Iterative Learning Control Design for Switched Systems

Abstract

In this paper, discrete-time linear systems with parameter switching in the repetitive mode are considered. A new iterative learning control design method is proposed. This method is based on the construction of an auxiliary 2D model in the form of a discrete repetitive process; the stability of the auxiliary model guarantees the convergence of the learning process. Stability conditions are derived using the divergent method of Lyapunov vector functions. The concept of the average dwell time in pass direction is introduced. An example that demonstrates the capabilities and features of the new method is presented.

1 Introduction

In modern control theory, switched systems are often understood as a class of models of dynamic systems consisting of a finite number of subsystems, of which only one is currently functioning, called the active subsystem, and the choice of the active subsystem is determined by some logical rule. The simplest example is a multi-mode system, in which subsystems are interpreted as separate modes of this system. Subsystems are usually described by an indexed set of differential or difference equations. The class of switched systems has been intensively studied in recent decades and continues to be actively developed nowadays, which is motivated by numerous applications in engineering, physics, biology, economics, and other fields, as well as by theoretical problems still open in this field of research. Like for other classes of control systems, the theory of stability and stabilization is of top priority, where a number of interesting and important results have been established. For an initial acquaintance with these results, in the first place the reader is recommended the monograph [1], the surveys [2, 3], and the recent books [4, 5].

Since the 1960s the theory of the so-called 2D systems began to develop actively. Its appearance was motivated by the problems of image processing and multidimensional electrical circuits, where the Roesser and Fornasini–Marchesini models [6] were constructed and subsequently became the classical 2D models; also, see a rich bibliography in the book [6]. A significant upsurge in the development of the theory of 2D systems was connected with the work of Arimoto [7], who first presented a theoretical justification of iterative learning control (ILC) algorithms for robots performing repetitive operations and revealed the natural 2D nature of the control process. (It includes a dynamic process on each separate repetition, also called pass or trial, and a dynamic process of transition from pass to pass.) 2D models in the form of repetitive processes [6, 8] serve as a natural description of ILC processes. The theory of repetitive processes was successfully applied to the design of ILC algorithms in [9, 10], where experimental results were also obtained. At present, the theory and applications of ILC continue to develop intensively, and numerous publications are devoted to this field of research. For an initial acquaintance, the reader is recommended the surveys [11, 12]. Among the recent works, note [13], where ILC was used for high-precision laser metal deposition and the results of experimental validation were presented. A very important application of ILC algorithms is robotic-assisted stroke rehabilitation. Well-known developments in this area were clinically tested [14, 15].

Switched repetitive processes were considered in [16, 17]. These works were motivated by metal rolling: a metal strip of a finite length is shaped by passing through a set of rolls, so that the output of a previous roll is the input for a next one. In [16], such systems were modeled by linear repetitive processes with switched dynamics. In both papers cited above, special switching rules were analyzed. The final results of these studies were ILC design procedures that can be implemented using calculations based on linear matrix inequalities (LMIs).

Finally, note a number of very recent works [18–21]. The paper [18] dealt with a class of discrete-time switched systems consisting of a linear part and a static nonlinearity satisfying special constraints. More specifically, the definitions of exponential stability and average dwell time were introduced, and sufficient conditions for exponential stability were established using the methods of the general and multiple 2D Lyapunov functions, respectively. The theoretical results obtained therein were applied to ILC design. Next, the authors [19] proposed high-order ILC for linear discrete-time switched systems under different initial conditions on repetitions and the action of disturbances bounded by norm. Linear discrete-time switched systems were also considered in [20], where the initial conditions on repetitions were assumed to be the same. The ILC algorithm constructed therein assumes the availability of the full state vector for the controller and ensures the monotonic convergence of the learning error. In [21], the systems consisting of a continuous linear part with mode switching and a Lipschitz nonlinearity were studied. An adaptive ILC algorithm assuming the availability of the full state vector for the controller was proposed. In all the publications listed, the technique of linear matrix inequalities was effectively used.

In this paper, linear discrete-time switched systems are considered. In contrast to the cited and other known works, only the output vector is assumed to be available for the controller and the ILC algorithm is formed using the error and an estimate of the state vector. The approach proposed below actually extends the earlier results of the authors (see [22–25]) to the class of switched systems. Unlike the well-known counterparts, this approach effectively utilizes the state estimates for improving the performance characteristics of the learning process and opens up the capabilities of nonlinear ILC design with mode switching depending on the accuracy achieved. An illustrative example of a dynamic model of a flexible rotating link operating in a repetitive mode [26] is presented. Switched and non-switched ILC algorithms are obtained and compared with one another.

2 Problem Statement

Consider a discrete-time system in repetitive mode described by the linear state-space model with switching

$$\begin{array}{rcl}{x}_{k}(p+1)&=&A(k){x}_{k}(p)+B(k){u}_{k}(p),\quad (A(k),B(k))\in {\mathcal{F}},\\ {y}_{k}(p)&=&C{x}_{k}(p),\quad p\in [0,T-1],\quad k=0,1,\ldots ,\end{array}$$

(2.1)

where an integer T denotes the number of samples over the pass length; on pass k, ${x}_{k}(p)\in {{\mathbb{R}}}^{{n}_{x}}$ is the state vector, ${y}_{k}(p)\in {{\mathbb{R}}}^{{n}_{y}}$ is the pass profile vector (output), and ${u}_{k}(p)\in {{\mathbb{R}}}^{{n}_{u}}$ is the control input; ${\mathcal{F}}=\{({A}_{1},{B}_{1}),({A}_{2},{B}_{2}),\ldots ,({A}_{N},{B}_{N})\}$ is the set of matrix pairs of compatible dimensions.

Following the standard notation of switched systems theory [1], consider a piecewise constant mapping of the set of nonnegative integers ${{\mathbb{Z}}}^{+}\to {\mathcal{F}}$. Such a mapping is defined by a piecewise constant function $\sigma :\,{{\mathbb{Z}}}^{+}\to {\mathcal{N}}=\{1,\ldots ,N\}$ so that A(k) = A_σ(k) and B(k) = B_σ(k), k = 0, 1, 2…. 

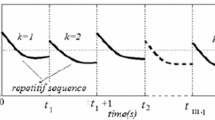
The function σ can be treated as the switching signal in pass direction. Assume that switchings occur at the beginning of each pass. Define the switching times in pass direction as the pass numbers k₁, k₂, … on which the pass profile vector of system (2.1) changes mode. Thus, for each pass k the switching signal specifies the index $\sigma (k)=i\in {\mathcal{N}}$ of the active subsystem whose dynamics are described by the equations

$$\begin{array}{rcl}{x}_{k}(p+1)&=&{A}_{i}{x}_{k}(p)+{B}_{i}{u}_{k}(p),\quad i\in {\mathcal{N}},\\ {y}_{k}(p)&=&C{x}_{k}(p),\quad p\in [0,T-1],\quad k=0,1,\ldots .\end{array}$$

(2.2)

Assume that the switching times are observable and there are no impulse effects: at a switching instant the value of the state vector does not change in jumps and remains constant.

On each pass the output of system (2.1) must track a reference trajectory y_ref (p), 0 ⩽ p⩽T − 1.  This goal can be achieved using iterative learning control. Denote by e_k(p) the tracking error of the reference trajectory (the learning error) on pass k:

$${e}_{k}(p)={y}_{ref}(p)-{y}_{k}(p),\quad 0\leqslant p\leqslant T-1.$$

(2.3)

If the initial conditions on each pass are the same, feedback control will give the same tracking error of the reference trajectory on all passes; moreover, this error may not match the existing accuracy requirements. The problem is to find a sequence of control inputs u_k(p), k = 0, 1, …,  that will ensure the achievement of a specified tracking accuracy of the reference pass profile in a finite number of passes k_fin with preserving this accuracy for all subsequent passes, i.e.,

$$| {e}_{k}(p)| \leqslant {e}^{* },\quad k\geqslant {k}_{fin},\quad 0\leqslant p\leqslant T-1.$$

(2.4)

This problem will be solved using iterative learning control. In accordance with this approach, the control input on a current pass is given by

$${u}_{k+1}(p)={u}_{k}(p)+\Delta {u}_{k+1}(p),$$

(2.5)

where Δu_k+1(t) is a control update to be designed. The problem stated above will be solved if the control input sequence satisfies the conditions

$$\mathop{\lim}\limits_{k\to \infty }| {e}_{k}(p)| =0,\quad \mathop{\lim}\limits_{k\to \infty }| {u}_{k}(p)-{u}_{\infty }(p)| =0,\quad 0\leqslant p\leqslant T-1,$$

(2.6)

where u_∞(p) is a bounded variable, often called the learned control.

3 Discrete 2D Model

Following [25], the control update law will be designed using the learning error and a state estimate ${\hat{x}}_{k}(p)$ obtained by a full-order observer:

$${\hat{x}}_{k}(p+1)={A}_{i}{\hat{x}}_{k}(p)+{B}_{i}{u}_{k}(p)+{F}_{i}({y}_{k}(p)-C{\hat{x}}_{k}(p)),\quad i\in {\mathcal{N}}.$$

(3.1)

Introduce the estimation error and also the increments of the state estimate and estimation error:

$$\begin{array}{rcl}{\tilde{x}}_{k}(p)&=&{x}_{k}(p)-{\hat{x}}_{k}(p),\\ {\hat{\xi }}_{k+1}(p+1)&=&{\hat{x}}_{k+1}(p)-{\hat{x}}_{k}(p),\\ {\tilde{\xi }}_{k+1}(p+1)&=&{\tilde{x}}_{k+1}(p)-{\tilde{x}}_{k}(p).\end{array}$$

(3.2)

Then the system’s dynamics with this observer can be described by the equations in the increments

$$\begin{array}{rcl}{\tilde{\xi }}_{k+1}(p+1)&=&({A}_{i}-{F}_{i}C){\tilde{\xi }}_{k+1}(p),\\ {\hat{\xi }}_{k+1}(p+1)&=&{F}_{i}C{\tilde{\xi }}_{k+1}(p)+{A}_{i}{\hat{\xi }}_{k+1}(p)+{B}_{i}{v}_{k+1}(p),\\ {e}_{k+1}(p)&=&-C{A}_{i}{\tilde{\xi }}_{k+1}(p)-C{A}_{i}{\hat{\xi }}_{k+1}(p)+{e}_{k}(p)-C{B}_{i}{v}_{k+1}(p),\quad i\in {\mathcal{N}},\end{array}$$

(3.3)

where

$${v}_{k+1}(p)=\Delta {u}_{k+1}(p-1).$$

Denote

$$\begin{array}{cc}{\eta }_{k}(p)={[{\tilde{\xi }}_{k}{(p)}^{{\rm{T}}}{\hat{\xi }}_{k}{(p)}^{{\rm{T}}}]}^{{\rm{T}}},\quad {A}_{i11}=\left[\begin{array}{cc}{A}_{i}-{F}_{i}C&0\\ {F}_{i}C&{A}_{i}\end{array}\right],\quad {B}_{i1}=\left[\begin{array}{c}0\\ {B}_{i}\end{array}\right],\quad {A}_{i12}=\left[\begin{array}{c}0\\ 0\end{array}\right],\\ {A}_{i21}=[-C{A}_{i}\,-C{A}_{i}],\quad {A}_{22}=I,\quad {B}_{i2}=-{C}_{i}B,\end{array}$$

and write (3.3) as the standard discrete repetitive process model [6]:

$$\begin{array}{rcl}{\eta }_{k+1}(p+1)&=&{A}_{i11}{\eta }_{k+1}(p)+{A}_{i12}{e}_{k}(p)+{B}_{i1}{v}_{k+1}(p),\\ {e}_{k+1}(p)&=&{A}_{i12}{\eta }_{k+1}(p)+{A}_{i22}{e}_{k}(p)+{B}_{i2}{v}_{k+1}(p),\quad i\in {\mathcal{N}}.\end{array}$$

(3.4)

Find the control update law as a feedback in the increments:

$$\Delta {u}_{k+1}(p-1)={v}_{k+1}(p)=\varphi ({\eta }_{k+1}(p),{e}_{k}(p)),\quad \varphi (0,0)=0.$$

(3.5)

If for all 0 ⩽ p⩽T − 1, ∣e_k(p)∣ → 0 as k → ∞, then there exists a number k_fin for which conditions (2.4) will be satisfied. Therefore, the problem will be solved if there exists a sequence v_k(p) such that

$$\mathop{\lim }\limits_{k\to \infty}| {e}_{k}(p)| =0,\quad | {u}_{\infty }(p)| <\infty ,\quad 0\leqslant p\leqslant T-1,$$

(3.6)

provided that the norm of the estimation error is bounded above by a monotonically decreasing function, where ${u}_{\infty }(p)={\mathrm{lim}\,}_{k\to \infty }{u}_{k}(p).$ Obviously, in this case there exists a number k_fin starting from which condition (2.4) will hold.

4 Main Results

4.1 Stability Conditions

Denote by N_σ(k_f, k_s) the number of switchings of the signal σ on an interval (k_s, k_f) and define the average dwell time as follows.

Definition 1.

A positive number ${\kappa }_{a}\in {{\mathbb{Z}}}^{+}$ is called the average dwell time under the switching signal in pass direction σ if, for some N₀ ⩾ 0,

$${N}_{\sigma }({k}_{f},{k}_{s})\leqslant {N}_{0}+\frac{{k}_{f}-{k}_{s}}{{\kappa }_{a}},\quad {k}_{f}\geqslant {k}_{s}\geqslant 0.$$

(4.1)

Inequality (4.1) means that on this interval the average number of passes between any two sequential switchings is not smaller than κ_a.

The solution will be obtained using the theory of stability and dissipativity of repetitive processes [22].

Definition 2.

[22] A discrete repetitive process (3.4), (3.5) is said to be exponentially stable if there exist real numbers κ > 0 and 0 < ϱ < 1 such that

$$| {\eta }_{k}(p){| }^{2}+| {e}_{k}(p){| }^{2}\leqslant \kappa {\varrho }^{k+p},$$

(4.2)

where ϱ does not depend on T.

Note that under condition (4.2) the error norm (see the previous section) is bounded above by a monotonically decreasing function, which in turn ensures the achievement of the given accuracy.

The switched system (3.4), (3.5) is generally nonlinear. A universal stability analysis method for nonlinear systems (Lyapunov’s second method) involves Lyapunov functions. However, the system equations under consideration are not resolved with respect to the total increments of the state variables, and this method becomes inapplicable here. To overcome this difficulty, the authors developed the so-called divergent method of vector Lyapunov functions, in which, unlike the classical version, stability is established based on the properties of the divergence operator (or its discrete counterpart) of these vector functions. In the case under study, introduce a vector Lyapunov function of the form

$${V}_{i}({\eta }_{k+1}(p),{e}_{k}(p))=\left[\begin{array}{c}{V}_{1}({\eta }_{k+1}(p))\\ {V}_{2i}({e}_{k}(p))\end{array}\right],\quad i\in {\mathcal{N}},$$

(4.3)

where V₁(x_k+1(p)) > 0, x_k+1(t) ≠ 0, V_2i(e_k(p)) > 0, y_k(p) ≠ 0, V₁(0) = 0, and V_2i(0) = 0, $i\in {\mathcal{N}}.$ Define a counterpart of the divergence operator as

$${\mathcal{D}}V({\eta }_{k+1}(p),{y}_{k}(p))={\Delta }_{p}{V}_{1}({\eta }_{k+1}(p))+{\Delta }_{k}{V}_{2}({e}_{k}(p)),$$

(4.4)

where Δ_pV₁(η_k+1(p)) = V₁(η_k+1(p + 1)) − V₁(η_k+1(p)), Δ_kV₂(e_k(p)) = V₂(e_k+1(p)) − V₂(e_k(p)). 

Theorem 1.

A discrete repetitive process (3.4), (3.5) is exponentially stable under any switching signal in pass direction σ with an average dwell time

$${\kappa }_{a}>\mathrm{ln}\,\left(\frac{{c}_{1}}{{c}_{2}}\right){\left(\mathrm{ln}\,\left(1-\frac{{c}_{3}}{{c}_{1}}\right)\right)}^{-1}$$

(4.5)

and an arbitrary number N₀ if there exist a vector function (4.3) and positive scalars c₁, c₂, and c₃ such that

$${c}_{1}| \eta {| }^{2}\leqslant {V}_{1}(\eta )\leqslant {c}_{2}| \eta {| }^{2},$$

(4.6)

$${c}_{1}| e{| }^{2}\leqslant {V}_{2i}(e)\leqslant {c}_{2}| e{| }^{2},$$

(4.7)

$${\mathcal{D}}{V}_{i}({\eta }_{k+1}(p),{e}_{k}(p))\leqslant -{c}_{3}\left(| {\eta }_{k+1}(p){| }^{2}+| {e}_{k}(p){| }^{2}\right).$$

(4.8)

Proof. Consider an interval (0, k_f), and let N_σ = N_σ(k_f, 0) be the number of switchings on this interval. From inequality (4.8) it follows that

$${\mathcal{D}}{V}_{\sigma (k)}({\eta }_{k+1}(p),{e}_{k}(p))\leqslant -{c}_{3}\left(| {\eta }_{k+1}(p){| }^{2}+| {e}_{k}(p){| }^{2}\right).$$

(4.9)

Using (4.6), (4.7), and (4.8), rewrite inequality (4.9) as

$$\begin{array}{l}{V}_{1}({\eta }_{k+1}(p+1))-{V}_{1}({\eta }_{k+1}(p))+{V}_{2\sigma (k+1)}({e}_{k+1}(p))-{V}_{2\sigma (k)}({e}_{k}(p))\\ \leqslant -{c}_{3}\left(| {\eta }_{k+1}(p){| }^{2}+| {e}_{k}(p){| }^{2}\right)\leqslant -\frac{{c}_{3}}{{c}_{2}}({V}_{1}({\eta }_{k+1}(p)+{V}_{2\sigma (k)}({e}_{k}(p)))),\end{array}$$

(4.10)

which is equivalent to

$${V}_{1}({\eta }_{k+1}(p+1))+{V}_{2\sigma (k+1)}({e}_{k+1}(p))\leqslant \left(1-\frac{{c}_{3}}{{c}_{2}}\right)\left({V}_{1}({\eta }_{k+1}(p))+{V}_{2\sigma (k)}({e}_{k}(p))\right).$$

(4.11)

The left-hand side of (4.11) is positive definite. Hence, $0<1-\frac{{c}_{3}}{{c}_{2}}<1.$ Denoting $\lambda =1-\frac{{c}_{3}}{{c}_{2}}$, rewrite (4.11) as

$${V}_{1}({\eta }_{k+1}(p+1))\leqslant \lambda {V}_{1}({\eta }_{k+1}(p))+\lambda {V}_{2\sigma (k)}({e}_{k}(p))-{V}_{2\sigma (k+1)}({e}_{k+1}(p)).$$

(4.12)

Solving inequality (4.12) in V₁(x_k+1(p)) gives

$${V}_{1}({\eta }_{k+1}(p))\leqslant {V}_{1}({\eta }_{k+1}(0)){\lambda }^{p}+\mathop{\sum }\limits_{h=0}^{p-1}\left[\lambda {V}_{2\sigma (k)}({e}_{k}(h))-{V}_{2\sigma (k+1)}({e}_{k+1}(h))\right]{\lambda }^{p-1-h}.$$

(4.13)

Introduce

$${H}_{k,\sigma (k)}(p)=\mathop{\sum }\limits_{h=0}^{p-1}{V}_{2,\sigma (k)}({e}_{k}(p)){\lambda }^{p-1-h}.$$

Then inequality (4.13) implies

$${H}_{k+1,\sigma (k+1)}(p)\leqslant \lambda {H}_{k,\sigma (k)}(p)+{\lambda }^{p}{V}_{1}({\eta }_{k+1}(0))-{V}_{1}({\eta }_{k+1}(p)).$$

(4.14)

Assume that on some pass k_n the active mode i is switched to mode j. From condition (4.7) it follows that

$${V}_{2j}(e)\leqslant \mu {V}_{2i}(e),\quad i,j\in {\mathcal{N}},$$

(4.15)

where $\mu =\frac{{c}_{2}}{{c}_{1}}\geqslant 1.$ Solving inequality (4.14) with using (4.15) yields

$${H}_{k,\sigma (k)}(p)\leqslant {\mu }^{{N}_{\sigma }}{\lambda }^{k}{H}_{0,\sigma (0)}(p)+{\mu }^{{N}_{\sigma }}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{k-1-n}\left({\lambda }^{p}{V}_{1}({\eta }_{n+1}(0))-{V}_{1}({\eta }_{n+1}(p))\right),$$

(4.16)

which is equivalent to

$$\begin{array}{ccc}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{k-1-n}{V}_{1}({\eta }_{n+1}(p))+\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2\sigma (k)}({e}_{k}(h))\\ \leqslant {\mu }^{{N}_{\sigma }}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{k-1-n}{V}_{1}({\eta }_{n+1}(p))+\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2\sigma (k)}({e}_{k}(h))\\ \leqslant {\mu }^{{N}_{\sigma }}\left({\lambda }^{p}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{k-1-n}{V}_{1}({\eta }_{n+1}(0))\right.+\left.{\lambda }^{k}\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2,\sigma (0)}({e}_{0}(h))\right).\end{array}$$

(4.17)

Inequality (4.17) implies

$$\begin{array}{cc}{\lambda }^{-(p-1)}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{-n}{V}_{1}({\eta }_{n+1}(p))+{\lambda }^{-(k-1)}\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{-h}{V}_{2\sigma (k)}({e}_{k}(h))\\ \leqslant {\mu }^{{N}_{\sigma }}\left({\lambda }^{-(k-1)}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{k-1-n}{V}_{1}({\eta }_{n+1}(0))+{\lambda }^{-(p-1)}\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2,\sigma (0)}({e}_{0}(h))\right).\end{array}$$

(4.18)

Recall that all passes have the same initial conditions; therefore, V₁(η_n+1(0)) = 0. In addition, since y_ref(p) is bounded for all p, ∣e_o(p)∣² = f(p)⩽M_f. Then the left-hand side of (4.18) can be estimated as

$$\begin{array}{cc}{\mu }^{{N}_{\sigma }}\left({\lambda }^{-(k-1)}\mathop{\sum }\limits_{n=0}^{k-1}{\lambda }^{k-1-n}{V}_{1}({\eta }_{n+1}(0))+{\lambda }^{-(p-1)}\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2,\sigma (0)}({e}_{0}(h))\right)\\ \leqslant {\mu }^{{N}_{\sigma }}{c}_{2}{M}_{f}\mathop{\sum }\limits_{h=0}^{T}{\lambda }^{-h}\leqslant {\mu }^{{N}_{\sigma }}\frac{{c}_{2}{M}_{f}({\lambda }^{-T}-1)}{{\lambda }^{-1}-1}={C}_{f}{\mu }^{{N}_{\sigma }}\end{array}$$

(4.19)

for all k ⩽ k_f and p ∈ [0, T].  Due to (4.19), from (4.18) it follows that

$${C}_{f}{\mu }^{{N}_{\sigma }}\geqslant {\lambda }^{-(p-1)}\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2}({y}_{0}(p))\geqslant {c}_{1}{\lambda }^{-(k-1)}{\lambda }^{-(p-1)}| {\eta }_{k}(p){| }^{2},$$

(4.20)

$${C}_{f}{\mu }^{{N}_{\sigma }}\geqslant {\lambda }^{-(p-1)}\mathop{\sum }\limits_{h=0}^{p-1}{\lambda }^{p-1-h}{V}_{2}({y}_{0}(h))\geqslant {c}_{1}{\lambda }^{-(k-1)}{\lambda }^{-(p-1)}| {e}_{k}(p-1){| }^{2}$$

(4.21)

for all k ⩽ k_f and p ∈ [0, T].  For k = k_f and (4.5), inequalities (4.18)–(4.21) finally give

$$| {\eta }_{{k}_{f}}(p){| }^{2}+| {e}_{{k}_{f}}(p){| }^{2}\leqslant \frac{C{\mu }^{{N}_{0}}}{{c}_{1}\lambda }{\lambda }_{0}^{{k}_{f}+p}$$

for any k_f and p ∈ [0, T], where ${\lambda }_{0}={\mu }^{{\kappa }_{a}^{-1}}={({c}_{2}/{c}_{1})}^{{\kappa }_{a}^{-1}}<1$. The proof of Theorem 1 is complete.

This theorem leads to an important result as follows.

Corollary. A discrete repetitive process (3.4), (3.5) is exponentially stable under an arbitrary switching signal in pass direction σ if there exist a vector function

$$V({\eta }_{k+1}(p),{e}_{k}(p))={[{V}_{1}({\eta }_{k+1}(p)){V}_{2}({e}_{k}(p))]}^{T}$$

(4.22)

and positive scalars c₁, c₂, and c₃ such that

$$\begin{array}{rcl}{c}_{1}| \eta {| }^{2}&\leqslant &{V}_{1}(\eta )\leqslant {c}_{2}| \eta {| }^{2},\\ {c}_{1}| e{| }^{2}&\leqslant &{V}_{2}(e)\leqslant {c}_{2}| e{| }^{2},\end{array}$$

(4.23)

$${\mathcal{D}}V({\eta }_{k+1}(p),{e}_{k}(p))\leqslant -{c}_{3}\left(| {\eta }_{k+1}(p){| }^{2}+| {e}_{k}(p){| }^{2}\right).$$

4.2 ILC Design Based on Dissipativity Theory

Consider the auxiliary vector

$${z}_{k+1}(p)={C}_{1}{\eta }_{k+1}(p)+{C}_{2}{e}_{k}(p)+D{v}_{k+1}(p),$$

(4.24)

where C₁, C₂,  and D are constant matrices of compatible dimensions. Following [22], introduce an important property of discrete repetitive processes.

Definition 3.

A discrete repetitive process (3.4) is said to be exponentially dissipative with respect to the input v_k+1(t) and the output z_k+1(t) defined by (4.24) if there exist a vector function (4.3) and positive scalars c₁, c₂, and c₃ such that

$$\begin{array}{rcl}{c}_{1}| {\eta }_{k+1}(p){| }^{2}&\leqslant &{V}_{1}({\eta }_{k+1}(p))\leqslant {c}_{2}| {\eta }_{k+1}(p){| }^{2},\\ {c}_{1}| {e}_{k}(p){| }^{2}&\leqslant &{V}_{2i}({e}_{k}(p))\leqslant {c}_{2}| {e}_{k}(p){| }^{2},\\ {\mathcal{D}}{V}_{i}({\eta }_{k+1}(t),{e}_{k}(t))&\leqslant &{S}_{i}({z}_{k+1}(p),{v}_{k+1}(p))-{c}_{3}\left(| {\eta }_{k+1}(t){| }^{2}+| {e}_{k}(t){| }^{2}\right),\quad i\in {\mathcal{N}},\end{array}$$

where S_i is a scalar function such that S_i(0, 0) = 0.

In the theory of dissipativity pioneered by Willems, the functions S_i and V_i are called a supply rate and a storage function, respectively. Clearly, if for some z sequence (3.5) satisfies the condition S_i(z_k+1(p), v_k+1(p)) ⩽ 0, $i\in {\mathcal{N}},$ then system (3.4), (3.5) will be exponentially stable under any switching signal in pass direction σ with an average dwell time (4.5); see Theorem 1. Thus, the ILC design problem is to find a stabilizing triplet {V, z, v}. Introduce the notations

$${\zeta }_{k+1}(p)=\left[\begin{array}{c}{\eta }_{k+1}(p)\\ {e}_{k}(p)\end{array}\right],\quad {\bar{A}}_{i}=\left[\begin{array}{cc}{A}_{i11}&{A}_{i12}\\ {A}_{i21}&{A}_{i22}\end{array}\right],\quad {\bar{B}}_{i}=\left[\begin{array}{c}{B}_{i1}\\ {B}_{i2}\end{array}\right],\quad i\in {\mathcal{N}}.$$

Define a block-diagonal matrix P_i = diag[P₁P_2i] ≻ 0 as the solution of the Riccati inequality

$${\bar{A}}_{i}^{{\rm{T}}}{P}_{i}\bar{A}-(1-\sigma ){P}_{i}-{\bar{A}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}{\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]}^{-1}{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{A}}_{i}+Q\preccurlyeq 0,\quad i\in {\mathcal{N}},$$

(4.25)

where 0 < σ < 1 is a positive scalar, and Q ≻ 0 and R ≻ 0 are weight matrices. Clearly, if the system of linear matrix inequalities

$$\left[\begin{array}{ccc}(1-\sigma ){X}_{i}&X{\bar{A}}^{T}&{X}_{i}\\ {\bar{A}}_{i}{X}_{i}&{X}_{i}+{\bar{B}}_{i}{R}^{-1}{\bar{B}}_{i}^{T}&0\\ {X}_{i}&0&{Q}^{-1}\end{array}\right]\succcurlyeq 0,\quad {X}_{i}\succ 0,\quad i\in {\mathcal{N}}$$

(4.26)

is solvable in X_i = diag[X₁X_2i] ≻ 0, then ${P}_{i}={X}_{i}^{-1}$, $i\in {\mathcal{N}}$.

The next theorem suggests a possible set of stabilizing triplets.

Theorem 2.

A discrete repetitive process (3.4) is exponentially dissipative with respect to the supply rate

$$\begin{array}{cc}{S}_{i}({v}_{k+1}(p),{z}_{k+1}(p))={z}_{k+1}^{{\rm{T}}}(p){\left({\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right)}^{-1}{z}_{k+1}(p)\\ +2{z}_{k+1}{(p)}^{{\rm{T}}}{v}_{k+1}(p)+{v}_{k+1}{(p)}^{{\rm{T}}}\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]{v}_{k+1}(p),\quad i\in {\mathcal{N}}\end{array}$$

(4.27)

with the input v_k+1(p) and the output

$${z}_{k+1}(p)={\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{A}}_{i}{\zeta }_{k+1}(p),\quad i\in {\mathcal{N}},$$

(4.28)

where ${P}_{i}={X}_{i}^{-1}$, ${X}_{i}={\rm{diag}}[{X}_{1}\,{X}_{2i}]\succ 0 \i\in {\mathcal{N}}$, is the solution of (4.25). The set of control update sequences (3.5) ensuring the exponential stability of system (3.4), (3.5) is given by

$${v}_{k+1}(p)=-{\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]}^{-1}{\bar{B}}_{i}^{{\rm{T}}}P{\bar{A}}_{i}{\Theta }_{i}({\zeta }_{k+1}(p)){\zeta }_{k+1}(p),\quad i\in {\mathcal{N}},$$

(4.29)

where Θ(ζ) is a symmetric matrix function that satisfies the relation

$${M}_{i}-{M}_{i}{\Theta }_{i}(\zeta )-{\Theta }_{i}(\zeta ){M}_{i}+{\Theta }_{i}(\zeta ){M}_{i}{\Theta }_{i}(\zeta )-Q-(\sigma -\mu ){P}_{i}\prec 0,\quad i\in {\mathcal{N}}$$

(4.30)

for all $\zeta \in {{\mathbb{R}}}^{2{n}_{x}+{n}_{y}}$, where

$${M}_{i}={\bar{A}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}{[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R]}^{-1}{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{A}}_{i},\quad 0<\mu <\sigma ,\quad i\in {\mathcal{N}}.$$

Proof. Choose the components of the vector storage function (4.3) as the quadratic forms

$${V}_{1}({\eta }_{k+1}(p))={\eta }_{k+1}{(p)}^{{\rm{T}}}{P}_{1}{\eta }_{k+1}(p),\quad {V}_{2i}({e}_{k}(p))={e}_{k}{(p)}^{{\rm{T}}}(t){P}_{2}{e}_{k}(p),\quad i\in {\mathcal{N}},$$

where P₁ ≻ 0 and P₂ ≻ 0 are the diagonal blocks of the matrix P representing the solution of (4.25). Calculating the counterpart of the divergence operator of (4.3) along the trajectories of (3.4) yields

$$\begin{array}{cccccc}{\mathcal{D}}{V}_{i}({\eta }_{k+1}(p),{e}_{k}(p))\\ ={{\zeta }_{k+1}(p)}^{{\rm{T}}}\left({\bar{A}}_{i}^{{\rm{T}}}P{\bar{A}}_{i}-(1-\sigma ){P}_{i}-{\bar{A}}_{i}^{{\rm{T}}}{P}_{i}\bar{B}{\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]}^{-1}{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{A}}_{i}+Q\right){\zeta }_{k+1}(p)\\ +{\zeta }_{k+1}{(p)}^{{\rm{T}}}{\bar{A}}_{i}^{{\rm{T}}}{P}_{i}\bar{B}{\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]}^{-1}{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{A}}_{i}{\zeta }_{k+1}(p)-{\zeta }_{k+1}{(p)}^{{\rm{T}}}(Q+\sigma {P}_{i}){\zeta }_{k+1}(p)\\ +2{\zeta }_{k+1}{(p)}^{{\rm{T}}}{\bar{A}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}{v}_{k+1}(p)+{v}_{k+1}{(p)}^{{\rm{T}}}{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}{v}_{k+1}(p)\\ \leqslant {\zeta }_{k+1}{(p)}^{{\rm{T}}}{\bar{A}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}{\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]}^{-1}{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}\bar{A}{\zeta }_{k+1}(p)+2{\zeta }_{k+1}{(p)}^{{\rm{T}}}{\bar{A}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}{v}_{k+1}(p)\\ +{v}_{k+1}{(p)}^{{\rm{T}}}\left[{\bar{B}}_{i}^{{\rm{T}}}{P}_{i}{\bar{B}}_{i}+R\right]{v}_{k+1}(p)-{\zeta }_{k+1}{(p)}^{{\rm{T}}}(Q+\sigma {P}_{i}){\zeta }_{k+1}(p),\quad i\in {\mathcal{N}}.\end{array}$$

(4.31)

From (4.31) it follows that (3.4) is exponentially dissipative with respect to the supply rate (4.27) with the input v_k+1(p) and the output (4.28). Moreover, from (4.31) it follows that if sequence (3.5) is determined by (4.29), then

$${\mathcal{D}}{V}_{i}({\eta }_{k+1}(p),{e}_{k}(p))\leqslant -\mu {\lambda }_{min}({P}_{i})\left(| {\eta }_{k+1}(p){| }^{2}+| {e}_{k}(p){| }^{2}\right)$$

and the discrete repetitive process (4.29), (3.4) is exponentially stable under any switching signal in pass direction σ with an average dwell time (4.5); see Theorem 1. The proof of Theorem 2 is complete.

Remark 1. Since the increment of the estimation error ${\tilde{\xi }}_{k+1}(p)$ is not available for the control update design, the matrix Θ_i always has the form ${\Theta }_{i}(\zeta )={\rm{diag}}[{0}_{{n}_{x}}\,{\Theta }_{i1}(\zeta )]$. In the simplest case, matrix Θ_i1 can be chosen independent of ζ and then, after the matrix P_i is found, condition (4.30) reduces to a system of linear matrix inequalities, and Theorem 2 gives a linear sequence of control updates. In the general case, Θ_i(ζ) depends on the variations of the error in pass direction; therefore, the control update coefficients can be decreased upon achieving the required accuracy and, conversely, increased when the error is large. In other words, adaptation to the error value can be introduced in the control update procedure. This approach will guarantee a reasonable compromise between the rate of learning and ILC costs. The simplest solution here is to use piecewise-constant variations of Θ, depending on the accuracy achieved. For discrete repetitive processes without switching, it was discussed in [24].

4.3 Alternative Approach

In a series of cases, it seems interesting to construct non-switched control. Here an alternative approach turns out to be more efficient. Consider a Lyapunov function (4.22) with the components

$${V}_{1}({\xi }_{k+1}(p))={\xi }_{k+1}^{T}(p){P}_{1}{\xi }_{k+1}(p),\quad {V}_{2}({e}_{k})={e}_{k}^{T}(p){P}_{2}{e}_{k}(p),$$

where P₁ ≻ 0 and P₂ ≻ 0. Find the control update law as a linear feedback in the increments of the measurable variable and the error:

$${v}_{k+1}(p)={K}_{1}{\hat{\xi }}_{k+1}(p)+{K}_{2}{e}_{k}(p)=KH{\zeta }_{k+1}(p),$$

(4.32)

where K = [K₁K₂], $H=[0\,{I}_{{n}_{x}+{n}_{y}}]$. Calculating the divergence operator of (4.22) along the trajectories of (3.4), (4.32) gives

$${\mathcal{D}}V={\bar{x}}^{T}\left({\bar{A}}_{ci}^{T}{P}_{i}{\bar{A}}_{ci}-P\right)\bar{x},\quad i\in {\mathcal{N}},$$

(4.33)

where

$${P}_{i}={\rm{diag}}[{P}_{1}\,{P}_{2i}],\quad {\bar{A}}_{ci}=\left[\begin{array}{ccc}{A}_{i}-{F}_{i}C&0&0\\ {F}_{i}C&{A}_{i}+{B}_{i}{K}_{1}&{B}_{i}{K}_{2}\\ -C{A}_{i}&-C({A}_{i}+{B}_{i}{K}_{1})&I-C{B}_{i}{K}_{2}\\ \end{array}\right],\quad i\in {\mathcal{N}}.$$

Assume that the matrices P ≻ 0 and K satisfy the system of inequalities

$${({\bar{A}}_{i}+{\bar{B}}_{i}KH)}^{T}P({\bar{A}}_{i}+{\bar{B}}_{i}KH)-{P}_{i}+Q+{H}^{T}{K}^{T}RKH\preccurlyeq 0,\quad i\in {\mathcal{N}},$$

(4.34)

where Q ≻ 0 and R ≻ 0 are some matrices, which play the same role as weight matrices in linear-quadratic control design. Due to (4.33), the discrete repetitive process (3.4), (4.32) is exponentially stable under an arbitrary switching signal in pass direction σ; see the corollary of Theorem 1. Using the well-known Schur’s complement lemma, inequalities (4.34) are easily reduced to the following linear matrix inequalities and equation in the variables $X={\rm{diag}}[{P}_{1}^{-1}\,{P}_{2}^{-1}]$, Y, and Z:

$$\left[\begin{array}{cccc}X&{({\bar{A}}_{i}X+{\bar{B}}_{i}YH)}^{T}&X&{(YH)}^{T}\\ {\bar{A}}_{i}X+{\bar{B}}_{i}YH&X&0&0\\ X&0&{Q}^{-1}&0\\ YH&0&0&{R}^{-1}\end{array}\right]\succcurlyeq 0,\quad X\succ 0,\quad HX=ZH,\quad i\in {\mathcal{N}}.$$

(4.35)

If the inequalities and equation of (4.35) are solvable, then K = [K₁K₂] = YZ⁻¹, since the matrix Z is nonsingular due to the structure of the matrix H.

5 Example

Consider the model of a single flexible link gantry robot [26] operating in a repetitive mode with a constant repetition period. The dynamics of the gantry robot are described by the state-space equations

$${\dot{x}}_{k}(t)={A}_{0}{x}_{k}(t)+{B}_{0}{u}_{k}(t),\quad {y}_{k}(t)=C{x}_{k}(t),\quad 0\leqslant t\leqslant {T}_{f},\quad k=0,1,2,\ldots ,$$

(5.1)

where $x(t)={\left[\theta (t)\alpha (t)\dot{\theta }(t)\dot{\alpha }(t)\right]}^{{\rm{T}}}$ in which θ(t) is the servo angle and α(t) is the flexible link angle;

$${A}_{0}=\left[\begin{array}{cccc}0&0&1&0\\ 0&0&0&1\\ 0&\frac{{K}_{s}}{{J}_{eq}}&-\frac{{B}_{eq}}{{J}_{eq}}&0\\ 0&-\frac{{K}_{s}({J}_{l}+{J}_{eq})}{{J}_{l}{J}_{eq}}&\frac{{B}_{eq}}{{J}_{eq}}&0\end{array}\right],\quad {B}_{0}=\left[\begin{array}{c}0\\ 0\\ \frac{1}{{J}_{eq}}\\ -\frac{1}{{J}_{eq}}\end{array}\right],\quad C=\left[1\,0\,0\,0\right],$$

in which B_eq is the viscous friction coefficient of the servo, K_s is the stiffness of the flexible link, J_l is the moment of inertia of the flexible link, and J_eq is the moment of inertia of the servo. The flexible link is moving in the horizontal plane.

The problem is to find an iterative learning control algorithm enabling the output variable y(t) = θ(t) to track a reference trajectory y_ref(t) with a given accuracy e^*. Only the servo angle θ is available for direct measurement.

Select the following nominal values of the parameters for simulation [26]: B_eq = 0.004N × m/(rad/s), K_s = 1.3N × m/rad, J_l = 0.0038kg × m², J_eq = 2.08 × 10⁻³kg × m².

Set the length of a repetition period equal to 3 s and the required accuracy to ${e}^{* }=0.5\,{\rm{grad}}=0.00873\,{\rm{rad}}$.

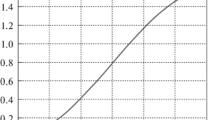
Let the reference trajectory of the output variable (see Fig. 1) be described by

$${y}_{ref}(t)=\frac{\pi {t}^{2}}{6}-\frac{\pi {t}^{3}}{27},\quad t\in [0,{T}_{f}].$$

Fig. 1

Reference trajectory of servo angle.

Assume that the ILC algorithm is implemented on computer with a sampling rate of T_s = 0.01s. The equivalent discrete model of (5.1), which connects the values of all variables at the time instants 0, T_s, 2T_s, …, has the form

$${x}_{k}(p+1)=A{x}_{k}(p)+B{u}_{k}(p),\quad p=0,1,\ldots ,{N}_{{T}_{f}},\quad k=0,1,2,\ldots ,$$

(5.2)

where $A=\exp ({A}_{0}{T}_{s})$, $B=\left(\mathop{\int}\nolimits_{0}^{{T}_{s}}\exp ({A}_{0}\tau )d\tau \right){B}_{0},$ and ${N}_{{T}_{f}}$ is the number of samples on the interval [0, T_f].

When the gantry robot begins operation, the first few passes are without load for presetting, and the parameters have their nominal values. After three passes, the gantry robot is loaded: J_l = 0.0076kg × m², J_eq = 3.3 × 10⁻³ kg × m². Based on the physical meaning of the state variables, set the weight matrices Q = diag[10⁻³I₈ 10⁶] and R = 0.01. Treating the stepwise change in the gantry robot’s load as a mode switching, use the results of Section 4.3, which are convenient for comparative analysis. Denote by A₁ and B₁ the matrices of the unloaded gantry robot and by A₂ and B₂ and the matrices of the loaded one. The switched iterative learning control algorithm is described by

$$\begin{array}{ccccc}{\hat{x}}_{k}(p)={A}_{i}{\hat{x}}_{k}(p-1)+{B}_{i}{u}_{k}(p-1)+{F}_{i}({y}_{k}(p-1)-C{\hat{x}}_{k}(p-1)),\\ i=\left\{\begin{array}{ll}1&{\rm{if}}\,k<3\\ 2&{\rm{if}}\,k\geqslant 3,\end{array}\right.\\ {F}_{i}=\left\{\begin{array}{ll}{F}_{1}={[1.9199-1.84159\, 1.1151-84.9936]}^{T}&{\rm{if}}\,k<3\\ {F}_{2}={[1.7575-1.70018\, 1.2812-78.3325]}^{T}&{\rm{if}}\,k\geqslant 3,\end{array}\right.\\ {u}_{k}(p)={u}_{k-1}(p)+{K}_{1}\left({\hat{x}}_{k}(p)-{\hat{x}}_{k-1}(p)\right)+{K}_{2i}\left({y}_{ref}(p)-{y}_{k-1}(p+1)\right),\\ {K}_{1}=[-31.0300\,-0.3018\,-0.4530\,-0.0444],\quad {K}_{2i}=\left\{\begin{array}{ll}9.5140&{\rm{if}}\,k<3\\ 27.1609&{\rm{if}}\,k\geqslant 3.\end{array}\right.\end{array}$$

The non-switched algorithm has the form

$$\begin{array}{cc}{u}_{k}(p)={u}_{k-1}(p)+{K}_{1}\left({\hat{x}}_{k}(p)-{\hat{x}}_{k-1}(p)\right)+{K}_{2}\left({y}_{ref}(p)-{y}_{k-1}(p+1)\right),\\ {K}_{1}=[-28.1965\,-0.2408\,-0.4345\,-0.0395],\quad {K}_{2}=12.8135.\end{array}$$

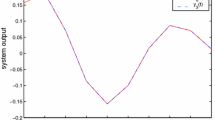
For assessing the tracking accuracy of the reference trajectory, select the mean-square learning error

$$E(k)=\sqrt{\frac{1}{{N}_{{T}_{f}}}\mathop{\sum }\limits_{p=0}^{{N}_{{T}_{f}}}| {e}_{k}(p){| }^{2}}.$$

(5.3)

The progressions of the mean-square learning error depending on the number of passes under the switched and non-switched control algorithms are presented in Figs. 2 and 3, respectively.

Fig. 2

Mean square learning error depending on number of passes: switched control.

Fig. 3

Mean square learning error depending on number of passes: non-switched control.

A direct analysis of these dependencies shows that in the case of switched control, the required accuracy is achieved immediately after the presetting passes; in the case of non-switched control, additional passes in the operating mode are required to achieve the required accuracy, which is obviously undesirable.

6 Conclusions

This paper has proposed a state observer-based iterative learning control design method for switched discrete repetitive processes. As it has been demonstrated by an example, in the case of observable switchings the switched iterative learning control algorithm accelerates the convergence of the learning process. In the authors’ viewpoint, further research in this area can be associated with the development of the theory for switched differential repetitive processes and its application to iterative learning control design problems. Also, an in-depth study is needed for the choice of the nonlinear function Θ_i(ζ) in the dissipativity-based design procedure (Theorem 2 and Remark 1). Of considerable interest are networked iterative learning control problems, where switching is a natural model of structural changes in the network configuration. The combination of iterative learning control and feedback control is another interesting area for future investigations.

7 Funding

This work was supported by the Russian Foundation for Basic Research, project no. 19-08-00528_a.