Introduction

Today airlines around the world are motivated to redefine the product offering methodology and customer experience through dynamic pricing. With the antiquated architecture present today, airlines can only file a limited number of price points for limited booking classes (on average 10–16 per cabin) that often end up with large gaps for each market. As a result, when the fare class of $300 is not available, the consumer is offered the next higher class of $400. However, if the consumer’s maximum willingness-to-pay (WTP) is $350, they go elsewhere. In the same example, the consumer could be offered the optimal dynamic fare of $350 (or less), which would satisfy the consumer while driving more revenue for an airline. The industry’s new distribution capability (NDC) will now allow for “continuous pricing” and “bucket-less distribution” and hence creates possibilities for dynamic pricing without the traditional constraints of a booking class (Isler and D’Souza 2009; Westermann 2013). Thus, a dynamically generated optimal price (based on customer’s WTP, choice set, as well as time-to-departure, and capacity left for the specific flight, etc.) becomes the determining factor in assigning seats and essentially makes integrating pricing and capacity allocation possible.

The successful implementation of dynamic pricing is contingent on effectively modeling the underlying market demand as a function of the offered price, and a good demand function on the other hand relies on well-modeled customers’ WTP (note in a competitive environment the WTP can be affected by other alternatives presented to the passenger). Built upon the success of the recent WTP model by Kambour (2014), in this article we model a customer’s WTP as a normal distribution with mean \(\mu\) and standard deviation \(\sigma\). In particular, we consider a single-leg flight with finite capacity, and customers are assumed to arrive according to a Poisson process with rate \(\lambda\) over a finite booking horizon. Upon the arrival of each customer, the airline offers a price based on its remaining seat inventory at that time, forecast for remaining demand as well as its estimated WTP of this customer. Then the customer compares the offered price with his/her maximum WTP, and decides whether to accept or reject the offer. The flight (which can also be equivalently considered as a selling horizon) is assumed to repeat on a regular basis, and both the WTP parameters (\(\mu\), \(\sigma\)) and the arrival rate \(\lambda\) are re-estimated through the learning-optimization cycle across the selling seasons.

More specifically, in this paper we first assume that the airline collects information only on the accepted offer prices throughout the selling horizon. We devise a maximum likelihood estimation (MLE) approach to learn the three unknown parameters under this framework. Meanwhile, we utilize a dynamic programming (DP) model to calculate bid prices for each seat in each small time period, and we use this information together with our estimated WTP parameters to calculate the optimal offered prices. Although the solution cannot be found in closed-form for the Gaussian demand model, we show an efficient way of computing the dynamic pricing policy.

To test our model, we set up a simulation environment. Beginning with some arbitrary guesses on the parameter values, we first solve the DP for bid prices. Then with simulated customer arrivals (which are based on the true parameter value \(\lambda\)), we calculate the optimal offer price for each, and observe the customer’s decision (based on his/her true WTP parameters \(\mu\) and \(\sigma\)). Finally, after each booking horizon has ended, we re-run our MLE with all the newly recorded sale prices to update our parameter estimations, and then kick off the next cycle.

Our simulation results show that the above approach (call it the “base model”) performs rather poorly in terms of parameter estimation. To overcome this inefficiency of MLE, we develop an enhancement to our base model using expectation–maximization (EM) and minimal active learning. More specifically, we first formulate an MLE by assuming that the airline has the capability to also collect information on those time periods when no customer arrived (loss information). As expected, the results rendered appear rather promising given the extra information used. However, we are well aware that in practice the loss information is not readily available, then built upon the extended MLE, we devise an EM approach to help estimate the parameters when such information is not available. The parameter learning process in this approach is still “passive,” in that, the variation of offered prices is generated purely by the optimal control, and the model does not “actively” generate any prices for the purpose of exploring the underlying demand model. In light of this, we devise an algorithm (EM-DZ’15) by combining the EM method with the minimal active learning method of den Boer and Zwart (2015); our numerical results show that active learning benefits the most when the demand-to-capacity ratio is medium.

Overall our contribution is three-fold. First, we consider a Gaussian demand model based on total demand volume and customer WTP and describe a computationally efficient way to find the dynamic pricing policy. Second, the parameter estimation of the Gaussian demand model is more difficult than the models considered in den Boer and Zwart (2015), and in addition to the simple MLE, we present a more sophisticated EM-based estimation methodology. Third, we confirm in a similar setting the result by den Boer and Zwart (2015) that when the inventory is finite the myopic policy works well and only minimal active learning is needed to achieve good revenue performance. We also show the performance of various estimation methods and identify the scenarios where active learning is most desired.

The remainder of this paper is organized as follows. We first present a brief literature review in the next section. Then we describe our model in details, including the demand model, price optimization, and the performance measure. Next we present various parameter estimation approaches, and describe the active learning methods. The numerical results and conclusions from our study are presented in the subsequent sections.

Literature review

This paper’s joint nature of learning and optimization makes us draw together two streams of literature, the revenue management (RM) literature, and the statistical learning literature.

For the RM research, the problem of evaluating a dynamic pricing policy over a selling horizon based on a well-defined and known demand model has been extensively studied and is well understood. In the seminal work of Gallego and van Ryzin (1994), a closed-form solution for exponential demand functions is found, and for general demand functions they derive a revenue upper-bound using a deterministic heuristic. In a similar setting, McAfee and te Velde (2008) develop an explicit solution for the constant elasticity demand model. More recently, Schlosser (2015) considers the dynamic pricing problem with time-dependent price elasticities of demand. However, in any practical implementation, the demand function is unknown and will have to be learned from the observed booking data. In this regard, some recent works have proposed to allow probing the demand function while optimizing the pricing policies through learning (den Boer and Zwart 2014; Wang et al. 2014).

The statistical learning literature generally falls into the parametric and non-parametric categories for the demand model. For a parametric model, the functional form of the demand function is assumed to be known; this form is typically based on a certain underlying distribution for the WTP. Most existing research has focused on parametric models (including ours). In particular, Bertsimas and Perakis (2006) consider a linear demand model where the parameters vary slowly; Broder and Rusmevichientong (2012) assume a Bernoulli demand distribution. Kambour (2014) proposes a Gaussian demand model and utilizes only products purchased and the prices paid, while in many other methods the availability of fare classes (or choice sets in broad term) are used. In this paper, we will also model our demand function as Gaussian. The non-parametric models do not assume a known functional form of demand and generally involve robust approaches for joint learning and optimization. Interested readers are referred to recent research including but not limited to Besbes and Zeevi (2012), Wang et al. (2014), etc., and for the remainder of the paper we focus only on parametric models.

Methods for parameter estimation commonly include Least Squares (Bertsimas and Perakis 2006), maximum likelihood estimation (MLE) (Broder and Rusmevichientong 2012), maximum quasi-likelihood estimation (MQLE) (den Boer and Zwart 2014). The observed historical booking data are typically constrained due to the interaction of optimal controls with the incoming demand. This complicates the estimation problem even further since some form of unconstraining method is required to recover demand volumes. For our parameter estimation, in addition to MLE we also formulate an EM approach tackling the incomplete demand information regarding lost sales. Moreover, it has also been observed that under the dynamic pricing framework, prices typically do not show much variation over the selling horizon especially in the low-to-medium load factor scenarios. Indeed, Gallego and van Ryzin (1994) show that open loop static pricing policies are close to optimal in the low-load factor scenarios. This lack of price variation may pose further challenges from the estimation perspective.

In this setting, the airline faces two challenges: firstly, the offered prices should have enough variance such that the underlying parameters \(\lambda\), \(\mu\), and \(\sigma\) can be discovered and secondly dynamic pricing decisions need to be made for each arriving customer such that the revenue is maximized. The end goal of the airline is to maximize expected revenue over the long run. This situation represents the classic exploration vs. exploitation trade-off: myopically offer prices that maximize the revenue for the current selling horizon based on their present knowledge of the demand model parameters, or offer prices that enable fast discovery of the unknown parameters to optimize total revenue over multiple selling horizons. Since we are concerned with revenue maximization over multiple selling horizons, a policy that achieves balance between these two criteria is desirable. In light of this, den Boer and Zwart (2014) recently propose a controlled variance pricing (CVP) approach for the infinite-capacity setting where a “taboo interval” is imposed around the average chosen prices to generate sufficient price variation to help improve the demand learning and revenue optimization. For the finite-capacity setting, den Boer and Zwart (2015) show that for certain family of demand models, a policy that offers optimal prices by assuming that the current known parameter estimates are correct during most of the selling horizon (the passive learning policy) and incorporates a minimal amount of active price exploration in the last few selling opportunities shows good performance. The demand model that we study is different from the one considered by den Boer and Zwart (2015). The survey paper by den Boer (2014) also gives an extensive overview of dynamic pricing and learning literature.

Model formulation

Consider the problem facing a monopolist selling a single product as described in Gallego and van Ryzin (1994). A firm has a finite number of perishable items to sell over selling horizons of length T, e.g., a small low-cost carrier operating a daily direct flight. The firm is able to influence the quantity demanded for its products by varying the price. In particular if the firm charges a price p, then their items are sold according to a Poisson process with rate \(\lambda (p)\) items per unit time. As one last assumption, we do not consider block sales (e.g., group requests in the airline industry) within the scope of this study as the structural properties of the underlying dynamic programming (DP) model may not necessarily hold.

We consider a parametric model for the demand function \(\lambda (p)\) based on an individual customer’s maximum WTP described in the “Demand model” Section. The firm has imperfect knowledge about the demand parameters and wants to maximize the total cumulative revenue over K consecutive selling horizons (flights).

At the start of each selling horizon, the firm has C units of capacity and each selling horizon is further subdivided into N periods (slots) of length \(\frac{T}{N}\). If there is inventory on hand in period t, then the firm must set a constant price \(p_t \in [p_{\min },p_{\max }]\) for this period. We assume that these time periods are small enough so that the probability of observing more than one arrival is negligible. Let \(d_t\) denote a variable that takes the value 1 if an item is sold in period t and is 0 otherwise. Due to the Poisson assumption, if the firm sets a price \(p_t\) in period t, then a single unit of the item is sold with probability λ(p t )/N, and with probability 1−λ(p t )/N there is no sale independent of the other time periods. The firm’s pricing policy can depend on all past prices and sales data observed in each period of this selling horizon (up to the current time) as well as the past selling horizons. The prices \(p_{\min }\) and \(p_{\max }\) are user-defined depending on the business requirements.

We assume that in case of no booking in a period, the firm cannot distinguish if this is due to lack of an arrival or the price exceeding the maximum WTP of an arriving customer. Given the historical observations, the firm wants to find a pricing policy \(\pi\) that maximizes the cumulative expected revenue over K selling horizons, \({\mathbb{E}}_{\pi }[\sum _{i=1}^{NK}p^{\pi }_id^{\pi }_i]\). This multiple selling horizon setting is similar to the one considered by den Boer and Zwart (2015) but with a different demand model.

In this paper, we assume there is a constant customer arrival intensity and a fixed WTP distribution over time for ease of exposition. In practice, airlines typically face time-varying demand model parameters. For such scenarios, we may easily extend the model and consider several periods in the booking horizon each having its own demand parameters.

Demand model

Our demand model is based on the assumption that each arriving customer has a maximum WTP W which is normally distributed with mean \(\mu\) and variance \(\sigma ^2\). Furthermore we assume the customers’ arrival process is Poisson with rate \(\lambda\). Therefore if the firm offers price p, then the demand rate for the firm’s product is

$$\begin{aligned} \lambda (p) = \lambda Pr[W>p] = \lambda \Big (1-\Phi \Big (\frac{p-\mu }{\sigma }\Big )\Big ) = \lambda \bar{\Phi }\Big (\frac{p-\mu }{\sigma }\Big ), \end{aligned}$$
(2.1)

where \(\Phi (\cdot )\) is the standard Normal cumulative distribution function and \(\bar{\Phi }(\cdot ) = 1-\Phi (\cdot )\) is the survival function. If the firm sets a price \(p_t\) in period t of a selling horizon and there is positive inventory then the demand, \(d_t(p_t)\), in that period is Bernoulli-distributed with the following probability mass function

$$\begin{aligned} d_t(p_t)= {\left\{ \begin{array}{ll} 1 \quad \text {w.p.} \quad \frac{\lambda }{N} \bar{\Phi }\left(\frac{p-\mu }{\sigma }\right) \\ 0 \quad \text {w.p.} \quad 1-\frac{\lambda }{N} \bar{\Phi }\left(\frac{p-\mu }{\sigma }\right). \end{array}\right. } \end{aligned}$$

The true value of the demand model parameter \(\varvec{\theta }_0 = (\lambda _0,\mu _0,\sigma _0)\) is unknown to the seller. We denote by \(\varvec{\theta }_k\) the firm’s estimate of these parameters at the beginning of selling horizon \(k \in \{1,2,\dots , K\}\). We assume that this estimate remains fixed throughout any selling horizon and the firm updates this estimate only at the start of the next selling horizon.

Given the parameters learned, there are many ways to obtain the control policy and hence derive revenue. The next subsection describes how to generate an optimal pricing policy for a selling season if the demand model parameters are known.

Optimal policy with known demand model parameters

If the demand model parameters are known then the optimal pricing policy for any selling horizon can be obtained by solving a DP problem (see for example Gallego and van Ryzin 1994). This framework can be used by a firm to generate a pricing policy based on myopically optimizing revenue for the current selling horizon with parameters estimated at the start of this horizon. The state space is the remaining inventory denoted by \(x \in \{0,1,\ldots ,C\}\). The action space is the optimal price to charge denoted by \(p \in [p_{\min },p_{\max }]\). If we set a price p for a seat at the start of period t with x seats remaining, then with probability \(\frac{\lambda }{N} \bar{\Phi }(\frac{p-\mu }{\sigma })\) a seat gets sold, we accumulate revenue p and move to the next time period with one less available seat, i.e., the state transitions to \(x-1\); with probability \(\Big (1-\frac{\lambda }{N}\bar{\Phi }(\frac{p-\mu }{\sigma })\Big ),\) there is no sale in the current time period; in this case we do not collect any revenue and move to the next period with all inventory intact, i.e., state remains as x. Let V(x, t) be the optimal expected revenue given that there are x seats left and we are at the start of time period t, then the following equation holds:

$$\begin{aligned} V(x,t)&=\sup _{p\in [p_{min}, p_{max}]}\left\{ \frac{\lambda }{N} \bar{\Phi }\Big (\frac{p-\mu }{\sigma }\Big )\Big (p+V(x-1,t+1)\Big ) + \Big (1-\frac{\lambda }{N}\bar{\Phi }\Big (\frac{p-\mu }{\sigma }\Big )\Big )V(x,t+1)\right\} \nonumber \\&=\sup _{p\in [p_{min}, p_{max}]}\left\{ \frac{\lambda }{N} \bar{\Phi }\Big (\frac{p-\mu }{\sigma }\Big )\Big (p-\Delta V(x,t+1)\Big ) +\, V(x,t+1)\right\} , \end{aligned}$$
(2.2)

where \(\Delta V(x,t)=V(x,t)-V(x-1,t)\) is the displacement cost (or bid price), and the boundary conditions are \(V(x,N+1)=0 \;\forall x\in \{1,2,\dots ,C\}\) and \(V(0,t)=0 \ \forall t\in \{1,2,\dots ,N+1\}\). Previous work in the RM literature shows that similar dynamic programs with exponential or constant elasticity demand models can be solved very efficiently (in closed-form), see for example Gallego and van Ryzin (1994) and McAfee and te Velde (2008). However for the Normal demand model a closed-form solution for the above model does not exist. Note that given the bid price \(\Delta V(x,t+1)\), the optimal price to offer in period t is generated by maximizing the expected margin over the bid price

$$\begin{aligned} \sup _{p\in [p_{\min }, p_{\max }]} \bar{\Phi }\Big (\frac{p-\mu }{\sigma }\Big )\Big (p-\Delta V(x,t+1)\Big ). \end{aligned}$$
(2.3)

Although the objective function in (2.3) may not be concave over the entire range of permissible prices, the next proposition shows that it is concave over an interval defined by the bid price and the WTP parameters, as well as the optimal price lies in this interval. Thus, the dynamic program defined in (2.2) can be solved efficiently.

Proposition

Denote the marginal cost by c, then there exists a unique \(p^{*}\in \Big (c,\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}}\Big )\) that maximizes expected margin:

$$\begin{aligned} U(p)&=(p-c)\cdot Pr(W\ge p)\\&=(p-c)\cdot \bar{\Phi }\big (\frac{p-\mu }{\sigma }\big ). \end{aligned}$$

This \(p^{*}\) can be numerically obtained by a line search over the interval. Furthermore, if \(\mu -c > 1.2534 \sigma\) , then \(p^*\) exists in \((c,\mu )\).

Proof

We shall pick our price from \((c,\infty )\) as otherwise the objective value is negative.

First, \(U^{'}(p)=\bar{\Phi }\big (\frac{p-\mu }{\sigma }\big )-\frac{p-c}{\sigma }\cdot \phi \big (\frac{p-\mu }{\sigma }\big )\). Notice \(U^{'}(c)=\bar{\Phi }\big (\frac{c-\mu }{\sigma }\big )>0\).

Next, see that

$$\begin{aligned} U^{''}(p)&=-\frac{2}{\sigma }\phi \Big (\frac{p-\mu }{\sigma }\Big )-\frac{p-c}{\sigma ^2}\phi ^{'}\Big (\frac{p-\mu }{\sigma }\Big )\\&=-\frac{2}{\sigma \sqrt{2\pi }}e^{-\frac{(p-\mu )^2}{2\sigma ^2}}+\frac{p-c}{\sigma ^2\sqrt{2\pi }}e^{-\frac{(p-\mu )^2}{2\sigma ^2}}\cdot \Big(\frac{p-\mu }{\sigma }\Big)\\&=\frac{1}{\sigma ^3\sqrt{2\pi }}e^{-\frac{(p-\mu )^2}{2\sigma ^2}}\cdot \big [ (p-c)(p-\mu )-2\sigma ^2\big ]\\&=\frac{1}{\sigma ^3\sqrt{2\pi }}e^{-\frac{(p-\mu )^2}{2\sigma ^2}}\cdot \bigg [\Big (p-\frac{\mu +c}{2}\Big )^2-\Big (2\sigma ^2+\frac{(\mu +c)^2}{4}\Big )\bigg ].\\ \end{aligned}$$

This is negative (i.e., U is concave) for \(p\in \Big (c,\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}}\Big )\) and positive (i.e., U is convex) for \(p\in \Big (\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}},\infty \Big )\).

Therefore, we have that \(U^{'}\) is positive at c, and that it decreases over \(\Big (c,\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}}\Big )\) and then increases over \(\Big (\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}},\infty \Big )\). But since \(U^{'}(p)<\bar{\Phi }\big (\frac{p-\mu }{\sigma }\big )\quad \forall p\in (c,\infty )\), and \(\underset{p\rightarrow \infty }{\lim }\bar{\Phi }\big (\frac{p-\mu }{\sigma }\big )=0\), it holds that \(U^{'}\) is negative over \(\Big (\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}},\infty \Big )\).

Consequently, we obtain that a unique \(p^{*}\) exists over \(\Big (c,\frac{\mu +c}{2}+\sqrt{2\sigma ^2+\frac{(\mu +c)^2}{4}}\Big )\) that satisfies \(U^{'}(p^{*})=0\) and that maximizes U. This \(p^{*}\) can be obtained by a simple line search over the interval.

Lastly, in the special case where \(U^{'}(\mu )=\frac{1}{2}-\frac{\mu -c}{\sigma \cdot \sqrt{2\pi }}<0\Leftrightarrow \frac{\mu -c}{\sigma }>\sqrt{\frac{\pi }{2}}\approx 1.2533\), we obtain \(p^*\) in \((c,\mu )\). \(\square\)

Performance measure

A popular metric in the demand learning and pricing literature to evaluate the quality of pricing policies is the Regret measure (e.g., see Besbes and Zeevi 2015 or den Boer and Zwart 2015). Seller’s Regret under a policy \(\pi\) after k selling horizons is defined as the difference between the total cumulative revenue earned if the parameters were known and the cumulative revenue earned under policy \(\pi\),

$$\begin{aligned} Regret_k^{\pi } = kV_{\varvec{\theta }_0}(C,1) - {\mathbb{E}}_{\pi }\left[ \sum _{i=1}^{Nk}p^{\pi }_id^{\pi }_i \right] , \end{aligned}$$
(2.4)

where \(\varvec{\theta }_0\) are the true demand model parameters and \(V_{\varvec{\theta }_0}(C,1)\) defined in (2.2) is the optimal expected revenue over a single selling horizon. In this paper, in addition to our focus on the quality of parameter estimation under various policies, we will use regret measure to evaluate their revenue performance. Note that minimizing the regret is equivalent to the originally stated objective of maximizing cumulative expected revenue.

Parameter estimation

Assume that we are at the start of selling horizon k and we have a dataset \(\mathcal {D}_k\) of the outcomes of each period in previous \(k-1\) selling horizons. Thus \(\mathcal {D}_k = \{(p_t,d_t), t = 1,2,\dots ,N(k-1)\}\), where \(p_t\) is the price offered in slot t and \(d_t\) is 1 if there was a booking in that slot and 0 otherwise. Based on our Normal demand model assumption, given the prices, \(d_t\) are independent draws from a Bernoulli distribution with success probability \(\frac{\lambda }{N} \bar{\Phi }(\frac{p_t-\mu }{\sigma })\). By some abuse of notation, in the rest of this and the next sections, we refer to \(\frac{\lambda }{N}\) as \(\lambda\). The firm’s goal is to estimate the demand model parameters \(\varvec{\theta }_k = (\lambda _k,\mu _k,\sigma _k)\) at the start of each selling horizon given historical observations. We next present an MLE for this purpose.

MLE for parameter estimation

With notations introduced above, our log-likelihood function for \(\lambda\), \(\mu\), and \(\sigma\) can be written as

$$\begin{aligned} \log \ \mathcal {L}(\varvec{\theta }_k \mid \mathcal {D}_k)&=\log \ \prod _{t=1}^{N(k-1)} \Big [\lambda \bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big ]^{d_t}\cdot \Big [1-\lambda \bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big ]^{1-d_t}\\&=\sum _{t=1}^{N(k-1)} d_t\cdot \log \Big [\lambda \bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big ]+(1-d_t)\cdot \log \Big [1-\lambda \bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big ].\nonumber \end{aligned}$$
(3.1)

Note our estimate of \(\varvec{\theta }_k\) is the point that maximizes the log-likelihood function (3.1), and we next illustrate the performance of the MLE in Example 3.1 below.

Example 3.1

Consider a case where a flight has 100 seats to sell, over 500 time periods in a selling horizon and we have 100 selling horizons. The true mean and standard deviation of customers’ WTP are, respectively, $200 and $75, and the effective demand-to-capacity ratioFootnote 1 of the flight is 90%. We study the performance of a myopic (passive learning) policy with the MLE. The seller at the start of each selling horizon estimates the demand model parameters using the MLE and then solves the dynamic pricing DP (2.2) using the estimated parameters.

Fig. 1
figure 1

Sample parameter errors—MLE

Full size image

Figure 1 shows the percentage relative parameter estimation errors, respectively, for \(\lambda\), \(\mu,\) and \(\sigma\) over the 100 selling horizons and averaged across 5 simulation runs.

As depicted, in this case the estimates take too long to converge, beginning to converge after about 50 selling horizons. Even by the end of 100 selling horizons, they are still far away from the true values (with approx. 16.9, 7.4, and 26.4% errors for \(\lambda\), \(\mu ,\) and \(\sigma,\) respectively). It also appears that \(\sigma\) has the largest estimation error among the 3 parameters. Our main observation based on this example and many other tests is that the MLE does not show robust convergence behavior and this necessitates a better parameter estimation method.

The complete information case

The main problem with the above estimation procedure is that for slots where there are no bookings, we do not know if this is because no one arrived or if someone arrived but the offered price was too high and hence no sale was made. Suppose that, in each time period, in addition to the booking information (\(d_t\)), the airline can also observe if there was an arrival (\(y_t\)) in a slot or not. In this case, the parameter estimation problem becomes more tractable. However, in practice, such information may not be available reliably. From this perspective our original estimation problem is an incomplete data problem. We next develop an MLE based on this additional information with two uses in mind: first if an airline is capturing this additional information then they can improve parameter estimation using the proposed methodology and second, when such information is not available, as a stepping stone for our formulation of the EM estimator (presented in the next section) which is especially suited for such incomplete data situations.

Let \(\mathcal {D}^{'}_k =\{(p_t, d_t, y_t)\}_{t=1}^{(k-1)N}\) be a dataset of the outcomes of each slot in previous \(k-1\) selling horizons with this additional customer arrival information \(y_t\). As before, \(p_t\) is the price charged in period t and \(d_t=1\) if a sale happens in period t and 0 otherwise. The new piece of information \(y_t\) equals 1 if a customer arrives in period t and 0 otherwise. Then \(\{y_t\}\) is a sequence of IID samples from a Bernoulli distribution with success probability \(\lambda\). Given that there was an arrival in slot t and a price \(p_t\) was charged, \(d_t\) is independently sampled from a Bernoulli distribution with success probability \(\bar{\Phi }(\frac{p_t-\mu }{\sigma })\). Note that if we observe a booking in any slot, then there must be an arrival in that slot (\(d_t = 1\) implies \(y_t = 1\)). Assuming that our dataset is consistent with this condition, the complete information log-likelihood function for \(\varvec{\theta }_k = (\lambda ,\mu ,\sigma )\) is

$$\begin{aligned} \log \mathcal {L}_c(\varvec{\theta }_k \mid \mathcal {D}^{'}_k)&= \log \left ( \prod _{t=1}^{(k-1)N} \lambda ^{{\mathbbm{1}}_{y_t = 1}}(1-\lambda )^{{\mathbbm{1}}_{y_t = 0}} \Big [\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\right ]^{{\mathbbm{1}}_{y_t = 1,d_t=1}}\cdot \Big [1-\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big ]^{{\mathbbm{1}}_{y_t = 1,d_t = 0}}\Big ) \end{aligned}$$
(3.2)
$$\begin{aligned}&=\log \Big (\lambda ^{\sum _{t=1}^{(k-1)N}y_t}(1-\lambda )^{(k-1)N-\sum _{t=1}^{(k-1)N}y_t}\Big )+\sum _{t:y_t=1} \Big [d_t\log \Big (\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )\\&\quad +\,(1-d_t)\cdot \log \Big (1-\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )\Big ]. \nonumber \end{aligned}$$
(3.3)

The parameters that maximize (3.3) lead to the following MLE estimators

$$\begin{aligned} \hat{\lambda } = \frac{\sum _{t=1}^{(k-1)N}y_t}{(k-1)N}, \end{aligned}$$
(3.4)

and

$$\begin{aligned} (\hat{\mu },\hat{\sigma }) = \mathop {\mathrm{arg \,\, max}}\limits _{\mu ,\sigma }{\sum _{t:y_t=1} \Big [d_t\log \Big (\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )+(1-d_t)\cdot \log \Big (1-\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )\Big ]}. \end{aligned}$$
(3.5)

The problem in (3.5) is relatively easier to solve as compared to the problem of maximizing the incomplete log-likelihood in (3.1). We next use this observation to provide an EM Algorithm for our original problem.

EM algorithm for the incomplete information case

To find the parameter estimates for our original incomplete information problem, we use the expectation–maximization (EM) approach introduced by Dempster et al. (1977). For applying this methodology, we consider our original dataset \(\mathcal {D}_k\) to be a partial version of the complete information dataset \(\mathcal {D}_k^{'}\). The EM algorithm is an iterative procedure which starts with an initial guess on the unknown parameters (\(\varvec{\theta }_k^0\)). We then find the expectation of the complete information log-likelihood function with respect to the unknown data \(\mathcal {Y}_k = (y_1,\ldots ,y_{(k-1)N})\) given the observed data and our current guess of the parameters. This constitutes the E step of the EM algorithm. The expected log-likelihood function has similar form as the complete information log-likelihood function; therefore, it can be maximized easily to find the updated parameter estimates (the M step). The algorithm iterates over the E and M steps until parameter convergence is achieved. This results in the following algorithm:

  • Choose initial parameter estimate \(\varvec{\theta }_k^0\) (ith iteration).

  • (E Step) Compute the expectation of complete information log-likelihood function w.r.t the current parameter estimate \(\varvec{\theta }_k^{(i-1)}\)

    $$\begin{aligned} Q(\varvec{\theta }_k,\varvec{\theta }_k^{(i-1)}) = {\mathbb{E}}_{\mathcal {Y}|\mathcal {D}_k,\varvec{\theta }_k^{(i-1)}}\Big [\log \mathcal {L}_c\Big (\varvec{\theta }_k|\mathcal {D}_k^{'},\varvec{\theta }_k^{(i-1)}\Big )\Big ] \end{aligned}.$$

  • (M Step) Compute the updated parameter estimates by maximizing the expected log-likelihood

    $$\begin{aligned} \varvec{\theta }_k^{(i)} = \mathop {\mathrm{arg \,\, max}}\limits _{\varvec{\theta }_k} Q(\varvec{\theta }_k,\varvec{\theta }_k^{(i-1)}) \end{aligned}.$$

The key step in this procedure is to find the expression for the expectation of complete information log-likelihood function in closed-form. In the E step for the \((i+1)\)st iteration, the unobserved data, given the observed data and current parameter estimate, \(\mathcal {Y}_k|\mathcal {D}_k,\varvec{\theta }_k^{(i-1)}\), comprise independent samples from the following distribution

$$\begin{aligned} {\mathbb{P}}[y_t|p_t,d_t,\varvec{\theta }_k^{(i)}]= {\left\{ \begin{array}{ll} \frac{\lambda _k^{(i)}\Phi _k^{(i)}(p_t)}{1-\lambda _k^{(i)}(1-\Phi _k^{(i)}(p_t))} &{}\quad \quad y_t=1,d_t=0,\\ \frac{1-\lambda _k^{(i)}}{1-\lambda _k^{(i)}(1-\Phi _k^{(i)}(p_t))} &{}\quad \quad y_t = 0, d_t = 0,\\ \qquad 1 &{}\quad \quad y_t = 1, d_t = 1,\\ \qquad 0 &{}\quad \quad y_t = 0,d_t = 1, \end{array}\right. } \end{aligned}$$
(3.6)

where \(\Phi _k^{(i)}(\cdot )\) is the cumulative distribution function of a Normally distributed random variable with mean \(\mu _k^{(i)}\) and standard deviation \(\sigma _k^{(i)}\). To simplify the expression for the expectation of complete information log-likelihood, we define the probability that a customer arrives in slot t given that there is no booking observed in that slot [in (3.6)] as

$$\begin{aligned} \alpha _t^{(i)}&:= {\mathbb{P}}[y_t=1|p_t,d_t=0,\varvec{\theta }_k^{(i)}] = \frac{\lambda _k^{(i)}\Phi _k^{(i)}(p_t)}{1-\lambda _k^{(i)}(1-\Phi _k^{(i)}(p_t))} \end{aligned}.$$
(3.7)

Taking the expectation of the complete log-likelihood function (3.2) with respect to the distribution (3.6), we get

$$\begin{aligned} Q(\varvec{\theta }_k,\varvec{\theta }_k^{(i)})&= {\mathbb{E}}_{\mathcal {Y}|\mathcal {D}_k,\varvec{\theta }_k^{(i)}}\Big [\log (\mathcal {L}_c\Big (\varvec{\theta }_k|\mathcal {D}_k^{'},\varvec{\theta }_k^{(i)}\Big )\Big ]\\&= \sum _{t:d_t=1}\Big [\log \Big (\lambda \bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )\Big ]\nonumber \\&\quad +\,\sum _{t:d_t=0}\Big [\alpha _t^{(i)}\log \Big (\lambda \Big (1-\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )\Big ) + (1-\alpha _t^{(i)})\log (1-\lambda )\Big ].\nonumber \end{aligned}$$
(3.8)

Then the parameters that maximize (3.8) as a function of \(\varvec{\theta }_k\) lead to the following updates for the parameter estimates:

$$\begin{aligned} \lambda _k^{(i+1)} = \frac{\sum _{t=1}^{(k-1)N}d_t+ \sum _{t:d_t=0}\alpha _t^{i}}{(k-1)N}, \end{aligned}$$
(3.9)

and

$$\begin{aligned} (\mu _k^{(i+1)},\sigma _k^{(i+1)}) = \mathop {\mathrm{arg \,\, max}}\limits _{\mu ,\sigma }{\sum _{t=1}^{(k-1)N} \Big [d_t\cdot \log \Big (\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )+\,(1-d_t)\cdot \alpha _t^{(i)}\cdot \log \Big (1-\bar{\Phi }\Big (\frac{p_t-\mu }{\sigma }\Big )\Big )\Big ]}. \end{aligned}$$
(3.10)

Note that the update for the probability that a customer arrives in a slot, \(\lambda _k^{(i+1)}\), is quite intuitive, i.e., the sum of total observed bookings and the expected number of slots where a customer arrived given there was no booking divided by the total number of slots. Equations (3.9) and (3.10) are essentially providing a mechanism for unconstraining (sometimes also referred to as uncensoring or detruncation) for the fully price-sensitive demand model in (2.1) defined over a continuum range of prices. The updates defined in (3.9) and (3.10) are similar to the MLE for the complete information case, thus the maximization (M) step can be computed efficiently.

Policies for dynamic pricing and learning

In this section, we discuss two pricing strategies that will be used to evaluate revenue performance and parameter convergence when demand model parameters are unknown.

Passive learning policy

The simplest learning policy that one can consider is the pure exploitation-based myopic policy. We assume that the seller at the start of the first selling horizon has some estimate of the demand model parameters. At the start of each selling horizon, the seller first uses one of the estimation methods discussed in the "Parameter estimation" Section to estimate demand model parameters based on historical observations. The estimated parameters are then used to evaluate a dynamic pricing policy for the current selling horizon by solving the dynamic program (2.2). This cycle is then repeated for each selling horizon. Such a policy is also referred to as the passive learning or certainty equivalent pricing policy in the Revenue Management literature. In the rest of the paper, this policy will be referred to as MLE-PAS or EM-PAS based on the estimation procedure used.

We also evaluated the performance of a policy assuming that the complete loss information is available and the MLE formulated in Section “The complete information case” (MLE-CPLT). As expected, since more information is available in this scenario, the performance will be better as compared to the incomplete information case. Nevertheless, such a comparison allows us to gage the value of obtaining additional loss information.

Policy based on minimal active learning

den Boer and Zwart (2015) develop a pricing strategy that modifies the passive learning policy slightly to incorporate minimal amount of price exploration. Under this scheme, one uses the passive learning policy throughout a selling horizon except perhaps for a small fraction of the selling horizon towards the end. The essential idea is that if we have not seen much price variation in a selling horizon and if there are few time periods left for exploration either because we are running out of inventory or the selling horizon is about to end, we generate prices that will benefit learning. We make a slight modification to the original algorithm of den Boer and Zwart (2015) mainly to suit the present setting and to increase the level of active learning. We state this algorithm (EM-DZ’15) here for completeness.

  • Initialization Assume initial parameter estimates \(\varvec{\theta }_1\). Choose \(0< \epsilon <(p_{max}-p_{min})/4\). Set parameters to define state space in which active learning may be triggered: \(\kappa \in \{ 1,2,\dots ,5\}\) and \(0.95< \tau < 1\) (Start of selling horizon k )

  • Estimation Estimate demand model parameters, \(\varvec{\theta }_k\), using the EM estimator and the historical dataset \(\mathcal {D}_{k-1}\)

  • Pricing Solve the Dynamic Program (2.2) for selling horizon k based on the estimated parameters \(\varvec{\theta }_k\) to evaluate the myopic price \(\pi ^k(x,t)\) for inventory state x and time period t. For determining prices in time slot \(t+1\) during selling horizon k, if inventory state \(x = 0\) then set \(p_{t+1} = p_{\max }\) else if \(x>0\):

    • If

      1. 1.

        \(\mid p_i - p_j\mid < \epsilon\) for all \(1\le i,j\le t\) in current selling horizon k, and

      2. 2.

        \(\mid p_i - \pi ^k(x,t+1)\mid < \epsilon\), for all \(1\le i \le t\) in the current selling horizon k, and

      3. 3.

        \(x \le \kappa\) or \(t > \tau N\) then choose \(p_{t+1} \in [\pi ^k(x,t+1)- 2\epsilon , \pi ^k(x,t+1)+2\epsilon ] \cap [p_{\min },p_{\max }]\).

    • Else, choose \(p_{t+1} = \pi ^k(x,t+1)\).

This algorithm in any selling horizon will generate prices based on the passive learning policy unless the price variation for a significant portion of selling horizon is less than a certain threshold. In case of low price variation, when the remaining capacity is less than \(\kappa\) or greater than \(\tau\) fraction of the selling horizon has elapsed then a price that deviates from the optimal price by at most 2\(\epsilon\) is generated. Parameters \(\kappa\) and \(\tau\) govern the aggressiveness of active learning; higher \(\kappa\) or lower \(\tau\) induce more exploration. den Boer and Zwart (2015) showed that for a different demand model, \(\kappa = 1\) and \(\tau = \frac{N-1}{N}\) (i.e., either inventory level is 1 or this is the last time slot in the selling horizon) is sufficient for convergence of parameter estimates and good (\(O(\log ^2(T))\)) regret performance. The demand model considered in this paper is arguably more complex at least from the perspective of number of model parameters. Therefore, it required a slightly more aggressive (\(\kappa = 2\) and \(\tau = 0.98\)) learning policy to see some advantages from active learning.

Numerical results

In this section, we conduct several numerical experiments to test the performance of the pricing policies described in the previous section. We conduct these experiments with the following aims:

  • to test whether the parameter estimation under various approaches converge to acceptable levels,

  • to evaluate the revenue performance of various policies,

  • to identify the conditions where active learning provides the most benefit.

Experiment setup

In our numerical study, we consider that the flight capacity is 100 and each selling horizon is of unit length (\(T = 1\)). Recall that the demand rate when price p is charged has the following functional form:

$$\begin{aligned} \lambda (p) = \lambda \Big (1-\Phi \Big (\frac{p-\mu }{\sigma }\Big )\Big ). \end{aligned}$$

We fix the true mean (\(\mu _0\)) and standard deviation (\(\sigma _0\)) of customers’ maximum WTP to be $200 and $75, respectively. Under this setting, we consider 6 arrival intensity (\(\lambda _0\)) values to simulate various congestion scenarios. To quantify different congestion scenarios, we define “effective” demand-to-capacity (D/C) ratio attained under a selected arrival intensity. More specifically, let \(p*\) be the revenue maximizing price in the infinite-capacity setting

$$\begin{aligned} p* = \underset{p\ge 0}{{\text {arg max}}}\quad p\cdot \bar{\Phi }\Big (\frac{p-200}{75}\Big ), \end{aligned}$$

which is the optimal price to charge if we have infinite capacity. Then the “effective” demand-to-capacity (D/C) ratio under arrival intensity \(\lambda _0\) is defined as

$$\begin{aligned} D/C = \frac{\lambda (p^{*})}{C} = \frac{\lambda _0}{C}\Big [1-\Phi \Big (\frac{p^{*}-200}{75}\Big )\Big ]. \end{aligned}$$

In this study, the six D/C scenarios range from 30 to 180%. We summarize the input parameters used in our experiments in Table 1. This table also shows the initial parameter estimate (\(\varvec{\theta }_1\)) used in our simulation studies. The initial parameter estimate is what the airline believes prior to the first selling season. These are used in solving the dynamic program (2.2) to generate the pricing policy for the first selling horizon, and also as the initial guess for parameter estimation problem to be solved at the end of this selling horizon. In practice there is often more uncertainty in the estimates of the willingness-to-pay parameters (\(\mu ,\sigma\)) than the volume parameter. Therefore, we set our initial estimate on \(\lambda\) at 70% of the true value, and guesses on \(\mu\) and \(\sigma\) both at 150% of the true values in all our experiments.

Table 1 Experiment input parameters
Full size table

For each of these scenarios, we consider 100 consecutive selling horizons (\(K = 100\)) and divide each selling horizon into 500 periods of equal length (\(N=500\)). For each scenario, we run 5 independent trials and compute the performance metrics and parameter estimation errors as the mean over these trials.

Performance and error metric

To evaluate the performance of policies described in the previous section, we use the following metrics:

  • Relative parameter errors: We evaluate relative parameter errors after each selling horizon ends. Let \(\epsilon _{\lambda }^r(k)\), \(\epsilon _{\mu }^r(k)\) , and \(\epsilon _{\sigma }^r(k)\) denote the relative errors in arrival intensity, mean WTP, and standard deviation of WTP, respectively, in trial r after selling horizon k. Then the overall relative parameter error for trial r after selling horizon k is \(\bar{\epsilon }^r(k) = \frac{\epsilon _{\lambda }^r(k)+ \epsilon _{\mu }^r(k)+\epsilon _{\sigma }^r(k)}{3}\). Finally the average percentage relative parameter error is \(\bar{\epsilon }(k) = \frac{\sum _{r=1}^R\bar{\epsilon }^r(k)}{R} \times 100\%\), which is the average over the total number of trials R. In our experiments, we considered \(R = 5\).

  • Relative regret: For revenue performance we define percentage relative regret for trial r after k selling seasons as \(\text {Relative\, regret}^r(k) = \frac{Regret^r_k}{k\cdot V_{\varvec{\theta }_0}(C,1)}\times 100\%,\) where \(V_{\varvec{\theta }_0}(C,1)\) is the optimal expected revenue per selling season if true parameters were known. As stated above, we take the average across trials to get the average percentage relative regret after selling season k denoted by avg. relative regret (k).

Results

We have organized the results of our numerical experiments in three parts. First, we analyze the parameter estimation performance of various methods in different D/C scenarios. Second, we discuss the revenue performance of various methods using the relative regret metric. Our results on parameter estimation and revenue performance show that in some cases revenue performance is still good even though the estimated parameters do not completely converge to the true parameters. In the third part of our results, we investigate this observation in depth and present insights on this.

Estimation performance

Figure 2 shows the average relative parameter error for the pricing policies across 100 selling horizons for each of the six D/C scenarios.

Fig. 2
figure 2

Parameter error

Full size image

A few observations are in order. The worst errors (20–30%) for all policies occur for the lowest D/C scenario. This is because when the demand is very low, there is very little price variation and the passive learning methods suffer. For the EM-DZ’15 method, since we have large inventory at hand throughout the selling horizon, the active learning takes effect only in last few periods in a selling horizon. However, given that the demand is low, it is unlikely to see bookings during the period when active learning is implemented. This renders active learning to be not as effective in discovering the full underlying demand curve.

For the medium D/C (60–90%) scenarios, the policy incorporating minimal active learning (EM-DZ’15) shows lower estimation errors (10%) than both passive learning policies: MLE-PAS and EM-PAS. This is to be expected since in medium D/C scenarios the prices generated by the passive learning (myopic) policies show less variation. Thus any form of active learning should improve parameter estimates.

We also note that the benefit of active learning begins to diminish as the D/C increases past the 90% level. Indeed for relatively high D/C (120–180%), EM-PAS performs as well as EM-DZ’15. Intuitively, for higher D/C scenarios, the passive learning policy inherently leads to higher price variation, thereby making active learning less useful.

Furthermore, we observe that the EM estimation method is more stable and robust than the incomplete information MLE. EM method converges close to the final value quickly (within 20 selling horizons), while the MLE takes much longer to converge and shows large fluctuations in estimated parameter values.

As expected, more information helps with parameter estimation; the complete information MLE with passive learning (MLE-CPLT) has the lowest error and converges to a very good estimate within 10 selling seasons.

Revenue performance

The relative regrets over selling seasons 5–100 for all four methods are plotted in Fig. 3. Clearly MLE-PAS performs the worst in all scenarios, mainly because of the high errors in parameter estimation in the earlier selling horizons.

Fig. 3
figure 3

Relative regret

Full size image

In scenarios with D/C 30 and 60%, both EM-DZ’15 and EM-PAS do well. Interestingly, in this case even when EM-DZ’15 has lower estimation error (for D/C 60%), the benefit does not translate to revenue performance. We will give more insight into the relationship between parameter estimation error and revenue performance in the next section.

EM-DZ’15 performs the best when we have medium D/C (e.g., 90%). In this case since the demand is capacity constrained, estimating parameters well and charging optimal prices become more critical. For high D/C scenarios, both EM-PAS and EM-ACT give good revenue performance. Overall we note that the EM-DZ’15 method leads to near-optimal revenues much faster than the MLE; it drives the regret to below 0.5% within 20 selling horizons in demand scenarios under 120% D/C, and 40 selling horizons in the rest.

Although MLE-CPLT has the least errors in parameter estimation, this does not translate to better revenue performance over EM-DZ’15 or EM-PAS in most scenarios. This seems to indicate that from a revenue perspective there is limited benefit of collecting the additional loss information and a good estimation procedure like EM can overcome the challenges posed by missing information.

In the appendix, we present a more detailed view of the relative errors in each of the three parameters as averaged across the last 10 simulation iterations in each demand scenario. The table also shows the relative regret and load factors achieved in each demand scenario.

Revenue performance under parameter errors

We observe from the results presented above that in most demand scenarios, although the parameter errors are in the 10–20% range at the end (the 100th selling season), the corresponding relative regret falls under 1%. To investigate why we observe good revenue performance under the observed parameter errors, we next present a deeper analysis on the 90% D/C scenario which is more representative of the load factors observed in practice.

We focus on the EM-DZ’15 model in this section (results for the other three models are similar), and Fig. 4 shows its corresponding offered prices spread along with that for the true model across all the 100 selling horizons. Note the bottom and top edges in the box plot represent the 25th and 75th percentile values, respectively, and the bottom and the top whiskers denote the 5th and 95th percentile values, respectively. Outliers beyond the 5th and 95th percentile values are also plotted as dots.

Fig. 4
figure 4

Spread of offered prices under the EM-DZ’15 and true model for 90% D/C scenario

Full size image

We observe from the last two boxes in this figure that the median offered prices for the EM-DZ’15 algorithm converge to that for the true model (\(p^{true}_{med} \approx \$ 160\)) in the last 10 selling horizons. In general, the EM-DZ’15 algorithm demonstrates a larger variation in offered prices due to the fact that the parameter values are re-estimated at the start of each selling horizon and hence differ slightly for each selling horizon. We also notice that most of the offered prices under the true model lie within the interval \(p^{true}_{med} \pm \sigma _0/2\), where \(\sigma _0\) denotes the standard deviation of the true WTP distribution, i.e., in the interval of \(160 \pm \frac{75}{2} = [122.5, 197.5]\). We next devote our attention to how the estimated demand function deviates from the true demand function over this “critical” price range.

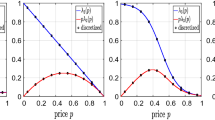
Figure 5a shows the true and estimated (averaged over the 5 trials) demand response functions \(\lambda (p)\) under the EM-DZ’15 pricing policy at the end of 1st, 34th, 67th, and 100th selling horizon (SH). To show the impact of error in estimated demand function on revenues, we also plot the corresponding total revenue \(p\lambda (p)\) in Fig. 5b.

Fig. 5
figure 5

Demand and revenue snapshots for EM-DZ’15 90% D/C scenario (SH selling horizon). a Demand response λ(p). Dotted vertical lines show 160 ± 2 range, b total revenue pλ(p) possible under infinite capacity setting

Full size image

Notice as we progress over selling horizons, better approximation of the estimated demand function to the true demand function is observed, and this is especially true for the portion of demand curve in the aforementioned price range of [122.5, 197.5], as marked by the vertical dashed lines in Fig. 5a. Moreover, the corresponding total revenue (Fig. 5b) shows even better convergence of the estimated revenue function to the true revenue function.

Thus, although the parameter error in the estimated model is as high as 11% for EM-DZ’15 in the 90% D/C Scenario (see Fig. 2 and Table 3), the estimated demand response is able to approximate the true demand function very well over the price range where most of the optimal offered prices lie. More specifically, Fig. 6 shows the mean relative error (MRE, also referred to as mean absolute percentage error in some literature) between the estimated demand function and the true demand function discretized using 200 equally spaced points over the price range [122.5, 197.5] for various methods. Table 2 shows the mean relative and root mean-squared errors (RMSE) in the demand response curves averaged over the last 10 selling horizons for all four schemes in the \(90\%\) D/C scenario. We see that for the EM-DZ’15 method the relative error quickly diminishes to less than \(5\%\) by selling horizon 20 and further decreases to less than \(2\%\) by selling horizon 100.

This suggests that by estimating the demand function correctly over a limited price range where most of the optimal offer prices lie, the EM-DZ’15 method is able to produce a good revenue performance. Note that a policy may be able to satisfy this less restrictive criterion even when the estimates of demand model parameters (\(\lambda ,\mu ,\sigma\)) converge to values different from the true values. This may explain the observed robustness of the revenue performance to the parameter estimation errors. Similar results have also been reported by Besbes and  Zeevi (2015) for the related problem of dynamic pricing under the infinite-capacity setting.

Fig. 6
figure 6

Errors in demand curve in price range [122.5, 197.5] for \(90\%\) D/C scenario

Full size image
Table 2 Errors in demand curve in price range [122.5, 197.5] for \(90\%\) D/C scenario averaged over the last 10 selling horizons
Full size table

Conclusion and future research

Airlines have been looking into leveraging dynamic pricing for more revenue-beneficial control of available capacity in an ever more competitive market. In this paper we investigate the problem of dynamic pricing in a single-leg setting when the airline has imperfect knowledge about the demand model parameters. We propose a framework for dynamic pricing based on a demand model with Gaussian WTP distribution. Under this assumption, we show how to formulate the revenue maximization problem over a single finite horizon as a dynamic program. We also show that a unique optimal solution exists for the pricing problem embedded in the DP and provide an interval in which this optimal price lies.

We develop MLE and EM-based estimators for the setting in which the demand model parameters are not known. Using these estimators, we study the revenue impact in a long-run (multiple selling horizons) setting and compare the performance of pricing policies that enforce small amounts of price variation designed to accelerate demand model learning (EM-DZ’15) and policies that myopically optimize single horizon revenues given estimated parameters (EM-PAS, MLE-PAS, MLE-CPLT). We observe from our numerical examples that with all the parameter estimation methods, the model will eventually output near-optimal revenues. However, the EM-DZ’15 method leads to near-optimal revenues much faster than the MLE. Moreover, congestion scenarios with load factors of 80–90% (D/C = 90%), which are closer to what is observed in practice, can benefit the most from incorporating a minimal amount of active price exploration.

Our numerical experiments also show that for good revenue performance, it is not necessary to learn the demand curve over the entire range of prices. The important characteristic of a method delivering good revenue performance is that it learns the demand curve well over a critical range of prices where most of the optimal prices under the true model lie. This is an important observation, since it suggests that low parameter estimation error is a sufficient but not a necessary condition for obtaining good revenue performance. From a practical perspective this indicates that models that are misspecified either in their functional form or model parameters may still be able to provide good revenues by learning the “critical” part of the true demand curve well.

Throughout the paper we have focused on a case where there is constant customer arrival intensity and a fixed WTP distribution. In practice, we note that this framework can be easily extended to situations where the underlying demand parameters vary by time-to-departure. To this end, the airline needs to assume certain time points when the average customer arrival and WTP characteristics change. After this, the same mechanism can be followed to solve the DP, collect booking history, and re-estimate parameters after each selling horizon. For future work, we plan to test our model with real data and extend our model to the network and multiple-product settings.