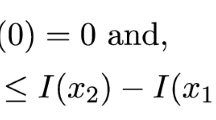Large losses and equilibrium in insurance markets

Abstract

We show that if losses are larger than wealth, then individuals with the option of declaring bankruptcy will not insure if the loss probability is above a threshold. In an insurance market with adverse selection, if the high risks’ loss probability is above the threshold, then no trade occurs at the Rothschild–Stiglitz equilibrium. Active trade in insurance requires cross-subsidization. When a subset of individuals with significant costs of bankruptcy and default is included in the market, then the equilibrium outcome always involves positive levels of insurance coverage for some individuals, but the parameters of the model determine whether all types receive coverage, or whether null contracts are received by both high and low risks with no bankruptcy costs or just the low risks from that group.

1 Introduction

Individuals can face large potential losses that exceed their wealth. The median net worth of U.S. households was $68,828 in 2011 (U.S. Census Bureau 2014). It is easy to see that a large medical expense or a large liability judgement could wipe out a household’s net worth.¹ We show that, when losses exceed wealth, risk averse individuals will not insure if the probability of loss exceeds a threshold. We examine the implications of this for insurance markets with adverse selection. We show that if the high risks do not buy insurance then there is no trade in the insurance market. The Rothschild–Stiglitz (1976) equilibrium contracts for both high and low risks are the null contracts. This is the reverse of the “adverse selection death spiral” since it is the high risks rather than the low risks that drop out of the market.

Shavell (1986) and Sinn (1982) consider the case where losses exceed wealth. Shavell shows that, for a fixed loss probability, there is a wealth threshold where individuals do not insure if their wealth is below the threshold and fully insure if it is above the threshold. Sinn notes that whether the premium exceeds the maximum willingness to pay depends on the probability of loss but does not consider threshold values. Neither author considers the case of asymmetric information. Our result is the obverse of Shavell’s. We show that, for fixed wealth, there is a probability threshold where individuals fully insure if the loss probability is below the threshold and do not insure if the loss probability is above the threshold.²

Hendren (2013, 2014) gives conditions under which the unique Rothschild–Stiglitz equilibrium contract in an insurance market with adverse selection is the null contract. The “no trade condition” is that lower risks are never willing to pay to be in a pool with higher risks. This leads to an adverse selection death spiral. If the no trade condition does not hold, then either there is an equilibrium where insurance is bought or there is no equilibrium. As Hendren (2014) points out the “equilibrium of market unraveling” (no trade) and the “unraveling of market equilibrium” (no equilibrium) are mutually exclusive.

We analyze the standard Rothschild–Stiglitz model of adverse selection. The no trade condition does not hold in this model, so we would expect active trade in equilibrium. We relax Hendren’s implicit assumption that losses do not exceed wealth. We show that if the high risks’ loss probability exceeds the threshold, then the unique Rothschild–Stiglitz equilibrium contracts are the null contracts—there is no trade—or else there is no equilibrium. The no trade equilibrium is the result of the high risks dropping out of the market. The high risks do not buy insurance at an actuarially fair price because it covers losses they would not be able to pay if uninsured and is therefore too expensive. The low risks would be willing to buy insurance at their actuarially fair price if it provided a minimum level of coverage. The need to screen the high risks limits the coverage for the low risks to a level that is below this minimum and the low risks choose not to insure. We extend the analysis to the Wilson (1977) E2 equilibrium and the Wilson (1977)–Miyazaki (1977)–Spence (1978) (WMS) equilibrium. For both the E2 and WMS equilibria, if the proportion of high risks is large enough, then the equilibrium contracts are the null contracts and there is no trade. If the proportion of high risks is small enough, then there is active trade in insurance. Active trade requires that the low risks subsidize the high risks.

A key factor in our analysis is the assumption that final wealth cannot be negative so that a portion of any loss that is greater than an individual’s wealth will be externalized. For example, the injured third party may not receive full compensation if the loss exceeds the wealth of the party liable for damages. Similarly, the medical expenses of uninsured or underinsured patients with insufficient wealth may ultimately be borne by medical providers. Our results may provide an explanation for why health insurance markets are not well-functioning for low-income populations.³

Although the existence of bankruptcy protection may alter the incentives to buy insurance, it is important to note that insurance policies are never written with coverage levels that are contingent upon the individual’s ex post bankruptcy status or wealth. For example, liability insurance policies are designed to pay for damages that would be the legal responsibility of the individual before bankruptcy protection is applied. The ISO commercial general liability policy states simply that the insurer “will pay those sums that the insured becomes legally obligated to pay as damages because of ‘bodily injury’ or ‘property damage’ to which this insurance applies,”⁴ and the Homeowners 3—Personal Liability Coverage E will “pay up to our limit of liability for the damages for which the ‘insured’ is legally liable.”⁵ Bankruptcy laws and courts determine how the financial resources of bankrupt individuals are allocated to claimants ex post, and insurance coverage is not designed to be a moving target during such proceedings.

The paper most closely related to ours is Strohmenger and Wambach (SW, 2000). They assume state-dependent utility in a health insurance model with two risk types where the cost of treatment may be less than the individual’s income yet exceed the individual’s willingness to pay for treatment. They show that individuals may be unwilling to buy insurance and that this may lead to no trade in insurance markets. In their paper, the willingness to pay for insurance is determined largely by the difference in state-dependent utility between the good state and bad state. Our analysis applies a similar model to the case of large losses with bankruptcy protection but there are differences. In SW, individuals have the choice of whether to accept and pay for treatment to cure their illness. Individuals who are unwilling to pay the full cost of treatment also may be unwilling to purchase insurance to cover the cost of treatment. This in turn depends on the difference in utility between the healthy and unhealthy states. In our model, individuals do not have this discretion, but are legally obligated to pay the loss to the extent possible. The extent to which individuals are obligated to pay the loss depends on the size of the loss and the level of bankruptcy protection.

We show that no trade may be second-best efficient and that an active market requires cross-subsidization. We present a formal proof of the WMS second-best equilibrium for our model. Strohmenger and Wambach limit their discussion to a graphical representation of the WMS equilibrium. We also extend our model to include a set of consumers who are unwilling to declare bankruptcy due to the stigma and reputational effects. We show that, in equilibrium, there is always an active market in insurance. However, not all consumers necessarily participate; depending on the parameters of the model, all consumers may purchase insurance or one or two of the four types may be absent from the market. Equilibria where all types participate in the market require cross-subsidization.⁶

2 The decision to buy full insurance

Assume individuals have the utility function u, which is strictly increasing, strictly concave, and at least twice differentiable. Individuals have initial wealth w. They face a potential loss l with probability p. Assume the loss is larger than wealth, l > w. If there is no bankruptcy protection, then, although consumption cannot be negative, a loss leaves the individual with negative final wealth because they have financial obligations they cannot meet. Many jurisdictions allow for bankruptcy, so that some amount of the individual’s wealth is protected. Let b ≥ 0 denote the wealth protected by bankruptcy; the most the individual can lose is w − b. Assume u(b) is finite. Insurance is actuarially fairly priced so if the individual buys insurance, full insurance is optimal (Mossin 1968). This can be shown as follows.

Expected utility with actuarially fair insurance (from the insurer’s perspective) for coverage level $\beta$ is U = Max $[\left( {1 - p} \right)u\left( {w - p\beta } \right) + pu\left( b \right), \left( {1 - p} \right)u\left( {w - p\beta } \right) + pu\left( {w - p\beta - l + \beta } \right)$]. Denote $u\left( {w - p\beta - l + \beta } \right) = U^{\beta }$. Setting the wealth level in $U^{\beta }$ equal to b gives the level of coverage above which purchasing actuarially fair insurance leads to an increase in wealth in the loss state above the minimum wealth guaranteed by bankruptcy protection. $w - p\beta - l + \beta = b$ implies that $\beta^{*} = \frac{b - w + l}{1 - p}.$ Below $\beta^{*}$, $u\left( b \right) > U^{\beta }$ and U is decreasing in $\beta$. Above $\beta^{*}$, $U^{\beta } > u\left( b \right),$ and U is increasing until $\beta$ reaches l, at which point it begins to decrease since $\frac{{{\text{d}}U}}{{{\text{d}}\beta }} = - \left( {1 - p} \right)u^{\prime}\left( {w - p\beta } \right)p + pu^{\prime}\left( {w - p\beta - l + \beta } \right)\left( {1 - p} \right)$ and $\frac{{{\text{d}}^{2} U}}{{{\text{d}}\beta^{2} }} < 0.$ Therefore, the utility maximizing level of coverage is either l or 0.

In this section, we consider the demand for actuarially fair full insurance when the probability of a loss is known to all parties. Expected utility with full insurance is u(w − pl). If the individual does not buy insurance, their expected utility is U = (1 − p)u(w) + pu(b). If p > w/l, then the individual cannot pay for full coverage. If p = (w − b)/l, the individual will not buy insurance since buying insurance leaves the individual with final wealth of b with certainty, while not buying insurance leaves the individual with final wealth of b or w with less than certainty. This implies there is a critical value p* < (w − b)/l, such that the individual will not buy insurance if p > p*.

The net benefit of buying full insurance when the loss probability is p and p ≤ (w − b)/l is

$$N\left( p \right) \, = u\left( {w{-}pl} \right) \, {-} \, \left( {1 \, {-}p} \right)u\left( w \right) \, {-}pu\left( b \right).$$

(1)

Observe that N(0) = 0 and N((w − b)/l) < 0. We have

$$N^{\prime}\left( p \right) = - u^{\prime}\left( {w - pl} \right)l + \left[ {u\left( w \right) - u\left( b \right)} \right]\,{ \lessgtr }\,0.$$

(2)

and $N^{\prime\prime}\left( p \right) = u^{\prime\prime}\left( {w - pl} \right)l^{2} < 0$. If $N^{\prime}(0$) < 0, then there is never a benefit to buying insurance and p* = 0.⁷ If $N^{\prime}(0$) > 0 then N(p) > 0, at least in some neighborhood of zero, and there is a net benefit to buying insurance if the risk of loss is low enough. Then there is a unique p* such that N(p*) = 0, where 0 < p* < (w − b)/l.

This proves the following result:

Proposition 1

Assume l > w. Then there is a p*, where 0 ≤ p* < (w − b)/l, such that individuals buy full insurance if p < p* and do not buy insurance if p$\ge$p*.

The threshold probability p* is increasing in initial wealth, decreasing in the amount of bankruptcy protection and decreasing in the amount of the loss. This result is analogous to Strohmenger and Wambach (2000) Sect. 2.2.

The insurer is responsible for the full amount of the loss, l, and charges a premium based on this amount, pl. Bankruptcy protects the individual’s wealth up to the limit b with no explicit cost. As a result, the individual only needs to insure their wealth above b. In order to obtain coverage above $\beta^{*}$, a consumer must pay a premium consisting of a fixed component equal to $p\beta^{*} = p\left( {\frac{b - w + l}{1 - p}} \right)$ as well as a variable component equal to the actuarially fair premium from the consumer’s perspective, $p\left[ {\beta - \beta^{*} } \right],$ where $\left[ {\beta - \beta^{*} } \right]$ is the amount of coverage the consumer is actually benefiting from. One can think of the marginal price as determining how much coverage the individual buys, and the fixed charge determining whether the individual buys or not. If p$\ge$p*, then the fixed charge is too large and the individual chooses not to buy insurance.

3 Rothschild–Stiglitz equilibrium

We now consider the implication of the decision not to buy insurance for equilibrium in the Rothschild–Stiglitz (1976) framework. We assume the proportion λ of the population is high-risk and the proportion 1 − λ is low-risk. The loss probabilities are p_H and p_L for high risk and low risks, where 0 < p_L < p_H < 1. Individuals’ types are private information. A contract consists of a premium, α, and an indemnity, β, paid in the event of a loss. Equivalently, a contract specifies wealth in the no loss, or good, state, w_G = w − α, and wealth in the loss, or bad, state, w_B = w − α − l + β. We let c = (w_G, w_B) denote a contract. Firms simultaneously offer contracts, and then individuals decide which, if any, contract they will buy. In equilibrium, contracts must break even, satisfy the self-selection constraint U_H(c_H) ≥ U_H(c_L), and there must be no other contract which, if offered, would earn positive profits.⁸ Let $H^{*} , L^{*}$ denote the standard Rothschild–Stiglitz equilibrium contracts when l < w. The low-risk contract $L^{*}$ is at the intersection of the self-selection constraint through the break-even high-risk full insurance contract $H^{*}$ and the low-risk fair odds. The Rothschild–Stiglitz equilibrium exists if the proportion of high risk is large enough, λ ≥ λ*.⁹

Now consider the no trade condition. Let $\bar{p}$ = λp_H + (1 − λ)p_L be the average or pooled loss probability. If l < w, as in Hendren’s case then the no trade condition can be written as

$$\left( {1 - p_{L} } \right)u^{\prime}\left( w \right)/p_{L} u^{\prime}\left( {w - l} \right) \ge \, ( 1 { } - \bar{p})/\bar{p}$$

(3)

and

$$\left( {1 - p_{H} } \right)u^{\prime}\left( w \right)/p_{H} u^{\prime}\left( {w - l} \right) \ge \, ( 1 { }{-}p_{H} )/p_{H} .$$

(4)

Condition (3) is that the slope of the low-risk indifference curve at the endowment is greater than the slope of the pooled fair odds line. The low risks are unwilling to pay the actuarially fair price of pooled coverage; they would rather be uninsured than buy a fairly priced pooled policy. Condition (4) is that the slope of the high-risk indifference curve at the endowment is greater than the slope of the high-risk fair odds line. As noted in Hendren (2014), in the canonical two type case with l < w, condition (4) can only hold for risk averse individuals if p_H = 1.¹⁰ Hendren’s analysis for losses less than wealth and two risk types with p_H <1 implies that either there is an equilibrium where non-null contracts are traded (if λ > λ*) or equilibrium does not exist (if λ < λ*).¹¹ We show that if losses are larger than wealth Hendren’s no trade condition does not apply.

The Rothschild–Stiglitz equilibrium when losses are larger than wealth is illustrated in Fig. 1. Also depicted are the standard Rothschild–Stiglitz equilibrium contracts $H^{*} , L^{*}$. With bankruptcy protection, if individuals are uninsured they are at the point E₀ = (w, b). All points other than E₀ represent insurance contracts without a declaration of bankruptcy.¹² The curves U ⁰ _H and U ⁰ _L are the high-risk and low-risk indifference curves through E₀. The traditional fair odds lines for high and low risks, P_H and P_L, as well as the pooling fair odds line, P_P, emanate from E = (w, w − l) since the insurer must receive a premium on all of the coverage provided. For each risk type, the wealth combinations actually faced by the policyholder level off at the horizontal line where w_L = b. Only the portions of the fairs odds lines above this horizontal line are relevant. It is assumed throughout that 1 > p_H > p* > $\bar{p}$, so U ⁰ _H crosses the full insurance line to the northeast of P_H and to the southwest of P_P, while U ⁰ _L crosses the full insurance line to the southwest of P_L.

Fig. 1

Rothschild–Stiglitz equilibrium with large losses

Let $\lambda^{\prime}$ be the value of λ at which the fair pooled price line is just tangent to the low-risk indifference curve through E₀.

We want to prove the following result:

Proposition 2

Assume l > w and 1 > p_H > p* > $\bar{p}$. If λ$\geq\lambda^{\prime}$, then the unique Rothschild–Stiglitz equilibrium contracts are the null contracts, c_H* = c_L* = (w, b) = E₀. If λ < $\lambda^{\prime}$, then equilibrium does not exist.

The proof is straightforward. U ⁰ _H and U ⁰ _L are the individual rationality constraints. The low risks would prefer to buy any policy along P_L above point B, and would prefer to remain uninsured rather than buy a policy along P_L below B. Since p_H > p*, the high-risk fair odds line lies completely below the indifference curve U ⁰ _H , so the high risks do not insure. The indifference curve U ⁰ _H is the self-selection constraint. Since U ⁰ _H is flatter than U ⁰ _L , it must intersect the fair odds line P_L below B, for example, at point A. The low risks prefer to remain uninsured. If the pooled fair odds line, labeled P_P in Fig. 1, lies below or tangent to the indifference curve U ⁰ _L , i.e., if λ$\geq\lambda^{\prime}$, then the equilibrium is at the null contracts, c_H* = c_L* = (w, b). There is no contract offering a positive level of coverage that at least breaks even and satisfies the self-selection constraint and the individual rationality constraints. Therefore, the equilibrium is unique.

Now suppose λ <$\lambda^{\prime}$, so the pooled fair odds line P_P intersects the low-risk indifference curve U ⁰ _L . Then a firm can offer a pooled policy, say, c_P, on P_P that attracts both high and low risks, breaking the equilibrium at the null contracts. But the low-risk indifference curve is steeper than the high-risk indifference curve through c_P. Then a firm can offer a profitable contract that attracts low risks but not high risks, breaking the equilibrium at c_P. Therefore, equilibrium does not exist.

Since both high and low risks obtain the null contract, this is a pooling equilibrium. However, the more important characteristic of the equilibrium is that no trade occurs.^13,14

As in the standard model where losses are less than wealth, the existence of an equilibrium depends on the location of the pooled fair odds line. In Fig. 1, the pooled fair odds line P_P lies below the low-risk indifference curve U ⁰ _L . Since the proportion of high risks is large enough, the equilibrium exists. If the proportion of high risks were too small, then the pooled fair odds line would intersect the low-risk indifference curve. Since there cannot be a pooling equilibrium with positive coverage, the Rothschild–Stiglitz equilibrium would fail to exist. Thus, there is either an equilibrium with no trade or there is no equilibrium.

The insurer must pay the full amount of the loss, l. Bankruptcy protects the individual’s wealth up to the limit b at no explicit cost. The individual only needs to insure their wealth above b. Thus, individuals face a type-specific fixed cost of $p_{i} \beta_{i}^{*}$, with an actuarially fair marginal price for coverage above $\beta_{i}^{*}$.¹⁵ If p_H > p*, then the high risks regard the fixed charge as too large, even for full insurance. As a result, they do not buy insurance. The low risks, who face a smaller fixed charge, would be willing to buy insurance if it provided enough coverage. The need to separate the high and low risks limits the amount of coverage that can be offered to the low risks. The low risks regard their fixed charge as too large for the limited coverage they are offered and also do not buy insurance. In the standard model where losses are less than wealth, the fixed charges are zero. This suggests why Hendren’s no trade conditions, Eqs. (3) and (4), apply in the standard model, but do not apply when losses are larger than wealth.

It is interesting to consider how the equilibrium changes as p_H changes (we assume equilibrium exists).¹⁶ Suppose that $p_{H}$ = p*. Then the high-risk fair odds line would be tangent to the indifference curve U ⁰ _H at full insurance. This is the lowest value of $p_{H}$ for which the equilibrium contracts would be the null contracts for both low and high risks. For $p_{H}$ < p*, the high-risk contract is the full insurance contract at the intersection of the high-risk fair odds line and the 45-degree full insurance line. This is illustrated in Fig. 2, where the high-risk fair odds line cuts the individual rationality constraint $U_{H}^{0}$. The high risks obtain full coverage at $c_{H}^{*}$. The high-risk indifference curve U ^* _H is the self-selection constraint, and intersects the low-risk fair odds line at L*. This would be the “usual” Rothschild–Stiglitz contract for the low risks. However, L* is below B, so the low-risk individual rationality constraint is violated. Therefore, the equilibrium contracts would be the full insurance contract for the high risks and the null contract for the low risks. As $p_{H}$ falls, the high-risk contract moves up along the full insurance line. The intersection between the high-risk indifference curve that is the self-selection constraint and the low-risk fair odds line moves up along the low-risk fair odds line. As long as the intersection is below or equal to B, the low risks will not insure. There is a probability, $p_{H}^{\prime }$ < p*, at which the intersection is at B. Then for $p_{H}$ < $p_{H}^{\prime }$, we have the usual Rothschild–Stiglitz equilibrium where the high risks fully insure and the low risks receive partial coverage.

Fig. 2

Rothschild–Stiglitz equilibrium with large losses: partial trade equilibrium

An alternative to the Rothschild–Stiglitz equilibrium is the Wilson (1977) “anticipatory” or E2 equilibrium. A set of contracts is a Wilson E2 equilibrium if “each policy earns non-negative profits and there is no other set of policies that would earn positive profits in the aggregate and non-negative profits individually, after the unprofitable policies in the original set have been withdrawn.” (Wilson 1977, p. 176). The E2 equilibrium is illustrated in Fig. 3, which replicates Fig. 1 except for the location of the pooled fair odds line P_P. If λ$\geq\lambda^{\prime}$, then the E2 equilibrium coincides with the Rothschild–Stiglitz equilibrium. If λ < $\lambda^{\prime}$, then the E2 equilibrium contract is the fairly priced pooling contract that maximizes low-risk expected utility. This is shown as point W in Fig. 3. If λ$\geq\lambda^{\prime}$, then there is no trade in equilibrium, and if λ < $\lambda^{\prime}$, then there is fully active trade in equilibrium. There is active trade in equilibrium if the low risks subsidize the high risks.

Fig. 3

Wilson E2 equilibrium with large losses

4 Wilson–Miyazaki–Spence equilibrium

Two important limitations of the Rothschild–Stiglitz equilibrium are the restriction of competition in single contracts rather than menus of contracts and that equilibrium may fail to exist. This leads us to consider the Wilson–Miyazaki–Spence equilibrium. We show that equilibrium always exists. We show that no trade equilibria can occur when firms compete in menus of contracts and that active trade requires that the low risks subsidize the high risks.

The Wilson–Miyazaki–Spence equilibrium is the solution to the constrained maximization problem:

The first two constraints are the self-selection constraints for the high and low risks, the third constraint is the resource constraint, and the fourth constraint is a lower bound on high risks’ expected utility.¹⁷ The last two constraints are the individual rationality constraints for the high and low risks. The resource constraint is affected by whether or not high risks, low risks, or both decide to buy insurance. The I_i are indicators equal to 1 if the constraint IR_i is slack and equal to 0 if IR_i is binding. Also, we have U_i(c_i) = (1 − p_i)u(w_iG) + p_iu(w_iB) if the individual buys insurance, and U_i($E_{0}$) = (1 − p_i)u(w) + p_iu(b) if the individual does not buy insurance.

Let δ and μ_H denote the Lagrangian multipliers for the constraints U_H and SS_H.

Proposition 3

Assume l > w and 1 > p_H > p* > $\bar{p}$. The WMS contracts satisfy the following conditions:

• A. (i) The resource constraint is binding, and (ii) either both IR constraints are binding or both IR constraints are slack.

• B. If IR_Hand IR_Lare both slack, then (i) SS_His binding, (ii) the high risks fully insure, and (iii)

  $$\frac{{{\text{d}}w_{LL} }}{{{\text{d}}w_{LN} }} = - \frac{{\left( {1 - p_{L} } \right)u^{\prime}\left( {w_{LG} } \right)}}{{p_{L} u^{\prime}\left( {w_{LB} } \right)}} - \frac{{\lambda \left( {1 - p_{H} } \right)u^{\prime}\left( {w_{LG} } \right) + \left( {1 - \lambda } \right)\left( {1 - p_{L} } \right)u^{\prime}\left( {w_{H} } \right)\left( {1 + \delta /\mu_{H} } \right)}}{{\lambda p_{H} u^{\prime}\left( {w_{LB} } \right) + \left( {1 - \lambda } \right)p_{L} u^{\prime}\left( {w_{H} } \right)\left( {1 + \delta /\mu_{H} } \right)}}.$$

  (5)

• C. If both IR_H and IR_L are binding, then (i) both SS_H and SS_L are binding, (ii) both types obtain the null contract, E₀.

• D. The solution is unique.

Proof

The proof is given in the Appendix.

Proposition 3 leaves unanswered the question of when the IR constraints are binding and when they are slack. Define the cross-subsidizing locus (CSL) as the locus of low-risk contracts that satisfy the resource constraint and the self-selection constraint as equalities for a high-risk full insurance contract. Let $c_{P}^{*}$ be the fairly priced pooled full insurance contract while $H^{*}$ is the contract at the intersection of the high-risk fair odds line and the full insurance line and $L^{*}$ is the contract at the intersection of the high-risk indifference curve U_H($H^{*}$) and the low-risk fair odds line. The CSL connects $c_{P}^{*}$ and $L^{*}$; the slope of the CSL is given by the right-hand side of (5). This is illustrated in Fig. 4 where the CSL is shown as the dashed line.¹⁸ Let $\lambda^{\prime\prime}$ be the largest value of λ such that the CSL is tangent to the low-risk IR constraint, U ⁰ _L . Since the CSL lies above the pooled fair odds line, $\lambda^{\prime\prime}$ > $\lambda^{\prime}$. The CSL in Fig. 4 is drawn so that λ < $\lambda^{\prime\prime}$, and the CSL crosses U ⁰ _L . The low-risk indifference curve through $\tilde{c}_{L}$ is just tangent to the CSL. The contracts $\tilde{c}_{H}$ and $\tilde{c}_{L}$ satisfy SS_H, U_H($\tilde{c}_{H}$) = U_H($\tilde{c}_{L}$). If λ < $\lambda^{\prime\prime}$, the WMS equilibrium is at the contracts ($\tilde{c}_{H}$, $\tilde{c}_{L}$) where the low-risk indifference curve is tangent to the CSL and the self-selection constraint SS_H is binding. At this equilibrium, the low risks subsidize the high risks. If λ$\ge$$\lambda^{\prime\prime}$ then IR_L is binding, which implies IR_H is binding, and the WMS equilibrium is at the null contracts.

Fig. 4

WMS equilibrium with large losses

Corollary

Assume l > w and 1 > p_H > p* > $\bar{p}$. (a) If λ$\ge$$\lambda^{\prime\prime}$, the WMS equilibrium is at the null contracts. (b) If λ < $\lambda^{\prime\prime}$, then the WMS equilibrium is at the cross-subsidized contracts ($\tilde{c}_{H}$, $\tilde{c}_{L}$).

In order for there to be active trade in the market, the low risks must subsidize the high risks.

The effect of the level of bankruptcy protection on the market equilibrium is an important issue. First, observe that the location of the candidate equilibria—the RS contracts (H* and L* in Fig. 1), the cross-subsidized Wilson E2 contracts (W in Fig. 3), and the WMS cross-subsidized contracts [($\tilde{c}_{H}$, $\tilde{c}_{L}$) in Fig. 4]—do not depend on the level of bankruptcy protection. The level of bankruptcy protection determines the location of the individual rationality constraints, which must be satisfied in order for the candidate contracts to be an equilibrium.

Suppose that bankruptcy protection is set at b and there is no trade in equilibrium. Then there will be no trade at higher levels of bankruptcy protection, but there may be trade at lower levels of bankruptcy protection. Conversely, if there is trade in equilibrium then there will be trade at lower levels of bankruptcy protection. But the level of bankruptcy protection can be raised high enough that there will not be trade. For example, consider the WMS cross-subsidized equilibrium ($\tilde{c}_{H}$, $\tilde{c}_{L}$) in Fig. 4. This is an equilibrium since the CLS crosses the low risk’s IR constraint. Lowering bankruptcy protection shifts the low risk’s IR constraint downward, so ($\tilde{c}_{H}$, $\tilde{c}_{L}$) remains the equilibrium. Increasing bankruptcy protection shifts the low risks’ IR constraint upward. A sufficiently large increase in bankruptcy protection may leave the CSL below the higher low-risk IR constraint, resulting in an equilibrium with no trade.

5 Equilibria with differential costs of bankruptcy and default

If bankruptcy protection is available to a given individual in a particular jurisdiction, it is also available to any other individual in that jurisdiction with an identical financial profile. Yet, some individuals choose to declare bankruptcy while others do not and at least part of that decision involves consideration of the psychic costs of bankruptcy and default. Individuals differ in terms of their sense of personal responsibility, fear of being stigmatized, and the impact that declaring bankruptcy would have on their reputation and sense of self-worth. In the previous sections, we assumed the psychic costs of bankruptcy and default were zero, but in this section a fraction $\theta$ of individuals incurs a psychic cost of defaulting on their financial responsibilities and of declaring bankruptcy.

Let those without bankruptcy and default costs be denoted type 0 individuals and those with bankruptcy and default costs be denoted type 1 individuals. There are four types altogether—type 0 high risks (type H0), type 0 low risks (type L0), type 1 high risks (type H1), and type 1 low risks (type L1). Whereas the type 0 individuals have utility function $u\left( {w_{ij} } \right)$, i = H or L and j = G or B, as in the prior sections, where $w_{ij}$ equals wealth, the type 1 individuals have utility function $u_{1} \left( {w_{ij} ;\, D_{ij} } \right)$ where $D_{ij}$ is defaulted financial obligations. Type 1 individuals’ utility is increasing in wealth and decreasing in defaulted financial obligations and, in particular, it is assumed that $u_{1} \left( {w_{ij} ;\,D_{ij} } \right) = u\left( {w_{ij} - D_{ij} } \right).$ In addition, a psychic cost of declaring bankruptcy of $\normalsize \kappa$ > 0 is experienced by type 1s, giving them utility in the case of bankruptcy of $u\left( {w_{ij} - D_{ij} } \right)$ − $\kappa$ so that they would prefer to pay the loss up to the full extent of their wealth rather than declare bankruptcy.¹⁹ We assume that the psychic costs of default and bankruptcy are unobservable. The psychic cost of bankruptcy introduces state-dependence for the fraction $\theta$ of individuals. Whether an individual is type 0 or type 1 is private information.

For type 1 individuals, the standard Rothschild–Stiglitz and Wilson–Miyazaki–Spence participation constraints apply. In all other respects, they are identical to the group without bankruptcy costs analyzed above, with proportion λ being high-risk types and proportion 1 − λ being low-risk types. If they were alone in the market, then under the equilibrium concept considered in Sect. 3, the equilibrium outcome would be the standard Rothschild–Stiglitz outcome ($H^{*} , L^{*} )$ as shown in Fig. 1 (or there would be no equilibrium if the proportion of high risks was too small). Under the equilibrium concept considered in Sect. 4, the equilibrium outcome would be the standard WMS cross-subsidizing outcome ($\tilde{c}_{H}$, $\tilde{c}_{L}$) as in Fig. 4. In neither case, would there be null contracts in equilibrium.

We next investigate how including both bankruptcy cost groups in the market alters the equilibrium outcome for each group, using a graphical analysis. It is important to keep in mind that the type 1 individuals are identical to their type 0 counterparts for this analysis except for their individual rationality constraints. Let $\lambda^{*}$ be the critical λ associated with the standard RS equilibrium. Under the Rothschild–Stiglitz equilibrium concept, when all four types are present and λ$\geq\lambda^{*}$, the equilibrium contracts are $H^{*}$ and $L^{*}$ for type 1 high risks and low risks, respectively, and the null contracts for type 0 individuals. In Fig. 1, the type 1 individuals do not have individual rationality constraints through E₀, but rather through E. E₀ is not obtainable without insurance because of their bankruptcy costs and is not obtainable with insurance because it would be unprofitable for insurers. When type 1 individuals are offered the standard Rothschild–Stiglitz equilibrium contracts ($H^{*} , L^{*} )$, they will self-select into the appropriate contracts and no contracts can be offered by insurers to attract either the high or low risks and make non-negative profits as in the standard Rothschild–Stiglitz problem. The type 0 individuals prefer not to buy insurance for the same reasons described in Sect. 2. Insurers cannot deviate and offer contracts to the type 0s and make non-negative profits. But if λ <$\lambda^{*}$, ($E_{0} , E_{0} ,H^{*} , L^{*} )$ cannot be sustained as an equilibrium because a pooling contract can attract type L1 policyholders, make non-negative profits, and break the equilibrium. But a pooling contract cannot be an equilibrium since low-risk indifference curves are steeper than those of high risks and an insurer can offer a contract which will be attractive to low risks, but not high risks, and will be profitable.

Therefore, we have

Proposition 4

Let l > w. Assume that there are four types H0, L0, H1, L1 and that 1 > p_H > p* > $\bar{p}$. (a) If λ$\geq\lambda$*, then the unique Rothschild–Stiglitz equilibrium contracts are (E₀, E₀, $H^{*} , L^{*} )$. (b) If λ < $\lambda$*, then equilibrium does not exist.

Under the Wilson–Miyazaki–Spence equilibrium concept, the equilibrium with four types present depends on the proportion of high risks, λ, and the proportion of type 1 individuals, $\theta$. If λ < $\lambda^{\prime\prime}$, then the WMS equilibrium will be ($\tilde{c}_{H}$, $\tilde{c}_{L} , \tilde{c}_{H}$, $\tilde{c}_{L}$) as depicted in Fig. 4. The type 0 individuals have the same indifference curves as their type 1 counterparts to the northeast of the type 0 individual rationality constraints. In this case, the standard WMS equilibrium is obtained because the proportion of high risks, λ, is the same when all four types are in the market as when only type 0s are in the market.

If λ$\ge$$\lambda^{\prime\prime}$, then the WMS equilibrium has a different character. In this case, there are two cross-subsidizing loci to consider as shown in Fig. 5. CSL, which connects $c_{P}^{*}$ and $L^{*}$, is equivalent to CSL in Fig. 4 and has a slope given by the right-hand side of (5). This is based on a proportion of high risks equal to λ. When λ$\ge$$\lambda^{\prime\prime}$, the individual rationality constraint for type 0 low risks is tangent to or to the northeast of CSL and type 0 low risks prefer not to purchase insurance contracts anywhere along this locus. The equilibrium will have either three types participating (H0, H1, and L1) or two types participating (H1 and L1). The fair pooled price line when H0, H1, and L1 are participating in the market is denoted P₃ in Fig. 5 and is to the southwest of P_p since it represents a higher proportion of high risks denoted $\lambda_{3} = \lambda /(\lambda + \left( {1 - \lambda )\theta } \right)$. The cross-subsidizing locus for these three types, CSL₃, is the curve connecting $c_{P}^{3}$ and $L^{*}$ and is to the southwest of CSL. The feasible portions of CSL and CSL₃ are depicted with dashes while the dotted segments are not feasible due to the individual rationality constraints. In particular, the individual rationality constraint for H0 types determines which contracts are feasible. Below U ⁰ _H , the H0 types will not participate in the market and the two-type CSL locus to the southeast of point M is feasible. Above U ⁰ _H , the H0 types will participate in the market so the two-type CSL locus will be unprofitable, but the three-type CSL₃ locus to the northwest of point N is feasible.

Fig. 5

WMS feasible contracts with large losses and two bankruptcy cost types

The value of $\lambda_{3}$ is critical to whether the WMS equilibrium involves two or three active types when λ$\ge$$\lambda^{\prime\prime}$. Let $\lambda_{3}^{*}$ be the value of $\lambda_{3}$ at which the low-risk indifference curve through point M is just tangent to CSL₃. When $\lambda_{3} > \lambda_{3}^{*}$, as in Fig. 5, there are points along the feasible portion of CSL that leave low risks better off than any point along CSL₃. In this case, to maximize low-risk expected utility, H0s will be left out of the market along with L0s. Let the WMS equilibrium in this case be denoted (E₀, E₀, $\tilde{c}_{H}^{2}$, $\tilde{c}_{L}^{2}$) since only two of the four types are active in equilibrium. If the low-risk indifference curve through point M is tangent to CSL or flatter (as in Fig. 5), then $\tilde{c}_{L}^{2}$ = M and $\tilde{c}_{H}^{2}$ is the corresponding incentive compatible high-risk contract. If the low-risk indifference curve though point M is steeper than tangent, then the type 1 individuals receive the traditional WMS equilibrium contracts for types H1 and L1 which would occur somewhere along the ML* segment. Again, types H0 and L0 obtain null contracts.

When λ$\ge$$\lambda^{\prime\prime}$ and $\lambda_{3} < \lambda_{3}^{*}$, as in Fig. 6, then there is a point of tangency between a low-risk indifference curve and the feasible portion of CSL₃, and this indifference curve is to the northeast of the feasible portion of CSL. Therefore, the expected utility maximizing feasible low-risk contract is along CSL₃ rather than CSL, and three types, H0, H1, and L1 will be active in the market in equilibrium. The equilibrium set of contracts is ($\tilde{c}_{H}^{3}$, E₀, $\tilde{c}_{H}^{3}$, $\tilde{c}_{L}^{3}$), where ($\tilde{c}_{H}^{3}$, $\tilde{c}_{L}^{3}$) is equivalent to the traditional WMS cross-subsidizing equilibrium contracts for a proportion of high risks equal to $\lambda_{3}$. Only the type 0 low risks will obtain the null contract.

Fig. 6

WMS equilibrium with large losses and three types (H0, H1, and L1) active in the market

These results for the WMS equilibrium concept can be summarized as

Proposition 5

Letl > w. that 1Assume that there are four types H0, L0, H1, L1 and > p_H > p* > $\bar{p}$.

• A. Ifλ < $\lambda^{\prime\prime}$, then the WMS equilibrium is at the cross-subsidized contracts ($\tilde{c}_{H}$, $\tilde{c}_{L} , \tilde{c}_{H}$, $\tilde{c}_{L}$).

• B. Ifλ$\ge$$\lambda^{\prime\prime}$ and$\lambda_{3} \ge \lambda_{3}^{*}$, then the WMS equilibrium is (E₀, E₀, $\tilde{c}_{H}^{2}$, $\tilde{c}_{L}^{2}$) where$\tilde{c}_{L}^{2}$is along the ML* segment of CSL and$\tilde{c}_{H}^{2}$is the incentive compatible cross-subsidizing contract for a proportion of high risks equal toλ. Type 0s obtain the null contract. The contract pair for type 1s, $(\tilde{c}_{H}^{2}$, $\tilde{c}_{L}^{2}$), is either the traditional WMS equilibrium contract for the two type case or, if the low-risk indifference curve through M is flatter than tangent,$\tilde{c}_{L}^{2}$ = M and$\tilde{c}_{H}^{2}$is the corresponding cross-subsidizing contract.

• C. Ifλ$\ge$$\lambda^{\prime\prime}$ and$\lambda_{3} < \lambda_{3}^{*}$, then the WMS equilibrium is ($\tilde{c}_{H}^{3}$, E₀, $\tilde{c}_{H}^{3}$, $\tilde{c}_{L}^{3}$), where$\tilde{c}_{L}^{3}$ is the point along CSL₃ that is tangent to the L1 indifference curve and$\tilde{c}_{H}^{3}$ is the incentive compatible cross-subsidizing contract when the proportion of high risks is$\lambda_{3}$. Only type 0 low risks obtain the null contract.

Compared to the case with only type 0 individuals described in Sect. 4, the inclusion of type 1 individuals in the market has the potential to induce the high-risk type 0s to purchase insurance when they otherwise would not have. If λ < $\lambda^{\prime\prime}$, the traditional WMS cross-subsidizing contracts are obtained by both type 0s and type 1s. But when λ$\ge$$\lambda^{\prime\prime}$, the proportion of individuals in the market who incur psychic costs of default and bankruptcy is a determining factor in whether H0 individuals obtain coverage or not, all else equal. Note that $\lambda_{3}$ is inversely proportional to $\theta$. When the proportion of type 1s, $\theta$, is relatively low, then $\lambda_{3} \ge \lambda_{3}^{*}$ and H0 and L0 individuals both obtain null contracts, just as they would have without the type 1s in the market. But when the proportion of type 1s is sufficiently large such that $\lambda_{3} < \lambda_{3}^{*}$, then H0s purchase insurance. In this case, L1s subsidize both H1 and H0 policyholders, something that would be too burdensome if the type 0s were more prominent in the market, all else equal.

Therefore, with a fixed number of potential policyholders, where a proportion λ is high risk and λ$\ge$$\lambda^{\prime\prime},$ no insurance is purchased when $\theta = 0$, and as $\theta$ begins to increase, the proportion buying insurance equals $\theta$. When $\theta$ reaches the critical point where $\lambda_{3} < \lambda_{3}^{*}$, then the proportion of individuals becoming insured is greater than $\theta$. This implies that if policymakers seek to reduce the number of uncompensated third-party claimants, they can have a more than proportional impact by increasing the proportion of individuals who experience psychic costs of default and bankruptcy beyond the level at which $\lambda_{3} = \lambda_{3}^{*}$.

6 Conclusion

We show that, if losses are larger than wealth, there is a threshold where individuals who have the option of declaring bankruptcy will not insure if the loss probability is above the threshold. In an insurance market with adverse selection, if the high risks’ loss probability is above the threshold, then no trade occurs at the Rothschild–Stiglitz equilibrium. We extend the analysis to the Wilson–Miyazaki–Spence equilibrium. We show that, if the proportion of high risks is large, then no trade occurs in equilibrium. If the proportion of high risks is small enough, then there is an equilibrium with active trade in insurance in which the high risks are subsidized. Hendren’s no trade condition does not apply when losses are larger than wealth. However, Hendren’s broader point, that the existence of active trade equilibria in markets with adverse selection is fragile, remains valid.

If a subset of individuals with sufficiently high bankruptcy costs is included in the market, then under the Rothschild–Stiglitz equilibrium concept, those with no bankruptcy costs obtain null contracts while the others obtain the standard R–S equilibrium contracts (unless the proportion of high risks is low enough that no equilibrium exists). Under the Wilson–Miyazaki–Spence equilibrium concept, the nature of the equilibrium depends on the proportion of high risks as well as the proportion of individuals with bankruptcy costs. Three possibilities exist, (1) the standard cross-subsidizing WMS contracts for high and low risk are obtained by both bankruptcy cost groups, (2) both high and low risks without bankruptcy costs obtain null contracts and those with bankruptcy costs obtain contracts with the low risks subsidizing high risks, or (3) only low-risk individuals without bankruptcy costs obtain the null contract while both sets of high risks receive an identical full insurance contract subsidized by the low risks with bankruptcy costs.

Our results have implications for public policy and the regulation of insurance markets. Our results suggest that insurance markets may not function well for low-income individuals. The no trade equilibrium is second best (Proposition 3) implying intervention in the market will not lead to welfare improvements. But this considers only the welfare of insurers and (potential) insureds. It does not consider the uncompensated losses born by, say, accident victims or health care providers. From a broader social welfare perspective, it may be desirable to implement policies that lead to an active insurance market.

Assuming, it is socially desirable to have active trade in the insurance market, there are two main policy alternatives. The first is to reduce the level of wealth protected by bankruptcy. A general reduction in bankruptcy protection will have repercussions beyond the insurance market. A possibility would be to eliminate some forms of debt, such as liability judgements or certain medical expenses, from discharge in bankruptcy. Reducing bankruptcy protection may offer only a partial solution since it may not be sufficient to induce high-risk individuals to buy insurance.

The second alternative is to subsidize insurance purchases. When losses are larger than wealth, individuals face a type-specific fixed charge equal to the portion of the loss they would not have to pay scaled by their risk of loss, p_i$\beta_{i}^{*}$. A subsidy to eliminate this fixed charge would lead to active trade in insurance. The subsidies could be implemented without the regulator having knowledge of individuals’ risk types. Analogous to Crocker and Snow (1985), policies with a premium to coverage ratio (α/(α + β) in our notation) above the average loss probability would receive a subsidy equal to the high-risk fixed charge while polices with a premium to coverage ratio below the average loss probability would receive a subsidy equal to the low-risk fixed charge. In terms of Fig. 1, the subsidy shifts E up to E₀. This requires tax revenue from other sources in order to relax the resource constraint and induce individuals to buy insurance. The expected cost is the same, so the subsidy shifts the cost from those who would bear the uncompensated losses to taxpayers. Whether this is desirable or not is a social value judgement about which group will bear the cost of unsubsidized losses.

Appendix: Proof of Proposition 3

The Lagrangian for the maximization problem is

$$\begin{aligned} {\mathcal{L}} =& U_{L} \left( {c_{L} } \right) \, + \mu_{H} \left[ {U_{H} \left( {c_{H} } \right) \, {-}U_{H} \left( {c_{L} } \right)} \right] \, + \mu_{L} \left[ {U_{L} \left( {c_{L} } \right) \, {-}U_{L} \left( {c_{H} } \right)} \right] \\ & + \gamma \{ \lambda \left[ {w{-}p_{H} l{-} \, \left( {1 \, {-}p_{H} } \right)w_{HG} {-}p_{H} w_{HB} } \right]I_{H} \\ & + \left( {1 \, {-}\lambda } \right)\left[ {w{-}p_{L} l{-} \, \left( {1 \, {-}p_{L} } \right)w_{LG} } \right) \, - p_{L} w_{LB} )]I_{L} \} \\ & + \delta \left[ {U_{H} \left( {c_{H} } \right) \, {-}U_{H} \left( {c_{H}^{*} } \right)} \right], \\ \end{aligned}$$

where μ_H, μ_L, γ, and δ are the Lagrange multipliers. The first-order conditions are

$$\partial {\mathcal{L}}/\partial w_{LG} = \, \left( {1 \, + \mu_{L} } \right)\partial U_{L} \left( {c_{L} } \right)/\partial w_{LG} - \mu_{H} \partial U_{H} \left( {c_{L} } \right)/\partial w_{LG} {-}\gamma \left( {1 \, {-}\lambda } \right)\left( {1 \, {-}p_{L} } \right) \, = \, 0$$

(6)

$$\partial {\mathcal{L}}/\partial w_{LB} = \, \left( {1 \, + \mu_{L} } \right)\partial U_{L} \left( {c_{L} } \right)/\partial w_{LB} - \mu_{H} \partial U_{H} \left( {c_{L} } \right)/\partial w_{LB} {-}\gamma \left( {1 \, {-}\lambda } \right)p_{L} = \, 0$$

(7)

$$\partial {\mathcal{L}}/\partial w_{HG} = \, \left( {\delta + \mu_{H} } \right)\partial U_{H} \left( {c_{H} } \right)/\partial w_{HG} - \mu_{L} \partial U_{L} \left( {c_{H} } \right)/\partial {\text{w}}_{HG} {-}\gamma \lambda \left( { 1 { }{-}p_{H} } \right) \, = \, 0$$

(8)

$$\partial {\mathcal{L}}/\partial w_{HB} = \, \left( {\delta + \mu_{H} } \right)\partial U_{H} \left( {c_{H} } \right)/\partial w_{HB} - \mu_{L} \partial U_{L} \left( {c_{H} } \right)/\partial w_{HB} {-}\gamma \lambda p_{L} ) \, = \, 0,$$

(9)

along with the complementary slackness conditions.

• A. (i) The resource constraint is binding: If at least one type buys insurance, then I_i =1 for some i, and non-satiation implies the resource constraint is binding. If neither type buys insurance, then I_H = I_L = 0 and the resource constraint becomes 0 = 0. (ii) Either both IR constraints are binding or both IR constraints are slack: We need to show (a) IR_H binding implies IR_L binding, (b) IR_L binding implies IR_H binding, (c) IR_H slack implies IR_L slack, and (d) IR_L slack implies IR_H slack. Observe that (a) and (d) are equivalent and (b) and (c) are equivalent. We first prove (b). Assume IR_L is binding. Suppose, by way of contradiction, that IR_H is slack, U_H(c_H) > U_H($E_{0}$). Since the Hs purchase a policy with positive coverage, either p_H < p* or the Hs are subsidized. The first possibility is ruled out by hypothesis. Since the Ls do not purchase insurance, the Hs cannot be subsidized without violating the resource constraint. We now prove (d), that if IR_L is slack then IR_H is slack. If IR_L is slack, then U_L(c_L) > U_L($E_{0} )$. Assume, by way of contradiction, the IR_H is binding, U_H(c_H) = U_H($E_{0}$). Since c_L must break even, it lies on the type L fair odds line above (w, b). But this implies U_H(c_L) > U_H($E_{0}$), which is the desired contradiction.

• B. If both IR constraints are slack, then (i) The SS_H constraint must be binding: Let (c_H, c_L) be a proposed solution to the maximization problem such that the resource constraint is binding. Suppose that SS_H is slack, U_H(c_H) > U_H(c_L). Let c_L = (w_LG, w_LB) and c_L′ = (w_LG − ε₁, w_LB + ε₂), where ε₂ = (1 − p_L)/p_L]ε₁, ε₁ > 0. If ε₁ is small enough then SS_H is still slack. But c_L′ is a mean preserving contraction relative to c_L, so U_L(c_L′) > U_L(c_L). So (c_H, c_L) cannot be a solution to the maximization problem. (ii) The high risks must be fully insured: If both self-selection constraints are binding, the equilibrium must be at a pooled policy c_H = c_L. Suppose the pooled policy offers less than full insurance. Then both types are better off at c_L′, so (c_H, c_L) cannot be a solution to the maximization problem. Any pooled equilibrium must be at the population pooled policy c_P. Now suppose SS_L is slack and SS_H is binding, U_H(c_H) = U_H(c_L), and c_H offers less than full insurance. Let c_H′ be a mean preserving contraction from c_H. Then there is a c_L′ such that SS_H is binding, U_H(c_H′) = U_H(c_L′). Both types are better off at (c_H′, c_L′), so (c_H, c_L) cannot be a solution to the maximization problem.

  (iii) Equation (5) in the text gives the slope of the CSL: If both self-selection constraints are slack, then the expected utility of both types can be increased. So at least one self-selection constraint must be binding. From (8) and (9), we have

  $$\frac{{\left( {1 - p_{H} } \right)u^{\prime}(w_{HG)} }}{{p_{H} u^{\prime}\left( {w_{HB} } \right)}} = \frac{{\mu_{L} \left( {1 - p_{L} } \right)u^{\prime}\left( {w_{HG} } \right) + \gamma \lambda \left( {1 - p_{H} } \right)}}{{\mu_{L} p_{L} u^{\prime}\left( {w_{HB} } \right) + \gamma \lambda p_{H} }}.$$

  (10)

  Evaluated at any full insurance contract (w_H, w_H), this becomes

  $$\frac{{1 - p_{H} }}{{p_{H} }} = \frac{{\mu_{L} \left( {1 - p_{L} } \right)u^{\prime}\left( {w_{H} } \right) + \gamma \lambda \left( {1 - p_{H} } \right)}}{{\mu_{L} p_{L} u^{\prime}\left( {w_{H} } \right) + \gamma \lambda p_{H} }}.$$

  (11)

  This can hold as an equality if and only if μ_L = 0. If both self-selection constraints are binding, then both types must be at the pooled contract c_P. Then high-risk utility is U_H(c_P). From (6) and (7), we have

  $$\frac{{\left( {1 - p_{L} } \right)u^{\prime}(w_{LG)} }}{{p_{L} u^{\prime}\left( {w_{LB} } \right)}} = \frac{{\mu_{H} \left( {1 - p_{H} } \right)u^{\prime}\left( {w_{LG} } \right) + \gamma \left( {1 - \lambda } \right)\left( {1 - p_{L} } \right)}}{{\mu_{H} p_{H} u^{\prime}\left( {w_{LB} } \right) + \gamma \left( {1 - \lambda } \right)p_{L} }}.$$

  (12)

  Evaluated at c_P, this becomes

  $$\frac{{1 - p_{L} }}{{p_{L} }} = \frac{{\mu_{H} \left( {1 - p_{H} } \right)u^{\prime}\left( {w_{H} } \right) + \gamma \left( {1 - \lambda } \right)\left( {1 - p_{L} } \right)}}{{\mu_{H} p_{H} u^{\prime}\left( {w_{H} } \right) + \gamma \left( {1 - \lambda } \right)p_{L} }}.$$

  (13)

  This holds as an equality if and only if μ_H = 0. Then (11) and (13) imply that μ_H = μ_L = 0 at c_P. If U_H(c_H) < U_H(c_P), then we have μ_L = 0, μ_H > 0, so that the low-risk self-selection constraint is slack and the high-risk self-selection constraint is binding.

  Using (8) to eliminate the Lagrangian multiplier γ in (12) yields

  $$\frac{{\left( {1 - p_{L} } \right)u'\left( {w_{LG} } \right)}}{{p_{L} u'\left( {w_{LB} } \right)}} = \frac{{\mu_{H} \left( {1 - p_{H} } \right)u^{\prime}\left( {w_{LG} } \right) + [\lambda \left( {1 - p_{H} } \right]^{ - 1} \left( {\mu_{H} + \delta } \right)\left( {1 - \lambda } \right)\left( {1 - p_{L} } \right)u'\left( {w_{H} } \right)}}{{\mu_{H} p_{H} u^{\prime}\left( {w_{LB} } \right) + [\lambda \left( {1 - p_{H} } \right]^{ - 1} \left( {\mu_{H} + \delta } \right)\left( {1 - \lambda } \right)p_{L} u'\left( {w_{H} } \right)}}.$$

  (14)

Rearranging (14) yields (5) in the text.

• C. If both IR constraints are binding, then (i) Both SS constraints are binding and (ii) both types obtain the null contract: This is Proposition 2. Observe that the IR and SS constraints coincide, so the SS constraints are binding and the null contract is unique.

• D. The solution is unique: Suppose that there are two distinct solutions to the constrained maximization problem, $(\tilde{c}_{H} ,\tilde{c}_{L}$) and $\left( {\hat{c}_{H} , \hat{c}_{L} } \right).$ Then we have U_L($\tilde{c}_{L}$) = U_L($\tilde{c}_{L}$). Since the CSL is downward sloping, one of the low-risk contracts, say,$\tilde{c}_{L} ,$ must have more coverage than the other low-risk contract. But then the tax on the low risks must be higher, and, since net transfers must balance, the subsidy to the high risks must also be higher. This implies $\tilde{w}_{H}$ > $\hat{w}_{H}$ making the high risks better off. Then the solution ($\tilde{c}_{H} ,\tilde{c}_{L}$) Pareto dominates $\left( {\hat{c}_{H} , \hat{c}_{L} } \right)$. Therefore, $(\tilde{c}_{H} ,\tilde{c}_{L}$) is the unique solution.