Analysis of some dynamical systems by combination of two different methods

Abstract

In this study, we introduce a novel iterative method combined with the Elzaki transformation to address a system of partial differential equations involving the Caputo derivative. The Elzaki transformation, known for its effectiveness in solving differential equations, is incorporated into the proposed iterative approach to enhance its efficiency. The system of partial differential equations under consideration is characterized by the presence of Caputo derivatives, which capture fractional order dynamics. The developed method aims to provide accurate and efficient solutions to this complex mathematical system, contributing to the broader understanding of fractional calculus applications in the context of partial differential equations. Through numerical experiments and comparisons, we demonstrate the efficacy of the proposed Elzaki-transform-based iterative method in handling the intricate dynamics inherent in the given system. The study not only showcases the versatility of the Elzaki transformation but also highlights the potential of the developed iterative technique for addressing similar problems in various scientific and engineering domains.

Introduction

Fractional calculus, deeply rooted in applied mathematics, has been a cornerstone in achieving more accurate modeling results when compared to traditional derivatives. Its significance extends across a multitude of disciplines, impacting fields like electronics, visco-elasticity damping, signal processing, transport systems, genetic algorithms, communication, biology, robotics, physics, chemistry, and finance. The ongoing research in this area, as reflected in the works of numerous scholars^1,2,3,4,5,6, underscores the continual exploration and discoveries within fractional calculus. In particular, the study of fractional-order partial differential equations (PDEs) has emerged as a focal point, attracting keen interest from researchers. This attention is justified given the diverse and novel applications fractional calculus offers. Researchers have responded by developing various methods to solve fractional linear and nonlinear PDEs, with innovative techniques like the local meshless approach finding application in addressing specific challenges such as the time-fractional and anomalous mobile–immobile solution transport mechanism^{7,8,9,10,11,12}. These advancements collectively contribute to the evolving landscape of fractional calculus applications and methodologies.

Fractional PDEs have attracted the attention of numerous academics in recent decades due to its applications in various fields of applied sciences. Fractional derivative (FD) has a higher level of adaptability in the model and generates wonderful tools for depicting the historical context of the variable and genetic traits of each dynamic framework. There has been extensive research towards the advancement of scientific and mathematical arrangements for all fractional PDEs. Burgers equation (BE) is one of the most important and fundamental nonlinear PDEs that includes diffusive and nonlinear proliferation affects¹³. BE was developed as a model of turbulent fluid movement, which is a complex field of study. For higher derivatives, Naiver-Stokes and BEs are comparable. The FBEs can depict the Unidirectional generating cycle of pitifully nonlinear sound waves through a gas-filled line. FD is the result of the memory-storage impact of the divider grating. By means of the boundary layer¹⁴. It is also used to exhibit in bubbly fluids and shallow water wave, in addition to a number of other fractional calculus applications^15,16.

In 2006, D.G. Jafari proposed a new iterative technique for solving nonlinear mathematics problems^17,18. Jafari et al. initially implemented Laplace transformation in the iterative method. In order to estimate the approximative effects of the FPDE scheme, they developed a modified version of the iterative Laplace transform algorithm¹⁹. ILTM to solve linear and nonlinear PDEs including fractional-order Fokker–Planck equations²⁰, time-fractional Zakharov–Kuznetsov equation²¹, and fractional-order Fokker–Planck equations²².

Preliminaries

Definition

We describe the fractional Abel-Riemann operator $D^{\varpi }$ of order $\varpi$ by^23,24,25:

$$\begin{aligned} D^{\varpi }\nu (\zeta )={\left\{ \begin{array}{ll}\frac{d^\jmath }{d\zeta ^\jmath }\nu {(\zeta )}, \ \ \varpi = \jmath ,\\ \frac{1}{\Gamma (\jmath -\varpi )}\frac{d}{d\zeta ^\jmath }\int _0^\zeta \frac{\nu (\zeta )}{(\zeta -\psi )^{\varpi -\jmath +1}}d\psi , \ \ \jmath -1< \varpi < \jmath , \end{array}\right. } \end{aligned}$$

where $\jmath \in Z^+$, $\varpi \in R^+$ and

$$\begin{aligned} D^{-\varpi }\nu (\zeta )=\frac{1}{\Gamma (\varpi )}\int _0^{\zeta }(\zeta -\psi )^{\varpi -1}\nu (\psi )d\psi , \ \ 0<\varpi \le 1. \end{aligned}$$

Definition

The Abel-Riemann fractional integral operator $J^{\psi }$ is given as^23,24,25

$$\begin{aligned} J^{\varpi }\nu (\zeta )=\frac{1}{\Gamma (\varpi )}\int _0^\zeta (\zeta -\psi )^{\varpi -1}\nu (\zeta )d\zeta , \ \ \zeta>0, \ \ \varpi >0. \end{aligned}$$

The operator of basic properties:

$$\begin{aligned}{} & {} J^{\varpi }\zeta ^\jmath =\frac{\Gamma (\jmath +1)}{\Gamma (\jmath +\varpi +1)}\zeta ^{\jmath +\psi },\\{} & {} D^{\varpi }\zeta ^\jmath =\frac{\Gamma (\jmath +1)}{\Gamma (\jmath -\varpi +1)}\zeta ^{\jmath -\psi }. \end{aligned}$$

Definition

We describe the Caputo fractional operator $D^{\varpi }$ of $\varpi$ by^23,24,25:

$$\begin{aligned} {}^CD^{\varpi }\nu (\zeta )={\left\{ \begin{array}{ll}\frac{1}{\Gamma (\jmath -\varpi )}\int _0^\zeta \frac{\nu ^\jmath (\psi )}{(\zeta -\psi )^{\varpi -\jmath +1}}d\psi ,\ \ \jmath -1<\varpi <\jmath ,\\ \frac{d^\jmath }{d\zeta ^\jmath }\nu (\zeta ), \ \ \jmath =\varpi . \end{array}\right. } \end{aligned}$$

(1)

Definition

$$\begin{aligned} J^\varpi _\zeta D^\varpi _\zeta {g}(\zeta )= & {} g(\zeta )-\sum _{k=0}^{m}g^{k}(0^{+})\frac{\zeta ^k}{k!},\ \quad for \ \ \zeta >0,\quad and \quad \jmath -1 < \varpi \le \jmath , \quad \jmath \in N.\nonumber \\ D^\varpi _{\zeta } J^\varpi _{\zeta }{g}(\zeta )= & {} g(\zeta ). \end{aligned}$$

(2)

Definition

The Elzaki fractional Caputo operator is defined as:

$$\begin{aligned} \texttt{E}[D^{\varpi }_\zeta g(\zeta )]=s^{-{\varpi }}{} \texttt{E}[g(\zeta )]-\sum _{k=0}^{\jmath -1}s^{2-{\varpi }+k}g^{(k)}(0), \ \ where \ \ \jmath -1<{\varpi } <\jmath . \end{aligned}$$

The general discussion of proposed method

Think about how the fractional PDEs are defined:

$$\begin{aligned} D_{\Im }^{\varpi } {{\mu }}({\zeta },{\Im })+ M {{\mu }}({\zeta },{\Im })+ N {{\mu }}({\zeta },{\Im })= h (\zeta ,\Im ), \ \ \ \ \ \jmath \in N, \ \ \jmath -1<\varpi \le \jmath , \end{aligned}$$

(3)

where M linear and N non-linear terms.

with the initial condition

$$\begin{aligned} {\mu }^{k}(\zeta ,0)=g_{k}({\zeta }), \ \ \ \ \ \ k=0,1,2,\ldots ,\jmath -1, \end{aligned}$$

(4)

Apply the Elzaki transformation of equation (3), we have

$$\begin{aligned}{} & {} {E}[D_{\Im }^{\varpi }{{\mu }}({\zeta },{\Im })]+{E}[M {{\mu }}({\zeta },{\Im })+ N {{\mu }}({\zeta },{\Im })]={E}[h(\zeta ,\Im )]. \end{aligned}$$

(5)

$$\begin{aligned}{} & {} {E}[{{\mu }}({\zeta },{\Im })]=\sum _{k=0}^{\jmath }s^{2-\varpi +k}u^{(k)}(\zeta ,0)+{s^{\varpi }}{E}[h(\zeta ,\Im )]-{s^{\varpi }} {E}[M {{\mu }}({\zeta },{\Im })+N {{\mu }}({\zeta },{\Im })], \end{aligned}$$

(6)

using the inverse Elzaki transformation Eq. (6), we get

$$\begin{aligned} {{\mu }}({\zeta },{\Im })={E}^{-1}\left[ \left\{ \sum _{k=0}^{\jmath }s^{2-\varpi +k} u^{k}(\zeta ,0)+{s^{\varpi }}{E}[h(\zeta ,\Im )]\right\} \right] -{E}^{-1}\left[ {s^{\varpi }} {E}[M {{\mu }}({\zeta },{\Im })+N {{\mu }}({\zeta },{\Im })]\right] . \end{aligned}$$

(7)

As through iterative method

$$\begin{aligned}{} & {} {{\mu }}({\zeta },{\Im })=\sum _{{\jmath }=0}^{\infty }{\mu }_{{\jmath }}(\zeta ,\Im ). \end{aligned}$$

(8)

$$\begin{aligned}{} & {} N \left( \sum _{{\jmath }=0}^{\infty }{\mu }_{{\jmath }}(\zeta ,\Im )\right) =\sum _{{\jmath }=0}^{\infty }N \left[ {\mu }_{{\jmath }}(\zeta ,\Im )\right] , \end{aligned}$$

(9)

the nonlinear terms N is given as

$$\begin{aligned} N\left( \sum _{{\jmath }=0}^{\infty }{\mu }_{{\jmath }}(\zeta ,\Im )\right) ={{\mu }}_{0} (\zeta ,\Im )+N\left( \sum _{k=0}^{{\jmath }}{{\mu }}_{k}(\zeta ,\Im )\right) -M \left( \sum _{k=0}^{{\jmath }}{{\mu }}_{k}(\zeta ,\Im )\right) . \end{aligned}$$

(10)

substituting Eqs. (8), (9) and (10) in Eq. (7), we can obtain the following solution

$$\begin{aligned} \sum _{{\jmath }=0}^{\infty }{{\mu }}_{{\jmath }}(\zeta ,\Im )= & {} {E}^{-1}\left[ {s^{\varpi }} \left( \sum _{k=0}^{\jmath }s^{{2-\zeta +k}}u^{k}(\zeta ,0)+{E}[h(\zeta ,\Im )]\right) \right] \nonumber \\{} & {} -{E}^{-1}\left[ {s^{\varpi }}E\left[ M\left( \sum _{k=0}^{{\jmath }}{{\mu }}_{k}(\zeta ,\Im )\right) -N\left( \sum _{k=0}^{{\jmath }}{{\mu }}_{k}(\zeta ,\Im )\right) \right] \right] . \end{aligned}$$

(11)

We using the following iterative technique

$$\begin{aligned}{} & {} {{\mu }}_{0}(\zeta ,\Im )={E}^{-1}\left[ {s^{\varpi }}\left( \sum _{k=0}^{\jmath }s^{{2-\zeta +k}} u^{k}(\zeta ,0)+{s^{\varpi }}E(g(\zeta ,\Im ))\right) \right] , \end{aligned}$$

(12)

$$\begin{aligned}{} & {} {{\mu }}_{1}(\zeta ,\Im )=-{E}^{-1}\left[ {s^{\varpi }}{E}[M[{{\mu }}_{0}(\zeta ,\Im )] +N[{{\mu }}_{0}(\zeta ,\Im )]\right] , \end{aligned}$$

(13)

$$\begin{aligned}{} & {} {{\mu }}_{m+1}(\zeta ,\Im )=-{E}^{-1}\left[ {s^{\varpi }}{E}\left[ -M\left( \sum _{k=0} ^{\jmath }{{\mu }}_{k}(\zeta ,\Im )\right) -N\left( \sum _{k=0}^{\jmath }{{\mu }}_{k}(\zeta ,\Im ) \right) \right] \right] ,\ \ m\ge 1. \end{aligned}$$

(14)

Finally, the Eq. (3) and (4) provide the m-terms solution in series form is define as

$$\begin{aligned} \ {{\mu }}({\zeta },{\Im })\cong {{\mu }}_{0}(\zeta ,\Im )+{{\mu }}_{1}(\zeta ,\Im )+{{\mu }}_{2}(\zeta ,\Im )+{\cdot\cdot\cdot} ,+{{\mu }}_{\jmath }(\zeta ,\Im ), \ \ \ m=1,2,\dots . \end{aligned}$$

(15)

Example

Take into account the following fractional system of partial differential equations in three dimensions:

$$\begin{aligned}{} & {} \frac{\partial ^\varpi {\mu }}{\partial {\Im ^\varpi }}-{\nu }\frac{\partial {\mu }}{\partial {\zeta }} -\frac{\partial {{\nu }}}{\partial {{\Im }}}\frac{\partial {\mu }}{\partial {\varphi }}=1-\zeta +\varphi +{\Im },\nonumber \\{} & {} \frac{\partial ^\varpi {{\nu }}}{\partial {{\Im }^\varpi }}-\mu \frac{\partial {{\nu }}}{\partial {\zeta }} +\frac{\partial {\mu }}{\partial {{\Im }}}\frac{\partial {{\nu }}}{\partial {\varphi }}=1-\zeta -\varphi -{\Im },\qquad 0<\varpi \le 1 \end{aligned}$$

(16)

with initial condition

$$\begin{aligned} u(\zeta ,\varphi ,0)=\zeta +\varphi -1, \qquad {\nu }(\zeta ,\varphi ,0)=\zeta -\varphi +1. \end{aligned}$$

(17)

When we use equation (refex1) to apply the Elzaki transform, we get

$$\begin{aligned}{} & {} {E}[\mu (\zeta ,\varphi ,{\Im })]={s}^2(\zeta +\varphi -1)+{s}^{{\varpi }}{E}\Bigg \{{\nu }\frac{\partial {\mu }}{\partial {\zeta }}+\frac{\partial {{\nu }}}{\partial {{\Im }}}\frac{\partial {\mu }}{\partial {\varphi }}+1-\zeta +\varphi +{\Im }\Bigg \},\nonumber \\{} & {} {E}[\nu (\zeta ,\varphi ,{\Im })]={s}^2(\zeta -\varphi +1)+{s}^{{\varpi }}{E}\Bigg \{\mu \frac{\partial {{\nu }}}{\partial {\zeta }}+\frac{\partial {\mu }}{\partial {{\Im }}}\frac{\partial {{\nu }}}{\partial {\varphi }} +1-\zeta -\varphi -{\Im }\Bigg \}. \end{aligned}$$

(18)

Using the inverse Elzaki transform

$$\begin{aligned}{} & {} \mu (\zeta ,\varphi ,{\Im })=\zeta +\varphi -1+E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{{\nu }\frac{\partial {\mu }}{\partial {\zeta }}+\frac{\partial {{\nu }}}{\partial {{\Im }}}\frac{\partial {\mu }}{\partial {\varphi }}+1 -\zeta +\varphi +{\Im }\Bigg \}\Bigg ],\nonumber \\{} & {} \nu (\zeta ,\varphi ,{\Im })=\zeta -\varphi +1+E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\mu \frac{\partial {{\nu }}}{\partial {\zeta }}+\frac{\partial {\mu }}{\partial {{\Im }}}\frac{\partial {{\nu }}}{\partial {\varphi }}+1 -\zeta -\varphi -{\Im }\Bigg \}\Bigg ]. \end{aligned}$$

(19)

First, we using the NITM, we get

$$\begin{aligned} {\mu _0(\zeta ,\varphi ,{\Im })}&=\zeta +\varphi -1, \ \ {\nu _0(\zeta ,\varphi ,{\Im })}=\zeta -\varphi +1,\\ \mu _1(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{{\nu }_0\frac{\partial {\mu }_0}{\partial {\zeta }}+\frac{\partial {{\nu }_0}}{\partial {{\Im }}}\frac{\partial {\mu }_0}{\partial {\varphi }} +1-\zeta +\varphi +{\Im }\Bigg \}\Bigg ],\\ \nu _1(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\mu _0\frac{\partial {{\nu }_0}}{\partial {\zeta }}+\frac{\partial {\mu }_0}{\partial {{\Im }}}\frac{\partial {{\nu }_0}}{\partial {\varphi }} +1-\zeta -\varphi -{\Im }\Bigg \}\Bigg ],\\ \mu _{1}(\zeta ,\varphi ,{\Im })&=\frac{2{\Im }^{\varpi }}{\Gamma (\varpi +1)}+\frac{{\Im }^{\varpi +1}}{\Gamma (\varpi +2)}, \ \ \nu _{1}(\zeta ,\varphi ,{\Im })=\frac{-{\Im }^{\varpi +1}}{\Gamma (\varpi +2)}.\\ \mu _2(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{{\nu }_1\frac{\partial {\mu }_1}{\partial {\zeta }}+\frac{\partial {{\nu }_1}}{\partial {{\Im }}}\frac{\partial {\mu }_1}{\partial {\varphi }} +1-\zeta +\varphi +{\Im }\Bigg \}\Bigg ],\\ \nu _2(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\mu _1\frac{\partial {{\nu }_1}}{\partial {\zeta }}+\frac{\partial {\mu }_1}{\partial {{\Im }}}\frac{\partial {{\nu }_1}}{\partial {\varphi }} +1-\zeta -\varphi -{\Im }\Bigg \}\Bigg ],\\ \mu _{2}(\zeta ,\varphi ,{\Im })&=\frac{-{\Im }^{2\varpi +1}}{\Gamma (2\varpi +2)}-\frac{{\Im }^{2\varpi }}{\Gamma (\varpi +2)},\\ \nu _{2}(\zeta ,\varphi ,{\Im })&=\left( \frac{2\Gamma (\varpi +2)-(\varpi +1)\Gamma (\varpi +1)}{\Gamma (2\varpi +1)\Gamma (\varpi +2)}\right) {{\Im }^{2\varpi }}+\frac{{\Im }^{2\varpi +1}}{\Gamma (2\varpi +2)}-\frac{2\varpi \Gamma (\varpi ){\Im }^{2\varpi -1}}{\Gamma (\varpi +1)\Gamma (2\varpi )},\\ \mu _3(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{{\nu }_2\frac{\partial {\mu }_2}{\partial {\zeta }}+\frac{\partial {{\nu }_2}}{\partial {{\Im }}}\frac{\partial {\mu }_2}{\partial {\varphi }} +1-\zeta +\varphi +{\Im }\Bigg \}\Bigg ],\\ \nu _3(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\mu _2\frac{\partial {{\nu }_2}}{\partial {\zeta }}+\frac{\partial {\mu }_2}{\partial {{\Im }}}\frac{\partial {{\nu }_2}}{\partial {\varphi }} +1-\zeta -\varphi -{\Im }\Bigg \}\Bigg ],\\ \mu _{3}(\zeta ,\varphi ,{\Im })&=\frac{{\Im }^{3\varpi +1}}{\Gamma (3\varpi +2)} +\left( \frac{2\Gamma (\varpi +2)-(\varpi +1)\Gamma (\varpi +1)}{\Gamma (3\varpi +1) \Gamma (\varpi +2)}\right) {\Im }^{3\varpi }+\frac{{\Im }^{3\varpi }}{\Gamma (2\varpi +2)}\\&\quad -\frac{2{\varpi \Gamma (\varpi )}{\Im }^{3\varpi -1}}{\Gamma (\varpi +1)\Gamma (3\varpi )} +\left( \frac{(2\Gamma (\varpi +2)-(\varpi +1)\Gamma (\varpi +1))2{\varpi \Gamma (\varpi )}}{\Gamma (3\varpi )\Gamma (2\varpi +1)\Gamma (\varpi +2)}\right) {\Im }^{3\varpi -1}\\&\quad -\left( \frac{2{\varpi \Gamma (\varpi )}}{\Gamma (2\varpi )\Gamma (\varpi +1)}\right) {\Im }^{3\varpi -2},\\ \nu _{3}(\zeta ,\varphi ,{\Im })&=\frac{-{\Im }^{3\varpi +1}}{\Gamma (3\varpi +2)} +\left( \frac{(\varpi +1)\Gamma (\varpi +1)2\varpi \Gamma (2\varpi )}{\Gamma {(3\varpi )} \Gamma (\varpi +2)\Gamma (\varpi +2)}\right) {\Im }^{3\varpi -1}.\\&\vdots \\ \mu _{m+1}(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{{\nu }_{\jmath } \frac{\partial {\mu }_{\jmath }}{\partial {\zeta }}+\frac{\partial {{\nu }_{\jmath }}}{\partial {{\Im }}} \frac{\partial {\mu }_{\jmath }}{\partial {\varphi }}+1-\zeta +\varphi +{\Im }\Bigg \}\Bigg ],\\ \nu _{m+1}(\zeta ,\varphi ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\mu _{\jmath } \frac{\partial {{\nu }_{\jmath }}}{\partial {\zeta }}+\frac{\partial {\mu }_{\jmath }}{\partial {{\Im }}} \frac{\partial {{\nu }_{\jmath }}}{\partial {\varphi }}+1-\zeta -\varphi -{\Im }\Bigg \}\Bigg ],\\ \end{aligned}$$

The series form answer is provided as

$$\begin{aligned}&\mu (\zeta ,\varphi ,{\Im })={\mu }_{0}(\zeta ,\varphi ,{\Im })+{\mu }_{1}(\zeta ,\varphi ,{\Im }) +{\mu }_{2}(\zeta ,\varphi ,{\Im })+{\mu }_{3}(\zeta ,\varphi ,{\Im })+{\cdot\cdot\cdot} {\mu }_{n}(\zeta ,\varphi ,{\Im }).\\&\nu (\zeta ,\varphi ,{\Im })={\nu }_{0}(\zeta ,\varphi ,{\Im })+{\nu }_{1}(\zeta ,\varphi ,{\Im }) +{\nu }_{2}(\zeta ,\varphi ,{\Im })+{\nu }_{3}(\zeta ,\varphi ,{\Im })+{\cdot\cdot\cdot} {\nu }_{n}(\zeta ,\varphi ,{\Im }). \end{aligned}$$

(20)

The approximate solutions is achieved as

$$\begin{aligned} \mu (\zeta ,\varphi ,{\Im })&=\zeta +\varphi -1+\frac{2{\Im }^{\varpi }}{\Gamma (\varpi +1)} +\frac{{\Im }^{\varpi +1}}{\Gamma (\varpi +2)}-\frac{{\Im }^{2\varpi +1}}{\Gamma (2\varpi +2)} -\frac{{\Im }^{2\varpi }}{\Gamma (2\varpi +1)}\\&\quad +\frac{{\Im }^{3\varpi +1}}{\Gamma (3\varpi +2)}+\left( \frac{2\Gamma (\varpi +2)-(\varpi +1) \Gamma (\varpi +1)}{\Gamma (3\varpi +1)\Gamma (\varpi +2)}\right) {\Im }^{3\varpi }+\frac{{\Im }^{3\varpi }}{\Gamma (2\varpi +2)}\\&\quad -\frac{2{\varpi \Gamma (\varpi )}{\Im }^{3\varpi -1}}{\Gamma (\varpi +1)\Gamma (3\varpi )} +\left( \frac{(2\Gamma (\varpi +2)-(\varpi +1)\Gamma (\varpi +1))2{\varpi \Gamma (\varpi )}}{\Gamma (3\varpi )\Gamma (2\varpi +1)\Gamma (\varpi +2)}\right) {\Im }^{3\varpi -1}\\&\quad -\left( \frac{2{\varpi \Gamma (\varpi )}}{\Gamma (2\varpi )\Gamma (\varpi +1)}\right) {\Im }^{3\varpi -2}+{\cdot\cdot\cdot} ,\\ \nu (\zeta ,\varphi ,{\Im })&=\zeta -\varphi +1-\frac{{\Im }^{\varpi +1}}{\Gamma (\varpi +2)} +\left( \frac{2\Gamma (\varpi +2)-(\varpi +1)\Gamma (\varpi +1)}{\Gamma (2\varpi +1)\Gamma (\varpi +2)} \right) {{\Im }^{2\varpi }}\\&\quad +\frac{{\Im }^{2\varpi +1}}{\Gamma (2\varpi +2)}-\frac{2\varpi \Gamma (\varpi ){\Im }^{2\varpi -1}}{\Gamma (\varpi +1)\Gamma (2\varpi )}-\frac{{\Im }^{3\varpi +1}}{\Gamma (3\varpi +2)}+\left( \frac{(\varpi +1) \Gamma (\varpi +1)2\varpi \Gamma (2\varpi )}{\Gamma {(3\varpi )}\Gamma (\varpi +2)\Gamma (\varpi +2)} \right) {\Im }^{3\varpi -1}+{\cdot\cdot\cdot} ,\\ \end{aligned}$$

when $\varpi =1$, then NITM solution is

$$\begin{aligned}{} & {} \mu (\zeta ,\varphi ,{\Im })=\zeta +\varphi +{\Im }-1,\nonumber \\{} & {} \nu (\zeta ,\varphi ,{\Im })=\zeta -\varphi -{\Im }+1. \end{aligned}$$

(21)

Figure 1

The Exact and NITM results of $\mu (\zeta ,\varphi ,\Im )$ of Example 1.

Figure 2

The graph of 3D and 2D various fractional-order $\varpi =1,0.8,0.6$ and 0.4 of Example 1.

Figure 3

The Exact and NITM results of $\mu (\zeta ,\varphi ,\Im )$ of Example 1.

Figure 4

The graphs of 3D and 2D different fractional-order $\varpi =1,0.8,0.6$ and 0.4 of Example 1.

Table 1 The exact and NITM results of $\mu (\zeta ,\varphi ,\Im )$ and absolute error of Example 1.

Table 2 The exact and NITM results of $\nu (\zeta ,\varphi ,\Im )$ and absolute error of Example 1.

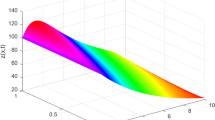
The graphical analysis presented in this study focuses on the comparison between the Numerical Iterative Technique Method (NITM) and the exact solutions for Issue 1 at $\varpi =1$. Figure 1a,b showcase the precision of NITM solutions at $varpi=1$. The close alignment between the NITM and exact solutions is evident in these graphs. Furthermore, Fig. 2 provides additional insights, with subgraph (c) illustrating the fractional-order differentials for $\varpi =1, 0.8, 0.6,$ and 0.4 in NITM results at $\varphi =0.5$. Subgraph (d) in Fig. 2 presents a 2D analysis of different fractional orders at $\varpi =1, 0.8, 0.6$ over time while keeping the space coordinates fixed at $\zeta =5$ and $\varphi =5$. Similarly, Fig. 3a,b depict the exact and NITM solutions for Issue 1 at ${{\varpi }}=1$. The graphical comparison continues in Fig. 4, where subgraph (c) exhibits the fractional-order differentials for $\varpi =1, 0.8, 0.6,$ and 0.4 in NITM results at $\varphi =0.5$. Subgraph (d) in Fig. 4 extends the analysis to a 2D view of different fractional orders at $\varpi =1, 0.8, 0.6$ over time, maintaining fixed space coordinates at $\zeta =5$ and $\varphi =5$. Complementing the graphical representation, Tables 1 and 2 provide quantitative insights, presenting absolute errors and the variations in fractional order of $\varpi$ for $\mu (\zeta ,\varphi ,\Im )$ and $\nu (\zeta ,\varphi ,\Im )$. These tables contribute to a comprehensive understanding of the accuracy and reliability of the NITM solutions under different scenarios.

Example

Consider the following fractional system of two non-linear equations:

$$\begin{aligned}{}&\frac{\partial ^\varpi {\mu }}{\partial {\zeta ^\varpi }}-\nu \frac{\partial {\mu }}{\partial {{\Im }}} +\mu \frac{\partial {\nu }}{\partial {{\Im }}}=-1+e^{\zeta }\sin {{\Im }},\\&\frac{\partial ^\varpi {\nu }}{\partial {\zeta ^\varpi }}+\frac{\partial {\mu }}{\partial {{\Im }}} \frac{\partial {\nu }}{\partial {\zeta }}-\frac{\partial {\nu }}{\partial {{\Im }}} \frac{\partial {\mu }}{\partial {\zeta }}=-1-e^{-\zeta }\sin {{\Im }},\qquad 0<\varpi \le 1 \end{aligned}$$

(22)

with initial conditions

$$\begin{aligned} \mu (0,{\Im })=\sin {{\Im }}, \qquad \nu (0,{\Im })=\cos {{\Im }}. \end{aligned}$$

(23)

Apply the Elzaki transform in equation (16), we get

$$\begin{aligned} {E}[\mu (\zeta ,{\Im })]&={s}^2(\sin {{\Im }})+{s}^{{\varpi }}{E}\Bigg \{\nu \frac{\partial {\mu }}{\partial {{\Im }}}-\mu \frac{\partial {\nu }}{\partial {{\Im }}}-1+e^{\zeta }\sin {{\Im }}\Bigg \},\\ {E}[\nu (\zeta ,{\Im })]&={s}^2(\cos {{\Im }})-{s}^{{\varpi }}{E}\Bigg \{\frac{\partial {\mu }}{\partial {{\Im }}}\frac{\partial {\nu }}{\partial {\zeta }}+\frac{\partial {\nu }}{\partial {{\Im }}} \frac{\partial {\mu }}{\partial {\zeta }}-1-e^{-\zeta }\sin {{\Im }}\Bigg \}. \end{aligned}$$

(24)

Using the inverse Elzaki transform

$$\begin{aligned} \mu (\zeta ,{\Im })&=\sin {{\Im }}+E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\nu \frac{\partial {\mu }}{\partial {{\Im }}}-\mu \frac{\partial {\nu }}{\partial {{\Im }}}-1+e^{\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \nu (\zeta ,{\Im })&=\cos {{\Im }}-E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\frac{\partial {\mu }}{\partial {{\Im }}} \frac{\partial {\nu }}{\partial {\zeta }}+\frac{\partial {\nu }}{\partial {{\Im }}}\frac{\partial {\mu }}{\partial {\zeta }}-1-e^{-\zeta }\sin {{\Im }}\Bigg \}\Bigg ]. \end{aligned}$$

(25)

First, we using the NITM, we get

$$\begin{aligned}{} & {} {\mu _0(\zeta ,{\Im })}&=\sin {{\Im }}, \ \ {\nu _0(\zeta ,{\Im })}=\cos {{\Im }},\\ \mu _1(\zeta ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\nu _0\frac{\partial {\mu _0}}{\partial {{\Im }}} -\mu _0\frac{\partial {\nu }_0}{\partial {{\Im }}}-1+e^{\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \nu _1(\zeta ,{\Im })&=-E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\frac{\partial {\mu _0}}{\partial {{\Im }}} \frac{\partial {\nu _0}}{\partial {\zeta }}+\frac{\partial {\nu _0}}{\partial {{\Im }}}\frac{\partial {\mu _0}}{\partial {\zeta }}-1-e^{-\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \mu _{1}(\zeta ,{\Im })&=\sin {{\Im }}\zeta ^{\varpi }\Sigma _{k=0}^{\infty }\frac{\zeta ^{k}}{\Gamma (k+\varpi +1)}, \\ \nu _{1}(\zeta ,{\Im })&=\frac{-{\Im }^{\varpi }}{\Gamma (\varpi +1)}-\cos {{\Im }}\zeta ^{\varpi }\Sigma _{k=0} ^{\infty }\frac{-\zeta ^{k}}{\Gamma (k+\varpi +1)}.\\ & {} \mu _2(\zeta ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\nu _1\frac{\partial {\mu _1}}{\partial {{\Im }}} -\mu _1\frac{\partial {\nu }_1}{\partial {{\Im }}}-1+e^{\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \nu _2(\zeta ,{\Im })&=-E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\frac{\partial {\mu _1}}{\partial {{\Im }}} \frac{\partial {\nu _1}}{\partial {\zeta }}+\frac{\partial {\nu _1}}{\partial {{\Im }}}\frac{\partial {\mu _0}}{\partial {\zeta }}-1-e^{-\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \mu _{2}(\zeta ,{\Im })&=\Sigma _{k=0}^{\infty }\frac{\zeta ^{2\varpi +k}}{\Gamma (2\varpi +k+1)} -\Sigma _{k=0}^{\infty }\frac{(-\zeta )^{2\varpi +k}}{\Gamma (2\varpi +k+1)}-\cos {{\Im }}\frac{\zeta ^{2\varpi }}{\Gamma (2\varpi +1)},\\ \nu _{2}(\zeta ,{\Im })&=\cos {{\Im }}\frac{\zeta ^{2\varpi -1}}{\Gamma (2\varpi )}+\cos ^{2}{{\Im }} \Sigma _{k=0}^{\infty }\frac{(-\zeta )^{2\varpi +k-1}}{\Gamma (2\varpi +k)}+\sin ^{2}{{\Im }} \Sigma _{k=0}^{\infty }\frac{\zeta ^{2\varpi +k-1}}{\Gamma (2\varpi +k)}.\\ & {} \quad \vdots \\{} & {} \quad \mu _{m+1}(\zeta ,{\Im })&=E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\nu _m\frac{\partial {\mu _1}}{\partial {{\Im }}}-\mu _m\frac{\partial {\nu }_m}{\partial {{\Im }}}-1+e^{\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \nu _{m+1}(\zeta ,{\Im })&=-E^{-1}\Bigg [{s}^{{\varpi }}{E}\Bigg \{\frac{\partial {\mu _m}}{\partial {{\Im }}}\frac{\partial {\nu _m}}{\partial {\zeta }}+\frac{\partial {\nu _m}}{\partial {{\Im }}} \frac{\partial {\mu _m}}{\partial {\zeta }}-1-e^{-\zeta }\sin {{\Im }}\Bigg \}\Bigg ],\\ \end{aligned}$$

The series form solution is given as

$$\begin{aligned}&\mu (\zeta ,{\Im })={\mu }_{0}(\zeta ,{\Im })+{\mu }_{1}(\zeta ,{\Im })+{\mu }_{2}(\zeta ,{\Im }) +{\mu }_{3}(\zeta ,{\Im })+{\cdot\cdot\cdot} {\mu }_{n}(\zeta ,{\Im }).\\&\nu (\zeta ,{\Im })={\nu }_{0}(\zeta ,{\Im })+{\nu }_{1}(\zeta ,{\Im })+{\nu }_{2}(\zeta ,{\Im }) +{\nu }_{3}(\zeta ,{\Im })+{\cdot\cdot\cdot} {\nu }_{n}(\zeta ,{\Im }).\\ \end{aligned}$$

(26)

The approximate solution is achieved as

$$\begin{aligned} \mu (\zeta ,{\Im })= & {} \sin {{\Im }}+\sin {{\Im }}\zeta ^{\varpi }\Sigma _{k=0}^{\infty }\frac{\zeta ^{k}}{\Gamma (k+\varpi +1)}+\Sigma _{k=0}^{\infty }\frac{\zeta ^{2\varpi +k}}{\Gamma (2\varpi +k+1)}\\{} & {} -\Sigma _{k=0}^{\infty }\frac{(-\zeta )^{2\varpi +k}}{\Gamma (2\varpi +k+1)}-\cos {{\Im }} \frac{\zeta ^{2\varpi }}{\Gamma (2\varpi +1)}...,\\ \nu (\zeta ,{\Im })= & {} \cos {{\Im }}-\frac{{\Im }^{\varpi }}{\Gamma (\varpi +1)}-\cos {{\Im }}\zeta ^{\varpi }\Sigma _{k=0}^{\infty }\frac{-\zeta ^{k}}{\Gamma (k+\varpi +1)}+\cos {{\Im }} \frac{\zeta ^{2\varpi -1}}{\Gamma (2\varpi )}\\{} & {} +\cos ^{2}{{\Im }}\Sigma _{k=0}^{\infty }\frac{(-\zeta )^{2\varpi +k-1}}{\Gamma (2\varpi +k)} +\sin ^{2}{{\Im }}\Sigma _{k=0}^{\infty }\frac{\zeta ^{2\varpi +k-1}}{\Gamma (2\varpi +k)}+{\cdot\cdot\cdot} , \end{aligned}$$

when $\varpi =1$, then NITM result is

$$\begin{aligned}{}&\mu (\zeta ,{\Im })=e^{\zeta }\sin {{\Im }},\\&\nu (\zeta ,{\Im })=e^{-\zeta }\cos {{\Im }}. \end{aligned}$$

(27)

Figure 5

The Exact and NITM results at $\mu (\zeta ,\Im )$ of Example 2.

Figure 6

The graph of different fractional-order $\varpi =0.8$ and 0.6 of Example 2.

Figure 7

The Exact and NITM results at $\mu (\zeta ,\Im )$ of Example 2.

Figure 8

The graph of different fractional-order $\varpi =1,0.8,06$ and 0.4 of Example 2.

The graphical and tabular analysis of example 2 is presented in Figs. 5, 6, 7 and 8, providing insights into the performance of the Numerical Iterative Technique Method (NITM) in comparison to the exact solutions. Figure 5a,b showcase the precision of NITM solutions at $\varpi =1$, revealing a close match with the actual findings. Moving to Fig. 6c,d illustrate the differential fractional-order for $\varpi =0.8$ and 0.6 in the NITM results for Issue 2. This differential analysis enhances the understanding of the fractional-order impact on the solutions. Similarly, Fig. 7a,b display the exact and NITM solutions for Issue 2 at ${{\varpi }}=1$, indicating a noteworthy alignment between the two sets of results. Figure 8 provides further insights, illustrating the differential fractional-order for $\varpi =1, 0.8, 0.6,$ and 0.4 in the NITM results for Issue 2. The analysis suggests that time-fractional problem results converge toward an integer-order effect as the time-fractional analysis approaches integer order. This observation contributes to understanding the relationship between time-fractional and integer-order effects in the context of the analyzed problem.

Conclusion

In conclusion, the Numerical Iterative Technique Method (NITM) has been applied to tackle two distinct problems, providing solutions for each at various fractional orders ($\varpi$). The graphical representations and tabular data presented in this study demonstrate the efficacy and accuracy of the NITM in obtaining solutions that closely align with the exact results. The close correspondence observed in both Issues 1 and 2 across different fractional orders suggests the robustness and reliability of the NITM in handling fractional partial differential equations. Furthermore, the differential fractional-order analysis presented in the figures enhances the understanding of how changes in the fractional order impact the solutions. Notably, the analysis indicates a convergence of time-fractional problem results toward an integer-order effect as the fractional order approaches integer values. This observation contributes valuable insights into the transition between time-fractional and integer-order dynamics within the analyzed problems. The findings of this study underscore the significance of the NITM as a powerful tool for solving fractional partial differential equations, providing a viable and accurate alternative to traditional methods. The successful application of NITM in the examined problems, coupled with the detailed analysis of fractional-order effects, contributes to the broader understanding of the dynamics governed by fractional calculus. Overall, this study highlights the NITM’s effectiveness in addressing complex mathematical and physical phenomena described by fractional partial differential equations.