1 Introduction

The reduction of pollutants from the environment is one of the main challenges of our society. Two tons of waste is released to water worldwide [1], and this value is increasing each year as population grows [2, 3]. Almost 900 million people still do not have access to safe water and some 2.6 billion do not have access to adequate sanitation [3], with 14,000 people dying daily by causes directly related to water contamination [2]. Polluted water also affects the biosphere by poisoning plants and animals [1, 2]. Air pollution is also a matter of concern, since the emission of greenhouse gases, the main contributors to the global warming emergency, has been increasing since 1970 [4]. The high atmospheric levels of acidifying pollutants (\(\textrm{SO}_2\) and \(\textrm{NO}_x\)) as well as other air contaminants such as volatile organic compounds (VOCs), ammonia, methane or particulate matter (PM) are also concerning [5]. Air pollution is a major cause of premature death and disease, and has a severe environmental impact in ecosystems by producing eutrophication and acidification of soil, lakes and rivers [5]. Indoor air pollution levels are commonly 2–5 times higher than outdoor levels, but can reach over 100 times higher [6]. In 2012, indoor air pollution was directly related to the cause of 4.3 million premature deaths, as well as several health problems related to breathing diseases and a reduction in decision-making performance [6].

The removal of contaminants from air and water effluents is essential in accomplishing the UN Sustainable Development Goals to ensure availability and sustainable management of water and sanitation for all, and to combat climate change and its impacts. The Paris Agreement at the COP21 conference in 2015 stated a need to keep the global temperature rise below \(2^{\circ }\textrm{C}\) above pre-industrial levels, and to pursue efforts to limit the temperature increase even further, to \(1.5^{\circ }\textrm{C}\). These new pledges for 2030 require a reduction of projected 2030 emissions by 30% for \(2^{\circ }\textrm{C}\) and 55% for \(1.5^{\circ }\textrm{C}\) [4]. The efficiency of the possible decontamination processes depends on the contaminant, the type of fluid and the required operating conditions. Some of the usual decontamination technologies are ultraviolet treatment, oxidation, clarification, biological treatment, membrane filtration, reverse osmosis, nanofiltration and adsorption. Among these, adsorption offers a higher removal efficiency than the others, allowing regeneration of the adsorbent and flexibility in designing the operation/disposal of both the spent media and the wastewater produced during regeneration [1]. Moreover, although high-performance adsorbents can be expensive, the disposal of more economical adsorbents extracted from geological rocks or carbonized wastes can make this technology very attractive [7].

Adsorption columns are a commonly used method for removing contaminants in water, such as fluoride and heavy metals, or gases such as \(\textrm{CO}_2\) and VOCs. In such devices, the fluid is fed into one end of the column, which is packed with small pellets onto which the contaminant adsorbs, thus removing the contaminant from the outlet stream. The performance of an adsorption column is strongly linked to the properties of the pellets used, in particular, their material composition, size and porosity. The adsorption can be chemical or physical in nature. In chemical adsorption, the adsorbate (captured pollutant) reacts with certain radicals located at the surface of the adsorbent creating a chemical bond with it. In physical adsorption, the adsorbate molecules are captured inside small pores inside the adsorbent via the establishment of electrostatic bonds [8].

Adsorption is a multiscale problem: when the fluid is fed into the column, it traverses the gaps between particles while also penetrating into small pores within the pellets themselves; the former transport is largely dominated by advection while the latter takes place via diffusion. The size of the pores is usually inhomogeneous in conventional adsorbents, and usually consists of a pore distribution that accounts for micropores (up to 2 nm) where physical adsorption occurs, mesopores (2 to 50 nm), and macropores (over 50 nm) through where contaminant molecules diffuse to reach micropores located in the inner regions of the adsorbent [9,10,11]. The work of Nepryahin et al. [12] and Fennell et al. [13] suggests that diffusion through the micropores is limited, so the meso/macropore structure is key for the adsorption capacity of the adsorbent and determines the concentration profile of the effluent.

The modelling of adsorption processes usually consists of an advection–diffusion equation, with concentrations averaged across the cross-section of the column, coupled with a sink term that accounts for either the average mass adsorbed inside the pellets [14,15,16,17,18,19], or the mass that diffuses through the boundary between the inner pores of the pellet and the region where the fluid is flowing. In the latter case, the concentration inside the pores might be volume averaged [20, 21] or a diffusion–reaction equation is also added to model the mass transport through the pores [7, 22, 23]. The adsorption kinetics are also highly dependent on the type of adsorption occurring. Although the Linear Driving Force approach [14,15,16] and Langmuir kinetics [17,18,19,20] are commonly used in the literature, some works use higher-order kinetic laws related to the type of adsorbate–adsorbent bonding [14, 17, 22, 23]. Although the velocity is usually assumed to be spatially uniform, some authors account for variable velocity when high concentrations, and thus volumes, of contaminant are being removed [16, 19]. Single-component adsorption is extensively studied in the literature [24,25,26,27] compared to multiple-component adsorption [28].

Despite the extensive work undertaken on the mathematical modelling of such systems, these have not examined the effect of pore size on the concentration effluent. To this end, we provide a novel mathematical model that accounts for the packing structure of the adsorbent pellets inside the column as well as their internal structure. There is a fraction of adsorption sites directly accessible from the fluid flow while there is another fraction that requires a multi-scale transport via the diffusion through internal pores. Thus, a fraction of the contaminant is adsorbed directly at the external surface of the adsorbent pellets while the rest is adsorbed inside the pores. We assess the balance between external and internal adsorption to identify the micro and macrostructure conditions that optimize the performance of the adsorption column.

In Sect. 2 we first define the problem and the assumptions on which the following sections will rely. In Sect. 3 we present the governing equations and the initial and boundary conditions of the model, considering momentum and mass conservation, and adsorption kinetics. In Sect. 4 we present a constrained reduced model considering the magnitude of the parameters defined in previous sections, which are based on lab-scale experimental data. In Sect. 5 we discuss the results obtained from the assessment of a range of parameters related to the structure and packing arrangement of the adsorbent. Finally, in Sect. 6 we conclude our work.

2 Assumptions and definition of the physical system

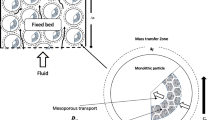
We consider an adsorption system comprising a cylindrical column of a bed, of length \(L_b\), loaded with cylindrical pellets of length \(L_b\) and radius \(L_p\), made of a porous adsorbent (see Fig. 1 left). We model the full system by considering a single representative cell comprising a cylindrical pellet surrounded by a cylindrical channel through which the fluid flows axially with a velocity u from the inlet to the outlet of the column. The length and radius of the cell are \(L_b\) and \(L_p+R_c\), respectively, where \(R_c\) is the radius of the channel (see Fig. 1 middle). We assume that the external perimeter of the channel coincides with the external perimeter of the surrounding cells. Thus, the points in this perimeter would be located in the middle point between two pellets.

The external surface of the pellets gives access to two different locations: adsorption sites onto which the molecules can be directly adsorbed, or pores through which the contaminant diffuses before subsequently attaching to adsorption sites on the pore walls. Physically, adsorption sites are micropores, which are narrow enough (diameter less than 2 nm) to establish bonds with the contaminant molecules and retain them inside (see Fig. 1 right). In this model, the pores are assumed to be cylinders with radius \(r_p\) and length \(L_p\), which represent the mean values from a pore distribution. The pores are assumed to extend radially, from the external surface of the pellet to its centre. Thus, \(L_p\) is assumed to be equal to the radius of the pellets.

Fig. 1
figure 1

Schematic of the physical set-up. Left: adsorption column filled with adsorbent pellets. Middle: Representative cell accounting for the porous pellet surrounded by a channel through which the fluid flows. Right: detail of a pore (top) and a section of this that shows the microstructure (bottom)

Full size image

The numbers in the detail at the bottom right of Fig. 1 indicate the steps of the process. These are: (1) adsorption in the adsorption sites at the external surface of the pellets in contact with the fluid flow; (2) molecular diffusion through the pores inside the pellets; (3) adsorption at the adsorption sites at the pore surface.

We use axisymmetric cylindrical polar coordinates to model the pellets, where the origin of the coordinate system is set in the centre of the pellet at the inlet of the column, and where the x axis coincides with the pellet axis. We denote the cylindrical coordinate variables inside the pores by (r,\(\varphi\),y), while the global coordinates are denoted by (R,\(\Phi\),x) (see Fig. 1). In Fig. 2 we show a transversal section and a cross-section of the cell considered in Fig. 1.

Fig. 2
figure 2

Schematic of the cell in 2D. a Transversal section of the cell. b Cross-section of the cell. The pores are assumed to be distributed randomly in angle and all over the column length

Full size image

In the mathematical model that follows, we make the following conventional assumptions:

  1. 1.

    Since the contaminant molecules are adsorbed inside the micropores, the volume of the pores is not occupied by the adsorbate. This leads us to assume that the pellet and pore geometries remain constant over time.

  2. 2.

    The distribution of the pores in the cross-section of the cell and x is assumed to be random (see Fig. 2). However, we assume that the number of pores per unit area of surface of the pellet \(n=N/(2\pi L_pL_b)\) is constant, where N is the total number of pores in the pellet. This way, the internal porosity of the pellet is the same in every transversal slice.

  3. 3.

    The length of the pores is assumed to be orders of magnitude larger than its radius.

  4. 4.

    The fluid is introduced parallel to the axis of the container and only exits at the outlet of the column.

  5. 5.

    The column has been previously washed with clean solvent. This, combined with the previous assumption, leads to the assumption that the contaminant is driven solely by diffusion from the outer flow to the inside of the pore.

  6. 6.

    The diffusion coefficient D (\(\hbox {m}^2\hbox {/s}\)) is assumed to be equal in all directions.

  7. 7.

    The inlet concentration of the contaminant in the fluid is low enough to neglect any effect of mass loss in the flow. This leads to the assumption of incompressible flow and constant diffusion coefficient of contaminant, D.

  8. 8.

    The velocity field in the cell is assumed to be radially symmetric. This assumption together with the fluid flow being parallel to the axis of the column means that the velocity is unidirectional. We further assume that the velocity field is steady.

  9. 9.

    The external boundary at \(L_p+R_c\) corresponds to the centre of the void regions through which the fluid flows from the inlet to the exit of the column. This boundary would in principle correspond to the intersection of multiple representative cells as the ones shown in Figs. 1 and 2. This leads us to assume axial symmetry at \(L_p+R_c\).

  10. 10.

    Given the length-to-width ratio of the column, the effect of the column wall on the fluid velocity is negligible in the representative cells.

3 Governing equations

In this section, the governing equations of the physical model in the channel and the pores of a representative cell will be derived.

3.1 Adsorption kinetics

The external and internal adsorption sink terms are both modelled using Langmuir kinetics [29]. This adsorption model is founded on the formation of a monolayer of adsorbate over the adsorbent surface. The adsorption rate is assumed to be proportional to the concentration of contaminant in the fluid and the available sites. The desorption rate is proportional only to the occupied sites, since the desorption potential increases as the surface becomes saturated. The available adsorption sites at the adsorbent surface are directly related to the surface concentration of contaminant. In Fig. 1 bottom-right we distinguish between the external (step 1) and the internal (step 3) adsorption. Hence, we define the variables \(\sigma _E\) and \(\sigma _I\) as the surface concentration of contaminant on the external and the internal surface of the adsorbent, respectively, with units \(\mathrm{kg/m}^2\). Note that this definition of the adsorption uptake as a surface density is convenient since we wish to assess the effect of pellet and pore dimensions. The considered areas are the lateral surfaces of the pellet and pore cylinders, not to be confused with the adsorption surface area (such as BET or Langmuir surface area), which also accounts for the internal area of the available sites (micropores). The adsorption–desorption equations for each case read

$$\begin{aligned} \frac{\partial \sigma _E}{\partial t}&=k_{Ea}c(\sigma _m-\sigma _E)-k_{Ed} \sigma _E \, , \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial \sigma _I}{\partial t}&=k_{Ia}c_p(\sigma _m-\sigma _I)-k_{Id} \sigma _I \, , \end{aligned}$$
(2)

where \(k_{Ea}\) and \(k_{Ia}\) are the external and internal adsorption constants, \(k_{Ed}\) and \(k_{Id}\) are the external and internal desorption constants, and \(\sigma _m\) is the maximum value that the surface concentration could reach on any of the surfaces. This last parameter encapsulates the available sites depending on the pellet or pore surface, namely the maximum mass per surface area that could be retained into the micropores accessible in that surface. The variables c(R, x, t) and \(c_p(r,y,x,t)\) denote the averaged concentrations of contaminant (\(\mathrm{kg/m}^3\)) in the channel and inside the pores, respectively. Equations governing their behaviour will be defined in Sects. 3.3 and 3.4. The adsorption and desorption constants usually depend on the velocity of the flow [17, 30]. Thus, the value of these constants could be different in the channel, where the fluid is advected, and inside the pores where the mass transport is driven by diffusion. Although the model accounts for this possibility, in Sect. 4.1, for simplicity, we consider a situation where the external and internal constants are equal. Equations (1) and (2) lead to the Langmuir isotherm when equilibrium is reached, i.e. when the time derivative is zero,

$$\begin{aligned} \sigma _e=\sigma _{Ee}=\sigma _{Ie}=\frac{\sigma _mK_Lc_e}{1+K_Lc_e} \, , \end{aligned}$$
(3)

where \(\sigma _e\) and \(c_e\) are the adsorbed surface density and the concentration in the fluid at equilibrium, respectively, and \(K_L=k_{Ea}/k_{Ed}=k_{Ia}/k_{Id}\) is the Langmuir constant of equilibrium. Note that in column tests the concentration at equilibrium both in the fluid and inside the pores must be the inlet concentration, i.e. \(c_e=c_{in}\), where \(c_{in}\) is the concentration of contaminant in the fluid that is being introduced to the inlet of the column.

We non-dimensionalize eqs. (1) and (2) using the following scaled variables

$$\begin{aligned} {\hat{c}}=\frac{c}{c_{in}} \, , \quad {\hat{c}}_p=\frac{c_p}{c_{in}} \, , \quad {\hat{\sigma }}_E=\frac{\sigma _E}{\sigma _{m}}\, , \quad {\hat{\sigma }}_I=\frac{\sigma _{I}}{\sigma _{m}}\, , \quad {\hat{t}}=\frac{t}{\tau } \, , \end{aligned}$$
(4)

where \(\tau =1/\left( k_{Ia}c_{in}\right)\) is the internal adsorption time-scale. This gives

$$\begin{aligned} \frac{\partial {\hat{\sigma }}_E}{\partial {\hat{t}}}&=k\left[ {\hat{c}}(1-{\hat{\sigma }}_E)-\delta {\hat{\sigma }}_E\right] \, , \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial {\hat{\sigma }}_I}{\partial {\hat{t}}}&={\hat{c}}_p(1-{\hat{\sigma }}_I)-\delta {\hat{\sigma }}_I \, , \end{aligned}$$
(6)

where \(k=k_{Ea}/k_{Ia}\).

3.2 Momentum conservation

As mentioned, we assume that the velocity field is purely axial and steady. We denote this velocity by u (m/s). Applying the incompressible flow condition gives \(\partial u/\partial x=0\) and so \(u=u(R)\).

The momentum conservation for the fluid is modelled using the steady-state Navier–Stokes equation for incompressible flow in the absence of external forces,

$$\begin{aligned} \frac{\mu }{R}\frac{\text {d}}{\text {d} R}\left( R\frac{\text {d} u}{\text {d} R}\right) =-G \, , \end{aligned}$$
(7)

where \(\rho\) and \(\mu\) are the density (\(\mathrm{kg/m}^3\)) and dynamic viscosity [kg/(ms)] of the carrier fluid, respectively, and \(G=-\text {d}p/\text {d}x>0\) is the pressure gradient where p is the pressure (Pa).

We may integrate eq. (7) to obtain

$$\begin{aligned} -\left[ R^2-(L_p+R_c)^2\right] G=2\mu R\frac{\text {d} u}{\text {d} R} \, , \end{aligned}$$
(8)

where we have used the symmetry condition \(\text {d} u/\text {d} R=0\) at \(R=L_p+R_c\).

Integrating again we get

$$\begin{aligned} -\left[ R^2-2(L_p+R_c)^2\ln {R}\right] G=4\mu u + A\, , \end{aligned}$$
(9)

where A is an integration constant. To determine this constant we apply a boundary condition at the surface of the pellet \(R=L_p\). Here we choose to use the Beavers–Joseph condition [31],

$$\begin{aligned} \frac{\text {d} u}{\text {d} R}\Bigg \vert _{R=L_p}=\alpha u\Bigg \vert _{R=L_p}\, , \end{aligned}$$
(10)

where \(\alpha\) (\(\textrm{m}^{-1}\)) is a parameter that determines the mechanism by which the slip velocity is induced. The parameter \(\alpha\) can be determined experimentally and depends on other parameters that characterize the behaviour at the boundary of the permeable material, such as the viscosity of the fluid or the permeability of the material [31].

Applying (10) to eq. (8) we obtain

$$\begin{aligned} u=\frac{1}{4\mu }\left[ L_p^2-R^2+2(L_p+R_c)^2\ln {\left( \frac{R}{L_p}\right) }+\frac{2R_c(R_c+2L_p)}{\alpha L_p}\right] G\, . \end{aligned}$$
(11)

The average of u over the cross-section of the channel coincides with the interstitial velocity \(u_{in}\), namely

$$\begin{aligned} u_{in}=\frac{1}{\pi R_c(R_c+2L_p)}\int _{0}^{2\pi }\int _{L_p}^{L_p+R_c}u R\,\text {d}R\,\text {d}\Phi \, . \end{aligned}$$
(12)

Thus, we can write

$$\begin{aligned} u_{in}=\frac{G(L_p+R_c)^2}{4\mu }\left[ \frac{2\phi }{\alpha (L_p+R_c)\sqrt{1-\phi }}-1-\frac{\phi }{2}-\frac{\ln {\left( 1-\phi \right) }}{\phi }\right] \, , \end{aligned}$$
(13)

where \(\phi\) is the porosity or void fraction of the cell and, by extension, the column. This porosity is the same as the ratio between the void area and the occupied area in the cross-section of a cell. Thus, \(\phi\) can be expressed in terms of the pellet and cell size as

$$\begin{aligned} \phi =1-\frac{L_p^2}{(L_p+R_c)^2}\, . \end{aligned}$$
(14)

The interstitial velocity is related to the superficial velocity \(U_s\) through the expression

$$\begin{aligned} u_{in}=\frac{U_s}{\phi }=\frac{U_s(L_p+R_c)^2}{R_c(R_c+2L_p)}. \end{aligned}$$
(15)

The superficial velocity is related to the flow rate at the inlet of the column \({\mathcal {Q}}\) (\(\textrm{m}^3\)/s) through the expression \({\mathcal {Q}}=U_s\pi \left( L_p+R_c\right) ^2\).

We non-dimensionalize the velocity u with the superficial velocity \(U_s\):

$$\begin{aligned} {\hat{u}}=\frac{u}{U_{s}}, \end{aligned}$$
(16)

which gives \({\hat{u}}_{in}=1/\phi\).

The dimensionless form of eq. (13) then reads

$$\begin{aligned} 1={\hat{G}}\phi \left[ \frac{2\phi }{\alpha (L_p+R_c)\sqrt{1-\phi }}-1-\frac{\phi }{2}-\frac{\ln {\left( 1-\phi \right) }}{\phi }\right] \, , \end{aligned}$$
(17)

where

$$\begin{aligned} {\hat{G}}=\frac{{\mathcal {L}}_b}{{\mathcal {P}}}G=\frac{(L_p+R_c)^2}{4\mu U_s}G \, , \end{aligned}$$
(18)

with \({\mathcal {P}}=4\mu U_s{\mathcal {L}}_b/\left( L_p+R_c\right) ^2\).

3.3 Mass conservation in the channel

We denote the concentration of contaminant in the fluid in the channel by \(\rho (R,\Phi ,x,t)\) (\(\mathrm{kg/m}^3\)), and the diffusion coefficient of the contaminant by D (\(\textrm{m}^2\)/s), which is assumed to be constant.

$$\begin{aligned} \frac{\partial \rho }{\partial t}+u\frac{\partial \rho }{\partial x}=D{\varvec{\nabla }}^2\rho \, . \end{aligned}$$
(19)

Now, we define the azimuthal average of the concentration of contaminant in the channel, c(R, x, t) (\(\mathrm{kg/m}^3\)) as

$$\begin{aligned} c=\frac{1}{2\pi }\int _{0}^{2\pi }\rho \, \text {d}\Phi \, . \end{aligned}$$
(20)

Taking into account the periodicity condition

$$\begin{aligned} \frac{\partial \rho }{\partial \Phi }\Bigg \vert _{\Phi =0} = \frac{\partial \rho }{\partial \Phi }\Bigg \vert _{\Phi =2\pi } \, , \end{aligned}$$
(21)

the azimuthally averaged advection–diffusion equation in a cylindrical coordinate system reads

$$\begin{aligned} \frac{\partial c}{\partial t}+u \frac{\partial c}{\partial x}=D\frac{\partial ^2 c}{\partial x^2}+D\frac{1}{R}\frac{\partial }{\partial R}\left( R\frac{\partial c}{\partial R} \right) \, . \end{aligned}$$
(22)

We now define the dimensionless form of eq. (19) taking into account the scaled variables

$$\begin{aligned} {\hat{x}}=\frac{x}{{\mathcal {L}}_b} \, , \quad {\hat{y}}=\frac{y}{{\mathcal {L}}_p} \, , \quad {\hat{R}}=\frac{R}{{\mathcal {R}}} \, , \end{aligned}$$
(23)

where \({\mathcal {L}}_b\) is the column length-scale, \({\mathcal {L}}_p\) is the pore length-scale and \({\mathcal {R}}\) is the radial length-scale in the channel, all of them to be chosen.

The dimensionless form of eq. (22) reads

$$\begin{aligned} \varepsilon ^2\text {Pe}\left[ \text {Da}\frac{\partial {\hat{c}}}{\partial {\hat{t}}}+{\hat{u}} \frac{\partial {\hat{c}}}{\partial {\hat{x}}}\right] =\varepsilon ^2\frac{\partial ^2 {\hat{c}}}{\partial {\hat{x}}^2}+\frac{1}{{\hat{R}}}\frac{\partial }{\partial {\hat{R}}}\left( {\hat{R}}\frac{\partial {\hat{c}}}{\partial {\hat{R}}} \right) \, , \end{aligned}$$
(24)

where

$$\begin{aligned} \varepsilon&=\frac{{\mathcal {R}}}{{\mathcal {L}}_b},&\text {Pe}&=\frac{U_s{\mathcal {L}}_b}{D},&\text {Da}=\frac{{\mathcal {L}}_b}{U_s\tau }. \end{aligned}$$
(25)

Here, \(\varepsilon\) denotes the pore aspect ratio, Pe denotes the Péclet number, which is defined as the ratio of the rate of advection to the rate of diffusion, and Da denotes the Damköhler number, which is the ratio between the internal adsorption time-scale and the advection rate.

The aspect ratio \(\varepsilon\) is expected to be small and we will exploit this in our subsequent analysis. We treat Da and \(\text {Pe}\) as \({\mathcal {O}}(1)\); in practice Da\(\ll 1\), but our model captures this scenario too. Although the Péclet number is usually greater than 1, it is reasonable to assume that \(\text {Pe}={\mathcal {O}}(1)\) since certain fluids such as gases usually exhibit high diffusivities [32].

We expand all dependent variables asymptotically in \(\varepsilon ^2\) via

$$\begin{aligned} f&=f^{(0)}+\varepsilon ^2f^{(1)}+{\mathcal {O}}(\varepsilon ^4) \, , \end{aligned}$$
(26)

for \(f=\{{\hat{c}},{\hat{c}}_p,{\hat{\sigma }}_E,{\hat{\sigma }}_I,{\hat{u}}\}\). To leading order in \(\varepsilon\), eq. (24) reads

$$\begin{aligned} \frac{1}{{\hat{R}}}\frac{\partial }{\partial {\hat{R}}}\left( {\hat{R}}\frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{R}}} \right) =0 \, . \end{aligned}$$
(27)

If we integrate eq. (27) and apply the axial symmetry condition at \(L_p+R_c\), i.e.

$$\begin{aligned} \frac{\partial {\hat{c}}}{\partial {\hat{R}}}\Bigg \vert _{{\hat{R}}=(L_p+R_c)/{\mathcal {R}}}=0 \, , \end{aligned}$$
(28)

we obtain that \({\hat{c}}^{(0)}={\hat{c}}^{(0)}({\hat{x}},{\hat{t}})\).

At \({\mathcal {O}}(\varepsilon ^2)\), eq. (24) reads

$$\begin{aligned} \text {Da}\frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{t}}}+{\hat{u}}^{(0)} \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}=\text {Pe}^{-1}\left[ \frac{\partial ^2 {\hat{c}}^{(0)}}{\partial {\hat{x}}^2}+\frac{1}{{\hat{R}}}\frac{\partial }{\partial {\hat{R}}}\left( {\hat{R}}\frac{\partial {\hat{c}}^{(1)}}{\partial {\hat{R}}} \right) \right] \, . \end{aligned}$$
(29)

We can integrate eq. (29) and exploit the fact that \({\hat{c}}^{(0)}\) is independent of R to obtain

$$\begin{aligned} \text {Da}\phi \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{t}}}+\frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}=\text {Pe}^{-1}\phi \frac{\partial ^2 {\hat{c}}^{(0)}}{\partial {\hat{x}}^2} - \frac{2\text {Pe}^{-1}L_p{\mathcal {R}}}{ (L_p+R_c)^2}\frac{\partial {\hat{c}}^{(1)}}{\partial {\hat{R}}}\Bigg \vert _{{\hat{R}}={\hat{L}}_p}, \end{aligned}$$
(30)

where we have used the fact that

$$\begin{aligned} \frac{\phi }{\pi R_c(R_c+2L_p)}\int _{0}^{2\pi }\int _{L_p}^{L_p+R_c}{\hat{u}}^{(0)} R\,\text {d}R\,\text {d}\Phi = 1 \end{aligned}$$
(31)

is the leading-order cross-sectionally averaged velocity. We have also made use of the symmetry condition in eq. (28).

The total amount of mass loss per column length at a given x [kg/(ms)] is divided into two sink terms: the mass sink by diffusion to the inside of the pellets through the base of the pores (\(Q_p(x,t)\)), and the mass sink by adsorption to the external surface of the pellets (\(Q_E(x,t)\)). Mathematically, this reads

$$\begin{aligned} -2\pi L_pD\frac{\partial c}{\partial R}\Bigg \vert _{R=L_p}=Q_p+Q_E \, . \end{aligned}$$
(32)

The mass sinks \(Q_p\) and \(Q_E\) are related to the fraction of internal and external surface, respectively, compared with the total surface of the pellet that is available for adsorption. This fraction is defined as

$$\begin{aligned} \chi =\frac{N\pi r_p^2}{2\pi L_p L_b}=\pi n r_p^2 \, . \end{aligned}$$
(33)

The external sink \(Q_E\) can be defined in terms of the Langmuir sink term (1)

$$\begin{aligned} Q_E=-2\pi L_p(1-\chi )\frac{\partial \sigma _E}{\partial t} \, . \end{aligned}$$
(34)

The sink term \(Q_p\) must also equal the diffusive flux into the pores. Thus,

$$\begin{aligned} Q_p=2\pi L_p\chi D\frac{\partial c_p}{\partial y}\Bigg \vert _{y=0} \, . \end{aligned}$$
(35)

We expect an \({\mathcal {O}}(1)\) amount of contaminant to be removed from the channel via diffusive transport for an efficient filter. To achieve this requires the concentration to fall quickly over a small boundary layer near the adsorbent boundary. This means that the first-order boundary condition in eq. (30) must match with the leading-order \(Q_E\) and \(Q_p\) from eqs. (34) and (35). Hence, the dimensionless condition that must be satisfied reads

$$\begin{aligned} -\frac{\partial {\hat{c}}^{(1)}}{\partial {\hat{R}}}\Bigg \vert _{{\hat{R}}={\hat{L}}_p}=\frac{\partial {\hat{c}}_p^{(0)}}{\partial {\hat{y}}}\Bigg \vert _{{\hat{y}}=0}-\frac{\sigma _m{\mathcal {L}}_p(1-\chi )}{D\tau c_{in}\chi }\frac{\partial {\hat{\sigma }}_E^{(0)}}{\partial {\hat{t}}} \, , \end{aligned}$$
(36)

where \({\mathcal {R}}={\mathcal {L}}_p\varepsilon ^2/\chi\). In this situation we assume \(\sigma _m{\mathcal {L}}_p(1-\chi )/(D\tau c_{in}\chi )\) is \({\mathcal {O}}(1)\) since this model can also capture the situation where \(\sigma _m{\mathcal {L}}_p(1-\chi )/(D\tau c_{in}\chi )\ll 1\). In the case where \(\sigma _m{\mathcal {L}}_p(1-\chi )/(D\tau c_{in}\chi )\gg 1\), the scale \({\mathcal {R}}\) should be defined in terms of this external adsorption instead.

Thus, we find that \({\mathcal {R}}=\chi {\mathcal {L}}_b^2/{\mathcal {L}}_p\) and \(\varepsilon =\chi {\mathcal {L}}_b/{\mathcal {L}}_p\). These results indicate that this approach is applicable when the length-scale over which removal of contaminant into the pores occurs is smaller than the length-scale over which the adsorption happens inside the pore.

Now, eq. (30) can be rewritten using eq. (36) as

$$\begin{aligned} \text {Da}\phi \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{t}}}+\frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}=&\text {Pe}^{-1}\phi \frac{\partial ^2 {\hat{c}}^{(0)}}{\partial {\hat{x}}^2} +\frac{\partial {\hat{c}}_p^{(0)}}{\partial {\hat{y}}}\Bigg \vert _{{\hat{y}}=0}-{\mathcal {A}}\frac{1-\chi }{\chi ^{\frac{3}{4}}}\frac{\partial {\hat{\sigma }}_E^{(0)}}{\partial {\hat{t}}}\, , \end{aligned}$$
(37)

where we have defined the column length-scale as \({\mathcal {L}}_b=(L_p+R_c)\sqrt{{\mathcal {L}}_p\text {Pe}/(2L_p\chi )}=(L_p+R_c)^2{\mathcal {L}}_pU_s/(2DL_p\chi )\), and \({\mathcal {A}}=\sqrt{\sigma _mk_{Ia}/(2D\sqrt{\pi n})}\).

3.4 Mass conservation in the pores

Within the pores we assume that the contaminant molecules travel only by diffusion. Thus, the concentration of contaminant in a pore \(\rho _p(\varphi ,r,y,x,t)\) (\(\mathrm{kg/m}^3\)), satisfies

$$\begin{aligned} \frac{\partial \rho _p}{\partial t}=D\frac{\partial ^2 \rho _p}{\partial y^2}+D\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial \rho _p}{\partial r} \right) \, , \end{aligned}$$
(38)

where we have assumed radial symmetry. Note that since the diffusion through the channels and the pores consist of the same contaminant and solvent, the diffusion coefficient is assumed to be the same.

We define the average concentration of contaminant in the pores, \(c_p\) (\(\mathrm{kg/m}^3\)), as

$$\begin{aligned} c_p=\frac{1}{\pi r_p^2}\int _{0}^{2\pi }\int _{0}^{r_p}\rho _p r\,\text {d}r\,\text {d}\varphi = \frac{2}{ r_p^2}\int _{0}^{r_p}\rho _p r\,\text {d}r \, . \end{aligned}$$
(39)

Integrating eq. (38) over the pore cross-section gives

$$\begin{aligned} \frac{\partial c_p}{\partial t}=D\frac{\partial ^2 c_p}{\partial y^2}+\frac{2D}{r_p}\frac{\partial \rho _p}{\partial r}\Bigg \vert _{r=r_p} \, . \end{aligned}$$
(40)

The boundary term in eq. (40) at \(r=r_p\) can be defined in terms of the Langmuir sink term (2) as

$$\begin{aligned} D\frac{\partial \rho _p}{\partial r}\Bigg \vert _{r=r_p}=-\frac{\partial \sigma _I}{\partial t} \, , \end{aligned}$$
(41)

and so (40) becomes

$$\begin{aligned} \frac{\partial c_p}{\partial t}=D\frac{\partial ^2 c_p}{\partial y^2}-\frac{2}{r_p}\frac{\partial \sigma _I}{\partial t} \, . \end{aligned}$$
(42)

We non-dimensionalize eq. (41), using the scalings introduced in (4) and (23) along with \({\hat{r}}=r/{\mathcal {R}}_p\). The dimensionless form of eq. (42) then reads

$$\begin{aligned} \text {Fo}^{-1}\frac{\partial {\hat{c}}_p}{\partial {\hat{t}}}=\frac{\partial ^2 {\hat{c}}_p}{\partial {\hat{y}}^2}-\frac{\partial {\hat{\sigma }}_I}{\partial {\hat{t}}} \, , \end{aligned}$$
(43)

where we have defined the pore length and radius scales as \({\mathcal {L}}_p=\sqrt{Dc_{in}r_p\tau /(2\sigma _m)}\) and \({\mathcal {R}}_p=D\tau c_{in}/\sigma _m\), respectively. The Fourier number \(\text {Fo}=D\tau /{\mathcal {L}}_p^2=2\sigma _m/(c_{in}r_p)\) is defined as the ratio of the internal adsorption time-scale to the diffusion time-scale.

3.5 Initial and boundary conditions

We consider the case where the channels, the pores inside the pellets and the adsorbent are all initially free of contaminant. Hence,

$$\begin{aligned} c^{(0)}(x,0)=\sigma _E(x,0)=c_p(x,y,0)=\sigma _I(x,y,0)=0 \, , \end{aligned}$$
(44)

which in dimensionless form reads

$$\begin{aligned} {\hat{c}}^{(0)}({\hat{x}},0)={\hat{\sigma }}_E({\hat{x}},0)={\hat{c}}_p({\hat{x}},{\hat{y}},0)={\hat{\sigma }}_I({\hat{x}},{\hat{y}},0)=0 \, . \end{aligned}$$
(45)

We assume that at the inlet the fluid enters in the axial direction with a uniform distribution of contaminant. Conserving flux of contaminant at the inlet provides the Danckwerts condition [33] (see [18] for a derivation),

$$\begin{aligned} (u\rho )\Bigg \vert _{x=0^-}=\left( u \rho -D\frac{\partial \rho }{\partial x}\right) \Bigg \vert _{x=0^+} \, . \end{aligned}$$
(46)

To leading order, the integral of (46) over the void region of fluid gives

$$\begin{aligned} u_{in}c^{(0)}_{in}=\left( u_{in}c^{(0)}-D\frac{\partial c^{(0)}}{\partial x}\right) \Bigg \vert _{x=0^+}\, , \end{aligned}$$
(47)

where we have used the fact that the free surface at \(x=0^-\) consists of all the area \(\pi (R_c+L_p)^2\) while the free surface at \(x=0^+\) only accounts for the channel area \(\pi R_c(R_c+2L_p)\).

Adopting the same approach at the outlet of the column gives

$$\begin{aligned} \left( u_{in} c^{(0)}-D\frac{\partial c^{(0)}}{\partial x}\right) \Bigg \vert _{x=L_b^-}=u_{in} c^{(0)}_b\, , \end{aligned}$$
(48)

where \(c^{(0)}_b\) is the concentration measured at the outlet (\(\mathrm{kg/m}^3\)), often called the breakthrough concentration. In order to use a practical boundary that avoids requiring knowing the concentration beyond the column outlet, we use the continuity condition \(c^{(0)}(L_b^-,t)=c^{(0)}_b\) [18] so that (48) becomes

$$\begin{aligned} \frac{\partial c^{(0)}}{\partial x}\Bigg \vert _{x=L_b^-} = 0\, . \end{aligned}$$
(49)

The dimensionless boundary conditions at the inlet and the outlet then read

$$\begin{aligned} \left( {\hat{c}}^{(0)}-\text {Pe}^{-1}\phi \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}\right) \Bigg \vert _{{\hat{x}}=0^+}=1 \, , \qquad \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}\Bigg \vert _{{\hat{x}}={\hat{L}}_b^-} = 0\, , \end{aligned}$$
(50)

respectively, where

$$\begin{aligned} {\hat{L}}_b=\frac{L_b}{{\mathcal {L}}_b}=\frac{2\beta D}{U_s}\left( \pi n\chi ^3\right) ^{\frac{1}{4}}\sqrt{\frac{2(1-\phi )}{ {\mathcal {R}}_p}} \, , \end{aligned}$$
(51)

with \(\beta =L_b/(L_p+R_c)\).

As for the pores, the boundary condition at \(y=0\) is based on the continuity condition between concentrations at the entrance of the pores:

$$\begin{aligned} c^{(0)}(x,t)=c_p(0,x,t) \, , \end{aligned}$$
(52)

while the boundary condition at \(y=L_p\) reads

$$\begin{aligned} \frac{\partial c_p}{\partial y}\Bigg \vert _{y=L_p^-}=0 \, , \end{aligned}$$
(53)

and corresponds to a symmetry condition where all the pores communicate at the ends.

The dimensionless conditions within the pore then read

$$\begin{aligned} {\hat{c}}^{(0)}({\hat{x}},{\hat{t}})={\hat{c}}_p({\hat{x}},0,{\hat{t}}), \quad \quad \frac{\partial {\hat{c}}_p}{\partial {\hat{y}}}\Bigg \vert _{{\hat{y}}={\hat{L}}_p^-}=0 \, , \end{aligned}$$
(54)

where

$$\begin{aligned} {\hat{L}}_p=(L_p+R_c)\left( \frac{\pi n}{\chi }\right) ^{\frac{1}{4}}\sqrt{\frac{2(1-\phi )}{ {\mathcal {R}}_p}} \, . \end{aligned}$$
(55)

4 Reduced dimensionless model

In the previous sections we have derived the governing equations and initial and boundary conditions. Since eq. (37) corresponds to the leading-order variables, the dependent variables in the rest of the governing equations and the initial and boundary conditions must be also asymptotically expanded. In the subsequent section we use typical experimental values to confirm the orders of magnitude of the parameters in the problem, which will enable us to consider a reduced model description.

4.1 Experimental values and reduced model

In Table 1 we provide typical laboratory-scale experimental values of an adsorption column process [20]. The case in consideration concerns the adsorption of toluene from nitrogen gas on activated carbon.

Table 1 Value of the parameters involved in a typical column adsorption process at laboratory scale [20]
Full size table

The value chosen for the parameter \(\alpha\) from the Beavers–Joseph condition in Table 1 will define the relation between flow rate and pressure drop (see eq. (13)). However, it does not affect the evaluation of the effect of the radius of the pores and the effect of the porosity that we consider in the following sections.

The experimental values validate the asymptotic analysis in \(\varepsilon\) carried out in Sect. 3.3. The parameter \(\text {Pe}^{-1}\phi\) is \({\mathcal {O}}(1)\) for the magnitude of \(r_p\) where the mass sink is more relevant (\(r_p=2.8\times 10^{-4}\) m). Since \(\text {Da}\phi\) and \(\text {Fo}^{-1}\) are both small we neglect these terms in (37) and (43) to obtain the reduced system

$$\begin{aligned} \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}= & \text {Pe}^{-1}\phi \frac{\partial ^2 {\hat{c}}^{(0)}}{\partial {\hat{x}}^2}+\frac{\partial {\hat{c}}_p^{(0)}}{\partial {\hat{y}}}\Bigg \vert _{{\hat{y}}=0}-{\mathcal {A}}\frac{1-\chi }{\chi ^{\frac{3}{4}}}\frac{\partial {\hat{\sigma }}_E^{(0)}}{\partial {\hat{t}}} , \end{aligned}$$
(56a)
$$\begin{aligned} \frac{\partial ^2 {\hat{c}}_p^{(0)}}{\partial {\hat{y}}^2}= & \frac{\partial \hat{\sigma _I^{(0)}}}{\partial {\hat{t}}} , \end{aligned}$$
(56b)
$$\begin{aligned} \frac{\partial {\hat{\sigma }}_E^{(0)}}{\partial {\hat{t}}}= & k\left[ {\hat{c}}^{(0)}(1-{\hat{\sigma }}_E^{(0)})-\delta {\hat{\sigma }}_E^{(0)}\right] , \end{aligned}$$
(56c)
$$\begin{aligned} \frac{\partial {\hat{\sigma }}_I^{(0)}}{\partial {\hat{t}}}= & {\hat{c}}_p^{(0)}(1-{\hat{\sigma }}_I^{(0)})-\delta {\hat{\sigma }}_I^{(0)} , \end{aligned}$$
(56d)

where

$$\begin{aligned} \tau =\frac{1}{k_{Ia}c_{in}} , \quad {\mathcal {R}}_p=\frac{D}{\sigma _m k_{Ia}} , \quad {\mathcal {L}}_b =\frac{U_s(L_p+R_c)^2}{\pi n L_p\sqrt{8Dr_p^3\sigma _mk_{Ia}}} , \quad {\mathcal {L}}_p=\sqrt{\frac{Dr_p}{2\sigma _m k_{Ia}}} , \end{aligned}$$
(57a)
$$\begin{aligned} \text {Pe}=\frac{U_s{\mathcal {L}}_b}{D} , \quad \text {Da}=\frac{{\mathcal {L}}_b}{U_s\tau } , \quad \text {Fo} =\frac{D\tau }{{\mathcal {L}}_p^2} , \quad {\mathcal {A}}=\frac{1}{\sqrt{2{\mathcal {R}}_p\sqrt{\pi n}}} , \quad k=\frac{k_{Ea}}{k_{Ia}} , \end{aligned}$$
(57b)
$$\begin{aligned} \delta =\frac{k_{Ed}}{k_{Ea}c_{in}}=\frac{k_{Id}}{k_{Ia}c_{in}} =\frac{1}{K_Lc_{in}} , \quad \phi =1-\left( \frac{L_p}{L_p+R_c}\right) ^2 , \quad \chi =\pi n r_p^2 . \end{aligned}$$
(57c)

The dimensionless initial conditions read,

$$\begin{aligned} {\hat{c}}^{(0)}({\hat{x}},0)={\hat{\sigma }}_E^{(0)}({\hat{x}},0)={\hat{c}}_p^{(0)}({\hat{x}},{\hat{y}},0)={\hat{\sigma }}_I^{(0)}({\hat{x}},{\hat{y}},0)=0 \, , \end{aligned}$$
(58)

and the boundary conditions at the inlet and the outlet read

$$\begin{aligned} 1=\left( {\hat{c}}^{(0)}-\text {Pe}^{-1}\phi \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}\right) \Bigg \vert _{{\hat{x}}=0^+} \, , \qquad \frac{\partial {\hat{c}}^{(0)}}{\partial {\hat{x}}}\Bigg \vert _{{\hat{x}}={\hat{L}}_b^-} = 0\, . \end{aligned}$$
(59)

Within the pore we have

$$\begin{aligned} {\hat{c}}^{(0)}({\hat{x}},{\hat{t}})={\hat{c}}_p^{(0)}({\hat{x}},0,{\hat{t}}) \quad \text {and} \quad \frac{\partial {\hat{c}}_p^{(0)}}{\partial {\hat{y}}}\Bigg \vert _{{\hat{y}}={\hat{L}}_p^-}=0 \, . \end{aligned}$$
(60)

4.2 Total adsorbed mass

In our results we will consider dimensionless adsorbed masses, \({\hat{m}}\) by scaling the dimensional mass m with the mass introduced into the adsorption column per unit time:

$$\begin{aligned} {\hat{m}}=\frac{m}{\pi (R_c+L_p)^2U_sc_{in}\tau }. \end{aligned}$$
(61)

The total mass of contaminant captured from \({\hat{x}}=0\) to a certain \({\hat{x}}\) can be calculated as

$$\begin{aligned} {\hat{m}}({\hat{x}},{\hat{t}})=\int _{0}^{{\hat{t}}} (1-{\hat{c}}^{(0)}({\hat{x}},\xi ))\,\text {d}\xi \, . \end{aligned}$$
(62)

The previous expression accounts not only for the adsorbed mass but also for the absorbed mass in the pores in the pellet. To calculate only the adsorbed mass, we can define it as an integral of the adsorbed densities over the surface of adsorption. Thus, we shall write

$$\begin{aligned} {\hat{m}}_{Ia}({\hat{L}}_b,{\hat{t}})&=\int _{0}^{{\hat{L}}_b} \int _{0}^{{\hat{L}}_p} {\hat{\sigma }}_I^{(0)}({\hat{y}},{\hat{x}},{\hat{t}}) \,\text {d}{\hat{y}}\text {d}{\hat{x}}\, , \end{aligned}$$
(63)
$$\begin{aligned} {\hat{m}}_{Ea}({\hat{L}}_b,{\hat{t}})&={\mathcal {A}}\frac{1-\chi }{\chi ^{\frac{3}{4}}}\int _{0}^{{\hat{L}}_b} {\hat{\sigma }}_E^{(0)}({\hat{x}},{\hat{t}}) \,\text {d}{\hat{x}}\, , \end{aligned}$$
(64)

where \({\hat{m}}_{Ia}({\hat{x}},{\hat{t}})\) and \({\hat{m}}_{Ea}({\hat{x}},{\hat{t}})\) are the mass adsorbed at the internal surface of the pores and the external surface of the pellet, respectively. The total adsorbed mass is \({\hat{m}}_{ad}={\hat{m}}_{Ia}+{\hat{m}}_{Ea}\).

The mass retained inside the channel, \({\hat{m}}_{c}({\hat{x}},{\hat{t}})\), and the pores, \({\hat{m}}_{p}({\hat{x}},{\hat{t}})\), can also be calculated as

$$\begin{aligned} {\hat{m}}_{c}({\hat{L}}_b,{\hat{t}})&=\text {Da}\phi \int _{0}^{{\hat{L}}_b} {\hat{c}}^{(0)}({\hat{x}},{\hat{t}}) \,\text {d}{\hat{x}}\, , \end{aligned}$$
(65)
$$\begin{aligned} {\hat{m}}_{p}({\hat{L}}_b,{\hat{t}})&=\text {Fo}^{-1}\int _{0}^{{\hat{L}}_b} \int _{0}^{{\hat{L}}_p} {\hat{c}}_p^{(0)}({\hat{y}},{\hat{x}},{\hat{t}}) \,\text {d}{\hat{y}}\text {d}{\hat{x}}\, , \end{aligned}$$
(66)

which are negligible due to the order of magnitude of \(\textrm{Fo}^{-1}\) and Da\(\phi\) reported in Table 1, respectively.

4.3 Parameter constraints

The size of the pores has an upper bound that depends on the available surface that surrounds the channel. In order to find the maximum surface that can be occupied by the base of the cylindrical pores, we consider a single cell of the size of the pore surrounded by pores in a hexagonal packing arrangement (see square in Fig. 3).

Fig. 3
figure 3

Surface of a pellet with an optimum hexagonal packing arrangement of pores

Full size image

Since the hexagonal packing density of the circles is the one that minimizes the area between circles, we can find the maximum surface ratio occupied by the pores around the channel. Taking into account the situation shown in Fig. 3, we can determine the area of one of the corners inside the square (yellow area). This is \(A_{corner}=br_p^2\), where

$$\begin{aligned} b=\frac{1}{2}\arccos {(\sqrt{3}-1)+\sqrt{2\sqrt{3}-3}-\sqrt{6-3\sqrt{3}}}\, . \end{aligned}$$
(67)

Thus, the maximum surface ratio is

$$\begin{aligned} \frac{\pi r_p^2+4br_p^2}{4r_p^2}=\frac{\pi }{4}+b \, . \end{aligned}$$
(68)

Now, the surface ratio retrieved from the parameters of the model must be less than the maximum found,

$$\begin{aligned} \frac{(2r_pn)\pi r_p^2}{2\pi L_p(2r_p)}< \frac{\pi }{4}+b \, , \quad \frac{Nr_p^2}{2L_b L_p}< \frac{\pi }{4}+b \, , \quad \chi < \frac{\pi }{4}+b \, . \end{aligned}$$
(69)

The equations above lead us to define the domain \(\chi \in [0,\pi /4+b)\).

Since the number of pores per unit area of pellet surface is fixed, the change in the porosity due to a change on \(L_p\) will lead to a change on the total number of pores in the cell N. This defines a constraint on \(\phi\) since there should be at least one pore, i.e. \(N\ge 1\). This constraint is

$$\begin{aligned} \phi \le 1-\frac{1}{\left( 2\pi nL_b(L_p+R_c)\right) ^2}\, . \end{aligned}$$
(70)

Taking into account the values in Table 1, this defines the boundary \(\phi \lesssim 0.999842\).

5 Results and discussion

We solve the model (56) subject to (58)–(60), using the method of lines in MATLAB. We discretize the spatial coordinate using the finite differences method with a central second-order scheme. The error committed in the discretization of time is controlled by the MATLAB function ode15s, which is a variable order method with default relative and absolute tolerances \(10^{-3}\) and \(10^{-6}\), respectively. The error committed by the spatial discretizations are \({\mathcal {O}}(\Delta x^2)\) and \({\mathcal {O}}(\Delta y^2)\), where \(\Delta x\) and \(\Delta y\) are the spatial steps throughout the column and the pores, respectively. Thus, the error in x is \({\mathcal {O}}(10^{-8})\) m with a bed length of 0.004 m, and for y is \({\mathcal {O}}(10^{-11})\) m with a pore length of \(7\times 10^{-4}\) m. These values stem from discretizing the bed length and the pore length in 30 and 100 portions, respectively. Once the solution at different positions and times is obtained, the concentration at the outlet (\({\hat{x}}={\hat{L}}_b\)) is evaluated at certain times. The values of \({\hat{m}}_{Ia}({\hat{L}}_b,{\hat{t}})\) and \({\hat{m}}_{Ea}({\hat{L}}_b,{\hat{t}})\) are calculated using expressions (63) and (64) by numerical integration of the results using the trapezoidal method. The calculation of \({\hat{G}}\) is obtained using eq. (17). The regressions made to assess the trend of the optimal values have been carried out using MATLAB’s Curve Fitting Toolbox, with a nonlinear least-squares method.

5.1 Effect of the pore radius

In the dimensionless model, variations in \(r_p\) correspond to variations in the parameter \(\chi\). Possible values of \(r_p\) range from the mean radius of the mesopore region (28 nm) to the macropore capillary region (280 \(\mu\)m) [35,36,37,38]. In dimensionless terms, this corresponds to \(10^{-8}\le \chi \le \pi /4+b\). To investigate the effect of the pore radius, the value of \(\chi\) is varied from \(10^{-8}\) to \(\pi /4+b\). For each value of \(\chi\), the values for the other dimensionless parameters are calculated, and the model in (56) with initial and boundary conditions (58)–(60) is then solved. Since we assume that the change in \(\chi\) is due to the change in \(r_p\), the rest of the dimensional values in Table 1 used to calculate the dimensionless parameters remain constant.

In Fig. 4 we show the dependence of the internal and the external mass adsorbed, \({\hat{m}}_{Ia}\) and \({\hat{m}}_{Ea}\), respectively, for increasing \(\chi\). The internal adsorbed mass follows a power-law relation of the form \({\hat{m}}_{Ia}\propto \chi ^{0.7}\) in most of the studied domain (see Fig. 4a). The external adsorbed mass though, is approximately constant with \(\chi\) until \(\chi \approx 10^{-1}\) (see Fig. 4b), when it sharply drops until \(\chi =1\).

Fig. 4
figure 4

Values of the dimensionless a internal \(m_{Ia}\) and b external \(m_{Ea}\) adsorbed mass using the parameter values in Table 1. From blue lines (early times) to red lines (later times): \({\hat{t}}=0.022\), 0.044, 0.088, 0.176, 0.264, 0.352, 0.44, 0.66, 0.88, 1.1, 1.32, 1.54, 1.76, 1.98, 2.2, 2.42, 2.64, 2.86, 3.08, 3.3, 3.52, 3.74, 3.96, 4.18, 4.4. The dimensionless times correspond to a time span from 45 s to 2.5 h

Full size image
Fig. 5
figure 5

Values of the dimensionless total adsorbed mass for a \({\hat{t}}=0.088\), b \({\hat{t}}=0.264\) and c \({\hat{t}}=1.76\). The dimensionless times correspond to 3 min, 9 min and 1 h respectively

Full size image

Summing the internal and external adsorbed masses uncovers an optimal pore radius \(\chi\) that maximizes the total adsorption (Fig. 5). The optimum value of \(\chi\) increases with increasing adsorption time until it disappears. This behaviour can be seen in Fig. 6, which shows the minima obtained in the outlet concentration, \({\hat{c}}_{out}\), at different times (a), and the evolution of the optimal \(\chi\) with time (b). There is a monotonic and exponential increase in the optimum \(\chi\) as time increases until \({\hat{t}}\approx 1.13\), beyond which, the optimal \(\chi\) coincides with the maximum possible value, \(\chi =1\).

Fig. 6
figure 6

a Evolution of outlet concentration \({\hat{c}}_{out}\) with \(\chi\). The values of the parameters used are given in Table 1. The black dashed line indicates the trend of the optimum of each line. From blue lines (early times) to red lines (later times): \({\hat{t}}=0.022\), 0.044, 0.088, 0.176, 0.264, 0.352, 0.44, 0.66, 0.88, 1.1, 1.32, 1.54, 1.76, 1.98, 2.2, 2.42, 2.64, 2.86, 3.08, 3.3, 3.52, 3.74, 3.96, 4.18, 4.4. The dimensionless times correspond to a time span from 45 s to 2.5 h. b Optimum \(\chi\) versus time \({\hat{t}}\). The red solid line is the regression of the optimum \(\chi\) with time

Full size image

The optimum values for \(\chi\) are all between \(10^{-1}\) and 1. This indicates that the optimum radius of pore is between 20 and 200 \(\mu\)m, which correlates to the macropore region of a capillary size. Although this is higher than the typical pore size of common adsorbents [39,40,41], it is appropriate for crafted materials with controlled structures [42,43,44,45]. Moreover, it indicates that the model is capable of predicting optimal pore size conditions, which will change with the physical parameters of a particular system.

5.2 Effect of the porosity

To assess the effect of the porosity we consider a value of \(\chi\) near the optimum region obtained in the previous section. We set a pore radius of 200 \(\mu\)m (\(\chi =0.5\)), which corresponds to a bed and pore length-scale \({\mathcal {L}}_b=1.36\times 10^{-4}\) m and \({\mathcal {L}}_p=1.17\times 10^{-4}\) m, respectively, and so \(\varepsilon ^2=0.4\). To investigate the effect of the porosity, we assume that the size of the representative cell remains constant. Hence, the value of \(L_p+R_c=7.8\times 10^{-4}\) is held constant, so when \(L_p\) is changed \(R_c\) varies accordingly. We use eq. (14) to calculate the value of \(\phi\) as we vary \(L_p\), considering a variation of \(1-\phi\) between \(10^{-8}\) and 0.9998, to ensure that we do not surpass the upper limit of \(\phi\) enforced by (70) (which requires \(\phi \lesssim 0.999842\)). When calculating all other dimensionless parameters, we vary \(L_p\) and \(R_c\) but hold all other parameters in Table 1 fixed. The model in (56) with initial and boundary conditions (58)–(60) is then solved for each value of \(\phi\).

Fig. 7
figure 7

Values of internal (a), external (b) and total (c) dimensionless adsorbed mass with different porosity values at the conditions given in Table 1 for \(\chi =0.5\). From blue lines (early times) to red lines (later times): \({\hat{t}}=0.022\), 0.044, 0.088, 0.176, 0.264, 0.352, 0.44, 0.88, 1.76, 2.64, 3.52, 4.4. The dimensionless times correspond to a time span from 45 s to 2.5 h

Full size image

In Fig. 7 we show the dependence of the dimensionless adsorbed mass on \(\phi\). Both the internal and the external adsorbed masses, \({\hat{m}}_{Ia}\) and \({\hat{m}}_{Ea}\), start at a non-zero value when \(\phi =0\) and tend to zero when \(\phi \rightarrow 1\) (Fig. 7a and 7b, respectively). Since the parameter \(\chi\) does not change with \(\phi\) (the number of pores per unit area is held constant), this relationship arises due to the effect of the porosity on the dimensionless column and pore lengths, i.e. \({\hat{L}}_b\) and \({\hat{L}}_p\) (eqs. (51) and (55), respectively). The dimensionless column length \({\hat{L}}_b\) is affected by \(\phi\) because of the column length-scale \({\mathcal {L}}_b\), which depends on the length of the pore. Both \({\hat{L}}_b\) and \({\hat{L}}_p\) are proportional to \(\sqrt{1-\phi }\), so if \(\phi\) increases then these lengths decrease. This correlation is translated to the calculation of the dimensionless internal and external adsorbed masses via eqs. (63) and (64), respectively. The external adsorbed mass displays an optimum close to \(\phi =1\), before dropping down to 0 (Fig. 7b). This is because of the effect of the linearly increasing diffusivity term with increasing \(\phi\). Since \(\text {Pe}^{-1}\) is \({\mathcal {O}}(1)\), the increase of \(\phi\) counteracts the decrease of the dimensionless column length \({\hat{L}}_b\). However, since the amount of internal adsorbed mass is generally higher than the external one, the total adsorbed mass is always decreasing for increasing \(\phi\) (Fig. 7c), and so there does not exist an optimum.

Fig. 8
figure 8

Evolution of outlet concentration with porosity at the conditions given in Table 1 for \(\chi =0.5\). From blue lines (early times) to red lines (later times): \({\hat{t}}=0.022\), 0.044, 0.088, 0.176, 0.264, 0.352, 0.44, 0.88, 1.76, 2.64, 3.52, 4.4. The dimensionless times correspond to a time span from 45 s to 2.5 h

Full size image

In Fig. 8 we show the relationship between the outlet concentration and porosity for different times. Here we see that higher values of \(\phi\) lead to higher concentrations at the column outlet. This is consistent with the total adsorbed mass shown in Fig. 7 (right).

5.3 Energetic considerations

Fig. 9
figure 9

a Pressure drop against outlet concentration when \({\hat{t}}=4.4\) (2.5 h) for different values of inlet flow rate. From blue lines [low \(U_s\)) to red lines (high \(U_s\))]: 0.005, 0.009, 0.013, 0.017, 0.021, 0.025, 0.029, 0.033, 0.037, 0.041, 0.045, 0.05 m/s. b Evolution of the product between the pressure drop and the outlet concentration with \(1-\phi\), for fixed \(U_s\). The black dashed line indicates the trend of the optimum of each line. From blue lines (early times) to red lines (later times): \({\hat{t}}=0.022\), 0.044, 0.088, 0.176, 0.264, 0.352, 0.44, 0.88, 1.76, 2.64, 3.52, 4.4. The dimensionless times correspond to a time span from 45 s to 2.5 h. In both figures, the parameter values used are given in Table 1, and we take \(\chi =0.5\)

Full size image

In Fig. 9a we show the evolution of the pressure drop with the outlet concentration for a range of inlet flow rates. To obtain different flow rates the superficial velocity \(U_s\) is varied from 0.001 m/s to 0.05 m/s. The rest of the dimensional values in Table 1 used to calculate the dimensionless parameters remain constant. The model in (56) with initial and boundary conditions (58)–(60) is then solved for each \(U_{s}\) for the associated values of the dimensionless parameters. We see that if we are willing to treat higher flow rates (red lines) and accept high outlet concentrations, we can input a significant flow rate for a low pressure drop, i.e. low energy cost. However, if we need to obtain low concentrations at the outlet, the energetic cost will be higher with a lower flow rate treated. This uncovers a trade-off between the required outlet concentration, the flow rate, and the energetic cost. Note that the dependence of \({\hat{G}}\) on \({\hat{c}}_{out}\) shown in Fig. 9a does not obey a power law. This is because the cost of maintaining \({\hat{c}}_{out}\) constant is to decrease \(\phi\) when a higher flow rate is treated. Thus, \({\hat{G}}\) rapidly diverges when this happens [see eq. (17)].

Fig. 10
figure 10

a Evolution of the optimum value of the product between the pressure drop and the outlet concentration with \(1-\phi\), for fixed \(U_s\). b Optimum porosity \(\phi _{opt}\) versus dimensionless time. The red solid line is the regression of \(\phi _{opt}\) with respect to \({\hat{t}}\). The black dots indicate the different optima and the red line indicates the regression. In both figures, the parameter values used are given in Table 1, and we take \(\chi =0.5\)

Full size image

In Fig. 9b we show the dependence of the product of the pressure drop \({\hat{G}}\) and the concentration \({\hat{c}}\) on the porosity \(\phi\), when flow rate is fixed. We choose to vary \(\phi\) in the same way as described in Sect. 5.2. As seen previously, the concentration increases with increasing \(\phi\) (see Fig. 8) whereas the pressure drop decreases with increasing \(\phi\) if flow rate is fixed (see Fig. 9a). Thus, the product of these two magnitudes exhibits an optimum porosity, \(\phi _{opt}\), as shown in Fig. 9b by the black dashed line. The location of this optimum obeys the approximate power-law relation \(({\hat{G}}{\hat{c}})_{opt} \propto (1-\phi _{opt})^{0.75}\). This is shown with more detail in Fig. 10a. In Fig. 10b we also show the dependence of \(\phi _{opt}\) with time. The identification of this optimal porosity is significant since in practice there is always a trade-off between the maximum permissible concentration from the filter and the energetic demand. These results indicate the suitability of the model presented in this work to determine the optimal packing arrangement of the column.

6 Conclusions

In this manuscript, we have presented a mathematical model to predict the behaviour of an adsorption column. The model is formed from equations that describe the fundamental laws of an advection–diffusion–reaction system. The approach as a multi-scale processes where adsorption can take place at both the external and internal surfaces of the pellets has shown the trade-off between these two when the size of the pores and the porosity of the column change. The conclusions obtained can be summarized in the following points:

  1. 1.

    The model presented is capable of predicting the optimal pore size of the adsorbent under given experimental conditions. The optimal pore radius is contained in the macropore region (\(r_p\approx 200\) \(\mu\)m), which makes the model useful for filtering applications where the pore size can be controlled and designed to create a capillary lattice.

  2. 2.

    The assessment of the effect of the porosity leads to the conclusion that a lower porosity provides a higher adsorption capacity. This means that a higher packing density and better packaging of the pellets is desirable for optimum adsorption.

  3. 3.

    The model provides a relation between pressure drop, inlet flow rate and outlet concentration. This allows us to determine the optimal packing arrangement for an optimal performance of the column given certain energetic constraints.

Since not all adsorbent pellets are cylindrical, different geometries and packing arrangements, such as spheres in a column, should be studied in the future. Moreover, although the results of the cell problem may be generalized to the whole column, the full column problem is also restricted by the packing arrangement of the different pellets of the column. Future work should also include testing for different applications.

In summary, the model presented in this work is capable of providing the optimal design and operating conditions of an adsorption filter.