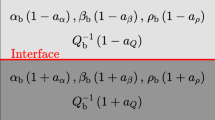Progress in acoustic measurements and geoacoustic applications

Abstract

Geoacoustic exploration is a rapidly evolving field investigating underground rock formations and sediment environments through acoustic waves. In this paper, we present a review of recent research progress, focusing on newly discovered physical phenomena, such as the reflection and refraction of acoustic waves at the interface between anisotropic rocks and between liquid and solid, the characteristics of electric-acoustic (and acoustic-electric) conversion of piezoelectric transducers, the physical mechanism of acoustic wave propagation in viscous media, and the generation of intrinsic noise. We developed new physical models, introduced a parallel transmission network describing piezoelectric transducers for electric-acoustic (and acoustic-electric) energy transfer, and derived new formulations and algorithms associated with the latest model. We will discuss the potential of abnormal incidence angle, acoustic attenuation, and acoustic Goos-Hänchen effect and propose a method of inversion of formation reflection coefficient using logging and seismic data acquired from anisotropic rocks with dip angle. We will also discuss the physical mechanism and potential applications of the intrinsic noise generated inside viscous solid media. Finally, we introduce a parallel/series lumped vibrational transmission network, explain the acoustic measurement process, and discuss applications of the Kaiser effect in petroleum engineering.

1 Introduction

The anisotropy of rock strata affects the propagation, polarization, and reflection/refraction of acoustic signals in seismic exploration and acoustic logging, which is essential for accurate forward modeling of geophysical prospecting and acoustic logging as well as correct inversion interpretation of seismic exploration data and acoustic logging data. Consequently, the impact of rock anisotropy on the propagation, polarization, and reflection/refraction of elastic waves has garnered increasing attention in geoacoustics and has been extensively researched and documented.

Backus [1] was the first to predict the macro-anisotropy behavior in underground rock formations under long wavelength conditions. The rock is transversely isotropic with a vertical axis of symmetry (VTI), and we use transverse isotropy with a tilted axis of symmetry (TTI) media models to describe the rock’s anisotropy of subterranean rock formation. Ĉervenŷ [2] utilized the stiffness coefficients of hexagonal crystals to characterize the macroscopic anisotropy of rock. Thomsen [3] and Wang [4, 5] reported the measured rock anisotropy parameters and gave the relationship between the rock anisotropy parameters and the stiffness coefficients of the hexagonal crystalline system solid. Crampin et al. [6] and Fa and Zhao et al. [7] investigated the polarization properties of homogeneous P waves propagating in anisotropic rock formations, and Helbig et al. [8] discussed the abnormal polarization of homogeneously elastic waves propagating in VTI media. Auld [9] and Carcione [10] elaborated that the direction and magnitude of the phase velocity vectors of P/SV waves propagating in VTI media are usually different from those of their energy velocity vectors, except for some specific directions. Based on reported rock anisotropy parameters [3,4,5], Fa and Zhao et al. [11] calculated the relationship between energy velocity vectors and phase velocity vectors, discussed the effect of rock anisotropy on the time-depth conversion of seismic data, and proposed an accurate time-depth conversion algorithm for seismic data for the case of considering rock anisotropy. Daley et al. [12, 13], Rüger [14], Tsvankin [15], Carcione [10], and Klimeš [16] discussed reflection/refraction coefficients at anisotropic rock interfaces, while Ostrander [17] and Castagna [18] focused on the application of reflection coefficients at isotropic rock interfaces to geophysical exploration. Fa et al. [19,20,21] derived the 4th polynomial for calculating the reflection/refraction angle at the VTI-VTI media interface, Fa and Zhao et al. [22] derived the 8th polynomial for calculating the refraction angle at the VTI-TTI media interface, and they proposed the fast and accurate algorithms for calculating the reflection/refraction coefficients at the VTI-VTI/VTI-TTI media interfaces. Fa and Zhao et al. [19, 21,22,23,24] conducted a theoretical simulation to analyze and explain the reflection and refraction characteristics of the interface of anisotropic media, the polarization state of the generated mode conversion wave, and some physical phenomena and predicted that the refracted P waves induced at some anisotropic rock interfaces may have an abnormal incidence angle in the region over the critical incidence angle, which can lead to an abrupt change in the polarization trajectory and direction of rotation of an inhomogenous elliptical polarized wave.

The Goos-Hänchen effect [25], a significant phenomenon in optics, is understood as follows:

• (i) Total reflection occurs when a beam of light waves is incident from a light-dense medium at the interface between a light-dense and light-sparse medium in the post-critical angle region.

• (ii) The reflected light wave produces coherent interference.

• (iii) The synthesized light wave produces a transverse offset at the interface concerning the point of incidence.

The concept of the Goos-Hänchen effect in optics has been extended to acoustics. Recent advancements in understanding the acoustic Goos-Hänchen effect have significantly enriched our knowledge. Atalar et al. [26] improved the assumption of the interface by replacing the mirror-reflected interface with an elastic interface. Briers et al. [27] also applied the model of the transverse offset effect of optics to ultrasonic nondestructive testing techniques. Liu et al. [28, 29] improved theoretical calculation with an all-directional sinusoidal incident wave (angular spectrum equals 1, and the frequency spectrum is a Delta function) and applied the acoustic Goos-Hänchen effect to the time-depth conversion technology of seismic exploration data. The image of the reflected acoustic field, as recorded by Zhu [30, 31], demonstrated the existence of the acoustic Goos-Hänchen effect generated at the interface of the liquid-void medium, i.e., the reflected waves exhibit lateral migration. This phenomenon of predicting the lateral migration of reflected waves at the interface can be applied to acoustic logging and geophysical exploration. However, their research and experimental verification did not address the issue of the propagation speed of reflected waves at the interface. Fa and Zhao et al. [32] introduced a novel physical model for the acoustic Goos-Hänchen effect, conducted further theoretical investigation on the lateral migration induced by reflected P wave signals with multifrequency components at the interface between liquid and isotropic solid, and proposed the potential existence of a new physical phenomenon: the propagation velocity of the reflected P wave at the liquid-solid interface is not only determined by the physical parameters of the media on both sides of the interface but also influenced by the incident angle. As an essential component in acoustic measurements, a transducer is fundamental for achieving the mutual conversion of acoustic and electric signals. A wide variety of piezoelectric transducers have been investigated and applied in many different fields. By introducing two frequency-dependent mechanical components (i.e., radiation resistance and radiation mass), Fa and Zhao et al. [33,34,35,36,37] established the parallel-electric equivalent circuit of the piezoelectric transducer excited by electric/acoustic signal with multifrequency components. Piezoelectric transducers are also extensively utilized in petroleum logging and geophysical exploration instruments.

Extensive theoretical, experimental, and applied studies have been carried out in many fields on the physical mechanisms that generate acoustic attenuation and intrinsic noise from both macroscopic and microscopic viewpoints. Wang et al. [38] investigated the relationship between the intrinsic frequency and the early strength development of cement mortar. That study showed that intrinsic frequency is related to the properties of the cement mortar around the transducer, which is the comprehensive response of the mechanical load of cement mortar and the electric-acoustic (or acoustic-electric) conversion of the piezoelectric transducer. Fa and Zhao et al. [33,34,35,36,37] investigated the damped attenuation characteristics of different piezoelectric transducers related to the intrinsic noise generated during the transducer’s electric-acoustic/acoustic-electric conversion. Alexet al. [39] introduced an extended mathematical framework for analyzing external and intrinsic noise. Jangir et al. [40] studied the influence of randomness inherent in biochemistry on the response (intrinsic noise) and the variability of cell state (external noise) on the information transmitted through the signal network. Fa and Zhao et al. [41] studied the effects of particle vibration-damping attenuation and wave propagation attenuation on the amplitude of measured acoustic signals, found that the particle vibration-damping attenuation is relative to the intrinsic noise, and anticipated that the obtained intrinsic noise (from actual acoustic logging signals) could be applied to invert the physical characteristics and internal structure of the formation around the oil well, to evaluate whether the measured rock formation was an oil and gas reservoir and the condition of the oil well, thereby enabling calculation of oil or gas content.

The Kaiser effect has also been widely used in many fields, e.g., for nondestructive testing of metal products. The Kaiser effect of rock can provide a design basis for geotechnical engineering. Li et al. [42], Zhang et al. [43], and Fu et al. [44] studied the characteristics of the Kaiser effect on rocks under different loading conditions. Zeng et al. [45] studied the influence of different confining pressures on acoustic emission events in rock samples. Based on the rock Kaiser effect, we can make several rock samples with drilling cores, slowly pressure them, observe the acoustic emission events caused by the rock samples with new micro-fractures (releasing rock stress for a short time), and evaluate the principal stresses of underground rock formations, providing fracturing design basis for low permeability rock oil wells to improve oil and gas production.

We present this review, focusing on a few selected progresses from our research group, specifically the following aspects, which we will discuss in detail in the following sections.

• (a) The possibility of abnormal incidence angles of reflection and refraction of acoustic waves at the interface of anisotropic rock layers directly impacts the amplitude versus offset (AVO) analysis used in seismic exploration. This analysis, crucial for evaluating variations in the reflection amplitude of seismic waves with distance changes between shot points and receivers and the time-depth conversion of seismic exploration data, underscores the urgent necessity of understanding abnormal incidence angles.

Our collaborative efforts have led to other closely associated studies, including acoustic attenuation, the acoustic Goos-Hänchen effect arising from the complex reflection coefficients, and the inverting rock-layer reflection coefficient-serials method by logging and seismic data. Together, we have established a seismic exploration wavelets dictionary to reflect possible geological structures of a region’s subsurface rock formations, highlighting the collective impact of our research.

• (b) The studies of the generation mechanism of intrinsic noise in viscous solids enhance our understanding of its physical nature.

Intrinsic noise in solids, a product of the inherent motion of particles within the material, is a fascinating area of study. When a harmonic force is applied, this motion transitions from a static state to a steady harmonic vibrational state, a process influenced by the particles’ inertia and viscosity. This natural motion, when externally disturbed, gives rise to intrinsic noise. The frequency spectrum corresponding to this transient process of particle motion mirrors the inherent noise generated by the particles within viscous isotropic solids. It is a subject of extensive research in a wide range of fields, including its impact on entropy noise in nozzles, mode coupling instability in friction-induced vibration, and the use of mathematical models to predict flow-acoustic noise. Notably, the investigation into the exact source of intrinsic noise is ongoing, adding to the intrigue and curiosity surrounding this topic. Therefore, understanding the physical mechanism is essential and a significant opportunity for scientific advancement.

• (c) An acoustic transducer is a reliable tool for converting acoustical waves into electrical signals and vice versa, which is crucial in many applications, including geological explorations.

An acoustic measurement consists of three processes. A transmitter, which generates an acoustic signal, is a crucial component. This signal is then transmitted through the medium, such as air, water, or a solid medium, to reach a receiver. The receiver, another critical component, accurately detects the transmitted acoustic waves. Thus, the transducer, i.e., the combination of the transmitter and receiver, enables precise and trustworthy measurements of acoustic properties.

Modeling the transmission process through an electric circuit has been a staple for decades. However, the transmitter signal that excites the transducer may contain numerous frequency components, and the radiation resistance and mass are frequency functions. Grasping the intricacies of signal transmission with multiple frequencies for accurate energy conversion is not just essential but also holds significant implications for practical use, underscoring the importance of our work.

This paper focuses on the transducer’s electric-acoustic conversion process in transmission signals with multiple frequencies in a parallel electrical circuit transmission network. This understanding has profound implications for practical applications, reinforcing the real-world impact of our research.

• (d) The Kaiser effect, a remarkable function of rock formation, allows it to memorize its history of enduring the most significant stresses. When a force surpasses the maximum stress applied to a rock sample, the rock promptly escalates the frequency of acoustic emission events. Grasping the Kaiser effect is a key to unlocking the mysteries of material behavior under stress, a crucial aspect in various scientific and engineering pursuits.

By examining the magnitudes of previous stresses applied to a specimen, we can gain valuable insights into material behavior under different loading conditions.

The Kaiser effect, which involves measuring acoustic emission, leverages internal or potential defects in a rock to automatically produce acoustic emission events as they change state in response to external action. This approach is beneficial in predicting how materials will behave under stress, enhancing our ability to design and engineer structures that can withstand such conditions. To measure acoustic emission, we use specialized sensors that detect the high-frequency acoustic waves emitted by the rock as it undergoes stress.

Numerous practical applications of the Kaiser effect exist, such as stress testing. We can measure acoustic emission in the laboratory by subjecting a rock sample to uniaxial pressure, which allows us to predict the stresses in subsurface rock formations or oil reservoirs based on the applied pressure corresponding to the initial moment of measured acoustic emission events rapidly increasing from the rock sample.

Further examples of the Kaiser effect include geological disaster warning and dam safety detection. We continuously review and advance our understanding of the Kaiser effect and its applications, a testament to this field’s ongoing progress and potential.

2 Theoretical study on the possibility of abnormal incidence angles

Most real subsurface rock formations have some degree of anisotropy and are often not 100% horizontal layers but rather oblique layers with a particular dip. The reflection/refraction of acoustic waves is one of the most fundamental problems in acoustics, involving theoretical studies, experimental verification, and practical applications. Investigating reflection/refraction coefficients at the interface of subsurface rock layers is very important for AVO analysis and time-depth conversion of seismic exploration data.

Based on the rock anisotropy parameters reported by Thomsen [3], Fa and Zhao [19, 20] et al. conducted a rigorous study of the reflection/refraction coefficients of anisotropic rock interfaces. They found that for some anisotropic rock interfaces, inhomogeneously refracted P waves create abnormal refraction, verified the reasonableness of the abnormal incidence angle by using Snell’s theorem and the law of energy conservation, and established the elliptic polarization equation of inhomogeneously refracted P waves [19, 21,22,23,24]. The computational results show that the abnormal incidence angle can not only cause an abrupt change in the size and shape of the elliptical polarization trajectory of the inhomogeneous mode-conversion wave but also cause an abrupt change in its elliptical polarization rotation direction. Many problems related to the potential abnormal incidence angles still need further study. In this section, we provide a theoretical discussion of the reflection/refraction of acoustic waves at interfaces between different rock layers and the possibility of abnormal incidence angles.

2.1 Establishment of 4th/8th polynomials for reflection/refraction angles at VTI-TTI media interfaces

In a good observation of the TTI medium model, we can rotate the VTI medium model around any horizontal axis by a given angle (φ), as shown in Fig. 1.

Fig. 1

Anisotropic VTI medium and TTI medium models: (a) VTI medium model; (b) TTI medium model

For a VTI medium with a hexagonal crystal solid structure, we may express the matrix of elastic stiffness coefficients in terms of the stiffness matrix [9].

$$C^{\left(V\right)}=\begin{bmatrix}c_{11}^{\left(V\right)}&c_{12}^{\left(V\right)}&c_{13}^{\left(V\right)}&0&0&0\\c_{12}^{\left(V\right)}&c_{11}^{\left(V\right)}&c_{13}^{\left(V\right)}&0&0&0\\c_{13}^{\left(V\right)}&c_{13}^{\left(V\right)}&c_{33}^{\left(V\right)}&0&0&0\\0&0&0&c_{44}^{\left(V\right)}&0&0\\0&0&0&0&c_{44}^{\left(V\right)}&0\\0&0&0&0&0&c_{66}^{\left(V\right)}\end{bmatrix}$$

(1)

The elastic stiffness coefficient matrix ($C^{\left(T\right)}$) corresponding to the TTI medium obtained by rotating the elastic stiffness coefficient matrix ($C^{\left(V\right)}$) of the VTI medium by an angle $\varphi$ around any horizontal coordinate axis using the Bond transformation is as follows.

$$C^{\left(T\right)}=\begin{bmatrix}c_{11}^{\left(T\right)}&c_{12}^{\left(T\right)}&c_{13}^{\left(T\right)}&0&c_{15}^{\left(T\right)}&0\\c_{12}^{\left(T\right)}&c_{11}^{\left(T\right)}&c_{23}^{\left(T\right)}&0&c_{25}^{\left(T\right)}&0\\c_{13}^{\left(T\right)}&c_{23}^{\left(T\right)}&c_{33}^{\left(T\right)}&0&c_{35}^{\left(T\right)}&0\\0&0&0&c_{44}^{\left(T\right)}&0&c_{46}^{\left(T\right)}\\c_{15}^{\left(T\right)}&c_{25}^{\left(T\right)}&c_{35}^{\left(T\right)}&0&c_{55}^{\left(T\right)}&0\\0&0&0&c_{46}^{\left(T\right)}&0&c_{66}^{\left(T\right)}\end{bmatrix}$$

(2)

Figure 2 shows the theoretical interface model of the VTI-TTI media interface, where the VTI medium is the incidence medium, the TTI medium is the refraction medium, and the incidence/reflection/refraction angles ($\theta^{(j)}$) correspond to responsive indices {j} = {0,1,2,3,4}.

Fig. 2

VTI-TTI media interface model

Figure 2a displays the angle (φ) between the symmetry axis of the VTI medium and the symmetry axis of the TTI medium, and Fig. 2b shows the wavefront normal and polarization directions of the incident P wave and the four mode conversion waves generated at the VTI-TTI medium interface. The solid line with arrows indicates the phase velocity direction, and the dashed line with arrows is the polarization direction. The $z$-axis and $Z$-axis are the symmetry axes of the VTI and TTI media. The displayed waves ($S^{(0)}$, $S^{(1)}$, $S^{(2)}$, $S^{(3)}$, and $S^{(4)}$) are the incident P wave, the reflected P wave, the refracted P wave, the reflected SV wave, and the refracted SV wave, respectively.

We can obtain the phase velocity solutions of the incident P wave, the reflected P wave, and the reflected SV wave on one side of the VTI medium by solving the Kelvin-Christoffel equation,

$$v_{1,2}^{(0,1,3)} = \left\{ {\left[ {A_{4}^{(V)} \sin^{2} \theta^{(0,1,3)} + A_{5}^{(V)} \pm Q^{(V)} (\theta^{(0,1,3)} )} \right]/2} \right\}^{1/2}$$

(3)

$$\textit{Q}^{(\text{V})}(\theta^{(0,1,3)})=\left[\left(\textit{A}_1^{(\text{V})}\sin^2\theta^{(0,1,3)}+\textit{A}_2^{(\text{V})}\cos^2\theta^{(0,1,3)}\right)^2+\left(\textit{A}_3^{(\text{V})}\right)^2\sin^22\theta^{(0,1,3)}\right]^{1/2}$$

(4)

The superscripts {0, 1, 3} denote the incident P wave, the reflected P wave, and the reflected SV wave, respectively.

The expressions for the phase velocity solutions of the refracted P wave and the refracted SV wave on one side of the TTI medium are as follows,

$$v_{1,2}^{(2,4)} = \left\{ {\left[ {c_{1} \sin^{2} \theta^{(2,4)} + c_{2} \sin 2\theta^{(2,4)} + c_{3} \cos^{2} \theta^{(2,4)} \pm Q^{(T)} (\theta^{(2,4)} )} \right]/2]} \right\}^{1/2}$$

(5)

where

$$\begin{gathered} Q_{{}}^{{({\text{T}})}} \left( {\theta^{(2,4)} } \right) = \left[ {b_{1} \sin^{4} \theta^{(2,4)} + b_{2} \cos^{4} \theta^{(2,4)} + b_{3} \sin^{2} 2\theta^{(2,4)} } \right. \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} \left. { + \sin 2\theta^{(2,4)} \left( {b_{4} \sin^{2} \theta^{(2,4)} + b_{5} \cos^{2} \theta^{(2,4)} } \right)} \right]^{1/2} \hfill \\ \end{gathered}$$

(6)

The superscripts {2, 4} denote the refracted P and SV waves. The coefficients $A_{i}^{(V)}$ are parameters related to the VTI medium, and c_j and b_j are some parameters related to the TTI medium, where the subscripts {i} = {1, 2, 3, 4, 5}, {j} = {1, 2, 3}, and {l} = {1, 2, 3, 4, 5}.

Based on Snell’s law, the 4th polynomials of the reflection angles of the reflected P wave and the reflected SV wave generated in the VTI medium are as follows,

$${B}_{1}^{\left(\text{1,3}\right)}\left(\theta \right)si{n}^{4} {\theta }^{\left(\text{1,3}\right)}+ {B}_{3}^{\left(\text{1,3}\right)}\left(\theta \right)si{n}^{2} {\theta }^{\left(\text{1,3}\right)}+{B}_{5}^{\left(\text{1,3}\right)}=0$$

(7)

The 8th polynomial of the refraction angle for refracted P waves and refracted SV waves in a TTI medium is

$$f_{1}{\prime} (\theta )\sin^{8} (\theta )^{(m)} + f_{2}{\prime} (\theta )\sin^{6} (\theta )^{(m)} + f_{3}{\prime} (\theta )\sin^{4} (\theta )^{(m)} + f_{4}{\prime} (\theta )\sin^{2} (\theta )^{(m)} + f_{5}{\prime} = 0$$

(8)

The coefficients ${B}_{j}^{\left(\text{1,3}\right)}$ ({j} = {1, 3, 5}) and $f_{l}{\prime}$ ({l} = {1, 2, 3, 4, 5}) are related to the incident angle and the physical parameters of the media on both sides of the interface.

2.2 A fast algorithm for calculating reflection/refraction coefficients at VTI-TTI media interfaces

Based on the acoustic-boundary conditions at the solid-solid interface, the continuity of the normal component and tangential component of particle displacement, and the continuity of the normal component of stress at the interface, the matrix equations of the reflection/refraction coefficients at the interface of VTI-TTI media are established as follows,

$$\left[ {\begin{array}{*{20}c} {M_{{1}1}} & {M_{12}} & {M_{13}} & {M_{14}} \\ {M_{21}} & {M_{22}} & {M_{23}} & {M_{24}} \\ {M_{31}} & {M_{32}} & {M_{33}} & {M_{34}} \\ {M_{41}} & {M_{42}} & {M_{43}} & {M_{44}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {R^{(1)} } \\ {R^{(2)} } \\ {R^{(3)} } \\ {R^{(4)} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {N_{1}} \\ {N_{2}} \\ {N_{3}} \\ {N_{4}} \\ \end{array} } \right]$$

(9)

The coefficients ($R^{(1)}$, $R^{(2)}$, $R^{(3)}$, and $R^{(4)}$) correspond to the P-P wave reflection, P-P wave refraction, P-SV wave reflection, and P-SV wave refraction at the interface. M-matrix and N-matrix elements are related to the physical properties of the VTI and TTI media and the incidence/reflection/refraction angles.

From Eqs. 7, 8 and 9, we can establish a fast algorithm for calculating the reflection/refraction coefficients at the VTI-TTI interface.

By setting angle φ = 0 in Fig. 2, the VTI-TTI interface becomes a VTI-VTI interface. Holding the anisotropic parameters (${\varepsilon }^{\left(in\right)}$, ${\delta }^{*\left(in\right)}$ 和 ${\delta }^{*\left(re\right)}$) as selected constants, we show the relationships of the reflection coefficients ($R^{(1)}$, $R^{(2)}$, $R^{(3)}$, and $R^{(4)}$) versus the anisotropic parameter of refraction ($\varepsilon^{(re)}$) and the incident angle ($\theta$) for the interface between A-shale (abbreviation of anisotropic shale) and O-shale (abbreviation of oil shale), as shown in Fig. 3. These results provided us with the following understandings:

Fig. 3

Reflection and refraction coefficients as functions of the incident angle and the anisotropic parameter for the interface between A-shale and O-shale: the left panel presents the amplitudes of the reflection and refraction coefficients, and the right panel presents their corresponding phase angles [19]

(i) Our algorithm, with its high accuracy and efficiency, reliably calculates the reflection/refraction coefficients of the VTI-TTI or VTI-VTI media interface. The calculated reflection/refraction angles adhere to Snell’s theorem, and the computed reflection/refraction coefficients uphold the law of energy conservation;

(ii) Considering rock strata’s anisotropy and the TTI medium’s inclination angle, the calculated reflection coefficient becomes a powerful tool for precise AVO analysis of seismic exploration data. This practical application underscores the relevance and usefulness of our research;

(iii) The enhanced understanding lays a robust theoretical foundation for studying the transverse displacement of reflected P waves on the interface between two different media when acoustic waves incident in the post-critical-angle range. It also provides a theoretical basis for accurate time-depth conversion of measured seismic data.

(iv) The anisotropy of rock and the TTI medium slope angle will significantly impact the amplitude, phase, and critical incident angle in reflection/refraction coefficients, underscoring our significance and depth.

2.3 Polarization coefficients of homogeneous/inhomogeneous mode-conversion waves generated at the anisotropic rock interface and elliptic polarization equation for inhomogeneous mode-conversion waves

Employing the rock anisotropy and physical parameters reported by Thomsen [3], we found that abnormal refraction occurs at some rock interfaces with strong anisotropy while calculating acoustic wave reflection/refraction coefficients [19]. This understanding led us to predict the existence of the potential abnormal incidence angles corresponding to the refracted P wave. These results are essential, as they show that the refracted P wave has different phase velocity solutions in “the pre-abnormal incidence range” and “the post-abnormal incidence angle region.” These findings have significant influences and implications for our understanding of wave propagation. We have also derived the analytical expressions of the polarization coefficient vectors of the inhomogenous mode-conversion wave generated at the interface for the first time. Furthermore, we have established the elliptic polarization trajectory equations of the inhomogenous refraction P wave generated at the anisotropic rock interface. We then discuss the effects of rock anisotropy and incidence angle on the elliptical polarization state of inhomogenous refracted P waves.

Based on Christoffel’s equation and the normalization condition, for the incident and mode-conversion waves at the anisotropic rock interface, we can obtain the $x$- and $z$-components of the polarization coefficients (i.e., vectors),

$$u_{x}^{(m)} \left( {u_{x}^{(m)} } \right)^{*} { = }\frac{{\Gamma_{13}^{(m)} \left[ {\Gamma_{33}^{(m)} - \left( {v^{(m)} } \right)^{2} } \right]^{*} }}{{(\Gamma_{13}^{(m)} )^{*} \left[ {\Gamma_{33}^{(m)} - \left( {v^{(m)} } \right)^{2} } \right] + \Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v^{(m)} } \right)^{2} } \right]^{*} }}$$

(10)

$$u_{z}^{(m)} \left( {u_{z}^{(m)} } \right)^{*} { = }\frac{{\Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v^{(m)} } \right)^{2} } \right]^{*} }}{{\left( {\Gamma_{13}^{(m)} } \right)^{*} \left[ {\Gamma_{33}^{(m)} - \left( {v^{(m)} } \right)^{2} } \right] + \Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v^{(m)} } \right)^{2} } \right]^{*} }}$$

(11)

The analytical expressions of the polarization coefficients in different incident angle regions are as follows.

• (i) For an incident wave, which is a line-polarized wave in all incidence angle ranges, the polarization coefficients are all real numbers and can be written as

$$u_x^{(m)}=\sqrt{\frac{\Gamma_{33}^{(m)}-\left(v_{1,2}^{(m)}\right)^2}{\Gamma_{11}^{(m)}+\Gamma_{33}^{(m)}-2\left(v_{1,2}^{(m)}\right)^2}}$$

(12)

$$u_{z}^{(m)} = \sqrt {\frac{{\Gamma_{11}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} }}{{\Gamma_{11}^{(m)} + \Gamma_{33}^{(m)} - 2\left( {v_{1,2}^{(m)} } \right)^{2} }}}$$

(13)

Where, $\phi^{(m)} = {\text{atan}}\frac{{{\text{Im}} [R^{(m)} ]}}{{{\text{Re}} [R^{(m)} ]}}$.

For the four mode-converted waves, which are all homogenously line-polarized, their polarization coefficients are all real numbers, and their analytical expressions, meticulously derived and verified, remain as Eqs. 12 and 13.

• (ii) In the region past the critical angle of incidence, the homogenous mode conversion waves generated at the anisotropic rock interface are still line-polarized. In this case, the corresponding reflection/refraction coefficients are complex numbers, and they create a phase shift relative to the incident wave, whose analytical expression is as below

$$u_{x}^{(m)} = \sqrt {\frac{{\Gamma_{33}^{(m)} - (v_{1,2}^{(m)} )^{2} }}{{\Gamma_{11}^{(m)} + \Gamma_{33}^{(m)} - 2(v_{1,2}^{(m)} )^{2} }}} \exp [\phi^{(m)} ]$$

(14)

$$u_{z}^{(m)} = \sqrt {\frac{{\Gamma_{11}^{(m)} - (v_{1,2}^{(m)} )^{2} }}{{\Gamma_{11}^{(m)} + \Gamma_{33}^{(m)} - 2(v_{1,2}^{(m)} )^{2} }}} \exp [\phi^{(m)} ]$$

(15)

• (iii) In the post-incidence critical-angle region, the inhomogenous mode conversion wave generated at the anisotropic rock interface is an elliptically polarized wave with one component of the polarization coefficients being a mathematically real number (not complex) and the other one being an imaginary number. The analytical expressions for the two sets of polarization coefficients can be written by

$$u_{x}^{(m)} = \sqrt {\frac{{\left| {\Gamma_{13}^{(m)} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}{{\left| {\left( {\Gamma_{13}^{(m)} } \right)^{*} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right] + \Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}}$$

(16)

$$u_{z}^{(m)} = i\sqrt {\frac{{\left| {\Gamma_{13}^{(m)} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}{{\left| {\left( {\Gamma_{13}^{(m)} } \right)^{*} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right] + \Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}}$$

(17)

or

$$u_{x}^{(m)} = i\sqrt {\frac{{\left| {\Gamma_{13}^{(m)} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}{{\left| {\left( {\Gamma_{13}^{(m)} } \right)^{*} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right] + \Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}}$$

(18)

$$u_{z}^{(m)} = \sqrt {\frac{{\left| {\Gamma_{13}^{(m)} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}{{\left| {\left( {\Gamma_{13}^{(m)} } \right)^{*} \left[ {\Gamma_{33}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right] + \Gamma_{13}^{(m)} \left[ {\Gamma_{11}^{(m)} - \left( {v_{1,2}^{(m)} } \right)^{2} } \right]} \right|}}}$$

(19)

In Eqs. 12, 13, 14, 15, 16, 17, 18 and 19, the superscripts {$m$} = {0, 1, 2, 3, 4} denote the incidence P wave, reflection P wave, refraction P wave, reflection SV wave, and refraction SV wave, respectively; $\Gamma_{11}^{(m)}$, $\Gamma_{13}^{(m)}$, and $\Gamma_{33}^{(m)}$ are parameters related to the properties of the anisotropic rocks and the angles of incidence/reflection/refraction.

Equations 16 and 17 are analytical expressions for the polarization coefficients of the inhomogenous mode-conversion wave. They are applicable in the region past the incidence critical angle without abnormal incidence angles or in the post-incidence critical angle region but smaller than the abnormal incidence angle. Equations 18 and 19 further contribute to our understanding by providing the polarization coefficients of the inhomogenous mode conversion wave in the post-abnormal incidence angle region. These equations are crucial for understanding the behavior of the mode-conversion wave under specific conditions.

The elliptical polarization equation, a precise representation of the inhomogenous mode conversion wave generated at the anisotropic rock interface, is established based on Eqs. 16, 17, 18 and 19. This equation is a testament to the meticulousness of our research as

$$\left[ {\frac{{{\text{Re}} \{ S_{x}^{(m)} \} }}{{\left| {({\text{u}}_{x}^{(m)} )} \right|}}} \right]^{2} + \left[ {\frac{{{\text{Re}} \{ S_{z}^{(m)} \} }}{{\left| {({\text{u}}_{z}^{(m)} )} \right|}}} \right]^{2} = \left[ {\left| {R_{{}}^{(m)} } \right|\exp \left( {\alpha_{{}}^{(m)} z} \right)} \right]^{2}$$

(20)

The expression for the polarization angle of an inhomogenous mode-converted elliptical polarized wave generated at the VTI-TTI media interface is as follows:

$$\text{tan}\,{{\xi }^{\left(m\right)}=\frac{\text{Re}\left({S}_{z}^{\left(m\right)}\right)}{\text{Re}\left({S}_{x}^{\left(2\right)}\right)}=\frac{{b}_{z}^{\left(m\right)}}{{a}_{x}^{\left(m\right)}} \text{tan}\left(\omega t-\frac{\text{sin}\theta }{{v}_{1}^{\left(0\right)}}x+{\phi }^{\left(m\right)}\right)\sqrt{\frac{\left|{\Gamma }_{11}^{\left(m\right)}-{\left({v}_{1}^{\left(m\right)}\right)}^{2}\right|}{\left|{\Gamma }_{33}^{\left(m\right)}-{\left({v}_{1}^{\left(m\right)}\right)}\right|}}\text{tan}\left(\omega t-\frac{\text{sin}\theta }{{v}_{1}^{\left(0\right)}}x+{\phi }^{\left(m\right)}\right)}$$

(21)

For the case of P wave incidence, the superscript m is only possible to choose 2 or 4.

Equations 18 and 19 indicate the possibility of abnormal incidence angles at some anisotropic rock interfaces. We use the rock interface consisting of A-shale and O-shale as a model sample for our calculations [3]. The refraction angle’s sine and the phase velocity of the refraction P wave versus the incidence angle are calculated and shown in Figs. 4 and 5.

Fig. 4

Relationship between the sine square of the angle of reflection and the angle of incidence of a P wave: (a) the relationship of ${\text{Re}} [\sin \theta^{(2)} ]$ versus ${\theta }^{\left(0\right)}$; (b) ${\text{Im}} [\sin \theta^{(2)} ]$ versus $\theta^{(0)}$

Fig. 5

Relationship between the phase velocity of the refracted P wave and the angle of incidence: (a) the real part of the phase velocity solution is ${v}_{1}^{\left(2\right)}$; (b) the imaginary part of the phase velocity solution is ${v}_{1}^{\left(2\right)}$; (c) the real part of the phase velocity solution is ${v}_{2}^{\left(2\right)}$; (d) the imaginary part of the phase velocity solution is ${v}_{2}^{\left(2\right)}$

Figure 4 shows that the angle’s sine for the refracted P wave ($sin {\theta }^{\left(2\right)}$) is real in the incidence angle range (${\theta }^{\left(0\right)}$) from $0^\circ$ to $62.04^\circ$ and is imaginary after ${\theta }^{\left(0\right)}=62.04^\circ$.

Figure 5 shows that the first phase velocity solution $v_{1}^{(2)}$ of the refracted P wave is real in all regions of incidence angles, and the maximum peak occurs at ${\theta }^{\left(0\right)}=62.04^\circ .$ In the region of incidence angle less than 48.34°, the second phase velocity solution $v_{2}^{(2)}$ of the refracted P wave is a real number, and in the region of incidence angles greater than 48.34°, the second phase velocity solution $v_{2}^{(2)}$ of the refracted P wave is an imaginary number. Its modulus has a maximum peak at ${\theta }^{\left(0\right)}=62.04^\circ$. The results of Figs. 4 and 5 indicate that the value of $\sin \theta^{(2)}$ and the solution of the phase velocity corresponding to the refraction P wave are abnormal at that incident angle ${\theta }^{\left(0\right)}=62.04^\circ$, defined as an abnormal incidence angle.

The ratio of the incidence angle’s sine to the phase velocity ($sin {\theta }^{\left(0\right)}/{v}_{1}^{\left(0\right)}$) for the refracted P wave versus the incidence angle (${\theta }^{\left(0\right)}$) is presented in Fig. 6a.

Fig. 6

The ratio of the refraction angle’s sine to the phase velocity ($\text{sin}{\theta }^{\left(2\right)}/{v}_{1+2}^{\left(2\right)}$) for the refracted P wave versus the incidence angle (${\theta }^{\left(0\right)}$) represents the phase velocity solution of the refraction P wave ${v}_{1}^{\left(2\right)}$ [for ${\theta }^{\left(0\right)}\upepsilon \left(0^\circ ,62.04^\circ \right)$] and ${v}_{2}^{\left(2\right)}$ [for ${\theta }^{\left(0\right)}\upepsilon \left(62.04^\circ ,90^\circ \right)$]

In Figs. 6b, c, the value of $sin {\theta }^{\left(02\right)}/{v}_{1}^{\left(2\right)}$ is equal to the value of $sin {\theta }^{\left(0\right)}/{v}_{1}^{\left(0\right)}$ for the incidence angle range ${\theta }^{\left(0\right)}\upepsilon \left(0^\circ ,62.04^\circ \right)$, and the value of $sin {\theta }^{\left(2\right)}/{v}_{2}^{\left(2\right)}$ is equal to the value of $sin {\theta }^{\left(0\right)}/{v}_{1}^{\left(0\right)}$ for the incidence angle range ${\theta }^{\left(0\right)}\upepsilon \left(62.04^\circ ,90^\circ \right)$. The curve segment $\overline{AB}$ in Fig. 6b combined with the curve segment $\overline{CD}$ in Fig. 6c forms the curve of Fig. 6d, where Fig. 6d is the same as Fig. 6a and satisfies Snell’s theorem.

Next, we can use the energy conservation law to verify the rationality and possibility of the abnormal incidence angle. If abnormal incidence angles exist, the z-component of the incidence P-wave Poynting vector must equal the sum of the real parts of the z-components of four mode conversion waves.

Figure 7 shows the relationship between the z-component of the Poynting vector and the incident angle at the interface between A-shale and O-shale. The solid line is the relationship between the z-component of the incidence P wave’s Poynting vector and the incident angle. In contrast, the dashed line represents the relationship between the sum of the real parts of the z-component of the four mode conversion waves’ Poynting vector and the incidence angle for the case without considering the existence of an abnormal incidence angle. The results indicate that for incidence angles that are smaller than the abnormal incidence angle (62.04°), the solid and dashed lines coincide entirely, demonstrating the conservation of energy as the sum of the real parts of the z-component of four mode conversion waves’ Poynting vector equals the z-component of the incidence P wave’s Poynting vector. However, there is a deviation between the dashed and solid lines for larger incidence angles beyond the abnormal incidence angle (62.04°), suggesting a violation of energy conservation. By switching from $v_{1}^{(2)}$ to $v_{2}^{(2)}$ the phase velocity solution for refraction P waves, we can achieve coincidence between the solid and dashed lines, thus upholding energy conservation.

Fig. 7

The z-component of the Poynting vector versus the angle of incidence

While the existence of the abnormal incidence angle is theoretically justified using Snell’s theorem and the law of conservation of energy, it is crucial to note that its existence requires two more prerequisites: (1) for the selected rocks, such as the rock samples reported as reported by Thomsen, the measurement errors of the physical and anisotropic parameters must be sufficiently small, and (2) the existence of the abnormal incidence angle needs to be experimentally verified, underscoring the necessity for further research and highlighting the urgency and importance of experimental validation.

Our calculations reveal a fascinating possibility: if an abnormal incidence angle exists, it could significantly alter the polarization direction and trajectory of the inhomogenous mode conversion waves generated at anisotropic rock interfaces. The theoretical deductions, which are of considerable importance, demonstrate the following:

• (i) Our research demonstrates that the polarization coefficients of the incidence wave and the four mode conversion waves generated at the VTI-TTI media interface are not only determined by the incidence angle but also influenced by the anisotropic and physical parameters of the VTI/TTI media and the dip angle of the TTI media.

• (ii) In the region of over-incidence critical angle, the homogenous mode conversion waves generated at the VTI-TTI media interface will have a phase shift relative to the incident wave. However, it is still a linearly polarized wave.

• (iii) In the region of over-incidence critical angle, one component of the polarization coefficient of the inhomogenous mode conversion wave generated at the interface of VTI-TTI media is real, and the other one is imaginary.

• (iv) The existence of an anomaly in some incidence angles can change the rotation direction and magnitude of the circular/elliptically polarized waves.

 

2.4 Acoustic attenuation studies

Electromagnetic waves propagate in a vacuum without internal energy loss, equal amplitude propagation, and no dispersion phenomenon; electromagnetic waves can also propagate in the medium, and acoustic waves can only reproduce in the medium.

All media in nature have a certain degree of viscosity and conductivity. Whether electromagnetic or acoustic waves propagate in the medium will produce different degrees of internal energy loss. Electromagnetic waves have no mass, there is energy, and their generation or disappearance does not undergo a transient transition process; thus, there is no damping attenuation with the increase of time. Heat loss will occur during the propagation process, and the electromagnetic wave will only produce propagation attenuation with increased propagation distance. Figure 8 shows the three-dimensional space-time diagram of a sinusoidal electromagnetic wave propagating in a non-ideal medium. The amplitude of sinusoidal electromagnetic waves propagating in a non-ideal medium decreases with the increase of the propagation distance in the space domain. In any space position inside the medium, the amplitude of a sinusoidal electromagnetic wave is constant, and there is no damping attenuation in the time domain.

Fig. 8

A schematic diagram of an electromagnetic wave propagating in a non-ideal medium

Acoustic vibration “particles” inside the medium have mass and energy. When a particle at any spatial position vibrates near its equilibrium position, heat loss caused by viscosity decreases the particle vibration amplitude with time, causing damping attenuation in the time domain.

The vibrating particles inside the media pass the energy on to the next particle in the adjacent position through internal stress and lead to adjacent particles’ vibrational motion. The continuous repetition of this process leads to the propagation of fluctuation in the media.

The viscosity reduces the cooperative force acting on the “next” particle, so the vibration amplitude of the “next” particle decreases with the increase of the propagation distance. The particle vibration has damping attenuation, and the fluctuation has propagation attenuation, leading to the amplitude of the acoustic wave decreasing with the increase of the propagation distance.

Both damping attenuation of vibration and propagation attenuation of fluctuation contribute to acoustic attenuation. Even if the acoustic source emits sinusoidal waves (which have a transient transition process from the stationary state to the stable sinusoidal vibration state, and their spectrum contains not only the frequency component of the stable sinusoidal vibration state but also the spectrum of the transient transition process, not a complete sine wave), in the propagation process through a viscous solid medium, inertia will cause particles around the acoustic source to undergo multifrequency vibration and dispersion phenomenon, leading to distortion of transmitted acoustic waveforms. The three-dimensional space-time diagram of an acoustic wave propagating in a viscous medium is shown in Fig. 9.

Fig. 9

A schematic presentation of acoustic waves propagating in a viscous solid

2.5 Acoustic Goos-Hänchen effect

The acoustic Goos-Hänchen effect arises from the complex reflection coefficient when a sinusoidal acoustic wave ($S^{(0)}$) impinges on the interface of two different media in the post-critical-angle range, and the reflection P wave ($S^{(1)}$) induces lateral displacement on the interface, as depicted in Fig. 10. The study of the acoustic Goos-Hänchen effect is based on examining reflection/refraction coefficients at interfaces between different elastic media. The incidence point (A) and reflection point (B) of the reflection P wave have different space locations, not identical positions on the interface. The sinusoidal acoustic wave travels along a path $T \to A \to B \to R_{R}$, and the reflection P wave is observed at the spatial position $R_{R}$.

Fig. 10

Schematic diagram of the model of transverse displacement generated by a reflected P wave, where T is the spatial position of the acoustic source, $R_{R}$ is the spatial position of the observation point, and $\Delta z$ is the lateral displacement of the sinusoidal reflection P wave at the interface of two different media

The equivalent propagation velocity of sinusoidal reflection P wave on the water-plexiglass interface is found to be dependent not only on the physical parameters of the media on both sides of the interface but also on the incident angle. Figure 11 illustrates that as the incidence angle increases, the equivalent propagation velocity of the sinusoidal reflection P wave on the water-plexiglass interface decreases monotonically. As the incident angle approaches the critical angle from the over-incidence angle range, the equivalent propagation velocity tends to approach that of the plexiglass side (refracting medium).

Fig. 11

The Equivalent propagation velocity of reflection P waves at the water-Plexiglas interface versus angle of incidence

When the P wave incidence angle approaches 90°, its equivalent propagation velocity tends to approach that of the water side (incident medium). The results also indicate that the sinusoidal reflection P wave with lower frequency results in more significant lateral displacement on the interface, which suggests that the first arrival of an acoustic logging signal is not a “sliding refraction P wave” with a fixed speed along borehole walls as traditionally considered, but rather a reflection P wave whose speed changes with variations in physical parameters and incidence angle.

Since the acoustic signal radiated by the acoustic source is usually composed of many sinusoidal components with different amplitudes, frequencies, and initial phases, these frequency components are reflected at the liquid-solid interface and reach the spatial position of the observation point along potentially different propagation paths. As shown in Fig. 12, different frequency components of acoustic signals produce different lateral displacements on the liquid-solid interface, so they have different propagation paths, resulting in different equivalent propagation speeds of each frequency component on the interface. Here {i} = {1, 2,…, n}, n is the number of different frequency components of acoustic wave signal discretized, that is, the number of propagation paths of each frequency component of the acoustic signal after discrete, and $\xi$ is the angle of geometric structure. Obviously, the larger the value of i, the higher the frequency of the represented frequency component and the smaller the lateral displacement. Therefore, the measured acoustic signal is the superposition of all different frequency components in the acoustic wave signal arriving at the observation point $R_{R}$ with different propagation paths and equivalent propagation speeds. Even if the media on both sides of the interface are elastic, due to the different propagation times above each frequency component from the acoustic source T to the observation point $R_{R}$, the acoustic wave waveform arriving at $R_{R}$ will also change.

Fig. 12

The propagation paths of different frequency components of an acoustic signal

To summarize, in the case of post-critical angle incidence, the equivalent propagation velocity of the sinusoidal reflection P wave on the liquid-solid interface is fundamentally related to the physical parameters of the media on both sides of the interface and the incident angle, and notably, not influenced by the frequency of the wave. This understanding is crucial as it allows us to comprehend the behavior of the acoustic signals at the liquid-solid interface, thereby enhancing our ability to manipulate and control these signals. Furthermore, the lateral displacement of the multifrequency reflection P wave signal is also influenced by the spectrum distribution of the multifrequency incidence P wave signal, underscoring the importance of considering the entire spectrum distribution in our analysis.

2.6 The method of inverting rock-layers reflection coefficient-serials by using logging data and seismic data for the case of considering rock anisotropy and formation dip angle

Using seismic data and logging data to invert the reflection coefficient serials of subsurface rock formations is a crucial seismic exploration inversion method. The logging data, obtained from measurements taken in boreholes, provides valuable information about the properties of the subsurface rock formations, such as their density, acoustic velocities, and porosity, and so on. We can use this information to construct a non-orthogonal subset, i.e., a seismic exploration signal wavelets dictionary that can reflect all possible geological structures of a region’s subsurface rock formations. On the other hand, the seismic data provides information about the subsurface structure, such as the depth and thickness of the rock layers. Based on this prior information, the seismic exploration data is matched and tracked with the basic units in the wavelet dictionary of seismic exploration signals, and the reflection coefficient serials of underground rock strata are reversed. Now, we can retrieve the reflection coefficient of underground rock formation by combining the two indispensable programs, i.e., the wavelet dictionary of seismic exploration signal and the matching tracking algorithm.

Based on the research results of the reflection/refraction coefficient of the VTI-TTI interface and for the case of considering the anisotropy and dip angle of the rock layer, we conducted research on the method of inversion of undersurface rock layers’ reflection coefficient serials by using logging data and seismic data [46, 47].

Using selected unique signal processing algorithms, we processed the logging data of several oil wells in a region and established many virtual wells. The processed virtual wells’ logging data are convolved with specific source functions to construct the seismic dictionary for this region. This dictionary, a crucial component of our method, contains a wide range of basic units of seismic wavelet, which can be used to construct a specific geological structure that may occur in the underground rock formation in this area. These basic units are designed to more accurately reflect various geological structures (such as top-lap, down-lap, and thin-out) that may occur in the underground rock formation in this area. Based on the match-pursuit algorithm, we use the actual measured seismic exploration signal and the basic unit (word) in the seismic wavelet dictionary to perform correlation and iteration operations, perform match and pursuit, and invert the reflection coefficient serials of the underground rock formation in the area around several actual oil wells for improving the accuracy of the inversion of oil and gas reservoirs. We construct a seismic wavelet dictionary that can reflect all possible underground geological structures near wells 1 and 2 by using unique algorithms such as internal and external interpolation, frequency compression and extension, and so on to process the logging data of these two oil wells.

Figures 13, 14 and 15 show examples of several underground geological structures constructed using the basic units of the seismic wavelet dictionary. The seismic wave is on the left, and the reflection intensity is on the right. The vertical coordinate is the travel time of the seismic wave, and the horizontal coordinate is the number of receiver channels.

Fig. 13

The thin-out for the case of without noticeable acoustic impedance difference between layer 2 and layer 4

Fig. 14

The thin-out with greater acoustic impedance difference

Fig. 15

An underground geological structure with down-lap and thin-out

Figure 13 provides a view of the underground geological structure with a thin-out constructed using the basic unit of the seismic wavelet dictionary. A key observation is the disappearance of the reflection wave in the area after the thin-out, a direct consequence of the acoustic impedance at layer 2 being essentially the same as in layer 4.

Figure 14 presents another underground geological structure with a thin-out, a construction also made using the basic unit of the seismic wavelet dictionary. The complexity of this structure is evident as there is still a rock layer interface after the thin-out disappears. This results from the significant acoustic impedance difference between the second and fourth layers, leading to an intense (strong) reflection even after the thin-out.

The underground geological structure with a down-lap is constructed by using the basic units of the seismic wavelet dictionary, as depicted in Fig. 15.

2.7 The effect of rock anisotropy on the time-depth conversion of seismic seismic signals

Given the escalating intricacy of the exploration object, the traditional primary method of horizontally stratified uniform medium and isotropic seismic exploration has proven inadequate to meet the application requirements. Its limitations in accurately capturing the complex geological structures and reservoirs are stark, necessitating the development of a new seismic exploration method to address these challenges.

Time-depth conversion, a crucial processing step, is the transformative force that turns seismic data from a time-domain signal to a space-domain signal. It is not just a step but a pivotal role player in the inversion of underground rock geological structure and reservoir interpretation using seismic data. This process is the cornerstone for obtaining precise imaging of underground rock geological structures.

Our research, based on the Thomsen rock anisotropy parameter [3], underscores the significant impact of anisotropy on the phase velocity, energy velocity, and depth-time conversion of seismic waves in subsurface rock formations. Neglecting anisotropy or failing to account for the difference between energy and phase velocities can lead to substantial errors in the depth-time conversion of seismic signals, which, in turn, hampers the accurate inversion of the geological structure of underground rock formations using seismic signal time information. Even when anisotropy is considered, omitting the difference between the phase velocity direction angle and the energy velocity direction angle can still result in errors in the time-depth conversion and the AVO analysis for the inversion of oil and gas reservoirs, thereby compromising their accuracy.

Based on the rock anisotropy parameters reported by Thomsen [3], we calculated the effects of anisotropy on the phase velocity, energy velocity, and time-depth conversion of elastic seismic waves propagating in subsurface formations, taking into account the difference between the energy velocity vector and the phase velocity vector. The results provide us with the following understandings:

Phase velocity and energy velocity are functions of anisotropy and phase angle; the more robust the anisotropy of the rock, the more significant the difference between the energy angle and the phase angle, and the larger the difference between phase and energy velocities; and the more substantial the effect on the phase velocity and energy velocity;

For the same propagation direction, the energy velocity is greater than or equal to the phase velocity, but for different propagation directions, the phase velocity can be greater than the energy velocity, i.e., the phase velocity in one direction can be greater than the energy velocity in another direction;

When using the travel time of seismic signals to perform the time-depth conversion, the anisotropy of the rock must be considered. Otherwise, the depth error of the reflection interface of the inversion will be generated, and the actual plane geological structure will be inverted into a curved geological structure [48]. When omitting anisotropy or ignoring the difference between the phase velocity and the energy velocity, the seismic data collected by the source-receiver array with different spatial arrangements and orientation will form a curved formation interface with various shapes and degrees after inversion, which will cause the error between the inversion depth and the actual formation depth;

Considering the influence of rock anisotropy on energy and phase velocities, we may employ the information related to the seismic travel time to accurately invert the geological structure of underground rock strata.

3 Intrinsic noise in viscous solids

The electromagnetic wave, being massless and devoid of transient processes in their generation and disappearance, does not inherently produce noise. However, in a viscous solid medium, the internal particles possess inertia, leading to a transient process from a static state to a stable sinusoidal vibration state under any frequency sinusoidal force acting on them. When this force abruptly ceases, the particle undergoes another transient process, returning to its static state. The frequency spectra corresponding to these two transitions represent the intrinsic noise these vibrating particles generate in the viscous solid medium.

Intrinsic noise can be used not only in the study of solid physics, for example, to invert the physical properties and internal microstructure of solid media, but also can be used in acoustic logging, such as conventional borehole acoustic-logging, MWD (measurement with drilling) acoustic-logging while drilling and cased-well cement bond quality logging. We may apply the intrinsic noise information obtained in acoustic logging to predict the acoustic wave propagation velocity of the formation around the borehole and the cement bonding quality of the primary and secondary interfaces of the cased well. In particular, the intrinsic noise information obtained from MWD acoustic logging can be used to effectively eliminate the influence of the direct wave from the drill collar on the measured P-wave head wave information to acquire the propagation velocity in the formation around the borehole more accurately.

In addition, the study includes the classification of intrinsic and external noise, the establishment of a noise library (dictionary) for marine underwater environmental noise, machine system-generated noise from stationary ships/submarines ensuring normal operations and personnel life, and navigation-related noise. The goal is to eliminate or suppress the intrinsic and external marine environment-generated noise. For instance, algorithms such as Match-Pursuit [46, 47] can extract external noise from ships and submarines. Then, the measured signals can be used to more accurately determine the characteristics of underwater targets, e.g., their locations.

Choose shale as a rock sample. The density, P wave velocity, and SV wave velocity for shale are 2.71 (g/cm³), 3377 (m/s), and 1490 (m/s), respectively. The frequency of the sinusoidal force is chosen to be less than, equal to, or greater than the center frequency of intrinsic noise generated from vibration particles within the medium, which allows for obtaining time-domain waveform and spectrum data on transient processes of particle vibrations inside shale (as shown in Fig. 16 with the following understandings:

• (i) When a different sinusoidal force is applied to the particle inside the medium, the corresponding particle vibration signals in the time domain have a different transient process at the beginning but gradually tend to a stable sinusoidal vibration state with the frequency of the sinusoidal force.

• (ii) The closer the frequency of the sinusoidal force is to the central frequency of intrinsic noise, the greater the amplitude of particle vibration.

• (iii) The frequency spectrum corresponding to the steady-state sinusoidal vibration of a particle is a single frequency impulse in the frequency domain, which is equal to the frequency of the sinusoidal force. In contrast, the frequency spectrum corresponding to the transient process is the intrinsic noise generated by the particle under the action of the sinusoidal force.

Fig. 16

The time-domain waveforms and frequency spectra of particle vibration

Of course, for the same sinusoidal force, different rock media have different transient processes for internal particle’s vibration, i.e., the intrinsic noise generated is different, and the frequency spectrum and center frequency are also different.

4 Research on piezoelectric transducers

Piezoelectric materials have been applied extensively to construct acoustic transducers and filters with high properties for different applications in different areas [49]. As an acoustic source, an acoustic transducer is an electric-acoustic filter; as a receiver, it is an acoustic-electric filter. Ogawa pointed out that in measuring biological properties, acoustic effects play an essential role in designing miniaturized electronic instruments [50]. The quality of acoustic measurements is determined by the acoustic effect and the characteristics of the acoustic transducer, which plays an essential role in acoustic measurements.

Fa and Zhao et al. [33,34,35,36,37] have meticulously investigated the characteristics of four types of piezoelectric acoustic wave transducers, namely, radially polarized thin spherical shells, radially and tangentially polarized thin circular tubes, and thickness-polarized thin disks. By introducing two mechanical components, i.e., radiation resistance and radiation mass whose values are frequency-dependent, an innovative parallel-dynamic machine-electrical equivalent circuit has been developed for the case of multifrequency electric/acoustic signal exciting the transducer, which provides a more comprehensive understanding of these transducers’ electric-acoustic/acoustic-electric conversions.

For a given sinusoidal frequency, applying the residue theorem, the electric-acoustic impulse response and system function of the piezoelectric transducer are derived as follows,

$$h_{1} (t) = A_{3} e^{ - \alpha t} \varepsilon \left( t \right) + B_{3} e^{ - \beta t} \cos \left( {\omega_{1d} t + \theta } \right)\varepsilon \left( t \right)$$

(22)

$$H_{1} \left( \omega \right) = \frac{i\omega d}{{ - i\omega^{3} - \omega^{2} a + i\omega b + c}}$$

(23)

The acoustic-electric impulse response and system function of the transducer are as follows,

$$h_{3} \left( t \right) = A^{\prime}_{3} e^{{ - \alpha^{\prime}t}} \varepsilon \left( t \right) + B^{\prime}_{3} e^{{ - \beta^{\prime}t}} \cos \left( {\omega_{3d} t + \theta^{\prime}} \right)\varepsilon \left( t \right)$$

(24)

$$H_{3} \left( \omega \right) = \frac{{i\omega d^{\prime}}}{{ - i\omega^{3} - \omega^{2} a^{\prime} + i\omega b^{\prime} + c^{\prime}}}$$

(25)

Besides the relevant parameters (${\text{A}}_{3}$, $B_{3}$, $A^{\prime}_{3}$, $B^{\prime}_{3}$, a, b, c, d, $a^{\prime}$, $b^{\prime}$, $c^{\prime}$ and $d^{\prime}$), there are factors, e.g., the angular frequency ($\omega$) and unit step function ($\varepsilon \left( t \right)$), the direct-current term attenuation coefficients of the electric-acoustic impulse response ($\alpha$) the attenuation coefficient of the oscillatory term ($\beta$), the oscillation angular frequency ($\omega_{1d}$), the initial phase shift ($\theta$), and the corresponding factors for acoustic-electric impulse response ($\alpha^{\prime}$,$\beta^{\prime}$, $\omega_{3d}$ and $\theta^{\prime}$).

The driving voltage signal that excites the transducer may contain many frequency components, and the transducer’s radiation resistance and mass are frequency functions. Using the principle of linear superposition, when a multifrequency voltage signal excites a piezoelectric transducer, the electric-acoustic conversion process of the transducer can be equated to a parallel transmission network, as shown in Fig. 17.

Fig. 17

A parallel equivalent network for electric-acoustic conversion of acoustic transducer

In Fig. 17, $U_{j} \left( t \right)$ is the j^th frequency component in the driving voltage signal $U\left( t \right)$ that excites the acoustic source transducer, where {$j$} = {1, 2, 3, …,$N$}, and $h_{j} \left( t \right)$ is the electric-acoustic impulse response of the transducer corresponding to the j^th frequency component ($U_{j} \left( t \right)$) in the driving voltage signal ($U\left( t \right)$). The driving voltage signal $U\left( t \right)$ is discretized into $N$ sinusoidal frequency components that excite the transducer separately. The acoustic signal wavelet radiated by the acoustic source transducer is regarded as a linear superposition of the acoustic signals radiated outward by each frequency component that separately excites the transducer.

The acoustic-electric conversion process of the transducer is the inverse process of its electric-acoustic conversion, as described above.

4.1 Physical mechanism of the acoustic measurement process

An acoustic measurement consists of three processes: the acoustic source transducer’s electric-acoustic conversion, the acoustic wave’s propagation in the medium, and the acoustic-electric conversion of the receiving transducer. The electric-acoustic/acoustic-electric conversion of the transducer has a transient transition process, which will produce intrinsic noise. A sinusoidal force acts on the particle inside a dense medium, and its vibration also has a transient process, producing intrinsic noise. The medium is composed of many particles. We may consider an acoustic wave propagating inside a medium as a vibration particle at any point in space acting on the next adjacent particle by internal stress, causing it to vibrate. This process is repeated in turn, resulting in the propagation of fluctuation, which refers to the variations in the amplitude and frequency spectrum of the acoustic wave as it travels through the medium.

The presence of viscosity, a crucial factor in the acoustic measurement process, not only causes damping attenuation of the vibration of each particle within the medium but also influences the next particle’s vibration due to friction resistance. This interaction leads to the propagation attenuation of the fluctuation. When a multifrequency force is applied to a particle within the medium, it provides an effect as a combination of the vibrations caused by each frequency component in the multifrequency force acting on the particle individually. Let us delve into the analysis and discussion of a scenario where a single sinusoidal force is applied to the next adjacent particle.

When a sinusoidal force is applied to the next adjacent particle, the adjacent particle is also transient from a stationary state to a stable sinusoidal vibration. Therefore, the vibration of all particles inside the viscous medium contains not only the frequency component of the stationary sinusoidal vibration of the particle but also the frequency components corresponding to the transient process of the particle from a stationary state to a stable sinusoidal vibration. Therefore, the force of any vibrating particle in the medium acting on adjacent particles is multifrequency. Thus, we may obtain the vibration state generated from a multifrequency force acting on the adjoining particle by superimposing the vibration generated by each frequency component in the multifrequency force acting on the adjacent particle, respectively. In this sense, regardless of any force acting on the particle inside the viscous medium, the particle vibration generated cannot be a pure sinusoidal vibration but a multifrequency vibration. In addition, the medium has viscosity, which will cause dispersion, that is, the propagation speed and attenuation of each frequency component in the multifrequency wave signal in the medium are functions of frequency. Therefore, compared with the propagation of electromagnetic waves in non-ideal media, the importance of developing more complex models to describe the propagation mechanism of acoustic waves in viscous media cannot be overstated.

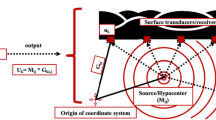
Our model of the acoustic measurement process is based on the study of the electric-acoustic/acoustic-electric conversions of piezoelectric transducers. Using signal and information transmission, we simulate this process as a signal transmission process. The model is a parallel/series lumped particle vibration acoustic measurement transmission network consisting of acoustic source transducers, media, and receiving transducer, as shown in Fig. 18. This model helps us understand the physical mechanism of the acoustic measurement process.

Fig. 18

A transmission network model for acoustic measurement of a multifrequency driving voltage to excite acoustic-source transducer

This physical model considers not only the electric-acoustic/acoustic-electric conversion of the transducer, particle vibration-damping attenuation, and fluctuation propagation attenuation but also the influence of the transient process of particle vibration inside the medium on the measured acoustic signal. This model can describe the actual propagation process of the acoustic wave in the viscous medium from the physical mechanism. In contrast, the wave acoustics research method primarily focuses on wave propagation and does not consider these additional factors. This physical model differs from the physical model established by the research method of wave acoustics. It considers the influences of all the damping attenuation and transient processes of particle vibration, the propagation attenuation of fluctuation, and the electric-acoustic/acoustic-electric conversion of the transducer on the measured acoustic signal. This model can describe the actual propagation process of the acoustic wave in the viscous medium from the physical mechanism.

The first part of Fig. 18 (Part I) describes the electric-acoustic conversion process generated by the multifrequency driving voltage signal to excite the acoustic source transducer, and the third part (Part III) describes the acoustic-electric conversion process of the multifrequency acoustic signal received by the receiving transducer at the observation point.

Next, we discuss the propagation of acoustic waves in a dense medium, i.e., Part II (P/SLPVTN) in Fig. 18, where P/SLPVTN is the abbreviation of “parallel/series lumped particle vibration transmission network.”

The vibration particles inside the medium have both mass and energy. Acoustic waves propagating in viscous media involve both particle vibration and fluctuation propagation. In the propagation of acoustic waves, heat dissipation will occur, which will cause the damping attenuation of particle vibration and the propagation attenuation of fluctuation, i.e., the amplitude of the acoustic wave decreases with the increasing propagation time and distance.

Even if the acoustic source continues to emit sinusoidal acoustic waves to the surrounding medium, it compensates for the damping attenuation (heat loss) of particle vibration caused by the medium’s viscosity so that the particle vibration can eventually reach a stable sinusoidal vibration. All particles in the medium have their unique transient transition process from the static state to a stable sinusoidal vibration or from the stable sinusoidal vibration to the static state.

The propagation of acoustic waves in a medium is a captivatingly intricate process. It commences with a particle vibrating at any point in space and exerting internal stress on the next adjacent particle, inducing its vibration. This sequence is then iterated, culminating in the propagation of fluctuations. It is essential to recognize that the intrinsic noise emanating from all particles in the propagation is not mere noise but a progressive characteristic that significantly influences the overall process.

The vibration of all particles inside the viscous medium contains the frequency component of the steady state sinusoidal vibration and the frequency components corresponding to the transient process from the static state to the stable sinusoidal vibration for particles. In this sense, all the particle vibration in the dense medium cannot be a pure sinusoidal vibration but a complex frequency vibration. After the particle vibration reaches a stable sinusoidal vibration state, the vibration amplitude of the particle at a fixed position in the medium does not change with time and remains constant. Only the amplitude of vibration of particles at different spatial positions in the medium decreases with the increase of the propagation distance, i.e., the amplitude of the fluctuation decreases with the increase of the propagation distance.

The particles’ inertia within a medium is a fundamental factor in their vibration, leading to a transient transition in their vibration state. The interaction force between adjacent particles is multifrequency, resulting in the wave propagating in the medium in a multifrequency form. Therefore, understanding particle inertia’s role in wave propagation is essential for comprehending the physics principles underlying acoustic wave propagation.

The acoustic wave propagating in the medium forms a wave group composed of all frequency components, each with a different propagation speed and producing different propagation attenuation. The measured signal encapsulates all the frequency components of fluctuations propagating to the observation point, inducing vibrations on the surface of the receiving transducer. Furthermore, the internal stress of the interaction between adjacent particles in different spatial locations varies, leading to changes in the time domain waveform and spectrum of the acoustic wave with increased propagation distance. This means that the propagation of the acoustic wave in a viscous medium results in distortion of the acoustic wave, highlighting the practical implications of our work.

Therefore, the propagation of acoustic waves in the viscous medium can be seen as a parallel/series lumped particle-vibration transmission network system. This system elucidates the connection between particle vibration-damping attenuation, interaction between the particle and adjacent particle, fluctuation propagation attenuation, internal noise, and acoustic wave propagation in a viscous medium. Let us say there are M particles in the propagation path of the acoustic wave, and the distance between two adjacent particles in the medium is $\Delta x$. It is crucial that, if the computer speed and memory capacity allow, the selected $\Delta x$ should be small enough to guarantee the accuracy of the calculation results, underscoring the importance of computational resources in our research.

5 The Kaiser effect

The Kaiser effect is a function of the solid, i.e., an ability to memorize a solid’s history of being subjected to the most significant stresses. The rock formation also has this function. When a more prominent force beyond its maximum stress is applied to a solid sample, the solid sample rapidly increases the frequency of acoustic emission events.

Measuring acoustic emission using the Kaiser effect relies on internal or potential defects in a rock to automatically produce acoustic emission events as they change state in response to external action. There are many applications, such as stress testing. Usually, acoustic emission measurements are made in the laboratory by applying a uniaxial pressure to a rock sample. We can predict the stresses in the subsurface rock formation or oil reservoir based on the applied pressure corresponding to the initial moment of measured acoustic emission events increasing rapidly from the rock sample.

As shown in Fig. 19, if the stress component in the Cartesian coordinate system is known under a particular stress state, converting the stress component to the polar coordinate system is straightforward using a simple relational equation.

Fig. 19

Coordinate transformation of stress

Let us consider setting the stress components ($\sigma_{x}$, $\sigma_{y}$ and $\tau_{xy}$) in a Cartesian coordinate system. Then, we convert it to a polar coordinate system ($\sigma_{r}$, $\sigma_{\theta }$, and $\tau_{r\theta }$). Take A to be a tiny triangular volume element with unit thickness. The side $\overline{ab}$ is parallel to the y-axis, the side $\overline{ac}$ is parallel to the x-axis, and the angle between the two sides ($\overline{ab}$ and $\overline{bc}$) is θ.

Let ${\text{d}}l$ be the length of $\overline{bc}$, then the lengths of the sides $\overline{ab}$ and $\overline{ac}$ are ${\text{d}}l\cos \theta$ and ${\text{d}}l\sin \theta$, respectively. The area corresponding to the side $\overline{bc}$ is ${\text{d}}s_{1} = {\text{d}}l \times 1$, then corresponding to the side $\overline{ab}$ and $\overline{ac}$, the areas are

$${\text{d}}s_{2} = {\text{d}}s_{1} \cos \theta$$

(26a)

$${\text{d}}s_{3} = {\text{d}}s_{1} \sin \theta$$

(26b)

The tiny triangular volume element A is stationary. Based on the static equilibrium condition, the sum of all the stress components in the direction perpendicular to the side $\overline{bc}$ is zero, i.e., $\sum F_{r} = 0$. Therefore, the stress equilibrium equation in this direction yields

$$\sigma_{r} {\text{d}}s_{1} - \sigma_{x} {\text{d}}s_{2} \cos \theta - \sigma_{y} {\text{d}}s_{3} \sin \theta - \tau_{xy} {\text{d}}s_{2} \sin \theta - \tau_{yx} {\text{d}}s_{3} \cos \theta = 0$$

(27)

Substituting Eqs. 26a and 26b in Eq. 27 leads to

$$\sigma_{r} = \sigma_{x} \cos^{2} \theta + \sigma_{y} \sin^{2} \theta + 2\tau_{xy} \sin \theta \cos \theta = \left( {\frac{{\sigma_{x} + \sigma_{y} }}{2}} \right) + \left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)\cos 2\theta + \tau_{xy} \sin 2\theta$$

(28)

The equilibrium equation for the stress component in the parallel direction of the side $\overline{bc}$ of the tiny triangular volume element A is $\sum F_{\theta } = 0$, i.e.,

$$\tau_{r\theta } = \left( {\sigma_{y} - \sigma_{x} } \right)\sin \theta \cos \theta + \tau_{xy} \left( {\cos^{2} \theta - \sin^{2} \theta } \right) = \tau_{xy} \cos 2\theta - \left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)\sin 2\theta$$

(29)

Similarly, we take the tiny triangle volume element B with the unit thickness. The sum of the stress components in the perpendicular direction of its hypotenuse is zero, and it yields the following relationships,

$$\sigma_{\theta } = \sigma_{x} \sin^{2} \theta + \sigma_{y} \cos^{2} \theta - 2\tau_{xy} \sin \theta \cos \theta = \left( {\frac{{\sigma_{x} + \sigma_{y} }}{2}} \right) - \left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)\cos 2\theta - \tau_{xy} \sin 2\theta$$

(30)

From Eqs. 28 and 30, eliminating $\theta$ yields

$$\left( {\sigma_{r} - \frac{{\sigma_{x} + \sigma_{y} }}{2}} \right)^{2} + \tau_{r\theta }^{2} = \left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)^{2} + \tau_{xy}^{2}$$

(31)

When the oblique section corresponding to the side $\overline{ob}$ varies with the azimuthal angle $\theta$, the trajectory of the stresses $\sigma_{r}$, $\tau_{r\theta }$ in Eq. 31 within the $\sigma - \tau$ Cartesian coordinate system is a circle with its center on the transverse axis σ-axis, at a distance $\left( {\frac{{\sigma_{x} + \sigma_{y} }}{2}} \right)$ from the origin and a radius $\left[ {\left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)^{2} + \tau_{xy}^{2} } \right]^{1/2}$. The circle described by Eq. 31 is referred to as the Mohr stress circle.

By selecting a scale within the $\sigma - \tau$ coordinate system and measuring $\overline{{OB_{1} }} = \sigma_{x}$ and $\overline{{B_{1} D_{1} }} = \tau_{xy}$, one can determine a point $D_{1} (\sigma_{x} ,\tau_{xy} )$ in the $\sigma - \tau$ two-dimensional space as shown in Fig. 20. The point $D_{1} (\sigma_{x} ,\tau_{xy} )$ represents the stress in the $x$-plane of the tiny triangular volume element.

Fig. 20

Determination of $D_{1} (\sigma_{x} ,\tau_{xy} )$ in the $\sigma - \tau$ coordinate system

Measuring $\overline{{OB_{2} }} = \sigma_{y}$ and $\overline{{B_{2} D_{2} }} = \tau_{yx}$, a point $D_{2} (\sigma_{y} ,\tau_{yx} )$ in two-dimension space can be determined as shown in Fig. 21. The point $D_{2} (\sigma_{y} ,\tau_{yx} )$ represents the stress in the $y$-plane of the tiny triangular volume element.

Fig. 21

Determination of $D_{2} (\sigma_{y} ,\tau_{yx} )$ in the $\sigma - \tau$ coordinate system

The line connecting the points $D_{1} (\sigma_{x} ,\tau_{xy} )$ and $D_{2} (\sigma_{y} ,\tau_{yx} )$ intersects with the $\sigma$-axis at point C. Since the relationship $\tau_{xy} = \tau_{yx}$ exists for shear stresses, $\overline{OC}$ is the median line of the trapezoid $AD_{1} D_{2} B$ and is equal to $\left( {\frac{{\sigma_{x} + \sigma_{y} }}{2}} \right)$. As depicted in Fig. 22, the Mohr stress circle is obtained with a point $C\left( {\frac{{\sigma_{x} + \sigma_{y} }}{2},0} \right)$, serving as the center of the circle and line segment either $\overline{{CD_{1} }}$ or $\overline{{CD_{2} }}$ serving as the radius.

Fig. 22

Establishment of Mohr’s stress circle

As long as the three principal stresses ($\sigma_{x}$, $\sigma_{y}$, and $\tau_{xy}$) are known, one can establish the corresponding Mohr’s stress circle. Then, one can obtain any of the principal stresses and shear stresses in the tiny volume with a horizontal angle $\theta$ from Mohr’s stress circle.

From Fig. 22, the maximum horizontal principal stresses can be obtained by determining the point $A_{1}$ in the $\sigma - \tau$ Cartesian coordinate system as follows,

$$\sigma_{1} = \left( {\frac{{\sigma_{x} + \sigma_{y} }}{2}} \right) + \sqrt {\left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)^{2} + \tau_{xy}^{2} }$$

(32)

By determining the point $A_{2}$, one can obtain the horizontal minimum principal stress as

$$\sigma_{2} = \left( {\frac{{\sigma_{x} + \sigma_{y} }}{2}} \right) - \sqrt {\left( {\frac{{\sigma_{x} - \sigma_{y} }}{2}} \right)^{2} + \tau_{xy}^{2} }$$

(33)

Let the angle between the horizontal direction and the maximum principal stress be $\beta$. One may obtain the following relationship from Fig. 22 and Eq. 28 by turning $2\beta$ clockwise from $\overline{{CD_{1} }}$ to $\overline{{CA_{1} }}$,

$$\tan 2\beta = \frac{{ - 2\tau_{xy} }}{{\left( {\sigma_{x} - \sigma_{y} } \right)}} = \frac{{\sigma_{{0^{ \circ } }} + \sigma_{{90^{ \circ } }} - 2\sigma_{{45^{ \circ } }} }}{{\sigma_{{0^{ \circ } }} - \sigma_{{90^{ \circ } }} }}$$

(34)

Since the subsurface rock formation is subject to triaxial stresses, we need to cut four rock samples for acoustic emission measurements from a subsurface core in the directions [51] as shown in Fig. 23: one rock sample is parallel to the axial direction of the rock core, and the other three rock samples are perpendicular to the axial direction of the rock core at 45° intervals. If one perpendicular to the rock core is determined horizontally oriented in the $x$-axis and the stress in the $x$-axis direction is $\sigma_{{0^{ \circ } }}$, then the stresses in the other two rock samples perpendicular to the core are $\sigma_{{45^{ \circ } }}$ and $\sigma_{{90^{ \circ } }}$, and the stress in the axial direction parallel to the core is $\sigma_{v0}$. By measuring the “Kaiser” stresses of the four rock samples above, the stresses in each of the four directions can be measured: $\sigma_{{0^{ \circ } }}$, $\sigma_{{45^{ \circ } }}$, $\sigma_{{45^{ \circ } }}$, and $\sigma_{v0}$. Bringing the square of Eq. 34 into Eqs. 32 and 33, the maximum, minimum, and vertical principal stresses in the horizontal direction of the rock layer can be obtained by the following equations, respectively

$$\sigma_{H} = \sigma_{1} + \alpha p_{p} { = }\left( {\frac{{\sigma_{{0^{ \circ } }} + \sigma_{{90^{ \circ } }} }}{2}} \right) + \left( {\frac{{\sigma_{{0^{ \circ } }} - \sigma_{{90^{ \circ } }} }}{2}} \right)\left( {1 + \tan^{2} 2\beta } \right)^{1/2} + \alpha p_{p}$$

(35)

$$\sigma_{h} = \sigma_{{2}} { + }\alpha p_{p} { = }\left( {\frac{{\sigma_{{0^{ \circ } }} + \sigma_{{90^{ \circ } }} }}{2}} \right) - \left( {\frac{{\sigma_{{0^{ \circ } }} - \sigma_{{90^{ \circ } }} }}{2}} \right)\left( {1 + \tan^{2} 2\beta } \right)^{1/2} + \alpha p_{p}$$

(36)

$$\sigma_{v} = \sigma_{v0} + \alpha p_{P}$$

(37)

and

$${\text{tan}}2\beta = \frac{{\sigma_{{0^{ \circ } }} + \sigma_{{90^{ \circ } }} - 2\sigma_{{45^{ \circ } }} }}{{\sigma_{{0^{ \circ } }} + \sigma_{{90^{ \circ } }} }}$$

(38)

where $\sigma_{H}$ and $\sigma_{h}$ are the maximum and minimum principal stresses in the horizontal direction, $\sigma_{v}$ is the principal stress in the vertical direction, $\alpha$ is the effective stress coefficient of the formation, $p_{p}$ is the pore pressure in the rock, $\sigma_{v0}$ is the Kaiser stress measured in the vertical direction, $\sigma_{{0^{ \circ } }}$, $\sigma_{{45^{ \circ } }}$, and $\sigma_{{90^{ \circ } }}$ are the Kaiser stresses obtained by measuring the rock samples at the 0°, 45°, and 90° directions, respectively, and $\beta$ is the angle between the 0° direction and the direction of the maximum principal stress.

Fig. 23

Orientation of the four rock samples cut from the core

By conducting measurements on the four rock samples depicted in Fig. 23, we can obtain the correlation between acoustic emission events and the pressure exerted on the rock samples. This correlation allows us to get four Kaiser stresses: $\sigma_{{0^{ \circ } }}$, $\sigma_{{45^{ \circ } }}$, $\sigma_{{90^{ \circ } }}$, and $\sigma_{v0}$.

Through a complex series of calculations using formulas [35,36,37,38], we can determine the maximum and minimum horizontal and vertical principal stresses of underground rock formations or reservoirs. Our apparatus’s acoustic transducer (AT) acts as an intricate acoustic-electric filter, generating electric signals. By leveraging these electrical signals and the electric-acoustic conversion characteristics of the acoustic transducer, we can invert the actual acoustic signal produced by a pressured rock sample. This inversion allows us to delve into the relationship between the frequency properties of the actual acoustic signal and the physical properties of the rock sample, the pressure applied to the rock sample, the confining pressure provided during the pressure process, the radius of the rock sample, the Kaiser effect, and the microcracks generated. Therefore, this in-depth analysis also enables us to use the recorded number of acoustic emission events produced by pressurized rock samples to obtain the geomechanical stress within underground rock formations or reservoirs to design oil well fracturing.

The acoustic emission data acquisition system consists of two acoustic receiver transducers (AT), pressure transducers (PT), preamplifiers, a data collector, a computer interface, and a desktop (laptop) computer, as shown in Fig. 24.

Fig. 24

The data acquisition system used in events of acoustic emission

Figure 25 shows the waveforms of the acoustic signals captured when the pressurized shale samples produced acoustic emissions. This experimental measurement suggests that the Kaiser effect exists in the Pierre Shale to some extent.

Fig. 25

The waveforms of acoustic emission signals collected before the rupture of pressurized shale samples

Figure 26 shows the waveforms of the acoustic signals captured when acoustic emissions were generated from the pressurized limestone samples. This experimental measurement indicates that the Kaiser effect is also present to some extent in limestone.

Fig. 26

The waveforms of acoustic emission signals collected before the pressurized limestone sample ruptured

The two experiments described above show that (i) the number and frequency of acoustic emission signals will suddenly increase when the rock sample breaks under pressure, and (ii) the influence of confining pressure on the relationship between acoustic emission and applied pressure decreases.

6 Conclusions

We present this review concerning the innovative approach primarily developed in our group, introducing novel 4th/8th polynomials to model the reflection/refraction angles in the VTI-TTI medium interface accompanied by a cutting-edge fast algorithm for calculating the reflection/refraction coefficients. This method is quick and highly effective. The calculated reflection/refraction angles adhere to Snell’s theorem, and the reflection/refraction coefficients strictly follow the energy conservation law, marking a significant advancement in our field.

The influence of the rock’s anisotropy and the TTI medium’s slope angle on the amplitude and phase of the reflection/refraction coefficients and the critical incidence angle is significant. However, what truly stands out is the substantial changes in the polarization direction and trajectory of inhomogenous mode conversion waves generated at anisotropic rock interfaces for the case with existing abnormal incidence angles. This key finding has direct implications for our field.

The mechanism of acoustic attenuation of acoustic waves propagating in viscous media is different from that of attenuation of electromagnetic waves propagating in non-ideal media. The amplitude attenuation of sinusoidal electromagnetic waves propagating in a non-ideal medium is only the propagation attenuation. In contrast, the amplitude attenuation of acoustic waves propagating in viscous solids is determined by the damping attenuation of the particle vibration and the propagation attenuation of the fluctuations together.

Our investigation into the acoustic Goos-Hänchen effect at the liquid-solid interface has led to a groundbreaking conclusion. We have challenged the conventional acoustic logging model’s assumption of a gliding refraction P wave, finding that the first arrival measured by acoustic logging is a reflected P wave, and its propagation speed on a fluid-solid interface is a function of incidence angle. This discovery and our exploration of joint inversion methods hold immense potential for the field, particularly in improving the accuracy of inverting oil and gas reservoirs.

Based on the study of depth-time conversion of seismic exploration signals propagating in two layers of anisotropic rock media and considering the difference between energy velocity vectors and phase velocity vectors, a new ray-tracing algorithm for the propagation of seismic exploration signals in multilayered anisotropic strata is established for the accurate time-depth conversion and AVO analysis of seismic exploration signals propagating in multilayered anisotropic rock layers. For the same sinusoidal acting force, the transient process of particle vibration inside different viscous media is different, i.e., the intrinsic noise generated is different, and its spectrum and center frequency are also different.

We have developed a parallel equivalent dynamic electric-acoustic/acoustic-electric conversion network model for piezoelectric transducers. This model comprehensively explains the acoustic measurement process when excited by electric/acoustic signals containing multifrequency components. These insights are invaluable for the field of wave propagation and exploration geophysics, offering new avenues for exploration and discovery. With the understanding of the Kaiser effect, we introduced the method of measuring acoustic emissions generated by rock samples under pressure to predict the principal stresses of underground rock, which can be fruitful for the fracturing engineering design of oil wells.

In summary, we have presented a review of the new advancements in acoustic exploration, focusing on the work of our research groups and shedding light on future practical applications. Our findings contribute to scientific, economic, and cultural knowledge while supporting innovations in exploration tools and capabilities. These new insights pave the way for future discoveries and advancements in the field.