1 Introduction

One of the long-standing puzzlements in Indian astronomy has been the calculation of latitude. By that, we mean the computation of the latitude of the five visible planets and the Moon. Various interpretations of the Indian latitude algorithm that the savants of the past have put forward have thus far been unsuccessful in calculating the actual latitude of these heavenly bodies with any reasonable accuracy, and there appear to be two reasons for this failure.

First, the terse and cryptic nature of ancient Indian texts, where information is presented in a highly compressed and minimalistic fashion, makes them prone to misinterpretation. Second, the curious fact that there appears to be missing information in the Sūryasiddhānta, perhaps erased unwittingly or withheld deliberately. Though the overall latitude algorithm given in the Sūryasiddhānta is entirely correct per modern spherical trigonometry, a vital sub-calculation in the process, namely, that of computing the maximum latitude, appears to be missing altogether. The mystery is compounded by the puzzling fact that Indian astronomers of yore have completely ignored this missing bit of information.

To summarize, the latitude conundrum in Indian astronomy comprises two related issues: (i) a missing sub-algorithm relating to the calculation of maximum latitude and (ii) the curious fact that this missing algorithm has never been noticed or mentioned by Indian astronomers of the past. In this paper, we take a detailed look at the Indian latitude algorithm while keeping our scope limited to that of the Moon. We do this primarily because the algorithm for the Moon is considerably simpler than that for the planets, and our current approach needs to be vetted on the simplest case first.

2 The wayward Moon

The study of Lunar motion has vexed not a few people in the past, including Sir Isaac Newton. It is well-known that our closest neighbor in space moves in a highly erratic fashion, making the accurate prediction of its motion a daunting task. This irregularity is because the motion of the Moon is influenced by two bodies–the Earth and the Sun. The combined gravitational effect of these two bodies produces great fluctuations in the motion of the Moon, as shown in Fig. 1a, b.

Fig. 1
figure 1

Irregular motion of the Moon

Full size image

Figure 1a shows the variation of the anomalistic period of the Moon over 200 orbits starting January 1, 2000. The anomalistic period is the time taken by the Moon to move from one perigee to the next. Its average duration is 27.55 days. As seen in the figure, the anomalistic period changes continuously from month to month, from orbit to orbit. It varies from about 27 days to nearly 28 days – almost a full day, which is a considerable variation for a 28 day cycle.

Similarly, Fig. 1b shows the variation of lunar apogee distance from the Earth for the same time range. The average distance is about 405,400 km. It can be observed that there is considerable variation in this distance from month to month. Quite a few short-term and long-term variations can be discerned in these figures.

The motion of the Moon is highly irregular due to the dual influences of the Earth and the Sun, and accurately predicting its longitude and latitude will be no easy task.

3 The Moon in Indian astronomy

The Moon occupies a central place in Indian calendric astronomy. Since time immemorial, the fundamental units of the Indian calendar have been the Lunar Day and the Lunar Month. In the Luni-Solar calendar, a new month always begins at Sun-Moon conjunctions. Furthermore, Lunar and Solar eclipse calculations depend critically on accurate prediction of the Moon’s position. Thus, it becomes apparent that an error-prone Moon calculation can throw the entire calendar into chaos, which is not the case in the long-standing traditional Indian Luni-Solar calendar that is brought out every year. The ancient Indians appear to have developed two techniques for astronomical computation: (i) the Siddhāntam method and (ii) the Vākiam, or Kārana method.

The former is a rigorous procedure that starts from first principles and adopts a complex planetary model involving multiple epicycles. This technique is suited for mathematicians and astronomers. The second is a practical approach that relies heavily on reference tables. This method is adopted by calendar makers, astrologers, and amateur astronomers, who want results quickly without dwelling deep into geometry and mathematics (Narayanan, 2022).

The extensive amount of ancient literature available on these two techniques is a strong testament to the antiquity and maturity of Indian astronomy and its popularity and widespread use among the masses. It becomes obvious that the ancient Indians expended a great deal of effort towards the science of astronomy, the Moon in particular, due to its paramount significance to the Indian calendar.

The Indian model for the planets, with its dual-pulsating epicycles, is, mathematically speaking, far greater in complexity than those of any other ancient civilization. Therefore, it is reasonable to suppose that the Moon too must have received an equally rigorous treatment at the hands of the ancient Indians, and their acumen must have produced a near-perfect prediction method for the Moon’s latitude as well. Proceeding with that assumption, let us look at the latitude algorithm for the Moon in Indian astronomy.

4 Latitude algorithm of the Moon

The Indian text we will refer to is the Sūryasiddhānta (Burgess, 1858), a revered, extant treatise among the various works of ancient Indian astronomy, many of which are now lost. The original text has been estimated to be older than 3000 BC (Brennand, 1988; Narayanan, 2010).

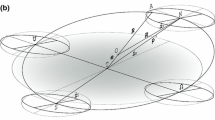
Figure 2 shows a schematic of the Moon’s latitude. The Moon (m) revolves around the Earth (e). The plane of the Moon’s orbit is observed to incline with respect to the ecliptic. The ecliptic, as we know, represents the plane of the Earth’s orbit around the Sun. This tilt is approximately five and ¼ degrees and varies a little from orbit to orbit due to the Sun's gravitational influence.

Fig. 2
figure 2

The Moon’s latitude

Full size image

The inclined orbit of the Moon meets the ecliptic at two points, the nodes. At the ascending node (a) the Moon moves from the southern side of the ecliptic to the northern, while at the descending node (d) it does the opposite.

At any point, the Moon’s latitude (L) is its angular distance from the ecliptic. In the diagram, this is represented by the arc bm. The maximum latitude (Lmax) is the arc cp.

The arc ab, which represents the longitude of the Moon along the ecliptic from the ascending node, is called the argument of latitude (AoL) since the Moon’s latitude has a direct relation to it. When the Moon is at either node (a or d) the AoL is 0° or 180°, and its latitude is zero. Conversely, when the Moon is at p or q, the AoL is 90° or 270°, and its latitude (north or south) is at a maximum.

Using standard laws of mathematics, we can calculate the arc bm, which is the latitude L. According to the laws of spherical geometry (Smart, 1977), Δabm and Δacp are similar spherical triangles. Thus, their sides are related by the following expression:

$$\frac{{\sin \left( {bm} \right)}}{{\sin \left( {ab} \right)}} = \frac{{\sin \left( {cp} \right)}}{{\sin \left( {ac} \right)}}.$$

Since Indian astronomy employs RSines instead of plain Sines, we will multiply both sides of the above expression by the radius (R).

$$\frac{{{\text{R}} \times \sin \left( {bm} \right)}}{{{\text{R}} \times \sin \left( {ab} \right)}} = \frac{{{\text{R}} \times \sin \left( {cp} \right)}}{{{\text{R}} \times \sin \left( {ac} \right)}},$$

Or,

$$\frac{{{\text{R}}{\text{Sin}} {\text{e }} \left( {bm} \right)}}{{{\text{R}}{\text{Sin}} {\text{e }} \left( {ab} \right)}} = \frac{{{\text{R}}{\text{Sin}} {\text{e }} \left( {cp} \right)}}{{{\text{R}}{\text{Sin}} {\text{e }} \left( {ac} \right)}}.$$

The standard radius in Indian astronomy is set as 3438 arc-minutes. Hence, RSine(bm) equals the arc bm in arc-minutes, which is the Latitude (L). Similarly, RSine(cp) gives the maximum latitude (Lmax) in arc minutes, and since angle ac = 90°, RSine(ac) simply equals the radius R.

In other words, the modern relation for calculating the Moon’s latitude equates to the following expression:

$$L = \frac{{{\text{R}}{\text{Sin}} {\text{e}}\,\left( {ab} \right) \times L_{\max } }}{{\text{R}}} .$$
(1)

Referring to the Sūryasiddhānta (Chapter-II/Verse-57), we find the following instructions for computing the Moon’s latitude:

The RSine of the arc found by subtracting the place of the node from that of the Moon, being multiplied by the extreme latitude, and divided by the radius, gives the latitude.

Thus, we see that the ancient Indian expression for computing the Moon’s latitude exactly matches the modern expression, indicating that the ancient Indians were well-versed in spherical trigonometry, as concluded by John Warren (Kāla Sankalita, 1825):

From modern rules of mathematics, it becomes apparent that the people of India, at some former period, were well acquainted with the theory of Spherical Trigonometry, if they be not acquainted with it at present.

We note from Eq. 1 that the Moon’s latitude algorithm is simplicity itself. However, there is one puzzling fact associated with it. Nowhere in the Sūryasiddhānta is mentioned how to compute the maximum latitude (Lmax), which, as we know, varies from orbit to orbit.

The text itself does provide a clear hint that Lmax is variable by presenting something called the Mean-Max latitude (Lindian-mean-max), which represents a sort of mean value for the maximum latitude, but it does not provide a way to compute Lmax. We may conjecture that perhaps Lmax is expected to be obtained in some well-known or obvious way from Lindian-mean-max, since nothing more is mentioned on the subject in the text. This is the crux of the puzzle we are investigating.

Let us begin our analysis by examining the actual month-to-month variation of the Moon’s maximum latitude.

5 The Moon’s maximum latitude

Figure 3, shows the actual variation of the Moon’s maximum northern latitude from orbit to orbit (month-to-month) for 100 consecutive months, starting from January 1, 2020, computed using modern formulae (Meeus, 2000). Each dot represents the maximum latitude for that month. A similar variation occurs for southern maximum latitudes as well.

Fig. 3
figure 3

Variation of maximum northern latitude of the Moon

Full size image

We can observe that Lmax changes periodically, varying from a minimum of around 5° to a maximum of about 5.3°, the mean value being 5.14° (upper dashed line in the figure), which we will call the Actual Mean-Max latitude.

Further below in the figure is shown another dashed line, which represents the mysterious Indian Mean-Max latitude (Lindian-mean-max) of Indian astronomy, which is defined as 4.5° for the Moon in the Sūryasiddhānta. It is obvious from the figure that the Indian Mean-Max latitude has no relation to the Actual Mean-Max latitude, which brings up the question–what exactly does the Indian Mean-Max represent?

Let us examine the verses that define the Indian Mean-Max latitude in the Sūryasiddhānta (Chapter-I/Verses-68, 69, 70):

The Moon is, by its node, caused to deviate from the limit of its declination, northward and southward, to a distance, when greatest, of an 80th part of the minutes in a circle.

Jupiter, to the 9th part of that multiplied by 2; Mars, to the same amount multiplied by 3; Mercury, Venus, and Saturn, to the same amount multiplied by 4

Thus: 270, 90, 120, 60, 120, and 120, are the number of minutes of Mean-Max Latitude of the Moon and the planets in their order.

The first verse indicates the physical reason, according to the ancient Indians, due to which the planet strays from the ecliptic, northward or southward. This is stated to be due to the action of the two nodes. The ascending node (Rāhu) attracts the planet northwards, while the descending node (Ketu) pulls it southwards. The net lateral movement of the planet at any point is a result of the ‘combined pull’ of the two nodes, which naturally depends upon the planet’s proximity to these nodes.

The first verse also indicates that the maximum latitude produced by the action of the nodes on the Moon is 4.5°, but it states so in a strange fashion–the 80th part of a circle (360°/80 = 4.5°). Why this strange wording? Why not say 4.5° directly? Is this simply an attempt by the author of the Sūryasiddhānta to fit the poetic meter of the verse, or are there deeper waters here? We will come back to this later.

The second verse indicates how to compute the Mean-Max latitudes for the five visible planets. To ensure no ambiguity, the third verse explicitly states these computed values of Mean-Max for each planet. For a terse and succinct text like the Sūryasiddhānta, this repetition of information is quite out of character and is indicative of the great significance attached to these Mean-Max latitudes by the text. This verse also explicitly states that these numbers are only mean values of the maximum latitude (madhyama-vikṣepa), which is important to note.

As an aside, the ‘order’ of the planets in the third verse refers to the order of weekdays: Monday (Moon), Tuesday (Mars), Wednesday (Mercury), Thursday (Jupiter), Friday (Venus), and Saturday (Saturn).

Before continuing our analysis any further, it may be useful to examine how various Indian astronomers of the past interpreted the Moon’s Mean-Max latitude.

6 Interpretations by various authorities

6.1 Āryabhaṭa (~ 495 CE)

We learn from ancient writers that Āryabhaṭa was the foremost astronomer of his time and that he had written several treatises on mathematics and astronomy, all of which have unfortunately been lost, except a minor pamphlet – the Āryabhaṭīyam (Clark, 1930). His major work, the Ārya-Siddhānta, was one of a trio of books from India that taught the first generation of Arab astronomers.

The Gola (spherics) section of the Āryabhaṭīyam presents the following verse (V3):

The Moon, from its nodes, moves northward and southward of the ecliptic.

Verse 6 of the Dasa-Gītika (ten verses) section has a single mention of the Moon’s maximum latitude:

The greatest deviation of the Moon from the ecliptic is 4.5 degrees.

Thus, while the Sūryasiddhānta clearly states that 4.5° is only a sort of mean of the maximum, Āryabhaṭa appears to consider this value as an absolute maximum for the Moon’s latitude.

6.2 Varāhamihira (~ 530 AD)

Varāhamihira was an astrologer who lived in the Ujjain region of central India. Though his date is not very certain, he is known to have lived after Āryabhaṭa, whose work he mentions. He wrote several books on astrology and one on astronomy—the Pacasiddhāntas (five treatises) (Thibaut, 1889), which is a compendium containing the distilled essence of five well-known astronomical works of his time, namely, the Sūryasiddhānta, Brahmasiddhānta, Vaśiṣṭhasiddhānta, Pauliṣasiddhānta, and the Romakasiddhānta.

In the Pauliṣasiddhānta chapter, we find:

When the Moon is 90° distant from the ascending node her latitude attains its maximum of 270 minutes (4.5°).

In the Romakasiddhānta chapter, the following expression is given to find the Moon’s latitude:

Multiply the Sine of the Moon’s distance from its node by 21 and divide by 9.

Instead of the usual Indian radius of 3438 units, the Romaka adopts the Greek radius of 120 units and its associated sine. Thus, Eq. 1 becomes:

$$L = \frac{{{\text{R}}{\text{Sin}} {\text{e }} \left( {ab} \right) \times L_{\max } }}{120} ,$$
$${\text{or }}, \frac{{L_{\max } }}{120} = \frac{21}{9}.$$

Therefore, Lmax = 120 21/9 = 280 min = 4.67˚.

We may conjecture that the Romaka intended to use the Indian value of 270 min (4.5°) for the maximum latitude and that 21/9 is an approximation for 270/120.

One interesting observation here is that according to Western scholars, both the Pauliṣa and Romakasiddhāntas were borrowed by the Indians from Greek sources. However, Ptolemy’s Almagest (mentioned further below) gives the maximum latitude of the Moon as 5.0°. If the Paulisa and Romaka are truly of Greek origin, it is puzzling why they did not adopt Ptolemy’s value for the Moon’s maximum latitude.

6.3 Brahmagupta (~ 630 CE)

The astronomer Brahmagupta is believed to have lived in the Bhinmal region of modern Rajasthan in India. In later life, he is said to have moved to Ujjain, one of two major centers for astronomy in India. After moving to Ujjain he composed his second major work, the Khanda Khādyaka (Sengupta, 1934). According to the Persian scholar Al-Birunī, this was a much sought-after book by both amateurs and experts alike in those times.

In the chapter on Lunar Eclipses of the Khanda khādyaka we find:

From the longitude of the Moon subtract that of the ascending node; The sine of the resulting arc multiplied by 9 and divided by 5 gives the latitude of the Moon in minutes.

Since Brahmagupta’s system employed a radius of 150 units, Eq. 1 becomes:

$$L = \frac{{{\text{R}}{\text{Sin}} {\text{e }}\,\left( {ab} \right) \times L_{\max } }}{150} ,$$
$$or{\text{ }},\frac{{L_{{\max }} }}{{150}} = \frac{9}{5}.$$

Therefore, Lmax = 150 9/5 = 270 min = 4.5°.

6.4 Lalla (~ 760 CE)

Lalla was an Indian astronomer who lived in the southern part of Gujarat. Only two of his works are currently extant. In the Lun ar Eclipse chapter of Śiṣyadhīvṛddhida Tantra (Chatterjee, 1981) the following verse is found:

Subtract from the Moon’s longitude the longitude of the ascending node.

Find RSine of the result, multiply it by 15, and divide by 191. The result is the latitude of the Moon.

Since Lalla used the standard Indian radius of 3438 units, Eq. 1 becomes:

$$L = \frac{{{\text{Sin}} {\text{e}}\,\left( {ab} \right) \times L_{\max } }}{3438} ,$$
$$Or, \frac{{L_{\max } }}{3438} = \frac{15}{{191}}.$$

Thus, Lmax = 3438 15 /191 = 270 min = 4.5°.

6.5 Mañjula (~ 935 CE)

Though the astronomer Mañjula’s location is not known for certain, he is thought to have lived in northern India, possibly near Patna in modern Bihar. In his Laghu-Mānasa we find the following reference to the Moon’s latitude (Shukla, 1990):

Subtract the longitude of the ascending node from that of the Moon; Find the RSine of the result and multiply it by 36. The result is the latitude of the Moon in minutes.

Mañjula’s system employed the unusual radius of 8′ 8′′, so Eq. 1 becomes:

$$L = \frac{{{\text{Sin}} {\text{e}}\,\left( {ab} \right) \times L_{\max } }}{8.133} ,$$
$$Or, \frac{{L_{\max } }}{8.133} = \frac{36}{1}.$$

Therefore, Lmax = 8.133 36 = 292.8 min = 4.88°.

6.6 Bhāskara-II (~ 1150 CE)

Bhāskara II, the great mathematician and astronomer who dates to the early part of the second millennium, is believed to have lived in the region of present-day Maharashtra. In his astronomical treatise, the Graha-Gaṇita (Arka Somayaji, 1980), within the section on Lunar Eclipses, is found the expression to calculate the latitude of the Moon:

$$L = \frac{{{\text{R}}{\text{Sin}} {\text{e}}\,\left( {ab} \right) \times 270}}{{\text{R}}} .$$

Thus, the maximum latitude will be 270 min = 4.5°, which will occur when RSine = R, that is, when the argument of latitude is 90°.

6.7 Nīlakaṇṭha (~ 1500 AD)

Nīlakaṇṭha Somayājī was an astronomer and mathematician who belonged to the Kerala School of Mathematics and flourished during medieval times. His most influential astronomical work, the Tantrasaṅgraha, was completed in 1501 CE (Ramasubramanian, 2011).

In the Lunar Eclipses chapter are found the following verses:

The RSine of the longitude of the node subtracted from the Moon is multiplied by 270 and divided by the Radius, which gives the latitude of the Moon.

This multiplied by the Moon’s orbital radius and divided by the actual distance between the Earth and the Moon gives the true value of latitude.

While the first verse appears to suggest that 270 min (4.5°) is the maximum latitude of the Moon, the second verse clarifies, in line with the general concept of the Sūryasiddhānta, that 4.5° is only the Mean-Max latitude.

Nīlakaṇṭha proclaims the actual latitude of the Moon as:

$$L_{\max } = \frac{{L_{{\text{Indian - mean - max}}} \times D_{{{\text{mean}}}} }}{{ D_{{{\text{actual}}}} }} ,$$
(2)

where Dmean is the mean distance of the Moon, and Dactual is the actual distance.

According to modern data, the mean distance of the Moon from the Earth is 239,000 miles, while the minimum and maximum are 226,000 and 252,000 miles, respectively. Plugging these values into Eq. 2 gives us the range of maximum latitude for the Moon as 4.27˚–4.76˚ according to Nīlakantha.

6.8 Ptolemy (~ 140 CE)

Finally, to round off our analyses of ancient savants, we must make a mention of the Greeks. Claudius Ptolemy was the greatest among the astronomers of Greek descent who lived in Alexandria, Egypt during the second century CE. His works represent the culmination of Greco-Roman science, particularly his work on astronomy, the ‘Mathematical Syntaxis’, known among the Arabs as the Almagest (Ptolemy, 1952).

In Book-V of the Almagest, he provides a lookup table for lunar latitudes, which presents the maximum latitude of the Moon as 5.0° exactly.

6.9 Summary of ancient literature

Table 1 shows a summary of information from ancient literature with regard to the maximum latitude of the Moon.

Table 1 Maximum lunar latitude according to various authorities
Full size table

We have added an extra column at the end that shows the obliquity of the ecliptic according to these ancient astronomers, which may have a bearing on the topic at hand, as will be explained later. From the third column of the table, we note that all Indian astronomers of yore have misconstrued the Sūryasiddhānta where it is explicitly stated that 4.5° is only a sort of mean value for the Moon’s maximum latitude and not the absolute maximum. In addition, all of them, except for Nīlakanṭha, have also assumed this supposed maximum of 4.5° (or near about) to be a constant as well.

This appears to indicate, quite shockingly, that none of these Indian or Greek savants of old ever made any actual observations of the Moon’s latitude themselves, or else they would have been aware that the maximum latitude is about 5.3°.

Figure 4 shows the Moon at 4.5° and 5.3° latitudes in a typical landscape, which indicates the magnitude of the error. It is seen that the difference between the two values amounts to more than 1 and ½ full-Moon widths; large enough to be easily perceived with the naked eye, and certainly not a trivial error. Yet, it appears that these leading lights of Indian and Greek astronomy have not noticed the substantial difference between their assumption and actuality.

Fig. 4
figure 4

Margin of Error for the Moon's Maximum Latitude

Full size image

The beginnings of modern European astronomy can be traced back to the 16th century when the Danish astronomer Tycho Brahe, vexed by the inaccurate astronomical tables of his time, decided to create a good observational data set for himself. His efforts over the years yielded an extensive collection of very accurate observational data, which eventually paved the way for significant discoveries by himself and others. This was the pre-telescope era, in which all observation was done with the naked eye. From his observations of the Moon, Tycho discovered, among other things, that the maximum inclination of the Moon’s orbit to the ecliptic was not 5° as stated by Ptolemy, but about 5.25°.

Thus, we are confronted with the startling realization that no Indian or Greek astronomer of old was able to determine by observation what Tycho Brahe found easily, namely, that the maximum latitude of the Moon is about 5.25°, and that this maximum varies from month to month. Note that the Moon attains its maximum latitude 2 times every month (north and south), therefore this is not one of those rare phenomena for which an astronomer must wait many years for a chance of observation.

A similar situation also occurs with the obliquity or tilt of the ecliptic. The tilt was 24° at about 3000 BC, and it has been decreasing slowly over the years, its current value being 23.44°. The obliquity is a parameter that can be determined easily by observation, and it is seen from the fourth column of the above table that 350 years before Āryabhaṭa, the Greek astronomer Ptolemy had determined this parameter to be 23.86°. Yet, like the Moon’s maximum latitude, all Indian astronomers have simply assumed the obliquity to be a constant 24° as stated in the ancient Sūryasiddhānta, without making any observational verification for themselves.

Summarizing our three findings thus far: (i) While the oldest extant Indian text, the Sūryasiddhānta, clearly indicates that 4.5° is only a sort of mean value for the Moon’s maximum latitude, the text does not provide a way to determine this maximum latitude; (ii) All Indian astronomers of old appear to have assumed the stated mean-max value of 4.5° to be the maximum latitude of the Moon, without making any observational verification themselves; (iii) These astronomers also appear to have assumed the obliquity of the ecliptic to be 24°, once again, without making any observational verification.

Let us take up the first item, and make a detailed study of the actual variation of the Moon’s maximum latitude from month to month, to see if we can perchance discover the missing algorithm in the Sūrya siddhānta.

7 Variation of the Moon’s maximum latitude

7.1 With anomaly

The first variable we will examine is the Moon’s anomaly. As depicted in Fig. 5, the anomaly (θ) is the angular distance of the Moon (m) from its apogee (a) as observed from the Earth (e). Note that when the anomaly is 0° the Moon is at its greatest distance from the Earth while at 180° it is the closest.

Fig. 5
figure 5

Moon's anomaly

Full size image

Recall from the previous section that the Indian astronomer Nīlakantha, unlike his compatriots, had stated that the Moon’s maximum latitude is not a constant but varies inversely with its distance from the Earth.

Figure 6 shows the variation of the Moon’s maximum latitude with respect to its anomaly over 600 consecutive months, starting from January 1, 2020. It is seen that the data is quite dispersed, with no perceivable linkage between the anomaly and maximum latitude, though we do observe a slight upward shift of the dataset when the anomaly is near 90°.

Fig. 6
figure 6

Variation of the Moon’s maximum latitude with anomaly

Full size image

7.2 With node-apogee separation

Another factor worth checking is the effect of the separation between the apogee and the node on the maximum latitude, for the same time range as above. The results are shown in Fig. 7.

Fig. 7
figure 7

Variation of the Moon’s maximum latitude with node-apogee separation

Full size image

Once again, we observe that the data appears to be highly dispersed with no clear correlation between the Node-Apogee separation and the maximum latitude, though there appears to be a slight downward shift of the dataset near 90°.

7.3 With elongation

Finally, we examine the variation of the Moon’s maximum latitude with its separation from the Sun, known as the Elongation, over 600 consecutive months starting January 1, 2020.

As seen in Fig. 8, we appear to have hit the jackpot with this parameter. Lmax is observed to have a direct relation to the elongation, almost a simple sinusoidal variation. We note that Lmax is a minimum when the elongation is 0° or 180°, and a maximum when it is 90° or 270°, and the entire variation closely resembles a sine wave.

Fig. 8
figure 8

Variation of the Moon’s maximum latitude with elongation

Full size image

Figure 9 depicts a physical summary of this finding. In Fig. A on the left, we see that when the separation between the Sun (s) and the Moon (m) is 90° or 270°, that is, first or third quarter Moon phase, and when the Sun is at either node, the Moon’s maximum latitude will be greatest (around 5.3°).

Fig. 9
figure 9

Configuration for Maximum and Minimum Lmax

Full size image

Conversely, as shown in Fig. B, when the Sun is aligned to the Earth-Moon axis, that is, at full Moon or new Moon, and the Sun is 90° from either node, the Moon’s maximum latitude will be least (around 5°).

8 Proposal for the missing algorithm

With these results, we are now in a position to make a broad-based proposal for the missing algorithm of the Moon’s maximum latitude in Indian astronomy.

Figure 10 shows two views of the standard Indian epicycle model for the Moon. The 2-D view depicts the Moon (m) revolving clockwise around the epicycle center, while the epicycle itself revolves counter-clockwise around the larger deferent circle, which has the Earth (e) at its center. The Mean Moon (mʹ) is located at the center of the epicycle. Note that the radius of the epicycle varies in time, as shown by the dashed line.

Fig. 10
figure 10

The Moon’s Epicycle

Full size image

In the 3-D view, we see that the deferent circle, on which the mean Moon revolves, is inclined to the ecliptic at 4.5°. This is the mean-max latitude (Lindian-mean-max) specified in the Sūryasiddhānta. Further, we note that the epicycle plane, in its turn, is inclined to the deferent plane. According to the Sūryasiddhānta, the nodes act upon both the Mean Moon (deferent) as well as the True Moon (epicycle), hence both will have separate inclinations of their own. Note that in this paper our focus is on the maximum latitude of the Moon, and Fig. 10 is only a general schematic representation to indicate that the deferent and epicycle circles have separate inclinations. This figure is not intended as a detailed model for the calculation of general latitude. The calculation of latitude in the epicycle model is an exceedingly complex affair. The interested reader can refer to available literature for further details (Swerdlow, 2005).

In the Indian epicycle model for the calculation of longitudes, the angular velocity of the mean planet on the deferent is set equal to the angular motion of the true planet on the epicycle. We may conjecture that a similar condition is applied implicitly to the calculation of latitudes as well, that is, the lateral motion of the mean planet on the deferent is proportionately equal to that of the true planet on the epicycle.

Now, while the Mean-Moon’s maximum latitude on the deferent is specified as 4.5°, how can we determine the maximum latitude of the True-Moon on the epicycle? We do that using the instruction in the Sūryasiddhānta (given in Sect. 5 above), which says that the maximum inclination equals an 80th part of the circumference. The Moon’s epicycle circumference (Cep) has been specified in the Sūryasiddhānta as approximately 32°, whose 80th part will be the inclination of the epicycle concerning the deferent, that is, 32/80 = 0.4°.

Putting all this together, we can propose the following empirical expression for the maximum latitude of the Moon, which comprises a base mean value over which a variation is superimposed:

$$L_{\max } = L_{Indian - mean - \max } + \frac{{ C_{ep} \times \left( {1 + {\text{Sin}} \left( E \right)} \right)}}{80},$$
(3)

where, the elongation (E) = (Sun’s Longitude)–(Moon’s Longitude).

The quantity (1 + sin(E)) can be regarded as a ‘pulsation factor’, which causes the circumference of the epicycle to vary (pulsate) in size from Cep to 2Cep.

Substituting known values into Eq. 3, we will have:

$$L_{{{\text{max}}}} = 4.5 + 0.4 \times \left( {1 + sin\left( E \right)} \right)$$
(4)

In the next section, we will compare the results of this proposed expression with actuality.

9 Results and discussion

Figure 11 compares the actual variation of the Moon’s maximum latitude with values obtained from Eq. 4 for 100 consecutive months starting January 1, 2020.

Fig. 11
figure 11

Variation of the proposed formula with actuality

Full size image

It can be seen that the proposed expression is in good agreement with actuality, except for a few points near the least maximum latitude, which is good enough for a first-cut estimate. The proposed expression can no doubt be improved with some simple extensions to bring it closer to actuality, but we will not attempt any further enhancements in this paper.

Using modern techniques such as the Fourier Transform, one can obtain a near-exact formula for the actual variation. However, that would likely result in very lengthy and complex expressions, which would be beyond what the ancient astronomer was capable of. Any future enhancements to the proposed expression for the missing algorithm should bear that in mind.

9.1 Possible reasons for the missing algorithm

Having shown that the variation of the Moon’s maximum latitude can be captured using a simple mathematical expression that is well within reach of the ancient Indian astronomer, we have now to deal with the question of why such an easy algorithm is missing in the Sūryasiddhānta in the first place, especially when the text indicates that the maximum latitude is variable. And there is the related question of why no Indian astronomer of old was even aware that the Moon’s maximum latitude is not 4.5° but 5.3°. Let us explore some possible answers to these questions.

9.1.1 The declination

It is, of course, quite inconceivable that no Indian astronomer ever made any actual observations. What is very likely, and practical moreover, is that the Moon’s latitude was not measured directly by the ancient astronomer, but only in an indirect manner, using the declination.

As mentioned, the latitude of heavenly bodies is measured regarding the ecliptic (see Fig. 2). To make this measurement directly without sophisticated instruments is not a simple task since the exact location of the ecliptic is not easy to pinpoint in the sky. Instead, the ancient astronomer usually based his observations on four easy-to-use reference points, namely: (i) The cardinal directions (north, south, east, west); (ii) The horizon; (iii) The pole star; (iv) The zenith point (directly overhead).

In Fig. 12, the observer is at O and his zenith point (Z) is directly overhead. His geographical latitude (Lo) is, say, 40° north, and therefore the north celestial pole (P) will appear to him 40° directly above the north point of the horizon (N). The southern horizon point (S) is directly opposite N. The great circle containing N, P, Z, and S is called the meridian for our observer. It is observed from the figure that the celestial equator, which lies 90° away from the pole, cuts the meridian at point E, which will be at a constant 40°south of the zenith for our observer.

Fig. 12
figure 12

Determining the declination of the Moon

Full size image

The declination (δ) of a heavenly body is defined as its angular distance, north or south, from the celestial equator. An ideal time to determine the declination of a heavenly body (including the Moon) is when it arrives at the observer’s meridian since the location of the celestial equator on the meridian is known (point E). Referring to the figure, the Moon’s declination is then simply the arc Em.

In practice, it is usual for the astronomer to measure either the altitude h (arc Sm) or the polar distance (arc Zm) of the body, both of which can be determined easily using instruments like the meridian circle. Given h, the declination (arc Em) can be found by Eq. 5 given below. Note that the Moon is south of the equator in the figure, so its declination will be negative.

$$\delta = \left( {L_{{\text{o}}} + h} \right) - 90^\circ .$$
(5)

Thus, we see that the Moon’s declination is a quantity that is fairly easy to determine.

Coming to the latitude, its determination is a different matter altogether. As mentioned, the latitude of a heavenly body is its angular distance, north or south, from the ecliptic. Now, while the location of the celestial equator on the observer’s meridian (point E) is fixed and known, as explained earlier, where the ecliptic cuts the meridian (point T) is variable throughout the year.

In standard works of spherical trigonometry (Smart, 1977), the relation between the latitude (β) and the declination (δ) involves the right ascension (α) and the obliquity of the earth’s axis (η). The full expression is as shown in Eq. 6.

$$\sin \left( {\upbeta } \right) = \sin \left( {\updelta } \right)\cos \left( {\upeta } \right) - \cos \left( {\updelta } \right)\sin \left( {\upeta } \right)\sin \left( {\upalpha } \right).$$
(6)

For the special case where \(\alpha = \, 90^\circ\), that is, when the Moon is on the meridian and the equinox point is located on our observer’s horizon, Eq. 6 will become:

$$\sin \left( {\upbeta } \right) = \sin \left( {\updelta } \right)\cos \left( {\upeta } \right) - \cos \left( {\updelta } \right)\sin \left( {\upeta } \right) .$$

Applying standard trigonometric identities we will have:

$$\sin \left( \beta \right) = \sin \left( {\delta - \eta } \right)$$

Therefore,

$$\beta = \delta - \eta$$

Or,

$$\delta = \beta + \eta$$
(7)

Thus, we see that for this special case, the declination, latitude, and obliquity have a simple relation among themselves. In general, the declination will be a maximum when latitude is a maximum since the obliquity of the ecliptic is a constant for a given epoch. However, the obliquity does change over longer periods, and it has been decreasing steadily for the past 8000 years. How does this affect the Moon’s maximum declination? The answer is shown in Fig. 13.

Fig. 13
figure 13

Variation of the Moon’s Maximum Declination in Time

Full size image

The solid line in the figure, which has been computed per modern astronomy (Meeus, 2000), shows that the Moon’s maximum declination has been decreasing steadily over the centuries due to the decreasing obliquity. Its current value is the sum of the Moon’s maximum latitude (5.3°) and the current obliquity (23.44°), which comes to 28.74°.

The dashed line in the figure shows the Indian value for the Moon’s maximum declination, which is a constant since both the Moon’s maximum latitude (4.5°) and the obliquity (24°) are deemed constants, their sum equating to 28.5°. Recall from the third and fourth columns of Table 1 that all Indian astronomers of old have assumed the obliquity to be constant at 24° and the Moon’s maximum latitude as 4.5° (or near about).

Thus, we see the interesting circumstance in Indian astronomy where the negative error in the Moon’s maximum latitude compensates for the positive error in the obliquity, such that their sum (the maximum declination) comes to within 0.5° of the actual maximum declination, as seen in Fig. 13.

The relative size of the full Moon is depicted on the right in Fig. 13 to indicate the magnitude of the Indian error for the Moon’s maximum declination. The width of the full Moon is 0.5°, and it is noted from the figure that the actual and Indian maximum declinations fall within the Moon’s orb, at least since Āryabhaṭa’s time (500 CE), which may have contributed to the Indian astronomer being satisfied that his values for the Moon’s maximum latitude (4.5°) and the obliquity (24°) were correct.

The important point being made here is that it is the declination that was of primary interest to the ancient astronomer, not the latitude.

9.1.2 Eclipses and Moon phase

Apart from the declination, there may have been other reasons that have contributed to the Indian astronomer’s lack of interest in the actual maximum latitude of the Moon. For the ancient astronomer, the three primary reasons to calculate the Moon were: (i) The regulation of months (new Moon); (ii) The calculation of eclipses; (iii) Calculation of the Moon’s phases.

For the first item, the Moon’s latitude does not figure anywhere in the calculation of New Moon. For the second, in the calculation of eclipses, the Moon’s latitude does matter, but not her maximum latitude. Both Lunar and Solar eclipses occur when the Moon is close to her node, in other words, close to zero latitude. For the third, in the calculation of the Moon’s phases, only her declination is employed, not her latitude.

9.1.3 Summary

For the ancient Indian astronomer, the Moon’s maximum latitude was perhaps only of academic interest since it is not used in any subsequent calculations. The Moon’s maximum declination far superseded her maximum latitude in importance.

10 Conclusions

Some conclusions that may be drawn from this study on the missing algorithm for the Moon’s maximum latitude in Indian astronomy are as follows:

  1. (1)

    The expression to calculate the Moon’s latitude, as given in various Indian texts, is precisely correct per modern spherical trigonometry.

  2. (2)

    One of the terms employed in the expression for latitude is the Maximum Latitude. Though the oldest extant Indian text, the Sūryasiddhānta, clearly indicates that the maximum latitude of the Moon is variable, it does not explicitly present a way to calculate this maximum latitude, providing instead only a mean value of the maximum latitude.

  3. (3)

    The analysis conducted in this paper discovered that the missing algorithm for the Moon’s maximum latitude may have had a simple form based on the elongation between the Sun and the Moon.

  4. (4)

    It is speculated that the missing algorithm may have been expunged from the Sūrya siddhānta due to long disuse since the Moon’s maximum latitude is not an essential parameter in any other calculations.

  5. (5)

    On the question of why the ancients were unaware that the Moon’s maximum latitude is not 4.5˚ but 5.3˚, it is conjectured that these astronomers were primarily concerned with the Moon’s maximum declination, and not the maximum latitude per se. Since the maximum declination is a combination of the maximum latitude and the obliquity, it is shown in this paper that the negative error due to assuming a maximum latitude of 4.5˚ is compensated by the positive error in assuming an obliquity of 24˚, resulting in the summed maximum declination of the Moon to be close to the actual observed maximum declination.

More research is needed before anything material can be established on the subject. The discovery of any ancient documents containing an algorithm for the maximum latitude would certainly be a fortuitous development in this regard and is eagerly awaited. In the meantime, one area to explore further is the possibility of improving upon the simple expression presented in this paper for the Moon’s maximum latitude to bring it closer to actuality.