Analytical solution of the electro-mechanical flexural coupling between piezoelectric actuators and flexible-spring boundary structure in smart composite plates

Abstract

An analytical solution has been developed developed in this research for electro-mechanical flexural response of smart laminated piezoelectric composite rectangular plates encompassing flexible-spring boundary conditions at two opposite edges. Flexible-spring boundary structure is introduced to the system by inclusion of rotational springs of adjustable stiffness which can vary depending on changes in the rotational fixity factor of the springs. To add to the case study complexity, the two other edges are kept free. Three advantages of employing the proposed analytical method include: (1) the electro-mechanical flexural coupling between the piezoelectric actuators and the plate’s rotational springs of adjustable stiffness is addressed; (2) there is no need for trial deformation and characteristic function—therefore, it has higher accuracy than conventional semi-inverse methods; (3) there is no restriction imposed to the position, type, and number of applied loads. The Linear Theory of Piezoelectricity and Classical Plate Theory are adopted to derive the exact elasticity equation. The higher-order Fourier integral and higher-order unit step function differential equations are combined to derive the analytical equations. The analytical results are validated against those obtained from Abaqus Finite Element (FE) package. The results comparison showed good agreement. The proposed smart plates can potentially be applied to real-life structural systems such as smart floors and bridges and the proposed analytical solution can be used to analyze the flexural deformation response.

1 Introduction

Composite materials application is rapidly growing in various industries. When improved stiffness, weight reduction, and greater durability and toughness are simultaneously sought, composite materials stand out as the best option [1, 2]. Laminated fiber reinforced composite structures have attracted many engineers in the fields of aerospace, automotive, civil, electrical, mechanical, structural, and biomedical engineering [3]. Plates and beams made of composite laminates are used to provide the better stiffness and lightness in numerous engineering structures [4]. Piezoelectric materials known as smart materials are small, consume less power, and rapidly respond when induced by external loads [5], which make them ideal to be incorporated with composite laminates [6]. Piezoelectric plates are an important part of smart engineering structures due to their electro-mechanical coupling characteristics. Smart piezoelectric structures have many engineering applications in aerospace, telecommunications, mechanical and civil systems, automotive, medical, military, sport, and science [7].

The vibration control of lightweight floor systems made of composite materials has recently attracted engineers in the construction and infrastructure industries. Some factors such as deflection reduction, enhancing the floor stiffness, and appropriate design of boundary conditions have all demonstrated to be successful in improving the vibration performance of floors [8]. Flexural deformation of floors and bridges are of significant importance due to their unstable geometrical shape (free edges) when subject to a moving mass and having a particular type of boundaries at the opposite edges which are neither clamped support nor simple support [9]. A floor/bridge system can be modelled as a plate with two rotationally flexible edges and two free edges. There are several studies regarding mechanical deformation of plates made of isotropic/orthotropic materials and under mechanical load. Some of the most recent studies are discussed in the following paragraphs.

There are several studies in which the conventional superposition and semi-inverse methods were used to derive the flexural equations of plates. Bhaskar and Sivaram [10] proposed a superposition method using infinite series equivalent to the complicated closed-form Levy-type solutions to calculate the elastic deformation of isotropic and orthotropic plates with various boundary conditions. In their study, the plates were subjected to concentrated load or uniformly distributed pressure. However, their analysis demonstrated that such procedure does not provide efficient results for orthotropic plates due to small convergence in the conventional Levy method. Liu and Li [11] introduced the symplectic geometry approach to calculate the rectangular thin plates bending under various boundary conditions. They employed Hamilton canonical equations in their analysis. The bending solutions of such problem were accurately calculated using the superposition method. Their approach demonstrated to be more effective and reliable than conventional superposition method due to enabling the elimination of the deformation function. Bhaskar and Kaushik [12] proposed a simple analytical solution using superposition method to calculate the mechanical deformation of cross-ply laminated plates under arbitrary boundary and loading conditions. The authors claimed that their proposed analytical solution was simple and straightforward and can conveniently calculate deflections and moments induced in laminated composite plates with either clamped or simple support boundaries. Lim et al. [13] proposed an analytical solution to calculate the elastic bending of plates with various boundary conditions. A symplectic elasticity approach was the base of their analysis. They developed an eigenvalue equation to analyze buckling and vibration of the plates. However, their proposed analytical solution was only limited to analysis of isotropic plates. Li and Zhong [14] used the symplectic geometry to calculate flexural response of thin rectangular plates made of laminated composite materials. The plate was fixed onto its two opposite edges. Their method provides rapid convergence and accurate results and does not require a trial function associated with deflection unlike the traditional semi inverse approaches. Shi et al. [15] and Zhang and Xu [16] proposed two distinct analytical solutions to inspect the flexural response of rectangular plates under mechanical load. They considered the effect of rotationally flexible springs at the boundaries. However, their proposed analytical solutions did not offer an analysis of smart plates integrated with piezoelectric actuators.

Finite integral Fourier transform is another method to obtain the flexural response of plates. Li et al. [17] proposed an analytical solution by employing the method of finite integral Fourier transform to calculate the analytical bending solutions of thin rectangular plates made of composite materials and with fully clamped boundaries. The results demonstrated that selecting sufficient Fourier terms leads to accurate and efficient results. Their proposed analytical solution was solvable without any need to obtain the deformation function. Li et al. [18] proposed an analytical solution to calculate flexural bending of all-edges-free laminated orthotropic plates with arbitrary boundary conditions. The double finite integral Fourier transform method was used in their analysis. The proposed method offered higher accuracy over those available in the literature when sufficient number of Fourier terms is selected. An et al. [19] proposed an analytical solution to calculate flexural response of thin rectangular plates made of composite laminates and with fully clamped boundary conditions. The generalized integral transform technique (GITT) was employed which led to a coupled system associated with fourth order differential equations (ODEs). The results obtained from their proposed method were validated by a numerical simulation using Abaqus FE package. Zhang and Shu [10, 16] proposed analytical solutions to calculate the elastic bending of laminated composite plates with rotational springs of adjustable stiffness using finite integral Fourier transform method. Although their proposed method was limited to plate type problems under single mechanical load, it demonstrated high accuracy and good convergence compared with the studies using the conventional superposition and semi-inverse methods. Gohari et al. [20, 21] proposed two analytical solutions to obtain the flexural and twisting deformation of laminated cantilevered composite plates induced by piezoelectric actuators. The higher order Fourier integral transform was the step stone of their analysis. The analytical results were later compared with and verified by the FE simulation and good agreement was observed.

In the present work, an analytical solution was derived to obtain the flexural response of smart laminated piezoelectric composite rectangular plates subjected to flexible-spring boundary structure at two opposite edges. The combined effect of the number of piezoelectric actuators, the fixity factor of springs, and the applied electrical voltage were further considered to enhance the structural stiffness of the plate. The authors, for the first time, used the higher-order Fourier integral and higher-order unit step function differential equations to analytically calculate the electro-mechanical flexural coupling between piezoelectric actuators and flexible spring boundary structures in smart composite plates. The results obtained from the proposed analytical method were verified using Abaqus FE simulation package. We addressed the electro-mechanical coupling between the piezoelectric actuators and the plate’s rotational springs of adjustable stiffness and demonstrated that trial deformation and characteristic function could be eliminated from the analytical equations. Furthermore, it enabled the calculation of the elastic bending of smart plates under all kinds of loads, including but not limited to, electrical load, mechanical patch loading, concentrated point load eliminating any restriction tied to the load position and the number of applied loads. The proposed analytical solution can be used as a positional guideline for engineers who are interested in the design and analysis of smart floors and bridges.

2 Problem statement and mathematical modelling

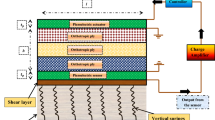
The schematic of a laminated piezoelectric composite rectangular plate with flexible-spring boundary structure is illustrated in Fig. 1. The plate has rectangular/square geometry, is made of composite laminates, and composed of N layers. The top and bottom layers are integrated with single/multiple pairs of piezoelectric actuator patches. The smart plate has flexible-spring boundary structure achieved by incorporating rotational springs of adjustable stiffness into two opposite edges. Hence, the boundary condition at the corresponding edges varies from simple support to clamped support depending on changes in the rotationally fixity factor of the springs. The other two edges of the plate are kept free. The electrical load is applied using piezoelectric actuators. The mechanical loading can be in the form of a concentrated force, patch loading, uniform pressure, or a combination of them. The plate’s width and length are defined as b and a, respectively. The length and width of piezoelectric patches are defined as L_a and W_a, respectively. The plate lamination with total thickness of H consists of several fiber reinforced polymer plies with fiber orientation and thickness defined as β_k and t_k, respectively. The index k stands for the layer number in a smart laminated piezoelectric composite plate. Each layer could be made of either composite or piezoelectric materials.

Fig. 1

Electro-mechanically induced bridge-typed laminated composite rectangular plate integrated with multiple piezoelectric patches and rotationally flexible springs at two opposite edges (note: for piezoelectric layers t_k = t_a)

In the current research, Kirchhoff hypothesis for small displacements within linear elastic zone is employed to obtain the displacements as stated in Eqs.1a–c [22, 23]. According to the Kirchhoff hypothesis, fibers and matrix are perfectly bounded. Furthermore, a linear strain-electric filed in the piezoelectric actuators is considered [24, 25].

$$u(x,y,z) = u_{0} (x,y) - z\frac{\partial w}{{\partial x}}$$

(1a)

$$v(x,y,z) = v_{0} (x,y) - z\frac{\partial w}{{\partial y}}$$

(1b)

$$w(x,y,z) = w_{0} (x,y)$$

(1c)

where, u₀, ν₀, and w₀ stand for the displacements in the mid-plane of a rectangular plate along the x, y, and z directions, respectively [26]. The coordinate z is defined as the distance normal to the xy-plane (Fig. 1). Equations 2a–c represents the strains and displacements in a composite laminate [27].

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{yy} } & {\gamma_{xy} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} & {\frac{\partial \nu }{{\partial y}}} & {\frac{\partial u}{{\partial y}} + \frac{\partial \nu }{{\partial x}}} \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } & {\varepsilon_{yy}^{0} } & {\gamma_{xy}^{0} } \\ \end{array} } \right]^{T} + z\left[ {\begin{array}{*{20}c} {\varepsilon_{xx}^{f} } & {\varepsilon_{yy}^{f} } & {\gamma_{xy}^{f} } \\ \end{array} } \right]^{T}$$

(2a)

where:

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } & {\varepsilon_{yy}^{0} } & {\gamma_{xy}^{0} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} & {\frac{{\partial v_{0} }}{\partial y}} & {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \\ \end{array} } \right]^{T}$$

(2b)

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx}^{f} } & {\varepsilon_{yy}^{f} } & {\gamma_{xy}^{f} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} & { - \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} & { - 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \\ \end{array} } \right]^{T}$$

(2c)

where, ε⁰_xx, ε⁰_yy, and γ⁰_xy are the mid-plane strains and ε_xx^f, ε_yy^f, and γ_xy^f are the flexural strains. The quantity w₀ is the mid-plane displacement along the z axis in a composite laminate. Equations 3a, b represents the 2D electro-mechanical plate equations when considering the plane stress for piezoelectric layer (Eq. 3a) and composite layer (Eq. 3b) [24]:

$$\left[ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\tau_{12} } \\ {\rho_{3} } \\ \end{array} } \right]^{k} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {G_{12} } \\ {e_{31} } & {e_{32} } & 0 \\ \end{array} } \right]^{k} \left[ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\gamma_{12} } \\ \end{array} } \right]^{k} - \left[ {\begin{array}{*{20}c} {e_{31} } \\ {e_{32} } \\ 0 \\ {\zeta_{33} } \\ \end{array} } \right]^{k} {\rm P}_{3}^{k}$$

(3a)

$$\left[ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\tau_{12} } \\ \end{array} } \right]^{k} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {G_{12} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\gamma_{12} } \\ \end{array} } \right]^{k}$$

(3b)

where, Q_ij are the stiffness matrix elements. The quantities e_ij are piezoelectric moduli of a piezoelectric layer. P₃ stands for the electrical filed component along the z direction in a piezoelectric layer. In Eq. 3b, 1 and 2 stand for the directions along the fibers and perpendicular to the fibers in a composite material, respectively. The entire stiffness matrix elements and piezoelectric components are discussed in Appendix A.

According to the Kirchhoff law (Appendix A), the transverse shear deformation effect is neglected (γ₁₃ = γ₂₃ = 0). The boundary condition applied to a rectangular plate with rotational springs of adjustable stiffness at two edges and two free edges are expressed in Eqs. 4a–e. Equations 4a, b are based on the fact that the bending moment M_xx at far side of the plate at x = 0 and x = a is dependent on the rotational fixity factors of the spring r_x0 and r_xa. This relationship was studied in detail in [16].

$$x = 0 \to M_{xx} = - \frac{{3D_{11} r_{x0} }}{{a(1 - r_{x0} )}}\frac{{\partial w_{0} }}{\partial x} \to - D_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - D_{12} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \frac{{3D_{11} r_{x0} }}{{a(1 - r_{x0} )}}\frac{{\partial w_{0} }}{\partial x} = 0$$

(4a)

$$x = a \to M_{xx} = \frac{{3D_{11} r_{xa} }}{{a(1 - r_{xa} )}}\frac{{\partial w_{0} }}{\partial x} \to - D_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - D_{12} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} - \frac{{3D_{11} r_{xa} }}{{a(1 - r_{xa} )}}\frac{{\partial w_{0} }}{\partial x} = 0$$

(4b)

$$x = \, 0{\text{ or}}\;\;x = a \to w_{0} (x,y) = 0$$

(4c)

$$y = \, 0 \; {\text{ or}}\;\;y = b \to M_{yy} = - \left[ {D_{22} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + D_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right] = 0$$

(4d)

$$y = \, 0\;\;{\text{ or}}\;\;y = b \to V_{yy} = - D_{22} \frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} - (H + 2D_{66} )\frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}} = 0$$

(4e)

where, M_xx and M_yy are the bending moment resultants acting over the x and y axes, respectively. V_yy is the total shear force resultants [N/m] which acts on yz plane in a plate element [28]. The terms r_x0 and r_xa are the rotational fixity factors of the springs at x = 0 and x = b edges, respectively, which were proposed by Zhang and Shu [16]. The stiffness of the springs changes depending on the r variation between 0 and 1. For instance, the higher the rotational fixity factor is, the stiffer the springs become. r = 0 and r = 1 are two special cases in which the springs provide simple support and clamped support to the plate, respectively.

Assuming thin symmetrical cross-ply lamination, the transverse bending and twisting moments in a smart laminated piezoelectric composite rectangular plate is calculated using Eqs. 5a–e [29]:

$$D_{11} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} + 2H\frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }} + D_{22} \frac{{\partial^{4} w_{0} }}{{\partial y^{4} }} = P_{m} (x,y) + P_{e} (x,y)$$

(5a)

where:

$$P_{e} (x,y) = \frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{yy}^{P} }}{{\partial y^{2} }}$$

(5b)

$$M_{xx}^{P} = \sum\limits_{k = 1}^{N} {\int\limits_{{h_{k} }}^{{h_{k + 1} }} {\left[ {Q_{1j} } \right]^{k} \left[ {d_{3j} } \right]^{k} P_{3}^{k} zdz} } = \tfrac{1}{2}\sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)$$

(5c)

$$M_{yy}^{P} = \sum\limits_{k = 1}^{N} {\int\limits_{{h_{k} }}^{{h_{k + 1} }} {\left[ {Q_{2j} } \right]^{k} \left[ {d_{3j} } \right]^{k} P_{3}^{k} zdz} } = \tfrac{1}{2}\sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{2j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)$$

(5d)

$$D_{ij} = \tfrac{1}{3}\sum\limits_{K = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {\overline{Q}_{ij} } \right]_{k} } } (h_{K}^{3} - h_{K - 1}^{3} )$$

(5e)

where, j = {1,2,6}, H = D₁₂ + 2D₆₆, and D₂₂, D₁₁, D₆₆, and D₁₂ are defined as the flexural rigidities about the y and x axes and torsional rigidity, respectively. The electrical and mechanical loads are defined as P_e(x,y) and P_m(x,y), respectively. In Eqs. 5c–e, the terms Q_1j, Q_2j are the stiffness and Q_ij with bar sign is the transformed stiffness (see Appendix A).

The geometry of a laminated composite rectangular plate integrated with the piezoelectric actuators is shown in Fig. 1. In this study, we assumed that the composite plate is incorporated with infinite number of arbitrarily positioned surface-bounded piezoelectric actuators. As such, the electrical bending moments induced along the x and y axes are expanded as a function of the higher-order unit step function differential equations as stated in Eqs. 6a–c, respectively. Equations 6a–c are derived based on the fact that the electrical bending is present at the edges of piezoelectric actuators. The detailed discussion can be found in [29].

$$\left[ {M_{xx} } \right]^{P} = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\left[ {U_{Lk}^{{}} (x - x_{1P}^{{}} ) - U_{Lk}^{{}} (x - x_{2P}^{{}} )} \right]\left[ {U_{Lk}^{{}} (y - y_{1P}^{{}} ) - U_{Lk}^{{}} (y - y_{2P}^{{}} )} \right]$$

(6a)

$$\left[ {M_{yy} } \right]^{P} = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{2j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\left[ {U_{Lk}^{{}} (x - x_{1P}^{{}} ) - U_{Lk}^{{}} (x - x_{2P}^{{}} )} \right]\left[ {U_{Lk}^{{}} (y - y_{1P}^{{}} ) - U_{Lk}^{{}} (y - y_{2P}^{{}} )} \right]$$

(6b)

$$P_{m} = \sum\limits_{L = 1}^{Mn} {P_{m} (x,y)\left[ {X_{L} (x - x_{1M} ) - X_{L} (x - x_{2M} )} \right]\left[ {X_{L} (y - y_{1M} ) - X_{L} (y - y_{2M} )} \right]}$$

(6c)

where, j = {1,2,6}. U_LK(x,y) and X_L indicate the electrical bending moment and the mechanical patch loading positions, respectively. L presents the piezoelectric actuator number and the mechanical patch loading number in a composite plate. The position vectors of mechanical loads are defined as x_1M, x_2M, y_1M, and y_2M and the position vectors of electrical loads are defined as x_1P, x_2P, y_1P, and y_2P, respectively.

The mid-plane vertical displacement in a bridge-typed plate can be expressed as the double finite integral Fourier transform as stated in Eq. 7:

$$w_{mn} = \int\limits_{0}^{a} {\int\limits_{0}^{a} {w_{0} (x,y)\sin (\alpha_{m} x)\cos (\beta_{n} y) {\text{d}}x {\text{d}}y} } \;(m = 1,3,5, \ldots )\;\;(n = 0,1,2, \ldots )$$

(7)

where, m and n are the components of the sine and cosine angles in a Fourier series. Practically, selection of the higher values for the terms m and n leads to more convergent and hence, more accurate results. There is a correlation between the boundary value problems and variation of the terms m and n in a Fourier series [30].

The inverse of Eq. 7 leads to the displacement of the function w₀(x,y) along the z direction as stated in Eqs. 8a, b [30]:

$$w_{0} (x,y) = \left( \frac{4}{ab} \right)\sum\limits_{m = 1,3,5,...}^{\infty } {\sum\limits_{n = 0,1,2,...}^{\infty } {w_{mn} \lambda_{n} \sin (\alpha_{m} x)\cos (\beta_{n} y)} }$$

(8a)

$$\alpha_{m} = \frac{m\pi }{a},\;\;\beta_{n} = \frac{n\pi }{b}\;\;{\text{and}}\;\;\lambda_{n} = \left\{ {\begin{array}{l} {0.5 \to (n = 0)} \\ {1 \to (n = 1,2,3,...)} \\ \end{array} } \right.$$

(8b)

In Eq. 8b, α_m and β_n are the angular functions depending on of m and n terms. The term λ_n is an author-defined coefficient which only takes 0.5 and 1 values depending on whether n = {0} or n = {1, 2, 3,…}.

The double integral transform over Eq. 5a leads to Eqs. 9a–h, which are the function of w₀(x,y).

$$\begin{gathered} \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {D_{11} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} + 2H\frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }} + D_{22} \frac{{\partial^{4} w_{0} }}{{\partial y^{4} }}} \right]\sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y} } \hfill \\ \;\;\;\;\;\;\;\;\; = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {P_{m} (x,y) + \frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{yy}^{P} }}{{\partial y^{2} }}} \right]} } \times \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y \hfill \\ \end{gathered}$$

(9a)

Equation 9a is rearranged to be represented as the function of f_n(w₀(x,y)) as stated in Eq. 9b:

$$\begin{aligned} D_{11} f_{1} (w_{0} (x,y)) + D_{22} f_{2} (w_{0} (x,y)) + 2Hf_{3} (w_{0} (x,y)) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {P_{m} (x,y)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y + \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }}} \right)} } \hfill \\ & \quad \times \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y + \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{yy}^{P} }}{{\partial y^{2} }}} \right)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y \hfill \\ \end{aligned}$$

(9b)

where:

$$f_{1} (w_{0} (x,y)) = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\frac{{\partial^{4} w_{0} }}{{\partial x^{4} }}} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y$$

(9c)

$$f_{2} (w_{0} (x,y)) = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\frac{{\partial^{4} w_{0} }}{{\partial y^{4} }}} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y$$

(9d)

$$f_{3} (w_{0} (x,y)) = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }}} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y$$

(9e)

$$I_{1} (x,y) = \int\limits_{0}^{a} {\int\limits_{0}^{b} {P_{m} (x,y)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y$$

(9f)

$$I_{2}^{A} (x,y) = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }}} \right)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y$$

(9g)

$$I_{2}^{B} (x,y) = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{yy}^{P} }}{{\partial y^{2} }}} \right)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y$$

(9h)

Considering the boundary conditions (Eqs. 4a–e) and with the use of higher-order integral transform, the higher-order partial derivatives of Eqs. 9c–e are expanded as stated in Eqs. 10a–c, which are the functions of w₀(x,y).

$$\begin{aligned} f_{1} (w_{0} (x,y)) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\frac{{\partial^{4} w_{0} }}{{\partial x^{4} }}} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = \int\limits_{0}^{b} {\left[ { - \alpha_{m} ( - 1)^{m} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right) + \alpha_{m} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \right.} \hfill \\ & \quad + \alpha_{m}^{4} \left. {\int\limits_{0}^{a} {w_{0} } \sin (\alpha_{m} x){\text{d}}x} \right]\cos (\beta_{n} y){\text{d}}y = - \alpha_{m} ( - 1)^{m} \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y + \alpha_{m} \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \hfill \\ & \quad \times \cos (\beta_{n} y){\text{d}}y + \alpha_{m}^{4} w_{{_{mn} }} \hfill \\ \end{aligned}$$

(10a)

$$\begin{aligned} f_{2} (w_{0} (x,y)) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\frac{{\partial^{4} w_{0} }}{{\partial y^{4} }}} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y \\ & = \int\limits_{0}^{b} {\left[ {( - 1)^{n} \left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right) - \left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \right.} - \beta_{n}^{2} ( - 1)^{n} \hfill \\ & \quad \left. { \times \left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right) + \beta_{n}^{2} \left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right) + \beta_{n}^{4} \int\limits_{0}^{b} {w_{0} } \cos (\beta_{n} y){\text{d}}y} \right]\sin (\alpha_{m} x){\text{d}}x \\ & = ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x \hfill \\ & \quad - \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - \beta_{n}^{2} ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x \\ & \quad + \beta_{n}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + \beta_{n}^{4} w_{mn} \hfill \\ \end{aligned}$$

(10b)

$$\begin{aligned} f_{3} (w_{0} (x,y)) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }}} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = \int\limits_{0}^{a} {\left[ {( - 1)^{n} \left( {\frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \right.} - \left( {\frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right) - \beta_{n}^{2} \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)} \hfill \\ & \quad \times \left. {\cos (\beta_{n} y){\text{d}}y} \right]\sin (\alpha_{m} x){\text{d}}x = ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - \beta_{n}^{2} \hfill \\ & \quad \times \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)} \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = - } \alpha_{m} ( - 1)^{n + m} \left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {x = a} \\ {y = b} \\ \end{array} } \right.} \right) + \alpha_{m} ( - 1)^{n} \left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {x = 0} \\ {y = b} \\ \end{array} } \right.} \right) - \alpha_{m}^{2} ( - 1)^{n} \hfill \\ & \quad \times \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + \alpha_{m} ( - 1)^{m} \left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {x = a} \\ {y = 0} \\ \end{array} } \right.} \right) - \alpha_{m} \left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {x = 0} \\ {y = 0} \\ \end{array} } \right.} \right) + \alpha_{m}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x \hfill \\ & \quad + \alpha_{m}^{2} \beta_{n}^{2} w_{mn} = \alpha_{m}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - \alpha_{m}^{2} ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + \alpha_{m}^{2} \beta_{n}^{2} w_{mn} \hfill \\ \end{aligned}$$

(10c)

We define P_m(x,y) = P₀ which is the uniform distributed pressure and/or the magnitude of the patch loading. With the use of higher-order integral transform, the partial derivatives of the mechanical load in the higher form are derived as stated in Eqs. 11a, b. The partial derivatives are obtained for two particular cases: (1) when n = {0} which provides an identical case with respect to Fourier term n, and (2) n = {1, 2, 3,…} which provides a variable case with respect to Fourier term n, i.e.

for n = {0} and m = {1,3,5…}, one has:

$$\begin{aligned} I_{1} (x,y) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {P_{m} (x,y)} } \sin (\alpha_{m} x){\text{d}}x{\text{d}}y = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\sum\limits_{L = 1}^{Mn} {P_{0} } } } \left[ {X_{L} (x - x_{1M} ) - X_{L} (x - x_{2M} )} \right]\left[ {X_{L} (y - y_{1M} )} \right. \hfill \\ & \quad - \left. {X_{L} (y - y_{2M} )} \right]\sin (\alpha_{m} x){\text{d}}x{\text{d}}y = \sum\limits_{L = 1}^{Mn} {\left( {\frac{{ - P_{0} }}{{\alpha_{m} }}} \right)\left[ {\cos (\alpha_{m} x_{1M} ) - \cos (\alpha_{m} x_{2M} )} \right]_{L} } \left( {y_{1M} - y_{2M} } \right)_{L} \hfill \\ \end{aligned}$$

(11a)

and for n = {1,2,3,…} and m = {1,3,5,…}, one has:

$$\begin{aligned} I_{1} (x,y) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {P_{m} (x,y)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y \\ & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\sum\limits_{L = 1}^{Mn} {P_{0} } } } \left[ {X_{L} (x - x_{1M} ) - X_{L} (x - x_{2M} )} \right] \hfill \\ & \quad \times \left[ {X_{L} (y - y_{1M} )} \right. - \left. {X_{L} (y - y_{2M} )} \right]\sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y \\ & = \sum\limits_{L = 1}^{Mn} {\left( {\frac{{ - P_{0} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} \left[ {\cos (\alpha_{m} x_{1M} ) - \cos (\alpha_{m} x_{2M} )} \right]_{L} } \hfill \\ & \quad \times \left[ {\sin (\beta_{n} y_{1M} )} \right. - \left. {\sin (\beta_{n} y_{2M} )} \right]_{L} \hfill \\ \end{aligned}$$

(11b)

The second derivatives of the electrical bending over the x and y axes are obtained according to Eqs. 12a and 12b, respectively. Equations 12a–c are obtained through taking the derivatives of the unit step functions representing the placements of the piezoelectric patches. The detailed discussions as to how the derivatives of a unit step function are taken can be found in [31].

$$\begin{aligned} \frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }} & = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\left( {\left[ {U_{Lk}^{{}} (x - x_{1P}^{{}} ) - U_{Lk}^{{}} (x - x_{2P}^{{}} )} \right]} \right.\left[ {U_{Lk}^{{}} (y - y_{1P}^{{}} )} \right. - \left. {\left. {U_{Lk}^{{}} (y - y_{2P}^{{}} )} \right]} \right) \hfill \\ & = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\left[ {\delta_{Lk}^{^{\prime}} (x - x_{1P}^{{}} )} \right. - \left. {\delta_{Lk}^{^{\prime}} (x - x_{2P}^{{}} )} \right]\left[ {U_{Lk}^{{}} (y - y_{1P}^{{}} )} \right. - \left. {U_{Lk}^{{}} (y - y_{2P}^{{}} )} \right] \hfill \\ \end{aligned}$$

(12a)

$$\begin{aligned} \frac{{\partial^{2} M_{yy}^{P} }}{{\partial y^{2} }} & = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {\overline{Q}_{2j} } \right]^{k} } } \left[ {\overline{d}_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\frac{{\partial^{2} }}{{\partial y^{2} }}\left( {\left[ {U_{Lk}^{{}} (x - x_{1P}^{{}} ) - U_{Lk}^{{}} (x - x_{2P}^{{}} )} \right]} \right.\left[ {U_{Lk}^{{}} (y - y_{1P}^{{}} )} \right. - \left. {\left. {U_{Lk}^{{}} (y - y_{2P}^{{}} )} \right]} \right) \hfill \\ & = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\left[ {U_{Lk}^{{}} (x - x_{1P}^{{}} ) - U_{Lk}^{{}} (x - x_{2P}^{{}} )} \right]\left[ {\delta_{Lk}^{^{\prime}} (y - y_{1P}^{{}} )} \right. - \left. {\delta_{Lk}^{^{\prime}} (y - y_{2P}^{{}} )} \right] \hfill \\ \end{aligned}$$

(12b)

Substituting Eqs. 12a, b into Eqs. 9g, h and then performing the higher-order integral transforms over Eqs. 12a, b result in Eqs. 13a–d.

For n = {0} and m = {1,3,5…}, one has:

$$\begin{aligned} I_{2}^{A} (x,y) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }}} \right)} } \sin (\alpha_{m} x){\text{d}}x{\text{d}}y = \tfrac{1}{2}\int\limits_{0}^{a} {\int\limits_{0}^{b} {\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)} } \left[ {\delta_{Lk}^{^{\prime}} (x - x_{1P}^{{}} )} \right. - \left. {\delta_{Lk}^{^{\prime}} (x - x_{2P}^{{}} )} \right] \hfill \\ & \quad \times \left[ {U_{Lk} (y - y_{1P}^{{}} ) - U_{Lk} (y - y_{2P}^{{}} )} \right]\sin (\alpha_{m} x){\text{d}}x{\text{d}}y = \sum\limits_{L = 1}^{Tn} {\alpha_{m} \left[ {M_{x}^{P} } \right]^{\Theta } } \left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left( {y_{1P} - y_{2P} } \right)_{L} \hfill \\ \end{aligned}$$

(13a)

$$I_{2}^{B} (x,y) = 0$$

(13b)

and for n = {1,2,3,…} and m = {1,3,5,…}, one has:

$$\begin{aligned} I_{2}^{A} (x,y) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{xx}^{P} }}{{\partial x^{2} }}} \right)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = \tfrac{1}{2}\int\limits_{0}^{a} {\int\limits_{0}^{b} {\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)} } \left[ {\delta_{Lk}^{^{\prime}} (x - x_{1P}^{{}} )} \right. \hfill \\ & \quad - \left. {\delta_{Lk}^{^{\prime}} (x - x_{2P}^{{}} )} \right]\left[ {U_{Lk} (y - y_{1P}^{{}} ) - U_{Lk} (y - y_{2P}^{{}} )} \right]\sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \hfill \\ & \quad \times \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\left( {\frac{{\alpha_{m} }}{{\beta_{n} }}} \right)\left[ {\cos (\alpha_{m} x_{1P} ) - \cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} )} \right. - \left. {\sin (\beta_{n} y_{2P} )} \right]_{L} \hfill \\ \end{aligned}$$

(13c)

$$\begin{aligned} I_{2}^{B} (x,y) & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} M_{yy}^{P} }}{{\partial y^{2} }}} \right)} } \sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = \tfrac{1}{2}\int\limits_{0}^{a} {\int\limits_{0}^{b} {\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{2j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)} } \left[ {U_{Lk}^{{}} (x - x_{1P}^{{}} )} \right. \hfill \\ & \quad - \left. {U_{Lk}^{{}} (x - x_{2P}^{{}} )} \right]\left[ {\delta_{Lk}^{^{\prime}} (y - y_{1P}^{{}} ) - \delta_{Lk}^{^{\prime}} (y - y_{2P}^{{}} )} \right]\sin (\alpha_{m} x)\cos (\beta_{n} y){\text{d}}x{\text{d}}y = \tfrac{1}{2}\sum\limits_{L = 1}^{Pn} {} \sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{2j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \hfill \\ & \quad \times \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)\left( {\frac{{\beta_{n} }}{{\alpha_{m} }}} \right)\left[ {\cos (\alpha_{m} x_{1P} ) - \cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} )} \right. - \left. {\sin (\beta_{n} y_{2P} )} \right]_{L} \hfill \\ \end{aligned}$$

(13d)

Equations 13a–d (I₂^A and I₂^B) are combined and then rearranged, leading to Eqs. 14a–e. The electrical intensity field along the z direction (through piezoelectric actuator thickness) is assumed to change linearly.

For n = {0} and m = {1, 3, 5…}, one gets:

$$I_{2} = I_{2}^{A} + I_{2}^{B} = 2\sum\limits_{L = 1}^{Tn} {\alpha_{m} \left[ {M_{x}^{P} } \right]^{\Theta } \left[ {\cos (\alpha_{m} x_{1P} ) - \cos (\alpha_{m} x_{2P} )} \right]_{L} \left( {y_{1P} - y_{2P} } \right)_{L} }$$

(14a)

and for n = {1, 2, 3,…} and m = {1, 3, 5,…}, one gets:

$$\begin{aligned} I_{2} = I_{2}^{A} + I_{2}^{B} & = \sum\limits_{L = 1}^{Tn} {\left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]} \left[ {\cos (\alpha_{m} x_{1P} ) - \cos (\alpha_{m} x_{2P} )} \right]_{L} \\ & \quad \left[ {\sin (\beta_{n} y_{1P} ) - \left. {\sin (\beta_{n} y_{2P} )} \right]} \right]_{L} \end{aligned}$$

(14b)

where:

$$\left[ {M_{x}^{P} } \right]^{\Theta } = \tfrac{1}{2}\sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{1j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)$$

(14c)

$$\left[ {M_{y}^{P} } \right]^{\Theta } = \tfrac{1}{2}\sum\limits_{k = 1}^{N} {\sum\limits_{j = 1,2,6} {\left[ {Q_{2j} } \right]^{k} } } \left[ {d_{3j} } \right]^{k} \left( {h_{k + 1}^{2} - h_{k}^{2} } \right)$$

(14d)

$$P_{3}^{k} = \frac{{V_{a}^{k} }}{{t_{a}^{k} }}$$

(14e)

where, V_a is the electrical voltage and t_a is the piezoelectric actuators thickness. The index k stands for the piezoelectric layer number.

Equations 10a–c and 14a, b are then substituted into Eq. 9b to find the relationship between the electro-mechanical coupling and the vertical displacements as stated in Eqs.15a–d:

$$\begin{aligned} - D_{11} \alpha_{m} ( - 1)^{m} \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y + D_{11} \alpha_{m} \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y + D_{11} \alpha_{m}^{4} w_{{_{mn} }} + D_{22} \hfill \\ & \quad \times ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - D_{22} \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - D_{22} \beta_{n}^{2} ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \hfill \\ & \quad \times \sin (\alpha_{m} x){\text{d}}x + D_{22} \beta_{n}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + D_{22} \beta_{n}^{4} w_{mn} + 2H\alpha_{m}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x - 2H \hfill \\ & \quad \times \alpha_{m}^{2} ( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + 2H\alpha_{m}^{2} \beta_{n}^{2} w_{mn} = \sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} \left[ {\cos (\alpha_{m} x_{1M} ) - \cos (\alpha_{m} x_{2M} )} \right]_{L} } \hfill \\ & \quad \times \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} \left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]_{{}} } \left[ {\cos (\alpha_{m} x_{1P} ) - \cos (\alpha_{m} x_{2P} )} \right]_{L} \hfill \\ & \quad \times \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} \hfill \\ \end{aligned}$$

(15a)

where:

$$n = 0,m = 1,3,5,... \to C_{mn}^{1} = \beta_{n} \left[ {\frac{{y_{1M} - y_{2M} }}{{\sin (\beta {}_{n}y_{1M} ) - \sin (\beta {}_{n}y_{2M} )}}} \right]_{L}$$

(15b)

$$\begin{aligned} n = 0,m = 1,3,5,... \to C_{mn}^{2} & = \frac{{2\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} \beta_{n} }}{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }} \\ & \quad \quad \left[ {\frac{{y_{1P} - y_{2P} }}{{\sin (\beta {}_{n}y_{1P} ) - \sin (\beta {}_{n}y_{2P} )}}} \right]_{L} \end{aligned}$$

(15c)

$$n = 1,2,3,...,m = 1,3,5,.. \to C_{mn}^{1} = C_{mn}^{2} = 1$$

(15d)

Above, C¹_mn and C²_mn are the electro-mechanical coefficients which are dependent on the m and n terms of the higher-order Fourier series.

Performing single finite sine transform over the boundary conditions in Eq. 4e, and integrating both sides, result in Eqs. 16a, b:

$$\begin{aligned} \int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin \left( {\alpha_{m} x} \right){\text{d}}x = \frac{{\left( {H + 2D_{66} } \right)}}{{D_{22} }} \alpha_{m}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)\sin \left( {\alpha_{m} x} \right){\text{d}}x} \end{aligned}$$

(16a)

$$\begin{aligned}\int\limits_{0}^{a} {\left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin \left( {\alpha_{m} x} \right){\text{d}}x = \frac{{\left( {H + 2D_{66} } \right)}}{{D_{22} }} \alpha_{m}^{2} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)\sin \left( {\alpha_{m} x} \right){\text{d}}x} \end{aligned}$$

(16b)

Equation 17 is derived by substituting Eqs. 16a, b into Eq. 15a:

$$\begin{aligned} & \left[ {2H\alpha_{m}^{2} + D_{22} \beta_{n}^{2} - \frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right]\int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + \left[ { - D_{22} ( - 1)^{n} \beta_{n}^{2} + \frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right. \hfill \\ & \quad \quad - \left. {2H\alpha_{m}^{2} ( - 1)^{n} } \right]\int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x + \left[ {D_{11} \alpha_{m} } \right]\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y + \left[ { - D_{11} \alpha_{m} ( - 1)^{m} } \right] \hfill \\ & \quad \quad \times \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y + \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]w_{mn} = \sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \left[ {\cos (\alpha_{m} x_{1M} )} \right. \hfill \\ & \quad \quad - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} \left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]_{{}} } \left[ {\cos (\alpha_{m} x_{1P} )} \right. \hfill \\ & \quad \quad - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} \hfill \\ \end{aligned}$$

(17)

In the next stage, four unknown functions Ω_m, ∆_m, Ψ_n, and Π_n are defined as stated in Eqs. 18a–d, respectively. Ω_m and ∆_m functions are merely dependent on the term m while Ψ_n and Π_n functions are merely dependent on the term n.

$$\Omega_{m} = \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x$$

(18a)

$$\Delta_{m} = \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x$$

(18b)

$$\Psi_{n} = \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y$$

(18c)

$$\Pi_{n} = \int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y$$

(18d)

Equation 19 is derived by substituting the unknown functions (Eqs. 18a–d) into Eq. 17:

$$\begin{gathered} \left[ {2H\alpha_{m}^{2} + D_{22} \beta_{n}^{2} - \frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right]\Omega_{m} + \left[ { - D_{22} ( - 1)^{n} \beta_{n}^{2} + \frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }} - 2H\alpha_{m}^{2} ( - 1)^{n} } \right]\Delta_{m} \hfill \\ + \left[ {D_{11} \alpha_{m} } \right]\Psi_{n} + \left[ { - D_{11} \alpha_{m} ( - 1)^{m} } \right]\Pi_{n} + \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]w_{mn} = \sum\limits_{L = 1}^{Mn} {_{{}} C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \hfill \\ \times \left[ {\cos (\alpha_{m} x_{1M} )} \right. - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} } \left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right] \hfill \\ \times \left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} \hfill \\ \end{gathered}$$

(19)

Rearranging Eq. 19 yields Eqs. 20a–f which present the double finite integral Fourier transform associated with the vertical displacements w_mn in the mid-plane, i.e.

$$w_{mn} = F_{mn}^{1} \Omega_{m} + F_{mn}^{2} \Delta_{m} + F_{mn}^{3} \Psi_{n} + F_{mn}^{4} \Pi_{n} + F_{mn}^{5} ,$$

(20a)

where:

$$\begin{aligned} F_{mn}^{1} & = \left[ {\frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }} - 2H\alpha_{m}^{2} - D_{22} \beta_{n}^{2} } \right] \\ & \quad \quad \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \end{aligned}$$

(20b)

$$\begin{aligned} F_{mn}^{2} & = \left[ {2H\alpha_{m}^{2} ( - 1)^{n} + D_{22} ( - 1)^{n} \beta_{n}^{2} - \frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right] \\ & \quad \quad \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1}\end{aligned}$$

(20c)

$$\begin{aligned} F_{mn}^{3} = \left[ { - D_{11} \alpha_{m} } \right]\left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \end{aligned}$$

(20d)

$$F_{mn}^{4} = \left[ {D_{11} \alpha_{m} ( - 1)^{m} } \right]\left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1}$$

(20e)

$$\begin{aligned} F_{mn}^{5} & = \left\{ {\sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \left[ {\cos (\alpha_{m} x_{1M} )} \right. - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} } \right. + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} } \hfill \\ & \quad \times \left. {\left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]\left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} } \right\} \hfill \\ & \quad \times \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \hfill \\ \end{aligned}$$

(20f)

Performing single finite cosine transform over the boundary conditions in Eqs. 4a, b, and integrating both sides, result in Eqs. 21a, b, respectively, one obtains:

$$\int\limits_{0}^{b} {\left( {\frac{{\partial w_{0} }}{\partial x}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \cos \left( {\beta_{n} y} \right){\text{d}}y = \frac{{D_{11} a(1 - r_{x0} )}}{{3D_{11} r_{x0} }}\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial^{2} x}}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \cos \left( {\beta_{n} y} \right){\text{d}}y = \frac{{a(1 - r_{x0} )}}{{3r_{x0} }}\Psi_{n}$$

(21a)

$$\int\limits_{0}^{b} {\left( {\frac{{\partial w_{0} }}{\partial x}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right)} \cos \left( {\beta_{n} y} \right){\text{d}}y = - \frac{{D_{11} a(1 - r_{xa} )}}{{3D_{11} r_{xa} }}\int\limits_{0}^{b} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial^{2} x}}\left| {\begin{array}{*{20}c} {} \\ {x = a} \\ \end{array} } \right.} \right)} \cos \left( {\beta_{n} y} \right){\text{d}}y = - \frac{{a(1 - r_{xa} )}}{{3r_{xa} }}\Pi_{n}$$

(21b)

Performing single finite sine transform over the boundary conditions in Eq. 4d, and integrating both sides, result in Eqs. 22a, b:

$$\int\limits_{0}^{a} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin \left( {\alpha_{m} x} \right){\text{d}}x = \frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} \int\limits_{0}^{a} {\left( {w_{0} \left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)\sin \left( {\alpha_{m} x} \right){\text{d}}x}$$

(22a)

$$\int\limits_{0}^{a} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin \left( {\alpha_{m} x} \right){\text{d}}x = \frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} \int\limits_{0}^{a} {\left( {w_{0} \left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)\sin \left( {\alpha_{m} x} \right){\text{d}}x}$$

(22b)

Performing the inverse finite cosine Fourier transform with respect to y of Eq. 8 results in Eq. 23. In particular cases when y = {0, b}, Eq. 23 is simplified to Eqs. 24a, b, respectively:

$$\int\limits_{0}^{a} {w_{0} \sin (\alpha_{m} x){\text{d}}x = \frac{2}{b}\sum\limits_{n = 0}^{\infty } {\delta_{n} w_{mn} \cos (\beta_{n} y)} }$$

(23)

$$\int\limits_{0}^{a} {\left( {w_{0} \left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)\sin (\alpha_{m} x){\text{d}}x = \frac{2}{b}\sum\limits_{n = 0}^{\infty } {\delta_{n} w_{mn} } }$$

(24a)

$$\int\limits_{0}^{a} {\left( {w_{0} \left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)\sin (\alpha_{m} x){\text{d}}x = \frac{2}{b}\sum\limits_{n = 0}^{\infty } {\delta_{n} ( - 1)^{n} w_{mn} } }$$

(24b)

Considering the principle of series higher derivatives [32], the second-order derivatives of Eqs. 24a, b can be calculated as stated in Eqs. 25a, b, respectively:

$$\begin{gathered} \frac{2}{b}\sum\limits_{n = 0}^{\infty } {\delta_{n} \left[ {( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)\sin (\alpha_{m} x){\text{d}}x} - \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)\sin (\alpha_{m} x){\text{d}}x - \beta_{n}^{2} w_{mn} } } \right]} \hfill \\ = \int\limits_{0}^{a} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x = \frac{2}{b}\sum\limits_{n = 0}^{\infty } {\delta_{n} \left[ {( - 1)^{n} \Delta_{m} - \Omega_{m} - \beta_{n}^{2} w_{mn} } \right]} \hfill \\ \end{gathered}$$

(25a)

$$\begin{gathered} \frac{2}{b}\sum\limits_{n = 0}^{\infty } {( - 1)^{n} \delta_{n} \left[ {( - 1)^{n} \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)\sin (\alpha_{m} x){\text{d}}x} - \int\limits_{0}^{a} {\left( {\frac{{\partial w_{0} }}{\partial y}\left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)\sin (\alpha_{m} x){\text{d}}x - \beta_{n}^{2} w_{mn} } } \right]} \hfill \\ = \int\limits_{0}^{a} {\left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}\left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)} \sin (\alpha_{m} x){\text{d}}x = \frac{2}{b}\sum\limits_{n = 0}^{\infty } {( - 1)^{n} \delta_{n} \left[ {( - 1)^{n} \Delta_{m} - \Omega_{m} - \beta_{n}^{2} w_{mn} } \right]} \hfill \\ \end{gathered}$$

(25b)

 Substituting Eqs. 22a, b into Eqs. 25a, b results in Eqs. 26a, b, respectively:

$$\frac{2}{b}\sum\limits_{n = 0}^{\infty } {\delta_{n} \left[ {( - 1)^{n} \Delta_{m} - \Omega_{m} - \beta_{n}^{2} w_{mn} } \right]} = \frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} \int\limits_{0}^{a} {\left( {w_{0} \left| {\begin{array}{*{20}c} {} \\ {y = 0} \\ \end{array} } \right.} \right)\sin \left( {\alpha_{m} x} \right){\text{d}}x}$$

(26a)

$$\frac{2}{b}\sum\limits_{n = 0}^{\infty } {( - 1)^{n} \delta_{n} \left[ {( - 1)^{n} \Delta_{m} - \Omega_{m} - \beta_{n}^{2} w_{mn} } \right]} = \frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} \int\limits_{0}^{a} {\left( {w_{0} \left| {\begin{array}{*{20}c} {} \\ {y = b} \\ \end{array} } \right.} \right)\sin \left( {\alpha_{m} x} \right){\text{d}}x}$$

(26b)

 Substituting Eqs. 24a, b into Eqs. 26a, b and rearranging both sides result in Eqs. 27a, b, respectively:

$$\sum\limits_{n = 0}^{\infty } {\delta_{n} \left\{ {\left[ {( - 1)^{n} \Delta_{m} - \Omega_{m} } \right] - \left[ {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right]w_{mn} } \right\}} = 0$$

(27a)

$$\sum\limits_{n = 0}^{\infty } {( - 1)^{n} \delta_{n} \left\{ {\left[ {( - 1)^{n} \Delta_{m} - \Omega_{m} } \right] - \left[ {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right]w_{mn} } \right\}} = 0$$

(27b)

Performing the inverse finite sine Fourier transform with respect to x of Eq. 8 results in Eq. 28:

$$\int\limits_{0}^{a} {w_{0} \cos (\beta_{n} y){\text{d}}y = \frac{2}{a}\sum\limits_{n = 0}^{\infty } {w_{mn} \sin (\alpha_{m} x)} }$$

(28)

Considering the principle of the series higher derivatives [30], the first-order derivatives of Eq. 28 at x = {0,a} can be calculated as stated in Eqs. 29a, b, respectively:

$$\int\limits_{0}^{b} {\left( {\frac{{\partial w_{0} }}{\partial x}\left| {\begin{array}{*{20}c} {} \\ {x = 0} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y = \frac{2}{a}\sum\limits_{m = 1}^{\infty } {\alpha_{m} w_{mn} }$$

(29a)

$$\int\limits_{0}^{b} {\left( {\frac{{\partial w_{0} }}{\partial x}\left| {\begin{array}{*{20}c} {} \\ {x = b} \\ \end{array} } \right.} \right)} \cos (\beta_{n} y){\text{d}}y = \frac{2}{a}\sum\limits_{m = 1}^{\infty } {( - 1)^{m} \alpha_{m} w_{mn} }$$

(29b)

 Substituting Eqs. 21a, b into Eqs. 29a, b and rearranging both sides result in Eqs. 30a, b, respectively:

$$\sum\limits_{m = 1}^{\infty } {\alpha_{m} w_{mn} } = \frac{{a^{2} (1 - r_{x0} )}}{{6r_{x0} }}\Psi_{n}$$

(30a)

$$\sum\limits_{m = 1}^{\infty } {( - 1)^{m} \alpha_{m} w_{mn} } = - \frac{{a^{2} (1 - r_{xa} )}}{{6r_{xa} }}\Pi_{n}$$

(30b)

 Substututing Eq. 20a into Eqs. 27a, b and 30a, b finally leads to Eqs. 31a–d which can be defined as four finite systems of linearized equations as the function of higher-order Fourier series and four unknown variables Ω_m, ∆_m, Ψ_n, and Π_n, namely:

$$\begin{aligned} & \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{1} } \Omega_{m} + \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{2} } \Delta_{m} + \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{3} } \Psi_{n} \\ & \quad + \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{4} } \Pi_{n} = \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{5} } \end{aligned}$$

(31a)

$$\begin{aligned} & \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{6} } \Omega_{m} + \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{7} } \Delta_{m} + \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{8} } \Psi_{n} \\ & \quad + \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{9} } \Pi_{n} = \sum\limits_{n = 0,1,2,...}^{\infty } {S_{mn}^{10} } \end{aligned}$$

(31b)

$$\sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{11} } \Omega_{m} + \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{12} } \Delta_{m} + \left[ {\frac{{ - a^{2} (1 - r_{xo} )}}{{6r_{xo} }} + \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{13} } } \right]\Psi_{n} + \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{14} } \Pi_{n} = \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{15} }$$

(31c)

$$\sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{16} } \Omega_{m} + \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{17} } \Delta_{m} + \left[ {\frac{{a^{2} (1 - r_{xa} )}}{{6r_{xa} }} + \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{18} } } \right]\Psi_{n} + \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{19} } \Pi_{n} = \sum\limits_{m = 1,2,3,...}^{\infty } {S_{mn}^{20} }$$

(31d)

where, Sⁱ_mn are twenty coefficients in four finite systems of the linearized equations. Once the unknown constants defined in Eqs. 18a–d are found from Eqs. 31a–d, they are substituted into Eq. 20a to obtain the higher order Fourier integral function of the mid-plane vertical displacement.

3 Results and discussions

Several case study examples are considered in this section to gauge the accuracy of the proposed analytical method. As such, the smart laminated piezoelectric composite rectangular plates are first subjected to pure electrical load induced by the bounded piezoelectric actuators and the final example (Case study 4) provides some insights into the application of electro-mechanical load. Matlab software [33] is used to solve Eqs. 31a–d. If m and n terms associated with each set of multivariable equations are sufficient, for example m = n = 50, the higher results accuracy can be achieved. In each case study, the composite laminate contains a particular stacking sequence configuration which is represented as [β₁, β₂,…, β_k], where, β stands for the fiber angle orientation with respect to x-direction in a composite layer and k stands for the layer number (see Fig. 1). For instance, a stacking sequence configuration [0, 90, 90, 0] represents a four-layered composite laminate with each layer from top to bottom having the fiber angle orientation of 0, 90, 90, and 0, respectively.

3.1 FE simulations

To validate the results obtained from the analytical approach developed in Sect. 2, a series of FE simulations are performed using the material parameters summarized in Table 1 [34, 35], and with the aid of Abaqus FE commercial code. In the FE simulations conducted in this work, Abaqus eight-node, hexahedron, reduced integration, three-dimensional continuum shell elements (SC8R) with hourglass control, and Abaqus eight-node, linear, piezoelectric three-dimensional brick elements (C3D8E) have been assigned to the laminated composite plates and piezoelectric patches, respectively. The SC8R elements with three displacement degrees of freedoms (DOFs) per node totally possess 24 DOFs, and the C3D8E elements with three displacement DOFs and one electric voltage DOF per node have a total of thirty two DOFs to be specified during the numerical solution process [36].

Table 1 Material properties of piezoelectric patches and composite laminates

The piezoelectric patches are attached to the laminated composite plate using the tie constraints available in Abaqus/Standard [36] which allows the existence of a mesh nonconformity between the piezoelectric patches and laminated composite plate.

To minimize the approximation error in the numerical analysis, a mesh refinement study has been performed to find the appropriate mesh densities. Based on the mesh convergence studies reported in Table 2, these mesh densities result in the most computationally-optimal solution, that is, the best balance between solution accuracy and computational time. Although, while adequate efforts have been made to preclude the approximation and discretization errors, the present verification needs more quantitative investigations due to the paucity of detailed numerical error analysis. Such analysis may require the application of the non-commercial software for parametric convergence studies and/or adaptive analysis to determine and control the numerical error, respectively. This is indeed an exciting topic for further investigation that is out of the scope of the present work. Refer to [37,38,39,40] for further details of numerical techniques used to model the electro-mechanical response of the piezoelectric structures.

Table 2 Mesh refinement study associated with Abaqus FE simulation

3.2 Case study examples

3.2.1 Case study 1

In this example, it is assumed that a smart laminated composite square plate (SLCSP) is induced by a pair of piezoelectric patches bounded to the top and bottom layers of the plate. The geometrical specifications of the composites plates are a = b = 0.3 [m], t_p = 1.2 [mm], and [0/90/90/0]. The geometrical specifications of the piezoelectric actuators are t_a = 0.3 [mm] and L_a = w_a = 0.1 [m]. 300 [V] and − 300 [V] are applied to the piezoelectric patches bounded to the top and bottom layers of the composite laminate, respectively. The piezoelectric patches are positioned at x₁ = y₁ = 0.1 [m] and x₂ = y₂ = 0.2 [m].

The rotational fixity factor of the springs are first chosen to be r_x0 = r_xa = 0, which causes the plate to have simple support boundaries at two opposite edges. The 3D results of the plate’s flexural response using the proposed analytical solution and Abaqus in the simple support case are illustrated in Fig. 2a, b, respectively. In the next attempt, the rotational fixity factor of the springs are chosen to be r_x0 = r_xa = 1, which causes the plate to have the clamped support boundaries at two opposite edges. The 3D results of the plate’s flexural response using the proposed analytical solution and Abaqus in the clamped case are illustrated in Fig. 3a, b, respectively. The comparison of the 3D results of both simple support and clamped support cases shows good agreement in terms of 3D flexural shape deformation. To evaluate the accuracy of the proposed analytical solution, the 2D results obtained from both approaches are compared together at the particular path w₀(x,b/2) (Fig. 4) which are in a good agreement. The results comparison between the proposed analytical solution and the FE simulation presented in Table 3 also demonstrates the accuracy of the analytical solution. The results clearly demonstrate that flexural response of the smart plate is significantly affected by variation in the rotational fixity factor of the springs. As such, flexural deformation is much higher in the simple support case than in the clamped support case, regardless of the effect of actuation voltage.

Fig. 2

3D flexural response of four-layered laminated composite plate induced by one pair of piezoelectric patches when r_x0 = r_xa = 0 at two opposite edges: (a) proposed analytical solution and (b) FE simulation. Note that the piezoelectric patches and laminated composite plate meshed with 1250 Abaqus C3D8E and 2888 Abaqus SC8R elements, respectively

Fig. 3

3D flexural response of four-layered laminated composite plate induced by one pair of piezoelectric patches when r_x0 = r_xa = 1 at two opposite edges: (a) proposed analytical solution and (b) FE simulation. Note that the piezoelectric patches and laminated composite plate meshed with 1250 Abaqus C3D8E and 2888 Abaqus SC8R elements, respectively

Fig. 4

2D flexural response of the SLCSP induced by one pair of piezoelectric patches at y = 0 (hollow circle and solid circle graphs) and y = b/2 (full line and dash line graphs). SS (r_x0 = r_xa = 0) and C (r_x0 = r_xa = 1) stand for simple support and clamped support, respectively

Table 3 Results comparison between the proposed analytical solution and the FE simulations in Fig. 4: SS (r_x0 = r_xa = 0) and C (r_x0 = r_xa = 1) stand for simple support and clamped support, respectively

3.2.2 Case study 2

In this example, a smart laminated composite rectangular plate (SLCRP) is induced by a pair of piezoelectric patches bounded to the top and bottom layers of the plate. The geometrical specifications of the composites plates are a = 0.2 [m], b = 0.1 [m], t_p = 1.2 [mm], and [0/90/90/0]. The geometrical specifications of the piezoelectric actuators are t_a = 0.3 [mm], L_a = 0.1 [m], and w_a = 0.05 [m]. 300 [V] and − 300 [V] are applied to the piezoelectric patches bounded to the top and bottom layers of the composite laminate, respectively. The piezoelectric patches are positioned at x₁ = 0.05 [m], x₂ = 0.15 [m], y₁ = 0.025 [m], and y₂ = 0.075 [m].

In the first attempt, the rotational fixity factor of the springs are chosen to be r_x0 = r_xa = 0, which causes the plate to have simple support boundaries at the corresponding edges. The 3D results of the plate’s flexural response using the proposed analytical solution and Abaqus in the simple support case are illustrated in Fig. 5a, b, respectively. In the next attempt, the rotational fixity factor of the springs are chosen to be r_x0 = r_xa = 1, which causes the plate to have the clamped support boundaries at the corresponding edges. The 3D results of the plate’s flexural response using the proposed analytical solution and Abaqus in the clamped case are illustrated in Fig. 6a, b, respectively. The comparison of the 3D results of both simple support and clamped support cases shows good agreement between two approaches in terms of 3D flexural deformation. In the next step, the 2D results are compared together at two particular paths (w₀(x,b/2) and w₀(x,0)) to evaluate and verify the accuracy of the proposed analytical solution. The overall results in the simple support case (Fig. 7) and in the clamped support case (Fig. 8) show good agreement. The results comparison between the proposed analytical solution and the FE simulation can be found in Table 4.

Fig. 5

3D flexural response of four-layered laminated composite plate induced by one pair of piezoelectric patches when r_x0 = r_xa = 0 at two opposite edges: (a) proposed analytical solution and (b) FE simulation. Note that the piezoelectric patches and laminated composite plate meshed with 272 Abaqus C3D8E and 4556 Abaqus SC8R elements, respectively

Fig. 6

3D flexural response of four-layered laminated composite plate induced by one pair of piezoelectric patches when r_x0 = r_xa = 1 at two opposite edges: (a) proposed analytical solution and (b) FE simulation. Note that the piezoelectric patches and laminated composite plate meshed with 272 Abaqus C3D8E and 4556 Abaqus SC8R elements, respectively

Fig. 7

2D flexural response of the SLCRP induced by one pair of piezoelectric patches at y = 0 and y = b/2 when r_x0 = r_xa = 0

Fig. 8

2D flexural response of the SLCRP induced by one pair of piezoelectric patches at y = 0 and y = b/2 when r_x0 = r_xa = 1

Table 4 The results comparison between the proposed analytical solution and the FE simulation in Figs. 7, 8: SS (r_x0 = r_xa = 0) and C (r_x0 = r_xa = 1) stand for simple support and clamped support, respectively

3.2.3 Case study 3

In this example, the flexural response of a SLCRP incorporated with several piezoelectric patches is evaluated. The geometrical specifications of the composites plates are a = 0.2 [m], b = 0.1 [m], t_p = 1.2 [mm], and [0/90/90/0]. The geometrical specifications of the piezoelectric actuators are t_a = 0.3 [mm], L_a = 0.1 [m], and w_a = 0.05 [m]. 300 [V] and − 300 [V] are applied to the piezoelectric patches bounded to the top and bottom layers of the composite laminate, respectively. The first pair of piezoelectric patches are positioned at x₁ = 0.05 [m], x₂ = 0.1 [m], y₁ = 0.0375 [m], and y₂ = 0.0625 [m] and the second pair of piezoelectric patches are positioned at x₁ = 0.125 [m], x₂ = 0.175 [m], y₁ = 0.0375 [m], and y₂ = 0.0625 [m].

The rotationally fixity factor of the springs are chosen to be the same as case study 2 (r_x0 = r_xa = 0 in the first attempt and r_x0 = r_xa = 1 in the second attempt). The 3D results of the plate’s flexural response using the proposed analytical solution and Abaqus in the simple support case are illustrated in Fig. 9a, b, respectively and in the clamped case in Fig. 10a, b, respectively. The comparison of the 3D results of both simple support and clamped support cases shows good agreement between two approaches in terms of 3D flexural deformation. In the next step, the 2D results are compared together at two particular paths (w₀(x,b/2) and w₀(x,0)). The overall results in the simple support case (Fig. 11) and in the clamped support case (Fig. 12) show good agreement. The results comparison between the proposed analytical solution and the FE simulation can be found in Table 5 which also demonstrates the proposed analytical solution accuracy when multiple piezoelectric patches are considered.

Fig. 9

3D flexural response of four-layered laminated composite plate induced by two pairs of piezoelectric patches when r_x0 = r_xa = 0 at two opposite edges: (a) proposed analytical solution and (b) FE simulation. Note that the piezoelectric patches and laminated composite plate meshed with 180 Abaqus C3D8E and 528 Abaqus SC8R elements, respectively

Fig. 10

3D flexural response of four-layered laminated composite plate induced by two pairs of piezoelectric patches when r_x0 = r_xa = 1 at two opposite edges: (a) proposed analytical solution and (b) FE simulation. Note that the piezoelectric patches and laminated composite plate meshed with 180 Abaqus C3D8E and 528 Abaqus SC8R elements, respectively

Fig. 11

2D flexural response of the SLCRP induced by two pairs of piezoelectric patches at y = 0 and y = b/2 when r_x0 = r_xa = 0

Fig. 12

2D flexural response of the SLCRP induced by two pairs of piezoelectric patches at y = 0 and y = b/2 when r_x0 = r_xa = 1

Table 5 The results comparison between the proposed analytical solution and the FE simulation in Figs. 11, 12: SS (r_x0 = r_xa = 0) and C (r_x0 = r_xa = 1) stand for simple support and clamped support, respectively

3.2.4 Case study 4

In the forth and final case study example, the effect of both piezoelectric patches and flexible-spring boundary structure on shape control of a SLCSP is investigated. The SLCSP is induced by one pair of piezoelectric patches. The shape control is based on classical trial and error techniques.

In the first attempt, a SLCRP is subjected to a mechanical patch loading (x₁ = y₁ = 0.05 [m], x₂ = y₂ = 0.15 [m], P_xy = − 6 [KPa]). The geometrical specifications of the composites plate are a = b = 0.2 [m], t_p = 1.2 [mm], and [0/90/90/0]. The geometrical specifications of the piezoelectric actuators are t_a = 0.3 [mm], L_a = w_a = 0.05 [m]. The piezoelectric patches are positioned at x₁ = y₁ = 0.075 [m] and x₂ = y₂ = 0.125 [m]. Piezoelectric patches are then activated by applying electrical voltages to them to induce stiffness in the plate and to ultimately control an undesired flexural deformation caused by the mechanical patch loading. − 400 [V] and 400 [V] are applied to the piezoelectric patches bounded to the top and bottom layers of the composite laminate, respectively. To observe the sole effect of the piezoelectric patches on shape control task, the rotational fixity factors of the springs are kept at r_x0 = r_xa = 0. It can be observed from the 2D results in Fig. 13 that the piezoelectric patches have significantly flexural deformation under pure mechanical patch loading. Comparison of the tip deflection results between the proposed analytical solution and the FE simulation can be found in Table 6. This table also presents the accuracy of the proposed analytical solution for shape control tasks. In the absence of electrical voltage, the plate’s maximum tip deflection reaches to − 1.26 [mm] and − 1.32 [mm] according to the proposed analytical solution and Abaqus, respectively. However, when the piezoelectric patches are activated by applying the electrical voltage, the bending stiffness of the plate considerably improves and the tip deflection magnitude reduces to 0.038 [mm] and 0.035 [mm] according to the proposed analytical solution and Abaqus, respectively.

Fig. 13

Flexural control of the SLCSP induced by one pair of piezoelectric patches at y = b/2 when r_x0 = r_xa = 0

Table 6 The results comparison between the proposed analytical solution and the FE simulation in Fig. 13

In the second attempt, the effect of flexible-spring boundary structure on shape control task is investigated. − 400 [V] and 400 [V] are applied to the piezoelectric patches bounded to the top and bottom layers of the composite laminate, respectively. The geometrical specifications of the composites plate are a = b = 0.2 [m], t_p = 1.2 [mm], and [0/90/90/0]. The geometrical specifications of the piezoelectric actuators are t_a = 0.3 [mm], L_a = w_a = 0.05 [m]. The piezoelectric patches are positioned at x₁ = y₁ = 0.075 [m] and x₂ = y₂ = 0.125 [m]. Several rotational fixity factors for the springs are considered and their effect on the shape control of the plate is explored. As seen in Fig. 14, an increase in the rotational fixity factor can improve flexural deflection according to both approaches. Therefore, by adapting a proper approach toward controlling both the electrical voltage and rotational fixity factor, one can achieve a highly desirable shape control performance of the plate versus arbitrary loads.

Fig. 14

Flexural control of the SLCSP induced by one pair of piezoelectric patches at y = b/2 considering various rotational fixity factors for springs at x = 0 and x = a

In the third attempt, the combined effects of rotational fixity factors for springs and the position of piezoelectric patches on shape control are investigated. The geometrical specifications of the composites plate are a = 0.2 [m] and b = 0.1 [m], t_p = 1.2 [mm], and [0/90/90/0]. The geometrical specifications of the piezoelectric actuators are t_a = 0.3 [mm], L_a = 0.1 [m] and w_a = 0.05 [m]. The piezoelectric patches are positioned at x₁ = 0.05 [m], x₂ = 0.15 [m], y₁ = 0.025 [m], and y₂ = 0.075 [m]. 400 [V] and − 400 [V] are applied to the piezoelectric patches bounded to the top and bottom layers of the composite laminate, respectively. In this example, the piezoelectric patches are either bounded to the top and bottom surfaces or only bounded to the top surface of the plate. The positional effect of piezoelectric patches coupled with the effect of rotational fixity factor is demonstrated to be significant as shown in Fig. 15a–c. In all cases, using a pair of piezoelectric patches rather than a single piezoelectric patch is shown to be more effective in improving the flexural deflection. The flexural deflection can further be using an appropriate rotational fixity factor. When the highest rotational fixity factor (r_x = 1) and a pair of piezoelectric patches are considered the flexural deflection is significantly reduced.

Fig. 15

Flexural control of the SLCSP induced by one pair of piezoelectric patches at y = b/2 considering the combined effects of rotational fixity factors for springs at x = 0 and x = a and piezoelectric patches position: (a) r_x0 = 0 and r_xa = 1, (b) r_x0 = 0.5 and r_xa = 1, and (c) r_x0 = r_xa = 1

4 Concluding remarks

This paper proposed an analytical solution for flexural response of smart laminated piezoelectric composite plates with flexible-spring boundary structure. Rotational springs encompassing adjustable stiffness are integrated with the smart plates to provide flexible boundaries at two opposite edges which vary depending on the rotational fixity factors of the springs. As such, the plate could have simple support, clamped support, and neither simple support nor clamped support boundary conditions at the corresponding edges. The proposed analytical solution enables (1) obtaining coupled electro-mechanical bending moments due to electro-mechanical load and (2) calculating flexural response which matches the particular type of boundary condition. The accuracy and the reliability of the proposed analytical solution are evaluated and qualitatively verified using the results achieved from Abaqus FE simulation. The findings reported in this study are summarized as follows:

• 1. The results comparison between the proposed analytical solution and the FE simulation showed good agreement.

• 2. The proposed analytical solution demonstrated that the trial deformation and characteristic function can be eliminated which leads to comparatively higher accuracy than employing conventional semi-inverse methods. Furthermore, it can be used to cover more general case study examples such as combined concentrated load and patch loading as well as electrical load applied by multiple piezoelectric actuators without any restriction to the load position and the number of loads applied.

• 3. The results obtained using the proposed analytical solution demonstrated that piezoelectric actuators and rotational fixity factor of springs can significantly influence flexural response of smart laminated piezoelectric composite plates.

• 4. The shape control using classical trial and error technique can be adopted to reduce the flexural deformation of plates which depends on the number of piezoelectric actuators, the fixity factor of springs, and the applied electrical voltage.

Future research will combine the expertise of the authors in analytical modeling, machine learning and artificial neural network algorithms [41,42,43], FEA, biomechanics and experimental protocol.

Appendices

Appendices

1.1 Appendix A

The relation between the global and local stresses in a composite layer is stated in Eq. 32. The transformation matrix [T] is calculated using Eq. 33 [44]:

$$\left[ {\begin{array}{*{20}c} {\sigma_{xx} } & {\sigma_{yy} } & {\tau_{xy} } \\ \end{array} } \right]_{k}^{T} = \left[ T \right]^{ - 1} \left[ {\begin{array}{*{20}c} {\sigma_{11} } & {\sigma_{22} } & {\tau_{12} } \\ \end{array} } \right]_{k}^{T}$$

(32)

where:

$$\left[ T \right] = \left[ {\begin{array}{lll} {c^{2} } & \quad {s^{2} } & \quad {2{\text{c}} s} \\ {s^{2} } & \quad {c^{2} } & \quad { - 2cs} \\ { - cs} & \quad {cs} & \quad {\left( {c^{2} - s^{2} } \right)} \\ \end{array} } \right]$$

(33)

where, c and s stand for cosine and sine of function β and β is the fiber angle of each composite layer.

The terms Q_ij present in Eqs. 3a, b stand for the elastic stiffness in composite and piezoelectric layers as stated in Eqs. 34–37 [45], i.e.

$$Q_{11} = \frac{{E_{11} }}{{1 - \nu_{12} \nu_{21} }}$$

(34)

$$Q_{22} = \frac{{E_{22} }}{{1 - \nu_{12} \nu_{21} }}$$

(35)

$$Q_{12} = \frac{{\nu_{12} E_{22} }}{{1 - \nu_{12} \nu_{21} }}$$

(36)

$$Q_{66} = G_{12}$$

(37)

where, E₁₁, E₂₂ are elastic modules along and perpendicular to fibers, respectively and v₁₂, and G₁₂ are the Poisson’s ratio and shear modules, respectively. The global stresses-strains in a composite layer is calculated using Eq. 38 [46]:

$$\left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ \end{array} } \right]^{k} = \left[ {\begin{array}{lll} {\overline{Q}_{11} } & \quad{\overline{Q}_{12} } & \quad {\overline{Q}_{16} } \\ {\overline{Q}_{12} } & \quad {\overline{Q}_{22} } &\quad {\overline{Q}_{26} } \\ {\overline{Q}_{16} } &\quad {\overline{Q}_{26} } & \quad {\overline{Q}_{66} } \\ \end{array} } \right]^{k} \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right]^{k}$$

(38)

where, σ_xx, σ_yy, and τ_xy are the global stress and strain components in the x and y directions, respectively. $\overline{Q}$ _ij^k in a composite layer are the transformed stiffness matrix terms which are calculated using Eqs. 39–44 [46]:

$$\overline{Q}_{11} = Q_{11} c^{4} + 2(Q_{12} + 2Q_{66} )c^{2} s^{2} + Q_{22} s$$

(39)

$$\overline{Q}_{12} = (Q_{11} + Q_{22} - 4Q_{66} )c^{2} s^{2} + Q_{12} (c^{4} + s^{4} )$$

(40)

$$\overline{Q}_{22} = Q_{11} s^{4} + 2(Q_{12} + 2Q_{66} )c^{2} s^{2} + Q_{22} c^{4}$$

(41)

$$\overline{Q}_{16} = - Q_{22} cs^{3} + Q_{11} c^{3} s - (Q_{12} + 2Q_{66} )(c^{2} - s^{2} )cs$$

(42)

$$\overline{Q}_{26} = - Q_{22} c^{3} s + Q_{11} cs^{3} - (Q_{12} + 2Q_{66} )(c^{2} - s^{2} )cs$$

(43)

$$\overline{Q}_{66} = (Q_{11} + Q_{22} - 2Q_{12} )c^{2} s^{2} + Q_{66} (c^{2} - s^{2} )^{2}$$

(44)

The piezoelectric modules in a piezoelectric layer are calculated using Eqs. 45–47 [24, 47]:

$$e_{31} = Q_{11} d_{31} + Q_{12} d_{32}$$

(45)

$$e_{32} = Q_{12} d_{31} + Q_{22} d_{32}$$

(46)

$$e_{36} = 0$$

(47)

where, d_ij stand for the piezoelectric dielectric constants under constant stress in a piezoelectric layer.

The electro-mechanical bending-twisting couplings are calculated using Eq. 48 [28]:

$$\left[ {\begin{array}{*{20}c} {M_{xx} } & {M_{yy} } & {M_{xy} } \\ \end{array} } \right]^{T} = \int\limits_{ - H/2}^{H/2} z \left( {\sigma_{xx} ,\sigma_{yy} ,\tau_{xy} } \right)dz - \left[ {\begin{array}{*{20}c} {M_{xx}^{P} } & {M_{yy}^{P} } & {M_{xy}^{P} } \\ \end{array} } \right]^{T}$$

(48)

where, [M_xx]^P and [M_yy]^P are defined as the bending moments and [M_xy]^P is the twisting moment induced by electrical load, respectively [48].

1.2 Appendix B

The twenty coefficients (Sⁱ_mn), i = {1,2,…,20} in four finite systems of the linear equations (Eqs. 31a–d) are as follows:

$$S_{mn}^{1} = \delta_{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( {\frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }} - 2H\alpha_{m}^{2} - D_{22} \beta_{n}^{2} } \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}} + 1} \right]$$

(49)

$$S_{mn}^{2} = \delta_{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( {2H\alpha_{m}^{2} ( - 1)^{n} + D_{22} ( - 1)^{n} \beta_{n}^{2} - \frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}} - ( - 1)^{n} } \right]$$

(50)

$$S_{mn}^{3} = \delta_{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( { - D_{11} \alpha_{m} } \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}}} \right]$$

(51)

$$S_{mn}^{4} = \delta_{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( {D_{11} \alpha_{m} ( - 1)^{m} } \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}}} \right]$$

(52)

$$\begin{aligned} S_{mn}^{5} & = - \delta_{n} \left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left \{ {\sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \left[ {\cos (\alpha_{m} x_{1M} )} \right. - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} } \right. \hfill \\ & \quad + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} } \left. {\left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]\left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} } \right\} \hfill \\ & \quad \times \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \hfill \\ \end{aligned}$$

(53)

$$S_{mn}^{6} = \delta_{n} ( - 1)^{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( {\frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }} - 2H\alpha_{m}^{2} - D_{22} \beta_{n}^{2} } \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}} + 1} \right]$$

(54)

$$S_{mn}^{7} = \delta_{n} ( - 1)^{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( {2H\alpha_{m}^{2} ( - 1)^{n} + D_{22} ( - 1)^{n} \beta_{n}^{2} - \frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}} - ( - 1)^{n} } \right]$$

(55)

$$S_{mn}^{8} = \delta_{n} ( - 1)^{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( { - D_{11} \alpha_{m} } \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}}} \right]$$

(56)

$$S_{mn}^{9} = \delta_{n} ( - 1)^{n} \left[ {\frac{{\left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left( {D_{11} \alpha_{m} ( - 1)^{m} } \right)}}{{\left( {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right)}}} \right]$$

(57)

$$\begin{aligned} S_{mn}^{10} & = - \delta_{n} ( - 1)^{n} \left( {\frac{{D_{12} }}{{D_{22} }}\alpha_{m}^{2} + \beta_{n}^{2} } \right)\left\{ {\sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \left[ {\cos (\alpha_{m} x_{1M} )} \right. - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} } \right. \hfill \\ & \quad + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} } \left. {\left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]\left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} } \right\} \hfill \\ & \quad \times \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \hfill \\ \end{aligned}$$

(58)

$$S_{mn}^{11} = \alpha_{m} \left[ {\frac{{\left( {\frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right) - 2H\alpha_{m}^{2} - D_{22} \beta_{n}^{2} }}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(59)

$$S_{mn}^{12} = \alpha_{m} \left[ {\frac{{2H\alpha_{m}^{2} ( - 1)^{n} + D_{22} ( - 1)^{n} \beta_{n}^{2} - \left( {\frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right)}}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(60)

$$S_{mn}^{13} = \alpha_{m} \left[ {\frac{{ - D_{11} \alpha_{m} }}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(61)

$$S_{mn}^{14} = \alpha_{m} \left[ {\frac{{D_{11} \alpha_{m} ( - 1)^{m} }}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(62)

$$\begin{aligned} S_{mn}^{15} & = - \alpha_{m} \left\{ {\sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \left[ {\cos (\alpha_{m} x_{1M} )} \right. - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} } \right. + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} } \hfill \\ & \quad \times \left. {\left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]\left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} } \right\} \hfill \\ & \quad \times \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \hfill \\ \end{aligned}$$

(63)

$$S_{mn}^{16} = \alpha_{m} ( - 1)^{m} \left[ {\frac{{\left( {\frac{{\alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right) - 2H\alpha_{m}^{2} - D_{22} \beta_{n}^{2} }}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(64)

$$S_{mn}^{17} = \alpha_{m} ( - 1)^{m} \left[ {\frac{{2H\alpha_{m}^{2} ( - 1)^{n} + D_{22} ( - 1)^{n} \beta_{n}^{2} - \left( {\frac{{( - 1)^{n} \alpha_{m}^{2} (H + 2D_{66} )}}{{D_{22} }}} \right)}}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(65)

$$S_{mn}^{18} = \alpha_{m} ( - 1)^{m} \left[ {\frac{{ - D_{11} \alpha_{m} }}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(66)

$$S_{mn}^{19} = \alpha_{m} ( - 1)^{m} \left[ {\frac{{D_{11} \alpha_{m} ( - 1)^{m} }}{{D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} }}} \right]$$

(67)

$$\begin{aligned} S_{mn}^{20} & = - \alpha_{m} ( - 1)^{m} \left\{ {\sum\limits_{L = 1}^{Mn} {C_{mn}^{1} \left( {\frac{{ - P_{o} }}{{\alpha_{m} \beta_{n} }}} \right)_{{}} } \left[ {\cos (\alpha_{m} x_{1M} )} \right. - \left. {\cos (\alpha_{m} x_{2M} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1M} ) - \sin (\beta_{n} y_{2M} )} \right]_{L} } \right. + \sum\limits_{L = 1}^{Tn} {C_{mn}^{2} } \hfill \\ & \quad \times \left. {\left[ {\frac{{\left[ {M_{x}^{P} } \right]^{\Theta } \alpha_{m}^{2} + \left[ {M_{y}^{P} } \right]^{\Theta } \beta_{n}^{2} }}{{\alpha_{m} \beta_{n} }}} \right]\left[ {\cos (\alpha_{m} x_{1P} )} \right. - \left. {\cos (\alpha_{m} x_{2P} )} \right]_{L} \left[ {\sin (\beta_{n} y_{1P} ) - \sin (\beta_{n} y_{2P} )} \right]_{L} } \right\} \hfill \\ & \quad \times \left[ {D_{11} \alpha_{m}^{4} + 2H\alpha_{m}^{2} \beta_{n}^{2} + D_{22} \beta_{n}^{4} } \right]^{ - 1} \hfill \\ \end{aligned}$$

(68)