Free vibration and buckling analyses of FG porous sandwich curved microbeams in thermal environment under magnetic field based on modified couple stress theory

Abstract

Porous sandwich structures include different numbers of layers and are capable of demonstrating higher values of strength to weight ratio in comparison with traditional sandwich structures. Free vibration and mechanical buckling responses of a three-layered curved microbeam was investigated under the Lorentz magnetic load in the current study. A viscoelastic substrate was considered and the effect of the thermal environment on its mechanical properties was assessed. The core was composed of the functionally graded porous materials whose properties changed across the thickness based on some given functions. The face sheets were FG-carbon nanotube-reinforced composites and the influence of the placement of CNTs was evaluated on the behavior of the faces. Using the extended rule of mixture, their effective properties were determined. Modified couple stress theory was used to predict the results in the micro-dimension. While the governing equations were derived based on the higher order shear deformation theory and energy method, and mathematically solved via Navier’s method. The results were validated with the previously published works, considering the effects of various parameters. As comprehensively explained in the results section, natural frequencies and critical buckling loads were reduced by enhancing the central opening angle. Moreover, an increase in the porosity coefficient declined the mentioned values, but increasing the CNTs content showed the opposite effect. The outcomes of this study may help in the design and manufacturing of various equipment using such smart structures, making high stiffness to weight ratios more accessible.

1 Introduction

Sandwich structures are often three-layered structures whose core (central layer) is integrated with two skins. Usually, the core has a lower strength in comparison with the face sheets. Porous materials are often used as core. The idea behind the development of such structures is the high demand of different industries for structures with low weight-to-strength ratios as the most important characteristics of sandwich structures. The extensive applications of porous materials in different fields have encouraged the researchers to further investigate them. For example, metal foams, a class of porous materials, have found wide applications in industries such as vehicles, high-speed trains, energy, and vibration absorbers (Fig. 1). Composites are multi-component materials whose properties are generally better than their components. Each composite consists of a matrix phase and one or more reinforcement phases. It should be noted that the components of a composite do not chemically merge as they fully maintain their chemical and natural properties; thus creating a definite common interface between the components [1]. Composites have several advantages, leading to their wide applications nowadays. Polymeric nanocomposites may be used in fuel tanks and tubes, military industries, automobile industries, marine structures, construction industry, sports equipment, and medical equipment [2]. Some of these applications are shown in Fig. 2. In recent years, nanotubes have been developed and applied by the rapid advancement in science and technology. In the past 2 decades, their usage has been accelerated with the advent of carbon nanotubes (CNTs) by Iijima [3]. CNTs have unique mechanical, magneto-electrical, and chemical properties. High rigidity and stiffness-to-weight ratio, electrical conductivity, and high-temperature strength are among some of their characteristics [4]. CNTs have been used as reinforcement of composites and significantly improved their properties. CNTs are divided into single-walled and multi-walled types. Single-walled carbon nanotubes (SWCNTs) consist of a simple structure. Some prediction suggests that SWCNTs can be conductive or semiconductor [5]. Its electrical conductivity depends on the exact geometry of carbon atoms. Based on the arrangement of the carbon atoms, SWCNTs are also divided into three major categories. Mechanical analysis of CNT-reinforced composites (CNTRCs) was presented by various researchers. Thostenson and Chou [6] modeled the elastic properties of CNTRCs in 2003. They investigated the effect of the size and structure of CNTs based on the elastic characteristics of the composite matrix. The bending behavior of a CNT-reinforced composite plate between two piezoelectric layers was investigated by Alibeigloo [7] under a uniform mechanical load. Duc et al. [8] considered thermal and mechanical stability of FG-CNTRC truncated conical shells. They used classical shells theory and Galerkin method to obtain the results and considered the effect of the most important variants such as semi-vertex angle and elastic medium on the linear thermal and mechanical buckling load. Shariati et al. [9] presented their study on the large-amplitude nonlinear vibrations in multi-sized hybrid nanocomposites disk rested on nonlinear elastic media and located in an environment whose temperature was gradually changed.

Fig. 1

Some of porous materials applications in different areas such as a frame/substructure of some cars; b kitchen pots and pans; c trains; d vibration absorbers in pipes

Fig. 2

Some of polymer nanocomposites applications

Many researchers have tried to investigate different types of sandwich structures with diverse theories, so far. One of them is a study by Khatua and Cheung [10] dated 1973 which addressed the bending and vibration behaviors of multilayer beams and plates. After that, Maheri and Adams [11] studied this topic and published the results of their study on the flexural vibration damping of honeycomb sandwich beams in 1992. Furthermore, transverse vibrations of a fluid-saturated thin rectangular porous plate were explored by Leclaire et al. [12] in 2001. Takahashi and Tanaka [13] investigated the flexural vibration of perforated plates and porous elastic materials under acoustic loads in 2002. Elastic buckling and static bending of shear deformable functionally graded (FG) porous beams were examined by Chen et al. [14]. As another paper, shock-absorbing characteristics and vibration transmissibility of honeycomb paperboard were studied by Yanfeng and Jinghui [15]. Ait Atmane et al. [16] studied the effect of thickness stretching and porosity on the mechanical response of FG beams. In another work, the vibrational behavior of shear deformable FG porous beams was estimated by Chen et al. [17] in both free and forced cases. More recently, Katunin [18], published an article about honeycomb sandwich structures and used wavelet analysis to consider the vibration-based spatial damage identification. After that, nonlinear free vibration and post-buckling behaviors of multilayer FG porous nanocomposite beams were evaluated by Chen et al. [19]. They used Graphene platelets (GPLs)-reinforced metal foams and indicated the essential role of the GPLs volume fraction in enhancing the stiffness of the structure. Moreover, they found the structure’s vibration and post-buckling performances were affected by the pore and GPL distribution types. Furthermore, in 2017, Duc et al. [20] hired the first-order shear deformation theory (FSDT) to study the vibration of sandwich composite cylindrical panels with an auxetic honeycomb core. They employed von Karman strain–displacement relations and Airy stress functions method to derive the equations and solved them using Galerkin and fourth-order Runge–Kutta methods. In 2018, Amir et al. [21] addressed the buckling behavior of sandwich plates considering the flexoelectricity effect. In another work, they investigated a similar effect but on the vibrational response of nanocomposite sandwich plates [22]. Besides this, nonlinear vibration of sandwich beams with entangled cross-linked fibers core was examined by Piollet et al. [23]. They compared two sandwich beams with the reference honeycomb beams. Safarpour et al. [24] assessed the frequency characteristics of GPL-reinforced composite viscoelastic thick annular plate with the aid of generalized differential quadrature method. Furthermore, Babaei et al. [25] investigated the thermal buckling and post-buckling responses of FG porous beams with geometrical imperfection. Kumar and Renji [26] conducted a profound study on composite honeycomb sandwich panels exposed to the diffusive acoustic field in a reverberation chamber in 2019 and succeed to measure the strains. The extended rule of mixture (ERM) and Halpin–Tsai micromechanical models were used by Moayedi et al. [27] to investigate the buckling and frequency responses of a GPL-reinforced composite microdisk.

Regarding different behaviors of structures in macro and small dimensions, and also due to the extensive application of small-scale structures (e.g. nano- and microbeams, plates, and shells) in measuring equipment, medicine, and industries, the researchers were encouraged to analyze the mechanical properties in small scales [28]. One of the first studies was conducted by Eringen who presented the nonlocal theory to evaluate the structures in the nanoscale [29, 30]. Earlier, small scales’ effects consideration extended rapidly by numerous authors. Amir et al. [31] used the modified couple stress theory (MCST) to capture the size effect for analyzing a sandwich beam with a porous core. In another study, Amir et al. [32] considered the size-dependent vibrational behavior of a three-layered nanoplate based on Eringen’s nonlocal elasticity theory. The effects of agglomerated CNTs as reinforcement on the size-dependent vibration of embedded curved microbeams based on MCST investigated by Allahkarami and Nikkhah-Bahrami [33]. Alipour and Shariyat [34] used nonlocal zigzag analytical solution for Laplacian hygrothermal stress analysis of annular sandwich macro/nanoplates with poor adhesions and FG porous cores. Also, a study conducted by Yi et al. [35] on size-dependent large-amplitude free oscillations of FG porous nanoshells incorporating vibrational mode interactions. A size-dependent exact theory was presented by Safarpour et al. [36] to analyze the thermal buckling and free and forced vibration of a temperature-dependent FG multilayer GPLs-reinforced composite nanostructure. The influence of modified strain gradient theory (MSGT) was investigated by Esmailpoor Hajilak et al. [37] on buckling, free and forced vibration characteristics of the GPL-reinforced composite cylindrical nanoshell in a thermal environment. As stated, their study was based on MSGT which suggested three material length-scale parameters (i.e. two parameters more than MCST). Earlier in 2020, Sobhy [38] used the differential quadrature method to evaluate the bending in three types of FG sandwich curved beams with honeycomb core in polar coordinate. He investigated magneto-hygrothermal effects on the deflection of the mentioned under consideration structure. In another paper, dynamic behaviors of the FG porous beams were presented by Lei et al. [39] under flexible boundary constraints. They examined two types of single- and multi-span beams.

Numerous theories have been developed to analyze the structures such as beams, plates, and shells; some of them consider the shear deformation effects while others neglected that. The theories accounting for these effects, especially those considering higher order functions, have found wide applications these days. First- and third-order, parabolic, trigonometric, and quasi-3D functions can be mentioned as the prominent higher order shear deformation theories. For example, Omidi Bidgoli et al. [40] used the FSDT to analyze the thermoelastic behavior of FGM rotating cylinders resting on a friction bed which was subjected to a thermal gradient and an external torque. This theory (i.e. FSDT) was also used by Mahani et al. [41] to consider thermal buckling of laminated nanocomposite conical shell reinforced with GPLs. Recently, Arshid et al. [42] took the shear deformation into account by employing the FSDT to investigate the static behavior of a three-layered sandwich circular microplate. Bousahla et al. [43] investigated the buckling and vibrational behaviors of the composite beam armed with SWCNTs resting on the Winkler-Pasternak elastic foundation. The CNTRCs beam was modeled by a novel integral FSDT. Also, hygrothermal and mechanical buckling responses of simply supported FG sandwich plates were investigated by a novel shear deformation theory in the study of Refrafi et al. [44]. Their model took into consideration the shear deformation effects and ensures the zero shear stresses on the free surfaces of the FG sandwich plate without requiring the correction factors. Moreover, a novel four-unknown integral model was introduced by Chikr et al. [45] for the buckling response of FG sandwich plates under various boundary conditions using Galerkin’s approach.

A review of the aforementioned studies shows the absence of a comprehensive study on vibrational and buckling characteristics of sandwich curved microbeams using higher order shear deformation theory (HSDT). Although there are some works about FG structures, no study has addressed the static and dynamic behaviors of a three-layer microstructure including an FG porous core and two nanocomposite face sheets. Therefore, the current paper aims to investigate the mechanical buckling and vibrational behavior of a sandwich curved microbeam placed on the visco-Pasternak substrate in a thermal environment. Also, the influence of the Lorentz magnetic load was investigated on the static and dynamic responses. Various patterns of CNTs’ dispersion were considered in this work, and the effective thermo-mechanical properties of the face sheets were determined via the ERM due to its simplicity and accuracy. By employing the extended Hamilton’s principle and variational formulation, the governing equations were derived, and since the classical elasticity theory does not consider the influence of dimension, the MCST was employed to capture the size effect. Navier’s solution method was used to analytically solve the differential equations system. Based on the results, it is possible to design and manufacture various equipment using such smart structures making the high stiffness to weight ratio more accessible than before.

2 Mathematical formulation

2.1 Geometry

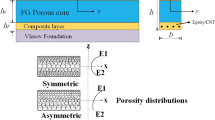
As stated in the previous section, the studied curved microbeam is composed of three layers, as shown in Fig. 3. The core was made from FG porous materials, while the skins were made from FG-CNTRCs. The curvature radius and length are presented by R and L, respectively. The central opening angle is denoted by θ, and the thicknesses of the layers from the bottom to the top are specified with h_b, h_c, and h_t, respectively. The effect of the Lorentz magnetic force was considered as a body force influencing the mechanical behavior of the structure. Moreover, the structure is located on a three-parameter viscoelastic substrate, which includes springs, shear layer, and dashpots. The thermo-mechanical properties of all three layers changed through their thicknesses according to some given functions; they also varied by temperature variations. The Cartesian coordinate system was selected to analyze the microstructure whose origin locates on the left corner of the mid-layer.

Fig. 3

Schematic of the sandwich curved micro beam under magnetic load effect resting on viscoelastic substrate in thermal environment

2.2 Constitutive law

The general stress–strain relations in the thermal environment for all layers of the curved microbeam can be demonstrated as follows [46]:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{i} } \\ {\sigma_{xz}^{i} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11}^{i} } & 0 \\ 0 & {Q_{55}^{i} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} - \alpha_{11}^{i} \Delta T} \\ {2\varepsilon_{xz} } \\ \end{array} } \right\},\quad i = t,c,b $$

(1)

in which σ_xj and ε_xj (j = x, z) are the stress and strain components, respectively. α₁₁ shows the thermal expansion coefficient, and ΔT represents the temperature variations relative to the ambient temperature. It should be noted that i superscript denotes each layer, namely top, core, and bottom. Also, Q₁₁ and Q₅₅ are the components of the stiffness matrix which can be separately defined for each layer:

2.2.1 FG porous core

The components of the stiffness matrix of the FG porous core can be determined through the below relations [47]:

$$ Q_{11} = \frac{E(z)}{{1 - \nu^{2} }},\quad \quad \quad \quad \quad \quad Q_{55} = G(z) = \frac{E(z)}{{2(1 + \nu )}} $$

(2)

where ν is the Poisson’s ratio, and E(z) is Young’s elasticity modulus, which depends on thickness. The mechanical properties of the porous core are graded functionally across its thickness based on three different patterns, called the porosity distributions. These patterns show the pore’s placement in the core. The elasticity modulus and density variations through the core’s thickness can be generally introduced as:

$$ \begin{aligned} E(z) = & E_{1} f(z) \\ \rho (z) = & \rho_{1} g(z), \\ \end{aligned} $$

(3)

where E₁ and ρ₁ are the maximum values of Young’s modulus and density, respectively. Also, f(z) and g(z) show the porosity functions specified for each pattern as follows:

Type A: In this type of porosity distribution, the pores are asymmetrically placed with respect to the mid-plane of the core. Therefore, the porosity functions are defined using a cosine pattern as follows [48]:

$$ \begin{aligned} f(z) = & 1 - \zeta \cos \left( {\frac{\pi z}{{2h_{c} }} + \frac{\pi }{4}} \right) \\ g(z) = & 1 - \psi \cos \left( {\frac{\pi z}{{2h_{c} }} + \frac{\pi }{4}} \right), \\ \end{aligned} $$

(4)

In the above relations, ζ and ψ are the porosity and mass density coefficients, respectively, and can be expressed as [49]:

$$ \zeta = 1 - \frac{{E_{0} }}{{E_{1} }},\quad \quad \quad \quad \quad \quad \psi = 1 - \frac{{\rho_{0} }}{{\rho_{1} }} = 1 - \sqrt {1 - \zeta } $$

(5)

The porosity coefficient shows the ratio of bulk volume to the total volume. Consequently, it was found that its minimum and maximum values are zero and one, respectively. Moreover, E₀ and ρ₀ are the minimum values of Young’s modulus and density, respectively.

Type B: As the second pattern of porosity distribution, symmetric cosine function is considered as follow [50]:

$$ f(z) = 1 - \zeta \cos \left( {\frac{\pi z}{{h_{c} }}} \right), $$

(6)

$g(z) = 1 - \psi \cos \left( {\frac{\pi z}{{h_{c} }}} \right)$.

This pattern states that the pores are distributed through the thickness of the core based on a symmetric function in which the maximum porosity occurs at the top and bottom surfaces, while the minimum porosity can be observed in the mid-plane.

Type C: Based on this type, the pore location does not depend on the z. Therefore, uniform functions with no dependence on z are employed [51]:

$$ f(z) = 1 - \zeta \chi ,\quad \quad \quad \quad \quad \quad g(z) = \sqrt {1 - \zeta \chi } $$

(7)

where [52]:

$$ \chi = \frac{1}{\zeta } - \frac{1}{\zeta }\left( {\frac{2}{\pi }\sqrt {1 - \zeta } - \frac{2}{\pi } + 1} \right)^{2} $$

(8)

On the other hand, the effect of temperature on the properties of the porous core was investigated. To this end, the following equation was used [53]:

$$ P_{c} (T) = P_{0} (P_{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} ) $$

(9)

in which P_c is the properties of the core, and T denotes the temperature in Kelvin. Also, temperature-dependent coefficients are presented by P_i (i = − 1, 0, 1, 2, 3). Table 1 [31] lists the values of these coefficients for SUS304 which is used in the studied core.

Table 1 Coefficients of temperature-dependent properties of the porous core (SUS304) [31]

2.2.2 FG-CNTRC face sheets

The stiffness components of the FG-CNTRC faces are determined via the following relations:

$$ Q_{11}^{t,b} = \frac{{E_{11} }}{{1 - \nu^{2} }},\quad \quad \quad \quad \quad \quad Q_{55}^{t,b} = G_{12} $$

(10)

in which t and b superscripts denote the top and bottom faces, respectively, and E₁₁ and G₁₂ are effective values of Young’s elasticity and shear moduli of the skins, respectively. Among the different methods used to determine these effective values, the ERM as selected due to its simplicity and accuracy. The mentioned values were determined using the following equations [8]:

$$ E_{11} = {\mkern 1mu} \eta_{1} E_{11CNT} {\mkern 1mu} V_{CNT} + V_{m} {\mkern 1mu} E_{m} , $$

(11)

$$ \frac{{\eta_{3} }}{{G_{12} }} = \frac{{V_{CNT} }}{{G_{12CNT} }} + \frac{{V_{m} }}{{G_{m} }} $$

(12)

where the subscripts CNT and m denote the CNTs reinforcement and matrix, respectively. Also, η₁ and η₃ are efficiency parameters of CNTs that can be achieved based on the molecular dynamics for different volume fractions of CNTs. It is noteworthy that the total volume of the faces (i.e. the summation of V_CNT and V_m) should equal one. Furthermore, other properties of the faces such as effective density and thermal expansion coefficient can also be determined by the ERM as [54]:

$$ \rho^{t,b} = V_{CNT} \rho^{CNT} + V_{m} \rho^{m} , $$

(13)

$$ \alpha_{11}^{t,b} = V_{CNT} \alpha_{11}^{CNT} + V_{m} \alpha_{11}^{m} $$

(14)

On the other hand, the Poisson’s ratio of the faces can be expressed as:

$$ \nu_{12} = V_{CNT}^{*} \nu_{12}^{CNT} + V_{m} \nu_{m} $$

(15)

in which, ${V}_{CNT}^{*}$ is the CNTs’ volume fraction:

$$ V_{CNT}^{*} = \frac{{w_{CNT} }}{{w_{CNT} + \left( {\frac{{\rho_{CNT} }}{{\rho_{m} }}} \right) - \left( {\frac{{\rho_{CNT} }}{{\rho_{m} }}} \right)w_{CNT} }} $$

(16)

Here, w_CNT is the mass fraction of CNTs. Similar to the core, the CNTs are distributed across the faces based on different patterns. These patterns determine the CNTs’ placement along the thickness of the face sheets. Therefore, the following functions are suggested to consider the variations of CNTs’ volume fraction [31]:

$$ V_{CNT}^{t,b} = V_{CNT}^{*} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;{\text{UD}} $$

(17)

$$ V_{CNT}^{t,b} = \left[ {1 - \frac{2}{{h_{t,b} }}\left( {z \mp \frac{{h_{c} + h_{t,b} }}{2}} \right)} \right]V_{CNT}^{*} \quad \quad \quad \quad {\text{FG - A}} $$

$$ V_{CNT}^{t,b} = \left[ {1 + \frac{2}{{h_{t,b} }}\left( {z \mp \frac{{h_{c} + h_{t,b} }}{2}} \right)} \right]V_{CNT}^{*} \quad \quad \quad \quad {\text{FG - V}} $$

$$ V_{CNT}^{t,b} = 2\left[ {1 - \frac{2}{{h_{t,b} }}\left( {z \mp \frac{{h_{c} + h_{t,b} }}{2}} \right)} \right]V_{CNT}^{*} \quad \quad \quad \;{\text{FG - O}} $$

$$ V_{CNT}^{t,b} = \frac{4}{{h_{t,b} }}\left[ {\left| {z \mp \frac{{h_{c} + h_{t,b} }}{2}} \right|} \right]V_{CNT}^{*} \quad \quad \quad \quad \quad \quad {\text{FG - X}} $$

where the upper sign (i.e., minus) is for to the top face, and the bottom sign (i.e., plus) represents the bottom face. It is important to note that the dispersion of CNTs in the top and bottom layers are symmetric relative to the mid-plane of structure.

The mechanical properties of the faces are also temperature dependent. Therefore, the temperature dependency of both CNTs reinforcements and matrix should be considered. To this end, the temperature-dependent properties of PMMA matrix including Young’s elasticity modulus, thermal expansion coefficient, mass density, and Poisson’s ratio are presented in Table 2 [55]. Note that in this table, ΔT is the temperature difference which changed linearly. Also, CNTs properties at different temperatures are presented in Table 3 [56]. Based on this table, the following polynomial can describe their dependence on the temperature [2]:

$$ P_{CNT} (T) = P_{0} (1 + P_{1} \Delta T + P_{2} \Delta T^{2} + P_{3} \Delta T^{3} ) $$

(18)

Table 2 Thermo-mechanical properties of PMMA [55]

Table 3 Temperature-dependent properties of the facesheets’ reinforcements (CNTs) [56]

P₀, P₁, P_2, and P₃ are CNTs’ temperature-dependent coefficients, which are shown in Table 4 [44]. Moreover, the density and Poisson’s ratio of CNTs are 1400 kg/m³ and 0.175, respectively.

Table 4 Coefficients of CNTs’ temperature-dependent properties [44]

2.3 Kinematic relations

To describe the displacements of the micro-curved beam, the following HSDT was chosen as the displacement field [57]:

$$ u\left( {x,z,t} \right) = u_{0} \left( {x,t} \right) - z\frac{\partial }{\partial x}w_{0} \left( {x,t} \right) + \Phi \left( z \right)\gamma \left( {x,t} \right), $$

(19)

$$ w\left( {x,z,t} \right) = w_{0} (x,t) $$

in which u and w are the displacements of each point in circumferential and radial directions, respectively. u₀ and w₀ represent the same ones but for the mid-plane. γ is the rotation of cross-section, and Φ(z) denotes the shear deformation function. Various theories have been developed to analyze the structure’s displacements some of which neglect the shear deformation effects; whereas others take then into account. Here, the shear deformation effect was investigated as higher order ones leading to the more complex and also, more accurate and reliable results. The following higher order shear deformation function was considered which is also known as third-order or parabolic shear deformation theory [58]:

$$ \Phi \left( z \right) = z(1 - {{4z^{2} } \mathord{\left/ {\vphantom {{4z^{2} } {3h^{2} )}}} \right. \kern-\nulldelimiterspace} {3h^{2} )}} $$

(20)

Here, h is the total thickness of the structure, i.e., the summation of h_t, h_c, and h_b. Based on the von Karman’s assumptions, the strain–displacement relations are given as follows:

$$ \varepsilon_{xx} = \frac{\partial }{\partial x}u\left( {x,z,t} \right) + \frac{{w\left( {x,z,t} \right)}}{R}, $$

$$ \varepsilon_{yy} = \frac{\partial }{\partial x}v\left( {x,z,t} \right), $$

$$ \gamma_{xy} = \frac{\partial }{\partial y}u\left( {x,z,t} \right) + \frac{\partial }{\partial x}v\left( {x,z,t} \right), $$

(21)

$$ \gamma_{yz} = \frac{\partial }{\partial y}w\left( {x,z,t} \right) + \frac{\partial }{\partial z}v\left( {x,z,t} \right), $$

$$ \gamma_{xz} = \left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right)\gamma \left( {x,t} \right) - \frac{{u_{0} \left( {x,t} \right)}}{R} + \frac{z}{R}\frac{\partial }{\partial x}w_{0} \left( {x,t} \right) - \frac{{\Phi \left( z \right)\gamma \left( {x,t} \right)}}{R} $$

Inserting the displacement components of Eq. (19) into Eq. (21), the non-zero stains can be obtained as:

$$ \varepsilon_{xx} = \frac{\partial }{\partial x}u_{0} \left( {x,t} \right) - z\frac{{\partial^{2} }}{{\partial x^{2} }}w_{0} \left( {x,t} \right) + \Phi \left( z \right)\frac{\partial }{\partial x}\gamma \left( {x,t} \right) + \frac{{w_{0} \left( {x,t} \right)}}{R}, $$

(22)

$$ \gamma_{xz} = \left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right)\gamma \left( {x,t} \right) - \frac{{u_{0} \left( {x,t} \right)}}{R} + \frac{z}{R}\frac{\partial }{\partial x}w_{0} \left( {x,t} \right) - \frac{{\Phi \left( z \right)\gamma \left( {x,t} \right)}}{R} $$

2.4 Modified couple stress theory

Since the classical elasticity theory fails to investigate the structure at small dimensions, and as the present study is aimed to consider the structure in the micro-dimension, the MCST was selected. The MCST suggests a material length-scale parameter and the strain energy of the structure which includes two parts: one related to the classical elasticity theory and the other relevant to the deviator part of the couple stress tensor as [59]:

$$ U = \frac{1}{2}\int_{V} {\left( {{\upsigma }:{\upvarepsilon } + {\text{m}}:{\upchi }} \right)\,\,{\text{dv}}} $$

(23)

in which χ and m are the symmetric part of the curvature tensor and deviatoric part of the couple stress tensor, respectively, which can be obtained as:

$$ {\text{m}}_{ij} = 2l^{2} \mu \left( z \right){\upchi }_{ij} \, $$

(24)

where l is the material length-scale parameter of MCST, and μ(z) is the Lame’s parameter.

To determine the components of the symmetric part of the curvature tensor, the following relations were employed [60]:

$$ \chi_{ij} = \frac{1}{2}\left[ {{\Theta }_{i,j} + {\Theta }_{j,i} } \right], $$

(25)

$$ \Theta = \frac{1}{2}\nabla \times {\text{u}} $$

(26)

In the above relations, Θ is the rotation vector, and u denotes displacements vector. As a result, the non-zero components of the symmetric part of the curvature tensor can be achieved:

$$ \begin{aligned} \chi_{xy} = & - \frac{1}{2}\frac{{\partial^{2} }}{{\partial x^{2} }}w_{0} \left( {x,t} \right) + \frac{1}{4}{\mkern 1mu} \left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right)\frac{\partial }{\partial x}\gamma \left( {x,t} \right) \\ & + \frac{1}{4R}{\mkern 1mu} \left( {\frac{\partial }{\partial x}u_{0} \left( {x,t} \right) - z\frac{{\partial^{2} }}{{\partial x^{2} }}w_{0} \left( {x,t} \right) + \Phi \left( z \right)\frac{\partial }{\partial x}\gamma \left( {x,t} \right)} \right), \\ \end{aligned} $$

(27)

$$ \chi_{yz} = \frac{1}{4}{\mkern 1mu} \left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }}\Phi \left( z \right)} \right)\gamma \left( {x,t} \right) + \frac{1}{4R}\left( { - {\mkern 1mu} \frac{\partial }{\partial x}w_{0} \left( {x,t} \right) + \left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right)\gamma \left( {x,t} \right)} \right) $$

3 Extracting the equations

3.1 Extended Hamilton’s principle

Hamilton’s principle and variational approach were employed to derive the governing equations. Based on the extended Hamilton’s principle [61]:

$$ \int_{0}^{t} {\delta \left[ {\Pi_{ext} + K - U} \right]} \,{\text{dt}}\, = 0 $$

(28)

in which Π_ext, K, and U are the external work, kinetic and strain energies, respectively. The variations of these terms should be obtained and then substituted in the above relation.

To calculate the strain energy of all three layers of the curved microbeam, the following relation can be used [62]:

$$ U = \frac{1}{2}\mathop \smallint \limits_{x} \mathop \smallint \limits_{y} \mathop \smallint \limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} \left\{ {\sigma_{xx}^{i} \varepsilon_{xx} + \sigma_{xz}^{i} \gamma_{xz} + 2m_{xy}^{i} \chi_{xy}^{i} + 2m_{yz}^{i} \chi_{yz}^{i} } \right\} {\text{dV,}}\quad \quad \quad \quad i = t,b,c $$

(29)

By separating the integrations respect to z and defining the stress resultants and using the variational approach, the following expression can be attained for strain energy variations:

$$ \delta U = \mathop \smallint \limits_{A} \left\{ \begin{gathered} \left( { - \frac{\partial }{\partial x}N_{xx} + \frac{{Q_{x} }}{R} - \frac{1}{4R}\frac{\partial }{\partial x}\alpha_{1} } \right)\delta u_{0} \hfill \\ + \left( { - \frac{{\partial^{2} }}{{\partial x^{2} }}M_{xx}^{b} + \frac{{N_{xx} }}{R} - \frac{1}{R}\frac{\partial }{\partial x}P_{x} - \frac{1}{2}\frac{{\partial^{2} }}{{\partial x^{2} }}\alpha_{1} - \frac{1}{4R}\frac{{\partial^{2} }}{{\partial x^{2} }}\alpha_{2} + {\mkern 1mu} \frac{1}{4R}\frac{\partial }{\partial x}\alpha_{5} } \right)\delta w_{0} \hfill \\ + \left( { - \frac{\partial }{\partial x}M_{xx}^{s} + T_{x} - \frac{{R_{x} }}{R} - \frac{1}{4}{\mkern 1mu} \frac{\partial }{\partial x}\alpha_{4} - \frac{1}{4R}\frac{\partial }{\partial x}\alpha_{3} + \frac{1}{4}{\mkern 1mu} \alpha_{7} + {\mkern 1mu} \frac{{\alpha_{6} }}{4R}} \right)\delta \gamma \hfill \\ \end{gathered} \right\} {\text{dA}} $$

(30)

The applied stress resultants are defined as:

$$ N_{xx} = Q_{110} \frac{{\partial u_{0} }}{\partial x} - Q_{111} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + Q_{113} \frac{\partial \gamma }{{\partial x}} + \frac{{Q_{110} w_{0} }}{R}, $$

$$ M_{xx}^{b} = Q_{111} \frac{{\partial u_{0} }}{\partial x} - Q_{112} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + Q_{115} \frac{\partial \gamma }{{\partial x}} + \frac{{Q_{111} w_{0} }}{R}, $$

$$ M_{xx}^{s} = Q_{113} \frac{{\partial u_{0} }}{\partial x} - Q_{115} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + Q_{114} \frac{\partial \gamma }{{\partial x}} + \frac{{Q_{113} w_{0} }}{R}, $$

$$ Q_{x} = Q_{556} \gamma + \frac{1}{R}\left( { - Q_{550} u_{0} + Q_{551} \frac{{\partial w_{0} }}{\partial x} - Q_{553} \gamma } \right), $$

$$ P_{x} = Q_{557} \gamma + \frac{1}{R}\left( { - Q_{551} u_{0} + Q_{552} \frac{{\partial w_{0} }}{\partial x} - Q_{555} \gamma } \right), $$

$$ R_{x} = Q_{558} \gamma + \frac{1}{R}\left( { - Q_{553} u_{0} + Q_{555} \frac{{\partial w_{0} }}{\partial x} - Q_{554} \gamma } \right), $$

$$ T_{x} = Q_{559} \gamma + \frac{1}{R}\left( { - Q_{556} u_{0} + Q_{557} \frac{{\partial w_{0} }}{\partial x} - Q_{558} \gamma } \right), $$

(31)

$$ \alpha_{1} = - l^{2} \beta_{1} {\mkern 1mu} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2}l^{2} \beta_{7} {\mkern 1mu} \frac{\partial \gamma }{{\partial x}} + \frac{{l^{2} }}{2R}\left( {{\mkern 1mu} \beta_{1} \frac{{\partial u_{0} }}{\partial x} - {\mkern 1mu} \beta_{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \beta_{4} {\mkern 1mu} \frac{\partial \gamma }{{\partial x}}} \right), $$

$$ \alpha_{2} = - l^{2} \beta_{2} {\mkern 1mu} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2}l^{2} \beta_{8} {\mkern 1mu} \frac{\partial \gamma }{{\partial x}} + \frac{{l^{2} }}{2R}\left( {\beta_{2} \frac{{\partial u_{0} }}{\partial x} - \beta_{3} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + {\mkern 1mu} \beta_{6} \frac{\partial \gamma }{{\partial x}}} \right), $$

$$ \alpha_{3} = - l^{2} \beta_{4} {\mkern 1mu} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2}{\mkern 1mu} l^{2} \beta_{9} {\mkern 1mu} \frac{\partial \gamma }{{\partial x}} + \frac{{l^{2} }}{2R}\left( {\beta_{4} \frac{{\partial u_{0} }}{\partial x} - \beta_{6} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + {\mkern 1mu} \beta_{5} \frac{\partial \gamma }{{\partial x}}} \right), $$

$$ \alpha_{4} = - l^{2} \beta_{7} {\mkern 1mu} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2}{\mkern 1mu} l^{2} \beta_{10} {\mkern 1mu} \frac{\partial \gamma }{{\partial x}} + \frac{{l^{2} }}{2R}\left( {{\mkern 1mu} \beta_{7} {\mkern 1mu} \frac{{\partial u_{0} }}{\partial x} - \beta_{8} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \beta_{9} \frac{\partial \gamma }{{\partial x}}} \right), $$

$$ \alpha_{5} = \frac{1}{2}l^{2} \beta_{11} {\mkern 1mu} \gamma - {\mkern 1mu} \frac{{l^{2} \beta_{1} {\mkern 1mu} }}{2R}\frac{{\partial w_{0} }}{\partial x} + {\mkern 1mu} \frac{{l^{2} \beta_{7} {\mkern 1mu} \gamma }}{2R}, $$

$$ \alpha_{6} = \frac{1}{2}{\mkern 1mu} l^{2} \beta_{12} {\mkern 1mu} \gamma - {\mkern 1mu} \frac{{l^{2} \beta_{7} {\mkern 1mu} }}{2R}\frac{{\partial w_{0} }}{\partial x} + {\mkern 1mu} \frac{{l^{2} \beta_{10} {\mkern 1mu} \gamma }}{2R}, $$

$$ \alpha_{7} = \frac{1}{2}{\mkern 1mu} l^{2} \beta_{13} {\mkern 1mu} \gamma - {\mkern 1mu} \frac{{l^{2} \beta_{11} {\mkern 1mu} }}{2R}\frac{{\partial w_{0} }}{\partial x} + \frac{{l^{2} \beta_{12} {\mkern 1mu} \gamma }}{2R} $$

Also, the kinetic energy of the microstructure can be calculated by [63]:

$$ K = \frac{1}{2}\mathop \smallint \limits_{x} \mathop \smallint \limits_{y} \mathop \smallint \limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} \rho \left( z \right)\left( {\left( {\frac{\partial u}{{\partial t}}} \right)^{2} + \left( {\frac{\partial w}{{\partial t}}} \right)^{2} } \right) {\text{dV}} $$

(32)

Replacing the displacements of Eq. (19) in the above relation, and similar to strain energy, i.e., separating the integrals respect to z and using the variational formulation, the below equation can be reached:

$$ \delta K = \mathop \smallint \limits_{A} \left\{ \begin{gathered} \left( { - I_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}u_{0} + I_{1} \frac{{\partial^{2} }}{{\partial x\partial t^{2} }}w_{0} - I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\gamma } \right)\delta u_{0} \hfill \\ + \left( {I_{2} \frac{{\partial^{4} }}{{\partial x^{2} \partial t^{2} }}w_{0} - I_{1} \frac{{\partial^{3} }}{{\partial x\partial t^{2} }}u_{0} - I_{5} \frac{{\partial^{3} }}{{\partial x\partial t^{2} }}\gamma - I_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}w_{0} } \right)\delta w_{0} \hfill \\ + \left( { - I_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}\gamma + I_{5} \frac{{\partial^{3} }}{{\partial x\partial t^{2} }}w_{0} - I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}u_{0} } \right)\delta \gamma \hfill \\ \end{gathered} \right\} {\text{dA}} $$

(33)

in which:

$$ \left\{ {\begin{array}{*{20}c} {I_{0} ,} & {I_{1} ,} & {I_{2} ,} & {I_{3} ,} & {I_{4} ,} & {I_{5} } \\ \end{array} } \right\} = \int_{z} {\rho (z)\left\{ {\begin{array}{*{20}c} {1,} & {z,} & {z^{2} ,} & {\Phi (z),} & {\Phi^{2} (z),} & {z\Phi (z)} \\ \end{array} } \right\}\,} {\text{d}}z $$

(34)

The external work in this study consists of three parts: the first one is due to the viscoelastic substrate, the second is the result of the thermal load, while the third one is related to the applied magnetic load:

$$ \Pi_{ext} = \Pi_{substrate} + \Pi_{thermo - mechanical\,load} + \Pi_{magnetic\,load} $$

(35)

To determine the work of the viscoelastic substrate, the visco-Pasternak type substrate was selected, which consisted of springs, shear layer, and dashpots. Therefore, the substrate force can be obtained via the following relation [64]:

$$ F_{substrate} = K_{1} w_{0} (x,t) - K_{2} \nabla^{2} w_{0} (x,t) + D\frac{\partial }{\partial t}w_{0} (x,t) $$

(36)

where K₁, K₂, and D are the springs, shear layer, and dashpots parameters, respectively.

Consequently, to obtain the work caused by the elastic substrate, the following relation may be used:

$$ \delta \Pi_{substrate} = \int_{x} {} \left[ { - F_{substrate} \,\delta w_{0} (x,t)} \right]\,\,{\text{dx}} $$

(37)

Moreover, the work of thermal load can be determined using the below equation [65]:

$$ \delta \Pi_{thermo - mechanical\,load} = \int_{x} {} \left[ {N\,\left( {\frac{{\partial w_{0} (x,t)}}{\partial x}} \right)\delta w_{0} (x,t)} \right]\,{\text{dx}} $$

(38)

where N includes both thermal (N_T) and mechanical (N₀) loads [66]:

$$ N = N_{0} + N^{T} , $$

(39)

$$ N^{T} = \int\limits_{ - h/2}^{h/2} {Q_{11}^{c,f} \,\alpha_{11}^{c,f} \,\Delta T} \,\,{\text{dz}} $$

(40)

The structure is exposed to longitudinal magnetic load (H_x), its force regarding Maxwell’s relations can be obtained by the following equation [67]:

$$ F_{magnetic\,load} = \eta H_{x}^{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) $$

(41)

In the above relation, magnetic field permeability is shown by η. Inserting displacements of Eq. (19) in Eq. (41) yields:

$$ F_{magnetic\,load} = \eta H_{x}^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}w_{0} (x,t) $$

(42)

Therefore, the work of Lorentz force can be demonstrated by:

$$ \delta \Pi_{magnetic\,load} = \int\limits_{ - h/2}^{h/2} {F_{magnetic\,load} \,\delta w_{0} (x,t)\,{\text{dx}}\,{\text{dy}}} $$

(43)

3.2 Governing equations

Using the obtained expressions for variations of strain and kinetic energies and works of external loads and substituting them into the extended Hamilton’s principle and separating coefficient of each variable, the below governing equations can be achieved in terms of displacements:

$$ \delta u_{0} : $$

$$ \begin{aligned} - Q_{110} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + & Q_{111} \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - Q_{113} \frac{{\partial^{2} \gamma }}{{\partial x^{2} }} - \frac{{Q_{110} }}{R}\frac{{\partial w_{0} }}{\partial x} - \frac{{Q_{556} \gamma }}{R} + \frac{{Q_{550} u_{0} }}{{R^{2} }} - \frac{{Q_{551} }}{{R^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{{Q_{553} \gamma }}{{R^{2} }} \\ & + \frac{{l^{2} \beta_{1} {\mkern 1mu} }}{4R}\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - {\mkern 1mu} \frac{{l^{2} \beta_{7} {\mkern 1mu} }}{8R}\frac{{\partial^{2} \gamma }}{{\partial x^{2} }} - \frac{{l^{2} \beta_{1} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{{l^{2} \beta_{2} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - {\mkern 1mu} \frac{{l^{2} \beta_{4} }}{{8R^{2} }}{\mkern 1mu} \frac{{\partial^{2} \gamma }}{{\partial x^{2} }} + I_{0} {\mkern 1mu} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} \\ & - I_{1} {\mkern 1mu} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }} + I_{3} {\mkern 1mu} \frac{{\partial^{2} \gamma }}{{\partial t^{2} }} = 0 \\ \end{aligned} $$

(44)

$$ \delta w_{0} : $$

$$ \begin{aligned} \frac{{Q_{110} }}{R}\frac{{\partial u_{0} }}{\partial x} + & \frac{{Q_{113} }}{R}\frac{\partial \gamma }{{\partial x}} + \frac{{Q_{110} w_{0} }}{{R^{2} }} - \frac{{Q_{557} }}{R}\frac{\partial \gamma }{{\partial x}} + \frac{{Q_{551} }}{{R^{2} }}\frac{{\partial u_{0} }}{\partial x} - \frac{{Q_{552} }}{{R^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{{Q_{555} }}{{R^{2} }}\frac{\partial \gamma }{{\partial x}} + \eta {\mkern 1mu} H_{x}^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} \\ & - 2{\mkern 1mu} \frac{{Q_{111} }}{R}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2}{\mkern 1mu} l^{2} \beta_{1} {\mkern 1mu} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - \frac{1}{4}{\mkern 1mu} l^{2} \beta_{7} {\mkern 1mu} \frac{{\partial^{3} \gamma }}{{\partial x^{3} }} - {\mkern 1mu} \frac{{l^{2} \beta_{8} {\mkern 1mu} }}{8R}\frac{{\partial^{3} \gamma }}{{\partial x^{3} }} - {\mkern 1mu} \frac{{l^{2} \beta_{2} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + {\mkern 1mu} \frac{{l^{2} \beta_{3} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} \\ & - {\mkern 1mu} \frac{{l^{2} \beta_{6} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{3} \gamma }}{{\partial x^{3} }} + {\mkern 1mu} \frac{{l^{2} \beta_{11} {\mkern 1mu} }}{8R}\frac{\partial \gamma }{{\partial x}} - {\mkern 1mu} \frac{{l^{2} \beta_{1} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{{l^{2} \beta_{7} {\mkern 1mu} }}{{8R^{2} }}\frac{\partial \gamma }{{\partial x}} - {\mkern 1mu} \frac{{l^{2} \beta_{1} {\mkern 1mu} }}{4R}\frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \frac{{l^{2} \beta_{2} {\mkern 1mu} }}{2R}\frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - {\mkern 1mu} \frac{{l^{2} \beta_{4} {\mkern 1mu} }}{4R}\frac{{\partial^{3} \gamma }}{{\partial x^{3} }} \\ & - Q_{111} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + Q_{112} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - Q_{115} \frac{{\partial^{3} \gamma }}{{\partial x^{3} }} + I_{{0{\mkern 1mu} }} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} + I_{{1{\mkern 1mu} }} \frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} - I_{2} {\mkern 1mu} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} + I_{5} {\mkern 1mu} \frac{{\partial^{3} \gamma }}{{\partial x\partial t^{2} }} \\ & + N^{T} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - K_{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - D\frac{{\partial w_{0} }}{\partial t} + K_{1} w_{0} + N_{0} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} = 0 \\ \end{aligned} $$

(45)

$$ \delta \gamma : $$

$$ \begin{aligned} \frac{1}{8}{\mkern 1mu} l^{2} \beta_{13} {\mkern 1mu} \gamma - & {\mkern 1mu} \frac{{l^{2} \beta_{11} {\mkern 1mu} }}{8R}\frac{{\partial w_{0} }}{\partial x} + \frac{{l^{2} \beta_{7} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial w_{0} }}{\partial x} - \frac{{l^{2} \beta_{10} {\mkern 1mu} \gamma }}{{8R^{2} }} - {\mkern 1mu} \frac{{l^{2} \beta_{7} {\mkern 1mu} }}{8R}\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{{l^{2} \beta_{8} {\mkern 1mu} }}{8R}\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - {\mkern 1mu} \frac{{l^{2} \beta_{9} {\mkern 1mu} }}{4R}\frac{{\partial^{2} \gamma }}{{\partial x^{2} }} + {\mkern 1mu} \frac{{l^{2} \beta_{4} {\mkern 1mu} }}{4R}\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} \\ & - {\mkern 1mu} \frac{{l^{2} \beta_{4} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + {\mkern 1mu} \frac{{l^{2} \beta_{6} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - \frac{{l^{2} \beta_{5} {\mkern 1mu} }}{{8R^{2} }}\frac{{\partial^{2} \gamma }}{{\partial x^{2} }} - Q_{113} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + Q_{115} \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - Q_{114} \frac{{\partial^{2} \gamma }}{{\partial x^{2} }} + I_{{3{\mkern 1mu} }} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} \\ & - I_{5} {\mkern 1mu} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }} + I_{4} {\mkern 1mu} \frac{{\partial^{2} \gamma }}{{\partial t^{2} }} + \frac{{Q_{553} u_{0} }}{{R^{2} }} - \frac{{Q_{555} }}{{R^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{{Q_{554} \gamma }}{{R^{2} }} - \frac{{Q_{113} }}{R}\frac{{\partial w_{0} }}{\partial x} + Q_{559} \gamma - \frac{1}{8}{\mkern 1mu} l^{2} \beta_{10} {\mkern 1mu} \frac{{\partial^{2} \gamma }}{{\partial x^{2} }} \\ & + \frac{1}{4}{\mkern 1mu} l^{2} \beta_{7} {\mkern 1mu} \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - \frac{{Q_{556} u_{0} }}{R} - 2{\mkern 1mu} \frac{{Q_{558} \gamma }}{R} + \frac{{Q_{557} }}{R}\frac{{\partial w_{0} }}{\partial x} = 0 \\ \end{aligned} $$

(46)

in which:

$$ Q_{iij} = \int\limits_{ - h/2}^{h/2} {Q_{ii} \,} z^{j} \,{\text{d}}z,\quad \quad \quad \quad i = 1,5;\quad \quad \quad \quad j = 0,1,2 $$

(47)

$$ \left\{ {\begin{array}{*{20}c} {Q_{ii3} ,} & {Q_{ii4} ,} & {Q_{ii5} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {Q_{ii} \,} \left\{ {\begin{array}{*{20}c} {\Phi \left( z \right),} & {\Phi^{2} \left( z \right),} & {z\Phi \left( z \right)} \\ \end{array} } \right\}\,{\text{d}}z,\quad \quad {\kern 1pt} \quad i = 1,5 $$

$$ \left\{ {\begin{array}{*{20}c} {Q_{556} ,} & {Q_{557} ,} & {Q_{558} ,} & {Q_{559} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {Q_{55} \,} \left\{ {\begin{array}{*{20}c} {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right),} & {z\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right),} & {\Phi \left( z \right)\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right),} & {\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right)^{2} } \\ \end{array} } \right\}\,{\text{d}}z, $$

$$ \beta_{k} = \int\limits_{ - h/2}^{h/2} {\mu \left( z \right)\,} z^{k - 1} \,{\text{d}}z,\quad \quad \quad k = 1,2,3 $$

$$ \left\{ {\begin{array}{*{20}c} {\beta_{4} ,} & {\beta_{5} ,} & {\beta_{6} ,} & {\beta_{7} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\mu \left( z \right)\,} \left\{ {\begin{array}{*{20}c} {\Phi \left( z \right),} & {\Phi^{2} \left( z \right),} & {z\Phi \left( z \right),} & {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \\ \end{array} } \right\}\,{\text{d}}z, $$

$$ \left\{ {\begin{array}{*{20}c} {\beta_{8} ,} & {\beta_{9} ,} & {\beta_{10} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\mu \left( z \right)\,} \left\{ {\begin{array}{*{20}c} {z\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right),} & {\Phi \left( z \right)\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right),} & {\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right)^{2} } \\ \end{array} } \right\}\,{\text{d}}z, $$

$$ \left\{ {\begin{array}{*{20}c} {\beta_{11} ,} & {\beta_{12} ,} & {\beta_{13} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\mu \left( z \right)\,} \left\{ {\begin{array}{*{20}c} {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }}\Phi \left( z \right),} & {\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }}\Phi \left( z \right)} \right)\left( {\frac{{\text{d}}}{{{\text{d}}z}}\Phi \left( z \right)} \right),} & {\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }}\Phi \left( z \right)} \right)^{2} } \\ \end{array} } \right\}\,{\text{d}}z $$

4 Analytical solution

To solve the governing equations and extracting the results, the analytical Navier’s solution method was employed for both ends of a simply supported curved microbeam. To satisfy the geometrical boundary condition, the following functions are introduced for the displacements [68]:

$$ \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {w_{0} } \\ \gamma \\ \end{array} } \right\} = \sum\limits_{m = 1}^{\infty } {\left\{ {\begin{array}{*{20}c} {U_{m} \,\cos \left( {\Xi x} \right)} \\ {W_{m} \,\sin \left( {\Xi x} \right)} \\ {\Upsilon_{m} \,\cos \left( {\Xi x} \right)} \\ \end{array} } \right\}} \,{\text{e}}^{{{\text{i}}\omega t}} $$

(48)

in which U, W, and ϒ are the unknowns, and m represents the number of the axial wave. Also, Ξ is defined as mπ/L.

Substituting the defined functions of Eq. (48) in the governing equations of (44)–(46) leads to the following matrix form for the vibrational and buckling analyses:

4.1 Vibration analysis

Solving the eigenvalue problem of Eq. (49) in the following form leads to the natural frequencies of the micro-curved beam:

$$ \left( {\left[ K \right] + {\text{i}}\omega \left[ C \right] - \omega^{2} \left[ M \right]} \right)\left\{ X \right\} = 0 $$

(49)

In the above relation, [K], [C], and [M] are the stiffness, damping, and mass matrices, and {X} is displacements vector which includes {U, W, ϒ}^T. ω denotes the natural frequency.

4.2 Buckling analysis

By dropping down the mass and damping matrices and setting the N₀ = − P_cr, the following eigenvalue equation can be used to determine the critical buckling load:

$$ \left( {\left[ K \right] - P_{cr} \left[ {K_{g} } \right]} \right)\left\{ X \right\} = 0 $$

(50)

where [K_g] is the geometric stiffness matrix.

The components of stiffness, damping, and mass matrices are presented in the “Appendix”.

5 Results and discussion

In the previous sections, the governing equations of a three-layered micro-curved beam exposed to a longitudinal magnetic load rested on the viscoelastic substrate were derived. Navier’s solution method was employed to solve these equations for simply supported edges. In this section, the numerical results are presented in two different parts, namely, vibrational and buckling responses, and the effect of various parameters on them was discussed.

5.1 Vibration analysis results

To obtain the natural frequencies of the microstructure, the eigenvalue problem of Eq. (49) should be solved. First, the reliability of the results was examined through a comparison of a simpler state with the previously published reports. To this goal, and due to the absence of similar work to compare with, some parameters have neglected the results were obtained for simpler cases. In this regard, the faces were ignored and the curvature radius was tended to infinity which implies a straight beam. The results for a microbeam were extracted and compared to those of Ansari et al. [69], and Ma et al. [70] as listed in Table 5. The results of this table are extracted with L/h = 10, ν = 0.38, ρ = 1220 kg/m³, E = 1.44 GPa and l = 17.6 μm. The current study indicated an excellent consistency with the previous results reflecting the reliability of our framework. As the second step to ensure the validity of the results, they were compared with those of Ansari et al. [69], Zhang et al. [71], and Allahkarami et al. [72] in Table 6 which are for a single-layer homogenous curved microbeam. The results are listed for both ceramic (i.e. SiC) and metal (i.e. aluminum) structure with the following mechanical properties: E_m = 70 GPa, ρ_m = 2702 kg/m³, ν_m = 0.3, E_c = 427 GPa, ρ_c = 3100 kg/m³, and ν_c = 0.17. Also, the results were obtained for the length-scale parameter of 15 μm and the central opening angle of π/4 with h/l = 2, and L/h = 20. It should be noted that the dimensionless natural frequency in Table 6 is defined as $\Omega =\omega L\sqrt{{I}_{0}/{Q}_{110}}$. This research showed an excellent agreement with the previously published works. Therefore, again the reliability of the equations, solution method, and finally the results is confirmed.

Table 5 Comparing the natural frequencies (MHz) for single-layer micro straight beam with those of previously published works (numbers in parenthesis are percentage error)

Table 6 Dimensionless frequency of homogenous curved microbeam (numbers in parenthesis are percentage error)

In the following, the effects of different parameters on the natural frequencies of the considered structure (i.e., the three-layered curved microbeam) will be investigated. It should be noted that the efficiency parameters of CNTs were introduced in Eqs. (11)–(12) for V_CNT = 0.11 as η₁ = 0.143 and η₃ = 0.934; for V_CNT = 0.14, as η₁ = 0.150 and η₃ = 0.941, and for V_CNT = 0.17 as η₁ = 0.149 and η₃ = 1.381 [73]. For all the presented results except those mentioned, the following specifications were used: h_c/l = 10, h_t = h_b, the core thickness was five times higher than that of the faces, L = 10 h, and θ = π/2. Moreover, the relationship between the central opening angle and length was L = Rθ.

Figure 4 considers the effect of the porosity coefficient and also thicknesses ratio on the first natural frequency. As mentioned before, the porosity coefficient refers to the void to bulk volume and its enhancement from zero means the increment of the pore volume. Therefore, it is expected that both stiffness and density of the structure reduce. On the other hand, it is well known that the frequency is generally proportional to the square root of stiffness-to-mass ratio. Thus, an increase in the porosity coefficient declines the mass more than stiffness, accordingly, the frequency will decrease. A rise in the h_c/h_f ratio decremented the natural frequency. Since the stiffness of the faces is much higher than the core, for constant total thickness, an increase in the core thickness means a reduction in the thickness of the faces, therefore, the stiffness of the structure will reduce giving rise to a reduction in the natural frequencies.

Fig. 4

Effect of porosity and thicknesses ratio variations on the fundamental natural frequency of the micro structure

Table 7 lists the exact values of natural frequencies for different dimensionless length-scale parameter (h/l) and porosity distribution types. As the h/l ratio grew, the frequencies decreased due to a reduction in stiffness. The results for different patterns of porosity distribution suggest that type C which (a uniform pores distribution) exhibited the least results, while type B (the symmetric pattern) caused the maximum values. In type B, the most stiffness occurred on the core surfaces causing higher stiffness compared to two other types.

Table 7 Size effect on the fundamental natural frequency (kHz) of the curved microbeam for different types of porosity distribution

The effect of the beam slenderness on the natural frequencies of the first four modes is illustrated in Fig. 5. By enhancing the length of the curved microbeam relative to its thickness, the natural frequencies reduced due to a decline in the structure stiffness. This phenomenon occurs for all first four modes. Note that the number of modes is specified by m.

Fig. 5

Slenderness ratio variations effects on the first four natural frequencies

Figure 6 shows the effects of CNTs volume fraction and the central opening angle (in Radian) on the fundamental natural frequency of the microstructure. By raising the content of CNTs in the faces, the faces, and thus the structure, got stiffer due to their extreme stiffness. The natural frequencies enhanced by increasing the volume fraction of CNTs. Furthermore, incrementing the central opening angle (i.e. length to curvature radius ratio) decremented the frequency. In other words, at a constant length, increasing θ elongated the beam, and similar to the previous findings, the natural frequencies showed a decline.

Fig. 6

Central opening angle and CNTs’ volume fractions variations effect on the natural frequency

The influence of temperature variations is examined in Fig. 7 for the different central opening angles. As can be seen in this figure, an increase in the temperature caused a slight reduction in the natural frequencies due to a drop in the stiffness of the microstructure. Also, comparing the curves for the different central opening angles confirmed the previous findings on its effect expressing that an increase in θ will decrease the natural frequency.

Fig. 7

Influence of temperature changes on the frequencies for different values of central opening angle

A longitudinal magnetic load was applied to the structure whose effect is investigated in Fig. 8. An increase in the magnetic field intensity made the structure stiffer, hence, the frequencies showed an increment. Moreover, Fig. 8 compares the effect of different patterns of CNTs dispersion on the natural frequencies. It was found that the FG-VA pattern resulted in the maximum values, while FG-AV led to the lowest ones. Since in the FG-VA pattern, the CNTs are more abundant in the surfaces of the structure, its stiffness is more than other patterns. In the FG-AV pattern, fewer CNTs can be found on surfaces which explains why the frequencies are the lowest in this pattern.

Fig. 8

Magnetic field effect on the frequencies for various types of CNTs’ dispersion

The effect of the parameters of the substrate on the natural frequencies of the microstructure is illustrated in Figs. 9, 10, 11. Figure 9 considers K₁ and K₂ influences (related to the springs and shear layer, respectively). An increment in both these parameters enhanced the natural frequencies due to the rigidity augmentation. Figure 10 considers the effect of the dashpots parameter, i.e., D. Unlike two other substrate’s parameters, a rise in the dashpots decremented the natural frequencies which occurred for all studied volume fractions of CNTs. Furthermore, a comparison between different types of substrates is made in Fig. 11. While the visco-Winkler type of substrate led to lower frequencies in comparison to the substrate-free case, the addition of the substrate to the structure enhanced its rigidity and accordingly, its frequencies. Based on this figure, the Pasternak type of substrate, which includes springs and shear layer, led to the highest frequencies.

Fig. 9

Springs and shear layer parameters’ variations effect on the fundamental natural frequency

Fig. 10

Dashpots’ parameter variations effect on the first natural frequency

Fig. 11

Comparing different types of substrate and their effect on the frequency of the micro structure

5.2 Buckling analysis results

Here, the results for the mechanical buckling response are presented. Similar to the vibration results, first, the results were compared with previous reports. To this end, the eigenvalue problem of Eq. (50) was solved, and the dimensionless critical buckling load of a macro straight beam was determined by setting the material length-scale parameter to zero and tending the curvature radius to infinity. The results were compared to those of Reddy [74], Aydogdu [75], and Eltaher et al. [76]. The presented results in Table 8 were gained with the following properties: L = 10 m, ν = 0.3, ρ = 1 kg/m³, E = 30 MPa. Also, they obey the following relation to be non-dimensionalized: P_cr^* = P_crL²/EI. A good agreement can be observed between the results of the current study and the previous ones reflecting the reliability of our method. The critical buckling loads were determined for the under consideration three-layered curved microbeam with the previously mentioned specifications.

Table 8 Comparing the dimensionless critical buckling load for single-layer macro straight beam with those of previously published works ($P_{cr}^{*} = {{P_{cr} L^{2} } \mathord{\left/ {\vphantom {{P_{cr} L^{2} } {EI}}} \right. \kern-\nulldelimiterspace} {EI}}$) (numbers in parenthesis are percentage error)

Figure 12 shows the effect of the porosity coefficient on the critical buckling load for different types of porosity distributions. The critical buckling load of the structure showed a decline by increasing the porosity due to a decline in the stiffness. Among three types of porosity distribution patterns, type C (uniform distribution) showed the least results, while type B (symmetric pattern) exhibited the highest critical buckling load.

Fig. 12

Investigation the effect of porosity increasing for three types of pores’ distribution on the critical buckling load

Figure 13 depicts the simultaneous effects of the central opening angle and thicknesses ratio. An increase in the central opening angle caused a reduction in stiffness by increasing the length, hence, the natural frequency decreased. As mentioned before, since the stiffness of the faces was more than the core, an increment in the h_c/h_f ratio declined the results. In this case, the total thickness of the structure remained constant.

Fig. 13

Central opening angle effect on the critical buckling load for different values of thicknesses ratio

Table 9 addresses the effect of slenderness ratio and CNTs dispersion patterns on the critical buckling load of the under consideration microstructure. The critical buckling load reduced as the length of the beam exceeded its thickness. Moreover, among different types of CNTs’ dispersion patterns, similar to vibrational response, FG-VA and FG-AV resulted in the most and the least critical buckling loads, respectively.

Table 9 Various patterns of CNTs’ dispersion and slenderness ratio effects on the critical buckling load (kN/m) of the curved microbeam

Figure 14 illustrates the influences of the temperature and magnetic field intensity on the critical buckling load. The critical buckling load was reduced by increasing the temperature difference from the ambient temperature. Moreover, a rise in the intensity of the magnetic field enhanced the critical buckling load.

Fig. 14

Magnetic field intensity effect on the critical buckling load for different temperature differences

The effect of the parameter of the springs of the substrate is examined in Fig. 15. As can be seen, enhancement of the parameter of springs (i.e. making the structure more rigid) augmented the critical buckling load. This figure also confirms the previous results about the effect of CNTs’ dispersion pattern on the critical buckling load.

Fig. 15

Influence of springs’ parameter on the critical buckling load for various types of CNTs’ dispersion

Figure 16 presents the effects of two factors: volume fraction of CNTs and the shear layer parameter of the substrate. Increasing the CNTs content of the faces increased their stiffness, causing an enhancement in the critical buckling load of the microstructure. Moreover, similar to the spring parameter, enhancing the shear layer elevated the critical buckling load.

Fig. 16

Shear layer’s parameter variations effect on the critical buckling load

Figure 17 compares different types of substrate in terms of the length-scale to thickness variations. Based on this figure, as the l/h ratio increased, its critical buckling load was enhanced since the stiffness of the structure was increased. Also, regardless of its type, the inclusion of a substrate increased the critical buckling among the two considered substrates, the Pasternak foundation led to a higher critical buckling load compared to the Winkler type.

Fig. 17

Size effect on the critical buckling load of the micro structure for different kinds of substrate

6 Conclusions

Free vibration and mechanical buckling responses of a three-layered curved microbeam were investigated under a longitudinal Lorentz magnetic load. The influence of a thermal environment was also considered on the mechanical behaviors of the structure. The core was made from FG porous materials whose properties vary through the thickness direction based on three patterns. The faces were composed of FG-CNTRCs and the impact of the placement of CNTs on the face properties was considered. Using ERM, the effective thermo-mechanical properties of the nanocomposite face sheets were also explored. Since this work analyzed the small-dimension structures, MCST was used to predict the results on the micro-scale. The kinematic relations were derived based on HSDT and using von Karman’s assumptions. The variational approach and energy method were used to derive the governing equations which were analytically solved for both simply supported ends via Navier’s solution method. The results in both vibrational and buckling domains were verified with the previously published reports on simpler states and the effects of various parameters on the results were considered. The chief conclusions are:

• Since increasing the porosity coefficient caused a reduction in stiffness of the structure, its enhancement will reduce both natural frequency and critical buckling load of the microstructure.

• Among the three considered types of porosity distribution, types B and C led to the maximum and minimum values of frequency and critical buckling load, respectively. Type B was related to symmetric pore pattern while type C reflected uniform pattern.

• Increasing the number of CNTs in the faces enhanced their stiffness, and accordingly, raised the natural frequency and critical buckling load.

• Comparing different patterns of CNTs’ dispersion, it was found that FG-VA and FG-AV resulted in the highest and lowest natural frequency and critical buckling load, respectively.

• Regarding higher stiffness of the face sheets than the core, an increment in the core thickness, at the constant total thickness, may decrement the stiffness of the structure; thus, both natural frequency and critical buckling load will be declined.

• Keeping the curvature radius constant and by increasing the central opening angle, the natural frequency and critical buckling load were enhanced.

• As the intensity of the applied longitudinal magnetic field increased, the natural frequency and critical buckling load were enhanced.

• Increasing the dimensionless length-scale parameter (h/l) declined the results.

• Regardless of its type inclusion of an elastic substrate incremented both frequency and critical buckling load.

• While increasing springs and shear layer parameters enhanced the results, an enhancement in the dashpots parameter declined them.

Appendix

The non-zero components of stiffness, damping, and mass matrices in Eq. (49) can be defined as:

$$ K_{11} = Q_{110} \Xi^{2} + \frac{{Q_{550} }}{{R^{2} }} + {\mkern 1mu} \frac{{l^{2} \beta_{1} {\mkern 1mu} \Xi^{2} }}{{8R^{2} }}, $$

$$ K_{12} = - Q_{111} \Xi^{3} - \frac{{Q_{110} \Xi }}{R} - \frac{{Q_{551} \Xi }}{{R^{2} }} - {\mkern 1mu} \frac{{l^{2} \beta_{1} {\mkern 1mu} \Xi^{3} }}{4R} - \frac{{l^{2} \beta_{2} {\mkern 1mu} \Xi^{3} }}{{8R^{2} }}, $$

$$ K_{13} = Q_{113} \Xi^{2} - \frac{{Q_{556} }}{R} + \frac{{Q_{553} }}{{R^{2} }} + \frac{{l^{2} \beta_{7} {\mkern 1mu} \Xi^{2} }}{8R} + \frac{{l^{2} \beta_{4} {\mkern 1mu} \Xi^{2} }}{{8R^{2} }}, $$

$$ K_{21} = - Q_{111} \Xi^{3} - \frac{{Q_{110} \Xi }}{R} - \frac{{Q_{551} \Xi }}{{R^{2} }} - \frac{{l^{2} \beta_{1} {\mkern 1mu} \Xi^{3} }}{4R} - \frac{{l^{2} \beta_{2} {\mkern 1mu} \Xi^{3} }}{{8R^{2} }}, $$

$$ \begin{gathered} K_{22} = \frac{{Q_{110} }}{{R^{2} }} + Q_{112} \Xi^{4} - N_{T} \Xi^{2} - N_{0} \Xi^{2} - K_{2} \Xi^{2} - K_{1} + \frac{{Q_{552} \Xi^{2} }}{{R^{2} }} - \eta {\mkern 1mu} H_{x}^{2} \Xi^{2} + 2{\mkern 1mu} \frac{{Q_{111} \Xi^{2} }}{R} + \frac{1}{2}{\mkern 1mu} l^{2} \beta_{1} {\mkern 1mu} \Xi^{4} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + \frac{{l^{2} \beta_{1} {\mkern 1mu} \Xi^{2} }}{{8R^{2} }}\, + {\mkern 1mu} \frac{{l^{2} \beta_{2} {\mkern 1mu} \Xi^{4} }}{2R} + {\mkern 1mu} \frac{{l^{2} \beta_{3} {\mkern 1mu} \Xi^{4} }}{{8R^{2} }}, \hfill \\ \end{gathered} $$

$$ \begin{gathered} K_{23} = - Q_{115} \Xi^{3} - \frac{{Q_{113} \Xi }}{R} + \frac{{Q_{557} \Xi }}{R} - \frac{{Q_{555} \Xi }}{{R^{2} }} - \frac{1}{4}{\mkern 1mu} l^{2} \beta_{7} {\mkern 1mu} \Xi^{3} - {\mkern 1mu} \frac{{l^{2} \beta_{6} {\mkern 1mu} \Xi^{3} }}{{8R^{2} }} - {\mkern 1mu} \frac{{l^{2} \beta_{11} {\mkern 1mu} \Xi }}{8R} - \frac{{l^{2} \beta_{7} {\mkern 1mu} \Xi }}{{8R^{2} }} - \frac{{l^{2} \beta_{4} {\mkern 1mu} \Xi^{3} }}{4R} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - {\mkern 1mu} \frac{{l^{2} \beta_{8} {\mkern 1mu} \Xi^{3} }}{8R}, \hfill \\ \end{gathered} $$

$$ K_{31} = Q_{113} \Xi^{2} - \frac{{Q_{556} }}{R} + \frac{{Q_{553} }}{{R^{2} }} + \frac{{l^{2} \beta_{7} {\mkern 1mu} \Xi^{2} }}{8R} + {\mkern 1mu} \frac{{l^{2} \beta_{4} {\mkern 1mu} \Xi^{2} }}{{8R^{2} }}, $$

$$ \begin{gathered} K_{32} = - Q_{115} \Xi^{3} + \frac{{Q_{557} \Xi }}{R} - \frac{1}{4}{\mkern 1mu} l^{2} \beta_{7} {\mkern 1mu} \Xi^{3} - \frac{{Q_{555} \Xi }}{{R^{2} }} - \frac{{Q_{113} \Xi }}{R} - {\mkern 1mu} \frac{{l^{2} \beta_{4} {\mkern 1mu} \Xi^{3} }}{4R} - \frac{{l^{2} \beta_{6} {\mkern 1mu} \Xi^{3} }}{{8R^{2} }} + \frac{{l^{2} \beta_{7} {\mkern 1mu} \Xi }}{{8R^{2} }}\, - {\mkern 1mu} \frac{{l^{2} \beta_{8} {\mkern 1mu} \Xi^{3} }}{8R} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - {\mkern 1mu} \frac{{l^{2} \beta_{11} {\mkern 1mu} \Xi }}{8R}, \hfill \\ \end{gathered} $$

$$ K_{33} = Q_{559} + \frac{1}{8}{\mkern 1mu} l^{2} \beta_{13} + \frac{{Q_{554} }}{{R^{2} }} + Q_{114} \Xi^{2} - 2{\mkern 1mu} \frac{{Q_{558} }}{R} - {\mkern 1mu} \frac{{l^{2} \beta_{10} }}{{8R^{2} }} + \frac{1}{8}l^{2} \beta_{10} {\mkern 1mu} \Xi^{2} + {\mkern 1mu} \frac{{l^{2} \beta_{5} {\mkern 1mu} \Xi^{2} }}{{8R^{2} }} + {\mkern 1mu} \frac{{l^{2} \beta_{9} {\mkern 1mu} \Xi^{2} }}{4R}, $$

$$ M_{11} = - I_{0} {\mkern 1mu} ,\quad \quad \quad M_{12} = I_{1} {\mkern 1mu} \Xi {\mkern 1mu} ,\quad \quad \quad \quad \quad M_{13} = - I_{3} {\mkern 1mu} , $$

$$ M_{21} = I_{1} {\mkern 1mu} \Xi {\mkern 1mu} ,\quad \quad \quad M_{22} = - I_{{0{\mkern 1mu} }} - I_{2} {\mkern 1mu} \Xi^{2} ,\quad \quad \;M_{23} = I_{5} {\mkern 1mu} \Xi , $$

$$ M_{31} = - I_{{3{\mkern 1mu} }} ,\quad \quad \quad M_{32} = I_{5} {\mkern 1mu} \Xi {\mkern 1mu} ,\quad \quad \quad \quad \quad M_{33} = - I_{4} , $$

$$ C_{22} = - D $$