Free and forced vibration analysis of a sandwich beam considering porous core and SMA hybrid composite face layers on Vlasov’s foundation

Abstract

This paper aims to investigate the free and forced vibration behavior of a sandwich beam with functionally graded porous core and composite face layers embedded with shape memory alloy (SMA). Three different porosity patterns are assumed through the thickness direction of the core, and composite face layers are reinforced with carbon nanotubes (CNT). The sandwich beam is resting on an elastic foundation which is simulated by Vlasov’s model. By using Hamilton’s principle and first-order shear deformation theory, the governing equations of motion are derived. The analytical solution is presented to solve the equations of motion using Navier’s solution. Results are verified with corresponding literatures. Finally, the effects of important parameters such as temperature, volume fraction of SMA, porosity distribution, weight fraction of CNT, and geometric parameters are explored in detail.

1 Introduction

The appearance of smart materials, which are a highly influential kind of materials, has opened a new horizon ahead of researchers. Shape memory alloys (SMA) are novel functional materials, and because of their shape memory effect and super elasticity they have been used in many applications from intelligent materials to modern industries. In the following, applications of SMA in a variety of research disciplines are presented.

1.1 Smart structures and applications of SMA

Jung et al. [1] designed a new type of SMA wire actuator for input shaping control of flexible structures by connecting two SMA wires with different martensitic-austenitic phase transformation temperatures. Vishal et al. [2] presented the active control of vibration using SMA as actuator. Suzuki and Kagawa [3] demonstrated a method for modeling an SMA actuator which is valid in all ranges of displacement and is capable of using in linear systems. Abdullah et al. [4] studied the effects of input measurements to the feedback control system in order to determine the optimal feedback variable. SMA is used in a wide variety of bioengineering applications such as dental wires, mending broken bones, and for medical devices that help open clogged veins and arteries.

1.2 Vibration analysis

Bayat and Ekhteraei Toussi [5] analyzed nonlinear transient vibration of a composite beam embedded with SMA wires at both high and low temperature. Helbert et al. [6] developed two NiTi-based damper devices, and they also observed the temperature effect on dampers. Kumbhar et al. [7] investigated the response of systems in which shape memory alloy and magneto-rheological elastomer are combined in order to be applied as smart damper in a tuned vibration absorber. Nejati et al. [8] studied the thermal vibration of a double-curved sandwich panel with soft core and embedded SMA wires hybrid composite face sheets. Nonlinear forced vibration of a composite sandwich doubly curved shell in hygrothermal environment is investigated by Karimiasl et al. [9]. Their results indicated that increasing SMA volume fraction leads to a decrease in nonlinear frequency. Garafolo and McHugh [10] explored the effect of embedded shape memory alloys as an active suppression system to decrease vibration produced by aeroelastic flutter. Their result illustrated that actuation of the embedded SMA wire increases the stiffness of the system which leads to a decrease in the amplitude of flutter.

1.3 Civil engineering

Dutta and Majumder [11] showed the potential of an SMA damper to control structural vibrations when exposed to underground blast. Their results indicated that SMA Nitinol dampers have reduced the response significantly. Ghafoori et al. [12] studied the structural fire behavior of Fe-SMA prestress-strengthened structural members. They performed a series of transient total deformation tests with Fe-SMA material samples, and they also derived a simple engineering model that allows to estimate the temperature-induced prestress loss occurring in a fire exposure. Abouali et al. [13] investigated the behavior of reinforced composite beams retrofitted by Fe-SMA numerically by developing a finite element model in ABAQUS, and its outcomes were compared with experimental results.

Sandwich structures, which are effectively light and have good mechanical properties such as strength and high durability to both normal and shear stresses, have been widely used in many areas, for instance automotive, marine, aerospace, and energy industries, and even in construction. Porous material due to its low density, light weight, heat insulation, efficient energy absorption, and high specific strength can be a great choice to be used as core in sandwich structures.

Trinh et al. [14] explored free vibration and nonlinear dynamic responses of functionally graded sandwich shells with double curvature under the effect of porosity and thermomechanical loading. Karamanli and Aydogdu [15] investigated the free vibration behavior of rotating two-directional functionally graded porous sandwich microbeams. The effect of some important parameters such as porosity volume fraction, dimensionless rotation speed and thickness to material length scale was studied. The mechanical behavior of porous beams was analyzed by Fang et al. [16]. They made use of an effective computational approach based on isogeometric analysis. Their obtained results indicated that the proposed approach can obtain the high accuracy and fast convergence for porous beam problems. Tsai and Taylor [17] analyzed the vibration behaviors of sandwich structures with single and double debonded regions. They compared the results of finite element simulation and vibration tests. They also discussed the effect of material chosen for core and facesheets. Demir et al. [18] performed a vibration analysis of three-layered curved sandwich beams with elastic face layers and viscoelastic core. The effect of parameters such as layer thickness, damping characteristics, and lamination angle of layers was investigated. Based on previous works, different recent investigations have focused on the analysis of sandwich structures with porous core [19,20,21] and composites reinforced by carbon nanotubes [22,23,24].

1.4 Numerical methods

In the last decade, various computational analysis methods have been developed which extended the finite element method, the meshfree methods, and non-nodal extended finite element methods that are the instances [24]. Zghal et al. [25] performed a static analysis of functionally graded carbon nanotube-reinforced shell and plate structures by using the finite element method. They studied the effect of various parameters such as CNT volume fraction, boundary conditions, and geometrical parameters. Their results illustrated that the skew angle has a significant effect on CNT-reinforced composite skew plates. In an other research by them [26, 27], linear free vibration of a CNT-reinforced composite shell and buckling analysis of curved composite panels were studied. They considered different CNT distributions through the thickness, and the influences of different parameters were studied. Frikha et al. [28] investigated the forced vibration behavior of a CNT-reinforced shell by employing the finite element method. They illustrated the applicability of the method with numerical examples, including square plates, spherical caps, and annular ring plates. Trabelsi et al. [29] proposed a nonlinear finite element procedure to analyze the thermal post-buckling response of a functionally graded plate and cylindrical shell. Their results indicated that increasing temperature leads to an increase in non-dimensional deflection, regardless of the boundary conditions. In another research by them [30], the thermal buckling behavior of functionally graded plates and cylindrical shells was investigated. They obtained governing equations based on modified first-order shear deformation theory, and the effects of geometrical parameters, thermal loading, and boundary conditions on shell were studied.

Belytschko et al. [31] presented a method to analyze failure by using multiscale methods. The significant feature of the method is that it is possible to extract a single discontinuity from the unit cell to be injected at the coarser scale. Song and Yoon [32] combined multiscale aggregating discontinuities method with extended finite element method and cracking nodes method for both macro- and micro-models.

Asareh and Song [33] used the non-nodal extended finite-element method to model a crack with two-dimensional four-node quadrilateral elements. They also presented two numerical examples to demonstrate the effectiveness of this method for dynamic failure. Asareh et al. [34, 35] applied the non-nodal extended finite-element method to analyze the dynamic fracture. It is worth mentioning that in these studies discontinuities are captured. Besides the Navier’s method, there are other alternative approaches to solve the governing equations. For instance, the extended particle difference method (EPDA) can be applied for solving a variety of problems, including discontinuity problems, transient heat transfer problems, elasticity problems, and moving boundary problems [36,37,38]. The particle difference method as a strong form of meshfree method is capable to be applied for various problems. Wind-driven ocean circulation, frictional contact on a rigid obstacle, and solidification and mechanical analysis of polycrystalline materials are remarkable examples [39,40,41,42]. Within the last years, there have been computational multiscale analyses. Some researchers worked about finite element method (FEM) [43, 44], differential quadrature method (DQM) [45, 46], extended Kantorovich method [47], and differential quadrature element method (DQEM) [48] for macro- , micro- , and nano-mechanics.

1.5 Research objectives

A comprehensive literature review on the applications of SMA in various industries and porous materials as well as sandwich beams and their usage in modern technology was completed. This review illustrates that although some influential works on the application of SMA materials and vibration analysis of sandwich structures have been published, there is no comprehensive research on the vibration analysis of a porous sandwich beam with composite face layers embedded with SMA resting on Vlasov’s foundation. It is assumed that composite face facesheets and the porous core are fully bonded, and simply supported boundary conditions are considered for this research. In order to obtain the governing equations, Hamilton’s principle is used, and also Navier’s solution method is applied to solve the equations.

The objective of this research is to quantify the effectiveness of parameters including SMA wires, porosity, and temperature as parameters which influence the vibration behavior of the sandwich beam. This was accomplished by a comprehensive study on free and forced vibration of the sandwich beam using FSDT and Hamilton’s principle. Furthermore, by employing Brinson’s model, constitutive equations of the SMA composite face sheets during the phase transformation are presented.

2 Problem description

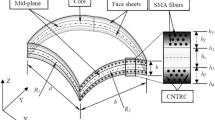
In this research, the vibration behavior of a sandwich beam with porous core and smart composite face sheets embedded with SMA is investigated. Composite layers consist of epoxy resin and carbon nanotube (CNT) reinforcements besides the SMA, and the porous pattern in the core is supposed to vary throughout the thickness direction of the beam, Fig. 1.

Fig. 1

Schematic view of the porous sandwich beam with porous core and composite face layers embedded with SMA resting on Vlasov’s foundation

2.1 Porous core of the sandwich beam

The material of the porous core is Ti–6Al–4V foam, and three different porosity distributions are assumed. Figure 1 illustrates the sandwich beam with the length of L, the thickness of h, and width of b.

Mechanical properties of the porous core including Young’s modulus and density can be presented as [49, 50]:

$$\begin{aligned} E_{c}\left( z \right)= & {} E^{*} \left[ 1-e_{0}\psi \left( z \right) \right] , \end{aligned}$$

(1)

$$\begin{aligned} \rho _{c}\left( z \right)= & {} \rho ^{*}\left[ \lambda \left( z \right) \right] \end{aligned}$$

(2)

where $E^{*}$ and $\rho ^{*}$ represent Young’s modulus and density of pure material without any porosity. $e_0$ denotes the porosity coefficient, and porosity distributions such as symmetry, asymmetry, and uniform are demonstrated by $\psi \left( z \right)$ and ${\uplambda }\left( z \right)$ which are explained in detail in “Appendix A”.

The Poisson’s ratio of the FG porous core can be calculated as [51]:

$$\begin{aligned} \upsilon \left( z \right) =0.221\left[ 1-\frac{\rho (z)}{\rho ^{*}} \right] +\upsilon ^{*}\left( 0.342\left[ 1-\frac{\rho (z)}{\rho ^{{*}}} \right] ^{{2}}-1.21\left[ 1-\frac{\rho (z)}{\rho ^{{*}}} \right] {+1} \right) . \end{aligned}$$

(3)

2.2 Face layers of the sandwich beam

Smart composite layers consist of three phases including CNT/Epoxy and SMA.

Young’s modulus of CNT/Epoxy composite is calculated using the Halpin–Tsai equation as follows [52]:

$$\begin{aligned} E_{{\mathrm {CNT/epoxy}}}= & {} \frac{3}{8}\frac{1+2\left( \frac{l_{\mathrm {CNT}}}{d_{\mathrm {CNT}}} \right) \left( \frac{\left( E_{eq} / E_{M} \right) -1}{\left( E_{eq} / E_{M} \right) +2\left( l_{\mathrm {CNT}} / d_{\mathrm {CNT}} \right) } \right) V_{\mathrm {CNT}}}{1-\left( \frac{\left( E_{eq} / E_{M} \right) -1}{\left( E_{eq} / E_{M} \right) +2\left( l_{\mathrm {CNT}} / d_{\mathrm {CNT}} \right) } \right) V_{\mathrm {CNT}}}\times E_\mathrm{epoxy} \nonumber \\&+\frac{5}{8}\frac{1+2\left( \frac{\left( E_{eq} / E_{M} \right) -1}{\left( E_{eq} / E_{M} \right) +2} \right) V_{\mathrm {CNT}}}{1-\left( \frac{\left( E_{eq} / E_{M} \right) -1}{\left( E_{eq} / E_{M} \right) +2} \right) V_{\mathrm {CNT}}}\times E_\mathrm{epoxy}, \nonumber \\ E_{eq}= & {} 4\left( \frac{t_{\mathrm {CNT}}}{d_{\mathrm {CNT}}} \right) \times E_{\mathrm {CNT}}, \nonumber \\ V_\mathrm{CNT}= & {} \frac{W_\mathrm{CNT}}{\left( \left( \rho _\mathrm{CNT} / \rho _\mathrm{epoxy}\right) -\left( \rho _\mathrm{CNT}/ \rho _\mathrm{epoxy} \right) W_\mathrm{CNT}+W_\mathrm{CNT} \right) }. \end{aligned}$$

(4)

Poisson’s ratio and mass density of CNT/Epoxy are expressed as:

$$\begin{aligned} \upsilon _{{\mathrm {CNT}} / {\mathrm {epoxy}}}= & {} V_{\mathrm {CNT}}\upsilon _{\mathrm {CNT}}+V_\mathrm{epoxy}\upsilon _\mathrm{epoxy},\nonumber \\ \rho _{{\mathrm {CNT}} / {\mathrm {epoxy}}}= & {} V_{\mathrm {CNT}}\rho _{\mathrm {CNT}}+V_\mathrm{epoxy}\rho _{epoxy}. \end{aligned}$$

(5)

The effective Young’s modulus, Poisson’s ratio, and mass density of composite layer (SMA and CNT/Epoxy) are calculated by using the rule of mixture as follows [53]:

$$\begin{aligned} E_{m}= & {} V_{SMA}E_{SMA}+V_{{\mathrm {CNT/epoxy}}}E_{{\mathrm {CNT /epoxy}}},\nonumber \\ \upsilon _{m}= & {} V_{\mathrm {SMA}}\upsilon _\mathrm{SMA}+V_{{\mathrm {CNT /epoxy}}}\upsilon _{{\mathrm {CNT/epoxy }}},\nonumber \\ \rho _{m}= & {} V_\mathrm{SMA}\rho _\mathrm{SMA}+V_{{\mathrm {CNT/epoxy}}}\rho _{{\mathrm {CNT /epoxy}}},\nonumber \\&{V_{{\mathrm {CNT/epoxy}}}=1-V}_{\mathrm {SMA}}, \end{aligned}$$

(6)

in which $V_\mathrm{SMA}$ is the volume fraction of SMA wires.

Nickel–Titanium is applied as shape memory alloy in this study, and its phase transformation is dependent upon temperature. Brinson’s model is used due to its capability in capturing the thermo-mechanical behavior at any temperature [54],

$$\begin{aligned} {\sigma }-\sigma _{0}=E\left( \xi \right) {\varepsilon }-E\left( \xi _{0} \right) \varepsilon _{0}+{\Omega }\left( \xi \right) \xi _{s}-{\Omega }\left( \xi _{0} \right) \xi _{s0}+\theta (T-T_{0}), \end{aligned}$$

(7)

in which $\sigma , E, T, \Omega , \varepsilon$ and $\theta$ illustrate stress, Young’s modulus, temperature, phase transformation coefficient, strain, and thermoelastic term, respectively. Subscript ‘zero’ denotes the value at the onset of the current phase transformation.

$\xi$ demonstrates, martensite volume fraction which ranges from zero to one. In case of $\xi =0$, SMA is in fully austenite phase, and when $\xi =1$, it can be understood that SMA is in fully martensite phase.

In the following equation, $\xi _{S}$ and $\xi _{T}$ illustrate martensite fraction induced by stress and temperature, respectively,

$$\begin{aligned} {\xi =\xi }_{S}+\xi _{T}, \end{aligned}$$

(8)

Based on Brinson’s model, the phase transformation coefficient can be expressed as:

$$\begin{aligned} {\Omega }\left( \xi \right) =-\varepsilon _{L}E\left( \xi \right) \end{aligned}$$

(9)

where $\varepsilon _{L}$ is the maximum residual strain of SMA that can be obtained from experimental tests.

Brinson’s model constitutive law can be rewritten by substituting Eq. (9) into Eq. (7) as follows:

$$\begin{aligned} {\sigma }=E\left( \xi \right) {(\varepsilon -}\varepsilon _{L}\xi _{s})+\theta \left( T-T_{0} \right) . \end{aligned}$$

(10)

Young’s modulus of SMA based on Reuss’ method is expressed as:

$$\begin{aligned} E(\xi )=\frac{E_{A}}{1+\left( \frac{E_{A}}{E_{M}}-1 \right) \xi }{.} \end{aligned}$$

(11)

The fully austenite and fully martensite modulus is denoted by $E_{A}$ and $E_{M}$, respectively.

Based on Brinson’s model, the martensitic fraction at low temperature (martensite phase) can be calculated as follows [55]:

$$\begin{aligned} M_{f}< & {} T<M_{s}, \nonumber \\ \xi _{T}= & {} \frac{{1-\xi }_{0}}{2}\left[ \cos \left( \frac{\pi \left( T-M_{f} \right) }{M_{s}-M_{f}} \right) +1 \right] . \end{aligned}$$

(12)

And at high temperature, the martensite fraction is expressed as follows:

$$\begin{aligned} A_{s}< & {} T<A_{f},\nonumber \\ \xi _{T}= & {} \frac{\xi _{0}}{2}\left[ \cos \left( \frac{\pi \left( T-A_{s} \right) }{A_{f}-A_{s}} \right) +1 \right] . \end{aligned}$$

(13)

3 Governing equations of motion

3.1 Displacement field

In the present research, first-order shear deformation theory (FSDT) is considered as displacement field [56, 57],

$$\begin{aligned} u^{i}\left( x,z \right)= & {} u_{0}^{i}\left( x \right) +z\varnothing ^{i}\left( x \right) ,\nonumber \\ w^{i}\left( x,z \right)= & {} w_{0}^{i}\left( x \right) , \quad \quad i=\text {core and face layers} \end{aligned}$$

(14)

where u and w indicate displacement components of an arbitrary point along the x and z direction, respectively. $\emptyset ^{i}$ represents the transverse normal rotation about the y-axis. $u_{0}^{i}$ and $w_{0}^{i}$ denote the axial and transverse displacements of the beam mid-plane, respectively.

The axial and transverse shear strains based on linear strain–displacement relationship take the form as [58]:

$$\begin{aligned} \left\{ {\begin{array}{l} {\varepsilon }_{xx}^{i}=\frac{{\partial }u^{i}\left( x,z \right) }{{\partial x}}=\frac{\mathrm {d}u_{0}^{i}\left( x \right) }{\mathrm {d}x}+z\frac{\mathrm {d}\emptyset ^{i}\left( x \right) }{\mathrm {d}x} \\ {\gamma }_{xz}^{i}=\frac{{\partial }u^{i}\left( x,z \right) }{{\partial z}}+\frac{{\partial }w^{i}\left( x,z \right) }{{\partial x}}=\emptyset ^{i}\left( x \right) +\frac{\mathrm {d}w_{0}^{i}\left( x \right) }{\partial x}. \\ \end{array}} \right. \end{aligned}$$

(15)

3.2 Constitutive equations

Linear elastic constitutive equations for SMA/FG smart composite sandwich beam subjected to thermal loading are given as:

(16)

where Q and C are elastic stiffness that are defined in “Appendix B”.

3.3 Strain Energy

The strain energy of an SMA/FG smart composite sandwich beam can be specified in the following form [59]:

$$\begin{aligned} {U}_{s}= & {} \frac{1}{2}\int _\mathrm{Core} {\left( \sigma _{xx}\varepsilon _{xx}+\tau _{xz}\gamma _{xz} \right) \mathrm{d}V} +\frac{1}{2}\int _\mathrm{upper sheet} {\left( \sigma _{xx}\varepsilon _{xx}+\tau _{xz}\gamma _{xz} \right) \mathrm{d}V} \nonumber \\&+\frac{1}{2}\int _{\mathrm {lower sheet}} {\left( \sigma _{xx}\varepsilon _{xx}+\tau _{xz}\gamma _{xz} \right) \mathrm{d}V}, \nonumber \\ {\delta {U}}_{s}= & {} \int _\mathrm{Core} {\left( \sigma _{xx}{\delta \varepsilon }_{xx}+\tau _{xz}\delta \gamma _{xz} \right) \mathrm{d}V} +\frac{1}{2}\int _\mathrm{upper sheet} {\left( \sigma _{xx}\delta \varepsilon _{xx}+\tau _{xz}\delta \gamma _{xz} \right) \mathrm{d}V} \nonumber \\&+\frac{1}{2}\int _{\mathrm {lower sheet}} {\left( \sigma _{xx}\delta \varepsilon _{xx}+\tau _{xz}\delta \gamma _{xz} \right) \mathrm{d}V}. \end{aligned}$$

(17)

In order to obtain Vlasov’s foundation’s strain energy, the displacement field is assumed to be [58]

$$\begin{aligned} u_{f}(x,z)= & {} 0, \nonumber \\ w_{f}(x,z)= & {} w_{0}(x)\chi (z). \end{aligned}$$

(18)

Based on this model, there is no horizontal displacement, $w_{{0}}(x)$ and $\chi (z)$ indicate transverse deflection in the mid-surface of the sandwich beam and shape function of foundation, respectively, with the following boundary conditions:

$$\begin{aligned} \chi \left( 0 \right) =1, \qquad \chi \left( -H \right) =0. \end{aligned}$$

(19)

Here, H represents the thickness of the foundation. Strain components can be expressed as follows according to strain–displacement equations:

$$\begin{aligned} f_{\varepsilon _{xx}}= & {} 0, \nonumber \\ f_{\varepsilon _{zz}}= & {} w_{0}(x)\frac{\mathrm{d}\chi (z)}{\mathrm{d}z},\nonumber \\ f_{\gamma _{xz}}= & {} \chi (z)\frac{\mathrm{d}w_{0}(x)}{\mathrm{d}x}. \end{aligned}$$

(20)

Constitutive equations for the isotropic foundation can be written as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{xx} \\ \sigma _{zz} \\ \tau _{xz} \\ \end{array}} \right\} ^{f}=\left[ {\begin{array}{lll} D_{11} &{}\quad D_{12} &{}\quad 0\\ D_{21} &{}\quad D_{11} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad D_{55}\\ \end{array} } \right] ^{f}\left\{ {\begin{array}{l} 0 \\ \varepsilon _{zz} \\ \gamma _{xz} \\ \end{array}} \right\} ^{f} \end{aligned}$$

(21)

where D is the elastic stiffness of the foundation that is determined in “Appendix C”.

The strain energy of Vlasov’s foundation can be derived as:

$$\begin{aligned} {U}_{f}= & {} \frac{1}{2}\int _f {\left( \sigma _{zz}\varepsilon _{zz}+\tau _{xz}\gamma _{xz} \right) \mathrm{d}V}, \nonumber \\ \delta {U}_{f}= & {} \int _f {\left( \sigma _{zz}{\delta \varepsilon }_{zz}+\tau _{xz}\delta \gamma _{xz} \right) \mathrm{d}V}. \end{aligned}$$

(22)

3.4 Kinetic energy

Variation of kinetic energy for the SMA/FG smart composite sandwich beam can be formulated as:

$$\begin{aligned} {T}= & {} \frac{1}{2}\int _\mathrm{Core} {\rho _{c}(z)\left( {\dot{u}}^{2}+{\dot{w}}^{2} \right) \mathrm{d}V} +\frac{1}{2}\int _{\text {upper sheet}} {\rho _{f}(z)\left( {\dot{u}}^{2}+{\dot{w}}^{2} \right) \mathrm{d}V} \nonumber \\&+\frac{1}{2}\int _{\text {lower sheet}} {\rho _{f}(z)\left( {\dot{u}}^{2}+{\dot{w}}^{2} \right) \mathrm{d}V}, \nonumber \\ \delta {T}= & {} \int _\mathrm{Core} {\rho _{c}(z)\left( {\dot{u}}\delta {\dot{u}}+{\dot{w}}\delta {\dot{w}} \right) \mathrm{d}V} +\frac{1}{2}\int _{\text {upper sheet}} {\rho _{f}(z)\left( {\dot{u}}\delta {\dot{u}}+{\dot{w}}\delta {\dot{w}} \right) \mathrm{d}V}, \nonumber \\&+\frac{1}{2}\int _{\text {lower sheet}} {\rho _{f}(z)\left( {\dot{u}}\delta {\dot{u}}+{\dot{w}}\delta {\dot{w}} \right) \mathrm{d}V}. \end{aligned}$$

(23)

3.5 External work

The variation of the total external work can be defined as follows:

$$\begin{aligned} \delta w=\int _0^l {f(x,t)\delta w\mathrm{d}x} \end{aligned}$$

(24)

in which f is the external force, and its value in free vibration analysis is supposed to be zero.

3.6 Hamilton’s principle

By applying Hamilton’s principle, the governing equations of a sandwich beam subjected to thermal loading are derived as [60]:

$$\begin{aligned}&\int _{t_{1}}^{t_{2}} {\delta \Pi } \mathrm{d}t=0, \nonumber \\&\int _{t_{1}}^{t_{2}} {(\delta T-\delta U-\delta W)\mathrm{d}t=0} \end{aligned}$$

(25)

where $\delta$ denote the variation operator, U, W,  and T are the strain energy, external work, and kinetic energy. The governing equations are presented in “Appendix D”.

4 Solution procedure

Assuming that the boundary conditions are simply supported in both ends of the sandwich beam, Navier’s type solution can be employed to solve the equations of motion as follows:

$$\begin{aligned} u\left( x,t \right)= & {} \sum \limits _{n=1}^\infty U_{n} \cos {\left( \frac{n\pi }{l}x \right) e^{-i\omega t}},\nonumber \\ w\left( x,t \right)= & {} \sum \limits _{n=1}^\infty W_{n} \sin \left( \frac{n\pi }{l}x \right) e^{-i\omega t},\nonumber \\ \emptyset \left( x,t \right)= & {} \sum \limits _{n=1}^\infty {\Phi }_{n} \cos {\left( \frac{n\pi }{l}x \right) e^{-i\omega t}}. \end{aligned}$$

(26)

Here, $U_{n}, W_{n}$, the and ${\Phi }_{n}$ are undetermined coefficients, $\omega$ is the vibration frequency. By substituting Navier’s assumptions into the governing equations of motion, the matrix form of free vibration equations of the sandwich beam is written as

$$\begin{aligned} \left( \left[ K \right] -[M]\omega ^{2} \right) \mathbf {q}= \end{aligned}$$

(27)

where K, M and ${\varvec{q}}$ indicate stiffness matrix, mass matrix, and displacement components, respectively.

In order to analyze forced vibration, the external force is assumed to be

$$\begin{aligned} F(x,t)=F_\mathrm{ext}\sin ({\Omega }t) \end{aligned}$$

(28)

where ${\Omega }$ is the frequency of forced vibration. The matrix form of the response system equations for the sandwich beam is obtained as follows:

$$\begin{aligned} \left\{ {\begin{array}{c} U_{n}\\ W_{n}\\ \end{array} } \right\} =\frac{{[M]}^{-1}\left\{ F \right\} }{\omega _{n}^{2}-{\Omega }_{n}^{2}}. \end{aligned}$$

(29)

In summary, the overall solution procedure can be shown as Fig. 2:

Fig. 2

A flowchart to obtain the governing equations and solution procedure

And then, by substituting Navier’s solution (Eq. (26)) into the governing equations of motion, the matrix form of free vibration equations (Eq. (27)) of the sandwich beam is obtained in which K, M,  and ${\varvec{q}}$ indicate stiffness matrix, mass matrix, and displacement components, respectively.

5 Results and discussion

5.1 Comparison studies

Before going into the details of the parametric analysis, it is necessary to validate the governing equations of motion. For this purpose, two different comparisons of obtained results are presented. As no published results for the SMA/FG smart composite sandwich beam under current consideration are available in the open literature, the vibration analysis is validated with [61]. The linear free vibration of sandwich beams is considered in Table 1 with a homogeneous core and composite face sheets reinforced by FG and uniformly CNT distribution.

Table 1 The comparison of natural frequencies of a sandwich beam with CNT-reinforced composite face sheets and simply supported boundary conditions

Natural frequencies presented in Table 1 illustrate good agreement with the literature.

Another verification is carried out for the free vibration of an SMA/FG smart composite sandwich beam, and it is indicated in Table 2. High-order shear deformation theory (HSDT) and Euler–Bernoulli beam theory are applied to compare the results. Besides various porosity coefficients, different variety of length-to-thickness ratio and porous distribution pattern are considered. As it is shown in Table 2, the symmetry porous pattern in the core provides the highest amount of the natural frequency, and that is due to the fact that in the symmetry pattern mass is distributed at the farthest distance from the neutral axis, and because of this, the moment of inertia of the beam has the maximum amount of itself, that means that the symmetry pattern of the porous core makes the beam stiffer and the natural frequency is the maximum.

Table 2 Comparison of natural frequency with three theories

5.2 Material properties

In this research, the geometric parameters of the sandwich beam and material properties of porous core are assumed as follows:

$$\begin{aligned} h_{c}/ h_{f}=8 ,b=0.5\left[ m \right] , h=0.2\left[ m \right] , E^{*}=113.8\times {10}^{9}\left[ Pa \right] ,\upsilon ^{*}=0.342,\rho ^{*} =4430\,[\mathrm{kg\,m}^{-3}]. \end{aligned}$$

Here, $h_{c}$ and $h_{f}$ describe the core and face layers thickness, respectively. And also $E^{*}, \upsilon ^{*},$ and $\rho ^{*}$ illustrate the pure Young’s modulus, Poisson’s ratio, and density of the porous core. The material properties of SMA are given in Table 3 [62].

Table 3 Thermomechanical properties of NiTi SMA [56]

Table 4 represents the material properties of the core.

Table 4 Material properties of the core

Table 5 indicates the material properties of CNT and epoxy, and Table 6 represents the material properties of silica aerogel.

Table 5 Material properties of CNT and Epoxy

Table 6 Material properties of silica aerogel

5.3 Thermo-mechanical behavior of SMA

During temperature change in Austenite phase, the Martensite volume fraction varies at each point. By increasing the temperature from $A_{s}$ to $A_{f}$, the molecular shape of SMA tends to get more organized order, and this change in molecular shape makes SMA wires have higher Young’s modulus, and by decreasing the temperature and transforming to the martensite phase, its molecular shape changes to irregular form, and it causes a decrease in Young’s modulus of SMA which is illustrated in Fig. 3.

Fig. 3

a Procedure of changing the martensite volume fraction for heating and cooling cycle. b Young’s modulus behavior of SMA in a wide range of temperature.

5.4 Volume fraction of SMA

In order to examine the effect of SMA’s volume fraction, Fig. 4 illustrates the dimensionless natural frequency of the sandwich beam versus temperature changing for different volume fractions of SMA. The numerical results indicate that with increase in SMA’s volume fraction, the dimensionless natural frequency is increased as well due to an increase in Young’s modulus. It is also noticeable that a higher volume fraction of SMA makes the sandwich beam become more sensitive to temperature, and the dimensionless natural frequency changes intensively.

Fig. 4

Dimensionless natural frequency of a sandwich beam in terms of temperature and SMA volume fraction (SYM porous distribution, $e_{0}=0.3)$

5.5 Porosity coefficient

For further study, the sensitivity of the structural response to the porosity coefficient in a heating/cooling cycle of SMA is calculated. Figure 5 indicates the variation of the dimensionless natural frequency of the sandwich beam in terms of temperature for various porosity coefficients. It is observed that the dimensionless natural frequency of a sandwich beam is increased with the increase in the porosity coefficient. One can conclude that by increasing the porosity coefficient, both stiffness and mass decrease, but the influence of mass reduction is more significant than stiffness decrease, and it leads to a higher natural frequency.

Fig. 5

Dimensionless natural frequency of a sandwich beam in terms of temperature and porosity coefficient (SYM porous distribution)

5.6 Effect of temperature

Figure 6 shows the effect of SMA wire’s existence in various temperatures. It can be seen that when SMA wires start the austenite phase (temperature $> 34.5$), the increase in stiffness results in the higher natural frequency. It should be noted that symmetric porous distribution provides a more stiffed structure which means a higher natural frequency for the sandwich beam.

Fig. 6

The effect of SMA wires on dimensionless natural frequency of the sandwich beam ($e_{0}=0.3)$

5.7 Frequency ratio

The variation of transverse amplitude for the sandwich beam with simply supported boundary conditions versus ratio of excitation frequency to natural frequency is illustrated in Fig. 7. It is clear that the excitation frequency ratio is the important factor to study the vibration behavior of sandwich structures. As can be seen, by approaching excitation frequency to natural frequency the amplitude of vibration significantly increases. Furthermore, it can be concluded that the amplitude of vibration is less when SMA wires are in austenite phase.

Fig. 7

Vibration amplitude in terms of excitation frequency ratio (SYM porous distribution, $e_{0}=0.3)$

Fig. 8

Vibration amplitude in terms of excitation frequency ratio for different porosity coefficients

5.8 Effect of porosity on amplitude

The influence of the porosity coefficient on the transverse amplitude for symmetric porous distribution of the core is demonstrated in Fig. 8. As it can be seen a higher amount of porosity coefficient leads to a higher transverse amplitude of the sandwich beam. Moreover, as it was predicted, by exciting the beam with frequencies around the natural frequency, significant rise in amplitude is resulted that shows the resonance.

5.9 External force

Figure 9 depicts the effect of different external forces on the vibration behavior of the sandwich beam, where the transverse amplitude of vibration is plotted versus time. It is brightly shown that an external force doesn’t have any effect on the time period. It is also indicated that the higher external forces result in higher transverse amplitude.

6 Concluding remarks

Free and forced vibration analysis of a sandwich beam including a functionally graded porous core and composite face layers embedded with shape memory alloy resting on Vlasov’s model was studied. Three different porosity distributions are supposed, and carbon nanotubes are added in order to reinforce the composite face layers. Constitutive relations were developed for graded porous core and composite face layers with embedded SMA wires. The governing equations of motion were derived using first-order shear deformation theory and Hamilton’s principle. By applying Navier’s solution method, the governing equations were solved. Results of this study are validated by comparing them to the ones already existing in literature, and a good agreement is observed. Then, parametric analyses are carried out, and the effects of such parameters as SMA volume fraction, temperature changing, porosity coefficient, and excitation frequency ratio are investigated. The main results of this study are expressed as:

• Although by increasing temperature the stiffness of the structure should decrease, due to the unique temperature properties of SMA, it gets stiffer by increasing temperature and entering the austenite phase. And this provides higher natural frequency for the sandwich beam.

• By increasing the SMA volume fraction in the face layers, the sandwich beam’s stiffness dramatically changes with temperature changing, and its stiffness changing is intensive when the phase transformation is happening.

• It is shown that for a sandwich beam with porous core the symmetric porous distribution provides higher stiffness than uniform and asymmetric porosity distribution, and consequently it results in higher natural frequency.

• As it comes out of the results, increasing porosity coefficient leads to higher natural frequency, and its reason is that by increasing porosity coefficient both mass and stiffness reduce, but the influence of mass reduction is more effective and it causes a higher natural frequency.

Fig. 9

Vibration amplitude in terms of time for different external forces (SYM porous distribution, $e_{0}=0.3)$

Appendix

1.1 Appendix A

$$\begin{aligned} \psi \left( z \right)= & {} \left\{ \begin{array}{ll} \cos \left( \frac{{\uppi z}}{{h}_{c}} \right) &{}\qquad { \rightarrow \text { Symmetry }} \\ \cos \left( \frac{{\uppi z}}{{2}{h}_{c}}+\frac{{\uppi }}{{4}} \right) &{}\qquad { \rightarrow \text { Asymmetry }} \\ \psi &{}\qquad \rightarrow \text { Uniform } \\ \end{array} \right. \nonumber \\ {\uplambda }\left( {z} \right)= & {} \left\{ {\begin{array}{ll} 1-{e}_{\mathrm {m}}\psi \left( z \right) &{} \qquad \quad \text {Symmetry, Asymmetry } \\ \sqrt{1-{e}_{{0}}\psi }&{}\qquad \quad \mathrm {Uniform } \\ \end{array}} \right. \nonumber \\ \psi= & {} \frac{{1}}{{e}_{{0}}}- \frac{{1}}{{e}_{{0}}}\left( \frac{{2}}{{\uppi }}\sqrt{1-{e}_{{0}}} -\frac{{2}}{{\uppi }}{+1} \right) ^{{2}} , \quad \quad {e}_{{m}}=1-\sqrt{1- e_{0}}. \end{aligned}$$

1.2 Appendix B

$$\begin{aligned} Q_{11}= & {} \frac{E_{m}}{1-\nu _{m}^{2}},\\ Q_{55}= & {} G_{m}=\frac{E_{m}}{2(1+\nu _{m})},\\ C_{11}= & {} \frac{E_{c}(z)}{1-{\nu _{c}(z)}^{2}},\\ C_{55}= & {} G_{c}=\frac{E_{c}}{2(1+\nu _{c})}. \end{aligned}$$

1.3 Appendix C

$$\begin{aligned} D_{11}= & {} \frac{E_{f}(\rho )}{1-{\nu _{f}(\rho )}^{2}},\\ D_{12}= & {} D_{21}=\frac{E_{f}(\rho )\nu _{f}(\rho )}{1-{\nu _{f}(\rho )}^{2}},\\ D_{55}= & {} G_{f}=\frac{E_{f}(\rho )}{2(1+\nu _{f}(\rho ))}. \end{aligned}$$

Subscript “f” denotes the foundation.

1.4 Appendix D

$$\begin{aligned}&{{{\delta }} }{{{u}}}_{\mathbf {0}}:\quad -\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {uc}_{110}+\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {uc}_{111}+2\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) T_{0}\theta -2\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) T\theta \\&\quad -\left( \frac{\partial ^{2}}{\partial x^{2}}\phi \left( x,t \right) \right) {uft}_{111}-\left( \frac{\partial ^{2}}{\partial x^{2}}u\left( x,t \right) \right) {ufb}_{110}-\left( \frac{\partial ^{2}}{\partial x^{2}}\phi \left( x,t \right) \right) {ufb}_{111}\\&\quad -\left( \frac{\partial ^{2}}{\partial x^{2}}u\left( x,t \right) \right) {uft}_{110}+2\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) \xi _{s}\varepsilon _{L}\xi +\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) T_{sur}\alpha _{f}{ufb}_{110} \\&\quad +\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) T_{sur}\alpha _{f}{uft}_{110}+\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) C\beta _{f}{ufb}_{110}+\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) C\beta _{f}{uft}_{110} \\&\quad +\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) C\beta {uc}_{110}+\left( \frac{\partial }{\partial x}u\left( x,t \right) \right) T_{sur}\alpha {uc}_{110}-\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {Ic}_{0}-\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {Ic}_{1} \\&\quad -\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {Ifb}_{0}-\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {Ifb}_{1}-\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {Ift}_{0}-\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {Ift}_{1}=0, \\&\varvec{\delta }\varvec{w}_{\mathbf {0}}:-\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) {uc}_{550}-\left( \frac{\partial ^{2}}{\partial x^{2}}w\left( x,t \right) \right) {uc}_{550}-w\left( x,t \right) K_{1f}-\left( \frac{\partial ^{2}}{\partial x^{2}}w\left( x,t \right) \right) K_{2f} \\&\quad -\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) {uft}_{550}-\left( \frac{\partial ^{2}}{\partial t^{2}}w\left( x,t \right) \right) {Ic}_{0}-\left( \frac{\partial ^{2}}{\partial t^{2}}w\left( x,t \right) \right) {Ift}_{0} \\&\quad -\left( \frac{\partial ^{2}}{\partial x^{2}}w\left( x,t \right) \right) {ufb}_{550}\left( \frac{\partial ^{2}}{\partial x^{2}}w\left( x,t \right) \right) {uft}_{550}-\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) {ufb}_{550} =0, \end{aligned}$$

$$\begin{aligned}&{{{\delta }} }{{{\phi }} }_{\mathbf {0}}:\quad \left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) \xi _{s}\varepsilon _{L}\xi {usb}_{1}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) \xi _{s}\varepsilon _{L}\xi {ust}_{1}+\left( \frac{\partial }{\partial x}w\left( x,t \right) \right) {uc}_{550} \\&\quad +\phi \left( x,t \right) {uc}_{550}+\phi \left( x,t \right) {ufb}_{550}+\phi \left( x,t \right) {uft}_{550}+\left( \frac{\partial }{\partial x}w\left( x,t \right) \right) {uft}_{550} \\&\quad +\left( \frac{\partial }{\partial x}w\left( x,t \right) \right) {ufb}_{550}-\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {Ic}_{1}-\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {Ic}_{2}-\left( \frac{\partial ^{2}}{\partial x^{2}}u\left( x,t \right) \right) {ufb}_{111} \\&\quad -\left( \frac{\partial ^{2}}{\partial x^{2}}\phi \left( x,t \right) \right) {ufb}_{112}-\left( \frac{\partial ^{2}}{\partial x^{2}}u\left( x,t \right) \right) {uc}_{111}-\left( \frac{\partial ^{2}}{\partial x^{2}}\phi \left( x,t \right) \right) {uc}_{112} \\&\quad -\left( \frac{\partial ^{2}}{\partial x^{2}}\phi \left( x,t \right) \right) {uft}_{112}-\left( \frac{\partial ^{2}}{\partial x^{2}}u\left( x,t \right) \right) {uft}_{111}-\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {Ifb}_{1}-\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {Ifb}_{2} \\&\quad -\left( \frac{\partial ^{2}}{\partial t^{2}}u\left( x,t \right) \right) {Ift}_{1}-\left( \frac{\partial ^{2}}{\partial t^{2}}\phi \left( x,t \right) \right) {Ift}_{2}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) \beta _{f}C{ufb}_{111} \\&\quad +\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) \beta _{f}C{uft}_{111}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T_{sur}\alpha _{f}{uft}_{111}-\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T\theta {usb}_{1}\\&\quad -\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T\theta {ust}_{1}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T_{0}\theta {usb}_{1}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T_{0}\theta {ust}_{1}\\&\quad +\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T_{sur}\alpha _{f}{ufb}_{111}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) \beta C{uc}_{111}+\left( \frac{\partial }{\partial x}\phi \left( x,t \right) \right) T_{sur}\alpha {uc}_{111}=0, \end{aligned}$$

$$\begin{aligned}&{uc}_{110}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \mathrm{d}z},&{uc}_{111}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \times z\mathrm{d}z}, \\&{uc}_{112}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \times z^{2}\mathrm{d}z},&{uc}_{113}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \times z^{3}\mathrm{d}z}, \\&{uc}_{114}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \times z^{4}\mathrm{d}z},&{uc}_{116}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \times z^{6}\mathrm{d}z},\\&{uc}_{550}=\int _{-h_{c}/2}^{h_{c}/2} {c_{55}\left( z \right) \mathrm{d}z},&{uc}_{552}=\int _{-h_{c}/2}^{h_{c}/2} {c_{11}\left( z \right) \times z^{5}\mathrm{d}z},\\&{uc}_{554}=\int _{-h_{c}/2}^{h_{c}/2} {c_{55}\left( z \right) \times z^{4}\mathrm{d}z},&{ufb}_{110}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{11}^{fb}\left( z \right) \mathrm{d}z}, \\&{ufb}_{111}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{11}^{fb}\left( z \right) \times z\mathrm{d}z},&{ufb}_{112}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{11}^{fb}\left( z \right) \times z^{2}\mathrm{d}z}, \\&{ufb}_{113}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{11}^{fb}\left( z \right) \times z^{3}\mathrm{d}z},&{ufb}_{114}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{11}^{fb}\left( z \right) \times z^{4}\mathrm{d}z}, \\&{ufb}_{116}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{11}^{fb}\left( z \right) \times z^{6}\mathrm{d}z},&{ufb}_{550}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{55}^{fb}\left( z \right) \mathrm{d}z}, \\&{ufb}_{552}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{55}^{fb}\left( z \right) \times z^{2}\mathrm{d}z},&{ufb}_{554}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {c_{55}^{fb}\left( z \right) \times z^{4}\mathrm{d}z}, \\&{uft}_{110}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{11}^{ft}\left( z \right) \mathrm{d}z},&{uft}_{111}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{11}^{ft}\left( z \right) \times z\mathrm{d}z}, \\&{utf}_{112}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{11}^{ft}\left( z \right) \times z^{2}\mathrm{d}z},&{uft}_{113}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{11}^{ft}\left( z \right) \times z^{3}\mathrm{d}z}, \\&{uft}_{114}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{11}^{ft}\left( z \right) \times z^{4}\mathrm{d}z},&{uft}_{116}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{11}^{ft}\left( z \right) \times z^{6}\mathrm{d}z}, \\&{uft}_{550}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{55}^{ft}\left( z \right) \mathrm{d}z},&{uft}_{552}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{55}^{ft}\left( z \right) \times z^{2}\mathrm{d}z}, \\&{uft}_{554}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {c_{55}^{ft}\left( z \right) \times z^{4}\mathrm{d}z},&{Ic}_{0}=\int _{-\frac{h_{c}}{2}-h_{f}-h_{p}}^{{-h}_{c}/2-h_{f}} {\rho _{c}(z)\mathrm{d}z}, \\&{Ic}_{1}=\int _{-\frac{h_{c}}{2}-h_{f}-h_{p}}^{{-h}_{c}/2-h_{f}} {\rho _{c}(z)\times {z}\mathrm{d}z},&{Ic}_{2}=\int _{-\frac{h_{c}}{2}-h_{f}-h_{p}}^{{-h}_{c}/2-h_{f}} {\rho _{c}(z)\times z^{2}\mathrm{d}z}, \\&{Ic}_{3}=\int _{-\frac{h_{c}}{2}-h_{f}-h_{p}}^{{-h}_{c}/2-h_{f}} {\rho _{c}(z)\times z^{3}\mathrm{d}z},&{Ic}_{4}=\int _{-\frac{h_{c}}{2}-h_{f}-h_{p}}^{{-h}_{c}/2-h_{f}} {\rho _{c}(z)\times z^{4}\mathrm{d}z}, \\&{Ic}_{6}=\int _{-\frac{h_{c}}{2}-h_{f}-h_{p}}^{{-h}_{c}/2-h_{f}} {\rho _{c}(z)\times z^{6}\mathrm{d}z},&{Ifb}_{0}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {\rho _{bf}(z)\mathrm{d}z}, \\&{Ifb}_{1}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {\rho _{bf}(z)\times z\mathrm{d}z},&{Ifb}_{2}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {\rho _{bf}(z)\times z^{2}\mathrm{d}z}, \\&{Ifb}_{3}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {\rho _{bf}(z)\times z^{3}\mathrm{d}z},&{Ifb}_{4}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {\rho _{bf}(z)\times z^{4}\mathrm{d}z},\\&{Ifb}_{6}=\int _{-\frac{h_{c}}{2}-h_{f}}^{{-h}_{c}/2} {\rho _{bf}(z)\times z^{6}\mathrm{d}z},&{Ift}_{0}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {\rho _{tf}(z)\mathrm{d}z}, \\&{Ift}_{1}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {\rho _{tf}(z)\times z\mathrm{d}z},&{Ift}_{2}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {\rho _{tf}(z)\times z^{2}\mathrm{d}z}, \\&{Ift}_{3}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {\rho _{tf}(z)\times z^{3}\mathrm{d}z},&{Ift}_{4}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {\rho _{tf}(z)\times z^{4}\mathrm{d}z}, \\&{Ift}_{6}=\int _\frac{h_{c}}{2}^{\frac{h_{c}}{2}+h_{f}} {\rho _{tf}(z)\times z^{6}\mathrm{d}z}. \\ \end{aligned}$$