1 Introduction

PMSMs exhibit high power density, wide speed range and high efficiency. Therefore, they have been employed in a variety of applications [1,2,3,4], such as industrial drives, electric vehicles, wind turbines, aerospace and marine uses. The output torque fluctuates with time, which is called torque ripple. The torque ripple of PMSMs can result in vibration and noise [5]. Therefore, it should be suppressed, especially in high-performance motion control applications.

Torque ripple is induced from many sources, such as flux linkage harmonics, cogging torque and current harmonics. There are two methods to suppress the torque ripple from flux linkage harmonics and cogging, i.e., motor design optimization [6,7,8,9,10] and current harmonic injection [11]. As for motor design optimization, it includes skewing of the rotor magnets and skewing slots, etc. Such methods reduce the power density of PMSMs. At the same time, they increase the motor manufacturing cost. Regarding current harmonic injection, it has been gradually used in industry. For current harmonic injection, some researchers have explored the speed ripple as the feedback signal [12,13,14]. Others have explored the PMSM model considering spatial harmonics. FEA data have been used by more and more researchers to describe the harmonics of PMSMs [15,16,17,18]. Meanwhile, the consistency between FEA data and the actual motor data has been verified. The inductance harmonics and flux linkage harmonics obtained from the FEA can be used to describe the link between the current harmonics and the torque ripple. Then the appropriate current harmonics are selected to suppress the torque ripple. By considering the inductance harmonics, a torque ripple function was established in [19,20,21]. However, the effect of magnetic saturation on the inductances was not considered. The torque ripple model was simplified by ignoring some of the minor components in [22], where the flux linkage was obtained by a voltage equation. The accuracy of the flux linkage obtained from voltage integration is affected by two factors, the high-pass filter and the voltage distortion caused by the inverter. In [23], the torque was described by a 2-D Fourier series and polynomial. In [24, 25], the torque was reconstructed by polynomials and Fourier series, and the analytical torque model was verified by experiments.

Based on a torque model considering spatial harmonics, current harmonics can be selected to suppress torque ripple. Torque ripple was minimized by fluctuating torque angle in [19, 21], and the current amplitude was fluctuated in [26]. In [20, 22], the q-axis current was fluctuated to suppress torque ripple, since the torque is more dependent on the q-axis than the d-axis current. However, it did not directly obtain the current harmonics and it was adjusted by a PI feedback controller. A genetic approach was used to select the optimal current harmonics for torque ripple minimization in [27]. A torque harmonic coupling model was established in [28]. However, it was not suitable for heavy loads.

In previous studies, the torque of PMSMs was described with flux linkage data, apparent inductance data and cogging torque data. Due to the high magnetic saturation of PMSMs, apparent inductances are not enough to describe the saturation of the motor. This paper mainly considered the effect of magnetic saturation, established a torque harmonic coupling model and selected current harmonics for torque ripple suppression.

2 Analytical torque model based on FEA

For automotive interior PMSMs, magnetic saturation is serious, and the amplitude and phase of the torque ripple change with the electrical loads. Therefore, an accurate PMSM model considering spatial harmonics and magnetic saturation is needed. In addition, the utilized analytical torque model [24] is expressed as follows:

$$ T_{e} (i_{d} ,i_{q} ,\theta ) = V_{\theta } P_{t} X(i_{d} ,i_{q} ), $$
(1)

where \(V_{\theta } = \left[ {\cos (6N_{2} \theta ), \cdots ,\cos (6\theta ),1,\sin (6\theta ), \cdots ,\sin (6N_{2} \theta )} \right]\), \(X(i_{d} ,i_{q} ) = \left[ {\begin{array}{*{20}c} 1 & {i_{d} } & {i_{q} } & {\begin{array}{*{20}c} {i_{d}^{2} } & {i_{d} i_{q} } & \cdots \\ \end{array} } & {i_{q}^{{N_{1} }} } \\ \end{array} } \right]^{\rm T}\). \(i_{d} ,i_{q}\) are the dq-axis currents, and \(\theta\) is the electrical rotor position. \(6N_{2}\) is the highest order of the Fourier series expansion. The value of \(N_{2}\) depends on the degree of the torque distortion. \(N_{1}\) denotes the highest order of the polynomial. \(P_{t}\) is the parameter matrix.

In [24], Fourier and Taylor series, expansions were utilized to find an analytical approximation of the flux linkage data from an FEA. Then an analytical approximation of the torque was derived through the mathematical relationship between the torque and flux linkage. However, the flux linkage model was not considered in the paper. Therefore, Fourier and Taylor expansions could be utilized to directly find an analytical approximation of the torque data from the FEA.

Figure 1a shows an FEA model of the studied PMSM. Table 1 shows the parameters of the PMSM. In Eq. (1), a Taylor series expansion was used to describe the saturated surface in Fig. 1b and a Fourier expansion was utilized to describe the spatial harmonics, such as the cogging torque in Fig. 1c. The analytical torque model has been verified by FEA and experiments in [24]. In addition, the analytical torque model showed high accuracy.

Fig. 1
figure 1

Diagrams showing: a mesh plot of the tested motor in an FEA; b saturated surface of the torque with dq-axis currents when \(\theta = 0^\circ\); c cogging torque

Full size image
Table 1 Parameters of a PMSM
Full size table

3 Torque harmonic coupling model

The analytical torque model describes the effects of magnetic saturation and spatial harmonics. To select current harmonics for torque ripple minimization, and to simplify the torque function, a plane was created near the current set \((i_{d0} ,i_{q0} )\) in Fig. 1b. The first-order Taylor of the torque function was expanded as follows:

$$ \begin{aligned} T_{e} (i_{d} ,i_{q} ,\theta ) = T_{e} (i_{d0} ,i_{q0} ,\theta ) + \left. {\frac{{\partial T_{e} (i_{d} ,i_{q} ,\theta )}}{{\partial i_{d} }}} \right|_{\begin{subarray}{l} i_{d} = i_{d0} \\ i_{q} = i_{q0} \end{subarray} } (i_{d} - i_{d0} ) \hfill \\ \, + \left. {\frac{{\partial T_{e} (i_{d} ,i_{q} ,\theta )}}{{\partial i_{q} }}} \right|_{\begin{subarray}{l} i_{d} = i_{d0} \\ i_{q} = i_{q0} \end{subarray} } (i_{q} - i_{q0} ), \hfill \\ \end{aligned} $$
(2)

where \(T_{e} (i_{d0} ,i_{q0} ,\theta )\) is the torque at the current \((i_{d0} ,i_{q0} )\). \((i_{d} - i_{d0} )\) and \((i_{q} - i_{q0} )\) are the incremental currents. \({{\partial T_{e} (i_{d} ,i_{q} ,\theta )} \mathord{\left/ {\vphantom {{\partial T_{e} (i_{d} ,i_{q} ,\theta )} {\partial i_{d} }}} \right. \kern-\nulldelimiterspace} {\partial i_{d} }}\) and \({{\partial T_{e} (i_{d} ,i_{q} ,\theta )} \mathord{\left/ {\vphantom {{\partial T_{e} (i_{d} ,i_{q} ,\theta )} {\partial i_{q} }}} \right. \kern-\nulldelimiterspace} {\partial i_{q} }}\) are the torque coefficients, where \(i_{d,0} ,i_{q,0}\) were chosen based on the maximum torque per ampere (MTPA) rule.

Torque under sinusoidal current excitation and torque coefficients were obtained through an analytical torque model, and the detailed equations can be derived as follows:

$$ \begin{gathered} \, T_{e} (i_{d0} ,i_{q0} ,\theta ) = V_{\theta } P_{t} X(i_{d0} ,i_{q0} ) = V_{\theta } E_{t} ; \hfill \\ \left. {\frac{{\partial T_{e} (i_{d} ,i_{q} ,\theta )}}{{\partial i_{d} }}} \right|_{\begin{subarray}{l} i_{d} = i_{d0} \\ i_{q} = i_{q0} \end{subarray} } = V_{\theta } P_{t} \left. {\frac{{\partial X(i_{d} ,i_{q} )}}{{\partial i_{d} }}} \right|_{\begin{subarray}{l} i_{d} = i_{d0} \\ i_{q} = i_{q0} \end{subarray} } = V_{\theta } E_{td} ; \hfill \\ \left. {\frac{{\partial T_{e} (i_{d} ,i_{q} ,\theta )}}{{\partial i_{q} }}} \right|_{\begin{subarray}{l} i_{d} = i_{d0} \\ i_{q} = i_{q0} \end{subarray} } = V_{\theta } P_{t} \left. {\frac{{\partial X(i_{d} ,i_{q} )}}{{\partial i_{q} }}} \right|_{\begin{subarray}{l} i_{d} = i_{d0} \\ i_{q} = i_{q0} \end{subarray} } = V_{\theta } E_{tq} . \hfill \\ \end{gathered} $$
(3)

\(E_{t}\), \(E_{td}\), and \(E_{tq}\) are the column vectors, which are composed of harmonic amplitudes. The torque coefficients are derivatives of the torque function with respect to currents. Similar to the definition of incremental inductances, torque coefficients describe the effect of incremental currents on the torque. In terms of high-saturated motors, derivatives such as the incremental inductances and torque coefficients are more accurate in describing the effects of incremental currents on the flux linkages and torque, respectively.

PMSMs are three-phase balanced and of half-wave symmetry. Therefore, there are only the 6kth torque harmonics. Figure 2 shows the spatial harmonics of the torque and torque coefficients under different loads. It can be seen that the 12th harmonic dominates the torque harmonic components. The amplitude of the torque ripple is 1.8 N·m when the average torque is 10 N·m. The amplitude of the torque ripple increases to 3.2 N·m when the average torque is 50 N·m. The q-axis torque coefficient decreases from 0.24 to 0.21 N·m/A when the average torque increases from 10 to 50 N·m. This indicates that the PMSM is highly saturated.

Fig. 2
figure 2

Spatial harmonics of the torque and torque coefficients under different loads: a average torque is 10 N·m, \(i_{d0} = - 6A\), \(i_{q0} = 40A\); b average torque is 25 N·m, \(i_{d0} = - 28A\), \(i_{q0} = 96A\); c average torque is 50 N·m, \(i_{d0} = - 82A\), \(i_{q0} = 193A\)

Full size image

Substituting Eq. (3) into Eq. (2), there is:

$$ \begin{gathered} V_{\theta } [T_{e,12c} ,T_{e,6c} ,T_{e,0} ,T_{e,6s} ,T_{e,12s} ]^{\rm T} \hfill \\ \, = V_{\theta } E_{t} + V_{\theta } E_{td} (i_{d} - i_{d0} ) + V_{\theta } E_{tq} (i_{q} - i_{q0} ). \hfill \\ \end{gathered} $$
(4)

Since the 6th and 12th harmonics of the torque and torque coefficients dominate the harmonic components, the harmonic components above the 12th are ignored here. Therefore, \(V_{\theta } = \left[ {\cos (12\theta ),\cos (6\theta ),1,\sin (6\theta ),\sin (12\theta )} \right]\). Similarly, the dq-axis currents can be expressed as below:

$$ i_{d} \left( \theta \right) = V_{\theta } \left[ {\begin{array}{*{20}c} {i_{d,12c} } \\ {i_{d,6c} } \\ {i_{d,0} } \\ {i_{d,6s} } \\ {i_{d,12s} } \\ \end{array} } \right],i_{q} \left( \theta \right) = V_{\theta } \left[ {\begin{array}{*{20}c} {i_{q,12c} } \\ {i_{q,6c} } \\ {i_{q,0} } \\ {i_{q,6s} } \\ {i_{q,12s} } \\ \end{array} } \right]. $$
(5)

When the base point \((i_{d0} ,i_{q0} )\) of the first-order Taylor expansion is the same as the current set \((i_{d,0} ,i_{{{\text{q}},0}} )\), i.e., \(i_{d0} = i_{d,0} ;i_{q0} = i_{q,0}\), substituting Eq. (5) into Eq. (4) yields:

$$ V_{\theta } \left[ {\begin{array}{*{20}c} {T_{e,12c} } \\ {T_{e,6c} } \\ {T_{e,0} } \\ {T_{e,6s} } \\ {T_{e,12s} } \\ \end{array} } \right] = V_{\theta } E_{t} + V_{\theta } E_{td} V_{\theta } \left[ {\begin{array}{*{20}c} {i_{d,12c} } \\ {i_{d,6c} } \\ 0 \\ {i_{d,6s} } \\ {i_{d,12s} } \\ \end{array} } \right] + V_{\theta } E_{tq} V_{\theta } \left[ {\begin{array}{*{20}c} {i_{q,12c} } \\ {i_{q,6c} } \\ 0 \\ {i_{q,6s} } \\ {i_{q,12s} } \\ \end{array} } \right]. $$
(6)

Assuming \(E_{td} = [e_{td,12c} ,e_{td,6c} ,e_{td,0} ,e_{td,6s} ,e_{td,12s} ]^{\rm T}\), and based on the double angle formula and the harmonic balance method, the harmonics above 12th order were ignored:

$$ \begin{aligned} V_{\theta } E_{td} V_{\theta } \left[ {i_{d,12c} ,i_{d,6c} ,0,i_{d,6s} ,i_{d,12s} } \right]^{\rm T} \hfill \\ \,& = \left[ {e_{td,0} + \sum\limits_{m = 1}^{2} {\left( {e_{td,6mc} \cos (6m\theta ) + e_{td,6ms} \sin (6m\theta )} \right)} } \right] \hfill \\ \, &\times \left[ {\sum\limits_{n = 1}^{2} {\left( {i_{d,6nc} \cos (6n\theta ) + i_{d,6ns} \sin (6n\theta )} \right)} } \right] \hfill \\ \, &= V_{\theta } F_{td} \left[ {i_{d,12c} ,i_{d,6c} ,0,i_{d,6s} ,i_{d,12s} } \right]^{\rm T} , \hfill \\ \end{aligned} $$
(7)

where \(F_{td}\) is the coupling matrix,

$$ \begin{gathered} F_{td} = \hfill \\ \left[ {\begin{array}{*{20}c} {e_{td,0} } & {0.5e_{td,6c} } & {e_{td,12c} } & { - 0.5e_{td,6s} } & 0 \\ {0.5e_{td,6c} } & {e_{td,0} + 0.5e_{td,12c} } & {e_{td,6c} } & {0.5e_{td,12s} } & {0.5e_{td,6s} } \\ {0.5e_{td,12c} } & {0.5e_{td,6c} } & {e_{td,0} } & {0.5e_{td,6s} } & {0.5e_{td,12s} } \\ { - 0.5e_{td,6s} } & {0.5e_{td,12s} } & {e_{td,6s} } & {e_{td,0} - 0.5e_{td,12c} } & {0.5e_{td,6c} } \\ 0 & {0.5e_{td,6s} } & {e_{td,12s} } & {0.5e_{td,6c} } & {e_{td,0} } \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

The main diagonal elements in \(F_{td}\) mean that \(i_{d,0}\) generates \(T_{{\text{e,0}}}\), and \(i_{d,6c}\) generates \(T_{e,6c}\). The harmonic amplitudes of the torque coefficients constitute the non-diagonal elements in \(F_{td}\). The non-diagonal elements mean that \(i_{d,0}\) generates torque harmonics and that \(i_{d,6c}\) generates not only \(T_{e,0}\), but also \(T_{e,6s} ,T_{e,12c} ,T_{e,12s}\).

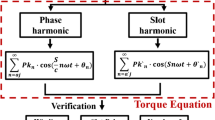
Therefore, the torque harmonic coupling model was obtained as follows:

$$ \left[ {\begin{array}{*{20}c} {T_{e,12c} } \\ {T_{e,6c} } \\ {T_{e,0} } \\ {T_{e,6s} } \\ {T_{e,12s} } \\ \end{array} } \right] = E_{t} + F_{td} \left[ {\begin{array}{*{20}c} {i_{d,12c} } \\ {i_{d,6c} } \\ 0 \\ {i_{d,6s} } \\ {i_{d,12s} } \\ \end{array} } \right] + F_{tq} \left[ {\begin{array}{*{20}c} {i_{q,12c} } \\ {i_{q,6c} } \\ 0 \\ {i_{q,6s} } \\ {i_{q,12s} } \\ \end{array} } \right], $$
(8)

where \(F_{tq}\) is the coupling matrix, which is similar to \(F_{td}\). Equation (8) shows that both the d-axis and the q-axis current harmonics generate torque harmonics. The torque harmonic coupling model illustrates the explicit relationship between the current harmonics and the torque harmonics.

4 Current harmonic selection for torque ripple suppression

For the given current harmonics, the torque harmonics can be calculated through Eq. (8). Conversely, the current harmonics can be calculated for given torque harmonics. Assigning \(T_{{{\text{e}},12c}}\), \(T_{e,6c}\), \(T_{e,6s}\) and \(T_{e,12s}\) zero in Eq. (8):

$$ \left[ {\begin{array}{*{20}c} {T_{e,12c} } \\ {T_{e,6c} } \\ {T_{e,6s} } \\ {T_{e,12s} } \\ \end{array} } \right] = {\rm E}_{t}^{^{\prime}} + F_{td}^{^{\prime}} \left[ {\begin{array}{*{20}c} {i_{d,12c} } \\ {i_{d,6c} } \\ {i_{d,6s} } \\ {i_{d,12s} } \\ \end{array} } \right] + F_{tq}^{^{\prime}} \left[ {\begin{array}{*{20}c} {i_{q,12c} } \\ {i_{q,6c} } \\ {i_{q,6s} } \\ {i_{q,12s} } \\ \end{array} } \right] = 0, $$
(9)

where \(E_{t}^{^{\prime}}\) is the column vector obtained by removing the middle element from \(E_{t}\). \(F_{td}^{^{\prime}} ,F_{tq}^{^{\prime}}\) are the matrices obtained by removing the middle row and the middle column from \(F_{td} ,F_{tq}\). Four equations are not enough to solve eight variables. Thus, there are countless current harmonic selection schemes for torque ripple suppression. Since current harmonics increase the iron loss, to suppress the torque ripple, the current harmonics need to be efficient. The torque is more dependent on the q-axis than the d-axis current (i.e., \(\left| {\frac{{\partial T_{{\text{e}}} }}{{\partial i_{d} }}} \right| < \left| {\frac{{\partial T_{e} }}{{\partial i_{q} }}} \right|\)). Therefore, an efficient method for current harmonic selection was to assign the d-axis current harmonics to zero:

$$ \left[ {\begin{array}{*{20}c} {i_{d,12c} } \\ {i_{d,6c} } \\ {i_{d,6s} } \\ {i_{d,12s} } \\ \end{array} } \right] = 0;\left[ {\begin{array}{*{20}c} {i_{q,12c} } \\ {i_{q,6c} } \\ {i_{q,6s} } \\ {i_{q,12s} } \\ \end{array} } \right] = - \left( {F_{tq}^{^{\prime}} } \right)^{ - 1} E_{t}^{^{\prime}} . $$
(10)

Table 2 shows the current harmonics under different loads calculated from Eq. (10). The current harmonics for torque ripple suppression change with the loads. When the load becomes larger, the torque ripple becomes larger and the q-axis torque coefficient becomes smaller. Correspondingly, the current harmonic amplitude for torque ripple suppression becomes larger. When the electrical load is 10 N·m, \(i_{q,12s}\) dominates. However, when the load is 50 N·m, \(i_{q,12c}\) dominates.

Table 2 q-Axis current harmonics selection
Full size table

5 FEA and experimental verification

5.1 FEA verification

To verify the accuracy of the torque harmonic coupling model and the effectiveness of the current harmonic selection, the currents with and without harmonics shown in Table 2 were used as excitations in the FEA. Figure 3 shows a torque comparison. Results show that the 12th torque ripples were suppressed by more than 95% through the current harmonic injection.

Fig. 3
figure 3

Comparison of torques with and without current harmonics in an FEA and their FFT analyses: a average torque is 10 N·m, \(i_{d0} = - 6A\), \(i_{q0} = 40A\); b average torque is 25 N·m, \(i_{d0} = - 28A\), \(i_{q0} = 96A\); c average torque is 50 N·m, \(i_{d0} = - 82A\), \(i_{q0} = 193A\)

Full size image

To study the effect of current harmonics on system efficiency, the iron loss was analyzed in an FEA. Table 3 shows a comparison of the average iron losses. The iron loss is related to the working frequency. In this simulation, the speed in the FEA was set to 2000 rpm. The data show that the iron loss increased by no more than 5% with the injection of current harmonics.

Table 3 Comparison of average iron losses
Full size table

5.2 Experimental verification

The current harmonic selection was tested by experiments on a laboratory PMSM drive system, which is shown in Fig. 4. The test bench consists of several parts, including the tested motor, high-precision servo motor, reducer, flexible coupling and high-precision torque sensor. The peak torque of the servo motor is 5 N·m. The servo motor is integrated with a reducer. The reduction ratio is 1:5, which can increase the loading torque to 25 N·m. The torque sensor has a measuring range of 0–100 N·m and a resolution of 0.05 N·m. Waveforms of phase current with and without harmonics were compared, as well as waveforms of the torque sensor.

Fig. 4
figure 4

Experimental platform

Full size image

Limited by the bandwidth and tracking static error of the PI controller, a multi-synchronous coordinate algorithm was used for current harmonic injection. The higher the speed, the more noise it brings during torque ripple measurements. Therefore, experiments were completed at 300 rpm. This paper mainly verifies the torque ripple suppression effect of current harmonic selection. As a result, the control algorithm has not been described here.

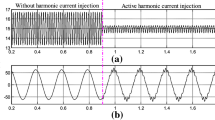
Figures 5, 6 and 7 show the effects of torque ripple suppression by injecting the desired current harmonics under different loads. Limited by the loading torque of the servo motor, the current harmonic injection under a heavy load \((T_{e} = 50N \cdot m)\) could not be implemented. Experiments of current harmonic injection under a medium load \((T_{e} = 17N \cdot m)\) were introduced. Vibration of the mechanical system results in the noise of torque measurement at different frequencies. However, only the motor produces torque ripple of specific frequencies. Therefore, the torque data were decomposed in the frequency domain. The 12th torque ripples were reduced by 78.3%, 60.8% and 67.4%. The average torque measured was less than that in the FEA due to the presence of unmolded mechanical losses. The obtained experimental results show a larger torque ripple than the FEA results. Firstly, the current harmonic injections in the experiments were not accurately achieved. For example, as shown in Fig. 5a, undesired current harmonics occurred during motor current control. Secondly, the vibration caused by inconsistent concentricity brought errors to the measurements. Flexible couplings resulted in resonance in the mechanical system, which also generated measurement errors.

Fig. 5
figure 5

Experimental comparisons with and without current harmonic injection, \(T_{{\text{e}}} = 10N \cdot m\): a waveforms of the phase current; b waveforms of the torque sensor; c FFT analysis of torque sensor waveforms

Full size image
Fig. 6
figure 6

Experimental comparisons with and without current harmonic injection, \(T_{{\text{e}}} = 17N \cdot m\): a waveforms of the phase current; b waveforms of the torque sensor; c FFT analysis of torque sensor waveforms

Full size image
Fig. 7
figure 7

Experimental comparisons with and without current harmonic injection, \(T_{{\text{e}}} = 25N \cdot m\): a waveforms of the phase current; b waveforms of the torque sensor; c FFT analysis of torque sensor waveforms

Full size image

6 Conclusion

This paper established a torque harmonic coupling model and accomplished a current harmonic selection methodology for torque ripple suppression. To verify the model, a torque comparison was accomplished with and without current harmonics through an FEA and experiments. The FEA results show that the torque ripple was suppressed to a great extent. Experimental results show that the 12th torque harmonic, the main torque harmonic component, was suppressed by more than 60% through an injection of current harmonics, which verifies the accuracy of the torque harmonic coupling model and the effectiveness of the current harmonic selection.

The torque harmonic coupling model describes the coupling relationship between the current harmonics and the torque harmonics. In addition to the model, current harmonic selection provided the basis for the active torque ripple suppression of PMSMs. When compared with previous studies on torque ripple suppression, magnetic saturation was fully taken into consideration. However, temperature affects the magnetic permeability of the motor. Therefore, the effect of temperature change on the torque harmonic coupling model requires more research.