Pyrolysis modeling of biomass: study of reaction yields using a single-particle model

Abstract

Pyrolysis has been essential in the context of renewable energies, offering an innovative approach for biomass and solid waste valorization. Therefore, mathematical models that can represent its phenomena are of fundamental importance in understanding the reaction progression and optimizing the process. In this sense, we sought to analyze the capability of single-particle models in representing the yields of pyrolysis reactions in fluidized  beds. To describe the behavior and interaction between the phases, we utilized an Eulerian–Lagrangian CFD modeling approach, solving the continuity, momentum, energy, species, and turbulence equations using OpenFOAM. We adopted the multicomponent and multi-stage model to describe the kinetics of pyrolysis in three different types of biomass. The numerical results obtained for the yields of pyrolysis reactions using the proposed modeling approach showed good agreement with the experimental data reported in the literature. We observed a maximum discrepancy of 3% in the study of pure cellulose reaction, 5.14% in red oak, and 0.56% in sugarcane bagasse. Therefore, we concluded that the single-particle model accurately represents the yields of pyrolysis reactions, making it suitable for estimating yields and conversion rates, providing valuable insights into pyrolysis behavior, and aiding in developing projects and optimization studies.

Introduction

Biomass has received significant attention as a renewable energy source for producing bioenergy and biofuels. These subject addresses various energy and environmental issues (Hameed et al. 2019). Unlike fossil fuels, biomass development does not take millions of years. For instance, plant biomass is derived from the process of photosynthesis, a chemical reaction involving carbon dioxide from the atmosphere, water from the soil, and sunlight at a specific wavelength catalyzed by chlorophyll (McCree 1971; Klass 1998). This process breaks the bonds of CO₂ and water, forming hydrocarbons (C_mH_nO_p), and releases oxygen into the atmosphere. Animal biomass, on the other hand, grows by consuming sources of biomass. As a result, unlike fossil fuels, biomass can be produced, making it a renewable source. This is the main appeal of using them as an energy or chemical resource (Basu 2018).

There are several processes to convert biomass into biofuels. Among the main ones, pyrolysis stands out as one of the most promising technologies for converting biomass into bio-oil, biochar, and gases (Clissold et al. 2020). In this process, biomass is thermally degraded in an inert atmosphere (in the absence of oxygen) and at moderate temperatures. This decomposition can last from a few seconds to several hours (Clissold et al. 2020).

Understanding the complex reaction mechanisms is crucial for improving the pyrolysis process, obtaining high-quality solid, liquid, and gaseous products, and designing industrial-scale reactor projects (Vikram et al. 2021). From an optimization standpoint, developing mathematical models to simulate biomass pyrolysis is becoming increasingly important (Hameed et al. 2019). During pyrolysis, the particle undergoes numerous intricate reactions with the reagents to release volatiles, which is very complex to model. Therefore, a comprehensive overview of theoretical approaches and simulation methods for modeling pyrolysis of lignocellulosic constituents, from the atomic/molecular level to the reactor level, is conducted to understand the kinetics of intraparticle and external diffusion rates (Vikram et al. 2021). Previous studies (Sheth and Babu 2006; Várhegyi et al. 1997; Ranzi et al. 2008; Vinu and Broadbelt 2012) have reported the understanding of fundamental reaction mechanisms and kinetics of biomass pyrolysis, ranging from simple single-step kinetic models to complex reaction models that include hundreds of reactions. Pyrolysis modeling of biomass generally considers the reactions of its three main components: cellulose, hemicellulose, and lignin. Models often simulate the reactions of each component individually so that biomass is modeled as the superposition of these components without considering potential interactions between them. At the reactor scale, attempts have also been made to couple the chemical reaction kinetics with intra and inter-particle heat transfer effects to simulate the pyrolysis of cellulose particles in a fluidized bed reactor (Blasi 2000).

A good understanding of the chemical and physical phenomena involved in biomass degradation within the reactor is necessary for process development, optimization, and scale-up. Due to the lack of fundamental knowledge of the system’s fluid and thermal behavior, process design has necessarily been based on empirical correlations and experiments carried out in laboratory scale or pilot-scale units. However, with the rapid advancement of Computational Fluid Dynamics (CFD) methods, detailed CFD models for the system should allow for the design and optimization of processes, minimizing the need for expensive and time-consuming experimental tests. Heat and mass transport models resolved by CFD are paramount in developing sophisticated particle scale models that incorporate the effect of reaction kinetics, extra particle transport, and particle size distribution. Coupling particle-scale models with reactor-scale models can provide a detailed analysis of bed hydrodynamics (Xue et al. 2011).

Most literature reports regarding Computational Fluid Dynamics (CFD) studies are centered on applying biomass pyrolysis in fluidized bed reactor (Hooshdaran et al. 2021). In the studies conducted by Papadikis et al. (b, c, 2010, 2012, 2009a), the effects of sphericity, drag, and particle size on heat transfer, momentum, mass, and chemical species were simulated in fluidized beds. Ferreira et al. (2023) employed an experimental design to assess the influence of temperature, velocity, and particle diameter on the yield of wood pyrolysis reaction using a semi-global, two-stage kinetic model. Hu et al. (2019) employed CFD-DEM to model fast pyrolysis reactions, investigating the effects of shrinkage and gas superficial velocity. Park and Choi (2019) analyzed the influence of reaction temperature and gas velocity on hydrodynamics, heat transfer, and pyrolysis reactions. Meanwhile, Yang et al. (2021) employed the Euler–Lagrange approach's MP-PIC method to model a three-dimensional bubbling fluidized bed reactor, aiming to study bubbles' physical and thermal dynamics at high temperatures.

The main objective of this study is to investigate the effectiveness of a CFD model in a pyrolysis reaction applied to a single particle with multi-component and multistage kinetics to achieve a precise understanding of the reaction progress and calculate pyrolysis yields and conversion. In order to achieve this objective, simulations were conducted using three different types of biomasses, constantly comparing the results with experimental data previously reported in the literature. This approach will allow the evaluation of the model’s ability to reproduce experimental results and provide valuable insights into pyrolysis behavior under the studied conditions.

Mathematical modeling

Four equations describe the gas phase in compressible dense gas–solid reactive flow: the continuity equation, the momentum equations, the energy equation, and the species equation. As we will see next, there is a term that represents the volumetric gas fraction (${\upalpha }_{\text{g}}$) and is calculated by:

$${\upalpha }_{\text{g}} = 1 - {\upalpha }_{\text{p}}$$

(1)

where ${\upalpha }_{\text{p}}$ is the volumetric fraction of the solid phase, given by:

$${\upalpha }_{\text{g}} = \frac{1}{{{\text{V}}_{{\text{elem}}} }} \sum\limits_{{\text{i}}= 1}^{\text{n}}\, {\text{W}}_{{\text{p,i}}} {\text{V}}_{{\text{p,i}}}$$

(2)

${\text{W}}_{{\text{p,i}}}$ is the portion of the particle volume occupied in the current mesh element, where ${\text{V}}_{{\text{p,i}}}$ is the particle volume and ${\text{V}}_{{\text{elem}}}$ is the mesh element volume.

The modeling of particles was carried out using the discrete particle model (DPM) coupled with the soft-sphere model. The Discrete Particle Model (DPM) approach describes the motion and collisions of particles. In this work, we used the soft-sphere model to represent wall-particle collisions. This approach assumes particles undergo a small deformation during contact with other particles or walls. This deformation is calculated using a simple analogy involving a mechanical spring, a potentiometer, and a slider. The equations that model both phases will be presented below.

Gas phase

The continuity equation of gas phase can be formulated as:

$$\frac{{\partial \left( {{\upalpha }_{\text{g}} {\uprho }_{\text{g}} } \right)}}{{\partial {\text{t}}}} + \nabla \cdot \left( {{\upalpha }_{\text{g}} {\uprho }_{\text{g}} {{\mathbf{u}}}_{\text{g}} } \right) = {\updelta} \dot{\text{m}}_{\text{s}}$$

(3)

where ${\upalpha }_{\text{g}}$, ${\uprho }_{\text{g}}$, and ${{\mathbf{u}}}_{\text{g}}$ are the volume fraction, density, and velocity, respectively. ${\updelta}\dot{\text{m}}_{\text{s}}$ represents the source term that models the chemical reactions between phases.

The term ${\updelta\dot{\text{m}}}_{\text{s}}$ in Eq. (3) represents the rate of mass consumption or generation caused by the interaction between the gas phase and the particulate phase, calculated by:

$${\updelta\dot{\text{m}}}_{\text{s}} =\frac{1}{{{\text{V}}_{{\text{elem}}} }} \sum \limits_{{\text{i}} = 0}^{{\text{N}}_{\text{p}} }\, {\text{W}}_{{\text{p,i}}} {\upchi }_{{\text{t,i}}}$$

(4)

${\upchi }_{{\text{t,i}}}$ are all the mass transfer terms between the gas phase and particulate phase that are acting on particle i.

The momentum equation of gas phase can be written as:

$$\frac{{\partial \left( {{\upalpha }_{\text{g}} {\uprho }_{\text{g}} {{\mathbf{u}}}_{\text{g}} } \right)}}{{\partial {\text{t}}}} + \nabla \cdot \left( {{\upalpha }_{\text{g}} {\uprho }_{\text{g}} {{\mathbf{u}}}_{\text{g}} {{\mathbf{u}}}_{\text{g}} } \right) = - {\upalpha }_{\text{g}} \nabla {\text{p}}_{\text{g}} + {\uprho }_{\text{g}} {\upalpha }_{\text{g}} {{\mathbf{g}}} + \nabla \cdot \left( {{\upalpha }_{\text{g}} {{\varvec{\tau}}}_{\text{g}} } \right) + {{\mathbf{F}}}_{{\text{gs}}}$$

(5)

where ${\text{p}}_{\text{g}}$ and ${{\mathbf{g}}}$ are the gas pressure and gravitational acceleration terms, respectively. The term ${{\varvec{\tau}}}_{\text{g}}$ represents the stress tensor calculated by:

$${{\varvec{\tau}}}_{\text{g}} = \left( {{\upmu }_{\text{l}} + {\upmu }_{\text{t}} } \right)\left( {\nabla {{\mathbf{u}}} + \left( {\nabla {{\mathbf{u}}}} \right)^{\text{T}} } \right) - \frac{2}{3}\left( {{\upmu }_{\text{l}} + {\upmu }_{\text{t}} } \right)\left( {\nabla \cdot {{\mathbf{u}}}} \right){{\varvec{I}}}$$

(6)

where ${\upmu }_{\text{l}}$ and ${\upmu }_{\text{t}}$ are the laminar and turbulent viscosity, respectively. The turbulent viscosity is calculated using the Smagorinsky (1963) model, which for large turbulent structures are solved directly while small ones are modeled by:

$${\upmu }_{\text{t}} = {\text{C}}{\uprho}_{\text{g}} {\Delta }^2 \sqrt {{\left( {\frac{{\partial {\text{u}}_{\text{i}} }}{{\partial {\text{x}}_{\text{j}} }} + \frac{{\partial {\text{u}}_{\text{j}} }}{{\partial {\text{x}}_{\text{i}} }}} \right)^2 }}$$

(7)

where ${\Delta }$ is the characteristic length, equal to the cube root of the volume of the element, ${\Delta } = (\Delta{\text{x}}\Delta{\text{y}}\Delta{\text{z}})^{1/3}$. C is the Smagorinsky constant, given as 0.01. The term ${{\mathbf{F}}}_{{\text{gs}}}$ in Eq. (5) represents the exchange of momentum between the solid and gas phases and can be calculated by:

$${{\mathbf{F}}}_{{\text{gs}}} = \frac{1}{{{\text{V}}_{{\text{elem}}} }} \sum \limits_{{\text{i}} = 0}^{{\text{N}}_{\text{p}} }\, {\text{W}}_{{\text{p,i}}} {{\mathbf{f}}}_{{\text{t,i}}}$$

(8)

where ${{\mathbf{f}}}_{{\text{t,i}}}$ are all the fluid-particle interaction forces acting on particle i.

The energy equation of gas phase in term of enthalpy can be written as:

$$\frac{{\partial \left( {\upalpha _{\text{g}} \uprho _{\text{g}} {\mkern 1mu} {\text{h}}_{\text{g}} } \right)}}{{\partial {\text{t}}}} + \nabla \cdot \left( {\upalpha _{\text{g}} \uprho _{\text{g}} {\mathbf{u}}_{\text{g}}{\mkern 1mu} {\text{h}}_{\text{g}} } \right) = \upalpha _{\text{g}} \left( {\frac{{\partial {\text{p}}_{\text{g}} }}{{\partial {\text{t}}}} + {\mathbf{u}}_{\text{g}} \cdot \nabla {\text{p}}_{\text{g}} } \right) - \nabla \cdot \left( {\upalpha _{\text{g}} {\mkern 1mu} {\text{q}}} \right) + {\dot{\text{Q}}}_{\text{D}} + {\text{Q}}_{{\text{gs}}} + {\text{Q}}_{{\text{gw}}} - \Delta {\text{H}}_{{\text{rg}}} + {\text{Q}}_{{\text{rad}}}$$

(9)

where ${\text{h}}_{\text{g}}$ and ${\Delta}{\text{H}}_{{\text{rg}}}$ are the enthalpy and heat of chemical reaction, respectively. The enthalpy is calculated by adding the enthalpy of each species (${\text{h}}_{\text{g}}$):

$${\text{h}}_{\text{g}} = \mathop \sum \limits_{{\text{k}} = 1}^{{\text{N}}_{\text{k}}}\, {\text{h}}_{\text{g}}^{\text{k}}\, {\text{Y}}_{\text{g}}^{\text{k}} = \mathop \sum \limits_{{\text{k}} = 1}^{{\text{N}}_{\text{k}}}\, {\text{Y}}_{\text{g}}^{\text{k}} \left({\mathop \int\nolimits_{{\text{T}}_0 }^{{\text{T}}_{\text{g}} }\, {\text{C}}_{\text{p}}^{\text{k}}\, {\text{dT}} + {\Delta}{\text{h}}_{\text{g}}^{\text{k}} } \right)$$

(10)

where ${\text{N}}_{\text{k}}$ is the number of chemical species present in the gaseous phase. ${\text{T}}_0$, ${\text{T}}_{\text{g}}$, ${\text{C}}_{\text{p}}^{\text{k}}$ and $\Delta{\text{h}}_{\text{g}}^{\text{k}}$ are respectively the reference temperature, the gas phase temperature, the specific heat of the species k and the heat of reaction. ${\text{Q}}_{{\text{gs}}}$ and ${\text{Q}}_{{\text{gw}}}$ represent the heat transfer terms between gas–solid and gas-wall, respectively. The convective heat transfer between the wall and the gas phase (${\text{Q}}_{{\text{gw}}}$) is calculated by:

$${\text{Q}}_{{\text{gw}}} = {\text{h}}_{{\text{gw}}}\, {\text{A}}_{{\text{gw}}}\, ({\text{T}}_{\text{w}} - {\text{T}}_{\text{g}} )$$

(11)

where ${\text{T}}_{\text{w}}$ and ${\text{A}}_{{\text{gw}}}$ are the temperature and surface area of the wall, respectively. The convection heat transfer coefficient ${\text{h}}_{{\text{gw}}}$ is calculated by:

$${\text{h}}_{{\text{gw}}} = \frac{{{\text{N}}_{\text{u}} {\uplambda }_{\text{g}} }}{{\text{L}}}$$

(12)

where ${\text{N}}_{\text{u}}$ is the Nusselt number, and L is the characteristic length. ${\dot{\text{Q}}}_{\text{D}}$ is the enthalpic diffusion calculated by:

$${\dot{\text{Q}}}_{\text{D}} = \mathop \sum \limits_{{\text{k}} = 1}^{{\text{N}}_{\text{k}} } \nabla \cdot \left( {{\upalpha }_{\text{g}}\, {\text{h}}_{\text{g}}^{\text{k}} {\uprho }_{\text{g}}\, {\text{D}}_{{\text{if, g}}}^{\text{k}} \nabla {\text{Y}}_{\text{g}}^{\text{k}} } \right)$$

(13)

The heat flux q is calculated by:

$${\text{q}} = {\uplambda }_{\text{g}} \nabla {\text{T}}_{\text{g}}$$

(14)

where the term ${\uplambda }_{\text{g}}$ is the thermal conductivity of the gas phase and includes the molecular (or laminar) ${\uplambda }_{\text{l}}$ and turbulent (${\uplambda }_{\text{t}}$) conductivity terms. ${\uplambda }_{\text{g}}$ is calculated by:

$${\uplambda }_{\text{g}} = \frac{{{\text{C}}_{\text{p}} {\upmu }_{\text{t}} }}{{{\text{Pr}}_{\text{t}} }}$$

(15)

where ${\text{Pr}}_{\text{t}}$ is the Prandtl turbulent number. The term ${\text{Q}}_{{\text{gs}}}$ in Eq. (9) represents the heat exchange between the gas phase and the solid phase, calculated by:

$${\text{Q}}_{{\text{gs}}} = \frac{1}{{{\text{V}}_{{\text{elem}}} }} \sum \limits_{{\text{i}} = 0}^{{\text{N}}_{\text{p}} }\, {\text{W}}_{{\text{p,i}}}\, {\text{Q}}_{{\text{t,i}}}$$

(16)

where ${\text{Q}}_{{\text{t,i}}}$ represents all the heat transfer terms between the gas phase and the particulate phase that are acting on particle i.

The transportation equation of gas species can be formulated as:

$$\frac{{\partial ({\upalpha }_{\text{g}} {\uprho }_{\text{g}}\, {\text{Y}}_{\text{g}}^{\text{k}} )}}{{\partial {\text{t}}}} + \nabla \cdot \left( {{\upalpha }_{\text{g}} {\uprho }_{\text{g}} {{\mathbf{u}}}_{\text{g}}\, {\text{Y}}_{\text{g}}^{\text{k}} } \right) = { }\nabla \left( {{\upalpha }_{\text{g}} {\uprho }_{\text{g}}\, {\text{D}}_{{\text{if, g}}}^{\text{k}} \nabla {\text{Y}}_{\text{g}}^{\text{k}} } \right) + { \dot{\text{m}}}_{{\text{react,g}}}^{\text{k}} + {\dot{\text{m}}}_{{\text{react,gs}}}^{\text{k}}$$

(17)

This equation is solved based on the chemical species k, and each computational element is summed to obtain the species change of the gaseous mixture. ${\text{D}}_{{\text{if, g}}}^{\text{k}}$ is the turbulent mass diffusivity calculated by:

$${\text{D}}_{{\text{if, g}}}^{\text{k}} = \frac{{{\upmu }_{\text{g}} }}{{{\uprho }_{\text{g}}\, {\text{S}}_{\text{c}} }}$$

(18)

where ${\upmu }_{\text{g}}$ is the viscosity of the gas and ${\text{S}}_{\text{c}}$ is the Schmidt number, which for this work was considered 0.9. ${\dot{\text{m}}}_{{\text{react, g}}}^{\text{k}}$ models the chemical reactions of the gas phase for each chemical species. This term is calculated by:

$${\dot{\text{m}}}_{{\text{react, g}}}^{\text{k}} = {\text{ k}}_{\text{i}}\, {\text{C}}_{\text{i}}$$

(19)

where ${\text{k}}_{\text{i}}$ and ${\text{C}}_{\text{i}}$ are the reaction rate constant and the concentration of component i, respectively. The reaction rate constant will be detailed in "Kinetics" section.

The term ${\dot{\text{m}}}_{{\text{react, gs}}}^{\text{k}}$ in Eq. (17) represents the rate of consumption or generation of species k caused by the interaction between the gas phase and the particulate phase, calculated by:

$${\dot{\text{m}}}_{{\text{react, gs}}}^{\text{k}} =\frac{1}{{{\text{V}}_{{\text{elem}}} }} \sum \limits_{{\text{i}} = 0}^{{\text{N}}_{\text{p}} }\, {\text{W}}_{{\text{p,i}}} {\upchi }_{{\text{t,i}}}^{\text{k}}$$

(20)

${\upchi }_{{\text{t,i}}}^{\text{k}}$ represents all the chemical species transfer terms between the gas phase and the particulate phase that are acting on particle i.

Solid phase

The motion of the particle i of mass ${\text{m}}_{\text{i}}$ and volume ${\text{V}}_{\text{i}}$ in a system is calculated according to Newton's second law of motion given by:

$${\text{m}}_{\text{i}} \frac{{{\text{d}}{{\mathbf{u}}}_{{\text{s, i}}} }}{{{\text{dt}}}} = {\text{m}}_{\text{i}} \frac{{{\text{d}}^2 {{\varvec{\xi}}}_{\text{i}} }}{{{\text{dt}}^2 }} = {\text{ f}}_{\text{i}}^{{\text{g}} - {\text{s}}} + {\text{f}}_{\text{i}}^{{\text{s}} - {\text{w}}} + {\text{f}}_{\text{i}}^{{\text{grav}}}$$

(21)

where ${{\mathbf{u}}}_{{\text{s, i}}}$ is the velocity, ${{\varvec{\xi}}}_{\text{i}}$ is the position of particle i, ${\text{f}}_{\text{i}}^{{\text{g}} - {\text{s}}}$ represents the forces acting on the particles due to interaction with fluids, ${\text{f}}_{\text{i}}^{{\text{grav}}}$ is gravity force on particle i and ${\text{f}}_{\text{i}}^{{\text{s}} - {\text{w}}}$ is the particle–wall collision term.

The angular momentum of a given particle i is calculated by:

$${{\mathbf{I}}}_{{\mathbf{i}}} \frac{{{\text{d}}{\upomega}}_{\text{i}}}{{\text{dt}}} = {{\mathbf{M}}}_{\text{i}}^{{\text{g}}-{\text{s}}}$$

(22)

${{\mathbf{M}}}_{\text{i}}^{{\text{g}}-{\text{s}}}$ is the torque caused by the fluid-particle effect. ${\mathbf{I}}_{\mathbf{i}}$ is the moment of inertia, which for a spherical particle of radius ${\text{r}}_{\mathbf{i}}$ is calculated by ${\mathbf{I}}_{\mathbf{i}} = \frac{2}{5}{\text{m}}_{\text{i}}\, {\text{r}}_{\text{i}}^2$.

Each particle assumes to have a uniform temperature, and thus the conservation of energy of particle i in a system is calculated by:

$${\text{m}}_{\text{i}}\, {\text{c}}_{{\text{p,i}}} \frac{{{\text{dT}}_{\text{i}} }}{{{\text{dt}}}} = {\text{Q}}_{{\text{gs}}} + {\text{Q}}_{{\text{rad}}} + {\Delta}{\text{H}}_{{\text{rs}}}$$

(23)

where ${\text{c}}_{{\text{p,i}}}$ and ${\text{T}}_{\text{i}}$ is the heat capacity and temperature of particle i, ${\text{Q}}_{{\text{gs}}}$ is the net heat by the interaction between the gas phase and the particle phase, calculated by:

$${\text{Q}}_{{\text{gs}}} =\frac{{{\uplambda }_{\text{g}}\, {\text{Nu}}_{\text{i}} }}{{{\text{d}}_{\text{s}} }}\,{\text{A}}_{\text{i}} \left( {{\text{T}}_{\text{g}} - {\text{T}}_{\text{s}} } \right)$$

(24)

where ${\text{d}}_{\text{s}}$ and ${\text{A}}_{\text{i}}$ is the diameter and surface area of the particle. ${\text{Nu}}_{\text{i}}$ is the Nusselt number of the particle calculated by:

$${\text{Nu}}_{\text{i}} = 2 + 0.6{\text{Re}}_{\text{s}}^{0.5} {\text{P}}_{\text{r}}^{0.33}$$

(25)

where ${\text{P}}_{\text{r}}$ and ${\text{Re}}_{\text{s}}$ are the particle's Prandtl numbers and Reynolds numbers, respectively. ${\Delta}{\text{H}}_{{\text{rs}}}$ is the heat of reaction of the solid phase, and ${\text{Q}}_{{\text{rad}}}$ is the effect of radiation on the particle, calculated by:

$${\text{Q}}_{{\text{rad}}} = {{\upsigma \upvarepsilon }}_{\text{s}}\,{\text{A}}_{\text{s}} \left( {{\text{T}}_{{\text{b, local}}}^4 - {\text{T}}_{\text{s}}^4 } \right)$$

(26)

where ${\upsigma }$ and ${\upvarepsilon }_{\text{s}}$ are the Stefan-Boltzmann constant and the emissivity of the particle.

The following equation calculates the mass of each particle i in a system:

$$\frac{{\text{dm}}_{\text{i}}}{{\text{dt}}} =\sum{\Omega }_{\text{i}}$$

(27)

${\Omega }_{\text{i}}$ represents the mass source term that can increase or decrease due to the chemical reaction of the solid phase.

The following equation calculates the composition of each particle i present in a system:

$$\frac{{{\text{d}}({\text{m}}_{\text{i}}\, {\text{Y}}_{{\text{i, k}}} )}}{{{\text{dt}}}} = \sum{\Omega }_{{\text{i, k}}}$$

(28)

${\Omega }_{{\text{i, k}}}$ represents the source term of the chemical species present in the particles that can increase or decrease due to a chemical reaction.

Gas-particle interaction

The drag model is vital in describing a gas-particle system, representing the momentum exchange between phases. The drag force of a single particle i is given by:

$${{\mathbf{f}}}_{\text{i}}^{{\text{g}} - {\text{s}}} = { }{{\mathbf{f}}}_{{\text{D, i}}} = { }\frac{{{\text{V}}_{\text{p}} {\Lambda }_{\text{p}} }}{{1 - {\upalpha }_{\text{g}} }}({{\mathbf{u}}}_{\text{g}} - {{\mathbf{u}}}_{{\text{s, i}}} )$$

(29)

The Gidaspow drag model combines the Ergun correlation applicable for dense systems (Ergun and Orning 1949) with the Wen-Yu correlation used for dilute systems (Yang et al. 2021) is appropriate for most gas–solid modeling. The Gidaspow model is written as follows:

$${\Lambda }_{\text{p}} = \left\{ \begin{array}{*{20}l}\frac{{150(1 - {\upalpha }_{\text{g}} )^2 {\upmu }_{\text{g}}}}{{{\upalpha }_{\text{g}}\, {\text{d}}_{\text{p}}^2 }} +\frac{{1.75{\uprho }_{\text{g}} \left( {1 - {\upalpha }_{\text{g}} }\right)|{{\mathbf{u}}}_{\text{g}} - {{\mathbf{u}}}_{{\text{s, i}}}|}}{{{\text{d}}_{\text{p}} }}, \hfill & {{\upalpha }_{\text{g}} \le0.8} \hfill \\ \frac{3}{4}\frac{{{\upalpha }_{\text{g}} {\uprho}_{\text{g}} \left( {1 - {\upalpha }_{\text{g}} }\right)|{{\mathbf{u}}}_{\text{g}} - {{\mathbf{u}}}_{{\text{s, i}}}|}}{{{\text{d}}_{\text{p}} }}\,{\text{C}}_{\text{D}} {\upalpha}_{\text{g}}^{ - 2.65}, \hfill & {{\upalpha }_{\text{g}} > 0.8}\hfill \\ \end{array} \right.$$

(30)

where

$${\text{C}}_{\text{D}} = \left\{ {\begin{array}{*{20}l} {\frac{24}{{{\text{Re}}_{\text{s}} }}\left( {1 + 0.15{\text{Re}}_{\text{s}}^{0.687} } \right),} \hfill & {{\text{Re}}_{\text{s}} < 1000} \hfill \\ {0.44,} \hfill & {{\text{Re}}_{\text{s}} \ge 1000} \hfill \\ \end{array} } \right.$$

(31)

and

$${\text{Re}}_{\text{s}} = { }\frac{{{\uprho }_{\text{g}} {\upalpha }_{\text{g}} |{{\mathbf{u}}}_{\text{g}} - {{\mathbf{u}}}_{{\text{s, i}}} |{\text{d}}_{\text{p}} }}{{{\upmu }_{\text{g}} }}$$

(32)

The force of gravity acting on the particle is given by:

$${\text{f}}_{\text{i}}^{{\text{grav}}} = \frac{{{{\mathbf{g}}}({\uprho }_{\text{g}} - {\uprho }_{\text{s}} )}}{{{\uprho }_{\text{g}} }}$$

(33)

where ${\uprho }_{\text{s}}$ is the density of particle i and ${{\mathbf{g}}}$ is the gravity acceleration.

Kinetics

The fast pyrolysis of biomass, which occurs in reactors, involves many elementary reactions (Bashir et al. 2017; Lee et al. 2017). As a result, biomass tar produces several chemical products, such as organic acid compounds, ketones, and phenols. In addition, some synthesis gas hydrocarbons were found in the gas compounds such as CH₄, CO₂, CO, H₂ and other synthesis gas hydrocarbons (Maduskar et al. 2018). However, the detailed kinetics of the reaction and the fundamental mechanisms of decomposition are still being studied, as these are complex chemical reactions, and the information on intermediate species is still unclear (Yang et al. 2021).

In CFD studies, chemical reactions are reduced to a set of main reactions that describes the pyrolysis process. Global devolatilization schemes derived from thermogravimetric analysis (TGA) experiments are often used to obtain these kinetic models, enabling studies of rapid biomass pyrolysis simulation (Xiong et al. 2014).

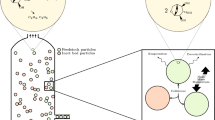
Figure 1 presents the multicomponent and multistage kinetics used in this work. This mechanism was proposed by Koufopanos et al. (1989), Di Blasi (1994), Ward and Braslaw (1985) and Miller and Bellan (1997) and has already been used, showing satisfactory results (Clissold et al. 2020; Park and Choi 2019).

Fig. 1

Multi-component and multi-stage reaction mechanism

This model correlates the pyrolysis rate of biomass with its composition, as shown below:

$$Biomass = {\Upsilon }_1 Cellulose + {\Upsilon }_2 Hemicellulose + {\Upsilon }_3 Lignin$$

(34)

In this model, the biomass reaction rate is considered the sum of the reaction rates of its main components: cellulose, hemicellulose, and lignin. Therefore, each component’s weight contributes to the forming of the virgin biomass (Xue et al. 2012). This assumption assumes that potential interactions between biomass components have a negligible effect on the course of pyrolysis. Thus, any biomass feedstock can be modeled based on the initial knowledge of cellulose, hemicellulose, and lignin composition.

As shown in Fig. 1, the products are grouped into char, gas, and tar. Y represents the formation ratio for the biochar component. Arrhenius’ law is used to calculate the rate of the chemical reaction and can be formulated as follows:

$$\psi_{\text{i}} = {\upgamma }_{\text{i}} \exp \left( {\frac{{ - {\text{E}}_{\text{i}} }}{{{\text{RT}}}}} \right)$$

(35)

where R is the universal gas constant, ${\upgamma }_{\text{i}}$ is the pre-exponential factor and ${\text{E}}_{\text{i}}$ is the activation energy. Table 1 details the kinetic parameters of the reaction.

Table 1 Arrhenius parameters for the multicomponent scheme

According to Di Blasi (1994), Koufopanos et al. (1989), and Curtis and Miller (1988), the enthalpies of reactions were obtained from measurements performed only for cellulose; however, these values are also used for the calculation of hemicellulose and lignin. Di Blasi (1994) states that the first reaction $\left( {\psi_1 } \right)$ of the virgin biomass for the active components has a tiny heat release, which can be neglected. Koufopanos et al. (1991) report that the tar formation reaction $\left( {\psi_2 } \right)$ is endothermic. Both the formation of char and gas $\left( {\psi_3 } \right)$ and the secondary cracking of bio-oil vapor $\left( {\psi_4 } \right)$ are exothermic.

Simulation setups

The present work was based on a study conducted by Xue et al. (2012), who experimentally studied the pyrolysis of pure cellulose and red oak in a bubbling fluidized reactor. In order to speed up simulations without compromising the quality of the results, it was decided to simplify the geometry of Xue et al. (2012) to a pseudo-2D format with a thickness of 7 mm. This simplification was inspired by the work of Li et al. (2012), where they concluded that the fluidized reactor thickness should be at least 12.3 times the particle size to neglect the wall effect and ensure it does not influence particle behavior. This consideration was validated by Hu et al. (2019) and Xu et al. (2016).

The accuracy of a CFD solution is directly influenced by the number of elements in the mesh. Generally, a higher number of elements leads to better simulation accuracy. However, increasing mesh refinement also results in higher computational processing costs and longer calculation times (Verteeg and Malalasekera 2017). Therefore, it is recommended to perform a mesh dependency analysis for CFD studies. This involves simulating the study with various mesh element sizes to determine the minimum number of elements required to obtain accurate results while minimizing computational costs. However, in CFD simulations employing the Eulerian–Lagrangian approach solved by the Discrete Phase Model (DPM) method, there is a particular consideration to be taken into account. The mesh element size is limited by the particle size, which must be sufficiently small to achieve accuracy and, at the same time, large enough to ensure a proper temporal and spatial variation of the solid particle fractions (Hu et al. 2019). It is common to follow recommendations from previous studies (Hu et al. 2019).

Based on the information presented, the findings of Peng et al. (2014) suggest that the ratio between element size (S_c) and particle size (d_p) should be greater than 1.6 to ensure accurate predictions. Clarke et al. (2018) also observed that ratios (S_c/d_p) below 1.6 resulted in poor predictions for particulate flow. Additionally, Boyce et al. (2014) ) recommended a ratio (S_c/d_p) around 3–4 for achieving the best agreement between experimental and numerical data in fluidized bed problems. Therefore, in this study, we followed these recommendations and used a ratio (S_c/d_p) of 3. Consequently, the computational mesh was composed of 20 × 4 × 176 elements in the x, y, and z directions. The study domain and the computational mesh are illustrated in Fig. 2.

Fig. 2

Fluidised bed geometry and mesh

The models presented in this work were implemented in OpenFOAM-v2012, an open-source program. Taking advantage of this characteristic, the reactingParcelFoam solver was modified, which is used to solve transient problems with compressible, turbulent flow, chemical reaction, and multiphase. The code was modified to include the DPM model, considering the volumetric fraction effects of the particles in the continuous phase and the collisions of particles/particles and particles/walls. Subsequently, the sub-models of the kinetics of heterogeneous pyrolysis reactions were implemented in the software’s source code.

This study performed three simulations, each with a different biomass particle: pure cellulose, red oak, and sugarcane bagasse. The compositions of each biomass are presented in Table 2.

Table 2 Composition of the studied biomasses

In the simulations, a single biomass particle was considered and inserted at the reactor’s center at the height of 0.01905 m, with a velocity of 0 m/s and a temperature of 303 K. The inlet flow consisted only of nitrogen, which entered the reactor from the base at a temperature of 773 K and a fixed velocity. The velocity value was adjusted for each scenario based on the gas phase residence time obtained from experiments reported in the literature. The reactor outlet was set at atmospheric pressure, and the walls were assumed to be non-slip and adiabatic. Initially, the reactor was filled with stagnant N₂ at a temperature of 303 K.

The particle has a thermal conductivity and specific heat proportionally calculated based on the solid mass fraction (cellulose, hemicellulose, lignin, and char). As the particle is heated, the biomass undergoes degradation into active cellulose, active hemicellulose, and active lignin, and then these activated compounds generate char, tar, and gas. The properties of N₂, pyrolysis gases, and biomass are shown in Table 3.

Table 3 Simulation parameters

The equations were solved using the finite volume method (FVM). In this approach, the transient term was discretized using the second-order Crank-Nicolson scheme, while the convection and diffusion terms were discretized using the Upwind and Gauss linear schemes, respectively. These discretization schemes were chosen because they demonstrated numerical stability in solving the linear matrix.

The result of the discretization is a set of algebraic equations constructed in the form A[ϕ] = b. The coefficients of the unknown variables in matrix A are obtained through the linearization procedure of the information within the computational mesh. Vector b contains all the source terms, including constants, boundary conditions, and non-linearizable components. The techniques for solving this algebraic system are not dependent on the specific discretization method employed. In this study, the GAMG (Greenshields and Weller 2022) method was used for solving the pressure field, the smoothSolver (Greenshields and Weller 2022) for the velocity field, and the PBiCGStab (Van der Vorst 1992; Barrett et al. 1994) for the other fields.

To calculate the velocity and pressure fields, Eq. (3) needs to be coupled with Eq. (5). This coupling is achieved using a pressure velocity coupling algorithm. In this work, a hybrid algorithm based on PISO and SIMPLE, called PIMPLE, was adopted, following the recommendation of Xiong et al. (2013). According to the authors, this algorithm allows for relatively large time steps while maintaining numerical stability and avoids pressure checkerboarding.

Each case is simulated for a physical time of 4 s, with a varied time step and a Courant number fixed at 0.5. The simulations were performed on a computer with an Intel core i9-12900k processor and 32 Gb of RAM, taking 0.5 h to be completed, using four processing cores.

Results

Pure cellulose

The pyrolysis of a single particle of pure cellulose was simulated, by implementing the boundary conditions used in the experiment conducted by Xue et al. (2012). The result of the reaction yields for the formation of tar, gas, char, and unreacted biomass are presented in Fig. 3. It also includes the results of the experimental work by Xue et al. (2012) and the simulations performed by Xue et al. (2012) and Yang et al. (2021).

Fig. 3

Yield of pure cellulose pyrolysis

When comparing the results obtained to those reported in the literature, it is clear that the yields found in the simulation are within the same magnitude range. However, the tar yield is slightly higher than in the experiment, while the gas yield is slightly lower. Table 4 was constructed to analyze the deviations in the results quantitatively.

Table 4 Yield values of the pyrolysis reaction for pure cellulose

When analyzing Table 4, it can be observed that the results obtained by the proposed model show some approximation to the results reported by Xue et al. (2012) and Yang et al. (2021). The difference observed in the tar vapor yield is approximately 7.17%, which is higher than expected, while the gas yield is 3.61% lower than the experimental value. The char yield is the closest, showing a difference of only 0.26%.

The discrepancies between the simulation and the experiment may be caused by the effect of the inert particle bed considered in the experiment but not adopted in the simulation of pure cellulose, where only a single biomass particle was considered. The presence of this bed reduces the velocity of nitrogen, causing the tar to remain in the reactor for a longer time, favoring gas formation. Additionally, a lower gas velocity reduces the convective heat transfer over the biomass particles. To examine this theory, the gas phase residence time in the reactor was calculated for the present work and the work of Xue et al. (2012) using Eq. (36).

$$\varrho_g = \frac{H}{{\overline{u}_g }}$$

(36)

where $\overline{u}_g$ is the average velocity of the gas phase in the bed, and H is the height of the reactor.

The results of the gas phase residence time are presented in Table 5.

Table 5 Residence time of pure cellulose and the work by Xue et al. (2012)

It can be observed from Table 5 that the gas phase residence time in Xue et al.’s work (2012) is nearly twice that of the pure cellulose simulation, resulting in the tar vapor staying in the reactor for almost one second longer, favoring the secondary reaction of gas production from tar vapor. The difference between the two cases is that Xue et al. (2012)’s experiment involves a bed of particles. In this experiment, when gas enters the bed with a velocity of 0.36 m/s, it decelerates due to the resistance provided by the inert particles, resulting in an average velocity of 0.18 m/s after passing through this region. In contrast, in the simulation conducted in this work, there is only one particle, which does not offer resistance to gas flow and does not reduce the velocity from 0.36 m/s to 0.18 m/s. Therefore, using the boundary condition of a reactor containing an inert particle bed to simulate the pyrolysis of a single particle introduces an error associated with the gas phase residence time.

In order to resolve this problem, the inlet velocity of the pure cellulose simulation was adjusted to match the gas phase residence time of Xue et al.’s work (2012). Consequently, the boundary condition for the inlet velocity was changed to 0.18 m/s. The new simulation was conducted with the calculated velocity, and the results for the new reaction yield of tar vapor, gas, char, and unreacted biomass are presented in Fig. 4.

Fig. 4

Pyrolysis yield of pure cellulose (${{\upvarrho }}_{\text{g}}$ = 1.905)

When comparing the results obtained from the new simulation ($\varrho_g$ = 1.905 s) to the data reported in the literature, a higher agreement is observed compared to the simulation with $\varrho_g$ = 0.95 s. The tar vapor and char yields showed almost the same behaviors as the experimental yields. The results presented in Table 6 allow for a more detailed analysis of the values obtained.

Table 6 Pyrolysis reaction yield for pure cellulose at ${{\upvarrho }}_{\text{g}}$ = 1.905 s

It can be observed from Table 6 that by reducing the nitrogen inlet velocity to adjust the gas phase residence time in the simulation to match the pyrolysis scenario with an inert particle bed, the yields of tar vapor, char, and unreacted biomass were practically the same as those found in the experiments conducted by Xue et al. (2012). The relative yield of gas showed a difference of almost 3% from the experimental data and 0.46% from the value reported by Yang et al. (2021). When summing up the mass fractions of the experimental data, a value of 96.7% is obtained, which may be attributed to experimental errors or imprecisions in the measurements. If such errors occurred in the biogas meter, the yield results would be very close. Therefore, it can be concluded that the observed discrepancy in Table 4 is due to the gas phase residence time.

Red oak

In order to study the behavior of the multicomponent and multi-stage kinetics model on varying types of biomass with different fractions of cellulose, hemicellulose, and lignin, a pyrolysis simulation was conducted on red oak biomass.

Similarly, to pure cellulose, the nitrogen velocity was adjusted so that the gas residence time matches the residence time of a reactor containing an inert particle bed. Therefore, the results from Clissold et al. (2020) were used to obtain the average gas velocity inside the reactor, and Eq. (36) was applied to calculate the residence time. The result is presented in Table 7.

Table 7 Residence time for the red oak simulation

Based on the gas phase residence time, the inlet velocity value was adjusted to match the residence time reported by Clissold et al. (2020). Thus, the boundary condition for the inlet velocity used was 0.26 m/s.

Based on the above, the pyrolysis simulation of red oak was performed. The results for the yield of tar vapor, gas, and char are presented in Fig. 5.

Fig. 5

Pyrolysis yield of red oak

Comparing the obtained results with the data reported in the literature, we observe that the yields found in the simulation fall within the same order of magnitude. However, the tar vapor yield is slightly below the experimental value and slightly above the value simulated by Xue et al. (2012) and Clissold et al. (2020). On the other hand, the gas yield is slightly below the experimental value and similar to the values reported by Xue et al. (2012) and Clissold et al. (2020). Analyzing the char yield, it was observed that it is higher than the results found by Xue et al. (2012) and Clissold et al. (2020).

From Table 8, it can be noted that the tar vapor yield shows a similarity to the information presented in existing literature, with a difference of 4.75% compared to the experimental data. When considering the yields of gas and char, a reversed behavior is noticed in the simulation for red oak. In this simulation, the biogas yield was expected to be around 20%, while the biochar yield was around 13%.

Table 8 Pyrolysis yield for red oak

Due to the inverse behavior of biogas and bio-oil yield presented in Table 8, it was necessary to adjust the multi-component and multistage kinetics parameters to accurately represent the pyrolysis reaction of red oak. This necessity arises from the difficulty of developing a generalized kinetic model capable of representing the pyrolysis behavior of any biomass source, as each biomass has its own peculiarities and complexity during the reaction. This adjustment is based on Miller and Bellan (1997), who state that multicomponent and multistage kinetics can be adjusted to better represent the pyrolysis reaction behavior. Therefore, this study adjusted the parameters of biochar formation proportion (y_c, y_h, y_l) to reduce biochar production and increase biogas production. Table 9 presents the old and new values.

Table 9 Values of the char formation ratio

With the adjusted values presented in Table 9, the pyrolysis of red oak was simulated again, and the results for the yields of bio-oil vapor, biogas, and biochar are shown in Fig. 6.

Fig. 6

Pyrolysis yield of red oak after adjustment

As shown in Fig. 6, the behavior of tar vapor yield remained the same after the adjustments. In contrast, the yields of gas and char closely approached the behavior observed in the experiment by Xue et al. (2012). Table 10 was constructed with the yield values reported in the literature for a more quantitative analysis.

Table 10 Pyrolysis yield for red oak after the adjustment

Upon analyzing Table 10, it can be observed that with the adjustment of the char formation ratio, the yields of gas and char fall within the margin of error of the experiments conducted by Xue et al. (2012). The yield of tar vapor showed a difference of nearly 5.14% from the experimental data and 4.06% from the value reported by Clissold et al. (2020). When summing up the mass fractions of the experimental data, a value of 105.2% was obtained, which could be attributed to experimental errors or inaccuracies in the readings. If such errors occurred in the tar vapor meter, the yield results would be very close.

Sugarcane bagasse

As presented in the cellulose and red bagasse section, modeling the pyrolysis of a single particle can provide a better insight into how the pyrolysis reaction progress is controlled and accurately predict the product yields. However, it was observed that an adjustment of the parameters in the multicomponent and multi-stage kinetic reaction was necessary for red oak. Therefore, the pyrolysis of sugarcane bagasse was simulated to investigate the need for adjusting the kinetic parameters.

Like the other analyses, the nitrogen velocity was adjusted so that the residence time of the gas phase was equal to that of a reactor containing an inert particle bed. For this purpose, the work of Suttibak (2017) was used as a basis. The results are shown in Table 11.

Table 11 Residence time for the simulation of sugarcane bagasse

Based on the residence time of the gas phase, the entry velocity for the simulation of sugarcane bagasse was adjusted to approximate the residence time reported in work by Suttibak (2017). Thus, the imposed inlet velocity boundary condition was set at 0.21 m/s. Considering this, the simulation of sugarcane bagasse was carried out, and the results for the tar, gas, and char yields are shown in Fig. 7.

Fig. 7

Pyrolysis yield of sugarcane

After comparing the results of the sugarcane pyrolysis simulation with the existing literature data, it is apparent that the yields obtained from the simulation are in good agreement. To analyze the deviations in the results more quantitatively, Table 12 was constructed.

Table 12 Pyrolysis yield of sugarcane bagasse

Upon analyzing Table 12, it can be observed that the yields of tar vapor, gas, and char are close to the experimental data obtained by Suttibak (2017). The tar vapor yield showed a difference of 0.27% from the experimental data, the gas yield showed a difference of 0.56%, and the char yield showed a difference of 0.83%. With slight differences between the simulated and experimental data, there was no need to adjust the kinetic parameters. Therefore, the multi-component and multi-stage kinetics accurately represented the behavior of the sugarcane bagasse pyrolysis reaction.

Conclusion

Based on the numerical simulation, the following conclusions can be drawn:

• (a) The results confirmed that the behavior of single-particle models could provide an excellent insight into how the pyrolysis reaction progress is controlled and can accurately predict conversions and product yields, provided that the boundary conditions are appropriate for a single particle.

• (b) Regarding the multicomponent and multistage kinetics, it was observed that the model represented the behavior of pure cellulose and sugarcane bagasse pyrolysis well. However, adjusting the char production ratios was necessary for red oak biomass. This indicates that adjustments to specific parameters may be necessary for some reactions.

• (c) The multicomponent and multi-stage kinetics’ pre-exponential factors and activation energies described the reaction behavior well in all studied scenarios.

• (d) The single-particle model coupled with the multicomponent and multi-stage kinetics adequately represented the behavior of pyrolysis reactions applied to biomass. Therefore, the proposed model helps estimate the conversion of various biomass sources and can be used in developing and optimizing industrial projects.