Review on Modelling Approaches Based on Computational Fluid Dynamics for Biomass Pyrolysis Systems

Abstract

Modelling is a complex task combining elements of knowledge in the field of computer science, mathematics and natural sciences (fluid dynamics, mass and heat transfer, chemistry). In order to correctly model the process of biomass thermal degradation, in-depth knowledge of multi-scale unit processes is necessary. A biomass conversion model can be divided into three main submodels depending on the scale of the unit processes: the molecular model, single particle model and reactor model. Molecular models describe the chemical changes in the biomass constituents. Single-particle models correspond to the description of the biomass structure and its influence on the thermo-physical behaviour and the subsequent reactions of the compounds released during decomposition of a single biomass particle. The largest scale submodel and at the same time, the most difficult to describe is the reactor model, which describes the behaviour of a vast number of particles, the flow of the reactor gases as well as the interaction between them and the reactor. This chapter contains a basic explanation about which models are currently available and how they work from a practical point of view.

1 Introduction

One of the most important processes of primary biomass conversion into carbonaceous materials is pyrolysis. It can be defined as the thermal conversion of biomass in an atmosphere with no oxygen to prevent its burnout. The “idea” of this process is not a new concept and has been known since ancient times [1]. As one can presume, these traditional technologies are based on very basic solutions, like kilns or burning pits, which are simple in use, but their efficiency and process control are relatively poor. In the past, the knowledge about the conversion process itself was not profound and did not allow for significant improvements in the technology. In the last four decades, due to social pressure favouring renewables and though research initiatives, the knowledge gaps started to fill, and new, more efficient solutions started to appear. Unfortunately, despite the increasing pressure for replacing fossil fuels, the alternative materials produced using novel renewable technologies are in many cases not sufficiently engineered, or their price is uncompetitive on the current market. For this purpose new and more sophisticated methods of research as well as new technological ideas, including modelling, are being developed to meet both economic and engineering ends of the problem.

2 Biomass Conversion: The Modeller’s Approach

2.1 General Overview of Simulation and Its Uncertainties

Substantial improvements in computer science in the last 30 years eased and spread access to a robust tool—numerical modelling. Simulations conducted on numerical models have allowed to significantly improve the pace of research and development in the biomass processing field.

Some commonly used terms need to be defined and clarified before the topic of computational modelling can be dealt with. A “model” is the mathematically described (by algorithms and equations) representation of a system existing in real life, and a “simulation” is an act of performing a test on a model. The term “numerical” means that the mathematical model will be translated through informatics into a numerical language, known by a numerical tool (more straightforward, a computer) to perform the computations [2, 3]. Models can be various, depending on the field where they are used, but in natural sciences and engineering, the most commonly used ones are numerical models.

A simplified scheme of a simulation study with the linkage between the experiments, theory, and model is shown in Fig. 13.1. As can be seen in this figure, the simulation has to be validated to obtain proof of its usefulness. Models based on experimental data are reliable only in a specified range of experimental values and only for this range results are valid. In general, it is always better to set the foundation of the model on fully established theories, which have a broader range of validity.

Fig. 13.1

Simplified scheme of a simulation study

It needs to be kept in mind that models are only a representation of a real system, and in most cases, they include simplifications and approximations. Moreover, the model background lies often in experimental data, which could be burdened with errors. Therefore, simulation results in most cases show discrepancies from “true/real” results, caused by unknown deviations of the model elements. These deviations are known as “uncertainties”. To be able to bring the model result’s closer to reality, the uncertainties need to be found, quantified and clarified. The sources of uncertainty can be divided into [4]:

• Parameter uncertainty—related to the parameters used in the model, which cannot be experimentally measured (too hard or too expensive) and have to be assumed in the model

• Model inadequacy—lack of full knowledge about the theory behind the modelled system or influence of the simplifying assumptions

• Residual variability—simulation output differs from experimentally obtained results through random fluctuations of parameters in a real situation (low repeatability of the real system)

• Parametric variability—the modelled system is not sufficiently described/measured, and input values have to be assumed

• Observation error (experimental uncertainty)—stemming from deviation in values due to the variability of experimental measurements

• Interpolation uncertainty—related to the assumption of the parameter trend in the range of experimental results between two consecutively measured data points

• Code uncertainty (numerical uncertainty)—the strongest uncertainty related to numerical procedures, caused by the inability to exactly solve the problem (technical boundaries) and the use of approximations while solving, e.g., in solving partial differential equations by a finite element solution method

A clear indication of the individual share of each uncertainty on the total uncertainty is not simple if at all possible, because of their strong interdependencies. For example, application of thermo-physical data from literature can influence parametric variability and residual variability. The initially implemented experimental correlations in the model and the simplification of a real system introduce model inadequacy, and the model’s validation with its consecutive adjustment to experimental data can increase the residual variability and the observation error. Proper clarification of errors can improve the modeller’s awareness about possible flaws within the model. Modellers are advised to keep a critical and very careful approach due to the possible implementation of unknown (unexpected) errors. The aforementioned errors, after implementation, are usually difficult to identify and time-consuming to remediate.

2.2 Simulation and Profit

Simulations on a properly constructed model provide valuable information about the system behaviour, which often cannot be obtained through experimental measurements. Such knowledge can give a significant boost for the development of innovative solutions and helps to identify the critical points within the system (bottlenecks). In general, the use of modelling studies brings four main advantages [2]:

• Allows for conduction of proof-of-concept (PoC) at the very beginning of the project (low sunk cost in case of failure)

• Allows for a performance of numerous tests with a low unit cost

• Increases the knowledge about dependencies in a real system

• Accumulates the obtained datasets and simplifies their treatment and sharing (big data processing)

All of the mentioned advantages can have a crucial impact on the economic feasibility of new technological solutions. As it is shown in Fig. 13.2, the application of simulations can reduce the overall cost of new solution implementations and reduce the risk of the project’s unprofitability, which in the development of new technologies is a strong benefit.

Fig. 13.2

Changes to the new idea implementation costs, through the project time (adapted with permission from [2] Copyright © 1990, Taylor and Francis Group, LLC, a division of Informa plc.)

Models are more flexible than real processes, so changes in modelled systems and their influence can be quickly verified. The model allows for solving technical problems in the early stage, which is the lowest cost extensive option. Modelling can also expand the knowledge about the investigated process. If the model is detailed and mimics the real system well, there is a possibility to investigate and validate new correlations and theories through large and detailed databases of the process history.

2.3 Theoretical Framework of a Comprehensive Model for Pyrolytic Biomass Conversion

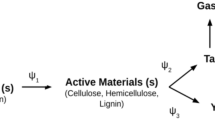
As it is illustrated in Fig. 13.3, a comprehensive/multi-scale model for biomass conversion can be divided into few submodels according to the scale in which the crucial processes take place. Besides combined implementation, each submodel can be studied separately, experimentally or through simulation, leading to expanding the knowledge of certain biomass conversion phenomena.

Fig. 13.3

Framework of a comprehensive biomass conversion model (adapted with permission from [5] Copyright © 2016, Elsevier)

The smallest considered scale in a comprehensive model is the molecular model. It describes the chemical reactions of organic compounds and catalytic effects of inorganic compounds which take place during biomass conversion. Chemical reactions themselves are not necessarily bound to spatial dimensions, so the implementation of geometry (i.e. biomass particle) can be omitted. The amount of data which is used for this model scale allows for simulations without the need for robust numerical solvers.

A submodel covering a larger size is the single-particle model. It describes the behaviour of one individual biomass particle for which temperature, species concentration and pressure gradients during the process play a crucial role. A single-particle model needs to contain a description of the heat and mass transport phenomena and fluid dynamics. The model may cover changes in particle size, shape and structure (porosity) as well as bio-polymers chemical reactions and water evaporation processes. The particle properties, intra-particle processes and boundary conditions have a strong influence on the final products yield and composition [5]. Therefore, the intra-particle phenomena, as well as their chemistry, has to be described in a very detailed manner. In the model, the gases and liquids are treated as fluids and biomass as a stagnant solid. The Eulerian description (see later) is sufficient to cope with such physical behaviour for both phases. The single particle model is strongly dependant on the geometry, so the use of a numerical solver is necessary to perform simulations at this stage.

The last submodel of a comprehensive biomass conversion model is the reactor model. It covers the description of every relevant process in a reactor for biomass thermochemical conversion. The behaviour of each biomass particle in most cases should be, if possible, described separately with a single-particle submodel. Besides the particles’ conversion, the model also consists of flow and thermal behaviour of gases, particles movement (collisions with each other and walls) and thermo-physical interactions between gas and solid phases. Therefore in the reactor model, the Eulerian description of fluids needs to be combined with biomass particles movement described with a Lagrangian approach (more complex and precise, simultaneously harder and more computationally extensive option), or with an Eulerian approach (this simplification is not always possible and valid but less complex and less computationally burdening). The quantity of equations and the amount of data needed to be processed in the reactor submodel is the largest among all submodels of a comprehensive biomass conversion model. To perform simulations in an efficient manner, the model requires appropriately large computational power resources, adequate to the chosen sub-models and their complexity.

3 Molecular Model

3.1 Brief Overview of Biomass Composition

Before the description of chemical reactions that occur in biomass during thermochemical conversion, a brief explanation of biomass composition should be made. There are several biomass sources such as wood and woody biomass, herbaceous and agricultural residues, starchy crops, oil crops, aquatic biomass and, animal and human biomass wastes. The most commonly employed biomasses for energetic purposes, such as woody biomass, herbaceous biomass or agricultural residues, have a lignocellulosic structure. In lignocellulosic biomass, organic matter is mainly made from 3 main structural biopolymers: cellulose, hemicellulose, lignin and other, minor compounds which are organics named extractives and inorganics called mineral matter. The concentration of each substance varies with biomass type, and even within the same species, they are distributed in different ways among the plant organs (e.g. leaves, stem, bark, roots in wood) [6]. Detailed characterisation of the structure of bio-polymers and their thermal degradation has been extensively investigated and can be found in numerous literature reports [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].

3.2 Single Component and Competitive Schemes

Historically, the description of the pyrolysis reaction started with the introduction of simple biomass thermal degradation models. Those models are largely based on mass-loss data obtained in thermo-gravimetric (TG) experiments and up to this day are very common among researchers due to their simplicity. The core of said models is the biomass degradation kinetic, in which biomass is treated as a bulk material. Those models only take into consideration the primary biomass degradation reactions. Models based on TG show strong fluctuations between publications in obtained kinetic values. Differences can be caused by using feedstocks with different bio-composition, size, and morphology as well as by the applied methodology and calculation procedures [5]. In order to systematise TG measurements, the International Confederation for Thermal Analysis and Calorimetry (ICTAC) presented guidelines for an experimental procedure for kinetic investigations, including researches related to biomass degradation [23]. Discrepancies between the kinetic data among publications can also be caused by inappropriate assumptions regarding the kinetic mechanism. In most cases, TG models consider only the primary biomass degradation and they do not take into account the low-temperature tar-char interactions (<500 °C). Additionally, the secondary charring reactions in most TG-based models are not distinguished nor considered. Those reactions are usually lumped together with the primary degradation reactions, which leads to a shift in the value of primary kinetic parameters and as such, discrepancies in values between sources. A detailed overview of the experimental approach of a mass-loss based biomass degradation study can be found in a recent and comprehensive review by Anca-Couce [5].

Introduction of the single-component competitive models led to an improvement of TG models accuracy. Those models, besides prediction of mass loss, aim to predict also the three main products of biomass pyrolysis: char, tar, and gas—without distinction on their detailed composition. Single-component competitive models are covering only primary biomass degradation reactions, which have an influence on the prediction accuracy of product’s yields [24]. Further development of the single-component competitive models was made by the introduction of cracking reactions of high molecular mass vapours (tars) at temperatures higher than 500 °C [25]. The most often used kinetic scheme is the one proposed by Shafizadeh and Chin [26].

When a higher prediction accuracy is required, the degradation of individual biomass components has to be considered in the kinetic scheme. Such schemes are named the multi-component parallel schemes, and they cover the degradation of the main biomass components (e.g. cellulose) and their intermediary products [27]. In literature extensions and improvements of the original Shafizadeh and Chin’s competitive scheme can be found, e.g. via the addition of intermediate compounds or considering the three main biomass constituents. Nevertheless, the expanded models show only moderate improvement regarding the accuracy in model prediction [28, 29]. For more detailed outcomes, kinetic schemes need to cover the description of the thermal degradation of all bio-components, combined with a description of the consecutive degradation of the primary pyrolysis products.

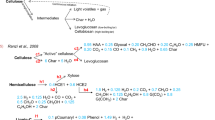
3.3 Detailed Reaction Schemes: Ranzi Scheme

A more detailed description of biomass degradation in a kinetic scheme was first introduced by Ranzi et al. [30], and was further improved by him and co-workers [31,32,33,34,35]. The most recent extension of the model was published by Debiagi et al. [36], which improves the accuracy of the prediction of char yield. In general, the Ranzi model combines all findings related to the thermal decomposition of each major component of biomass: cellulose, hemicellulose (2 types), and lignin [11, 16, 37]. In the scheme, the overall lignin is divided into 3 artificial types of lignin: LIG-H, LIG-O, and LIG-C (hydrogen-, oxygen- and carbon-rich, respectively). Another innovation of the Ranzi model is a description of char, which distinguishes “pure” char and the volatiles “trapped” within a char metaplastic phase. Thermally unstable “traps” degrade according to the applied kinetic, releasing captured volatiles. Such a description allows for the introduction of the char devolatilisation into the kinetic scheme. The Ranzi model does not cover all possible evolved species in pyrolysis, but reduces their amount to 20 representative volatile compounds, being the most abundant in non- and condensable vapours. The Ranzi scheme allowed for the derivation of a complex reaction scheme, combining separate mechanisms into a consolidated form. The latest version of the composition of vapours, kinetic parameters, and the reaction heats can be found in the work of Ranzi et al. [34, 35].

The Ranzi model is a milestone in the description of pyrolysis kinetics, but there are a few areas in which improvements or extensions can be made. The kinetic scheme was developed for a description of fast pyrolysis, so it does not cover the secondary charring reactions. Moreover, it does not consider the catalytic influence of the of mineral matter (mainly AAEM’s) contained in biomass, which leads to overprediction of the sugars and underprediction of the non-condensable gases and char. Also, the pyrolytic mechanism of the evolution of phenolic compounds is not contained in the base scheme, causing an underprediction of BTXs at higher temperatures [5, 19]. Accuracy improvement can be made by the implementation of secondary cracking reactions of the primary pyrolysis products in the gas phase. For example, it can be done by the implementation of the POLIMI kinetic mechanism, developed by the CRECK modelling group, recently revised by Ranzi et al. [35]. The POLIMI kinetic mechanism is a complex, radical, kinetic scheme, whose application improves the accuracy of prediction, but is also time-consuming to implement and increases the computational burden significantly.

3.4 Detailed Reaction Schemes: Ranzi—Anca-Couce Model

As was mentioned in the previous section, the Ranzi model was intended for the prediction of products from fast pyrolysis, so it shows some limitations in terms of describing biomass conversion in less severe thermal regimes. Lower thermal gradients or extended gas-solid reactions, e.g. in pyrolysis of larger samples, can lead to losses in prediction accuracy in case of application of the Ranzi model. An extension of secondary charring reactions to the Ranzi scheme, named as RAC (Ranzi—Anca-Couce) scheme was introduced by Anca-Couce et al. [19]. Their adaptation aimed to incorporate the secondary charring phenomena with the possibility of their adjustment to the severity of the conversion regime. A full description of the model with its kinetic parameters and reactions heat values can be found in the works of Anca-Couce et al. [19, 37].

The RAC model introduces an adjustable parameters “x” which defines the share of the alternative degradation, named “charring” or “secondary charring” in the overall degradation process. The adjustable parameter also partially takes into account the influence of inorganics which have a role in promoting “charring” reactions. As the main factors which increase the extent of charring, the adjustable parameter value can be modified to account for [5]:

• Decrease in the pyrolysis temperature,

• Decrease in the heating rate,

• Increase in volatiles retention time in the particle (larger particle or slower gas movements),

• Increase of the pressure in the reactor,

• High concentration of the mineral matter, especially AAEMs.

The extent of secondary charring can be different for each bio-component, so the value of the “x” parameter should be assigned separately. Unfortunately, lack of quantitative correlations between the pyrolysis conditions, biomass composition and amount of secondary charring reactions cause the need for the iterative fitting of the “x” parameter to the experimental results. A common approach is to set the adjustable parameter for all bio-components a priori, based on the available experimental data and then slightly adjust to the experimental result [5, 38]. It is worth to mention that the amount of secondary charring reactions have as well a noticeable influence on the heat of the reaction, as it was observed by Rath et al. [39].

The RAC scheme also does not cover all areas which the Ranzi scheme lacks, e.g., a detailed description of AAEM’s influence or insights into polycyclic aromatic compounds formation. The base RAC scheme does not take into account the secondary gas-phase tar cracking kinetics. As well as the Ranzi scheme, it can be extended with the POLIMI kinetic mechanism. Another possible option is the simple one-step kinetics firstly introduced by Blondeau and Jeanmart [40], and consecutively improved by Mellin et al. [41] and most recently by Anca-Couce et al. [42]. Application of the one-stage kinetic cracking scheme is relatively simple, and it improves the accuracy of predictions of the vapour composition.

Constant work and recent findings on the subject gives promise of improvement and further extension of the pyrolysis reaction schemes, which would allow for better understanding of biomass pyrolysis and the ability to predict its outcome with higher accuracy [17, 43, 44]. In Table 13.1 is shown a brief summary of the comparison of kinetic models. As it can be anticipated, the more detailed the model, the better the accuracy of the predictions that can be attained. From the practical point of view, the application of a detailed model needs a lot more initial information about the processed feedstock. It also increases the complexity of the model, which leads to a higher computational burden. Therefore, the complexity of the calculation has to be chosen with caution, in relation to the desired precision of the model outcome.

Table. 13.1 Brief summary of the comparison of kinetic models

4 Single-Particle Model

As was mentioned previously in Sect. 13.2.3, the single-particle model focuses on the influence of the composition of a particle and its thermo-physical properties on the particle’s behaviour during pyrolysis. The biomass particle, due to its structure, cannot be treated as an impermeable solid object, so the description of a porous structure needs to be implemented. In practical pyrolysis applications, the biomass is rarely fed to the process in a completely dry state. Therefore, besides the description of the pyrolytic behaviour, the drying process and description of water movement within the particle have to be included in single particle models.

Due to the geometrical dependence as well as the complexity of the phenomena occurring in this stage, robust numerical solvers have to be applied. Having in mind that the Eulerian approach is able to handle the description of the processes, suitable numerical tools have to be applied, such as the Computational Fluid Dynamics (CFD).

4.1 Modelling Conversion Based on CFD

Prior to the mathematical description of the thermo-physical phenomena occurring in the single particle, a brief explanation of CFD will be provided here. It should give the reader a basic insight in the Eulerian approach, which is applied in single particle models as well as in the modelling of gas flow at the reactor scale.

Computational Fluid Dynamics (CFD) is the analysis of systems involving fluid flow, heat transfer and associated phenomena (e.g., chemical reactions) by using computer-based simulation [45]. In general, CFD can be treated as the integration of the following fields: natural sciences (physics and chemistry), mathematics and computer science [46].

The model behaviour is based on governing equations—in which physical phenomena like transport phenomena are mathematically described through differential equations (e.g. Navier-Stokes equation). To solve the governing equations, high-level computer programs and software packages convert them with the use of computer programming languages to numerous, simple commands that can be understood by a computing machine.

CFD for its computation needs dimensional geometrical domains. As the first step of the model’s construction, the initially specified geometry (“domain”) needs to be subdivided into a finite number of smaller, non-overlapping subdomains called “cells”. The process of dividing a domain into subdomains is called “meshing”, and it results in a grid of cells (“mesh”), that occupies the whole geometry. The cell can be defined as a representative element or a representative volume, depending on the division method (“finite element” or “finite volume”, respectively). Geometry division techniques are already included in most commercially available CFD software packages. Each cell in the domain has a “node”, which holds information about this certain area in the geometry. Information stored in the node changes according to the applied physical phenomena and chemical reactions.

The fluid dynamics principle employed in CFD means that it treats the flow of matter (fluid) as a continuum (Eulerian approach). In the Eulerian description of fluid dynamics, points in the geometry do not change their position with respect to the fluid motion [47, 48]. The only change that occurs is the change of the values of parameters stored at specific, fixed points (nodes). Therefore, it allows only for a description of changes taking place in nodes in the investigated geometry. As a consequence, the approach makes no distinction of single molecules or particles, so their time-based investigation is not possible.

The accuracy and precision of a CFD simulation are determined by the number of cells contained in the grid (“mesh coarseness”). An increase in the number of cells improves a simulation accuracy, until the moment when a simulation becomes grid-independent. In other words, there exists a number of cells above which the addition of new cells no longer influences the simulation quality. The simulation is called a grid-independent simulation when further mesh densification does not lead to an improvement in solution accuracy [45]. Grid independent simulations have a major advantage, which is the smallest numerical error is achieved with the most coarse mesh (least computational burden).

A detailed explanation of the CFD solution procedure is complex and goes beyond the purpose of this chapter. Nevertheless, a brief introduction to the matter will be provided. The CFD framework consists of three main elements [46]:

• Pre-processor—is a part of a CFD code that is responsible for the creation of an investigated geometry and its consecutive meshing. The mesh obtained in the pre-processor is a foundation for implementation of governing equations.

• Solver—through implemented solution methods, the solver simulates the changes of the variables in the nodes according to the applied governing equations and boundary conditions. The solver processes information regarding the applied physics and chemistry located on the nodes of the grid. Therefore, the solver is responsible for performing the simulation.

• Post-processor—is responsible for the visualisation of the simulation results. Most post-processors allow for quick creation of 1D, 2D or 3D plots and representation of variables of interest on the applied geometry.

The CFD solution scheme which can be found in [45] provides a general scheme, which is valid for any model based on the Eulerian approach. The specification of parameter values in the governing equations depend on the characteristics of the process which one needs to solve. Moreover, the reliability of a simulation’s results is linked directly to data and auxiliary correlations, so to their compliance with the modelled system and range of application. Therefore further subsections will be focused on the reliable description of the phenomena occurring in the single particle models as well as the validity of the thermo-physical parameters applied in modelling of biomass pyrolysis.

4.2 Definitions of Phases in a Particle’s Structure

Biomass feedstock which has not been dried previously, and is typically used for conversion, consists in most cases of four different phases: liquid water, bound water, solid and gas. The bound water is distinguished from liquid water due to its significant difference in behaviour. Each of the mentioned phases needs to be identified and described separately.

A detailed theoretical description of each phase was first made by Whitaker [49], in which a boundary surface between each phase has to be differentiated and known during the whole process. Wood has a very complex geometric structure, which strongly changes during pyrolysis, so identification of boundary surfaces at every point in time is a very difficult and complex task. Also, the amount of computation for such a sophisticated model would be very high.

The efficient description of phases has been investigated by Perre and his co-workers [50, 51], and on this basis, an elegant description of the system was presented in the work of Grønli [52]. In their approach, all of the phases are treated as a continuum for which conservation laws must be satisfied. The description assumes averaging of variables and parameters over a finite volume, which can simultaneously contain all phases. This results in a set of conservation equations for every phase, valid within the applied geometry.

For further model description, it will be helpful to define the spatial average over the geometry’s total volume for any given variable (φ) valid for every phase. The spatial average is defined as:

$$ <\varphi >=\frac{1}{V}\underset{V}{\int}\varphi\ dV $$

(13.1)

The spatial average for one of the phases (γ) is defined as:

$$ <\varphi {>}^{\gamma }=\frac{1}{V_{\gamma }}\underset{V_{\gamma }}{\int}\varphi\ dV $$

(13.2)

where <φ>^γ is the variable ‘s averaged value in the phase γand V_γ is the volume of the phase in the representative volume V. The volume fraction occupied by the phase γ is defined as:

$$ {\varepsilon}_{\gamma }=\frac{V_{\gamma }}{V} $$

(13.3)

A relation between the averaged value in phase γ and a spatial average is described as:

$$ <\varphi >={\varepsilon}_{\gamma }<\varphi {>}^{\gamma } $$

(13.4)

In other words, <φ>^γ is an intrinsic or true value of the variable and <φ> is an averaged value in the representative volume. For example, if <ρ_S>^S would be defined as the true density of the solid phase, then <ρ_S> will be defined as the density of contained solids in a representative volume of the porous particle structure (i.e. bulk density). The notation with the <,> brackets is based on the authors believe that it is clearer, and of course, it is not mandatory.

Since the particle is made in most cases out of four phases, the representative volume can be treated as a sum of volumes of each phase:

$$ V={V}_S+{V}_L+{V}_B+{V}_G $$

(13.5)

where subscripts S, L, B, and G represent solid, liquid water, bound water and gas, respectively. Sum of volume fractions occupied by each phase sums into one, so:

$$ {\varepsilon}_G=1-\left({\varepsilon}_S+{\varepsilon}_L+{\varepsilon}_B\right)=1-\left(\frac{<{\rho}:S>}{<{\rho}:S{>}^S},+,\frac{<{\rho}:L>}{<{\rho}:L{>}^L},+,\frac{<{\rho}:B>}{<{\rho}:B{>}^B}\right) $$

(13.6)

which means that knowing the intrinsic and average density of a solid, and both types of water, a volume fraction occupied by the gas can be calculated. Visual representation of a real system in the Whitaker theory is shown in Fig. 13.4.

Fig. 13.4

Visual representation of the conversion of a real system (woody biomass) into a model system according to Whitaker’s theory

4.3 Governing Equations

In this section, an explanation of the conservation laws will be provided. Nonetheless, the theoretical derivation of the formulas will be omitted. In here, the fundamental description of the mathematical description of the governing equations is applied. Therefore, the negative signs in the equations originated purely from mathematical derivations, and they are reflecting the actual values of parameters (positive or negative). All equations mentioned in this subsection are valid only within the applied particle geometry, and they do not describe the interactions of the particle with its external environment. Reading this subsection is worth to keep in mind that all conservation equations are referring to a single, finite and representative volume.

For clarity purposes, the one component kinetic scheme will be used for explaining the principles. All kinetic schemes described in this section are treated as first-order Arrhenius kinetics with the pre-exponential parameter set as constant or temperature dependent. Additionally, from now on, wood will be treated as the exemplary lignocellulosic biomass type in the model description.

4.3.1 Mass Conservation Equations: Solids

At any given time of a pyrolysis reaction, the solid is represented by a mix of unconverted biomass and biochar, so it can be stated that:

$$ <{\rho}:S>=<{\rho}:{BM}>+<{\rho}:{BC}> $$

(13.7)

where <ρ_S>, <ρ_BM> and <ρ_BC> are the volume-averaged densities of solid, biomass and biochar respectively. Mass conservation equation of biomass is defined as:

$$ \frac{\partial }{\partial t}<{\rho}:{BM}>={\dot{\omega}}_{BM} $$

(13.8)

where ${\dot{\omega}}_{BM}$ is the mass change rate of biomass caused by degradation and devolatilisation reactions. Although the degradation reactions lead to a reduction in mass, a negative sign is not used in Eq. (13.8). Similarly, the mass conservation equation of biochar is defined as:

$$ \frac{\partial }{\partial t}<{\rho}:{BC}>={\dot{\omega}}_{BC} $$

(13.9)

In most general form, the mass conservation equation is defined as:

$$ \frac{\partial }{\partial t}<{\rho}:S>={\dot{\omega}}_S $$

(13.10)

where ${\dot{\omega}}_S$ is the total mass change of a solid obtained from a sum of the biomass degradation and char formation.

4.3.2 Mass Conservation Equations: Single Component in the Gas Mixture

The equation for mass conservation of the i^th component in a gas mixture is defined as:

$$ \frac{\partial }{\partial t}\left({\varepsilon}_G<{\rho}:i{>}^G\right)+\nabla <{u}_i{\rho}_i>={\dot{\omega}}_i $$

(13.11)

where <ρ_i>^G is the density of the i^th component in the gaseous phase, <u_iρ_i> is i^th component’s transport term and ${\dot{\omega}}_i$ is the mass change rate caused due to formation/degradation reactions of the i^th gas component. Transport of the gas is driven by two phenomena: convection and diffusion. Therefore the transport term can be described as:

$$ <{u}_i{\rho}_i>={u}_G<{\rho}:i{>}^G-<{\rho}:G{>}^G{D}_{eff}\nabla \left(\frac{<{\rho}:i{>}^G}{<{\rho}:G{>}^G}\right) $$

(13.12)

where u_G is the superficial gas velocity, <ρ_G>^G is the total density of the gas mixture, D_eff is the effective gas diffusion coefficient. The low permeability of biomass structures (small pores) leads to relatively low Reynolds numbers (<10) for the gas movement inside a particle. Therefore the viscous resistance force is much larger than the inertial one, which simplifies the description of flow from Darcy and Forchheimer’s description to a pure Darcy’s description [53]:

$$ {u}_G=\frac{K_{G, eff}}{\mu_G}\nabla \left(<{P}:G{>}^G\right) $$

(13.13)

where K_G,eff is the effective gas permeability, μ_G is the gas dynamic viscosity and <P_G>^G is the pressure in the gas mixture.

4.3.3 Mass Conservation Equations: Liquid Water

Mass conservation equation for liquid water is defined as:

$$ \frac{\partial }{\partial t}<{\rho}:L>+\nabla <{u}_L{\rho}_L>={\dot{\omega}}_L $$

(13.14)

where <ρ_L> is the volume-averaged liquid water density, <u_Lρ_L> is its transport term and ${\dot{\omega}}_L$ is a mass change rate caused by evaporation or re-condensation. It is assumed that liquid water migrates through the structure entirely due to a pressure change (convectively), so its transport term is expressed as:

$$ <{u}_L{\rho}_L>={u}_L<{\rho}:L> $$

(13.15)

where u_L is a superficial velocity of the liquid water. Similar to the gas mixture, Darcy’s law is also avalid to obtain the superficial liquid velocity:

$$ {u}_L=\frac{K_{L, eff}}{\mu_L}\nabla \left(<{P}:L{>}^L\right) $$

(13.16)

where K_L,eff is the effective liquid water permeability, μ_L is the liquid water dynamic viscosity and <P_L>^L is the pressure in the liquid water.

4.3.4 Mass Conservation Equations: Bound Water

Mass conservation equation of bound water is defined as:

$$ \frac{\partial }{\partial t}<{\rho}:B>+\nabla <{u}_B{\rho}_B>={\dot{\omega}}_B $$

(13.17)

where <ρ_B> is the volume-averaged bound water density, <u_Bρ_B> is the bound water’s transport term and ${\dot{\omega}}_B$ is the mass change rate caused by water’s unbinding. In opposition to the liquid water, it is assumed that the bound water migrates entirely by diffusion, so its transport term is:

$$ <{u}_B{\rho}_B>=-<{\rho}:S>{D}_B\nabla \left(\frac{<{\rho}:B>}{<{\rho}:S>}\right) $$

(13.18)

where D_B is the bound water’s diffusion coefficient.

4.3.5 Energy Conservation Equation

The energy conservation equation is based on the assumption that the Péclet number for heat transfer is sufficiently large, so a local thermal equilibrium is obtained by all phases [53]. Therefore the equation is defined as:

$$ \frac{\partial T}{\partial t}\left(<{\rho}:S>{C}_{P,S}+<{\rho}:L>{C}_{P,L}+<{\rho}:B>{C}_{P,B}+{\varepsilon}_G<{\rho}:G{>}^G{C}_{P,G}\right)+\nabla T\left(<,{u}_L,{\rho}_L,>,{C}_{P,L},+,<,{u}_B,{\rho}_B,>,{C}_{P,B},+,{\varepsilon}_G,\sum \limits_{i=1}^N,<,{u}_i,{\rho}_i,>,{C}_{P,i}\right)=\nabla \left({\lambda}_{eff}\nabla T\right)+Q $$

(13.19)

where C_P is the heat capacity/specific heat and subscripts S, L, B and i indicate solid, liquid water, bound water, and the i^th component of the gas mixture, respectively, λ_eff is the effective thermal conductivity and Q is the total heat produced by the occurring reactions, and it is defined as:

$$ Q=\sum \limits_i^N{H}_i{\dot{\omega}}_i+{H}_L{\dot{\omega}}_L+{H}_B{\dot{\omega}}_B+{H}_S{\dot{\omega}}_S $$

(13.20)

where H is the overall heat of the reaction. In the most general case, the transport terms are implemented in the conservative form, so the energy conservation equation takes into account the heat transfer through conductive, convective and diffusion transport [52, 54, 55]. Some authors apply simplifications in defining the transport, by omitting the heat transported through diffusion, assuming that the amount of heat exchanged through this phenomenon is negligible [28, 56,57,58]. Taking abovementioned simplification into account, the energy conservation equation takes the form:

$$ \frac{\partial T}{\partial t}\left(<{\rho}:S>{C}_{P,S}+<{\rho}:L>{C}_{P,L}+<{\rho}:B>{C}_{P,B}+{\varepsilon}_G<{\rho}:G{>}^G{C}_{P,G}\right)+\nabla T\left({u}_L<{\rho}:L>{C}_{P,L}+{u}_B<{\rho}:B>{C}_{P,B}+{u}_G{\varepsilon}_G<{\rho}:G{>}^G{C}_{P,G}\right)=\nabla \left({\lambda}_{eff}\nabla T\right)+Q $$

(13.21)

4.3.6 Reactions

The mass change rate of every reaction in the kinetic scheme is defined as:

$$ {\dot{\omega}}_j={k}_j<{\rho}:j>={k}_j{\varepsilon}_{\gamma }<{\rho}:j{>}^{\gamma } $$

(13.22)

where ${\dot{\omega}}_j$ is the mass change rate of the j^th species (e.g., biomass, tar, gas), k_j is a reaction rate of the j^th species, <ρ_j> is the averaged volume density of the j^th species and <ρ_j>^γ is the intrinsic density of the j^th species in phase γ. Water can be an exception to this definition. Depending on the applied drying/evaporation model (equilibrium, heat sink, kinetic model) the mass change rate for the liquid and bound water will take a form suitable for the chosen model.

4.4 Evaporation of Water

Moisture evaporation is one of the most energy-intensive phenomena occurring during pyrolysis of wet biomass particles. Therefore, its appropriate description has much importance. Three common ways of implementing biomass drying can be used in practice: the kinetic model, heat sink model and equilibrium model.

4.4.1 Kinetic Model

The kinetic model represents the simplest way of describing evaporation. It was first introduced by Chan et al. [59], and then, due to its simplicity, it has been widely applied by other authors [60,61,62,63]. The kinetic model assumes a first-order Arrhenius reaction of the liquid water phase turning into vapour. In work by Haberle et al. [64] a summary of the commonly used parameters for this model can be found.

The kinetic model is very convenient, but it treats a physical phenomenon via a chemical description, so it does not reflect the process well in real terms. In practice, in the kinetic model, water evaporation starts before water obtains its boiling temperature (100 °C at 1 atm), and the temperature during evaporation does not stay constant during the whole process. Therefore, such a model may be suitable for specific cases, but it is not advised for general application.

4.4.2 Heat Sink Model

The heat sink model (thermal drying model, heat flux model) [57, 64, 65] assumes that water evaporation in a representative volume occurs only at the boiling temperature, and the temperature stays constant until all water is evaporated. To maintain a constant temperature, the evaporation reaction needs to consume all the energy transferred to the representative volume. Thus all the energy delivered to the volume is absorbed (sunk) by the evaporation reaction. Mathematically the model is formulated as:

$$ {\dot{\omega}}_e=\left\{\begin{array}{c}\frac{j_{Heat}}{H_e}\kern0.75em T\ge {T}_e\ and<{\rho}:L>>0\\ {}\ \\ {}\begin{array}{c}\kern0.75em \\ {}0\kern5em otherwise\kern1.5em \end{array}\end{array}\right. $$

(13.23)

where ${\dot{\omega}}_e$ is the evaporation rate, T_e is the water boiling temperature, H_e is the heat of water evaporation and j_Heat is the heat flux towards to the representative volume. With the assumption that heat is not transferred by water, the heat flux is defined as:

$$ {j}_{Heat}=\nabla \left({\varepsilon}_G{u}_G<{\rho}:G{>}^G{C}_{p,G}-{\lambda}_{eff}\nabla T\right) $$

(13.24)

The heat sink model of Lu et al. [65] assumes that the boiling temperature of water is fixed at 373 K. Nevertheless, strong local evaporation can cause noticeable changes in pressure which shifts the boiling temperature. The pressure effect on the boiling temperature can be modelled as [64]:

$$ {T}_e={T}_{e,0}\log \left(\frac{<{P}:G{>}^G}{P_0}\right)+{T}_0 $$

(13.25)

where <P_G>^G is the actual gas pressure, P₀ is atmospheric pressure (1 atm), T_{e, 0} is an empirical constant (32.7 K) and T₀ is the water boiling temperature at atmospheric pressure (373 K).

The heat sink model describes the evaporation phenomena more accurately than the kinetic model, and it suits very well the models of large particles, which are subjected to a high temperature and a high heating rate. Nevertheless, it also has its flaws. The model assumes an infinitely thin moving volume where evaporation takes place, so it is not valid in case if the thickness of the drying volume is not negligible in comparison to the size of the domain [5]. Another disadvantage of the model is the application of a step function (Eq. (13.23)), which is hard to handle by a numerical solver and results in numerical instability [57, 66]. The step function was investigated by Haberle et al. [64], who advised using an evaporation fraction factor (f_evap) as the multiplier of the heat flux. The purpose of this limiting factor is to reduce the amount of the heat sunk by the evaporation reaction. In that way, the drying is distributed over neighbouring nodes, leading to the smoothing of the step and reduction of numerical instability. The disadvantage of such an approach is the forced broadening of the thickness of the drying volume.

4.4.3 Equilibrium Model

The equilibrium model assumes that an equilibrium between liquid water and water vapour exists inside the particle’s pores. The water vapour’s partial pressure at any given time tends to be equal to the saturation vapour pressure (when the biomass moisture content is above the fibre suration point, or FSP) or saturation vapour pressure reduced by the relative humidity factor (moisture content below the FSP). For a whole range of moisture concentrations, it can be stated that:

$$ <{P}:v^{eq}{>}^G=\left\{\begin{array}{c}\kern0.5em {P}_{sat}(T)\kern5.5em \left( MC>{MC}_{FSP}\right)\\ {}\begin{array}{c}\ \\ {}{P}_{sat}(T)\ \kappa \left({MC}_B,T\right)\kern0.5em \left( MC\le {MC}_{FSP}\right)\end{array}\end{array}\right. $$

(13.26)

where $<{P}:v^{eq}{>}^G$ is the equilibrium’s partial pressure of water vapour, P_sat(T) is the saturation pressure in function of the temperature, κ(MC_B, T) is the relative humidity factor calculated from the wood isotherm. This parameter depends on the bound water content and the temperature. The saturation pressure in function of temperature can be obtained from Raznjevic’s [67] experimental correlation:

$$ {P}_{sat}=\exp\ \left(24.21,-,\frac{467.35}{T}\right) $$

(13.27)

The equation for the wood’s relative humidity can be obtained based on data from the Encyclopedia of Wood [68], which was obtained by Grønli [52]:

$$ \kappa \left({MC}_B,T\right)=1-{\left(1-\frac{MC_B}{MC_{FSP}}\right)}^{6.453\cdotp {10}^{-3}\ T} $$

(13.28)

From the equilibrium partial pressure, the vapour density can be obtained through:

$$ <{\rho}:v^{eq}{>}^G=\frac{<{P}:v^{eq}{>}^G{M}_{H_2O}}{RT} $$

(13.29)

where ${M}_{H_2O}$ is the molecular mass of water. Taking into account all above, the final equation for water evaporation rate can be defined as:

$$ {\dot{\omega}}_e=\frac{\varepsilon_G\left(<{\rho}:v^{eq}{>}^G-<{\rho}:v{>}^G\right)}{t_{eq}} $$

(13.30)

where $<{\rho}:v^{eq}{>}^G$ is the equilibrium vapour density, <ρ_v>^G is the water vapour density at a given time and t_eq is the time it takes to reach equilibrium between the actual vapour density and theoretically assumed saturation vapour density (“equilibration time”). Jahili et al. [54] stated that the equilibration time has to be appropriately short in relation to the pore diameter of wood and proposed a constant value of 10⁻⁵ s. Lu et al. [65] proposed a correlation of the equilibration time based on particle specific surface area and pore diameter, expressed as:

$$ {t}_{eq}={S}_{SSA}\frac{3.66\ {D}_{eff,{H}_2O}}{d_{pore}} $$

(13.31)

where S_SSA is the specific surface area of a porous particle, ${D}_{eff,{H}_2O}$ is the effective diffusivity of water, calculated according to the work of Olek et al. [69] and d_pore is the average pore diameter. In their work, Lu et al. applied values obtained experimentally from N₂ adsorption [65].

The equilibrium model was designed initially for the modelling of slow, low-temperature drying. Nevertheless, it was also applied in the modelling of fast, high-temperature drying, but only with moderate success [57, 64, 65, 70, 71]. In the literature, hybrid evaporation models can also be found. Those models combine different models for liquid and bound water evaporation [63, 64].

4.4.4 The Heat of Water Evaporation

The most convenient way to implement the heat of evaporation is by using a constant value. For models without differentiation between liquid and bound water or models with liquid water only, the heat of evaporation can be assumed to be equal to 2440 kJ/kg (at 20 °C) [64, 65] or as 2257 kJ/kg (at 100 °C) [57]. A more appropriate way to implement the heat of evaporation can be done by using a temperature-dependent heat of evaporation correlation, e.g. the equation suggested by Ranzjevic [67]:

$$ {H}_L=3179-2.5\ T $$

(13.32)

where H_L is the heat of water evaporation. In models where both liquid and bound water are distinguished, a more complex approach for describing the heat of evaporation is needed. Such a model should include an additional term to account for the energy required for unbinding of the bound water prior to its evaporation. As such, the heat of evaporation for a whole range of moisture contents (liquid and bounded water) can be defined as:

$$ {H}_e=\left\{\begin{array}{c}{H}_L\kern0.75em if\ MC\ge {MC}_{FSP}\\ {}\ \\ {}\ {H}_L+{H}_B\kern0.75em if\ MC<{MC}_{FSP}\end{array}\right.\operatorname{} $$

(13.33)

where H_e is the total evaporation heat of water and H_B is the the energy needed to unbind the water. The latter can be calculated using the equation proposed by Stanish [72]:

$$ {H}_B=0.4\ {H}_L{\left(1-\frac{MC_B}{MC_{FSP}}\right)}^2 $$

(13.34)

4.5 Shape Specification and Coordinate Systems

The most common coordinate system for fluid dynamics is the Cartesian coordinate system. In cases where the particle anisotropy in a direction other than Cartesian’s the implementation of another coordinate system can be beneficial. A wood particle does not have large property differences in the radial and tangential direction. Therefore in case of a wood particle, despite the particle’s anisotropy, the Cartesian system can be applied without significant error. Table 13.2 shows the changes in description between coordinate systems for particles of different shapes: block (Cartesian), cylinders (Cylindrical) and spheres (Polar).

Table. 13.2 Coordinate systems for CFD systems

5 Thermal and Physical Properties of Lignocellulosic Biomass

5.1 Density

5.1.1 Density of Biomass

The composition and the structure of biomass differ significantly not only with plant species but also within individual specimens of the same species. Moreover, the climate, the availability of nutrients, solar radiation and genetic changes have an influence on the plant growth, hence its structure and composition. Also, different plant organs differ in structure and composition. This leads to significant differences in biomass densities among others. Analysis of apparent density (oven dry) data of 167 measurements of the Pinaceae family from the Global Wood Density Database shows a significant heterogeneity within one family of a single plant (n =167, average = 435 kg/m³, st. dev. = 65 kg/m³).

Measurement of the solid’s apparent density can be conducted by a simple measurement of weight over mass. This is not a very accurate method, especially for finely ground biomass or char samples, due to the free spaces between the grains of a solid. A more sophisticated method for measuring the apparent density is mercury porosimetry, in which Hg displaces gas around the grain. At atmospheric pressure, mercury is not able to penetrate pores whose size is below 15 μm. Therefore, the result of the measurement by mercury porosimetry is only slightly overestimated [52]. Due to the high toxicity of mercury, recently more interest is devoted to measurement methods with micro-granular suspensions. Their role is similar to mercury and relies on displacement of the gas from spaces between the grains. Some sources call the density measured with micro-granular suspensions as “envelope” density [73], in order to distinguish it from bulk density, but stay with the name “apparent” [74].

The true (skeletal, intrinsic) density is measured by helium pycnometry. The method uses helium as the pore displacement gas because it can penetrate pores with a diameter larger than 40 nm [52]. If the analysed material does not have closed pores, helium pycnometry allows for very accurate true density measurements. As is shown in the work by Brewer et al. [75], some pores in the biochar structure are not penetrable by helium, without prior grinding of the material.

Knowing both true and apparent densities and in case that samples were measured with zero moisture (dry state), the volume fraction occupied by gas, can be calculated using:

$$ {\varepsilon}_G=1-{\varepsilon}_S $$

(13.35)

The orientation of the cut plane of a sample during true density measurement influences the result due to the anisotropy within the wood cell walls. Table 13.3 shows a summary of the apparent and true densities together with resulting porosity for selected biomasses. If not specified, the sample anisotropy was not taken into account in the measurement.

Table. 13.3 Apparent and true densities together with resulting porosity of selected biomasses

5.1.2 Density of Char

The char’s density and porosity depend on the initial composition and structure of biomass, as well as on the conditions of a pyrolysis process. The production temperature has a significant effect on the char’s true density, as opposed to the heating rate, which seems to not have a relevant influence [75, 77]. In Table 13.4 data of the true and apparent (if available) density as well as the porosity of chars obtained from different biomasses distinguished by pyrolysis conditions is summarised. The theoretical maximum of the true density of a char is 2250 kg/m³, which refers to the true density of graphite [78], but in practice, the maximum that can be obtained is within the range between 2000 kg/m³ and 2100 kg/m³.

Table 13.4 True and apparent (if available) densities with resulting porosity of chars obtained from different biomasses

5.1.3 Densities of Bound and Liquid Water

Bound water is water that exists in the biomass structure, and which is partially incorporated into the cell wall. In literature an explanation of the interaction between bound water and the cell structure as well as information about the storage locations of bounded water can be found [79]. In general, the cell wall of biomass, due to its chemical structure, is hydrophilic in its nature, and it has the ability to interact with water molecules through hydrogen bonding. Through this mechanism, water is able to stick to the wall and occupy empty spaces in its structure [80].

The cells wall of biomass has only a finite ability to bind water. To describe the amount of water that can be bound to a wall, the term fibre saturation point (FSP) was introduced first by Tiemann in 1906 [79]. It is defined as the moisture content below which only bound water exists in a biomass structure. Above the fibre saturation point, cell walls cannot bind more water, so both bound and liquid water can exist. In literature, the two most commonly applied values of the base FSP have been reported: 30% proposed by Stamm in 1971 [81] and 40% proposed by Skaar in 1988 [82]. Measurements show that above the FSP, the density of the bound water is close to 1110 kg/m³ and with moisture content close to zero its value rises up to 1300 kg/m³ [83]. The bound water’s density increases at lower moisture content, according to the cell wall binding strength per amount of available water molecules [80]. In order to avoid over-complexity of the problem, authors typically use a constant value of 1000 kg/m³ for the true density of the bound water [52, 54, 57, 64, 65].

The true density of the liquid water depends on the temperature, due to its thermal expansion. In the pyrolysis conditions, the water does not significantly exceed 100 °C, so the simplification that the true density of water has a constant value of 1000 kg/m³ does not induce strong inaccuracies in the model.

5.1.4 Density and Pressure of Gases and Vapours

Temperatures and intrinsic pressures during pyrolysis allow for the assumption that gases and vapours can be treated as ideal gases, so:

$$ <{P}:i{>}^G=\frac{<{\rho}:i{>}^G RT}{M_i} $$

(13.36)

where <P_i>^G and M_i are the partial pressure and molar mass of i^th component in the gas mixture, respectively. The total gas density can be calculated from:

$$ <{\rho}:G{>}^G=\sum \limits_i^N<{\rho}:i{>}^G $$

(13.37)

The molecular mass of the gas mixture is defined as:

$$ {M}_G={\left(\sum \limits_i^N,\frac{<{\rho}:i{>}^G}{<{\rho}:G{>}^G{M}_i}\right)}^{-1} $$

(13.38)

where M_G is the mean molar mass of the gas mixture. The total gas pressure can be calculated as:

$$ <{P}:G{>}^G=\frac{<{\rho}:G{>}^G RT}{M_G} $$

(13.39)

where <P_G>^G is the total pressure. In case of the application of a simple, single-component model, permanent gases and tars are often treated not as a product mixture, but as single representative species of the mixture. For example in the work of Grønli [52], tars are represented by benzene with a molecular mass of 110 g/mol and gases are represented by a 1:1 mixture of carbon monoxide and carbon dioxide with a molecular mass of 38 g/mol.

5.2 Moisture Content and Saturation

The amount of water in biomass is described by the moisture content (MC), and calculated as:

$$ MC=\frac{mass\ of\ water}{mass\ of\ biomass\ (db.)} $$

(13.40)

The water in biomass can exist in two phases, so:

$$ MC={MC}_L+{MC}_B $$

(13.41)

where MC_L is the moisture related to the liquid water and MC_B is the moisture related to the bound water. To calculate both moisture contents, the value of the fibre saturation point (function of the temperate) has to be obtained, for example, with the equation proposed by Siau [84]:

$$ {MC}_{FSP}(T)=\left({M}_{FSP}^o+0.298\right)-0.001\ T $$

(13.42)

where MC_FSP is the fibre saturation point at a certain temperature, and ${M}_{FSP}^o$ is the base fibre saturation point (value between 0.3 or 0.4). Knowing that only above the fibre saturation point both types of water can be found in biomass, it can be stated that:

$$ {MC}_B=\min \left({MC}_{FSP}, MC\right) $$

(13.43)

$$ {MC}_L=\max \left( MC-{MC}_{FSP},0\right) $$

(13.44)

With the assumption that the water content in the gas phase is negligible, the apparent density of bound and liquid water can be calculated respectively:

$$ {MC}_B=\frac{<{\rho}:B>}{<{\rho}:S>} $$

(13.45)

$$ {MC}_L=\frac{<{\rho}:L>}{<{\rho}:S>} $$

(13.46)

where <ρ_S> is the solid’s apparent density in the dry state. Having the value of the true and apparent density for both water types, the volume fraction occupied by these phases can be calculated.

Saturation of a particle quantifies to what extent the space within pores is occupied by water. This value should not be confused with the MC_FSP. Saturation is defined as:

$$ S=\frac{liquid\ volume}{pore\ volume\ } $$

(13.47)

where pore volume is a particle’s empty (filled with gas) volume which theoretically can be occupied by the liquid water. When equal representative volumes are considered:

$$ S=\frac{MC_L}{MC_{sat}-{M}_{FSP}} $$

(13.48)

where MC_sat is the maximum moisture content which can be retained by a biomass structure:

$$ {MC}_{sat}={MC}_{FSP}+{MC}_{sat,L} $$

(13.49)

where MC_sat,L is the maximum liquid water content which can be retained by a biomass structure. Assuming that during the maximum saturation state all pores of biomass are filled with water, and that liquid and bound water have the same density, MC_sat can be obtained from the equation:

$$ {MC}_{sat}=<{\rho}:L{>}^L\left(\frac{1}{<{\rho}:S>},-,\frac{1}{<{\rho}:S{>}^S}\right) $$

(13.50)

In the literate devoted to wood drying, a parameter “irreducible water content of structure” (S_irr) can be found. It refers to the water bound so strongly to a cell wall structure that it is not removed during a conventional drying processes (up to 120 °C). In the model of a pyrolysis process of biomass, it is not advisable to implement such parameter for two reasons. First, the energy flux added to water is much higher than in conventional drying due to higher temperatures. Theoretically, it should allow for complete unbinding of water. Second, even if the energy flux would be insufficient during the pyrolysis, the structure of biomass changes and cell walls lose their binding ability (hydrophilicity).

5.3 Capillary Pressure

For models in which the transportation term for the liquid water is included in the mass conservation equation, the capillary pressure needs to be defined. Capillary pressure in the lumens of wood is defined as:

$$ <{P}:L{>}^L=<{P}:G{>}^G+{P}_C $$

(13.51)

where P_C is a capillary pressure and <P_L>^L is pressure in of the liquid water. In literature different correlations for the capillary pressure can be found. An extensive comparison can be found in the work of Jalili et al. [54]. Here are shown only two, most commonly used empirical correlations, one by Spolek and Plumb [85]:

$$ {P}_C=\frac{8.4\cdotp {10}^4}{S^{0.63}} $$

(13.52)

where S is the saturation. The second, by Perre and Degiovanni [86]:

$$ {P}_C=\frac{1.364\cdotp {10}^5\ \sigma (T)}{{\left({MC}_L+1.2\cdotp {10}^{-4}\right)}^{0.63}} $$

(13.53)

where σ(T) is the temperature-related coefficient, defined as:

$$ \sigma (T)=\left(128-0.185\ T\right)\cdotp {10}^{-3} $$

(13.54)

Both above mentioned empirical correlations were established for softwood. Therefore they should be applied only for modelling those biomasses due to significant differences in pore size, pore shape and surface wettability with other wood types.

5.4 Permeability

The permeability has a major influence on the fluid movement through a porous structure. The permeability determines the superficial velocity and pressure formation of gases and transport of liquid water in a porous biomass structure.

5.4.1 Intrinsic Permeability of Biomass

The proper assumption regarding biomass permeability is not an easy task. As it was pointed out by Grønli [52], the value of the intrinsic gas permeability of wood shows high variability and strongly depends on:

• type of wood: hardwood or softwood

• position in the plant from which the wood sample was taken: heartwood (older part) or sapwood (younger part)

• cut plane direction (related to sample anisotropy): longitudinal, tangential or radial

Table 13.5 contains experimental data of the intrinsic gas permeability of selected biomasses. As it can be noticed, sapwoods show higher intrinsic gas permeability than heartwoods. Regarding the cut plane direction, the permeability in the longitudinal direction is much higher than in the radial or tangential direction, for which values are comparable. Taking this into account, the assumption that radial and tangential permeability are equal does not lead to a significant loss in model accuracy. In publications related to modelling, the implemented values of the intrinsic gas permeability sometimes differ significantly from those experimentally obtained. For example, some authors adjust the permeability values according to the simulation’s result, or, as it was done by Di Blasi [71], the author adapted permeability to obtain the same pressure as in the experimental data from Lee et al. [87].

Table 13.5 Intrinsic gas permeability for selected biomass in different directions

Analysis of the intrinsic gas permeability with differentiation on the cut plane direction, for c.a. 100 different wood samples was made by Smith and Lee in 1958 [84]. Results of their study are presented in Fig. 13.5. Values of the longitudinal permeability used by modellers are in general within the range of experimental data, but for the radial permeability, values are usually overstated by at least one order of magnitude [50, 71, 90,91,92,93]. From experimental data, it can be stated that the valid range for the longitudinal intrinsic gas permeability is between 10⁻¹¹ m² and 10⁻¹⁷ m² and for the radial between 10⁻¹⁵ m² and 10⁻¹⁹ m².

Fig. 13.5

Intrinsic gas permeability range for woods, based on the data from Smith and Lee [84] (s sapwood, h heartwood,∗ sample from the coast, ∗∗ sample from mountains)

5.4.2 Intrinsic Permeability of Char

The thermal decomposition of biomass increases the internal volume of the structure. Therefore, chars formed in pyrolysis show higher permeability than the initial biomass due to an increase of the size of the channels (pore size) and development of new pores and cracks in the cell walls. Experimentally measured permeabilities of char are rarely found in the literature. Hence, most works related to the modelling of biomass pyrolysis estimate its value. Usually, the permeability of a char in the longitudinal direction is estimated to be about 1–2 orders of magnitude higher, and in the radial and tangential direction from 1 to 4–5 orders of magnitude higher than a value of the initial biomass. In Table 13.6 data of the intrinsic permeability of a pinewood char is presented. Unfortunately, the data source did not provide information regarding the direction other than the longitudinal.

Table 13.6 Pinewood char’s longitudinal intrinsic gas permeability as a function of pyrolysis temperature [94]

5.4.3 Intrinsic Permeability of Liquid Water

Table 13.7 shows a summary of the relationship between the intrinsic permeability of a gas and liquid water in biomass. According to the literature, the liquid permeability should be in the range of ±1 order of magnitude different than that of the gas permeability. It is worth to mention that during pyrolysis at any given time, the liquid water does not co-exist with the char.

Table 13.7 Relationship between gas and liquid intrinsic permeability in biomass

5.4.4 Intrinsic, Relative and Effective Permeability

The intrinsic permeability at any time of the reaction is defined as:

$$ {K}_{ph}={X}_{BM}{K}_{ph, BM}+{X}_{BC}{K}_{ph, BC} $$

(13.55)

where K_ph is the intrinsic permeability of a phase and X_BM and X_BC are the mass ratio of the unreacted biomass and biochar in the solid matrix, respectively. The subscript ph refers to a particular phase (gas or liquid).

The relative permeability reflects the difference between a material effective permeability in a wet state and the intrinsic permeability in a dry state. The correlation of moisture content and the permeability is expressed by the saturation. The most commonly used correlation is the one developed by Perre et al. [97] and is shown in Table 13.8. It is based on experimental data retrieved on softwood. In literature, other correlations between saturation and relative permeability are also available [54].

Table 13.8 Most commonly used correlations for relative gas and liquid permeabilities [96]

The effective permeability consists of two parts: a first related to the solid porous structure (intrinsic permeability) and a second related to the effect of saturation of pores on the fluid movement (relative permeability). Effective permeability can be calculated as:

$$ {K}_{ph, eff}={K}_{ph}\cdotp {K}_{ph, rel} $$

(13.56)

where K_ph,eff is the effective permeability of a phase, K_ph is the intrinsic permeability of a phase, and K_ph,rel is the relative permeability of a phase.

5.5 Diffusion

5.5.1 Bound Water Diffusion

The migration of bound water arises only from diffusion through cell walls of biomass. Mathematically, such transport can be described using Fick’s law [98]. During pyrolysis and at any given time, bound water does not co-exist with biochar.

By fitting the experimental data of bound water diffusivity in a transverse direction, the following correlations based on the Arrhenius expression were proposed:

Perre and Degiovanni [86]:

$$ {D}_{B,T}=\exp \left(-9.9+9.8\ {MC}_B-\frac{4300}{T}\right) $$

(13.57)

Perre and Turner [98]:

$$ {D}_{B,T}=\exp \left(-12.818+10.895\ {MC}_B-\frac{4300}{T}\right) $$

(13.58)

Stamm [99] stated that the following dependency exists between diffusion of bound water in different directions:

$$ {D}_{B,T}\cong \frac{1}{3}{D}_{B,L}\cong \frac{2}{3}{D}_{B,R} $$

(13.59)

where subscripts T, L, and R denote the transverse, longitudinal and radial direction respectively. More complex dependency between bound water diffusion and direction can be found in the works of Pierre and Turner [98, 100].

5.5.2 Gas Binary Diffusion

The gas-vapour mixture, which exists in the pores during pyrolysis consists of a variety of compounds in different concentrations and its composition changes as the process progresses. Mathematical description of such a process is not straightforward.

Application of binary diffusion description is valid only for systems where only two major components interact with each other, and there are no other components or their influence on a mixture is negligible. Also, binary diffusion is based on the assumption that one compound has to be indicated as an inert during the whole process. Such a situation is far different from the one that takes place in the pores during the pyrolysis process of biomass. Therefore, the application of the binary diffusion description can lead to significant inaccuracies in prediction. Hence, other more complex ways of describing diffusion have to be applied. A satisfactory procedure which is always valid for a multi-component system is the Maxwell-Stefan equations system, so in theory, its application would be the most valid option [101].

Diffusion is the dominating transport phenomenon only in systems where large pressure gradients do not exist. An increase in the pressure gradient leads to a reduction of the diffusion’s share in the overall transport of gases, as convection becomes the dominating phenomenon of transport [52]. During pyrolysis of dry biomass, especially at high temperatures and with a high heating rate, the pressure gradients are significant, which indicates that the diffusion does not play a major role in gas transport. It leads to the conclusion that implementation of the binary diffusion model, which will be rather inaccurate, but fairly simple in implementation and easy in computation should not add a significant inaccuracy to the prediction of fast pyrolysis. In general, it is always advised to try to avoid the application of a robust, global description, which can be overcomplex and simultaneously not lead to visible improvement in modelling accuracy.

On the other hand, for a pyrolysis process of wet biomass, so combined with particle’s drying, the diffusion of water vapour can be significant. Especially for pyrolysis of a large particle that is exposed to moderate thermal conditions, where evolved pressure gradients can be insufficient to shift the convection into the dominant transport process. For such situations, an assumption that diffusion is negligible will not be valid. During drying, an inert (most often nitrogen)—water vapour system will appear, which can be described satisfactorily by binary diffusion. Often in practice, the binary diffusion of an inert-water vapour system is treated as an air-water vapour system instead of nitrogen-water vapour system due to the marginal difference in gas properties and higher availability of data for the air-water vapour system.

The air-water vapour binary diffusion coefficient (D_A/V), in function of the temperature and the pressure inside a particle, can be calculated with the equation proposed by Siau [84]:

$$ {D}_{A/V}=2.23\cdot {10}^{-5}\frac{\ {T}^{1.81}}{<{P}:G{>}^G} $$

(13.60)

Alternatively, it can be calculated with a more often used equation, proposed by Grønli [52]:

$$ {D}_{A/V}=1.192\cdot {10}^{-4}\frac{\ {T}^{1.75}}{<{P}:G{>}^G} $$

(13.61)

Correlations above can be used not only for the water vapour but also for other compounds in the pyrolysis gas mixture without introduction of a significant error. If higher accuracy is needed, a discrete description of the binary diffusion coefficient for each component of a system can be calculated with the Chapman-Enskog equation, based on the kinetic gas theory, or with the equation proposed by Poling et al. [102]:

$$ {D}_{inert/i}=1.43\cdotp {10}^{-7}\frac{T^{1.75}}{P\ {M_{inert/i}}^{1/2}\ {\left[{\left({\Sigma}_v^{inert}\right)}^{1/3}+{\left({\Sigma}_v^i\right)}^{1/3}\right]}^2} $$

(13.62)

where D_inert/i is the binary diffusion coefficient between an inert and an i^th component, Σ_v is the sum of the atomic diffusion volumes (from Poling et al. [102]) and M_inert/i is the mean molecular mass ratio between an inert and an i^th compound.

The diffusion phenomena are omitted in certain publications related to modelling of pyrolysis of dry biomass [28, 42, 56, 103]. Authors who modelled the pyrolysis of wet biomass have treated the diffusion coefficients as constant values (range from 10⁻⁶ m²/s to 10⁻⁵ m²/s) for all gas species in order not to overcomplicate the model [59, 91, 92, 104]. Such approaches are not fully invalid with respect to the minor role of diffusion in the overall transport of gases in specific cases.

5.5.3 Effective Gas Diffusion Coefficient

Besides the gas mixture composition, the structure of the porous material in which the diffusion process takes place has an influence on the diffusion coefficient. The effective gas diffusion coefficient can be defined as:

$$ {D}_{eff,\kern0.75em inert/i}=\uptheta\ {D}_{inert/i} $$

(13.63)

where D_{eff,  inert/i} is the effective inert—i^th component diffusion coefficient, D_inert/i is the inert—i^th component diffusion coefficient and θ is the structure resistance factor (tortuosity factor). The structure resistance factor is an artificial parameter describing the restriction of diffusion in narrow pores, which can be linked to the porosity. The correlation of the structure resistance factor to porosity is obtained by fitting a function to the experimental data. A summary of the correlations available in literature is shown in Table 13.9.

Table 13.9 Proposed correlations for the structure resistance factor

5.6 Heat Capacities

5.6.1 Heat Capacity of Biomass

In the literature devoted to drying of biomass, empirical correlations can be found which combine the influence of temperature and moisture content (liquid and bound water) on the specific heat of biomass. Since there are no theoretical reasons to combine the effects of both parameters into one correlation, the specific heat of biomass and water will be treated separately.

Biomass starts its degradation in the temperature range from 200 °C to 250 °C. Therefore the range of temperature for which specific heat of biomass has to be described is more narrow than for gas and vapour compounds. One of the most commonly used correlations is the one obtained experimentally by Grønli [52] for spruce wood and is valid in the range from 80 °C to 230 °C:

$$ {C}_{P, BM}=1500+T $$

(13.64)

where C_{P, BM} is the specific heat of biomass. Dupont et al. [110] conducted an analysis of the specific heat of 19 different biomasses in the temperature range from 40 °C to 80 °C. The result for every biomass shows a linear change of the specific heat with temperature in the investigated range. Taking into account Grønli’s correlation, it can be assumed that this trend will be kept until the temperature at which biomass starts to thermally decompose. Averaged for all biomasses used in the study of Dupont et al., the correlation between the specific heat and the temperature has the form:

$$ {C}_{P, BM}=1032.8+3.783\ T $$

(13.65)

It is proven that the specific heat of biomass is a function of temperature, but in some older publications, it can be found that the parameter as a constant value [87, 91, 92]. Recent work of Gorensek et al. [111] deserves attention in where the authors, starting from fundamentals of thermodynamics, calculated missing heat capacities of artificial, initial components and their transitional forms from the Ranzi scheme. Thereby, they allowed for the implementation of biomass into the model as a mixture of individual bio-components.

5.6.2 Heat Capacity of Char

The most well-known correlation between the specific heat of char and the temperature is the one provided by Raznjevic [67], valid in the range from 0 °C to 1000 °C:

$$ {C}_{P, BC}=1430+0.355\ T+6.85\cdotp {10}^{-4}\ {T}^2 $$

(13.66)

where C_{P, BC} is the specific heat of biochar. In literature, also other correlations for specific heat capacity can be found, e.g. one proposed by Larfeldt et al. [93], valid in the range from 0 °C to 800 °C:

$$ {C}_{P, BC}=420+2.09\ T-\frac{7.32\cdotp {10}^7}{T^2} $$

(13.67)

The specific heat for solids at any given time of the reaction is defined as:

$$ {C}_{P,S}={X}_{BM}{C}_{P, BC}+{X}_{BC}{C}_{P, BM} $$

(13.68)

where C_P,S is the specific heat of the solid.

5.6.3 Heat Capacity of Bound and Liquid Water

Liquid water heat capacity (C_P,L) at the atmospheric pressure does not change significantly within the range from 20 °C to 100 °C. Therefore the value of its heat capacity can be assumed as a constant value of 4.20 kJ/(kg K), which is an averaged value within the mentioned temperature range. The specific heat of the bound water (C_P,B) is assumed to be slightly higher than the liquid water. Hunt et al. [112] proposed a value of 4.66 kJ/(kg K), but this is a rough estimated value, not measured analytically. For the sake of simplicity, the value of C_P,B can be treated as equal to C_P,L without introducing significant error.

5.6.4 Heat Capacity of Gases and Vapours

The specific heat correlation of compounds in the gas mixture applied in a model depends on the complexity of the kinetic scheme. For all low-molecular compounds and most of the high-molecular compounds data can be obtained from the NIST Chemistry WebBook [113] and Gorensek et al. [111]. In case of missing heat capacity data for a specific compound, the authors suggest to find the data record of a compound with similar mass, chemical structure, and chemical properties and treat it as a representative. If more accuracy is needed, the use of thermodynamically based approaches provided by Gordon and McBride [114] is advised.

For the single component reaction scheme, only four representative compounds have to be described: air, water vapour, gas (1:1 mixture of CO and CO₂) and tar (benzene). For the mentioned compounds, Grønli’s correlations [52] can be used:

$$ {C}_{P, Air}=950+0.188\ T $$

(13.69)

$$ {C}_{P,v}=1670+0.64\ T $$

(13.70)

$$ {C}_{P, Tar}=-100+4.4\ T-1.57\cdotp {10}^{-3}\ {T}^2 $$

(13.71)

$$ {C}_{P, Gas}=770+0.629\ T-1.91\cdotp {10}^{-4}\ {T}^2 $$

(13.72)

where C_P, is the specific heat and subscript Air, v, Tar and Gas denotes air, water vapour, tars and gases, respectively. The specific heat for the gas-vapour mix at any time in the process can be obtained from an equation:

$$ {C}_{P,G}=\frac{\sum \limits_i^N{C}_{P,i}<{\rho}:i{>}^G}{<{\rho}:G{>}^G} $$

(13.73)

where C_P,G is the specific heat of the gas-vapour mix and C_P,i is the specific heat for the i^th component of the gas mixture.

5.7 Dynamic Viscosities of Fluids

5.7.1 Dynamic Viscosity of Gases-Vapour Mixture

According to the definition, viscosity is a property of a fluid which indicates its resistance to flow (i.e. continual deformation). The viscosity of fluids depends strongly on temperature and pressure. In the atmospheric pyrolysis, a pressure change during the process is not significant in relation to viscosity, so the pressure influence on fluid viscosity can be omitted. The temperature between the start and the end of the pyrolysis usually exceeds a few hundred degrees, so its influence on the viscosity is significant. Therefore, the temperature dependence of the viscosity should be to implemented into a model.

Similar to heat capacity, the correlations of the viscosity of compounds in the gas mixture applied in a model depend on the complexity of the kinetic scheme. Data for permanent gases and light organic compounds can be found in the NIST database [113]. Heavy organic compounds, for which data is lacking, can be replaced by other, similar compounds and treat them as representatives. The missing data can also be calculated, according to the procedure provided by Poling et al. [102]. For the single component kinetic scheme, the correlations valid in the range from 0 °C to 1000 °C, for air, water vapour, tars and gases, provided by Grønli [52] can be applied:

$$ {\mu}_{G, Air}=9.12\cdotp {10}^{-6}+3.27\cdotp {10}^{-8}\ T $$

(13.74)

$$ {\mu}_{G,v}=-1.47\cdotp {10}^{-6}+3.78\cdotp {10}^{-8}\ T $$

(13.75)

$$ {\mu}_{G, Tar}=-3.73\cdotp {10}^{-7}+2.62\cdotp {10}^{-8}\ T $$

(13.76)

$$ {\mu}_{G, Gas}=7.85\cdotp {10}^{-6}+3.18\cdotp {10}^{-8}\ T $$

(13.77)

where μ_G is the dynamic viscosity of gaseous matter and subscript Air, v, Tar and Gas denote air, water vapour, tars and non-condensable gases, respectively. To calculate the viscosity of a gas mix at any given time, the Graham model can be used:

$$ {\mu}_G=\frac{\sum \limits_i^N{\mu}_{G,i}<{\rho}:i{>}^G}{<{\rho}:G{>}^G} $$

(13.78)

where μ_G is the viscosity of the gas mix and μ_{G, i} is the viscosity of the i^th component of the mixture. Above mentioned Eq. (13.78) is appropriate for rough calculations, and it is fully valid only when the molar masses of the mixture components are relatively similar [115]. For a more accurate calculation it is advised to use the Wilkie model with the Herning and Zipperer approximation:

$$ {\mu}_G=\frac{\sum \limits_i^N{\mu}_{G,i}<{\rho}:i{>}^G\sqrt{M_i}}{\sum \limits_i^N<{\rho}:i{>}^G\sqrt{M_i}} $$

(13.79)

where M_i is the molar mass of the i^th component in the mixture. In most of the publications related to modelling, the subject of viscosity is treated with neglect. Most of the authors apply the assumption that the viscosity of gases and vapours is invariant to either the gas mix composition and the temperature and its value is constant, equal to 3 × 10⁻⁵ Pa s.

5.7.2 Dynamic Viscosity of Liquid Water

As it was mentioned in Sect. 13.4.3.3, only the liquid water has the ability to move actively through convection. The viscosity of liquid water as a function of temperature can be calculated with the equation proposed by Grønli [52]:

$$ {\mu}_L=1.40\cdotp {10}^{-2}-7.30\cdotp {10}^{-5}\ T+9.73\cdotp {10}^{-8}\ {T}^2 $$

(13.80)

where μ_L is the liquid water viscosity. Alternatively the correlation proposed by de Paiva Souza et al. [116] can be used:

$$ \log \left({\mu}_L\right)=-13.73+\frac{1828}{T}+1.97\cdotp {10}^{-2}\ T-1.97\cdotp {10}^{-5}\ {T}^2 $$

(13.81)

5.8 Thermal Conductivity

5.8.1 Thermal Conductivity of Biomass

For particles in the thermally thick regime, thermal conductivity and radiative thermal conductivity have a major influence on the thermal behaviour of the biomass sample. Therefore their appropriate implementation into the model is crucial in terms of the model accuracy.

In Table 13.10 is shown a summary of thermal conductivity data of different biomasses. The thermal conductivity of biomass depends on the bio-composition and structure of the cell wall as well as on the direction of the cut plane (direction of fibres). A rough analysis of the data indicates that the thermal conductivity of hardwoods in the longitudinal direction is c.a. 1.6 times higher than the thermal conductivity in the radial direction. The difference for softwoods is much higher and the ratio of longitudinal to radial thermal conductivity has a value of 2.7. On average, the difference in thermal conductivity in the longitudinal direction between both wood types is relatively low. The difference between both wood types is more visible for the radial thermal conductivity, where hardwoods show c.a. 1.5 times higher thermal conductivity than for softwoods.

Table 13.10 Data of thermal conductivity of different biomasses

5.8.2 Thermal Conductivity of Char

The thermal conductivity of char depends strongly on the initial thermal conductivity of the parent biomass, as well as on the pyrolysis process conditions. In Table 13.11 summarised data of char thermal conductivity originating from different biomasses are shown, at different pyrolysis temperatures. In general, an increase in the pyrolysis temperature results in a decrease in the char thermal conductivity. Data indicate that the thermal conductivity in the longitudinal direction is much less sensitive to the pyrolysis temperature than the one in the radial direction (relative change of 1.3 for the longitudinal direction and 2.4 for the radial direction). For chars originating from softwood and pyrolysed at 470 °C, the longitudinal thermal conductivity is on average five times higher than the radial thermal conductivity. It is suspected that such a large change in the radial direction is related by breaking the continuity of the cell wall’s structure caused by the bio-polymers degradation.

Table 13.11 Data of thermal conductivity of char originated from different biomasses

The thermal conductivity of solids in a given direction (D = L, R, T) at any given time of the reaction is defined as:

$$ {\lambda}_{S,D}={X}_{BM}{\lambda}_{BM,D}+{X}_{BC}{\lambda}_{BC,D} $$

(13.82)

where λ_BM,D and λ_BM,D denote the thermal conductivity in a given direction for biomass and biochar, respectively.

5.8.3 Thermal Conductivity of Liquid and Bound Water

The thermal conductivity of liquid water as a function of temperature can be obtained through the correlation of data from the NIST database [113]:

$$ {\lambda}_L=0.7695+7.5\cdotp {10}^{-3}\ T-1\cdotp {10}^{-5}\ {T}^2 $$

(13.83)

In literature, constant values of thermal conductivity of liquid water, i.e. 0.658 W/(m K) [52] can be found. Due to a lack of experimental data regarding the thermal conductivity of bound water, it has to be assumed that its thermal conductivity value is similar to that of liquid water.

5.8.4 Thermal Conductivity: Gas Mixture

The thermal conductivity of most of the permanent gases, light and heavy organic compounds can be found in tables [67, 122, 123] or in the NIST database [113]. Heavy organic compounds, for which data is lacking, can be replaced by other, similar compounds and treat them as representatives. The missing data can also be calculated, according to the procedure provided by Poling et al. [80]. For the single component kinetic scheme, correlations between the thermal conductivity and the temperature for air, water vapour and permanent gases are based on data from NIST [113], and they are valid in range from 0 °C to 1000 °C. The correlation for tar (benzene) can be obtained from the work of Zaitseva et al. [124], and it is valid in the range from 320 °C to 660 °C.

$$ {\lambda}_{G, Air}=9.3\cdotp {10}^{-3}+6\cdotp {10}^{-5}\ T $$

(13.84)

$$ {\lambda}_{G,v}=-8.1\cdotp {10}^{-3}+1\cdotp {10}^{-3}\ T $$

(13.85)

$$ {\lambda}_{G, Tar}=-5.07\cdotp {10}^{-1}+1.1\cdotp {10}^{-3}\ T $$

(13.86)

$$ {\lambda}_{G, Gas}=1.01\cdotp {10}^{-2}+4\cdotp {10}^{-5}\ T $$

(13.87)

Analogous to the viscosity, the thermal conductivity of a gas mixture at any time in the pyrolysis process can be calculated with the equation:

$$ {\lambda}_G=\frac{\sum \limits_i^N{\lambda}_{G,i}<{\rho}:i{>}^G}{<{\rho}:G{>}^G} $$

(13.88)

where λ_G,i is the thermal conductivity of the i^th component in the gas mix. For more accurate calculations, the Wassilijewa’s equation with the Herning and Zipperer approximation can be used:

$$ {\lambda}_G=\frac{\sum \limits_i^N{k}_{G,i}<{\rho}:i{>}^G\sqrt{M_i}}{\sum \limits_i^N<{\rho}:i{>}^G\sqrt{M_i}} $$

(13.89)

where M_i is the molar mass of the i^th component in the mixture. Many authors use simplifications and implement the thermal conductivity of the gas mix as a constant value in the range from 0.025 W/(m K) to 0.026 W/(m K) [52, 56, 91, 103].

5.8.5 Radiative Heat Transfer

When the pyrolysis temperature exceeds 600 °C, the share of the heat transferred through radiation within the particle starts to become significant. In such cases, implementation of the radiative heat transfer into the model is necessary. Radiative thermal conductivity within a particle can be defined as:

$$ {\lambda}_{rad}=A\ {\ell}_n\ \sigma\ {T}^3 $$

(13.90)

where λ_rad is the radiative thermal conductivity, ℓ_n is the photon’s mean free path, σ is the Stefan-Boltzman constant and A is the coefficient of the radiative model. In Table 13.12 are presented the most commonly used correlations for radiative thermal conductivity, others can be found in work of Grønli [52].

Table 13.12 Models of radiative thermal conductivity

Table 13.13 Exemplary values of final shrinkage parameter in pyrolysis, and obtained experimentally

Where ω is the surface emissivity and d_pore is the average diameter of the pores, calculated as:

$$ {d}_{pore}={X}_{BM}\ {d}_{pore, BM}+{X}_{BC}\ {d}_{pore, BC} $$

(13.91)

where d_pore is the average pore’s size and subscripts BM and BC denote the biomass and the biochar, respectively. The average pore size of biomass or biochar in the equation above is obtained from the whole range of pores existing in the structure (micro-, meso- and macropores). Therefore, its value should be obtained by helium pycnometry.

Regarding the influence of the pore size on the radiative thermal conductivity, the work of the Janse et al. [104] is worth to mention. They proposed a division of the radiative thermal conductivity in the macropore radiative conductivity and the micropore radiative conductivity. Such an approach seems intuitively reasonable and in theory, it should be more accurate. Nonetheless, the lack of reliable data regarding the pore size distribution of the biochar and its evolution throughout pyrolysis does not allow to obtain solid proof. In the literate applications of Janse et al.’s radiative heat transfer model with an averaged pore size [57, 65] can be found.

5.8.6 Effective Thermal Conductivity

The effective thermal conductivity depends on the following factors: anisotropy of the structure, porosity and pore size distribution, bio-composition of the cell wall and water content. In literature examples of correlations for the thermal conductivity of wet biomass particles obtained empirically can be found. In most cases, they were applied for the description of a drying process, not pyrolysis combined with drying [50, 72, 84, 86, 126]. In order to describe the thermal conductivity of biomass, the following general equation is often used:

$$ {\lambda}_{eff,D}={\lambda}_{cond,D}+{\lambda}_{rad} $$

(13.92)

where λ_eff,D is the effective thermal conductivity, λ_cond,D is the thermal conductivity, λ_rad is the internal radiative thermal conductivity and the subscript D denotes the direction of the conduction. The thermal conductivity can also be treated as a function based on conduction through the solid matter with respect to the heat transfer direction (λ_S,D), the conduction through the liquid and bound water (λ_L, λ_B) and the conduction through gas filling the pores (λ_G). The last three terms are not directionally dependent.

$$ {\lambda}_{cond,D}=f\left({\lambda}_{S,D}+{\lambda}_L+{\lambda}_B+{\lambda}_G\right) $$

(13.93)

The share of each thermal conductivity component is proportional to its volume fraction, so the effective thermal conductivity within a particle can be defined as:

$$ {\lambda}_{eff,D}=\left({\varepsilon}_S\ {\lambda}_{S,D}+{\varepsilon}_L\ {\lambda}_L+{\varepsilon}_B\ {\lambda}_B+{\varepsilon}_G\ {\lambda}_G\right)+{\lambda}_{rad} $$

(13.94)

More detailed approaches on the modelling of the thermal conductivity can be found in work of Suleiman et al. [120], Thunman and Leckner [127], Blondeau and Jeanmart [40] and Gentile et al. [53]. All mentioned approaches are based on the comprehensive thermal conduction model developed by Kollmann and Côte [128].

5.9 Surface Emissivity

Radiative heat emissivity from natural surfaces is usually modelled as a “grey body”. According to the definition and the Stefan-Boltzmann law, a “grey body” is an intermediate material between a perfect absorber of light (ideal “black body”) and a perfect reflector of light (ideal “white body”). The value of the emissivity of the “grey body” depends on the surface’s temperature, colour and roughness. For biomass, emissivity (ω_BM) is usually assumed to be in the range between 0.7 and 0.85 [64, 65] and for biochar (ω_BC) in the range between 0.9 and 0.95 [52, 59]. The surface emissivity (ω) at any time of the process can be defined as:

$$ \omega ={X}_{BM}{\omega}_{BM}+{X}_{BC}{\omega}_{BC} $$

(13.95)

5.10 Particle Shrinking

Drying and thermal degradation of a biomass particle have an influence not only on its porosity and thermo-physical properties but also on its overall geometry and shape. To model a particle’s change in geometry and shape, usually, one out of three methods of shrinking process description is applied: uniform shrinkage, shrinking shell, or shrinking cylinder.

An analysis of shrinkage during pyrolysis shows that final shrinkage in the longitudinal direction is lower than in the radial direction. Additionally, for small particles, the shrinking takes place mostly at the end of the conversion. During the conversion under a high heating rate, strong mechanical tensions occur within a particle, which leads to particle cracking and in some cases, even to the fragmentation of a particle. Besides the reduction in particle shape by shrinking, the expansion via the swelling can take place. The expansion can be observed usually at the beginning of the conversion, especially for large particles [129]. The details regarding cracking and swelling are not incorporated in mentioned models of shrinking.

A detailed description of mentioned shrinking models can be found in the work of Bryden et al. [61] and Bellais [130]. The most commonly used shrinking model is the uniform shrinking model, so its basis will be briefly described here. Shrinking in a selected direction can be defined as [61]:

$$ {f}_D=\frac{current\ dimension}{original\ dimension}=\frac{L_D}{L_{D0}} $$

(13.96)

where f_D is the shrinkage factor in the D direction, L_D is the dimension after shrinkage in the D direction and L_D0 is the original dimension in the D direction. The uniform shrinking model assumes, that particle size change is directly proportional to the mass loss, so it can be stated that:

$$ {f}_D=\left[\left(\overline{\eta}-1\right){p}_D+\left(\overline{\mathrm{M}}-1\right){m}_D\right] $$

(13.97)

where $\overline{\eta}$ is the conversion extent of pyrolysis, averaged over the particle’s geometry, p_D is the parameter of final shrinkage due to pyrolysis in direction D, $\overline{M}$ is the progress of the particle’s drying, averaged over the particle’s geometry, m_D is the parameter of final shrinkage due to drying in the D direction. The drying influence on the shrinkage in any direction is not large (6–7%) [61], so its omission does not introduce significant accuracy loss in modelling [131]. Applying the aforementioned simplification, the following equation is obtained:

$$ {f}_D=\left[\left(\overline{\eta}-1\right){p}_D\right] $$

(13.98)

The averaged conversion extent of the pyrolysis reaction is defined as:

$$ \overline{\eta}=\frac{current\ mass\ of\ biomass}{inital\ mass\ of\ biomass}=\frac{<{\rho}:{BM}>}{<{\rho}:{BM0}>} $$

(13.99)

where <ρ_BM0> is the initial apparent density of biomass. A more in-depth description of changes to the conservation equations due to implementation of the uniform shrinking model can be found in the work of Bryden et al. [61] and Anca-Couce et al. [56].

Exemplary final shrinkage parameters that can be found in the literature are summarised in Table 13.13. The symbols α, β and γ denote the final shrinkage in the longitudinal (p_L), radial (p_R) and transversal (p_T) direction, respectively. The data in the table indicates that the final particle shrinkage depends not only on the pyrolysis temperature but also on the heating rate.

An extensive analysis of particle shrinkage was performed by Davidson et al. [133]. It resulted in a correlation between the highest temperature in pyrolysis and the final shrinkage parameter in direction D. The correlation is valid for temperatures from 350 °C to 700 °C.

$$ {p}_D={a_D}^2\left[{a}_D+{b}_DT+{c}_D{T}^2\right] $$

(13.100)

where a_D, b_D and c_D are correlation parameters obtained by fitting to experimental data. Their values are shown in Table 13.14.

Table 13.14 Parameters of Davidson et al. correlation [133]

6 Boundary Conditions

6.1 Boundary Conditions Equations

Boundary conditions are the drivers of the modelled process through the description of phenomena occurring on the geometrical surface of a particle. In other words, boundary conditions define the behaviour of the nodes located on the geometry edge. In the most general case, they are defined as [134]:

• For pressure:

$$ {\left.\operatorname{}<{P}:G{>}^G\ \right|}_{x={x}_p}={P}_{\infty } $$

(13.101)

• For heat transfer:

$$ {\left.\nabla \left({\lambda}_{eff}\nabla T\right)\ \right|}_{x={x}_p}={h}_T\left({\left.{T}_{flow,\infty }-T\ \right|}_{x={x}_p}\right)+\sigma \omega \left({\left.{T}_{wall}^4-{T}^4\right|}_{x={x}_p}\right) $$

(13.102)

• For mass transfer:

$$ {\left.\operatorname{}{D}_{eff}\nabla \left(<{\rho}:i{>}^G\right)\ \right|}_{x={x}_p}={h}_m\left[{\left.\operatorname{}{\rho}_{i,\infty }-<{\rho}:i{>}^G\right|}_{x={x}_p}\right] $$

(13.103)

where $\mid {}_{x={x}_p}$ denotes the position (x_p point of the surface, “x” can be adapted according to the appropriate coordinate system), P_∞ is the pressure of the environment (ambient), h is the convective transfer coefficient, subscript T and m denote heat and mass respectively, T_flow,∞ is the temperature of the flowing fluid at a considerable distance from the particle’s surface, T_wall is the temperature of the reactor wall, σ is Stefan-Boltzmann coefficient, ω is surface emissivity and ρ_i,∞ is the density of the i^th compound at a considerable distance from the particle’s surface. Even though the radiative heat transfer at a temperature below 600 °C does not have a large share in the total heat exchange [135], its implementation is not complex and can result in improvements in model accuracy.

6.2 Dimensionless Numbers and Transfer Coefficients

Convective heat and mass transfer coefficients can be obtained from correlations of the dimensionless numbers.

• The convective heat transfer coefficient from the Nusselt number:

$$ Nu=\frac{h_T\ L}{\lambda_{eff}} $$

(13.104)

• The convective mass transfer from the Sherwood number:

$$ Sh=\frac{h_m\ L}{D_{eff}} $$

(13.105)

where L is the characteristic dimension of a particle, h_T is the convective heat transfer coefficient, h_m is the convective mass transfer coefficient, λ_eff is the effective thermal conductivity and D_eff is the effective diffusion coefficient. For laminar flow, the dimensionless numbers can be obtained from flow-shape correlations presented in Table 13.15.

Table 13.15 Dimensionless number correlations as a function of shape [134, 136]

Where Pr is Prandtl’s number, Sc is Schmidt’s number, μ is the dynamic viscosity of the gas mix, and subscript ∞ and S denote the free stream and the surface (on the fluid’s side) respectively. Above mentioned correlations are valid only for particles immersed in a single-phase flow. It is advised to use other correlations to calculate the convective heat and mass transfer coefficient of particles immersed in two-phase flows (e.g. gas-solid systems in a fluidised bed), [92, 137,138,139,140].

Rapid evaporation or ignition of evolved pyrolysis gases can cause a temporary disturbance in the convective transfer. In order to account for it in a model, Stefan’s correlation can be used to calculate the mass and heat convective transfer coefficients with an extensive outflow from surfaces [57, 65, 92, 101]. Correlations are defined as:

• Heat transfer:

$$ {h}_{Ts}=\frac{A_S{u}_G{\varepsilon}_G<{\rho}:G{>}^G{C}_{P,G}}{\exp\ \left(\frac{A_S{u}_G{\varepsilon}_G<{\rho}:G{>}^G{C}_{P,G}}{h_T}\right)-1} $$

(13.106)

• Mass transfer:

$$ {h}_{ms}=\frac{A_S{u}_G}{\exp \left(\frac{A_S{u}_G}{h_m}\right)-1} $$

(13.107)

where h_Ts is the convective heat transfer coefficient with surface outflow, h_ms is the convective mass transfer coefficient with surface outflow and A_S is the external surface area of a particle.

In literature, exemplary values of the convective heat transfer coefficient can be found: flat plate—5 W/(m² K) [52], sphere—20 W/(m² K) [28], shapes with different size from 8.4 W/(m² K) to 20 W/(m² K) [141], particles in a fixed bed—50 W/(m² K) [142] or particles in a fluidised bed—400 W/(m² K) [143]. Not as many examples for the convective mass transfer coefficient can be found: flat plate—0.03 m/s [52]. It is possible that many authors consider that the mass transfer from a particle is not hindered nor enhanced. Therefore the convective mass transfer coefficient is equal to the superficial gas velocity on the surface.

7 Reactor Model and Multiscale

The gases and the solid phase (processed biomass) in a given reactor have significant differences in physical, chemical and thermal behaviour. Therefore, in this section, the description of each phase separately needs to be considered as well as interactions between the phases.

7.1 Lagrangian method: Particle Movement Description

In reactor systems, the movement of every single particle is independent. The method which allows for describing the behaviour of each individual particle is the Lagrangian approach, which is based on Newton’s second law of motion [56, 144]. In the Lagrangian framework, each particle is modelled with its own body (subdomain), which moves independently in an applied geometry according to the forces affecting the particle. This framework allows for investigating the time-position relation of each particle (e.g. trajectory).

The framework of the Lagrangian method also allows for the implementation of mechanical interactions between particles and between phases. Consecutively, it opens the possibility for implementation and investigation of particle-particle and particle-wall interactions. The visualisation of the basic difference between the Eulerian and the Lagrangian approach is shown in Fig 13.6.

Fig. 13.6

Simplified visualisation of the difference between Eulerian and Lagrangian approach

7.2 Methods of Two-Phase Flow Description

The Eulerian approach is sufficient to describe a single-phase flow and all significant unit processes occurring in it. Unfortunately, such an approach may not be sufficient to describe two-phase flows (e.g. gas-solid systems) appropriately.

A comprehensive and complete description of the behaviour of two-phase flow is provided by a combination of Computational Fluid Dynamics (CFD) with the Discrete Element Method (DEM) resulting in the so-called Eulerian-Lagrangian approach (CFD-DEM method). The first part of the name indicates that the gas phase description (fluid with continuum properties) is done according to the Eulerian method. In the Eulerian approach, fluid properties are stored in grid nodes of the applied geometry. The fluid movement does not interfere with the grid arrangement. The second part of the name indicates that the description of the solid phase (particles) is done with the Lagrangian approach. In this approach, solid particles are not linked to the grid used for modelling fluid dynamics, and the subdomains of particles can move freely through the applied geometry. Nevertheless, both phases are interconnected, so, e.g. the movement of the particles causes changes in the fluid phase, and the flow of the fluid can alter the movement of particles.

With an increase in the number of investigated particles as well as with an increase of the complexity of the single-particle behaviour, the quantity of data that needs to be handled by the solver grows exorbitantly. Therefore, a proper description of the investigated system with the full Eulerian-Lagrangian method, besides an in-depth knowledge about its fundamentals, needs robust numerical software tools and powerful computing hardware.

The Discrete Phase Model (DPM) is a hybrid method, and it is based on a partial simplification of the DEM method. The DPM method still has its base in the Lagrangian description and takes into accountsthe particle’s movement resulting from forces like: gravity, drag force, pressure force and Magnus force, but the particle-particle collisions are neglected. Additionally, the Discrete Phase Model method omits the fluid volume’s displacement by particles, so the volume of a fluid phase remains constant. Recommendations with respect to choosing the simplification from DEM to DPM, are not clear in the literature. The cause of this can be linked to the difference in types of reactors that were modelled with the use of the simplification. The most general recommendation is to apply the simplification in cases when the solid phase is strongly dispersed, and its volume fraction is less than 5 vol. % [145].

The Dense Discrete Phase Model method (DDPM), an improved version of the DPM is an another, more recently developed hybrid method. The DDPM method is capable of handling higher volume fractions of the solid phase, and it has an in-built particle-particle collision sub-model through a collision component taken from the DEM method. One of the drawbacks of the DDPM method is that the flow around particles is not taken into account during the simulation, so the dynamic behaviour of particles still can differ from reality. Both hybrid approaches (simplifications) lead to a significant reduction in the computational burden in comparison to the full DEM description method. Also, the influence of applying these simplifications on the accuracy loss strongly depends on the modelled scenario (reactor type, number of particles and their size).

In peculiar cases, when the size of the particles is sufficiently small and the particles are strongly dispersed among the fluid phase (suspension), there is the possibility of a strong simplification with the assumption that the particles suspended in a fluid are “dissolved” in it. Therefore they can be treated as part of the fluid, and they can behave as such (quasi-continuous solid phase). The method of describing a two-phase system where both phases are treated as a continuum is called the Eulerian-Eulerian approach. It indicates that both phases, fluid and solid, are described by the Eulerian approach, so the model does not distinguish each particle in the solid phase. Therefore in this approach, it is impossible to investigate the single particle movement. The Eulerian-Eulerian approach is the least computationally burdening method of simulating two-phase flow. Moreover, the simplification is very convenient in terms of mathematical description. Expressions used for describing the movement, thermal and chemical behaviour of the solid phase have the same construction as those used for the fluid phase description. There is a strong restriction regarding the application of this simplification. The Eulerian-Eulerian approach for particles with relatively large size introduces a significant deviation from reality in the model. In such cases, the result of the simulation is burdened with a considerable inadequacy, so its accuracy is low.

7.3 Particle Conversion Regimes and Two-Phase Flow Models

The fluid phase in a reactor is always described with the Eulerian approach. In comparison to the description of the solid phase, it makes the fluid phase a less challenging part of the reactor model. The description of the fluid phase has to contain, among others: fluid motion within the reactor geometry, changes of fluid phase volume due to particle movement and rotary elements (if any), the heat exchange between the fluid and reactor’s walls and particles. The description of the fluid phase in the reactor has to cope also with the chemical behaviour of the compounds (e.g., secondary tar cracking) that are contained in it.

As it has been mentioned, the possibility of simplifying the description of the two-phase flow into the a quasi-one phase fluid flow (Eulerian-Eulerian) is only valid when particles immersed in the fluid are sufficiently small. To assess if this simplification is valid, values of two non-dimensional numbers have to be checked: the thermal Biot number (Bi) and the Pyrolysis number (Py), the latter is also called reversed thermal Thiele modulus [56]. Those numbers indicate to which thermal regime the investigated particles belong. Each of the regimes indicate which thermal phenomena (chemical reactions, intra-particle or extra-particle heat exchange) have the strongest influence on the rate of the particle’s conversion [24, 91, 146,147,148]. Particles can be assigned to one of the four following thermal regimes: pure kinetic, thermally thin, thermal wave and thermally thick.

The simplification through the Euler-Euler approach is the most valid for particles in the pure kinetic regime, whose size usually is smaller than 1 mm in any direction [5]. Conversion of particles in the thermal thin regime is also driven mostly by the reaction kinetics, but also external heat transfer starts to play a significant role. Due to a relatively small size, those particles do not show high thermal or internal pressure gradients during conversion. The application of this simplification for particles in the thin thermal regime is not advised, but it would not introduce a critical error to the model. For this regime, the dilution of the solid phase also has to be taken into account. In case of a highly concentrated solid phase, the Eulerian-Eulerian approach is not valid, so more sophisticated description methods (DPM or DDPM) have to be applied to obtain more accurate and reliable description.

The conversion of particles assigned to the thermal wave regime is mostly driven by the internal and external heat transfer. Additionally, a significant temperature and pressure gradient is formed during the conversion. For particles in the thermal wave regime, the particle’s location during the process starts to play a major role in its conversion. Therefore, applying the Euler-Euler simplification is not valid for particles in this regime, and thus they have to be described with a Lagrangian approach. It is expected that, in the thermal wave regime the conversion of the particle takes place in a thin surface front, so the assumption that the conversion front thickness strives to 0, is not a large departure from reality. Such an approach opens a possibility of a partial simplification of describing the conversion process. The simplification can be made by implementation of the unreacted shrinking core model or the layer model [5, 24, 149].

The internal heat transfer has the largest share in the control of the conversion of particles in the thermally thick regime. To this regime are assigned the largest particles, which show the highest temperature and pressure gradients during conversion. There is no stiff border, from which point the particles have to be assigned to the thermally thick regime. In literature, it can be found that the particle is considered to be in the mentioned regime if the Bi number is higher than 40 or 100 and the thermal Thiele modulus (1/Py) number is higher than 100 or 1400 [148, 150]. The conversion of the particle in the thermally thick regime is the most complex and cannot be simplified, so only a detailed description via the Eulerian-Lagrangian approach is valid (DDPM or DEM).

7.4 Appropriate Model for Different Kinds of Beds

For fixed bed reactors, the only limitation for the particle size are the reactor dimensions. Therefore relatively large biomass particles (e.g. logs or large chunks) can be processed in a fixed bed. For this reactor type, the movement of particles is negligible, and the mixing of solids is insignificant. Taking this into account, Wurzenberger et al. [151] proposed the Representative Particle Model (RPM), suitable for the description of the conversion of single particles in fixed bed reactors. The method assumes that parameters of biomass conversion can be treated as homogenous for the whole reactor, so all processed particles show the same behaviour. In consequence, it leads to the conclusion that for the RPM, the single-particle model needs to be solved for one representative particle only once for the applied boundary and initial conditions. Application of the RPM method for modelling fixed beds reduces the computational time significantly and shows moderately good agreement with experimental results [5, 152, 153].

An additional challenge is brought into the reactor model description for systems in which particles are in motion. Movement of particles can be driven by changes in pressure of a fluid (pneumatically driven) or by the physical forces transmitted to the particles via the reactor’s rotary elements (mechanically driven). In the second scenario, the moving element also has an influence on the gas motion in the reactor, and this needs to be taken into account in the description of a model. The selection of the driver of the particle’s movement imposes practical boundaries on the size of particles that can be processed in the reactor.

For fluidised beds, the particle size has to be significantly small to be able to be suspended and/or dragged by the fluidising gas. In general, the size of particles that can be applied in fluidised bed reactors does not exceed 2–3 mm. Application of such small particles in fluidised bed reactors opens possibilities for model simplification (Eulerian-Eulerian, DPM or DDPM). An implementation of the simplification leads to a significant reduction in complexity of the description and simultaneously, it lowers the computational burden.

In processing in rotary reactors (auger/screw or rotary kiln reactors), the size of particles is usually larger than in fluidised bed reactors. The maximum size of particles for rotary reactors is limited by the dimensions of the reactor and its moving parts (e.g. size of a screw and its pitch), the reactor’s mechanical durability and the homogeneous distribution of solid material in the reactor. The particles processed in rotary reactors cannot be assigned to the kinetic thermal regime due to their large size. Therefore there is no possibility of applying the Euler-Euler approach for those systems. For rotary reactors, the Eulerian-Lagrangian approach of the two-phase flow has to be implemented (DPM, DDPM, or DEM). It has to be kept in mind that for rotary reactors, the influence of the movement of the reactor’s elements as well as of the particles on the fluid phase has to be included in the model description. Models for rotary reactors are the most demanding, both for the modeller (interdependences between phases, number of correlations and parameters), as well as for the software and hardware used to conduct computation on such complex systems.

An extensive and comprehensive overview of the application of different approaches for describing specific reactor modelling cases can be found in the recent work of Xiong et al. [154]. The work contains numerous references to examples from literature, so the authors strongly recommend this review for readers interested in the subject. Among many others, the works of Subramaniam [155], Ku et al. [156, 157] and Xie et al. [158] are worth to mention, as they contain the mathematical description of the Eulerian-Lagrangian method, as well as the work of Funke et al. [159] in which, for the first time the heat transfer between particles in an auger type reactor was calculated using a combined fundamental heat transfer model with DEM simulation.

7.5 Reactor Model and Limitations

Increase in complexity of a comprehensive model for biomass conversion, in principle, is done to bring a model closer to reality and improve its prediction accuracy. Simultaneous application of detailed models causes the issue requiring a vast amount of data and correlations that need to be handled and computed by a solver. A vast increase in computational load requires simultaneously a higher need for hardware power to obtain adequate solving efficiency. A very complex model and limited computational resources result in elongated computational time, which does not allow for a rapid refinement of the model to the investigated scenario. Therefore, model complexity is a bottleneck for the investigation and the development of the reactor technology under study. For a modeller, it is crucial to select the level of complexity that simultaneously will fulfil a required, satisfactory accuracy of a prediction, will be technically possible in implementation and will be feasible in terms of time and cost.

The reactor submodel of a comprehensive biomass conversion model is the most difficult and the most complex part among all model parts, so a short elaboration on its problems is provided here. An increase of the computational demand needed to solve a reactor model, besides the increased complexity of solid phase movement description (e.g. via application of DEM), is caused by expanding the meshed geometry of a reactor domain as well as by an increase in number of particles that have to be considered. Besides high requirement of the hardware computational resources, an additional issue is connected to the application of the DEM method in the solid phase description. A detailed description of solid-phase interactions and mechanical changes of particles is not fully developed yet, so there is no certainty that already established solid-phase descriptions are accurate in their predictions. Another issue that hinders the effective use of the complex reactor models is the in-depth knowledge on how to use the computational resources in an economical and an effective manner (e.g. parallelisation of computation, adjustment of the procedure of a solver) [5]. From the side of practice, there also exists a problem with the insufficiently developed software, which can have problems with mesh adaptation in more complex scenarios which form a barrier in modelling, like in e.g. modelling a double-screw rotary reactor [160].

8 Conclusions

Numerical modelling is a very robust tool, which allows for cost-effective research and development of technologies within the field of biomass thermal processing. As it is indicated in this chapter, proper construction and use of a comprehensive model needs knowledge from different areas of science. Only through their combination in an efficient manner, the model will lead to reasonable and useful results.

In theory, there is no limitation to model every processing technology or to base the model on parameters for any range (feedstock or process-related). Nonetheless, from a practical point of view, the selected environment of conversion, as well as the applied processed material, imposes strong boundaries on the modelled system. Those boundaries impose limits on possibilities of the model’s validation against experimental data, which is the only reliable method to assess model performance.

The level of complexity and the proper selection of components of the model has a significant influence on the model’s accuracy and reliability. A general, descriptive summary of the submodels of a comprehensive biomass conversion model is presented in Table 13.16. In general, the balance between accuracy and computational efficiency as well as the technical feasibly have to be obtained. It is advised to apply the most detailed description when it is feasible, and always a check if the model cannot be simplified without loss in model accuracy. This balance has to be taken as one of the priorities in modelling practice.

Table 13.16 Descriptive summary of components of a comprehensive biomass conversion model