Minimax-regret treatment rules with many treatments

Abstract

Statistical treatment rules map data into treatment choices. Optimal treatment rules maximize social welfare. Although some finite sample results exist, it is generally difficult to prove that a particular treatment rule is optimal. This paper develops asymptotic and numerical results on minimax-regret treatment rules when there are many treatments. I first extend a result of Hirano and Porter (Econometrica 77:1683–1701, 2009) to show that an empirical success rule is asymptotically optimal under the minimax-regret criterion. The key difference is that I use a permutation invariance argument from Lehmann (Ann Math Stat 37:1–6, 1966) to solve the limit experiment instead of applying results from hypothesis testing. I then compare the finite sample performance of several treatment rules. I find that the empirical success rule performs poorly in unbalanced designs, and that when prior information about treatments is symmetric, balanced designs are preferred to unbalanced designs. Finally, I discuss how to compute optimal finite sample rules by applying methods from computational game theory.

1 Introduction

The purpose of empirical work is often to inform decision-making. Manski (2000, 2004, 2007a, 2009) argued that our statistical methods should reflect the underlying decision problem. He proposed using Wald’s (1950) statistical decision theory framework to formally analyze methods for converting sample data into policy decisions. From a Bayesian perspective, Chamberlain (2000) and Dehejia (2005) also argue for the relevance of decision theory to econometrics.

In this paper, I consider statistical decision problems when there are many possible treatments to choose from. In the first part, I show that an empirical success rule which assigns everyone to the treatment with the largest estimated welfare is locally asymptotically minimax optimal under regret loss, a result proved for the two treatment case by Hirano and Porter (2009). As in Hirano and Porter (2009), this asymptotic approach allows the distribution of the data to be arbitrary with unbounded support, whereas most existing finite sample results require the distribution of the data to have bounded support (e.g., (Schlag, 2003, 2006; Stoye, 2009a)).¹ In the second part, I examine the performance of various treatment rules in finite samples. In particular, I show that the empirical success rule performs poorly when the sampling design is highly unbalanced—when some treatments are purposely given a larger proportion of subjects than other treatments. My computations also suggest that balanced designs are preferred to unbalanced designs. I end by discussing how to numerically compute optimal treatment rules by applying results from computational game theory.

Several papers (e.g., (Manski, 2004; Schlag, 2006; Stoye, 2009a, 2012; Tetenov, 2012; Hirano & Porter, 2009)) have analyzed statistical decision problems using the minimax-regret criterion when there is a binary treatment. The first part of this paper extends a result of Hirano and Porter (2009) to the many treatment case. In the second part of this paper, I show how to use the proof strategy of Stoye (2009a) to numerically compute optimal treatment rules when the analytical solution appears intractable.

Few papers discuss minimax-regret treatment rules with many treatments. Prior to 2013, I am only aware of two previous results: First, Stoye (2007b) derives population level treatment rules for more than two treatments (where ambiguity arises due to missing data), but does not consider finite sample rules. Second, a series of papers by Bahadur (1950), Bahadur and Goodman (1952), and Lehmann (1966) showed that the empirical success rule is minimax-regret optimal with many treatments, assuming the data comes from a known parametric family satisfying monotone likelihood ratio in a scalar parameter and under a balanced sampling design (see appendix B for further details). In the first part of this paper, I show how this result may be used to extend a result of Hirano and Porter (2009). There has been more work since 2013: Manski and Tetenov (2016) extend the large deviations analysis of Manski (2004) to multiple treatments to derive a finite sample bound on the maximum regret of the empirical success rule. They then use that result to study the choice of sampling design. Appendix B.3 of Kitagawa and Tetenov (2017) discusses an extension of empirical welfare minimization to multiple treatments (also see (Kitagawa & Tetenov, 2018)). Kallus (2018) and Zhou et al. (2023) derive regret bounds for treatment rules with more than two treatments that also incorporate covariate information.

The asymptotic results here and in Hirano and Porter (2009) apply to arbitrary sampling designs,² and hence do not allow us to compare specific designs. Likewise, the Bahadur et al results do not apply to unbalanced designs. Regardless of the number of treatments, the finite-sample minimax-regret treatment rule for an unbalanced design is currently unknown. Nonetheless, unbalanced designs are important in practice. First, when there are a large number of treatments, it may be difficult or impossible to gather data on all treatments. Moreover, the costs of treatment may differ, in which case we need to trade off potential gains from a balanced design versus the different costs of treatment. Finally, the traditional statistics literature on experimental design, based on power analysis of hypothesis tests, sometimes recommends unbalanced designs. Depending on the a priori information available, this recommendation may not be optimal when the minimax-regret treatment choice criterion is used instead. My computational results suggest that, without a priori restrictions on treatment response, balanced designs are preferred to unbalanced designs. My results also suggest that designs which do not commit to an allocation in advance, and instead allocate subjects with equal probability to all treatments, are preferred to balanced designs.

Although results on binary treatments are insightful, policy-makers often have to choose between many different options. In these cases, previous research provides insufficient guidance for decision-making. While analytical finite-sample optimality results are preferred, this paper shows that asymptotic and numerical results can be a useful substitute when analytical results are unavailable.

2 Asymptotics for statistical treatment rules with many treatments

Finite sample optimality results are often difficult to derive. For years, asymptotic theory has been used instead when finite sample result are unavailable. Much of the foundational work on asymptotics followed Wald’s (1945) statistical decision function approach, culminating in Le Cam’s (1986) magnum opus. In this general formulation, statistics is viewed as a formal tool for making decisions with finite sample data, where the decision maker incurs real losses if she makes a suboptimal decision. This view was seemingly forgotten along the way, as researchers focused on convenient choices of loss functions which led to now-standard work on estimation problems and hypothesis tests. Recent work by Chamberlain (2000), Dehejia (2005), and Manski (2000, 2004), has renewed interest in the decision theory view of statistics.

In particular, Hirano and Porter (2009) applied Le Cam’s (1986) local asymptotic theory to the comparison of statistical treatment rules when there are two treatments to choose from.³ This approach allows them to derive locally asymptotically optimal rules under weaker assumptions than needed to derive exact finite-sample results, as in Stoye (2009a). This asymptotic approach allows the data to have unbounded support, and the sampling design may be anything which point identifies the parameters.

In this section, I extend one of Hirano and Porter’s (2009) results to show that an empirical success rule is asymptotically optimal under the minimax-regret criterion when there are an arbitrary, but finite, number of treatments. Specifically, letting $\delta _{k,N}^*$ denote the proportion of people to be assigned to treatment k, and letting ${\mathcal {M}}_k = \{ s \in \{1,\ldots ,K \}: w({\hat{\theta }}_{k,N}) = w({\hat{\theta }}_{s,N}) \}$, I show that

$$\begin{aligned} \delta _{k,N}^* = {\left\{ \begin{array}{ll} 1 / | {\mathcal {M}}_k | &{} \text{if} \; w({\hat{\theta }}_{k,N}) \ge w({\hat{\theta }}_{s,N}) \; \text{for all} \; s \ne k \\ 0 &{}\text{otherwise,} \end{array}\right. } \end{aligned}$$

(1)

is locally asymptotically minimax optimal under regret loss, where $w({\hat{\theta }}_{k,N})$ is a ‘best’ estimate of the welfare achieved by treatment k. Such a function which maps data into an allocation of treatments to individuals is called a treatment rule.

As in Hirano and Porter (2009), I use Le Cam’s limits of experiments framework. This framework splits the problem of deriving asymptotically optimal rules into four steps: (1) establish that the data generating process converges to a ‘limit experiment’, where one observes a single draw from a specific distribution, often a mean-shifted normal, (2) show that no sequence of rules can do better than the optimal rule in the limit experiment, a result called the asymptotic representation theorem, (3) derive the optimal rule in the limit experiment, and (4) construct a sequence of rules which converges to the optimal rule from step 3. The key difference between my result and that of Hirano and Porter is step 3: solving the limit experiment. Since they consider only two treatments, they are able to apply finite sample optimality results from hypothesis testing theory, namely the Neyman–Pearson lemma. For more than two treatments, I instead apply results of Bahadur (1950), Bahadur and Goodman (1952), and Lehmann (1966) on picking the normal population with the largest mean, which use permutation invariance arguments.

The rest of this section is organized as follows: In section 2.1 I specify the setup of the statistical decision problem. In section 2.2 I derive the distribution of plug-in estimators of welfare based on estimators like the MLE. I then state an asymptotic representation theorem in section 2.3. Consequently, in section 2.4, I derive the optimal treatment rule in the limit experiment. Finally, I show in section 2.5 that the plug-in rule matches the optimal treatment rule in the limit experiment, and hence is locally asymptotically optimal.

2.1 Setup

I begin by describing the general setup of a statistical decision problem used in Manski (2004). I then specialize that setup to the case of finitely many treatments and describe the data generating processes under consideration.

2.1.1 General statistical decision theory setup

A treatment $t \in {\mathcal {T}}$ can be applied at the individual level to members of some population. When individual i receives treatment t, she experiences the outcome $Y_i(t) \in {\mathcal {Y}}$. Let $P_t$ denote the distribution of outcomes in the population that would occur if we assigned everyone to treatment t. Assume $P_t$ is in a parametric family of distributions, so that for each treatment t, $P_t = P_{\theta _t}$ for some finite vector $\theta _t$ and a known function $P_{\theta _t} = P(\theta _t)$. Let $\theta = \{ \theta _t: t \in {\mathcal {T}} \}$. $\theta$ is called the state of the world.

Example 1

A simple example is to let the density of $P_t$ be the location model $f(y - \theta _t)$, where f is a known density function, symmetric about zero. In this model, $\theta _t \in {\mathbb {R}}$ is the median of $P_t$. $\theta _t$ is also the mean of $P_t$, if it exists.

Suppose outcome distributions are ranked by a scalar mapping W, called the welfare function. Larger values of welfare are preferred. For example, we may rank outcome distributions by their average outcome: $W(P_t) = {\mathbb {E}}_{\theta _t} [Y_i(t)]$. Let $w(\theta _t) = W(P_{\theta _t})$ denote the welfare achieved when all people are assigned to treatment t and the true state of the world for treatment t is $\theta _t$. If we knew $\theta$, then the welfare $w(\theta _t)$ would be known for all treatments t and hence to maximize welfare we would solve

$$\begin{aligned} \sup _{t \in {\mathcal {T}}} \; w(\theta _t). \end{aligned}$$

(2)

Unfortunately, we do not know the true state of the world $\theta$. To learn about $\theta$, we gather sample data $\omega$ which lies in some sample space $\Omega$. Given the sample data, we make a decision about what distribution of treatments t we will assign in the population. Denote this distribution by $\delta (t \mid \omega )$. This $\delta (\cdot \mid \omega )$ is a density function on ${\mathcal {T}}$ for all $\omega$. That is,

$$\begin{aligned} \int _{{\mathcal {T}}} \delta (t \mid \omega ) \; d\nu (t) = 1, \end{aligned}$$

where $\nu$ is a $\sigma$-finite measure on ${\mathcal {T}}$. Call $\delta (\cdot \mid \cdot ) \in {\mathcal {D}}$ a statistical treatment rule.

Let $Q_\theta$ denote the sampling distribution of the data $\omega$ when the true state of the world is $\theta$. Following Wald (1950), we evaluate statistical treatment rules according to their mean performance across repeated sampling. Performance is measured using a function $L(\delta ,\theta )$, called a loss function. The mean loss of a rule $\delta$ is called the risk:

$$\begin{aligned} R(\delta ,\theta ) = \int _\Omega L(\delta (\cdot \mid \omega ),\theta ) \; dQ_\theta (\omega ). \end{aligned}$$

Although many loss functions may be considered, I focus on regret loss, defined as follows. For a given dataset $\omega$, the rule $\delta$ yields the welfare

$$\begin{aligned} W[\delta (\cdot \mid \omega ),\theta ] = \int _{{\mathcal {T}}} \delta (t \mid \omega ) w(\theta _t) \; d\nu (t). \end{aligned}$$

Define the regret from the rule $\delta$ at state $\theta$ to be

$$\begin{aligned} \text{Regret}[\delta (\cdot \mid \omega ), \theta ] = U_\theta ^* - W[\delta (\cdot \mid \omega ),\theta ], \end{aligned}$$

where

$$\begin{aligned} U^*_\theta = \sup _{t \in {\mathcal {T}}} \; w(\theta _t) \end{aligned}$$

is the maximal welfare if we knew the state of the world was $\theta$. Then the risk of $\delta$ under regret loss is

$$\begin{aligned} R(\delta ,\theta )&= \int _\Omega L(\delta (\cdot \mid \omega ),\theta ) \; dQ_\theta (\omega ) \\&= \int _\Omega \text{Regret}[\delta (\cdot \mid \omega ), \theta ] \; dQ_\theta (\omega ) \\&= U_\theta ^* - \int _\Omega W[\delta (\cdot \mid \omega ),\theta ] \; dQ_\theta (\omega ) \\&= U_\theta ^* - \int _\Omega \left\{ \int _{{\mathcal {T}}} \delta (t \mid \omega ) w(\theta _t) \; d\nu (t) \right\} dQ_\theta (\omega ) \\&= U_\theta ^* - \int _{{\mathcal {T}}} {\mathbb {E}}_{\omega }[ \delta (t \mid \omega )] w(\theta _t) \; d\nu (t) . \end{aligned}$$

Since $\theta$ is unknown, the risk $R(\delta ,\theta )$ cannot be used directly to evaluate statistical treatment rules. Two common ways of eliminating $\theta$ are: (1) averaging risk over $\theta$ with respect to some distribution $\pi (\theta )$, or (2) looking at the worst case $\theta$. I focus on worst case analysis. Since regret is bad, larger values of risk are bad. Hence the worst case risk is

$$\begin{aligned} \sup _{\theta } R[\delta ,\theta ]. \end{aligned}$$

Define a finite sample minimax-regret treatment rule $\delta ^*$ as a solution to

$$\begin{aligned} \inf _{\delta } \sup _{\theta } \; R[\delta ,\theta ]. \end{aligned}$$

2.1.2 Finitely many treatments

Deriving finite sample minimax-regret treatment rules for an arbitrary set of treatments ${\mathcal {T}}$ is quite challenging. Most previous work has focused on the binary treatment case. In this paper, I consider the case where ${\mathcal {T}}$ is a finite set of K distinct treatments, ${\mathcal {T}} = \{ t_1, \ldots , t_K \}$. In this case, $\delta (\cdot \mid \omega )$ is a probability mass function, with $\delta _k(\omega ) \equiv \delta (t_k \mid \omega )$ denoting the percentage of the population to be assigned to treatment $t_k$ given data $\omega$. Note that $\sum _{k=1}^K \delta _k(\omega ) = 1$ must hold for all $\omega$. From here on, I suppress dependence on $\omega$ and just write $\delta _k$ instead.

For simplicity, I assume there is a unique solution to equation (2). That is, there is a unique optimal treatment. Under this assumption, the infeasible optimal treatment rule is

$${\delta_{k}^{*}} = { \mathbbm{1}} ( w(\theta _k) > w(\theta _s) \;\text{for all}\; s \ne k)$$

where I let $\theta _k = \theta _{t_k}$. It is helpful to rewrite the regret loss function using this infeasible optimal rule:

$$\begin{aligned} \text{Regret}[\delta ,\theta ]&= \max \{ w(\theta _1),\ldots ,w(\theta _K) \} - \sum _{k=1}^K w(\theta _k) \delta _k \\ &= \sum _{k=1}^K w(\theta _k) [{ \mathbbm{1}}( w(\theta _k) > w(\theta _s) \; \text{for all} \; s \ne k) - \delta _k].\\ \end{aligned}$$

Note that, when $K=2$, this loss function simplifies to that in Hirano and Porter (2009). The risk is then

$$R[\delta ,\theta ] = \sum _{k=1}^K w(\theta _k) [{ \mathbbm{1}}( w(\theta _k) > w(\theta _s) \; \text{for all}\; s \ne k) - {\mathbb {E}}\delta _k].$$

Next I specify the sampling process. Here I let $N = n_1 + \cdots + n_K$ denote the total number of observations.

Assumption 1

(Data generating process)

• 1. For each k we observe a random sample of size $n_k$ of data from $P_{\theta _k}$. This sample is independent of the other datasets.

• 2. $n_k / N \rightarrow \lambda _k \in (0,1)$ as $N \rightarrow \infty$.

Throughout this paper I also assume the parameters $\theta _k$ are point identified. See Song (2014) for some related asymptotic results in the partially identified case

Assumption 2

(Identification) Each $\theta _k$ is point identified.

Assumptions 1 and 2 together let us use the data from sample k to consistently estimate $\theta _k$.

2.2 Distribution of plug-in estimators of welfare under local alternatives

The purpose of this paper is to give conditions under which the plug-in rule

$$\begin{aligned} \delta _{k,N}^* = {\left\{ \begin{array}{ll} 1 / | {\mathcal {M}}_k | &{}\text{if} \; w({\hat{\theta }}_{k,N}) \ge w({\hat{\theta }}_{s,N}) \; \text{for all} \; s \ne k \\ 0 &{}\text{otherwise,} \end{array}\right. } \end{aligned}$$

(1)

is locally asymptotically minimax under regret loss, where ${\hat{\theta }}_{k,N}$ is a ‘best regular’ estimator of $\theta _k$ and ${\mathcal {M}}_k = \{ s \in \{1,\ldots ,K \}: w({\hat{\theta }}_{k,N}) = w({\hat{\theta }}_{s,N}) \}$. Many treatment rules will be consistent, in the sense that they asymptotically select the optimal treatment:

$$\begin{aligned} \lim _{N \rightarrow \infty } {\mathbb {E}}\delta _{k,N} = {\left\{ \begin{array}{ll} 1 &{} \text{if}\; k = \mathop {\textrm{argmax}}\limits _k w(\theta _k) \\ 0 &{}\text{otherwise.} \end{array}\right. } \end{aligned}$$

Local asymptotic theory allows us to more finely distinguish between any two treatment rules, by considering a sequence of parameter values such that the best treatment is not clear, even asymptotically. This ‘local sequence’ prevents the decision problem from becoming trivial asymptotically. To this end, I consider parameter sequences of the form

$$\begin{aligned} \left( \theta _0 + \frac{h_1}{\sqrt{N}}, \ldots , \theta _0 + \frac{h_K}{\sqrt{N}} \right) , \qquad h = (h_1,\ldots ,h_K), \end{aligned}$$

(3)

where $\theta _0$ is, without loss of generality, such that $w(\theta _0) = 0$.⁴ Thus, under this sequence, all treatments are eventually equivalent (since w is continuous by assumption 3 below). The parameters $h_k$ are called local parameters.

Assumption 3

(Model regularity)

• 1. For each k, $\theta _k \in \Theta$ where $\Theta$ is an open subset of the Euclidean space ${\mathbb {R}}^{d_\theta }$. $\theta _0 \in \Theta$ satisfies $w(\theta _0) = 0$.

• 2. The class $\{ P_\theta : \theta \in \Theta \}$ is differentiable in quadratic mean (QMD): There exists a vector of measurable functions ${\dot{\ell }}_\theta$, called the score functions, such that

  $$\begin{aligned} \int \left[ \sqrt{ p_{\theta + h} } - \sqrt{p_\theta } - \frac{1}{2} h' {\dot{\ell }}_\theta \sqrt{ p_\theta } \right] ^2 d\mu = o( \Vert h \Vert ^2) \end{aligned}$$

  as $h \rightarrow 0$, where $p_\theta$ denotes the density of $P_\theta$ with respect to the measure $\mu$. Let the information matrix $I_0 = {\mathbb {E}}_{\theta _0}[ {\dot{\ell }}_{\theta _0} {\dot{\ell }}_{\theta _0}' ]$ be nonsingular.

• 3. $w(\theta )$ is continuous, and is differentiable at $\theta _0$.

It is not necessary that the distribution of outcomes under each treatment lies in the same parametric family, or that $\theta _k$ all have the same dimensions, but it simplifies the exposition to do so. This generality follows from assumption 1.1, which says that all the samples are jointly independent, and the fact that the joint distribution of independent normals is the multivariate normal distribution. Also see remark 1 below.

Let ${\hat{\theta }}_{k,N}$ be a best regular estimator of $\theta _k$, meaning that

$$\begin{aligned} \sqrt{N} \left( {\hat{\theta }}_{k,N} - \left[ \theta _0 + \frac{h_k}{\sqrt{N}} \right] \right) {\mathop {\rightsquigarrow }\limits ^{h_k}} {\mathcal {N}}(0, \lambda _k^{-1} I_0^{-1}) \end{aligned}$$

(4)

for all $h_k$. For example, ${\hat{\theta }}_{k,N}$ can be the MLE of $\theta _k$. Let ${\hat{\varvec{\theta }}}_N = ({\hat{\theta }}_{1,N}',\ldots ,{\hat{\theta }}_{K,N}')'$, ${\textbf{w}}({\hat{\varvec{\theta }}}_N) = (w({\hat{\theta }}_{1,N}),\ldots ,w({\hat{\theta }}_{K,N}))'$,

$$\begin{aligned} {\dot{w}} = \frac{\partial w}{\partial \theta } \Big |_{\theta = \theta _0}, \quad {\dot{{\textbf{w}}}}' = \begin{pmatrix} {\dot{w}}' &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} {\dot{w}}' \end{pmatrix}, \quad \text{and} \quad {\textbf{I}}_0 = \begin{pmatrix} \lambda _1 I_0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \lambda _2 I_0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \lambda _K I_0 \end{pmatrix}. \end{aligned}$$

Then we have the following result on the distribution of plug-in estimators of welfare under the sequence of local alternatives (3).

Proposition 1

Suppose assumptions 1, 2, and 3 hold. Then, for every h,

$$\begin{aligned} \sqrt{N} {\textbf{w}}({\hat{\varvec{\theta }}}_N) {\mathop {\rightsquigarrow }\limits ^{h}} {\mathcal {N}}\left( {\dot{{\textbf{w}}}}'h, {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\dot{{\textbf{w}}}} \right) , \end{aligned}$$

where ${\hat{\theta }}_{k,N}$ are best regular estimators of $\theta _{k,N}$.

This proof, along with all others, is given in appendix A. It follows by applying Le Cam’s third lemma to the asymptotic linear representations of $\sqrt{N} {\textbf{w}}({\hat{\varvec{\theta }}}_N)$ (obtained via the delta method and since ${\hat{\varvec{\theta }}}_N$ is best regular) and the log-likelihood ratio (which satisfies local asymptotic normality due to the QMD assumption).

In particular, this proposition gives

$$\begin{aligned} \sqrt{N} w({\hat{\theta }}_{k,N}) {\mathop {\rightsquigarrow }\limits ^{h_k}} {\mathcal {N}}\left( {\dot{w}}'h_k, \lambda _k^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} \right) \end{aligned}$$

for each k. It’s important that we have obtained the asymptotic distribution under the sequence of local alternatives, and not under the fixed ‘true’ distribution $P_{\theta _0}$. Indeed, as used in the proof of this proposition, standard asymptotic theory shows that $\sqrt{N} w({\hat{\theta }}_{k,N})$ converges to a normal distribution centered at zero under $P_{\theta _0}$. Proposition 1 is analogous to lemma 3 of Hirano and Porter (2009).

2.3 The asymptotic representation theorem

In the previous section I derived the limiting distribution of plug-in estimators of welfare under a sequence of local alternatives. In this section, I first scale the risk and loss functions to keep them nontrivial asymptotically. I then state an asymptotic representation theorem, which formalizes the notion that no sequence of treatment rules can be better than the best treatment rule in the limit experiment.

To prevent regret loss from going to zero asymptotically, I scale it by $\sqrt{N}$:

$$\begin{aligned} \sqrt{N} \;&\text{Regret} \left[ \delta , \theta _0 + \frac{h}{\sqrt{N}} \right] \\ &= \sum _{k=1}^K \sqrt{N} w\left( \theta _0 + \frac{h_k}{\sqrt{N}} \right) \left[ { \mathbbm{1}}\left( \sqrt{N} w\left( \theta _0 + \frac{h_k}{\sqrt{N}} \right)> \sqrt{N} w\left( \theta _0 + \frac{h_s}{\sqrt{N}} \right)\; \text{for\,all} \; s \ne k \right) - \delta _k \right] \\ &\rightarrow \sum _{k=1}^K {\dot{w}}' h_k [{ \mathbbm{1}}( {\dot{w}}' h_k > {\dot{w}}' h_s \; \text{for all} \; s \ne k) - \delta _k] \qquad \text{as} \; N \rightarrow \infty \\ &\equiv L_\infty (\delta ,h),\\ \end{aligned}$$

where the third line follows since

$$\begin{aligned} \sqrt{N} w \left( \theta _0 + \frac{h_k}{\sqrt{N}} \right) \rightarrow {\dot{w}} ' h_k \quad \text{as} \; N \rightarrow \infty , \end{aligned}$$

which holds by a Taylor expansion and since $w(\theta _0) = 0$.

Scaled finite sample risk under the local sequence is

$$\begin{aligned}&\sqrt{N} R_N \left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] \\ &= \sqrt{N} {\mathbb {E}}_{\theta _0 + h/\sqrt{N}} \; \text{Regret}\left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] \\ &= \sum _{k=1}^K \sqrt{N} w\left( \theta _0 + \frac{h_k}{\sqrt{N}} \right) \left[ { \mathbbm{1}}\left( \sqrt{N} w\left( \theta _0 + \frac{h_k}{\sqrt{N}} \right) > \sqrt{N} w\left( \theta _0 + \frac{h_s}{\sqrt{N}} \right) \; \text{for all}\; s \ne k \right) - \beta _{k,N}(h) \right] ,\\ \end{aligned}$$

where I have defined

$$\begin{aligned} \beta _{k,N}(h) = {\mathbb {E}}_{\theta _0 + h/\sqrt{N}} \delta _{k,N}. \end{aligned}$$

Assumption 4

(Pointwise convergence) The rule $\delta _N$ is such that for each component k and each h, $\beta _{k,N}(h)$ converges to some limit $\beta _k(h)$.

Under this pointwise convergence assumption, scaled finite sample risk converges to asymptotic risk as follows:

$$\sqrt{N} R_N \left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] \rightarrow \sum _{k=1}^K {\dot{w}}' h_k [{ \mathbbm{1}}( {\dot{w}}' h_k > {\dot{w}}' h_s \; \text{for all} \; s \ne k) - \beta _k(h)].$$

Theorem 1

(Asymptotic representation theorem) Suppose assumptions 1–4 hold. Then for each k there exists a function $\delta _k: {\mathbb {R}}^{\dim (h_k)} \rightarrow [0,1]$ such that for every $h_k$,

$$\begin{aligned} \beta _k(h) = \int \delta _k(\Delta _k) \; d{\mathcal {N}}(\Delta _k \mid h_k, \lambda _k^{-1} I_0^{-1}), \end{aligned}$$

and $\sum _{k=1}^K \delta _k(\Delta _k) = 1$ for all $\Delta = (\Delta _1,\ldots ,\Delta _K)$.

Assumption 3 implies that $\{ P_{\theta _1}^{n_1} \otimes \cdots \otimes P_{\theta _K}^{n_K}: \theta \in \Theta ^K \}$ converges to the limit experiment $\{ {\mathcal {N}}(h_1,\lambda _1^{-1} I_0^{-1}) \otimes \cdots \otimes {\mathcal {N}}(h_K,\lambda _K^{-1} I_0^{-1}) \}$ (see Van der Vaart (1998) chapter 9 for a formal discussion of convergence of experiments). The asymptotic representation theorem states that for any rule $\delta _N = (\delta _{1,N},\ldots ,\delta _{K,N})$ which has a limit in the sense of assumption 4, there exists a rule $\delta = (\delta _1,\ldots ,\delta _K)$ in the limit experiment whose risk $R_\infty (\delta ,h)$ equals the limiting risk of $\delta _N$. We say that $\delta _N$ is matched by $\delta$ in the limit experiment. This theorem is a special case of theorem 9.3 on page 127 of Van der Vaart (1998) (see also theorem 15.1 on page 215 and proposition 7.10 on page 98 for similar special cases), and hence its proof is omitted.

2.4 The optimal treatment rule in the limit experiment

Because of the asymptotic representation theorem, no rule can do better than the best rule in the limit experiment, which I derive in this section. In the limit experiment, $\{ {\mathcal {N}}(h_1,\lambda _1^{-1} I_0^{-1}) \otimes \cdots \otimes {\mathcal {N}}(h_K,\lambda _K^{-1} I_0^{-1}) \}$, we observe a single draw $\Delta = (\Delta _1',\ldots ,\Delta _K')'$ from the distribution

$$\begin{aligned} {\mathcal {N}}\left( \begin{pmatrix} h_1 \\ \vdots \\ h_K \end{pmatrix}, \begin{pmatrix} \lambda _1^{-1} I_0^{-1} &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \lambda _K^{-1} I_0^{-1} \end{pmatrix} \right) . \end{aligned}$$

The risk of a rule $\delta$ in this limit experiment is

$$R_\infty (\delta ,h) \equiv \sum _{k=1}^K {\dot{w}}' h_k [{ \mathbbm{1}}( {\dot{w}}' h_k > {\dot{w}}' h_s \; \text{for all} \; s \ne k) - \beta _k(h)]$$

where

$$\begin{aligned} \beta _k(h) = \int \delta _k(\Delta _k) \; d{\mathcal {N}}(\Delta _k \mid h_k, \lambda _k^{-1} I_0^{-1}). \end{aligned}$$

A rule $\delta ^*$ is minimax optimal in this experiment if it solves

$$\begin{aligned} \inf _{\delta } \sup _h \; R_\infty (\delta ,h). \end{aligned}$$

Because of the form of the limit risk $R_\infty$, the (infeasible) optimal choice of treatments in the limit experiment is

$$\begin{aligned} \delta _k = {\left\{ \begin{array}{ll} 1 &{}\text{if} \; {\dot{w}}' h_k > {\dot{w}}' h_s \; \text{for all}\; s \ne k \\ 0 &{}\text{otherwise.} \end{array}\right. } \end{aligned}$$

In the main result of this section, I show that if we replace the unknown mean $h_k$ by the observed realization $\Delta _k$, we obtain a minimax optimal treatment rule:

$$\begin{aligned} \delta _k^* = {\left\{ \begin{array}{ll} 1 &{}\text{if} \; {\dot{w}}' \Delta _k > {\dot{w}}' \Delta _s \; \text{for all}\; s \ne k \\ 0 &{}\text{otherwise.} \end{array}\right. } \end{aligned}$$

(5)

Because the limit risk $R_\infty$ only depends on h through the linear combinations ${\dot{w}}' h_k$, for all k, the random variable ${\dot{{\textbf{w}}}}' \Delta$ is a sufficient statistic in the following sense.

Lemma 1

For any rule $\delta _k(\Delta )$ which is a function of the entire vector $\Delta$, there exists a rule ${\tilde{\delta }}_k({\dot{{\textbf{w}}}}' \Delta )$ which is a function of only ${\dot{{\textbf{w}}}}'\Delta$, and yet achieves the same risk as $\delta _k$.

This result is a kind of complete class theorem. Hence it suffices to consider the limit experiment where we observe a single draw ${\dot{{\textbf{w}}}}' \Delta$ from the distribution

$$\begin{aligned} {\mathcal {N}}\left( \begin{pmatrix} {\dot{w}}' h_1 \\ \vdots \\ {\dot{w}}' h_K \end{pmatrix}, \begin{pmatrix} \lambda _1^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \lambda _2^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \lambda _K^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} \end{pmatrix} \right) . \end{aligned}$$

The following assumption states that, asymptotically, the sample sizes are equal.

Assumption 5

(Asymptotically balanced samples) $\lambda _1 = \cdots = \lambda _K = 1/K$.

This assumption implies that the only differences between treatments in the limit experiment are their means $h_k$. Consequently, the question of finding the optimal treatment rule is simply that of finding the optimal rule when the goal is to pick the normal population with the largest mean, when all populations have equal variance. This problem was solved in a series of papers by Bahadur (1950), Bahadur and Goodman (1952), and Lehmann (1966).

Theorem 2

The rule $\delta ^*$ defined in equation (5) is minimax optimal in the limit experiment:

$$\begin{aligned} \sup _h R_\infty (\delta ^*,h) = \inf _\delta \sup _h R_\infty (\delta ,h). \end{aligned}$$

This result follows immediately from the above discussion and the results of Bahadur, Goodman, and Lehmann, which I discuss in appendix B. Their results use permutation invariance arguments. This is quite different from the approach in Hirano and Porter (2009), who apply results from hypothesis testing. In particular, they use the Neyman-Pearson lemma; see Van der Vaart (1998) proposition 15.2 on page 217. The hypothesis testing approach does not appear to generalize to the case with more than two treatments.

Theorem 2 relies on assumption 5 to ensure equal variances in the limit. Practically, this means that rules which approximate $\delta ^*$ (see section 2.5) can only be guaranteed to be optimal when the sample sizes in finite samples are roughly equal. Such rules may have poor finite sample performance when the sample sizes are dramatically different. Relaxing this assumption has proven to be quite difficult analytically. In the binary treatment case, Hirano and Porter (2009) do not require an assumption like 5. Nonetheless, their main results are similar to theorem 2, in that they also show that an empirical success rule is asymptotically optimal. This empirical success rule may also have poor finite sample performance when sample sizes are dramatically different (see section 3), and hence this calls into question the value of the local asymptotic approximation for these cases.⁵

Remark 1

As mentioned earlier, the results generalize to allow different parametric models across treatments. In this case, assumption 5 must be modified to require the variances $\lambda _k^{-1} {\dot{w}}_k' I_{0,k}^{-1} {\dot{w}}_k$ to be equal for all k, where $I_{0,k}$ is the information matrix corresponding to the kth treatment, evaluated at the centering point $\theta _{0,k}$, and $w_k(\theta _k) = W(P_k(\theta _k))$.

2.5 Local asymptotic minimaxity of the plug-in rule

Theorem 2 shows that the optimal decision rule in the limit experiment is

$$\begin{aligned} \delta _k^* = {\left\{ \begin{array}{ll} 1 &{}\text{if} \; {\dot{w}}' \Delta _k > {\dot{w}}' \Delta _s \; \text{for all} \; s \ne k \\ 0 &{}\text{otherwise.} \end{array}\right. } \end{aligned}$$

(2)

Proposition 1 shows that $\sqrt{N} w({\hat{\theta }}_{k,N})$ has an asymptotic normal distribution with mean ${\dot{w}}'h_k$ under the sequence of local alternatives; i.e., the same distribution as ${\dot{w}}' \Delta _k$. This suggests that an optimal rule might be obtained by replacing ${\dot{w}}' \Delta _k$ with $\sqrt{N} w({\hat{\theta }}_{k,N})$ in $\delta ^*$. In this section, I show that this plug-in rule,

$$\begin{aligned} \delta _{k,N}^* = {\left\{ \begin{array}{ll} 1 / | {\mathcal {M}}_k | &{}\text{if} \; w({\hat{\theta }}_{k,N}) \ge w({\hat{\theta }}_{s,N})\; \text{for all} \;s \ne k \\ 0 &{}\text{otherwise,} \end{array}\right. } \end{aligned}$$

(1)

matches the optimal rule in the limit experiment, and hence that this plug-in rule is locally asymptotically minimax under regret loss.

Let ${\mathcal {D}}$ denote the set of all sequences of rules $\delta _N$ that converge in the sense of assumption 4. The following result shows that the minimax value in the limit experiment is an asymptotic risk bound.

Lemma 2

(Asymptotic minimax bound) Suppose assumptions 1–5 hold. Then for all $\delta _N \in {\mathcal {D}}$,

$$\begin{aligned} \sup _J \liminf _{N \rightarrow \infty } \sup _{h \in J} \; \sqrt{N} R_N\left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] \ge \inf _\delta \sup _h R_\infty (\delta ,h), \end{aligned}$$

where the outer supremum over J is taken over all finite subsets J of ${\mathbb {R}}^{\dim (h)}$.

We call any $\delta _N$ which achieves the lower bound a locally asymptotically minimax rule. The following theorem is the main asymptotic result of this paper.

Theorem 3

Suppose assumptions 1–5 hold. Let ${\hat{\varvec{\theta }}}_N$ be a best regular estimator, as described by equation (4). Then the plug-in rule $\delta _N^*$ defined in (1) is locally asymptotically minimax:

$$\begin{aligned} \sup _J \liminf _{N \rightarrow \infty } \sup _{h \in J} \; \sqrt{N} R_N \left[ \delta _N^*, \theta _0 + \frac{h}{\sqrt{N}} \right] = \inf _\delta \sup _h R_\infty (\delta ,h), \end{aligned}$$

where the outer supremum over J is taken over all finite subsets J of ${\mathbb {R}}^{\dim (h)}$.

Compared to the finite sample results discussed in appendix B, this asymptotic result has several advantages. It does not require each treatment distribution to lie in the same parametric class (although I have assumed this in the exposition for simplicity). It does not require sample sizes to be exactly balanced, although the approximation will likely be poor if the sample size is far from being balanced. It does not require the parameters $\theta _k$ to be scalar, and does not require the distribution of data to have monotone likelihood ratio.

2.6 Discussion

In this section, I have shown that, when there are a finite number of treatments, the rule which assigns everyone to the treatment with the largest estimated welfare is locally asymptotically minimax under regret loss. This extends one of the results in Hirano and Porter (2009), and relies on applying permutation invariance results by Bahadur (1950), Bahadur and Goodman (1952), and Lehmann (1966) in the limit experiment, instead of results from hypothesis testing. One limitation of this result is that I required the sample sizes to be asymptotically balanced, which was not required by Hirano and Porter when there are only two treatments. This requirement suggests that the empirical success rule defined in equation (1) may perform poorly when the sample size is far from balanced. More generally, the performance of the rule (1) depends on how well the limit experiment approximates the actual finite-sample distribution of ${\hat{\varvec{\theta }}}_N$. I leave a further exploration of the quality of the finite-sample approximation to future research. Likewise, I leave the problem of asymptotically unbalanced samples to future research.

3 Numerical computation of finite-sample minimax-regret treatment rules

Finite-sample minimax-regret treatment rules are often difficult to derive analytically. When analytical results are not available, we can instead numerically compare the performance of any proposed treatment rules, and also compute optimal treatment rules. In this section, I first compare selected treatment rules. I show that optimal rules for certain sampling designs may perform quite poorly for other designs. In particular, the empirical success rule does poorly for unbalanced designs. I next show how optimal rules can be computed. Minimax-regret rules can be thought of as solutions to a fictitious game between nature and the decision-maker. Consequently, numerical techniques used to compute equilibria of games can be used to compute minimax-regret rules.

3.1 Setup

The general setup is as in section 2. Here I describe several additional assumptions I use for the numerical finite-sample results, and I describe the sampling designs I consider throughout the section.

3.1.1 Additional assumptions

Assume the welfare function is the population mean outcome: $W(P_{\theta _t}) = {\mathbb {E}}_{\theta _t}[Y_i(t)] \equiv m_\theta (t)$, where $\theta = \{ \theta _t: t \in {\mathcal {T}} \}$. Assume outcomes have an arbitrary distribution on a common bounded support, which is normalized to [0, 1]. Using Schlag’s (2003) ‘binary randomization’ technique, described below, it suffices to only consider the case where outcomes are binary, $Y_i(t) \in {\mathcal {Y}} = \{ 0, 1 \}$, where 1 is a success and 0 is a failure. Under this assumption, the population mean function is just the proportion of individuals in the population who achieve a success, $m_\theta (t) = {\mathbb {P}}[Y_i(t) = 1]$. Since outcomes are binary, the state of the world is fully described by the vector $\theta = (\mu _1,\ldots , \mu _K)$ of means $\mu _k = m_{\theta }(t_k)$. Assume $\Theta$ is the product space $[0,1]^K$.

Our sample data $\omega$ has the form $\{ (Y_i,k_i) \}_{i=1}^N$. Let $N_k$ denote the number of observations with treatment k. Each $Y_i$ is an independent draw from the Bernoulli distribution with mean $\mu _{k_i}$. Let $n_k$ denote the number of successes among subjects with treatment k. If the number of observations $N_k$ of each treatment is non-random, the vector of success counts $(n_1,\ldots ,n_K)$ is a sufficient statistic for the sample data, and so from now on we view $\omega$ as producing this vector. If the number of observations $N_k$ is random, then we augment the vector of success counts with the realized number of observations of each treatment.

Remark 2

Schlag (2003) showed that by performing a ‘binary randomization’ it suffices to only consider binary outcomes. This technique is described as follows. As above, we assume outcomes have an arbitrary distribution with a common bounded support, normalized to [0, 1]. Replace each observation $Y_i \in [0,1]$ by ${\tilde{Y}}_i \in \{ 0, 1 \}$, obtained by making a single draw of a $\text{Bernoulli}(Y_i)$ random variable. Now apply a treatment rule ${\tilde{\delta }}$ to the binary data ${\tilde{Y}}_i$. Let $\delta$ denote the overall rule, including both the binary randomization step and the application of ${\tilde{\delta }}$. It turns out that if ${\tilde{\delta }}$ is minimax-regret optimal for binary data, then $\delta$ is minimax-regret optimal for the original data.

3.1.2 Sampling designs

Thus far I have not fully described how the data $\omega$ is gathered. I consider two kinds of sampling designs. For simplicity, I describe them in terms of just two treatments. Call the pair $(N_1,N_2)$ of sample sizes an allocation.

• Ex ante known allocation. The researcher chooses $N_1$ and $N_2$. Among all the possible combinations of subjects which achieve this allocation, one of them is chosen at random with equal probability. When $N_1=N_2$, we say the design is balanced. Otherwise, it is unbalanced.⁶

• Ex ante unknown allocation. The researcher chooses the total sample size $N = N_1 + N_2$. Individuals are independently assigned to treatment 1 or 2 with equal probability. Thus, before performing the experiment, any pair $(N_1, N_2)$ such that $N_1 + N_2 = N$ is possible. In particular, it is possible that all subjects are assigned to the same group and we make no observations in the other group. For this design, I assume the decision-maker commits to a decision rule $\delta$ before the allocation $(N_1,N_2)$ is revealed.⁷

The ex ante unknown allocation is easy to implement, but it may lead to extremely unbalanced samples ex post. This feature makes it intuitively unattractive to many researchers, who consequently prefer an ex ante known balanced design. On the other hand, traditional design of experiments based on analysis of power often recommends an ex ante known unbalanced design.⁸ For example, suppose there are two treatments with normally distributed outcomes and known variances but unknown means. Then the power of a t-test for a difference in the means is maximized by making more observations of the treatment with a larger variance. In section 3.2, I consider optimal sampling designs based instead on minimizing maximum regret.

3.2 Comparison of selected rules

In this section, I consider several cases where the analytical optimal rule is unknown. I compare several ‘reasonable’ rules by numerically calculating the maximal regret associated with each rule. These are the empirical success rule, various Bayes’ rules, and Stoye’s (2009a) rule, which is minimax-regret optimal for the ex ante unknown allocation and two treatments.

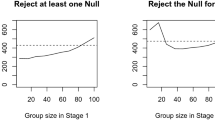
I begin with ex ante known allocations with an unbalanced design and two treatments. The main findings are that the empirical success rule is not optimal for unbalanced designs, and that balanced designs are preferred to unbalanced designs. Moreover, the empirical success rule does worse as the design becomes even more unbalanced, and its maximal regret may actually increase with the sample size. The same results hold for three treatments. With ex ante unknown allocations and three treatments, the obvious extension of Stoye’s rule is not optimal. Finally, my calculations here suggest that an ex ante unknown design is preferred to any ex ante known design.

3.2.1 Ex ante known allocation, unbalanced design

Suppose there are two treatments with sample sizes $N_1 \ne N_2$. I consider three different treatment rules.⁹ All rules have the form

$$\begin{aligned} \delta _2 = {\left\{ \begin{array}{ll} 1 &{}\text{if} \; I_{21} > 0 \\ 1/2 &{}\text{if} \; I_{21} = 0 \\ 0 &{}\text{if} \; I_{21} < 0, \end{array}\right. } \qquad \delta _1 = 1 - \delta _2. \end{aligned}$$

Define the comparison numbers $I_{21}$ as follows.

• Empirical success: Define

  $$\begin{aligned} I_{ij}^{\textsc {ES}} = \frac{n_i}{N_i} - \frac{n_j}{N_j}. \end{aligned}$$

• Stoye’s rule: Define

  $$\begin{aligned} I_{ij}&= n_i - n_j - \frac{N_i - N_j}{2} \\&= N_i \left( \frac{n_i}{N_i} - \frac{1}{2} \right) - N_j \left( \frac{n_j}{N_j} - \frac{1}{2} \right) . \end{aligned}$$

  Note that when $N_j = 0$, we choose i if and only if the sample success proportion $n_i / N_i$ is greater than 1/2. Thus 1/2 is the a priori mean.

• Squared error minimax: Define

  $$\begin{aligned} I_{ij}^{\textsc {M}} = \frac{(1/2) \sqrt{N_i} + n_i}{\sqrt{N_i} + N_i} - \frac{(1/2) \sqrt{N_j} + n_j}{\sqrt{N_j} + N_j}. \end{aligned}$$

Note that all rules are equivalent when $N_1=N_2$.¹⁰ “Stoye’s rule” is the minimax-regret optimal rule for $K=2$ and an ex ante unknown allocation, as shown by Stoye (2009a). The squared error minimax rule is derived as follows. Consider group 1. We observe $n_1 \sim \text{Bin}(\mu _1,N_1)$. With a $\text{Beta}(\alpha ,\beta )$ prior on $\mu _1$, the Bayes estimator of $\mu _1$ under squared error loss is

$$\begin{aligned} {\hat{\mu }}_1^\textsc {B}&= \frac{\alpha +n_1}{\alpha +\beta +N_1} \\&= \left( \frac{\alpha +\beta }{\alpha +\beta + N_1} \right) \frac{\alpha }{\alpha +\beta } + \left( \frac{N_1}{\alpha +\beta +N_1} \right) \frac{n_1}{N_1}. \end{aligned}$$

Rule $\delta _1^{\textsc {M}}$ uses the prior $\alpha = \beta = (1/2)\sqrt{N_1}$ for treatment 1 and $\alpha =\beta =(1/2)\sqrt{N_2}$ for treatment 2.¹¹ This corresponds to the minimax optimal rule for estimating $\mu _1$ and $\mu _2$ separately, each under squared error loss. Thus, in rule $\delta ^{\textsc {M}}$, we first estimate $\mu _1$ and $\mu _2$ separately by their Bayes’ estimators under squared error loss and a particular prior. These estimators are just the posterior means, a consequence of using squared error loss. The rule then picks the treatment with the largest Bayes’ estimator. The Bayes’ estimator biases the sample proportion toward 1/2, the a priori mean. For example, if $N_1=1$,

$$\begin{aligned} {\hat{\mu }}_1^{\textsc {B}}(n_1) = {\left\{ \begin{array}{ll} 1/4 &{}\text{if}\;n_1 = 0 \\ 3/4 &{}\text{if} \; n_1 = 1. \end{array}\right. } \end{aligned}$$

For large $N_1$, the Bayes estimators are approximately equal to the sample proportions; ${\hat{\mu }}_1^{\textsc {B}} \approx n_1/N_1$. Despite the fact that the beta-prior Bayes estimators were derived for a different purpose, they lead to treatment rules that often perform better than the empirical success rule.¹² Tables 1, 2, and 3 show maximal regret for various sample sizes.

Table 1 Maximal regret for Stoye’s rule. Row is $N_1$, Column is $N_2$

Table 2 Maximal regret for Empirical success rule

Table 3 Maximal regret for Squared error minimax rule

Among the rules considered, Stoye’s rule performs the worst. This outcome underlines the importance of the sampling design for evaluating optimality. Stoye’s rule is optimal if we commit to it before seeing the allocation, but it is not optimal if we allow ourselves to condition on the realized allocation. The empirical success rule performs better, but the beta-prior Bayes rule typically performs best. In particular, it improves upon the empirical success rule significantly more as the the allocation becomes more unbalanced; that is, as $N_1 - N_2$ gets large. This latter fact follows since the maximal regret of the empirical success rule is increasing in $N_2$, when $N_1$ is fixed (likewise if we fix $N_2$). In fact, most of the rules have this property (including the uniform prior and Jeffreys prior Bayes rules, not shown). Only the squared error minimax rule seems to mostly escape it. This result is related to the fact that the probability the empirical success rule makes a correct selection is decreasing in the sample size of the best population.¹³ Thus, neither Stoye’s rule nor the empirical success rule are minimax-regret optimal with ex ante known unbalanced allocations.¹⁴ The apparently good performance of the beta-prior Bayes rules suggests the true optimal rule may look similar.

These results also shed light on Manski’s example from Stoye (2009a). Suppose $N=1100$, $N_1 = 1000$, $n_1 = 550$, $N_2 = 100$, $n_2 = 99$. Then Stoye’s rule chooses treatment 1. The empirical success rule and the beta-prior Bayes rule both choose treatment 2. Thus the counterintuitive result that Stoye’s rule chooses treatment 1 with this data may just reflect the fact that Stoye’s rule is not optimal for an ex ante known unbalanced allocation.

Tables 1, 2, and 3 allow us to examine optimal sample size allocation. Equal sample size allocations are essentially always preferred to unequal allocations. For example, suppose $N=6$. Compare the allocation $N_1=5$, $N_2 =1$ to the allocation $N_1 = 3$, $N_2 = 3$. Maximal regret for empirical success is cut in half, from 0.143 to 0.071. Maximal regret for Stoye’s rule goes from 0.209 to 0.071. Maximal regret for the squared error minimax rule goes from 0.108 to 0.071. For an equal allocation, $N_1 = N_2$, increasing total sample size N always lowers maximal regret. For $N=10$, all rules deliver a regret of 5.5%. For $N=11$, regret is below 5%.¹⁵ The sampling cost and importance of decreasing regret by a small percent will lead to an optimal total sample size.

Next suppose there are three treatments. As in the two treatment case, I computed maximal regret for the three-treatment generalization of the three rules considered above. All rules have the form

$$\begin{aligned} \delta _1 = {\left\{ \begin{array}{ll} 1 &{} \text{if} \;I_{12}> 0, I_{13}> 0 \\ 1/2 &{}\text{if} \;I_{12}> 0, I_{13} = 0 \\ 1/2 &{}\text{if} \;I_{12} = 0, I_{13} > 0 \\ 1/3 &{}\text{if} \;I_{12} = 0, I_{13} = 0 \\ 0 &{}\text{if} \;I_{12}< 0 \,\, {\text{or}} \,\, I_{13} < 0 \end{array}\right. } \end{aligned}$$

for some pairwise comparison numbers $I_{ij}$ defined as in the previous section on two treatments. $\delta _2$ and $\delta _3$ are defined analogously. Since Bayes rules form a complete class, and Bayes rules can be defined in terms of pairwise comparisons, we can restrict attention to rules with the form above.

Table 4 Maximal regret for three treatment rules when $K=3$ under ex ante known allocations

Table 4 shows the maximal regret for various allocations. The findings here are similar to the two treatment case—the beta-prior Bayes rule does the best, then the empirical success rule, and then Stoye’s rule. Note, in particular, the poor performance of Stoye’s rule when the sample sizes are most unequal. For example, when $N_3=1, N_1=8, N_2 = 10$.

3.2.2 Ex ante unknown allocations

Thus far I have only considered ex ante known allocations. In this section, I briefly consider ex ante unknown allocations. For these allocations, Stoye (2009a) derived the minimax-regret optimal rule for $K=2$. I show that the obvious generalization of this rule is not minimax-regret optimal. Furthermore, I show that ex ante unknown allocations appear to be preferred to ex ante known allocations. Intuitively, committing to an allocation in advance gives nature an advantage in choosing her least favorable prior.

Table 5 shows maximal regret for Stoye’s rule and the beta-prior Bayes rule using the Jeffreys prior, both described in the previous section. The Jeffreys Bayes rule beats Stoye’s rule when $N=4$ and $N=6$, while Stoye’s rule wins when $N=8$ and $N=10$. Although this shows that Stoye’s rule is not optimal, its maximal regret is not much larger than that of the Jeffreys Bayes rule in the cases where it loses.

Table 5 Maximal regret when the allocation is ex ante unknown and $K=3$

When $K=2$ and N is even,¹⁶ the ex ante unknown allocation design and the ex ante known balanced design lead to identical values of regret.¹⁷ Neither is preferred over the other. This conclusion no longer holds when $K=3$. Tables 4 and 5 provide a counter-example. When $N=3$, the ex ante known balanced allocation $N_1=N_2=N_3=1$ yields minimal maximal regret 0.21038 (due to the Bahadur–Goodman–Lehmann theorem; see appendix B). Stoye’s rule under an ex ante unknown allocation, however, has a smaller maximal regret of 0.1860. The optimal rule for an ex ante unknown allocation may do even better than 0.1860.

When $K=3$, ex ante unknown allocations also appear to perform better than ex ante known unbalanced allocations. For example, when $N=4$, Stoye’s rule under an ex ante unknown allocation has maximal regret 0.1630, while Stoye’s rule under the ex ante known allocation $N_1 = 2, N_2 = 1, N_3 = 1$ has maximal regret 0.2243. Likewise, when $N=6$, Stoye’s rule under an ex ante unknown allocation has maximal regret 0.1335, while Stoye’s rule under the ex ante known allocation $N_1 = 4, N_2 = 1, N_3 = 1$ has maximal regret 0.2557.

3.3 Computation of optimal rules

Although analytical finite-sample optimal treatment rules are often unknown, in this section I show how they can be computed numerically. I first consider a simple, but naive approach to numerically calculating optimal rules. I illustrate it by computing optimal rules for various unbalanced allocations. These calculations suggest that there exists an optimal rule which mixes at more than just one realization of the data, a distinct feature of minimax rules (e.g., (Manski, 2007b; Manski & Tetenov, 2007)). I next discuss a more sophisticated approach based on results from computational game theory.

Consider the two treatment case. With binary outcomes, the sample space is finite. Thus any treatment rule can be written as a finite vector specifying the fraction allocated to treatment 1 versus 2 for each element of the sample space. Specifically, the sample space for the sufficient statistics $n_k$ is

$$\begin{aligned} \Omega = \{&(0,0),(0,1),\ldots ,(0,N_2), \\&(1,0),(1,1),\ldots ,(1,N_2), \\&\vdots \\&(N_1,0),(N_1,1),\ldots ,(N_1,N_2) \}. \end{aligned}$$

Any treatment rule $\delta$ is completely defined by $(N_1+1)\cdot (N_2+1)$ constants

$$\begin{aligned} \lambda _{ij} \equiv {\mathbb {P}}[\delta \text{selects\,treatment\,2} \mid \omega = (i,j)]. \end{aligned}$$

The probability that $\delta$ selects treatment 2, prior to gathering the data, is

$$\begin{aligned} {\mathbb {E}}\delta _2&= \sum _{i,j} \lambda _{ij} {\mathbb {P}}(\omega = (i,j)) \nonumber \\&= \sum _{i=0}^{N_1} \sum _{j=0}^{N_2} \lambda _{ij} {N_1 \atopwithdelims ()i} a^i (1-a)^{N_1 - i} {N_2 \atopwithdelims ()j} b^j (1-b)^{N_2-j}, \end{aligned}$$

(6)

where a and b are the unknown probabilities of success from treatments 1 and 2, respectively. Regret is

$$\begin{aligned} R(\delta ,\theta )&= R[\{ \lambda _{ij} \}, (a,b)] \nonumber \\&= \max \{ a,b\} - (a {\mathbb {E}}\delta _1 + b {\mathbb {E}}\delta _2). \end{aligned}$$

(7)

The minimax-regret problem is

$$\begin{aligned} \min _{\lambda _{ij} \in [0,1]} \max _{(a,b) \in [0,1]^2} R[\{ \lambda _{ij} \}, (a,b)]. \end{aligned}$$

For small sample sizes, we can solve the minimax-regret problem by using nonlinear optimization packages like KNITRO to solve a nested optimization problem, where we first solve the inner problem, and then solve the outer problem. I implemented this approach for several cases. The solutions are displayed in table 6. Note that there may not be a unique optimal rule, and therefore the numerical solutions are just one possible optimal rule.

Table 6 Some minimax-regret optimal rules for unbalanced allocations

These calculations suggest several things. The rules are monotonic in $n_2$ holding $n_1$ fixed (likewise if we swap $n_1$ and $n_2$). That is, for each fixed $n_1$, the probability that we choose treatment 2 is increasing in $n_2$. For the first three cases, mixing only occurs in the extreme cases where either there are no successes for both treatments, or there are only successes for both treatments. In the second two cases, when $N_1=1$ and $N_2=4$ or 5, the rule mixes for more than just those extreme cases.

Table 7 lists the value of maximal regret for the three rules considered previously, and the optimal rules computed above. Reassuringly, maximal regret is strictly decreasing in sample size, although the benefits of increasing sample size on a treatment which already has most of the observations are quite small.

Table 7 Maximal regret for the optimal rule, along with several other rules

Although these initial computations are helpful, more sophisticated numerical approaches have been developed for solving these kinds of computational problems. Schlag (2003, 2006) and Stoye (2009a) reconsidered Wald’s (1945) game theory technique for deriving exact, analytical finite sample results. Stoye (2009a) describes this approach in detail (see also (Berger, 1985)), so I will only briefly review the main idea. Under conditions that are satisfied here, any minimax-regret rule $\delta ^*$ is equivalent to a Bayes rule with respect to some prior $\pi ^*$ on $\Theta$, called the least favorable prior. We envision a fictional game between the decision-maker, who must choose the rule $\delta ^*$, and nature, who chooses the prior $\pi ^*$. It is well known that $\delta ^*$ is a minimax-regret rule if $(\delta ^*,\pi ^*)$ is a Nash equilibrium of this game. Thus it suffices to derive a Nash equilibrium of this game. Schlag (2003, 2006) and Stoye (2009a) use this idea to derive analytical results, but these proofs often rely on symmetry properties of the setup, which make them difficult to extend to more general settings, such as allowing for many treatments with differing costs, or for unbalanced sampling designs. Rather than analytically finding equilibria, we can compute equilibria numerically, and hence numerically compute optimal treatment rules. I sketch the game to be solved numerically in chapter 2 of Masten (2013), and I discuss the computational methods that can be used below. I leave actual implementation of these methods to future research, however.

Several papers ((Judd, Renner, and Schmedders, 2012; Kubler & Schmedders, 2010), and (Borkovsky, Doraszelski, and Kryukov, 2010)) discuss computational techniques for solving for equilibria of games with continuous strategies, with a particular emphasis on computing all equilibria, when there are multiple equilibria. This feature is particularly important in statistical decision theory: two player games often have multiple equilibria, and hence it is likely the game considered here will also have multiple equilibria. If there are many qualitatively different optimal rules, the minimax-regret criterion will suffer from the same problem that Bayes rules users face when choosing priors.¹⁸ The presence of multiple minimax-regret treatment rules will require a method for choosing a particular rule.

These methods compute equilibria by solving the system of first order conditions for the two players subject to any required constraints (e.g., Judd (1998) pages 162–165). Consequently, these methods can be seen as simply numerical methods for solving systems of equations. The first approach is called all-solutions homotopy. The idea behind homotopy methods is to start with a system of equations $g(x)=0$ whose solutions are known, and to then continuously transform that system into the system of interest $f(x)=0$, whose solutions are desired. Assuming $g(x)=0$ has as many solutions as $f(x)=0$, each solution of $g(x)=0$ will map into a solution of $f(x)=0$. Judd et al. (2012) discuss the theory, application, and implementation of this method; also see Borkovsky et al. (2010). The second approach is called the Gröbner basis method. This approach is based on a result in algebraic geometry which lets us reduce the problem of solving for all solutions to a system of equations to the problem of finding all solutions to just a single equation with a single unknown. Kubler and Schmedders (2010) describe this approach and illustrate its application in economics.

Both approaches require the system to be a polynomial, which is satisfied here.¹⁹ The Gröbner basis method has the nice feature that when the system of interest is polynomial with rational coefficients, it proves exact analytical solutions, not just numerical approximations. If we restrict the decision-maker’s $\lambda _{ij}$’s to be rational, then the first-order conditions of the statistical decision game are rational, since binomial coefficients are rational. The downside of Gröbner basis methods is that it can only handle smaller systems of equations, compared to all-solutions homotopy. One limitation of the numerical approach is that as the sample size increases, so does the number of equations in the system, eventually making the problem infeasible under either method. Nonetheless, at such sample sizes, the asymptotic approximation results of section 2 are likely to be reasonable, and can be used instead.

3.4 Discussion

The results in this section show that when no analytical finite-sample optimality results are available, numerical computations can be a useful substitute. I showed that optimality depends importantly on the sampling design. The empirical success rule, while optimal for balanced designs, performs poorly in highly unbalanced designs. My results suggest that, when choosing the sampling design, all treatments should be treated as symmetrically as possible. For example, ex ante known allocations with balanced designs yield lower regret for many rules compared to ex ante known allocations with unbalanced designs. Likewise, ex ante unknown allocations are preferred to ex ante known allocations.

Much future work remains. In particular, implementing the computational methods discussed will help analyze more complicated settings, such as larger sample sizes, more than three treatments, and asymmetric costs of treatment.

Appendices

A Proofs

Proof of proposition 1

Assumption 3.2 implies that the sequence of experiments

$$\begin{aligned} \{ P_{\theta _1}^{n_1} \otimes \cdots \otimes P_{\theta _K}^{n_K}: \theta \in \Theta ^K \} \end{aligned}$$

is locally asymptotically normal with norming rate $\sqrt{N}$. Let

$$\begin{aligned} P_{N,h} = P_{\theta _0 + h_1/\sqrt{N}}^{n_1} \otimes \cdots \otimes P_{\theta _0 + h_K/\sqrt{N}}^{n_K}. \end{aligned}$$

where $h = (h_1',\ldots ,h_K')'$. Then

$$\begin{aligned} \log \frac{dP_{N,h}}{dP_{\theta _0}^N}&= h' \Delta _{N,\theta _0} - \frac{1}{2} h' {\textbf{I}}_0 h + o_{P_{\theta _0}}(1), \end{aligned}$$

where

$$\begin{aligned} \Delta _{N,\theta _0} = \begin{pmatrix} \Delta _{N,\theta _0,1} \\ \vdots \\ \Delta _{N,\theta _0,K} \end{pmatrix} = \begin{pmatrix} \dfrac{\sqrt{\lambda _1}}{\sqrt{n_1}} \displaystyle \sum _{i=1}^{n_1} {\dot{\ell }}_{\theta _0}(X_{1i}) \\ \vdots \\ \dfrac{\sqrt{\lambda _K}}{\sqrt{n_K}} \displaystyle \sum _{i=1}^{n_K} {\dot{\ell }}_{\theta _0}(X_{Ki}) \end{pmatrix}, \qquad \text{and} \qquad {\textbf{I}}_0 = \begin{pmatrix} \lambda _1 I_0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \lambda _2 I_0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \lambda _K I_0 \end{pmatrix}. \end{aligned}$$

Here $\Delta _{N,\theta _0} {\mathop {\rightsquigarrow }\limits ^{\theta _0}} {\mathcal {N}}(0,{\textbf{I}}_0)$. The corresponding limit experiment consists of observing K independent normally distributed variables with means $h_k$ and variances $\lambda _k^{-1} I_0^{-1}$.

Since ${\hat{\theta }}_{k,N}$ is a best regular estimator of $\theta _k$, the converse part of lemma 8.14 of Van der Vaart (1998) implies that the estimator sequence ${\hat{\theta }}_{k,N}$ satisfies the expansion

$$\begin{aligned} \sqrt{N} ({\hat{\theta }}_{k,N} - \theta _0) = \lambda _k^{-1} I_0^{-1} \Delta _{N,\theta _0,k} + o_{P_{\theta _0}}(1). \end{aligned}$$

By the delta method,

$$\begin{aligned} \sqrt{N} [ w({\hat{\theta }}_{k,N}) - w(\theta _0)]&= \sqrt{N} w({\hat{\theta }}_{k,N}) \\&= {\dot{w}}' \lambda _k^{-1} I_0^{-1} \Delta _{N,\theta _0,k} + o_{P_{\theta _0}}(1), \end{aligned}$$

where recall that

$$\begin{aligned} {\dot{w}} = \frac{\partial w}{\partial \theta } \Big |_{\theta = \theta _0}. \end{aligned}$$

Recall that ${\hat{\varvec{\theta }}}_N = ({\hat{\theta }}_{1,N}',\ldots ,{\hat{\theta }}_{K,N}')'$, ${\textbf{w}}({\hat{\varvec{\theta }}}_N) = (w({\hat{\theta }}_{1,N}),\ldots ,w({\hat{\theta }}_{K,N}))'$, and

$$\begin{aligned} {\dot{{\textbf{w}}}}' = \begin{pmatrix} {\dot{w}}' &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} {\dot{w}}' \end{pmatrix}. \end{aligned}$$

Then the previous results show that

$$\begin{aligned} \sqrt{N} {\textbf{w}}({\hat{\varvec{\theta }}}_N) = {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} \Delta _{N,\theta _0} + o_{P_{\theta _0}}(1), \end{aligned}$$

where note that

$$\begin{aligned} {\textbf{I}}_0^{-1} = \begin{pmatrix} \lambda _1^{-1} I_0^{-1} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \lambda _2^{-1} I_0^{-1} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \lambda _K^{-1} I_0^{-1} \end{pmatrix}. \end{aligned}$$

Hence, by Slutsky’s theorem (this allows us to drop the $o_{P_{\theta _0}}(1)$ terms) and a multivariate CLT, we have

$$\begin{aligned} \left( \sqrt{N} {\textbf{w}}({\hat{\varvec{\theta }}}_N), \quad \log \frac{dP_{N,h}}{dP_{\theta _0}^N} \right)&= \left( {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} \Delta _{N,\theta _0}, \quad h' \Delta _{N,\theta _0} - \frac{1}{2} h' {\textbf{I}}_0 h \right) + o_{P_{\theta _0}}(1) \\&{\mathop {\rightsquigarrow }\limits ^{\theta _0}} {\mathcal {N}}\left( \begin{pmatrix} 0 \\ -\frac{1}{2} h' {\textbf{I}}_0 h \end{pmatrix}, \begin{pmatrix} {\mathbb {E}}_{\theta _0} \psi _{\theta _0} \psi _{\theta _0}' &{} {\mathbb {E}}_{\theta _0} \psi _{\theta _0} h' \dot{\varvec{\ell }}_{\theta _0} \\ {\mathbb {E}}_{\theta _0} \psi _{\theta _0}' h' \dot{\varvec{\ell }}_{\theta _0} &{} h' {\textbf{I}}_0 h \end{pmatrix} \right) \\&= {\mathcal {N}}\left( \begin{pmatrix} 0 \\ -\frac{1}{2} h' {\textbf{I}}_0 h \end{pmatrix}, \begin{pmatrix} {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\dot{{\textbf{w}}}} &{} {\dot{{\textbf{w}}}}' h \\ {\dot{{\textbf{w}}}}' h &{} h' {\textbf{I}}_0 h \end{pmatrix} \right) \end{aligned}$$

where $\psi _{\theta _\theta } = {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} \dot{\varvec{\ell }}_{\theta _0}$, and we have defined

$$\begin{aligned} \dot{\varvec{\ell }}_{\theta _0} = (\sqrt{\lambda _1} {\dot{\ell }}_{\theta _0}(X_1)', \ldots , \sqrt{\lambda _K} {\dot{\ell }}_{\theta _0}(X_K)'). \end{aligned}$$

Then ${\mathbb {E}}_{\theta _0} \dot{\varvec{\ell }}_{\theta _0} \dot{\varvec{\ell }}_{\theta _0}' = {\textbf{I}}_0$, where note that the off-diagonal entries are zero since the K samples are independent and the expected score is zero. Hence the third line follows since

$$\begin{aligned} {\mathbb {E}}_{\theta _0} \psi _{\theta _0} \psi _{\theta _0}'&= {\mathbb {E}}_{\theta _0} {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} \dot{\varvec{\ell }}_{\theta _0} ({\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} \dot{\varvec{\ell }}_{\theta _0})' \\&= {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\mathbb {E}}_{\theta _0}[\dot{\varvec{\ell }}_{\theta _0} \dot{\varvec{\ell }}_{\theta _0}' ] {\textbf{I}}_0^{-1} {\dot{{\textbf{w}}}} \\&= {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\dot{{\textbf{w}}}} \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}_{\theta _0} \psi _{\theta _0}' h' \dot{\varvec{\ell }}_{\theta _0}&= {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\mathbb {E}}_{\theta _0}[ \dot{\varvec{\ell }}_{\theta _0} \dot{\varvec{\ell }}_{\theta _0}'] h \\&= {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\textbf{I}}_0 h \\&= {\dot{{\textbf{w}}}}' h. \end{aligned}$$

Thus, by Le Cam’s third lemma (see example 6.7, page 90 of (Van der Vaart, 1998)):

$$\begin{aligned} \sqrt{N} {\textbf{w}}({\hat{\varvec{\theta }}}_N)&{\mathop {\rightsquigarrow }\limits ^{h}}{\mathcal {N}}\left( 0 + {\dot{{\textbf{w}}}}'h, {\dot{{\textbf{w}}}}' {\textbf{I}}_0^{-1} {\dot{{\textbf{w}}}} \right) \\&= {\mathcal {N}}\left( \begin{pmatrix} {\dot{w}}' h_1 \\ \vdots \\ {\dot{w}}' h_K \end{pmatrix}, \begin{pmatrix} \lambda _1^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \lambda _2^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \lambda _K^{-1} {\dot{w}}' I_0^{-1} {\dot{w}} \end{pmatrix} \right) . \end{aligned}$$

$\square$

Proof of theorem 2

This result follows from the results in appendix B, as summarized in corollary S1. Note that assumption 5 ensures that the variances are equal in the limit experiment, as needed to apply those results. $\square$

The following lemma restates the parts of lemma 4 of Hirano and Porter (2009) which are relevant here, for reference.

Lemma S1

(Hirano and Porter (2009) lemma 4) Suppose assumptions 1–4 hold. Let $\delta _N$ be a sequence of treatment assignment rules which is matched by a rule $\delta$ in the limit experiment, as given by the asymptotic representation theorem. Let J be a finite subset of ${\mathbb {R}}^{\dim (h)}$. If

$$\begin{aligned} \lim _{N \rightarrow \infty } \; \sqrt{N} R_N\left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] = R_\infty (\delta ,h) \end{aligned}$$

holds for all $h \in {\mathbb {R}}^{\dim (h)}$, then

$$\begin{aligned} \sup _J \liminf _{N \rightarrow \infty } \sup _{h \in J} \; \sqrt{N} R_N \left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] = \sup _h R_\infty (\delta ,h), \end{aligned}$$

where the outer supremum over J is taken over all finite subsets J of ${\mathbb {R}}^{\dim (h)}$.

Proof of lemma 2

By the asymptotic representation theorem, $\delta _N \in {\mathcal {D}}$ is matched by a rule ${\tilde{\delta }}$, meaning that ${\mathbb {E}}_{\theta _0 + h/\sqrt{N}} \delta _{k,N} \rightarrow {\mathbb {E}}_h {\tilde{\delta }}_k$ for all h. Consequently, by our risk function calculations in section 2.3, we have

$$\begin{aligned} \lim _{N \rightarrow \infty } \sqrt{N} R_N\left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right] = R_\infty ({\tilde{\delta }},h) \end{aligned}$$

for all h. Thus

$$\begin{aligned} \sup _J \liminf _{N \rightarrow \infty } \sup _{h \in J} \; \sqrt{N} R_N\left[ \delta _N, \theta _0 + \frac{h}{\sqrt{N}} \right]&= \sup _h R_\infty ({\tilde{\delta }},h) \\&\ge \inf _\delta \sup _h R_\infty (\delta ,h), \end{aligned}$$

where the first line follows by lemma 4 of Hirano and Porter (2009). $\square$

Proof of theorem 3

By proposition 1,

$$\begin{aligned} \beta _{k,N}^*(h)&\equiv {\mathbb {E}}_{\theta _0 + h/\sqrt{N}} \delta _{k,N}^* \\&= P_{\theta _0 + h/\sqrt{N}} \left( \sqrt{N} w({\hat{\theta }}_{k,N})> \sqrt{N} w({\hat{\theta }}_{s,N})\; \text{for all} \;s \ne k \right) \\&\rightarrow {\mathbb {P}}_h({\dot{w}}' \Delta _k > {\dot{w}}' \Delta _s\; \text{for all} \;s \ne k)&\text{as} \; N \rightarrow \infty \\&= {\mathbb {E}}_h [ \delta _k^*(\Delta )] \\&= \int \delta _k^*(\Delta _k) \; d{\mathcal {N}}(\Delta _k \mid h_k, \lambda _k^{-1} I_0^{-1}) \\&\equiv \beta _k^*(h) \end{aligned}$$

for all h. Thus, by our risk calculations in section 2.3, $\delta _N^*$ is matched in the limit experiment by $\delta ^*$; that is,

$$\begin{aligned} \lim _{N \rightarrow \infty } \sqrt{N} R_N\left[ \delta _N^*, \theta _0 + \frac{h}{\sqrt{N}} \right] = R_\infty (\delta ^*,h) \end{aligned}$$

for all h. Then

$$\begin{aligned} \sup _J \liminf _{N \rightarrow \infty } \sup _{h \in J} \; \sqrt{N} R_N \left[ \delta _N^*, \theta _0 + \frac{h}{\sqrt{N}} \right]&= \sup _h R_\infty (\delta ^*,h) \\&= \inf _\delta \sup _h R_\infty (\delta ,h), \end{aligned}$$

where the outer supremum over J is taken over all finite subsets of ${\mathbb {R}}^{\dim (h)}$. The first line follows by lemma 4 of Hirano and Porter (2009). The second line follows since $\delta ^*$ is optimal in the limit experiment, by theorem 2. $\square$

B The finite-sample results of Bahadur, Goodman, and Lehmann

In this appendix I reproduce several results from Lehmann (1966), who built on Bahadur (1950) and Bahadur and Goodman (1952). Theorem 2 in the present paper is an immediate corollary of these results. None of the results in this section are new (except for corollary S2, which is a minor extension); I include them here for reference and accessibility. I have also made a few notational changes. The basic approach is to first show that the empirical success rule is uniformly best within the class of permutation invariant rules, and then show that this implies that it is a minimax rule among all possible rules. Although theorem 2 only requires this result to hold for normally distributed data, the result holds more generally, and so I present the general result here.

Suppose there are K treatments. From each treatment group $k=1,\ldots ,K$ we observe a vector of outcomes $X_k$. Let $P_\theta$ denote the joint distribution of the data $X = (X_1,\ldots ,X_K)$, where $\theta = (\theta _1,\ldots ,\theta _K)$ and $\theta _k \in {\mathbb {R}}$. Let $L(k,\theta ) = L_k(\theta )$ denote the loss from assigning everyone to treatment k. Let

$$\begin{aligned} G = \{ g_1,\ldots , g_J \} \end{aligned}$$

be a finite group of transformations.

Example 2

(Permutation group) Let $\pi : \{1,\ldots ,K \} \rightarrow \{ 1,\ldots , K \}$ be a function which permutes the indices of $\theta$. So $\pi (k)$ denotes the new index which k is mapped into. $\pi ^{-1}(k)$ denotes the old index which maps into the new kth spot. Let $\{ \pi _j \}$ be the set of all J permutations of indices. The set of transformations

$$\begin{aligned} g_j(\theta ) = (\theta _{\pi _j^{-1} 1},\ldots ,\theta _{\pi _j^{-1} K}) \end{aligned}$$

which permute the indices of $\theta$ is called the permutation group. For example, let $\theta = (\theta _1,\theta _2,\theta _3)$. Consider the particular permutation $\pi _j$ with $\pi _j(1) = 2$, $\pi _j(2) = 1$, and $\pi _j(3) = 3$. Then

$$\begin{aligned} g_j(\theta ) = (\theta _2, \theta _1, \theta _3). \end{aligned}$$

Assume from now on that G is the permutation group. Let $\delta$ denote an arbitrary treatment rule. We say $\delta$ is invariant under G if

$$\begin{aligned} g_j[(\delta _1(X),\ldots ,\delta _K(X))] = (\delta _1(g_j X),\ldots ,\delta _K(g_j X)) \quad\; \text{for all} \;j \text{and\,all} \; X. \end{aligned}$$

Assumption S1

The following hold.

• 1. (Invariant distribution). $P_\theta$ is invariant under G. That is, the distribution of $g_j(X)$ is $P_{g_j(\theta )}$ for all j.²⁰

• 2. (Invariant loss). $L(k,\theta )$ is invariant under G. That is, if $L((1,\ldots ,K),\theta )$ is the vector of losses then

  $$\begin{aligned} L(g_j((1,\ldots ,K)),g_j(\theta )) = L((1,\ldots ,K),\theta ) \end{aligned}$$

  for all j.

• 3. (Independence). $X = (X_1,\ldots ,X_K)$ has a probability density of the form

  $$\begin{aligned} h_\theta (T) = C(\theta ) f_{\theta _1}(T_1) \cdots f_{\theta _K}(T_K), \end{aligned}$$

  with respect to a $\sigma$-finite measure $\nu$, where $T_k = T_k(X_k)$, are real valued statistics, and $T = (T_1,\ldots ,T_K)$.

• 4. (MLR). $f_{\theta _k}$ has monotone (non-decreasing) likelihood ratio in $T_k$ for each k.

• 5. (Monotone loss). Larger parameter values are weakly preferred. That is, the loss function L satisfies

  $$\begin{aligned} \theta _i < \theta _j \qquad \Rightarrow \qquad L_i(\theta ) \ge L_j(\theta ). \end{aligned}$$

Example 3

(Independent normal observations with equal variances) Let $X_k \sim {\mathcal {N}}(\theta _k,\sigma ^2)$, and $X_k$ is independent of all other observations. Then this data satisfies assumptions (1), (3), and (4), with $T_k = X_k$.

Example 4

(Regret loss) The regret loss function

$$\begin{aligned} L(k,\theta ) = \max _i \; \theta _i - \theta _k \end{aligned}$$

satisfies (2) and (5).

Let

$$\begin{aligned} {\mathcal {M}} = \{ k: T_k \ge T_j\; \text{for all} \;j \} \end{aligned}$$

denote the set of treatments which yield the largest observed statistics $T_k$. Define the empirical success rule by

$$\begin{aligned} \delta _k^*(X) = {\left\{ \begin{array}{ll} 1/|{\mathcal {M}}| &{}\text{if} \;T_k \ge T_j\; \text{for all} \;j \\ 0 &{}\text{if} \; T_k < T_j \; \text{for some}\; j. \end{array}\right. } \end{aligned}$$

(8)

When the $T_k$ are continuously distributed, it is not necessary to define what $\delta ^*$ does in the event of ties, since they occur with probability zero. When $T_k$ are discretely distributed, however, ties may occur with positive probability.

Theorem S1

(Bahadur–Goodman–Lehmann) Suppose assumption S1 holds. Then the empirical success rule (8) uniformly over $\theta$ minimizes the risk $R(\delta ,\theta )$ among all rules $\delta$ based on T which are invariant under G.

Proof

First note that $\delta ^*$ is invariant under G. By lemma 1 of Lehmann (1966) (see below), it suffices to prove that, for all $\theta$, $\delta ^*$ minimizes risk averaged over all permutations,

$$\begin{aligned} r(\delta ,\theta ) \equiv \frac{1}{J} \sum _{j=1}^J R(\delta , g_j \theta ), \end{aligned}$$

among all procedures (not just invariant ones). The risk of a rule $\delta$ is

$$\begin{aligned} R(\delta ,\theta )&= \sum _{k=1}^K L_k(\theta ) {\mathbb {E}}[ \delta _k(T) ] \\&= \sum _{k=1}^K L_k(\theta ) \int \delta _k(t) h_\theta (t) \; d\nu (t). \end{aligned}$$

Average risk is

$$\begin{aligned} r(\delta ,\theta )&= \frac{1}{J} \sum _{j=1}^J R(\delta , g_j \theta ) \\&= \frac{1}{J} \sum _{j=1}^J \sum _{k=1}^K L_k(g_j \theta ) \int \delta _k(t) h_{g_j \theta }(t) \; d\nu (t) \\&= \frac{1}{J} \sum _{k=1}^K \int \left[ \sum _{j=1}^J L_k(g_j \theta ) h_{g_j \theta }(t) \right] \delta _k(t) \; d\nu (t) \\&= \frac{1}{J} \sum _{k=1}^K \int A_k(t) \delta _k(t) \; d\nu (t), \end{aligned}$$

where we defined

$$\begin{aligned} A_k(t) = \sum _{j=1}^J L_k(g_j \theta ) h_{g_j \theta }(t). \end{aligned}$$

Suppose without loss of generality that $\theta _1< \cdots < \theta _K$. We will show that, for a fixed t, $A_k(t)$ is minimized over k by any i such that

$$\begin{aligned} t_i = \max _k \; t_k \end{aligned}$$

Consequently, the average risk $r(\delta ,\theta )$ is minimized for any rule $\delta$ which puts $\delta _k(t) = 0$ whenever $t_k < \max t_i$. Finally, since the lemma requires the procedure $\delta ^*$ to be invariant under G, we break ties between maxima at random with equal probability.

Thus all we have to do is show that for a fixed t,

$$\begin{aligned} A_i(t) = \min _k \; A_k(t) \qquad \text{if\,and\,only\,if} \qquad t_i = \max _k \; t_k. \end{aligned}$$

$A_i$ minimized means $A_i \le A_k$ for all k, or $A_i - A_k \le 0$ for all k. Thus consider the difference

$$\begin{aligned} A_i - A_k = \sum _{j=1}^J [L_i(g_j \theta ) - L_k(g_j \theta )] h_{g_j \theta }(t). \end{aligned}$$

We will look at each term in the sum separately. Consider a permutation g defined by $\pi$ such that $\pi ^{-1} i < \pi ^{-1} k$. By our ordering of the parameters, this implies that $\theta _{\pi ^{-1} i} < \theta _{\pi ^{-1} k}$. Let $g'$ be the permutation obtained from g by swapping $\pi ^{-1} i$ and $\pi ^{-1} k$.

The contribution to $A_i - A_k$ from the terms corresponding to g and $g'$ is

$$\begin{aligned} {[}L_i(g \theta ) - L_k(g \theta )] h_{g\theta }(t) + [L_i(g' \theta ) - L_k(g'\theta )] h_{g' \theta }(t). \end{aligned}$$

Since the loss function is invariant,

$$\begin{aligned} L_i(g \theta ) = L_k(g'\theta ) \qquad \text{and} \qquad L_k(g \theta ) = L_i(g' \theta ). \end{aligned}$$

So the previous equation reduces to

$$\begin{aligned} {[}L_i(g\theta ) - L_k(g\theta )][ h_{g \theta }(t) - h_{g'\theta }(t)]. \end{aligned}$$

The first piece is positive (nonnegative at least) since $\theta _{\pi ^{-1} k} > \theta _{\pi ^{-1} i}$. Consider the sign of the second term. By the form of the density,

$$\begin{aligned} h_{g \theta }(t) = C(g \theta ) f_{\theta _{\pi ^{-1} 1}}(t_1) \cdots f_{\theta _{\pi ^{-1} K}}(t_K) \end{aligned}$$

Since $g'$ is the same permutation as g, except that $j_i$ and $j_k$ are switched, $h_{g'\theta }(t)$ is the same as above, except that $f_{\theta _{\pi ^{-1} i}}$ is evaluated at $t_k$ and $f_{\theta _{\pi ^{-1} k}}$ is evaluated at $t_i$. Thus, when we compare the difference $h_{g \theta }(t) - h_{g'\theta }(t)$ to zero, we can divide by all the shared terms (including the constant C, which is invariant), which all cancel, leaving just the $\pi ^{-1} i$ and $\pi ^{-1} k$ terms remaining.

Thus

$$\begin{aligned} h_{g \theta }(t) - h_{g'\theta }(t) \ge (\le ) 0&\qquad \Leftrightarrow \qquad f_{\theta _{\pi ^{-1} i}}(t_i) f_{\theta _{\pi ^{-1} k}}(t_k) \ge (\le ) f_{\theta _{\pi ^{-1} k}}(t_i) f_{\theta _{\pi ^{-1} i}}(t_k) \\&\qquad \Leftrightarrow \qquad \frac{f_{\theta _{\pi ^{-1} k}}(t_k)}{f_{\theta _{\pi ^{-1} i}}(t_k)} \ge (\le ) \frac{f_{\theta _{\pi ^{-1} k}}(t_i)}{f_{\theta _{\pi ^{-1} i}}(t_i)} \\&\qquad \Leftrightarrow \qquad t_k \ge (\le ) t_i . \end{aligned}$$

The last line follows since $\theta _{\pi ^{-1} k} \ge \theta _{\pi ^{-1} i}$ and $f_\theta$ has MLR. Thus, when $t_k \le t_i$, the second term is negative, and hence the entire term is negative.

Now, every permutation $g_{\pi }$ must have either $\pi ^{-1} i < \pi ^{-1} k$ or $\pi ^{-1} i > \pi ^{-1} k$. So if we consider the set of all permutations with $\pi ^{-1} i < \pi ^{-1} k$ then we can uniquely pair each one of these with a permutation with $\pi ^{-1} k < \pi ^{-1} i$. This is what we did above. By doing so, we have considered every term in the summation which defines $A_i - A_k$. Thus, when $t_k \le t_i$, every term in the sum has the desired sign, and hence

$$\begin{aligned} A_i - A_k \le 0, \end{aligned}$$

as desired. $\square$

Lemma S2

(Lehmann (1966) lemma 1) Fix $\theta$. A necessary and sufficient condition for an invariant procedure $\delta ^*$ to minimize the risk $R(\delta ,\theta )$ among all invariant procedures is that it minimizes the average risk

$$\begin{aligned} r(\delta ,\theta ) = \frac{1}{J} \sum _{j=1}^J R(\delta ,g_j \theta ) \end{aligned}$$

among all procedures (not just the invariant ones).

Proof

• 1. (Sufficient). Let $\delta ^*$ be an invariant procedure which minimizes average risk $r(\delta ,\theta )$ among all procedures. Let $\delta '$ be any other invariant procedure. Now, the risk function of any invariant procedure is constant over each orbit²¹

  $$\begin{aligned} \{ g_j \theta : j =1,\ldots ,J \}. \end{aligned}$$

  Thus

  $$\begin{aligned} R(\delta ',\theta ,) = r(\delta ', \theta ) \qquad \text{and} \qquad R(\delta ^*,\theta ) = r(\delta ^*, \theta ), \end{aligned}$$

  since both $\delta '$ and $\delta ^*$ are invariant. By the assumption that $\delta ^*$ minimizes average risk among all procedures,

  $$\begin{aligned} r(\delta ^*, \theta ) \le r(\delta ', \theta ). \end{aligned}$$

  Hence

  $$\begin{aligned} R(\delta ^*, \theta ) \le R(\delta ', \theta ). \end{aligned}$$

• 2. (Necessary). Suppose that $\delta ^*$ minimizes risk $R(\delta , \theta )$ among all invariant procedures. Let $\delta '$ be any procedure. There exists an invariant procedure $\delta ''$ such that

  $$\begin{aligned} r(\delta ', \theta ) = r(\delta '', \theta ). \end{aligned}$$

  For example, we can take

  $$\begin{aligned} \delta '' = \frac{1}{J} \sum _{j=1}^J g_j [\delta ' (g_j^{-1} X)]. \end{aligned}$$

  Thus we have

  $$\begin{aligned} r(\delta ', \theta )&= r(\delta '', \theta ) \\&= R(\delta '', \theta ) \\&\ge R(\delta ^*, \theta ) \\&= r(\delta ^*, \theta ). \end{aligned}$$

$\square$

Finally, this result implies certain optimality properties among all rules, not just permutation invariant ones. To this end, suppose all rules are ranked by a complete and transitive ordering $\succeq$.

Example 5

The minimax criterion orders rules as follows: $\delta ' \succeq \delta$ if

$$\begin{aligned} \sup _\theta \; R(\delta ', \theta ) \le \sup _\theta \; R(\delta , \theta ). \end{aligned}$$

This ordering satisfies all the assumptions of Lehmann’s lemma 2 below.

Lemma S3

(Lehmann (1966) lemma 2)

• 1. If the ordering $\succeq$ is such that

  • (a) $\delta ' \succeq \delta$ implies $g \delta g^{-1} \succeq g \delta ' g^{-1}$, and

  • (b) for any finite set of rules $\delta ^{(i)}$, $i=1,\ldots ,r$, $\delta ^{(i)} \succeq \delta$ for all i implies $\frac{1}{r} \sum _{i=1}^r \delta ^{(i)} \succeq \delta$.

  then given any procedure $\delta$ there exists an invariant procedure $\delta '$ such that $\delta ' \succeq \delta$.

• 2. Suppose that in addition to (a) and (b) above, the ordering satisfies

  • (c) $R(\delta ',\theta ) \le R(\delta , \theta )$ for all $\theta$ implies $\delta ' \succeq \delta$.

  Then, if there exists a procedure $\delta ^*$ that uniformly minimizes the risk among all invariant procedures, $\delta ^*$ is optimal with respect to the ordering $\succeq$. That is, $\delta ^* \succeq \delta$ for all $\delta$.

Proof

• 1. Note that

  $$\begin{aligned} \delta ' = \frac{1}{r} \sum _{j=1}^r g_j \delta g_j^{-1} \end{aligned}$$

  is invariant and, by (a) and (b), at least as good as $\delta$.

• 2. Let $\delta$ be any rule. By part 1, there exists an invariant $\delta '$ that is preferred to $\delta$. $\delta ^*$ uniformly minimizes risk among all invariant procedures. In particular, it has uniformly smaller risk than $\delta '$. Thus, by (c), $\delta ^* \succeq \delta ' \succeq \delta$.

$\square$

Thus, combining the BHL theorem with Lehmann’s lemma 2 yields the following result.

Corollary S1

The empirical success rule (8) is minimax optimal under regret loss in the experiment where, for all k, $X_k \sim {\mathcal {N}}(\theta _k,\sigma ^2)$ and $X_k$ is independent of all other observations.

As a final remark, Schlag (2003) showed that when outcomes have an arbitrary distribution on a common bounded support, it suffices to only consider binary outcomes by performing a ‘binary randomization’. This technique can be used to extend the Bahadur-Goodman-Lehman result as follows.

Corollary S2

Let $X_k$ be a vector $(X_{k,1},\ldots ,X_{k,n_k})$ of $n_k$ scalar observations. Suppose $n_1 = \cdots = n_K$. Suppose the parameter space for the distribution of $X_{k,i}$ is the set of all distributions with common bounded support, for all $i=1,\ldots ,n_k$, for all k. Then the empirical success rule (8) is minimax optimal under any loss function satisfying assumptions (2) and (5).