1 Introduction

In this work, we consider the autonomous, additively partitioned system of ordinary differential equations (ODEs)

$$\begin{aligned} y' = f(y) + g(y), \quad y(t_0) = y_0, \quad t_0 \leqslant t \leqslant t_{\rm{F}}, \end{aligned}$$
(1.1)

where f is nonstiff, g is stiff, and \(y \in \mathbb {R}^d\). Such systems frequently arise from applying the methods of lines to semidiscretize a partial differential equation (PDE). For example, processes such as diffusion, advection, and reaction all have different stiffnesses, CFL conditions, and optimal integration schemes. Implicit-explicit (IMEX) methods offer a specialized approach for solving Eq. (1.1) by treating f with an inexpensive explicit method and limiting the application of an implicit method, which is generally more expensive, to g.

The IMEX strategy has a relatively long history in the context of Runge–Kutta methods [2, 4, 17, 25, 28] and linear multistep methods [3, 19, 21]. Zhang et al. proposed IMEX schemes based on two-step Runge–Kutta (TSRK) and general linear methods (GLM) [33, 34, 36] with further developments reported in [5, 6, 12,13,14, 22, 24, 35]. Similarly, peer methods, a subclass of GLMs, have been utilized for IMEX integration in the literature such as [18, 27, 31, 32].

High-order IMEX GLMs do not face the stability barriers that constrain multistep counterparts and have much simpler order conditions than IMEX Runge–Kutta methods. Moreover, they can attain high stage order making them resilient to the order reduction phenomena seen in very stiff problems and PDEs with time-dependent boundary conditions.

A major challenge when deriving high-order IMEX GLMs is ensuring the stability region is large enough to be competitive with IMEX Runge–Kutta schemes. One can directly optimize for the area of the stability region under the constraints of the order conditions, but this is quite challenging as the objective and constraint functions are highly nonlinear and expensive to evaluate. In addition, this optimization is not scalable, with sixth order appearing to be the highest order achieved with this strategy [24].

Parallelism for IMEX schemes is scarcely explored [16, 18], but it is well studied for traditional, unpartitioned GLMs [8,9,10, 23]. One step of a GLM is

$$\begin{aligned} Y_i&= h \sum _{j=1}^s a_{i,j} \left( f(Y_j) + g(Y_j) \right) + \sum _{j=1}^r u_{i,j} \, y^{[n-1]}_j,&\qquad i&= 1, \cdots , s, \\ y^{[n]}_i&= h \sum _{j=1}^s b_{i,j} \left( f(Y_j) + g(Y_j) \right) + \sum _{j=1}^r v_{i,j} \, y^{[n-1]}_j,&\qquad i&= 1, \cdots , r. \end{aligned}$$

Methods are frequently categorized into one of four types to characterize the suitability for stiff problems and parallelism [7]. Types 1 and 2 are serial and have the structure

$$\begin{aligned} {\mathbf {A}}= \begin{bmatrix} \lambda \\ a_{2,1} &{} \lambda \\ \vdots &{} \vdots &{} \ddots \\ a_{s,1} &{} a_{s,2} &{} \cdots &{} \lambda \end{bmatrix}. \end{aligned}$$
(1.2)

When \(\lambda = 0\), the method is of type 1, and of type 2 for \(\lambda > 0\). Of interest to this paper are methods of types 3 and 4, which have \(A = \lambda \, {{\mathbf {I}}_{{s}\times {s}}}\), so that all internal stages are independent and can be computed in parallel. Type 3 methods are explicit with \(\lambda = 0\), while type 4 methods are implicit with \(\lambda > 0\).

This work extends traditional, parallel GLMs into the IMEX setting and proposes two systematic approaches for designing stable methods of arbitrary order. The first uses the popular DIMSIM framework for the base methods. In particular, we use a family of type 4 methods proposed by Butcher [9] for the implicit base and show an explicit counterpart is uniquely determined. This eliminates the need to perform a sophisticated optimization procedure to determine coefficients. The second approach can be interpreted as a generalization of the simplest IMEX scheme: IMEX Euler. It starts with an ensemble of states each approximating the ODE solution at different points in time. In parallel, they are propagated one timestep forward using IMEX Euler, which is only first-order accurate. A new, highly accurate ensemble of states is computed by taking linear combinations of the IMEX Euler solutions. This scheme, which we call parallel ensemble IMEX Euler, can be described in the framework of IMEX GLMs. Notably, it maintains the exact same stability region and roughly the same runtime in a parallel setting as IMEX Euler while achieving arbitrarily high orders of consistency. Again, coefficients are determined uniquely, and we show that they are very simple to compute using basic matrix operations.

To assess the quality of the two new families of parallel IMEX GLMs, we apply them to a PDE with time-dependent forcing and boundary conditions, as well as to a singularly perturbed PDE. Convergence is verified as high as eighth order for these challenging problems which can cause order reduction for methods of low stage order. For the performance tests, the parallel methods were run on several nodes in a cluster using MPI and compared to existing, high-quality, serial IMEX Runge–Kutta and IMEX GLMs run on a single node. The best parallel methods could reach a desired solution accuracy approximately two to four times faster.

The structure of this paper is as follows. Section 2 reviews the formulation, order conditions, and stability analysis of IMEX GLMs. This is then specialized in Sect. 3 for parallel IMEX GLMs. Sections 4 and 5 present and analyze two new families of parallel IMEX GLMs. The convergence and performance of these new schemes are compared to other IMEX GLMs and IMEX Runge–Kutta methods in Sect. 6. We summarize our findings and provide final remarks in Sect. 7.

2 Background on IMEX GLMs

An IMEX GLM [34] computes s internal and r external stages using timestep h according to:

$$\begin{aligned} Y_i&= h \sum _{j=1}^{i-1} a_{i,j} \, f(Y_j) + h \sum _{j=1}^{i} {\widehat{a}}_{i,j} \, g(Y_j) + \sum _{j = 1}^r u_{i,j} \, y^{[n-1]}_j,&\qquad i&= 1, \cdots , s, \end{aligned}$$
(2.1a)
$$\begin{aligned} y^{[n]}_i&= h \sum _{j=1}^s \left( b_{i,j} \, f(Y_j) + {\widehat{b}}_{i,j} \, g(Y_j) \right) + \sum _{j = 1}^r v_{i,j} \, y^{[n-1]}_j,&\quad i&= 1, \cdots , r. \end{aligned}$$
(2.1b)

Using the matrix notation for the coefficients

$$\begin{aligned} {\mathbf {A}}:= (a_{i,j}), \quad {\mathbf {B}}:=(b_{i,j}), \quad {\mathbf {U}}:=(u_{i,j}), \quad \widehat{{\mathbf {A}}}:= ({\hat{a}}_{i,j}), \quad \widehat{{\mathbf {B}}}:=({\hat{b}}_{i,j}), \quad {\mathbf {V}}:=(v_{i,j}), \end{aligned}$$

the IMEX GLM can be represented in the Butcher tableau

(2.2)

Assuming the incoming external stages to a step satisfy

$$\begin{aligned} \begin{aligned} y^{[n-1]}_i&= w_{i,0} \, y(t_{n-1}) + \sum _{k=1}^{p} w_{i,k} \, h^k \, \frac{\hbox {d}^{k-1}{f(y(t))}}{\hbox {d}t^{k-1}}(t_{n-1}) \\&\quad + \sum _{k=1}^{p} {\widehat{w}}_{i,k} \, h^k \, \frac{\hbox {d}^{k-1}{g(y(t))}}{\hbox {d}t^{k-1}}(t_{n-1}) + {\mathcal {O}}\left( {h^{p+1}}\right) , \quad i = 1, \cdots , r, \end{aligned} \end{aligned}$$
(2.3)

an IMEX GLM is said to have stage order q if

$$\begin{aligned} Y_i = y(t_{n-1} + c_i \, h) + {\mathcal {O}}\left( {h^{q+1}}\right) , \quad i = 1, \cdots , s, \end{aligned}$$

and order p if

$$\begin{aligned} y^{[n]}_i&= w_{i,0} \, y(t_{n}) + \sum _{k=1}^{p} w_{i,k} \, h^k \, \frac{\hbox {d}^{k-1}{f(y(t))}}{\hbox {d}t^{k-1}}(t_n) \\&\quad + \sum _{k=1}^{p} {\widehat{w}}_{i,k} \, h^k \, \frac{\hbox {d}^{k-1}{g(y(t))}}{\hbox {d}t^{k-1}}(t_n) + {\mathcal {O}}\left( {h^{p+1}}\right) , \quad i = 1, \cdots , r. \end{aligned}$$

The Taylor series weights for the external stages are also described in the matrix form

$$\begin{aligned} {\mathbf {W}}= (w_{i,j}) \in \mathbb {R}^{r \times (p+1)}, \quad \widehat{{\mathbf {W}}}= ({\widehat{w}}_{i,j}) \in \mathbb {R}^{r \times (p+1)} \end{aligned}$$
(2.4)

with \(w_{i,0} = {\widehat{w}}_{i,0}\) for \(i = 1, \cdots , r\).

The order conditions for IMEX GLMs are discussed in detail in [34]. Notably, a preconsistent IMEX GLM has order p and stage order \(q \in \{p, p-1\}\) if and only if the base methods have order p and stage order \(q \in \{p, p-1\}\). Here, we present the order conditions in a compact matrix form. First, we define the Toeplitz matrices

$$\begin{aligned} {\mathbf {K}}_{n} = \begin{bmatrix} 0 &{} 1 \\ &{} 0 &{} 1 \\ &{} &{} \ddots &{} \ddots \\ &{} &{} &{} 0 &{} 1 \\ &{} &{} &{} &{} 0 \end{bmatrix} \in \mathbb {R}^{n \times n}, \qquad {\mathbf {E}}_{n} = \exp ({\mathbf {K}}_{n}) = \begin{bmatrix} 1 &{} 1 &{} \frac{1}{2} &{} \cdots &{} \frac{1}{(n-1)!} \\ &{} 1 &{} 1 &{} \cdots &{} \frac{1}{(n-2)!} \\ &{} &{} \ddots &{} \ddots &{} \vdots \\ &{} &{} &{} 1 &{} 1 \\ &{} &{} &{} &{} 1 \end{bmatrix} \in \mathbb {R}^{n \times n}, \end{aligned}$$

and the scaled Vandermonde matrix

$$\begin{aligned} {{\mathbf {C}}_{n}} = \begin{bmatrix} \mathbb {1}_s&{\mathbf {c}}&\frac{{\mathbf {c}}^2}{2}&\cdots&\frac{{\mathbf {c}}^{n-1}}{(n-1)!} \end{bmatrix} \in \mathbb {R}^{s \times n}. \end{aligned}$$
(2.5)

Powers of a vector are understood to be component-wise, and \(\mathbb {1}_s\) represents the vector of ones of dimension s.

Theorem 2.1

(Compact IMEX GLM order conditions [34]) Assume \(y^{[n-1]}\) satisfies Eq. (2.3). The IMEX GLM Eq. (2.1) has order p and stage order \(q \in \{p, p-1\}\) if and only if

$$\begin{aligned}&{{\mathbf {C}}_{q+1}} - {\mathbf {A}}\, {{\mathbf {C}}_{q+1}} \, {\mathbf {K}}_{q+1} - {\mathbf {U}}\, {\mathbf {W}}_{:,0:q} = {{\mathbf {0}}_{{s}\times {(q+1)}}}, \end{aligned}$$
(2.6a)
$$\begin{aligned}&{{\mathbf {C}}_{q+1}} - \widehat{{\mathbf {A}}}\, {{\mathbf {C}}_{q+1}} \, {\mathbf {K}}_{q+1} - {\mathbf {U}}\, \widehat{{\mathbf {W}}}_{:,0:q} = {{\mathbf {0}}_{{s}\times {(q+1)}}}, \end{aligned}$$
(2.6b)
$$\begin{aligned}&{\mathbf {W}}\, {\mathbf {E}}_{p+1} - {\mathbf {B}}\, {{\mathbf {C}}_{p+1}} \, {\mathbf {K}}_{p+1} - {\mathbf {V}}\, {\mathbf {W}}= {{\mathbf {0}}_{{r}\times {(p+1)}}}, \end{aligned}$$
(2.6c)
$$\begin{aligned}&\widehat{{\mathbf {W}}}\, {\mathbf {E}}_{p+1} - \widehat{{\mathbf {B}}}\, {{\mathbf {C}}_{p+1}} \, {\mathbf {K}}_{p+1} - {\mathbf {V}}\, \widehat{{\mathbf {W}}}= {{\mathbf {0}}_{{r}\times {(p+1)}}}, \end{aligned}$$
(2.6d)

where \({\mathbf {W}}_{:,0:q}\) is the first \(q+1\) columns of \({\mathbf {W}}\), and \(\widehat{{\mathbf {W}}}_{:,0:q}\) is defined analogously.

Remark 2.1

The first column in each of the matrix conditions in Eq. (2.6) corresponds to a preconsistency condition.

2.1 Linear Stability of IMEX GLMs

The standard test problem used to analyze the linear stability of an IMEX method is the partitioned problem

$$\begin{aligned} y' = \xi \, y + {\widehat{\xi }} \, y, \end{aligned}$$
(2.7)

where \(\xi \, y\) is considered nonstiff and \({\widehat{\xi }} \, y\) is considered stiff. Applying the IMEX GLM Eq. (2.1) to Eq. (2.7) yields the stability matrix

$$\begin{aligned} \begin{aligned} y^{[n]}&= {\mathbf {M}}(w,{\widehat{w}}) \, y^{[n-1]}, \\ {\mathbf {M}}(w,{\widehat{w}})&= {\mathbf {V}}+ \left( w \, {\mathbf {B}}+ {\widehat{w}} \, \widehat{{\mathbf {B}}}\right) \left( {{\mathbf {I}}_{{s}\times {s}}} - w \, {\mathbf {A}}- {\widehat{w}} \, \widehat{{\mathbf {A}}}\right) ^{-1} {\mathbf {U}}, \end{aligned} \end{aligned}$$

where \(w=h \, \xi \) and \({\widehat{w}}=h \, {\widehat{\xi }}\). The set of \((w, {\widehat{w}}) \in \mathbb {C}\times \mathbb {C}\) for which \({\mathbf {M}}(w,{\widehat{w}})\) is power bounded, and thus, the IMEX GLM is stable, is a four-dimensional region that can be difficult to analyze and visualize. Following [34], we also consider the simpler stability regions

$$\begin{aligned} \widehat{{\mathcal {S}}}_{\alpha }&= \left\{ {\widehat{w}} \in \widehat{{\mathcal {S}}}\, : \, \vert \hbox {Im}({\widehat{w}})\vert < \tan (\alpha ) \, \vert \hbox {Re}({\widehat{w}})\vert \right\} , \end{aligned}$$
(2.8a)
$$\begin{aligned} {\mathcal {S}}_{\alpha }&= \left\{ w \in {\mathcal {S}}\, : \, {\mathbf {M}}(w,{\widehat{w}}) \text { power bounded, } \forall {\widehat{w}} \in \widehat{{\mathcal {S}}}_{\alpha }\right\} , \end{aligned}$$
(2.8b)

where \({\mathcal {S}}\) and \(\widehat{{\mathcal {S}}}\) are the stability regions of the explicit and implicit base methods, respectively. Equation (2.8a) is referred to as the desired stiff stability region and Eq. (2.8b) as the constrained nonstiff stability region.

3 Parallel IMEX GLMs

An IMEX GLM formed by pairing a type 3 GLM with a type 4 GLM has stages of the form

$$\begin{aligned} Y_i&= h \, \lambda \, g(Y_i) + \sum _{j = 1}^r u_{i,j} \, y^{[n-1]}_j,&\quad i&= 1, \cdots , s, \end{aligned}$$
(3.1a)
$$\begin{aligned} y^{[n]}_i&= h \sum _{j=1}^s \left( b_{i,j} \, f(Y_j) + {\widehat{b}}_{i,j} \, g(Y_j) \right) + \sum _{j = 1}^r v_{i,j} \, y^{[n-1]}_j,&\quad i&= 1, \cdots , r. \end{aligned}$$
(3.1b)

The only shared dependencies among the internal stages are the previously computed external stages \(y^{[n-1]}_j\). This allows the IMEX method to inherit the parallelism of the base methods.

The tableau for a parallel IMEX GLM is of the form

(3.2)

We note that one could more generally define \(\widehat{{\mathbf {A}}}= {{\,\mathrm{diag}\,}}{(\lambda _1, \cdots , \lambda _s)}\); however, this introduces additional complexity and degrees of freedom that are not needed for the purposes of this paper.

3.1 Simplified Order Conditions

In this paper, we will consider methods with \(p=q=r=s\), distinct \({\mathbf {c}}\) values (nonconfluent method), and an invertible \({\mathbf {U}}\). By transforming the base methods into an equivalent formulation, we can then assume without loss of generality that \({\mathbf {U}}= {{\mathbf {I}}_{{s}\times {s}}}\). With these assumptions, we start by determining the structure of the external stage weights \({\mathbf {W}}\) and \(\widehat{{\mathbf {W}}}\).

Lemma 3.1

For a parallel IMEX GLM with \({\mathbf {U}}= {{\mathbf {I}}_{{s}\times {s}}}\) and \(p=q\), the internal stage order conditions (2.6a) and (2.6b) are equivalent to

$$\begin{aligned} {\mathbf {W}}= {{\mathbf {C}}_{p+1}} \quad \text {and} \quad \widehat{{\mathbf {W}}}= {{\mathbf {C}}_{p+1}} - \lambda \, {{\mathbf {C}}_{p+1}} \, {\mathbf {K}}_{p+1}, \end{aligned}$$
(3.3)

respectively.

Proof

This follows directly from substituting \({\mathbf {A}}= {{\mathbf {0}}_{{s}\times {s}}}\), \(\widehat{{\mathbf {A}}}= \lambda \, {{\mathbf {I}}_{{s}\times {s}}}\), and \({\mathbf {U}}= {{\mathbf {I}}_{{s}\times {s}}}\) into Eqs. (2.6a) and (2.6b).

Our main theoretical result on parallel IMEX GLMs is presented in Theorem 3.1 and provides a practical strategy for method derivation.

Theorem 3.1

(Parallel IMEX GLM order conditions) Consider a nonconfluent parallel IMEX GLM with \({\mathbf {U}}= {{\mathbf {I}}_{{s}\times {s}}}\). All of the following are equivalent:

  1. i)

    the method satisfies \(p=q=r=s\);

  2. ii)

    the explicit base method satisfies \(p=q=r=s\) and

    $$\begin{aligned} \widehat{{\mathbf {W}}}&= {{\mathbf {C}}_{s+1}} - \lambda \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1}, \end{aligned}$$
    (3.4a)
    $$\begin{aligned} \widehat{{\mathbf {B}}}&= {\mathbf {B}}- \lambda \, {{\mathbf {C}}_{s}} \, {\mathbf {E}}_{s} \, {{\mathbf {C}}_{s}^{-1}} + \lambda \, {\mathbf {V}}; \end{aligned}$$
    (3.4b)
  3. iii)

    the implicit base method satisfies \(p=q=r=s\) and

    $$\begin{aligned} {\mathbf {W}}&= {{\mathbf {C}}_{s+1}}, \end{aligned}$$
    (3.5a)
    $$\begin{aligned} {\mathbf {B}}&= \widehat{{\mathbf {B}}}+ \lambda \, {{\mathbf {C}}_{s}} \, {\mathbf {E}}_{s} \, {{\mathbf {C}}_{s}^{-1}} - \lambda \, {\mathbf {V}}. \end{aligned}$$
    (3.5b)

Remark 3.1

With Theorem 3.1, once the implicit base method has been chosen, all coefficients for the explicit counterpart are uniquely determined by the order conditions. Conversely, if the explicit base is fixed, then all implicit method coefficients are uniquely determined, but parameterized by \(\lambda \).

Proof

To start, we will show the first statement of Theorem 3.1 is equivalent to the second. Assume that a nonconfluent parallel IMEX GLM with \({\mathbf {U}}= {{\mathbf {I}}_{{s}\times {s}}}\) has \(p=q=r=s\). By Theorem 2.1, the explicit (and implicit) base method also has \(p=q=r=s\) and satisfies the order conditions in Eq. (2.6). Furthermore, by Lemma 3.1, Eq. (3.4a) holds. Subtracting Eq. (2.6d) from Eq. (2.6c) gives

$$\begin{aligned} \lambda \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} \, {\mathbf {E}}_{s+1} + \left( \widehat{{\mathbf {B}}}- {\mathbf {B}}\right) {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - \lambda \, {\mathbf {V}}\, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} = {{\mathbf {0}}_{{s}\times {(s+1)}}}. \end{aligned}$$
(3.6)

The three terms summed on the left-hand side of Eq. (3.6) have zeros in the leftmost column. Removing this yields the following equivalent statement:

$$\begin{aligned} \lambda \, {{\mathbf {C}}_{s}} \, {\mathbf {E}}_{s} + \left( \widehat{{\mathbf {B}}}- {\mathbf {B}}\right) {{\mathbf {C}}_{s}} - \lambda \, {\mathbf {V}}\, {{\mathbf {C}}_{s}} = {{\mathbf {0}}_{{s}\times {s}}}. \end{aligned}$$

A bit of algebraic manipulation recovers the desired result of Eq. (3.4b).

Now, assume that a nonconfluent parallel IMEX GLM with \({\mathbf {U}}= {{\mathbf {I}}_{{s}\times {s}}}\) satisfies the properties of the second statement of Theorem 3.1. Condition (3.4a) ensures that the implicit method has stage order q, and Eq. (3.4b) ensures that it has order p,

$$\begin{aligned}&\quad \widehat{{\mathbf {W}}}\, {\mathbf {E}}_{s+1} - \widehat{{\mathbf {B}}}\, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - {\mathbf {V}}\, \widehat{{\mathbf {W}}}\\&\quad = \widehat{{\mathbf {W}}}\, {\mathbf {E}}_{s+1} - \left( {\mathbf {B}}- \lambda \, {{\mathbf {C}}_{s}} \, {\mathbf {E}}_{s} \, {{\mathbf {C}}_{s}^{-1}} + \lambda \, {\mathbf {V}}\right) \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - {\mathbf {V}}\, \widehat{{\mathbf {W}}}\\&\quad = \left( \widehat{{\mathbf {W}}}- \lambda \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} \right) \, {\mathbf {E}}_{s+1} - {\mathbf {B}}\, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - {\mathbf {V}}\left( \widehat{{\mathbf {W}}}- \lambda \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} \right) \\&\quad = {\mathbf {W}}\, {\mathbf {E}}_{s+1} - {\mathbf {B}}\, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - {\mathbf {V}}\, {\mathbf {W}}\\&\quad = {{\mathbf {0}}_{{s}\times {(s+1)}}}. \end{aligned}$$

Now, both base methods have \(p=q=r=s\), so by Theorem 2.1, the combined IMEX scheme also has \(p=q=r=s\).

The process to show statement one is equivalent to statement three, thus completing the proof, follows nearly identical steps, and is therefore omitted.

3.2 Stability

Applying parallel IMEX GLMs to linear stability test Eq. (2.7) gives

$$\begin{aligned} {\mathbf {M}}(w, {\widehat{w}})&= {\mathbf {V}}+ \frac{w}{1 - \lambda \, {\widehat{w}}} \, {\mathbf {B}}\, {\mathbf {U}}+ \frac{{\widehat{w}}}{1 - \lambda \, {\widehat{w}}} \, \widehat{{\mathbf {B}}}\, {\mathbf {U}}\end{aligned}$$
(3.7a)
$$\begin{aligned}&= {\mathbf {M}}\left( \frac{w}{1 - \lambda \, {\widehat{w}}} \right) + \widehat{{\mathbf {M}}}({\widehat{w}}) - {\mathbf {V}}, \end{aligned}$$
(3.7b)

where \({\mathbf {M}}(w)\) and \(\widehat{{\mathbf {M}}}({\widehat{w}})\) are the stability matrices of the explicit and implicit base methods, respectively. When the implicit partition becomes infinitely stiff,

$$\begin{aligned} {\mathbf {M}}(w, \infty ) = \widehat{{\mathbf {M}}}(\infty ) = {\mathbf {V}}- \frac{1}{\lambda } \widehat{{\mathbf {B}}}\, {\mathbf {U}}. \end{aligned}$$

Stability matrices evaluated at \(\infty \) are understood to be the value in the limit.

3.3 Starting Procedure

The starting procedure for nontrivial IMEX GLMs is more complex than traditional GLMs because the external stages for IMEX GLMs weight time derivatives of f and g differently. When computing \(y^{[0]}\), the high-order time derivatives are usually not readily available, but can be approximated by finite differences [11, 34]. A one-step method can be used to get very accurate approximations to y, and, consequently, f and g, at a grid of time points around \(t_0\) to construct these finite-difference approximations. While this generic approach is applicable to parallel IMEX GLMs, we also describe a specialized strategy that is simpler and more accurate.

Based on the \({\mathbf {W}}\) and \(\widehat{{\mathbf {W}}}\) weights derived in Eq. (3.3),

$$\begin{aligned} \begin{aligned} y^{[0]}_i&= y(t_0) + \sum _{k=1}^{p} \frac{c_i^k}{k!} \, h^k \, \frac{\hbox {d}^{k-1}{f(y(t))}}{\hbox {d}t^{k-1}} (t_0) \\&\quad + \sum _{k=1}^{p} \left( \frac{c_i^k}{k!} - \frac{\lambda \, c_i^{k-1}}{(k-1)!} \right) h^k \, \frac{\hbox {d}^{k-1}{g(y(t))}}{\hbox {d}t^{k-1}} (t_0) + {\mathcal {O}}\left( {h^{p+1}}\right) \\&= y(t_0 + h \, c_i) - h \, \lambda \, g(y(t_0 + h \, c_i)) + {\mathcal {O}}\left( {h^{p+1}}\right) . \end{aligned} \end{aligned}$$
(3.8)

Now, a one-step method can be used to get approximations to y and g at times \(t_0 + h \, c_i\) to compute \(y^{[0]}\). This eliminates the need to use finite differences and eliminates the error associated with them. Note that negative abscissae would require integrating backwards in time. Although the interval of integration may be quite short, this could still lead to stability issues, and is easily remedied. If \(c_\text {min}\) is the smallest abscissa, then the one-step method can produce an approximation to \(y^{[\ell ]}\), where \(\ell = \lceil -c_\text {min}\rceil \), instead of \(y^{[0]}\). Note, \(t_\ell + c_i \, h \geqslant t_0\), and the IMEX GLM will start with \(y^{[\ell ]}\) to compute \(y^{[\ell +1]}\) and so on.

3.4 Ending Procedure

We will consider the ending procedure for an IMEX GLM to be of the form

$$\begin{aligned} y(t_n) \approx h \sum _{j=1}^s \left( \beta _{j} \, f(Y_j) + {\widehat{\beta }}_{j} \, g(Y_j) \right) + \sum _{j = 1}^r \gamma _{j} \, y^{[n-1]}_j. \end{aligned}$$
(3.9)

Frequently, IMEX GLMs have the last abscissa set to 1, which allows for a particularly simple ending procedure for high stage order methods. The final internal stage \(Y_s\) can be used as an \({\mathcal {O}}\left( {h^{\min (p, q+1)}}\right) \) accurate approximation to \(y(t_n)\). One can easily verify that the coefficients for such an ending procedure are

$$\begin{aligned} \beta ^{\rm{T}} = e_s^{\rm{T}} \, {\mathbf {A}}, \quad {\widehat{\beta }}\,^{\rm{T}} = e_s^{\rm{T}} \, \widehat{{\mathbf {A}}}, \quad \gamma ^{\rm{T}} = e_s^{\rm{T}} \, {\mathbf {U}}, \end{aligned}$$
(3.10)

where \(e_i\) is the ith column of \({{\mathbf {I}}_{{s}\times {s}}}\). Indeed, all parallel IMEX GLMs tested in this paper have \(c_s=1\); however, we present an alternative strategy to approximate \(y(t_n)\). Suppose a parallel IMEX GLM has \(c_i=0\) for some \(i \in \left\{ 1, \cdots , s - 1 \right\} \) and \(c_s=1\). Then, based on the relation in Eq. (3.8), we have that

$$\begin{aligned}&h \sum _{j=1}^s \left( b_{i,j} \, f(Y_j) + {\widehat{b}}_{i,j} \, g(Y_j) \right) + h \, \lambda \, g(Y_s) + \sum _{j = 1}^r v_{i,j} \, y^{[n-1]}_j \\& = y^{[n]}_i + h \, \lambda \, g(Y_s) \\& = y(t_n) + {\mathcal {O}}\left( {h^{\min (p, q+1)}}\right) . \end{aligned}$$

This ending procedure has the coefficients

$$\begin{aligned} \beta ^{\rm{T}} = e_i^{\rm{T}} \, {\mathbf {B}}, \quad {\widehat{\beta }}\,^{\rm{T}} = e_i^{\rm{T}} \, \widehat{{\mathbf {B}}}+ \lambda \, e_s^{\rm{T}}, \quad \gamma ^{\rm{T}} = e_i^{\rm{T}} \, {\mathbf {V}}. \end{aligned}$$
(3.11)

For the parallel ensemble IMEX Euler methods of Sect. 5, numerical tests revealed that this new ending procedure is substantially more accurate. For the parallel IMEX DIMSIMs, the coefficients in Eqs. (3.10) and (3.11) gave similar results in tests as the accumulated global error dominated the local truncation error of the ending procedure.

4 Parallel IMEX DIMSIMs

Diagonally implicit multi-stage integration methods (DIMSIMs) have become a popular choice of the base method to build high-order IMEX GLMs. IMEX DIMSIMs are characterized by the following structural assumptions:

  1. i)

    \({\mathbf {A}}\) is strictly lower triangular, and \(\widehat{{\mathbf {A}}}\) is lower triangular with the same element \(\lambda \) on the diagonal as in Eq. (1.2);

  2. ii)

    \({\mathbf {V}}\) is rank one with the single nonzero eigenvalue equal to one to ensure preconsistency;

  3. iii)

    \(q \in \{p, p-1\}\) and \(r \in \{s, s+1\}\).

Based on Theorem 2.1, to build a parallel IMEX DIMSIM with \(p=q=r=s\), we only need to choose one of the base methods and the rest of the coefficients will follow. If we start by picking an explicit base, it may be difficult to ensure that the resulting implicit method has acceptable stability properties, ideally L-stability. Instead, we start by picking a stable, type 4 DIMSIM for the implicit base method.

In [8, 9], Butcher developed a systematic approach to construct DIMSIMs of type 4 with “perfect damping at infinity”. One of his primary results is presented in Theorem 4.1.

Theorem 4.1

(Type 4 DIMSIM coefficients [9, Theorem 4.1]) For the type 4 DIMSIM,

with \(p=q=r=s\) and \({\mathbf {V}}\, \mathbb {1}_s = \mathbb {1}_s\), the transformed coefficients

$$\begin{aligned} {\overline{{\mathbf {B}}}} = {\mathbf {T}}^{-1} \, \widehat{{\mathbf {B}}}\, {\mathbf {T}}, \qquad {\overline{{\mathbf {V}}}} = {\mathbf {T}}^{-1} \, {\mathbf {V}}\, {\mathbf {T}} \end{aligned}$$

satisfy

$$\begin{aligned} {\overline{{\mathbf {V}}}} e_1&= e_1, \end{aligned}$$
(4.1a)
$$\begin{aligned} {\overline{{\mathbf {B}}}}&= \widehat{{\mathbf {E}}}_{s} - \lambda \, {\mathbf {E}}_{s} + {\overline{{\mathbf {V}}}} \left( \lambda \, {{\mathbf {I}}_{{s}\times {s}}} - {\mathbf {K}}_{s}^{\rm{T}} \right) , \end{aligned}$$
(4.1b)

where

$$\begin{aligned} {\mathbf {T}} = \begin{bmatrix} P^{(s)}(c_1) &{} P^{(s-1)}(c_1) &{} \cdots &{} P'(c_1) \\ P^{(s)}(c_2) &{} P^{(s-1)}(c_2) &{} \cdots &{} P'(c_2) \\ \vdots &{} \vdots &{} &{} \vdots \\ P^{(s)}(c_s) &{} P^{(s-1)}(c_s) &{} \cdots &{} P'(c_s) \\ \end{bmatrix}, \qquad P(x) = \frac{1}{s!} \prod _{i=1}^s (x-c_i), \end{aligned}$$

and

$$\begin{aligned} \widehat{{\mathbf {E}}}_{n} = \begin{bmatrix} 1 &{} \frac{1}{2} &{} \frac{1}{6} &{} \cdots &{} \frac{1}{(n-1)!} &{} \frac{1}{n!} \\ 1 &{} 1 &{} \frac{1}{2} &{} \cdots &{} \frac{1}{(n-2)!} &{} \frac{1}{(n-1)!} \\ 0 &{} 1 &{} 1 &{} \cdots &{} \frac{1}{(n-3)!} &{} \frac{1}{(n-2)!} \\ \vdots &{} \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 &{} \frac{1}{2} \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 &{} 1 \end{bmatrix} \in \mathbb {R}^{n \times n}. \end{aligned}$$

Theorem 4.1 fully determines the \(\widehat{{\mathbf {B}}}\) coefficient for a type 4 DIMSIM, but \({\mathbf {c}}\), \(\lambda \), and most of \({\mathbf {V}}\) remain undetermined. Fortunately, this offers sufficient degrees of freedom to ensure that \(\widehat{{\mathbf {M}}}(\infty )\) is nilpotent. In [9, Theorem 5.1], Butcher proved \(\lambda \) must be a solution to.

$$\begin{aligned} L'_{s+1} \left( \frac{s+1}{\lambda } \right) = 0, \end{aligned}$$
(4.2a)

and

$$\begin{aligned} {\overline{{\mathbf {V}}}} = \begin{bmatrix} v_1 &{} v_2 &{} \cdots &{} v_s \\ 0 &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 \end{bmatrix}, \qquad v_i = (-1)^{s+1} \frac{s-i+2}{s+1} \lambda ^{i-1} L_{s+1}^{(s-i+2)} \left( \frac{s+1}{\lambda } \right) . \end{aligned}$$
(4.2b)

Here, \(L_n(x) = \sum\limits_{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) (-x)^i / i!\) is the Laguerre polynomial and \(L_n^{(m)}(x)\) is its mth derivative.

With the implicit base method determined, we now turn to the explicit method. Indeed, Theorem 2.1 could be applied to recover \({\mathbf {B}}\), but Theorem 4.1 provides a more direct approach. Equation (4.1b), which is normally used for type 4 methods, remains valid when \(\lambda =0\), and Eq. (4.1a) is fulfilled, because the implicit and explicit base methods share \({\mathbf {V}}\).

In summary, the coefficients for a parallel IMEX DIMSIM with \(p=q=r=s\) are given by

$$\begin{aligned} {\mathbf {A}}&= {{\mathbf {0}}_{{s}\times {s}}}, \qquad&{\mathbf {B}}&= {\mathbf {T}} \left( \widehat{{\mathbf {E}}}_{s} - \lambda \, {\mathbf {E}}_{s} + {\overline{{\mathbf {V}}}} \left( \lambda \, {{\mathbf {I}}_{{s}\times {s}}} - {\mathbf {K}}_{s}^{\rm{T}} \right) \right) {\mathbf {T}}^{-1}, \\ \widehat{{\mathbf {A}}}&= \lambda \, {{\mathbf {I}}_{{s}\times {s}}}, \qquad&\widehat{{\mathbf {B}}}&= {\mathbf {T}} \left( \widehat{{\mathbf {E}}}_{s} - {\overline{{\mathbf {V}}}} \, {\mathbf {K}}_{s}^{\rm{T}}\right) {\mathbf {T}}^{-1}, \\ {\mathbf {U}}&= {{\mathbf {I}}_{{s}\times {s}}}, \qquad&{\mathbf {V}}&= {\mathbf {T}} \, {\overline{{\mathbf {V}}}} \, {\mathbf {T}}^{-1} \end{aligned}$$

with \({\mathbf {c}}\) remaining as free parameters. The two most “natural” and frequently used choices are \({\mathbf {c}}= [0,1/(s-1),2/(s-2),\cdots ,1]^{\rm{T}}\) and \({\mathbf {c}}= [2-s,1-s,\cdots ,1]^{\rm{T}}\). This presents a trade-off where the first option has smaller local truncation errors, but the second option results in coefficients that grow slower with order, thus reducing the accumulation of finite precision cancellation errors. Table 1 presents the magnitude of these largest coefficients for both strategies.

Table 1 Approximate values for the largest coefficient in absolute value from \({\mathbf {B}}\), \(\widehat{{\mathbf {B}}}\), and \({\mathbf {V}}\) for parallel IMEX DIMSIMs of orders 2~10
Full size table

Before proceeding to the stability analysis, we present two examples of parallel IMEX DIMSIMs. A second-order method has the tableau

where \(\lambda = (3 - \sqrt{3}) / 2\). In a more compact form, a third-order method has the coefficients:

$$\begin{aligned} {\mathbf {c}}&= \begin{bmatrix} 0&\frac{1}{2}&1 \end{bmatrix}^{\rm{T}}, \\ {\mathbf {B}}&= \begin{bmatrix} \frac{6 \lambda ^2-15 \lambda +7}{2} &{} \frac{6 \lambda -5}{3} &{} -\frac{(3 \lambda -2) (6 \lambda -13)}{6} \\ \frac{72 \lambda ^2-180 \lambda +89}{24} &{} \frac{6 \lambda -7}{3} &{} \frac{-24 \lambda ^2+68 \lambda -27}{8} \\ \frac{(3 \lambda -4) (6 \lambda -7)}{6} &{} 2 \lambda -5 &{} \frac{-18 \lambda ^2+51 \lambda -7}{6} \\ \end{bmatrix}, \\ \widehat{{\mathbf {B}}}&= \begin{bmatrix} \frac{72 \lambda ^3-156 \lambda ^2+34 \lambda +21}{6} &{} \frac{-72 \lambda ^3+192 \lambda ^2-88 \lambda -5}{3} &{} \frac{36 \lambda ^3-114 \lambda ^2+80 \lambda -13}{3} \\ \frac{288 \lambda ^3-624 \lambda ^2+112 \lambda +89}{24} &{} \frac{-72 \lambda ^3+192 \lambda ^2-79 \lambda -7}{3} &{} \frac{288 \lambda ^3-912 \lambda ^2+592 \lambda -81}{24} \\ \frac{2 \left( 18 \lambda ^3-39 \lambda ^2+4 \lambda +7\right) }{3} &{} \frac{-72 \lambda ^3+192 \lambda ^2-64 \lambda -15}{3} &{} \frac{72 \lambda ^3-228 \lambda ^2+130 \lambda -7}{6} \\ \end{bmatrix}, \\ {\mathbf {V}}&= \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \begin{bmatrix} \frac{72 \lambda ^2-174 \lambda +79}{6} &{} -\frac{2 \left( 36 \lambda ^2-96 \lambda +47\right) }{3} &{} \frac{72 \lambda ^2-210 \lambda +115}{6} \\ \end{bmatrix}, \\ \lambda&= \frac{2 \cos \left( \frac{\pi }{18}\right) \sec \left( \frac{\pi }{9}\right) }{\sqrt{3}} \approx 1.210\,138\,312\,730\,603. \end{aligned}$$

4.1 Stability

While Eq. (4.2) ensures \(\rho ( \widehat{{\mathbf {M}}}(\infty ) ) = 0\), it is not a sufficient condition for L-stability of a type 4 DIMSIM. In [9], appropriate values of \(\lambda \) for L-stability are provided for orders 2~10, excluding nine. If the weaker condition of L\((\alpha )\)-stability is acceptable, smaller values of \(\lambda \) may be used, as well.

With \({\mathbf {c}}\) available as the free parameters, it is natural to see if they can be used to optimize the stability of parallel IMEX DIMSIMs. It is easy to verify that the stability is, in fact, independent of \({\mathbf {c}}\),

$$\begin{aligned} {\mathbf {T}}^{-1} \, {\mathbf {M}}(w, {\widehat{w}}) \, {\mathbf {T}}&= {\overline{{\mathbf {V}}}} + \frac{w}{1 - \lambda \, {\widehat{w}}} \left( \widehat{{\mathbf {E}}}_{s} - {\overline{{\mathbf {V}}}} \, {\mathbf {K}}_{s}^{\rm{T}} \right) \\&\quad + \frac{{\widehat{w}}}{1 - \lambda \, {\widehat{w}}} \left( \widehat{{\mathbf {E}}}_{s} - \lambda \, {\mathbf {E}}_{s} + {\overline{{\mathbf {V}}}} \left( \lambda \, {{\mathbf {I}}_{{s}\times {s}}} - {\mathbf {K}}_{s}^{\rm{T}} \right) \right) . \end{aligned}$$

The stability matrix is similar to a matrix completely independent of \({\mathbf {c}}\), and thus, \({\mathbf {c}}\) has no effect on the power boundedness of \({\mathbf {M}}\).

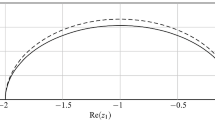
Plots of the constrained nonstiff stability region for several methods appear in Fig. 1. Roughly speaking, the area of the stability region shrinks as the order increases. Furthermore, the smaller values of \(\lambda \) satisfying Eq. (4.2a) tend to provide larger stability regions for a fixed order.

Fig. 1
figure 1

Stability regions \({\mathcal {S}}_{\alpha }\) with \(\alpha = {0}^{\circ }, 75^{\circ }, 90^{\circ }\) for parallel IMEX DIMSIMs. Note the scale for (a) is different than for the other plots

Full size image

5 Parallel Ensemble IMEX Euler Methods

If one seeks to minimize communication costs for parallel IMEX GLMs, the choice \({\mathbf {U}}= {\mathbf {V}}= {{\mathbf {I}}_{{s}\times {s}}}\) is attractive, as it eliminates the need to share external stages among parallel processes. As we will show in this section, this choice of coefficients also leads to particularly favorable structures for the order conditions and stability matrix.

Theorem 5.1

(Parallel ensemble IMEX Euler order conditions) A nonconfluent parallel ensemble IMEX Euler method, which starts with the structural assumptions

$$\begin{aligned} {\mathbf {A}}= {{\mathbf {0}}_{{s}\times {s}}}, \quad \widehat{{\mathbf {A}}}= \lambda \, {{\mathbf {I}}_{{s}\times {s}}}, \quad {\mathbf {U}}= {\mathbf {V}}= {{\mathbf {I}}_{{s}\times {s}}} \end{aligned}$$

has \(p=q=r=s\) if and only if the remaining method coefficients are

$$\begin{aligned} {\mathbf {W}}&= {{\mathbf {C}}_{s+1}}, \qquad&\widehat{{\mathbf {W}}}&= {{\mathbf {C}}_{s+1}} - \lambda \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1}, \end{aligned}$$
(5.1a)
$$\begin{aligned} {\mathbf {B}}&= {{\mathbf {C}}_{s}} \, {\mathbf {F}}_{s} \, {{\mathbf {C}}^{-1}_{s}}, \quad&\widehat{{\mathbf {B}}}&= {{\mathbf {C}}_{s}} \, {\mathbf {F}}_{s} \left( {{\mathbf {I}}_{{s}\times {s}}} - \lambda \, {\mathbf {K}}_{s} \right) {{\mathbf {C}}^{-1}_{s}}, \end{aligned}$$
(5.1b)

where

$$\begin{aligned} {\mathbf {F}}_{n} = \begin{bmatrix} 1 &{} \frac{1}{2} &{} \frac{1}{6} &{} \dots &{} \frac{1}{n!} \\ &{} 1 &{} \frac{1}{2} &{} \dots &{} \frac{1}{(n-1)!} \\ &{} &{} \ddots &{} \ddots &{} \vdots \\ &{} &{} &{} 1 &{} \frac{1}{2} \\ &{} &{} &{} &{} 1 \end{bmatrix} \in \mathbb {R}^{n \times n}. \end{aligned}$$
(5.2)

Remark 5.1

An alternative representation for Eq. (5.2) is \({\mathbf {F}}_{n} = \varphi _1({\mathbf {K}}_{n})\), where \(\varphi _1\) is the entire function

$$\begin{aligned} \varphi _1(z) = \sum _{k=0}^{\infty } \frac{z^k}{(k+1)!} = \frac{{\rm{e}}^z - 1}{z}. \end{aligned}$$

Proof

With Theorem 3.1, we only need to show that the explicit base method for parallel ensemble IMEX Euler satisfies \(p=q=r=s\) and \({\mathbf {B}}\) and \(\widehat{{\mathbf {B}}}\) are related by Eq. (3.4b). By Lemma 3.1, the internal stage order condition for the explicit method, given in Eq. (2.6a), holds. For the external stage order conditions,

$$\begin{aligned} {\mathbf {W}}\, {\mathbf {E}}_{s+1} - {\mathbf {B}}\, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - {\mathbf {V}}\, {\mathbf {W}}&= {{\mathbf {C}}_{s+1}} \, {\mathbf {E}}_{s+1} - {{\mathbf {C}}_{s}} \, {\mathbf {F}}_{s} \, {{\mathbf {C}}^{-1}_{s}} \, {{\mathbf {C}}_{s+1}} \, {\mathbf {K}}_{s+1} - {{\mathbf {C}}_{s+1}} \\&= {{\mathbf {C}}_{s+1}} \, {\mathbf {E}}_{s+1} - {{\mathbf {C}}_{s+1}} \, {\mathbf {F}}_{s+1} \, {\mathbf {K}}_{s+1} - {{\mathbf {C}}_{s+1}} \\&= {{\mathbf {C}}_{s+1}} \left( {\mathbf {E}}_{s+1} - {\mathbf {F}}_{s+1} \, {\mathbf {K}}_{s+1} - {{\mathbf {I}}_{{(s+1)}\times {(s+1)}}} \right) \\&= {{\mathbf {0}}_{{s}\times {(s+1)}}}. \end{aligned}$$

Therefore, the explicit method satisfies all order conditions and has \(p=q=r=s\). Finally,

$$\begin{aligned} {\mathbf {B}}- \lambda \, {{\mathbf {C}}_{s}} \, {\mathbf {E}}_{s} \, {{\mathbf {C}}^{-1}_{s}} + \lambda \, {\mathbf {V}}&= {{\mathbf {C}}_{s}} \, {\mathbf {F}}_{s} \, {{\mathbf {C}}^{-1}_{s}} - \lambda \, {{\mathbf {C}}_{s}} \, {\mathbf {E}}_{s} \, {{\mathbf {C}}^{-1}_{s}} + \lambda \, {{\mathbf {I}}_{{s}\times {s}}} \\&= {{\mathbf {C}}_{s}} \left( {\mathbf {F}}_{s} - \lambda \, {\mathbf {E}}_{s} + \lambda \, {{\mathbf {I}}_{{s}\times {s}}} \right) {{\mathbf {C}}^{-1}_{s}} \\&= {{\mathbf {C}}_{s}} \left( {\mathbf {F}}_{s} - {\mathbf {F}}_{s} \, {\mathbf {K}}_{s} \right) {{\mathbf {C}}^{-1}_{s}} \\&= {{\mathbf {C}}_{s}} \, {\mathbf {F}}_{s} \left( {{\mathbf {I}}_{{s}\times {s}}} - \lambda \, {\mathbf {K}}_{s} \right) {{\mathbf {C}}^{-1}_{s}} \\&= \widehat{{\mathbf {B}}}, \end{aligned}$$

which completes the proof.

While the parallel IMEX DIMSIMs of Sect. 4 require symbolic tools to derive and have coefficients that can be expressed as roots of polynomials, ensemble methods have simple, rational coefficients that can be derived with basic matrix multiplication. The following parallel ensemble IMEX Euler method, for example, is second order,

A third-order method is given by

and a fourth-order method is given by

When the order of the method increases, so does the magnitude of the method coefficients: a phenomenon previously described for parallel IMEX DIMSIMs. Similarly, the distribution of abscissae can limit the growth of coefficients, and thus, the floating-point errors associated with them. Table 2 lists these maximum coefficients for \({\mathbf {c}}\)’s evenly spaced between [0, 1], as well as \([2-s,1]\).

Table 2 Approximate values for the largest coefficient in absolute value from \({\mathbf {B}}\) and \(\widehat{{\mathbf {B}}}\) for parallel ensemble IMEX Euler methods of orders 2~10 with \(\lambda =1\)
Full size table

5.1 Stability

An interesting property of parallel ensemble IMEX Euler methods is that \({\mathbf {B}}\), \(\widehat{{\mathbf {B}}}\), \({\mathbf {A}}\), and \(\widehat{{\mathbf {A}}}\) all simultaneously triangularize. The stability matrix Eq. (3.7) can, therefore, be put into an upper triangular form with a simple similarity transformation,

$$\begin{aligned} {{\mathbf {C}}^{-1}_{s}} \, {\mathbf {M}}(w, {\widehat{w}}) \, {{\mathbf {C}}_{s}} = {{\mathbf {I}}_{{r}\times {r}}} + \frac{w}{1 - \lambda \, {\widehat{w}}} \, {\mathbf {F}}_{s} + \frac{{\widehat{w}}}{1 - \lambda \, {\widehat{w}}} \, {\mathbf {F}}_{s} \left( {{\mathbf {I}}_{{s}\times {s}}} - \lambda \, {\mathbf {K}}_{s} \right) . \end{aligned}$$
(5.3)

The diagonal entries of Eq. (5.3) are all \(1 + (w+{\widehat{w}})/(1 - \lambda \, {\widehat{w}}) \) and identically are the eigenvalues of the stability matrix. Note that the geometric multiplicity of this repeated eigenvalue is r when \(w = {\widehat{w}} = 0\) and 1 otherwise. To ensure the L-stability of the implicit base method as well as \(\rho ({\mathbf {M}}(w, \infty )) = 0\), we set \(\lambda = 1\). In this case, the eigenvalues simplify to \((1+w)/(1-{\widehat{w}})\) matching the stability of the IMEX Euler scheme

$$\begin{aligned} y_{n} = y_{n-1} + h \, f(t_{n-1}, y_{n-1}) + h\, g(t_{n}, y_{n}). \end{aligned}$$

There are several other interesting stability features for parallel ensemble IMEX Euler methods. First, stability is independent of the order and the choice of abscissae, allowing a systematic approach to develop stable methods of arbitrary order. The constrained nonstiff stability region has the simple form

$$\begin{aligned} {\mathcal {S}}_{\alpha }= {\mathcal {S}}= \left\{ w \in \mathbb {C}: \vert 1 + w\vert < 1 \vee w=0 \right\} \end{aligned}$$

when \(s > 1\). Except for the origin, the boundary of this circular stability region is carefully excluded, because the 1 eigenvalue of \({\mathbf {M}}\) is defective at those points. This family of methods is stability decoupled in the sense that linear stability of the base methods for their respective partitions implies linear stability of the IMEX scheme.

We note that aside from the origin, \({\mathcal {S}}_{\alpha }\) does not contain any of the imaginary axis, indicating potential stability issues when f is oscillatory. This analysis is a bit pessimistic, however, as \({\mathcal {S}}_{\alpha }\) represents the explicit stability when \({\widehat{w}}\) is chosen in a worst-case scenario. Only when \({\widehat{w}}=0\) is there instability for all purely imaginary w. As the modulus of \({\widehat{w}}\) grows, the range of imaginary w for which the IMEX method is stable also grows.

6 Numerical Experiments

We provide numerical experiments to confirm the order of convergence and to study the performance of our methods compared to other IMEX methods. We use the CUSP and Allen–Cahn problems in our experiments.

6.1 CUSP Problem

The CUSP problem [20, Chapter IV.10] is associated with the equations

$$\left\{\begin{array}{ll} \frac{\partial y}{\partial t}&= -\frac{1}{\varepsilon } \left( y^3 + a \, y + b \right) + \sigma \, \frac{\partial ^{2}y}{\partial x^{2}}, \\ \frac{\partial a}{\partial t}&= b+ 0.07 \, v + \sigma \, \frac{\partial ^{2}a}{\partial x^{2}},\\ \frac{\partial b}{\partial t}&= b \, (1-a^2) - a- 0.4 \, y + 0.035 \, v + \sigma \, \frac{\partial ^{2}b}{\partial x^{2}}, \end{array} \right.$$
(6.1)

where \(v = \frac{u}{u+ 0.1}\) and \(u = (y-0.7) \, (y-1.3)\). The timespan is \(t \in [0,1.1]\), the spatial domain is \(x \in [0,1]\), and the parameters are chosen as \(\sigma = \frac{1}{144}\) and \(\varepsilon = 10^{-4}\). Spatial derivatives are discretized using second-order central finite differences on a uniform mesh with \(N=32\) points and periodic boundary conditions. The initial conditions are

$$\begin{aligned} y_i(0) =0, \quad a_i(0) = -2 \cos \left(\frac{2\pi i}{N}\right), \quad b_i(0) = 2\sin \left(\frac{2\pi i}{N}\right) \end{aligned}$$

for \(i=1,\cdots ,N\). Note that the problem is singularly perturbed in the y component and the stiffness of the system can be controlled using \(\varepsilon \). Following the splitting used in [24], the diffusion terms and the term scaled by \(\varepsilon ^{-1}\) form g, while the remaining terms form f. The MATLAB implementation of the CUSP problem is available in [15, 29].

We performed a fixed time-stepping convergence study of the new methods. Figure 2 shows the error of the final solution versus number of timesteps. Error is computed in the \(\ell ^2\) sense using a high-accuracy reference solution. In all cases, the parallel IMEX GLMs converge at least at the same rate as theoretical order of accuracy.

Fig. 2
figure 2

Convergence of parallel IMEX DIMSIM and parallel ensemble IMEX Euler methods for the CUSP problem Eq. (6.1)

Full size image

6.2 Allen–Cahn Problem

We also consider the two-dimensional Allen–Cahn problem described in [35]. It is a reaction-diffusion system governed by the equation

$$\begin{aligned} \frac{\partial u}{\partial t} = \alpha \, \nabla ^{2}{u} + \beta \, (u - u^3) + s, \end{aligned}$$
(6.2)

where \(\alpha = 0.1\) and \(\beta = 3\). The time-dependent Dirichlet boundary conditions and source term s(t, x, y) are derived using the method of manufactured solutions, such that the exact solution is

$$\begin{aligned} u(t,x,y) = 2 + \sin (2\pi \left( x -t \right) ) \cos (3 \pi \left( y-t \right) ). \end{aligned}$$

We discretize the PDE on a unit square domain using degree two Lagrange finite elements and a uniform triangular mesh with \(N=32\) points in each direction. The diffusion term and forcing associated with the boundary conditions are treated implicitly, while the reaction and source term are treated explicitly.

The problem is implemented using the FEniCS package [1] leveraging OpenMP parallelism to speed up f and g evaluations, as well as MPI parallelism of stage computations made possible by the structure of the parallel IMEX GLMs. All tests were run on the Cascades cluster maintained by Virginia Tech’s Advance Research Computing center (ARC). Parallel experiments were performed on \(p=q=r=s\) nodes, each using 12 cores. Serial experiments were done on a single node with the same number of cores. The error was computed using the \(\ell _2\) norm by comparing the nodal values of the numerical solution against a high-accuracy reference solution.

Figure 3 summarizes the results of this experiment by comparing several additive Runge–Kutta (ARK) methods and IMEX DIMSIMs with parallel IMEX GLMs derived in this paper. At order 3, serial methods are ARK3(2)4L[2]SA from [25] and IMEX-DIMSIM3 from [14]. At order 4, comparisons are done against ARK4(3)7L[2]SA1 from [26] and IMEX-DIMSIM4 from [35]. Order 5 serial methods are ARK5(4)8L[2]SA2 from [26] and IMEX-DIMSIM5 from [35]. Finally, the order 6 baseline is IMEX-DIMSIM6(\({\mathcal {S}}_{\pi /2}\)) from [24]. The results show that parallel ensemble IMEX Euler methods are the most efficient in all cases. Parallel IMEX DIMSIMs are competitive at orders 3 and 6 and surpass the efficiency of serial schemes at orders 4 and 5.

Figure 4 plots convergence of the methods used in the experiment. We can see that the ARK methods exhibit order reduction for this problem, which explains their poor efficiency results. All other methods achieve the expected order of accuracy. For a fixed number of steps, the parallel IMEX GLMs are less accurate than the serial IMEX GLMs, which indicates that parallel methods have larger error constants and are not the most efficient when limited to serial execution. This is to be expected given parallel methods have a more restrictive structure and fewer coefficients available for optimizing the principal error and stability.

Fig. 3
figure 3

Work-precision diagrams for the Allen–Cahn problem Eq. (6.2)

Full size image
Fig. 4
figure 4

Convergence diagrams for the Allen–Cahn problem Eq. (6.2)

Full size image

7 Conclusion

This paper studies parallel IMEX GLMs and provides a methodology to derive and solve simple order conditions for methods of arbitrary order. Using this framework, we construct two families of methods, based on existing DIMSIMs and on IMEX Euler, and provide linear stability analyses for them.

Our numerical experiments show that parallel IMEX GLMs can outperform existing serial IMEX schemes. Between parallel IMEX DIMSIMs and parallel ensemble IMEX Euler methods, the latter proved to be the most competitive. The error for the ensemble methods is generally smaller than that of the DIMSIMs, due in part to the improved ending procedure. Moreover, the magnitude of method coefficients grows slower for ensemble methods as documented in Tables 1 and 2, reducing the impact of accumulated floating-point errors. For orders 5 and higher, we have to carefully select the method and distribution of the abscissae to control these errors. In addition, one notes that parallel ensemble IMEX Euler methods tend to have smaller values of \(\lambda \), which improves convergence of iterative linear solvers used in the Newton iterations.

Owing to their excellent stability properties, the ensemble family shows great potential for constructing other types of partitioned GLMs. Of particular interest are alternating directions implicit (ADI) GLMs [30], as well as multirate GLMs. The authors hope to study these in future works.