1 Introduction

In this research, the focus is on the study of Remotely Operated Vehicles (ROVs) [1, 2]. The design models of ROVs [3] have received limited attention, and the achieved results are still constrained due to the challenges involved in procuring ROV accessories. Moreover, with the increasing depths and durations of underwater work required in offshore structures such as drilling rigs and oil and gas pipelines, there is an urgent need to research and design a compact remotely controlled submersible vehicle that can be applied in offshore and ocean-related research fields. Figure 1 illustrates ROVs operating underwater.

Fig. 1
figure 1

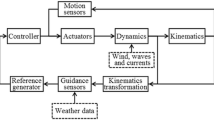
ROV and its operating system [1]

Full size image

Currently, ROVs, widely known as Remotely Operated Vehicles, are extensively utilized globally, particularly in deep-sea resource exploration, scientific research, and underwater maintenance work. Companies specializing in ROVs have been developing increasingly advanced and diverse equipment to meet the requirements of diverse customers in various fields.

Furthermore, advancements in remote-control technology and data transmission have facilitated easier and more precise ROV operations. Intelligent control systems and automation are being researched and developed to enable ROVs to autonomously carry out complex tasks.

However, the utilization of ROVs still encounters challenges, including cost reduction and increased safety measures to ensure the well-being of humans and the environment [4]. Companies are actively exploring and developing solutions to address these challenges, making ROVs increasingly valuable and effective in numerous fields.

ROVs play a crucial role in multiple domains [5], particularly in deep-sea resource exploration, scientific research, and underwater maintenance work. The progress in ROV technology [6] has expedited tasks, enhanced efficiency, and improved safety for humans, while minimizing environmental impacts. ROVs serve as valuable tools for geological, biological, meteorological, and hydrological research. Additionally, ROVs are instrumental in the search for and extraction of natural resources on the ocean floor, such as oil, gas, and minerals.

Electric ROVs receive power [7] from the ship or shore, which is transmitted through cables to the ROV. This type of ROV employs electric motors to control its legs and other movable components.

Hydraulic ROVs [8, 9], on the other hand, employ hydraulic oil to manipulate their movable parts. Hydraulic power is supplied from the ship or shore and transmitted through cables to the ROV. Hydraulic motors are utilized to control the legs and other movable parts of this type of ROV.

Depending on the intended use and technical requirements, ROVs can be equipped with various types of propulsion systems. The study of ROV dynamics has significantly contributed to the development and enhancement of propulsion systems for ROVs [10]. These studies aid ROV designers in gaining a better understanding of the functioning of movable parts and optimizing their performance. Consequently, control and positioning of ROVs [11] are enhanced, resulting in improved accuracy and efficiency of underwater tasks [12].

The study of ROV dynamics also plays a pivotal role in optimizing the design and performance of different propulsion systems, including electric and hydraulic motors. Such research endeavors contribute to the operational efficiency of ROVs by reducing operational time and maintenance costs.

Moreover, the study of ROV dynamics brings forth numerous other benefits in the realm of underwater science and technology. These benefits encompass improved performance of resource extraction equipment on the seafloor, optimization of underwater environmental control systems, assessment of the impact of human activities on the underwater environment, and exploration of issues related to climate change and oceans [1, 13,14,15].

Additionally, the article places emphasis on developing fundamental controllers for ROVs as a crucial initial step towards intelligent controller development for ROVs. These fundamental controllers aid researchers in gaining a better understanding of ROV operations and the factors influencing their performance.

The approach to the topic involves research methods, the subject and scope of re-search, and the research content:

  • Overview and development of dynamic modeling and control of underwater ROV vehicles.

  • Designing fuzzy logic controllers to govern the motion of underwater ROV vehicles.

  • Utilizing Matlab Simulink software [16] for simulating the motion of underwater ROV vehicles.

2 Kinetics and Dynamic of ROV Submarine

2.1 Modeling of Kinetics Behavior and Control of ROV

Operating underwater robots [12] involves the utilization of a control system. Accurate modeling of the kinematic behavior [17] of underwater robots is crucial for designing the robot's control system. This task entails not only determining the mathematical model of the robot but also describing the interaction between the robot and the surrounding water. The motion equation of the underwater robot is derived by applying the Newton–Euler equation [13] to the freely moving rigid body, accounting for the fluid–structure interaction. However, many factors used in the kinematic modeling of underwater robots still exhibit relatively high inaccuracies.

In addition to the challenging description of the fluid–structure interaction, predicting and accurately modeling the impact of water flow on the robot poses further difficulties. Moreover, the cable used for power supply and signal transmission between the robot and the mothership exerts varying forces on the robot based on its position, velocity, ocean current speed, and cable configuration. These forces are not readily accessible for feedback control systems. Therefore, the selection of a control strategy for underwater robots holds great significance. Traditional control methods such as PD, and PID [18] are still employed due to their simplicity and ease of implementation. Additionally, modern control techniques like sliding control [14], adaptive control [19], and fuzzy control [20] have garnered research attention from experts.

2.2 ROV Kinetics

Underwater vehicles [21], such as ROVs, are considered to be rigid bodies with six degrees of freedom. The position and orientation of the vehicle are determined by the position of a point on the vehicle, known as the pole, and the orientation of the vehicle with respect to a fixed reference frame. The kinetics problem presents the position and orientation parameters, as well as the longitudinal and angular velocity trans-formations in the reference frame. This involves the concept of direction cosine matrix, the angles of position, and the transformations of longitudinal and angular velocities.

According to the international symbols, the six components of motion for ships and submarines are designated as follows: the three translational motions along the axes of the ship are surge (longitudinal), sway (transverse), and heave (vertical); and the three rotational motions are roll (about the longitudinal axis), pitch (about the transverse axis), and yaw (about the vertical axis), as shown in Fig. 2 and Table 1.

Fig. 2
figure 2

ROV model with two coordinate systems

Full size image
Table 1 The symbols are used for ROV
Full size table

Let \(q={\left[x, y, z, \phi , \theta , \psi \right]}^{T}\) be the generalized coordinates vector that defines the position and orientation of the ROV, where x, y, z are the coordinates of the origin O of the ROV-fixed frame in the fixed frame; and \(\phi , \theta , \psi\) are the Roll–Pitch-Yaw angles; q1 = [x, y, z]T and q2 = [\(\phi , \theta , \psi\)]T. Let y = [u, v, w, p, q, r]T be the vector containing the components of the velocity of point O and the angular velocity of the body in the body-attached reference frame (v0 = [u, v, w]T) and \(\omega\) = [p, q, r]T or set y1 = [u, v, w]T, y2 = [p, q, r]T

The rotation matrix determines the direction of the object according to the three Roll-Pitch-Yaw angles as follows:

$$A\left({q}_{2}\right)={A}_{x0}\left(\psi \right){A}_{y1}\left(\theta \right){A}_{z2}\left(\phi \right)$$
(1)
$$A\left({q}_{2}\right)=\left[\begin{array}{ccc}c\psi c\theta & -s\psi c\phi +c\psi s\theta s\phi & s\psi s\phi +c\psi s\theta c\phi \\ s\psi c\theta & s\psi c\phi +s\psi s\theta c\phi & -c\psi s\phi +s\psi s\theta \\ -s\theta & s\phi c\theta & c\phi c\theta \end{array}\right]$$
(2)

The kinematic differential equations for submarines are written as:

$${\dot{q}}_{1}=A\left({q}_{2}\right){v}_{0}\iff \left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=\left[\begin{array}{ccc}c\psi c\theta & -s\psi c\phi +c\psi s\theta s\phi & s\psi s\phi +c\psi s\theta c\phi \\ s\psi c\theta & c\psi c\phi +s\psi s\theta c\phi & -c\psi s\phi +s\psi s\theta c\phi \\ -s\theta & s\phi c\theta & c\phi s\theta \end{array}\right]\left[\begin{array}{c}u\\ v\\ w\end{array}\right]$$
(3)
$${\dot{q}}_{2}={J}_{2}\left({q}_{2}\right)\omega \iff \left[\begin{array}{c}\dot{\psi }\\ \dot{\theta }\\ \dot{\varphi }\end{array}\right]=\left[\begin{array}{ccc}1& sin\phi tan\theta & cos\phi tan\theta \\ 0& cos\phi & -sin\phi \\ 0& \frac{sin\phi }{c\mathrm{\acute{o} }\theta }& \frac{cos\phi }{cos\theta }\end{array}\right]\left[\begin{array}{c}p\\ q\\ r\end{array}\right]$$
(4)

Combine the two Eqs. (3) and (4) above to get:

$${q}_{2}={J}_{2}\left({q}_{2}\right)y$$
(5)

With the overall transformation matrix as follows:

$$J\left({q}_{2}\right)=\left[\begin{array}{cccccc}c\psi c\theta & -s\psi c\phi +c\psi s\theta s\phi & s\psi s\phi +c\psi s\theta c\phi & 0& 0& 0\\ s\psi c\theta & c\psi c\phi +s\psi s\theta c\phi & -c\psi s\phi +s\psi s\theta c\phi & 0& 0& 0\\ -s\theta & s\phi s\theta & c\phi c\theta & 1& 0& 0\\ 0& 0& 0& 0& s\phi t\theta & c\phi t\theta \\ 0& 0& 0& 0& c\phi & -s\phi \\ 0& 0& 0& 0& \frac{s\phi }{c\theta }& \frac{c\phi }{c\theta }\end{array}\right]$$
(6)

2.3 Body

An ROV, AUV or a submarine moving in water is modeled as a solid body. Setting up a dynamic equation [15] for a moving solid can use the following tools: momentum theorem [22], angular momentum theorem [23], kinetic energy theorem [24], Lagrange 2 equation [25], etc. This section presents the solid-body dynamics then applies the motion differential equation setting to the underwater robot. The differential equation of motion describing the motion of a rigid body in space is written in matrix form:

$$\left[\begin{array}{cc}mS\left(\omega \right){\mathrm{v}}_{o}& -mS\left(\omega \right)S{(u}_{c})\omega \\ mS{(u}_{c})S\left(\omega \right){\mathrm{v}}_{o}& -S{(J}_{O}\omega )\omega \end{array}\right]=\mathrm{CRB}(\mathrm{v})\mathrm{v }=\mathrm{ CRB }(\mathrm{v})\left[\begin{array}{c}{\mathrm{v}}_{O}\\ \omega \end{array}\right]$$
(7)

To use this equation for submersibles, we need to add the forces that act when the submersible moves through the water. The force acting on the robot as it moves through the water depends on many factors such as the shape of the object, the flow of water around it. However, for a robot moving at a low speed, the force of the environment acts, so the robot includes:

 + Acceleration ratios drag: \({\tau }_{A}\)

 + Velocity dependent drag \({\tau }_{D}\)

 + Gravity and force due to displaced volume of water: g(η).

 + Control force due to engine propellers: τ

 + Other components not mentioned above are considered as noise: \({\tau }_{E}\)

Such:

$${\tau }_{RB}={\tau }_{A}+{\tau }_{D}+\mathrm{g}\left(\eta \right)+\tau +{\tau }_{E}$$
(8)

Acceleration ratios drag \({\tau }_{A}\):

Since the robot moves a portion of the liquid surrounding the robot to be accelerated accordingly, this effect will be accounted for in the drag component proportional to the acceleration \({\tau }_{A}\), or sub-mass.

$${\tau }_{A}=-{M}_{A}\dot{v}-{C}_{A}\left(v\right)v$$
(9)

where the \({M}_{A}\) sub-mass matrix of size 6 × 6 has experimentally determined components and is divided into four 3 × 3 blocks:

$${M}_{A}=\left[\begin{array}{cc}{A}_{11}& {A}_{12}\\ {A}_{21}& {A}_{22}\end{array}\right]$$
(10)

The CA(v) matrix is calculated similarly to the CRB(v) matrix.

$${C}_{A}\left(v\right)=\left[\begin{array}{cc}{0}_{3x3}& -S({A}_{11}{\mathrm{v}}_{1}+{A}_{12}{\mathrm{v}}_{2})\\ -S({A}_{11}{\mathrm{v}}_{1}+{A}_{12}{\mathrm{v}}_{2})& -({A}_{21}{\mathrm{v}}_{1}+{A}_{22}{\mathrm{v}}_{2})\end{array}\right]$$
(11)

In case the robot has three planes of symmetry, completely submerged in water, \({M}_{A}\) is a positively definite symmetry matrix. The components on the main diagonal are larger than many other components. Then it is possible to approximate:

$${M}_{A}=diag({A}_{11},{A}_{22},{A}_{33}, {A}_{44},{A}_{55}, {A}_{66})$$
(12)

And:

$${C}_{A}\left(v\right)=\left[\begin{array}{cccccc}0& 0& 0& 0& {A}_{33}w& -{A}_{22v}\\ 0& 0& 0& -{A}_{33}w& 0& {A}_{11}u\\ 0& 0& 0& {A}_{22}v& -{A}_{11}u& 0\\ 0& {A}_{33}w& {-A}_{22}v& 0& {A}_{66}r& {A}_{55}q\\ {-A}_{33}w& 0& {A}_{11}u& {A}_{66}r& 0& {A}_{44}p\\ -{A}_{22v}& {-A}_{11}u& 0& {A}_{66}q& -{A}_{44}p& 0\end{array}\right]$$
(13)

Velocity dependent drag \({\tau }_{D}\)

The velocity-dependent drag can be written in matrix form as follows:

$${\tau }_{D}=D\left(v\right)v$$
(14)

where D(v) is a matrix of size 6 × 6, positive definite real, its elements depend on the speed of the robot.

In the simplest case, it can be considering the resistances to each move independently of each other and that these resistances are proportional to the first and second order with respect to the velocity to get:

$$\begin{aligned} {\text{D}}\left( {\text{v}} \right) \, = & {\text{ D}}_{L} + {\text{ D}}_{N} = {\text{ diag }}\{ X_{u} ,Y_{v} ,Z_{w} ,K_{p} ,M_{q} ,N_{r} \} \, \\ & + diag\{ X_{u\left| u \right|} \left| u \right|,Y_{v\left| v \right|} \left| v \right|, Z_{w\left| w \right|} \left| w \right|,Z_{w\left| w \right|} \left| w \right|,K_{p\left| p \right|} \left| p \right|,M_{q\left| q \right|} \left| q \right|, N_{r\left| r \right|} \left| r \right|\} \\ \end{aligned}$$
(15)

where the coefficients \({X}_{u}\), \({Y}_{v}\), \(\dots\), \({N}_{r}\), \({Y}_{v\left|v\right|}\), …, \({N}_{r\left|r\right|}\left|r\right|\) are determined from experiment.

Gravity and repulsion due to displaced volume of water g(η):

Gravity fG is applied at the center rG = [\({X}_{G}\), \({Y}_{G}\),\({Z}_{G}\)], and buoyancy force fB is applied at the center of buoyancy. Reducing these forces to the origin O, expressed in a body-connected system to get:

$$\mathrm{g}(\eta ) =\left[\begin{array}{c}{\mathrm{f}}_{G}(\eta )+{\mathrm{f}}_{B}(\eta )\\ S{(r}_{G}),{\mathrm{f}}_{G}\left(\eta \right)+S{(r}_{B}).{\mathrm{f}}_{B}(\eta )\end{array}\right]$$
(16)

With \({\text{f}}_{G} \left( \eta \right) = \, - {\text{J}}_{{1}}^{{ - {1}}} \left( \eta \right)\; \left[ {\begin{array}{*{20}c} 0 & 0 & {\text{W}} \\ \end{array} } \right]^{{\text{T}}}\), \({\text{f}}_{G} \left( \eta \right) = \, - {\text{J}}_{{1}}^{{ - {1}}} \left( \eta \right) \left[ {\begin{array}{*{20}c} 0 & 0 & {\text{B}} \\ \end{array} } \right]^{{\text{T}}}\) (W- robot weight, B- rebound force).

Expanding to get:

$$\mathrm{g}(\eta ) =\left[\begin{array}{c}\left(B-W\right)s\theta \\ -\left(B-W\right)c\theta s\phi \\ -\left(B-W\right)s\theta c\phi \\ -\left({y}_{B}B- {y}_{G}W\right)c\theta c\phi +({z}_{B}B-{z}_{B}Wc\theta s\phi )\\ \left({z}_{B}B- {y}_{G}W\right)s\theta +({x}_{B}B-{x}_{G}W)c\theta s\phi \\ -\left({z}_{B}B-{x}_{G}W\right)c\theta s\phi -\left({z}_{B}B-{y}_{G}W\right)s\theta \end{array}\right]$$
(17)

Driven force by the motor propellers τ.

Usually, the robot is driven by electric motors with propellers, the propellers rotating in the water will create thrust to make the robot move. Thrust depends on many factors such as: propeller diameter, blade inclination angle, rotational speed of the moving fan creating a thrust \({F}_{i}\)(i = 1,2…p = number of propellers on the robot), force This thrust is proportional to the square of the rotational velocity of the propeller. Then, the sum of the forces and moments to make the robot move is as follows:

$$\uptau =\mathrm{Bu}$$
(18)

where:\(\tau = \, [F_{x} ,F_{y} ,F_{z} ,m_{x} ,m_{y} ,m_{z} ]^{{\text{T}}}\), \({\text{u}} = \, [F_{1} ,F_{2} , \ldots F_{p} ]^{{\text{T}}}\).

The 6xp matrix B is called the distribution matrix, which depends on the arrangement of motors on the robot body.

2.4 Equation of Motion for Submersible ROV

With the forces described above, instead of the equation of motion of the object, we get the equation of motion of the robot underwater as follows:

$${\text{M}}\dot{\text v} + {\text{ C}}\left( {\text{v}} \right){\text{v }} + {\text{ D}}\left( {\text{v}} \right){\text{v }} + {\text{ g}}(\eta ) + \tau _{E} = {\text{ Bu}}$$
(19)

where:

M = MRB + MA

C(v) = CRB(v) + CA(v).

Combined with kinematic differential equations, we get a system of 12 differential equations of first order describing underwater robot dynamics.

$$\left\{\begin{array}{c}M\dot{\mathrm{v}} + C(v)v + D(v)v + g(\eta ) + {\tau }_{E} = \tau = Bu\\ \dot{\upeta }=J(\eta )v\end{array}\right.$$
(20)

Because of the kinematic relation \({\dot{\upeta }} = {\text{ J}}(\eta ){\text{v}}\), can be transform the differential equation of motion of the submersible into a system of 6 differential equations of two for generalized coordinate systems \(\eta = \left[ {x_{0} ,y_{0} ,z_{0} ,\phi ,\theta ,\varphi } \right]^{{\text{T}}}\) as follows:

$$\left\{ {\begin{array}{*{20}c} {{\dot{\upeta }} = {\text{J}}\left( \eta \right){\text{v}} \Rightarrow {\text{v}} = {\text{J}} - 1\left( \eta \right){\dot{\upeta }}} \\ {{\ddot{\upeta }} = {\text{J}}\left( \eta \right){\dot{\text{v}}} + {\dot{\text{J}}}\left( \eta \right){\text{v}} \Rightarrow {\dot{\text{v}}} = {\text{J}}^{ - 1} \left( \eta \right)\ddot{\eta }{\text{J}} - 1\left( \eta \right){\dot{\text{J}}}\left( \eta \right){\text{J}}^{ - 1} \left( \eta \right){\dot{\upeta }}} \\ \end{array} } \right.$$
(21)

Substituting the quantities just received (19), to get the differential equation of motion as follows:

$${\text{M}}_{\left( \eta \right)} (\eta )\ddot{\eta } + {\text{C}}_{{\eta { }}} (\eta ,{\dot{\upeta }}) {\dot{\upeta }} + {\text{D}}_{{\eta { }}} (\eta ,{\dot{\upeta }}) {\dot{\upeta }} + {\text{ g}}(\eta )(\eta ) + {\text{d}}_{{\eta { }}} = \tau_{\eta }$$
(22)

where:

$$\left\{ {\begin{array}{*{20}c} {{\text{M}}_{{\left( \eta \right)}} (\eta ) = {\text{J}} - {\text{T}}(\eta ){\text{MJ}} - 1(\eta )} \\ {{\text{C}}_{{\left( \eta \right)}} (\eta )\dot{\upeta } = {\text{J}} - {\text{T}}(\eta )[{\text{C}}({\text{v}}) - {\text{MJ}} - 1(\eta )\mathop {\text{J}}\limits^{.} (\eta )]{\text{J}} - 1(\eta )} \\ {{\text{g}}_{{(\eta )}} = {\text{J}} - {\text{T}}(\eta ){\text{g}}(\eta )} \\ {{\text{d}}_{\eta } = {\text{J}} - {\text{T}}(\eta ){\text{d}}_{0} } \\ {\tau _{\eta } = {\text{J}} - {\text{T}}(\eta )\tau } \\ \end{array} } \right.$$
(23)

Some properties of differential equations of motion:

1. M = MT > 0 \(\Rightarrow\) xTMx > 0, \(\forall\) x \(\ne\) 0.

2. C(v) = − CT(v) \(\Rightarrow\) xTC(v)x = 0 \(\forall\) x.

3. D(v) > 0 \(\Rightarrow\) xTD(v)x \(\frac{1}{2}\) xT(D(v) + DT(v))x > 0 \(\forall\) × \(\ne\) 0.

4. BBT and τ are not singular matrices.

5. J(η) is a Euler angle dependent transformation matrix (undefined when \(\theta\)=\(\pm\) 90°).

2.5 Individual Cases

 + In case the ROV moves (according to the x-axis)

$$\left\{ {\begin{array}{*{20}c} {{\text{m}}_{x} {\dot{\text{v}}} + Y_{{{\text{v}}\left| {\text{v}} \right|}} \left| {\text{v}} \right|{\text{v}} + {\text{d}}\left( {\text{t}} \right) = {\text{t}}_{x} } \\ {{\dot{\text{x}}} = {\text{v}}} \\ \end{array} } \right.$$
(24)

 + In case the train moves in the horizontal plane (z = const, ϕ = θ = 0):

$$\left[ {\begin{array}{*{20}c} {m_{x} } & 0 & 0 \\ 0 & {m_{y} } & 0 \\ 0 & 0 & {I_{z} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{r}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 & { - m_{y} v} \\ 0 & {m_{y} } & {m_{x} u} \\ {m_{y} v} & { - m_{x} u} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} u \\ v \\ r \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {D_{u\left| u \right|} \left| u \right|} & 0 & 0 \\ 0 & {D_{v\left| v \right|} \left| v \right|} & 0 \\ 0 & 0 & {D_{r\left| r \right|} \left| r \right|} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} u \\ v \\ r \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} X \\ Y \\ N \\ \end{array} } \right]$$
(25)

And the kinematic differential equation:

$$\left[ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{\psi }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \psi } & { - \sin \psi } & 0 \\ {\sin \psi } & {\cos \theta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} u \\ v \\ q \\ \end{array} } \right]$$
(26)

2.6 Individual Cases

As shown above, in the expression (18) linear relationship between the driving force and the thrust of the engines, the calculation of the thrust forces needs to distribute those forces evenly to each engine to optimize the thrust for each engine propellers:

$$\tau =Bu$$
(27)

In the case of driving residuals, B is not a square matrix with each vector τ, it can be solved for many different u vectors. The following will present the method to find an "optimal" u. Will find the vector u satisfying Eq. (27) with the condition.

$$J = \frac{1}{2}u^{T} {\text{Wu}}$$
(28)

where W is a square matrix of size \({n}_{p}\) x \({n}_{p}\)—called the weight matrix. If all motors are of the same type and have the same role, W will be chosen as the unit matrix. With the help of the Lagrange multiplier λ to get u by finding the value of the following function:

$$L(u,\lambda ) \, = \frac{1}{2}u^{T} Wu + \lambda^{T} (\tau - Bu)$$
(29)

Derivative L and then taking the solution of the equation then substituting into Eq. (27) to get the optimal solution u:

$$u = W^{ - 1} B^{T} (BW^{ - 1} B^{T} )^{ - 1} \tau \hat{ = }B_{w}^{\dag } \tau$$
(30)

The matrix \(B_{w}^{\dag }\) = W−1BT(BW−1BT)−1 is called the weighted general inverse matrix of matrix B. If choose W as the unit matrix and \({n}_{p}\)=6 and \(B^{\dag }\)=B−1, to get thrust for propellers:

$${\text{u}} = {\text{ B}}^{{ - {1}}} \tau$$
(31)

The differential equations are obtained on the basis of the angular momentum theorems, as well as the kinetic energy theorem. Combined with the 12-way differential equations of kinematics. The forces exerted by the aquatic medium are described by the enclosed mass, the drag force, and the hydrostatic force. The force and torque controlling the submersible are represented by a linear relationship with respect to the thrust of the propeller system.

3 Design Control Method for ROV, Simulation, Results and Discussion

In Chapter 2, a dynamic model for ROV has been established. It is a system of differential equations that shows the relationship between the force acting on the ROV and its motion. This chapter will present some motion control algorithms for ROV. The motion control for ROV [26] can be classified into 3 types:

  • Control to the point aka position control problem—and keep the ROV stable at that position.

  • Control the ROV to follow a given trajectory, here showing both the path and the law of motion along that trajectory.

  • Control the ROV to follow a given path without regard to the law of motion along that trajectory.

In the third problem, after the operator preselects the motion rule along the trajec-tory s(t), this problem will become the second problem. Therefore, here only two prob-lems of motion control are examined here. first and second moves.

Regarding the problem of motion control of ROV, there are many control methods in this chapter. In this chapter, we will present some control laws that design and cal-culate it based on the dynamic model established from Chapter 2:

$$\dot{\upeta }=\mathrm{J}(\eta )\mathrm{v}$$
(32)
$$\text{M}\dot{\text{v}} + {\text{C}}({\text{v}}){\text{v}} + {\text{D}}({\text{v}}){\text{v}} + {\text{g}}(\eta ) + \tau _{E} = \tau$$
(33)

The parameters of ROV used for the survey are as follows:

m = 80; \({\text{r}}_{{\text{C}}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}\), \({\text{r}}_{{\text{B}}} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - 0.040} \\ \end{array} } \right]^{{\text{T}}}\)

$${\text{M}}_{{{\text{RB}}}} = {\text{ diag }}\left( {\begin{array}{*{20}c} {80} & {80} & {80} & {4.39} & {8.06} & {9.17} \\ \end{array} } \right)$$
$${\text{M}}_{{\text{A}}} = {\text{diag}}\left( {\begin{array}{*{20}c} {63.84} & {87.36} & {102.48} & {3.512} & {6.448} & {7.336} \\ \end{array} } \right)$$

Matrix of inertia: \(\mathrm{Jo}=\mathrm{Io}= \left[\begin{array}{ccc}4.39& 0& 0\\ 0& 8.06& 0\\ 0& 0& 9.17\end{array}\right]\)

In this paper, the author proposes a Fuzzy-PD controller [27] for ROV. The author chose the Fuzzy-PD controller for the research object due to the following characteristics:

Ability to handle nonlinear dynamics: ROVs typically operate in water environments where there are nonlinear factors such as dynamic environment, resistance from water, and forces exerted by surrounding objects. The Fuzzy-PD controller is capable of effectively handling nonlinear impacts and providing flexible control feedback to respond to different situations.

Flexibility in design and adjustment: The Fuzzy-PD controller allows for easy customization of control rules based on the knowledge and experience of the controller. The Fuzzy-PD system can be adjusted flexibly to meet the specific requirements of the ROV and the working environment.

Noise and uncertainty tolerance: The water environment can introduce noise and uncertainty in measurements and control feedback. The Fuzzy-PD controller has the ability to resist noise and handle uncertain parameters. This helps improve the stability and responsiveness of the ROV in challenging environments.

Simplicity and comprehensibility: Compared to some other complex control methods, Fuzzy-PD has a simple and understandable structure. This means it is easy to deploy and effective in controlling ROVs. The Fuzzy-PD control rules can be expressed clearly and easily optimized and adjusted.

The Fuzzy controller is based on the Takagi–Sugeno fuzzy rule and performs online adjustment of the coefficients of the PD controller. The hybrid fuzzy controller takes the error 'e' and derivative error 'ce' as inputs, and this process is used to determine the control parameters. Linear transformation is used to determine the Kp and KD parameters of the PD controller as follows:

PD control + gravity compensation is the simplest control law that meets the control requirements of ROV submersibles. The control force is calculated from the desired position and the moving state of the ship at the present time obtained by sensors mounted on the hull.

$$\tau_{\upeta } = \, - {\text{K}}_{{\text{p}}} \dot{\tilde{\upeta }} - {\text{K}}_{{\text{d}}} \dot{\tilde{\upeta }} - {\text{g(}}\upeta {)}$$
(34)

where \({\tilde{\upeta }} = {\upeta } - {\upeta }_{{\text{d}}}\) is the position difference between the actual and the desired, Kp, Kd are positive definite matrices and are usually chosen as diagonal matrices.

To investigate the stability of this rule, to consider the Lyapunov function:

$${\text{V}} = \frac{1}{2}\dot{\tilde{\upeta }}^{{\text{T}}} {\text{M}}_{\eta } \dot{\tilde{\upeta }} + \frac{1}{2}\tilde{\upeta }^{{\text{T}}} {\text{K}}_{{\text{p}}} \tilde{\upeta }$$
(35)

Based on the above expressions, we see that the function V decreases when \({\dot{\upeta }} \ne 0\) and the submersible will reach the desired position η = ηd. The function \({\dot{\text{V}}}\) = 0 only if \(\dot{\upeta} = 0\), then ῆ = consts.

Paying attention to the differential equation of motion of the submersible, to get:

$${\text{M}}\left( {\upeta } \right) {\ddot{\upeta }} + {\text{C}}({\upeta },{\dot{\upeta }}){\dot{\upeta }} + {\text{ D}}({\upeta }, {\dot{\upeta }}){\dot{\upeta }} + {\text{ g}}\left( {\upeta } \right) \, = \, - {\text{K}}_{{\text{p}}} {\tilde{\upeta }} - {\text{Kd}}_{{\text{p}}} {\dot{\upeta }} + {\text{g}}\left( {\upeta } \right)$$
(36)

To choose the parameters for the controller Kp, Kd considers the model with independent movements—ignoring the reciprocal effects between the movements, assuming that the robot's motion velocity is small.

Have:

$$m_{ii} {\ddot{\upeta }}_{i} + \, K {}_{d}^{ii} {\dot{\upeta }} + \, K_{p} \eta_{i} = \, 0, \, i \, = \overline{1,6}$$
(37)

From here, rewrite as:

$${\ddot{\upeta }}_{i} + 2\delta \omega_{0i} {\dot{\upeta }}_{i} + \omega_{0i}^{2} \eta_{i} = 0,\;i = \overline{1,6}$$
(38)

To choose 0 < δ ≤ 1, while the value ω0i depends on the maximum magnitude of the control forces. From that, the coefficients Kp and Kd are deduced:

 + Choose = 1.

 + Choose ω0i = 0.5 =  > Kp = 30*diag (20, 20, 20, 20, 20, 20).

 =  > Kd = 100*diag (5, 5, 5, 5, 5, 5).

In this research, the Fuzzy-PD controller is used based on the Takagi–Sugeno fuzzy principle. The typical rule in the Sugeno fuzzy rule has the form: "If Input 1 = x and Input 2 = y, then Output is z = ax + by + c". The structure of the Fuzzy-PD controller for ROV is described in Fig. 3. Initially, the trajectory block will set a trajectory based on the parameters provided by the controller. Then, the controller will control the ROV's motion according to the predetermined trajectory.

Fig. 3
figure 3

ROV model with two coordinate systems

Full size image

The Fuzzy-PD hybrid controller takes the error 'e' and derivative error 'ce' as inputs with 7 fuzzy set values (NB (Negative Big), NM (Negative medium), NS (Negative small), Z (Zero), PS (Positive small), PM (Positive medium), PB (Positive Big)) related according to Table 2. The output of the controller consists of 4 values: Z (zero), S (Small), M (Medium), B (Big).

Table 2 Fuzzy rule table for Kp, Kd
Full size table

From the above data, we conducted simulations using Matlab Simulink with two different reference signals and compared them with a PID controller and Fuzzy Logic Controller to demonstrate clearer results.

The simulation results are as follows in Fig. 4 and Fig. 5:

Fig. 4
figure 4

The graph over time when using the controller PD

Full size image
Fig. 5
figure 5figure 5

The graph over time when using the controller fuzzy logic control

Full size image

Through the graphs above, we see that when the submersible stops (\({\dot{\upeta }} \equiv 0\), \({\ddot{\upeta }} \equiv 0\) then Kpῆ = 0 so ῆ = ƞ-ƞd = 0. That means the ROV only moves to the desired position. It can be shown that the equilibrium position \(\left( {\dot{\upeta },\tilde{\upeta }} \right)\) of the submersible is globally asymptotically stable with the PD plus gravity controller.

A problem arises, if the D-component is too large for the P-component or the P-component itself is small, when the train approaches the desired point B (not actually to B), the train may come to a complete stop, the D-component equal to 0 (because the error e does not change anymore), force τ = Kpe. While Kp and e are both small now, the force τ is also small and may not be able to overcome the acsimeter push and flow resistance. Imagine a situation where force is used to push a truck weighing several tens of tons, although thrust exists but the vehicle cannot move. Thus, the car will be stationary forever even though the error e is still not zero. The error e in this situation is called the error of the static state. In order to avoid static state errors, a component is added to the controller with the function of "accumulating" errors. When the static state error occurs, the two components P and D lose their effect, the new control component will "accumulate" the error over time and increase the force τ over time. At some point, the force τ is large enough to overcome the acsimeter thrust and the flow resistance, the submersible will continue to move to point B. This "accumulative" component is the I component (Integral) in the set PID controller.

The results of trajectory tracking and a comparison with the PID controller [28] are shown below Figs. 6 and 7.

Fig. 6
figure 6

Compare 2 controllers with set signal as ellipse

Full size image
Fig. 7
figure 7

Compare 2 controllers with set signal as Square

Full size image

From the simulation results and compare with [29, 30], there are the following find-ings:

Nonlinear motion handling capability: ROV operates in a water environment with nonlinear factors such as hydrodynamics, water resistance, and forces exerted by surrounding objects. The Fuzzy-PD controller excels in handling nonlinear impacts and provides flexible control feedback to adapt to different situations.

Flexibility in design and tuning: The Fuzzy-PD controller allows easy customiza-tion of control rules based on the knowledge and experience of the controller. The Fuzzy-PD system can be flexibly tuned to meet specific requirements of the ROV and the working environment.

Noise and uncertainty resilience: The water environment can introduce noise and uncertainty in measurements and control feedback. The Fuzzy-PD controller has the ability to resist noise and handle uncertain parameters. This improves the stability and responsiveness of the ROV in challenging environments.

Simplicity and comprehensibility: Compared to other complex control methods, Fuzzy-PD has a simple and understandable structure. This facilitates easy deploy-ment and effectiveness in ROV control. The control rules of Fuzzy-PD can be explic-itly represented and easily optimized and adjusted.

In general, the Fuzzy-PD controller brings benefits in handling nonlinear motion, flexibility in design, noise and uncertainty resilience, as well as simplicity and com-prehensibility compared to the PID controller. These characteristics make it a suitable choice for controlling ROVs in water environments.

4 Conclusion

The study achieved the following results:

  1. (1)

    Building kinematics and dynamics models of ROV

  2. (2)

    Build basic controllers to solve 2 problems of position and follow the given trajectory of ROV

  3. (3)

    Building a fuzzy controller for ROV

From there, using Matlab Simulink software to simulate the movement of ROV submersibles, under the influence of different control methods and laws, different desired results were obtained. Thereby helping readers orient how to choose the control law in each specific control case for ROV.

Through the research paper, it can be seen that the advantages of fuzzy logic control in controlling ROVs:

  1. (1)

    Accuracy and Stability: fuzzy logic control has demonstrated the ability to maintain and control high precision in various parameters of the ROV, such as position, inclination, depth, and movement speed. This indicates stability and compatibility with the dynamic marine environment.

  2. (2)

    Quick and Flexible Responsiveness: fuzzy logic control has shown fast and flexible responsiveness in diverse and complex situations, enabling the ROV to adapt well to rapid changes in the marine environment.

  3. (3)

    Advantageous Fuzzy Nature: The ability to handle inaccurate or noisy data in the marine environment, and the fuzzy inference capability of fuzzy logic control, have made the ROV control system more versatile and reliable.

  4. (4)

    Cost-Efficient: Compared to traditional control methods or more complex control systems, fuzzy logic control can bring cost savings in the deployment and maintenance of the ROV system.