Modeling orthotropic elastic-inelastic response of growing tissues with application to stresses in arteries

Abstract

This paper generalizes previous work on physically based nonlinear orthotropic invariants for thermomechanical response of soft materials to include the inelastic process of homeostasis, which causes a biological tissue to approach its homeostatic state. This process of homeostasis can cause a homogeneous material (one with the same constitutive equations and material constants as each material point) to develop a nonuniform state. Within the context of biological tissues, this means that the tissue cannot be unloaded elastically to a zero-stress state. A simplified version of the theory is used to describe elastic response of an artery from its nonuniform homeostatic state using a Fung-type exponential orthotropic strain energy function with material constants determined for a human carotid artery. As discussed in Safadi and Rubin (Int. J. Eng. Sci. 118(40), 2017), the approach of assuming a homeostatic state at systolic pressure and limiting extrapolation of the constitutive response to the physiological pressure range reduces uncertainty in the stress distributions in the artery. The specific results here show that the circumferential stress in the physiological pressure range exhibits a strong sensitivity to residual stresses known to exist in the cut unloaded state. This approach suggests that detailed experimental data on the response of the artery in its physiological pressure range and more complete understanding of mechanobiological processes during homeostasis are essential for determining an accurate constitutive equation of an artery.

1 Introduction

Biological materials are heterogeneous mixtures of components that can flow relative to each other and can interact mechanically, chemically and electrically [2,3,4,5,6]. Within the context of continuum mechanics, it is natural to model the response of tissues using mixture theory [7,8,9] and a simplified mixture theory with only one velocity field was proposed in [2]. Continuum models for growth and remodeling can be found in [10,11,12,13,14,15,16,17,18,19]. Specifically, in [15, 17], a Lagrangian formulation was proposed with constitutive equations based on the elastic deformation tensor F_e, defined by

$$ \mathbf{F}_{e} = \mathbf{F} \mathbf{F}_{g}^{-1} , $$

(1)

where F is the total deformation from a reference configuration and the growth tensor F_g is determined by integrating an evolution equation of the form

$$ \dot{\mathbf{F}}_{g} = \boldsymbol{\Lambda}_{g} \mathbf{F}_{g} , $$

(2)

with the growth rate Λ_g specified by a constitutive equation. The theory of multiple natural configurations in [20] can also be expressed in a form characterized by Eqs. 1 and 2.

Eckart [21] developed an Eulerian formulation of a theory for inelastic response of solids based on an evolution equation for an elastic deformation measure. Leonov [22] proposed a similar theory for polymeric liquids. Both of the theories modeled elastically isotropic response. An Eulerian formulation for elastically anisotropic response was developed in [23] which proposed evolution equations for a triad of microstructural vectors that model elastic deformations and the changing orientations of anisotropy. Based on these ideas, an Eulerian formulation of growth was developed in [24]. Physical invariants for large deformation orthotropic elastic response were proposed in [25, 26] and recently [27] these invariants were generalized for orthotropic thermomechanical response of soft materials.

In contrast with Lagrangian formulations of inelastic response, the Eulerian formulation is insensitive to arbitrariness of specifications of a reference configuration, an intermediate configuration, a total deformation measure, and an inelastic deformation measure. This is particularly important for materials that grow and remodel due to homeostasis, which is the process of the material attempting to achieve a homeostatic state, because homeostasis occurs in the current state of the material and depends only on the current state variables.

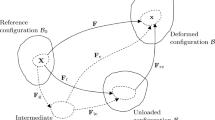
One objective of the present paper is to generalize the nonlinear orthotropic invariants developed in [27] for the themoelastic response of soft materials to include the inelastic effect of homeostasis. General forms of the evolution equations are proposed but specific forms for homeostasis still need to be discovered. Another objective is to examine the influence of homeostasis on the prediction of stress distributions in the passive behavior of arteries. The classical approach to modeling stresses in arteries [28, 29] is to model the artery as a homogeneous, uniform circular cylindrical tube made of a hyperelastic material. These works assume that the artery has zero-stress in its cut unloaded state (see Fig. 1) and that stresses in other intact states can be determined by considering the artery to be an incompressible material with applied internal pressure, zero external pressure, and applied uniform axial stretch relative to its cut unloaded state. Further axial cuts of the cut unloaded artery revealed that the curvature of the cut segments remains nearly uniform [29], which indicates that any residual stress in the cut unloaded artery is independent of circumferential coordinate but does not ensure that the stress field is independent of the radial coordinate.

Fig. 1

Deformations from the homeostatic state loaded with internal pressure P_h to the cut unloaded state with the opening angle ω_c and to the intact loaded state with internal pressure P

Holzapfel et al. [30] described the artery as having three layers: the intima, media, and adventitia. Since the intima has little mechanical strength, the artery was modeled using two layers, each with orthotropic elastic response but it was also assumed that the cut unloaded state is at zero stress. Later [31] sectioned the cut unloaded state and determined that the residual stress distributions are three-dimensional and cannot be fully characterized by the geometry of the cut unloaded state. Also, constitutive equations based on structurally motivated orthotropic invariants are discussed in [32].

Using the formulation for growth of biological tissues developed in [24], Safadi and Rubin [1] studied the influence of homeostasis on stresses in arteries. Following this work, it is assumed that homeostasis is a slow process relative to normal deformations of the artery due to cyclic loading from the diastolic pressure P_d to the systolic pressure P_s and due to deformations caused by unloading and cutting the artery. This assumption suggests that the artery has had sufficient time to remodel to its homeostatic state (i.e., the homeostatic state is in mechanobiological equilibrium) and that deformations from this homeostatic state can be approximated as elastic with no influence of homeostasis.

Based on engineering considerations, different proposals for the mechanical response to homeostasis have been suggested. Much of the research on homeostasis, discussed in [1], suggests that homeostasis tends to cause the circumferential and axial stresses in the artery to become more uniform through thickness of the artery. These assumptions are used in the examples in this paper. In this regard, it is noted that [33] discusses the fundamental roles of axial stress, and flow-induced shear stress applied to the interior artery wall in the axial direction, which is not included in the present analysis.

Since the stresses in the artery are highest in its systolic state, Safadi and Rubin [1] specified this state as the homeostatic state of the artery with the homeostatic pressure P_h = P_s and predicted the stress distributions in the cut unloaded and intact unloaded states for a rabbit thoracic artery. Specifically, the circumferential and axial stresses in the homeostatic systolic state were assumed to be uniform, with these uniform values determined to match the measured cut unloaded geometry. This approach was also used to predict stress distributions due to homeostasis caused by hypertension.

In addition, in [1] estimates of the influence of residual stresses in a cut unloaded state were obtained by cutting the intact unloaded state into two layers, each of which produce different cut unloaded geometries with different internal and external radii and different opening angles. Furthermore, Safadi [34] examined the influence of residual stresses in the intact unloaded state on the stress distributions in the systolic state. Specifically, different homeostatic stress distributions were proposed for the intact unloaded state which are consistent with the measured geometry of the cut unloaded state. It was found that these different stress distributions have a significant influence on the predicted stresses in the systolic state.

Following with work in [1, 34], here, it is also assumed that the arterial tube is made of a homogeneous material (i.e., identical material properties at each point) but that homeostasis causes the arterial material to become nonuniform (i.e., the material cannot be fully unloaded elastically with a compatible deformation field to a zero-stress configuration). This is consistent with the experimental observations in [31] which showed that the geometry of the cut unloaded artery continues to change as more cuts are made that relieve residual stresses. Also, here, the loaded nonuniform homeostatic systolic state is used as a reference state for the determination of the stress-distributions in other states of the artery. Specifically, the systolic state has inner radius a_s, outer radius b_s, and applied internal pressure P_s; the diastolic state has inner radius a_d, outer radius b_d, and applied internal pressure P_d; the intact unloaded state has inner radius a_u, outer radius b_u, and zero applied internal pressure; and the cut unloaded state has inner radius a_c, outer radius b_c, and opening angle ω_c (see Fig. 1). In this regard, it is noted that the opening angle of the cut unloaded state in Fig. 1 is identified as ω_c/2 in [28, 29] and by ω_c here and in [35]. The word intact is used to distinguish between an artery that is not cut and a cut artery. The equivalent uniform axial stress in the homeostatic state, which is taken to be the systolic state, is specified (see Eq. 86). Also, the equivalent uniform axial stress in the diastolic state is assumed to be reduced relative to that in the systolic state by the ratio of the applied pressures in the two states [see Eq. 84].

The purely mechanical form of the model developed here introduces a homeostatic state of the tissue with the elastic dilatation J_e and the elastic distortional microstructural vectors $\mathbf {m}_{i}^{\prime }$ given by

$$ \begin{aligned} &J_{e} = J_{h} > 0 , &&\mathbf{m}_{i}^{\prime} = \mathbf{h}_{i}^{\prime} , \\ &\mathbf{h}_{1}^{\prime} = h_{1} \mathbf{p}_{1} , &&\mathbf{h}_{2}^{\prime} = h_{2} \mathbf{p}_{2} , &&\mathbf{h}_{3}^{\prime} = h_{3} \mathbf{p}_{3} , \\ &h_{1} > 0 , &&h_{2} > 0 , &&h_{3} > 0 , \\ &h_{1} h_{2} h_{3} = 1 , \\ &\mathbf{p}_{i} \cdot \mathbf{p}_{j} = \delta_{ij} , &&\mathbf{p}_{1} \times \mathbf{p}_{2} \cdot \mathbf{p}_{3} = 1 . \end{aligned} $$

(3)

where the homeostatic values J_h,h₁, and h₂ are specified by constitutive equations and p_i is a right-handed orthonormal triad that determines the directions of elastic orthotropy. Next, it is convenient to define the relative deformation gradient F_r from the homeostatic state to another deformed state and to define the relative dilatation J_r and relative unimodular deformation tensor $\mathbf {F}_{r}^{\prime }$ [36], by

$$ J_{r} = \det \mathbf{F}_{r} , \quad \mathbf{F}_{r}^{\prime} = J_{r}^{-1/3} \mathbf{F}_{r} , \quad \det \mathbf{F}_{r}^{\prime} = 1 . $$

(4)

Now, confining attention to elastic deformations from the homeostatic state, it follows that the deformed elastic dilatation J_e and elastic distortional deformation microstructural vectors $\mathbf {m}_{i}^{\prime }$ in a general deformed state are given by

$$ J_{e} = J_{r} J_{h} , \quad \mathbf{m}_{i}^{\prime} = \mathbf{F}_{r}^{\prime} \mathbf{h}_{i}^{\prime} . $$

(5)

As is common, the elastic response from the homeostatic state is assumed to be incompressible. However, this does not prevent homeostasis of growth and remodeling from changing the volume of the artery when it is active.

The sensitivity of the material parameters and errors in measurements has been considered in [35, 37,38,39,40] for different material models of arterial tissue. Finite element solutions were also used in [41] to examine influences of different test protocols on the determination of stress in tube models of orthotropic materials.

Recently, Emuna et al. [35] determined the sensitivity of material model parameters in two constitutive equations to uncertainties in stress-free measurements. To determine the sensitivity of the Fung model to residual stresses in the cut unloaded state, a modified Fung model (MF-c) is developed here which uses scaled values of the residual stresses predicted for the cut unloaded state as the homeostatic state. Then, the stress distributions in the unloaded, diastolic, and systolic states are predicted by elastically deforming this cut unloaded homeostatic state. When the scale parameter α vanishes, these stress fields are the same as those predicted by the standard Fung model. However, when 0 < α ≤ 1, the predictions of the MF-c model suggest that the circumferential stress predicted by extrapolating from the cut unloaded state is particularly sensitive to the residual stress field.

An outline of this paper is as follows. Section 2 presents the basic equations and balance laws. Section 3 introduces the evolution equations for the elastic dilatation J_e, the distortional microstructural vectors $\mathbf {m}_{i}^{\prime }$ with the influence of homeostasis and the nonlinear orthotropic thermoelastic invariants. General constitutive equations are developed in Section 4 and modeling of the homeostatic state is discussed in Section 5. Section 6 discusses the application of a simplified version of the model to determining stresses in arteries and Section 7 presents results of specific examples. Conclusions are discussed in Section 8 and details of some of the mathematical expressions are recorded in Appendix A.

2 Basic equations

The location of a material point in the current configuration at time t is denoted by x and the velocity v, velocity gradient L, rate of deformation tensor D, and spin tensor W are defined by

$$ \begin{aligned} &\mathbf{v} = \dot{\mathbf{x}} , \quad \mathbf{L} = \partial \mathbf{v}/\partial \mathbf{x} = \mathbf{D} + \mathbf{W} , \\ &\mathbf{D} = \frac{1}{2}(\mathbf{L}+\mathbf{L}^{T}) = \mathbf{D}^{T} , \\ &\mathbf{W} = \frac{1}{2}(\mathbf{L}-\mathbf{L}^{T}) = - \mathbf{W}^{T} , \end{aligned} $$

(6)

where a superposed dot $\dot {()}$ denotes material time differentiation.

Following the work in [24, 27], the local forms of the balance laws of mass, linear momentum and entropy are given by

$$ \begin{aligned} &\dot{\rho} + \rho \mathbf{D} \cdot \mathbf{I} = \rho r_{m} , \\ &\rho \dot{\mathbf{v}} = \rho \mathbf{b} + \text{div} \mathbf{T} , \\ &\rho \dot{\eta} = \rho (s + \xi) - \text{div} \mathbf{p} , \end{aligned} $$

(7)

where ρ is the current mass density, r_m is the external rate of mass supply per unit mass, b is the external body force per unit mass, T is the Cauchy stress, η is the entropy per unit mass, s is the external rate of entropy supply per unit mass, ξ is the internal rate of entropy production per unit mass due to dissipative mechanisms, and p is the entropy flux per unit current area. In these equations, I is the second-order unity tensor and A ⋅B = tr(AB^T) is the inner product between two second-order tensors A and B. Also, the balances of angular momentum and energy are given by

$$ \begin{aligned} &\mathbf{T}^{T} = \mathbf{T} , \\ &\rho \dot{\varepsilon} = \rho \theta s - \text{div} (\theta \mathbf{p}) + \mathbf{T} \cdot \mathbf{D} + \rho b , \end{aligned} $$

(8)

where ε is the internal energy per unit mass, 𝜃 is the absolute temperature, and b is the external rate of energy supply per unit mass due to mechanobiological processes. Using the result

$$ \text{div}(\theta \mathbf{p}) = \theta \text{div} \mathbf{p} + \mathbf{p} \cdot \mathbf{g} , \quad \mathbf{g} = \frac{\partial \theta}{\partial \mathbf{x}} , $$

(9)

the definition

$$ \rho \theta \xi = - \mathbf{p} \cdot \mathbf{g} + \rho \theta \xi^{\prime} , $$

(10)

and the balance of entropy, the balance of energy can be expressed in the form

$$ \rho \theta \xi^{\prime} = \mathbf{T} \cdot \mathbf{D} - \rho \dot{\varepsilon} + \rho \theta \dot{\eta} + \rho b . $$

(11)

Moreover, using the definition of the Helmholtz free energy

$$ \psi = \varepsilon - \theta \eta . $$

(12)

it follows that

$$ \rho \theta \xi^{\prime} = \mathbf{T} \cdot \mathbf{D} - \rho (\dot{\psi}+\eta \dot{\theta}) + \rho b . $$

(13)

3 Evolution equations

Following the work in [27], the elastic dilatation J_e is determined by the equation

$$ J_{e} = \frac{\rho_{0}}{\rho} , \quad \frac{\dot{J}_{e}}{J_{e}} = \mathbf{D} \cdot \mathbf{I} - {\varGamma}_{v} \ln \left( \frac{J_{e}}{J_{h}} \right) , $$

(14)

where ρ₀ is the density of the material in a zero-stress state at reference temperature 𝜃₀, Γ_v controls the rate of volumetric homeostasis and J_h controls the homeostatic value of elastic dilatation. Also, the elastic distortional deformations and the orthotropic orientations are determined by the right-handed triad of linearly independent distortional vectors $\mathbf {m}_{i}^{\prime }$

$$ \mathbf{m}_{1}^{\prime} \times \mathbf{m}_{2}^{\prime} \cdot \mathbf{m}_{3}^{\prime} = 1 , $$

(15)

which satisfy the evolution equations

$$ \dot{\mathbf{m}}_{i}^{\prime} = (\mathbf{L}^{\prime\prime} - {\varGamma} \bar{\mathbf{L}}_{g}^{\prime\prime}) \mathbf{m}_{i}^{\prime} , $$

(16)

where Γ controls the rate of distortional homeostasis, $\bar {\mathbf {L}}_{g}^{\prime \prime }$ controls its direction, and the deviatoric part of a tensor is denoted by $()^{\prime \prime }$ so, for example

$$ \bar{\mathbf{L}}_{g}^{\prime\prime} = \bar{\mathbf{L}}_{g} - \frac{1}{3} (\bar{\mathbf{L}}_{g} \cdot \mathbf{I}) \mathbf{I} . $$

(17)

Also, the symmetric $\bar {\mathbf {D}}_{g}^{\prime \prime }$ and skew-symmetric $\bar {\mathbf {W}}_{g}$ parts of $\bar {\mathbf {L}}_{g}^{\prime \prime }$ are defined by

$$ \bar{\mathbf{D}}_{g}^{\prime\prime} = \frac{1}{2} (\bar{\mathbf{L}}_{g}^{\prime\prime} + \bar{\mathbf{L}}_{g}^{\prime\prime T}) , \quad \bar{\mathbf{W}}_{g}= \frac{1}{2} (\bar{\mathbf{L}}_{g}^{\prime\prime} - \bar{\mathbf{L}}_{g}^{\prime\prime T}) . $$

(18)

In addition, the reciprocal vectors $\mathbf {m}^{i\prime }$ are defined by

$$ \begin{aligned} &\mathbf{m}^{1 \prime} = \mathbf{m}_{2}^{\prime} \times \mathbf{m}_{3}^{\prime} , &&\mathbf{m}^{2 \prime} = \mathbf{m}_{3}^{\prime} \times \mathbf{m}_{1}^{\prime} , \\ &\mathbf{m}^{3 \prime} = \mathbf{m}_{1}^{\prime} \times \mathbf{m}_{2}^{\prime} , \end{aligned} $$

(19)

and the covariant metric $m_{ij}^{\prime }$ and contravariant metric $m^{ij \prime }$ satisfy the equations

$$ \begin{aligned} &m_{ij}^{\prime} = \mathbf{m}_{i}^{\prime} \cdot \mathbf{m}_{j}^{\prime} , \\ &\dot{m}_{ij}^{\prime} = 2 (\mathbf{m}_{i}^{\prime} \otimes \mathbf{m}_{j}^{\prime} - \frac{1}{3} m_{ij}^{\prime} \mathbf{I}) \cdot (\mathbf{D} - {\varGamma} \bar{\mathbf{D}}_{g}^{\prime\prime}) , \\ &m^{ij \prime} = \mathbf{m}^{i \prime} \cdot \mathbf{m}^{j \prime} , \quad m_{in}^{\prime} m^{nj \prime} = {\delta_{i}^{j}} , \end{aligned} $$

(20)

where ${\delta _{i}^{j}}$ is the Kronecker delta and the usual summation convention for repeated indices is applied.

In these equations, $\bar {\mathbf {D}}_{g}^{\prime \prime }$ controls the direction of the homeostasis distortional deformation rate and $\bar {\mathbf {W}}_{g}$ controls the direction of inelastic spin. To motivate a form for $\bar {\mathbf {D}}_{g}^{\prime \prime }$ it is recalled from [27] that the metrics $m_{ij}^{\prime }$ and $m^{ij \prime }$ in any hydrostatic state of stress (HSS) take the forms

$$ \begin{aligned} &m_{11}^{\prime} = {\eta_{1}^{2}} , &&m_{22}^{\prime} = {\eta_{2}^{2}} , &&m_{33}^{\prime} = {\eta_{3}^{2}} , \\ &m_{12}^{\prime} = 0 , &&m_{13}^{\prime} = 0 , &&m_{23}^{\prime} = 0 , \\ &m^{11 \prime} = \frac{1}{{\eta_{1}^{2}}} , &&m^{22 \prime} = \frac{1}{{\eta_{2}^{2}}} , &&m^{33 \prime} = \frac{1}{{\eta_{3}^{2}}} , \\ &m^{12 \prime} = 0 , &&m^{13 \prime} = 0 , &&m^{23 \prime} = 0 , \end{aligned} $$

(21)

where η_i are positive dependent constitutive functions of the elastic dilatation J_e and temperature 𝜃 satisfying the restrictions

$$ \eta_{i} = \eta_{i}(J_{e},\theta) > 0 , \quad \eta_{1} \eta_{2} \eta_{3} = 1 , \quad \eta_{i}(1,\theta_{0}) = 1 . $$

(22)

It also follows that for any HSS

$$ \begin{aligned} &\mathbf{m}_{1}^{\prime} = \eta_{1} \mathbf{p}_{1} , \quad \mathbf{m}^{1 \prime} = \frac{1}{\eta_{1}} \mathbf{p}_{1} , \\ &\mathbf{m}_{2}^{\prime} = \eta_{2} \mathbf{p}_{2} , \quad \mathbf{m}^{2 \prime} = \frac{1}{\eta_{2}} \mathbf{p}_{2} , \\ &\mathbf{m}_{3}^{\prime} = \eta_{3} \mathbf{p}_{3} , \quad \mathbf{m}^{3 \prime} = \frac{1}{\eta_{3}} \mathbf{p}_{3} , \end{aligned} $$

(23)

where the right-handed orthonormal triad p_i

$$ \mathbf{p}_{i} \cdot \mathbf{p}_{j} = \delta_{ij} , \quad \mathbf{p}_{1} \times \mathbf{p}_{2} \cdot \mathbf{p}_{3} = 1 , $$

(24)

characterizes the principal directions of orthotropy.

The six invariants β_i introduced in [27] are defined by

$$ \begin{aligned} &\beta_{1} = \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} + {\eta_{1}^{2}} m^{11 \prime} , &&\beta_{2} = \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} + {\eta_{2}^{2}} m^{22 \prime} , \\ &\beta_{3} = \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} + {\eta_{3}^{2}} m^{33 \prime} , &&\beta_{4} = \frac{m_{12}^{\prime 2}}{m_{11}^{\prime} m_{22}^{\prime}} , \\ &\beta_{5} = \frac{m_{13}^{\prime 2}}{m_{11}^{\prime} m_{33}^{\prime}} , &&\beta_{6} = \frac{m_{23}^{\prime 2}}{m_{22}^{\prime} m_{33}^{\prime}} . \end{aligned} $$

(25)

Moreover, it can be shown that

$$ \begin{aligned} &\dot{\eta}_{i} = J_{e} \frac{\partial \eta_{i}}{\partial J_{e}} \left[ \mathbf{D} \cdot \mathbf{I} - {\varGamma}_{v} \ln \left( \frac{J_{e}}{J_{h}} \right) \right] + \frac{\partial \eta_{i}}{\partial \theta} \dot{\theta} , \\ &\dot{\beta}_{i} = 2 (- N_{i} \mathbf{I} + \mathbf{B}_{i}^{\prime\prime}) \cdot \left[ \mathbf{D} - \frac{1}{3} {\varGamma}_{v} \ln \left( \frac{J_{e}}{J_{h}} \right) \mathbf{I} - {\varGamma} \bar{\mathbf{D}}_{g}^{\prime\prime} \right] \\ &\quad \quad \quad \quad \quad \quad \quad + 2 A_{i} \dot{\theta} \quad (i=1,2,3) , \\ &\dot{\beta}_{i} = 2 \mathbf{B}_{i}^{\prime\prime} \cdot \left[ \mathbf{D} - \frac{1}{3} {\varGamma}_{v} \ln \left( \frac{J_{e}}{J_{h}} \right) \mathbf{I} - {\varGamma} \bar{\mathbf{D}}_{g}^{\prime\prime} \right] \\ &\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (i=3,4,5) , \end{aligned} $$

(26)

where the scalar functions N_i and A_i and the deviatoric tensors $\mathbf {B}_{i}^{\prime \prime }$ are defined in Appendix A.

4 Constitutive equations

The Helmholtz free energy per unit mass is specified in the form

$$ \psi = \psi(J_{e},\beta_{i},\theta) , $$

(27)

and the stress and entropy are determined by

$$ \begin{aligned} &\mathbf{T} = - p \mathbf{I} + \mathbf{T}^{\prime\prime} , \\ &p = - J_{e} \rho \frac{\partial \psi}{\partial J_{e}} + \sum\limits_{i=1}^{3} 2 \rho \frac{\partial \psi}{\partial \beta_{i}} N_{i} , \\ &\mathbf{T}^{\prime\prime} = 2 \rho \sum\limits_{i=1}^{6} \frac{\partial \psi}{\partial \beta_{i}} \mathbf{B}_{i}^{\prime\prime} , \\ &\rho_{0} \eta = - \frac{\partial \psi}{\partial \theta} - \sum\limits_{i=1}^{3} 2 \frac{\partial \psi}{\partial \beta_{i}} A_{i} . \end{aligned} $$

(28)

Now, using Eqs. 14, 26, and 28, the constitutive equation for $\xi ^{\prime }$ in Eq. 13 is given by

$$ \begin{aligned} &\rho \theta \xi^{\prime} =\rho b - \frac{2}{3} \rho {\varGamma}_{v} \left[ \sum\limits_{i=1}^{3} \frac{\partial \psi}{\partial \beta_{i}} N_{i} \right] \ln (\frac{J_{e}}{J_{h}}) \\ &\quad \quad \quad \quad + 2 \rho {\varGamma} \left[ \sum\limits_{i=1}^{6} \frac{\partial \psi}{\partial \beta_{i}} \mathbf{B}_{i}^{\prime\prime} \cdot \bar{\mathbf{D}}_{g}^{\prime\prime} \right] . \end{aligned} $$

(29)

Furthermore, the Helmholtz free energy is restricted by the conditions that

$$ \begin{aligned} &\psi = 0 , \quad \frac{\partial \psi}{\partial J_{e}} = 0 , \quad \frac{\partial^{2} \psi}{\partial {J_{e}^{2}}} > 0 \\ &\quad \quad \quad \quad \quad \quad \text{for} \quad J_{e} = 1 \text{and} \theta = \theta_{0} , \end{aligned} $$

(30)

so that a zero-stress state is characterized by

$$ \begin{aligned} &\mathbf{T} = 0 \quad \text{for} \quad J_{e} = 1 , \quad \theta= \theta_{0} , \\ &\mathbf{m}_{1}^{\prime} = \mathbf{p}_{1} , \quad \mathbf{m}_{2}^{\prime} = \mathbf{p}_{2} , \quad \mathbf{m}_{3}^{\prime} = \mathbf{p}_{3} . \end{aligned} $$

(31)

5 Modeling a homeostatic state

A homeostatic state of the material is defined by Eq. 3, where J_h,h₁,h₂, and h₃ characterize the homeostatic state. It then follows from Eq. 102 that for a homeostatic state

$$ \begin{aligned} &\mathbf{B}_{1}^{\prime\prime} = \left( \frac{{h_{1}^{2}}}{{\eta_{1}^{2}}} - \frac{{\eta_{1}^{2}}}{{h_{1}^{2}}} \right) (\textbf{P}_{1} - \frac{1}{3} \mathbf{I}) , &&\textbf{P}_{1} = \mathbf{p}_{1} \otimes \mathbf{p}_{1} , \\ &\mathbf{B}_{2}^{\prime\prime} = \left( \frac{{h_{2}^{2}}}{{\eta_{2}^{2}}} - \frac{{\eta_{2}^{2}}}{{h_{2}^{2}}} \right) (\textbf{P}_{2} - \frac{1}{3} \mathbf{I}) , &&\textbf{P}_{2} = \mathbf{p}_{2} \otimes \mathbf{p}_{2} , \\ &\mathbf{B}_{3}^{\prime\prime} = \left( \frac{{h_{3}^{2}}}{{\eta_{3}^{2}}} - \frac{{\eta_{3}^{2}}}{{h_{3}^{2}}} \right) (\textbf{P}_{3} - \frac{1}{3} \mathbf{I}) , &&\textbf{P}_{3} = \mathbf{p}_{3} \otimes \mathbf{p}_{3} , \\ &\mathbf{B}_{4}^{\prime\prime} = \mathbf{B}_{5}^{\prime\prime} = \mathbf{B}_{6}^{\prime\prime} = 0 , \end{aligned} $$

(32)

which indicates that the stress in a homeostatic state can be controlled by the values J_h and h_i, and P_i are orthogonal second-order unit tensors.

From the evolution (14), it also follows that in the absence of deformation rate D = 0, the process of homeostasis causes J_e to approach its homeostatic value J_h. To ensure that in the absence deformation rate L = 0, the evolution (16) causes $\mathbf {m}_{i}^{\prime }$ to approach constant homeostatic values (3), the inelastic spin $\bar {\mathbf {W}}_{g}$ is restricted to vanish in the homeostatic state. Also, $\bar {\mathbf {W}}_{g}$ is restricted to vanish in a zero-stress state. Then, it is convenient to define the deviatoric tensors $\bar {\mathbf {H}}_{i}^{\prime \prime }$ by

$$ \begin{aligned} &\bar{\mathbf{H}}_{1}^{\prime\prime} = \frac{1}{{h_{1}^{2}}} \mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime} - {h_{1}^{2}} \mathbf{m}^{1 \prime} \otimes \mathbf{m}^{1 \prime} \\ &\quad \quad \quad \quad - \frac{1}{3} \left( \frac{m_{11}^{\prime}}{{h_{1}^{2}} } - {h_{1}^{2}} m^{11 \prime} \right) \mathbf{I} , \\ &\bar{\mathbf{H}}_{2}^{\prime\prime} = \frac{1}{{h_{2}^{2}}} \mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime} - h_{2} \mathbf{m}^{2 \prime} \otimes \mathbf{m}^{2 \prime} \\ &\quad \quad \quad \quad- \frac{1}{3} \left( \frac{m_{22}^{\prime}}{{h_{2}^{2}}} -{h_{2}^{2}} m^{22 \prime} \right) \mathbf{I} , \\ &\bar{\mathbf{H}}_{3}^{\prime\prime} = \frac{1}{{h_{3}^{2}}} \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime} - {h_{3}^{2}} \mathbf{m}^{3 \prime} \otimes \mathbf{m}^{3 \prime} \\ &\quad \quad \quad \quad- \frac{1}{3} \left( \frac{m_{33}^{\prime}}{{h_{3}^{2}} } - {h_{3}^{2}} m^{33 \prime} \right) \mathbf{I} , \\ &\bar{\mathbf{H}}_{4}^{\prime\prime} = \mathbf{B}_{4}^{\prime\prime} , \quad \bar{\mathbf{H}}_{5}^{\prime\prime} = \mathbf{B}_{5}^{\prime\prime} , \quad \bar{\mathbf{H}}_{6}^{\prime\prime} = \mathbf{B}_{6}^{\prime\prime} , \end{aligned} $$

(33)

to express the tensor $\bar {\mathbf {D}}_{g}^{\prime \prime }$ by

$$ \bar{\mathbf{D}}_{g}^{\prime\prime} = \sum\limits_{i=1}^{6} \bar{\mathbf{H}}_{i}^{\prime\prime} , $$

(34)

which vanishes for a homeostatic state given by Eq. 3. A more general form of $\bar {\mathbf {D}}_{g}^{\prime \prime }$ with constitutive coefficients times each of the terms $\bar {\mathbf {H}}_{i}^{\prime \prime }$ in the series to describe orthotropic homeostasis could be considered but is not pursued here.

Thus, with the help of Eqs. 14, 16, 22, 31, 33, and the restriction that $\bar {\mathbf {W}}_{p}$ vanishes in a zero stress state, it follows that the zero-stress growth rate D_g, with constant $\mathbf {m}_{i}^{\prime }$, is given by

$$ \begin{aligned} &\mathbf{L} = \mathbf{D}_{g} = - \frac{1}{3} {\varGamma}_{v} \ln(J_{h}) \mathbf{I} + {\varGamma} \left[\left( {h_{1}^{2}} - \frac{1}{{h_{1}^{2}}} \right) (\textbf{P}_{1} - \frac{1}{3} \mathbf{I})\right. \\ &\left.\quad \quad + \left( {h_{2}^{2}} - \frac{1}{{h_{2}^{2}}} \right) (\textbf{P}_{2} - \frac{1}{3} \mathbf{I}) + \left( {h_{3}^{2}} - \frac{1}{{h_{3}^{2}}} \right) (\textbf{P}_{3} - \frac{1}{3} \mathbf{I}) \right] . \end{aligned} $$

(35)

6 Application to stresses in arteries

Motivated by the work in [1], use is made of the orthotropic model proposed in this paper to study stress distributions in a human carotid artery. All solutions are consistent with measured values of the cut unloaded state. The HS-Ps model described below specifies the systolic state as the homeostatic state and considers the influence of a nonuniform homeostatic circumferential stress on the stress distributions in other states. Also, the modified Fung model MF-c described below specifies the cut unloaded state as the homeostatic state and considers the influence of a family of homeostatic stress distributions on the stress distributions in other states. In this regard, it is recalled that [34] considered of the influence of different homeostatic stress fields specified for the intact unloaded state of a rabbit thoracic artery.

6.1 Constitutive equation of Fung

Within the context of the purely mechanical theory, the Fung model for biological tissues can be expressed in the form

$$ \rho_{0}\psi_{F} = \frac{c}{w} \left[\exp(w Q_{F}) -1 \right] , $$

(36)

where Q_F is a normalized strain energy function of the Lagrangian strain E defined in terms of the total deformation gradient F from a zero-stress reference configuration by

$$ \mathbf{E} = \frac{1}{2}(\mathbf{C} - \mathbf{I}) , \quad \mathbf{C} = \mathbf{F}^{T} \mathbf{F} , $$

(37)

the scalar w controls the nonlinearity caused by the exponential function and c is a constant that has magnitude unity with the dimensions of stress. When this function is used for an incompressible material it describes distortional deformation only. Consequently, it is more convenient to write Q_F in terms of the distortional Lagrangian strain $\mathbf {E}^{\prime }$ defined by

$$ \begin{aligned} &\mathbf{E}^{\prime} = \frac{1}{2}(\mathbf{C}^{\prime} - \mathbf{I}) , &&\mathbf{C}^{\prime} = \mathbf{F}^{\prime T} \mathbf{F}^{\prime} , \\ &\mathbf{F}^{\prime} = J^{-1/3} \mathbf{F} , &&J = \det \mathbf{F} , \end{aligned} $$

(38)

where J is the total dilatation and $\mathbf {F}^{\prime }$ and $\mathbf {C}^{\prime }$ are unimodular tensors with their determinants equal to unity.

To describe deformations of a cylindrical tube from a zero-stress reference configuration, use is made of the cylindriical polar base vectors

$$ \begin{aligned} &\mathbf{e}_{r}({\varTheta}) = \cos {\varTheta} \mathbf{e}_{1} + \sin {\varTheta} \mathbf{e}_{2} , \\ &\mathbf{e}_{\theta}({\varTheta}) = - \sin {\varTheta} \mathbf{e}_{1} + \cos {\varTheta} \mathbf{e}_{2} , \\ &\mathbf{e}_{z} = \mathbf{e}_{3} , \end{aligned} $$

(39)

and the unit tensors

$$ \begin{aligned} &\mathbf{N}_{R}({\varTheta}) = \mathbf{e}_{r}({\varTheta}) \otimes \mathbf{e}_{r}({\varTheta}) , \\ &\mathbf{N}_{{\varTheta}}({\varTheta}) = \mathbf{e}_{\theta}({\varTheta}) \otimes \mathbf{e}_{\theta}({\varTheta}) , \\ &\mathbf{N}_{z} = \mathbf{e}_{z} \otimes \mathbf{e}_{z} . \end{aligned} $$

(40)

to write Q_F in the form

$$ \begin{aligned} &Q_{F} = \frac{1}{2} \left[ c_{R} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{R})^{2} + c_{{\varTheta}} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{{\varTheta}})^{2}\right. \\ &\quad \quad \quad \quad+ c_{Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{z})^{2} \\ &\quad \quad \quad \quad+2\left\{c_{R {\varTheta}} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{R})(\mathbf{E}^{\prime} \cdot \mathbf{N}_{{\varTheta}})\right. \\ &\quad \quad \quad \quad+c_{RZ} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{R}) (\mathbf{E}^{\prime} \cdot \mathbf{N}_{z}) \\ &\left.\left.\quad \quad \quad \quad +c_{{\varTheta} Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{{\varTheta}}) (\mathbf{E}^{\prime} \cdot \mathbf{N}_{z}) \right\} \right] , \end{aligned} $$

(41)

where c_R,c_Θ,c_Z,c_RΘ,c_RZ, and c_ΘZ are material constants. In the limit of small strains, cQ_F characterizes the small deformation strain energy function for any positive value of w. Furthermore, it can be shown that

$$ \begin{aligned} &\dot{J} = J \mathbf{I} \cdot \mathbf{D} , \\ &\frac{d}{dt}(\mathbf{E}^{\prime} \cdot \mathbf{N}_{R}) = \left[ \mathbf{F}^{\prime} \mathbf{N}_{R} \mathbf{F}^{\prime T} - \frac{1}{3} (\mathbf{F}^{\prime} \mathbf{N}_{R} \mathbf{F}^{\prime T} \cdot \mathbf{I}) \mathbf{I} \right] \cdot \mathbf{D} , \end{aligned} $$

(42)

with similar expressions for the derivatives of $\mathbf {E}^{\prime } \cdot \mathbf {N}_{{\varTheta }}$ and $\mathbf {E}^{\prime } \cdot \mathbf {N}_{z}$. Then, the deviatoric stress $\mathbf {T}^{\prime \prime }$ in Eq. 28 is given by

$$ \begin{aligned} &\mathbf{T}^{\prime\prime} = c \exp (w Q_{F}) J_{e}^{-1} \left[c_{R} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{R}) + c_{R {\varTheta}} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{{\varTheta}})\right. \\ &\left.\qquad+ c_{R Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{z}) \right] \left[ \mathbf{F}^{\prime} \mathbf{N}_{R} \mathbf{F}^{\prime T} - \frac{1}{3} (\mathbf{F}^{\prime} \mathbf{N}_{R} \mathbf{F}^{\prime T} \cdot \mathbf{I}) \mathbf{I} \right] \\ & \qquad + c \exp (w Q_{F}) J_{e}^{-1} \left[ c_{R {\varTheta}} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{R}) +c_{{\varTheta}} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{{\varTheta}})\right. \\ &\left. \qquad + c_{{\varTheta} Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{z}) \right] \left[ \mathbf{F}^{\prime} \mathbf{N}_{{\varTheta}} \mathbf{F}^{\prime T} - \frac{1}{3} (\mathbf{F}^{\prime} \mathbf{N}_{{\varTheta}} \mathbf{F}^{\prime T} \cdot \mathbf{I}) \mathbf{I} \right] , \\ & \qquad + c \exp (w Q_{F}) J_{e}^{-1} \left[ c_{R Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{R}) +c_{{\varTheta} Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{{\varTheta}})\right. \\ &\left. \qquad + c_{Z} (\mathbf{E}^{\prime} \cdot \mathbf{N}_{z}) \right] \left[ \mathbf{F}^{\prime} \mathbf{N}_{z} \mathbf{F}^{\prime T} - \frac{1}{3} (\mathbf{F}^{\prime} \mathbf{N}_{z} \mathbf{F}^{\prime T} \cdot \mathbf{I}) \mathbf{I} \right] . \end{aligned} $$

(43)

For an incompressible material, J_e = J = 1 and the pressure p in Eq. 28 is an arbitrary function of position and time.

The material constants for a human carotid artery based on the experiments in [42], as reported in [35] for the Fung model, are recorded in Table 1. Due to the presence of w in the definition of ψ in Eq. 36, the values of the constants in Table 1 are those in [35] multiplied by the numerical value of c₀ without units there so, for example, c_R in Table 1 is equal to c₀c_R in [35]. Also the numerical value of w is given by w = 2/c₀ without units for c₀.

Table 1 List of material parameters for a human carotid artery

6.2 Purely mechanical response of an incompressible material

For the purely mechanical response of an incompressible material at constant reference temperature 𝜃₀, the functions η_i = 1 in Eq. 22 and there is no advantage to using the formulation based on the invariants β_i defined in Eq. 25. Moreover, for incompressible response, it is assumed that there is no volumetric growth with

$$ J_{e} = J_{h} = 1 , \quad \rho =\rho_{0} . $$

(44)

However, distortional homeostasis still causes distortions of the material due to $\mathbf {D}_{g}^{\prime \prime }$ in Eq. 18. Specifically, the Helmholtz free energy for distortional deformation is specified by

$$ \psi = \psi(m_{ij}^{\prime}) . $$

(45)

Then, with the help of the evolution (20) for $m_{ij}^{\prime }$, the constitutive equation for the Cauchy stress is given by Eq. 28 with the deviatoric tensor $\mathbf {T}^{\prime \prime }$ determined by

$$ \mathbf{T}^{\prime\prime} = 2 \rho_{0} \frac{\partial \psi}{\partial m_{ij}^{\prime}} (\mathbf{m}_{i}^{\prime} \otimes \mathbf{m}_{j}^{\prime} - \frac{1}{3} m_{nn}^{\prime} \mathbf{I}) , $$

(46)

where due to the incompressibility constraint, the pressure p is an arbitrary function of position and time.

6.3 Specific constitutive equation

When the (i = 1,2,3) directions of $\mathbf {m}_{i}^{\prime }$ are identified with the e_r,e_𝜃, and e_z material directions, respectively, the Helmholtz free energy

$$ \begin{aligned} \rho_{0} \psi &= \frac{c}{w} \left[\exp(w Q) -1 \right] , \quad E_{ij}^{\prime} = \frac{1}{2} (m_{ij}^{\prime} - \delta_{ij}) , \\ Q &= \frac{1}{2} \left[ c_{R} E_{11}^{\prime 2} + c_{{\varTheta}} E_{22}^{\prime 2} + c_{Z} E_{33}^{\prime 2}\right. \\ & \qquad+2\left( c_{R {\varTheta}} E_{11}^{\prime} E_{22}^{\prime} +c_{RZ} E_{11}^{\prime} E_{33}^{\prime}\right. \\ &\left.\left.\qquad +c_{{\varTheta} Z} E_{22}^{\prime} E_{33}^{\prime} \right) \right] , \end{aligned} $$

(47)

yields identical elastic response to the Fung model in Eqs. 36 and 41 with the material constants

$$ \{ c , w , c_{R} , c_{{\varTheta}} , c_{Z} , c_{R {\varTheta}} , c_{RZ} , c_{{\varTheta} Z} \} , $$

(48)

specified in Table 1. Also, the associated deviatoric stress is given by

$$ \begin{aligned} &\mathbf{T}^{\prime\prime} = \frac{c}{2} \exp (w Q) \left[ \left\{c_{R} (m_{11}^{\prime}-1) + c_{R {\varTheta}} (m_{22}^{\prime}-1)\right.\right. \\ &\left.\quad \quad + c_{R Z} (m_{33}^{\prime}-1) \right\} (\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime} - \frac{1}{3} m_{11}^{\prime} \mathbf{I} ) \\ &\quad \quad +\left\{ c_{R {\varTheta}} (m_{11}^{\prime}-1) +c_{{\varTheta}} (m_{22}^{\prime}-1)\right. \\ &\left.\quad \quad+ c_{{\varTheta} Z} (m_{33}^{\prime}-1) \right\}(\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime} - \frac{1}{3} m_{22}^{\prime} \mathbf{I} ) , \\ &\quad \quad +\left\{c_{R Z} (m_{11}^{\prime}-1) +c_{{\varTheta} Z} (m_{22}^{\prime}-1)\right. \\ &\left.\left.\quad \quad+ c_{Z} (m_{33}^{\prime}-1) \right\} (\mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime} - \frac{1}{3} m_{33}^{\prime} \mathbf{I} ) \right] . \end{aligned} $$

(49)

6.4 Homeostatic state

Using $\mathbf {m}_{i}^{\prime }$ in Eq. 3, the homeostatic expression for $\mathbf {T}^{\prime \prime }$ in Eq. 49 is given by

$$ \begin{aligned} &\mathbf{T}^{\prime\prime} = \frac{c}{2} \exp (w Q) \left[m_{11}^{\prime} \left\{c_{R} (m_{11}^{\prime}-1) + c_{R {\varTheta}} (m_{22}^{\prime}-1)\right.\right. \\ &\left.\qquad + c_{R Z} (m_{33}^{\prime}-1) \right\} \left\{\mathbf{N}_{r}(\theta) - \frac{1}{3} \mathbf{I} \right\} \\ &\qquad + m_{22}^{\prime} \left\{ c_{R {\varTheta}} (m_{11}^{\prime}-1) +c_{{\varTheta}} (m_{22}^{\prime}-1)\right. \\ &\left.\qquad + c_{{\varTheta} Z} (m_{33}^{\prime}-1) \right\} \left\{\mathbf{N}_{\theta}(\theta) - \frac{1}{3} m_{22}^{\prime} \mathbf{I} \right\} \\ &\qquad + m_{33}^{\prime} \left\{c_{R Z} (m_{11}^{\prime}-1) +c_{{\varTheta} Z} (m_{22}^{\prime}-1)\right. \\ &\left.\left.\qquad + c_{Z} (m_{33}^{\prime}-1) \right\} \left\{\mathbf{N}_{z} - \frac{1}{3} \mathbf{I} \right\} \right] , \end{aligned} $$

(50)

where $m_{11}^{\prime }, m_{22}^{\prime }$ and $m_{33}^{\prime }$ are specified by

$$ m_{11}^{\prime} = {h_{1}^{2}}(r) , \quad m_{22}^{\prime} = {h_{2}^{2}}(r) , \quad m_{33}^{\prime} = {h_{3}^{2}}(r) , $$

(51)

with h_i interpreted as elastic stretches.

6.5 Specific expressions for the homeostatic stress

Figure 1 shows an artery modeled as a circular cylindrical tube in its homeostatic state with inner radius a_h outer radius b_h and internal pressure P_h. For the deformations of the artery considered in the following examples, the stress T and pressure are given by

$$ \begin{aligned} \mathbf{T}(r,\theta) &= - p \mathbf{I} + \mathbf{T}^{\prime\prime} = T_{rr}(r) \mathbf{N}_{r}(\theta) + T_{\theta \theta}(r) \mathbf{N}_{\theta}(\theta) \\ &\quad+ T_{zz}(r) \mathbf{N}_{z}(\theta) , \\ p(r) &= - \frac{1}{3}(T_{rr} + T_{\theta \theta} + T_{zz}) , \\ \mathbf{T}^{\prime\prime}(r,\theta) &= T_{rr}^{\prime\prime}(r) \mathbf{N}_{r}(\theta) + T_{\theta \theta}^{\prime\prime}(r) \mathbf{N}_{\theta}(\theta) + T_{zz}^{\prime\prime}(r) \mathbf{N}_{z}(\theta) , \end{aligned} $$

(52)

where T_rr,T_𝜃𝜃, and T_zz are the cylindrical polar components of stress, which satisfy the equilibrium equation

$$ \frac{d (rT_{rr})}{dr} -T_{\theta \theta} = 0 , $$

(53)

and the functional forms of N_r,N_𝜃, and N_z are defined in Eq. 40. Moreover, the homeostatic state is characterized by Eqs. 50 and 51.

To study the influence of the stress field in the homeostatic state, it is convenient to consider the following homeostatic stress fields, which satisfy the equilibrium (53)

$$ \begin{aligned} &T_{rr} = \frac{a_{h}}{r} \left[ - \frac{b_{h}-r}{b_{h}-a_{h}} +\frac{c_{1}}{2} \left( \frac{r^{2}-{a_{h}^{2}}}{{b_{h}^{2}}} + \frac{{a_{h}^{2}}}{r^{2}}-1 \right) \right] P_{h} , \\ &T_{\theta\theta}=\left[ \frac{a_{h}}{b_{h}-a_{h}} +c_{1} \left( \frac{a_{h} r}{{b_{h}^{2}}} -\frac{{a_{h}^{3}}}{r^{3}} \right) \right] P_{h} , \quad T_{zz} = c_{2} P_{h} , \end{aligned} $$

(54)

and the boundary conditions

$$ T_{rr}(a_{h}) = - P_{h} , \quad T_{rr}(b_{h}) = 0 . $$

(55)

In these expressions, c₁ and c₂ are constants to be determined. Also, the pressure p and deviatoric components of stress are given by

$$ \begin{aligned} p(r) &= - \frac{1}{3} \left[T_{rr}(r) + T_{\theta \theta}(r) + T_{zz}(r)\right] , \\ T_{rr}^{\prime\prime}(r) &= T_{rr}(r) + p(r) , \quad T_{\theta \theta}^{\prime\prime}(r) = T_{\theta \theta}(r) + p(r) , \\ T_{zz}^{\prime\prime}(r) &= T_{zz}(r) + p(r) . \end{aligned} $$

(56)

The force f_𝜃 per unit axial length applied in the e_𝜃 direction and the moment m_z per unit axial length about the middle surface of artery applied in the e_z direction, both on the cross-section with outward normal e_𝜃, and the equivalent uniform axial stress σ_z applied in the e_z direction on the cross-section with outward normal e_z over the region a ≤ r ≤ b are defined by

$$ \begin{aligned} &f_{\theta} = {{\int}_{a}^{b}} T_{\theta \theta} dr , \quad m_{z} = {{\int}_{a}^{b}} (r - \frac{a+b}{2}) T_{\theta \theta} dr , \\ &\sigma_{z} = \frac{2}{b^{2}-a^{2}} {{\int}_{a}^{b}} T_{zz} r dr , \end{aligned} $$

(57)

The homeostatic stress field (54) is defined so that

$$ \begin{aligned} &f_{\theta} = f_{\theta h} = a_{h} P_{h} , \\ &m_{z} = m_{zh} = c_{1} \left[\frac{a_{h} (b_{h}-a_{h})^{3} P_{h}}{3 {b_{h}^{2}}} \right] , \\ &\sigma_{z} = \sigma_{zh} = c_{2} P_{h} , \end{aligned} $$

(58)

when the region of interest is the homeostatic state with a = a_h and b = b_h. These expressions show that c₁ controls the magnitude of the moment m_zh and c₂ controls the equivalent uniform axial stress σ_zh.

6.6 Determination of the homeostatic values h ₁,h ₂, and p _h

Given values of the material constants (48) and the constants c_i in Eq. 54, the values of h₁(r) and h₂(r) are determined by solving the equations

$$ T_{rr}^{\prime\prime} = \mathbf{T}^{\prime\prime} \cdot \mathbf{N}_{r} , \quad T_{\theta \theta}^{\prime\prime} = \mathbf{T}^{\prime\prime} \cdot \mathbf{N}_{\theta} , $$

(59)

where $T_{rr}^{\prime \prime }$ and $T_{\theta \theta }^{\prime \prime }(r)$ are specified by Eq. 56 and $\mathbf {T}^{\prime \prime }(r)$ is specified by Eq. 52. Also, p_h is specified by .

$$ p_{h}(r) = p(r) , $$

(60)

with p given by Eq. 56.

6.7 Deformations from a homeostatic state

For the analysis in this paper, it is assumed that deformations from the homeostatic state are elastic with no influence of homeostasis (Γ_m = Γ = 0). This means that the evolution (16) for elastic changes in $\mathbf {m}_{i}^{\prime }$ are given by

$$ \dot{\mathbf{m}}_{i}^{\prime} = \mathbf{L}^{\prime\prime} \mathbf{m}_{i}^{\prime} . $$

(61)

Next, it is noted that the unimodular relative distortional deformation gradient $\mathbf {F}_{r}^{\prime }$ in Eq. 4 from the homeostatic state of the artery satisfies the evolution equation and initial condition

$$ \dot{\mathbf{F}}_{r}^{\prime} = \mathbf{L}^{\prime\prime} \mathbf{F}_{r}^{\prime} , \quad \mathbf{F}_{r}^{\prime}(0) = \mathbf{I} . $$

(62)

It follows that the solution of Eq. 61 is given by

$$ \mathbf{m}_{i}^{\prime}(r,\theta,t) = \mathbf{F}_{r}^{\prime}(r,\theta,t) \mathbf{h}_{i}^{\prime}(r) . $$

(63)

with h_i specified by Eq. 3. To be specific, the homeostatic state is specified by the systolic state of the intact artery with applied systolic pressure P_s.

6.7.1 Deformation to the cut unloaded state

The radial r, circumferential 𝜃 and axial z coordinates in the homeostatic state are deformed to $\tilde {r}$, $\tilde {\theta }$, and $\tilde {z}$, respectively, in the cut unloaded state such that

$$ \begin{aligned} &\tilde{r}^{2} = {a_{c}^{2}} + \frac{1}{\tilde{\lambda}_{c}} \left( \frac{2 \pi}{2 \pi-\omega_{c}} \right) (r^{2}-{a_{s}^{2}}) , \quad a_{s} \le r \le b_{s} , \\ &\tilde{\theta} = \left( \frac{2\pi- \omega_{c}}{2 \pi}\right) \theta - \frac{\omega_{c}}{4} , \quad - \frac{3\pi}{2} < \theta \le \frac{\pi}{2} , \\ &\tilde{z} = \tilde{\lambda}_{c} z , \end{aligned} $$

(64)

where $\tilde {\lambda }_{c}$ is axial stretch from the homeostatic systolic state. It therefore follows that the radii of the cut unloaded state satisfy the equation

$$ {b_{s}^{2}} = {a_{s}^{2}} + \tilde{\lambda}_{c} \left( \frac{2 \pi - \omega_{c}}{2 \pi} \right) ({b_{c}^{2}}-{a_{c}^{2}}) . $$

(65)

This assumed deformation field satisfies the incompressibility condition with $\mathbf {F}_{r}^{\prime }$ given by

$$ \begin{aligned} &\mathbf{F}_{r}^{\prime} = \frac{r}{\tilde{\lambda}_{c} \tilde{r}} \left( \frac{2 \pi}{2 \pi-\omega_{c}} \right) \mathbf{e}_{r}(\tilde{\theta}) \otimes \mathbf{e}_{r}(\theta) \\ &\quad \quad + \frac{\tilde{r}}{r} \left( \frac{2 \pi-\omega_{c}}{2 \pi} \right) \mathbf{e}_{\theta}(\tilde{\theta}) \otimes \mathbf{e}_{\theta}(\theta) + \tilde{\lambda}_{c} \mathbf{N}_{z} , \end{aligned} $$

(66)

which determines the value of $\mathbf {T}^{\prime \prime }$ by Eq. 50 with 𝜃 replaced by $\tilde {\theta }$, $m_{11}^{\prime }, m_{22}^{\prime }$, and $m_{33}^{\prime }$ given by

$$ \begin{aligned} &m_{11}^{\prime} = m_{11s}^{\prime} = \left[\frac{r h_{1}(r)}{\tilde{\lambda}_{c} \tilde{r}(r)} \left( \frac{2 \pi}{2 \pi-\omega_{c}} \right)\right]^{2} , \\ &m_{22}^{\prime} = m_{22s}^{\prime} = \left[\frac{\tilde{r}(r)h_{2}(r)}{r} \left( \frac{2 \pi-\omega_{c}}{2 \pi} \right) \right]^{2} , \\ &m_{33}^{\prime} = m_{33s}^{\prime} = \left[\tilde{\lambda}_{c} h_{3}(r)\right]^{2} , \end{aligned} $$

(67)

and h_i determined by the homeostatic systolic state.

6.7.2 Deformation to another intact state

The functional forms for $\tilde {r}$, $\tilde {\theta }$ and $\tilde {z}$ in another intact state are given by

$$ \tilde{r}^{2} = \tilde{a}^{2} + \frac{1}{\tilde{\lambda}} (r^{2}-{a_{s}^{2}}) , \quad \tilde{\theta} = \theta , \quad \tilde{z} = \tilde{\lambda} z , $$

(68)

where $\tilde {\lambda }$ is the axial stretch relative to the homeostatic systolic state. It therefore follows that the inner and outer radii (a_u,b_u) of the intact unloaded state and (a_d,b_d) of the diastolic state are related by the equations

$$ \begin{array}{@{}rcl@{}} &&{b_{u}^{2}} = {a_{u}^{2}} + \frac{1}{\tilde{\lambda}_{u}} ({b_{s}^{2}}-{a_{s}^{2}}) , \end{array} $$

(69)

$$ \begin{array}{@{}rcl@{}} &&{b_{d}^{2}} = {a_{d}^{2}} + \frac{1}{\tilde{\lambda}_{d}} ({b_{s}^{2}}-{a_{s}^{2}}) , \end{array} $$

(70)

where $\tilde {\lambda }_{u}$ and $\tilde {\lambda }_{d}$ are, respectively, the axial stretches in the intact unloaded and diastolic states relative to the homeostatic systolic state.

Also, this assumed deformation field satisfies the incompressibility condition with $\mathbf {F}_{r}^{\prime }$ given by

$$ \mathbf{F}_{r}^{\prime} = \frac{r}{\tilde{\lambda} \tilde{r}} \mathbf{N}_{r}(\theta) + \frac{\tilde{r}}{r} \mathbf{N}_{\theta}(\theta) + \tilde{\lambda} \mathbf{N}_{z} , $$

(71)

which determines the value of $\mathbf {T}^{\prime \prime }$ by the expression (50) with $m_{11}^{\prime }, m_{22}^{\prime }$, and $m_{33}^{\prime }$ given by

$$ \begin{aligned} &m_{11}^{\prime} = \left[\frac{r h_{1}(r)}{\lambda \tilde{r}(r)} \right]^{2} , \quad m_{22}^{\prime} = \left[\frac{\tilde{r}(r)h_{2}(r)}{r} \right]^{2} , \\ &m_{33}^{\prime} = \left[\lambda h_{3}(r)\right]^{2} . \end{aligned} $$

(72)

In Eq. 68$(\tilde {a}, \tilde {b}, \tilde {\lambda })$, respectively, take the values $(a_{u}, b_{u}, \tilde {\lambda }_{u})$ for the intact unloaded state and $(a_{d}, b_{d}, \tilde {\lambda }_{d})$ for the diastolic state.

6.8 Equilibrium and boundary conditions

All of the solutions satisfy the equilibrium equation, which can be written in the equivalent forms

$$ \begin{array}{@{}rcl@{}} \frac{d T_{rr}(\tilde{r})}{d \tilde{r}} + \frac{T_{rr}^{\prime\prime}(\tilde{r}) - T_{\theta \theta}^{\prime\prime}(\tilde{r})}{\tilde{r}} &=& 0 , \end{array} $$

(73)

$$ \begin{array}{@{}rcl@{}} \frac{d [\tilde{r} T_{rr}(\tilde{r})]}{d \tilde{r}} - T_{\theta \theta}(\tilde{r}) &=& 0 , \end{array} $$

(74)

and the boundary conditions

$$ T_{rr}(a) = -P , \quad T_{rr}(b) = 0 , $$

(75)

where P is the applied internal pressure. Also, the pressure $p(\tilde {r})$ is determined by integrating (73) to obtain

$$ p(\tilde{r}) = P + T_{rr}^{\prime\prime}(\tilde{r}) + {\int}_{a}^{\tilde{r}} \left[\frac{T_{rr}^{\prime\prime}(x) - T_{\theta \theta}^{\prime\prime}(x)}{x} \right] dx , $$

(76)

with x being a dummy variable of integration.

6.9 Boundary conditions for the cut unloaded state

For the cut unloaded state, the internal pressure P = 0 vanishes and integration of Eq. 73 requires

$$ {\int}_{a_{c}}^{b_{c}} \left[\frac{T_{rr}^{\prime\prime}(x) - T_{\theta \theta}^{\prime\prime}(x)}{x} \right] dx = 0 . $$

(77)

Moreover, using Eq. 57 with P = 0, integration of Eq. 74 automatically yields the result

$$ f_{\theta c} = {\int}_{a_{c}}^{b_{c}} T_{\theta \theta}(\tilde{r}) d\tilde{r} = 0 , $$

(78)

which indicates that the circumferential force applied to the cut artery vanishes. In addition, the equivalent uniform axial stress in the cut unloaded state must vanish which, with the help of Eq. 57, requires

$$ \sigma_{c} = \frac{2}{{b_{c}^{2}}-{a_{c}^{2}}} {\int}_{a_{c}}^{b_{c}} T_{zz}(\tilde{r}) \tilde{r} d\tilde{r} = 0 . $$

(79)

6.10 Boundary conditions for other intact states

For all intact states, the boundary condition at the inner surface is satisfied by specifying the appropriate value of the pressure P, and the boundary condition (75)₂ at the outer boundary imposes the restrictions

$$ \begin{array}{@{}rcl@{}} {\int}_{a_{u}}^{b_{u}} \left[\frac{T_{rr}^{\prime\prime}(x) - T_{\theta \theta}^{\prime\prime}(x)}{x} \right] dx &= 0 , \end{array} $$

(80)

$$ \begin{array}{@{}rcl@{}} P_{d} + {\int}_{a_{d}}^{b_{d}} \left[\frac{T_{rr}^{\prime\prime}(x) - T_{\theta \theta}^{\prime\prime}(x)}{x} \right] dx &= 0 , \end{array} $$

(81)

$$ \begin{array}{@{}rcl@{}} P_{s} + {\int}_{a_{s}}^{b_{s}} \left[\frac{T_{rr}^{\prime\prime}(x) - T_{\theta \theta}^{\prime\prime}(x)}{x} \right] dx &= 0 , \end{array} $$

(82)

for the intact unloaded, diastolic and systolic states, respectively. This boundary condition for the systolic state is automatically satisfied by this solution since the systolic state is assumed to be the homeostatic state specified by the stress field (54), which satisfies the boundary conditions (55).

In addition, it is necessary to specify a condition on the axial load for each state. For the intact unloaded state, the equivalent uniform axial stress vanishes

$$ \sigma_{u} = \frac{2}{{b_{u}^{2}}-{a_{u}^{2}}} {\int}_{a_{u}}^{b_{u}} T_{zz}(\tilde{r}) \tilde{r} d\tilde{r} = 0 . $$

(83)

Motivated by the results in Figs. 9.4-9.6 in [28], the equivalent uniform axial stress in the diastolic state is assumed to be proportional to applied internal pressure so that

$$ \sigma_{d} = \frac{2}{{b_{d}^{2}}-{a_{d}^{2}}} {\int}_{a_{d}}^{b_{d}} T_{zz}(\tilde{r}) \tilde{r} d\tilde{r} = \left( \frac{P_{d}}{P_{s}}\right) \sigma_{s} , $$

(84)

where the equivalent uniform axial stress σ_s in the systolic state is determined by

$$ \sigma_{s} = \frac{2}{{b_{s}^{2}}-{a_{s}^{2}}} {\int}_{a_{s}}^{b_{s}} T_{zz}(\tilde{r}) \tilde{r} d\tilde{r} . $$

(85)

For this solution, the systolic state is specified by the homeostatic state so that σ_s is given by Eq. 58

$$ \sigma_{s} = c_{2} P_{s} . $$

(86)

6.11 A modified Fung model

The cut unloaded state is not a physiological state and therefore most likely is also not a homeostatic state, which is specified by values of J_h and h_i. However, within the context of the proposed theory, it is possible to study the influence of different residual stress distributions in the cut unloaded state by specifying J_h and h_i to be consistent with these residual stresses.

To this end, the modified Fung model, which uses the cut unloaded state as a homeostatic state, is defined by

$$ \begin{aligned} &\tilde{r} = R , \quad a_{c} \le R \le b_{c} , \quad \tilde{z}=Z , \\ &\tilde{\theta} = {\varTheta} , \quad - \frac{3\pi}{2} + \frac{\omega_{c}}{2} < {\varTheta} \le \frac{\pi}{2} - \frac{\omega_{c}}{2} , \end{aligned} $$

(87)

with the stress field given by Eq. 50 with 𝜃 replaced by $\tilde {\theta }$ and using the specifications (51). A deformed intact configuration is determined by

$$ \begin{aligned} &\tilde{r}^{2} = \tilde{a}^{2} + \frac{1}{\lambda} \left( \frac{2 \pi-\omega_{c}}{2 \pi} \right) (R^{2}-{a_{c}^{2}}) , \quad a_{c} \le R \le b_{c} , \\ &\tilde{\theta} = \left( \frac{2\pi}{2\pi- \omega_{c}}\right) ({\varTheta} + \frac{\omega_{c}}{4}) , \quad - \frac{3 \pi}{2} \le {\varTheta} \le \frac{\pi}{2} , \\ &\tilde{z} = \lambda Z . \end{aligned} $$

(88)

It then follows that the inner and outer intact radii (a_u,b_u) of the intact unloaded state, (a_d,b_d) of the diastolic state and (a_s,b_s) of the systolic state are related by the equations

$$ \begin{aligned} &{b_{u}^{2}} = {a_{u}^{2}} + \frac{1}{\lambda_{u}} \left( \frac{2 \pi-\omega_{c}}{2 \pi} \right) ({b_{c}^{2}}-{a_{c}^{2}}) , \\ &{b_{d}^{2}} = {a_{d}^{2}} + \frac{1}{\lambda_{d}} \left( \frac{2 \pi-\omega_{c}}{2 \pi} \right) ({b_{c}^{2}}-{a_{c}^{2}}) , \\ &{b_{s}^{2}} = {a_{s}^{2}} + \frac{1}{\lambda_{s}} \left( \frac{2 \pi-\omega_{c}}{2 \pi} \right) ({b_{c}^{2}}-{a_{c}^{2}}) , \end{aligned} $$

(89)

where λ_u,λ_d, and λ_s are axial stretches from the cut unloaded state. Furthermore, the relative deformation gradient $\mathbf {F}_{r}^{\prime }$ from the cut unloaded state and the elastic deformation measures are given by

$$ \begin{aligned} &\mathbf{F}_{r}^{\prime} = \frac{1}{\lambda} \left( \frac{2 \pi-\omega_{c}}{2 \pi}\right) \frac{R}{\tilde{r}} \mathbf{e}_{r}(\tilde{\theta}) \otimes \mathbf{e}_{r}({\varTheta}) \\ &\quad \quad + \left( \frac{2 \pi}{2 \pi-\omega_{c}}\right) \frac{\tilde{r}}{R} \mathbf{e}_{\theta}(\tilde{\theta}) \otimes \mathbf{e}_{\theta}({\varTheta}) + \lambda \mathbf{N}_{3} , \\ &m_{11}^{\prime} = \left[\frac{1}{\lambda} \left( \frac{2 \pi-\omega_{c}}{2 \pi}\right) \frac{R}{\tilde{r}} h_{1}\right]^{2} , \\ &m_{22}^{\prime} = \left[ \left( \frac{2 \pi}{2 \pi-\omega_{c}}\right) \frac{\tilde{r}}{R} h_{2}\right]^{2} , \\ &m_{33}^{\prime} = (\lambda h_{3})^{2} , \end{aligned} $$

(90)

where h_i are determined by the homeostatic cut unloaded state and λ is the axial stretch from the cut unloaded state to the intact state in consideration. Also, the stresses are obtained by substituting these values of $m_{11}^{\prime }, m_{22}^{\prime }$, and $m_{33}^{\prime }$ into Eq. 50 with 𝜃 replaced by $\tilde {\theta }$.

6.12 Solution procedure

The examples in this paper discuss solutions based on two models. Both models use the same constitutive (50) with 𝜃 replaced by $\tilde {\theta }$ and the material constants for a human carotid artery recorded in Table 1. For clarity, the proposed model, which takes the systolic state to be the homeostatic state of the artery, is referred to as the HS-Ps model. The second model is the modified Fung model, which takes the homeostatic state to be the cut unloaded state predicted by the HS-Ps model, and is referred to as the MF-c model.

The solutions of both models satisfy the geometry of the cut unloaded state determined by [35]

$$ a_{c} = 4.66 [mm] , \quad b_{c} = 6.16 [mm] , \quad \omega_{c} = 103^{\circ} . $$

(91)

Both the HS-Ps and MF-c models are parameterized by two constants

$$ \{ c_{1} , \tilde{\lambda}_{c} = \frac{1}{\lambda_{s}} \} , $$

(92)

with λ_s determining the axial stretch of the systolic state relative to the cut unloaded state. For the examples considered in this paper, λ_s is specified by

$$ \lambda_{s} = 1.3 , $$

(93)

and the influence of c₁ in Eq. 54 on the homeostatic systolic state is examined by considering the following three values

$$ c_{1} = 0 , 15 , - 15 . $$

(94)

For each solution, the value of c₂ in Eq. 54 is determined by the solution procedure. Specifically, the numerical solutions for the two models discretize the integrals over the radial coordinate using the trapezoidal rule with 21 integration points, including the boundaries. Moreover, this value of λ_s was specified so that the HS-Ps solution with c₁ = 0 causes the uniform systolic values of T_𝜃𝜃 and T_zz to be identical, which is consistent with an isotropic state of stress in plane normal to the radial direction.

6.13 Solution procedure for the HS-Ps model

For the HS-Ps model, the value of c₁ is specified by one of the values (94), the values of h₁,h₂, and p are determined for the 21 numerical integration points by solving (59) and (60), with the homeostatic stress given by Eq. 54 with P_h = P_s and the constitutive equation for $\mathbf {T}^{\prime \prime }$ given by Eqs. 50 and 51. These equations include three unknown variables

$$ \{a_{s} , b_{s} , c_{2} \} , $$

(95)

which are determined by the Eqs. 65, 77, and 79. Once these values have been determined, the value of σ_s in Eq. 85 is known, use is made of Eqs. 69, 80, and 83 to determine the values of a_u,b_u, and $\tilde {\lambda }_{u}$ in the intact unloaded state. Similarly, use is made of Eqs. 70, 81, and 84 to determine the values of a_d,b_d, and $\tilde {\lambda }_{d}$ in the diastolic state. For both of these solutions the pressure is determined by solving (76).

6.14 Solution procedure for the MF-c model

For the MF-c model, only one value of c₁ = 0 is considered and the values of h₁,h₂, and p are determined for the 21 numerical integration points by solving scaled version of Eq. 59

$$ T_{rr}^{\prime\prime} = \alpha \mathbf{T}_{c}^{\prime\prime} \cdot \mathbf{N}_{r}(\theta) , \quad T_{\theta \theta}^{\prime\prime} = \alpha \mathbf{T}_{c}^{\prime\prime} \cdot \mathbf{N}_{\theta}(\theta) , $$

(96)

with the pressure p_h specified by a scaled version of Eq. 60

$$ \quad p_{h} = \alpha p_{c} , $$

(97)

and α is a scale factor (0 ≤ α ≤ 1). In these equations, $\mathbf {T}_{c}^{\prime \prime }$ and p_c are the HS-Ps solution for the cut unloaded state and $T_{rr}^{\prime \prime }$ and $T_{\theta \theta }^{\prime \prime }$ are determined by substituting the values of $m_{11}^{\prime }, m_{22}^{\prime }$, and $m_{33}^{\prime }$ in Eq. 90 into the constitutive (50) with 𝜃 replaced by $\tilde {\theta }$.

Next, the MF-c solutions for the intact unloaded, diastolic, and systolic states are determined by solving (80), (81), (82), (83), (84) and (89), for the eight unknowns

$$ \{a_{u} , b_{u} , \lambda_{u} , a_{d} , b_{d} , \lambda_{d} , a_{s} , b_{s} \} , $$

(98)

with σ_s determined by Eq. 85 and λ_s specified by Eq. 93. Again, the pressure is determined by solving (76).

7 Examples

For the solutions discussed in this section, the diastolic pressure P_d and systolic pressure P_s are specified by the typical values for a healthy human

$$ \begin{aligned} &P_{d} = 80 [mm\text{-}Hg] = 10.66 [kPa] , \\ &P_{s} = 120 [mm\text{-}Hg] = 16.00 [kPa] . \end{aligned} $$

(99)

7.1 The HS-Ps solution

Predictions of the HS-Ps model are shown for the cut unloaded state, the intact unloaded state, the diastolic state and the homeostatic systolic state in Figs. 2, 3, 4, and 5, respectively. These figures examine the influence of the constant c₁ in Eq. 54, and the Fung solution (which is determined by the MF-c model with α = 0) is shown for comparison. Table 2 records the value of c₂, the equivalent uniform axial stresses σ_d,σ_s in the diastolic and systolic states, the values of the inner and outer radii, the stretches predicted by the HS-Ps solution for each of theses states, and the minimum T_𝜃𝜃(min) and maximum T_𝜃𝜃(max) values of the circumferential stress T_𝜃𝜃, with the stretches λ_u,λ_s,λ_d relative to the intact unloaded state defined by

$$ \lambda_{u} = \frac{\tilde{\lambda}_{u}}{\tilde{\lambda}_{c}} , \quad \lambda_{s} = \frac{\tilde{\lambda}_{s}}{\tilde{\lambda}_{c}} , \quad \lambda_{d} = \frac{1}{\tilde{\lambda}_{c}} . $$

(100)

Also, the value ΔT_𝜃𝜃(max) in Table 2 represents the increase in the maximum circumferential stress relative to that predicted by the HS-Ps solution for c₁ = 0 for each stress state. In addition, the original Fung solution is included in Table 2 for comparison.

Fig. 2

Influence of c₁ on the stress distributions in the cut unloaded state predicted by the HS-Ps model. The predictions of the Fung model (F) are included for comparison

Fig. 3

Influence of c₁ on the stress distributions in the intact unloaded state predicted by the HS-Ps model. The predictions of the Fung model (F) are included for comparison

Fig. 4

Influence of c₁ on the stress distributions in the diastolic state predicted by the HS-Ps model. The predictions of the Fung model (F) are included for comparison

Fig. 5

Influence of c₁ on the stress distributions in the systolic state predicted by the HS-Ps model. The predictions of the Fung model (F) are included for comparison

From the results presented in these figures and Table 2, it is observed that c₁ has a significant effect on the circumferential distribution of stress. The value of c₁ = 15 has a smaller influence than c₁ = − 15 on the value of c₂, which controls the equivalent uniform axial stress. The predicted values of the compressive circumferential stress in Fig. 3b for the state (u) are similar for the HS-Ps model with c₁ = 0,− 15 and the Fung model, but the large magnitude of the compressive circumferential stress for c₁ = 15 seems unphysical. Also, the large magnitude of the compressive axial stress for c₁ = − 15 in Fig. 3c seems unphysical. Furthermore, it is seen from Fig. 5b that the prediction of the circumferential stress using the HS-Ps model with c₁ = − 15 is similar to that of the Fung model for the systolic state but the prediction for c₁ = 15 has the opposite slope. From Table 2, it is observed that changes in c₁ cause minor changes in the geometries of the predicted states. Moreover, it can be seen that the Fung solution predicts significantly larger values of the circumferential stress, especially for the systolic state.

Table 2 Influence of c₁ on the predictions of the HS-Ps model for the cut unloaded (c), intact unloaded (u), diastolic (d) and systolic (s) states. Values of the inner radius (a), outer radius (b), axial stretch (λ) from the cut unloaded state, minimum [T_𝜃𝜃(min)] and maximum [T_𝜃𝜃(max)] values of the circumferential stress T_𝜃𝜃 are recorded. The value ΔT_𝜃𝜃(max) represents the increase in the maximum circumferential stress relative to that predicted by the HS-Ps solution for c₁ = 0 for each stress state. Also, the predictions of the Fung model (F) are included for comparison

7.2 The MF-c solution

Figures 6, 7, and 8 show results based on the MF-c model. Figures 6 and 7 show, respectively, the stress and stretch distributions for the cut unloaded homeostatic state and Fig. 8 shows the stress distributions predicted for the systolic state. For clarity, the values h₁,h₂, and h₃ are denoted by h_rc,h_𝜃c, and h_zc, respectively, in Fig. 7. Also, the value ΔT_𝜃𝜃(max) in Table 3 represents the increase in the maximum circumferential stress relative to that predicted by the HS-Ps solution for α = 1.0 for each stress state. These figures and Table 3 examine the influence of residual stresses in the cut unloaded state on the predictions of the stress distributions in the other states. Specifically, when the scale parameter α = 0, the cut unloaded state has zero stress and the MF-c model predicts the standard Fung extrapolations for the intact unloaded, diastolic, and systolic states. However, when 0 < α ≤ 1, the predictions of the MF-c model show influences of the residual stresses in the cut unloaded state. In particular, it is seen that the results for the intact unloaded, diastolic, and systolic states in Tables 2 of the HS-Ps model for c₁ = 0, which specifies the systolic state as the homeostatic state, are identical to those of the MF-c model in Table 3 with α = 1, which specified the cut unloaded state as the homeostatic state. This is because for both choices of the homeostatic state, the deformations from the homeostatic state are elastic. The original Fung solution with α = 0 is included in Table 3 for comparison.

Fig. 6

Influence of the scale factor α on the stresses determined by the MF-c solution for the cut unloaded state. The value α = 0 corresponds the the original Fung solution and the value α = 1 calibrates the homeostatic state in the MF-c solution with the stress distribution in the cut unloaded state predicted by the HS-Ps model with c₁ = 0

Fig. 7

Influence of the scale factor α on the homeostatic stretches determined by the MF-c solution for the cut unloaded state. The value α = 0 corresponds the the original Fung solution and the value α = 1 calibrates the homeostatic state in the MF-c solution with the stress distribution in the cut unloaded state predicted by the HS-Ps model with c₁ = 0

Fig. 8

Influence of the scale factor α on the stresses determined by the MF-c solution for the systolic state. The value α = 0 corresponds to the original Fung solution and the value α = 1 calibrates the homeostatic state in the MF-c solution with the stress distribution in the cut unloaded state predicted by the HS-Ps model with c₁ = 0

The elastic stretches shown in Fig. 7 indicate that this kinematic approximation of the cut unloaded state as a section of a circular tube with uniform axial stretch is not accurate. The predicted axial stretch is small so planes normal to e_z would remain nearly planar but the planes normal to e_𝜃 would tend to shear relative to e_𝜃 if the bounding surfaces were actually traction free. This is qualitatively consistent with the work reported in [31] which observed that additional cuts of the cut unloaded state cause additional deformations of the cut sections due to stress relief.

From the results in Table 3 it can be seen that the predicted geometries of the other states are only slightly affected by the residual stresses in the cut unloaded state. However, small changes in these residual stresses can have a large influence on the predicted circumferential stress. For example, from the results in Table 3 for α = 0.2 it is seen that ΔT_𝜃𝜃(max)=-3.47 [kPa] in the cut unloaded state causes ΔT_𝜃𝜃(max)= 65.9 [kPa] in the systolic state. This same large sensitivity to the residual stresses in the cut unloaded state is also seen in Figs. 6b and 8b.

8 Conclusions

The nonlinear orthotropic invariants developed in [27] for themoelastic response of soft materials have been generalized to include the inelastic effect of homeostasis. The evolution (14) for the elastic dilatation J_e and Eq. 16 for the distortional microstructural vectors $\mathbf {m}_{i}^{\prime }$ are Eulerian formulations which are insensitive to arbitrariness of the specifications of: a reference configuration, an intermediate configuration, a total deformation measure, and an inelastic deformation measure. This Eulerian formulation is naturally suited to model growth, remodeling and homeostasis of tissues since the evolution equations depend only on state variables which can be determined in the present configuration.

As an example, the stress distributions in a human carotid artery are studied. The inelastic process of homeostasis is used to specify the residual homeostatic stress state and the inelastic process of homeostasis is assumed to be slow relative to physiological times for cardiac cycles from diastolic to systolic pressures and relative to unloading to cut unloaded and intact unloaded states. Consequently, homeostasis during these processes is ignored and the artery is modeled as an incompressible, orthotropic nonlinear hyperelastic material. Due to the incompressibility constraint, the special features of the orthotropic invariants developed in the generalized model are not needed and a Fung-type exponential strain energy function can be used directly.

The HS-Ps model developed here specifies the systolic state as the homeostatic state and deformations from this loaded systolic state are used to analyse the stresses in the cut unloaded, intact unloaded and diastolic states and the influence of different homeostatic stress states is considered. In addition, a modified Fung model MF-c is developed which uses the cut unloaded state with residual stresses as a reference state for predicting stresses in the other intact states and the influence of a family of residual stress states is analyzed.

The results indicate that:

• The geometry of the cut unloaded state does not uniquely determine the stresses in other intact states

• The circumferential stress in the artery is particularly sensitive to the distribution of residual stress in the cut unloaded state

• Extrapolation should be limited to the physiological pressure range to improve the accuracy of the predicted stress distributions

These conclusions are consistent with those in previous work on a rabbit thoracic artery in [1, 34]. In addition, the results in Table 3 indicate that relatively small changes in the residual stresses in the cut unloaded state, which cause significant changes in the circumferential stress in the systolic state, have little effect on the geometries of the diastolic and systolic states. However, measured differences in the in vivo geometries of the diastolic and systolic states of an artery can be used to validate constitutive equations. Also, from Figs. 4b,c and 5b,c, it is interesting to note that the engineering assumption of uniform circumferential and axial stresses of equal values in the systolic homeostatic state cause the circumferential and axial stresses to remain of the same order in the diastolic state.

Table 3 Influence of scaling factor α using the cut unloaded state HS-Ps solution with c₁ = 0 as the homeostatic state for the MF-c model on the predictions of the cut unloaded (c), intact unloaded (u), diastolic (d) and systolic (s) states. Values of the inner radius (a), outer radius (b), axial stretch (λ) from the cut unloaded state, minimum [T_𝜃𝜃(min)] and maximum [T_𝜃𝜃(max)] values of the circumferential stress T_𝜃𝜃 are recorded. The value ΔT_𝜃𝜃(max) represents the increase in the maximum circumferential stress relative to that predicted by the HS-Ps solution for α = 1.0 for each stress state. Also, the predictions of the Fung model (F) are included for comparison

Improved constitutive equations for modeling of biological tissues should be inspired by in vivo experimental measurements of mechanical response and mechanobiological processes that control homeostasis and the homeostatic state. Also, differences in the mechanical properties, homeostasis and the homeostatic states of the media and adventitia layers of the artery, which were not considered here, need to be investigated.

Appendix A: Details of some the mathematical expressions

1.1 A.1 Details of the functions N _i and A _i

The scalar functions N_i and A_i in Eq. 26 are defined by

$$ \begin{aligned} &\quad \quad \quad N_{1} =\frac{J_{e}}{\eta_{1}} \left( \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} - {\eta_{1}^{2}} m^{11 \prime}\right) \frac{\partial \eta_{1}}{\partial J_{e}} , \\ &\quad \quad \quad N_{2} =\frac{J_{e}}{\eta_{2}} \left( \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} - {\eta_{2}^{2}} m^{22 \prime}\right) \frac{\partial \eta_{2}}{\partial J_{e}} , \\ &\quad \quad \quad N_{3} =\frac{J_{e}}{\eta_{3}} \left( \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} - {\eta_{3}^{2}} m^{33 \prime}\right) \frac{\partial \eta_{3}}{\partial J_{e}} , \\ &\quad \quad \quad A_{1} =- \frac{1}{\eta_{1}} \left( \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} - {\eta_{1}^{2}} m^{11 \prime} \right) \frac{\partial \eta_{1}}{\partial \theta} , \\ &\quad \quad \quad A_{2} =- \frac{1}{\eta_{2}} \left( \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} - {\eta_{2}^{2}} m^{22 \prime} \right) \frac{\partial \eta_{2}}{\partial \theta} , \\ &\quad \quad \quad A_{3} =- \frac{1}{\eta_{3}} \left( \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} - {\eta_{3}^{2}} m^{33 \prime} \right) \frac{\partial \eta_{3}}{\partial \theta} . \end{aligned} $$

(101)

1.2 A.2 Details of the tensors $\mathbf {B}_{i}^{\prime \prime }$

The deviatoric tensors $\mathbf {B}_{i}^{\prime \prime }$ in Eq. 26 are defined by

$$ \begin{aligned} &\mathbf{B}_{1}^{\prime\prime} = \frac{1}{{\eta_{1}^{2}}} \mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime} - {\eta_{1}^{2}} \mathbf{m}^{1 \prime} \otimes \mathbf{m}^{1 \prime} \\ &\quad \quad - \frac{1}{3} \left( \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} - {\eta_{1}^{2}} m^{11 \prime} \right) \mathbf{I} , \\ &\mathbf{B}_{2}^{\prime\prime} = \frac{1}{{\eta_{2}^{2}}} \mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime} - {\eta_{2}^{2}} \mathbf{m}^{2 \prime} \otimes \mathbf{m}^{2 \prime} \\ &\quad \quad- \frac{1}{3} \left( \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} - {\eta_{2}^{2}} m^{22 \prime} \right) \mathbf{I} , \\ &\mathbf{B}_{3}^{\prime\prime} = \frac{1}{{\eta_{3}^{2}}} \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime} - {\eta_{3}^{2}} \mathbf{m}^{3 \prime} \otimes \mathbf{m}^{3 \prime} \\ &\quad \quad- \frac{1}{3} \left( \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} - {\eta_{3}^{2}} m^{33 \prime} \right) \mathbf{I} , \\ &\mathbf{B}_{4}^{\prime\prime} = \frac{m_{12}^{\prime}}{m_{11}^{\prime} m_{22}^{\prime}} \left[(\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{2}^{\prime}+ \mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{1}^{\prime})\right. \\ &\left.\quad \quad- \frac{m_{12}^{\prime}}{m_{11}^{\prime}} (\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime}) - \frac{m_{12}^{\prime}}{m_{22}^{\prime}} (\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime}) \right] , \\ &\mathbf{B}_{5}^{\prime\prime} = \frac{m_{13}^{\prime}}{m_{11}^{\prime} m_{33}^{\prime}} \left[(\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{3}^{\prime}+ \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{1}^{\prime})\right. \\ &\left.\quad \quad- \frac{m_{13}^{\prime}}{m_{11}^{\prime}} (\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime}) - \frac{m_{13}^{\prime}}{m_{33}^{\prime}} (\mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime}) \right] , \\ &\mathbf{B}_{6}^{\prime\prime} = \frac{m_{23}^{\prime}}{m_{22}^{\prime} m_{33}^{\prime}} \left[(\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{3}^{\prime}+ \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{2}^{\prime})\right. \\ &\left.\quad \quad- \frac{m_{23}^{\prime}}{m_{22}^{\prime}} (\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime}) - \frac{m_{23}^{\prime}}{m_{33}^{\prime}} (\mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime}) \right] . \end{aligned} $$

(102)