Inception of Material Instabilities in Arteries

Abstract

We propose a theoretical approach to predict the onset of cracks in arterial wall. The arterial wall is a soft composite made up of hydrated ground matrix of proteoglycans reinforced by elastin and collagen fibers spatially dispersed in the matrix. Like any other material, the arterial tissue cannot store and dissipate strain energy above a certain threshold. This threshold value is introduced in the constitutive theory via energy limiters. The limiters naturally constrain reachable stresses and enable analysis of mathematical condition of strong ellipticity. Loss of the strong ellipticity corresponds to the juncture when superimposed waves cease to propagate due to localization of material failure into cracks perpendicular to a possible wave direction. Thus, the direction in which crack starts to appear can be analyzed in addition to its inception. We enrich the recently developed constitutive theories that account for fiber dispersion of the arterial wall by including 8 and 16 structure tensors with energy limiters. We analyze the loss of strong ellipticity in uniaxial tension in circumferential and axial directions of the arterial wall. We find that cracks appear in the direction perpendicular to tension, when the speed of the superimposed longitudinal wave vanishes. We also find that the appearance of cracks is predicted in the direction inclined (non-perpendicular) to tension, when the speed of the superimposed transverse wave vanishes.

1 Introduction

In this paper, we describe a procedure to find the inception of material instabilities in arterial tissue. This requires developing constitutive models of arteries capable of failure description and examining the mathematical condition of strong ellipticity of the model for the given deformation.

Constitutive models of the arterial wall have a great wealth of literature. Experiments [1] showed anisotropic and heterogeneous characteristics of arteries. Fung with collaborators introduced nonlinear elasticity models [2, 3] to capture the large deformation response at low stresses. In these models the characteristic material directions were along the radial, circumferential and axial directions of artery. Numerous Fung-type phenomenological theories were proposed since then [4,5,6]. Subsequently, frame-invariant forms of these models were developed by introducing the structure tensors [7,8,9]. Furthermore, the anisotropy was accounted for by introducing the angular dispersion of collagen fibers in the strain energy density to develop more physically appealing structural models [10,11,12,13,14]. These models with analytically defined angular fiber dispersion needed angular integration on a unit sphere that was computationally intensive. The approach of generalized structure tensors (GST), which included fiber dispersion in structure tensor instead of strain energy density, was introduced to reduce the computational cost [15, 16]. Inability to easily exclude the compressed fibers was the major drawback of the GST approach although it was computationally attractive. An alternative approach that allowed for an easy exclusion of compressed fibers, without forgoing the advantages of the fiber dispersion models, was developed recently in [17]. This latter approach used 16 and 8 specially chosen structure tensors to describe the fiber dispersion.

A systematic method capable of describing material failure, which was based on the introduction of the energy limiters in the strain energy functions, was proposed in [18,19,20]. The violation of the strong ellipticity condition can be readily examined using this approach [21].

We enhance these recently developed constitutive theories of the arterial wall including 8 and 16 structure tensors fiber dispersion models [17] with energy limiters. We analyze the loss of strong ellipticity in uniaxial tension in circumferential and axial directions of the arterial wall. We find that the imposition of the incompressibility constraint can have a significant effect on the crack direction.

2 Constitutive Theory

We assume that the arterial wall exhibits hyperelastic response. Arterial wall is made of collagen fibers dispersed in isotropic ground matrix. The strain energy function W of the intact artery wall involves two terms

$$\begin{aligned} W=g+f, \end{aligned}$$

(1)

where

$$\begin{aligned} g=\frac{c}{2}(I_{3}^{-1/3}I_{1}-3)+K(I_{3}^{1/2}-1)^{2}, \end{aligned}$$

(2)

is the neo-Hookean strain energy for the isotropic ground matrix, where c and K are the shear and bulk modulus respectively and $I_{1}$ and $I_{3}$ are the first ad third strain invariants. In the limit of incompressibility, $I_{3}=1$ is imposed in (2).

The total energy of dispersed fibers integrated on a unit sphere is

$$\begin{aligned} f=\int \rho wd\varXi =\sum \limits _{i}\gamma ^{(i)}w^{(i)}, \end{aligned}$$

(3)

where the cubature formula for numerical integration appears on the right hand side.

Here, $\gamma ^{(i)}$ is the weight coefficient, $\varXi$ is a solid angle; $\rho$ is the angular density of the fiber distribution (see [17, 22, 23]), which is normalized as $\int \rho d\varXi =4\pi$; w is the strain energy of single fiber per unit reference volume [7] and

$$\begin{aligned} w^{(i)}=\frac{k_{1}}{2k_{2}}(\exp [k_{2}\left\langle I_{4}^{(i)}-1\right\rangle ^{2}]-1), \end{aligned}$$

(4)

where $k_{1}$ and $k_{2}$ are material parameters; the strain invariant $I_{4}^{(i)}=\mathbf {C}:\mathbf {a}^{(i)}\otimes \mathbf {a}^{(i)}>1$; and triangular brackets denote Macaulay brackets to exclude the fiber response in compression, where $\left\langle x\right\rangle =0\, \forall \, x<0$ and x otherwise.

We choose a unit vector in the direction of a generic material fiber in the initial configuration as

$$\begin{aligned} \mathbf {a}^{(i)}(\varPhi ^{(i)},\varTheta ^{(i)})=\cos \varPhi ^{(i)}\sin \varTheta ^{(i)}\mathbf {e}_{1}+\sin \varPhi ^{(i)}\sin \varTheta ^{(i)}\mathbf {e}_{2}+\cos \varTheta ^{(i)}\mathbf {e}_{3}, \end{aligned}$$

(5)

where $0\,\le \varPhi \le \,2\pi$ and $0\,\le \varTheta \le \,\pi$ and integration points $(\varPhi ^{(i)},\varTheta ^{(i)})$ are taken on the unit sphere.

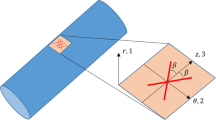
$\varPhi$ is the angle in the tangent plane measured from the circumferential direction $\mathbf {e}_{1}$ to the axial direction $\mathbf {e}_{2}$. $\varTheta$ is the angle in the normal plane measured from the radial direction $\mathbf {e}_{3}$ in this plane. $\mathbf {a}^{(i)}\otimes \mathbf {a}^{(i)}$ denote a finite number of structure tensors representing fiber dispersion that account for anisotropy.

The limited bond energy of the particles in a representative volume restricts the strain energy density on the macroscopic scale. Bounded strain energy implies that a material can not sustain stress beyond a limit which leads to material failure. Thus, we introduce a limiter in the strain energy in the following form [20], to analyse the onset of failure,

$$\begin{aligned} \psi (\mathbf {F})=\psi _{\mathrm {f}}-\psi _{\mathrm {e}}(\mathbf {F}), \end{aligned}$$

(6)

where, $\psi _{\mathrm {e}}(\mathbf {F})=\phi m^{-1}\varGamma (m^{-1},W(\mathbf {F})^{m}\phi ^{-m}),\, \, \psi _{\mathrm {f}}=\psi _{\mathrm {e}}(\mathbf {1})$, and $\varGamma (s,x)=\int _{x}^{\infty }t^{s-1}e^{-t}dt$ is the upper incomplete gamma function.

Here, $\psi _{\mathrm {f}}$ is the failure energy; $\psi _{\mathrm {e}}(\mathbf {F})$ is the elastic energy; $\mathbf {1}$ is identity tensor; $\phi$ is the energy limiter (average bond energy); and m is a material parameter. A regularized formulation as in [26, 27], for example, should be used, if the failure propagation is also of interest.

3 Strong Ellipticity Condition

Incremental equations of momenta balance and constitutive equation in the Eulerian form, where the current configuration $\varOmega$ is referential [19], can be written as follows

$$\begin{aligned} \rho \ddot{\tilde{\mathbf {y}}}=\mathrm {div}\tilde{\varvec{\sigma }},\quad \tilde{\varvec{\sigma }}+\varvec{\sigma }\tilde{\mathbf {L}}^{\mathrm {T}}=(\tilde{\varvec{\sigma }}+\varvec{\sigma }\tilde{\mathbf {L}}^{\mathrm {T}})^{\mathrm {T}}, \end{aligned}$$

(7)

and

$$\begin{aligned} \tilde{\varvec{\sigma }}=\mathbb {A}:\tilde{\mathbf {L}}+\{\varPi \tilde{\mathbf {L}}^{\mathrm {T}}-\tilde{\varPi }\mathbf {1}\},\quad \{\tilde{\mathbf {L}}:\mathbf {1}=0\}, \end{aligned}$$

(8)

where $\rho =I_{3}^{-1/2}\rho _{0}$ is the current mass density; $\varvec{\mathbf {\sigma }}=I_{3}^{-1/2}\mathbf {P}\mathbf {F}^{\mathrm {T}}$ is the Cauchy stress tensor and $(\mathrm {div}\tilde{\varvec{\sigma }})_{i}=\partial \sigma _{ij}/\partial y_{j}$; $\tilde{\varvec{\sigma }}=I_{3}^{-1/2}\tilde{\mathbf {P}}\mathbf {F}^{\mathrm {T}}$ is the incremental Cauchy stress; $\tilde{\mathbf {L}}=\tilde{\mathbf {F}}\mathbf {F}^{-1}$ is the incremental velocity gradient. Note that terms in braces $\{...\}$ should be considered for incompressible material models only.

The fourth order instantaneous elasticity tensor $\mathbb {A}$ has Cartesian components

$$\begin{aligned} A_{ijkl}=I_{3}^{-1/2}F_{js}F_{lm}\frac{\partial ^{2}\psi }{\partial F_{is}\partial F_{km}}. \end{aligned}$$

(9)

We use the strain energy defined by (6) to calculate,

$$\begin{aligned} \frac{\partial ^{2}\psi }{\partial F_{is}\partial F_{km}}=\left( \frac{\partial ^{2}W}{\partial F_{is}\partial F_{km}}-mW^{m-1}\phi ^{-m}\frac{\partial W}{\partial F_{km}}\frac{\partial W}{\partial F_{is}}\right) \exp [-W^{m}\phi ^{-m}]. \end{aligned}$$

(10)

Substitution of (10) in (9) yields

$$\begin{aligned} A_{ijkl}=I_{3}^{-1/2}F_{js}F_{lm}\left( \frac{\partial ^{2}W}{\partial F_{is}\partial F_{km}}-mW^{m-1}\phi ^{-m}\frac{\partial W}{\partial F_{km}}\frac{\partial W}{\partial F_{is}}\right) \exp [-W^{m}\phi ^{-m}]. \end{aligned}$$

(11)

We choose the following form for a plane wave solution of the incremental initial-boundary-value problem

$$\begin{aligned} \tilde{\mathbf {y}}=\mathbf {r}g(\mathbf {s}\cdot \mathbf {y}-vt),\quad \{\tilde{\varPi }=\varUpsilon g^{\prime }(\mathbf {s}\cdot \mathbf {y}-vt),\} \end{aligned}$$

(12)

where $\mathbf {r}$ and $\mathbf {s}$ are the unit vectors in the directions of wave polarization and wave propagation respectively; v is the wave speed; $g^{'}$ denotes the differential of g with respect to the argument of the function.

We get the incremental stress $\tilde{\varvec{\sigma }}$ by substituting for $\tilde{\varPi }$ and $\tilde{\mathbf {L}}=\mathrm {grad}\tilde{\mathbf {y}}=\partial \tilde{\mathbf {y}}/\partial \mathbf {y}$ from (12) to (8)$_{1}$. Then, substituting this incremental stress $\tilde{\varvec{\sigma }}$ and $\tilde{\mathbf {y}}$ from (12) into the linear momentum balance (7)$_{1}$, we get

$$\begin{aligned} \rho v^{2}\mathbf {r}=\varvec{\varLambda }(\mathbf {s})\mathbf {r}-\{\varUpsilon \mathbf {s}\}, \end{aligned}$$

(13)

where $\mathbf {\Lambda }(\mathbf {s})$ is the acoustic tensor with Cartesian components $\varLambda _{ik}=A_{ijkl}s_{j}s_{l}$.

Taking the scalar product of (13) with $\mathbf {r}$, we obtain for the wave speed

$$\begin{aligned} I_{3}^{1/2}\rho v^{2}=I_{3}^{1/2}\mathbf {r}\cdot \varvec{\varLambda }\mathbf {r}=f_{1}f_{2}, \end{aligned}$$

(14)

where

$$\begin{aligned} f_{1}= & {} f_{3}-mW^{m-1}\phi ^{-m}f_{4}^{2},\quad f_{2}=\exp [-W^{m}\phi ^{-m}],\end{aligned}$$

(15)

$$\begin{aligned} f_{3}= & {} s_{j}s_{l}r_{i}r_{k}F_{js}F_{lm}\frac{\partial ^{2}W}{\partial F_{is}\partial F_{km}},\quad f_{4}=r_{k}s_{l}F_{lm}\frac{\partial W}{\partial F_{km}}. \end{aligned}$$

(16)

The mathematical condition of the strong ellipticity of the incremental initial boundary-value-problem is violated when the wave speed becomes zero and, physically, it means material fails to propagate a wave in direction $\mathbf {s}$. The latter notion can also be interpreted as the onset of a crack perpendicular to $\mathbf {s}$.

Here, we will take into account longitudinal wave (P-wave) and transverse wave (S-wave) in the plane of the arterial sheet for calculating the condition of vanishing wave speed.

We write

$$\begin{aligned} \mathbf {s}=\mathbf {r}=\cos \alpha \mathbf {e}_{1}+\sin \alpha \mathbf {e}_{2} \end{aligned}$$

(17)

for the P-wave and

$$\begin{aligned} \mathbf {s}=\cos \alpha \mathbf {e}_{1}+\sin \alpha \mathbf {e}_{2},\quad \mathbf {r}=-\sin \alpha \mathbf {e}_{1}+\cos \alpha \mathbf {e}_{2} \end{aligned}$$

(18)

for the S-wave, where $\alpha$ is unknown angle in the tangent plane spanned by the unit tangent vectors $\mathbf {e}_{1}$ in the circumferential and $\mathbf {e}_{2}$ in axial directions of the arterial wall, respectively.

4 Specialization of Material

We use the material models that were experimentally calibrated for the intact material behavior [17]. We enhance them with a failure description by incorporating energy limiters. The model using 16 structure tensors includes out of plane fiber dispersion while the model using 8 structure tensors does not. Parameters for these models are given in Table 1. For details on integration points and weight coefficients, reader is referred to [17].

Table 1. Material constants for models with 16 and 8 structure tensors

5 Results and Discussion

In this section, we present the results of the analysis of the loss of strong ellipticity for the vanishing wave speed when the arterial wall is subjected to uniaxial tension in circumferential and axial directions.

We analyze the loss of strong ellipticity for the “stiff” displacement-controlled loading. The unknown out-of-plane principal stretch $\lambda _{3}$ is determined in terms of the known in-plane stretches $\lambda _{1}$ and $\lambda _{2}$ using the plane stress condition for a plane sheet of arterial wall. Uniaxial tension in circumferential and axial directions are described as follows: $\lambda _{2}=\lambda _{1}^{-0.5}$ and $\lambda _{1}=\lambda _{2}^{-0.5}$.

The condition of the vanishing wave speed: $I_{3}^{1/2}\rho v^{2}=f_{1}f_{2}=0$; enables us to find the critical stretches that mark the loss of strong ellipticity. We obtain the results for longitudinal P-waves and transverse S-waves in slightly compressible and incompressible (for S-waves only) material models. We found that the results for the slightly compressible and incompressible materials are numerically very close.

Figure 1 shows results of the analysis of loss of strong ellipticity for the model with 16 structure tensors presented in the previous sections:

• (a) Figure on top-left shows stretches as a function of direction (angle) of the propagating longitudinal (P-) or transverse (S-) waves. The minimal stretches indicate the loss of the strong ellipticity and the onset of cracks.

• (b) Figure on top-right shows convergence of the exponential function $f_{2}$ to zero. Theoretically, $f_{2}$ should approach zero at infinity. However, the numerical infinity occurs fast!

• (c) Bottom left shows the points on the stress-stretch curve, denoting the loss of the strong ellipticity for P- and S-waves.

• (d) Bottom right presents schematic showing the loading and possible directions of the onset of cracks predicted by P- and S-waves.

Fig. 1.

Uniaxial tension in circumferential direction (the model with 16 structure tensors): (a) stretch $\lambda _{1}$ versus the orientation of the superimposed wave for $f_{1}=0$ and $f_{2}=0$; (b) convergence of the exponential function $f_{2}(\lambda _{1})$ to zero; (c) Cauchy stress [kPa] versus stretch; (d) crack directions

The main findings can be summarized as follows:

• 1. The condition of the vanishing P-wave speed predicts the direction of cracks, perpendicular to tension in uniaxial tension. It should be noted that the incompressibility constraint suppresses this prediction. This constraint eliminates the possibility of consideration of the longitudinal wave and cracks associated with it. The incompressibility constraint acts as a Trojan Horse for the study of the onset of cracks. Results akin to these have been reported in [24] for purely isotropic soft material.

• 2. The condition of the vanishing S-wave speed predicts the direction of cracks, inclined (non-perpendicular) to tension in uniaxial tension. Such cracks seem unreasonable at first. However, in the recent experimental work [25], peculiar form of cracks in the direction of tension in a silicone elastomer were observed. The authors of the work associated these “sideways” cracks with “microstructural anisotropy (in a nominally isotropic elastomer)”.

We should note that the present approach can provide new insights in the design of experiments with cracking. Information about material anisotropy can be obtained from the character and direction of cracks - the inverse problem. However, this is outside the purview of the present work.

We emphasize that the proposed approach is suitable for the analysis of the onset of cracks only. Regularized formulations (e.g. [26, 27]), necessary for monitoring the crack development were not considered in this work.

Finally, we note that more results concerning the present study can further be found in [28].