Abstract
We consider the active learning problem for a supervised learning model: That is, after training a black box model on a given dataset, we determine which (large batch of) unlabeled candidates to label in order to improve the model further. We concentrate on the large batch case, because this is most aligned with most machine learning applications, and because it is more theoretically rich. Our approach blends three ideas: (1) We quantify model uncertainty with jackknife-like 50-per cent sub-samples (“half-samples”). (2) To select which n of C candidates to label, we consider (a rank-\((M-1)\) estimate of) the associated \(C\times C\) prediction covariance matrix, which has good properties. (3) Our algorithm works only indirectly with this covariance matrix, using a linear-in-C object. We illustrate by fitting a deep neural network to about 20 percent of the CIFAR-10 image dataset. The statistical efficiency we achieve is \(3\times\) random selection.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In part, machine learning (ML) technology has developed in response to the large data volumes of online systems, so-called big data. In parallel, physical laboratories have applied automation to scale up the range and scale of their experiments. DNA encoded libraries [28] enable in vitro selection of molecules of interest. Gregoire et al. [17] develop high-throughput experiments in order to discover new materials. Gongara et al. [16] apply such methods to additive manufacturing to optimize macroscopic structural properties. Such combinatorial experiments combine two technologies: high-throughput fabrication and high-throughput measurement.
Such high volumes of experimental data are good candidates for machine learning technology. Further, they suggest an iterative experimentation loop: fabricate, measure, model, predict, select, validate by fabrication, and measurement. Contemporary deep neural network (DNN) technology is readily useful for the modeling and prediction steps. Active learning—ML algorithms that can actively query for additional observations—has potential for the selection and validation steps. And high-throughput fabrication implies that any proposed new data (“selection”) are likely to be fabricated and measured in batches of substantial size.
This work considers active learning for such high-throughput experiments. We abstract two key properties: batches and continuous measurements. As we do so, we implicitly explore the boundary between the statistical theory of experimental design and a relatively contemporary ML technology, deep neural networks (DNNs). To this end, as we attend to notions of statistical efficiency, we consider primarily objects in the prediction—not parameter—domain.
Our key contributions revolve around three interconnected ideas: (1) We represent prediction uncertainty by a jackknife-like method called here half-sampling. Even in the canonical case where we predict a scalar, this representation of uncertainty is multivariate. (2) In a principled way, we construct batches of new candidates for labeling. This update-without-label property exploits the multivariate representation of uncertainty. Unlike other batch active learning algorithms, which require something ad hoc in order to achieve diverse samples, our algorithm, with its multivariate representation of uncertainty, intrinsically ensures diversity. (3) We quantify the benefit of active learning by comparing sample sizes required to achieve the same global precision; this is a computational version of relative statistical efficiency. Each of these ideas has roots in statistical theory.
By way of introduction, we briefly recap some linear model theory, optimal experimental design, and active learning. In Sect. 2, we discuss model ensembles. This motivates Sect. 3, where we introduce a jackknife-like approach to model uncertainty, interesting in its own right. To quantify the benefit of using model uncertainty, we develop an active learning algorithm in Sects. 4 and 5.
As our exposition proceeds, we are aware of two audiences. For statistics researchers, please note that two of our efficiency claims, in Sects. 3.5 and 6, are based on simulations. These are perhaps amenable to theoretical analysis, so we anticipate that this work may attract further research on this important topic from the statistical community. For ML researchers and practitioners, we have included a little more statistical background than might otherwise be expected, and for this audience, we have endeavored to make our statistical arguments more accessible, if perhaps less formal.
1.1 Supervised Training
We have a training dataset S consisting of N i.i.d. data points, \(S= \lbrace ({{\varvec{x}}}_i,y_i): i=1,2,\ldots ,N\rbrace ,\) where \({{\varvec{x}}}_i\in {\mathbb {R}}^D\) are D-dimensional features. For classification, \(y_i\) denotes one of K classes, \(y_i \in \lbrace 1,2,\ldots ,K\rbrace\). For regression, \(y_i \in {\mathbb {R}}\).
Our development and algorithm emphasize regression; our example (Sect. 6) involves classification.
A note on index notation: Observed, that is, labeled data \(({{\varvec{x}}}_i,y_i)\) are typically indexed by the letters h and i. Candidates for labeling are known by their features \({{\varvec{x}}}_a\) and are typically indexed by the letters a, b, and c. Subsets of data are denoted by S, with subscripts j, m, and \(m^\prime\). We are not aware of any statement in the following that depends on these details of notation, but hope this i-vs-a-vs-j convention may assist the reader in inferring the author’s implied context. At any rate, in this paper, AL algorithms propose a batch \(\lbrace {{\varvec{x}}}_a, a \in S_{\mathcal {C}}\rbrace\), \(\#S_{{\mathcal {C}}}=n\), for which the labels \(\lbrace y_a, a \in S_{\mathcal {C}}\rbrace\) are then requested.
1.2 Experimental Design Theory
1.2.1 Linear Models and Experimental Design
Consider the regression problem and linear models: \({\mathbb {E}}\lbrace y_i\rbrace = {{\varvec{x}}}_i^\top {\varvec{\beta }}\), its matrix form \({\mathbb {E}}\lbrace {{\varvec{y}}} \rbrace = {{\varvec{X}}}{\varvec{\beta }}\), with uncorrelated errors: \({\mathbb {E}}\lbrace (y_h-{{\varvec{x}}}_h^\top {\varvec{\beta }})(y_i-{{\varvec{x}}}_i^\top {\varvec{\beta }}) \rbrace =\sigma ^2\delta _{hi}\) where \(\delta _{hi}\) is Kronecker’s delta. The ordinary least squares estimate of \({\varvec{\beta }}\) is \(\hat{{\varvec{\beta }}}=({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}{{\varvec{X}}}^\top {{\varvec{y}}}\), with covariance matrix \(\mathbb {COV}\lbrace \hat{{\varvec{\beta }}} \rbrace = \sigma ^2 ({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}\).
Experimental design is based on such linear models. The theory underlying, say, Box and Hunter [2, 3] and Hunter [4] is that of orthogonal arrays, arrays such that \({{\varvec{X}}}^\top {{\varvec{X}}}\) are diagonal, and for which all of the diagonal elements of \(({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}\) are in some sense small.
The algorithm-oriented branch of experimental design theory, optimal design, emphasizes the computational problem of making good design matrices \({{\varvec{X}}}\). Optimal design can proceed in settings where orthogonal arrays are unavailable.
Optimal experimental design needs to map the design or feature matrix \({{\varvec{X}}}\) into a scalar, to enable the scoring, ranking, and selection of better designs. Consider the error ellipse defined by this equation in \({\varvec{\beta }}:\) \((\hat{{\varvec{\beta }}}-{\varvec{\beta }})^\top ({{\varvec{X}}}^\top {{\varvec{X}}})^{-1} (\hat{{\varvec{\beta }}}-{\varvec{\beta }})=\texttt {constant}\). Its (squared) volume is proportional to \(\texttt {det}(({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}),\) which is Wald’s (1943) D-optimality criterion and is to be minimized.
In the prediction domain, \(y_a\) is predicted as \({{\varvec{x}}}_a^\top \hat{{\varvec{\beta }}}\) with a squared standard error of \(\sigma ^2 {{\varvec{x}}}_a^\top ({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}{{\varvec{x}}}_a\), and \(\mathbb {COV}\lbrace {{\varvec{x}}}_a^\top \hat{{\varvec{\beta }}},{{\varvec{x}}}_b^\top \hat{{\varvec{\beta }}}\rbrace =\sigma ^2 {{\varvec{x}}}_a^\top ({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}{{\varvec{x}}}_b\) follows easily.
G-optimality [22] also acts in the prediction domain; it seeks to minimize \(\texttt {max} \texttt {diag}({{\varvec{X}}}({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}{{\varvec{X}}})\), while I-optimality [40] minimizes the average prediction error. A numerical calculation of I-optimality involves minimizing this criterion:
the summation over some integration grid \(\lbrace {{{\varvec{x}}}_a, a \in S_{\mathcal {G}}} \rbrace\) with \(\#S_{\mathcal {G}}\) elements.
The more standard implementation of I-optimality minimizes instead this criterion, which is free of the numerically enumerated integration grid \(S_{\mathcal {G}}\).
the integration taking place over a specified experimental domain which is ultimately represented by the constant matrix \({\varvec{\Omega }}.\) In the following, we implement a version of I-optimality that depends on a numerical integration grid like \(S_{\mathcal {G}}\).
1.2.2 Rank-1 Updates
Optimal experimental design is inherently computationally intensive, and techniques that reduce computational burden are therefore quite attractive. One class of such techniques updates the inverse matrix \(({{\varvec{X}}}^\top {{\varvec{X}}})^{-1}\) rather than recalculating it from scratch. An example is the rank-1 update of Sherman-Morrison (1949): If \({{\varvec{X}}}_1 = ({{\varvec{X}}}_0^\top ,{{\varvec{x}}})^\top\), the one-more-row version of \({{\varvec{X}}}_0\), then
An analogous result updates when a row \({{\varvec{x}}}\) is deleted:
(Eq. (2) follows from (1) by replacing \({{\varvec{x}}}\) with \(\sqrt{-1}{{\varvec{x}}}\).) Equation (2) has at least a pair of uses: (a) When \({{\varvec{x}}}={{\varvec{x}}}_i\), the i-th row in \({{\varvec{X}}}_1\), then Eq. (2), or its second term, can be fashioned as a measure of influence for observation \({{\varvec{x}}}_i\). (b) There is a class of optimal design algorithms that alternately add and delete rows to matrices like \({{\varvec{X}}}_1\) and \({{\varvec{X}}}_0\). The canonical exchange algorithm is that of Fedorov [15]. Equations (1) and (2) can be applied in tandem to accelerate such algorithms.
Sherman-Morrison is the rank-1 version of Woodbury’s (1950) rank-k result. The author is not aware of Woodbury’s update being used for optimal design algorithms, but this potential remains.
In the prediction domain, of particular interest are the prediction variances and covariances of candidates. An analog to (1) can update prediction variances and covariances:
In the case where \({{\varvec{x}}}_a={{\varvec{x}}}_b={{\varvec{x}}},\) the first term, \({{\varvec{x}}}^\top ({{\varvec{X}}}_0^\top {{\varvec{X}}}_0)^{-1}{{\varvec{x}}}\), is reduced by the multiplier \(1/(1+{{\varvec{x}}}^\top ({{\varvec{X}}}_0^\top {{\varvec{X}}}_0)^{-1}{{\varvec{x}}}).\) This makes precise an often-cited intuition about experimental design: prediction variances are most reduced near where the new observations are added. Further, such updates as (3) work intrinsically to discourage the repeated selection of any particular \({{\varvec{x}}}\); once selected, prediction variances nearby to \({{\varvec{x}}}\) are reduced, so points further from \({{\varvec{x}}}\) represent relatively better opportunities for variance reduction.
If we define the covariance function \({{\varvec{V}}}_1[{{\varvec{x}}}_a,{{\varvec{x}}}_b]\) as \({{\varvec{x}}}_a^\top ({{\varvec{X}}}_1^\top {{\varvec{X}}}_1)^{-1}{{\varvec{x}}}_b\) and \({{\varvec{V}}}_0[{{\varvec{x}}}_a,{{\varvec{x}}}_b]\) as \({{\varvec{x}}}_a^\top ({{\varvec{X}}}_0^\top {{\varvec{X}}}_0)^{-1}{{\varvec{x}}}_b\), Eq. (3) can be re-expressed as
This remains a rank-1 update, involving the outer product of the column \({{\varvec{V}}}_0[\cdot ,{{\varvec{x}}}]\) with itself. Note the following is the analog to (2):
The utility of updates (4) and (5) derive from four properties: (1) They operate in the prediction domain, making them more suitable for deep neural network applications. (2) They do not require the label y associated with new observation \({{\varvec{x}}}\). This update-before-label property helps us select batches of new observations. (3) \({{\varvec{V}}}_0\) and \({{\varvec{V}}}_1\) can be used to quantify useful design criteria, e.g., G-optimality minimizes quantities like \(\texttt {max}(\texttt {diag}({{\varvec{V}}}_1))\), while I-optimality minimizes objective functions of the form \(\texttt {trace}({{\varvec{V}}}_1).\) (4) These updates work intrinsically to ensure diversity among selected candidates.
We pause to recognize two open issues. (a) \({{\varvec{V}}}\) is a \(C\times C\) matrix. When the number of candidates C to label is not small, \({{\varvec{V}}}\) does not appear scalable. This we address in Sect. 5, algorithm 2. (b) We have not specified how to calculate the initial value of \({{\varvec{V}}}\). This we address in Sect. 4, which in turn depends importantly on Sect. 3.
1.3 Active Learning
Active learning (AL) is the machine learning specialty that addresses the problem of which additional candidates to label for training. Settles [35] offers a still well-cited survey of this field. Lewis and Gale [26] describe the classic sequential algorithm, and Seung et al. [36] present what has come to be called the query-by-committee algorithm. Cohn et al [10] implement AL for statistical models, while Schohn and Cohn [34], Tong and Koller [42], and Tong and Chang [41] interweave AL with support vector machines.
For batch labeling problems, Brinker [5] and Xu et al. [48] build on Tong and Koller [42] by explicitly incorporating a diversity measure; Brinker uses a minimax correlation, Xu et al a Kullback-Liebler density distance. Working within the framework of logistic regression, Hoi et al [20] consider the parameters’ Hessian matrix. Guo and Schuurmans [18] propose the entropy of any proposed batch, working around the problem of not knowing labels by an “optimistic” heuristic. Zhou and Sun [49] extend margin sampling to the batch case; their approach (manifold-preserving graph reduction, MPGR) uses the distances between feature vectors of nearest-neighbor observations.
In the context of language models, Hartford et al. [19] adapt AL algorithms to increase observations of rare categories. Oversampling of rare cases is relatively robust to diversity issues. Hu et al. [21] consider small-batch active learning on graph neural networks, and in particular on the problem of transferring or borrowing knowledge from labeled graphs to unlabeled ones. They seek to label the candidates with maximum entropy—most uncertainty—in their predicted labels.
2 Ensembles
Given input features \({{\varvec{x}}}\), let us consider DNN predictions of y given \({{\varvec{x}}}\) from a model \(f({{\varvec{x}}}),\) say. In particular, we are interested in an ensemble of such neural network models, indexed by m: \(\lbrace f_m(\cdot ): m=1,2,\ldots ,M\rbrace\).
Ensembles are sets of predictive models. Their predictions are typically averaged together to achieve better results than that of any single ensemble member. DNNs can be sensitive to the starting point of its internal coefficients (its “weights”); ensembling several such models mitigates this sensitivity. Ensembles are naturally trained in parallel, which makes them quite amenable to cloud-based approaches to model fitting. For online applications, the extra computations that ensembles involve make them rather unattractive; in the present context, supporting experiments performed in physical laboratories, the extra computation of ensembles is much less of an issue. Research continues to reduce ensemble computation; see Wenzel et al. [46] and Singh and Jaggi (2020) and references therein.
Cross-validation, e.g., Allen [1] and Stone [39], is one popular approach to ensemble making: A training set is partitioned into M mutually exclusive folds, and model m is trained on the \(M-1\) folds \(\lbrace 1,2,...,M\rbrace \setminus \lbrace m \rbrace\), resulting in M different models. Cross-validation solves a particular problem, quantifying the effect of fitting and over-fitting by comparing predictions to out-of-sample labels. For this reason, cross-validation-based ensembles are rather popular in practice.
Breiman (1996) offers an alternative form of ensemble making, bagging, whereby each model is fit to a with-replacement (bootstrap) sample of training data. Breiman observes that bagging helps most with unstable models, of which DNNs are an example.
Perrone and Cooper (1992) recognize that for neural networks, ensembles work better (a) when each individual ensemble member predicts well, and (b) when the ensemble members correlate less with one another. The latter has come to be called ensemble diversity.
Considerable research goes into increasing ensemble diversity. In addition to manipulating training data just alluded to, Dietterich [12] enumerates Bayesian voting [31], feature subsets [7], bit-vector encoding target classes [13], and randomized initial values [23].
Building on Liu’s (1998) negative correlation learning, Brown et al. [6] propose a term penalizing the systematic agreement of the predictions of different ensemble members. Mariet et al. [29] propose an analogous term to inhibit the correlation among a DNN’s internal coefficients (the so-called weights).
Lakshminarayanan, et al. (2017) combine neural network ensembles with adversarial training to fit a two-output model, one that predicts the prediction mean function and prediction variance functions, jointly.
By data structure, ensembles would seem to be useful for estimating a prediction’s uncertainty. Section 2.1 shows this limitations of this idea, while Sect. 3 constructs a new class of ensembles to estimate uncertainty better.
2.1 Minimum Variance Ensemble Weights
Perrone and Cooper (1992) calculate variance-minimizing weights on ensemble members, which we briefly recap and slightly expand.
Consider an ensemble of M models, each of which predicts the same quantity, i.e., has the same estimand. Let us postulate an \(M\times M\) matrix \({{\varvec{U}}}\) of the covariances of the predictions among the M ensemble members. We want weights \({{\varvec{w}}}\), which sum to one, and minimize the variance of the combined predictions:
This yields the solution \({\textit{w}}^{*}= {{\varvec{U}}}^{-1}{{\varvec{1}}}/{{\varvec{1}}}^\top {{\varvec{U}}}^{-1}{{\varvec{1}}}.\)
When \({{\varvec{U}}}'\) is diagonal, \({{\varvec{w}}}^*\) is proportional to the reciprocals of \({{\varvec{U}}}\)’s diagonal elements; this recapitulates a well known rule of thumb.
Of course, ensembles constructed by symmetric processes such as bootstrapping and cross-validation do not to benefit from calculating optimal weights, since such symmetry implies equal weights. In particular, if \({{\varvec{U}}}_{ij}=\) constant for all \(i\ne j\), then the off-diagonal elements of \({{\varvec{U}}}_{ij}^{-1}\) also equal a constant. That fact, and that the diagonal elements are also constant, together imply the row sums \({{\varvec{U}}}^{-1}{{\varvec{1}}}\) are constant too.
Note, however, that \({{\varvec{w}}}^*\) sets a lower limit on the variance achievable from reweighting the ensemble with covariance \({{\varvec{U}}}\): \(1/{{\varvec{1}}}^\top {{\varvec{U}}}^{-1}{{\varvec{1}}}\), one that is quite informative:
A symmetric ensemble’s covariance matrix is proportional to its correlation matrix \({{\varvec{U}}}_{\rho }=(1-\rho ){{\varvec{I}}}+\rho {\varvec{11}}^\top\), where \(\rho\) is the (constant) correlation between any pair of ensemble members \(m, m^\prime .\) In this case, its inverse is also symmetric: \({{\varvec{U}}}_{\rho }^{-1}=({{\varvec{I}}}-a{\varvec{11}}^\top )/(1-\rho ),\) where \(a=\rho /(\rho M+1-\rho ).\) This implies that \({{\varvec{1}}}^\top {{\varvec{U}}}_{\rho }^{-1}{{\varvec{1}}}=M/(\rho M+1-\rho ),\) so it follows that the lower bound on the ensemble variance is
As \(M \rightarrow \infty\), the lower bound approaches \(\rho ,\) not 0, so this relationship limits the practical benefits of reducing variance by increasing ensemble size.
2.2 Prediction Correlations for Cross-Validation and Bagging
Consider M i.i.d. folds fully and equally partitioning the training data. Suppose the estimand is the population average, \(\mu\), estimated by the overall average \(\bar{y}=\sum _{m=1}^M \bar{y}_m /M\), the average over all M folds. Consider two cross-validation samples, \(\bar{y}_{(m)}\) and \(\bar{y}_{(m^\prime )}\), each based on folds \(\lbrace 1,2,\ldots ,M \rbrace \setminus m\) and \(\lbrace 1,2,\ldots ,M \rbrace \setminus m^\prime\), respectively. Then \(\mathbb {COR}(\bar{y}_{(m)},\bar{y}_{(m^\prime )}) = (M-2)/(M-1),\) for \(m \ne m^\prime\). This correlation generalizes to model families amenable to convex optimization, that converge to unique solutions, that is, the stable models in the sense of Breiman (1996). (Section 3.4.2 also offers an analysis in the framework of stable models.)
A simple approximation allows us to estimate the correlation between two bootstrap samples. For observations \(i=1,2,\ldots , N\), define two \(N-\)vectors of weights as i.i.d. draws from the Poisson distribution with mean rate \(\lambda ; \lambda =1\) is the standard bootstrap, \({{\varvec{w}}}_{1}\) and \({{\varvec{w}}}_{2}\), respectively.
So for the standard bootstrap with \(\lambda =1,\) this correlation is 0.5. The \(2\times\) bootstrap, which uses bootstrap samples of size 2N and \(\lambda =2\), the inter-ensemble correlation grows to 2/3. Again, this correlation generalizes to model families amenable to convex optimization, i.e., stable models.
Using the value of 0.5, one can observe that an ensemble size of \(M=10\) achieves a variance only 10 percent higher than the lower bound in (6); this reproduces a rule of thumb that Breiman (1996) observed empirically: “[M]ost of the improvement us[es] only 10 bootstrap replicates. More that 25 bootstrap replicates is love’s labor lost.”
2.3 Zero-Correlation Ensembles?
Given the lower bound in (6) of \(\rho ,\) can ensembles be formed with correlations of \(\rho =0\)? Were that achieved, then the squared standard errors gained by ensembles becomes proportional to 1/M, the more ensembles the better.
Note that there are two effects here: For an ensemble member m using weights \({{\varvec{w}}}_m\) on observations in S to estimate the prediction function \(f_m(\cdot )\), then
And,
(8) quantifies the efficiency of ensemble member m—proportional to the amount of data, while (9) quantifies ensemble diversity.
So, of course, one can achieve zero correlations, trivially, by defining ensembles that have no observations in common. But (8) tells us how such a practice would be highly inefficient.
However, when the weights \({{\varvec{w}}}_m \in \lbrace -1,+1 \rbrace ,\) rather than \(\lbrace 0, +1 \rbrace ,\) (8) can be minimized and in (9) zero correlations achieved. Such weights are available from two-level orthogonal arrays.
Orthogonal arrays (OAs) are matrices with a finite set of symbols; two-level orthogonal arrays consist of two symbols, \(\lbrace 0, 1\rbrace\) or \(\lbrace -1, 1\rbrace ,\) say. The defining property of an orthogonal array is that for any pair of columns, \(m, m^\prime\), all combinations of symbol pairs occur with equal frequency. For an M-row two-level orthogonal array \({{\varvec{Z}}}\) encoded with \(\pm 1,\) orthogonality implies that \({{\varvec{Z}}}^\top {{\varvec{Z}}}=M{{\varvec{I}}}\).
OA(M) signifies an orthogonal array of M rows; two-level OAs have \(M-1\) columns. In this paper, we use only two-leval OAs with \(M=2^k, k=4, 5, 6,\) and 7. Plackett and Burman (1946) construct many two-level OAs for integer multiples of 4. Under the term “fractional factorial designs,” OAs are typically the concluding topic in an undergraduate class in experimental design for engineers (Box, Hunter, and Hunter [4]; Montgomery [30]).
Obviously, applying \({{\varvec{w}}}_m \in \lbrace -1,+1 \rbrace\) requires some interpretation. This is the topic of Sect. 3, to which we now turn.
3 Half-Samples
3.1 Signed Weights and Half-Samples
We interpret the signed weights \({{\varvec{w}}}_m\) of Sect. 2.3 as follows:
We denote our training data by S, where \(S=\lbrace ({{\varvec{x}}}_i,y_i), i=1,2,...,N \rbrace\) is comprised of i.i.d observations.
Let us denote a model trained on a dataset \(S_j \subseteq S\) by \(f(\cdot | S_j)\).
Consider a given signed weight N-vector \({{\varvec{w}}},\) and assume the sign of \({{\varvec{w}}}[i]\) assigned at random.
Denote two half-samples \(S_+=\lbrace i \in S: {{\varvec{w}}}[i]=+1 \rbrace\) and \(S_-=\lbrace i \in S\rbrace : {{\varvec{w}}}[i]=-1 \rbrace\) for some signed weight vector \({{\varvec{w}}}\). By construction, \(S_+ \cap S_- = \emptyset\) and \(S_+ \cup S_- = S\). Without much loss of much generality, we assume both \(S_+\) and \(S_-\) have N/2 observations, i.e., \(\#S_+=\#S_-=N/2\).
Consider the predictions based on models \(f(\cdot |S_+)\) and \(f(\cdot |S_-)\), and in particular consider their half-difference \(d({{\varvec{x}}}) \equiv (f({{\varvec{x}}}|S_+)-f({{\varvec{x}}}|S_-))/2.\) Because the observations of S are i.i.d. and \(S_+\) and \(S_-\) are mutually exclusive, \(\mathbb {COR}\lbrace f({{\varvec{x}}}|S_+),f({{\varvec{x}}}|S_+)\rbrace\) = 0. By the symmetry in constructing \(S_+\) and \(S_-\), which are both random half-samples of \(S, \mathbb {VAR}\lbrace f({{\varvec{x}}}|S_+)\rbrace = \mathbb {VAR}\lbrace f({{\varvec{x}}}|S_+)\rbrace\). Therefore,
The argument for equating the terms \(\mathbb {VAR}\lbrace f({{\varvec{x}}}|S_+)\rbrace\) and \(\mathbb {VAR}\lbrace f({{\varvec{x}}}|S_-)\rbrace\) to \(\mathbb {VAR}\lbrace f({{\varvec{x}}}|S)\rbrace\) has three steps: (1) asserts a square-root-N rule:
(2) recalls that \(\#S_+=\#S_-=\#S/2\), and (3) divides both sides by \(N=\#S.\)
In the following, \(d({{\varvec{x}}})^2\) is treated as an estimate of \(\mathbb {VAR}\lbrace f({{\varvec{x}}}|S)\rbrace\)—with one degree of freedom.
3.2 File Shards
In what follows, we break the training set S into mutually exclusive, exhaustive, equally sized, i.i.d. partitions called shards. Our resampling scheme is in terms of these shards.
When implemented in a computer file system, large datasets often consist of multiple physical files, shards. A computationally convenient interpretation of half-sampling is that each half-sample uses half the shards. A recognizably natural practice is for the number of shards to be \(M=2^k\) for some integer k; \(k=5\) to 12 give shard counts ranging from 32 to 4096. Using a two-level OA ensures that each shard is used in exactly half the samples \(S_j\).
For each observation \(i\in S\), it is convenient to assign it to a single shard (i), where \(\texttt{shard:} \lbrace \textrm{1, 2, }\ldots , \textit{N}\rbrace \rightarrow \lbrace \textrm{0, 1, }\ldots , M-1 \rbrace .\) Any given half-sample is defined by a set H, where \(S_H=\lbrace i:\texttt{shard}(\textit{i})\in \textit{H} \rbrace\), where \(H \subset \lbrace 0,1,\ldots ,M-1 \rbrace\) and \(\#H=M/2,\) exactly half the shards. For observations in approximately random order, a common sharding function is \(\texttt {shard}(\textit{i})=(\textit{i}{-1}) \textrm{ mod } \textit{M}\), which assigns observations to shards as most card games deal out cards into players’ hands.
3.3 Half-Sampling and the Jackknife
Half-sampling is a particular form of the jackknife of Quenouille [33] and Tukey [43]. In our use, half-samples (a) are not exhaustive of all possible half-samples and (b) are guided by an orthogonal array. For these—arguably second-order—distinctions, we find it appropriate to designate this jackknife-like scheme by its own term, hence half-sampling. Half-sampling is random to the extent that the initial assignment of observations \((y_i,{{\varvec{x}}}_i)\) to shards can be considered random.
Half-samples have a minor, if intriguing, property. The variance among random half-samples is an unbiased estimate of the variance of estimates based on the whole sample.
As above, denote all available observations by S, which has N observations and denote the j-th half-sample by \(S_j\), which has \(N_j=N/2\) observations. Denote the estimand by \(\tau ={\mathbb {E}}\lbrace T(S) \rbrace ={\mathbb {E}}\lbrace T(S_j) \rbrace\). Of primary interest is \(\mathbb {VAR}(T(S)) = {\mathbb {E}}\lbrace (T(S)-\tau )^2 \rbrace\). Of course, this cannot be calculated directly because \(\tau\) is unknown. However,
When \(N_j=N/2\), then \({\mathbb {E}}\lbrace (T(S_j)-\tau )^2 \rbrace = 2\times {\mathbb {E}}\lbrace (T(S)-\tau )^2 \rbrace\), so
Note that the right hand side of (11) is estimable, and of course, it estimates \({\mathbb {E}}\lbrace (T(S)-\tau )^2 \rbrace\), exactly the squared standard error we want to estimate. This derivation has a geometric version, presented in Fig. 1a.
Many ML practitioners find \(N_j > N/2\) of special interest, and, indeed, this case is the more traditional use of the jackknife. Consider a random subset \(S_j \subset S\), consisting of \(\#S_j=N_j < N\) observations. \(N_j\) now is not necessarily equal to N/2 :
As before, \({\mathbb {E}}\lbrace (T(S_j)-\tau )^2 \rbrace = {\mathbb {E}}\lbrace (T(S_j)-T(S))^2 \rbrace + {\mathbb {E}}\lbrace (T(S)-\tau )^2 \rbrace\). Now, \({\mathbb {E}}\lbrace (T(S_j)-\tau )^2 \rbrace = (N/N_j) {\mathbb {E}}\lbrace (T(S)-\tau )^2 \rbrace\), so
The geometric argument for this calculation is presented in Fig. 1(b).
In our applications below, we consistently use half-sampling, so \(N_j=N/2\) uniformly.
3.4 Orthogonal Arrays and Half-Samples
A two-level orthogonal array such as OA(M) has \(M-1\) columns. Each column j of orthogonal array \(OA,{ }j=1,2,\ldots ,M-1\) defines two half-samples: \(S_{j+}=\lbrace i: OA[\texttt {shard}(i),j]=+1 \rbrace\) and \(S_{j-}=\lbrace i: OA[\texttt {shard}(i),j]=-1 \rbrace\). These pairs of sets \((S_{j+},S_{j-})\) and especially the associated models fit to them, \(f(\cdot |S_{j+}),f(\cdot |S_{j-})\) we call an ensemble pair. Indeed, as suggested in Sect. 3.1, the critical quantity for any such ensemble pair is, for a given feature vector \({{\varvec{x}}}\), their half-difference, \(d({{\varvec{x}}}|j)=(f({{\varvec{x}}}|S_{j+})-f({{\varvec{x}}}|S_{j-}))/2\).
The orthogonality property ensures that these \(M-1\) columns have approximately zero correlation, that is, for \(j\ne k\), \({\mathbb {E}}\lbrace d({{\varvec{x}}}|j),d({{\varvec{x}}}|k) \rbrace \approx 0\).
The case for zero correlation has two elements, the assertion of additive attribution and an heuristic argument in favor of additive attribution. These are the respective topics of Sects. 3.4.1 and 3.4.2, which might reasonably be by-passed on first reading.
3.4.1 Additive Attribution and Zero Correlation
Consider two pairs of half-samples, \((S_{j+},S_{j-})\) and \((S_{m+},S_{m-})\), \(j \ne m.\) Additive attribution means that any estimator of interest \(T(S_{j})\) can be decomposed in to a sum its shards’ contributions:
for some function L(s) of shard s. For Sect. 3.1, recall that we are interested in the half-differences \((T(S_{j+})-T(S_{j-}))/2\):
where \(\omega _j\) is the j-th column in the orthogonal array and \(\omega _j(s)=+1\) when \(s\in S_{j+}\) and \(\omega _j(s)=-1\) when \(s\in S_{j-}\).
Consider now the covariance of such differences:
The first term factors into \(\sum _{s_1 \in S} \omega _j(s_1) {\mathbb {E}}\lbrace L(s_1) \rbrace\) \(\times\) \(\sum _{s_1 \in S} \omega _j(s_1) {\mathbb {E}}\lbrace L(s_1) \rbrace\). Because the shards are randomly assigned their observations, \({\mathbb {E}}\lbrace L(s)\rbrace\) is constant. Because orthogonal arrays are balanced, \(\sum _{s\in S}\omega _j(s)=\) \(\sum _{s\in S}\omega _m(s)=0\). As a result, both factors of this first term are zero.
For the same reason, \(\mathbb {COV}\lbrace L(s_1), L(s_2)\rbrace\) is constant for \(s_1\ne s_2\), and \(\mathbb {VAR}\lbrace L(s)\rbrace\) is also constant. The second term simplifies as follows:
Because orthogonal arrays are balanced, \(\sum _s \omega _j(s)=0,\) and the C term becomes zero. By defining property of two-level orthogonal arrays, \(\sum \omega _j(s)\omega _m(s) = 0\), so the \((V-C)\) term is also zero.
3.4.2 Heuristic for Additive Attribution
In this section, we make the case for additive attribution. Our development uses linear approximations reminiscent of maximum likelihood theory, and implicitly assumes that small changes in the underlying data induce approximately linear changes.
Our heuristic assumes we can uniquely fit a model by maximizing an objective function \({\mathcal {L}}_S({\varvec{\beta }})\) with respect to parameters \({\varvec{\beta }}\). Further, we assume \({\mathcal {L}}_S(\cdot )\) is a sum over i.i.d. shards indexed by t: \({\mathcal {L}}_S({\varvec{\beta }})=\sum _t {\mathcal {L}}_t({\varvec{\beta }})\). For dataset S, define \({\varvec{\beta }}_S\) as the solution to this equation in \({\varvec{\beta }}\):
Now let us consider the dataset S without exactly one shard, \(S\setminus u\), denoted more compactly as \(-u\) with solution \({\varvec{\beta }}_{-u}\) such that \(\nabla {\mathcal {L}}_{-u}({\varvec{\beta }}_{-u})={{\varvec{0}}}\).
Because \(-u\) is only a small perturbation of S, our heuristic assumes we can approximate \({\varvec{\beta }}_{-u}\) linearly:
The second line recognizes that \({\mathcal {L}}_S={\mathcal {L}}_{-u}+{\mathcal {L}}_u\), the latter term specific to shard u. The third line notes that \({\varvec{\beta }}_{-u}\) solves the equation \(\nabla {\mathcal {L}}_{-u}({\varvec{\beta }}_{-u})={{\varvec{0}}}\). The fourth line asserts that the hessian \(\nabla {\mathcal {L}}_{S}\nabla ^\top\) evaluated at \({\varvec{\beta }}_{-u}\) can be approximated by evaluating it at \({\varvec{\beta }}_S\). The fifth line approximates the u-shard-specific gradient \(\nabla {\mathcal {L}}_u(\cdot )\) evaluated at \({\varvec{\beta }}_{-u}\) with one evaluated nearby at \({\varvec{\beta }}_{S}.\) The last line merely shifts notation from \(+\nabla {\mathcal {L}}_S({\varvec{\beta }}_{S}) \nabla ^\top\) to \(-{{\varvec{H}}}_S\).
Expressions (15) suggests this approximation:
Note that \({{\varvec{H}}}_S\) is the sum over all shards, so \({{\varvec{H}}}_S\) is rather big—at least compared to \(\nabla {\mathcal {L}}_u(\cdot ),\) which is based on only one shard. For this reason, approximation (16) approximates \({\varvec{\beta }}_{-u}\) by only a small shift from \({\varvec{\beta }}_S\).
Now consider a generic estimator T based on parameters \({\varvec{\beta }}_{-u}\). By approximation (16),
If we sum the latter expression over all shards \(u \in S\), the right hand side sums to zero, because \(\sum _{u \in S} \nabla {\mathcal {L}}_{u}({\varvec{\beta }}_S) =\nabla {\mathcal {L}}_S({\varvec{\beta }}_S)= 0,\) and the operator \(\nabla _{\beta } T({\varvec{\beta }}_S)^\top {{\varvec{H}}}_S^{-1}\) does not depend on u. This implies that \(\sum _u \big ( T({\varvec{\beta }}_{-u}) - T({\varvec{\beta }}_S) \big ) \approx 0\), and, on rearranging terms,
where M is the number of shards. Approximation (17) motivates the linear attribution of the quantity \(T({\varvec{\beta }}_S)\) to the u-shard-specific quantities
Equation (12) assumes attributions have a constant correlation. Note that for shards \(t\ne u, \mathbb {COV}\lbrace \nabla {\mathcal {L}}_{t}({\varvec{\beta }}), \nabla {\mathcal {L}}_{u}({\varvec{\beta }}) \rbrace = {{\varvec{0}}},\) while the constraint \(\sum _t \nabla {\mathcal {L}}_{t}({\varvec{\beta }}_S)=0\) implies \(\mathbb {COV}\lbrace \nabla {\mathcal {L}}_{t}({\varvec{\beta }}_S), \nabla {\mathcal {L}}_{u}({\varvec{\beta }}_S) \rbrace\) is slightly negative, corresponding to correlations of about \(-1/(M-1),\) so ever smaller as the number of shards increases.
3.4.3 Recap
Sections 3.4.1 and 3.4.2 help motivate how half-differences guided by orthogonal arrays might plausibly achieve nearly zero correlation. Their common framework assumes that the equation \(\nabla {\mathcal {L}}_S({\varvec{\beta }}) = {{\varvec{0}}}\) yields a unique \({\varvec{\beta }}\) solution. Of course, this assumption is in substantial tension with our primary application of interest, deep neural networks, which are quite sensitive to their initial \({\varvec{\beta }}\) starting point.
This same tension shapes the implementation of half-sampling for DNNs: All half-samples are given the same initial starting point, those to which the full training set S has converged. Computationally, this can be accomplished through checkpoints. Checkpoints consist of recording parameter states before an algorithm has converged. Usually recorded as insurance against computer crashes, checkpoints allow restarting a computation from an intermediate state rather than at the beginning. In our applications, we use checkpoints to reduce the sensitivity to the initial values of parameters, which are often initialized by pseudo-random values, giving them instead the parameters to which the fully trained model has converged, \({\varvec{\beta }}_S\). Half-samples thereby move away from \({\varvec{\beta }}_S\) as a result of (randomly) subsetting the underlying training data and not from the more arbitrary mechanisms of resetting the initial starting point.
To conclude, Sect. 3.1, for each j, \(d({{\varvec{x}}}|j),j=1,2,\ldots ,M-1\) gives a one degree-of-freedom estimate of \(\mathbb {VAR}\lbrace f({{\varvec{x}}}|S) \rbrace\). For this reason,
so the mean square term in the left hand side of (19) estimates the uncertainty of \(f({{\varvec{x}}}|S)\) and does so with \(M-1\) degrees of freedom. (The half-normal plots of Daniel [11] depend on similar contrasts and a similar relationship.) The result (19) gives an interesting estimate of model uncertainty in its own right. Our basic plan is to apply Eqs. (19) and (4) to achieve a batch-based active learning algorithm.
The next Sect. (3.5) is a slight detour from this effort, an attempt to quantify the benefit of implementing half-sampling by orthogonal arrays rather than by random selection.
3.5 Orthogonal Arrays and Efficiency
Intuitively, the careful balancing among shards achieved by orthogonal arrays should be somehow better than half-sampling by random selection. Here, by simulation, we assess the magnitude of this benefit by simulation. We construct orthogonal arrays of size \(m=2^k, k \in \lbrace 4,5,6,7,8 \rbrace ,\) which we assess for \(p \in \lbrace 0,1,2,4,8 \rbrace\) boolean features. The results are presented in Fig. 2. Note that the largest p considered is 8, while the smallest m is 16; this boundary is chosen to reduce the probability of random half-samples becoming fatally collinear to something manageably small and ignorable.
For 80,000 simulations, Fig. 2 plots the relative statistical efficiencies of orthogonal arrays versus random half-sampling. The quantity estimated is the average prediction variance of a linear model at the \({{\varvec{q}}}=(1,1,\ldots ,0)\)-corner, where \(\texttt {sum}({{\varvec{q}}}_i)=p.\) Figure 2 plots ratio of two prediction variances, the numerator is the median prediction variance from random halves, and the denominator is that estimated from orthogonal array-based halves. The group labeled \(p=1+0\) corresponds to an intercept and no two-level features, \(p=1+1\) to an intercept and one two-level feature, and so on. (The median prediction variance is chosen to mitigate the problem of right-tailed outliers among the random half-samples.)
Note that when p/n is small, the benefit of orthogonal arrays is small also. When p/n is larger, by eye one can see the relative efficiency become roughly \(1+p/n\). Plotted by a red “|” symbol, a curve-fitting exercise empirically suggests the relative statistical efficiency can be usefully approximated as \((n-1)/(n-1-p)=\sum _{k=0}^\infty [p/(n-1)]^k\). According to the uppermost right point pair, this appears to underestimate the relative efficiency gain for the highest p/n, where it approaches a relative efficiency of \(2\times\). Note that, in practice, DNNs often fit models in this range, with relatively high p-to-n ratios, that is, relatively high ratios of parameter count to observation count. For this reason, the gain in efficiency using orthogonal arrays would seem especially useful for a parameter-rich model.
The results reported in this section seem amenable to theoretical analysis, and we encourage further research into quantifying more precisely the benefit of using OAs for half-sampling.
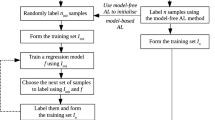
4 Considerations for Active Learning Algorithms
In this section, we describe broadly our approach to batch active learning. In Sect. 5, we become more precise in specifying our algorithm. Section 6 works out an example and calculates some relative statistical efficiencies.
Suppose we have C candidates for labeling; this is an external and prescribed data structure, known by their features \(\lbrace {{\varvec{x}}}_c, c \in {\mathcal {C}}_0\rbrace\). Values of \(C=\#{\mathcal {C}}_0 \approx 10^6\text {--}10^7\) are common enough. We want to determine which subset of size \(n, n \ll C,\) might best improve model prediction error, or best improve model prediction error and something else, a yield or other measure of economic consequence.
Our approach combines three ideas.
Idea#1 Suppose we have the \(C\times C\) prediction covariance matrix \({{\varvec{V}}}\). For any candidate c, we can update \({{\varvec{V}}}\) by Eq. (4) to \({{\varvec{V}}}_c\), say. We choose that candidate that minimizes \(\texttt {trace}({{\varvec{V}}}_c)\). As we accept (greedily) a candidate c, by Eq. (4) we update \({{\varvec{V}}}\).
Idea#2 Before any candidate selection can proceed, we need an initial estimate of \({{\varvec{V}}}, {{\varvec{V}}}_0\), say. We form the following \(C\times (M-1)\) matrix \({\varvec{\Delta }}\): \({\varvec{\Delta }}[c,j]=d({{\varvec{x}}}_c|j), j=1,2,\ldots ,M-1\). \({\varvec{\Delta }}{\varvec{\Delta }}^\top /(M-1)\) estimates \({{\varvec{V}}}\) with \(M-1\) degrees of freedom. (Note that, in spite of being motivated by Eqs. (6)–(8), this estimate \({{\varvec{V}}}_0\) involves no matrix inversion.)
Idea#3 For even moderate C, \({{\varvec{V}}}\) has on the order of \(C^2\) elements, awkwardly large. However, by idea#2, \({{\varvec{V}}}\) is of rank \(M-1,\) and we are able to select from and update \({\varvec{\Delta }}\) directly with operations on the \(C\times (M-1)\) matrix instead.
4.1 Idea#1: The Prediction Covariance Matrix
Consider two candidates \(a\ne b \in {\mathcal {C}}_0\), with feature vectors \({{\varvec{x}}}_a\) and \({{\varvec{x}}}_b\), respectively, and unobserved labels \(y_a\) and \(y_b\).
We have a model \(f(\cdot |S)\) that predicts \(f({{\varvec{x}}}_a|S)\) and \(f({{\varvec{x}}}_b|S)\), respectively. Let us suppose we can estimate \({{\varvec{V}}}[a,b]=\mathbb {COV}\lbrace f({{\varvec{x}}}_a|S), f({{\varvec{x}}}_b|S) | {{\varvec{x}}}_a, {{\varvec{x}}}_b, S \rbrace\). When \({{\varvec{x}}}_a={{\varvec{x}}}_b\), \({{\varvec{V}}}[a,b]={{\varvec{V}}}[a,a]\) and is merely the squared standard error of prediction \({\hat{y}}({{\varvec{x}}}_a)\). It is obvious, in a way approaching tautological, that \({{\varvec{V}}}[a,b] \rightarrow {{\varvec{V}}}[a,a]\) as \({{\varvec{x}}}_b \rightarrow {{\varvec{x}}}_a\). In this way, \({{\varvec{V}}}\) captures a sense in which observing \({{\varvec{x}}}_a\) might make observing \({{\varvec{x}}}_b\) unnecessary. This issue we call the problem of near duplicates: When \({{\varvec{x}}}_b \approx {{\varvec{x}}}_a\), \({{\varvec{V}}}[a,a] \approx {{\varvec{V}}}[b,b] \approx {{\varvec{V}}}[a,b]\) and \(\mathbb {COR}({\hat{y}}({{\varvec{x}}}_a),{\hat{y}}({{\varvec{x}}}_b)) \rightarrow 1\), and there is not much incremental improvement in uncertainty from observing both a and b beyond that from just observing one of a or b.
By Sherman-Morrison update in Eq. (4), we can reflect the consequence of including c as
We now make three observations regarding \({{\varvec{V}}}\):
(1) First, various optimal design criteria are functions of \({{\varvec{V}}}\). In particular, its largest diagonal element, \(\texttt {max}(\texttt {diag}({{\varvec{V}}}))\), corresponds to the G-optimal criterion. In similar vein, \(\texttt {ave}(\texttt {diag}({{\varvec{V}}}))\) gives the I-optimal criterion, \(\texttt {trace}({{\varvec{V}}})/C\).
(2) \({{\varvec{V}}}\) is a precision matrix, and if we newly observe \({{\varvec{x}}}_c\), we can again update \({{\varvec{V}}}\) by the Sherman-Morrison (1949) rank-1 update (and Eq. (4)):
The (scalar) decrement from \(\texttt {trace}({{\varvec{V}}}_k)\) is given by
This decrement has two components: (a) The scalar \({{\varvec{V}}}_k[c,c]^2/(1+{{\varvec{V}}}_k[c,c])\) is the influence of candidate c on its own prediction, classical leverage. (b) \(\sum _{d \ne c} {{\varvec{V}}}_k[d,c]^2/(1+{{\varvec{V}}}_k[c,c])\) is the influence of including candidate c upon the mean squared prediction error of all the other candidates. When (a) dominates, the I-optimal criterion prescribes labeling the most uncertain candidates (“direct observation”). When (b) dominates, the I-optimal criterion prioritizes those candidates whose predictions are more thickly correlated with many other candidates (“interpolation”).
(3) Note that this Sherman-Morrison update can be calculated without actually needing to observe \(y({{\varvec{x}}}_c)\) (“update before label”). This update-before-label property makes \({{\varvec{V}}}\) attractive for designing supplemental batches, because we can reflect the impact of including \({{\varvec{x}}}_c\) without observing its associated label/response until later.
By these three properties, \({{\varvec{V}}}\) emerges as a principled object for constructing supplemental batches.
(Of course, for batches of size 1, one can and should update models to reflect the newly observed label. We strictly limit our proposal to active learning contexts where the batch size is intrinsically bigger than 1 by the nature of the laboratory setup.)
The case against using \({{\varvec{V}}}\) is computational: as a \(C\times C\) matrix, which we mitigate by idea#3. Viswanathan et al [44] likewise manage and manipulate a \(C\times C\) precision matrix, in their case by using sparse matrix representations; their approach is a qualitatively different from that presented here.
4.2 Idea#2: Contrast Matrix \({\varvec{\Delta }}\)
For any given column of an orthogonal array, we have two half-samples, \(S_{j+}\) and \(S_{j-}\), so we fit two predictive models, \(f({{\varvec{x}}}|S_{j+})\) and \(f({{\varvec{x}}}|S_{j-})\). A natural common estimate is their average,
Further, their (signed) half-difference,
estimates in some sense the sensitivity of this estimate to perturbing data. In particular, \(|\Delta [{{\varvec{x}}},j]|\) estimates—with one degree of freedom—the standard error of \(f({{\varvec{x}}}|S) \approx\) the standard error of \((f({{\varvec{x}}}|S_{j+})+f({{\varvec{x}}}|S_{j-}))/2\).
For a typical candidate c with features \({{\varvec{x}}}_c\), we have the \(M-1\) half-sample contrasts \(\Delta [{{\varvec{x}}}_c,j], j=1,2,\ldots ,M-1\), one for each column in the orthogonal array. The \(C\times (M-1)\) matrix \({\varvec{\Delta }}\) has four properties:
-
1.
It estimates (approximately) \(\mathbb {VAR}\lbrace f({\textit{x}}|S) \rbrace\):
$$\begin{aligned} {\mathbb {E}}\left\{ \sum _j^{M-1} \Delta ^2[{{\varvec{x}}},j]/(M-1) \right\} \approx \mathbb {VAR}\lbrace f({{\varvec{x}}}|S)\rbrace .\end{aligned}$$ -
2.
As a modest extension, \({{\varvec{\Delta }}\, {\varvec{\Delta }}^\top }/(M-1)\) estimates \({{\varvec{V}}}\).
-
3.
For each j, each value \(\Delta [{{\varvec{x}}},j]\) makes use of all the data in S.
-
4.
For two different half-samples, \(j\ne k, \mathbb {COR}(\Delta [{{\varvec{x}}},j],\Delta [{{\varvec{x}}},k])\approx 0.\)
Properties 1 and 2 give us an estimate of the important prediction covariance matrix \({{\varvec{V}}}.\) Properties 3 and 4 suggest this estimate has high statistical efficiency, as is typical when using two-level orthogonal arrays.
4.3 Idea#3: Updating \({\varvec{\Delta }}\) not \({{\varvec{V}}}\)
Our initial prediction covariance matrix \({{\varvec{V}}}={\varvec{\Delta }}{\varvec{\Delta }}^\top /(M-1)\). Were we to include candidate c, the updated matrix would be \({{\varvec{V}}}_c\leftarrow {{\varvec{V}}} - {{\varvec{V}}}[,c] {{\varvec{V}}}[,c]^\top /(1+{{\varvec{V}}}[c,c])\). In this section, we work out that \((M-1)\times (M-1)\) matrix \({{\varvec{H}}}_c\) such that \({\varvec{\Delta }}_c = {\varvec{\Delta }}{{\varvec{H}}}_c\) is such that \({\varvec{\Delta }}_c {\varvec{\Delta }}_c^\top /(M-1) = {{\varvec{V}}}_c\). With such a matrix \({{\varvec{H}}}_c\) in hand, we can form algorithms that operate on \(C\times (M-1)\) matrices like \({\varvec{\Delta }}\) — linear in the number of candidates C — rather than \(C\times C\) matrices like \({{\varvec{V}}}\), which are quadratic in C.
It is convenient to shift notation: Let us define \({\varvec{\Delta }}_0 = {\varvec{\Delta }}/\sqrt{M-1}\), so now \({{\varvec{V}}}={\varvec{\Delta }}_0{\varvec{\Delta }}_0^\top\). Denote by the column vector \({\varvec{\delta }}_c\) equal the c-th row of \({\varvec{\Delta }}_0;\) formally, \({\varvec{\delta }}_c={\varvec{\Delta }}_0[c,]^\top .\) A consequence of this notation is that \({{\varvec{V}}}[c,c]={\varvec{\delta }}_c^\top {\varvec{\delta }}_c\) and \({\varvec{\Delta }}_0{\varvec{\delta }}_c = {{\varvec{V}}}[,c] = {{\varvec{V}}}[c,]^\top\).
Consider the \((M-1)\times (M-1)\) matrix \({{\varvec{H}}}_c = {{\varvec{I}}} - \lambda {\varvec{\delta }}_c {\varvec{\delta }}_c^\top\), where \(\lambda\) is to be determined below. The key property we seek is for \({\varvec{\Delta }}_0{{\varvec{H}}}_c{{\varvec{H}}}_c^\top {\varvec{\Delta }}_0^\top\) to equal \({{\varvec{V}}}-{{\varvec{V}}}[c,]{{\varvec{V}}}[c,]^\top /(1+{{\varvec{V}}}[c,c])\), and we choose \(\lambda\) to make it so.
Consider the following as an equation in the scalar \(\lambda\):
from which we can conclude this quadratic equation in the scalar \(\lambda ,\)
which yields the solutions
The matrix \({{\varvec{H}}}_c = {{\varvec{I}}}-\lambda {\varvec{\delta }}_c {\varvec{\delta }}_c^\top = {{\varvec{I}}}-(1-\sqrt{1/(1+{{\varvec{V}}}[c,c])}) {\varvec{\delta }}_c {\varvec{\delta }}_c^\top / \Vert {\varvec{\delta }}_c\Vert ^2,\) recalling that \({{\varvec{V}}}[c,c]={\varvec{\delta }}_c^\top {\varvec{\delta }}_c=\Vert {\varvec{\delta }}_c\Vert ^2\). If we compare \({{\varvec{H}}}_{c}\) to \({{\varvec{I}}}- {\varvec{\delta }}_c {\varvec{\delta }}_c^\top /\Vert {\varvec{\delta }}_c\Vert ^2\), the latter is a projection matrix with exactly one zero eigenvalue, that associated with \({\varvec{\delta }}_c/\Vert {\varvec{\delta }}_c\Vert\). In contrast, \({{\varvec{H}}}_c\) does not fully zero out the eigenvalue associated with the unit vector \({\varvec{\delta }}_c/\Vert {\varvec{\delta }}_c\Vert ,\) but \({{\varvec{H}}}_c\) does move to reduce its associated eigenvalue away from 1 and toward 0.
We close this section with one more observation. The I-optimal criterion can be defined operationally by \(\texttt {trace}\lbrace {{\varvec{V}}}-{{\varvec{V}}}[c,]{{\varvec{V}}}[c,]^\top /(1+{{\varvec{V}}}[c,c])\rbrace\) \(=\texttt {trace}\lbrace {\varvec{\Delta }}_0{{\varvec{H}}}_c {{\varvec{H}}}_c^\top {\varvec{\Delta }}_0^\top \rbrace\). With operators like \({{\varvec{H}}}_c\) available, the \(({{\varvec{H}}},{\varvec{\Delta }})\)-form of this same quantity is \(\texttt {trace}\lbrace \mathbf {{\varvec{\Delta }}_0{{\varvec{H}}}_c{{\varvec{H}}}_c^\top {\varvec{\Delta }}_0^\top }\rbrace =\) \(\texttt {trace}\lbrace \mathbf {{{\varvec{H}}}_c{{\varvec{H}}}_c^\top {\varvec{\Delta }}_0^\top {\varvec{\Delta }}_0}\rbrace\), where both \({{\varvec{H}}}_c{{\varvec{H}}}_c^\top\) and \({\varvec{\Delta }}_0^\top {\varvec{\Delta }}_0\) are \((M-1)\times (M-1)\) matrices. In this way, the \(({{\varvec{H}}},{\varvec{\Delta }})\)—representation enables us to avoid calculating \(C\times C\) objects.
5 Algorithms
Let us now assemble ideas #1, #2, and #3 into working algorithms. For clarity, we define algorithm 1, which uses ideas #1 and #2, then add in idea #3 to form algorithm 2.
For a criterion, we use that of I-optimality, which works to minimize \(\texttt {trace}\lbrace {{\varvec{V}}}\rbrace\). In principle, one could apply instead G-optimality, which minimizes \(\texttt {max}(\texttt {diag}\lbrace {{\varvec{V}}} \rbrace )\). However, G-optimality has performed too poorly empirically to include in this investigation. Further, for our applications, the boundaries of protein, molecule, and alloy space are not well defined, and G-optimality is a poor match conceptually.
The algorithms we present are greedy algorithms. This is because of the rather large number C of candidates we screen. In principle, one could implement exchange algorithms instead, alternately adding and deleting candidates, but we have not explored such an implementation yet.
Algorithm 1 assumes we can calculate and hold in memory the \(C\times C\) matrix \({{\varvec{V}}}\) in memory based on the half-sample \(C\times (M-1)\) matrix \({\varvec{\Delta }}\). It then proceeds to include one-by-one candidates (“greedily”) until the batch quota is filled.

Algorithm 2 incorporates idea #3, so maintains the \(C\times (M-1)\) matrix \({\varvec{\Delta }}\) and \((M-1)\times (M-1)\) matrix H.

Algorithm 2 makes use of an \((M-1)\times (M-1)\) matrix \({{\varvec{H}}}\): Note that one can form from new candidates another \({\varvec{\Delta }}\)-matrix, \({\varvec{\Delta }}^{(1)}\), say, and re-enter algorithm 2 by initializing \({\mathcal {C}} \leftarrow {\mathcal {C}}\), \({{\varvec{H}}} \leftarrow {{\varvec{H}}}\), and \({\varvec{\Delta }}_0 \leftarrow {\varvec{\Delta }}^{(1)} {{\varvec{H}}}/(M-1)^{1/2}\). This enables the construction of a series of supplemental batches, each of which presents its own list of candidates. Matrix \({{\varvec{H}}}\) therefore records the variance-reducing effect of including the previously selected candidates \({\mathcal {C}}\).
6 Example
For DNNs, it may be fairly said that the ideas#1 and #2 that underlie algorithms 1 and 2 are mere heuristics, extrapolated from a linear context to a nonlinear one. In this section, we work out an example using a particular neural network, and see what can be achieved in practice.
For an example, we consider the CIFAR-10 dataset [24], which consists of \(32\times 32\) pixel color images. Our model follows the vignette of Chollet, et al [9] for convolutional neural networks and this data: four 2-dimensional convolutional layers and two subsequent layers. The ground truths for the image labels are represented by 10-tuples of mutually exclusive booleans coded in alphabetic order: The category airplane is represented by (1, 0, 0, 0, 0, 0, 0, 0, 0, 0), the category truck by (0, 0, 0, 0, 0, 0, 0, 0, 0, 1), and so on.
For training, we use the first \(12,288(=96 \times 128)\) images, and for candidates the second 12,288 images of the 50,000-image training set. For a test set, we use the standard 10, 000 CIFAR-10 test set.
By the considerations of appendix A, we use the orthogonal arrays OA(128), OA(64), OA(32), and OA(16), corresponding to \(b=3, 2.5, 2\), and 1.5 bits relative precision, respectively. Following Chollet (2017), we fit an initial keras model using 64 iterations (“UpdateEpochs=64”) using all 128 shards; this model \(f(\cdot |S)\) defines the warm start for all subsequent half-sample models \(f(\cdot |S_{j+})\) and \(f(\cdot |S_{j-}), j=1,2,...,127\). Each half-sample model is fit with an 24 additional iterations ((“UpdateEpochs=24”)). The result is for each of the 12,288 candidates, the 127 contrasts for each of the 10 categories, that is, \(10\; {\varvec{\Delta }}\) matrices. Using algorithm 2, we identify \(C=768\) without-replacement samples, maintaining records for each of the \(10\; {\varvec{\Delta }}\) and \({{\varvec{H}}}\) matrices, one pair for each of the CIFAR-10 classes.
For OA(16), OA(32), and OA(64), algorithm 2 takes, respectively, 9, 19, and 48 seconds, respectively, per sample. For OA(128), algorithm 2 takes 7 minutes per sample.
For comparison, we compute two reference models, updating with no new data and with all \(C=12,288\) candidates, both using 24 iterations (“Update Epochs=24”). In addition, we take 512 random without-replacement samples of sizes \(768, 2\times 768=1536,\) and \(3\times 768=2304\), additional cases, respectively. These latter are essentially simulations of 512 different random case selections. Each random \(2\times\) sample extends a \(1\times\) sample, likewise each \(3\times\) sample extends a \(2\times\) sample.
We evaluate average prediction variance on the 10, 000 images in the CIFAR-10 test data. Of course, random selection of candidates imposes random distributions on any resulting prediction variance on the test data. Figure 3 presents the cumulative distribution functions (and averages) of the prediction variances for random selections of \(n=768, n=1536,\) and \(n=2304,\) \(1\times , 2\times ,\) and \(3\times ,\), respectively. 87 percent of the time, algorithm 2 using OA(64) outperforms a similar amount of random data (labeled “random \(1\times (n=768)\)”).
Simulations indicating half-sampling’s relative efficiency. X-axis is the smaller-is-better average variance in predicting the test set. Plotted are three CDFs and six scalar values. The CDFs consist of 512 without-replacement random case selections. Scalar values: variance achieved by (left to right) including all \(n=12,288\) available candidates; for half-sampling using OA(128), OA(64), OA(32), and OA(16), all with \(n=768\), respectively. And by including no additional data (\(n=0\)). CDFs (left to right): dark red, from including \(n=2304\) additional random candidates (without replacement); red, \(n=1536\) additional random candidates; orange, \(n=768\) additional random candidates. Vertical dashed lines denote the average values of the respective CDFs
We also measure how far from “no new” data to “all C candidates.” Presented in Table 1 as the rightmost column, it is the percentage as quantified by the “ave var” column (and x-axis in Fig. 3). Algorithm 2 moves the average prediction variance for OA(32) and OA(64) 38.8 and 42.4 percent of the way toward using 12,288 candidates, respectively, while \(1\times\) random sampling moves only 30 percent, \(2\times\) random sampling 36 percent, OA(16) 35 percent, and \(3\times\) random sampling 42 percent.
These results indicate that on average, algorithm 2 using OA(64) performs equivalent to three times as much data selected at random (labeled “random \(3\times (n=2304)\)”). The relative efficiency of half-sampling with OA(32) is between 2 and \(3\times\). So larger ensembles buy some efficiency, but with decreasing marginal rates of return. Based on Table 1, it becomes quite difficult to recommend OA(128) over OA(64).
Note that the model employed by this example, a convolutional neural network, is quite non-linear, yet we achieve substantial gain from algorithm 2. This should be reassuring: Idea#1 in algorithms 1 and 2, which is motivated by linear model theory, seems to work effectively in this nonlinear context.
7 Summary
The problem we consider is that of supplementing training data for a machine learning model.
For our purposes, there is a pre-existing model, of a modern ML type, a deep neural network, say, fit using a current dataset, so there is some ability to make model predictions. For candidate c drawn from C potential candidates, we have available the associated feature vector \({{\varvec{x}}}_c\) but not the associated label/response \(y_c\). Consistent with many big data applications, any data supplement likely needs to consist of a batch of substantial size, drawn from an even larger set of potential candidates.
Common also with many ML models, we balance statistical considerations with those of computational feasibility, both in terms of computing complexity and data object size.
In general, we pursue a paradigm of multivariate model uncertainty, recognizing early that merely adding error bars to our model predictions is insufficient. This is because of the near-duplicates problem: Two cases close together in feature space may share about the same prediction and the same, larger error bars. If we observe only one of them, we may gain enough information about the other that observing both becomes wasteful. This redundancy can be detected, for instance, were we to have available the prediction covariance matrix; this would signal near-duplicates by the high correlation between the two candidates’ predictions.
Our approach is built on three ideas. The first consists in recognizing the theoretical centrality of the \(C\times C\) prediction covariance matrix \({{\varvec{V}}}\). \({{\varvec{V}}}\) is a precision matrix, and quite suitable for this batch supplement problem, even for, especially for, modern ML models such as deep neural networks, for four reasons: (1) I-optimality: Consistent with such semi-parametric models, \({{\varvec{V}}}\) is defined in the prediction domain. (2) Update before label: \({{\varvec{V}}}\) does not require observing the label/response \(y_c\) in order to be updated by the prospect of including candidate c, with features \({{\varvec{x}}}_c\), in the supplement. (3) Training case influence: When constructed from a training set, \({{\varvec{V}}}\) can be used to quantify for each observation the impact on overall model fit. (4) Theory generalization: The underlying theory for \({{\varvec{V}}}\) is comfortably compatible with linear model theory and classical experimental design ideas.
The statistically efficient estimation of \({{\varvec{V}}}\) defines the second idea for our approach, called here half-sampling. Half-sampling strongly resembles a fifty-percent jackknife. This work focuses on deep neural networks; contemporary DNNs approach interpolators/memorizers to such an extent that without-replacement sampling seems preferable to with-replacement bootstrap resampling. As presented here, half-sampling depends on defining mutually exclusive, equally sized data shards, and the careful balancing properties of a two-level orthogonal array. (Note that when shards correspond to physical computer files, half-sampling reduces file reads by half.) The use of the orthogonal array buys something substantial: relative efficiencies approaching \(2\times\) when the ratio of parameter count to sample size becomes large—exactly the case inhabited by many applications of deep neural networks. Also, note that half-sampling admits highly parallel model fitting. Thus, half-sampling adapts to ML-type models four ways: without-replacement sampling, file sharding, orthogonal-array-based sample balancing, and parallel computing.
Our third idea recognizes that the \(C\times C\) matrix \({{\varvec{V}}}\) is, for C even moderately sized, awkwardly large. We therefore reformulate our algorithm 1 into algorithm 2, which operates on the linear-in-C matrix \({\varvec{\Delta }}\).
The resulting matrix of prediction contrasts \({\varvec{\Delta }}\) inherits the well-known statistical efficiency properties of two-level orthogonal arrays: (1) For every candidate, each half-sample contrast uses all the training data. (2) The (signed) weights on each shard are equal in absolute value. (3) Between any two half-samples, the weights are uncorrelated. In this sense, the construction of \({\varvec{\Delta }}\) has high statistical efficiency and estimates \({{\varvec{V}}}={{\varvec{\Delta }}{\varvec{\Delta }}}^{\top }/(M-1)\) with \(M-1\) degrees of freedom. Balancing between computational burden and efficiency gain, we recommend around \(M=64,\) that is, OA(64), which gives 63 degrees of freedom for estimating prediction covariances.
Our main result is that statistically efficient estimates of error buy something: for the problem of supplementing training data, half-sampling and algorithm 2 combine to give three times “(\(3\times\))” the statistical efficiency of random without-replacement case selection. So for each case proposed by half-sampling and algorithm 2, the reduction in average prediction variance is on average about the same as selecting 3 random cases, 50 percent beyond the \(2\times\) rule of thumb associated with active learning performance. To our knowledge, this is the first of the use of the concept of relative statistical efficiency for assessing active learning algorithms.
We give due diligence to computational issues: (1) Fitting by half-sampling can be accelerated by warm starts, reduced file reads, and parallel computation. (2) By using algorithm 2, we can avoid direct calculation of the \(C\times C\) prediction covariance matrix \(\user2{V}\). Instead, we maintain a \(C\times (M-1)\) matrix, essentially a data table with \(M-1\) features for C candidates. (3) We quantify the precision-computation trade-offs in the appendix A and Sect. 6.
The present work is limited in several directions: (a) Our framework is developed by analogy with linear models and continuous responses (continuous labels, a.k.a. “regression”). In contrast, much of ML involves categorical labels. (b) Further, our efficiency claim is worked out only for one dataset, CIFAR-10. This places this work in substantial tension with much of ML literature, which favor extensive empirical exercises over common task frameworks [14]. (c) Our proposed algorithms are “greedy”, and the benefit of non-greedy, exchange-type algorithms has not yet been explored. (d) Finally, each of our particular claims, orthogonal arrays to implement half-sampling, the efficiency gains from Sherman-Morrison batch construction, even the number of shards M to implement half-sampling, although theoretically motivated, each is fundamentally an empirical or simulation result. For these reasons, we find it appropriate to invite further study, empirical and theoretical, in other experimental settings, for other model families, and with additional datasets.
References
Allen DM (1974) Relationship between variable selection and data augmentation and a method for prediction. Technometrics 16:25–127
Box GEP, Hunter JS (1961a) The \(2^{k-p}\) fractional factorial designs, Pt. I. Technometrics 3(3):311–351
Box GEP, Hunter JS (1961b) The \(2^{k-p}\) fractional factorial designs, Pt. II. Technometrics 3(4):449–458
Box GEP, Hunter JS, Hunter WG (2005) Statistics for experimenters: design, discovery, and innovation. Wiley, New York
Brinker K (2003) Incorporating diversity in active learning with support vector machines. In: Proceedings of the International Conference on Machine Learning, pp 59–66. AAAI Press
Brown G, Wyatt JL, Tin̆o P (2005) Managing diversity in regression ensembles. J Mach Learn Res 6:1621–1650
Cherkauer KJ (1996) Human expert-level performance on a scientific image analysis task by a system using combined artificial neural networks. In: Chan P (ed) Working notes of the AAAI Workshop on Integrating Multiple Learned Models, pp 15–21
Chollet F, Allaire JJ (2018) Deep learning with R. Manning, Shelter Island
Chollet F, Allaire JJ, et al (2017) R Interface to Keras. https://github.com/rstudio/keras
Cohn DA, Ghahramani Z, Jordan MI (1996) Active learning with statistical models. J Artif Intell Res 4:129–145
Daniel C (1959) Use of Half-Normal Plots in Interpreting Factorial Two-Level Experiments. Technometrics 1(4):311–341
Dietterich TG (2000) Multiple classifier systems, MCS. Lecture Notes in Computer Science, vol 1857. Springer, Berlin, Heidelberg
Dietterich TG, Bakiri G (1995) Solving multiclass learning problems via error-correcting output codes. J Artif Intell Res 2:263–286
Donoho D (2017) 50 years of data science. J Comput Graph Stat 26:745–766
Fedorov VV (1972) Theory of optimal experiments. Academic Press, New York
Gongora AE, Xu B, Perry W, Okoye C, Riley P, Reyes KG, Morgan EF, Brown KA (2020) A Bayesian experimental autonomous researcher for mechanical design. Sci Adv 6(15):eaaz1708
Gregoire JM, Boyd DA, Guevarra D, Haber JA, Jones R, Kan K, Marcin M, Newhouse PF, Shinde A, Soedarmadji E, Suram SK, Zhou L (2018) High throughput experimentation for the discovery of water splitting materials. Integrated solar fuel generators. The Royal Society of Chemistry, London, pp 305–340
Guo Y, Schuurmans D (2008) Discriminative batch mode active learning. Adv Neural Inf Process Syst 20:593–600
Hartford J, Leyton-Brown K, Raviv H, Padnos D, Shahar L, Lenz B (2020) Exemplar guided active learning. In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H (eds) Advances in Neural Information Processing Systems, vol. 33
Hoi SCH, Jin R, Lyu MR (2006) Large-scale text categorization by batch mode active learning. In: Proceedings of the International Conference on the World Wide Web. ACM Press, New York, pp 633–642
Hu S, Xiong Z, Qu M, Yuan X, Côté M-A, Liu Z, Tang J (2020) Graph policy network for transferable active learning on graphs, In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H (eds) Advances in Neural Information Processing Systems, vol. 33
Kiefer JC, Wolfowitz J (1960) The equivalence of two extremum problems. Canadian J Math 12:363–366
Kolen JF, Pollack JB (1991) Back propagation is sensitive to initial conditions. Advances in neural information processing systems, vol 3. CA. Morgan Kaufman, San Francisco, pp 860–867
Krizhevsky A, Nair V, Hinton G (2012). Imagenet classification with deep convolutional neural networks. In: Advances in Nueral Information Processing, vol. 25.
Lakshminarayana B, Pritzel A, and Blundell C (2017). Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in Neural Information Processing Systems, vol. 30, pp 6402–6413
Lewis D, Gale W (1994) A sequential algorithm for training text classifiers. In: Proceedings of the ACM SIGIR, Conference on Research and Development in Information Retrieval. ACM/Springer, New York, pp 3–12
Liu Y (1998) Negative Correlation Learning and Evolutionary Neural Network Ensembles. PhD thesis, University College, The University of New South Wales, Australian Defence Force Academy, Canberra, Australia
Mannocci L, Leimbacher M, Wichert M, Scheuermann J, Neri D (2011) 20 years of DNA-encoded libraries. Chem Commun 47(48):12747–12753
Mariet Z, Jerfel G, Wang Z, Angermüller C, Belanger D, Vora S, Bileschi M, Colwell L, Sculley D, Tran D, Snoek J (2020) Deep Uncertainty and the Search for Proteins, Workshop: Machine Learning for Molecules, 2020, preprint.
Montgomery DC (2019) Design and analysis of experiments. Wiley, New Jersey
Neal R (1993) Probabilistic inference using Markov chain Monte Carlo method. Technical report CRG-TR-93-1, Department of Computer Science, University of Toronto, Toronto, CA
Plackett RL, Burman JP (1946) The design of optimum multifactorial experiments. Biometrika 33:305–25
Quenouille MH (1956) Notes on bias in estimation. Biometrika 43(3–4):353–360
Schohn G, Cohn D (2000) Less is more: Active learning with support vector machines. Int Conf Mach Learn 2:4
Settles B (2009) Active learning literature survey. Computer Sciences Technical Report 1648, University of Wisconsin–Madison
Seung HS, Opper M, Sompolinsky H (1992) Query by committee. Proceedings of the ACM Workshop on Computational Learning Theory, pp 287–294
Sherman J, Morrison WJ (1949) Adjustment of an inverse matrix corresponding to changes in the elements of a given column or a given row of the original matrix (abstract). Ann Math Stat 20:621
Singh SP, Jaggi M Model fusion via optimal transport. In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H (eds) Advances in Neural Information Processing Systems, vol. 33
Stone M (1974) Cross-validation choice and assessment of statistical predictions. J R Stat Soc Ser B 36:111–147
Studden WJ (1977) Optimal designs for integrated variance in polynomial regression. In: Gupta SS, Moore DS (eds) Statistical decision theory and related topics II. Academic Press, New York
Tong S, Chang E (2001) Support vector machine active learning for image retrieval. Proceedings of the Ninth ACM International Conference on Multimedia, ACM
Tong S, Koller D (2001) Support vector machine active learning with applications to text classification. J Mach Learn Res 2:45–66
Tukey JW (1958) Bias and confidence in not quite large samples (abstract). Ann Math Stat 29(2):614
Viswanathan K, Sachdeva S, Tomkins A, Ravi S (2019) Improved semi-supervised learning with multiple graphs. Proc Mach Learn Res 89:3032–3041
Wald A (1943) On the efficient design of statistical investigations. Ann Math Stat 14(2):134–140
Wenzel F, Snoek J, Tran D, Jennatton R (2020) Hyperparameter ensembles for robustness and uncertainty quantification. In: Larochelle H, Ranzato M , Hadsell R, Balcan MF, Lin H (eds) Advances in Neural Information Processing Systems, vol. 33
Woodbury MA (1950) Inverting modified matrices, Memorandum Report 42. Princeton University, Princeton, NJ, Statistical Research Group, p 4
Xu Z, Akella R, Zhang Y (2007) Incorporating diversity and density in active learning for relevance feedback. In: Proceedings of the European Conference on IR Research. Springer, New York, pp 246–257
Zhou J, Sun S (2014) Improved margin sampling for active learning. In: Li S, Liu C, Wang Y (eds) Pattern Recognition, CCPR 2014
Acknowledgements
The author benefited from the interest, comments, and questions of Anton Geraschenko, Zelda Mariet, John Platt, Patrick Riley, the editor, and two anonymous referees.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Advances in Deep Learning” guest edited by David Banks, Ernest Fokoué, and Hailin Sang.
A Sample Sizes for Variances
A Sample Sizes for Variances
For histograms, one rule of thumb for recommended sample size is \(n=30\). The detailed rationale for this is as follows: (a) The proxy for the precision of a histogram is the precision of its spread, e.g., its standard deviation. (b) Based on Gaussian theory, the delta method, and the chi-square distribution with \(\nu\) degrees of freedom, an approximate \(1-\alpha\) percent confidence interval for a standard deviation s is \(s(1+ z_{\alpha /2}/\sqrt{2\nu })^{\pm 1}\). Since the standard Gaussian deviate \(z_{\alpha /2}=1.96 \approx 2\) for 95 percent confidence intervals, this expression can be usefully approximated by \(s(1+2/\sqrt{2\nu })^{\pm 1}\), Note that the second term, \(t=2/\sqrt{2\nu }\), gives the relative precision. Suppose we replace t with \(2^b\) and \(\nu\) with \(2^h\). b now denotes the relative precision and h gives the degrees of freedom/sample size, both in bits. It follows that we achieve b bits relative precision when \(\texttt {log}_2(\nu )=h=2b+1.\)
Examples:
- (\(b=2\)):
-
When \(b=2\), relative precision of two bits, \((1+1/4)^{\pm 1}\), one needs \(h=5,\) hence a sample size of \(n\approx \nu =2^5=32\).
- (\(b=3\)):
-
When \(b=3\), three bits, \(h=7\) and the associated sample size is \(n\approx \nu =2^7=128.\)
- (\(b=4\)):
-
\(b=4\) gives 512.
Each incremental bit of relative precision increases sample size requirements by \(4\times ,\) a manifestation of the familiar square root rule for confidence intervals.
In Sect. 6, the recommended OA(64) gives 2.5 bits relative precision, about one part in six.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heavlin, W.D. On Ensembles, I-Optimality, and Active Learning. J Stat Theory Pract 15, 66 (2021). https://doi.org/10.1007/s42519-021-00200-4
Accepted:
Published:
DOI: https://doi.org/10.1007/s42519-021-00200-4