1 Introduction

Influenced by early diagenesis or late geological processes, various discontinuities are extensively distributed in natural rocks, e.g., joint, bedding, fault, fissure, pore, and cave. Since stress concentration easily occurs near the corners of these flaws, new cracks usually emanate from these places first, and then propagate in a certain direction until they intersect each other to form a macroscopic failure. In other words, the failure of rock is generally progressive, which is different from the instantaneous failure of glass material. This makes it possible to warn of rock instability and rock disasters. Also, provided that the rock mass is excavated by drilling and blasting method, the internal flaws are conducive to reducing the consumption of explosives and improving rock fragmentation. On the other hand, the existing flaws make the mechanical properties of rocks greatly weakened and complicate the failure behavior. A couple of reasons can account for these behaviors: (1) The internal structure of the rock is seriously deteriorated by the flaws, which brings about a pronounced degradation in rock strength and stiffness; (2) under the action of external force, micro-cracks tend to appear around the perimeters of the flaws because of high concentrated stress, resulting in further weakening of rock mechanical properties [1,2,3,4]; and (3) the number of flaws is unclear and their spatial distribution is random.

According to the shape of flaws, we can classify them into two kinds: crack-type flaw and cavity-type flaw. To find out how pre-existing cracks affect the strength, deformation, and failure features of rocks, a multitude of studies have been performed on jointed rock or rock-like samples under different load conditions in recent years. For prismatic samples embedded with a single joint in uniaxial loading, two typical sorts of cracks have been widely identified, namely, wing crack (also known as primary-tensile crack) and secondary crack [5, 6]. The wing crack initiating from the joint tip propagates crookedly in a stable manner as the imposed load increases, and finally remains consistent with the loading direction. The secondary crack whose propagation direction is largely related to rock material generally occurs later than the wing crack, and plays a leading role in the eventual failure. Additionally, several other types of cracks such as anti-wing crack, shear crack, and far-field crack are sometimes found in the uniaxial compression tests, which depend on the length and inclination of the pre-fabricated joint in the sample [7]. Under biaxial and triaxial loading, the confining pressure and joint angle are found to be the prominent factors influencing the failure mode [8,9,10]. Moreover, the failure characteristics of samples with one joint under other loading methods, e.g., tensile loading, cyclic loading, impact loading, and static-dynamic coupled loading, have also been surveyed and discussed [11,12,13,14,15], which plays a positive role in understanding the mechanism of rock mass instability.

Apart from one crack, considerable research has focused on the situations of two, three, and multiple pre-fabricated joints in gypsum, PMMA, cement mortar, and rock samples as well [16,17,18,19,20,21]. Results manifested that the sample strength and cracking response are corporately impacted by the number, dimension and configuration of joints, material properties, loading forms, and filling conditions. The failure is an evolutionary process of initiation and propagation of various cracks and different types of joint coalescence. Occurrence of diverse coalescence patterns is a result of competition between a few mechanisms in forming tensile or shear cracks [22]. Moreover, some researchers, e.g., Dyskin et al.[23], Zhang et al. [24], Mondal et al. [25], and Zhou et al. [26, 27] have further explored the crack evolution in samples with 3D-joints under compressive loads, and observed three common classes of cracks growing from the joint tips; that is, wing crack, anti-wing crack, and far-field crack.

Likewise, the cavities ranging from tiny pores to large caves are also widespread in the rock mass, and it is widely shared that the rock having cavities has a higher potential for instability than the intact rock. Besides, in engineering practice, rock burst or V-notched failure often happens at sidewalls or roof of deep-buried hard rock tunnel. Essentially, the tunnel, roadway, and shaft excavated in deep-buried rock mass can be simplified as an artificial cavity in rock sample. Therefore, studying the effect of cavity on mechanical performance and failure features of holey rock is beneficial to control rock stability and reveal tunnel failure mechanism. For this purpose, growing attention has been paid to the cracking behavior of rock or rock-like samples having cavity-type flaws under various loading conditions. For sample having a single cavity under uniaxial compression, Hoek [28] first discovered three categories of cracks (primary-tensile fracture on roof-floor, spalling fracture on sidewalls, and remote fracture on corners) formed around a circular cavity in photo elastic tests. Wong et al. [29] found that the primary-tensile crack is inclined to initiate and propagate in sample with a small width and a large diameter cavity, which is fairly agreeable with the theoretical results by Sammis-Ashby model [30]. Zhao et al. [31] applied acoustic emission (AE) technique to investigate the fracture evolution around circular cavities, and argued that the peak strength and crack initiation stress mainly rely on the cavity size. Carter et al. [32] measured the initiation stress of the tensile cracks by attaching a number of strain gauges close to the circular cavity. However, the applicability of this method is limited because the propagation paths of the cracks are uncertain. Besides, Zeng et al. [33] experimentally investigated the influence of cavity shape on strength, deformation, and fracturing behavior, and explained the initiation locations of cracks based on the force fields obtained by PFC modeling. To deeply reveal the fracturing mechanisms of different shaped cavities, Wu et al. [34] analytically derived the stress distributions around the cavities using complex variable approach, and reproduced the real-time crack development combining AE and DIC techniques. If the biaxial load is applied, tensile cracks squeezed by lateral pressure no longer appear, and the spalling failure on the cavity sides is more severe [32, 35]. For the case of triaxial compression, the crack initiation stress is larger than that of the biaxial and uniaxial loading, and the failure mode is prominently controlled by the orientation and amplitude of the intermediate principal stress [36]. In regard to the Brazilian disc sample with a central circular cavity under splitting tension, the failure is induced by the coalescence of the primary crack along the loading diameter and the secondary crack parallel with the horizontal diameter [37]. Besides, the failure processes of samples having two or multiple cavities of circular, elliptical, inverted U-shaped, and rectangular cavities under different forms of static loads were reported experimentally and numerically [38,39,40,41,42,43,44,45,46]. Furthermore, to be close to the actual situation of natural rocks, many factors like rock heterogeneity, porosity, and ambient temperature were considered [47,48,49], which promotes the development of rock mechanics.

From the above review, it can be seen that most studies were conducted under static loads. In practice, openings in hard rock mass are mostly excavated by using drilling and blasting method; that is, the rock mass and opening are subjected to strong dynamic loads caused by mechanical drilling and explosive blasting [50, 51]. Additionally, literature indicates that many rock disasters, especially rock bursts, are caused by dynamic load disturbances [52,53,54,55, ]. Thus, carrying out investigations on cracking behavior of samples containing a cavity under dynamic loads is helpful to grasp the deformation and failure mechanism of rock tunnel. In this work, several groups of prismatic sandstone samples with a circular cavity of different diameters were prepared for impact tests by a modified split Hopkinson pressure bar (SHPB) test system. The dynamic failure processes of these samples were monitored by a high-speed camera. Further on, the energy changes during rock failure and fragmentation feature were also analyzed and discussed.

2 Material and Experimental Method

2.1 Sample Preparation

Considering that sedimentary rocks are widely distributed in the Earth’s crust, we chose representative brown sandstone with medium strength as the test material in this work. This sort of rock originating from a quarry in Linyi City in eastern China was transported to a professional geotechnical company in Liuyang City for processing. The results of optical microscopy analysis show that the rock has good homogeneity and integrity, and the main mineral components are SiO2 (46%), Na[AlSi3O8]-Ca[Al2Si2O8] (35%), CaCO3 (9%), AmBpO2p·nH2O (8%), K[AlSi3O8] (5%), and 1% other transparent substances (see Fig. 1) [56]. Additionally, the rock owns a massive structure, and its particle size varies from 0.15 to 0.50 mm, which belongs to the medium-fine grade.

Fig. 1
figure 1

Photos of mineral compositions in brown sandstone slice by polarizing microscope: a under single polarized light; b under orthogonal polarized light (quartz—SiO2; plagioclase—Na[AlSi3O8]-Ca[Al2Si2O8]; calcite—CaCO3; zeolite—AmBpO2p·nH2O; K-feldspar—K[AlSi3O8]).

Full size image

In this research, we prepared a total of four groups of samples: group D-1, group D-2, group D-3, and group D-4. Each group contains three identical samples. The samples of group D-1, namely, D-1-A, D-1-B, and D-1-C (A/B/C represents the sample number in the same group) are intact and used for comparison with other groups. Group D-2 are samples containing a circular cavity with a radius of 3 mm, while the radius of the hole inside the samples of group 3 and group 4 are 4 mm and 5 mm. All the samples were separated from a complete sandstone block and machined into prisms with sizes of 45 × 45 × 20 mm (length × width × thickness) via a rock cutter, as illustrated in Fig. 2. The size design is mainly based on the following reasons: (1) The cross-sectional areas of the loading ends of the sample shall be smaller than those of the bars; (2) the length-width ratio of the sample should meet 1:1, and the length and width of the sample should be large enough to eliminate the boundary effect caused by cavity excavation; and (3) the sample should be thin enough to ensure that the surface cracking and internal fracture are consistent. As the hydraulic cutting method causes less damage to the rock than the mechanical cutting method, the high-pressure water jet technique was adopted to excavate the central circular cavities in the samples. Besides, the six surfaces of each specimen need to be polished so that the unevenness does not exceed 0.02 mm, and the non-perpendicularity between parallel surfaces is less than 0.001 radian.

Fig. 2
figure 2

Diagram of four groups of processed samples for SHPB test: a sample D-1; b sample D-2; c sample D-3; d sample D-4

Full size image

Before the start of the impact test, several conventional physico-mechanical property indexes of this rock were measured firstly in accordance with the relevant experimental specifications, as shown in Table 1.

Table 1 Main physico-mechanical property indexes of brown sandstone sample
Full size table

2.2 Testing Equipment and Principle

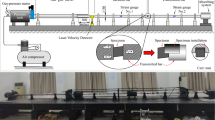
A set of modified SHPB test equipment [57] in the rock dynamics laboratory of Central South University was used to carry out impact tests on these samples, which is presented in Fig. 3. It consists of three parts: impact loading system, signal acquisition system, and image acquisition system.

Fig. 3
figure 3

SHPB equipment for impact loading tests

Full size image

The impact loading system is comprised of a nitrogen container, an excitation device, a self-designed spindle-shaped striker, an incident bar, a transmission bar, a buffer bar, and a pedestal. Compared with the conventional loading method of rectangular waves generated by a cylindrical striker, the loading method of half-sine wave induced by the spindle-shaped striker can solve the problems of wave dispersion, large change of strain rate, repeated loading, and unloading during rock impact loading, which is particularly suitable for rock dynamic performance testing [58]. The striker and bars are both made of 40Cr alloy steel with an elastic modulus of 233 GPa and a density of 7821 kg/m3. The diameters of the incident, transmission, and buffer bars are all 50 mm, and the lengths are 2.0 m, 1.5 m, and 0.5 m, respectively. The average wave speed of these bars is measured as 5461 m/s.

With respect to the signal acquisition system, it is made up of two strain gauges (B120-2AA), two bridge boxes, a dynamic strain meter and an oscilloscope. The oscilloscope with model of DL-850E is produced by Yokogawa, Japan. It has a data update rate of 1 MHz (1 μs), a minimum measurement resolution of 625 ps, and a measurement range (frequency) of 0.01 Hz to 500 kHz. The model of the dynamic stain meter purchased from Beidaihe practical electronic technology research institute is SDY2107A. The frequency band of the dynamic strain gauge is 0~1 MHz, and the applicable range of the bridge resistance is 60~1000 Ω. It has automatic balancing and calibration functions, and the quarter-bridge strain gauge measuring mode is adopted. Besides, a laser velocimeter was placed near the end of excitation device to monitor the impact speed of the striker.

For the image acquisition system, it is composed of a high-speed camera and a light source. The high-speed camera used for recording the failure process of sample is produced by Photron company, with a model of Fastcam Sa1.1. Its chip is a 12-bit CMOS sensor with a maximum shooting speed of 675,000 FPS. To clearly capture the photos of the sample during the tests, a high-power fill light is usually arranged next to the high-speed camera. The acquisition rate of the camera is designed to be 75,000 FPS, namely, one photo is taken every 13.33 μs. Note that the camera starts to work when the strain gauge on the incident bar is first triggered by the stress wave, so the loading time of sample ts can be calculated according to: ts = t–t0, where t is the oscilloscope running time and t0 is the time that the stress wave propagates from the strain gauge to the interface between the incident bar and the specimen minus the signal processing time. Literature shows that t0 is 147.20 μs [58]. That is, the twelfth picture taken by the camera in this study is the initial moment of sample deformation under loading.

Figure 4 shows the propagation process of the stress wave in the impact loading system. When the excitation device is started, a certain pressure of nitrogen from the nitrogen tank will drive the striker to hit the incident bar, leading to the formation of incident stress wave. The amplitude of the stress wave is positively related to the nitrogen pressure, and this system has a maximum impact load of 500 MPa. In this work, the impact pressure for each test is set to 0.45 MPa. The stress wave first propagates at a constant speed along the incident bar, and then transmits and reflects at the interface I between the incident bar and the sample. After that, the stress wave propagates steadily in the sample, and transmits and reflects again at the interface II between the sample and the transmission bar. The signals of the first incident and reflected waves can be picked up by the strain gauge 1, while those of the transmitted wave appeared firstly in the transmission bar can be monitored by the strain gauge 2. Since the length of the sample is very small, the time for the stress wave to go back and forth in the rock sample is very short. After several times of transmissions and reflections, the stress and strain in the rock sample are basically the same. That is to say, the stress uniformity hypothesis can be satisfied.

Fig. 4
figure 4

Propagation of stress wave in impact loading tests

Full size image

According to the one-dimensional stress wave theory [58,58,60], the displacement u(t) of particle can be written as follows:

$$ u(t)=C{\int}_0^t\varepsilon (t)\mathrm{d}t $$
(1)

where C denotes the wave speed, t means the time, and ε is the strain.

If the incident, reflected and transmitted strains are denoted by εi(t), εr(t) and εt(t), respectively, the displacements (u1 and u2) of the interfaces I and II can be expressed as follows:

$$ \left\{\begin{array}{l}{u}_1=C{\int}_0^t\left({\varepsilon}_{\mathrm{i}}(t)-{\varepsilon}_{\mathrm{r}}(t)\right)\mathrm{d}t\\ {}{u}_2=C{\int}_0^t{\varepsilon}_{\mathrm{t}}(t)\mathrm{d}t\end{array}\right. $$
(2)

Therefore, the average strain εs of the sample whose length is represented by ls can be concluded as follows:

$$ {\varepsilon}_{\mathrm{s}}(t)=\frac{u_1-{u}_2}{l_{\mathrm{s}}}=\frac{C}{l_{\mathrm{s}}}{\int}_0^t\left({\varepsilon}_{\mathrm{i}}(t)-{\varepsilon}_{\mathrm{r}}(t)-{\varepsilon}_{\mathrm{t}}(t)\right)\mathrm{d}t $$
(3)

Based on the uniformity hypothesis, substituting εi + εr = εt into Eq. (3), we have as follows:

$$ {\varepsilon}_{\mathrm{s}}(t)=-\frac{2C}{l_{\mathrm{s}}}{\int}_0^t{\varepsilon}_{\mathrm{r}}(t)\mathrm{d}t $$
(4)

By differentiating Eq. (4), the strain rate of the sample can be solved, namely

$$ {\dot{\varepsilon}}_{\mathrm{s}}(t)=\frac{2C}{l_{\mathrm{s}}}{\varepsilon}_{\mathrm{r}}(t) $$
(5)

where \( {\dot{\varepsilon}}_{\mathrm{s}} \) represents the strain rate of the sample.

The loads at both ends of the sample can be calculated by the following:

$$ {F}_1= EA\left({\varepsilon}_{\mathrm{i}}(t)+{\varepsilon}_{\mathrm{r}}(t)\right),\kern1em {F}_2= EA{\varepsilon}_{\mathrm{t}}(t) $$
(6)

where F1 and F2 are the loads on the left and right ends of the specimen, respectively. A and E means the cross-sectional area and elastic modulus of the bars.

For the average stress in the sample, it can be found according to the following:

$$ {\sigma}_{\mathrm{s}}=\frac{F_1+{F}_2}{2{A}_{\mathrm{s}}} $$
(7)

where σs denotes the stress in the sample and As represents the cross-sectional area of the sample.

Substituting Eq. (7) into Eq. (6) and combining the stress uniformity hypothesis, we get the following:

$$ {\sigma}_{\mathrm{s}}=E\left(\frac{A}{A_{\mathrm{s}}}\right){\varepsilon}_{\mathrm{t}}(t) $$
(8)

To conclude, based on the monitored strain signals, the dynamic mechanical parameters (ε(t), \( {\dot{\varepsilon}}_{\mathrm{s}}(t) \), σs) of the samples can be calculated by Eqs. (4), (5), and (8).

3 Experimental Results

3.1 Verification of Stress Uniformity

Firstly, impact tests without placing a sample were carried out to calibrate the SHPB system. When the amplitudes of the incident and transmitted waves in three consecutive tests are basically equal and the reflected wave is close to a straight line, the accuracy of the SHPB system can be deemed to meet the test requirements.

In the present study, the sample D-1-A was taken as an example to verify the stress equilibrium in the sample. Based on the monitored voltage signals of the incident, reflected and transmission waves, the changes of stresses on the two loading surfaces (I and II) of the sample with the loading time can be plotted in Fig. 5a.

Fig. 5
figure 5

Curves of different stress waves versus loading time: a sample D-1-A; b Sample D-2-A

Full size image

As can be seen in Fig. 5a, the curve of stress I agrees well with that of the stress II, especially before the peak point. This suggests that the stress state of the two loading ends of the prismatic sample is the same before failure. Prior to the peak, the sample can be regarded as an elastomer and is macroscopically intact. After the peak stress, damage occurs in the sample and many cracks are formed. Thus, the amplitude of the propagating stress wave will decrease when it encounters cracks. Moreover, Fig. 5b further illustrates the stress states of the loading ends of the sample having a small circular cavity under the same impact load. It is found that the stress at interface II is slightly smaller than that at interface I. The reason is that the stress wave reflects and scatters when it encounters a crack on the propagation path, and then its amplitude is reduced. To sum up, the stress uniformity hypothesis of the prismatic sample under impact loading using SHPB system can be satisfied, which is consistent with the viewpoint of Li et al [61].

3.2 Dynamic Mechanical Properties of Samples

Table 2 lists the mechanical properties of the four groups of samples subjected to dynamic loading. In each experiment, the speed of the striker is approximately 10 m/s, so the dynamic load applied to each sample is basically the same. According to Table 2, it is calculated that the average dynamic compressive strength (DCS) of the samples from group D-1 to group D-4 is 186.69 MPa, 161.23 MPa, 150.46 MPa, and 145.95 MPa, respectively. Compared with the intact sample, the DCS of the samples with small, medium, and large cavities decreases by 13.64%, 19.40%, and 21.82%, respectively. It is clearly seen that the embedded cavities obviously degrade the DCS of the rock samples, and the degree of weakening is positively related to the cavity size.

Table 2 Physical-mechanical property parameters of samples under impact loading
Full size table

The dynamic elastic modulus (DEM) is defined as the slope of the dynamic stress-strain curve where the dynamic stress is half the peak. From Table 2, the average DEM of the four groups of samples (D1~D4) is 26.54 GPa, 25.41 GPa, 25.48 GPa, and 24.36 GPa, respectively. Therefore, it can be summarized that the DEM of the sample is also weakened by the cavity to a certain extent, but the weakening effect is not very significant. Besides, the average peak strains of the four groups of samples are 8.92‰, 8.11‰, 7.38‰, and 7.51‰, respectively. The peak strain of the rock samples having a cavity decreases slightly compared with that of the intact samples, which basically shows a linear relationship with the cavity size. In addition, we found that the strain rate of the sample generally rises with the increase of the cavity radius, with a range of 60 to 80 s−1. It is also shown that the DCS of the samples in the same group increases as the strain rate increases, which is called strain rate effect.

The representative dynamic stress–strain curves of the four sets of samples under impact loading are presented in Fig. 6. Since the dynamic loading process is quite short, there is no obvious initial pores and micro-cracks compaction stage at the beginning of loading. Only elastic deformation stage, plastic deformation stage, and post-peak deformation stage are formed. The slope of the stress–strain curve of the intact sample in the post-peak stage is very large, suggesting the brittleness of the sample is extremely significant. By contrast, the brittleness of the samples having cavities is not very significant as that of the intact sample. Accordingly, the existence of the cavity enhances the plasticity of the rock sample. Moreover, compared with the samples with a cavity under uniaxial loads [62], no significant stress drops on the stress–strain curves under dynamic loads is observed. This shows that the dynamic crack development is exceedingly fast.

Fig. 6
figure 6

Dynamic stress-strain curves of representative samples under impact loading

Full size image

3.3 Dynamic Fracture Process and Failure Mode

According to the recorded photos of the samples by a high-speed camera during the impact tests, we selected several representative photos for failure analysis. The failure states of the samples at different loading times are shown in Table 3. In the table, the marked cyan notes at the bottom of the sample indicate the dynamic loading time, and the blue notes denote the appeared cracks during the loading. Among the blue notes, the number indicates the crack type (numbers 1, 2, and 3 are defined as tensile cracks, shear cracks, and spalling cracks, respectively), and the superscript letters mean the order in which the cracks form.

Table 3 Failure processes of samples under impact loading
Full size table

As can be seen in Table 3, the failure behavior of these samples under impact loading is clearly displayed. For the intact sample D-1-C, several splitting tensile cracks gradually appear as the loading time T increases. When T = 2172 μs, a splitting tensile crack 1a induced by the axial load is formed at the top of the sample and propagates along the impact direction, and a shear crack 2a with an angle to the loading direction is also observed at the bottom. When the loading time rises to 2200 μs, the above two cracks develop further. Meanwhile, the other two tensile cracks (1b and 1c) initiate from the two loading ends and propagate horizontally. At T = 2269 μs, another tensile crack 1d is found to grow from the left towards the right loading end. Also, the other non-penetrating shear crack 2a at the central of the sample surface starts to propagate, which is caused by surface spalling. When T reaches 2408 μs, it is found that the tensile cracks 1a~1c have connected the left and right ends, leading to instability of the sample. Obviously, the failure of the intact sample is attributed to the splitting tensile cracks, while the shear cracks that result from the end friction effect do not dominate it. Thus, the failure mode of the intact sample subjected to dynamic loads can be regarded as tensile failure.

With respect to the sample D-2-B, its dynamic failure process is presented in Table 3. When T = 2013 μs, it can be seen that spalling failure occurs on the roof and floor of the cavity, leading to the appearance of spalling cracks 3a and 3b and the ejection of rock slices. With the increase of loading time to T = 2039 μs, three shear cracks 2a~2c on the diagonals begin to develop towards the cavity. At T = 2066 μs, the shear cracks 2b and 2c have been connected with the cavity and the shear crack 2a is about to reach the cavity. Besides, the other two shear cracks 2c and 2d are also formed and have merged with the shear crack 2b. At T = 2146 μs, the sample loses its integrity due to the intersection of the shear cracks 2a~2c with the cavity. To summarize, the failure mode of the sample D-2-B is still shear-dominated failure. Table 3 also illustrates the dynamic failure processes of the samples D-3-C and D-4-A, which are similar to that of the sample D-2-B. To put it differently, the spalling failure occurs first at the top and bottom of the cavity, and then different numbers of shear cracks appear on the diagonals and extend toward the cavity until they are connected. The failure patterns of the two samples under dynamic uniaxial loading also belong to shear-typed failure.

3.4 Energy Dissipation and Rock Fragmentation

According to the energy conservation equation, the calculation formulas of incident energy WI, reflected energy WR, transmitted energy WT, and dissipated energy WS in the SHPB test system can be derived, namely [59]:

$$ {W}_{\mathrm{I}}=\frac{AC}{E}{\int}_0^t{\sigma}_{\mathrm{i}}^2(t) dt $$
(9)
$$ {W}_R=\frac{AC}{E}{\int}_0^t{\sigma}_{\mathrm{r}}^2(t) dt $$
(10)
$$ {W}_T=\frac{AC}{E}{\int}_0^t{\sigma}_{\mathrm{t}}^2(t) dt $$
(11)
$$ {W}_{\mathrm{S}}={W}_I\hbox{-} {W}_R\hbox{-} {W}_T $$
(12)
$$ {\rho}_W={W}_{\mathrm{S}}/{V}_{\mathrm{S}} $$
(13)

where σi, σr, and σt represent the incident wave stress, reflected wave stress, and transmitted wave stress, respectively, which can be solved according to Hooke’s law. ρW and VS are the dissipated energy density and the volume of the sample.

Based on the picked strain signals, the detailed values of WI, WR, WT, WS, and ρW of each sample can be achieved according to Eqs. (9)~(13), as shown in Table 4. It is seen that the incident energy range is within 130~150 J at the same pressure, and the reasons for the slight difference are (1) affected by the pressure in the nitrogen tank and manual operation, the amount of nitrogen flowed into the excitation device in each test may be a little different; (2) the initial position of the manually placed striker cannot be exactly the same. Generally, the energy absorbed during the failure of the specimens is mainly used for crack initiation, propagation, and coalescence. Hence, the rock fragmentation highly depends on the dissipated energy. In this research, the dissipated energy density was employed to characterize the rock fragmentation. The larger the value of this indicator, the more cracks generated inside the sample, that is, the smaller the size of the sample fragment after failure. The average values of the dissipated energy density of the four groups of samples are 1.64 J∙cm−3, 1.71 J∙cm−3, 1.73 J∙cm−3, and 1.81 J∙cm−3, respectively. Clearly, the larger the size of the pre-fabricated cavity, the more severe the failure of the specimens.

Table 4 Energy characteristic parameters of samples under impact loading
Full size table

To further analyze the failure degree of the sample having a cavity under dynamic loading, fractal theory was applied to study the fractal characteristics of rock fragmentation. In this work, a cuboid iron box was placed on the experimental platform to collect rock fragments during the tests. As the front surface of the box needs to be opened for the high-speed camera to take photos, some rock fragments will be ejected from the front opening, but most rock debris can be collected. For the collected sample fragments, a series of standard sieves with mesh diameters of 5, 10, 15, 20, and 40 mm were used to sift them. The cumulative weight of rock fragments at each particle size grade is shown in Table 5.

Table 5 Energy characteristic parameters of samples under impact loading
Full size table

Literature demonstrates that the distribution of rock fragments can be formulated as [60]:

$$ \frac{m_d}{m_t}={\left(\frac{d}{d_m}\right)}^{3-D} $$
(14)

where md means the cumulative weight of sample fragments with a particle size smaller than d. mt denotes the total weight of the collected rock fragments. d is the particle size of rock fragments, and dm is the maximum size of rock fragments (40 mm in this study). D represents the fractal dimension of the sample fragments.

Taking the logarithms on both sides of Eq. (14), it is found that (3-D) is the slope of lg (md/mt)-lg(d/dm) curve. Based on the data in Table 5, the D-value of each sample can be solved via linear fitting, which is listed in Table 5. The average fractal dimensions of the four groups of samples are 1.91, 1.96, 2.09, and 2.20, respectively. Clearly, the fractal dimension of the sample having a cavity is larger than that of the intact sample. The larger the cavity size, the larger the fractal dimension of the sample. Research has shown that the larger the fractal dimension, the more severe the failure of the sample and the smaller the rock fragments [63]. Thus, the rock fragment of the sample having the largest cavity is the smallest, while that of the intact sample is the largest. As illustrated in Fig. 7, both the fractal dimension and the dissipated energy density of the rock sample fragments increase with the growing of the hole radius. This indicates that the existence of hole defects promotes the failure of samples. In summary, the rock fragmentation features of these samples characterized by fractal dimension index are agreeable with that by dissipated energy density index.

Fig. 7
figure 7

Average fractal dimension and dissipated energy density of different groups of samples under impact loading

Full size image

4 Discussion

The crack development in the specimen under load is largely associated with the internal stress state. Generally, tensile cracks are more likely to appear in the tensile stress concentration area, while shear cracks are caused by the high concentrated compressive stress. Therefore, understanding the stress distribution in the sample subjected to different forms of loads is useful to explain the cracking mechanism and failure behavior.

In our previous study, we have conducted uniaxial compression experiments on the prismatic brown sandstone sample with a circular-shaped cavity, and have examined the crack evolution around the cavity via digital image correlation technique [64]. It is observed that four kinds of cracks sequentially appear next to the cavity during the compression process, i.e., primary-tensile cracks (1a~1b), secondary-tensile cracks(2a~2c), spalling cracks (3a~3b), and shear cracks (4a~4b), which is presented in Fig. 8. In this figure, UCS and σ denote the uniaxial compressive strength and axial stress. According to the Kirsch equation, the hoop stress distribution on the boundary of a circular hole only under vertical load p can be plotted in Fig. 9a. Consequently, the primary-tensile cracks first appear in the tensile stress concentration areas (top and bottom of the circular cavity), and propagate along the loading direction. When the cracks reach the edges of the tensile stress areas, the critical stress zones transfer from the tips of the primary-tensile cracks to their either side. It can be calculated that the length of the primary-tensile cracks is (\( \sqrt{3} \)-1)r0 (r0 denotes the cavity radius). This results in the occurrence of the secondary-tensile cracks, which distribute at the corners of the cavity and also propagate parallel to the loading direction. Owing to the lateral squeeze caused by the secondary-tensile cracks, the primary-tensile cracks close progressively. Actually, the presence of the two types of cracks both results from the concentrated tensile stress. With the gradual increase of the applied load, the concentrated compressive stress (3p) on the two sidewalls of the cavity significantly increases, which eventually leads to flaking of the spalling cracks. Moreover, affected by the friction effect at the loading ends of the sample, the shear stress on the diagonal of the sample becomes larger and larger, which will form a shear band and evolve into shear cracks. When they extend to the cavity sidewalls, the specimen loses integrity and fails, resulting in a shear-dominated failure mode.

Fig. 8
figure 8

Distributions of major principal strain of sample with a circular cavity under uniaxial loading

Full size image
Fig. 9
figure 9

Hoop stress distributions on the boundary of circular cavity: a under uniaxial compressive load; b under one-dimensional dynamic load

Full size image

By contrast, the dynamic stress distribution on the boundary of the circular cavity under one-dimensional impact loads can be obtained using the wave function expansion method, as shown in Fig. 9b. The detailed derivation process can be found in reference [65]. It is found that the stress distributions around the circular cavity under dynamic and static loads are different. Note that the circular hole is symmetric with respect to the x-axis and y-axis, so only the stresses of the six monitoring points in the figure have been marked, and the stress magnitude of their symmetric points is the same. Since there is no external force applied to the cavity boundary, the radial stress on the perimeter of the hole is zero. For the hoop stress distribution on the cavity boundary, at the position θ = 0, r = r0, the static and dynamic compressive stress are 3p and 2.8p. At θ = π/2, r = r0, the static and dynamic compressive stress concentration factors are −1 and 0. Interestingly, no tensile stress is observed on the boundary of the circular cavity subjected to dynamic loads. As a result, no tensile cracks can be formed around the circular cavity under impact loads. Also, drastic spalling failure occurs at the top and bottom of the cavity (see Table 3) because of high concentrated compressive stresses. With the regard to the shear cracks appeared in the impact loading tests, its formation mechanism is the same as that under uniaxial compression; that is, the end friction effect leads to the appearance of the shear band. As the imposed load increases further, the shear band evolves into shear cracks and merges with the cavity eventually. Clearly, the dynamic failure behavior of the cavity under impact loads can be well explained based on the dynamic stress distribution on the periphery of the cavity.

With regard to the rock fragmentation characteristics, the greater the energy absorbed, the more easily the sample is broken. Therefore, it is easy to understand that the sample with large dissipated energy density tends to fail violently. If the size of rock fragmentation is small, the fractal dimension is large according to fractal theory of rock. Besides, it is universally acknowledged that rock burst and spalling failure or V-notched failure in hard rock tunnel under high in situ stresses can be induced by blasting loads. Studies have shown that these disasters in deep rock engineering usually occur at the bottom/top or two sides of the tunnel [66,67,68], depending on the stress distribution. In this study, the spalling failure is found to happen where the dynamic concentrated compressive stress is greatest, i.e., the roof and floor of the circular cavity in the samples. Obviously, the laboratory findings are consistent with the actual engineering, which is beneficial to the prevention and control of rock disasters. Given that the cross-sectional shapes of the openings in rock engineering are mostly noncircular, such as horseshoe, rectangle, trapezoid, and inverted U-shape. Therefore, the dynamic failure response and stress distributions around these openings in rock samples under impact loads will be further studied in the next work. Also, considering the dual effects of the blasting dynamic load and geo-stress exerted on the tunnel, we will explore the failure behavior of rock samples with openings under static-dynamic coupled loads in the future. Moreover, the possible influencing factors such as lithology, discontinuities, loading methods, opening shape, number as well as their configuration will be taken into account.

5 Conclusions

In this paper, the dynamic mechanical response and energy dissipation of rock samples having a circular cavity of different sizes were deeply investigated via a modified SHPB test equipment. Based on the experimental and theoretical analysis results, the following points can be concluded:

  1. (1)

    The mechanical parameters of the rock sample having a cavity such as dynamic compressive strength, peak strain and brittleness index are greatly degraded by the cavity, and the weakening degree relies on the cavity radius.

  2. (2)

    Under dynamic loads, no tensile cracks as in uniaxial loading tests are formed, and spalling cracks occur first on the top and bottom of the cavity, followed by the shear cracks appearing on the diagonals. The intersection of the shear cracks with the cavity brings about the instability of the sample, with a shear failure mode. With the rise of the cavity radius, both the dissipated energy density and fractal dimension increases gradually. This indicates that the sample failure is more and more severe, and the rock fragments are getting smaller and smaller.

  3. (3)

    On the boundary of the circular cavity, the maximum compressive stress concentration factor is about 2.8 on the roof and floor, while the minimum value is close to zero on the sidewalls. The dynamic stress distribution law can fully explain the fracture development around the cavity under impact loading.