1 Introduction

The origin of light and matter has been a profound mystery. However, our inherently induced curiosity and quest for understanding nature led us to study them. We wonder how we exist, and how and why the universe formed and evolved. As human intelligence evolved, many scientific theories were proposed to explain the formation of the universe. Of these theories, the Big Bang theory is the most widely accepted, as it has relatively the most logical statements and arguments in it. Further, nowadays mathematical proofs, simulations, and experimental explanations are available to support it. However, there are many fundamental questions, for instance, the cause of the Big Bang, the existence of the universe, and its expansion are yet to be addressed by Big Bang theory [1,2,3].

Soon after the Big Bang, the universe was superhot (nearly 1015 Kelvin) and a super-dense gravy of elementary particles namely up-quarks, down-quarks, gluons, electrons, photons, and neutrinos [4,5,6]. The exponential expansion of the early universe helped to cool down the elementary particles, enabling the interaction and formation of heavier particles such as protons and neutrons. According to Big Bang theory, between 2 and 20 min after the Big Bang, nuclear fusion reactions occurred, which, in turn, produced the light elements, namely, hydrogen, helium, and deuterium in the form of ions, the phenomenon is called Big Bang nucleosynthesis [7]. In the first 380,000 years after the Big Bang, the universe was too hot for light to shine [8]. The photons also took birth with nuclear fusion but they were constantly being scattered by the free ions, making the universe misty. In the dense plasma, photons were scattered by ions and nearly trapped. After 380,000 years, the universe had cooled enough for electrons to get bound with protons and neutrons in such a way that electrons formed a cloud of probability around the nucleus (made up of protons and neutrons) of the atom. This process is known as the epoch of recombination[9]. When the density of free electrons was reduced significantly, the photons were no longer trapped and they had a high degree of freedom to travel freely through the universe with their natural velocity. The light that we see today as the cosmic microwave background is the remnant radiation from the Big Bang [10]. In the first few hundred million years, the first stars and galaxies were formed. These stars and galaxies then began to produce heavier elements through nuclear fusion reactions. The heavier elements eventually formed planets, including Earth. The evolution of light and matter after the Big Bang was a complex process. It is fascinating to explore how the universe evolved from a hot and dense soup of elementary particles to the complex, beautiful, and nonlinear place that we see today [11].

Nonlinear dynamics is abundant in nature and hence nonlinear waves are ubiquitous. For the first time, in 1834, John Scott Russell observed a wave solitary in nature in the Union Canal. He named this wave as "great wave of translation," and he conducted extensive experiments to study its properties [12, 13]. However, this solitary wave is considered to be a fundamental property of nature that dates back to the beginning of the universe and may be as old as the inflationary epoch. The solitary wave can be induced in a wide variety of systems such as water medium, plasma, acoustic medium, magnetic medium, dielectric medium, biological systems, etc. [14]. Of these media, nonlinear waves, namely, tsunamis, rouge waves, and solitary waves are commonly observed in water medium. In biological systems, nonlinear waves have been observed in the propagation of nerve impulses, and they play a role in the transmission of genetic information as well [15, 16].

Unfortunately, initial observations made by John Scott Russell on solitary wave met with scepticism. Later, his work was ultimately validated by the theoretical research of Dutch physicists Diederik Korteweg and Gustav de Vries. In 1895, Korteweg and de Vries derived a mathematical equation for describing the propagation of solitary wave. This equation, now known as the Korteweg-de Vries (KdV) equation, is one of the most important equations in the theory of nonlinear waves [17, 18]. After the successful theoretical modelling of solitary waves, there has been a growing interest in nonlinear waves. The concept of solitons emerged in the 1960s within the realm of integrable models. In 1965, Zabusky and Kruskal demonstrated a stable solitary wave solution to the KdV equation numerically and coined the term "soliton" for its particle-like behavior [19]. Then, in 1967, Gardner et al. developed the Inverse Scattering Transform (IST) for analytically solving nonlinear evolution equations like the KdV [20]. This paved the way for further exploration of solitons in integrable systems.

In 1972, a significant breakthrough took place by Zakharov and Shabat who applied the IST to solve the nonlinear Schrödinger (NLS) equation and reported the soliton solution [21]. The NLS equation, describing wave propagation in dispersive media like optical fibers, offered a more general framework than the KdV. Notably, Hasegawa and Tappert theoretically predicted the stable soliton propagation in optical fibers in 1973 due to the interplay between dispersion and nonlinearity [22]. This finding laid the groundwork for experimental observations. Seven years later in the year 1980, for the first time, Mollenauer et al. successfully demonstrated the soliton pulse propagation in single-mode optical fibers [23]. Then, subsequently, Mitschke and Mollenauer explored the interactions of soliton pulses in detail in the year 1987[24]. Further, in 1987, Curtis Menyuk published a pivotal paper where he derived the coupled nonlinear Schrödinger (CNLS) equation to describe the soliton pulse propagation in single-mode optical fibers under weak birefringence [25]. In 1988, Christodoulides and Joseph predicted a novel form of phase-locked vector solitons in birefringent dispersive media called higher-order phase-locked vector solitons [26]. In 1991, Malomed achieved a significant theoretical advance by demonstrating that bound soliton states could exist within a perturbed NLS equation [27]. Then, in 1997, Akhmadiev et.al analyzed the stable soliton-bound states by solving the complex Ginzburg–Landau (CGL) equation [28, 29]. Later, stable bound soliton was demonstrated experimentally in a mode-locked fiber laser in 2001. Further, between 2001 and 2009, various natures of bound states of solitons such as various types of phase oscillations and temporal vibrations, pulsation, weak and strong interactions were observed experimentally [28, 30, 31]. Initially, these bound states of solitons were referred as soliton pairs and then they were renamed as soliton molecules [28, 32]. In subsequent years, investigations were extended to encompass soliton complexes and soliton crystals [33, 34].

This review article aims to illuminate the captivating phenomenon of solitons, from their fundamental formation in conservative media to their intricate behavior in dissipative systems. In order to introduce the idea of solitary wave and its entire evolution, especially, the formation of solitons in optical fibers and fiber lasers to the novice and to illuminate the promising avenues for future research directions, this review article provides a foundational understanding of wave propagation in diverse media and the intriguing phenomenon of soliton formation. The article provides a comprehensive review of research studies on optical soliton formation in various nonlinear systems. It reviews a few important research works on optical soliton formation and multi-soliton interaction in systems that are described by the NLS equation, modified and extended forms of the NLS equation, and coupled NLS equations. Further, it also reviews the recent research studies and advancement on dissipative soliton, soliton molecules, and soliton complexes in the dissipative optical systems where the wave propagation is usually governed by the complex Ginzburg–Landau (CGL) equation and its variants. Besides, it also includes research studies on soliton crystal and optical soliton microcomb in the optical microresonators which are modelled by the Lugiato-Lefever (LL) equation.

This transition unlocks a treasure trove of intriguing dynamics and potential applications that were previously unseen in conservative environments. It unveils how solitons, once confined to conservative systems, exhibit fascinating new behaviors and functionalities when introduced into dissipative environments. Notably, the review emphasizes the generation of a rich tapestry of interaction dynamics of higher-order solitons by tuning the physical parameters. Thus, the ability to control the dynamics of optical solitons paves the way for their applications in a diverse range of scientific and technological domains. If the light pulses could be sculpted and manipulated at will, then this will lead to ground-breaking advancements in various fields such as optical communication, optical signal processing, biomedical Imaging, quantum technologies, etc.

Through a critical analysis of existing literature, the review identifies the following intriguing research gaps. We find that there is a limited understanding of how weak and long-range interactions between solitons more than 2 solitons affect their dynamics. Further, there is a need for more comprehensive models that can capture the broad spectrum of soliton behaviour under various influences such as optomechanical interplay, anisotropy (direction-dependence) in dispersion, diffraction, nonlinearity, etc. By addressing these research gaps, one can gain a deeper understanding of solitons and unlock their full potential for applications in various fields. This review article distinguishes itself from others by offering a unique perspective. Table 1 clearly demonstrates how this review addresses research gaps not covered in previous works.

Table 1 To provide a clearer context for this review's contribution, the following table summarizes previously published review articles on soliton molecules. It highlights how this review expands the discussion by incorporating dissipative solitons, soliton molecules, and soliton crystals
Full size table

The review article is laid out as follows. Section 2 briefly explores the evolution of the theory of light and matter and the nature of light-matter interaction. Section 3 then delves into wave and wave packet behavior across various media, highlighting their unique properties. Section 4 introduces optical solitons within the framework of integrable models. It emphasizes the crucial roles of nonlinearity and dispersion in soliton formation. Additionally, this section reviews several unique soliton interaction phenomena and explores bound states of solitons in integrable models. In Sect. 5, we turn our attention to solitons that arise from the CNLS equation. Here, the resulting solitons are known as vector solitons and they are discussed, in detail, by emphasizing their nature as bound states of two orthogonally polarized solitons. Section 6 incorporates comprehensive information on optical spatial solitons, photorefractive solitons, and quadratic solitons, detailing their formation, nature, recent studies, and applications. Additionally, Sects. 7, and 8 incorporate information on spatiotemporal solitons and soliton bubbles respectively. Finally, Sect. 9 explores solitons in dissipative optical media by examining their interaction dynamics. In this section, we also briefly discuss the formation of soliton molecules, soliton complexes, soliton crystals, and soliton combs. Finally, we also point out their potential applications and how current and future research endeavors would lead us to Photobot.

2 Light and matter

There is a long scientific history where the nature of atoms and light was studied extensively by many scientists. Figure 1 presents a timeline of key contributions to the understanding of atomic structure and the nature of light.

Fig. 1
figure 1

Flowchart Top-row shows the evolution of the atomics’ model [38, 39]; Bottom-row shows the evolution of the theory of light [40]

Full size image

It should be emphasized that Aryabhata's theory of light is based on his observations of the eclipses of the Sun and Moon in 500 BC. Unfortunately, it was not noticed by the scholars. He noticed that the eclipses are always sharp and well-defined even when the sun and moon are very close to each other. Based on this fact, he suggested that light must be made up of very small particles that could travel in a straight line [41,42,43,44]. As depicted in the flowchart of Fig. 1, other theories are well-known to the world and the corresponding details are available in the literature. Hence, we do not emphasize them here. At this juncture, we would like to emphasize that the research works of these scientists also led to a quantum mechanical explanation of light-matter interaction.

2.1 Interaction of light with matter

When photons interact with atoms, they can undergo various processes, such as absorption, emission, scattering, etc. In general, these interactions can be understood from various theoretical perspectives. According to the corpuscular theory, light particles travel in a straight line collide with matter, and scatter like particles. In contrast, wave theory describes light as a wave, which is capable of explaining reflection, refraction, diffraction, and interference when light interacts with matter, passes through the boundary between two media, or slit [40]. With experiments like black-body radiation, photoelectric effect, and Compton effect, one understands that the light is quantized in nature where each quanta is referred as a photon of energy 'hϑ'. Thus, light exhibits wave-particle duality. When electromagnetic radiation is shined in a dielectric material, material polarization takes place when energy of photon is not equal to the excitation energy of the atom. That is, owing to wave nature of photon, oscillating electric field components create an oscillating electron cloud around the nucleus. On the other hand, when energy of a photon matches with the energy required to excite an electron, it excites an atom i.e. owing to its particle nature. Hence wave-like or particle-like nature of photons can dominate, depending on the energy of the photon and the energy band of the material. Figure 2 illustrates the interaction of light with an atom where the photon is treated as both wave and particle and the corresponding probability is represented by \({P}_{1}^{2}\) and \({P}_{2}^{2}\), respectively that results in the possibility of photon emission and/or polarization of the atom with the probability of \({P}_{3}^{2}\) and \({P}_{4}^{2}\), respectively.

Fig. 2
figure 2

Illustration of the interaction of light with matter in two primary ways, either as photons (P1) or as electromagnetic waves (P2). These interactions can lead to two possible phenomena: photon emission (P3) or the polarization of atoms (P4)

Full size image

With the help of the particle nature of a photon, the fundamental processes, namely, absorption (that leads to energy level transitions and plays a key role in absorption spectroscopy), spontaneous emission (results in natural light sources and is fundamental in fluorescence and phosphorescence), stimulated emission (crucial for laser operation, produces coherent and amplified light), and multi-photon absorption and emission (in which atom can absorb multiple photons and can emit photons of double or triple frequency called higher-order harmonic generation) can be explained [45]. These interactions are used in various scientific techniques such as lasers, environmental monitoring, material characterization, etc. When highly intense light interacts with a dielectric material, it linearly as well as nonlinearly polarizes the atoms [45]. The polarization oscillation of atoms due to electromagnetic waves can be represented as follows.

$$\overrightarrow{P}={\varepsilon }_{0}\left({\chi }^{\left(1\right)}.\overrightarrow{E}+{\chi }^{\left(2\right)}:\overrightarrow{E}\overrightarrow{E}+{\chi }^{\left(3\right)}\vdots \overrightarrow{E}\overrightarrow{E}\overrightarrow{E}+\cdots \right)$$
(1)

Here, \({\varepsilon }_{0}\) is permittivity of free space, \({\chi }^{\left(i\right)}\) is ith order susceptibility of dielectric medium where i = 1, 2, 3…; \(\overrightarrow{E}\) is the electric field vector of electromagnetic wave. Higher-order susceptibilities get induced to a non-negligible value whenever intense light interacts with the atom. In nonlinear polarization, diverse phenomena occur such as self-phase modulation, cross-phase modulation, four-wave mixing of light, etc. In silica optical fiber, due to centrosymmetric nature, even-order susceptibilities are zero, and odd-order susceptibilities only contribute [21].

3 Dynamics of waves in diverse optical media

Having understood the fundamental light-matter interaction and the corresponding linear and nonlinear characteristics, in what follows, we discuss the light wave propagation in both linear and nonlinear media. Thus, in this section, we intend to explore the dynamics of light wave propagation individually in the linear non-dispersive medium, linear dispersive medium, nonlinear non-dispersive medium, and nonlinear dispersive medium. Here, we discuss these four special cases in the following sub-sections.

3.1 Wave propagation in a linear non-dispersive medium

A wave in a linear non-dispersive medium, in general, is modelled by a wave equation and the same is given by

$$\frac{{\partial }^{2}q}{\partial {z}^{2}}- \frac{1}{{v}^{2}}\frac{{\partial }^{2}q}{\partial {t}^{2}}=0$$
(2)

The general solution of the wave equation is given by the following form

$$q\left(z,t\right)=f\left(z-vt\right)+g\left(z+vt\right)$$
(3)

here q(z,t) is the amplitude of the wave. The parameters f and g are arbitrary functions. Here, v is the velocity of the wave. One of the possible solutions of Eq. (2) is given by \(q=Acos\left(kz-\omega t\right)\). On substituting it in Eq. (2), we get the dispersion relation as \(\omega = \pm vk\). i.e. \({v}_{p}= {v}_{g}= \pm v\). Hence individual wave travels with the same phase velocity irrespective of its frequency. Thus, in linear non-dispersive medium, all waves travel with the same velocity ‘\(v\)’. Even if they form wave packets by superposition, then the wave packet does not experience dispersion. Hence, the wave packet does propagate without change in its shape throughout the propagation. This type of wave propagation is called non-dispersive as the waves or wave packets do not spread out during the propagation [46]. This kind of light wave propagation can be understood in a vacuum.

3.2 Wave propagation in a linear dispersive medium

In many materials such as beams, rods, damped oscillators, and even air, the inherent nature of the material forces atoms to vibrate back and forth with respect to equilibrium position. These materials are called linear dispersive media. This means that waves traveling through these materials will spread out over time as the different frequencies travel with different velocities. Examples of other linear dispersive media include water waves on various water bodies, propagation of sound waves and light waves. The inclusion of such effects necessarily modifies the wave Eq. (2) [46]. To study the effect of dispersion, we use the following wave equation.

$$i\frac{\partial q}{\partial z}+ \sigma \frac{{\partial }^{2}q}{\partial {t}^{2}}=0$$
(4)

here, \(\sigma\) is called dispersion coefficient of medium. General solution of a linear dispersive wave can be considered as a linear superposition of elementary waves of the following form

$$q\left(z,t\right)=q\left(k\right){e}^{i\left(kz-\omega t\right)}$$
(5)

here ‘\(k\)’ is a propagation constant and \(\omega\) is an angular frequency of the wave [13]. Substituting Eq. (5) in Eq. (4), we get the dispersion relation of the following form,

$$k+ \sigma {\omega }^{2}=0$$
(6)

Using this relation, one can obtain the expressions for phase velocity \({(v}_{p})= \pm \sqrt{\frac{k}{\sigma }}\) and group velocity \({(v}_{g})= \pm \frac{1}{2\sqrt{\sigma k}}\). From these relations, it is very clear that, in any dispersive media, the phase velocity is not equal to group velocity (\({v}_{p}\ne {v}_{g}\)). Here phase velocity of the individual wave depends on the frequency of the wave. Thus, when a wave packet travels in a medium for example electromagnetic (EM) wave in optical fiber, the different spectral components experience different refractive indices and hence they move with different phase velocities. As a result, the wave packet experiences a dispersion called group velocity dispersion (GVD). To account for the effects of fiber dispersion mathematically, the mode-propagation constant \(\beta (\omega )\) of traveling EM wave can be expanded in a Taylor series around the central frequency \({\omega }_{0}\) of the pulse spectrum:

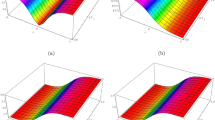
$$\begin{array}{c}\beta (\omega )=n(\omega )\frac{\omega }{c}={\beta }_{0}+{\beta }_{1}\left(\omega -{\omega }_{0}\right)+\frac{1}{2}{\beta }_{2}{\left(\omega -{\omega }_{0}\right)}^{2}+\cdots \\ {\beta }_{m}={\left(\frac{{d}^{m}\beta }{d{\omega }^{m}}\right)}_{\omega ={\omega }_{0}}(m=\text{0,1},2,\dots )\end{array}$$
(7)

Here \({\beta }_{0}\) corresponds to the diffraction parameter of the traveling wave, \({\beta }_{1}\) is the first-order dispersion parameter that is inverse of group velocity at the central frequency, \({\beta }_{2}\) is the second-order dispersion parameter also known as the GVD coefficient. There are two types of GVDs, namely, normal/ positive GVD and anomalous/negative GVD. In positive GVD, the shorter-wavelength components of a wave travel slower than that of longer-wavelength components. Hence, the wave packet acquires positive chirp/up-chirp. On the other hand, in negative GVD, the shorter-wavelength components of a wave travel faster than that of longer-wavelength components. Here, the wave packet undergoes negative chirp/down-chirp. The propagation of wave packet in various optical media is illustrated in Fig. 3c where one can observe the wave packet undergoing different chirps depending on the nature of the medium [21].

Fig. 3
figure 3

a Classification of optical media based on the type of dispersion and nonlinearity for conservative and b non-conservative media c Effect on wave packet when it propagates through optical media that has the induvial effect of positive and negative dispersions, nonlinearity and dissipation

Full size image

3.3 Wave propagation in a nonlinear non-dispersive medium

Linear dynamics is an inherent simplification of nonlinear dynamics for the sake of mathematical tractability. Rather than shying away from the mathematical complexity of nonlinearity to make our models easier to solve, we should embrace its ubiquity in nature and explore its profound significance, beauty, consequences, and applications [14, 46, 47]. Owing to the presence of intense driving forces, sensitive media and intricate interactions among dynamical components of the systems, the system naturally becomes complex and nonlinear.

In general, nonlinearity depends on the properties of the medium and wave. Even though it is highly challenging to realize the nonlinear non-dispersive media, it is highly useful to understand the influence of nonlinearity over wave packets. In this case, the wave propagation is described by the following nonlinear equation without dispersion,

$$i\frac{\partial q}{\partial z}+\mu {\left|q\right|}^{2}q=0$$
(8)

here \(\mu\) is called the nonlinear coefficient of the medium. By substituting \(q=\left|{q}_{0}\right|{e}^{i\varphi \left(t\right)}\) into Eq. (8), the following phase relationship can be obtained,

$$\varphi \left(t\right)= \varphi \left(0\right)-{\mu \left|q\left(0\right)\right|}^{2}t$$
(9)

Equation (9) gives a physical intuition about the modulation in phase over time that is proportional to the intensity of the input pulse. This effect is called self-phase modulation (SPM). It is named as SPM because the phase of the light pulse gets modulated by its own intensity. This SPM causes a wave packet to spread its energy over a larger bandwidth keeping the temporal profile of the pulse unchanged. In Eq. (9), as \(t\to \infty\), \(\varphi \left(t\right) \to \infty\), i.e. SPM increases without any bound. However, in realistic media, energy loss is unavoidable due to inherent attenuation. Consequently, the SPM reaches a saturation point [21, 48].

3.4 Wave propagation in a nonlinear dispersive medium

In this subsection, we consider the wave propagation in a realistic medium that exhibits both dispersive and nonlinear effects. When an intense light pulse or a train of wave packets is formed due to the superposition of a few intense waves in optical fibers (or some other dielectric media), it induces higher-order susceptibility and hence nonlinear refractive index in the media [21]. The NLS equation can be derived from Maxwell’s equations under the assumption of nonlinear material polarization, slowly varying envelope approximation, and paraxial approximation. Thus, NLS equation successfully describes the pulse propagation in optical fibers.

$$i\frac{\partial A}{\partial z}-\frac{{\beta }_{2}}{2}\frac{{\partial }^{2}A}{\partial {T}^{2}}+\gamma {\left|A\right|}^{2}A- \frac{i\alpha }{2}A=0$$
(10)

here, A = A(z,T) is the slowly varying amplitude of envelope, \({\beta }_{2}\) is the GVD parameter, \(\gamma\) is nonlinear parameter, \(\alpha\) is loss parameter and T is measured in a frame of reference moving with the pulse at group velocity vg (T = \(\tau -z/{v}_{g})\) inside single mode optical fibers. By using a time scale normalized to the input pulse T0 as \(t=\frac{T}{{T}_{0}}= \frac{\tau -\frac{z}{{v}_{g}}}{{T}_{0}}\), and normalized amplitude U as \(A\left(z,t\right)= \sqrt{{P}_{0}}\text{exp}\left(-\frac{\alpha z}{2}\right)q\left(z,\tau \right)\) [21]. Here, P0 is peak power of the incident pulse. By introducing these scaling Eq. (10), can be re-written as,

$$i\frac{\partial q}{\partial z}-\frac{sgn\left({\beta }_{2}\right)}{2{L}_{D}}\frac{{\partial }^{2}q}{\partial {t}^{2}}+\frac{\text{exp}\left(-\alpha z\right)}{{L}_{NL}}{\left|q\right|}^{2}q=0$$
(11)

here, \(sgn\left({\beta }_{2}\right)=\pm 1\) and it represents the type of GVD. Further, LD and LNL are dispersion and nonlinear lengths, respectively and they are expressed by \({L}_{D}=\frac{{T}_{0}^{2}}{\left|{\beta }_{2}\right|}, {L}_{NL}=\frac{1}{\gamma {P}_{0}}\). When the fiber and pulse parameters are such that \(\frac{{L}_{D}}{{L}_{NL}}\ll 1\), the regime is dispersion dominant and when \(\frac{{L}_{D}}{{L}_{NL}}\gg 1\), the regime is nonlinearity dominant. If the fiber length is longer or comparable to both LD and LNL, then dispersion and nonlinearity effects interplay. Finally, this process leads to different behavior when compared with GVD or SPM effect alone. In anomalous dispersion (\({\beta }_{2}<0)\), the formation of optical soliton pulse takes place and the normal dispersion \({(\beta }_{2}>0)\) can be used for pulse compression [21].

In order to provide the more insightful information on the dynamics of optical pulse propagation in conservative media with four different special cases, we provide the graphical representation in Fig. 3 where the effects due to non-conservative media is also taken into account. Further, Table 2 summarizes the effects, due to various conservative and non-conservative media, over the pulse propagation. It is known that in a non-conservative system, either gain or loss is dominant depending upon the nature of the system. Further, both gain and loss can also be equally present in the system. Here, in what follows, we delineate the wave propagation in the above-mentioned special cases of both conservative and non-conservative systems. Figure 3a depicts the various possible media in terms of χ (nonlinearity coefficient) and β (dispersive coefficient) for wave propagation in the conservative system. On the other hand, gain (α) and loss (-α) media are portrayed in Fig. 3b in a non-conservative system. Further, the propagation of wave packet is also presented in various optical media that cover both conservative and non-conservative systems as shown in Fig. 3c.

Table 2 The following table summarises various types of medium, their properties, and the effect on wave packets in that media
Full size table

4 Nonlinearity in optical fibers and formation of optical soliton

When an intense light pulse propagates through an optical fiber, its high power density interacts with the silica glass that makes up the fiber core. This interaction distorts the balance between the electric field of the light and the response of the electrons within the glass molecules. The result is a nonlinear effect, where the refractive index of the fiber becomes dependent on the intensity of the light itself. This intensity-dependent refractive index is a key characteristic of optical nonlinearity. In centrosymmetric materials such as silica glass, the second-order susceptibility (which gives rise to effects like second-harmonic generation) cancels out due to symmetry. However, odd-order susceptibilities remain nonzero and play a key role in the nonlinear behavior of optical fibers [21]. Thus, the third-order nonlinearity is the fundamental nonlinearity and is also called the Kerr effect which basically induces SPM effect in optical pulses.

Having understood the origin of nonlinearity in optical fibers, the next step is to investigate the formation of optical solitons. For convenience, we introduce the following scaling variables for getting the dimensionless variables [21].

$$q=\frac{q}{\rho },t=\frac{\text{t}}{{a}_{0}},z=\frac{\text{z}}{{L}_{D}}, \psi =\frac{A\rho }{{\sqrt{P}}_{0}},\gamma =\frac{\mu {P}_{0}{L}_{D}}{{\rho }^{2}}$$
(12)

here \(\rho\) is the radius of the beam,\({a}_{0}\) is initial pulse width, \({P}_{0}\) is peak power of the pulse. By using the above scaling variables in Eq. (11), the dimensionless NLS equation can be written as

$$i\frac{\partial q}{\partial z}+\sigma \frac{{\partial }^{2}q}{\partial {t}^{2}}+\mu {\left|q\right|}^{2}q=0$$
(13)

here, \(\sigma\) and \(\mu\) are the dimensionless GVD and nonlinear coefficients, respectively. Here, a dynamic balance between the chirp produced by the anomalous GVD and the chirp induced by SPM leads to the formation of a fundamental soliton. The solitons described by Eq. (13) are known as temporal solitons. This is because they arise from a balance between the effects of nonlinearity and group velocity dispersion (GVD) along the propagation axis, which preserves the pulse shape during transmission. The term "soliton" is the Latin word "solum" meaning "whole" or "unbroken". An optical soliton can be understood as a self-localized wave-packet of electromagnetic energy that maintains its shape and integrity over long propagation distances due to a delicate dynamical interplay between dispersion and nonlinearity. It can also be thought of as a well-confined electromagnetic field around a stable equilibrium point in phase space.

It is obvious that the NLS equation possesses the one-soliton solution. Mathematically, the one soliton solution is represented by the hyperbolic secant function, i.e., “sech”. One soliton solution can be of the order N where order of soliton can be determined by \(({N}^{2}= \frac{{L}_{D}}{{L}_{NL}}).\) Here N = 1, Soliton will be of the order one also called one fundamental soliton. Higher-order soliton solutions in some systems can display breather-like characteristics Here, an Nth-order order soliton breather is represented by \(q\left(t, z=0\right)= \sum_{j=1}^{N}{a}_{j}\text{sech}\left(t\right)\) where the pulse amplitude is given by aj = (2j − 1) for j = 1, 2,….,N. In addition to the one soliton, NLS equation has 2,3,…,n soliton solution. Note that Nth-order soliton refers to a higher energy single soliton pulse that maintains its shape and can break to multiple fundamental soliton due to the instability various the combined waveform of an n-soliton solution results from the nonlinear superposition of these individual soliton pulses. Unlike linear superposition, the solitons can influence each other's shape and dynamics in complex ways. N-soliton solutions represent a special type of solution where ‘N’ individual solitons interact nonlinearly while maintaining their overall shape and identities. Each soliton within the solution is characterized by its amplitude, width, phase, and velocity. At this juncture, it should be emphasized that there is no binding energy between the solitons in the breathers. That is, the total energy of the breather is equal to the sum of the energies of its constituent solitons [49]. The continuous interaction of the N-solitons gives rise to the periodic behaviour of the combined pulse. So far, several analytical methods [13, 50,51,52] have been proposed for studying 1 to N soliton solutions. For brevity, in what follows, we present the general form of a 2-soliton solution which was derived by using Hirota bilinear transformation [13].

$$q\left(z,t\right)=\frac{{e}^{{\eta }_{1}}+{e}^{{\eta }_{2}}+{e}^{{\eta }_{1}+{\eta }_{1}^{*}+{\eta }_{2}+{\delta }_{1}}+{e}^{{\eta }_{1}+{\eta }_{1}+{\eta }_{2}^{*}+{\delta }_{2}} }{1+{e}^{{\eta }_{1}+{\eta }_{1}^{*}+{R}_{1}}+{e}^{{\eta }_{1}+{\eta }_{2}^{*}+{\delta }_{0}}+{e}^{{\eta }_{1}^{*}+{\eta }_{2}+{\delta }_{0}^{*}}+{e}^{{\eta }_{2}+{\eta }_{2}^{*}+{\eta }_{2}+{R}_{2}}+{e}^{{\eta }_{1}+{\eta }_{1}^{*}+{\eta }_{2}^{*}+{\eta }_{2}+{R}_{3}}}$$
(14)

where;

k1 and k2 are complex propagation constants in the seed solution,

$${\eta }_{1}={k}_{1}x+i{k}_{1}^{2}t, {\eta }_{2}={k}_{2}x+i{k}_{2}^{2}t, {e}^{{\delta }_{0}}=\frac{1}{{\left({k}_{1}+{k}_{2}^{*}\right)}^{2}}, { e}^{{R}_{1}}=\frac{1}{{\left({k}_{1}+{k}_{1}^{*}\right)}^{2}}, { e}^{{R}_{2}}=\frac{1}{{\left({k}_{2}+{k}_{2}^{*}\right)}^{2}}, { e}^{{\delta }_{1}}=\frac{{\left({k}_{1}-{k}_{2}\right)}^{2}}{{\left({k}_{1}+{k}_{2}^{*}\right)}^{2}{\left({k}_{1}^{*}+{k}_{2}\right)}^{2}}, { e}^{{\delta }_{2}}=\frac{{\left({k}_{1}-{k}_{2}\right)}^{2}}{{\left({k}_{2}+{k}_{2}^{*}\right)}^{2}{\left({k}_{1}+{k}_{1}^{*}\right)}^{2}}$$
(15)

In general, it is difficult to have a complete understanding of the above-presented two-soliton solution as it is a nonlinear superposition of two solitons. However, this multifaceted two-soliton solution offers a wide range of optical operations such as all-optical switching, all-optical universal logic gates of NAND and NOR, pulse compression by higher-order solitons, etc. for various values of k1 and k2 [53]. We find the most important and interesting special cases when the eigenvalues k1 and k2 maintain a ratio of 1 and 3. Under these parametric conditions, the general two-soliton solution becomes a familiar hyperbolic secant shape whose initial amplitude is doubled i.e., 2sech(t) [54]. For the first time, Satsuma and Yajima [49] reported this special 2-soliton breather and later it was also observed experimentally in both planar waveguides and optical fibers [55,56,57].

The typical 1-soliton solution and 2-soliton solutions are depicted in Fig. 4a, b for various propagation constants and phase differences.

Fig. 4
figure 4

a Illustrate particle-like shape preservation and energy stability in soliton when it propagates for k1 = 1 + 0.3i and in b particle-like perfect elastic collision can be observed where two solitons collide and reemerge without any change in its energy and shape chosen prorogation constants are k1 = 2 + 2i, k2 = 1 – 1i, \({\eta }_{10}=0,\) and \({\eta }_{20}=0\)

Full size image

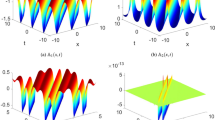
From Fig. 4a, it is clear that a single soliton propagates without any change in its shape, energy, or velocity. Further, when two solitons collide with each other as in Fig. 4b, all the important physical parameters (i.e. shape, energy, and velocity) remain constant except the phase. From this, one can understand the particle-like behaviour of soliton pulses. This kind of behaviour of higher-order solitons has been observed under the influence of higher-order linear and nonlinear effects where the pulse propagation is governed by a modified NLS equation [58, 59]. In addition to the two soliton interactions, as depicted in Fig. 5a, one can also observe the two distinct soliton pulses, separated by a finite distance, also known as a soliton pair which occurs for the following physical parameters of k1 = 1 + 1i, k2 = 1.1 + 1.1i, \({\eta }_{10}=0,\) and \({\eta }_{20}=1+i\). In this case, the soliton pair propagates without energy exchange. Figure 5b represents the evolution of a special 2-soliton pulse whose amplitude is twice of the fundamental soliton when k1 = 3 + 1i, k2 = 1 + 1i, \({\eta }_{10}=1+i,\) and \({\eta }_{20}=0\).

Fig. 5
figure 5

a Illustrate Soliton pair propagation for k1 = 1 + 1i, k2 = 1.1 + 1.1i, \({\eta }_{10}=0,\) and \({\eta }_{20}=1+i\) and b is periodic interaction between 2-soliton for k1 = 3 + 1i, k2 = 1 + 1i, \({\eta }_{10}=0,\) and \({\eta }_{20}=0\)

Full size image

In Fig. 5b, it is found that the periodic interaction between two solitons causes periodic pulsation in amplitude where the period of oscillation is \(\frac{\pi }{2}.\) Similarly, a few other cases like periodic, quasi-periodic, and aperiodic oscillation between 2-solitons were also observed. Such soliton solutions are also studied by solving the modified NLS-type equations[58, 60].

Soliton propagation is described by various models beyond the ubiquitous NLS-equation. Examples include the complex Ginzburg–Landau equation, Lakshmanan-Porsezian-Daniel model, Radhakrishnan–Kundu–Lakshmanan (RKL) model, Chen-Lee-Liu equation, cascaded systems, Gerdjikov-Ivanov equation, Kudryashov’s generalized nonlocal nonlinear model, Kaup-Newell equation, and the Sasa-Satsuma equation [61,62,63,64,65,66]. Recently, an exploration of soliton behavior in a perturbed Gerdjikov-Ivanov equation was also proposed [67]. In an another recent study, with the Darboux transformation approach, exact two and three-soliton solutions for a higher-order NLS equation with variable coefficients were obtained. These studies explore soliton interaction, propagation, and even show attosecond regime-switching for the first time. Additionally, the impact of variable coefficients is investigated [68]. Further Darboux transformation was used to obtain 3 and 4 soliton solutions for high-speed data transmission applications and to investigate the generation of non-autonomous rogue waves [69, 70].

5 Birefringence in optical fibers and formation of vector soliton-bound state

Birefringence in optical fibers can be either linear or nonlinear. Linear birefringence arises from inherent asymmetries in the fiber's geometry or stress, causing a constant difference in refractive index for different polarization modes. Nonlinear birefringence, on the other hand, is caused by the intensity of the light itself and is mediated through the Kerr effect. Cross-phase modulation (XPM), a consequence of the Kerr effect, allows the two polarization components to interact. Vector soliton formation requires this nonlinear interaction: the nonlinear coupling from XPM must precisely counterbalance the linear birefringence and dispersive effects that tend to separate the polarization components. This balance leads to a stable pulse with a fixed polarization state that propagates as a vector soliton. Pulse propagation in such optical fibers can be modeled using a coupled CNLS equation, which accounts for the interplay of dispersion, linear birefringence, and nonlinear effects like XPM [21, 26, 71].

$$\begin{array}{c}i{q}_{1,z}+{q}_{1,tt}+2\mu \left({\left|{q}_{1}\right|}^{2}+{\left|{q}_{2}\right|}^{2}\right){q}_{1}=0\\ i{q}_{2,z}+{q}_{2,tt}+2\mu \left({\left|{q}_{1}\right|}^{2}+{\left|{q}_{2}\right|}^{2}\right){q}_{2}=0\end{array}$$
(16)

Hirota bilinear transform can be used to obtain the 1, and 2 soliton solutions of the above Eq. 2 -soliton solution of Eq. (14) has the following form[72, 73].

$${q}_{j}=\frac{{\alpha }_{1}^{(j)}{e}^{{\eta }_{1}}+{\alpha }_{2}^{(j)}{e}^{{\eta }_{2}}+{e}^{{\eta }_{1}+{\eta }_{1}^{*}+{\eta }_{2}+{\delta }_{1j}}+{e}^{{\eta }_{1}+{\eta }_{2}+{\eta }_{2}^{*}+{\delta }_{2j}}}{1+{e}^{{\eta }_{1}+{\eta }_{1}^{*}+{R}_{1}}+{e}^{{\eta }_{1}+{\eta }_{2}^{*}+{\delta }_{0}}+{e}^{{\eta }_{1}^{*}+{\eta }_{2}+{\delta }_{0}^{*}}+{e}^{{\eta }_{2}+{\eta }_{2}^{*}+{R}_{2}}+{e}^{{\eta }_{1}+{\eta }_{1}^{*}+{\eta }_{2}+{\eta }_{2}^{*}+{R}_{3}}}, j=\text{1,2}$$
(17)

where,

$$\begin{array}{c} {\eta }_{j}={k}_{j}\left(t+i{k}_{j}z\right),\\ {e}^{{\delta }_{0}}=\frac{{\kappa }_{12}}{{k}_{1}+{k}_{2}^{*}},{e}^{{R}_{1}}=\frac{{\kappa }_{11}}{{k}_{1}+{k}_{1}^{*}},{e}^{{R}_{2}}=\frac{{\kappa }_{22}}{{k}_{2}+{k}_{2}^{*}},\\ \\ {e}^{{\delta }_{1j}}=\frac{\left({k}_{1}-{k}_{2}\right)\left({\alpha }_{1}^{\left(j\right)}{\kappa }_{21}-{\alpha }_{2}^{\left(j\right)}{\kappa }_{11}\right)}{\left({k}_{1}+{k}_{1}^{*}\right)\left({k}_{1}^{*}+{k}_{2}\right)},\\ {e}^{{\delta }_{2j}}=\frac{\left({k}_{2}-{k}_{1}\right)\left({\alpha }_{2}^{(j)}{\kappa }_{12}-{\alpha }_{1}^{(j)}{\kappa }_{22}\right)}{\left({k}_{2}+{k}_{2}^{*}\right)\left({k}_{1}+{k}_{2}^{*}\right)},\\ { e}^{{R}_{3}}=\frac{{\left|{k}_{1}-{k}_{2}\right|}^{2}}{\left({k}_{1}+{k}_{1}^{*}\right)\left({k}_{2}+{k}_{2}^{*}\right){\left|{k}_{1}+{k}_{2}^{*}\right|}^{2}}\left({\kappa }_{11}{\kappa }_{22}-{\kappa }_{12}{\kappa }_{21}\right),\\ {\kappa }_{jl}=\frac{\mu \left({\alpha }_{j}^{\left(1\right)}{\alpha }_{l}^{\left(1\right)*}+{\alpha }_{j}^{\left(2\right)}{\alpha }_{l}^{\left(2\right)*}\right)}{{k}_{j}+{k}_{l}^{*}}, j,l=\text{1,2}\end{array}$$
(18)

For the above 2-soliton solutions, several forms of vector soliton interactions have been observed with the following conditions of \({\alpha }_{1}^{(j)}={\alpha }_{2}^{(j)}=1, j=\text{1,2}\). Of these solutions, we present the following four interesting bound states.

From Fig. 6a–d, in all the above cases, the two solitons interaction facilitates the formation of a stable soliton pair and periodically interacting solitons. The beauty lies in tailoring soliton interactions by adjusting their propagation vectors. It shows how manipulating just a few key parameters can generate a rich tapestry of interaction dynamics within solitons. However, it has been proved that these interacting solitons do not have binding energy within them in the absence of dissipative effects, namely, gain and loss. Thus, they are unstable to any perturbations. As a result, these unstable soliton pairs cannot be treated as soliton molecules [27, 29].

Fig. 6
figure 6

a Periodic interaction between two orthogonally polarized soliton due to XPM for k1 = 1.0, k2 = 0.95 b Stable soliton pair of two orthogonally polarized soliton for k1 = 1.0, k2 = -0.95; c Pulsating vector soliton for k1 = 0.95, k2 = 1.95; d Pulsating vector soliton pairs for k1 = 1.90, k2 = 1.95

Full size image

To demonstrate the impact of gain and loss on the soliton dynamics observed in Fig. 6, we incorporate gain and loss terms into the vector soliton solution of Eq. (16). This modification includes a periodic gain term and an exponential loss term.

$${q}_{modified}= {q}_{j}\times {e}^{g \;\text{sin}(\frac{2\pi t}{T})}{e}^{-\alpha z}$$
(19)

here, g is the gain coefficient, T is time period of periodic gain, and \(\alpha\) as a loss coefficient. For T = 10, we have re-plotted plots of Fig. 6 for various gain and loss values.

Figure 7 incorporates the plots to summarize key dynamical features of vector solitons in the presence of gain and loss.

Fig. 7
figure 7

llustration of the variations in two-soliton interaction dynamics under different propagation constants (k1 and k2), both with and without the influence of gain and loss effects. Column 1 (Figs. 1a, 2a, 3a, and 4a) displays the pure solution of the CNLS equation (gain g = 0 and loss α = 0). Columns 2 (Figs. 1b, 2b, 3b, and 4b) and 3 (Figs. 1c, 2c, 3c, and 4c) show the effects on the pure two-soliton solutions of column 1 for (g = 0.1, α = 0.01) and (g = 5, α = 0.001) respectively

Full size image

Figure 7 demonstrates the change in the 2 soliton interaction dynamics for various values of propagation constants in the absence and presence of gain and loss effects. Each row in the figure shows the results for a specific propagation constant value of k1 and k2. Columns correspond to different gain and loss coefficients listed across the top row. In the first column of Fig. 3 (where gain, g = 0 and loss, α = 0), the vector solitons propagate without any change in shape or energy, as expected. In contrast, the second column (g = 0.1, α = 0.01) showcases the interplay between gain and loss. While the gain (g = 0.1) attempts to counteract the loss (α = 0.01), an exponential decrease in soliton intensity is observed as the loss value is higher. Finally, the third column (g = 5, α = 0.001) demonstrates a stronger gain (g = 5) that significantly mitigates the loss effect (α = 0.001) for relatively shorter distance propagation but the intensity of the pulse gets decayed when the pulse travels for a long distance. Further, at this juncture, it can be also observed that high gain (g = 5) alters the dynamics of the vector soliton pulses at propagation constant values k1 = 1.9, k2 = 1.95, and k1 = 1.0, k2 = 0.95.

In the integrable regime of Manakov systems (coupled NLS system), multi-soliton solutions and vector soliton solutions were studied extensively [50, 74,75,76,77]. A recent research study explores the RKL equation for dispersive optical solitons in birefringent optical fibers. While various numerical schemes successfully retrieved soliton solutions, a common flaw emerged—none captured "soliton radiation." This limits their robustness. Future work should focus on analytically capturing radiation effects using variational principles, asymptotic methods, or unfolding theory[61].

6 Optical spatial soliton

The solitons that are discussed in the previous sections are temporal solitons which demand a balance between GVD and nonlinearity for the formation. Unlike temporal solitons, the optical spatial solitons are self-trapped light beams which maintain the shape during the propagation. This self-trapping occurs due to a balance between diffraction, which tends to spread the beam, and nonlinear effects, which counteract this spreading. It is well established that optical spatial solitons are governed by the NLS equation of the following form, instead of GVD term, it incorporates the transverse diffraction.

$$i\frac{\partial \text{q}}{\partial z}+\frac{1}{2{\beta }_{0}}{\nabla }_{\perp }^{2}\text{q}+{\gamma |q|}^{2}q=0$$
(20)

here \({\nabla }_{\perp }^{2}=\frac{{\partial }^{2}}{{\partial x}^{2}}+ \frac{{\partial }^{2}}{{\partial y}^{2}}, {\beta }_{0}= \frac{2\pi n}{\lambda }, n\) is the refractive index, λ is the wavelength of the beam and \(\gamma\) represents self-focusing nonlinearity.

Like temporal solitons, these solitons also exhibit particle-like behavior, including attraction and repulsion, depending on their relative phase and distance. For example, in-phase solitons attract each other, whereas out-of-phase solitons repel. This interaction mimics the behavior of particles under various forces, providing a unique platform to study nonlinear dynamics and optical information processing [78,79,80]. A study demonstrates the potential of nematic liquid crystals for nonlinear optics applications by showcasing the formation and control of optical spatial solitons through reorientational nonlinearity, requiring minimal power and being influenced by light polarization and external electric fields [81, 82]. All-optical switching and logic operations using spatial solitons were demonstrated in nematic liquid crystals. Further, AND and NOR gates through soliton-induced waveguide formation and their collisional behaviours were also reported [82]. Recent advancements have focused on the practical implementation of nonlocal nonlinear media in photonic devices, exploring new materials and configurations to optimize soliton properties. Advances in material science and fabrication techniques are driving the development of highly stable and controllable soliton systems for next-generation optical technologies [83, 98]. The enhanced stability and interaction control provided by nonlocality open new avenues for designing complex photonic devices and systems that leverage the unique properties of spatial solitons [82, 85]. The two primary new classes of spatial solitons that were identified, particularly concerning nonlinear mechanisms, are photorefractive solitons and quadratic solitons.

6.1 Photorefractive solitons

Photorefractive solitons form in photorefractive materials where the refractive index change is induced by the redistribution of charge carriers under the illumination of light [84, 86]. This nonlocal response due to the diffusion of charge carriers makes photorefractive solitons particularly stable and attractive for low-power applications. These solitons require minimal power for the generation. Hence, these solitons are ideal for integrated photonic circuits and optical data storage [84]. The photorefractive effect leads to a nonlocal nonlinear response, often resulting in a modified NLS equation incorporating this nonlocality. One of the simplest modified NLS equations that produces bright photorefractive soliton has the following form [78, 87].

$$i\frac{\partial q}{\partial z}+\frac{1}{2{\beta }_{0}}{\nabla }_{\perp }^{2}\text{q}-\frac{\delta }{|q{|}^{2}+1}q=0$$
(21)

here, \(\delta\) represents the strength of photorefractive nonlinearity.

A study reveals that photorefractive waveguide structures enhance self-focusing and lower the power threshold for self-trapping of bright screening solitons, leading to the prediction of bistable states and the identification of four power regimes for soliton behavior [88]. Recent research has demonstrated the formation of two-dimensional photorefractive solitons with enhanced stability and interaction control. In a recent study by directing spatial solitons towards bias electrodes in a photorefractive crystal, the authors achieved an anchoring effect that significantly reduced beam movement, enabling the creation of stable and addressable optical waveguides [89]. A few Research developments also include the observation of self-trapping in photorefractive waveguides, where the nonlocal response induced by charge carrier diffusion plays a crucial role in soliton stabilization [90, 91]. Another important study predicts the existence of various coherently coupled soliton pairs in unbiased photorefractive pyroelectric materials, influenced by temperature change, mutual phase difference, and beam intensity ratio [92]. Temporal evolution of optical spatial solitons in photorefractive media was investigated in both linear and quadratic electro-optic effects. Here, the distinct soliton formation regimes were identified based on intensity ratio and the influence of individual electro-optic coefficients on soliton characteristics was also reported [93]. Recently, researchers leveraged the photorefractive effect in lithium niobate microresonators to enable stable, single-soliton generation without active feedback, leading to a robust and compact soliton microcomb platform [94].

6.2 Quadratic soliton

Quadratic solitons, also known as second-harmonic generation solitons, form in media with a quadratic nonlinearity (\({\chi }^{\left(2\right)}\)). These solitons result from the interaction between a fundamental wave and its second harmonic, with energy exchange leading to mutual trapping and self-focusing. Quadratic solitons can exist in both local and nonlocal nonlinear media, offering a versatile platform for studying nonlinear wave dynamics [84, 95]. The modified NLS equation for quadratic soliton includes terms representing the interaction between two waves

$$\begin{array}{c}i\frac{\partial {q}_{1}}{\partial z}+\frac{1}{2{\beta }_{0}}{\nabla }_{\perp }^{2}{q}_{1}+\kappa {q}_{2}{q}_{1}^{*}{e}^{-i\varphi z}=0\\ i\frac{\partial {q}_{2}}{\partial z}+\frac{1}{2{\beta }_{0}}{\nabla }_{\perp }^{2}{q}_{2}+\kappa {q}_{1}^{2}{e}^{i\varphi z}=0\end{array}$$
(22)

here q1 is the complex envelope of the fundamental frequency, q2 is the envelope of the second harmonic, \(\varphi\) is normalized phase mismatch and k is the coupling coefficient representing the second-order nonlinearity.

In nonlocal nonlinear media, the quadratic solitons benefit from the extended interaction range, which can enhance their stability and control. Nonlocal interactions help maintain the phase matching required for efficient second-harmonic generation, supporting robust soliton formation even in the presence of perturbations[96]. This makes quadratic solitons highly useful for frequency conversion and parametric amplification applications [97, 98]. Recent advances have focused on the dynamics of quadratic solitons in nonlocal media by exploring their stability, interaction dynamics, and potential applications in integrated photonic devices. Studies have shown that nonlocality can significantly enhance the robustness and tunability of quadratic solitons, making them ideal for complex optical systems [99].

7 Spatiotemporal soliton

We know that the spatial optical soltions are confined in the transverse plane to the propagation of beam and the temporal optical solitons are confined in the time domain or in the direction of propagation. However, the spatiotemporal solitons, also known as light bullets, are localized wave packets that maintain their shape in both space and time during propagation through a nonlinear medium. An interplay of diffraction and nonlinearity happens in the transverse plane along with an interplay between GVD and nonlinearity in the propagation direction. They are solutions to the (3 + 1)D NLS equation, which combines the effects of diffraction, dispersion, and nonlinearity [100,101,102].

$$\text{i}\frac{\partial q}{\partial z}+\left(\frac{1}{2{\beta }_{0}}{\nabla }_{\perp }^{2}-\frac{{\beta }_{2}}{2}\frac{{\partial }^{2}}{\partial {t}^{2}}\right)q+{\gamma }_{1}|q{|}^{2}q+{\gamma }_{2}|q{|}^{4}q=0$$
(23)

Here \({\gamma }_{1}\) is the cubic nonlinearity and \({\gamma }_{2}\) is the quintic nonlinearity. Spatiotemporal solitons have been extensively studied in semiconductor lasers and metamaterials due to their potential applications in optical communication and photonic devices [103, 104]. The stability of these solitons in semiconductor lasers is influenced by the carrier dynamics and the interplay between gain and absorption. Recent studies have shown that the spatiotemporal solitons can be stabilized in semiconductor waveguides with tailored dispersion and nonlinearity profiles. Formation of stable light bullets demand high nonlinearity and spatiotemporal balance between nonlinearity, dispersion and diffraction which, in general, are difficult to achieve in conventional materials [105,106,107]. In metamaterials, spatiotemporal solitons benefit from engineered dispersion and nonlinearity properties, enabling the formation of stable light bullets. Spatiotemporal soliton was proved to be stable theoretically in quintic nonlinearity metamaterials. Stable light bullets are studied extensively in cubic-quintic nonlinear media [101, 108]. A recent study proposes a novel method to generate 3D linear light bullets in free space using a single passive nonlocal optical surface, enabling simultaneous control over both external and internal properties of the light bullets without the need for complex pulse-shaping techniques [109].

8 Soliton bubbles

Soliton bubbles, or electromagnetic (EM) bubbles, are solitary pulses of a unipolar electromagnetic field exhibiting high stability and resistance to dispersion. These pulses, with amplitudes up to atomic field strength of 109 V/cm and durations as short as 10–16 s, can propagate through atomic gases without significant changes due to gas density variations [110]. Although bubble-like soliton solutions are generally unstable across various dimensions according to NLS equation [111]. However, they can be stabilized in media with a Gaussian potential barrier, supported by repulsive Kerr nonlinearity [112].

In one- and two-dimensional media with a central maximum in local self-repulsion strength, ground states and excitations like dark solitons and vortices can form stable flat-floor bubbles, accurately described by Thomas–Fermi expressions [113]. Additionally, soliton bubbles in the form of strong, subcycle electromagnetic solitons have been demonstrated in gases of two-level atoms, generated by subpicosecond half-cycle pulses or short laser pulses, offering insights into their characteristics and transient phenomena [114]. Additionally, 3D relativistic electromagnetic subcycle solitons in 3D particle-in-cell simulations show an oscillating electric dipole structure with poloidal electric and toroidal magnetic fields. These solitons oscillate with the electron density below the Langmuir frequency, undergoing a core Coulomb explosion, which accelerates ions and evolves into an expanding quasineutral cavity [115].

9 New avatar of optical solitons in dissipative optical systems

Dissipative optical systems are systems where energy is exchanged with the external environment, in contrast to conservative systems where energy is preserved. Examples include lasers, optical resonators, and fiber-optic systems with amplifiers. For the first time, solitons were studied theoretically only in conservative systems. Later, this idea was also extended to dissipative media. In the dissipative media, in addition to dispersion and nonlinearity balancing, gain and loss also involved in the formation of soliton pulses. These solitons are known as dissipative optical solitons (DOSs). Thus, DOSs are localized, self-sustaining pulses of light that exist as a delicate balance between nonlinearity, dispersion, loss, and gain mechanisms. Unlike their conservative counterparts, DOSs require continuous energy input to maintain their shape. The complex Ginzburg–Landau (CGL) equation is a powerful mathematical model for describing the evolution of DOSs in various dissipative optical systems. It incorporates the various linear and nonlinear effects, namely, dispersion, spectral filtering, SPM, linear and nonlinear loss/gain, and has the following form [63, 116].

$$i{q}_{z}+\frac{{\beta }_{2}}{2}{q}_{tt}+\gamma |q{|}^{2}q+\nu |q{|}^{4}q=i\delta q+i\epsilon |q{|}^{2}q+i\beta {q}_{tt}+i\mu |q{|}^{4}q$$
(24)

here, z is the propagation distance in the cavity, t is the retarded time, q is the normalized envelope of the field, δ is the linear gain–loss coefficient, β accounts for spectral filtering or linear parabolic gain dispersion (β > 0), ϵ represents the nonlinear gain, μ represents the saturation of the nonlinear gain and ν corresponds to the saturation of the nonlinear refractive index. Equation (24) is a non-integrable equation, that gives dissipative soliton solution and can be analyzed using the methods like Lagrange variational analysis, moment method, and Linear stability analysis and also can be simulated for soliton solution using split-step fourier method [28, 29, 102, 117].

It is known that DOSs exhibit a rich variety of dynamical behaviours far beyond simple steady-state propagation. They can undergo periodic pulsations where their amplitude or width varies in a regular pattern as well as aperiodic pulsations with more complex fluctuations. In some cases, dissipative solitons demonstrate a 'creeping' behavior where they gradually shift their position over time. Under certain conditions, the dynamics of DOSs becomes chaotic, they exhibit unpredictable fluctuations and they are also highly sensitivity to initial conditions. Further, bifurcations, where the qualitative behavior of the soliton changes abruptly as parameters are varied, are also commonly observed. These diverse dynamics reflect the complex interplay between nonlinearity, dispersion, gain, and loss within dissipative optical systems [35, 63, 116]. In the following sub-section, we delineate the various possibilities of the DOSs in terms of soliton molecules, soliton complexes, soliton crystals, etc.

9.1 Soliton molecules

Unlike conservative optical systems where solitons do exist as individual pulses and self-reinforcing pulses, dissipative media can support the formation of bound states called soliton molecules (SMs). In these systems, soliton interactions are primarily driven by the overlap of their optical fields. This dissipation manifests as oscillating intensity tails trailing behind each soliton. Crucially, these oscillations create localized regions of minimal interaction force within the tails. These minima act like "traps" that can bind multiple solitons together, forming stable soliton molecules [27]. The formation of a typical soliton molecule is depicted in Fig. 8.

Fig. 8
figure 8

Illustrates that potential minimum in the interaction potential between solitons causes the formation of soliton molecules (i.e. stable bound state of solitons)

Full size image

These molecules are bound states of two or more individual solitons, interacting and propagating together as a single entity. The key to their stability lies in the interplay between nonlinearity, dispersion, and dissipation within the dissipative medium. We know that small perturbations can disrupt solitons in conservative systems and cause them to decay or split. However, the dissipative nature introduces energy exchange that helps SMs maintain their bound state. The interplay between nonlinearity, which tends to bind the solitons, dispersion, which influences their interaction, and the energy exchange with the environment creates a stable configuration for the SM. This allows them to persist even under minor external fluctuations. It is a unique characteristic of SMs and is not observed in conservative systems where solitons are more vulnerable to perturbations [29, 31, 118].

Thus, the SMs display a variety of intriguing dynamics that go beyond the behaviour of individual solitons. They show bifurcations, pulsation, molecule-like periodic and aperiodic temporal vibrations, annihilation, and many more complex dynamics [28, 31, 118]. Time stretch dispersive Fourier transform (TS-DFT) facilitates to study such dynamics in real time. During their formation, SMs exhibit complex build-up dynamics where individual solitons coalesce into a bound state, often involving oscillations and adjustments before reaching equilibrium. These were studied using the TS-DFT technique. Once formed, their interaction dynamics can be remarkably intricate. The relative spacing and phases of the constituent solitons within the molecule can change, leading to internal vibrations or pulsations. In some instances, SMs can even experience periodic switching between different bound states. Additionally, external perturbations can lead to SM collisions and interactions, revealing the complex scattering or even annihilation behaviour [119,120,121]. These diverse dynamics make SMs a subject of active research, both for their fundamental interest in nonlinear physics and their potential applications in optical communications and information processing.

9.2 Soliton complexes

Beyond simple two-soliton bound states, researchers have also investigated the formation of "soliton compounds" that contain more than two tightly bound solitons or even pre-existing SMs. These compounds arise due to strong inter-soliton forces within the cavity [122,123,124]. However, the process doesn't end here. Further, the weaker inter-molecular forces can come into play and they act between individual SMs or even soliton compounds. These weaker forces can then lead to the formation of even larger structures called soliton molecular complexes and they are also referred to as soliton supramolecule. These complexes represent a fascinating level of organization within the laser cavity with multiple tightly bound SMs or soliton compounds can also interact and propagate together. As discussed previously, when individual soliton pulses are tightly bound through interactions like cross-phase modulation, they synchronize their phases and velocities, forming a stable entity known as a SM. This tightly bound structure behaves like a single entity for propagation purposes. Soliton molecular complexes are also studied to show many interesting dynamics such as synchronization, reconfiguration, and self-configuration (self-assembly) of SMs in the complex [31, 122, 125, 126]. We note that the SMs and soliton molecular complexes are also studied in CNLS systems such as coupling dynamics of modes in model-locked fiber lasers that are called vector dissipative optical SMs [71, 104, 127, 128]. The formation of soliton complexes or supramolecules with the help of soliton molecules is clearly illustrated in Fig. 9.

Fig. 9
figure 9

Formation of soliton supramolecule also called soliton complex due to interaction between multi solitons, soliton molecules and/or soliton compounds

Full size image

Soliton supramolecular complexes are attracting significant research interest due to their intriguing dynamics. Understanding the behavior of these complex structures is crucial for unlocking their potential in various applications, particularly in the realm of ultrafast all-optical signal processing, and optical information storage.

9.3 Soliton crystals

Further soliton interaction in the presence of dissipation also gives rise to optical soliton microcomb, perfect soliton comb, and soliton crystal. In a microresonator, solitons can circulate and interact, leading to the formation of stable, organized structures like crystals. A perfect soliton crystal is a particularly desirable type of soliton crystal where the solitons are perfectly equidistant from each other [129]. Optical soliton micro-combs are formed within micro-resonators, tiny ring-shaped structures that trap and confine light. When a continuous-wave (CW) laser is coupled into the micro-resonator, complex interactions between nonlinearity (specifically the Kerr effect), dispersion, and the resonator geometry can give rise to dissipative Kerr solitons (DKS). These solitons are self-sustaining optical pulses that circulate within the resonator, forming a comb-like spectrum of equally spaced frequencies. A perfect soliton comb refers to a type of DKS micro-comb where the repetition rate and spectral envelope are exceptionally smooth and stable. Optical soliton crystals arise when multiple DKS solitons in the microresonator form a temporally ordered pattern with regular spacing akin to a crystal lattice. The Lugiato-Lefever equation (LLE) provides a powerful theoretical framework for modelling these phenomena [130, 131]. It is a driven, detuned, and damped NLS equation that describes the evolution of the optical field within the microresonator. (3 + 1)D LL equation has the following form that can be reduced to (1 + 1)D form by removing the paraxial term (\({\nabla }_{\perp }^{2}\)) from equation.

$$\frac{\partial A}{\partial t}={A}_{\text{i}}-(\alpha +i\delta )A-i\left({\frac{1}{2{\beta }_{0}}\nabla }_{\perp }^{2}+\frac{{\beta }_{2}}{2}\frac{{\partial }^{2}}{\partial {z}^{2}}\right)A+i\gamma |A{|}^{2}A$$
(25)

here A = A(x,y,z,t) is electromagnetic field, \(\delta\) is cavity detuning parameter, \(\alpha\) is the loss coefficient, and \({A}_{\text{i}}\) is an external pump field.

Equation (25) is employed to model and study spatiotemporal soliton crystals. Its reduced form, the (1 + 1)D Lugiato-Lefever equation, is used to model various phenomena in optical microresonators, including soliton crystals, soliton molecules, and soliton frequency combs [132,133,134].

The soliton crystal formed by a continuous wave laser in a fiber ring microresonator is portrayed in Fig. 10.

Fig. 10
figure 10

showcases a remarkable soliton crystal formation achieved using a continuous-wave laser in a fiber ring microresonator

Full size image

The LLE takes into account essential optical effects like dispersion, Kerr nonlinearity, losses, and the continuous-wave pump lasing that drives the system. Solving the LLE allows researchers to simulate the formation of DKS, predict conditions for perfect soliton combs, soliton crystals, and analyse their stability. Soliton-based microcombs and soliton crystals have a remarkable range of applications. In metrology, their stable and evenly spaced spectral lines enable precise frequency measurements and distance determination. Their ability to broaden the spectral bandwidth of lasers makes them ideal for high-resolution spectroscopy, leading to advances in chemical sensing and similar fields. Additionally, soliton microcombs offer the potential to generate high-speed data streams, making them valuable for next-generation optical communications systems. Finally, their use in calibrating astrophysical spectrometers is key to the ongoing search for exoplanets [34, 129, 133, 135, 136].

9.4 Intelligent soliton molecules – photo-bot

In the near future, we envisage that intelligent soliton molecules will be achieved soon. We trust that these intelligent soliton molecules may manipulate nearby atoms by varying their own physical parameters. Understanding the interactions and behaviours of soliton molecules has the potential to unlock precise control. Researchers are actively exploring the manipulation of quantum states in atoms and molecules for controlling the rate of chemical reaction and it paves the way for on-demand control of chemical reactions using laser pulses [137, 138]. Recently, there have been few research studies that suggest that in the near future we will have intelligent control over the pulse dynamics for some potential applications [139, 140]. This control could lead to the engineering of "soliton molecules" with tailored interactions, potentially enabling complex behaviors ideal for light-based information processing. Finally, this will revolutionize the world of computing and communication. As of now, these applications are still under development. We note that the potential for precise control over the quantum world is highly challenging and it holds the promise of groundbreaking advancements in various sectors. The concept of 'intelligent soliton molecules' is intriguing, it is important to focus on the achievable possibilities of controlled soliton interactions for future technological applications.

In this review article, for the first time, we propose the name "photo-bot" for representing these intelligent soliton molecules due to their potential resemblance to nanobots in the nanotechnology. It is well established that the nanobots are nanomaterials-based microscopic machines envisioned to manipulate objects physically or chemically. Similarly, photobots may be used to dynamically control their own energy, frequency, chirp, and polarization states. Such precise control would enable manipulation of nearby atoms: changing their polarization, promoting excitation through chirped pulses, or even enhancing molecular vibrations to ultimately induce, control, and engineer desired chemical reactions. While nanobots may influence chemical reactions by providing a surface for enzymes to work on, photobots promise to operate on a quantum level. They may potentially control these reactions by manipulating the quantum states of the reacting atoms and molecules themselves. We firmly believe that this would open the untapped avenues in photonics very soon.

10 Research gaps in soliton science

Despite the significant progress made, several research gaps remain unaddressed and they have to be explored:

  1. 1. Stability of Solitons in Complex Systems:

    Understanding how solitons interact and maintain stability in complex, multi-component systems are crucial for practical applications.

  2. 2. AI-powered Unveiling of Multi-Soliton Complexity for Self-stability and Self-induced Interactions:

    While traditional methods have helped to gain the significant insights into soliton behavior, a crucial research gap lies in the exploration of complex multi-soliton dynamics and their interaction. Here, the power of artificial intelligence (AI) offers a promising avenue for further exploration.

  3. 3. Solitons in Novel Materials:

    Exploring the behavior of solitons in newly developed materials with exotic properties can lead to unforeseen functionalities and applications.

  4. 4. Integration with Nanophotonic Devices:

    Investigating the seamless integration of solitons with miniaturized photonic devices will be essential for building future soliton-based technologies.

Addressing these gaps will not only deepen our theoretical understanding of solitons but also will pave a way for their practical implementation in various scientific and technological endeavours.

11 Conclusion

In this review article, we have begun with the origins of light and matter at the Big Bang and explored their fundamental interactions. Then, we have also briefly discussed the light-matter interaction. After this, we have examined the wave propagation in diverse linear and nonlinear optical media. Of all, we have discussed the formation of optical solitons, in detail, in optical fibers that exhibit both anomalous dispersion and self-phase modulation. In order to provide more insight on the wave propagation in various linear and nonlinear optical media, we have provided the self-explanatory type geometrical illustrations for the novice of the subject. In addition, we have also presented a Table where the gist of all these ideas is coherently summarized for both conservative and non-conservative media. Then, we have discussed the basic studies on stability and interaction dynamics of both scalar and vector solitons in conservative media. In addition to temporal solitons, we have expanded our discussion to include optical spatial solitons, photorefractive solitons, quadratic solitons, spatiotemporal solitons, and soliton bubbles. Finally, we have delved into the fascinating world of dissipative optical systems where the new avatar of optical solitons has been discussed. That is, we have reviewed the birth of soliton molecules, soliton complexes, soliton combs, and soliton crystals. Eventually, we have also pointed out the realization of ‘photobot’ using intelligent soliton molecules. Undoubtedly, this new idea would definitely pave a path for future micro and nano-photonics. While control over soliton dynamics offers exciting prospects for various applications, certain key gaps remain and they have to be addressed. The careful literature survey dictates that there is a limited understanding of weak soliton interactions and the need for proposing various theoretical models for exploring the optomechanical interplay and anisotropic effects. We firmly believe that bridging these gaps will definitely unlock the full potential of solitons for future scientific and technological advancements. Key research gaps beckon further investigation, including the stability and complicated interaction dynamics of solitons in complex systems, their behavior in novel materials, and seamless integration with nanophotonic devices. Additionally, the potential of AI to unveil the intricate dynamics and interactions within multi-soliton systems presents a promising avenue for future research.