1 Introduction

The advancement of computing and sensing has made the field of autonomous driving a hot research area in recent years [1]. Path following, as an indispensable technological aspect of autonomous driving, aims to ensure that the vehicle adheres to the predetermined reference path [2]. The autonomous ground vehicle presents itself as a promising architectural solution for the implementation of path following, due to its notable attributes of increased adaptability, maneuverability, and efficient transmission. Nonetheless, the nonlinear dynamics and the under-actuated characteristics of AGV pose considerable challenges to the task of path following control [3]. Hence, there exists a pressing need for further examination and exploration of the control scheme related to path following in the context of AGV.

In the past years, several path tracking control strategies have been proposed for the AGV to achieve the desired path tracking performance. The control strategies for the AGV can be broadly classified as linear and nonlinear [4]. For example, linearizing the model of the AGV around an operating point enables the application of linear quadratic regulator control [5], linear quadratic Gaussian control [6], proportional-integral-derivative controller [7], model predictive control [8], model predictive control based on proportional-integral-derivative controller [9], linear matrix inequality-based control [10], and \(\text {H}_{\infty }\) control [11]. However, these linear controllers are only valid around the operating point where the AGV model is linearized.

The limitations of linear controllers are usually overcome by using nonlinear controllers with global operating points. Tao et al. [12] applied a sliding mode control for the path tracking of an AGV with uncertainties. In [13], a finite-time robust sliding mode path following control was studied for a linearized AGV dynamic model. In [14], a particle swamp optimization algorithm was used to optimize the gains of the sliding mode controller to improve path tracking accuracy and robustness. In [15], immersion and invariance control is proposed to minimize tracking errors. In [16], a recursive backstepping control is developed for path tracking of AGV with asymptotic convergence. In [17], robust backstepping control is used to achieve trajectory tracking and counter uncertainties. In [18], backstepping and sliding mode controllers with optimal gains were designed for the kinematic and dynamic subsystems of the AGV to realize the trajectory following. In [19], a robust sliding mode control is proposed for an AGV with state constraints to follow the desired trajectory. In [20], a passivity-based lateral control is proposed for the AGV. In [21], backstepping sliding mode control is utilized to achieve automatic steering control of the AGV. In [22], a backstepping controller with optimal gains is used to follow the trajectory and avoid obstacles. In [23], a robust differential flatness-based control protocol is proposed to realize path tracking of the AGV.

To enhance the robustness of the controllers against disturbances and parametric uncertainties, it is essential to incorporate estimation mechanisms into the controllers to compensate for the disturbances. In [24], adaptive backstepping control is designed for path tracking and estimating the uncertain parameters of the AGV. In [25], adaptive terminal sliding mode control is proposed for the AGV to follow the target path while accounting for parametric perturbations. Baosen et al. [26] designed a recursive integral terminal sliding mode control scheme with adaptive gains to realize accurate path following. A disturbance observer-based sliding mode control is employed in [27] to estimate the disturbances and steer the AGV to track the desired trajectory. In [28], a nonsingular terminal sliding mode controller with disturbance observer was designed for the AGV path following. In [29], a robust adaptive sliding mode path tracking control law optimized with particle swamp optimization was formulated for the AGV. In [30], an observer-based differential flatness-based control has been suggested for path tracking of an AGV subjected to disturbances.

Recently, researchers have been using the universal approximating capability of fuzzy logic systems and neural networks to approximate unknown and continuous nonlinear functions and external disturbances [31]. Since fuzzy logic systems require heuristic knowledge of the plants and the formation of large sets of fuzzy rules and membership functions, neural networks are preferred for approximating nonlinear functions. In [32], a neural network-based control has been proposed for steering control of AGV to keep tracking the target path. In [33], a neural network-based super-twisting sliding mode control has been designed for an AGV subjected to parametric variations. In [34], the authors presented a chattering-free sliding mode control with a neural network approximator to minimize the impact of unknown perturbations. In [35], a neuro-adaptive sliding mode control strategy has been proposed for uncertain AGV. In [36], a nonsingular terminal sliding mode control with an adaptive recurrent neural network has been designed for path tracking of an AGV. Jin et al. [37] utilized adaptive backstepping variable structure control with a neural estimator to tackle vehicle trajectory following deviation and suppress environmental disturbances. However, updating the weights of the neural network’s hidden layer leads to a high computation load. The high computational burden will cause some delays in the control action and slow convergence speed. To lessen the computational burden and enhance the control performance, a minimum parameter learning approach is employed to replace the neural network’s weight vector with its norm which is a single parameter [38].

Whilst the path tracking control techniques had shown promising results in the previously mentioned studies, the controller synthesis did not consider the actuators’ nonstructured nonlinear characteristics. The actuator nonlinearities such as backlash, deadzone, and saturation can degrade the path following performance or even lead to instability of the control system [39, 40]. In [41], an observer-based path tracking control based on convex optimization has been proposed for an AGV with Input Saturation. In [42], an adaptive path tracking control problem of an AGV with input saturation has been studied. In [43], an adaptive path tracking control problem of an AGV with steering angle backlash has been studied. The authors in [44] proposed a gain-scheduling control of an AGV with steering backlash. In [45], the model of the backlash in the steering system is first identified using the recursive identification algorithm and then an appropriate controller is designed.

Although the above works were wonderful, the path following control problem of the AGV with input deadzone has rarely been addressed [46, 47]. When the control input encounters a deadzone, the actuator output signal is blocked, which deteriorates the accuracy of the AGV path tracking. In [46], an observer-based state feedback control law has been designed to take care of the deadzone. In [47] an adaptive sliding mode control was proposed to estimate and compensate the upper bounds of the deadzone parameters. Considering the low volume of literature that investigated the path following control of AGV with deadzone, this paper is motivated to contribute in this direction to improve the path tracking accuracy.

In recent years, the command filtered scheme has been widely used to solve the problem of the “explosion of the complexity” associated with backstepping control. The command filter estimates the time-derivative of the virtual error while the associated filtering error is compensated through an auxiliary error signal [48]. Considering the complexity of the AGV kinematic model in the presence of disturbances and input deadzone, command filtered scheme is essential.

Motivated by the above discussion, this paper aims to develop a neural network-based backstepping control with a command filter and integral error action for path following control of AGV subjected to input deadzone. Compared with the existing path following control methods for AGV, this article considers the problems of external disturbances, the explosion of the complexity, and the input deadzone simultaneously, and incorporates the integral error term to improve the path following performances. Considering that it is difficult to determine the upper bounds of external disturbances and nonlinear dynamics in practical applications, neural networks are used to approximate them. The neural networks’ weights are adjusted using the minimum parameter learning scheme to lighten the computational burden. The low computational complexity of the controller makes its practical implementation easier. In addition, the knowledge of the AGVs’ nonlinearities or external disturbances is no longer required. The contributions of this paper compared to the existing path following control of the AGV are summarized as follows:

  • Different from the studies [46, 47] where an observer-based state feedback controller and adaptive sliding mode controller were designed respectively to compensate the actuator deadzone and achieve the AGV path tracking, a neural network-based backstepping controller is proposed.

  • Unlike the backstepping path following control in [16,17,18, 24], a command filter is used to tackle the "explosion of complexity" problem of the conventional backstepping arising due to successive differentiation of the virtual control input. The filtering errors are removed with the aid of filtered-error compensation signals to enhance the control accuracy. Moreover, contrary to [16,17,18, 24], an integral error term is added to the proposed backstepping controller to reduce steady-state tracking errors and enhance the tracking accuracy.

  • In contrast to the neural networks in [31,32,33,34,35,36,37] where the whole weight vector is updated, in this paper, a single parameter that corresponds to the norm of the weight vector of the neural network is updated. This significantly reduces the computational load and improves the convergence speed of the controller.

  • Simulation results and comparison studies are provided to justify the superior performance of the proposed controller compared to existing path tracking controllers.

The remaining sections of the paper are arranged as follows: The problem formulation is described in Sect. 2. The formulation of the proposed path following controller is presented in Sect. 3. The Simulation results and discussions are provided in Sect. 4. Finally, the conclusions of the paper are given in Sect. 5.

Fig. 1
figure 1

Schematic diagram of the AGV

Full size image

2 Problem formulation

2.1 Kinematic model of the AGV

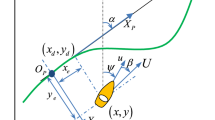
This article considers a two-wheeled mobile robot as the AGV as shown in Fig. 1. The AGV modeled disregards the side-slip angle, the AGV dynamics and tire models. The AGV kinematic model is widely used in the literature and it is described by the following equations [8, 22].

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} =v \cos \psi \\ \dot{y} =v \sin \psi \\ \dot{\psi } =\omega \end{array}\right. } \end{aligned}$$
(1)

where x and y present the location of the AGV, v and \(\omega\) denote the linear and angular (yaw rate) velocities of the AGV, respectively, and \(\psi\) is the orientation angle.

Due to the fact that (1) is non-holonomic, a new reference point \(\left( x_{n }, y_{n }\right)\) is defined with \(\left( x, y\right)\) being the inertial position. The new coordinate transforms (1) into a holonomic system as follows [49]:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{n }=x+L \cos \psi \\ y_{n }=y+L \sin \psi \end{array}\right. } \end{aligned}$$
(2)

where L is the wheelbase.

Differentiating (2) twice with respect to time gives:

$$\begin{aligned} {\left[ \begin{array}{c} \ddot{x}_{n } \\ \ddot{y}_{n } \end{array}\right] =\left[ \begin{array}{ll} \cos \psi &{} -L \sin \psi \\ \sin \psi &{} L \cos \psi \end{array}\right] \left[ \begin{array}{c} \dot{v} \\ \dot{\omega } \end{array}\right] } \nonumber \\ +\left[ \begin{array}{l} -v \omega \sin \psi {-L \omega ^{2} \cos \psi } \\ v \omega \cos \psi {-L \omega ^{2} \sin \psi } \end{array}\right] \end{aligned}$$
(3)

We let

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left[ \begin{array}{c} \dot{v} \\ \dot{\omega } \end{array}\right] } &{} =\left[ \begin{array}{cc} \cos \psi &{} \sin \psi \\ -\frac{1}{L} \sin \psi &{} \frac{1}{L} \cos \psi \end{array}\right] \left[ \begin{array}{l} {u_x } \\ {u_y } \end{array}\right] \\ {\left[ \begin{array}{c} f_{ 1} \\ f_{ 2} \end{array}\right] } &{} =\left[ \begin{array}{l} -v \omega \sin \psi -L \omega ^{2} \cos \psi \\ v \omega \cos \psi -L \omega ^{2} \sin \psi \end{array}\right] \end{array}\right. } \end{aligned}$$
(4)

Therefore, the holonomic model of the AGV is derives as:

$$\begin{aligned} \left[ \begin{array}{c} \ddot{x}_{n } \\ \ddot{y}_{n } \end{array}\right] =\left[ \begin{array}{l} {u_x } \\ {u_y} \end{array}\right] +\left[ \begin{array}{l} f_{ 1} \\ f_{ 2} \end{array}\right] \end{aligned}$$
(5)

where \({u_x }\) and \({u_y }\) denote the new control inputs under deadzone, \(f_{ 1}\) and \(f_{ 2}\) are non-linear functions.

By considering the unknown lumped uncertainties and external disturbance, the dynamic equation of the orientation angle and (5) can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{l}\dot{\chi }_{1}=\chi _{2} \\ \dot{\chi }_{2}=F(\chi )+ {U}+\delta _{\chi } \\ \dot{\psi } =\omega +\delta _{\psi } \end{array}\right. \end{aligned}$$
(6)

The vectors of the dynamic states, control inputs under deadzone, and lumped disturbances are given by (7), (8), and (10), respectively, as:

$$\begin{aligned}&\left\{ \begin{array}{rl}\chi _{1}&=\left[ \begin{array}{ll} x_{n } &{} y_{n } \end{array}\right] ^{T} \\ \chi _{2} &{} =\left[ \begin{array}{ll}\dot{x}_{n } &{} \dot{y}_{n } \end{array}\right] ^{T}\end{array}\right. \end{aligned}$$
(7)
$$\begin{aligned}&\quad {U}=\left[ \begin{array}{ll}{u_x}&{u_y} \end{array}\right] ^{T} \end{aligned}$$
(8)
$$\begin{aligned}&{F(\chi ) = \left[ \begin{array}{ll}{f_1}&{f_2} \end{array}\right] ^{T} } \end{aligned}$$
(9)
$$\begin{aligned}&\delta _{\chi } =\left[ \begin{array}{ll}\delta _{x}&\delta _{y} \end{array}\right] ^{T} \end{aligned}$$
(10)

2.2 Dead-zone

When the input of a mechanical system falls into the deadzone effect, the actuator signals are blocked which leads to the loss of control performance and system stability. The model of the deadzone output can be written as [50]:

$$\begin{aligned} {u_i}= {{\left\{ \begin{array}{ll} \Pi _{ir} \left( {\bar{u}_i \left( {t}\right) -s_{ir} }\right) ,&{}{\textrm{ if}}~\bar{u}_i \left( {t}\right) \ge s_{ir} \\ 0, &{} {\textrm{ if}} \,\, {-}s_{il}< \bar{u}_i \left( {t}\right) < s_{ir} \\ \Pi _{il} \left( {\bar{u}_i \left( {t}\right) +s_{il} }\right) ,&{} {\textrm{ if}}~\bar{u}_i \left( {t}\right) \le -s_{il} \end{array}\right. } } \nonumber \\ { i = (x,y)} \end{aligned}$$
(11)

where \(s_{il}\) and \(s_{ir}\) are the deadzone thresholds, \(\Pi _{il}\) and \(\Pi _{ir}\) are the deadzone slopes. Equation (11) can be transformed into the following form:

$$\begin{aligned} U=\Pi \bar{U}+d(\bar{U}) \end{aligned}$$
(12)

where \(\bar{U} { \in \mathbb {R}^{2}}\) is the vector of the actual control inputs without deadzone, \(d(\bar{U}) { \in \mathbb {R}^{2}}\) is the vector of disturbance-like terms, \({\Pi = \text {diag} \{ \Pi _x,~ \Pi _y \} \in \mathbb {R}^{2 \times 2}}\) is a diagonal matrix with each element defined as follows:

$$\begin{aligned} {\Pi _i }=&{{\left\{ \begin{array}{ll} {\Pi _{ir} }, &{}~{\textrm{ if}}~\bar{u}_i \left( {t}\right) >0 \\ {\Pi _{il} }, &{}~{\textrm{ if}}~\bar{u}_i \left( {t}\right) \le 0 \end{array}\right. }~ ~~ ~~ ~~ ~~~ ~~ ~ i = (x,y)}\end{aligned}$$
(13)
$$\begin{aligned} {d(\bar{u}_i)}=&{{\left\{ \begin{array}{ll} {-\Pi _{ir} s_{ir} }, &{}~{\textrm{ if}}~\bar{u}_i \left( {t}\right) \ge s_{ir} \\ {-\Pi _i\left( {t}\right) \bar{u}_i \left( {t}\right) }, &{}~{\textrm{ if}} \,\, {-}s_{il}< \bar{u}_i \left( {t}\right) < s_{ir}\\ {\Pi _{il} s_{il} }, &{}~{\textrm{ if}}~\bar{u}_i \left( {t}\right) \le -s_{il} \end{array}\right. }} \end{aligned}$$
(14)

It is easy to see that

$$\begin{aligned} {{\left\{ \begin{array}{ll} {\underline{\Pi }_i\le \left| {\Pi _i }\right| \le \bar{\Pi }_i} \\ {\underline{d}_i\le \left| { d\left( {\bar{u}_i}\right) }\right| \le \bar{d}_i} \end{array}\right. } } \end{aligned}$$
(15)

where \(\underline{\Pi }_i = \min \left( {\Pi _{ir},\Pi _{il} }\right)\), \(\bar{\Pi }_i = \max \left( {\Pi _{ir},\Pi _{il} }\right)\), \(\underline{d}_i = \min \left( {\Pi _{ir} s_{ir},\Pi _{il} s_{il} }\right)\), and \(\bar{d}_i = \max \left( {\Pi _{ir} s_{ir},\Pi _{il} s_{il} }\right)\)

Similar to (12), the deadzone output of the orientation angle can be written as:

$$\begin{aligned} \omega = \Pi _{\psi } \bar{\omega } + d(\bar{\omega }) \end{aligned}$$
(16)

where

$$\begin{aligned} \Pi _{\psi } =&{\left\{ \begin{array}{ll} {\Pi _{\psi r} }, &{}~{\textrm{ if}}~\bar{\omega } \left( {t}\right) >0 \\ {\Pi _{\psi l} }, &{}~{\textrm{ if}}~\bar{\omega } \left( {t}\right) \le 0 \end{array}\right. } \end{aligned}$$
(17)
$$\begin{aligned} d(\bar{\omega })=&{\left\{ \begin{array}{ll} {-\Pi _{\psi r} s_{\psi r} }, &{}~{\textrm{ if}}~\bar{\omega } \left( {t}\right) \ge s_{\psi r} \\ {-m\left( {t}\right) \bar{\omega } \left( {t}\right) }, &{}~{\textrm{ if}} \,\, {-}s_{\psi l}< \bar{\omega } \left( {t}\right) < s_{\psi r}\\ {\Pi _{\psi l} s_{\psi l} }, &{}~{\textrm{ if}}~\bar{\omega } \left( {t}\right) \le -s_{\psi l}. \end{array}\right. } \end{aligned}$$
(18)

2.3 Neural network approximation

A radial basis function neural network is a powerful approximation algorithm commonly utilized in the control of nonlinear systems. The approximation equation of the RBFNN is given by:

$$\begin{aligned} f(\chi )=W^{T} S(\chi ) + {\varepsilon }(\chi ) \end{aligned}$$
(19)

where \(\chi =\left[ \chi _{1}, \chi _{2}, \ldots , \chi _{q}\right] ^{T} \in \mathbb {R}^{q}\) is the input vector, \(W=\left[ W_{1}, W_{2}, \ldots , W_{N}\right] ^{T} \in \mathbb {R}^{N}\) is a weight vector, N is the number of nodes in the hidden layer, \({\varepsilon }(\chi )\) is the approximation error satisfying \(\Vert {\varepsilon }(\chi )\Vert \le \bar{\varepsilon }\), with \(\bar{\varepsilon }\) being a positive constant, \(S(\chi )=\left[ S_{1}(\chi ), S_{2}(\chi ), \ldots , S_{N}(\chi )\right] ^{T} \in \mathbb {R}^{N}\) is the vector of the Gaussian function with \(S_{i}(\chi )\) expressed as

$$\begin{aligned} S_{i}(\chi )=\exp \left( \frac{-\left( \chi - \bar{\eta } \right) ^{T}\left( \chi -\bar{\eta } \right) }{\underline{\eta }}\right) , i=1,2, \ldots , N \end{aligned}$$
(20)

where \(\bar{\eta }\) and \(\underline{\eta }\) represent the center and width of the Gaussian function.

3 Design of the path following controller

Step l: The path following error is defined as:

$$\begin{aligned} \left\{ \begin{array}{l}Z_{1}=\chi _{1}-\chi _{1 d}=\left[ \begin{array}{ll}z_{1} &{} z_{3} \end{array}\right] ^{T} \\ Z_{2}=\chi _{2}- {\phi _{1}}=\left[ \begin{array}{ll}z_{2} &{} z_{4} \end{array}\right] ^{T}\end{array}\right. \end{aligned}$$
(21)

where \(\chi _{1 d} = { [x_d~y_d]^T}\) is the vector of the target trajectories, \({\phi _{1} { \in \mathbb {R}^{2}}}\) stands for the output vector of the command filter which is the estimate of the virtual control inputs \(\alpha _{1} { \in \mathbb {R}^{2}}\) . The virtual controller \(\alpha _{1}\) will be designed later.

To tackle the issue of “explosion of complexity” associated with the conventional backstepping method as a result of continuous differentiation of \(\alpha _{1}\), a command filter is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l}\dot{\phi }_{1}=\omega _{n} \phi _{2} \\ \dot{\phi }_{2}=-2 \Psi \omega _{n} \phi _{2}-\omega _{n}^{2}\left( \phi _{1}-\alpha _{1}\right) \end{array}\right. \end{aligned}$$
(22)

where \(\omega _{n} >0\) represents the undamped natural frequency, \(\Psi \in (0,1]\) denotes the damping ratio, the initial condition of the filter satisfies \(\phi _{1}(0)=\alpha _{1}(0), \phi _{2}(0)= {[0~0]^T}\), and \(\left\| \phi _{1}-\alpha _{1}\right\| \le \eta\) with \(\eta >0\).

The filtering error \({\phi _{1}}-\alpha _{1}\) is compensated by an error compensation signal designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l}\dot{\xi }_{1}=\xi _{2}+\left( {\phi _{1}}-\alpha _{1}\right) -k_{1} \xi _{1} \\ \dot{\xi }_{2}=-k_{2} \xi _{2}\end{array}\right. \end{aligned}$$
(23)

where \({\xi _1, \xi _2 \in \mathbb {R}^{2}}\), \(\xi _1(0) =\xi _2(0)= {[0~0]^T}\), and \(k_{1},k_2>0\) are constants chosen such that \(\Vert \xi _1|\) and \(\Vert \xi _2\Vert\) are bounded. The path following errors are rewritten as:

$$\begin{aligned} \left\{ \begin{array}{l}\bar{Z}_{1}=Z_{1}-\xi _{1} \\ \bar{Z}_{2}=Z_{2}-\xi _{2}\end{array}\right. \end{aligned}$$
(24)

where \(\bar{Z}_{1},\bar{Z}_{2} \in \mathbb {R}^{2}\) are new error variables. An integral term \({\beta _1 \in \mathbb {R}^{2}}\) is added to the system to lessen the steady-state errors in the presence of deadzone and external disturbances.

$$\begin{aligned} \beta _{1}=\int _{0}^{t} Z_{1}(\tau ) d \tau \end{aligned}$$
(25)

Select a candidate Lyapunov as follows:

$$\begin{aligned} L_{1}=\frac{1}{2} \bar{Z}_{1}^{2}+\frac{1}{2} \Lambda \beta _{1}^{2} \end{aligned}$$
(26)

where \(\Lambda >0\), and the time-derivative of \(L_{1}\) gives

$$\begin{aligned} \dot{L}_{1}&=\bar{Z}_{1} \dot{\bar{Z}}_{1}+\Lambda \beta _{1} \dot{\beta }_{1} =\bar{Z}_{1} \dot{\bar{Z}}_{1}+\Lambda \beta _{1} Z_{1} \end{aligned}$$
(27)

Inserting (24) into (27) leads to:

$$\begin{aligned} \dot{L}_{1}=\bar{Z}_{1}\left( \dot{\bar{Z}}_{1}+\Lambda \beta _{1}\right) +\Lambda \beta _{1} \xi _{1} \end{aligned}$$
(28)

From (24), we can have the following:

$$\begin{aligned} \dot{\bar{Z}}_{1}&=\dot{Z}_{1}-\dot{\xi }_{1} =\dot{\chi }_{1}-\dot{\chi }_{1 d}-\dot{\xi }_{1} \nonumber \\&=\chi _{2}-\dot{\chi }_{1 d}-\dot{\xi }_{1} \end{aligned}$$
(29)

Inserting (29) into (28) gives:

$$\begin{aligned} \dot{L}_{1}=\bar{Z}_{1}\left( \chi _{2}-\dot{\chi }_{1 d}-\dot{\xi }_{1}+\Lambda \beta _{1}\right) +\Lambda \beta _{1} \xi _{1} \end{aligned}$$
(30)

From (21) and (24), we can have \(\chi _2 = Z_{2}+ {\phi _{1}}\) and \(Z_{2} = \bar{Z}_{2}+\xi _{2}\), respectively. Then, (30) can be evaluated as follows:

$$\begin{aligned} \dot{L}_{1}&=\bar{Z}_{1}\left( Z_{2}+ {\phi _{1}}-\dot{\chi }_{1 d}-\dot{\xi }_{1}+\Lambda \beta _{1}\right) +\Lambda \beta _{1} \xi _{1} \nonumber \\&=\bar{Z}_{1}\left( \bar{Z}_{2}+\xi _{2}+\alpha _{1}+\left( {\phi _{1}}-\alpha _{1}\right) -\dot{\chi }_{1 d}-\dot{\xi }_{1}\right. \nonumber \\&\quad \left. +\Lambda \beta _{1}\right) +\Lambda \beta _{1} \xi _{1} \end{aligned}$$
(31)

Using the error compensating signal (23), (31) leads to:

$$\begin{aligned} \dot{L}_{1}&=\bar{Z}_{1}\left( \bar{Z}_{2}+\alpha _{1}+k_{1} \xi _{1}-\dot{\chi }_{1 d}+\Lambda \beta _{1}\right) +\Lambda \beta _{1} \xi _{1} . \end{aligned}$$
(32)

The virtual control law is designed as \(\alpha _{1}=-k_{1} Z_{1}+\dot{\chi }_{1 d}-\Lambda \beta _{1}\). Inserting it into (32) gives the following equation:

$$\begin{aligned}&\dot{L}_{1} =\bar{Z}_{1}\left( \bar{Z}_{2}-k_{1} Z_{1}+k_{1} \xi _{1}\right) +\Lambda \beta _{1} \xi _{1} \nonumber \\&\quad =\bar{Z}_{1}\left( \bar{Z}_{2}-k_{1} \bar{Z}_{1}\right) +\Lambda \beta _{1} \xi _{1} . \end{aligned}$$
(33)

Choose \(k_{1}\) and \(\Lambda\) such that \(\dot{L}_{1} \le 0\) is realized.

Step 2: Design a candidate Lyapunov function \(L_{2}\) as follows:

$$\begin{aligned} L_{2}=L_{1}+\frac{1}{2} \bar{Z}_{2}^{2}+\frac{\Pi }{2 \gamma _{1}} \tilde{\varphi }^{2} \end{aligned}$$
(34)

where \(\gamma _{1}>0\) is a design constant, \(\tilde{\varphi }=\varphi -\hat{\varphi }\) is the estimation error and \(\hat{\varphi }\) is the estimate of \(\varphi\).

Remark 1

Note that the unknown parameter \(\varphi\) will be discussed later.

The time-derivative of \(L_{2}\) yields:

$$\begin{aligned}&\dot{L}_{2} =\dot{L}_{1}+\bar{Z}_{2} \dot{\bar{Z}}_{2}-\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }} \nonumber \\&\quad =-k_{1} \bar{Z}_{1}^{2}+\bar{Z}_{1} \bar{Z}_{2}+\Lambda \beta _{1} \xi _{1}+\bar{Z}_{2}\left( \dot{Z}_{2}-\dot{\xi }_{2}\right) -\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }} \nonumber \\&\quad =-k_{1} \bar{Z}_{1}^{2}+\bar{Z}_{1} \bar{Z}_{2}+\Lambda \beta _{1} \xi _{1}+\bar{Z}_{2}\left( \dot{\chi }_{2}- {\dot{\phi }_{1}}-\dot{\xi }_{2}\right) \nonumber \\&\quad -\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }} \nonumber \\&\quad =-k_{1} \bar{Z}_{1}^{2}+\bar{Z}_{1} \bar{Z}_{2}+\Lambda \beta _{1} \xi _{1}\nonumber \\&\quad +\bar{Z}_{2}\left( F(\chi )+ U+\delta _{\chi }- {\dot{\phi }_{1}}-\dot{\xi }_{2}\right) -\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }} \end{aligned}$$
(35)

From (12), one gets \(U=\Pi \bar{U}+d(\bar{U})\), and

$$\begin{aligned}&\dot{L}_{2} =-k_{1} \bar{Z}_{1}^{2}+\Lambda \beta _{1} \xi _{1}\nonumber \\&\quad +\bar{Z}_{2}\left( f_{2}(\chi )+ \Pi \bar{U}- {\dot{\phi }_{1}}\right) -\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }} \end{aligned}$$
(36)

where \(f_{2}(\chi )=\bar{Z}_{1}+\delta _{\chi }-\dot{\xi }_{2}+F(\chi )+d(\bar{U}) { \in \mathbb {R}^{2}}\). The neural network approximation of \(f_2\) is given by:

$$\begin{aligned} f_{2}(\chi )=W^{T} S(\chi )+\varepsilon (\chi ) \end{aligned}$$
(37)

where \(\Vert \varepsilon (\chi )\Vert \le \bar{\varepsilon }\) Substituting (37) into (36), we have:

$$\begin{aligned}&\dot{L}_{2} = {-k_{1} \bar{Z}_{1}^{2}+\Lambda \beta _{1} \xi _{1}} \nonumber \\&\quad {+\bar{Z}_{2}\left( W^{T} S(\chi )+\varepsilon (\chi )+ \Pi \bar{U}- {\dot{\phi }_{1}}\right) -\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }} } \end{aligned}$$
(38)

Remark 2

The RBFNN weight vector \(W \in \mathbb {R}^{N}\) in (38) contains N weights which requires N adaptive rules to adjust them online. However, updating the N weights adds to the computational cost of the controller. We define an unknown parameter \(\varphi = W^T W = \Vert W \Vert\) with \(\hat{\varphi }\) as its estimate. So, updating a single parameter \(\hat{\varphi }\) instead of the N weights reduces the computational burden of the controller.

To avoid updating the weight vector W in the control law, we utilize Young’s inequality to derive the following equation:

$$\begin{aligned} \bar{Z}_{2} f_{2}(\chi )&=\bar{Z}_{2}\left( W^{T} S(\chi )+\varepsilon (\chi )\right) \nonumber \\&\le { \frac{\bar{Z}_{2}^{2} W^T W S^{T} S}{2 b_{1}^{2}}}+\frac{b_{1}^{2}}{2}+\frac{\bar{Z}_{2}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2} \nonumber \\&\le \frac{\bar{Z}_{2}^{2} \varphi S^{T} S}{2 b_{1}^{2}}+\frac{b_{1}^{2}}{2}+\frac{\bar{Z}_{2}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2} \end{aligned}$$
(39)

where \(\varphi = W^T W = \Vert W\Vert\) is an unknown parameter, \(b_{1} >0\) is a constant, inserting (39) into (38), one gets:

$$\begin{aligned} \dot{L}_{2} \le&-k_{1} \bar{Z}_{1}^{2}+\bar{Z}_{2}\Pi \bar{U}+\frac{\bar{Z}_{2}^{2} \varphi S^{T} S}{2 b_{1}^{2}}+\frac{b_{1}^{2}}{2} \nonumber \\&+\frac{\bar{Z}_{2}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2}-\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }}+\Lambda \beta _{1} \xi _{1} -\bar{Z}_{2} {\dot{\phi }_{1}} . \end{aligned}$$
(40)

Then, \(\bar{U}\) can be obtained as follows:

$$\begin{aligned} \bar{U}=-k_{2} \bar{Z}_{2}-\frac{\bar{Z}_{2} \hat{\varphi } S^{T} S}{2 b_{1}^{2} \Pi }+\frac{ {\dot{\phi }_{1}}}{\Pi } \end{aligned}$$
(41)

It follows that

$$\begin{aligned} \Pi \bar{Z}_{2} \bar{U}=-\Pi k_{2} \bar{Z}_{2}^{2}-\frac{\bar{Z}_{2}^{2} \hat{\varphi } S^{T} S}{2 b_{1}^{2}}+\bar{Z}_{2} {\dot{\phi }_{1}} \end{aligned}$$
(42)

Inserting (42) into (40) gives:

$$\begin{aligned} \dot{L}_{2} \le&-k_{1} \bar{Z}_{1}^{2}+\frac{\bar{Z}_{2}^{2} \varphi S^{T} S}{2 b_{1}^{2}}+\frac{b_{1}^{2}}{2}+\frac{\bar{Z}_{2}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2} \nonumber \\&-\Pi k_{2} \bar{Z}_{2}^{2}-\frac{\bar{Z}_{2}^{2} \hat{\varphi } S^{T} S}{2 b_{1}^{2}} -\frac{\Pi }{\gamma _{1}} \tilde{\varphi } \dot{\hat{\varphi }}+\Lambda \beta _{1} \xi _{1} \end{aligned}$$
(43)

Evaluating (43) yields:

$$\begin{aligned} \dot{L}_{2} \le&-k_{1} \bar{Z}_{1}^{2}+\frac{b_{1}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2}-\left( \Pi k_{2}-\frac{1}{2}\right) \bar{Z}_{2}^{2} \nonumber \\&+\frac{\Pi }{\gamma _{1}} \tilde{\varphi }\left( -\dot{\hat{\varphi }}+\frac{\gamma _{1} \bar{Z}_{2}^{2} S^{T} S}{2 \Pi b_{1}^{2}}\right) +\Lambda \beta _{1} \xi _{1} . \end{aligned}$$
(44)

The parameter update law for \(\hat{\varphi }\) is designed as follows:

$$\begin{aligned} \dot{\hat{\varphi }}=\frac{\gamma _{1} \bar{Z}_{2}^{2} S^{T} S}{2 \Pi b_{1}^{2}}-\eta _{1} \hat{\varphi } \end{aligned}$$
(45)

where \(\eta _{1} >0\) is a constant.

Remark 3

The lone adaptive rule (45) will be used to adjust the RBFNN instead of the weight vector W.

3.1 Stability analysis

Inserting (45) into (44) leads to the following equation:

$$\begin{aligned} \dot{L}_{2} \le&-k_{1} \bar{Z}_{1}^{2}+\frac{b_{1}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2} -\left( \Pi k_{2}-\frac{1}{2}\right) \bar{Z}_{2}^{2} \nonumber \\&+\frac{\Pi \eta _{1}}{\gamma _{1}} \tilde{\varphi } \hat{\varphi }+\Lambda \beta _{1} \xi _{1} \end{aligned}$$
(46)

By using the Young’s inequality, we have:

$$\begin{aligned} \left\{ \begin{array}{l} \Lambda \beta _{1} \xi _{1} \le \frac{1}{2} \Lambda ^{2} \beta _{1}^{2}+\frac{1}{2} \xi _{1}^{2} \\ \tilde{\varphi } \hat{\varphi } \le -\frac{1}{2} \tilde{\varphi }^{2}+\frac{1}{2} \varphi ^{2} \end{array}\right. \end{aligned}$$
(47)

Inserting (47) into (46), we achieve:

$$\begin{aligned} \dot{L}_{2} \le&-k_{1} \bar{Z}_{1}^{2}-\left( \Pi k_{2}-\frac{1}{2}\right) \bar{Z}_{2}^{2}-\frac{\Pi \eta _{1}}{2 \gamma _{1}} \tilde{\varphi }^{2}+\frac{\Pi \eta _{1}}{2 \gamma _{1}} \varphi ^{2} \nonumber \\&+\frac{1}{2} \Lambda ^{2} \beta _{1}^{2}+\frac{1}{2} \xi _{1}^{2}+\frac{b_{1}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2} \nonumber \\ \le&-a_1 L_{2}+a_2 . \end{aligned}$$
(48)

where \(a_1=\min \left[ \begin{array}{lll}2 k_{1},~2\left( \Pi k_{2}-\frac{1}{2}\right) ,~ \eta _{1}\end{array}\right]\) and \(a_2=\frac{\xi _{1}^{2}}{2}+\frac{b_{1}^{2}}{2}+\frac{\bar{\varepsilon }^{2}}{2}\).

From (48) we can obtain:

$$\begin{aligned} L_{2}(t)&\le \frac{a_2}{a_1}+\left( L_{2}\left( t_{0}\right) -\frac{a_2}{a_1}\right) e^{-a_1\left( t-t_{0}\right) } \nonumber \\&\le \frac{a_2}{a_1}+L_{2}\left( t_{0}\right) e^{-a_1\left( t-t_{0}\right) } \quad \forall t \ge t_{0} \end{aligned}$$
(49)

This implies that the closed-loop signals \(\chi _{1}, \chi _{2}\), \(\bar{Z}_{1}, \bar{Z}_{2}\) and \(\tilde{\varphi }\) are semi-globally uniformly ultimately bounded. From (21), \(Z_{1}=\bar{Z}_{1}+\xi _{1}\), and \(\left| \xi _{1}\right|\) is bounded. This implies that there exists a constant \(N_{1} >0\) such that \(\left| \xi _{1}\right| \le N_{1}\). This implies that \(Z_{1}\) converges to the vicinity of zero.

$$\begin{aligned} \lim _{t \rightarrow \infty }\left| Z_{1}\right| \le \left( \sqrt{\frac{2 a_2}{a_1}}+N_{1}\right) \end{aligned}$$
(50)

Select a candidate Lyapunov function for \(\xi _{1}\) as follows:

$$\begin{aligned} L_{3}=\frac{1}{2} \xi _{1}^{2}+\frac{1}{2} \xi _{2}^{2} \end{aligned}$$
(51)

The time-derivative of \(L_{3}\) gives:

$$\begin{aligned} \dot{L}_{3}&=\xi _{1} \dot{\xi }_{1}+\xi _{2} \dot{\xi }_{2} \nonumber \\&=\xi _{1}\left( \xi _{2}+\left( {\phi _{1}}-\alpha _{1}\right) -k_{1} \xi _{1}\right) -k_{2} \xi _{2}^{2} \nonumber \\&\le \xi _{1} \xi _{2}+\xi _{1} \eta -k_{1} \xi _{1}^{2}-k_{2} \xi _{2}^{2} \nonumber \\&\le \frac{1}{2} \xi _{1}^{2}+\frac{1}{2} \xi _{2}^{2}+\frac{1}{2} \xi _{1}^{2}+\frac{1}{2} \eta ^{2}-k_{1} \xi _{1}^{2}-k_{2} \xi _{2}^{2} \nonumber \\&\le -\left( k_{1}-1\right) \xi _{1}^{2}-\left( k_{2}-\frac{1}{2}\right) \xi _{2}^{2}+\frac{1}{2} \eta ^{2} \nonumber \\&\le -a_{3} L_{3}+a_{4} \end{aligned}$$
(52)

By integrating (52), one has:

$$\begin{aligned} L_{3} \le \left( L_{3}\left( t_{0}\right) -\frac{a_{4}}{a_{3}}\right) e^{-a_{3}\left( t-t_{0}\right) }+\frac{a_{4}}{a_{3}} \end{aligned}$$
(53)

From (53), one obtains:

$$\begin{aligned} \lim _{t \rightarrow \infty }\left| \xi _{i}\right| =\sqrt{\frac{2 a_{4}}{a_{3}}}, i=1,2 \end{aligned}$$
(54)

Therefore, (54) shows that the signals of the filtering error compensator are bounded.

Considering (16), the dynamic equation of the orientation angle can be rewritten as follows:

$$\begin{aligned} \dot{\psi } =\Pi _{\psi }\bar{\omega } + d(\bar{\omega }) + \delta _{\psi } \end{aligned}$$
(55)

From Fig. 1, by using plane geometry, we know that \(\frac{y}{x} = \frac{y_n}{x_n}\). Therefore, the desired heading angle of the AGV is calculated as follows:

$$\begin{aligned} \psi _d = \text {atan2}(y_d,x_d) \end{aligned}$$
(56)

The heading angle tracking error is calculated as \(Z_3 = \psi - \psi _d\). The integral of \(Z_3\) is given by:

$$\begin{aligned} \beta _2 = \int _{0}^{t} Z_{3}(\tau ) d \tau \end{aligned}$$
(57)

The Lyapunov function for the heading angle is chosen as:

$$\begin{aligned} L_{4}= \frac{1}{2} {Z}_{3}^{2}+ \frac{1}{2}\Lambda _{\psi } \beta _2^2 + \frac{\Pi _{\psi }}{2 \gamma _{2}} \tilde{\varphi }_{\psi }^{2} \end{aligned}$$
(58)

where \(\gamma _{2}>0\) is a design constant. Define a parameter \(\varphi =\Vert W\Vert ^{2}\), with \(\tilde{\varphi }_{\psi }=\varphi -\hat{\varphi }\) is the estimation error and \(\hat{\varphi }\) is the estimate of \(\varphi\). The time-derivative of \(L_{4}\) yields:

$$\begin{aligned} \dot{L}_{4}&={Z}_{3} \dot{Z}_{3} + \Lambda _{\psi } \beta _2 \dot{\beta }_2-\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi } \nonumber \\&={Z}_{3}\left( \dot{\psi }-\dot{\psi }_{d}\right) + \Lambda _{\psi } \beta _2 Z_3-\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi } \nonumber \\&={Z}_{3}\left( \omega + \delta _{\psi }-\dot{\psi }_{d} + \Lambda _{\psi } \beta _2\right) -\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi } \nonumber \\&={Z}_{3}\left( \Pi _{\psi }\bar{\omega } + d(\bar{\omega })+\delta _{\psi }-\dot{\psi }_{d} + \Lambda _{\psi } \beta _2\right) -\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi } \nonumber \\&={Z}_{3}\left( \Pi _{\psi }\bar{\omega } + F_{\psi }-\dot{\psi }_{d}+ \Lambda _{\psi } \beta _2\right) -\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi } \end{aligned}$$
(59)

where \(F_{\psi }=d(\bar{\omega })+\delta _{\psi }\) which is approximate with neural network as follows:

$$\begin{aligned} F_{\psi }=W_{\psi }^{T} S_{\psi }(\psi )+\varepsilon (\psi ) \nonumber \\ \Vert \varepsilon (\psi )\Vert \le \bar{\varepsilon }_{\psi } \end{aligned}$$
(60)

To avoid updating the weight vector \(W_{\psi }\) in the control input, we employ Young’s inequality to derive the following equation:

$$\begin{aligned} {Z}_{3} F_{\psi }&={Z}_{3}\left( W_{\psi }^{T} S_{\psi }(\psi )+\varepsilon (\psi )\right) \nonumber \\&\le \frac{{Z}_{3}^{2} \varphi _{\psi }S_{\psi }^{T} S_{\psi }}{2 b_{2}^{2}}+\frac{b_{2}^{2}}{2}+\frac{{Z}_{3}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2} \end{aligned}$$
(61)

where \(\varphi _{\psi } = W_{\psi }^T W_{\psi } = \Vert W_{\psi }\Vert\) is an unknown parameter, and \(b_{2} >0\) is a constant. Using (61), (59) becomes:

$$\begin{aligned} \dot{L}_{4} \le&{Z}_{3} \Pi _{\psi }\bar{\omega }+\frac{{Z}_{3}^{2} \varphi _{\psi }S_{\psi }^{T} S_{\psi }}{2 b_{2}^{2}}+\frac{b_{2}^{2}}{2} +\frac{{Z}_{3}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2}\nonumber \\&-\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi }+\Lambda _{\psi } \beta _{2} {Z}_{3} -{Z}_{3} \dot{\psi }_{d} . \end{aligned}$$
(62)

The control law for the heading angle is designed as follows:

$$\begin{aligned} \bar{\omega }=\left( -k_{3} {Z}_{3}-\frac{{Z}_{3} \hat{\varphi }_{\psi }S_{\psi }^{T} S_{\psi }}{2 b_{2}^{2} \Pi _{\psi }}+\frac{\dot{\psi }_{d}}{\Pi _{\psi }}-\frac{\Lambda _{\psi } \beta _{2}}{\Pi _{\psi }}\right) \end{aligned}$$
(63)

Then,

$$\begin{aligned} \Pi _{\psi } {Z}_{3} \bar{\omega }=-\Pi _{\psi } k_{3} {Z}_{3}^{2}-\frac{{Z}_{3}^{2} \hat{\varphi }_{\psi }S_{\psi }^{T} S_{\psi }}{2 b_{2}^{2}}+{Z}_{3} \dot{\psi }_{d}-\Lambda _{\psi } \beta _{2} Z_3 \end{aligned}$$
(64)

Substituting (64) into (62) yields:

$$\begin{aligned} \dot{L}_{4} \le&\frac{{Z}_{3}^{2} \varphi _{\psi }S_{\psi }^{T} S_{\psi }}{2 b_{2}^{2}}+\frac{b_{2}^{2}}{2}+\frac{{Z}_{3}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2} -\Pi _{\psi } k_{3} {Z}_{3}^{2} \nonumber \\&-\frac{{Z}_{3}^{2} \hat{\varphi }_{\psi }S_{\psi }^{T} S_{\psi }}{2 b_{2}^{2}} -\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi } \dot{\hat{\varphi }}_{\psi } \end{aligned}$$
(65)

Simplifying (65) yields:

$$\begin{aligned} \dot{L}_{4} \le&\frac{b_{2}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2}-\left( \Pi _{\psi } k_{3}-\frac{1}{2}\right) {Z}_{3}^{2} \nonumber \\&+\frac{\Pi _{\psi }}{\gamma _{2}} \tilde{\varphi }_{\psi }\left( -\dot{\hat{\varphi }}_{\psi }+\frac{\gamma _{2} {Z}_{3}^{2} S_{\psi }^{T} S_{\psi }}{2 \Pi _{\psi } b_{2}^{2}}\right) \end{aligned}$$
(66)

The update rule for \(\hat{\varphi }_{\psi }\) is thus:

$$\begin{aligned} \dot{\hat{\varphi }}_{\psi }=\frac{\gamma _{2} {Z}_{3}^{2} S_{\psi }^{T} S_{\psi }}{2 \Pi _{\psi } b_{2}^{2}}-\eta _{2} \hat{\varphi }_{\psi } \end{aligned}$$
(67)

where \(\eta _{2} >0\) is a small constant.

Remark 4

The single adaptive rule (67) will be deployed to adjust the RBFNN instead of the weight vector \(W_{\psi }\).

3.2 Stability analysis

Substituting (67) into (66) gives:

$$\begin{aligned} \dot{L}_{4} \le&\frac{b_{2}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2}-\left( \Pi _{\psi } k_{3}-\frac{1}{2}\right) {Z}_{3}^{2} +\frac{\Pi _{\psi } \eta _{2}}{\gamma _{2}} \tilde{\varphi }_{\psi } \hat{\varphi }_{\psi } \end{aligned}$$
(68)

Considering the Young’s inequality, one gets:

$$\begin{aligned} \tilde{\varphi }_{\psi } \hat{\varphi }_{\psi }\le -\frac{1}{2} \tilde{\varphi }_{\psi }^{2}+\frac{1}{2} \varphi _{\psi }^{2} \end{aligned}$$
(69)

Substituting (69) into (68) yields:

$$\begin{aligned} \dot{L}_{4} \le&-\left( \Pi _{\psi } k_{3}-\frac{1}{2}\right) {Z}_{3}^{2}-\frac{\Pi _{\psi } \eta _{2}}{2 \gamma _{2}} \tilde{\varphi }_{\psi }^{2}+\frac{\Pi _{\psi } \eta _{2}}{2 \gamma _{2}} \varphi _{\psi }^{2} \nonumber \\&+\frac{b_{2}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2} \nonumber \\ \le&-a_5 L_{4}+a_6 . \end{aligned}$$
(70)

where \(a_5=\min \left[ \begin{array}{lll}2\left( \Pi _{\psi } k_{3}-\frac{1}{2}\right) ,~ \eta _{2}\end{array}\right]\) and \(a_6=\frac{\xi _{1}^{2}}{2}+\frac{b_{2}^{2}}{2}+\frac{\bar{\varepsilon }_{\psi }^{2}}{2}\). By integrating both sides of (70), one has:

$$\begin{aligned} L_{4}(t)&\le \frac{a_6}{a_5}+\left( L_{4}\left( t_{0}\right) -\frac{a_6}{a_5}\right) e^{-a_5\left( t-t_{0}\right) } \nonumber \\&\le \frac{a_6}{a_5}+L_{4}\left( t_{0}\right) e^{-a_5\left( t-t_{0}\right) } \quad \forall t \ge t_{0} \end{aligned}$$
(71)

The inequality above highlights that \(Z_{3}\) is semi-globally uniformly ultimately bounded and converges to:

$$\begin{aligned} \lim _{t \rightarrow \infty }\left| Z_{3}\right| \le \sqrt{\frac{2 a_6}{a_5}} \end{aligned}$$
(72)

The block diagram of the proposed path following control of the UGV is depicted in Fig. 2.

Fig. 2
figure 2

Block diagram of the proposed UGV control

Full size image

Remark 5

The controller parameters are adjusted by trial and error technique until the desired path tracking performances are achieved.

4 Simulation results

This section presents simulation results to highlight the performance of the proposed path following control protocol. The AGV kinematic model is obtained from [8, 22]. The initial conditions of the AGV are set as \(x_n(0) = -0.5\), \(y_n(0) = 0.5\), \(\dot{x}_n(0) = 0.1\), \({y}_n(0) = 0.1\), and \(\psi (0) = 0.1\). The external disturbances are set as \(\delta _x= 0.2 \text {cos}(0.5t)\), \(\delta _y= 0.2 \text {cos}(0.5t)\), and \(\delta _{\psi }= 0.2 \text {cos}(0.5t)\). The deadzone parameters are set as \(\Pi _r=0.6\), \(\Pi _l = 0.8\), \(s_r = 0.5\), \(s_l = -0.4\), \(\Pi _{\psi r}=0.91\), \(\Pi _{\psi l} = 0.72\), \(s_{\psi r} = 0.66\), and \(s_{\psi l} = -0.53\). The parameters of the filter are set as \(\omega _n = 90\) and \(\Phi = 0.75\). The controller gains are set as \(\Lambda = 16\), \(\Lambda _{\psi } = 9\), \(k_1 = 20\), \(k_2 = 20\), and \(k_3 = 12\). The RBFNN in this study consists of five nodes; the centers of the Gaussian functions are selected between \(-3\) and 3, whereas the width of the functions is chosen as 0.5; the parameters of the RBFNN parameter update laws are chosen as \(\gamma _1 = 0.1\), \(\eta _1=0.001\), \(\gamma _2 = 0.1\), \(\eta _2=0.001\); the initial values of the RBFNN parameter update laws are chosen as 0.1. The desired path is a dumbbell shape described by \(x_d = \text {sin} \left( \frac{1}{3}. \frac{22}{7}.t \right)\), \(y_d = \text {sin} \left( \frac{1}{6}. \frac{22}{7}. t \right)\). The desired orientation angle is calculated as \(\psi _d = \text {atan2}(x_d,y_d)\).

The simulation results are depicted in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, and 16. The Figs. 3, 4, 5, 6 shows the performance of the proposed path following controller compared with the recently reported literature that investigated the path following control of the AGV subjected external disturbances to actuator deadzone such as observer-based state feed control (OSFC) [46] and adaptive sliding mode control (ASMC) [47]. Figures 3, 4 depict the time-varying position and orientation of the AGV. It can be observed that all three controllers were able to achieve path tracking in the presence of external disturbances and deadzone. However, the proposed controller has better tracking accuracy compared to OFSMC and ASMC. The tracking errors of the time-varying position and orientation of the AGV under the three controllers are shown in Figs. 5, 6, respectively. These figures show that the tracking errors are much closer to zero under the proposed controller. The dumbbell path tracking is shown in Fig. 7 which shows that the proposed controller can track the path faster. The responses of the proposed control inputs capable of compensating input deadzone and external disturbances are presented in Figs. 8, 9. The evolution of the parameters for adjusting the RBFNN for the position and the orientation angle are depicted in Figs. 10, 11, respectively. Each of the parameters corresponds to the norm-2 of the RBFNN weights. Updating a single parameter instead of the whole weight vector lessens the computational cost of the controller. Table 1 presents the performance of the proposed controller in terms of settling time and root-mean-square-errors (RMSE) under different RBFNN weights. It can be seen that by using a single parameter to adjust the RBFNN, the RMSE and the settling time of the proposed controller are smaller, which signifies enhanced tracking performance. On the other hand, when multiple weights are used to adjust the RBFNN, the RBFNN approximation errors tend to increase as the number of weights increases. The increase in the RBFNN approximation errors coupled with the increase in the computational complexities leads to an increase in the tracking errors and slows down system response.

Table 1 Comparisons of settling time and RMSE of the proposed controller with different RBFNN weights
Full size table
Fig. 3
figure 3

Time-varying positions of the AGV

Full size image
Fig. 4
figure 4

Steering angle of the AGV

Full size image
Fig. 5
figure 5

Path following tracking errors of the AGV

Full size image
Fig. 6
figure 6

Steering angle tracking errors of the AGV

Full size image
Fig. 7
figure 7

Path tracking graph of the AGV

Full size image
Fig. 8
figure 8

Control inputs of the AGV position

Full size image
Fig. 9
figure 9

Control inputs of the AGV orientation angle

Full size image
Fig. 10
figure 10

Norm-2 of the neural network weights of the AGV position

Full size image
Fig. 11
figure 11

Norm-2 of the neural network weights of the AGV steering angle

Full size image

To highlight the negative impact of the input deadzone on the path tracking performance of the AGV, the differential flatness-based controller (DFC) [23] and the finite-time sliding mode control (FTSMC) [13] are applied to the AGV under deadzone. The time-varying position and orientation of the AGV under the DFC and FTSMC deviated from the target trajectories as depicted in Figs. 12, 13, respectively. The tracking errors of the AGV under both DFC and FTSMC are large and unacceptable as shown in Figs. 14, 15. The dumbbell path tracking is presented in Fig. 16 which shows that both DFC and FTSMC failed to steer the AGV to track the desired path because they were not designed to compensate for the input deadzones.

Fig. 12
figure 12

Time-varying positions of the AGV

Full size image
Fig. 13
figure 13

Steering angle of the AGV

Full size image
Fig. 14
figure 14

Path following tracking errors of the AGV

Full size image
Fig. 15
figure 15

Steering angle tracking errors of the AGV

Full size image
Fig. 16
figure 16

Path tracking graph of the AGV

Full size image

To further demonstrate the superior robustness of the proposed controller against external disturbances and input deadzone, its performance in terms of settling time and RMSE is compared with that of the OSFC, ASMC, TOSMC, and DFC as shown in Table 2. From this table, it is clear that the proposed controller is superior. Meanwhile, both TOSMC and DFC could not settle and converge to the desired trajectories as a result of the input deadzone.

Table 2 Comparisons of settling time and RMSE of the three controllers
Full size table

5 Conclusion

This paper studied the problem of path following control of an AGV subjected to input deadzone and external disturbances. An RBFNN has been employed to approximate the AGV nonlinearities, external disturbances, and the input deadzone. A minimum learning parameter scheme is put in place to minimize the computational cost of the RBFNN. A backstepping controller with integral error action is proposed to achieve the path following with much smaller tracking errors. The problem of ’explosion of the complexity’ associated with traditional backstepping has been dealt with using the command filter and the filtering errors were removed via filtering error compensation signals. The comparison results showed that the proposed control strategy provided Superior path tracking performance. The limitations of this work include the use of Ackerman’s model which disregards some important parameters of the AGV, and a lack of experimental verification. In the future, fractional-order backstepping will be used to improve the robustness and convergence speed of the path tracking controller. In addition, to further minimize the computation cost of the controller, an event-triggered mechanism will be incorporated into the controller. Furthermore, a detailed model of AGV will be considered and an experiment will be conducted to further verify the effectiveness of the proposed controller.