1 Introduction

Overpopulation is a magnificent challenge in the existing decade, as the continuous increase leads to a boost in resource usage, including energy consumption causing the energy demand more exaggerated than the energy generation. Still, fossil fuels and chemical and nuclear reactors represent master energy resources; Unfortunately, these resources are non-renewable and non-ecofriendly. Subsequently, these reasons led to finding renewable, eco-friendly replacements [1].

Renewable energy is counter to fossil fuels, generated from the sun, tidal waves, geothermal heat, rain, and wind. Furthermore, the essential need to change to renewable energy is forced by the necessity to deal with climate change, global warming, greenhouse gas emission reduction, ensure energy security, and enhance the sustainability of human activities. The most well-known and prevalent renewable energy source is solar energy [2, 3]. Moreover, the efficiency of solar photovoltaic (PV) cells was reinforced corresponding to technology development recently while the manufacturing cost was reduced [1, 2]. The capacity of solar energy increased by 22% between 1994 and 2004 [1]. By the end of 2021, the installed solar capacity reached 843.1 Gigawatts [4]. Furthermore, according to the PV technology road map by the International Energy Agency, solar energy will contribute to more than 16% of the total electricity generated by 2050 [5]. The applications of solar energy were mounted a short while ago to power lights, pumps, engines, refrigerators, and construction sites [3].

Approximately \(3.8 \times 10^{23}\) KW per second is the total energy transmitted from the sun while only \(1.8 \times 10 ^{14}\) KW per second is intercepted by the earth; however, approximately 30% of the radiation reaches the earth’s surface on a clear day and around 10% on cloudy days [6, 7]. On the other side, conventional photovoltaic cells require an extensive area for installation; for instance, 1 kWp PV cell requires \(10\,m^2\) of land [5]. Whereas the unavailability of free land in cities and transmission losses due to long distances, traditional PV cells are not an optimal solution. Consequently, A new configuration of PV cells has been used to minimize the footprint while maximizing the generated electricity which is an artificial tree design where the panels are arranged in the Fibonacci series method [1].

The quality of urban life in Egypt has decreased over the years as Cairo lost a significant quantity of green spaces due to overpopulation. According to data collected between 2017 and 2020 regarding the green spaces in Cairo, the results illustrate a limited presence of gardens as Cairo lost \(910,894 m^2\) of green lands. As a result, conventional PV cells should replaced with a solar tree to produce the same energy quantity in less area [8].

The main objective of this paper is the achieve a trade-off between power generated and structural cost to increase the efficiency of the solar tree. The optimization procedure is to optimize the solar panels’ positions to minimize the shaded area which leads to maximizing the generated power. Solar panel Orientation has been generated using a single-objective genetic algorithm to allocate tilt angle and surface azimuth angle for each panel while a multi-objective genetic algorithm has been used to optimize the panel’s position.

Most of the real applications contain numerous factors and boundaries that need to be considered during the design of the system despite its changeability either over time or per each system component. Sequentially, the genetic algorithm optimization technique has been used as it works a vector-valued cost function to optimize the components which are represented as a family of points known as the Pareto-optimal set where each point on the surface is in the optimal orientation as long as the other points are in the optimal orientation as well; also, the adjustment of each point leads to different orientations for other points [9]. In addition, the study considers the Egyptian clear sky climate.

The paper is organized as Sect. 1 presents the introduction of the paper. In Sect. 2, the literature review illustrates the development of solar tree applications and optimization techniques; besides, the mathematical model and algorithm, including the constraints and limitations, have been discussed in Sect. 3. Section 4 represents the results and their explanation. Section 5 includes the conclusion of the performance analysis of the optimization technique over the solar tree.

2 Literature review

2.1 Solar tree

Solar trees are a PV system that blends PV technology and the art of biomimicry structures. It mainly consists of a tree-like structure with solar panels arranged as leaves on the branches of the steel structure of the tree. There is no optimum standard structure for solar trees; it is designed to effectively capture the maximum amount of solar energy simultaneously while occupying the minimum land area and avoiding the shading of the panels on one another. These structures result in increasing the power density of the PV system. Also, The solar tree is designed to please the public. Researchers developed different designs for solar trees, which can be categorized as Multi-branch single stem solar trees, Fibonacci pattern solar trees, Spiraling phyllotaxy solar trees, 3D solar trees, and Simple solar trees.

2.1.1 Multi-branch single-stem solar tree

A multi-branch single stem solar tree is a unique solar structure that features a tree stem-like column with branches extending out at different heights, each carrying solar modules oriented in different directions to prevent shading, as shown in ([3], Fig. 1). While this design may trade off some efficiency in capturing solar radiation throughout the day, it offers several advantages over other solar structures.

Recent studies, such as those by Dey and Pesala [5], Cuce et al. [10], Eltayeb et al. [11], Hyder et al [12], and Kumar et al. [13], have investigated the design and performance of multi-branch single stem solar trees. These studies have shown that the multi-branch single stem solar tree design is simple and easy to develop, and can offer improved power generation compared to other solar structures. The optimal design of these structures, including maximum power point tracking (MPPT), has also been explored in some studies ([7, 14]). There are a variety of solar structures that resemble trees in their appearance or function. Some common patterns of solar trees will be introduced below subsections.

Fig. 1
figure 1

Multi-branch single stem

Full size image

2.1.2 Fibonacci pattern solar tree

The Fibonacci pattern solar tree is the most popular design for solar trees nowadays. In this design, the branches’ lengths and angles follow a Fibonacci pattern. “It takes n branches to complete m turns around the trunk, with \((m,n)\in F\)” [12]. Furthermore, the vertical separation follows the same pattern, while the angular separation is \(144 ^{\circ }\), as shown in ([12], Fig. 2). This design is considered to be a bio-inspired design by oak trees which also have the same pattern. The Fibonacci pattern solar tree has a relatively high efficiency as it ensures that the tree’s leaves, and solar panels, face the sun absorbing most of the energy. This pattern helps direct the tree’s leaves toward the sun to ensure that the most energy is absorbed [3, 12]. On the other hand, this design is complicated, not suitable for large power production, and costlier than the other designs.

Fig. 2
figure 2

Fibonacci pattern solar tree

Full size image

2.1.3 Spiraling phyllotaxy solar tree

The spiraling phyllotaxy solar trees mimic the nature of plants in which a spiral on the stem is formed by lines touching the basses of successive leaves, as shown in ([3], Fig. 3). This structure enhances the sunlight capturing of the solar tree, but it uses considerable space for the leaves and is expensive to manufacture [3, 12]. The common patterns of this structure are 2/5 and 3/8 phyllotaxy patterns; the fraction in the name determines the angle between each branch.[3, 15]. Researchers found that the 3/8 phyllotaxy pattern produces more power than the 2/5 phyllotaxy pattern under the same operating conditions. [15].

Fig. 3
figure 3

Spiraling phyllotaxy solar tree

Full size image

2.1.4 3D solar tree

The 3D solar tree includes many 3D shapes. The Hemispherical dome solar tree is developed by placing solar cells along the surface of a hemispherical contour. Researchers [16] considered half of the hemisphere for the design, and the panels were oriented on random angles so that while some PV panels have oblique angles with the sunrays, others have normal angles with the incident rays, as shown in ([16], Fig. 4). Hence max power generation for these oriented panels is obtained. Another advantage is encountering the 3D space rather than the 2D footprint to capture sunlight. By using this configuration, a gain of 227% and 54% over the flat panel configuration was observed in the winter and summer, respectively. However, 3D solar trees are costly designs as they need a large number of panels [16]. Other 3D shapes were investigated by [17], including open cube and open parallelepiped shown in ([17], Fig. 5). They found a higher annual energy generation of a factor ranging from 2.1\(-\)3.8 depending on the longitude in which the system is placed as compared to the flat orientation.

Fig. 4
figure 4

Hemispherical dome solar tree

Full size image
Fig. 5
figure 5

Open cube and open parallelepiped configurations

Full size image

2.1.5 Simple Solar tree

The simple solar tree is similar to the solar module surface systems; the difference is that the modules are installed on steel structures with suitable heights and slopes to harvest the sunlight more efficiently, as shown in ([3], Fig. 6). It is characterized to be inhomogeneous and perpendicular to the sunlight [3]. Researchers [18] developed a roughly 5-meter simple solar tree with 7 PV panels at an angle of 28 degrees with different heights. The tree generated 28% more power in comparison to the land-based system. The problem with this design is that it is less effective in light capturing as all panels are placed in the same direction. [3].

Fig. 6
figure 6

Simple solar tree

Full size image

2.1.6 Application on solar tree

The main value of solar trees appears in situations where a small area is provided, like urban areas and highways. The solar tree has the following applications [19]:

  • Urban areas: To provide electricity for houses with much less area than the traditional PV systems.

  • Rural areas: where many places do not have access to an electricity grid. It can also be used in agriculture applications as shown in ([3], Fig. 7a).

  • Highways: It is often expensive to bring an electricity grid for highways, so in this situation, the solar tree will be a much more cost-effective choice.

  • Street Lighting: as Ross Lovegrove tree in the United Kingdom as shown in ([14], Fig. 7b).

  • Parking spots: To provide both shadow and energy.

  • Garden lighting: to provide electricity for walkways and gardens’ streetlights, illuminating the area and enhancing its look. As shown in ([20], Fig. 7c).

  • Airports: airports have a large land area for runways, so the solar tree can provide energy for airports and uses only a small land area.

  • Charging purpose: Solar trees can provide energy for charging as they may contain wireless charges and USB chargers to charge phones and laptops.

  • Charging stations: to charge electric vehicles as shown in ([20], Fig. 7d).

Ultimately, solar trees offer a variety of possible uses and can help create a cleaner and more sustainable future.

Fig. 7
figure 7

Solar tree application

Full size image

2.2 Optimization technique

Usually, any optimization model is dependent on applying a what-if analysis. A well-designed optimization model can help by highlighting potential areas for improvement. Each category of optimization has a different subset. The first approach uses statistics, but the second employs probabilistic thinking. The best option is selected after a series of data models have been evaluated using a mathematical method. Constraints, like the range of potential values for a function, are very important to define the problem domain correctly. Finding the ideal answer necessitates evaluating the performed function. The output of the optimization problem should be zero errors [21].

Several kinds of optimization problems exist. A few straightforward ones, including those with obvious solutions or no decision variables, do not require formal optimization. Nonetheless, a mathematical solution is typically required, and the aim is to produce the best outcomes. So most issues need to be optimized in some way. The main goal of any optimization problem despite its kind is to cut the expense and risks of the required model. On the other hand, the problem can need several decisions, and this time it is called a multi-objective optimization problem.

As ([22], Fig. 10) illustrates, the mathematical process of any optimization problem must be solved by identifying two stages which are the modeling of the problem and the solving algorithms. The modeling stage has three main elements: Objective: To get the best value from all possible outcomes. Variables: identify each variable to predict its different and possible values Constraints: put all possible constraints into consideration, Then solve the problem by applying a suitable optimization technique and finally get the optimal solution [23].

The optimal solution to a required problem is found using mathematical approaches called optimization techniques, which entail making choices that maximize or minimize the objective function according to the selected application; several optimization techniques can be performed for the application of solar tree as they are considered as soft computing techniques such as genetic algorithms, fuzzy logic, particle swarm optimization, etc [12]. Genetic algorithm (GA): is a technique based on natural selection, the process that propels biological evolution, for addressing both constrained and unconstrained optimization problems. The genetic algorithm repeatedly modifies a population of unique solutions. The genetic algorithm chooses individuals of the existing population to serve as parents at each stage and uses them to create offspring for the following generation. The population “evolves” towards the best option over the subsequent generations. As [5] show in their research a genetic algorithm based on multi-objective optimization is used while designing a model of a solar tree to avoid the maximization of the shading losses and they used a ray optic simulation to verify the shading losses and power generation.

2.2.1 Fuzzy logic

Fuzzy logic: This optimization model addresses how to carry out optimization while dealing with uncertainty. When it is impossible to determine the accuracy of a system’s performance criteria, parameters, and decision variables, this optimization strategy is applied. Particularly, the system’s truth values can be either fully false (zero), completely truthful (one) or some value in between. The idea of partial truth is intended to be captured by this. As [24] mentioned in his paper, a fuzzy logic algorithm has the advantage of using linguistic variables to simplify the required problem in an obvious manner so he used it in the estimation of the total amount of solar irradiance.

2.2.2 Particle swarm optimization

Particle Swarm Optimization (PSO) is a population-based algorithm that is similar to the genetic algorithm in that it evaluates each particle’s objective function at each step and determines each particle’s new velocity based on this assessment. In PSO, particles represent a group of individuals that move in steps across an area. The algorithm re-evaluates after particles move to determine the optimal solution.[25]. PSO has been utilized in research studies such as [26], where it was used to optimize a solar tree system. The benefits of PSO include its simplicity of implementation, unique memory properties, and the fact that it does not require the gradient of an objective function like other optimization algorithms. When selecting an optimization technique, it is important to consider the application and the desired output characteristics. A simulator such as Matlab can then be used to perform the necessary mathematical operations. Overall, PSO is a useful optimization algorithm for complex systems such as solar trees and can provide better results than other optimization methods.

2.2.3 Genetic algorithm

The single-objective optimization problem is a relatively simple problem with only one variable in its objective function. This problem can be classified as either constrained or unconstrained, depending on the presence of constraints. In [27], the authors provided an example of a single-objective optimization problem with constraints. Consider an objective function \(f(x')\) with a constraint \(g(x')\). The goal is to minimize \(f(x')\) subject to the constraint \(g(x') \ge 0,\) where \(x'\) is a vector of decision variables belonging to the n-dimensional space \(X \subset \mathbb {R}^n\). The solution to this problem is a vector \(x' = (x_1, x_2, x_3, \ldots , x_n)^T\), which minimizes the objective function while satisfying the constraint.

3 Methodology

Since one of the advantages of using GAs is their ability to efficiently search and explore the solution space, considering multiple conflicting objectives simultaneously [28] and according to [29] application of PSO in Multi-objective optimization is not justified as the possibility of finding a non-dominated solution drop deeming it useless in multi-objective optimization. Also, they mentioned that a study was performed on a validation comparison of results among Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), and the sequential search technique. When dealing with problems involving more than multiple parameters for optimization, the validation analysis demonstrated that GAs outperformed both the sequential search and PSO methods. It was observed that the GA approach can achieve the best solution with 0.5% accuracy while using only half the number of iterations required by PSO and the sequential search techniques. Consequently, GAs have garnered significant attention in the realm of optimization methods due to their ability to efficiently address various scheduling problems within reasonable timeframes [29]; taking previous statements into consideration the genetic algorithm optimization technique is chosen to optimize our problems.

3.1 Limitation, assumption, and uncertainties

This study contains some limitations, assumptions, and uncertainties mentioned below:

  • Limitations

    • Upper and lower boundaries of (X, Y, Z) coordinates of structure.

    • Due to the computational power limit, A 5 mm area is used for mesh in analysis.

    • There is no software available to calculate the energy yield curve for solar trees.

    • Solar panels are fixed that limit the power generated.

  • Assumption

    • The first-panel position has been set as the original point (0, 0, 0).

    • For single-objective genetic algorithms, the year is assumed to start on January 1st, and the day length is from 7 a.m. to 5 p.m.

    • For solar energy treatment, similar to solar trees known for their low to medium power generation, the harvested energy can either be instantly utilized or stored in a conventional solar battery

    • The partial shading due to branches is neglected in this study

  • Uncertainties

    • The calculations assumed that hourly radiation data are given; however, the data available is monthly irradiance.

3.2 Optimal orientation for the solar panels using single objective genetic algorithm

Firstly, we considered maximizing individual solar panels’ output by changing their orientation. These outputted orientations are then used in the second part of the methodology in which the position of each oriented solar panel is determined in the tree with the consideration of both the cost and the efficiency of the solar panel [22]. For the solar panel to have a maximum output, the sun’s direct irradiance lines should be perpendicular to the panel’s surface. Due to the continuous movement of the sun, this objective could only be established using a rotating solar panel with a tracking mechanism. However, tracking solar panels adds to the cost of regular maintenance and the existence of large moving parts [22]. Therefore, the fixed orientation of the solar panels is used in this paper. Irradiance is divided into four main types: DNI, DHI, BHI,  and GHI is the amount of solar radiation received per unit area by a surface that is always held perpendicular to the direction of the Sun. DHI is the amount of radiation received per unit area by a horizontal surface due to the solar radiation scattered by molecules and particles in the atmosphere. Beam Horizontal Irradiance (BHI) is the subtraction of global horizontal irradiance GHI and diffused radiation DHI on a horizontal surface as per the below equation [30].

$$\begin{aligned} BHI = GHI - DHI \end{aligned}$$
(1)

where

$$\begin{aligned} BHI= DHI+DNI \cos \left( \theta _z\right) \end{aligned}$$
(2)

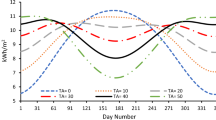
where \(\theta _z\) is the zenith angle defined by the angle between the observer surface normal and the line joining the Sun and the observer. The monthly direct normal irradiance values and the diffused horizontal irradiance are obtained from the Egyptian atlas[31]. As shown in ([31], Fig. 8) and ([31], Fig. 9) show DNI and GHI Obtained from Atlas [31], while taking Sheikh Zayed city GPS co-ordinate 30.08N, 31.34E when observing the value.

Fig. 8
figure 8

DNI from Atlas

Full size image
Fig. 9
figure 9

GHI from Atlas

Full size image

A mathematical formulation of the irradiance on a tilted surface given the DNI and DHI is obtained from the literature [22, 32,33,34]. It is dependent on the solar angles and orientation that change daily and even hourly. The total irradiance on an inclined surface is determined using the following equation

$$\begin{aligned} I(\beta , \gamma )=I_b \frac{\cos \theta _i}{\cos \theta _z}+I_d \frac{1+\cos \beta }{2}+(I_b+I_d) \rho _g \frac{1-\cos \beta }{2} \end{aligned}$$
(3)
Fig. 10
figure 10

Sun’s and tilted surface’s angles

Full size image

where \(I_b\) is hourly direct irradiance on a horizontal surface, \(I_d\) is Hourly diffuse irradiance on a horizontal surface, \(\theta _i\) is the angle of incidence of the sun rays on the tilted surface, \(\beta\) (tilt angle of the surface) is the angle between the plane of the surface and horizontal, \(\gamma\) is the surface azimuth angle which is the angular measurement between the direction of true South and the horizontal projection of the surface normal vector [35]. \(\theta _z\) is the zenith angle and \(\rho _g\) is the ground albedo which equals to 0.2 according to the literature [33, 34]. The term \((I_b+I_d) \rho _g \frac{1-\cos \beta }{2}\) represents the sky-diffuse irradiance and the direct components of the irradiance are \(I_b \frac{\cos \theta _i}{\cos \theta _z}\). The term \((I_b+I_d) \rho _g \frac{1-\cos \beta }{2}\) represents the ground reflected irradiance; this term is considered insignificant and omitted from our calculations due to the relatively higher height of the solar tree when compared traditional PV system and the low multiplication factor (\(\rho _g\)). ([22], Fig. 10) illustrates the sun-earth angles for a tilted surface described earlier.

The \(cos\theta _i\) and \(cos\theta _z\) can be obtained by the following two equations

$$\begin{array}{lllll} \cos {\theta _i} = & \sin \delta \sin \phi \cos \beta - \sin \delta \cos \phi \sin \beta \cos \gamma \\ & \; + \cos \delta \cos \phi \cos \beta \cos \omega + \cos \delta \sin \phi \sin \beta \cos \gamma \cos \omega \\ & \, + \cos \delta \sin \beta \sin \gamma \sin \omega \end{array}$$
(4)
$$\begin{aligned} \begin{aligned}&\cos \theta _z = \cos \delta \cos \phi \cos \omega +\sin \delta \sin \phi \\&\end{aligned} \end{aligned}$$
(5)

\(\phi\) is the latitude, \(\delta\) is the sun’s declination angle, \(\omega\) is solar hour angle [35].

$$\begin{aligned} \delta =-23.45^{\circ } \times \cos \left( \frac{360}{365} \times (d+10)\right) \end{aligned}$$
(6)

where d is the day of the year with Jan 1 as d = 1. The equations require the irradiance to be measured each hour while the available data was the monthly irradiance; therefore, the Sunshine Hours Mean Method was used to convert the monthly irradiance into hourly one [36]. In this method, the hourly irradiance is obtained by dividing the monthly accumulated irradiance by the total sunshine hours in a month. The total yearly energy incident is the cost function that should to be maximized in order to get the maximum output from the solar panel. The total energy per day is obtained by summing the irradiance of each hour from 7 a.m. to 5 p.m. The daily energy is summed for 365 days to calculate the annual energy incident on the solar panel. The final cost function is shown below.

$$\begin{aligned} E(\beta , \gamma )=\sum _{\text{ day } =1}^{365} \sum _{h=7 \text{ a.m. } }^{5 \text{ p.m. } } I_{(h, \text{ day } )}(\beta , \gamma ) \end{aligned}$$
(7)

To obtain the maximum irradiance for each solar panel, the genetic optimization tool on the Matlab simulator is used; its default is to minimize the error, so an inverter is performed over the objective function to maximize our cost function.

The following diagram, Fig. 11, shows the procedure for applying an optimization technique to this solar tree model.

Fig. 11
figure 11

Optimization technique

Full size image

For the genetic algorithm option, there are five main parameters that should be identified shown in Fig. 12.

Fig. 12
figure 12

Single-objective optimization technique

Full size image

3.3 Optimal position using multi-objective genetic algorithm

The branches of solar trees are supported by a metallic structure, allowing them to withstand the winds and other weather conditions in the metropolitan area [3, 14]. The structural steel of the solar tree can be optimized because it is one of the most expensive elements, and although many solar configurations were used, the simple solar tree design obtained the most energy with PV panels spread, which can be identified by the net area projected on the ground, but this raises the cost, whereas stacking panels can cause partial shading, which leads to an optimization problem between minimizing projected net area on the ground and power loss [5]. The position uses the optimal orientation so that the shading loss is minimized. Based on light transmission principles, the annual power loss due to shading is defined as a function of solar panel positions \(\left( P_n\left( x_n, \textrm{y}_n, \textrm{z}_n\right) \right)\), length (L), breadth (B), orientation \(\left( \beta _n, \gamma _n\right)\), DNI and DHI of the location. The light from the sun is assumed to come from infinity, whereas the lines travel in straight lines in parallel. The area of the shadow projected by one solar panel “Panel 1” on another solar panel “Panel 2” is calculated using the algorithm in Fig. 14 Given the center point O(x, y, z), the endpoints of the solar panel 1 (ABCD) can be calculated according to the [5] in the following equations

$$\begin{aligned} O= & {} \left[ \left( \textrm{x}_0-\left( \frac{\textrm{H}}{2}\right) \cos \beta \sin \left( \gamma +180^{\circ }\right) \right) , \right. \nonumber \\{} & {} (\textrm{y}_0-\left( \frac{\textrm{H}}{2}\right) \cos \beta \cos (\gamma +180^{\circ })), \nonumber \\{} & {} (\textrm{z}_0-(\textrm{H} / 2) \sin \beta ] \end{aligned}$$
(8)
$$\begin{aligned} A= & {} [(O_{\textrm{x}}+(\textrm{L} / 2) \cos \left( \gamma +180^{\circ }\right) , \nonumber \\{} & {} \left( \textrm{O}_{\textrm{y}}-(\textrm{L} / 2) \sin (\gamma +180)\right) ,\left( \textrm{O}_{\textrm{z}}\right) ] \end{aligned}$$
(9)
$$\begin{aligned} B= & {} [\left( A_x+H \cos \beta \sin \left( \gamma +180^{\circ }\right) \right) , \nonumber \\{} & {} \left( A_y+H \cos \beta \cos \left( \gamma +180^{\circ }\right) \right) ,\left( A_z+H \sin \beta \right) ] \end{aligned}$$
(10)
$$\begin{aligned} C= & {} [\left( \textrm{A}_{\textrm{x}}-\textrm{L} \cos \left( \gamma +180^{\circ }\right) \right) , \left( \textrm{A}_{\textrm{y}}+{\text {Lsin}} \left( \gamma +180^{\circ }\right) \right) ,\nonumber \\{} & {} \left( \textrm{A}_{\textrm{z}}\right) ] \end{aligned}$$
(11)
$$\begin{aligned} D= & {} [\left( C_x+H \cos \beta \sin \left( \gamma +180^{\circ }\right) \right) ,\nonumber \\{} & {} \left( C_y+H \cos \beta \cos \left( \gamma +180^{\circ }\right) \right) ,\left( C_z+H \sin \beta \right) ] \end{aligned}$$
(12)

The same process is used to obtain the endpoint of the second solar panel PQSR. At a certain time instant, the sun ray directional vectors are calculated through the next equation

$$\begin{aligned} \text{s}=\left[ \cos \gamma _s \cos \alpha , \sin \gamma _s \cos \alpha , \sin \alpha \right] \end{aligned}$$
(13)

where

$$\begin{aligned}{} & {} \alpha : \,Altitude \,angle \,of \,the \,sun \\{} & {} \gamma _s: \,Azimuth \,angle \,of \,the \,sun \end{aligned}$$

Following that, a line segment is drawn through each point on “Panel 1” in the direction of the Sun vector (\(\text{s}\)). The “Panel 1” coordinate is one of the line segment’s ends (For example Point A). In equation 13, The relationship used to determine a second endpoint for point A of “Panel 1” is represented by a line segment. In equation 13, the value ofk is any constant integer value. In our case, we choose 1 as the constant integer value. As a result, \(S_AA\) represents the line segment representing Sun rays passing through point A. A similar relation is used for all four points in panel 1 to obtain a line segment representing Sun rays.

$$\begin{aligned} \textrm{S}_{\textrm{A}}=\textrm{A}+\textrm{k} \times \overrightarrow{\textrm{s}} \end{aligned}$$
(14)

The point of intersection of solar ray lines (whose direction is given by the directional vector \(\text{s}\)) passing through points A, B, C, and D with the plane of the “Panel 2” (PQSR) gives the endpoints of the shadow (\(I_A I_B I_C I_D\)) cast by “Panel 1” (ABDC). To find the shadow of “Panel 1” (ABDC) in the plane of “Panel 2” (PQSR), use equation 14 to calculate the normal vector (\(\text{n}\)) to the “Panel 2” plane.

$$\begin{aligned} \overrightarrow{\textrm{n}}=\overrightarrow{\textrm{PQ}} \times \overrightarrow{\textrm{PR}} \end{aligned}$$
(15)

In Fig. 14, the projection of panel 1 onto panel 2 employs the algorithm for determining the intersection point of a line and a plane. The algorithm takes as inputs the normal for vector to Panel 2 (\(\text{n}\)), any point in the plane of Panel 2 (For example, Point “P”), and endpoints of the line segment as mentioned above (for example, P0 = A, P1 = SA). The process is repeated for each of “Panel 1’s” four points to obtain the shadow on the “Panel 2” plane. Our coordinate system is defined by point O which is defined as the origin of the first solar panel to be the origin and the downward direction as the positive z-axis; therefore the top of the tree is our origin as shown in Fig. 13.

Fig. 13
figure 13

Projection of shadow on panel 2

Full size image

To prevent false shading while calculating, panel 1 should be between the sun and the shadow. The algorithm followed to prevent false shading is shown in the intersection between a point and a plane, whereas check D checks if there is false shading. Considering sun position determined by \(\textrm{S}_{\textrm{A}} \textrm{S}_{\textrm{B}} \textrm{S}_{\textrm{D}} \textrm{S}_{\textrm{C}}\) which was determined in a previous equation, the following equation uses dot product to determine if the solar panel 1 lies between the shadow and the sun.

$$\begin{aligned} \text{ Condition } =T . Y \end{aligned}$$
(16)

where T is the difference between shadow and center point of the solar panel 1 Y is the difference between solar panel 1 and the sun.

First, we calculate the line segment \(\text{u}\)

$$\vec u = \overrightarrow {O{P_1}} - \overrightarrow {O{P_0}}$$
(17)

Second, the solar panel’s line segment intersects with a point on the plane of the second solar panel.

$$\vec w = \overrightarrow {O{P_0}} - \vec V$$
(18)

where V is any point on the plane of the second, solar panel

$$D = \vec n \cdot \vec u$$
(19)

Then the absolute value of D will determine if the line segment of solar panel 1 is parallel to the plane where If the D is equal to zero then the line segment is parallel to the plane of the second panel therefore there is no shading. Since the sun rays are assumed to be parallel the position we can get the position of one point only, Where

$$\begin{aligned} \begin{aligned}&\textrm{I}_{\textrm{x}}=\textrm{P}_{0 \textrm{x}}+\left( \frac{\mathrm {-(\text{n} \cdot \text{w})}}{\textrm{D}} \times \textrm{u}_{\textrm{x}}\right) \\&\textrm{I}_{\textrm{y}}=\textrm{P}_{0 \textrm{y}}+\left( \frac{\mathrm {-(\text{n} \cdot \text{w})}}{\textrm{D}} \times \textrm{u}_{\textrm{y}}\right) \\&\textrm{I}_{\textrm{z}}=\textrm{P}_{0 \textrm{z}}+\left( \frac{\mathrm {-(\text{n} \cdot \text{w})}}{\textrm{D}} \times \textrm{u}_{\textrm{z}}\right) \end{aligned} \end{aligned}$$
(20)

The process is repeated to get the other three points, after removing the z component, the MATLAB command poly shape was used to draw these points and the solar panel 2, then the area of the intersection is calculated using the command area, and the process is repeated for each panel on the other 19 panels to get the total shaded area. Then, after plotting the total solar panel, the enclosed shape is calculated through the function area.

Fig. 14
figure 14

The algorithm to calculate the Intersection between a point and a plane

Full size image

The partial shading due to the branches is not considered in this study, as the branches have a low cross-sectional area compared to the large area of the solar panel. Since the diffuse radiation incident on the solar panel is not affected by shading, the power loss due to partial shading is calculated by multiplying the beam radiation on each solar panel by the efficiency of the solar panel (\(\eta _e\)) and shaded area (\(A_h\)). The net power loss is calculated by adding the energy losses(\(P_l\)) at each instant.

$$\begin{aligned} \textrm{P}_{\textrm{l}}=\sum _{\textrm{h}} \sum _{\textrm{n}} \textrm{I}_{\textrm{b}}\left( \beta _{\textrm{n}}, \gamma _{\textrm{n}}\right) \times \textrm{A}_{\textrm{h}} \times \eta _{\textrm{e}} \end{aligned}$$
(21)

The net estimated annual power generated (\(P_g\)) from a solar tree made up of ’n’ solar panels is calculated by subtracting the shading loss (\(P_l\)) from the estimated annual power without considering shading loss. This essentially means that Pg is made up of energy generation from the diffuse component of solar radiation received by the entire solar panel as well as energy generation from the non-shaded parts of the solar panel. It is worth noting that the current study did not account for interconnection losses in the solar tree. Using the first solar panel as the reference panel (0, 0, 0), the number of variables, i.e., the positions of solar panels to be optimized, is three (n-1). The net projected ground footprint area (Ap) is also defined as a function of the positions and orientation of solar panels. Similar to the calculation of shaded area, the solar panels are projected onto the ground for the calculation of projected area (i.e., the xy plane) whereas the z component is removed. The negative z-axis [0, 0, -1] represents the direction vector for projecting the solar panels on the xy plane. The net projected area is the area of the largest rectangle enclosing all the solar panels (Ap). The multi-objective optimization problem fitness function is the minimization of Power loss (\(P_l\)) and minimization of the Projected net area on the ground, whereas the algorithm compromises between them. The initial population size is 200, the crossover fraction is 0.8, and the selection function is tournament selection, where 2 individuals from the current generation are selected randomly, then the best is chosen to be the parents. Crossover mutation 0.001, as a measure of population concentration, the distance crowding function. The stopping criteria are the difference between two consecutive generations to be around 0.02, the constraints for the solar tree were the upper and lower limit for x,y, and z of the solar tree where they satisfied an existing defined volume. The selected solution was per the criteria of power generated per unit ground footprint area for the given constraints.

Fig. 15 shows the flow of the code in MATLAB

Fig. 15
figure 15

Flowchart for the multiobjective genetic algorithm

Full size image

3.4 Simulink model

The designed solar tree model consists of 20 solar panels using Simulink as illustrated in Fig. 16. Each solar panel receives the average temperature for Egypt and the irradiance value obtained by the genetic algorithm. The used PV module is based on M-Si technology which has the highest power output performance in various locations throughout Egypt. Table 1 provides an overview of the electrical and thermal properties of the used PV module JA Solar JAM6(k)-72-335/PR [37].

Table 1 The electrical and thermal characteristics of JA Solar JAM6(k)-72-335/PR module
Full size table
Fig. 16
figure 16

Simulink model for the solar tree

Full size image

3.5 Finite element analysis

The selected solar tree design does not have equal branches so each branch has a unique length according to the solar panel position, however, the outer diameter and thickness of the branches and trunk are selected to be of the same size whereas the pipe size selected from SolidWorks is 21.3 × 2.3 mm. Using Ansys 19.2 for finite element analysis for the solar tree, we consider the following loading conditions: Weight due to the solar panel assembly on the branches to be 270 N, and the wind load to be 17 KN. The fixed support is considered to be the main branch as it will be fixed to the ground, the study considers the longest branch as it would be the weakest link due to the longest arm of the moment due to the limited computational power of the PC used. The mesh size is 5 mm, and the selected material is steel The material property can be found in Engineering data in ANSYS under the name of structural steel as shown in Table 2.

Table 2 Structural steel material data from ANSYS
Full size table

The structural analysis will show von-mises stresses and deflection, Fig. 17 shows the loading condition and solar tree shape.

Fig. 17
figure 17

Ansys loading condition

Full size image

4 Results

4.1 Single objective genetic algorithm

The objective of our algorithm is to maximize the output energy of the solar tree while considering various constraints such as available space, shading effects, and the orientation of the panels. By employing a single-objective optimization approach, we generated 20 optimal combinations of tilt and azimuth angles for each solar panel in order to capture the highest perpendicular irradiance.

4.2 Power loss due to partial shading and multi-objective genetic algorithm

The values of beta and gamma in Table 3 are related to shading losses in the solar panels. Panels with higher values of beta and gamma may experience higher power losses due to shading. For example, panels 1 and 4 have high beta and gamma values and relatively high power losses due to partial shading compared to some other panels. Panels 9 and 10 have low beta and gamma values and relatively low power losses due to partial shading. The power loss has an inverse relation with the area shaded as the area shaded increases the power loss decreases. The minimization of power loss and the projected net area on the ground are the multi-objective genetic algorithm optimization problem and fitness function, while the algorithm compromises between them (Table 4).

Table 3 The optimal tilt and azimuth angle for each solar panel
Full size table
Table 4 power loss due to partial shading
Full size table

The results, in Table 5, show the optimal position of each solar panel;the origin point (0,0,0) is located at the mid-top of the tree, achieving the minimum of both power loss and area projected on the ground. It is observed that the maximum coordinate of x,y, and z is around 1.

Table 5 Optimal position for the 20 solar panels
Full size table

4.3 Matlab simulink result

Based on the information provided, the solar panels were arranged into two parallel columns of 10 series panels each. This arrangement allowed for a maximum power output of 10.75 KW. The I–V graph in Fig. 18 shows how the current (I) and voltage (V) characteristics of a solar tree vary under different conditions. Lastly, the maximum energy density of the proposed solar tree is calculated to be 2.9341 Kwatt/m2. Therefore, it has a much higher energy density than the stand-alone large photovoltaic installations which have a power density of 35-37 W/m2 on average (including inter-row spacing and other ancillary facilities).

Fig. 18
figure 18

I–V Characteristics of the PV-tree

Full size image

4.4 Finite element analysis

The result in Fig. 19 shows that the maximum stress in the longest branch is 230 MPa, and Fig. 20 shows that the deflection is approximately 0.003 m which verifies that the structure can withstand real-world conditions after mass reduction where the boundary of the tree-width was 3 m and after decreasing it to approximately 1.3m which caused a mass reduction accordingly a cost reduction.

Fig. 19
figure 19

Von-Mises stress analysis

Full size image
Fig. 20
figure 20

Deflection

Full size image

4.5 Advantage and disadvantage

Table 6 summarizes the advantage and disadvantage of our structure:

Table 6 Advantage and disadvantage of the used solar tree structure
Full size table

5 Conclusion

The solar tree is a viable energy collecting technique as it takes much less area than the traditional PV systems about only 1% of traditional PV space. Two main obstacles for the solar tree are shadow loss and the high cost of implementation due to the expensive cost structure of its pleasant shape. A single objective genetic algorithm is used to minimize the shadow loss by orienting the panels. To minimize the structure cost a multi-objective genetic algorithm has been used to obtain solar panel positions. In conclusion, we obtained a design for a 10 KW solar tree in Elsheikh Zayed City, Egypt located at \(30.08^{\circ }\hbox {N}, 31.34^{\circ }\hbox {E}\). To validate the results a Simulink model is built to obtain the energy curve for the 20 connected solar panels. ANSYS software is used to do a finite element analysis to ensure that the tree maintains its structure under wind and load conditions.