1 Introduction

Optimization involves successive iterative processes aiming to obtain the best decision variables among the set of candidate solutions for a particular problem. The quality of the solution is evaluated by the optimization objective function, which is to be maximized or minimized depending on the optimization purposes. The iterative search process is subjected to a predefined number of problem-specific restrictions called constraints, which can be mathematically formulated in terms of equality or inequality expressions. There are several options for solving a typical optimization problem. Deterministic and stochastic optimization strategies are the most prominent methods between the available alternatives. Deterministic methods provide reliable tools for finding the global optimum point of the problem also claiming that the obtained solution is the global one. They strongly rely on the analytic information of the problem to probe the search space efficiently. The optimum solution is converged within a lower number of function evaluations in comparison with the stochastic solvers. These types of solvers are successful in solving the unimodal problems having linear search spaces. However, they experience difficulties in solving non-convex-problems as local optimum entrapment is highly possible due to the singularities and non-differentiable points on the function space. One can conquer these characteristic drawbacks by modifying or hybridizing the algorithm [1].

Efficient design of an ORC becomes a hot spot research area for designers as well as researchers for many years. Many research studies have been devoted for thermodynamical design and optimization of ORC systems [2,3,4]. Some other completed studies cover experimental and theoretical applications of ORC along with its viable utilization in different type of hybrid power generation systems[5,6,7]. Besides, more and more studies about the ORC systems are finding their places in the literature every day [8,9,10]. Haghparast et al. [2] have investigated the impact of ejector geometry and power output capacity on cycle performance. A sensitivity study has been carried out by the researchers to find out the most significant parameters that have impact on cycle efficiency. The results of the parametric studies that have been conducted by the authors showed that the net power output increases as the ejector area ratio or secondary fluid mass flow rate rises; and decreases as the throat diameter, primary inlet pressure or primary inlet temperature increases. Furthermore, it has been concluded that area duct diameter is one of the most important geometrical parameter that effects the cycle performance. Chen et al. [3] have proposed a novel zeotropic ORC that the mixture composition can be adjusted based on the environmental temperature variation utilizing liquid-seperation condensation. The optimization model has been developed to optimize the mixture composition with respect to the changing environmental temperature. A parametric optimization study has been performed and the results showed that the proposed ORC system significantly improved the output power compared to the conventional ORC in terms of 100 °C heat source. Feng et al. [8] have investigated and optimized a waste-heat regenerative ORC by utilizing classical and finite-time thermodynamics. The authors have accomplished to maximize the power output and thermal efficiency of the cycle by fixing total heat transfer area of all heat exchangers and changing the superheat, mass flow rate of the working fluid and heat transfer area ratios of the heat exchangers. As a result of this study, the authors have found out that there exists an optimal ORC design with optimal superheat, working fluid mass flow rate and heat transfer area ratio values. Moreover, the power output and thermal efficiency of the cycle are increased by 25.22% and 12.16% after the optimization process finished. Baldasso et al. [9] have proposed a model to optimize the design of an ORC for waste heat recovery in maritime applications. The findings of the authors showed that the combination of minimum exhaust gas velocity and maximum engine backpressure acts as a constraint on the maximum amount of heat that can be drawn out from the waste heat recovery boiler. The authors have considered ten design variables and one objective function for the development of the optimization problem. The results have shown that the overall system fuel consumption can be lowered by 0.52–1.45 g/kWh by allowing higher backpressure levels on the engine. Liu et al. [10] have analyzed the performances of single—and dual-pressure ORCs with combined heat and compressed air energy storage modifications. The authors have developed thermodynamic models of the mentioned cycles and compared the performances of the cycles with each other. As a result of this study, the authors have come to the following conclusions. The dual-pressure ORC has produced more power compared to the single-pressure ORC. The optimum superheat temperature of the dual-pressure ORC with combined heat and compressed air energy storage modifications is much smaller compared to its single-pressure counterpart.

In this study, Salp Swarm Algorithm (SSA) [11] is hybridized with the Jaya algorithm (JAYA) [12] and a variant of opposition-based learning (OBL) [13] to improve the solution diversity and convergence rate. SSA is a swarm-based metaheuristic simulating the intelligent foraging and navigating behaviors of a salp chain in the ocean. Some of the recent applications of SSA can be exemplified as parameter extraction of PEM fuel cells [14], feature selection [15], and optimum allocation of power sources [16]. JAYA is a population-based algorithm with a very simple search mechanism and successfully applied to engineering design problems from various disciplines [17,18,19]. The optimization performance of the proposed hybrid is enhanced by utilizing a variant of OBL called quasi-opposition based learning (QOBL). OBL takes simultaneously advantage of a current estimate solution and its opposite point to improve the search capacity of the included algorithm. OBL concept has been incorporated into many metaheuristics such as Particle Swarm Optimization [20], Harmony Search [21] and Whale Optimization Algorithm [22]. SSA, JAYA and OBL methods have been coupled with each other in the literature before to solve various optimization problems [23, 24], however, to the best knowledge of the authors, these three techniques have never been incorporated before. Besides the above mentioned successful applications of these algorithms on various optimization problems, they lack some algorithm-specific deficiencies similar to the other metaheuristics. For instance, SSA suffers from the slow convergence and local minima entrapment resulting from the redundant intensification of the fertile areas on the search space, which is occurred by the salp chain movement of the followers. Apart from the favorable advantages of being a parameter-free algorithm with an accelerated convergence rate, JAYA still has some tedious disadvantages such that the algorithm has only one manipulation scheme that may lead to obtaining candidate solutions with lower diversity. JAYA performs such iterative calculations that perturbated population individuals get closer to the best solutions while moving away from the worst ones. This tendency may occur a premature convergence due to the extensive exploitation of the potential best solutions. The hybridization of metaheuristic algorithms with OBL greatly increases the solution accuracy along with convergence speed. Thanks to the enhanced diversification produced by using the mirror point rather than the randomly generated point, OBL has the capability of reaching unvisited regions of the solution space [25]. Literature applications of QOBL [26, 27] reveal that using quasi-opposition instead of an opposition point enables us to acquire sample solutions much closer to the global optimum. Another strong point of QOBL has iteratively updated search regions that are dynamically shrunk throughout iterations. Updated extremum values of the search space pave the way for capitalizing on the historical knowledge of the previous generations and increase the possibility of finding better solution outcomes. This study hybridizes these three algorithms to eliminate their inherent structural drawbacks and benefit from their intrinsic advantages on the optimization framework called OPSSAJ. Optimization efficiency of the proposed OPSSAJ is firstly assessed on twenty-four benchmark problems composed of unimodal and multimodal test functions. Numerical results are compared and evaluated against those obtained from some recently emerged renowned metaheuristics. Comparative results show the superiority of the proposed algorithm over its constituent algorithms along with the challenging contenders. Then, OPSSAJ is applied to a highly complex real-world optimization problem of the multi-objective design of an organic ranking cycle (ORC). Finally, a sensitivity analysis is performed to observe the effects of seventeen design variables on the problem objectives.

This research study aims to provide an essential solution framework for optimum thermal design optimization for an Organic Rankine Cycle (ORC) working with a binary mixture. This study also proposes a brand new variant of SSA in which basic mutation scheme of JAYA and rudimentary manipulation equations of another variant OBL scheme called QOBL are successfully integrated. This kind of integration entails a plausible balance in the exploration and exploitation phases of the proposed hybrid method. Then, this proposed hybrid method is applied to maintain a design optimization of an ORC. The foremost novelty occurring in this paper is that this is the first research study deeply investigating the thermal behavior of an ORC system taken into account of two conflicting but complementary designs of objectives of Specific Investment Cost and second law efficiency of the cycle. Several literature studies [28,29,30] have been accomplished up to now dealing with thermo-economic design optimization of ORCs running with binary mixtures. However, most of them consider a limited number of cycle parameters to be optimized and remaining parameters are taken constant during the iterations. This study offers a comprehensive examination of the influences of cycle parameters on considered conflicting design objectives. Moreover, limited research papers attempted to perform a comparative study between ORCs working with pure fluids and binary mixtures, which is detailly investigated in this work. Another significant contribution of this study is that this is the first consideration of the refrigerant mass flow rate and mass fraction of refrigerants in the binary mixture as design variables. Pareto curves for different cycle configurations are constructed and final optimum solution among the non-dominated solutions is chosen by the highly-reputed TOPSIS decision-maker [31]. Another novelty of this paper is that the improved solution accuracy and robustness which is resulted from the meticulously created synergy between JAYA and QOBL method. Proposed hybridization procedure leads to a significant boost in the probing mechanism of ordinary SSA by enhancing the exploration and exploitation capacities of the algorithm.

To achieve the main goals of the research study, the following contributions are proposed,

  • Improved version of the SSA called OPSSAJ is proposed to solve complex optimization problems in this research study.

  • Hybridization of the JAYA with the QOBL is adapted into the leader phase of the SSA to diversify the swarm individuals, which has never been studied before in such utilization so far.

  • The proposed method (OPSSAJ) is then applied to obtain the optimal design of an Organic Rankine Cycle working operating with a binary mixture of R227EA and R600. This is the first application of a metaheuristic algorithm on multi-objecive optimization of a thermal cycle running with a binary mixture.

  • Influence of optimum design parameters of the ORC cycle on conflicting but complementary problem objectives has been comprehensively analyzed, much deeper than most of the literature studies dealing with an ORC design.

The rest of the paper is organized as follows: Sect. 2 provides brief instruction on Salp Swarm Algorithm, Opposition-based Learning, and Jaya Algorithm. The essentials of the proposed hybrid are expressed in Sect. 3. Numerical results of the hybrid method along with the related discussions are provided in Sect. 4. Section 5 reports the single and multi-objective optimization results of ORC. Section 6 concludes this research study with remarkable comments.

2 Related work

2.1 Salp Swarm algorithm

Salp Swarm Algorithm (SSA) is a new bio-inspired metaheuristic algorithm developed by Mirjalili et al. [11]. SSA mimics the swarming behavior of salps during navigating in the deep sea. The movement of salps is modeled as salp chains that compose of two groups. The first group consists of the leader, and the second group is formed by the followers. The leader is located at the front of the chain and directs the whole chain. On the other hand, the followers go after the leader and at the same time they follow each other. The updated position of the leader in the n-dimensional search space is given as:

$$x_{1,j} = \left\{ {\begin{array}{*{20}c} {F_{j} + c_{1} \left( {\left( {ub_{j} - lb_{j} } \right)c_{2} + lb_{j} } \right),\,c_{3} \ge 0.5} \\ {F_{j} - c_{1} \left( {\left( {ub_{j} - lb_{j} } \right)c_{2} + lb_{j} } \right),\,c_{3} < 0.5} \\ \end{array} } \right.$$
(1)

where \(x_{1,j}\) represents the j-th position of the first salp (leader), \(F_{j}\) is the position of the food source, and \(lb_{j}\) and \(ub_{j}\) denote lower and upper bounds of the j-th dimension, respectively.

The coefficients \(c_{1} ,c_{2} ,c_{3}\) are random numbers. The coefficients \(c_{1}\) is used to balance exploration and exploitation and defined as:

$$c_{1} = 2e^{{ - \left( {\frac{4 \times iter}{{maxIter}}} \right)^{2} }}$$
(2)

where \(iter\) and \(maxIter\) represent current iteration and the maximum number of iterations, respectively. The coefficients \(c_{2}\) and \(c_{3}\) are random numbers lying in the range [0,1].

The position update rule of the followers obeys Newton’s law of motion as:

$$x_{i,j} = \frac{1}{2}at^{2} + v_{0} t$$
(3)

where \(i \ge 2\) and \(x_{i,j}\) shows the position of i-th follower salp in the j-th dimension, \(t\) denotes the time, \(v_{0}\) is the initial speed, \(a = {{v_{final} } \mathord{\left/ {\vphantom {{v_{final} } {v_{0} }}} \right. \kern-\nulldelimiterspace} {v_{0} }}\) and \(v = {{\left( {x - x_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {x - x_{0} } \right)} t}} \right. \kern-\nulldelimiterspace} t}\). Considering the discrepancy between iterations as equal to one and \(v_{0} = 0\), position update equation of the follower salps can be written as:

$$x_{i,j} = \frac{1}{2}\left( {x_{i,j} + x_{i - 1,j} } \right)$$
(4)

where \(i \ge 2\) and \(x_{i,j}\) shows the position of i-th follower salp in the j-th dimension. The pseudocode of the SSA is given in Algorithm 1 [11].

2.2 Opposition based learning

There are seven widely used OBL approaches in the literature [32, 33]. These are, basic OBL [13], quasi-opposition [34], quasi-reflection [35], current optimum opposition [36], extended opposition [33], reflected extended opposition [33], and comprehensive opposition [33]. Among these seven variants of OBL, quasi OBL approach has enjoyed a visible position in the literature. It has been mathematically proved that the probability of the quasi-opposite point being closer to the unknown optimal solution is higher than being closer to the basic opposite point [34, 37]. Therefore, the present study employs quasi-OBL approach. Before giving details, basic definitions are introduced as follows.

Definition (Opposite Number)

Let \(x \in \left[ {a,b} \right]\) be a real number. The opposite number of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}\) is defined by

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} = a + b - x$$
(5)

Extending this definition to higher dimensions, the opposite point can be defined as the following.

Definition (Opposite point)

Let \(P\left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right)\) be a point in the n-dimensional space, where \(x_{1} ,x_{2} , \ldots ,x_{n} \in R\) and \(x_{i} \in \left[ {a_{i} ,b_{i} } \right]\) \(\forall i \in \left\{ {1,2, \ldots ,n} \right\}\). The opposite point is defined by its components as

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}_{i} = a_{i} + b_{i} - x_{i}$$
(6)

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}_{i}\) represents opposite-point.

Based on the opposite point definition, quasi-opposite point is defined as a uniform random point generated between the center point and the opposite point. In the quasi-OBL, the opposite of each variable and center point is updated in each iteration dynamically. Because the search space is shrunk over the course of iterations, going through the initial static boundaries of variables might result in boundary violations and poor search capability. Therefore, the minimum and maximum values of each variable in the current iteration \(\left( {\left[ {MIN_{j}^{t} ,MAX_{j}^{t} } \right]} \right)\) are used to calculate center point \(M_{j}^{t}\), which denotes the mean value of minimum and maximum values, respectively. By updating the boundary intervals in each step, the knowledge of previous generations is implicitly capitalized. The calculation of the quasi-opposite population is shown in Algorithm 2 [13].

2.3 Jaya algorithm

Jaya algorithm is a recent population-based metaheuristic algorithm developed by Rao [12]. The main rationale underlying the Jaya algorithm is that individuals try to escape from the non-promising solutions and tend towards the best solution. Java algorithm has a very simple search mechanism that is computationally efficient and straightforward. Jaya algorithm does not require any parameters pertaining to its search mechanisms. It only requires the knowledge of population size and number of generations. Main steps of the Jaya algorithm can be given as follows:

  • Step 1 Population initialization: Initial positions of individuals are randomly generated within the range of boundaries.

    $$x_{i,j} = x_{\min ,j}^{{}} + rand(0,1)(x_{\max ,j}^{{}} - x_{\min ,j}^{{}} )$$
    (7)

    where \(x_{i,j}\) represents jth position value of the ith individual in the population, \(rand(0,1)\) denotes uniformly distributed random number lying between 0 and 1, \(x_{\min ,j}^{{}}\) and \(x_{\max ,j}^{{}}\)are the lower and upper bounds of the jth dimension, respectively.Once the initial population is formed, the fitness value of each solution vector is calculated. Then, the best and worst individuals are identified. Afterwards, each individual is subjected to repeated cycles of the search processes, which is described below, until the predefined termination criterion is met.

  • Step 2 Generating a new solution. The new solution vector is calculated as follows:

    $$x^{\prime}_{i,j} = x_{i,j} + r_{1,j} \left( {x_{best,j} - \left| {x_{i,j} } \right|} \right) - r_{2,j} \left( {x_{worst,j} - \left| {x_{i,j} } \right|} \right)$$
    (8)

    where \(r_{1,j}\) and \(r_{2,j}\) represent the jth dimension of the uniform random numbers, \(x_{best,j}\) and \(x_{worst,j}\)are the jth dimension of the best and worst solutions, respectively. In Eq. 2., the term \(\left( {x_{best,j} - \left| {x_{i,j} } \right|} \right)\) serves as guiding the solution towards the best solution and \(\left( {x_{worst,j} - \left| {x_{i,j} } \right|} \right)\) is used to ensure that the new solution gets away from the worst solution.

  • Step 3 Checking for the boundaries: In this step, each dimension of the solution vector is checked against the allowable regions.

    $$x^{\prime}_{i,j} = \left\{ {\begin{array}{*{20}c} {x^{\prime}_{\min ,j} } & {if\,x^{\prime}_{i,j} < x^{\prime}_{\min ,j} } \\ {x^{\prime}_{\max ,j} } & {if\,x^{\prime}_{i,j} > x^{\prime}_{\max ,j} } \\ {x^{\prime}_{i,j} } & {{\text{otherwise}}} \\ \end{array} } \right.,\,\,\forall i \in \left\{ {1, \ldots ,N} \right\},\,j \in \left\{ {1, \ldots ,D} \right\}$$
    (9)

  • Step 4 Giving solution acceptance decision: In this step, the fitness value of a new solution is compared with that of the current solution. If the new solution is better than the current solution, than the new solution is accepted, and the current solution is replaced by the new solution. Otherwise, the current solution remains in the population and the new solution is discarded.

    $$X^{\prime}_{i} = \left\{ {\begin{array}{*{20}c} {X^{\prime}_{i} ,} & {{\text{if}}\,fitness\left( {X^{\prime}_{i} } \right) \le fitness\left( {X_{i} } \right)} \\ {X_{i} ,} & {otherwise} \\ \end{array} } \right.$$
    (10)

    where \(X_{i}\) and \(X^{\prime}_{i}\) represent the current and new solutions, respectively.

3 Proposed algorithm

This section gives the basics of the opposition-based Salp Swarm Algorithm with the Jaya (OPSSAJ). In particular, the OPSSAJ method hybridizes quasi-opposition-based learning with the SSA and Jaya algorithms. There are three main steps in the proposed algorithm, which are the generation of the initial population, the movement of the salp chain, and updating the best solutions.

The procedural steps of the OPSSAJ method can be given as follows:

3.1 Generating initial population

The proposed algorithm starts with generating an initial population randomly. The initial population of salps is formed based on the predefined bounds, which are represented as \(x_{\min ,j}\) and \(x_{\max ,j}\) respectively. Mathematically speaking, the ith salp of the population \(\vec{X}_{i} = \left\{ {x_{i,1} ,x_{i,2} , \ldots ,x_{i,D} } \right\}\) is generated based on Eq. 11.

$$x_{ij} = x_{\min ,j}^{{}} + rand(0,1)(x_{\max ,j}^{{}} - x_{\min ,j}^{{}} )$$
(11)

where \(x_{i,j}\) denotes the value at the jth position of the ith salp.

After generating the initial population of salps, the neighboring solutions are identified within the search space.

3.2 Movement of the salp chain

In the canonical SSA, the first salp is regarded as the leader salp, and the rest of the salps follow the leader. This mechanism has been improved by hybridizing the SSA with the oppositional based learning and Jaya algorithms. The use of multiple leaders avoids trapping into local optima and improves the exploration capability of the algorithm.

In order to balance exploration and exploitation during the search, the leader salps randomly select either the oppositional-based learning or Jaya algorithm. In this study, quasi-opposition based learning has been employed, since the probability of the quasi-oppositional point being closer to the unknown optimal solution is higher than being closer to the opposite point [37]. To perform quasi-opposition-based learning, minimum, and the maximum values of each dimension are found based on the following equations:

$$min_{j} = \mathop {\min }\limits_{{i \in \left\{ {1,2, \ldots ,N/2} \right\}}} \left\{ {x_{i,j} } \right\}$$
(12)
$$max_{j} = \mathop {\max }\limits_{{i \in \left\{ {1,2, \ldots ,N/2} \right\}}} \left\{ {x_{i,j} } \right\}$$
(13)

The oppositional position vector is calculated as:

$$x_{i,j}^{o} = \min_{j} + \max_{j} - x_{i,j}^{{}}$$
(14)

where \(x_{i,j}^{o}\) represents the oppositional point of the jth position of the ith salp. Once the minimum and maximum values are identified for each dimension, medium value is calculated as:

$$med_{j} = {{\left( {min_{j} + max_{j} } \right)} \mathord{\left/ {\vphantom {{\left( {min_{j} + max_{j} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$$
(15)

where \(med_{j}\) denotes the mean value of the jth dimension.

Eventually, the quasi-oppositional position is calculated as follows:

$$x_{i,j}^{qo} = \left\{ {\begin{array}{*{20}l} {med_{j} + \left( {x_{i,j}^{o} - med_{j} } \right) \times rand(0,1),} \hfill & {{\text{if}}\,x_{i,j} < med_{j} } \hfill \\ {x_{i,j}^{o} + \left( {med_{j} - x_{i,j}^{o} } \right) \times rand(0,1),} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(16)

where \(x_{i,j}^{qo}\) is the value of the jth dimension of the ith quasi-oppositional salp. On the other hand, if the leader salps perform movements based on Jaya algorithm, the indices of the best and worst solutions are calculated as:

$$best = \mathop {\arg \min }\limits_{{i \in \left\{ {1,2, \ldots ,N/2} \right\}}} \left\{ {f\left( {\vec{X}_{i} } \right)} \right\}$$
(17)
$$worst = \mathop {\arg \max }\limits_{{i \in \left\{ {1,2, \ldots ,N/2} \right\}}} \left\{ {f\left( {\vec{X}_{i} } \right)} \right\}$$
(18)

where best and worst represent the indices of the best and worst salps, respectively. Let \(x_{best}\) and \(x_{worst}\) denote the best and worst solution vectors among the first \(N/2\) individuals in the population, respectively. The movement of leader salps, according to Jaya algorithm, can be given as:

$$x_{i,j}^{jaya} = x_{i,j} + r_{1,j} \left( {x_{best,j} - \left| {x_{i,j} } \right|} \right) - r_{2,j} \left( {x_{worst,j} - \left| {x_{i,j} } \right|} \right)$$
(19)

where \(x_{i,j}^{jaya}\) is the value of the jth position of the ith salp as a result of Jaya move. The new position is accepted if the fitness of the new salp is better than the previous salp. Otherwise, the current salp is not replaced with the new salp. On the other hand, the follower salps move their positions following the salp chain movement, which is defined as:

$$x_{i,j} = \frac{1}{2}\left( {x_{i,j} + x_{i - 1,j} } \right)$$
(20)

where \(i\) denotes the index of the followers and \(i \ge \left( {N/2} \right) + 1\). Once the movements of the salp chains are completed, the fitness value of each salp is calculated. Then, the population is sorted based on the fitness values, and the leader and follower salps are identified. The population of salps is subjected to repeated cycles of the search processes until a termination criterion is met. The pseudo-code of the proposed algorithm is given in Algorithm 3.

figure c

3.3 Implementation of the proposed OPSSAJ algorithm

The step-wise description for the execution of the proposed OPSSAJ is given below.

  • Step 1 Initialize the set of algorithm parameters and define the objective function. Population size and dimension of the decision variables are respectively set to N and D. Objective function f() is set and upper and lower bounds (UB and LB) of the search space are defined.

  • Step 2 Initialize the population within the prescribed search boundaries. Randomly generated solutions \(S = [S]_{N \times D}\) can be described by the following matrix expression,

    $$S_{1,...,N,1,...,D} = \left[ {\begin{array}{*{20}c} {S_{11} } & {S_{12} } & {...} & {S_{1D} } \\ {S_{21} } & {S_{22} } & {...} & {S_{2D} } \\ \vdots & \vdots & {} & \vdots \\ {S_{N1} } & {S_{N2} } & {...} & {S_{ND} } \\ \end{array} } \right]$$

    Subsequently, the solution quality of each member is evaluated by \(f = f\left( {S_{i} } \right), \, i = 1,...,N\). Selected the best and the worst quality member based on their solution fitness.

  • Step 3 Sort the population from best to worst and apply randomly Jaya and Quasi-oppositional based learning for the best half (N/2) of the population, which are the leader salps. The pseudocode of this step is given in Algorithm 4.

    figure d

  • Step 4 For the worst half part of the population which are knowns as followers, apply the chain movement method given in Algorithm 5.

    figure e

  • Step 5 Check the boundaries and restrict the violated solution into the predefined search ranges.

  • Step 6 Update the current solution.

  • Step 7 Repeat Step 3 to Step 6 until the termination criterion is reached.

  • Step 8 Output the best solution.

4 Numerical investigations over unconstrained benchmark suite

In this study, 24 benchmark functions comprising of multimodal and unimodal problems with 30 dimensions have been used to test the performance of the proposed algorithm. The statistical results obtained from the OPSSAJ method are compared with the state-of-the-art algorithms including colliding bodies algorithm (CB) [38], cuckoo search algorithm (CS) [39], fruit fly algorithm (FF) [40], tree-seed algorithm (TS) [41], spotted hyena algorithm (SH) [42], emperor penguin algorithm (EPA) [43], vibrating particles system algorithm (VPS) [44], butterfly algorithm (BF) [45], jaya algorithm [12], crow search algorithm [46]. The above-mentioned algorithms have essential parameters that are tuned employing a trial-and-error approach. The selection of the best parameters is highly dependent on the problem characteristics. In general, finding the best parameter is a time-consuming and tedious task that incurs a considerable amount of computation time. Table 1 reports the statistical results of the multimodal benchmark functions, which are collected after 50 independent replications. The termination criterion is set to 4000 function evaluations. The algorithms are developed in Java and computations are run on an Intel Core i5 computer with 3.00 GHz CPU and 6 GB RAM. The best, worst, mean, and standard deviation values of the multi-modal test functions are reported in Table 1. According to results, OPSSAJ method finds superior results than its counterparts in f1-Ackley, f4-Zakharov, f5-Alpine, f7-Csendes, f9-Salomon, f10-Inverted cosine, and f12-Pathological functions. On the other hand, BFA algorithm finds slightly better solutions in f2-Griewank, f3-Rastrigin, f8-Schaffer, and f11-Wavy functions. BFA algorithm produces better results only in f6-Quintic function. Apart from the best solutions, OPSSAJ outperformed other optimizers in terms of robustness and solution accuracy. Analysis of the standard deviation values reveals that the OPSSAJ gives robust results with small standard deviations. On the other hand, the worst solutions obtained by OPSSAJ are usually better than those found by the second-best optimizer in comparison.

Table 1 Statistical results for multimodal optimization test functions
Full size table

Figures 1, 2 depict the convergence charts of the compared algorithms for each multimodal test function. The x-axis represents the number of function evaluations, and the y-axis shows the best objective function value in the logarithmic scale obtained during iterations. The convergence performance of OPSSAJ is highly satisfactory in comparison with the remaining algorithms. The evolution history of the OPSSAJ method clearly shows that the algorithm reaches its optimum point gradually and consistently, while other algorithms stagnate at the early phases of the search, which is due to the lack of exploration capability. The OPSSAJ takes firm steps forward to the global optimum point as a result of a plausible balance between intensification and diversification. Table 2 gives the statistical results of unimodal test functions. OPSSAJ has found better solutions in f13-Sphere, f15-Schwefel 2.22, f16-Schwefel 2.23, f18-Brown, f20-Powell, f21-Sum of different powers, f22-High conditioned elliptic, f23-Sum squares, and f24-Bent cigar functions. BFA algorithm has found better solutions in f19-Streched V Sine Wave functions. Jaya algorithm has managed to outperform other algorithms in only f17-Schwefel 2.25 function. The Rosenbrock function is known to be one of the most challenging instances in which there are many long and carved valleys. OPSSAJ has found the solution of 2.7917E + 01 in the Rosenbrock function, which is much closer to the optimal solution in comparison with the results of other algorithms. The evolution histories of the algorithms for unimodal benchmark instances are depicted in Figs. 3, 4. As can be seen from the figures, OPSSAJ quickly converges to its optimum solution. In many instances, compared algorithms fall behind the OPSSAJ results in terms of solution quality and speed of convergence towards the global optimum point.

Fig. 1
figure 1

Evolution characteristics of the algorithms for the test functions f1-f6

Full size image
Fig. 2
figure 2

Evolution characteristics of the algorithms for the test functions f7-f12

Full size image
Table 2 Statistical results for unimodal optimization test functions
Full size table
Fig. 3
figure 3

Evolution characteristics of the algorithms for the test functions f13-f18

Full size image
Fig. 4
figure 4

Evolution characteristics of the algorithms for the test functions f19-f24

Full size image

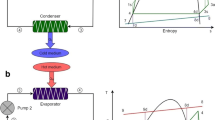
5 Thermodynamic modeling and optimization of Organic Rankine Cycle

5.1 Mathematical modeling of a thermal ORC system

The following assumptions have been made not only to simplify the optimization process but also to eliminate the excessive amount of the computational burden resulted from the iterative calculations [47].

  • It is assumed that ORC operates under steady-state conditions and running fluid at the outlet of the condenser and evaporator is presumed to be saturated

  • Leakages from the pipes and heat losses to the surroundings are neglected

  • Shell and tube heat exchangers are considered for condenser and evaporator

  • Thermal analysis of the cycle disregards the effects of kinetic and potential energy changes

  • Heat transfer calculations are made based on fully developed flow conditions

There are also some precautionary system design constraints taken such that evaporator pressure should not exceed 90% of the critical pressure of the running cycle fluid. All design constraints considered in the optimization problem are modeled as hard inequality constraints. Obeying the above-given assumptions, mathematical modeling ORC is constructed in step-by-step formulations. Mass and energy balance equations along with irreversibility generation formulations govern the basics of thermal modeling of ORC. Heat and mass balance equations are related to the first law of thermodynamics while irreversibility equations are concerned with the second law of thermodynamics. Mass balance is expressed by,

$$\sum {\dot{m} = 0}$$
(21)

Energy balance in each cycle component is maintained by using the merits of first law and equated by

$$\sum {\dot{Q}} + \sum {\dot{W}} + \sum {\left( {\dot{m} \cdot h} \right)} = 0$$
(22)

The irreversibility equation reflects the effects of entropy generation. If a substance changes its state from a to b, irreversibility generation of the system is formulated by the following equation

$$I_{a \to b} = T_{0} \cdot \left( {S_{b} - S_{a} - \frac{{\dot{Q}_{0} }}{{T_{0} }} - \frac{{\dot{Q}_{source(sink)} }}{{T_{source(sink)} }}} \right) = T_{0} \cdot \Delta S_{gen} \ge 0$$
(23)

The above equation can be applied to determine the current irreversibility rate of the working fluid flowing through the related cycle component. Based on the formulations given in the Electronic Supplementary Material, second law efficiency of the cycle, which is also one of the design objectives considered in this study, is calculated by the following expression

$$\eta_{II} = W_{net} /\left( {W_{net} + \dot{I}_{tot} } \right)$$
(24)

where \(\dot{I}_{tot}\) is the total irreversibility of the cycle.

Mathematical modeling of condenser and evaporator takes a great role in determining the overall efficiency and cost of the thermal cycle. It is known that the investment cost of the heat exchanger is directly related to the total heat exchange area, which is a function of the overall heat transfer coefficient of the system. Therefore, the utmost concern should be given to the proper use of the correct heat transfer correlation. Although there are plenty of correlations available in the literature for modeling two-phase flow heat transfer occurring in condenser and evaporator, they are correlated with their experimental conditions. For this reason, it is a huge task for a designer to use the correct heat transfer correlation for the governing operational conditions.

Gnielinski [48] correlation, which is a highly reputed equation for modeling single-phase flow, is used to evalulate the heat transfer mechanism taking place in the evaporator and condenser. Correlation developed by Thome [49] is a modified form of Gungor-Winterton [50] correlation which takes into account the contribution of binary mixtures on flow boiling mechanism and used for estimating the evaporative heat transfer coefficient. Florides et al. [51] correlation is used to calculate the total amount of heat transfer in the annulus flow, which takes place between outer and inner tube regions. Shah [52] correlation is very effective in predicting the in-flow condensation heat transfer rates and so is used in this study for thermal modeling of the condenser. Therminol VP-1 is used as a secondary fluid that conveys the available low grade heat to the working fluid of the system. Cooling water absorbs the rejected heat in the condenser and considered as a secondary fluid for this process. Shell and tube type heat exchanger is used for condenser and evaporator and heat exchange area of each cycle component is calculated by the below given generic formulation

$$A = \frac{{\dot{Q}}}{{U \cdot \Delta T_{LMTD} }}$$
(25)

where A is the total heat exchange surface, Q is the imposed heat load on the heat exchanger, \(\Delta T_{LMTD}\) is the logarithmic mean temperature difference between two streams, and U is the overall heat transfer coefficient computed by the following equation

$$U = \frac{1}{{\left( {\left( {\frac{1}{{h_{out} }}} \right) + R_{out} + \left( {\frac{{d_{out} }}{2k}} \right)\ln \left( {\frac{{d_{out} }}{{d_{in} }}} \right) + R_{in} + \left( {\frac{{d_{out} }}{{d_{in} }}} \right)\left( {\frac{1}{{h_{in} }}} \right)} \right)}}$$
(26)

Applying reliable capital cost correlations to cycle components is also very crucial in obtaining the best possible thermoeconomic design outcomes. However, this important issue has not been carefully analyzed in most of the literature studies regarding ORC design. This is because most of the available cost model is correlated for a very specific experimental region of temperatures and pressures. Economic information of cycle components is generally not conveyed by the component manufacturers, however affordable data from different sources is sufficient enough to develop reliable cost correlations. Among the various type of cost correlations available in the literature, the most reputed alternative is the chemical engineering plant cost ındex (CEPCI) whose updated model parameters have been reported in Chemical Engineering publication since 1963 [53]. Most of the published studies in the literature use the correlations developed by Turton et al. [54] to estimate the equipment investment cost of ORC components and apply the CEPCI index to each component to obtain their updated and current cost values.

Based on the proposed economic model, specific ınvestment cost (SIC) rate is the ratio between total ORC system cost and net power output which is expressed by the following equation [55]

$$SIC = \frac{{C_{cap} \cdot CRC + C_{mi} }}{{W_{net} \cdot h}}$$
(27)

where Ccap is the capital cost accounting for the investment cost of the ORC elements of the evaporator, condenser, expander, fans, pump and working fluid.

$$C_{cap} = \left( {C_{evap,bm} + C_{exp,bm} + C_{pump,bm} + C_{cond,bm} } \right)\frac{{CEPCI_{2019} }}{{CEPCI_{1996} }} + C_{fan,bm} \left( {\frac{{CEPCI_{2019} }}{{CEPCI_{2011} }}} \right) + C_{wf,bm}$$
(28)

wherein CEPCI2019 = 619, CEPCI2011 = 582, and CEPCI1996 = 382 [56]. In Eq. (29), CRC represents the capital recovery cost which is calculated by

$$CRC = \frac{{i\left( {1 + i} \right)^{{LT_{plant} }} }}{{\left( {\left( {1 + i} \right)^{{LT_{plant} }} - 1} \right)}}$$
(29)

where i symbolizes the interest rate which is considered to be 8% in this case; LTplant is the plant life time and assumed to be 15 years of operation; h stands for the working hours of the ORC system per annual year and presumed to 8000 h. Insurance and management cost of the system is expressed by Cmi and estimated by [57]

$$C_{mi} = 0.165 \cdot C_{cap}$$
(30)

Cost correlations for expanders are expressed as

$$\log C_{exp} = K_{1,\exp } + K_{2,\exp } \log \left( {W_{Exp} } \right) + K_{3,\exp } \left( {\log \left( {W_{Exp} } \right)} \right)^{2}$$
(31)
$$C_{exp,bm} = C_{exp} \cdot F_{Exp,bm}$$
(32)

Investment cost correlations for the pump are formulated by

$$\log C_{pump} = K_{1,pump} + K_{2,pump} \log \left( {W_{pump} } \right) + K_{3,pump} \log \left( {W_{pump} } \right)^{2}$$
(33)
$$p_{diff} = p_{evap} - p_{cond}$$
(34)
$$\log F_{pump,p} = C_{1,pump} + C_{2,pump} \log \left( {p_{diff} } \right) + C_{3,pump} \log \left( {p_{diff} } \right)^{2}$$
(35)
$$F_{pump,bm} = B_{1,pump} + B_{2,pump} \cdot F_{m,pump} \cdot F_{pump,p}$$
(36)
$$C_{pump,bm} = C_{pump} \cdot F_{pump,bm}$$
(37)

For calculation of heat exchanger (HEX) cost in the cycle (valid for both condenser and evaporator)

$$\log F_{HEX,p} = C_{1} + C_{2} \log \left( {p_{HEX} - p_{0} } \right) + C_{3} \log \left( {p_{HEX} - p_{0} } \right)^{2}$$
(38)
$$F_{HEX,bm} = B_{1,HEX} + B_{2,HEX} \cdot F_{m,HEX} \cdot F_{HEX,p}$$
(39)
$$\log C_{HEX} = K_{1,HEX} + K_{2,HEX} \log \left( {A_{HEX} } \right) + K_{3,HEX} \log \left( {A_{HEX} } \right)^{2}$$
(40)
$$C_{HEX,bm} = C_{HEX} \cdot F_{HEX,bm}$$
(41)

For the investment cost of the fan,

$$\log F_{fan,p} = C_{1,fan} + C_{2,fan} \log p_{fan} + C_{3,fan} \left( {\log p_{fan} } \right)^{2}$$
(42)
$$\log C_{fan} = K_{1,fan} + K_{2,fan} \log \dot{V} + K_{3,fan} \left( {\log \dot{V}} \right)^{2}$$
(43)
$$C_{fan,bm} = C_{fan} \cdot F_{fan,p} \cdot F_{fan,bm}$$
(44)

For working fluid cost

$$C_{wf,bm} = c_{wf} \cdot m_{wf}$$
(45)

where cwf is the unit price of the working fluid in $/kg and mfw is the mass of the working fluid circulating through the cycle in kg.

5.2 Discussion on the optimization results

Numerical modeling of the thermal system and the proposed OPSSAJ algorithm are both developed in Java environment. Due to the intrinsic random behavior of the hybrid metaheuristic OPSSAJ optimizer, simulations are run for 50 times for each optimization objective and the best results are collected and evaluated in terms of statistical analysis. The developed program is run at quad-core Intel i5-4460 @ 3.20 GHz with 16.0 GB RAM on a desktop computer. Table 3 reports the single objective optimization results of the ORC system running with different single working fluids obtained by OPSSAJ. For the cycle operating with R227EA refrigerant, it is seen that minimum obtained SIC value is 7529.457 ($/W) while the maximum second law efficiency of the cycle 0.431 when these conflicting objectives are separately optimized. Design variables of superheat temperature and evaporator pinch temperature hit the maximum allowable limits when SIC is minimized. Temperature mismatch between the heat source and evaporator increases with increasing superheat and pinch-point temperatures. This increase leads to a decline in the heat exchange area of the evaporator which entails a decrease in SIC rates. Similar tendencies can be observed for the condenser and heat sink temperature relationship. Outer tube diameters of the condenser and evaporator hit the prescribed lower bound which is 0.015 m. This is because when tube diameter values decrease, convective heat transfer coefficient of the running cycle fluid increases. This increase consequently gives rise in the net power output of the cycle, resulting in a decrease in SIC values. Triangular tube arrangement is observed for evaporator and condenser when SIC is minimized. Condenser and evaporator shell diameters reach the minimum allowable bounds. As shell diameters decrease, the cross-sectional area of the normal to secondary fluid flow decreases. This decrease results in an increase in secondary fluid flow velocity and consequently gives rise to overall heat transfer coefficient rates. Enhancement in heat transfer rates resulted from the increased convective heat transfer coefficient values increases the net power generation rates and decreases SIC of the cycle. Optimum refrigerant (R227EA) mass flow rate obtained by OPSSAJ is at its higher limit, which is 0.799 kg/s. One can easily see the relationship between the refrigerant mass flow rate and single and multi-phase convective heat transfer correlations reported in the Electronic Supplementary Material. It is observed from the correlations that convective heat transfer coefficient of the running fluid is directly influenced by the increasing flow rates, which eventually enhances the power generation of the ORC system. It is also observed that baffle spacing in the condenser and evaporator is closer to minimum allowable bound rather than its maximum. When ORC system running with R227EA is optimized to obtain maximum second law efficiency of the cycle, evaporator and condenser pinch point temperatures reach their minimum value. A thermodynamic system with minimum entropy generation is the system having higher exergetic (second law) efficiency. It is a thermodynamic principle that entropy of a system increases with the increasing temperature differences between the surroundings. Therefore, it is logical to obtain the minimum allowable value of these design variables, which reduces the temperature mismatch between two mediums and thereby increasing the exergetic efficiency of the cycle. Superheat temperature in the evaporator is obtained 17.168 K. Baffle spacing in the condenser and evaporator reaches its upper limits of 0.499 m. Triangular and square pitch arrangements are respectively obtained for the condenser and evaporator. The optimum number of tube passes in the evaporator and condenser is found to be 1. Single optimization results of the ORC running with R600 working fluid indicates that minimum SIC and maximum second law efficiency values are correspondingly 5351.095 ($/W) and 0.496. These objective function values are respectively 28.9% lower and 15.1% higher than those found by the cycle running with R227EA. Enhancement in the numerical value of these cycle performance indexes results from the intrinsic thermophysical characteristics of R600 refrigerant. The inclination of the design variables of ORC operating with R600 is in accordance with that of running with R227EA, except one case which is the superheat temperature in the evaporator when SIC is minimized. 6.379 K superheat is obtained which is closer to its lower limit contrary to the evaporator superheat of 29.998 K obtained by the cycle running with R227EA. It is also interesting to see that the design variable of condenser temperature reaches its minimum value for both cycles running with R227EA and R600. The net power output of the cycle is the direct function of the mass flow rate of the running refrigerant stream while it has no significant influence on second law efficiency rates as it is understood from Eq. (24). Regarding single objective optimization results obtained by the proposed hybrid algorithm reported in Table 3, Specific Investment Cost rate of the cycle gets its minimum value when mass flow rates hit the maximum value between the allowable value for ORC operated with R227EA refrigerant. A moderate mass flow rate of 0.363 kg/s, which is close to the minimum value between the defined search span, is obtained in the case of SIC minimization of ORC with R600 refrigerant. As respective Specific Investment Cost and second law efficiency rates acquired for R227EA and R600 refrigerants are comparatively evaluated, it is seen that ORC running with R600 is much more favorable to that of operated with R227EA because of its compatible thermal characteristics. In most of the related literature studies concerning with thermal design of ORC working with a binary mixture, the fluid composition is taken constant value and generally is not considered as a design variable. Parametric optimization is applied to observe the variational effects of mixture composition on the problem objectives. However, this type of optimization procedure has several shortcomings [28]. A significant drawback is that singularities can be observed in calculating the objective function values when the mixture composition is varied within the defined interval. This deficiency in calculation reduces the credibility and reliability of the obtained optimization results. For this important reason, mixture composition is considered as an accompanying decision variable along with remaining cycle design parameters. ORC with mixture fluid shows much better thermoeconomic performance in comparison with the cycle operating with pure fluids of R227EA and R600. The maximum exergetic efficiency of the ORC with mixture fluid is correspondingly 4.6% lower and 9.7% higher than that of the cycle operating with R600 and R227EA. Minimum SIC acquired by R227EA/R600 mixture is respectively 29.6% and 1.1% lower than that of the R227EA and R600 pure fluids. In this sense, working with mixture fluid leads to lower capital cost rates entailing a smaller physical scale of ORC plant compared to pure fluids. Evaporator pinch point and superheat temperatures are correspondingly 8.0 and 15.0 K when second law efficiency is maximized. Besides, the optimum condenser temperature of the mixture fluid is obtained 303.150 K, which is its minimum allowable value, in this optimization case. Based on the Carnot principle of thermodynamics higher temperature difference between evaporator and condenser yields better exergy efficiency. Increasing evaporator temperatures results in an increased enthalpy difference in the expander. This increase causes a reduction in mass flow rates of the mixture fluid. The effect of variations in enthalpy difference and mass flow rate entails an increase in the net power output of the cycle. It is noted that the mass fraction of R227EA in the mixture is found respectively 0.590 when exergetic efficiency is maximized and 0.20 when SIC is minimized. Tables 4 and 5 respectively report the single-objective optimization results of the ORC system for the NSGA-II and MOPSO algorithms. By looking at the results, it is realized that OPSSAJ outperformed the other two competing algorithms for the single-objective optimization task.

Table 3 Single objective optimization results of the ORC system obtained with OPSSAJ
Full size table
Table 4 Single objective optimization results of the ORC system obtained with NSGA-II
Full size table
Table 5 Single objective optimization results of the ORC system obtained with MOPSO
Full size table

Figure 5 shows the Pareto solutions found by the NSGA-II [58], MOPSO [59] and OPSSAJ algorithms for the base ORC system running with R600 working fluid. Each sample solution on the Pareto curve represents a trade-off and no solution is superior to the other on the frontier. It is seen that the final solution selected by TOPSIS from the alternative sample points on the curve is much closer to minimum SIC rather than maximum second law efficiency. Moreover, the pareto curve generated by the OPSSAJ algorithm has more desirable desirable solutions compared to that of NSGA-II and MOPSO optimizers. Referring to the final optimum solution on the Pareto curve constructed by OPSSAJ and obtained by TOPSIS, optimal values of exergetic efficiency and Specific Investment Cost are respectively 0.3758 and 5499.612 ($/W). Optimal solutions attained by TOPSIS for SIC and exergetic efficiency are correspondingly 2.7% higher and 24.2% lower compared to the optimum ORC system running with single R600 refrigerant when design objectives are seperately optimized. Figure 6 depicts the distribution of the non-dominated solutions on the Pareto curve for ORC running with R227EA. TOPSIS results of ORC for OPSSAJ with R227EA for second law efficiency and SIC are respectively 0.3228 and 7636.917 ($/W). The optimization results indicate that SIC and exergetic efficiency rates are correspondingly increased by 1.4% and 2.1% compared to that of the optimum solutions obtained from single-objective optimization. Furhermore, it is seen that the Pareto curve constructed by OPSSAJ has better solutions compared to that of NSGA-II and MOPSO algorithms. Figure 7 shows the non-dominated solutions of the conflicting objectives residing on the Pareto curve for the ORC system with the R227EA/R600 mixture refrigerant. TOPSIS results of OPSSAJ for the ORC cycle employing the refrigerant mixture are 0.4534 for exergetic efficiency and 7031.801 ($/W) which are respectively 32.7% higher and 4.1% lower than those of the solutions obtained for the case of single-objective optimization. It is also realized that the OPSSAJ Pareto curve consists of more desirable solutions compared to that of NSGA-II and MOPSO algorithms. Table 6 reports the TOPSIS results of OPSSAJ along with their corresponding design variables for the ORC system operating with different refrigerants. Tables 7 and 8 respectively report the TOPSIS results of NSGA-II and MOPSO algorithms for the ORC system. The results show that TOPSIS solution of OPSSAJ is more desirable than that of the NSGA-II and MOPSO algorithms.

Fig. 5
figure 5

Non dominated solutions obtained by the OPSSAJ, MOPSO and NSGA-II for ORC running with R600 refrigerant

Full size image
Fig. 6
figure 6

Pareto optimal solutions obtained by OPPSAJ, MOPSO and NSGA-II for ORC operating with R227EA working fluid

Full size image
Fig. 7
figure 7

Pareto solutions for the ORC cycle employing R227EA/R600 refrigerant mixture

Full size image
Table 6 Optimal values of cycle parameters and conflicting design objectives obtained with the OPSSAJ algorithm
Full size table
Table 7 Optimal values of cycle parameters and conflicting design objectives obtained with the NSGA-II algorithm
Full size table
Table 8 Optimal values of cycle parameters and conflicting design objectives obtained with the MOPSO algorithm
Full size table

6 Conclusion

This study proposed a hybrid Oppositional Salp Swarm—Jaya optimization (OPSSAJ) algorithm for solving multi objective design optimization of an Organic Rankine Cycle operating with a binary mixture composed of R227EA/R600. The proposed hybridization procedure focuses on enhancing the diversity of the population and manintaining a plausible balance between the diversification and intensification whih are two important phases of any optimization algorithm. SSA is a powerful optimizer having plenty of applications in the literature. However, major drawback of SSA is too much exploitation caused by the chain movement of the salps on the fertile areas. This deficiency is conquered by using opposite point of the current solution which can diversify the search space and enables to reach unknown paths of the solution domain. Jaya algorithm is an effective metaheuristic optimizer having a superior capability in local minima avoidance thanks to its dexterious manipulation schemes. It is aimed to compansate for the algorithm-specific disadvantages of SSA by hyridizing it with Jaya and Oppositonal-based algorithms, both of which having an exceptional exploration capability. The proposed hybrid OPSSAJ is applied to a suite of twenty-four test functions comprised of unimodal and multimodal problems in order to benchmark its optimization efficiency on multidimensional test problems. Statistical analysis have been performed and numerical results obtained from OPSSAJ have been compared with those acquired by some of recently developed metaheuristic optimizers. The proposed algorithm outperforms the contender algorithms with regards to the solution accuracy and robustness in most of the cases. Integrating the basic mutation scheme of JAYA with QOBL method significantly boosts the optimization performance of the hybrid method such that the proposed algorithm obtains the best optimum results ins 20 out of 24 test functions and hows the best predictive accuracy when ranking-point based assessment is performed. As a real-world case application, OPPSAJ is evaluated on solving a multi objective design of and Organic Rankine Cycle. Optimum cycle design parameters have been acquired by the proposed algorithm considering single and multi objective optimization cases. Multi-objective optimization of ORC system results shows that using a binary mixture instead of a single refrigerant greatly enhances the second law efficiency of the cycle. However, using binary mixture increases the SIC of the system compared to the system running with R600 refrigerant, based on the numerical outcomes of the TOPSIS decision-maker. During sensitivity analysis, it is also interesting to see that the second law efficiency of the thermal cycle is increased then enters a declining zone as the mass fraction of R227EA in the refrigerant mixture increases. This behavior can be attributed to the intrinsic thermal characteristic of R227EA refrigerant. Furthermore, a sensitivity analysis have been performed based on the non-dominated solution of the Pareto curve chosen by TOPSIS to observe the influences of the varying cycle parameters on the problem objectives.