1 Introduction

Although robot technologies that greatly simplify our lives is a very important technology, it is known inverse kinematics solution of robots is one of the difficult and very time-consuming problems and has a non-linear characteristic [1,2,3]. Therefore, it is of great importance to overcome these problems which have a very widespread research, such as reducing the computation time, getting the right solution, to achieve the shortest path planning [4]. Recently, 7-DOF robot manipulators, which have come to the forefront with their skill in avoiding obstacles, have become the focus of the research world. However, control of this robot so difficult and complicated owing to the large number of joint [5]. The basis of robot control is the kinematic calculations which are divided into two as forward and inverse kinematics. These calculations, which express robot movements, are a very common field of study. Forward kinematics that is used to obtain the position of the end effector in cartesian space from the joint angles is relatively easy [6]. On the other hand, inverse kinematics that is conversion of the position and orientation of the robot manipulator end-effector from Cartesian space to joint space is a more complex, non-linear equations and impossible to solution by conventional methods such as geometric, iterative and algebraic [7, 8]. Moreover, it has a large number of solutions. Hence, inverse kinematics problem is suitable for the heuristic methods such as particle swarm optimization, artificial bee colony, firefly algorithm and artificial neural network [9,10,11]. Because artificial intelligence techniques are indispensable methods for solving difficult, complex and long-time problems, it is actively used at every stage of robot technology [12, 13].

Momani et al. have implemented an inverse kinematics solution of an articulated robot manipulator using traditional and improved genetic algorithm methods [14]. Tejomurtula and Kak perform the inverse kinematic solution of 3-jointed robot arm using artificial neural networks that eliminates some of the disadvantages of this method BP algorithm, such as training time and accuracy [15]. Dash et al. [16] perform solution a new method based on artificial neural network and simulated this solution via six-jointed robot arm. Huang et al. [17] carry out inverse kinematics solution of seven-joined robot manipulator quickly and accurately using particle swarm optimization. Ayyıldız and Çetinkaya [18] have designed a 4-DOF robot manipulator and inverse kinematics solutions of its have achieved the four different (PSO, QPSO, GSA and GA) optimization algorithm and they demonstrated comparatively results obtained. Rokbani and Alimi studied the contribution to the solution of inverse kinematics using variants of PSO, such as inertia weight, constriction factor and linear decreasing weight. In addition, they have used a two-jointed robotic arm for simulation test [19]. Rokbani et al. prefer to use the firefly intelligent method which is a new heuristic algorithm based on swarm, in their work and tested the proposed method in a three-jointed robot arm [20]. Koker has proposed a hybrid method which was used with the neural network and genetic algorithm to solve the inverse kinematics solution of a six-joint robotic manipulator to minimize the error of the end effector [21]. Similarly, Pam et al. use together bee algorithm and artificial neural network of the inverse kinematics of an articulated robotic manipulator which has a three-joint. The bee algorithm was used to train the neural network which has a multilayer perceptron structure [22].

In general, the calculation steps used for heuristic methods have been also preferred in this study. The robot manipulator is manually directed to a predetermined position. The artificial bee colony algorithm and particle swarm optimization are used to obtain the optimal joint angles that reach the nearest point to this position of the end effector. The main focus of the study is to perform the inverse kinematics calculation with ABC technique and to compare the results with PSO which is another widely used technique in the literature. Therefore, the following parts of the study are organized in this framework. In Chapter 2, the newly designed robot manipulator used in this study is introduced and kinematics equations of this robotic arm are created. In the following, the artificial bee colony algorithm and particle swarm optimization is briefly summarized and the fitness function that finds the distance between the desired position and the actual position, to be used in this algorithm is introduced. In Chapter 3, simulation results are obtained and presented. In the last section, the results have been analyzed and compared with previous studies.

2 Materials and methods

2.1 Kinematics analysis of a 7-DOF redundant robot manipulator

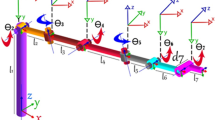
Robotic manipulators which are available in two forms: prismatic and rotational, consist of links sequentially connected to each other with joints which perform a movement mechanism taking certain angles or by a certain percentage of elongation and shortening by actuators [23]. Designed robot manipulator for this study has seven rotational joints and is shown in Fig. 1. A 7-DOF robotic manipulator not only performs the movement from one position to another position in a comfortably but also has infinite inverse kinematics solutions. Of course, objective is to provide the end effector to be positioned correctly.

Fig. 1
figure 1

The structure of robot manipulator

Full size image

Today, kinematics calculations are done by homogeneous transformation matrices which are created with the help of four parameters that is called Denavit–Hartenberg parameters.

In Table 1, i shows the joint sequence. The lengths are given in meters and the angles are given in degree. The homogeneous transformation matrix can be used to obtain the forward kinematics of the robot manipulator, using the DH parameters in Eq. (1) [24, 25].

$${}_{i - 1}^{i} T = \left[ {\begin{array}{*{20}c} {cos\theta {\text{i}}} & { - cos\alpha i \cdot sin\theta {\text{i}}} & {sin\alpha i \cdot sin\theta {\text{i}}} & {ai \cdot cos\theta {\text{i}}} \\ {sin\theta {\text{i}}} & {cos\alpha i \cdot cos\theta {\text{i}}} & { - cos\theta {\text{i}} \cdot { \sin }\upalpha{\text{i}}} & {ai \cdot sin\theta {\text{i}}} \\ 0 & {sin\alpha i} & {cos\alpha i} & {di} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(1)
$$A_{\text{EE}} = {}_{0}^{7} T = {}_{0}^{1} T \cdot {}_{1}^{2} T \cdot {}_{2}^{3} T \cdot {}_{3}^{4} T \cdot {}_{4}^{5} T \cdot {}_{5}^{6} T \cdot {}_{6}^{7} T = \left[ {\begin{array}{*{20}c} {n_{x} } & {s_{x} } & {a_{x} } & {P_{x} } \\ {n_{y} } & {s_{y} } & {a_{y} } & {P_{y} } \\ {n_{z} } & {s_{z} } & {a_{z} } & {P_{z} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(2)
$$\begin{aligned} & {}_{0}^{1} T = \left[ {\begin{array}{*{20}c} {c\theta_{1} } & 0 & { - s\theta_{1} } & 0 \\ {s\theta_{1} } & 0 & {c\theta_{1} } & 0 \\ 0 & { - 1} & 0 & {l_{1} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \;{}_{1}^{2} T = \left[ {\begin{array}{*{20}c} {c\theta_{2} } & 0 & {s\theta_{2} } & {l_{2} c\theta_{2} } \\ {s\theta_{2} } & 0 & { - c\theta_{2} } & {l_{2} s\theta_{2} } \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ & {}_{2}^{3} T = \left[ {\begin{array}{*{20}c} {c\theta_{3} } & 0 & { - s\theta_{3} } & {l_{3} c\theta_{3} } \\ {s\theta_{3} } & 0 & {c\theta_{3} } & {l_{3} s\theta_{3} } \\ 0 & { - 1} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ & {}_{3}^{4} T = \left[ {\begin{array}{*{20}c} {c\theta_{4} } & 0 & {s\theta_{4} } & {l_{4} c\theta_{4} } \\ {s\theta_{4} } & 0 & { - c\theta_{4} } & {l_{4} s\theta_{4} } \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] {}_{4}^{5} T = \left[ {\begin{array}{*{20}c} {c\theta_{5} } & 0 & { - s\theta_{5} } & {l_{5} c\theta_{5} } \\ {s\theta_{5} } & 0 & {c\theta_{5} } & {l_{5} s\theta_{5} } \\ 0 & { - 1} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ &\; {}_{5}^{6} T = \left[ {\begin{array}{*{20}c} {c\theta_{6} } & { - s\theta_{6} } & 0 & {l_{6} c\theta_{6} } \\ {s\theta_{6} } & {c\theta_{6} } & 0 & {l_{6} s\theta_{6} } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] {}_{6}^{7} T = \left[ {\begin{array}{*{20}c} {c\theta_{7} } & { - s\theta_{7} } & 0 & {l_{7} c\theta_{7} } \\ {s\theta_{7} } & {c\theta_{7} } & 0 & {l_{7} s\theta_{7} } \\ 0 & 0 & 1 & {d7} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$
(3)

where iTi+1 is the transfer matrix of link i. 0T7 matrix produces a Cartesian coordinate for any seven joint angles. Because the fitness function of the proposed approach is the Euclidian distance in Cartesian space between the obtained and the target points. 0T7 can be used to calculate the Cartesian coordinate of the obtained point in the cost function.

Table 1 D–H parameters for robot manipulator
Full size table

In Eq. (2), px, py, and pz denotes the elements of the position vector whereas nx, ny, nz, sx, sy, sz, ax, ay, az denote the rotational elements of the transformation matrix. In this study, only the position vector will be used to calculate the position error. The position vector equation is as follows (where s and c denote the sine and cosine functions):

$$\begin{aligned} & P_{x} = \left( {c\theta_{1} c\theta_{2} c\theta_{3} c\theta_{4} - s\theta_{1} s\theta_{3} s\theta_{4} - c\theta_{1} s\theta_{2} s\theta_{4} } \right)\left( {c\theta_{5} c\theta_{6} l_{7} c\theta_{7} - c\theta_{5} s\theta_{6} l_{7} s\theta_{7} - s\theta_{5} d_{7} + c\theta_{5} l_{6} c\theta_{6} + l_{5} c\theta_{5} } \right)\left( { - c\theta_{1} c\theta_{2} s\theta_{3} - s\theta_{1} c\theta_{3} } \right) \\ & \quad \left( {s\theta_{5} c\theta_{6} l_{7} c\theta_{7} - s\theta_{5} s\theta_{6} l_{7} s\theta_{7} + c\theta_{5} d_{7} + s\theta_{5} c\theta_{6} l_{6} + l_{5} s\theta_{5} } \right)\left( {c\theta_{1} c\theta_{2} c\theta_{3} s\theta_{4} s\theta_{1} s\theta_{3} s\theta_{4} c\theta_{1} c\theta_{4} s\theta_{2} } \right)\left( { - s\theta_{6} l_{7} c\theta_{7} - c\theta_{6} l_{7} s\theta_{7} - l_{6} s\theta_{6} } \right) \\ & \quad + \;c\theta_{1} c\theta_{2} \left( {c\theta_{3} c\theta_{4} l_{4} + l_{3} c\theta_{3} } \right) - s\theta_{1} \left( {s\theta_{3} c\theta_{4} l_{4} + l_{3} s\theta_{3} } \right) - c\theta_{1} s\theta_{2} l_{4} s\theta_{4} + c\theta_{1} c\theta_{2} l_{2} \\ \end{aligned}$$
(4)
$$\begin{aligned} & P_{y} = s\theta_{1} c\theta_{2} c\theta_{3} c\theta_{4} + c\theta_{1} s\theta_{3} c\theta_{4} - s\theta_{1} s\theta_{2} s\theta_{4} )\left( {c\theta_{5} c\theta_{6} l_{7} c\theta_{7} - c\theta_{5} s\theta_{6} l_{7} s\theta_{7} - s\theta_{5} d_{7} + c\theta_{5} c\theta_{6} l_{6} + l_{5} c\theta_{5} } \right) \\ & \quad + \;\left( { - s\theta_{1} c\theta_{2} s\theta_{3} + c\theta_{1} c\theta_{3} } \right)\left( {s\theta_{5} c\theta_{6} l_{7} c\theta_{7} - s\theta_{5} s\theta_{6} l_{7} s\theta_{7} + c\theta_{5} d_{7} + s\theta_{5} c\theta_{6} l_{6} + l_{5} s\theta_{5} } \right) \\ & \quad + \;\left( {s\theta_{1} c\theta_{2} c\theta_{3} s\theta_{4} + c\theta_{1} s\theta_{3} s\theta_{4} + s\theta_{1} s\theta_{2} c\theta_{4} } \right)\left( { - s\theta_{6} l_{7} c\theta_{7} - c\theta_{6} l_{7} s\theta_{7} - l_{6} s\theta_{6} } \right) + s\theta_{1} c\theta_{2} \left( {c\theta_{3} c\theta_{4} l_{4} + l_{3} c\theta_{3} } \right) \\ & \quad + \;c\theta_{1} \left( {s\theta_{3} c\theta_{4} l_{4} + l_{3} s\theta_{3} } \right) - s\theta_{1} s\theta_{2} s\theta_{4} l_{4} + s\theta_{1} c\theta_{2} l_{2} \\ \end{aligned}$$
(5)
$$\begin{aligned} & P_{z} = \left( { - s\theta_{2} c\theta_{3} c\theta_{4} - c\theta_{2} s\theta_{4} } \right)\left( {c\theta_{5} c\theta_{6} l_{7} c\theta_{7} - c\theta_{5} s\theta_{6} l_{7} s\theta_{7} - s\theta_{5} d_{7} + c\theta_{5} c\theta_{6} l_{6} + l_{5} c\theta_{5} } \right) \\ & \quad + \;s\theta_{2} s\theta_{3} \left( {s\theta_{5} c\theta_{6} l_{7} c\theta_{7} - s\theta_{5} s\theta_{6} l_{7} s\theta_{7} + c\theta_{5} d_{7} + s\theta_{5} c\theta_{6} l_{6} + s\theta_{5} l_{5} } \right) \\ & \quad + \;\left( { - s\theta_{2} c\theta_{3} s\theta_{4} + c\theta_{2} c\theta_{4} } \right)\left( { - s\theta_{6} l_{7} c\theta_{7} - c\theta_{6} l_{7} s\theta_{7} - s\theta_{6} l_{6} } \right) - s\theta_{2} \left( {c\theta_{3} c\theta_{4} l_{4} + l_{3} c\theta_{3} } \right) - c\theta_{2} s\theta_{4} l_{4} - s\theta_{2} l_{2} + l_{1} \\ \end{aligned}$$
(6)

2.2 Artificial bee colony (ABC) algorithm

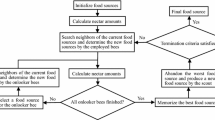
Heuristic algorithms such as artificial neural network, simulated annealing, genetic algorithm, particle swarm optimization and firefly algorithm have the ability to easily solve NP problems which are very complex, non-linear and time-consuming problem to be solved by normal methods [26]. Recently, Artificial Bee Colony (ABC) based on search of food by honey bees, is a very popular heuristic method and was presented by Karaboğa in 2005 [27, 28].

According to ABC, this algorithm is consist of from three kinds of bees that their names are employed, onlooker and scout bee. Steps of ABC Algorithm are as follows [29, 30]:

  • The initial food sources are generated randomly.

  • Employed bees select a food source and return to the hive by storing nectar.

  • After onlooker bees watch the waggle dance of the employed bees that came to the hive, they chose the food source with a certain probability.

  • Onlooker bees that turned to the selected food sources begin to nectar storage like employed bees.

  • Onlooker bees continue to nectar storage, until the limit value takes the maximum value.

  • Employed bees convert into scout bees, as soon as the limit value reaches the maximum value.

  • Scout bees search the new food source randomly and continue to nectar storage.

  • All these steps constitute one cycle algorithm and these steps continue by the time the termination criterion is achieved.

When the basic steps of the ABC algorithm is examined in Fig. 2, in the first step, the random food sources are constructed as follows:

$$x_{i,j} = x_{j}^{min} + rand\left( {0,1} \right)\left( {x_{j}^{max} - x_{j}^{min} } \right)$$
(7)

where i = 1…N, j = 1…D, N is the number of nectar sources, D is the number of optimization parameters, \(x_{min}^{j}\) and \(x_{max}^{j}\) are the maximum and minimum of parameter j. Initially, the value of limit parameters are reset.

Fig. 2
figure 2

Flowchart of basic ABC algorithm

Full size image

Employed bees find neighbors solution in search of new sources of food and make comparisons between existing solutions for new solutions. If the new solution is kept in memory it is better than the old solution and the other is abandoned. If the new solution is not a good solution the counter of existing solutions is incremented.

$$v_{i,j} = x_{i,j} + \varphi_{i,j} \left( {x_{i,j} - x_{k,j} } \right)$$
(8)

where xi indicates that the current solution which is selected by the employed bees. vi is a new solution in neighborhood of xi. k ∈ (1, N) is a randomly chosen and must be different than i, j is a random integer in the range [1, D]. φi,j coefficients are randomly chosen value in the range [− 1.1].

Meanwhile, if the new neighborhood values exceed limit values, it is prevented by Eq. (9).

$$x_{i} = \left\{ {\begin{array}{*{20}l} {x_{min}^{i} ,} \hfill & {x_{i} < x_{min}^{i} } \hfill \\ {x_{max}^{i} , } \hfill & {x_{i} > x_{max}^{i} } \hfill \\ \end{array} } \right.$$
(9)

After employed bees complete their research, probability values are calculated as in Eq. (10) so as to selection food sources of scout bees.

$$P_{i} = fit_{i} /\mathop \sum \limits_{j = 1}^{N} fit_{i}$$
(10)

where \(fit_{i}\) is normalized fitness function value. After probability values for each solution is calculated, employed bees compare with random-determined value and the probability value of the solution. If the selected probability value of the solution is greater than this value, scout bee tends to the food supply and search for new solution [31].

After all employed and scout bees complete their search, the abandonment counter of each solution is controlled. If the counter value of the solution has reached the limit value which is an important control parameter of the ABC algorithm, the employed bee that uses that resource, convert into scout bee. It is directed to a new point in the solution space using Eq. (7) than continues to search from here. All operations will continue until it reaches the maximum number of cycles [32].

2.3 Particle swarm optimization

It is a heuristic algorithm first used by Kennedy, inspired by the co-movement of birds and fishes [33]. Like other heuristic algorithms, it works by searching in a certain solution space within the frame of certain movements and stands out with its good values despite the small number of parameters [34].

As shown in Fig. 3, the PSO algorithm process depends on only two parameters, speed (Eq. 11) and position (Eq. 12) of particles. Because all the particles move to a defined position, depending on their own velocities. Therefore, each movement results in a new position [35].

$$v_{id} = v_{id} + c_{1} \cdot r_{1} \cdot \left( {p_{best} - x_{id} } \right) + c_{2} \cdot r_{2} \cdot \left( {g_{best} - x_{id} } \right)$$
(11)
$$x_{id} = x_{id} + v_{id}$$
(12)
Fig. 3
figure 3

Flowchart of basic ABC algorithm

Full size image

2.4 Method

Here, the optimization problem is to find the optimum angle value for each joint with the given initial Cartesian coordinate and the target coordinate, so the end-effector of robot arm is transferred to desired location by joint angles. Obviously, the accurate calculations of joint angles values are very important. For this purpose the following scenario is followed. Firstly, the optimal values of the 7-joint angles of the robot manipulator are found by the ABC algorithm. Then, the distance between the position of the end effector obtained by these optimal angles and the predetermined position is calculated.

$$Error = \sqrt {\left( {x_{2} - x_{1} } \right)^{2} + \left( {y_{2} - y_{1} } \right)^{2} + \left( {z_{2} - z_{1} } \right)^{2} }$$
(13)

The main goal of this study is to solve this optimization problem by implementing the ABC. For this purpose, we designed a fitness function that is based on Euclidian distance given Eq. (13) between the desired location (x2, y2, z2) and the current location (x1, y1, z1) described. This cost can be used to calculate fitness function (Fig. 4).

Fig. 4
figure 4

Illustrating the position error

Full size image

3 Simulation results

The purpose of this study is to demonstrate the effectiveness and performance of the artificial bee colony algorithm to solve the inverse kinematics solution of the 7-DOF robot arm. The initial and final positions of the end effector are seen Fig. 5a, b. However, the final position and angles appears in Fig. 5b is a position created by manual. Because the designed 7-DOF robotic arm has a redundant structure, it can be formed in the same position at different angles.

Fig. 5
figure 5

Initial (a) and final (b) position of 7-DOF redundant robot arm end effector

Full size image

The desired position of the end effector for the robot arm is illustrated in Fig. 5b. The joint angles for the robot manipulator orientation shown in this figure are 45°, 0°, 45°, 0°, 45°, 0°, 0° from θ1 to θ7, respectively. However, the values obtained by the algorithm have resulted in different orientations. Because the robot manipulator used in this study has an unlimited number of solutions. The subject of this study is to position the robot arm to the destination with the minimum error using artificial bee colony algorithm and compare the result with the PSO (Table 2).

Table 2 Joint angles obtained from calculation
Full size table

The proposed approach has been simulated in MATLAB IDE software. Figure 6 presents the performance fitness function (position error) of the ABC algorithm to solve the redundant problem of the 7-DOF robotic manipulator. As can been seen in Fig. 6, the ABC algorithm successfully search for the optimal configurations of the robotic manipulator.

Fig. 6
figure 6

Position error of end effector

Full size image

According to Fig. 7, the evolved optimal solution is (θ1f, θ2f, θ3f, θ4f, θ5f, θ6f, θ7f) = (101.190080691136°, − 9.51890813773679°, − 14.3155800174267°, − 4.35578591323361°, 39.6787526304158°, 35.9420677837833°, 72.6774064516414°).

Fig. 7
figure 7

The values of 7-joint angles during iteration

Full size image

In this study, in order to reveal the performance of ABC algorithm, it has compared with PSO that is a swarm algorithm. As shown in Fig. 8, the ABC algorithm yielded a better result than the PSO algorithm in terms of position error.

Fig. 8
figure 8

ABC and PSO position error comparison

Full size image

Figure 9 shows the computation times of both the ABC and the PSO algorithm 500 iterations. Graphs clearly show that the computation times of both algorithms are very close to each other.

Fig. 9
figure 9

ABC and PSO computation time comparison

Full size image

Figure 10 shows the orientations of joint angles resulting from position error calculated by ABC and PSO algorithms. Here, the final positions of the manipulator have been revealed in the RoboAnalyzer [36] interface through the joint angles obtained with each algorithm. That is, the expression of accuracy which redundant robot has numerous solutions for inverse kinematics problem is shown.

Fig. 10
figure 10

According to obtained joint angles, the end effector position of the robot manipulator

Full size image

A more detailed comparison of the values obtained by ABC and PSO algorithms appears in Table 3. The ABC algorithm uses 100 population while the PSO is 300. In these algorithms, the number of population affects the quality of the solution positively while extending the solution time. Although the time for computation of the algorithm was similar to each other, the ABC solution reached a much shorter time.

Table 3 Comparison of ABC and PSO
Full size table

In order to ensure the accuracy of the ABC algorithm, the calculation of 100 different points selected from the workspace of the robot manipulator is also performed in this article. Figure 11 shows a comparison of the position error of both algorithms for 100 different points, and Fig. 12 shows the solution time comparison.

Fig. 11
figure 11

Position error calculated for 100 different points

Full size image
Fig. 12
figure 12

Computation time for 100 different points

Full size image

It is clear that the ABC algorithm produces much better results than the PSO algorithm, except for the two of the results, which produce different results in both algorithms as position errors. When the calculation period is considered, the results are close to each other. However, the ABC algorithm has also shown slightly better results than the PSO algorithm.

Intelligent optimization techniques have emerged as a result of the complexity of the problems encountered today and have provided effective solutions. For this reason, these techniques have left their mark on the last 20 years, have settled in the focus of the research world and many engineering problems that take long time to solve by classical methods have been solved in a short time (Table 4).

Table 4 Literature summary similar to this article
Full size table

4 Conclusion

In this paper, Artificial Bee Colony algorithm has been proposed for the inverse kinematics problem of the robot arms, and it has been simulated on 7-DOF redundant robot manipulator. The most important innovation in this study is the use of a newly designed 7-jointed robot arm in the test process. In this study, artificial bee colony algorithm is used to approximate the robot manipulator to a predetermined position in the workspace with minimum error. The obtained position error and calculation times have been compared with particle swarm optimization which is another heuristic algorithm technique. In order to determine the accuracy of the algorithm used, a second scenario has been applied in 100 different tests. The simulations show the proposed ABC algorithm successfully search for the optimal joint angles of the robotic manipulator. So the ABC algorithm is a candidate method to solve inverse kinematics problem of robot arms with the high numbers of joint just like other heuristic methods. Despite all its performance, the long process stages of the algorithm and the excess of the parameters are seen as disadvantages of the artificial bee colony. If these disadvantages are eliminated or the algorithm is improved, this technique will be used more widely in the coming period. Especially after this study, it can be used to control complex robots.