Introduction

In the dynamic field of marine propulsion, the complex interaction of coupled torsional and transverse vibrations within shaft systems constitutes a critical challenge with far-reaching implications for stability and operational efficiency. This research addresses this challenge by delving into applying Magnetorheological (MR) dampers, enriched through incorporating an Adaptive Neuro-Fuzzy Inference System (ANFIS) for advanced control. The impetus behind this inquiry arises from the urgent need to refine dynamic control strategies, presenting a novel pathway to optimize the performance of marine propulsion systems [1,2,3]. Historically, research on vibration control predominantly centered around passive damping systems. While effective within specific parameters, these systems exhibit limitations in adaptability and responsiveness. The integration of MR dampers, particularly synergized with ANFIS, emerges as a promising avenue to overcome these limitations, offering a semi-active control system that can dynamically adjust damping forces in response to varying operational conditions [4,5,6,7,8].

A comprehensive review of the existing literature underscores the importance of understanding the dynamic behavior of marine propulsion shaft systems under coupled vibrations. The approach of this manuscript is to build upon the foundation of the Jeffcott rotor model, modified to encapsulate the subtleties of cross-section eccentricity arising from excessive shaft vibrations [9,10,11,12]. This model, combined with a meticulously crafted mathematical representation of the MR damper, establishes a robust framework for predicting and controlling coupled vibrations in marine propulsion systems.

Examining literature surrounding marine propulsion dynamics and the control of coupled torsional and transverse vibrations reveals a multifaceted landscape of challenges and advancements. Esteemed researchers have contributed significantly, addressing specific aspects of this specialized field [13,14,15,16,17,18]. Noteworthy works, such as Firouzi et al. [5] providing a comprehensive review of recent advancements and Marijančević et al. [2] delving into the modeling intricacies of torsional vibrations, offer valuable insights. Additionally, studies like Huang et al. [13] exploring the applications of ANFIS in semi-active control systems. Also, Quanchao and Rui [3] scrutiny of the technological aspects of MR dampers plays a pivotal role in understanding adaptive control methodologies and the critical role of MR dampers in vibration control.

Huang et al. 's [10] dynamic analysis of coupled vibrations in marine propulsion systems, Halilbeşe et al. [4] examination of adaptive control strategies for MR dampers, and Kim et al.'s (2013) empirical validation of Jeffcott rotor models further enrich our understanding. Moreover, Chen et al. 's [8] investigation into the effectiveness of ANFIS in adaptive vibration control and Firouzi et al. 's [5] exploration of advancements in numerical modeling techniques contribute significantly to refining dynamic analysis tools. Hence, from the literature, there is a scarcity of studies examining the application of the Adaptive Neuro-Fuzzy Inference System (ANFIS) in conjunction with Magnetorheological (MR) dampers, specifically within marine propulsion dynamics as per the authors' best knowledge. While the literature underscores the limitations of traditional passive damping systems in adapting to the dynamic marine environment, the potential of MR dampers controlled by ANFIS to overcome these constraints remains relatively unexplored. The dynamic adjustment capability of MR dampers, a key attribute for addressing variable conditions in marine propulsion systems, necessitates a closer examination within the context of ANFIS regulation. Additionally, the literature underscores the importance of precise numerical modeling and experimental validation yet needs a focused exploration of these aspects concerning integrating ANFIS-regulated MR dampers. Consequently, our research aims to fill this identified gap by investigating how the application of ANFIS with MR dampers can optimize the control of coupled torsional and transverse vibrations in marine propulsion shaft systems.

Therefore, in this manuscript, a meticulous exploration of coupled torsional and transverse vibrations is developed, introducing a sophisticated numerical model and a validated mathematical model for the MR damper. The experimental protocol involves subjecting the MR damper to sinusoidal displacement inputs across a range of current levels within a controlled testing environment. Integrating ANFIS as a controller for the MR damper further enhances adaptability and responsiveness. Subsequent analyses, including validating our numerical model through experimental analysis and investigating MR dampers controlled by ANFIS, contribute to a holistic understanding of the potential for mitigating vibrations and improving stability in marine propulsion shaft systems.

Mathematical Modeling of the System

Mathematical Model of Coupled Torsional–Transverse Vibrations

In this study, a Jeffcott rotor model was employed to simulate the coupled torsional–transverse vibrations in a rotor system. The model includes a massless shaft with a central disk, and instead of a propeller, a loading system was connected to the shaft [6]. The shaft, represented with three degrees of freedom, undergoes deformations in torsional and transverse directions. Due to operating forces, the mass center of the shaft shifted by a distance 'e.' shown in Fig. 1. The rotational speed is denoted by 'ω,' with 'θ' for torsional displacement and 't' for time. The Lagrangian dynamics approach was used to derive the system's behavior equation, with Eq. (1) determining the kinetic energy of the shaft (Han and Lee, 2019).

$$T = \frac{1}{2}m\left( {\dot{x}_{c}^{2} + \dot{y}_{c}^{2} } \right) + \frac{1}{2}J(\omega + \dot{\theta })^{2} .$$
(1)
Fig. 1
figure 1

Unbalanced shaft model

Full size image

In the given system, the new locations of the mass center, \(x_{c}\) and \(y_{c}\) are determined by Eqs. (2) and (3).

$$x_{c} = x + e\cos \varphi ,$$
(2)
$$y_{c} = y + e\cos \varphi ,$$
(3)
$$\varphi = \theta + \omega t.$$
(4)

Here, \(\varphi = \theta + \omega t\) represents the overall angular displacement due to torsional and transverse deformations, and e accounts for the cross-section eccentricity caused by external forces. The kinetic energy (T) of the shaft, described by Eq. (5), is obtained.

$$T = \frac{1}{2}m\left( {\dot{x} - e\left( {\omega + \dot{\theta }} \right)\sin \left( {\omega t + \theta } \right)} \right)^{2} + \frac{1}{2}m\left( {\dot{y} + e\left( {\omega + \dot{\theta }} \right)\cos \left( {\omega t + \theta } \right)} \right)^{2} + \frac{1}{2}J\left( {\omega + \dot{\theta }} \right)^{2} .$$
(5)

Additionally, the potential energy (V) and dissipation energy (D) of the system are defined in Eqs. (6) and (7), respectively [6]:

$$V = \frac{1}{2}k_{x} x^{2} + \frac{1}{2}k_{y} y^{2} + \frac{1}{2}k_{\theta } \theta^{2} ,$$
(6)
$$D = \frac{1}{2}c_{x} \dot{x}^{2} + \frac{1}{2}c_{y} \dot{y}^{2} + \frac{1}{2}c_{\theta } {\dot{\theta }}^{2} ,$$
(7)

where \(k_{x} ,k_{y}\), and \(k_{\theta }\) represent the stiffness coefficients, and \(c_{x} ,c_{y}\), and \(c_{\theta }\) represent the damping coefficients in the torsional and transverse directions. The equations of motion for the shaft system, considering the coupled torsional–transverse vibrations, are derived using Lagrange's Eq. (8),

$$\frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial \grave{\varvec{q}}}}} \right) - \frac{{\partial T}}{{\partial \user2{q}}} + \frac{{\partial V}}{{\partial \user2{q}}} + \frac{{\partial D}}{{\partial \grave{\varvec{q}}}} = \user2{Q,}$$
(8)

where \({\varvec{Q}}\) represents the non-conservative forces, and \({\varvec{q}} = \left[ {\begin{array}{*{20}l} x \hfill & y \hfill & \theta \hfill \\ \end{array} } \right]^{{\text{T}}}\) denotes the generalized coordinates. Equation (9) describes the equations of motion for the torsional–transverse coupled vibration of the system

$$\left\{ {\begin{array}{*{20}c} {m\dot{x} - me\dot{\theta }\sin \left( {\omega t + \theta } \right) + c_{x} \dot{x} + k_{x} x = me(\omega + \dot{\theta })^{2} \cos \left( {\omega t + \theta } \right)} \\ {m\dot{y} + me\dot{\theta }\cos \left( {\omega t + \theta } \right) + c_{y} \dot{y} + k_{y} y = me(\omega + \dot{\theta })^{2} \sin \left( {\omega t + \theta } \right)} \\ {\left( {J + me^{2} } \right)\dot{\theta } - me\dot{x}\sin \left( {\omega t + \theta } \right) + me\dot{y}\cos \left( {\omega t + \theta } \right) + c_{\theta } \dot{\theta } + k_{\theta } \theta = 0.} \\ \end{array} } \right.$$
(9)

In Eq. (9), torsional acceleration terms \(me\dot{\theta }\sin \left( {\omega t + \theta } \right)\) and \(me\dot{\theta }\cos \left( {\omega t + \theta } \right)\) influence transverse movements, while transverse acceleration terms \(me\dot{x}{\text{sin}}\left( {\omega t + \theta } \right)\) and \(me\dot{y}\cos \left( {\omega t + \theta } \right)\) impact torsional motion. This interplay, involving inertia components, results from the mass of imbalanced loads, indicating a direct interaction between transverse and torsional vibrations in the system.

When considering the coupling of lateral and torsional vibrations in an unbalanced rotor system, the resulting equations of motion become nonlinear due to the interaction between these motions. In many rotor systems, torsional displacements are often small and are estimated based on the primary terms of their development processes, considering torsion as a rotational force. To handle the low amplitude of torsional vibration, \({\text{sin}}\theta\) and \({\text{cos}}\theta\) can be approximated using the first terms of their Taylor series expansions. This allows for a simplified representation, as shown in Eq. (10)[6].

$$\left\{ {\begin{array}{*{20}l} {{\text{cos}}\left( {\omega t + \theta } \right) = {\text{cos}}\left( {\omega t} \right){\text{cos}}\theta - {\text{sin}}\left( {\omega t} \right){\text{sin}}\theta \approx {\text{cos}}\omega t - \theta {\text{sin}}\omega t} \hfill \\ {{\text{sin}}\left( {\omega t + \theta } \right) = {\text{sin}}\left( {\omega t} \right){\text{cos}}\theta + {\text{cos}}\left( {\omega t} \right){\text{sin}}\theta \approx {\text{sin}}\omega t + \theta {\text{cos}}\omega t.} \hfill \\ \end{array} } \right.$$
(10)

By neglecting higher-order terms in Eq. (9) and incorporating the approximations from Eq. (10), we arrive at the equation of motion (Eq. 11)

$$\left\{ {\begin{array}{*{20}l} {m\dot{x} - me\dot{\theta }\sin \omega t + c\dot{x} - 2me\omega \dot{\theta }\cos \omega t + kx + me\omega^{2} \theta \sin \omega t} \hfill \\ { = me\omega^{2} \cos \omega t} \hfill \\ {m\dot{y} + me\dot{\theta }\cos \omega t + c\dot{y} - 2me\omega \dot{\theta }\sin \omega t + ky - me\omega^{2} \theta \cos \omega t} \hfill \\ { = me\omega^{2} \sin \omega t} \hfill \\ { \left( {J + me^{2} } \right)\dot{\theta } - me\dot{x}\sin \omega t + me\dot{y}\cos \omega t + c_{\theta } \dot{\theta } + k_{\theta } } \hfill \\ { = 0.} \hfill \\ \end{array} } \right.$$
(11)

This equation, representing the combined effects of torsional and transverse vibrations, can be reformulated in matrix form as shown in Eq. (12).

$$\begin{array}{*{20}r} \hfill {} & \hfill {\left[ {\begin{array}{*{20}c} m & 0 & { - me{\text{sin}}\left( {\omega t} \right)} \\ 0 & m & {me{\text{cos}}\left( {\omega t} \right)} \\ { - me{\text{sin}}\left( {\omega t} \right)} & {me{\text{cos}}\left( {\omega t} \right)} & {J + me^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ {{\dot{\theta }}} \\ \end{array} } \right] + } \\ \hfill {} & \hfill {\left[ {\begin{array}{*{20}c} {c_{x} } & 0 & { - 2me\omega {\text{cos}}\left( {\omega t} \right)} \\ 0 & {c_{y} } & { - 2me\omega {\text{sin}}\left( {\omega t} \right)} \\ 0 & {} & {0c_{\theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ {{\dot{\theta }}} \\ \end{array} } \right] + } \\ \hfill {} & \hfill {\left[ {\begin{array}{*{20}c} {k_{x} } & {0me\omega^{2} {\text{sin}}\left( {\omega t} \right)} \\ 0 & {k_{y} - me\omega^{2} {\text{cos}}\left( {\omega t} \right)} \\ 0 & {0k_{\theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \theta \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {me\omega^{2} {\text{cos}}\left( {\omega t} \right) + F_{x} \left( t \right)} \\ {me\omega^{2} {\text{sin}}\left( {\omega t} \right) + F_{y} \left( t \right)} \\ {M_{\theta } \left( t \right)} \\ \end{array} } \right].} \\ \end{array}$$
(12)

This matrix representation captures the coupled dynamics of the system under the influence of both lateral and torsional vibrations [6].

Mathematical Model of Magnetorheological (MR) Damper

MR dampers are highly nonlinear devices that have a force–velocity connection that displays a hysteretic behavior. This relationship is not simple to represent theoretically since it shows hysteretic activity. Hysteresis may lead to significant issues in regulated systems, including loss of robustness and instability, respectively. In the recent past, the area of modeling MR dampers has been a very active one, and various different methods have previously been offered. The Bouc–Wen model is an example of a model that is both numerically tractable and has seen a great deal of application in the context of describing hysteretic systems. The Bouc–Wen model is very flexible and may demonstrate a wide range of hysteretic behaviors. To more accurately forecast how the damper would react, the authors of [12] presented a modified design, which can be seen in Fig. 2. To derive the equations that control this model, one part, namely the top one, is used exclusively.

Fig. 2
figure 2

MR damper was developed using a modified version of the Bouc–Wen model

Full size image

A semi-active control model for an MR damper that is connected to the linked torsional and transverse shaft systems may be developed with the use of a modified version of the Bouc–Wen model (Eq. (13)). Because the forces on each side of the rigid bar are equal to one another.

$$C_{1} \dot{y} = \left[ {\alpha z + c_{0} \dot{x} + k_{0} \left( {x - y} \right) + c_{0} \left( {\dot{x} - \dot{y}} \right)} \right],$$
(13)

where the evolutionary variable z is governed by

$$\begin{array}{*{20}c} {} \\ {\dot{z} = - \gamma \left| {\dot{x} - \dot{y}} \right|z\left| {z|^{n - 1} - \beta \left( {\dot{x} - \dot{y}} \right)} \right|z|^{n} + A\left( {\dot{x} - \dot{y}} \right)} \\ {} \\ \end{array} .$$
(14)

Solving for ẏ results in

$$\dot{y} = \frac{1}{{\left( {c_{0} + c_{1} } \right)}}\left[ {\alpha z + c_{0} \dot{x} + k_{0} \left( {x - y} \right)} \right].$$
(15)

The total force that is produced by the system may then be calculated by adding the forces that are shown in Fig. 2 to be present in the system's upper and lower parts.

$$F_{{\text{d}}} = \alpha z + k_{0} \left( {x - y} \right) + c_{0} \left( {\dot{x} - \dot{y}} \right) + k_{1} \left( {x - y} \right).$$
(16)

The total force can also be written as

$$F_{{\text{d}}} = c_{1} \dot{y} + k_{1} \left( {x - x_{0} } \right).$$
(17)

In this model, the adjustable parameters are denoted by the symbols γ, β, and A, the accumulator stiffness is denoted by the symbol k1, and the viscous damping that is seen at higher velocities is denoted by the symbol c0. k0 is present to control the stiffness at large velocities, and x0 is the initial displacement of spring k1 associated with the nominal damper force due to the accumulator. The model includes a dashpot, which is represented by c1, to produce the roll-off that was observed in the experimental data at low velocities.

ANFIS Controller

To enhance the fuzzy logic controller's capacity for learning, the ANFIS is applied in this research work. An artificial neural network known as ANFIS is a neural network that merges the functionalities of neural networks with fuzzy logic. The non-parametric ANFIS model is trained and considered. The ANFIS model is considered to be a "non-parametric model" due to the fact that it is trained using the input signals and output signals from the modified Bouc Wen model. Figure 3 presents a visual representation of the training process for the ANFIS model, which was derived from the MR damper model (also known as the modified Bouc–Wen model). According to the information shown in this Fig. 3, the force that was generated by the MR damper model is referred to as the target force (FMR), whereas the force that was generated by the forward ANFIS model is referred to as the forecast force fmr.

Fig. 3
figure 3

ANFIS controller training from the MR damper model

Full size image

The ANFIS model's internal architecture is shown in Fig. 3, which may be found here. The output of the ANFIS model is the expected force if the signals that are inputted into it are (V, V(k-1), \(\dot{x,}\) \(\dot{x}\left({\text{k}}-1\right)\), \(x\)), which are based on the signals that are inputted into the MR damper model. The following principles are used to determine the value of this force, and they are provided in Eq. (18).

$$\begin{gathered} {\text{Rule 1}}:{\text{ If}}\;x\;{\text{is}}\;\pi_{1} {\text{and}} \dot{x}\;{\text{is}}\;\pi_{2} ,\;{\text{then}}\;f_{1} = N_{1} x + W_{1} \dot{x} + r_{1} . \hfill \\ {\text{Rule 2}}:{\text{ If}}\;\dot{x}\;{\text{is}}\;\pi_{2} {\text{and}} \dot{x}\left( {k - 1} \right)\;{\text{is}}\;\pi_{3} ,\;{\text{then}}\;f_{2} = N_{2} \dot{x} + W_{2} \dot{x}\left( {{\text{k}} - 1} \right) + r_{2} . \hfill \\ {\text{Rule 3}}:\;{\text{If}}\;\dot{x}\left( {k - 1} \right){\text{ is }}\pi_{3} {\text{and}} V {\text{is}}\;\pi_{4} ,\;{\text{then}}\;f_{3} = N_{3} \dot{x}\left( {{\text{k}} - 1} \right) + W_{3} {\text{V}} + r_{3} . \hfill \\ {\text{Rule }}N:{\text{ If}}\;x_{n} \;{\text{is}}\;\pi_{n} {\text{and}} \dot{x}\;is\;\pi_{n} \;{\text{then}}\;f_{n} = N_{n} x + W_{n} \dot{x} + r_{n} . \hfill \\ \end{gathered}$$
(18)

V is the voltage input to the MR damper and ANFIS models; V (k-1) is the prior voltage input to the ANFIS model; \(\dot{x}\) is the relative velocity input to the MR damper and ANFIS models \(\dot{x}\left({\text{k}}-1\right)\) is the previous relative velocity input to the ANFIS model; \(x\) is the relative displacement input to the MR damper and ANFIS models; \({\pi }_{1}\dots \dots \dots \dots {\pi }_{n}\) and \({\pi }_{2}\dots \dots \dots \dots {\pi }_{n}\) are the ANFIS membership functions. Hence, when the MR damper produces the required ideal force (\(f={f}_{d}\)), the voltage provided to the MR damper should be maintained at a constant level. The voltage that is applied to the current driver is increased to its maximum level to increase the damper force to match the desired control force [19]. The semi-active strategies were studied in three modes semi-active-off (Sa-off), semi-active-on (Sa-on), and semi-active control (Sa-C). The damper is set to a low damping rate with a current of 0.25 A in Sa-off mode. When a specified vertical threshold velocity is reached, the damper is set to a high damping rate with a current of 1 A in Sa-on mode. In Sa-C mode, the damper continually controls the damping rate depending on real-time sensor inputs [20].

Training and Validation

In this paper, training and validation data sets of the proposed ANFIS are obtained by prescribing displacement and voltage signals to an MR damper. The output of \({F}_{{\text{MR}}}\) and \({f}_{{\text{mr}}}\) are compared for a displacement amplitude of X = 0.007 m and a voltage range of 0–1.5 V. The traces in Fig. 4 show good agreement between the non-parametric force estimates of \({F}_{{\text{MR}}}\) calculated using the ANFIS model and the parametric force estimate (\({F}_{{\text{MR}}}\)) calculated using the modified Bouc–Wen model. The checking data validation case is shown in Fig. 4 and it has been discovered that the accuracy of the checking data is comparable to the accuracy of the training data. Because the inverse model of the MR damper is used primarily for the purpose of controlling the damping force of the MR damper, this may fulfill the requirements for the inverse model of the MR damper.

Fig. 4
figure 4

The traces of \({F}_{{\text{MR}}}\) and \({f}_{{\text{mr}}}\) with uniform input voltages set

Full size image

Numerical–Experimental Validation

Validation of MR Damper

The validation of the proposed Magnetorheological (MR) damper is substantiated through a meticulous comparison between simulation outcomes and empirical data. The experimentation conducted by Hu et al. [14] focused on exploring the displacement characteristics of the damper at a frequency of 1 Hz and an amplitude of 5 mm. The investigation involved direct currents of 0.1 A and 0.4 A. The experimental setup, illustrated in Fig. 5, provided a comprehensive platform for scrutinizing the MR damper's performance.

Fig. 5
figure 5

Experimental setup of MR damper

Full size image

The comparative analysis of MR damper characteristics is graphically depicted in Fig. 6. Notably, and the damping force registers an approximate 180 N in the absence of applied current. This baseline damping force is attributed to the stiffness of the accumulator and the MR fluid within the damper, operating in accordance with the Newtonian fluid model. However, a significant augmentation in damping force is observed upon introducing an electrical current. Specifically, with a current of 0.4 A, the damping force substantially increases from 180 N to approximately 456 N. This amplification in force is concomitant with a power consumption of around 1.4 watts.

Fig. 6
figure 6

Experimental and Simulation comparison of MR damper characteristics at 0.4 A

Full size image

The results unequivocally demonstrate that the damping force is contingent upon the magnitude of the administered current, showcasing a dynamic response to input variations. The numerical analysis of the mathematical model aligns well with empirical findings, affirming the proposed MR damper's capability to generate a modifiable damping force while consuming a comparatively low amount of power. The correlation between simulation and experimentation establishes the damper's potential as a viable solution for applications requiring effective damping control.

Validation of Coupled Torsional–Transverse Vibrations Model

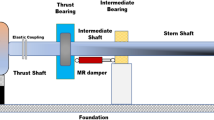
To evaluate the reliability of the proposed numerical model, experimental measurements were performed on the marine propeller shaft systems of a ship, following the methodology outlined in [10]. The experimental setup incorporated diverse instruments, including a laser torsional vibration transducer for capturing torsional measurements and a tri-axial accelerometer for transverse measurements. The schematic of the tested shaft system is shown in Fig. 7. Additional details regarding the experimental setup and procedures can be found in the work [10].

Fig. 7
figure 7

The schematic of the tested shaft system

Full size image

During the experiments, torque values and corresponding rotational speeds (ω) were recorded using stress sensors and signal acquisition. The rotational speeds ranged from 100 to 500 rpm in 100-rpm increments. Transient responses in Y-transverse and torsional directions were simultaneously captured and are shown in Table 1.

Table 1 Experimental and numerical simulation comparison of torsional–transverse vibration control in marine propulsion shaft systems at 100 rpm and 500 rpm
Full size table

The results show a good agreement between the numerical predictions and experimental measurements in both Y-transverse and torsional directions across different rotational speeds shown in Fig. 8. The observed trends in amplitude variations align well, validating the accuracy of the numerical model in capturing the coupled transverse–torsional vibrations of the propeller shaft system. This validation process provides confidence in the numerical model's reliability for predicting the system's dynamic behavior under various operating conditions.

Fig. 8
figure 8

Experimental and numerical simulation comparison of torsional–transverse vibration control in marine propulsion shaft systems at a 100 rpm and b 500 rpm

Full size image

Results and Discussion

In this investigation into the influence of rotational speed on the time domain response of a marine engine employing a semi-active system, the investigation into the influence of rotational speed on the time domain response of a marine engine utilizing a semi-active system reveals a dependence on specific design and control parameters. In semi-active systems, damping force is adaptively adjusted based on incoming vibrations through feedback control mechanisms. As the marine engine's rotational speed increases, the frequency and amplitude of engine-generated vibrations escalate, necessitating the semi-active system to respond for effective vibration control dynamically. Acceleration responses of torsional and transverse vibrations at the Center of Mass (CoM) of the engine at a rotational speed of 250 rpm are illustrated in Figs. 9 and 10. These responses suggest that the semi-active systems yield smaller acceleration amplitudes compared to the passive Magnetorheological (MR) strategies system.

Fig. 9
figure 9

Acceleration response of transverse vibration at a rotational speed of 250 rpm

Full size image
Fig. 10
figure 10

Acceleration response of torsional vibration at a rotational speed of 250 rpm

Full size image

To evaluate the system's performance, Root Mean Square (RMS) values of acceleration at the CoM of the engine's well and percentage reduction index (PRI) for both torsional and transverse vibrations are calculated across rotational speeds ranging from 150 to 650 RPM. A thorough analysis was conducted for transverse and torsional vibrations. The detailed results presented in Table 2 for transverse acceleration and Table 3 for torsional acceleration shed light on the system's performance at various rotational speeds, revealing a nuanced picture of its efficacy.

Table 2 Transverse acceleration and PRI at different strategies
Full size table
Table 3 Torsional RMS acceleration and PRI at different strategies
Full size table

The in-depth study shows that the semi-active system always provides lower acceleration amplitudes at all rotational speeds. Comparisons with the passive MR strategy demonstrate superior performance in damping acceleration effects. Notably, employing semi-active technology, especially incorporating MR dampers and an Adaptive Neuro-Fuzzy Inference System (ANFIS), substantially reduces both RMS values and PRI for torsional and transverse vibrations. As a result, the semi-active controlled system works better than other MR strategy systems, showing big gains in PRI for both transverse and torsional vibrations. The PRI enhancements range from 13.03% to 29.36% for Sa-C in transverse vibrations and from 9.65 to 21.01% for Sa-C in torsional vibrations.

As shown in the radar chart in Fig. 11b, d, at 150 rpm, the Sa-C strategy exhibited a transverse RMS acceleration of 0.164 m/s2, showcasing its ability to mitigate vibrations effectively. The corresponding 13.03% PRI emphasizes the substantial reduction achieved compared to the passive strategy (P). As the rotational speed increased to 250 rpm, the Sa-C strategy maintained its superiority, with an RMS acceleration of 1.281 m/s2 and a remarkable PRI of 17.12%. The PRI reached its highest point of 28.36% at 650 rpm, showing that this trend persisted at all rotational speeds. This shows that the Sa-C strategy worked very well and consistently. Similarly, the analysis of torsional vibrations in Table 3 revealed a parallel trend. At 150 rpm, Sa-C exhibited a torsional RMS acceleration of 0.154 rad/s2 and a PRI of 9.65%. The performance of Sa-C continued to shine as rotational speed increased, reaching an RMS acceleration of 2.748 rad/s2 with a 21.01% PRI at 650 rpm.

Fig. 11
figure 11

Comparison of different semi-active strategies with passive system a transverse rms Acceleration b PRI for Transverse Acceleration c Torsional rms Acceleration d PRI for Torsional Acceleration

Full size image

These findings indicate that the semi-active system, particularly the Sa-C strategy, consistently outperforms passive strategies across the entire spectrum of rotational speeds. The notable reductions in transverse and torsional vibrations underscore the efficacy of the semi-active system in maritime engineering applications. This detailed discussion provides valuable insights into the nuanced dynamics of the system's response to varying rotational speeds, offering a robust foundation for further exploration and practical application in marine engine vibration control.

Conclusion

This study represents a significant contribution to marine propulsion dynamics, aiming to unravel the complexities of coupled torsional and transverse vibrations in shaft systems while proposing an innovative solution for effective mitigation. The Main focus on incorporating Magnetorheological (MR) dampers controlled by an Adaptive Neuro-Fuzzy Inference System (ANFIS) has revealed promising avenues for enhancing adaptability and responsiveness in marine propulsion systems. The numerical model, built on a modified Jeffcott rotor model, has proven to be a sophisticated and accurate tool for forecasting the intricate dynamics of the shaft system. Validation through experimental investigations reinforces the reliability of the mathematical model predictions. Additionally, the mathematical model for the MR damper, subjected to sinusoidal displacement inputs at varying current levels, has been rigorously validated through comprehensive analyses of force–displacement profiles. These results underscore the efficacy of MR dampers in effectively mitigating coupled torsional and transverse vibrations.

The semi-active control system, comprising MR dampers and the ANFIS controller, has demonstrated superior performance compared to passive strategies. The reduction in torsional vibrations by a percentage reduction index of 21.01% and transverse vibrations by 28.36% underscores the potential of this innovative approach in dynamically controlling marine propulsion systems. The ANFIS controller's ability to dynamically adjust damping force has proven crucial in ensuring optimal performance. These findings underscore the potential application of the semi-active system, particularly the Sa-C strategy, in effectively minimizing vibrations in marine engines across a range of rotational speeds. Hence, this study enhances our understanding of the Complex dynamics of vibration control in marine propulsion systems and suggests practical and innovative solutions. With its superior performance and promising results, the semi-active control system opens new avenues for exploration and implementation in the maritime industry. The findings contribute to the ongoing efforts to address vibration-related challenges, emphasizing the potential resilience and optimization achievable through integrating advanced control systems in marine engineering applications.