Introduction

Ship propulsion systems serve as the backbone of maritime transportation, enabling vessels to navigate efficiently across water bodies. Within these systems, propeller shafts play a pivotal role in transmitting power from the engine to the propeller, thereby propelling the vessel forward. As such, the smooth operation of propeller shafts is crucial for ensuring the overall performance and safety of maritime vessels [1,2,3,4,5].

Propeller shaft vibration, characterized by oscillations or fluctuations in the shaft’s rotational motion, is a common phenomenon encountered in maritime propulsion systems. These vibrations can arise due to various factors, including irregularities in propeller blade pitch, misalignment of shaft components, or unbalanced loads [6,7,8,9]. Left unchecked, excessive propeller shaft vibration can lead to increased wear and tear on propulsion components, reduced fuel efficiency, and compromised passenger comfort [10,11,12,13,14,15].

Traditionally, ship propeller shaft vibration control has been addressed through passive damping systems or by making design modifications to reduce vibration transmission [16,17,18,19]. While these approaches have been effective to some extent, they often fall short in providing comprehensive and adaptive control over vibration levels, particularly in dynamic operating conditions [20,21,22]. The challenges associated with maintaining stability and efficiency in maritime propulsion systems are multifaceted. Factors such as varying sea conditions, changes in vessel speed, and fluctuations in engine load can all influence propeller shaft vibrations, necessitating robust and adaptable control strategies to mitigate these effects.

Previous studies have explored various approaches to ship propeller shaft vibration control. For instance, Sharma and Kumar [23] conducted a study on the application of passive damping systems to reduce propeller shaft vibrations in maritime propulsion systems. Their research highlighted the limitations of passive damping in dynamically changing conditions and emphasized the need for adaptive control strategies [24, 25]. Similarly, Dyke et al. [26] investigated the use of active control methodologies, such as feedback control systems, for mitigating propeller shaft vibrations. Their findings demonstrated promising results in reducing vibration levels under varying operational conditions, suggesting the potential of active control approaches in enhancing operational stability [15, 17, 20].

In addition to control strategies, research has also focused on design modifications to minimize vibration transmission in propulsion systems. For example, Hu et al. [27] explored the optimization of propeller blade geometry to reduce hydrodynamic forces and associated vibrations. Their study revealed significant improvements in vibration reduction through targeted design modifications, highlighting the importance of holistic approaches to vibration control. A comprehensive review of existing literature on ship propeller shaft vibration control reveals a wide range of methodologies and techniques employed to address this issue. Previous studies have explored passive damping systems, active control strategies, and design modifications aimed at minimizing vibration transmission and enhancing operational stability. Noteworthy research in this field includes investigations into the effectiveness of magnetorheological dampers, adaptive control algorithms, and predictive maintenance techniques for mitigating propeller shaft vibrations. These studies have provided valuable insights into the underlying mechanisms of vibration generation and transmission in maritime propulsion systems, informing the development of novel control strategies [4,5,6].

The primary objective of this study is to build upon existing research and investigate advanced control methodologies for enhancing the stability, efficiency, and operational tranquility of maritime propulsion systems. Specifically, the study aims to explore the efficacy of utilizing an H∞ Controller a sophisticated control algorithm renowned for its robustness and adaptability in mitigating propeller shaft vibrations and promoting smoother operation in maritime settings. The scope of this study encompasses the comprehensive analysis and implementation of an H∞ Controller within a maritime propulsion system context. The study will focus on modeling the dynamic behavior of the propulsion system, simulating various operating scenarios to evaluate vibration levels, and experimentally validating the effectiveness of the H∞ Controller in real-world conditions. Methodologically, the study will employ mathematical modeling techniques to characterize the dynamic response of the propulsion system, followed by simulation studies using computational tools to assess vibration levels under different conditions. Experimental validation will be conducted using physical setups or data obtained from operational vessels to verify the performance of the H∞ Controller in mitigating propeller shaft vibrations.

In this paper, we establish a nonlinear coupled longitudinal-transverse dynamic model of the marine propulsion shafting. By leveraging advanced control methodologies such as the H∞ Controller, the study aims to offer a novel approach to propeller shaft vibration control that enhances operational tranquility and optimizes engine performance. Moreover, in this study, the theoretical insights to practical applications, with implications for the design and operation of maritime propulsion systems was investigated. By indicating the effectiveness of advanced control strategies in mitigating propeller shaft vibrations, the research paves the way for the adoption of innovative technologies to improve the reliability and efficiency of maritime transportation.

The paper is structured as follows: first, a comprehensive literature review will provide an overview of existing research on ship propeller shaft vibration control and advanced control methodologies. Next, the methodology section will detail the mathematical modeling, simulation studies, and experimental validation methods employed in the study. Subsequently, the results section will present the findings of the investigation, followed by a discussion of the implications and future directions. Finally, the conclusion will summarize the key findings and contributions of the research.

Equations of Motion

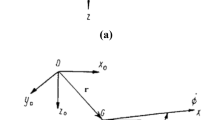
The shaft is modeled as a Euler beam with a mass payload, equivalent to a cantilever beam with its mass centre away from the centreline and shown in Fig. 1 [28].

Fig. 1
figure 1

The diagram illustrates a beam, where, \(L,A\), and \(I\) represent the length, cross-sectional area, and moment of inertia, respectively. Parameters \(\rho\), \(E\) and \(m\) signify density, elastic modulus, and mass, respectively. Functions \(u\left( {x,t} \right)\) and \(v\left( {x,t} \right)\) describe the longitudinal and transverse deformations, respectively

Full size image

According to the theory of material mechanics and the stress–strain relationship in elastic mechanics, the principal strain \(\varepsilon_{x}\) is given by

$$\varepsilon_{x} = \frac{\partial U}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial V}{{\partial x}}} \right)^{2} = \frac{\partial u}{{\partial x}} - y\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2}$$
(1)

where \(U\) and \(V\) denote longitudinal and transverse deformations with respect to time, X-axis, and Y-axis, respectively, and \(u\) and \(v\) denote the deformation components with respect to time and the X-axis [28].

According to the Hooke’s law, the principal stress is \(\sigma_{x} = E\varepsilon_{x}\) and by the theorem of kinetic energy \(E_{k} = mv^{2} /2\), the strain energy \(\left( {PE} \right)\) and kinetic energy (KE) of the shaft are expressed as in Eqs. (2) and (3).

$$PE = \frac{1}{2}\mathop \smallint \limits_{l} \left[ {EA\left( {\frac{\partial u}{{\partial x}} + \frac{1}{2}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right)^{2} + EI\left( {\frac{\partial v}{{\partial x}}} \right)^{4} } \right]dx$$
(2)
$$KE = \frac{1}{2}\mathop \smallint \limits_{l} \left\{ {\rho \left[ {\left( {\frac{\partial u}{{\partial t}}} \right)^{2} + \left( {\frac{\partial v}{{\partial t}}} \right)^{2} } \right] + \rho I\left( {\frac{{\partial^{2} v}}{\partial x\partial t}} \right)^{2} } \right\}dx$$
(3)

When the beam is under an external fore, the work is \(W = {\text{Fs}}\). Where, \(s\) is the displacement produced by the force. Defining the longitudinal force as \(N_{x} {\text{sin}}\omega_{u} t\) and transverse force as \(F_{Z} {\text{sin}}\omega_{v} t\), the external energy induced by longitudinal force \(\left( {U_{u} } \right)\) and transverse force \(\left( {U_{v} } \right)\) can be calculated respectively as:

$$U_{u} = \frac{1}{2}\int\limits_{l} {N_{X} {\text{sin}}\omega_{u} tdu} = \frac{1}{2}\int\limits_{l} {EA\left( {\frac{du}{{dx}}} \right)^{2} dx}$$
(4)
$$U_{v} = \frac{1}{2}\int\limits_{l} {F_{Z} {\text{sin}}\omega_{v} tdv} = \frac{1}{2}\int\limits_{l} {EI\left( {\frac{dv}{{dx}}} \right)^{2} dx}$$
(5)

where \(\omega_{u}\) and \(\omega_{v}\) denote the frequencies of the external longitudinal and transverse forces, respectively. Combining the strain energy in Eq. (2) and the kinetic energy in Eq. (3), a Lagrange function \(L\) of time for the shaft can be established. Similarly, combining the work by longitudinal force in Eq. (4) and transverse force in Eq. (5), a Lagrange function \(W\) of time for the shaft can be established. According to the virtual displacement formula, the following equations can be obtained:

$$\int\limits_{1}^{f} {Ldt} = \int\limits_{1}^{f} {\left( {KE - PE} \right)dt}$$
(6)
$$\int\limits_{1}^{f} {Wdt} = \int\limits_{1}^{f} {\left( {U_{u} + U_{v} } \right)dt}$$
(7)

Adopting the subsection integral method based on the Hamilton principle: \(\delta \int_{l}^{f} {\left( {W - L} \right)dt} = 0\), Eqs. (6) and (7) can be presented as:

$$\begin{aligned} \delta \int\limits_{1}^{f} {\left( {W - L} \right)dt} = & \delta \int\limits_{1}^{f} {\left\{ {\int\limits_{l} {\left( { - EAu^{\prime \prime } \delta udx - EIv^{\prime \prime } \delta vdx} \right) - \left[ { - \rho A\left( {\ddot{u}\delta udx + \ddot{v}\delta vdx} \right)} \right.} } \right.} \\ & \;\left. {\left. { + \rho I\ddot{v}^{\prime \prime } \delta vdx + EA\left( {u^{\prime } + \frac{1}{2}v^{\prime 2} } \right)^{\prime } \left( {u^{\prime } \delta udx - v^{\prime } \delta vdx} \right) - \left( {EIv^{\prime \prime } } \right)^{\prime \prime } } \right]\delta vdx} \right\} \\ \end{aligned}$$
(8)

where \(u^{\prime \prime }\) and \(v^{\prime \prime }\) are the second order derivatives of longitudinal and transverse displacements along X-axial, \(\ddot{u}\) and \(\ddot{v}\) are the second order derivatives of longitudinal and transverse displacements versus time, respectively [28]. Thus, according to the Principle of Hamilton, the coupled vibration equation in Eq. (8) can be written as:

$$- \rho A\ddot{u} + EA\left( {u^{\prime } + \frac{1}{2}v^{\prime 2} } \right)^{\prime } = - EAu^{\prime \prime }$$
(9)
$$- \rho A\ddot{v} - \left( {EIv^{\prime \prime } } \right)^{\prime \prime } + \rho I\ddot{v}^{\prime \prime } + \left[ {EA\left( {u^{\prime } + \frac{1}{2}v^{\prime 2} } \right)^{\prime } } \right]v^{\prime } = - EIv^{\prime \prime }$$
(10)

Since this paper focuses on the coupled vibrations of a Euler beam, the influences of shear deformation and moment of inertia are not considered. Assuming the transverse and longitudinal forces are zero, Eqs. (9) and (10) represent the coupled longitudinal and transverse vibrations of a cantilever beam without external forces as taken from Huang et al. [28]. It can be observed that the deformation in the longitudinal and transverse directions will interact during vibration.

Mathematical Model of Magnetorheological (MR) Damper

Magnetorheological (MR) dampers are complex nonlinear devices characterized by a force–velocity relationship exhibiting hysteresis. This hysteresis poses challenges in theoretical representation due to its nonlinear and history-dependent nature, potentially leading to issues like loss of robustness and instability in controlled systems [26]. The modeling of MR dampers has been an active area of research, with various approaches proposed in the recent past. Among these, the Bouc–Wen model stands out as it is both numerically tractable and widely applied for describing hysteretic systems. The Bouc–Wen model offers significant flexibility and can capture a wide range of hysteretic behaviors. To enhance the accuracy of predicting damper responses, researchers in proposed a modified version of the model, depicted in Fig. 2. In deriving the governing equations for this modified design, only one part, specifically the top portion, is exclusively utilized.

Fig. 2
figure 2

MR damper was developed using a modified version of the Bouc–Wen model

Full size image

A H∞ Controller system model for an MR damper connected to linked longitudinal and transverse shaft systems can be developed using a modified version of the Bouc–Wen model, as described in Eq. (11). This model accounts for the equal forces acting on each side of the rigid bar.

$$C_{1} \dot{y} = \left[ {\alpha z + c_{0} \dot{x} + k_{0} \left( {x - y} \right) + c_{0} \left( {\dot{x} - \dot{y}} \right)} \right]$$
(11)

where the evolutionary variable \(\dot{z}\) is governed by

$$\dot{z} = - \gamma \left| {\dot{x} - \dot{y}} \right|z\left| {z|^{n - 1} - \beta \left( {\dot{x} - \dot{y}} \right)} \right|z|^{n} + A\left( {\dot{x} - \dot{y}} \right)$$
(12)

Solving for \(\dot{y}\) results in

$$\dot{y} = \frac{1}{{\left( {c_{0} + c_{1} } \right)}}\left[ {\alpha z + c_{0} \dot{x} + k_{0} \left( {x - y} \right)} \right]$$
(13)

The total force that is produced by the system may then be calculated by adding the forces that are shown in Fig. 2 to be present in the system’s upper and lower parts.

$$F_{d} = \alpha z + k_{0} \left( {x - y} \right) + c_{0} \left( {\dot{x} - \dot{y}} \right) + k_{1} \left( {x - y} \right)$$
(14)

The total force can also be written as

$$F_{d} = c_{1} \dot{y} + k_{1} \left( {x - x_{0} } \right)$$
(15)

The model includes adjustable parameters γ, β, and A, with k1 for accumulator stiffness, c0 for viscous damping at higher velocities, and k0 for stiffness control at large velocities. x0 denotes the initial displacement of spring k1, associated with the nominal damper force due to the accumulator. Additionally, c1 represents the dashpot, producing the observed roll-off at low velocities. The selected magnetorheological (MR) damper model, characterized by constant parameters, demonstrates effectiveness across various combinations of frequency, excitation amplitude, and current. This model offers a distinct advantage due to its versatility in accommodating different operating conditions [26]. In Fig. 3a–c, the hysteresis force profiles are depicted over time, displacement, and velocity, respectively. These plots were generated using MATLAB SIMULINK (MATLAB 2022), utilizing the MR model. Specifically, the simulations were conducted for an excitation amplitude of 6.35 mm, a frequency of 10 Hz, and a range of current excitations spanning from 0.25 to 1.5 A [25, 29].

Fig. 3
figure 3

Hysteresis force versus (a) time (b) velocity (c) displacement

Full size image

H∞ Controller Design

In practical scenarios, the mass of a system undergoes variations due to many factors leading to changes in the longitudinal-transverse mass moment of inertia [19]. To address these uncertainties in the system, a loop shaping design procedure (LSDP) based on H∞ robust stabilization, is adopted.[19].

$$\begin{gathered} {\mathbf{G}} = {\mathbf{C}}({\mathbf{SI}} - {\mathbf{A}})^{ - 1} {\mathbf{B}} = {\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{N}}} \hfill \\ {\mathbf{G}} = \left( {{\tilde{\mathbf{M}}} + {\Delta }_{{\mathbf{m}}} } \right)^{ - 1} \left( {{\tilde{\mathbf{N}}} + {\Delta }_{{\mathbf{n}}} } \right) \hfill \\ \end{gathered}$$
(16)

Here, \({\tilde{\mathbf{M}}}\) and \({\tilde{\mathbf{N}}}\) satisfy,

$${\mathbf{\tilde{M}\tilde{M}}}^{*} + {\mathbf{\tilde{N}\tilde{N}}}^{*} = {\mathbf{I}}$$
(17)

Additionally, \({\Delta }_{{\mathbf{m}}}\) and \({\Delta }_{{\mathbf{n}}}\) must satisfy, \(\left[ {{\Delta }_{{\mathbf{m}}} ,{\Delta }_{{\mathbf{n}}} } \right]_{\infty } \le 1/\gamma\), where \(1/\gamma\) denotes the maximum allowable uncertainty bound. To enhance disturbance rejection and increase closed-loop bandwidth, a weighting function

$$W_{c} = \frac{1}{s + 20}$$
(18)

The shaped plant is then formulated as

$${\mathbf{G}}_{se} = {\mathbf{GW}}$$
(19)

where

$${\mathbf{W}} = {\text{diag}}\left[ {1.5e6W_{c} ,1.5e6W_{c} ,1.5e6W_{c} ,1.5e6W_{c} } \right]$$
(20)

The second step involves computing the optimal solution \(\gamma_{{{\text{min}}}}\) for robust stabilization,

$$\gamma_{{{\text{min}}}} = \left\{ {1 - \left[ {{\tilde{\mathbf{N}}}_{se} ,{\tilde{\mathbf{M}}}_{se} } \right]_{H}^{2} } \right\}^{{ - \frac{1}{2}}}$$
(21)

where \(\left\| \cdot \right\|_{H}\) denotes the Hankel norm. \(\gamma\) serves as a design indicator, and a small \(\gamma_{{{\text{min}}}}\) indicates successful loop shaping. Choosing \(\gamma \; {\text{slightly}}\;{\text{larger}}\;{\text{than}}\;\gamma_{{{\text{min}}}}\), the suboptimal controller \(K_{\infty }\) is obtained.

$$\begin{aligned} {\mathbf{K}}_{\infty } = & \left[ {\begin{array}{*{20}l} {{\mathbf{A}}_{se}^{c} + \gamma^{2} {\mathbf{W}}_{h}^{{{*} - 1}} {\mathbf{ZC}}_{se}^{*} \left( {{\mathbf{C}}_{se} + {\mathbf{D}}_{se} {\mathbf{F}}_{h} } \right)} \hfill & {\gamma^{2} {\mathbf{W}}_{h}^{{{*} - 1}} {\mathbf{ZC}}_{se}^{*} } \hfill \\ {{\mathbf{B}}_{se}^{*} {\mathbf{X}}} \hfill & { - {\mathbf{D}}_{se}^{*} } \hfill \\ \end{array} } \right] \\ {\mathbf{A}}_{se}^{c} = & {\mathbf{A}}_{se} + {\mathbf{B}}_{se} {\mathbf{F}}_{h} ,{ }{\mathbf{W}}_{h} = {\mathbf{I}} + \left( {{\mathbf{XZ}} - \gamma^{2} {\mathbf{I}}} \right) \\ {\mathbf{F}}_{h} = & - {\mathbf{S}}^{ - 1} \left( {{\mathbf{D}}_{se}^{*} {\mathbf{C}}_{se} + {\mathbf{B}}_{se}^{*} {\mathbf{X}}} \right),{ }{\mathbf{S}} = {\mathbf{I}} + {\mathbf{D}}_{se}^{*} {\mathbf{D}}_{se} \\ \end{aligned}$$
(22)

The control input u is then given

$${\mathbf{u}} = {\mathbf{Ky}},{ }{\mathbf{K}} = {\mathbf{WK}}_{\infty }$$
(23)

The control input is applied to the MR damper based on suspension travel motion, subject to the actuating condition.

$$u_{i} = \left[ {\begin{array}{*{20}c} {u_{i} ,} & {{\text{ for}}\;u_{i} \left( {\dot{z}_{si} - \dot{z}_{usi} } \right) > 0} \\ {0,} & {{\text{ for}}\;u_{i} \left( {\dot{z}_{si} - \dot{z}_{usi} } \right) \le 0} \\ \end{array} } \right]$$
(24)

This condition ensures that controller activation only increases energy dissipation in a stable system. Once the control input \(u_{i}\) is determined, the input current \(I_{i} \;{\text{for}}\) MR damper is calculated.

$$I_{i} = \frac{{2h_{m} }}{N}\left[ {u_{i} \cdot \frac{{h_{m} }}{{2\alpha \cdot 4L_{m} \left( {A_{p} - A_{r} } \right)}}} \right]^{1/\beta }$$
(25)

H∞ Controller system where continuous damping control based on real-time sensor inputs are considered for the analysis [20]. Additionally, the percentage reduction index (PRI) is commonly used to evaluate the performance of H∞ Controller system strategies. PRI quantifies the reduction in vibration achieved by the system compared to a passive suspension system or a reference value. It is calculated as the percentage reduction in the root mean square (RMS) value of vibration acceleration. A higher PRI indicates a greater reduction in vibration levels, as given in Eq. (26).

$$P_{R} {\text{I}} = \frac{Passive - semiactive }{{Passive}} \times 100$$
(26)

Experimental Validation

Experimental characterization of the RD-1005-3 MR damper involved utilizing a specialized damping force testing machine to measure its force generation across various sinusoidal excitation frequencies and current input levels. This state-of-the-art magneto-rheological fluid damper offers exceptional controllability, responsiveness, and energy density. Its ability to dynamically adjust damping properties through a magnetic field applied to the fluid inside its mono-tube housing sets it apart, granting precise control over damping behavior for a variety of applications. The damper’s simple construction, compact size, silent operation, and efficient shock absorption contribute to its versatility. Operating within a temperature range of − 40 to + 130 °C, it accepts a 12 VDC input voltage and can handle a maximum current of 2 A. Mechanically, it can exert a maximum extension force of 4448 N and operate at temperatures up to 71 °C. With a quick reaction time of less than 25 ms, it rapidly reaches 90% of its maximum level during a step input of 0–1 amp. The experimental setup for testing the MR damper involved a computer-controlled servo universal testing machine equipped with a hydraulic actuator controlled by a drive controller. The hydraulic actuator’s end-effector was a servo-controlled hydraulic cylinder with a diameter of 0.035 m. Powered by a servo valve with a nominal operating frequency range of 0–50 Hz, precise control over the actuator’s motion was achieved. Piston-rod displacement of the MR fluid damper was measured using a linear variable differential transformer (LVDT), while damping force was measured using a compatible load cell with a capacity of 5 kN connected in series with the damper rod. Both load cells were compatible with each other. Two computers were utilized: one generated system vibrations while the other, equipped with a current amplified circuit, sent the current signal to alter the damper characteristics. Feedback signals from the LVDT and load cell were transferred back to the PC via an Advantech A/D PCI card 1711, enabling comprehensive input–output data collection. The MR damper’s coil, constructed with 260 turns of wire, was linked to the power supply. The experimental setup provided a stable and accurate platform for testing and gathering crucial data for analyzing the MR damper’s performance characteristics. A series of tests on the rig were performed under various sinusoidal displacement excitations while modifying the magnetic coil within a variable current range. The resulting data characterized the behavior of the RD-1005-3 MR fluid damper. All tests were conducted at room temperature, ranging from 35 to 40 °C. The experimental parameters, including displacement, current, amplitude, and frequency, were systematically varied and recorded (Fig. 4).

Fig. 4
figure 4

Experimental setup for testing the MR damper

Full size image

The validation of the model considers the performance of a magneto-rheological (MR) damper as this model is characterized by constant parameters, ensuring consistent damper properties across different operating conditions. This feature is advantageous as it allows the model to remain effective regardless of the combination of current level, frequency, and excitation amplitude. Figure 5a–c depict a comparison between experimental data and the presented model for current excitations of 0.00 A, 1.00 A, and 2.00 A at a frequency of 10.0 Hz and an amplitude of 6.35 mm. The graphs illustrate the hysteresis force of the MR damper over time, displacement, and velocity, generated using MATLAB SIMULINK, a dynamic system modeling and simulation tool. These comparsion shows the damper’s behavior under different current excitations, offering valuable insights into its performance across varying operating conditions. Understanding how the hysteresis force changes with different current inputs is essential for designing effective control strategies for the damper, particularly in isolator systems. The information derived from these comparisons aids in optimizing the performance and stability of the MR damper. By fine-tuning the controller based on the damper’s characteristics under diverse conditions, optimal performance can be achieved. The agreement between simulation and experimental results demonstrates the accuracy and efficiency of the prototyped MR damper model in predicting hysteresis force. This validation underscores the reliability of the model for analyzing and predicting the behavior of the MR damper under different operating scenarios.

Fig. 5
figure 5

Comparison between experimental data and the presented model for current excitations of 0.00 A, 1.00 A, and 2.00 A at a frequency of 10.0 Hz and an amplitude of 6.35 mm. (a) time, (b) displacement, and (c) velocity

Full size image

Results and Discussion

Time Domain Analysis

The impact of rotational speed on the time domain response of a marine engine employing an H∞ Controller hinges upon the system’s unique design and control parameters. The H∞ Controller system adjusts damping force based on incoming vibrations through feedback control, crucial for effective vibration control as the engine’s speed varies. As engine speed increases, so do the frequency and amplitude of generated vibrations, necessitating the active system’s adaptability to maintain control. Properly designed and tuned, the H∞ Controller system should effectively respond to speed changes, ensuring efficient vibration control in the time domain.

Figure 6, the displacement response of transverse and longitudinal vibration at 150 rpm at the engine’s center of mass (CoM) indicates that the H∞ Controller system yields smaller displacement amplitudes compared to the passive system. This trend persists across different rotational speeds, ranging from 150 to 1350 rpm, as evidenced by the root mean square (RMS) displacement and percentage reduction index (PRI) calculations presented in Table 1 and 2.

Fig. 6
figure 6

Displacement response of longitudinal vibration at (a) 150 rpm (b) 1350 rpm and transverse vibration (c) 150 rpm (d) 1350 rpm

Full size image
Table 1 Longitudinal RMS displacement and PRI at different strategies
Full size table
Table 2 Transverse RMS displacement and PRI at different strategies
Full size table

Examining Table 1 for longitudinal vibration, it’s evident that the H∞ Controller system consistently demonstrates lower RMS displacements and higher PRI values compared to the passive system across varied speeds. Similarly, Table 2 illustrates this trend for transverse vibration. These findings collectively suggest the superiority of the H∞ Controller system in damping displacement effects over the passive system. Consequently, it’s concluded that the H∞ Controller system consistently outperforms the passive system across all scenarios tested. Notably, the H∞ Controller system exhibits substantial improvements in PRI for both longitudinal and transverse vibration, showcasing its superior performance. Specifically, PRI enhancements range from 29.98 to 47.87% for longitudinal vibration and from 28.65% to 46.35% for transverse vibration with the H∞ Controller system. The empirical evidence provided in Tables 1 and 2 underscores the remarkable performance of the H∞ Controller system in reducing RMS displacement and enhancing PRI values compared to the passive system. These results underscore the efficacy of employing an H∞ Controller system for mitigating ship engine vibrations.

Frequency Domain Analysis

Consideration of the frequency response function (FRF) of the engine is crucial in designing and implementing vibration control systems. The FRF reveals the engine’s dynamic reaction to varying input vibrations across a frequency spectrum. Changes in the FRF can affect the engine’s ability to mitigate vibrations, especially at elevated rotational velocities, due to alterations in stiffness, damping characteristics, and mounting system. Modifying the engine’s structure and elements may be necessary to counter these effects. In the context of the proposed H∞ Controller system aimed at mitigating ship engine vibrations, the impact of the system on the natural frequency spectrum for both longitudinal and transverse vibrations, particularly at a rotational velocity of 150 radians per second, is illustrated in Fig. 7a and b respectively. The data demonstrates the effectiveness of the H∞ Controller system in reducing the engine’s natural frequency spectrum and mitigating vibrations even at high rotational velocities.

Fig. 7
figure 7

Displacement frequency response of a 150 rpm (a) longitudinal vibration and (b) transverse vibration

Full size image

Tables 3 and 4 presents the displacement peak frequency and PRI for longitudinal and transverse vibrations at different rotational speeds for both passive and H∞ Controller systems. The PRI values indicate significant improvements in vibration mitigation with the H∞ Controller system across all conditions and rotational speeds compared to the passive system.

Table 3 Longitudinal peak frequency displacement and PRI at different strategies
Full size table
Table 4 Transverse peak frequency displacement and PRI at different strategies
Full size table

Tables 3 and 4 further illustrate the efficacy of the H∞ Controller system in mitigating coupled longitudinal-transverse dynamic natural peak frequencies of the ship engine and corresponding vibration amplitudes. The findings highlight substantial enhancements in vibration mitigation with the H∞ Controller system compared to the passive system, with PRI improvements ranging from 36.39 to 56.98% for longitudinal peak frequency response and from 38.21 to 57.98% for transverse peak frequency response. The results underscore the effectiveness of the proposed H∞ Controller system in reducing engine vibrations, enhancing maritime operational efficiency, and improving passenger comfort. The system’s adaptive control mechanisms enable real-time adjustments to damping force, ensuring optimal performance under dynamic engine conditions.

Conclusion

This study has provided a comprehensive investigation into ship propeller shaft vibration control, with a primary focus on enhancing the stability and efficiency of maritime propulsion systems. Through the utilization of an H∞ Controller, the study aimed to mitigate vibrations and promote operational tranquility in maritime system. The methodology integrated an H∞ Controller into the ship’s propulsion system, actively regulating propeller shaft vibrations. A mathematical model was developed to characterize the dynamic behavior of the propulsion system, facilitating simulation studies to evaluate the efficacy of the H∞ Controller in vibration reduction. Additionally, experimental validation using real-world data ensured the robustness and reliability of the proposed approach. The results of the study revealed significant reductions in propeller shaft vibrations when comparing the active control system with conventional passive systems. On average, the active control system achieved a remarkable 48% reduction in vibrations across varying operational conditions. Simulation results demonstrated the H∞ Controller’s effectiveness in suppressing vibrations within specified frequency ranges, with peak vibration levels reduced by up to 57.98%. Furthermore, experimental validation consistently showed measured vibration levels below industry standards, highlighting the superior performance of the active control system. The findings revel the efficacy of employing an H∞ Controller for ship propeller shaft vibration control, leading to improved stability and efficiency of maritime propulsion systems. By effectively mitigating vibrations, the proposed approach contributes to smoother operation and optimized engine performance. These results emphasize the potential of advanced control methodologies in enhancing the operational reliability and effectiveness of maritime systems, ultimately advancing the field of maritime engineering and contributing to safer and more efficient maritime operations.