Introduction

Severe vibration is one of the main challenges for suspension systems since serious vibration may cause terrible health and safety issues [1]. Seat suspension is widely used to isolate uneven road vibration and provide good ride comfort to drivers, passengers, and cargo [2]. The seat suspension system can be categorized into passive, semi-active, and active seat suspension [3]. Traditional passive seat suspensions have been adopted in many kinds of vehicles and have been studied widely for their simple structure and low cost. However, passive seat suspensions cannot provide good vibration isolation performance at all frequencies considered because of their fixed stiffness and damping parameters [4, 5].

To improve vibration suppression performance further, intelligent suspensions, including active and semi-active suspensions, have been applied to seat suspensions. Some intelligent materials are used in the design of semi-active suspensions due to their fast response speed, good controllability, and large force output range. The most common semi-active magnetorheological (MR) suspensions have been used in seats and achieved good performance [6,7,8]. However, the cost of intelligent materials is still high and obstructs their actual application.

Compared with semi-active seat suspensions, active seat suspensions usually have better comprehensive performance because active suspensions can provide ideal controllable force. There are two research hotspots of active seat suspensions: actuator design and control algorithms. Reputable control algorithms, such as robust control [9], neural network control [10], PID control [11], fuzzy control [12,13,14], sliding mode control [15, 16] and event-triggered control [17,18,19], have been adopted in seat suspensions in recent years. Although active seat suspensions have better performance than semi-active seat suspensions, the energy consumption and cost of active suspensions are high.

Electromagnetic seat suspension, which can transform electrical energy into mechanical energy to attenuate vibration and provide an ideal active control force, is a typical active suspension. Additionally, electromagnetic suspensions also can work as a generator to transform vibration energy into electrical energy. The energy can be consumed by electrical components, which can achieve vibration isolation. Additionally, the energy also can be harvested by storage components, such as batteries and supercapacitors. Therefore, semi-active electromagnetic suspensions have drawn increasing attention [14, 20,21,22]. Semi-active electromagnetic seat suspensions can achieve vibration suppression performance by varying damping [23], stiffness [24], and inertance [25] ways. In addition, some novel seat suspensions, which combine variable damping, variable stiffness, and variable inertance characteristics, achieve better vibration isolation performance than traditional dampers [14, 26, 27].

The energy dissipated by vehicle suspensions is very considerable, which accounts for about 3–12% of the total vehicle fuel consumption [20]. Therefore, it is necessary to study the energy recovery capacity of electromagnetic suspensions. The energy-harvesting characteristic of electromagnetic suspensions has been researched by many scholars and engineers, but few studies combine energy saving and vibration control. To cut this edge, a novel H-bridge-based electromagnetic damper (EMD) is designed [28]. To maximize the energy harvesting efficiency, an energy harvesting model and an optimal circuit structure are proposed for an electromagnetic inertial mass damper (EIMD) [22].

A continuously controllable EMD system is proposed, and the vibration control capacity is validated [23]. The damping of the EMD system can be controlled by changing the pulse-width modulation (PWM) duty cycle exerted on the MOSFET. Based on the EMD system, another variable damping strategy is developed by controlling the circuit resistance of the EMD system [3]. The EMD system has excellent vibration isolation performance, and the energy consumption of the EMD system can be neglected, which shows good application potential.

Although the above research has proved the vibration control performance of the EMD system, the robust controller [23] and sliding controller [3] are designed based on the assumption that absolute signals in the suspension system can be measured. Nevertheless, absolute signals cannot be measured easily because of the uneven road. In addition, the suspension system's disturbance has a serious effect on vibration control, so it is necessary to compensate for the disturbance of the seat suspension system [29].

To overcome the above issues, this paper proposes a robust controller based on state estimation and disturbance compensation and adopts the EMD seat suspension system with outstanding vibration isolation performance and energy-saving potential. The main contributions of this paper are highlighted below:

  1. (a)

    Disturbance force of the EMD seat suspension system is compensated. A simple bench test is established to measure disturbance force–displacement data of the seat suspension. The Bouc–Wen model has been selected to represent the disturbance force.

  2. (b)

    A robust \({H}_{\infty }\) controller based on state observer and disturbance compensation is proposed. Since some state variables cannot be measured easily, a state observer is designed to estimate state variables that cannot be measured easily.

  3. (c)

    Experimental studies of the robust controller based on disturbance compensation and state estimation are conducted on a six-DOF motion platform.

This paper is organized as follows: the next section introduces the seat suspension model, EMD model, and the system's disturbance model; the following section designs the robust controller based on disturbance compensation and state observer; the next section discusses the experimental platform and the experimental results; Conclusions are discussed in the last section.

Modelling of Seat Suspension System Equipped with the EMD System

The Variable Damping Seat Suspension Model

The vertical vibration influences the ride comfort most and generally has the highest magnitude in the seat suspension. Thus, considering the system cost and effectiveness, most researchers study the vertical motion of the seat suspension without considering other directions' motions.

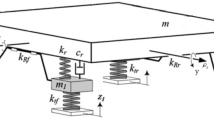
Figure 1a shows the schematic diagram of a seat with the EMD suspension system. The seat system consists of a spring, a seat with a scissor structure, and an EMD system. To simplify the controller design process, some simplified suspension models are adopted in previous studies [13, 16]. Seat suspension model supplemented with a human body model has been studied in previous studies, such as the four-DOF human body model [16]. However, most researches adopted a single DOF human model during the design process of controllers to simplify the problem [16]. A two-DOF suspension model is employed in this research and can be seen in Fig. 1b, where \({z}_{b}, {z}_{s}\) and \({z}_{v}\) are absolute displacements of driver body, suspension upper platform and vehicle cabin floor; \({m}_{\text{b}}\) and \({m}_{\text{s}}\) are the equivalent masses of the human body and seat suspension; \({k}_{\text{b}}\) and \({k}_{\text{s}}\) are the equivalent stiffness of human body and seat suspension; \({c}_{\text{b}}\) and \({c}_{\text{s}}\) are the equivalent damping coefficient of human body and seat suspension; \({f}_{\text{r}}\) and \(u\) are equivalent disturbance force and output force of the EMD system, respectively.

Fig. 1
figure 1

Seat suspension system a schematic diagram of a seat with suspension; b seat suspension mathematical model

Full size image

The mathematical model of the seat suspension system equipped with the EMD system can be described as:

$${m}_{\mathrm{b}}\ddot{{z}_{\mathrm{b}}}=-{k}_{\mathrm{b}}\left({z}_{\mathrm{b}}-{z}_{\mathrm{s}}\right)-{c}_{\mathrm{b}}(\dot{{z}_{\mathrm{b}}}-\dot{{z}_{\mathrm{s}}})$$
(1)
$${m}_{\mathrm{s}}\ddot{{z}_{\mathrm{s}}}={k}_{\mathrm{b}}\left({z}_{\mathrm{b}}-{z}_{\mathrm{s}}\right)+{c}_{\mathrm{b}}\left(\dot{{z}_{\mathrm{b}}}-\dot{{z}_{\mathrm{s}}}\right)-{k}_{\mathrm{s}}\left({z}_{\mathrm{s}}-{z}_{\mathrm{v}}\right)-{c}_{\mathrm{s}}\left(\dot{{z}_{\mathrm{s}}}-\dot{{z}_{\mathrm{v}}}\right)-{f}_{\mathrm{r}}+u$$
(2)

The system state variables are selected as \({x}_{1}={z}_{s}-{z}_{v}, { x}_{2}=\dot{{z}_{s}}, { x}_{3}={z}_{b}-{z}_{s}, { x}_{4}=\dot{{z}_{b}}\). Then, the system state-space equation can be obtained based on Eqs. (1) and (2),

$$\dot{{\varvec{x}}}={\varvec{A}}{\varvec{x}}+{{\varvec{B}}}_{1}w+{{\varvec{B}}}_{2}(u-{f}_{\text{r}})$$
(3)

where \(\dot{{\varvec{x}}}={\left[\begin{array}{cccc}{x}_{1}& {x}_{2}& {x}_{3}& {x}_{4}\end{array}\right]}^{\mathrm{T}}\), \(w=\dot{{z}_{\mathrm{v}}}\), \({\varvec{A}}=\left[\begin{array}{cccc}0& 1& 0& 0\\ -\frac{{k}_{\mathrm{s}}}{{m}_{\mathrm{s}}}& -\frac{{c}_{\mathrm{b}}+{c}_{\mathrm{s}}}{{m}_{\mathrm{s}}}& \frac{{k}_{\mathrm{b}}}{{m}_{\mathrm{s}}}& \frac{{c}_{\mathrm{b}}}{{m}_{\mathrm{s}}}\\ 0& -1& 0& 1\\ 0& \frac{{c}_{\mathrm{b}}}{{m}_{\mathrm{b}}}& -\frac{{k}_{\mathrm{b}}}{{m}_{\mathrm{b}}}& -\frac{{c}_{\mathrm{b}}}{{m}_{\mathrm{b}}}\end{array}\right]\), \({{\varvec{B}}}_{1}=\left[\begin{array}{c}-1\\ \frac{{c}_{\mathrm{s}}}{{m}_{\mathrm{s}}}\\ 0\\ 0\end{array}\right]\), \({{\varvec{B}}}_{2}=\left[\begin{array}{c}0\\ \frac{1}{{m}_{\mathrm{s}}}\\ 0\\ 0\end{array}\right]\).

In the practical situation, the vertical human body acceleration \(\ddot{{z}_{b}}\), seat suspension upper platform acceleration \(\ddot{{z}_{s}}\) and suspension relative displacement \({z}_{s}-{z}_{v}\) can be measured easily. Therefore, the control output can be written as,

$${\varvec{Y}}={[\ddot{{z}_{b}} \ddot{{z}_{s}} {z}_{s}-{z}_{v}]}^{\mathrm{T}}={{\varvec{C}}}_{1}{\varvec{x}}+{{\varvec{D}}}_{1}w+{{\varvec{D}}}_{2}(u-{f}_{r})$$
(4)

where \({{\varvec{C}}}_{1}=\left[\begin{array}{cccc}0& \frac{{c}_{b}}{{m}_{b}}& -\frac{{k}_{b}}{{m}_{b}}& -\frac{{c}_{b}}{{m}_{b}}\\ -\frac{{k}_{s}}{{m}_{s}}& -\frac{{c}_{b}+{c}_{s}}{{m}_{s}}& \frac{{k}_{b}}{{m}_{s}}& \frac{{c}_{b}}{{m}_{s}}\\ 1& 0& 0& 0\end{array}\right],\) \({{\varvec{D}}}_{1}=\left[\begin{array}{c}0\\ \frac{{C}_{S}}{{m}_{s}}\\ 0\end{array}\right],\) \({{\varvec{D}}}_{2}=\left[\begin{array}{c}0\\ \frac{1}{{m}_{s}}\\ 0\end{array}\right]\).

The main research objective of the seat suspension controller is to improve ride comfort, and the human body acceleration is regarded as a ride comfort index. In addition, many operation devices, such as the accelerator pedal, brake pedal, and transmission lever, are fixed on the cabin floor. Therefore, an excessive seat suspension deflection may cause handling problems. Additionally, the seat suspension with a large deflection may hit the stop block, which will deteriorate the ride comfort. Therefore, seat suspension acceleration \(\ddot{{z}_{b}}\) and seat suspension deflection \({z}_{\text{s}}-{z}_{v}\) are defined as two main performance criteria. Thus, the controllable output is defined as \({\varvec{Z}}={[\ddot{{z}_{s}} {z}_{s}-{z}_{v}]}^{\mathrm{T}}\) and can be obtained as,

$${\varvec{Z}}={[\ddot{{z}_{b}} {z}_{s}-{z}_{v}]}^{T}={\varvec{\delta}}{\varvec{C}}{\varvec{x}}$$
(5)

where \({\varvec{\delta}}=\left[\begin{array}{cc}{\delta }_{1}& 0\\ 0& {\delta }_{2}\end{array}\right]\), \({\varvec{C}}=\left[\begin{array}{cccc}0& \frac{{c}_{b}}{{m}_{b}}& -\frac{{k}_{b}}{{m}_{b}}& -\frac{{c}_{b}}{{m}_{b}}\\ 1& 0& 0& 0\end{array}\right]\); \({\varvec{\delta}}\) is the weighting matrix, which determines seat suspension ride comfort and handling stability performance. \({\delta }_{1}\) and \({\delta }_{2}\) are the weighting parameters, which are identified by trial and error. A larger \({\delta }_{1}\) usually was selected compared with \({\delta }_{2}\) because ride comfort is the primary control objective of the designed controller.

Modelling of the EMD System

The prototype and equivalent circuit frame diagram of the EMD system can be seen in Figs. 2 and 3. As can be seen from Fig. 2 the EMD system consists of a permanent magnet synchronous motor (PMSM), a three-phase rectifier, an external resistor, and an N-channel metal–oxide–semiconductor field-effect transistor (MOSFET). Figure 3 shows the circuit diagram in detail, where \(e, L_{i} , R_{i}\) are the generated voltage, inner inductance, and inner resistance of the EMD system, respectively; \(R_{{\text{e}}}\) is the external resistance of the EMD system. The MOSFET is connected with \(R_{{\text{e}}}\) in parallel. The functionality of the circuit is to provide controllable varying damping force by changing the equivalent circuit current. The controller sends PWM duty cycle signals to the MOSFET, and the equivalent resistance of the whole circuit can be changed with the change of the PWM signals. Therefore, the equivalent circuit current is changed according to the change of circuit equivalent resistance.

Fig. 2
figure 2

EMD seat suspension prototype

Full size image
Fig. 3
figure 3

Control circuit diagram

Full size image

When the seat suspension moves, the PMSM will generate a voltage, which is proportional to the circuit current [30, 31]. The PMSM will generate an output torque proportional to the circuit current. The output torque will be converted into vertical force through the scissors structure of the seat suspension. Therefore, the damping force can be controlled by controlling circuit current, which can be realized by changing circuit equivalent resistance. Therefore, the equivalent circuit resistance of the EMD system can be controlled by exerting different PWM duty cycles of the MOSFET switch.

The EMD system is installed on a seat suspension, and its structures can be seen in Fig. 4. The reducer shell is fixed on the outer rod of the scissors structure, while the rotating shaft of the reducer is fixed on the inner rod of the scissors structure. When the vehicle moves vertically, the sliders of the seat suspension slide in the guide rail, and the two rods of the scissors structure drive the shell and the shaft of the motor to rotate respectively. Therefore, the scissors structure can output a changing angle \(\theta\). The vertical movement of the seat suspension transformed into the rotary movement of the EMD system in this way. In this way, the rotary output torque \(T\) is transformed into the vertical force \(u\) to the seat suspension.

Fig. 4
figure 4

The kinetic model of the seat suspension

Full size image

When the rotor of the PMSM is rotating, a voltage proportional to rotational speed is generated in the circuit. PMSM will output a real-time changing torque proportional to circuit current because of the changing resistance, and the torque of the PMSM will be amplified by the reducer. The amplified torque is transmitted to the scissors structure of the seat suspension by the motion transmission path. Then the sliders slide into the guide rail, and the torque is transformed into vertical force and acts on the seat suspension.

The output force of the EMD system can be obtained by the relationship between the seat suspension and the EMD system [23],

$$u = \frac{{4r_{g}^{2} k_{i}^{2} }}{{\left( {L^{2} - \left( {h + h(t} \right)^{2} } \right)\left( {R_{i} + \left( {1 - D} \right)R_{e} } \right)}}\dot{h}\left( t \right)$$
(6)

where \(r_{g}\) is the gear ratio of the reducer; \(k_{i}\) is the torque constant of the PMSM; \(L\) is the length of the seat suspension rod; \(h_{0}\) is the initial height of the seat suspension; \(h\) is the relative displacement of the seat suspension; \(\dot{h}\) is the relative velocity of the seat suspension; \(R_{i}\) is the internal resistance; \(R_{{\text{e}}}\) is the external resistance; \(D\) is the PWM duty cycle.

The Equivalent Disturbance Force Model

In the seat suspension system equipped with the EMD system, there are two disturbances. One is caused by the road roughness, which is the cabin floor acceleration \(\ddot{z}_{v}\). In the robust controller design process, the cabin floor acceleration \(\ddot{z}_{v}\) is defined as system disturbance. Another one is friction and equivalent inertial force. The friction force comes from the mechanical system, and the equivalent inertial force is caused by the rotor of the permanent magnet synchronous motor (PMSM) and the reducer. The friction and the inertial force have an unneglectable impact on the seat suspension dynamics. Therefore, the disturbance force containing the friction and equivalent inertial force is estimated for enhancing controlling performance.

To compensate for the disturbance force, a 6-DOF vibration platform and a force sensor are applied to measure the force–displacement relationship of the seat suspension (the damper of the seat suspension is removed). The experimental bench is shown in Fig. 5 and the displacement excitation data can be seen in Fig. 6.

Fig. 5
figure 5

The experimental setup of test bench for seat suspension disturbance force

Full size image
Fig. 6
figure 6

Disturbance force–displacement relationship

Full size image

The six-DOF vibration platform is fixedly connected with the seat suspension system to provide the vertical displacement excitation and the real-time suspension force is measured by the force sensor. Since the damper is removed, the force obtained from the experiments includes disturbance force and stiffness force. As the suspension stiffness is already known, the disturbance-displacement responses can be obtained in Fig. 6. Since the disturbance force–displacement response is known, the disturbance force–velocity can be obtained by deriving the displacement.

Compared with the equivalent inertial force, the friction force has a greater influence on suspension vibration control. The friction forces with the excitation frequencies of 1 Hz, 1.5 Hz, and 2 Hz are overlapping. When the seat suspension deflection directions are inversed, there is an apparent hysteresis phenomenon in the change of friction force.

Therefore, a hysteresis model (Bouc–Wen model) is chosen to describe the disturbance because the model widely used in the MR model to describe the hysteresis characteristics [32]. The Bouc-Wen model is given as:

$$\left\{ {\begin{array}{*{20}c} {\widehat{{f_{r} }} = \alpha z_{d} } \\ {\dot{z}_{d} = - \gamma_{d} \left| {v_{s} } \right|z_{d} \left| {z_{d} } \right| - \beta_{d} v_{s} \left| {z_{d} } \right|^{2} + A_{d} \left( {\dot{z}_{s} - \dot{z}_{v} } \right)} \\ \end{array} } \right.$$
(7)

where \(\dot{z}_{s} - \dot{z}_{v}\) is the relative velocity of the seat suspension; \(z_{d}\) is the intermediate variable; \(\alpha\), \(\gamma_{d}\), \(\beta_{d}\) and \(A_{d}\) are the parameters to be identified.

Robust Controller Design

Design of State Observer

In the practical scene, human body deflection, human body, and seat suspension's absolute velocity cannot be measured easily because sensors cannot be installed easily. Therefore, only seat suspension relative displacement \(x_{1}\) is easy to be measured in all state variables.

A state observer is designed to solve the problem and the estimated control output can be defined based on Eq. (4),

$$\hat{\varvec{Y}} = {\varvec{C}}_{1} \hat{\varvec{x}} + {\varvec{D}}_{2} \left( {u - \widehat{{f_{r} }}} \right),$$
(8)

where \(\widehat{{f_{r} }}\) is the estimated disturbance force.

The estimation error is,

$${\varvec{e}} = {\varvec{x}} - \hat{\varvec{x}}\varvec{.}$$
(9)

Therefore, the state observer can be obtained by,

$$\varvec{\dot{\hat{x}}} = \varvec{A\hat{x}} + {\varvec{B}}_{2} \left( {u - \widehat{{f_{r} }}} \right) + {\varvec{L}}\left( {{\varvec{Y}} - \hat{\varvec{Y}}} \right),$$
(10)

where \(\hat{\varvec{x}}\) is the estimated state variables, \({\varvec{L}}\) is the state observer gain. Therefore, state variables can be estimated by damping force, disturbance force and control output.

By differentiating Eq. (9), the derivative of the estimation error can be obtained by substituting Eqs. (3), (4), (8) and (10) into Eq. (9):

$$\dot{\varvec{e}} = \dot{\varvec{x}} - \varvec{\dot{\hat{x}}} = \left( {{\varvec{A}} - {\varvec{LC}}_{1} } \right){\varvec{e}} + \left( {{\varvec{B}}_{1} - {\varvec{LD}}_{1} } \right)w + \left( {{\varvec{LD}}_{2} - {\varvec{B}}_{2} } \right)e_{f} .$$
(11)

Robust \({\varvec{H}}_{\infty }\) controller design

The robust \(H_{\infty }\) controller is designed as,

$$u = \varvec{K\hat{x}} + \widehat{{f_{r} }}$$
(12)

where \({\varvec{K}}\) is the feedback gain to be solved.

The state equation can be rearranged by substituting Eqs. (9), (12) into Eq. (3),

$$\dot{\varvec{x}} = \left( {{\varvec{A}} + {\varvec{B}}_{2} {\varvec{K}}} \right){\varvec{x}} + {\varvec{B}}_{1} w - {\varvec{B}}_{2} {\varvec{Ke}} - {\varvec{B}}_{2} e_{f} .$$
(13)

A new state-space equation is obtained by augmenting matrix,

$$\varvec{\dot{\overline{x}}} = {\varvec{A}}_{{\varvec{h}}} \overline{\varvec{x}} + {\varvec{B}}_{{\varvec{h}}} \varvec{d,}$$
(14)

where \(\overline{\varvec{x}} = \left[ {\begin{array}{*{20}c} {\varvec{x}} \\ {\varvec{e}} \\ \end{array} } \right]\); \({\varvec{A}}_{{\varvec{h}}} = \left[ {\begin{array}{*{20}c} {{\varvec{A}} + {\varvec{B}}_{2} {\varvec{K}}} & { - {\varvec{B}}_{2} {\varvec{K}}} \\ 0 & {{\varvec{A}} - {\varvec{LC}}_{1} } \\ \end{array} } \right]\); \({\varvec{B}}_{{\varvec{h}}} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}_{1} } & { - {\varvec{B}}_{2} } \\ {{\varvec{B}}_{1} - {\varvec{LD}}_{1} } & {{\varvec{LD}}_{2} - {\varvec{B}}_{2} } \\ \end{array} } \right]\); \({\varvec{d}} = \left[ {\begin{array}{*{20}c} w \\ {e_{f} } \\ \end{array} } \right]\).

Then Eq. (5) can be rewritten as

$${\varvec{Z}} = {\varvec{C}}_{{\varvec{h}}} \overline{\varvec{x}}$$
(15)

where \({\varvec{C}}_{{\varvec{h}}} = \left[ {\begin{array}{*{20}c} {\varvec{C}} & 0 \\ \end{array} } \right]\).

To satisfy system's \(H_{\infty }\) performance, the designed controller should be asymptotically stable when \({\tilde{\mathbf{w}}} \equiv 0\). The \(H_{\infty }\) norm is chosen as the control performance measure. The \(L_{2}\) gain of the system (14) and (15) is defined as,

$$\left\| {\begin{array}{*{20}c} {T_{zd} } \\ \end{array} } \right\|_{\infty } = {\text{sup}}\frac{{\left\| {\varvec{Z}} \right\|_{2} }}{{\begin{array}{*{20}c} {\left\| {\varvec{d}} \right\|} \\ \end{array}_{2} }},$$
(16)

where \(\left\| {\varvec{Z}} \right\|_{2} = \mathop \smallint \limits_{0}^{\infty } {\varvec{Z}}_{\left( t \right)}^{{\text{T}}} {\varvec{Z}}_{\left( t \right)} {\text{d}}t\); \(\left\| {\varvec{d}} \right\|_{2} = \mathop \smallint \limits_{0}^{\infty } {\varvec{d}}_{\left( t \right)}^{{\text{T}}} {\varvec{d}}_{\left( t \right)} {\text{d}}t\).

The Lyapunov function of (14) is,

$${\varvec{V}} = \overline{\varvec{x}}^{{\text{T}}} \varvec{P\overline{x}}$$
(17)

where \({\varvec{P}} = \left[ {\begin{array}{*{20}c} {{\varvec{P}}_{1} } & 0 \\ 0 & {{\varvec{P}}_{2} } \\ \end{array} } \right]\) is a positive matrix, \({\varvec{P}} = {\varvec{P}}^{{\text{T}}}\), and \({\varvec{P}}_{1}\) and \({\varvec{P}}_{2}\) are both positive definite matrices.

By differentiating Eq. (17), and the equation can be obtained,

$$\dot{\varvec{V}} = \varvec{\dot{\overline{x}}}^{{\text{T}}} \varvec{P\overline{x}} + \overline{\varvec{x}}^{{\text{T}}} \varvec{P\dot{\overline{x}}}.$$
(18)

Adding \({\varvec{Z}}^{{\text{T}}} {\varvec{Z}} - \gamma^{2} {\varvec{d}}^{{\text{T}}} \varvec{d }\) to the two sides of Eq. (18) can obtain,

$$\dot{\varvec{V}} + {\varvec{Z}}^{{\text{T}}} {\varvec{Z}} - \gamma^{2} {\varvec{d}}^{{\text{T}}} {\varvec{d}} = \left[ {\begin{array}{*{20}c} {\overline{\varvec{x}}^{{\text{T}}} } & {{\varvec{d}}^{{\text{T}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{A}}_{{\varvec{h}}}^{{\mathbf{T}}} {\varvec{P}} + {\varvec{PA}}_{{\varvec{h}}} + {\varvec{C}}_{{\varvec{h}}}^{{\text{T}}} {\varvec{C}}_{{\varvec{h}}} } & {{\varvec{PB}}_{{\varvec{h}}} } \\ {{\varvec{B}}_{{\varvec{h}}}^{{\mathbf{T}}} {\varvec{P}}} & { - \gamma^{2} {\varvec{I}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{\varvec{x}}} \\ {\varvec{d}} \\ \end{array} } \right]$$
(19)

where \(\gamma\) is the \(H_{\infty }\) performance criteria.

If we define

$${\varvec{\varOmega}}= \left[ {\begin{array}{*{20}c} {{\varvec{A}}_{{\varvec{h}}}^{{\mathbf{T}}} {\varvec{P}} + {\varvec{PA}}_{{\varvec{h}}} + {\varvec{C}}_{{\varvec{h}}}^{{\text{T}}} {\varvec{C}}_{{\varvec{h}}} } & {{\varvec{PB}}_{{\varvec{h}}} } \\ {{\varvec{B}}_{{\varvec{h}}}^{{\mathbf{T}}} {\varvec{P}}} & { - \gamma^{2} {\varvec{I}}} \\ \end{array} } \right] < 0,$$
(20)

then \(\dot{\varvec{V}} + {\varvec{Z}}^{{\text{T}}} {\varvec{Z}} - \gamma^{2} {\varvec{d}}^{{\text{T}}} {\varvec{d}} < 0\).

By the Schur complement, \({\varvec{\varOmega}}< 0\) is equivalent to

$${{\varvec{\Omega}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{{\mathbf{h}}}^{{\mathbf{T}}} {\mathbf{P}} + {\mathbf{PA}}_{{\mathbf{h}}} } & {{\mathbf{PB}}_{{\mathbf{h}}} } & {{\mathbf{C}}_{{\mathbf{h}}}^{{\text{T}}} } \\ {{\mathbf{B}}_{{\mathbf{h}}}^{{\mathbf{T}}} {\mathbf{P}}} & { - \gamma^{2} {\mathbf{I}}} & 0 \\ {{\mathbf{C}}_{{\mathbf{h}}} } & 0 & { - 1} \\ \end{array} } \right] < 0.$$
(21)

Equation (21) is post- and pre-multiplied by diag (\({\mathbf{P}}_{1}^{ - 1} , {\mathbf{I}}, {\mathbf{I}}, {\mathbf{I}},{\mathbf{I}})\) and its transposition matrix, respectively. Then we define \({\mathbf{P}}_{1}^{ - 1} = {\mathbf{Q}}\), \({\mathbf{KQ}} = {\mathbf{Y}},\;{\mathbf{P}}_{2} {\mathbf{L}} = {\mathbf{G}}\), where \({\mathbf{P}}_{2}\) is a constant matrix. The controller gain and observer gain can be obtained by solving the following linear matrix inequality (LMI),

$${{\varvec{\Omega}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{AQ}} + {\mathbf{B}}_{2} {\mathbf{Y}} + *} & { - {\mathbf{B}}_{2} {\mathbf{K}}} & {{\mathbf{B}}_{1} } & { - {\mathbf{B}}_{2} } & {{\mathbf{QC}}^{{\text{T}}} } \\ * & {{\mathbf{P}}_{2} {\mathbf{A}} - {\mathbf{GC}}_{1} + *} & {{\mathbf{P}}_{2} {\mathbf{B}}_{1} - {\mathbf{GD}}_{1} } & {{\mathbf{GD}}_{2} - {\mathbf{P}}_{2} {\mathbf{B}}_{2} } & 0 \\ * & * & { - {{\varvec{\upgamma}}}^{2} {\mathbf{I}}} & 0 & 0 \\ * & * & * & { - {{\varvec{\upgamma}}}^{2} {\mathbf{I}}} & 0 \\ * & * & * & * & { - {\mathbf{I}}} \\ \end{array} } \right] < 0$$
(22)

where \({\mathbf{Q}} = {\mathbf{Q}}^{{\mathbf{T}}} ,{ }{\mathbf{Q}} > 0\). After solving the Eq. (22) for matrices \({\mathbf{Q}},{ }{\mathbf{Y}}\) and \({\mathbf{G}}\), the controller gain and the observer gain are obtained as \({\mathbf{K}} = {\mathbf{YQ}}^{ - 1} ,\;{\mathbf{L}} = {\mathbf{P}}_{2}^{ - 1} {\mathbf{G}}\).

Case Study

To validate the effectiveness of the proposed control algorithm, a specific case is studied. The seat suspension system and controller parameters are listed in Table 1. The parameters of the seat system are measured in a laboratory, while the human body stiffness and damping coefficients are from reference [33]. It is worth mentioning that although there is no damper in the suspension system, a small damping coefficient is selected since the system still exists a linear damping part. The control gain can be obtained as \({\mathbf{K}} = \left[ {\begin{array}{*{20}c} {7828.3} & {1711.1} & { - 68153} & { - 1726.2} \\ \end{array} } \right]\), and the state observer gain is \({\mathbf{L}} = \left[ {\begin{array}{*{20}c} { - 7.9229} & { - 1.4855} & { - 244.8603} \\ {0.0012} & 1 & 0 \\ 0 & 0 & { - 0.0011} \\ {0.9988} & 0 & 0 \\ \end{array} } \right]\).

Table 1 Parameters of seat suspension system and controller
Full size table

The Simulink design optimization toolbox is used to identify parameters of the Bouc-Wen model and these parameters can be identified as \(A_{d}\) = − 517,920, \(\alpha = - 110.22\), \(\beta_{d}\) = 1,724,900, \(\gamma_{d}\) = 2,586,600. The simulated disturbance force is compared with the measured disturbance force in Fig. 7. Figure 7 shows that the Bouc-Wen model is highly consistent with experimental data, which validates the effectiveness of the disturbance compensation method.

Fig. 7
figure 7

Disturbance force simulation

Full size image

Experimental Validation

Experimental Setup

The seat suspension system equipped with the EMD system is tested on a 6-DOF vibration platform, and the test rig is shown in Fig. 8. The 6-DOF vibration platform is applied to generate vertical vibration excitation. A c-RIO 9076 and three NI 9401 are used to control the motion of the 6-DOF vibration platform.

Fig. 8
figure 8

Test rig setup

Full size image

A displacement sensor is used to measure seat suspension deflection. Two acceleration sensors (ADXL 203EB) are used to measure acceleration data of the seat suspension upper platform and six-DOF upper platform, respectively. In addition, an inertial measurement unit (IMU) is applied to measure the human body’s acceleration since the human body has coupled motions. An NI 9041 can send PWM duty cycle signals to control the EMD system. A current sensor is used to measure the current of the circuit diagram. The measurement and control frequency is set as 500 Hz. Measurement data from these sensors are required by this controller and then the desired PWM duty cycles are sent out to the EMD system.

To validate the effectiveness of the controller, a well-tuned commercial suspension is selected to compare with the semi-active seat suspension. Besides that, three different types of experiments (sinusoidal vibration, bump excitation, and random excitation) were carried out.

Experimental Results

Sinusoidal Excitation

To systematically research the EMD seat suspension's vibration suppression performance under different frequencies, sinusoidal excitations are applied. Acceleration transmissibility is used to evaluate the controller's performance, and Table 2 shows sinusoidal excitations' frequency and amplitude.

Table 2 Sinusoidal excitations signals
Full size table

The acceleration transmissibility of the system can be obtained,

$$T_{bv} = \frac{{{\text{RMS}}\left( {\ddot{z}_{b} } \right)}}{{{\text{RMS}}\left( {\ddot{z}_{v} } \right)}}$$
(23)

where \({\text{RMS}}\left( {\ddot{z}_{b} } \right)\) is the root mean square (RMS) value of human body acceleration; \({\text{RMS}}\left( {\ddot{z}_{v} } \right)\) is the RMS value of the 6-DOF upper platform; \({\text{RMS}}\left( a \right) = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {a_{i}^{2} } }\).

The comparison of suspension acceleration transmissibility is shown in Fig. 9. It can be seen that the resonance frequency of the seat suspension is around 1.6 Hz and the designed controller can reduce resonance vibration effectively. In addition, the robust controller can isolate vibration effectively in the lower frequency band (1–2.5 Hz), while the robust controller can keep a similar passivity performance with the passive suspension in the higher frequency band (f > 2.5 Hz).

Fig. 9
figure 9

Acceleration transmissibility

Full size image

It is worth mentioning that the high-frequency excitation of the uneven road will be filtered by the vehicle suspension in practice. Therefore, the designed controller is useful in practical scenarios because it can reduce vibration effectively in low frequency and keep passivity in high frequency.

Bump Excitation

Bump excitation usually is used to evaluate the suspension system's transient response characteristics, and the excitation is given in reference [13]. Relevant excitation can be obtained by exerting the bump excitation on a seven-DOF vehicle model. The response of the 7-DOF vehicle model is used as the input of the seat suspension. The Bump excitation is given as follows

$$Z_{r} \left( t \right) = \left\{ {\begin{array}{*{20}c} {\frac{a}{2}\left( {1 - \cos \left( {\frac{{2\pi v_{0} }}{l}t} \right)} \right),\;0 \le t \le \frac{l}{{v_{0} }}} \\ {0,\; t > \frac{l}{{v_{0} }}} \\ \end{array} } \right.$$
(24)

where \(a = 0.04\;{\text{m}},{ }l = 0.4\;{\text{m}}\) are the height and length of the Bump excitation, and the forward velocity \(v_{0} = 9.7 {\text{m}}/{\text{s}}\).

Figure 10 demonstrates that the robust controller can improve the seat suspension system's transient response performance effectively. The first peak acceleration values of the passive suspension and EMD seat suspension are 1.858 \({\text{m}}/{\text{s}}^{2}\) and 1.706 \({\text{m}}/{\text{s}}^{2}\), and the second peak acceleration values are 2.3505 \({\text{m}}/{\text{s}}^{2}\) and 1.5863 \({\text{m}}/{\text{s}}^{2}\), respectively.

Fig. 10
figure 10

Human body acceleration response under bump excitation

Full size image

This means that the EMD seat suspension's peak acceleration values have declined by 8.18% and 32.5% compared with the passive suspension. In addition, the robust controller can reduce shock quickly compared with the passive one.

Figure 11 shows that EMD seat suspension's handling performance is improved, which means that the relative displacement has declined compared with the passive suspension. The EMD seat suspension and passive suspension's relative displacement peak values are 11.451 mm and 8.975 mm, separately. This means that the relative displacement peak value of the EMD seat suspension has declined by nearly 21.6% compared with the passive suspension.

Fig. 11
figure 11

Seat suspension relative displacement response under bump excitation

Full size image

Figure 12 demonstrates the comparison between the active force obtained by the robust controller and the actual output force, and the semi-active force can track the active force well. Based on the above analysis, only the state variable \(x_{1}\) can be easily measured in practice. Therefore, the estimated state variable \(\widehat{{x_{1} }}\) and practical state variable \(x_{1}\) are compared in Fig. 13, and the error between \(\widehat{{x_{1} }}\) and \(x_{1}\) is very little. The effectiveness of the designed state observer is validated. In addition, the real-time duty cycle calculated by the robust controller is shown in Fig. 14.

Fig. 12
figure 12

The actual output force and ideal active force

Full size image
Fig. 13
figure 13

The performance of state observer

Full size image
Fig. 14
figure 14

PWM duty cycle

Full size image

Random Excitation

The random excitation is closer to the actual road excitation, the random excitation is selected as the seat suspension's input,

$$\dot{z}_{r} \left( t \right) + \rho VZ_{r} \left( t \right) = VW_{n}$$
(25)

where \(W_{n}\) is the intensity \(2\sigma^{2} \rho V\) of the white noise, \(\sigma^{2}\) is the covariance of road irregularity; \(V\) is the vehicle forward velocity; \(\rho\) is the road roughness parameters. \(\rho = 0.45\;{\text{m}}^{ - 1}\), \(\sigma^{2} = 300{\text{ mm}}^{2}\), \(v = 20{\text{ ms}}^{ - 1}\) are chosen in this paper. Similarly, the 7-DOF vehicle model is used to generate random responses and the response signals are used as seat suspension random input.

The acceleration response and seat suspension relative displacement are shown in Figs. 15 and 16, respectively. The seat suspension based on the robust controller achieves better vibration isolation and handling performance compared with the passive suspension under random excitation conditions.

Fig. 15
figure 15

Human body acceleration under random excitation

Full size image
Fig. 16
figure 16

Seat suspension relative displacement response under random excitation

Full size image

To evaluate the controller's performance under random excitation quantitatively, ISO 2631-1 is applied to evaluate the two kinds of seat suspensions. The RMS, frequency-weighed root mean square (FW-RMS), and fourth power vibration dose value (VDV) are calculated as follows,

$${\text{RMS}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} a_{i}^{2} } ,$$
(26)
$$a_{{\text{FW - RMS}}} = \left[ {\frac{1}{T}\mathop \smallint \limits_{0}^{T} a_{w}^{2} \left( t \right){\text{d}}t} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}$$
(27)
$${\text{VDV}} = \left[ {\frac{1}{T}\mathop \smallint \limits_{0}^{T} a_{w}^{4} \left( t \right){\text{d}}t} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}}} ,$$
(28)

where \(a_{w}\) is the frequency-weighted acceleration.

It can be seen from Fig. 17 that the VDV, RMS, and FW-RMS values of the EMD seat suspension are 4.3706 m/\({\text{s}}^{2}\), 1.4098 m/\({\text{s}}^{2}\), and 0.7266 m/\({\text{s}}^{2}\), while the corresponding values of the passive suspension are 3.6145 m/\({\text{s}}^{2}\), 1.1763 m/\({\text{s}}^{2}\), and 0.6142 m/\({\text{s}}^{2}\), respectively. This means that the VDV, RMS and FW-RMS values of the EMD seat suspension have dropped 17.30%, 16.56%, and 11.24% compared with the passive one, respectively.

Fig. 17
figure 17

The comparison of the VDV, RMS and FW-RMS

Full size image

In addition, the RMS values of relative displacement are calculated to evaluate seat suspension's handling performance quantitatively. Figure 18 illustrates the seat suspension relative displacement RMS values. The relative displacement RMS values are 3.5049 mm and 4.0328 mm for the EMD seat suspension and the passive suspension, which means that the EMD seat suspension's handling stability has increased by 13.09% than the passive one.

Fig. 18
figure 18

The relative displacement RMS values

Full size image

To further investigate the robust controller's frequency characteristics, the acceleration power spectral density (APSD) is compared in Fig. 19. Figure 19 shows that the passive suspension and the EMD seat suspension both have a peak value of around 1.46 Hz. The robust controller can suppress the vibration to a very low magnitude in a wide frequency range (0.1–4 Hz). The APSD peak values of the EMD seat suspension and the passive suspension are 5.8097 \({\text{(m/s}}^{2} )^{2} {\text{/Hz}}\) and 3.611 \({\text{(m/s}}^{2} )^{2} {\text{/Hz}}\), which means that the APSD peak value of the EMD seat suspension has decreased by 37.84% compared with the passive one.

Fig. 19
figure 19

PSD of human body acceleration

Full size image

The performance of actual output force, state observer, and output PWM duty cycle is shown in Figs. 20, 21 and 22. The EMD system can achieve the requirement of ideal active force to a larger extent, and the state observer has good performance with little estimation error.

Fig. 20
figure 20

Response of actual output force under random excitation

Full size image
Fig. 21
figure 21

State observer performance

Full size image
Fig. 22
figure 22

PWM duty cycle

Full size image

Conclusions

This paper proposes an applicable robust controller, which can compensate for the system disturbance and estimate state variables effectively. Compared with a well-tuned commercial passive suspension, the proposed controller has better overall performance. Conclusions are summarized as follows.

  1. 1.

    The state controller can be implemented with the human body acceleration, seat suspension acceleration, and the seat suspension relative displacement signals. Experimental results show that the proposed observer has excellent performance with an acceptable estimation error.

  2. 2.

    The seat suspension disturbance force, including friction force, and inertia force, is measured on a test bench. The Bouc-Wen model is selected to compare with actual disturbance, which shows high accuracy.

  3. 3.

    Experimental results show that the controller has great vibration isolation performance and handling performance than a passive suspension under three typical road excitations. The VDV, RMS and FW-RMS values of the designed controller decreased by 17.30%, 16.56%, and 11.24%, respectively.