Introduction

In recent years, the demand for the improvement of ride comfort has motivated much research. Nowadays, using the control strategy to study the vibration damping performance of the suspension system has become a hot topic among scholars [1,2,3]. According to different methods of implementing control, it divides the suspension system with control function into an active control suspension system and semi-active control suspension system, thus breaking the damper mode of a passive suspension system [4,5,6]. The semi-active control suspension does not require active input energy compared to a fully active control suspension. It only needs to adjust the damping or spring stiffness of the suspension system according to the driving condition of the vehicle. It is safe, reliable, and easy to implement. It has promotion and the value of the application.

The magnetorheological (MR) damper is utilized extensively as a nonlinear component in semi-active suspension systems because of its excellent damping effect [7]. Seat MR suspension is an important part of the vehicle vibration damping system. It can avoid passengers from high-intensity vibration, especially heavy-duty vehicles, agricultural vehicles and construction vehicles at poor working environment, and the heavy load. Through the improvement of vehicle suspension structure, the damping effect is not ideal, but through the research of control method, improving the damping performance of seat MR suspension has the advantages of convenience, short cycle, and quick effect.

Owing to the complex dynamic constitutive relationship of MR fluids, it is difficult to establish a MR damper model and an effective control method for MR suspensions. For the MR suspension control system, the forward and reverse models of the MR damper to be study, mainly to make the MR damper model in the suspension control modeling system closer to the dynamics of the real MR damper characteristics, the suspension control simulation system will replace the actual system and achieve the purpose of experiment and research. Therefore, accurately establishing the MR damper model is essential to get a satisfactory control effect. However, it has very few reverse models suitable for practical control applications. Most of them resort to the inverse dynamics model of the Bingham model, and it rarely considers the influence of acceleration excitation on the damper characteristics in the existing MR damper dynamics model.

In the semi-active's control seat suspension, different control strategies are adopted, and the damping effect that the suspension can achieve is also very different, so the control method is actually the core of the semi-active suspension. The study of variable structure control (VSC) began in the 1950s when former Soviet Scholar Emelyanov et al. proposed the concept of variable structure control [8, 9]. Subsequently, Utkin, Itkis, and other scholars summarized and developed the sliding mode variable structure control theory, which laid the theoretical foundation of sliding mode variable structure control [10,11,12]. The sliding mode control method has strong robustness and anti-interference in the active's control suspension [13]. The Lyapunov type adaptive law usually uses as back-stepping [14, 15], the method integrates the control law and the adaptive law to achieve the goal of dynamic performance and static performance of the entire closed-loop system. With the emergence of many control methods, the research of intelligent control problems has gradually changed into the direction of combining intelligent control methods with modern control methods, the combination of control methods has further changed the performance of semi-active suspensions to improve the smoothness. The combination of back-stepping and other control methods has been successful in many successful applications in control systems, such as automatic underwater vehicles [16], air-breathing hypersonic vehicles [17], electric vehicles [18], and permanent magnet synchronous generator [19].

Consequently, in this paper, it focuses on designing a back-stepping sliding mode controller for seat suspension systems with the MR damper. First, by constructing a MR damper experimental platform, it collects the measured data, then put the data into the particle swarm optimization training system to get the MR damper models. Second, to improve the ride comfort of the seat MR suspension based on the establishment and analysis of the quarter-body MR suspension dynamic model, the controller will use the approximate skyhook-damping system as the reference model. The error dynamic equation is obtained through the MR suspension model and the reference model, and the error dynamic component is used as the back-stepping control parameter. On the premise of ensuring the system is asymptotically stable, adding the sliding mode surface to the dynamic equation of the third error subsystem can complete design of the back-stepping sliding mode controller. Finally, it adds the obtained MR damper model to the control simulation model, to verify the effectiveness of the proposed back-stepping sliding mode controller.

Formulation

Structural Motion Equation

The vehicle system is a complex multi-degree-of-freedom nonlinear system. To analyze the dynamic characteristics of the suspension system, it needs to be simplified. Suspension dynamics models include single degree of freedom model, two-degree-of-freedom model, half-car model, and complete vehicle model.

The vehicle suspension system model is shown in Fig. 1. It is a three-dimensional model that regards the body mass of a car as a rigid body. The sprung (body) mass of a car is \(m\). It is composed of the body, frame, and parts. It is connected to the axle and wheels through shock absorbers and suspension springs. The unsprung (wheel) masses composed of wheels and axles are \(m_{1}\), \(m_{2}\), \(m_{3}\), and \(m_{4}\), and the wheels are supported on uneven roads through tires with certain elasticity and damping. When discussing driving comfort, the body quality of this three-dimensional model mainly considers three degrees of freedom: vertical, pitch, and roll, and the four-wheel masses are four vertical degrees of freedom, for a total of seven degrees of freedom.

Fig. 1
figure 1

The vehicle suspension system model

Full size image

When a car is symmetrical on its longitudinal axis and has the same left and right rut unevenness, the vertical vibration and pitching vibration of the vehicle have the greatest impact on the ride comfort. Therefore, the vehicle suspension vibration system is simplified to a half-vehicle model with four degrees of freedom as shown in Fig. 2.

Fig. 2
figure 2

Half-vehicle suspension system model

Full size image

In the model shown in Fig. 2, because the damping of the tires is small and negligible, the body with mass \(m\) and moment of inertia \(I_{y}\) is decomposed into the front axle, the rear axle, and the center of mass C according to the dynamic equivalent adjustment. The three concentrated masses are \(m_{{\text{q}}}\), \(m_{{\text{h}}}\) and \(m_{{\text{c}}}\). These three masses are connected by massless rigid rods, and their size is determined by the following three conditions:

  1. (1)

    The total mass remains unchanged:

    $$m_{{\text{q}}} + m_{{\text{h}}} + m_{{\text{c}}} = m.$$
    (1)
  2. (2)

    The position of the center of mass remains unchanged:

    $$m_{{\text{q}}} l_{1} - m_{{\text{h}}} l_{2} = 0$$
    (2)

(3) The value of the moment of inertia remains unchanged:

$$I_{y} = m\rho _{y}^{2} = m_{{\text{q}}} l_{1}^{2} + m_{{\text{h}}} l_{2}^{2} ,$$
(3)

where \(\rho _{y}\) is the radius of gyration around the horizontal axis y; \(l_{1}\) and \(l_{2}\) are the distances from the center of mass of the car body to the front and rear axles.

The three quality values are:

$$m_{{\text{q}}} = m\frac{{\rho _{y}^{2} }}{{l_{2} (l_{1} + l_{2} )}},\;m_{{\text{h}}} = m\frac{{\rho _{y}^{2} }}{{l_{1} (l_{1} + l_{2} )}},\;m_{{\text{c}}} = m\left( {1 - \frac{{\rho _{y}^{2} }}{{l_{1} l_{2} }}} \right).$$
(4)

Generally, let \(\varepsilon = \frac{{\rho _{y}^{2} }}{{ab}}\) be called the sprung mass distribution coefficient. When the sprung mass distribution coefficient is \(\varepsilon = 1\), the contact mass is \(m_{{\text{c}}} = 0\). According to statistics, the \(\varepsilon =\) 0.8–1.2 of most cars is close to 1. In the case of \(\varepsilon = 1\) and the following assumptions are made: (1) the body is rigid and symmetrical to the vertical plane; (2) the left and right wheels are stimulated by the same unevenness of the road surface; (3) when the vehicle is running in a straight line at a constant speed, the tires are always in contact with the ground and there is no jump; (4) the road surface is not smooth and the vehicle does not vibrate much; (5) vehicle suspension stiffness and tire stiffness are linear functions of displacement, suspension damping and tire damping are relative velocities linear function of degrees; (6) the pavement displacement input function acts on the center of the contact point between the tire and the pavement; (t) tire-road contact is considered point contact. The mass of the body part above the front and rear axles is concentrated in the vertical direction of \(m_{{\text{q}}}\) and \(m_{{\text{h}}}\), and the body movement above the front and rear axles is independent of each other, in this case, the front wheel encounters uneven road surface when the vibration is caused, the mass \(m_{{\text{q}}}\) moves, but the mass \(m_{{\text{h}}}\) does not move. The same is true when the rear wheels encounter uneven road surfaces. Therefore, when the system is in this special situation, the two-degree-of-freedom vibration model of the two-mass system composed of the front and rear wheels can be discussed separately.

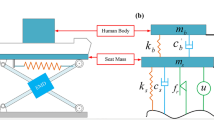
Figure 3 shows the structural model of a quarter-vehicle-seat suspension. We base it on the following assumptions: (1) the human body and the seat are treated; (2) the human seat mass, suspension mass, and unsprung mass are considered rigid bodies; (3) it simplifies the chair and suspension to only consider stiffness and damped components; (4) the tire has linear stiffness which ignoring tire damping on vibration and the road input is at the point of contact between the tire and the road surface. In the figure \(m_{\rm{s}}\),\(m_{\rm{v}}\), and \(m_{\rm{t}}\) are the masses of the seat suspension (including the human body), quarter body, and tire quality, respectively. \(z_{\rm{s}}\), \(z_{\rm{v}}\), and \(z_{\rm{t}}\) are their corresponding displacements, respectively. \(k_{\rm{s}}\),\(k_{\rm{v}}\), \(k_{\rm{t}}\), and \(c_{\rm{s}}\), \(c_{\rm{v}}\) are the stiffness coefficient and damping coefficient of the corresponding system. \(F_{\rm{d}}\) is the variable damping force of the damper, \(z_{0}\) is the displacement excitation of the external road surface to the system.

Fig. 3
figure 3

Quarter-vehicle-seat structural model

Full size image

According to Newton's second law, it establishes the corresponding dynamic equation:

$$\left\{ \begin{gathered} m_{\rm{s}} \ddot{z}_{\rm{s}} = - c_{\rm{s}} (\dot{z}_{\rm{s}} - \dot{z}_{\rm{v}} ) - k_{\rm{s}} (z_{\rm{s}} - z_{\rm{v}} ) - F_{\rm{d}} \hfill \\ m_{\rm{v}} \ddot{z}_{\rm{v}} = c_{\rm{s}} (\dot{z}_{s} - \dot{z}_{\rm{v}} ) + k_{\rm{s}} (z_{\rm{s}} - z_{\rm{v}} ) + F_{\rm{d}} - c_{\rm{v}} (\dot{z}_{\rm{v}} - \dot{z}_{t} ) - k_{\rm{v}} (z_{\rm{v}} - z_{t} ) \hfill \\ m_{\rm{t}} \ddot{z}_{\rm{t}} = c_{\rm{v}} (\dot{z}_{\rm{v}} - \dot{z}_{\rm{t}} ) + k_{\rm{v}} (z_{\rm{v}} - z_{\rm{t}} ) - k_{\rm{t}} (z_{\rm{t}} - z_{0} ). \hfill \\ \end{gathered} \right.$$
(5)

It selects the system state variable is \(Z = \left[ {z_{\rm{s}} ,\dot{z}_{\rm{s}} ,z_{\rm{v}} ,\dot{z}_{\rm{v}} ,z_{\rm{t}} ,\dot{z}_{\rm{t}} } \right]^{\rm{T}}\), the output variable is \(Y = \left[ {\dot{z}_{\rm{s}} ,\ddot{z}_{\rm{s}} ,\dot{z}_{\rm{v}} ,z_{\rm{v}} - z_{\rm{t}} ,z_{\rm{s}} } \right]^{\rm{T}}\), and then the system state equation corresponding to Eq. (5) is:

$$\left\{ \begin{gathered} \dot{Z} = \user2{AZ} + \user2{BU} \hfill \\ \user2{Y} = \user2{CZ} + \user2{DU} \hfill \\ \end{gathered} \right.,$$
(6)
$$\user2{A} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 & 0 \\ {\frac{{ - k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{ - c_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ {\frac{{k_{\rm{s}} }}{{m_{\rm{v}} }}} & {\frac{{c_{\rm{s}} }}{{m_{\rm{v}} }}} & {\frac{{ - (k_{\rm{s}} + k_{v} )}}{{m_{\rm{v}} }}} & {\frac{{ - (c_{\rm{s}} + c_{v} )}}{{m_{\rm{v}} }}} & {\frac{{k_{v} }}{{m_{\rm{v}} }}} & {\frac{{c_{v} }}{{m_{\rm{v}} }}} \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & {\frac{{k_{\rm{v}} }}{{m_{\rm{t}} }}} & {\frac{{c_{\rm{v}} }}{{m_{\rm{t}} }}} & {\frac{{ - (k_{t} + k_{\rm{v}} )}}{{m_{\rm{t}} }}} & {\frac{{ - c_{\rm{v}} }}{{m_{\rm{t}} }}} \\ \end{array} } \right],\user2{B} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ {\frac{{ - 1}}{{m_{\rm{s}} }}} & 0 \\ 0 & 0 \\ {\frac{1}{{m_{\rm{v}} }}} & 0 \\ 0 & 0 \\ 0 & {\frac{{k_{\rm{t}} }}{{m_{\rm{t}} }}} \\ \end{array} } \right],$$
$$\user2{C} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 & 0 \\ {\frac{{ - k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{ - c_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & { - 1} & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\;{\mathbf{D}} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ {\frac{{ - 1}}{{m_{\rm{s}} }}} & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right],\;\user2{U} = \left[ \begin{gathered} F_{\rm{d}} \hfill \\ z_{0} \hfill \\ \end{gathered} \right].$$

This paper considers the influence of acceleration excitation on the damper characteristics based on the hyperbolic tangent model. A modified hyperbolic tangent model is proposed. The formula for the improving hyperbolic tangent MR damper is:

$$F_{{\text{d}}} = f_{0} + k_{{\text{d}}} x + c_{{{\text{po}}}} \dot{x} + m_{{\text{f}}} \ddot{x} + f_{y} \tan {\text{sig}}\left( {(\dot{x} + \lambda _{1} \text{sgn} (\ddot{x}))\lambda _{2} } \right),$$
(7)

where \(k_{{\text{d}}}\) is the stiffness element, \(c_{{{\text{po}}}}\) is the post-yield damping, \(f_{y}\) is the yielding force, \(m_{{\text{f}}}\) is the fluid inertia, \(x\) is the damper body displacement \(z_{v} - z_{s}\), \(f_{0}\) is the force offset, and \(F_{{\text{d}}}\) is the force generated by the MR damper.

Reference Design

The idea of approximate skyhook-damping control is to install a skyhook damper between the body and the imaginary "skyhook". When the damping coefficient reaches a certain value, a specified damping effect can be obtained. Although the ceiling damping control is a hypothetical model, it has a suitable damping effect. The approximate skyhook-damping system is shown in Fig. 4.

Fig. 4
figure 4

Reference model

Full size image

The dynamic equation for this reference model is:

$$\left\{ \begin{gathered} m_{\rm{s}} \ddot{z}_{{\rm{rs}}} = - c_{\rm{s}} (\dot{z}_{{\rm{rs}}} - \dot{z}_{{\rm{rv}}} ) - k_{\rm{s}} (z_{{\rm{rs}}} - z_{{\rm{rv}}} ) - c_{{\rm{sh}}} \dot{z}_{{\rm{rs}}} \hfill \\ m_{\rm{v}} \ddot{z}_{{\rm{rv}}} = c_{\rm{s}} (\dot{z}_{{\rm{rs}}} - \dot{z}_{{\rm{rv}}} ) + k_{\rm{s}} (z_{{\rm{rs}}} - z_{{\rm{rv}}} ) - c_{\rm{v}} (\dot{z}_{{\rm{rv}}} - \dot{z}_{{\rm{rt}}} ) - k_{\rm{v}} (z_{{\rm{rv}}} - z_{{\rm{rt}}} ) \hfill \\ m_{\rm{t}} \ddot{z}_{{\rm{rt}}} = c_{\rm{v}} (\dot{z}_{{\rm{rv}}} - \dot{z}_{{rt}} ) + k_{\rm{v}} (z_{{\rm{rv}}} - z_{{\rm{rt}}} ) - k_{\rm{t}} (z_{{\rm{rt}}} - z_{0} )\rm{ } \hfill \\ \end{gathered} \right.,$$
(8)
$$c_{{\rm{sh}}} = \left\{ \begin{gathered} c_{{\rm{sky}}} \hfill \\ 0 \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\dot{z}_{{\rm{rs}}} (\dot{z}_{{\rm{rs}}} - \dot{z}_{{\rm{rv}}} ) \ge 0} \\ {\dot{z}_{{\rm{rs}}} (\dot{z}_{{\rm{rs}}} - \dot{z}_{{\rm{rv}}} ) < 0} \\ \end{array} ,$$
(9)

where \(z_{{\rm{rs}}}\),\(\dot{z}_{{\rm{rs}}}\),\(z_{{\rm{rv}}}\),\(\dot{z}_{{\rm{rv}}}\), \(z_{{\rm{rt}}}\), and \(\dot{z}_{{\rm{rt}}}\) are the reference displacement and speed corresponding to the seat suspension (including the human body), the body and the tire, respectively; \(c_{{sh}}\) is the damping coefficient of the skyhook damper.

It selects state variable \(\user2{Z}_{r} = \left[ {z_{{rs}} ,\dot{z}_{{rs}} ,z_{{rv}} ,\dot{z}_{{rv}} ,z_{{rt}} ,\dot{z}_{{rt}} } \right]^{T}\), output variable \(\user2{Y}_{r} = \left[ {z_{{rs}} ,\dot{z}_{{rs}} ,z_{{rv}} ,\dot{z}_{{rv}} } \right]^{T}\). The system state equation corresponding to Eq. (8) is:

$$\left\{ \begin{gathered} \mathbf{\dot{Z}}_{\rm{r}} = \mathbf{A}_{\rm{r}} \mathbf{Z}_{\rm{r}} + \mathbf{B}_{\rm{r}} u_{\rm{r}} \hfill \\ \mathbf{Y}_{\rm{r}} = \mathbf{C}_{\rm{r}} \mathbf{Z}_{\rm{r}} + \mathbf{D}_{\rm{r}} u_{\rm{r}} \hfill \\ \end{gathered} \right.,$$
(10)
$$\begin{aligned} A_{\rm{r}} & = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 & 0 \\ {\frac{{ - k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{ - (c_{\rm{s}} + c_{{\rm{sh}}} )}}{{m_{\rm{s}} }}} & {\frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ {\frac{{k_{\rm{s}} }}{{m_{\rm{v}} }}} & {\frac{{c_{\rm{s}} }}{{m_{\rm{v}} }}} & {\frac{{ - (k_{\rm{s}} + k_{\rm{v}} )}}{{m_{\rm{v}} }}} & {\frac{{ - (c_{\rm{s}} + c_{\rm{v}} )}}{{m_{\rm{v}} }}} & {\frac{{k_{\rm{v}} }}{{m_{\rm{v}} }}} & {\frac{{c_{\rm{v}} }}{{m_{\rm{v}} }}} \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & {\frac{{k_{\rm{v}} }}{{m_{\rm{t}} }}} & {\frac{{c_{\rm{v}} }}{{m_{\rm{t}} }}} & {\frac{{ - (k_{\rm{t}} + k_{\rm{v}} )}}{{m_{\rm{t}} }}} & {\frac{{ - c_{v} }}{{m_{\rm{t}} }}} \\ \end{array} } \right],C_{\rm{r}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array} } \right]. \\ B_{\rm{r}} & = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {\frac{{k_{\rm{t}} }}{{m_{\rm{t}} }}} \\ \end{array} } \right]^{\rm{T}} ,D_{\rm{r}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ \end{array} } \right]^{\rm{T}} ,u_{\rm{r}} = \left[ {z_{0} } \right]. \\ \end{aligned}$$

Controller Design

The controller takes the approximate skyhook-damping system as the reference model, and introduces the acceleration component of the generalized state tracking error vector between the actual system and the reference model into the back-stepping sliding mode control. First, the system is decomposed into subsystems that do not exceed the order of the system. Then, the intermediate virtual control rate \(\alpha _{1}\) is designed to make the system stable. Finally, sliding mode control is added to make the actual control system track the reference model effectively and stably. The acceleration of the seat will be reduced and the comfort will be improved.

Because the controller designed in this paper is to make the actual control system of the seat suspension track the movement of the reference model, and use the back-stepping sliding mode method to control the error dynamic system. According to the aforementioned dynamic model of the seat and reference model, the integral of the seat suspension displacement error, the seat suspension displacement error and its velocity error are defined as generalized errors vector \(\user2{e}\):

$$e = \left[ {\begin{array}{*{20}c} {e_{1} } & {e_{2} } &{e_{3} } \\ \end{array} } \right]^{\rm{T}} = \left[ {\begin{array}{*{20}c} {\int {(z_{\rm{s}} - z_{{\rm{rs}}} )\rm{d}t} } & {z_{\rm{s}} - z_{{\rm{rs}}} } & {\dot{z}_{\rm{s}} - \dot{z}_{{\rm{rs}}} } \\ \end{array} } \right]^{\rm{T}} ,\dot{e} = \left[ {\begin{array}{*{20}c} {z_{\rm{s}} - z_{{\rm{rs}}} } & {\dot{z}_{\rm{s}} - \dot{z}_{{\rm{rs}}} } &{\ddot{z}_{\rm{s}} - \ddot{z}_{{\rm{rs}}} } \\ \end{array} } \right]^{\rm{T}} .$$
(11)

The error dynamics equation is further organized into a matrix form:

$$\dot{e} = E\mathbf{e} + Fu + G\mathbf{Z} + H\mathbf{Z}_{\rm r}$$
(12)

where

$$E = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & {\frac{{ - k_{\rm{s}} }}{{{\text{m}}_{\rm{s}} }}} & {\frac{{ - c_{\rm{s}} }}{{m_{\rm{s}} }}} \\ \end{array} } \right],G = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\frac{{k_{\rm{s}} }}{{{\text{m}}_{\rm{s}} }}} & {\frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}} & 0 & 0 \\ \end{array} } \right],H = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{{c_{{\rm{sh}}} }}{{m_{\rm{s}} }}} & {\frac{{ - k_{\rm{s}} }}{{m_{\rm{s}} }}} & {\frac{{ - c_{\rm{s}} }}{{m_{\rm{s}} }}} & 0 & 0 \\ \end{array} } \right],F = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{{ - 1}}{{{\text{m}}_{\rm{s}} }}} \\ \end{array} } \right]^{\rm{T}} ,u = \left[ {F_{\rm{d}} } \right].$$

The equation of state for the vehicle seat suspension to establish a control system is:

$$\left\{ \begin{gathered} x_{1} = e_{1} \hfill \\ x_{2} = \dot{x}_{1} = e_{2} \hfill \\ x_{3} = \dot{x}_{2} = e_{3} \hfill \\ \dot{x}_{3} = - \frac{{k_{s} }}{{m_{s} }}x_{2} - \frac{{c_{s} }}{{m_{s} }}x_{3} - \frac{1}{{m_{s} }}F_{d} + \frac{{c_{{sh}} }}{{m_{s} }}\dot{z}_{{rs}} + \frac{{k_{s} }}{{m_{s} }}(z_{v} - z_{{rv}} ) + \frac{{c_{s} }}{{m_{s} }}(\dot{z}_{v} - \dot{z}_{{rv}} ) \hfill \\ \end{gathered} \right..$$
(13)
  1. (1)

    First, it defines the following two error variables:

    $$\left\{ \begin{gathered} z_{1} = x_{1} \hfill \\ z_{2} = x_{2} - \alpha _{1} \hfill \\ \end{gathered} \right.$$
    (14)

where: \(\alpha _{1}\) is virtual control and needs to be further determined.

(2) For the first error subsystem, the virtual control quantity \(\alpha _{1} = - z_{1}\) and the energy function \(V_{1} = \frac{1}{2}z_{1}^{2}\) are designed. The dynamic equation of the error system is:

$$\dot{z}_{1} = x_{2} = z_{2} + \alpha _{1} = z_{2} - z_{1} ,$$
(15)

and \(\dot{V}_{{\text{1}}}\) is:

$$\dot{V}_{1} = z_{1} \dot{z}_{1} = z_{1} (z_{2} - z_{1} ) = - z_{1}^{2} + z_{1} z_{2} .$$
(16)

(3) It lets \(s = \dot{z}_{2} + c_{1} z_{2} + z_{1}\) and the energy function is \(V_{2} = \frac{1}{2}z_{2}^{2} + V_{1}\)

$$\dot{V}_{2} = \dot{V}_{1} + z_{2} \dot{z}_{2} = - z_{1}^{2} + z_{1} z_{2} + z_{2} \dot{z}_{2} = - z_{1}^{2} + z_{1} z_{2} + z_{2} (s - c_{1} z_{2} - z_{1} ) = - c_{1} z_{2}^{2} - z_{1}^{2} + z_{2} s,$$
(17)
$$\begin{aligned} \dot{s} & = \ddot{z}_{2} + c_{1} \dot{z}_{2} + \dot{z}_{1} = - \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}e_{2} - \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}e_{3} - \frac{1}{{m_{\rm{s}} }}F_{\rm{d}} + \frac{{c_{{\rm{sh}}} }}{{m_{\rm{s}} }}\dot{z}_{{\rm{rs}}} + \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}(z_{\rm{v}} - z_{{\rm{rv}}} ) + \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}(\dot{z}_{\rm{v}} - \dot{z}_{{\rm{rv}}} ) - \ddot{\alpha }_{1} + c_{1} \dot{z}_{2} + \dot{z}_{1} , \\ & {\text{ = }} - \frac{{k_{\rm{s}} }}{{m_{s} }}e_{2} - \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}e_{3} - \frac{1}{{m_{\rm{s}} }}F_{\rm{d}} + \frac{{c_{{\rm{sh}}} }}{{m_{\rm{s}} }}\dot{z}_{{\rm{rs}}} + \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}(z_{\rm{v}} - z_{{\rm{rv}}} ) + \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}(\dot{z}_{\rm{v}} - \dot{z}_{{\rm{rv}}} ) + \ddot{z}_{1} + c_{1} \dot{z}_{2} + \dot{z}_{1} , \\ & = - \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}e_{2} - \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}e_{3} - \frac{1}{{m_{\rm{s}} }}F_{\rm{d}} + \frac{{c_{{\rm{sh}}} }}{{m_{\rm{s}} }}\dot{z}_{{\rm{rs}}} + \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}(z_{\rm{v}} - z_{{\rm{rv}}} ) + \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}(\dot{z}_{\rm{v}} - \dot{z}_{{\rm{rv}}} ) + \dot{z}_{2} - \dot{z}_{1} + c_{1} \dot{z}_{2} + \dot{z}_{1} , \\ & = - \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}e_{2} - \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}e_{3} - \frac{1}{{m_{\rm{s}} }}F_{\rm{d}} + \frac{{c_{{\rm{sh}}} }}{{m_{\rm{s}} }}\dot{z}_{{\rm{rs}}} + \frac{{k_{\rm{s}} }}{{m_{\rm{s}} }}(z_{\rm{v}} - z_{{\rm{rv}}} ) + \frac{{c_{\rm{s}} }}{{m_{\rm{s}} }}(\dot{z}_{\rm{v}} - \dot{z}_{{\rm{rv}}} ) + \left( {c_{1} + 1} \right)\dot{z}_{2} , \\ \end{aligned}$$
(18)

where \(c_{1} > 0\).

It lets:

$$\begin{aligned} F_{\rm{d}} & = - k_{\rm{s}} e_{2} - c_{\rm{s}} e_{3} + c_{{\rm{sh}}} \dot{z}_{{\rm{rs}}} + k_{\rm{s}} (z_{\rm{v}} - z_{{\rm{rv}}} ) + c_{\rm{s}} (\dot{z}_{\rm{v}} - \dot{z}_{{\rm{rv}}} ) \\ & + \left( {c_{1} + 1} \right)\dot{z}_{2} m_{\rm{s}} + m_{\rm{s}} \eta \rm{sgn}(s) + z_{2} m_{\rm{s}} . \\ \end{aligned}$$
(19)

Then:

$$\dot{s} = - \eta \rm{sgn}(s) - z_{2} .$$
(20)

It lets: \(V_{3} = V_{2} + \frac{1}{2}s^{2}\).

Then:

$$\begin{gathered} \dot{V}_{3} = \dot{V}_{2} + s\dot{s} = - c_{1} z_{2}^{2} - z_{1}^{2} + z_{2} s + s\dot{s} = - c_{1} z_{2}^{2} - z_{1}^{2} + s(\dot{s} + z_{2} ) \hfill \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} = - c_{1} z_{2}^{2} - z_{1}^{2} + s( - \eta \rm{sgn}(s) - z_{2} + z_{2} ) = - c_{1} z_{2}^{2} - z_{1}^{2} - \eta \left| s \right| \le 0. \hfill \\ \end{gathered}$$
(21)

where \(\eta = 3\).

In summary, the expected damping force under the back-stepping sliding mode control is:

$$F_{{{\text{back}} - {\text{steppingsliding}}}} = \left\{ {\begin{array}{*{20}c} {F_{{\text{d}}} } & {} & {\dot{z}_{{\text{s}}} (\dot{z}_{{\text{s}}} - \dot{z}_{{\text{v}}} ) \ge 0} \\ 0 & {} & {\begin{array}{*{20}c} {\dot{z}_{{\text{s}}} (\dot{z}_{{\text{s}}} - \dot{z}_{{\text{v}}} ) < 0} \\ \end{array} } \\ \end{array} } \right.,$$
(22)

where \(F_{{{\text{fb}}}}\) required force for the calculated MR damper.

To understand the difference between sliding mode, fuzzy sliding mode, skyhook back-stepping, and the back-stepping sliding mode control in the later simulation, the control forces are listed as follows:

$$F_{{{\text{sliding}}}} = (c_{1} m_{{\text{s}}} - k_{{\text{s}}} )e_{2} + (c_{2} m_{{\text{s}}} - c_{{\text{s}}} )e_{3} + k_{{\text{s}}} (x_{{\text{v}}} - x_{{{\text{rv}}}} ) + c_{{\text{s}}} (\dot{x}_{{\text{v}}} - \dot{x}_{{{\text{rv}}}} ) + c_{{{\text{sh}}}} \dot{x}_{{{\text{rs}}}} {\text{ + }}\varepsilon m_{{\text{s}}} \text{sgn} (s) \cdot \varepsilon {\text{ = 3,}}$$
(23)
$$F_{{\_{\text{sliding}}\_{\text{fuzzy}}}} = (c_{1} m_{{\text{s}}} - k_{{\text{s}}} )e_{2} + (c_{2} m_{{\text{s}}} - c_{{\text{s}}} )e_{3} + k_{{\text{s}}} (x_{{\text{v}}} - x_{{{\text{rv}}}} ) + c_{{\text{s}}} (\dot{x}_{{\text{v}}} - \dot{x}_{{{\text{rv}}}} ) + c_{{{\text{sh}}}} \dot{x}_{{{\text{rs}}}} + \varepsilon _{{{\text{fuzzy}}}} m_{{\text{s}}} \text{sgn} (s),$$
(24)
$$F_{{\rm{skyhook back} - \rm{stepping}}} = - k_{\rm{s}} e_{2} - c_{\rm{s}} e_{3} + c_{{\rm{sh}}} \dot{x}_{{\rm{rs}}} + k_{\rm{s}} (x_{\rm{v}} - x_{{\rm{rv}}} ) + c_{\rm{s}} (\dot{x}_{\rm{v}} - \dot{x}_{{\rm{rv}}} ) + 3z_{3} m_{\rm{s}} - 2z_{1} m_{\rm{s}} - z_{2} m_{\rm{s}} .$$
(25)

MR Damper Model

(1) Experimental setup

The MR damper test and in-loop simulation system is shown in Fig. 5. The construction of the MR damper experimental platform is shown in Fig. 6, which realizes the experiment of MR damper modeling.

Fig. 5
figure 5

MR damper test and in-loop simulation system

Full size image
Fig. 6
figure 6

MR damper experimental platform

Full size image

Model Identification Experiment of MR Damper

In this paper, the PSO algorithm is used to solve the parameters. The parameter least-squares method is used for parameter fitting. The nonlinear least-squares method is used to estimate parameters of the nonlinear model according to the minimum criterion of the gap. It determines the objective function as Eq. (26).

$$\mathop {\min }\limits_{\theta } e = \mathop {\min }\limits_{\theta } \sum\limits_{{i = 1}}^{n} {\left[ {y_{i} - f(x_{i} ,\dot{x}_{i} ,\ddot{x}_{i} ,k_{{\text{d}}} ,c_{{{\text{po}}}} ,m_{{\text{f}}} ,f_{y} ,\lambda _{1} ,\lambda _{2} ,f_{0} )} \right]^{2} } ,$$
(26)

where \(\theta\) is a vector of parameters \(k_{{\text{d}}} ,c_{{{\text{po}}}} ,m_{{\text{f}}} ,f_{y} ,\lambda _{1} ,\lambda _{2} ,f_{0}\) to be determined.

The gap function for each particle in the definition formula (26) is the square of the difference between the force calculated by the current parameter of each particle and the experimental force obtained by the Eq. (7).

Figure 7 is a comparison of the velocity-force and displacement-force of the experimental MR damper and the modified hyperbolic tangent model. It can be seen from the figure that the modified hyperbolic tangent model obtained by PSO parameter training can basically match the experimental results. Since the above parameters are obtained under a specific voltage, to obtain the variation of each parameter with voltage, in the following sub-section, the quadratic equations are fitted to each parameter to obtain the quadratic coefficient, the primary coefficient and the constant of each parameter under different voltages, so as to obtain a hyperbolic tangent positive model under different voltages.

Fig. 7
figure 7

The comparison displacement speeds of experimental data and modified model at various input voltages

Full size image

(3) Determine the reverse and positive model of the MR damper

Since the changes of \(\lambda _{1}\) and \(f_{0}\) are not obvious under different voltages, it can be considered as a constant value. It sets \(\lambda _{1}\) to 0.000016 and \(f_{0}\) to 0.08. To get the fitting results of parameters \(k_{{\text{d}}}\), \(c_{{{\text{po}}}}\), \(m_{{\text{f}}}\), \(f_{y}\), and \(\lambda _{2}\), it makes the following settings, where \(\hat{\varphi }\) is the voltage:

$$k_{{\text{d}}} = k_{{{\text{d}},2}} \hat{\varphi }^{2} + k_{{{\text{d}},1}} \hat{\varphi } + k_{{{\text{d}},0}} ,$$
(27)
$$c_{{{\text{po}}}} = c_{{{\text{po}},2}} \hat{\varphi }^{2} + c_{{{\text{po}},1}} \hat{\varphi } + c_{{{\text{p}},0}} ,$$
(28)
$$m_{{\text{f}}} = m_{{{\text{f}},2}} \hat{\varphi }^{2} + m_{{{\text{f}},1}} \hat{\varphi } + m_{{{\text{f}},0}} ,$$
(29)
$$f_{y} = f_{{y,2}} \hat{\varphi }^{2} + f_{{y,1}} \hat{\varphi } + f_{{y,0}} ,$$
(30)
$$\lambda _{2} = \lambda _{{2,2}} \hat{\varphi }^{2} + \lambda _{{2,1}} \hat{\varphi } + \lambda _{{2,0}} .$$
(31)

The fitting coefficients of each parameter are shown in Table 1. Through the above analysis, the voltage function of the modified hyperbolic tangent model at different voltages can be obtained. It substitutes the formulas (27), (28), (29), (30), and (31) into the formula (7), and then it can be obtained:

$$\begin{gathered} f = f_{0} + k_{{\text{d}}} x + c_{{{\text{po}}}} \dot{x} + m_{{\text{f}}} \ddot{x} + f_{y} \tan {\text{sig}}\left( {(\dot{x} + \lambda _{1} \text{sgn} (\ddot{x}))\lambda _{2} } \right) \hfill \\ \begin{array}{*{20}c} {} \\ \end{array} = f_{0} + \left( {k_{{{\text{d}},2}} \hat{\varphi }^{2} + k_{{{\text{d}},1}} \hat{\varphi } + k_{{{\text{d}},0}} } \right)x + \left( {c_{{{\text{po}},2}} \hat{\varphi }^{2} + c_{{{\text{po}},1}} \hat{\varphi } + c_{{{\text{p}},0}} } \right)\dot{x} + \left( {m_{{{\text{f}},2}} \hat{\varphi }^{2} + m_{{{\text{f}},1}} \hat{\varphi } + m_{{{\text{f}},0}} } \right)\ddot{x} \hfill \\ \begin{array}{*{20}c} {} \\ \end{array} + \left( {f_{{y,2}} \hat{\varphi }^{2} + f_{{y,1}} \hat{\varphi } + f_{{y,0}} } \right)\tan {\text{sig}}\left( {\left( {\dot{x} + \lambda _{1} \text{sgn} (\ddot{x})} \right)\left( {\lambda _{{2,2}} \hat{\varphi }^{2} + \lambda _{{2,1}} \hat{\varphi } + \lambda _{{2,0}} } \right)} \right). \hfill \\ \end{gathered}$$
(32)
Table 1 Fitting coefficient of each parameter
Full size table

Therefore, the force, fitting coefficients and damper state of the modified hyperbolic tangent model can be expressed as:

$$f = g\left( {f_{0} ,k_{{{\text{d}},2}} ,k_{{{\text{d}},1}} ,k_{{{\text{d}},0}} ,c_{{{\text{po}},2}} ,c_{{{\text{po}},1}} ,c_{{{\text{p}},0}} ,m_{{{\text{f}},2}} ,m_{{{\text{f}},1}} ,m_{{{\text{f}},0}} ,f_{{y,2}} ,f_{{y,1}} ,f_{{y,0}} ,\lambda _{1} ,\lambda _{{2,2}} ,\lambda _{{2,1}} ,\lambda _{{2,0}} ,\hat{\varphi },x,\ddot{x},\dot{x}} \right).$$
(33)

When the control force is used to obtain the desired control force of the MR damper, the voltage corresponding to this force is obtained, and the Eqs. (27), (28), (29), (30) and (31) are substituted into (7), and is obtained:

$$0 = a\hat{\varphi }^{2} + b\hat{\varphi } + c,$$
(34)

where: \(a = k_{{{\text{d}},2}} q_{i} + c_{{{\text{po}},2}} \dot{q}_{i} + m_{{{\text{f}},2}} \ddot{q}_{i} + f_{{y,2}} \tan {\text{sig}}((\dot{q}_{i} + \lambda _{1} \text{sgn} (\ddot{q}_{i} ))\lambda _{{2,2}}^{ - } )\), \(b = k_{{{\text{d}},1}} q_{i} + c_{{{\text{po}},1}} \dot{q}_{i} + m_{{{\text{f}},1}} \ddot{q}_{i} + f_{{y,1}} \tan {\text{sig}}((\dot{q}_{i} + \lambda _{1} \text{sgn} (\ddot{q}_{i} ))\lambda _{{2,1}}^{ - } )\), \(c = k_{{{\text{d}},0}} q_{i} + c_{{{\text{po}},0}} \dot{q}_{i} + m_{{{\text{f}},0}} \ddot{q}_{i} + f_{{y,0}} \tan {\text{sig}}((\dot{q}_{i} + \lambda _{1} \text{sgn} (\ddot{q}_{i} ))\lambda _{{2,0}}^{ - } ) - f - f_{0}\)

\(q_{i}\) is the displacement that changes at any time during the experiment. \(\lambda _{{2,2}}^{ - }\), \(\lambda _{{2,1}}^{ - }\) and \(\lambda _{{2,0}}^{ - }\) are the parameters of the fitting parameters \(\lambda _{{2,2}}\), \(\lambda _{{2,1}}\), and \(\lambda _{{2,0}}\) after the tansig function for the square of the voltage, the one-time term and the constant term.

Then use the quadratic formula to find the command voltage:

$$\hat{\varphi } = \frac{{ - b + \sqrt {b^{2} - 4ac} }}{{2a}}.$$
(35)

This article establishes a saturation range to limit voltage \(\hat{\varphi }\) below the maximum voltage \(\varphi _{{\max }}\) available from the external power supply and above the actual minimum zero voltage. The case of \(\hat{\varphi } < 0\) usually occurs in passive dampers. The damper used in this paper is a MR semi-active damper whose voltage is given as:

$$\hat{\varphi } = \left\{ \begin{gathered} \varphi _{{\max }} ,\begin{array}{*{20}c} {} & {} \\ \end{array} \hat{\varphi } > \varphi _{{\max }} \hfill \\ 0,\begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \hat{\varphi } < 0 \hfill \\ \hat{\varphi },\begin{array}{*{20}c} {} & {} \\ \end{array} 0 \le \hat{\varphi } \le \varphi _{{\max }} \hfill \\ \end{gathered} \right..$$
(36)

Numerical Simulation

Simulation Process

In this paper, Fig. 8 shows back-stepping sliding mode control feedback loop associated with MR dampers.

Fig. 8
figure 8

Back-stepping sliding mode control feedback loop associated with MR dampers

Full size image

In Fig. 8, first, the excitation is input to the vehicle suspension model and the reference model, and then the two model states are input to the controller. The controller obtains the force required by the MR process in three steps. After that, the required force and suspension states are input to the inverse model of the MR damper to obtain the voltage. Finally, voltage and suspension states are input to reverse and positive MR model to implement the sliding mode control system with MR dampers. The forward and inverse models of MR damper used in the simulation are obtained by the above-mentioned 2.4 MR damper model through three steps.

Simulation Experiment with MR Damper

To verify the effect of the proposed back-stepping sliding mode controller, the dynamic model of the system was established for simulation analysis. The road surface excitation can be expressed as: \(\dot{z}_{0} = - 2\pi f_{0} z_{0} + 2\pi n_{0} w\sqrt {G_{n} (n_{0} )v}\) where \(n_{0} = 0.1\;{\text{m}}^{{ - 1}}\), \(G_{n} (n_{0} ) = 3.2 \times 10^{{ - 5}} {\text{m}}^{3}\), \(f_{0} = 0.011v({\text{Hz}})\), \(v = 20\;{\text{m}}/{\text{s}}\). The simulation parameters are set as shown in Table 2.

Table 2 MR damper and control parameters
Full size table

This paper to verify the control effect of the designed back-sliding mode controller, it is according to the dynamic equation of the three-degree-of-freedom seat suspension, reference model and error system, the experiment is carried out. Figure 9 shows the control system for a seat suspension system. The back-stepping sliding mode, sliding mode, fuzzy sliding mode and the skyhook back-stepping control are compared with the passive system.

Fig. 9
figure 9

The system for a seat suspension system

Full size image

Figure 10 is a three-dimensional diagram of the \(e_{1} ,e_{2} ,e_{3}\) each control method coordinates, the grade of \(e_{1}\) is \(10^{{ - 7}}\); the grade of \(e_{2}\) is \(10^{{ - 7}}\); the grade of \(e_{3}\) is equal to the number of \(10^{{ - 6}}\) of the back-stepping sliding mode method, and this method of \(e_{1} ,e_{2} ,e_{3}\) grades are smallest than others. It can be seen that the back-stepping sliding mode control method can best follow the approximate skyhook-damping reference model compared with the sliding mode, the fuzzy sliding mode and skyhook back-stepping control method.

Fig. 10
figure 10

Three-dimensional maps of \(e_{1} ,e_{2} ,e_{3}\) coordinates for each control method

Full size image

Figures 11, 12, and 13 are the simulation results of the seat suspension acceleration, velocity, and displacement of each control method, and Tables 3, 4, and 5 are the maximum, minimum, mean, root mean square, and RMS reduction rate of the acceleration, velocity and displacement simulation results.

Fig. 11
figure 11

Acceleration of seats for each control and approximate skyhook-damping reference model

Full size image
Fig. 12
figure 12

Velocity of seats for each control and approximate skyhook-damping reference model

Full size image
Fig. 13
figure 13

Displacement of seats for each control and approximate skyhook-damping reference model

Full size image
Table 3 Parameters of seat suspension acceleration obtained by various control methods
Full size table
Table 4 Parameters of seat suspension velocity obtained by various control methods
Full size table
Table 5 Parameters of seat suspension displacement obtained by various control methods
Full size table

It can be seen from Figs. 11, 12, and 13, in terms of suspension acceleration, velocity, and displacement, the back-stepping sliding mode can best follow the reference model. Tables 3, 4, and 5 show that the sliding mode, fuzzy sliding mode, skyhook back-stepping and back-stepping sliding mode control methods compared with the passive suspension, their acceleration root mean squares are reduced by 31.0%, 44.7%, 51.0%, and 52.6%, their velocity root mean squares are reduced by 31.4%, 40.7%, 42.4%, and 44.4% and their displacement root mean squares are reduced by 26.3%, 28.2%, 30.0%, and 30.3%, respectively. So, the back-stepping sliding mode control method has the greatest reduction in RMS acceleration, velocity, and displacement.

The power spectrum density of seat suspension acceleration under random road surface excitation is shown in Fig. 14. It can be seen from Fig. 14, the seat acceleration under the action of the back- stepping sliding mode controller is significantly reduced in most frequency bands, which improve the ride comfort of the vehicle. In the frequency range of 4–12 Hz, the internal organs of the human body are most prone to resonance, so zoom in this part, it can be seen that the back-stepping sliding mode controller has a significantly lower acceleration than other control methods, thereby reducing vibration.

Fig. 14
figure 14

Acceleration of seats for each control and approximate skyhook-damping reference model

Full size image

Experiment

To verify the proposed back-stepping sliding mode semi-active control algorithm, the hardware in the loop schematic diagram of vehicle suspension is built, as shown in Fig. 15. The hardware-in-loop test bench of MR-damper is constructed with reference to article [20]. The control method is verified by hardware in the loop simulation. In the control model, a quarter vehicle dynamic model is established, and the back-stepping sliding mode control algorithm is used to obtain the control force provided by the MR damper and the dynamic deflection of the seat suspension. By establishing the inverse model of MR damper, the voltage is obtained, and the voltage is supplied to MR damper through data acquisition system and damper drive circuit. Through the data acquisition system and servo amplifier, the dynamic deflection of the seat suspension obtained from the control model is provided to the electro-hydraulic servo system. The electro-hydraulic servo system drives the MR damper to move according to the dynamic deflection and voltage required by the experiment. The force sensor detects the real-time force of MR damper and transmits it to the control model through signal adapter and data acquisition system, thus completing the construction of vehicle semi-active hardware in the loop suspension control experiment, as shown in Fig. 16.

Fig. 15
figure 15

The hardware in the loop schematic diagram of vehicle suspension

Full size image
Fig. 16
figure 16

The vehicle suspension hardware in the loop experimental platform

Full size image

To verify the semi-active control algorithm, a sinusoidal signal with amplitude of 0.03 m and frequency of 4Pi is used as road excitation, and the test time is 50000 ms. Due to the use of magnetorheological fluid damper, the passive suspension takes the minimum damping as the reference. Figure 17 shows the road excitation signal input by hardware in the loop. Figure 18 shows the forces generated by the control algorithm and the forces actually generated. Figure 19 shows the displacement produced by the hardware in the loop hydraulic cylinder and the displacement of the suspension dynamic deflection in the control model. Figure 20 shows the seat acceleration of passive and back-stepping sliding mode control of hardware in the loop system. Figure 21 shows the seat speed of passive and back-stepping sliding mode control of hardware in the loop system. Figure 22 is a 3D diagram \(e_{1} ,e_{2} ,e_{3}\) of the hardware in the loop back-stepping sliding mode control system. Figure 23 shows the sliding surface of the hardware in the loop back-stepping sliding mode control system.

Fig. 17
figure 17

The road excitation signal input by hardware in the loop

Full size image
Fig. 18
figure 18

The forces generated by the control algorithm and the forces actually generated

Full size image
Fig. 19
figure 19

The displacement produced by the hardware in the loop hydraulic cylinder and the displacement of the suspension dynamic deflection in the control model

Full size image
Fig. 20
figure 20

The seat acceleration of passive and back-stepping sliding mode control of hardware in the loop system

Full size image
Fig. 21
figure 21

The seat speed of passive and back-stepping sliding mode control of hardware in the loop system

Full size image
Fig. 22
figure 22

A 3D diagram \(e_{1} ,e_{2} ,e_{3}\) of the hardware in the loop back-stepping sliding mode control system

Full size image
Fig. 23
figure 23

The sliding surface of the hardware in the loop back-stepping sliding mode control system

Full size image

It can be found from Fig. 18 that the force generated by MR damper can well follow the force required by the back-stepping sliding mode control model, and the time lag is small. It shows that the forward and inverse model of MR damper can reproduce the hysteresis characteristics of MR damper, and can be applied to hardware in the loop control system.

In the experiment, the hydraulic cylinder will follow the seat dynamic deflection displacement of the control model to drive the MR damper, so that the MR damper receives the displacement input similar to the control model, and the required input voltage to the MR damper is obtained through the inverse model of the MR damper, so as to generate the required control force. Figure 19 shows that the displacement of the hydraulic cylinder in the hardware loop can well follow the seat dynamic deflection in the control model. From the experimental data, it can be seen that the root mean square of the overall displacement data provided by the hydraulic cylinder is 0.0021 smaller than the root mean square of the seat dynamic deflection provided by the control model, so the hydraulic cylinder can better follow the seat dynamic deflection of the control model in the experiment. This provides an experimental basis for the research of hardware in the loop control experiment in the future.

It can be found from Figs. 20 and 21 that the acceleration and velocity of seat mass center obtained by hardware in the loop of back-stepping sliding mode are smaller than those of passive suspension. It can be seen from the experimental data that the root mean square of the acceleration and velocity of the center of mass of the back-stepping sliding mode in the ring is 0.3643 and 0.0318 smaller than that of the corresponding data of the passive suspension, respectively. It shows that the back-stepping sliding mode algorithm has a certain control effect.

Figures 22 and 23 are the generalized error vector and sliding surface of the back-stepping sliding mode. It can be seen that the quantity unit of the generalized error vector and sliding surface is relatively small, which indicates that the back-stepping sliding mode can follow the reference model well, and further illustrates the effectiveness of the algorithm.

Conclusion

Based on the quarter-vehicle-seat suspension, this paper uses the particle swarm training algorithm to build the experimental platform and input the experimental data into the training system. Through the training of the improved hyperbolic tangent model parameters, the positive and inverse models of the improved hyperbolic tangent MR damper are obtained. The dynamic model of the system was established for simulation analysis. The semi-active suspension control uses sliding mode, fuzzy sliding mode, skyhook back-stepping, and back-stepping sliding mode control methods. The control results under test conditions are given; the data and charts are analyzed and evaluated. Through the hardware in the loop experiment, the effectiveness of forward and inverse model of MR damper is verified, and the effectiveness of back-stepping sliding mode control is verified. The results show that the back-stepping sliding mode proposed in this paper is better than the seat suspension under other control and passive systems, which proves that the back-stepping sliding mode controller is effective. It also shows that the forward and inverse model of MR damper is effective.