1 Introduction

The inverse simulation typically involves computing control inputs required to perfectly track a prescribed trajectory. This predictive capability of required controls is extremely valuable for the flight dynamic investigations and controller design studies. The development history, application areas, numerical methods, and stability issue related to the currently available methods are well overviewed in Ref. [1, 2]. On the other hand, Linghai Lu et al. [3] pointed out that all inverse simulation algorithms widely used today are subject to various types of numerical accuracy and stability problems. Many researches have been carried out to identify the origins of associated numerical problems and to develop more robust algorithms by controlling numerical processes in an extremely detailed manner. Numerical optimization approaches of Celi [4], two-time scale approach by Avanzini et al. [5], optimal search algorithm adopted by Linghai Lu et al. [3] are a few examples of such efforts and there exist too many to list every single effort. These examples indicate that further studies are required to resolve numerical accuracy and stability problems associated with currently available inverse simulation methods.

An inverse simulation problem is inherently formulated in a form of the differential algebraic equations (DAEs) due to the imposed path constraints. Thomson et al. [2] proved that the formulation associated with the inverse simulation problem reduces to index 2 DAEs in that the ordinary differential equations (ODEs) for control inputs can be obtained by applying twice differentiations of the algebraic constraints. Higher index DAE is much more difficult to solve than the ODEs or index 1 DAEs. Petzold et al. recommended the application of index reduction techniques for the solution of higher index systems to use implicit solvers of the ODEs and index 1 DAEs [6, 7]. On the other hand, the most widely used integration-based approach simply adopts the multi-stage explicit integrators or single-step implicit methods without detail consideration on these problem characteristics [8]. Therefore, it may be natural that the currently available inverse simulation methods suffer from various types of numerical instability and accuracy problems addressed in Ref. [2]. Without detailed algorithmic modifications, these methods can be applied only to the problems over a relatively short time period due to the deficiency in the robustness for long-term simulations.

Based on the above considerations, this paper proposes a new algorithm to solve the inverse simulation problems in an efficient and robust manner. The pseudo-spectral method is adopted as an implicit time integrator in a moving horizon framework [9, 10]. And, the quasi-Newton and fixed-point iterative methods are applied to efficiently solve the resultant nonlinear algebraic equations (NAEs) to minimize computational burden in estimating Jacobean matrices [11, 12]. Because of these specific features, the proposed algorithms are collectively called by the pseudo-spectral inverse simulation techniques (PIST) throughout the paper. A detailed pseudo-code to implement the PIST is formally proposed for researchers hoping to apply the present approach in the future. In addition, various numerical tips used to enhance the solution robustness and efficiency are explained in detail for each step of major routines, some of which are valuable even for the conventional approaches. The performance measures such as the number of iterations required to obtain a converged solution, function residuals in NAEs, and the minimum values of adaptive under-relaxation factors are used to compare the relative computing time and convergence status with varying solution control parameters.

The PIST is applied to maneuvering flights using the BO105 flight dynamic model generated by the HETLAS (Helicopter Trim, Linearization, and Simulation) program, which has been developed for the rotorcraft fly-by-wire flight control system program [13, 14]. The trajectories for the inverse simulations are prescribed using the 7th order polynomial functions of a non-dimensional time to connect the prescribed waypoints along the trajectory in a realizable manner. The important numerical properties of the PIST algorithm are thoroughly investigated through the applications to the popup maneuver. Thereby, the solution control parameters including the average time-step size and number of quadrature points can be optimally selected using the results of simulations. The long-term simulation capability with the PIST is demonstrated through the applications to the pirouette maneuver with varying maneuver exit times. Finally, to analyze the robustness characteristics to the level of maneuver aggressiveness, the depart/abort maneuver defined in ADS-33E-PRF [15] is analyzed with different levels of maneuver aggressiveness. From the results of these applications, it can be concluded that the present PIST can provide extremely efficient and robust solution to the inverse simulation problems related to aggressive aircraft maneuvers over relatively long period time with much less accuracy and instability problems than the conventional integration inverse simulation methods.

2 Inverse Simulation Problems and Solution Methods

2.1 General Formulation of Inverse Simulation Problems

Inverse simulation problems typically intend to determine the control inputs required to produce a prescribed trajectory using system dynamics. For this purpose, general nonlinear aircraft dynamics and system output may be represented by the equations of the following form [2]:

$$ \begin{aligned} &{\dot{\mathbf{x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{u}},t), \hfill \\ &{\mathbf{y}}(t) = {\mathbf{g}}({\mathbf{x}},t). \hfill \\ \end{aligned} $$
(1)

The first equation represents the Euler equation with the system states x and controls u, which are defined by x = (u, v, w, p, q, r, ϕ, θ, ψ, x, y, z)T and u = (δ0, δ1C, δ1S, δP)T for the rotorcraft. The system states consist of the linear and angular velocities (u, v, w, p, q, r) in each body-fixed axis, the Euler angles (ϕ, θ, ψ), and position vector (x, y, z), respectively. Also, the controls (δ0, δ1C, δ1S, δP) contain the main-rotor collective, longitudinal and lateral cyclic, and tail-rotor collective pitch angles, respectively. For the inverse simulation purpose, the system output is typically defined with the aircraft trajectory such as y = (x, y, z, ψ)T. In a case when the system output y(t) is related to the prescribed trajectory yp(t), the inverse simulation problem can be formulated as:

$$ \begin{aligned} {\dot{\mathbf{x}}} & = {\mathbf{f}}({\mathbf{x}},{\mathbf{u}},t), \hfill \\ {\mathbf{0}} &= {\mathbf{g}}({\mathbf{x}},t) - {\mathbf{y}}^{p} (t). \hfill \\ \end{aligned} $$
(2)

Twice differentiations of the 2nd equation produce the following ODEs for control inputs.

$$ \begin{aligned} {\mathbf{0}} &= {\mathbf{g}}_{{\mathbf{x}}} {\mathbf{f}} + {\mathbf{g}}_{t} - {\mathbf{y}}_{t}^{p} \hfill \\ {\mathbf{0}} &= {\mathbf{g}}_{{{\mathbf{xx}}}} {\mathbf{f}}^{2} + {\mathbf{g}}_{{\mathbf{x}}} \left( {{\mathbf{f}}_{{\mathbf{x}}} {\mathbf{f}} + {\mathbf{f}}_{{\mathbf{u}}} {\dot{\mathbf{u}}} + {\mathbf{f}}_{t} } \right) + {\mathbf{g}}_{tt} - {\mathbf{y}}_{tt}^{p} . \hfill \\ \end{aligned} $$
(3)

Therefore, the control inputs required to exactly track the prescribed trajectory can be computed from the second equation when the matrix gxfu is nonsingular. As a result, it can be concluded that the general inverse simulation problem formulated in the form of Eq. (2) is an index 2 DAEs [6, 7] under this non-singularity condition. However, the mentioned DAE index can be increased with the singular gxfu when the trajectory yp(t) is specified with the position vector and heading angle. On the other hands, smooth controls can be obtained from Eq. (3) only when the 2nd time derivative of the prescribed trajectory exists. It is generally known that higher than index 1 DAEs are much more difficult to solve than the ODEs or index 1 DAEs [6,7,8]. Therefore, many literatures on DAE solvers recommend the application of index reduction techniques for the solution of higher index systems to use index 1 DAE solvers or implicit integrators. However, an exact implementation of these kinematics in an exact manner is not a simple task. The present paper confines its scope in the direct solution of the index 2 DAE form of the formulation using the pseudo-spectral integrator and efficient NAE solvers.

Importance of an adequate trajectory prescription cannot be overemphasized in the inverse simulation. The maneuver trajectories for a specific aircraft should be designed considering their realizability. Furthermore, they should meet special conditions imposed by the problem formulation as shown in Eq. (3), which says that the realizable smooth control inputs can be obtained only when the trajectory is prescribed with enough smoothness to guarantee the existence of y p tt in Eq. (3). Otherwise, the predicted control inputs may show unreasonable discontinuities and highly oscillatory behaviors which are rarely seen in real flights. Trajectories required for the inverse simulation are typically prescribed by the following parameter sets [2, 3, 17]:

$$ {\mathbf{y}}^{p} (t) = \left( {V^{p} ,\gamma^{p} ,\chi^{p} } \right)^{\text{T}} , $$
(4)

or

$$ {\mathbf{y}}^{p} (t) = \left( {x^{p} ,y^{p} ,z^{p} ,\chi^{p} } \right)^{p} . $$
(5)

Here, Vp, γp, and χp denote the flight speed, climb angle, and track angle, respectively. Two sets of the prescribed trajectory shown above are interchangeable using the following kinematical relations:

$$ \begin{aligned} \dot{x}^{p} &= V^{p} \cos \gamma^{p} \cos \chi^{p}, \hfill \\ \dot{y}^{p} &= V^{p} \cos \gamma^{p} \sin \chi^{p}, \hfill \\ \dot{z}^{p} &= - V^{p} \sin \gamma^{p}, \hfill \\ V^{p} &= \sqrt {\left( {\dot{x}^{p} } \right)^{2} + \left( {\dot{y}^{p} } \right)^{2} + \left( {\dot{z}^{p} } \right)^{2} } . \hfill \\ \end{aligned} $$
(6)

In general, the track angle differs from the heading angle. As an example, the track and heading angles are different by 90° in the sidestep and pirouette maneuvers [15]. The heading angle for a specific mission-task-element (MTE) largely depends on the pilot strategy. However, the heading angle may be easily defined considering the maneuver characteristics or it can assign the same value as the track angle for the forward flight without deviating greatly from the purpose of the inverse simulations. For this reason, this paper prescribes the required trajectories using the heading angle rather than the track angle.

2.2 Pseudo-Spectral Time Integrator

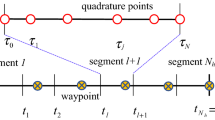
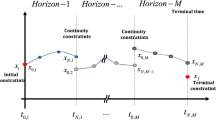
The pseudo-spectral integrator is adopted in the present inverse simulation algorithm to transform the system dynamics into the solvable NAEs. For this purpose, the time horizon of interests is divided by several small segments as shown in Fig. 1 and a moving horizon concept is used to accelerate convergence [10]. Detailed methods used in this paper can be found in Ref. [9]. Here, we will briefly introduce for completeness of the paper using the following initial value problem:

Fig. 1
figure 1

Time segments, quadrature points, and waypoints in computational domain

Full size image
$$ {\dot{\mathbf{x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{u}},t)\quad {\text{with}}\quad {\mathbf{x}}(t_{0} ) = {\mathbf{x}}_{0} \quad {\text{over}}\quad t \in [t_{0} ,t_{f} ]. $$
(7)

The above equations can be expressed in a form of the following integral equation:

$$ {\mathbf{x}}(t) = {\mathbf{x}}_{0} + \int_{{t_{0} }}^{t} {{\mathbf{f}}({\mathbf{x}},{\mathbf{u}},\xi )} {\text{d}}\xi . $$
(8)

To utilize a standard integration formula, the following affine transformation is applied to Eq. (8) to obtain Eq. (10):

$$ \tau = \frac{2t}{{t_{f} - t_{0} }} - \frac{{t_{f} + t_{0} }}{{t_{f} - t_{0} }},\quad \tau \in [ - 1,\;1], $$
(9)
$$ {\mathbf{x}}(t) = {\mathbf{x}}_{0} + \frac{{t_{f} - t_{0} }}{2}\int_{ - 1}^{\tau } {{\mathbf{f}}\left\{ {{\mathbf{x}},{\mathbf{u}},t(\xi )} \right\}{\text{d}}\xi } . $$
(10)

The pseudo-spectral method utilizes the Lagrange interpolation over a given set of quadrature nodes {τk} k= N k=0 . The forcing function can be approximated using the corresponding Lagrange interpolating functions {ϕk(τ)} k= N k=0 as:

$$ {\mathbf{f}}(\tau ) \approx \sum\limits_{k = 0}^{k = N} {\phi_{k} (} \tau ){\mathbf{f}}_{k} \quad {\text{with}}\quad {\mathbf{f}}_{k} = {\mathbf{f}}\left\{ {{\mathbf{x}}_{k} ,{\mathbf{u}}_{k} ,t(\tau_{k} )} \right\}. $$
(11)

Then, Eq. (10) can be transcribed as:

$$ \begin{aligned} & {\mathbf{x}}_{j} = {\mathbf{x}}_{0} + \frac{{t_{f} - t_{0} }}{2}\sum\limits_{k = 0}^{k = N} {I_{jk} } {\mathbf{f}}_{k} ,\quad (j = 1,2, \ldots ,N), \\ & {\text{where}}\quad I_{jk} = \int_{ - 1}^{{\tau_{j} }} {\phi_{k} (\tau )} {\text{d}}\tau . \\ \end{aligned} $$
(12)

The coefficients {Ijk} j, k= N j, k=1 are components of the integration matrix for the pseudo-spectral integrator and Ref. [9] described their computational methods regardless of types of node distribution using the generalized spline interpolation (G-SPIN) formula. This paper uses the Legendre–Gauss–Lobatto (LGL) quadrature points, which contain two end points and allows an easy definition of initial and final conditions.

As a result, the systems of NAEs for the inverse simulation can be obtained in the following form using Eq. (12) and by applying the path constraints given in Eq. (2):

$$ \begin{array}{lll} {{\mathbf{h}}_{j} = \left( \begin{aligned} {\mathbf{h}}_{1,j} \hfill \\ {\mathbf{h}}_{2,j} \hfill \\ \end{aligned} \right) = {\mathbf{0}}}, & {} & {} \\ {{\mathbf{h}}_{1,j} = {\mathbf{x}}_{0} + \frac{{t_{f} - t_{0} }}{2}\sum\limits_{k = 0}^{k = N} {I_{jk} } {\mathbf{f}}_{k} - {\mathbf{x}}_{j} } & {\text{for}} & {j = 1,2, \ldots ,N,} \\ {{\mathbf{h}}_{2,j} = {\mathbf{g}}({\mathbf{x}}_{j} ,t_{j} ) - {\mathbf{y}}^{p} (t_{j} ),} & {} & {} \\ \end{array} $$
(13)

where h1,j and h2,j correspond to Eqs. (12) and (2), respectively.

2.3 NAE Solvers

The solution algorithm of NAEs shown in Eq. (13) should be carefully selected because the iterative solution of NAEs consumes most of computing time to approximate the Jacobean matrix. The present paper implements two different methods. The first one is the quasi-Newton method and the other one is the fixed-point iteration algorithm [11, 12]. The quasi-Newton method requires no repeated computations of the Jacobean matrix after available in the 1st iterative step, whereas the 2nd method needs no Jacobean computations. Therefore, the computational efficiency can be greatly enhanced once their algorithmic implementations work well. For the above NAEs represented by h(y) = {hj} j= N j=1  = 0 with y = {xj, uj} j= N j=1 , the standard Newton–Raphson method can be described by

$$ \begin{aligned} {\mathbf{y}}_{i + 1} &= {\mathbf{y}}_{i} + \Delta {\mathbf{y}}_{i} ,\quad (i = 0,1,2, \ldots ) \hfill \\ \Delta {\mathbf{y}}_{i} &= - {\mathbf{J}}_{i}^{ - 1} {\mathbf{h}}({\mathbf{y}}_{i} ), \hfill \\ {\mathbf{J}}_{i} & = \frac{{\partial {\mathbf{h}}({\mathbf{y}}_{i} )}}{{\partial {\mathbf{y}}}}, \hfill \\ \end{aligned} $$
(14)

where the subscript i represent the i-th solution iterates. The Jacobean matrix Ji for the i-th iterate is typically approximated using the finite difference formula around the current iterate yi. The quasi-Newton method uses an approximate inverse of Jacobean B −1 i to update the solution as:

$$ \Delta {\mathbf{y}}_{i} = - {\mathbf{B}}_{i}^{ - 1} {\mathbf{g}}({\mathbf{y}}_{i} ),\quad {\mathbf{B}}_{i}^{ - 1} \approx {\mathbf{J}}_{i}^{ - 1} . $$
(15)

This paper selects the Martinez’s column-updating method among various quasi-Newton methods since it has shown much higher robustness and efficiency than other methods in our trial solutions for the NAE test problems in Ref. [11]. The Martinez’s method updates each column of B −1 i+1 with different basis vectors using the following formula:

$$ \begin{aligned} {\mathbf{B}}_{i + 1}^{ - 1} & = {\mathbf{B}}_{i}^{ - 1} + \frac{{\left\{ {\Delta {\mathbf{y}}_{i} - {\mathbf{B}}_{i}^{ - 1} \left( {{\mathbf{g}}_{i + 1} - {\mathbf{g}}_{i} } \right)} \right\}\left( {{\mathbf{e}}_{j} } \right)^{T} {\mathbf{B}}_{i}^{ - 1} }}{{\left( {{\mathbf{e}}_{j} } \right)^{T} {\mathbf{B}}_{i}^{ - 1} \left( {{\mathbf{g}}_{i + 1} - {\mathbf{g}}_{i} } \right)}},\\ &\quad (j = 1,2, \ldots ,m). \end{aligned} $$
(16)

Here, ej is an orthogonal basis vector and each row can be expressed using the Kronecker Delta function (ejk = δjk) k= m k=1 .

Next, the fixed-point y of a function vector h is defined by a point satisfying Eq. (17) [12]. The problem of finding such a fixed point is called the fixed-point problem.

$$ {\mathbf{y}} = {\mathbf{h}}({\mathbf{y}}). $$
(17)

Among various fixed-point algorithms, the simplest one is the Piccard iterative method represented in Eq. (18) and the standard Newton–Raphson method can be considered as the Piccard iterative method for the modified NAEs as expressed in Eq. (19):

$$ {\mathbf{y}}_{i + 1} = {\mathbf{h}}({\mathbf{y}}_{i} ), $$
(18)
$$ {\mathbf{y}}_{i + 1} = {\mathbf{y}}_{i} - {\mathbf{J}}^{ - 1} ({\mathbf{y}}_{i} ){\mathbf{h}}({\mathbf{y}}_{i} ). $$
(19)

Also, the pseudo-spectral integration formula given in Eq. (12) is the same form as the fixed-point problem. Therefore, the Piccard or other fixed-point algorithms are applicable to iteratively update differential variables without resorting to expensive computations of the Jacobean matrices. This approach generally works well for the solution of non-stiff ODEs [10, 16]. Two methods mentioned above are effectively applied to the present PIST under the moving horizon approach. Their implementation will be explained later in detail with reference to the associated pseudo-code. In a case when there exists a probable risk of numerical divergence as in highly aggressive maneuver analyses, the solution can be updated after applying the under-relaxation as shown in Eq. (20) and the under-relaxation factor αi can be adaptively adjusted using the vector norms of ‖h(yk)‖ or ‖Δyk‖, (k = i, i − 1, …) to guarantee numerical convergence. Equation (21) is used in the present paper to achieve this.

$$ \left( {{\mathbf{y}}_{i + 1} } \right)_{\text{update}} = {\mathbf{y}}_{i + 1} + \alpha_{i} ({\mathbf{y}}_{i + 1} - {\mathbf{y}}_{i} ),\quad \alpha_{i} \in (0,1], $$
(20)
$$ \alpha_{i} = \hbox{min} \left( {\alpha_{\hbox{max} } ,\;1.5\alpha_{i - 1} ,\;\frac{{\left\| {{\mathbf{g}}_{i - 1} } \right\|}}{{\left\| {{\mathbf{g}}_{i} } \right\|}}\alpha_{\hbox{max} } } \right),\quad \alpha_{\hbox{max} } \in (0,1]. $$
(21)

The maximum value of αi is typically set to αmax = 1 and the second term intends to accelerate convergence when functional residuals are monotonically decreased. The last term is to guarantee the converged solution even when functional residuals are monotonically increased over several iterates.

2.4 Spline Trajectory Generator

The generation of the realizable trajectory is treated as one of the most important parts in the inverse simulations. As an example, Thomson and Bradly have addressed only this topic in Ref. [17], cited in most of the literatures related to inverse simulations. Furthermore, the generalization of a trajectory description method for arbitrary realizable flight paths is not an easy task. Above all, the generated trajectory should meet the continuity conditions imposed by Eq. (3). Even when an index reduction method is applied to the index 2 DAEs as formulated in Eq. (2), the mentioned conditions become more stringent in that it requires preserving the continuity up to the 3rd order derivative of the trajectory function as a minimum over whole time horizon of interests. In a case when the polynomial function is used, it should be not less than 7th order to independently meet this requirement at both end points. The present paper applies the spline trajectory generation techniques to meet the above requirements and to provide a unified approach to arbitrary flyable trajectories including those composed of multiple maneuver phases. The attitude trajectory generation techniques used in Ref. [18] and the spline interpolation method in Ref. [9] are adopted for this purpose.

A flight path can be explained using multiple waypoints along the trajectory such as {tk, r w k  = (x w k , y w k , z w k , ψ w k )} k= K k=0 . A spline curve-fitting can be straightforwardly defined over each time interval t ∊ [tk, tk+1] using a non-dimensional time variable τ as:

$$ \begin{aligned} {\mathbf{r}}_{k} (\tau ) & = {\mathbf{a}}_{k} + {\mathbf{b}}_{k} \tau + {\mathbf{c}}_{k} \tau^{2} + {\mathbf{d}}_{k} \tau^{3} + {\mathbf{e}}_{k} \tau^{4} + {\mathbf{f}}_{k} \tau^{5} + \cdots, \\ \tau & = \frac{{t - t_{k} }}{{\Delta t_{k} }} \in [0,1], \\ \Delta t_{k} & = t_{k + 1} - \Delta t_{k}.\\ \end{aligned} $$
(22)

The coefficient vectors {ak, bk, …} k= K k=0 can be determined by applying the prescribed waypoint data and the continuity and smoothness conditions at each waypoint. The spline polynomials in the form of Eq. (22) are extremely convenient in that coefficients (ak, bk, ck) are directly related to the position, velocity and acceleration vectors at the initial point, respectively.

$$ {\mathbf{r}}_{k} (0) = {\mathbf{a}}_{k} ,\;\quad {\dot{\mathbf{r}}}_{k} (0) = \frac{{{\mathbf{b}}_{k} }}{{\Delta t_{k} }},\;\quad {\ddot{\mathbf{r}}}_{k} (0) = \frac{{2{\mathbf{c}}_{k} }}{{\Delta t_{k}^{2} }}. $$
(23)

Furthermore, Eqs. (24) and (25) can be used to obtain time derivatives or integrations of trajectory parameters with an initial parameter vector α0.

$$ {\dot{\mathbf{r}}}_{k} (\tau ) = \frac{1}{{\Delta t_{k} }}\left( {{\mathbf{b}}_{k} + 2{\mathbf{c}}_{k} \tau + 3{\mathbf{d}}_{k} \tau^{2} + 4{\mathbf{e}}_{k} \tau^{3} + 5{\mathbf{f}}_{k} \tau^{4} + \cdots } \right), $$
(24)
$$ \int_{0}^{\tau } {{\mathbf{r}}_{k} {\text{d}}\tau } = {\varvec{\upalpha}}_{0} + \Delta t_{k} \left( {{\mathbf{a}}_{k} \tau + \frac{1}{2}{\mathbf{b}}_{k} \tau^{2} + \frac{1}{3}{\mathbf{c}}_{k} \tau^{3} + \frac{1}{4}{\mathbf{d}}_{k} \tau^{4} + \cdots } \right). $$
(25)

The same spline approach can be applied to accurately estimate any scalar parameters. As an example, the spline coefficients for the speed and arc length can be computed using Eqs. (24) and (25). To achieve this, first the velocity vector is computed by applying Eq. (26) and the spline coefficients for the speed variation are obtained using the data set {tk, vk} k= K k=0 . Finally, the distribution of the arc length along the trajectory can be determined by applying the integration formula shown in Eq. (25) rather than by performing the numerical integration of the speed with Eq. (26).

$$ \begin{aligned} v(t) & = \left\| {{\dot{\mathbf{r}}}(t)} \right\| = \sqrt {\dot{x}^{2} (t) + \dot{y}(t)^{2} + \dot{z}(t)^{2} } , \hfill \\ s(t) & = \int_{{t_{0} }}^{t} {v(t){\text{d}}t} . \hfill \\ \end{aligned} $$
(26)

This arc length is an extremely convenient parameter when a maneuver is performed with a constant speed since the elapsed time along the trajectory is straightforwardly determined by t = s(t)/v.

2.5 Formal PIST Algorithm

Using the results of previous subsections, the formal algorithm for the present PIST is proposed as shown in Table 1. Waypoints and quadrature nodes are defined with different time sets to provide their independent handling. After a converged solution over a time-horizon segment is obtained, the solution at the final time τN is used to initialize the solutions over the next segment. The loop in STEP 6 represents such moving horizon approaches. Techniques used in the present study and tips for efficient implementation of each step are addressed in detail in a step-by-step sequence.

Table 1 Formal pseudo-code for the present PIST
Full size table

STEP 1 intends to provide waypoint data and solution parameters. The number of quadrature points N and the number of time-horizon segments Nh are extremely important since these parameters determine overall accuracy and solution convergence in PIST. The number of quadrature points directly affects the computing time of the Jacobean matrix and numerical accuracy at each segment. A larger value of N can enhance time-integration accuracy but poor initial estimates can cause numerical divergence over the segment. Therefore, trial analyses for their combinations are highly recommended to consider their effects on the solution accuracy and convergence. The spline coefficients are used in the present algorithm rather than the waypoints to generalize the usage of trajectory information and to use the integration and differentiation formula shown in Eqs. (24) and (25). STEP 2 represents this process. The time-horizon segments in STEP 3 are uniformly generated for all analyses in this paper. STEPS 4 and 5 explain the initialization process of the PIST. An aircraft trim solution is required to initiate the inverse simulation and the corresponding trim conditions can be computed using Eq. (23) and the spline trajectory coefficients at the first segment. The trim analysis results are used to initialize all solutions at each quadrature point within the first segment. The unknown vectors can be defined by the rigid-body states {xj} j= N j=1 and controls {u = (δ0, δ1C, δ1S, δTR) T j } j= N j=1 for the rotorcraft inverse simulation problems, respectively.

The present algorithm adopts a moving horizon approach as shown in the loop of Step 6. STEP 7 represents the initialization process for a new segment. STEP 8 intends to refine the initial guesses of the solutions for better convergence. For this purpose, the rigid-body states {xj} j= N j=1 satisfying Eq. (12) with control inputs fixed are iteratively computed. Here, the Piccard iterative method represented in Eq. (18) is applied to get the solutions rather than the quasi-Newton method. In a case when a large value of N is used, the under-relaxation using Eqs. (20) and (21) may be adopted to enhance the robustness. A few iterations are enough to get a fully converged solution in most cases. As in all inverse simulation methods, the proposed algorithm may spend most of computing time in estimating the Jacobean matrix with respect to the unknown variables y = {xj, uj} j= N j=1 . Therefore, the computational procedure related to the Jacobean evaluation should be carefully designed to enhance overall computational efficiency. The present algorithm adopts the Martinez’s column-updating method shown in Eq. (16). The inverse Jacobean can be recursively updated using the current values of the inverse Jacobean, the residuals in NAEs, and the corrections for the unknown variables. Given an initial Jacobean at each segment, all subsequent inverse Jacobean can be obtained without resorting to expensive computation of the new Jacobean. However, STEP 9 intentionally limits this computation only at the first segment. If the number of quadrature nodes and the time step Δtj = tj+1 − Δtj are small enough, the final inverse Jacobean at a segment can be used as a good approximation of the initial one for the next segment. Therefore, overall computational time can be greatly reduced. A new computation of the initial Jacobean at every single segment may contribute to enhance overall robustness of the PIST. However, STEP 9 provides the converged solutions without numerical failures for all applications in this paper. The algorithm solves all unknowns y = {xj, uj} j= N j=1 in a fully coupled manner as shown by STEPs 7–12. Some inverse simulation methods use an independent computation of control inputs to reduce the computing time, but most of the DAE literature do not recommend such an approach due to the probable problems of slow convergence and numerical instability.

3 Applications and Discussion

The present PIST is applied to the analyses of the aggressive maneuvers of Bo-105. The flight dynamics model for Bo-105 is implemented in the HETLAS [13, 14]. All applications of this paper utilize the rotor trim solutions to eliminate the effects of the high-frequency oscillatory forces and moments due to rotor and inflow dynamics. There exist various solution control parameters in the PIST algorithm, which greatly affect the robustness and efficiency of the analyses. Table 2 shows how these parameters are selected for a specific application in this paper. In addition, it is valuable to define other parameters providing good information on the robustness and efficiency of the analysis. The number of iterations required to obtain a fully converged solution at each segment may be a good indicator for the efficiency of an analysis. The functional residuals at the final iteration determine whether a solution is converged or not. Finally, the minimum values of the adaptive relaxation factor can be used to check both the robustness and efficiency of the analyses. In a case when this value reaches 1.0, it denotes that the functional residuals decrease monotonically. Hence, the required number of iterations can be reduced at each segment. These three parameters are selected in this paper as the measures of the robustness and efficiency of the present PIST.

Table 2 Solution control parameters for the PIST
Full size table

3.1 Popup Maneuver

The schematic view and the trajectory parameters for the popup maneuver used in the analyses are represented in Fig. 2, where the final time tf can be selectable to adjust the level of the maneuver aggressiveness. The aircraft enters the maneuver from the trimmed level flight condition at 60 knots and exits with 100ft height change. The simulations are performed with five quadrature points and with the number of segments allocated with 10 segments per a second (Nh ≈ 10tf). Figure 3 presents the simulation results for different final times. The simulations for all maneuvers except that with tf = 7 s are successfully performed up to the specified final times. Figure 4 shows that around 10 iterations are enough to obtain the converged solution and the functional residuals at each time-horizon segment are monotonically decreased with tf = 9 and tf = 10. The simulation for relatively higher aggressive maneuvers with tf < 9 required a greater number of iterations. The solution with tf = 7 failed at around 4 s, where the rate of climb reaches around 2000 ft/min and it may be much greater than the operational limit of BO-105 helicopter. The computed controls in the converged solutions exhibit smooth variations with which a normal pilot can manage his aircraft without exceptional skills.

Fig. 2
figure 2

Simulation parameters for popup maneuver

Full size image
Fig. 3
figure 3

Simulation results for popup maneuver

Full size image
Fig. 4
figure 4

Simulation status for popup maneuver with varying final time

Full size image

The time-step size of each segment can affect the robustness of the present PIST. Table 3 shows the design of numerical experiments and the corresponding results to clarify the effects of the number of quadrature points and time segments with the average time-step size fixed. The smaller the number of quadrature points, the more favorable results from a computational efficiency point of view can be achieved. However, it may be afraid that an accurate analysis will be difficult to obtain with three quadrature points with N = 2. Also, it is worth considering the numerical failure with N = 32, which corresponds to the extremely large step-length of 0.3125 s. The time variations of the required iteration number and the minimum under-relaxation factor as shown in Fig. 5 indicate that the solution robustness is degraded with the increased value of N. Based on the above investigations, most of the present analyses utilize five-point quadrature formula for the numerical integration of the motion equations and the number of tome-horizon segments is allocated with Nh = 10 per a second.

Table 3 Summary of test cases for solution control parameters (popup)
Full size table
Fig. 5
figure 5

Simulation status for popup maneuver with varying node distribution

Full size image

3.2 Piroutte Maneuver

The next application intends to test the long-term simulation capability of the PIST. The pirouette maneuver of ADS-33E-PRF is selected to address these issues. Figure 6 shows the maneuver parameters and ADS-33E-PRF recommends around steady 8 knots lateral velocity. Time fractions for the entry and exit phases are defined by κ0 and κf in the figure, respectively. These fractions may be independently used to determine each aggressiveness at the entry and exit phases, but these values are set to 0.1 in the present applications because overall aggressiveness can be controlled by changing the final time.

Fig. 6
figure 6

Trajectory parameters for pirouette maneuver (ADS-33E-PRF with tf = 45 s)

Full size image

The heading trajectories for each phase can be built in 7th order polynomials using the similar steps in the popup maneuver by applying the following conditions for each phase:

$$ \begin{aligned} \psi (t_{0} ) = 0, \hfill \\ \dot{\psi }(t_{0} ) = 0, \hfill \\ \ddot{\psi }(t_{0} ) = 0, \hfill \\ \dot{\psi }(t_{1} ) = \dot{\psi }_{\text{steady}}, \hfill \\ \ddot{\psi }(t_{1} ) = 0, \hfill \\ \dot{\psi }(t_{2} ) = \dot{\psi }_{\text{steady}}, \hfill \\ \ddot{\psi }(t_{2} ) = 0, \hfill \\ \psi (t_{f} ) = 2\pi, \hfill \\ \dot{\psi }(t_{f} ) = 0, \hfill \\ \ddot{\psi }(t_{f} ) = 0. \hfill \\ \end{aligned} $$
(25)

After generating the uniformly spaced time nodes{t w k } k= K k=0 , the position data for {(x w k , y w k )} k= K k=0 are computed using the circular radius R and the heading angles for each waypoint. The total number of waypoints consists of those allocated to each maneuver phase. Through a rigorous investigation, the allocated number of waypoints of (Kentry, Ksteady, Kexit) = (31, 301, 31) is selected to minimize the oscillatory behaviors in the accelerations. Detailed results of numerical trials to determine an adequate allocation are not included due to the page limitation. However, it does not mean disregarding the importance of such trials.

Figure 7 shows the simulation results with variations in the final time. The fully converged solutions up to the final time can be obtained over tf = 45–75 s. In addition, there exists no indication of numerical failures even with the relatively long simulation time of tf = 75 s, which says that the present PIST has the long-term simulation capability. Figure 8 represents the number of iterations at each segment to obtain the fully converged solutions. The higher the level of maneuver aggressiveness (with shorter duration time), the more iterations are required to get the converged solution. However, all analyses can be completed with the less than 30 iterations for each time-horizon segment. Therefore, the results of the present analyses prove the robustness of the PIST to the long-term simulation.

Fig. 7
figure 7

Simulation results for piroutte maneuver with varying final time

Full size image
Fig. 8
figure 8

Simulation status for piroutte maneuver with varying final time

Full size image

3.3 Depart/Abort Maneuver

The effects of a math model and the level of handling qualities of a specific aircraft are also an important topic in the inverse simulation. These effects are extremely difficult to adequately address because they are related to every details of the simulation environment. Therefore, this subsection simply intends to gather information on how the solutions with the PIST respond to the different levels of maneuver aggressiveness. For this purpose, the depart/abort MTE of ADS-33E-PRF is analyzed with the variation in the maximum velocity at the beginning time for the deceleration to hover (abort phase). Figure 9 shows the schematic of the depart/abort MTE described in ADS-33E-PRF and the desired time to complete the maneuver is recommended by less than or equal to 25 s in a good visual environment.

Fig. 9
figure 9

Schematic description of depart/abort maneuver (ADS-33E-PRF)

Full size image

A series of analyses are performed with variations of the maximum velocity vmax(= v1) ranging from 25 to 50 knots. The simulation results are compared in Fig. 10 and the corresponding required number of iterations are shown in Fig. 11. All numerical trials provide fully converged solutions. However, some of the simulated states and control inputs exhibit oscillatory responses with vmax = 40 and 50 knots. Especially, the oscillatory longitudinal cyclic control δ1S required to perfectly track the prescribed trajectory seems not to be accomplishable by the pilot with normal piloting skills. On the other hand, the analyses for the reduced aggressiveness level with vmax = 25 and 30 knots show smooth variation of all states and controls. Therefore, it can be concluded that oscillatory controls mentioned above were caused by factors other than algorithmic problems of the PIST such as inherent deficiency in the handling qualities of Bo-105 or the fidelity of the present flight dynamic model. The related issues are too extremely difficult to adequately treat in this paper. On this other hand, the results also provide valuable information on the robustness of the proposed algorithm to the maneuver aggressiveness.

Fig. 10
figure 10

Simulation results for depart/abort maneuver with varying final time

Full size image
Fig. 11
figure 11

Simulation status for depart/abort maneuver with varying maximum velocity

Full size image

4 Conclusion

A new inverse simulation technique has been proposed to cope with the numerical stability and accuracy problems frequently encountered with the currently available methods. The pseudo-spectral integrator, quasi-Newton method, and Piccard iterative solution are integrated to develop an efficient and robust inverse simulation algorithm. The proposed algorithm has been successfully applied to the analyses of the popup, pirouette, and depart/abort maneuvers, the last two of which are classified as highly aggressive mission-task-elements in the ADS-33E-PRF. Numerical characteristics of the proposed algorithm were thoroughly investigated using the analyses of the popup maneuver with various combinations of the solution control parameters such as the numbers of quadrature nodes and time-horizon segments. In addition, the robustness and efficiency of the algorithm could be identified using various performance measures such as the required number of iterations at each segment, the minimum value of the adaptive under-relaxation factor, and the final functional residuals for convergence check.

Based on the results of the popup maneuver, the paper could recommend using the five-point quadrature formula and 10 time-horizon segments for the enhanced robustness and numerical efficiency of the inverse simulations with the proposed techniques. The simulation results for the piroutte maneuvers with variations in the final time showed that the present method has the favorable robustness to the simulations over relatively long period of time. Finally, the effects of the level of maneuver aggressiveness on the simulation results have been studied through the analysis of the depart/abort maneuver defined in ADS-33E-PRF. Even though oscillatory responses became dominated at the simulation results for highly aggressive maneuvers, the fully converged solutions could be obtained. Therefore, it can be concluded that the present method has a strong robustness to the inverse simulation of highly aggressive maneuvers and can be used as another efficient alternative of the inverse simulation methods.