1 Introduction

The Category-A (Cat-A) flight performance should be demonstrated through extensive flight tests for a type certification of the transport-category rotorcraft [1]. The engine failures and the pilot delay in the failure-recognition and the follow-on reactions must be suitably simulated during the tests. A series of relevant flight tests should be carefully designed and must be performed through a strict buildup process to avoid unexpectable mishaps during the tests. On the other hand, the Federal Aviation Administration (FAA) allows the use of the analytical and/or simulation tools as a means of compliance for the Cat-A performance [2, 3] in a case when these tools have FAA approval. The FAA Part-29 Advisory Circular (AC) addresses the usage conditions of above tools for the performance extrapolation in AC-29.59, AC-29.75, and AC-29.79. Large-scale piloted simulations, trajectory optimizations, and maneuver simulations with a paper pilot are representative methods typically used today for design, data reduction, and pilot training [4] for the Cat-A certification. Among them, trajectory optimizations are most promising in that they allow a direct prediction of the required Cat-A flight performance, while others required complex numerical treatments in extrapolating the Cat-A performance using their results.

E. B. Carlson et al. showed that many of Cat-A maneuvers including those for the height-velocity diagram can be predicted using the trajectory optimization method [5,6,7]. Even though a low-fidelity point-mass model has been adopted in their predictions, the results well correlated with the flight test data could be obtained by carefully adjusting various model parameters. Bottasso et al. [8] analyzed the emergency landing procedures for both helicopters and tiltrotors. They used a nonlinear longitudinal dynamic equation to adequately consider the pitch variation during the flare. The rotor aerodynamic forces and moments are computed using the blade element method, but only the rigid-body dynamics are considered in their formulation using the rotor trim solution.

A trajectory optimization can be formulated with the corresponding nonlinear optimal control problem (NOCP), which can be solved using various methods. Carlson et al. analyzed various Cat-A performance by applying the collocation method and SNOPT (Sparse Nonlinear OPTimizer), which is a commercial solver of nonlinear programming problem (NLP) [4]. Chen and Zhao solved the one-engine-inoperative (OEI) landing problem using sequential gradient restoration algorithm (SGRA) developed by Miele et al. [1]. Also, Floros [9] studied on the autorotation and descent phases using the same SGRA. All studies mentioned above applied the point-mass rotorcraft model, the applicable flight areas of which are far below the operational flight envelope of typical rotorcrafts due to its extremely low fidelity. In this regard, Padfield classified the model fidelity as Level 1, 2 and 3, depending on how rotor dynamics and aerodynamics are modeled [10]. Also, he distinguished the applicable area of each Level. The point-mass model can be said as a Level 0 in accordance with his classification. All three Levels include the rotor and inflow dynamics, which are much faster than the rigid-body dynamics. The NLP derived from an NOCP formulated with these models inevitably suffers from a serious dimensionality problem. This point may become a strong reason why most of the previous studies adhere to the point-mass model [4,5,6,7,8,9].

This paper proposes various efficient methods to mitigate the mentioned dimensionality problem in solving the NOCP related to the Cat-A maneuvers. These methods are developed by combining a direct method for NOCP with a simple idea that the system states can be completely determined by the initial states and the imposed controls over a time-horizon. In other words, the system states can be uniquely determined through the simulation of the system dynamics over whole time-horizon using the controls computed at each of the iterative NOCP-solution step. Thus, the dynamic constraints can be removed in the transformed NLP and the size of the resultant Karush–Kuhn–Tucker (KKT) systems can be greatly reduced. The concept mentioned above is easily understandable and has already adopted in the direct-multiple-shooting method (DMS) [11,12,13,14]. However, DMS typically adopts an explicit time integrator and parameterizes controls with piecewise constant function and interpolating polynomials with a global support. Therefore, it cannot efficiently solve the NOCP with global path constraints because the evaluation of constraint Jacobians requires a formidable computing-time. Furthermore, DMS commonly presents much worse convergence than other direct methods like the pseudo-spectral method [12].

The present paper tries to remove main drawbacks of the DMS framework to enjoy various advantages provided by the KKT system with smaller size. First, the pseudo-spectral integrator developed in Ref.17 is adopted for an efficient and accurate simulation of the dynamical system. It is an implicit integrator, but the adopted Piccard iterative method provides fast convergence without resorting to Jacobian evaluations. In addition, such an implicit integrator outperforms the explicit counterpart in computing the constraint Jacobians based on the numerical perturbation. More details on this integrator are described in the Sect. 3.3. Secondly, the control is parameterized using the Hermit spline (HS) with a local support rather than the polynomial interpolation with a global support as in the traditional DMS. Using the local support property of the HS interpolation, Jacobians for the initial states and control parameters can be evaluated only with the simulations over two adjacent collocation points. The global effects of every single perturbation are efficiently reflected using simple recursive formulas. Whereas, the traditional DMS requires a simulation over whole shooting interval for each of single perturbation of design variables. Or, it needs to solve the additional differential equations which are introduced for each design variable of NLP [13,14,15]. It is complicated, because additional equations must be derived for each application and solved along with the state equation. The present paper derives the new approach of an NOCP formulation by removing the drawbacks of the DMS framework, and this technique is collectively named by the direct dynamic-simulation approach (DDSA) throughout this paper.

The NOCPs for rotorcraft emergency procedures are solved in the present paper. Those procedures contain one-engine-inoperative (OEI) operation and autorotation. The dynamic model is used as a point-mass model considering longitudinal dynamics, main rotor RPM, and power supplied during engine shutdown. The NOCP is transformed into an NLP thorough the DDSA, and the robust sequential quadratic programming (SQP) is used to solve the NLP. Further work for this study is that solving the NOCP with a high-fidelity model and developing the M&S (modeling and simulation) certification tool for extrapolation, interpolation, and simulation. It is expected that the solution of NOCPs with a high-fidelity model using DDSA will be much easier than that using the typical direct method.

2 Nonlinear Optimal Control Problem

2.1 Formulation of an NOCP for Trajectory Optimization Problems

The flight performance can be predicted by solving a trajectory optimization problem. The trajectory optimization problems can be formulated NOCPs which minimize an objective function. The objective function is formulated as ‘Bolza form’ which contains boundary objective and path integral form.

$$\begin{gathered} \min J = \phi ({\mathbf{x}}_{0} ,{\mathbf{x}}_{f} ,t_{f} ) + \int_{{t_{0} }}^{{t_{f} }} {f_{obj} ({\mathbf{x}},{\mathbf{u}},t)} dt \hfill \\ {\text{subject to}} \hfill \\ \quad \quad {\dot{\mathbf{x}}}(t) = {\mathbf{f}}({\mathbf{x}},{\mathbf{u}},t),\quad {\mathbf{x}} \in R^{n} ,\quad {\mathbf{u}} \in R^{m} ,\hfill \\ \quad \quad {{\boldsymbol{\psi}}}({\mathbf{x}}_{0} ,{\mathbf{x}}_{f} ) = 0,\quad \;\;{{\boldsymbol{\psi}}} \in R^{{L_{e} }}, \hfill \\ \quad \quad {\mathbf{g}}({\mathbf{x}},{\mathbf{u}},t) \le 0,\;\;\;\;\quad {\mathbf{g}} \in R^{{L_{i} }} . \hfill \\ \end{gathered}$$
(1)

The most important constraint for the NOCP is system dynamics \({\dot{\mathbf{x}}}(t)\), which can be considered the system limitation. Initial and terminal states constraint functions \({{\boldsymbol{\psi}}}({\mathbf{x}}_{0} ,{\mathbf{x}}_{f} )\) and global inequality constraint functions \({\mathbf{g}}({\mathbf{x}},{\mathbf{u}},t)\) for both states and controls are defined over time-horizon \(t \in [t_{0} ,t_{f} ]\).

2.2 Direct Dynamic-Simulation Approach for NOCP Solution

The continuous form of NOCP is transformed into NLP form by discretizing states and controls at prescribed time nodes. There are lots of discretizing methods; generally, the pseudo-spectral method is used in the collocation approach. In the collocation method, all state and control variables in particular time nodes are used for the design variable of NLP. This method has the advantage of fast local convergence and can handle unstable systems well [12]. However, the dynamic constraints of state variables must be considered when solving NLP. When it comes to solving NOCP with a high-fidelity model, the large size of the KKT system which is from the first optimality condition makes it hard to solve.

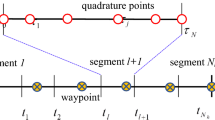
The DDSA is based on the following several simple ideas. To reduce the size of the KKT system, only control variables and initial state variables are used as design variables for the NLP. State variables satisfying the dynamic constraints can be uniquely defined through time integration over a particular time-horizon using the previous states and controls. Therefore, the dynamic constraint does not need to be considered in an NLP. These following processes can reduce the size of the KKT system even if the dynamic system is large. Because the unstable systems are difficult to treat, the simulation was performed by dividing simulation time into several independent short-time horizons, which is called a multi-horizon approach illustrated in Fig. 1. This multi-horizon approach can solve the poor convergence problem of unstable systems. However, first, it needs to consider the continuity conditions between two facing horizons.

Fig. 1
figure 1

Illustration of DDSA with multi-horizon approach

Full size image

The present paper proposes the DDSA. The pseudo-spectral time integration [17] and multi-horizon approach are used for the simulation in the DDSA. The effective recursive formula is applied for the Jacobian evaluation for NLP solver. Also, the robust SQP method is applied to solve NLP [16].

3 Numerical Technique

3.1 Formulation of DDSA

The general NOCP formulation Eq. (1) can be transformed into “Mayer form” and can be discretized using the dynamic simulation. The continuity condition \({\mathbf{c}}({\mathbf{x}}_{N,k} ,{\mathbf{x}}_{0,k + 1} )\) for multi-horizon approach is added. The discretized NOCP formulation is presented by the following form:

$$\begin{gathered} \min J = \phi ({\mathbf{x}}_{0} ,{\mathbf{x}}_{N,M} ,t_{N,M} ) + J_{N,M} \hfill \\ {\text{subject to}} \hfill \\ \,\,\,\,\,\,\,\,\,\,(k = 1,2, \cdots ,M),\,\,(j = 0,1, \cdots ,N - 1), \hfill \\ \quad \quad ({\mathbf{x}}_{j + 1} )_{k} = ({\mathbf{x}}_{j} + \Delta {\mathbf{x}}_{j} )_{k}, \quad \hfill \\ \quad \quad (J_{j + 1} )_{k} = (J_{j} + \Delta J_{j} )_{k}, \quad \hfill \\ \quad \quad {{\boldsymbol{\psi}}}({\mathbf{x}}_{0} ,{\mathbf{x}}_{N,M} ) = 0, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,{\mathbf{c}}({\mathbf{x}}_{N,k} ,{\mathbf{x}}_{0,k + 1} ) = 0,\,\,\,\,\,\,\,\,\, \hfill \\ \quad \quad ({\mathbf{g}}({\mathbf{x}}_{j} ,{\mathbf{u}}_{j} ,t_{j} ))_{k} \le 0\quad (j = 0,1, \ldots ,N), \hfill \\ \end{gathered}$$
(2)
$${\text{where }}\left\{ \begin{gathered} {\mathbf{x}}_{j + 1} = {\mathbf{x}}_{j} + \Delta {\mathbf{x}}_{j} = {\mathbf{x}}_{j} + \int_{{t_{j} }}^{{t_{j + 1} }} {{\mathbf{f}}({\mathbf{x}},{\mathbf{u}},\xi )d\xi } \hfill \\ J_{j + 1} = J_{j} + \Delta J_{j} = J_{j} + \int_{{t_{j} }}^{{t_{j + 1} }} {f_{obj} ({\mathbf{x}},{\mathbf{u}},\xi )d\xi }. \hfill \\ \end{gathered} \right.$$
(3)

Using the “Mayer form” above, the design variables can be formulated with the state variables at an initial time node of each time-horizon and control variables of all-time nodes using this relation. It can be expressed \({\overline{\mathbf{y}}}_{k} = ({\mathbf{x}}_{0,k}^{T} ,{\overline{\mathbf{v}}}_{k}^{T} )^{T}\) where \({\overline{\mathbf{v}}}_{k} = ({\mathbf{v}}_{0}^{T} ,{\mathbf{v}}_{1}^{T} , \cdots ,{\mathbf{v}}_{N}^{T} )_{k}^{T}\),\({\mathbf{v}}_{j} = \left( {{\mathbf{u}}_{j}^{T} ,{\dot{\mathbf{u}}}_{j}^{T} ,{\ddot{\mathbf{u}}}_{j}^{T} , \ldots } \right)^{T}\)\((k = 1,2, \cdots ,M)\). Equation (2) can be transformed into an NLP with the following equations:

$$\begin{gathered} \min \sum\limits_{k = 1}^{M} {J({\overline{\mathbf{y}}}_{k} )} \hfill \\ {\text{subject to}} \hfill \\ \,\,(j = 0,1, \cdots ,N),\,\,\,(k = 1,2, \ldots ,M) ,\hfill \\ \quad \quad {\overline{\mathbf{h}}}({\overline{\mathbf{y}}}_{k} ) = 0, \hfill \\ \quad \quad {\overline{\mathbf{g}}}_{j} ({\overline{\mathbf{y}}}_{k} ) \le 0,\quad \hfill \\ where\,\,{\overline{\mathbf{h}}}({\overline{\mathbf{y}}})\left\{ \begin{gathered} {{\boldsymbol{\psi}}}({\overline{\mathbf{y}}}_{k} ) = 0 \hfill \\ {\mathbf{c}}({\overline{\mathbf{y}}}_{k} ) = 0. \hfill \\ \end{gathered} \right.\,\, \hfill \\ \end{gathered}$$
(4)

The Lagrangian function \(L\) is used to derive the first-order optimality conditions, called the KKT condition:

$$L({\overline{\mathbf{y}}},{{\boldsymbol{\mu}}},\,{{\boldsymbol{\gamma}}}) = \sum\limits_{k = 1}^{k = M} {J({\overline{\mathbf{y}}}_{k} )} + {{\boldsymbol{\mu}}}^{T} {\overline{\mathbf{h}}}({\overline{\mathbf{y}}}_{k} ) + \sum\limits_{k = 1}^{k = M} {\sum\limits_{j = 0}^{j = N} {\,{{\boldsymbol{\gamma}}}_{j}^{T} } {\overline{\mathbf{g}}}_{j} ({\overline{\mathbf{y}}}_{k} )} .$$
(5)

In this paper, the robust SQP method is used to solve NLP. This method showed robustness by solving example problems that have inconsistency problems and Martos effect in Ref.[16].

3.2 Control Parameterization

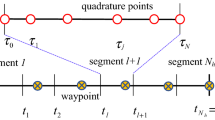
In the process of NLP transcription using DDSA technique, the states of NLP are defined by the dynamic simulations using the initial states and distributed controls. Therefore, the appropriate time integration method and control parameterization is an essential part. Because the details are the same on each horizon, this chapter focused on a single horizon to explain the numerical technique. Two type of grids for variables are defined over a time-horizon and it is illustrated in Fig. 2. The first type of grid is the collocation node, where both the system dynamics and constraints will be satisfied. The second type is the computational node for simulation, and it follows the Legendre–Gauss–Lobatto (LGL) points [17] to apply the pseudo-spectral time integrator.

Fig. 2
figure 2

Illustration of DDSA grid in one horizon

Full size image

The control variables on computation node can be interpolated using control value on the collocation nodes. The interpolating controls and states on the initial collocation node are used for the time integration. In this paper, the Hermit spline interpolation method [18] is adopted for control parameterization, and the continuous controls over \(t \in [t_{j} ,t_{j + 1} ]\) are approximated using the following formula:

$${\mathbf{u}}(\tau ) = \sum\limits_{l = 0}^{l = K} {\left( {\Delta t_{j} } \right)^{l} \left\{ {\alpha_{l} (\tau ){\mathbf{u}}_{j}^{(l)} + \beta_{l} (\tau ){\mathbf{u}}_{j + 1}^{(l)} } \right\}} .$$
(6)

Here, the time interval \(\Delta t_{j}\) and nondimensional time \(\tau\) are defined by:

$$\begin{gathered} \Delta t_{j} = t_{j + 1} - t_{j} ,\hfill \\ \tau = (t - t_{j} )/\Delta t_{j} \in [0,1]. \hfill \\ \end{gathered}$$
(7)

And, the functions \(\left\{ {\alpha_{l} (\tau ),\beta_{l} (\tau )} \right\}_{l = 0}^{l = K}\) represent the Hermit basis polynomials with \((2K + 1)\) order. The coefficients of each polynomial can be computed by imposing the following conditions for \(l = 0, \cdots ,K\) at two-end nodes:

$$\frac{{d^{l} {\mathbf{u}}(0)}}{{d\tau^{l} }} = \frac{{{\mathbf{u}}_{k}^{(l)} }}{{\left( {\Delta t_{j} } \right)^{l} }},\quad \frac{{d^{l} {\mathbf{u}}(1)}}{{d\tau^{l} }} = \frac{{{\mathbf{u}}_{j + 1}^{(l)} }}{{\left( {\Delta t_{j} } \right)^{l} }}.$$
(8)

Therefore, the continuous control over the time interval is parameterized using the control derivatives \({\mathbf{u}}_{j}^{(l)} = d^{l} {\mathbf{u}}/dt^{l}\) at each collocation node. It can provide the local support for the recursive formula which is the Jacobian calculation method for robust SQP and can provide an extremely accurate interpolation.

3.3 Jacobian Matrices for Robust SQP Method

The Jacobian matrices of the KKT system used in the robust SQP must be derived for the design variables. Originally, the Jacobian matrix is calculated using the central difference formula through integration in the whole time-horizon, when design variables are perturbed. Or, a less common alternative to the calculation of Jacobian is to solve the additional differential equations obtained through the sensitivity analysis. However, these are not suitable for DDSA, because it takes long time to integrate and solve the additional equations. Therefore, the efficient recursive formula is derived for efficiently calculating the Jacobian matrices. This formula is based on Eq. (3).

The Jacobian matrix of Eq. (3) for the design variables derived as using the chain rules:

$$\begin{gathered} \frac{{\partial {\mathbf{x}}_{0} }}{{\partial {\mathbf{x}}_{0} }} = {\mathbf{I}},\quad \frac{{\partial {\mathbf{x}}_{0} }}{{\partial {\mathbf{v}}_{0} }} = {\mathbf{0}},\quad \frac{{\partial {\mathbf{x}}_{0} }}{{\partial t_{f} }} = {\mathbf{0}}, \hfill \\ \frac{{\partial {\mathbf{x}}_{j + 1} }}{{\partial {\mathbf{x}}_{0} }} = \frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }} = \left( {{\mathbf{I}} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }}} \right)\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }}, \hfill \\ \frac{{\partial {\mathbf{x}}_{j + 1} }}{{\partial {\mathbf{v}}_{k} }} = \frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{k} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{k} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{j} }}\frac{{\partial {\mathbf{v}}_{j} }}{{\partial {\mathbf{v}}_{k} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, = \left( {{\mathbf{I}} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }}} \right)\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{k} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{j} }}\delta_{jk} ,\quad (k = 0,1, \cdots ,j), \hfill \\ \frac{{\partial {\mathbf{x}}_{j + 1} }}{{\partial {\mathbf{v}}_{j + 1} }} = \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{j + 1} }}, \hfill \\ \frac{{\partial {\mathbf{x}}_{j + 1} }}{{\partial t_{f} }} = \frac{{\partial {\mathbf{x}}_{j} }}{{\partial t_{f} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial t_{f} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial t_{f} }} = \left( {{\mathbf{I}} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }}} \right)\frac{{\partial {\mathbf{x}}_{j} }}{{\partial t_{f} }} + \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial t_{f} }}, \hfill \\ \end{gathered}$$
(9)
$$\begin{gathered} \frac{{\partial J_{j + 1} }}{{\partial {\mathbf{x}}_{0} }} = \frac{{\partial J_{j} }}{{\partial {\mathbf{x}}_{0} }} + \frac{{\partial \Delta J_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }} ,\hfill \\ \frac{{\partial J_{j + 1} }}{{\partial {\mathbf{v}}_{k} }} = \frac{{\partial J_{j} }}{{\partial {\mathbf{v}}_{k} }} + \frac{{\partial \Delta J_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{k} }},\,\,\,\,(k = 0,1,2, \cdots ,j - 1), \hfill \\ \frac{{\partial J_{j + 1} }}{{\partial {\mathbf{v}}_{j} }} = \frac{{\partial J_{j} }}{{\partial {\mathbf{v}}_{j} }} + \frac{{\partial \Delta J_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{j} }} + \frac{{\partial \Delta J_{j} }}{{\partial {\mathbf{v}}_{j} }} ,\hfill \\ \frac{{\partial J_{j + 1} }}{{\partial {\mathbf{v}}_{j + 1} }} = \frac{{\partial \Delta J_{j} }}{{\partial {\mathbf{v}}_{j + 1} }}. \hfill \\ \end{gathered}$$
(10)

In Eqs. (9)–(10), using \(\left\{ {\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }},\frac{{\partial {\mathbf{x}}_{j} }}{{\partial t_{f} }},\frac{{\partial J_{j} }}{{\partial {\mathbf{x}}_{0} }},\frac{{\partial J_{j} }}{{\partial t_{f} }}} \right\}_{j = 0}^{j = N}\), the Jacobian matrix of \(\Delta {\mathbf{x}}_{j}\),\(\Delta \,J_{j}\) can be estimated using the following relation:

$$\begin{gathered} \frac{{\partial \Delta {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{j} }} = \frac{{\partial {\mathbf{x}}_{j + 1} }}{{\partial {\mathbf{x}}_{0} }}(\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }})^{ - 1} - {\mathbf{I}}, \hfill \\ \frac{{\partial \Delta J_{j} }}{{\partial {\mathbf{x}}_{j} }} = \left( {\frac{{\partial J_{j + 1} }}{{\partial {\mathbf{x}}_{0} }} - \frac{{\partial J_{j} }}{{\partial {\mathbf{x}}_{0} }}} \right)\left( {\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }}} \right)^{ - 1} . \hfill \\ \end{gathered}$$
(11)

The number of simulations for calculating Jacobian using Eq. (11) can be reduced. The control Jacobians are computed straightforwardly using the hermit spline interpolation:

$$\begin{gathered} \frac{{\partial {\mathbf{u}}_{j} }}{{\partial {\mathbf{v}}_{k} }} = \left( {\frac{{\partial {\mathbf{u}}_{j} }}{{\partial {\mathbf{v}}_{j} }}} \right)\delta_{jk} ,\quad (k = 0,1, \cdots ,N) ,\hfill \\ \frac{{\partial {\mathbf{u}}_{j} }}{{\partial {\mathbf{u}}_{j}^{(k)} }} = {\mathbf{I}}\delta_{0k} ,\quad \quad \;\;(k = 0,1, \cdots ,K). \hfill \\ \end{gathered}$$
(12)

For example, the Jacobian matrix of the global inequality function \({\mathbf{g}}_{j} ({\mathbf{x}}_{j} ,{\mathbf{u}}_{j} ,t_{j} )\) can be defined by the following local Jacobian matrices:

$$\begin{gathered} \frac{{\partial {\mathbf{g}}_{j} }}{{\partial {\mathbf{x}}_{0} }} = \frac{{\partial {\mathbf{g}}_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{x}}_{0} }} ,\hfill \\ \frac{{\partial {\mathbf{g}}_{j} }}{{\partial {\mathbf{v}}_{k} }} = \frac{{\partial {\mathbf{g}}_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial {\mathbf{v}}_{k} }} + \frac{{\partial {\mathbf{g}}_{j} }}{{\partial {\mathbf{u}}_{j} }}\frac{{\partial {\mathbf{u}}_{j} }}{{\partial {\mathbf{v}}_{k} }},\quad (k = 0,1, \cdots ,N), \hfill \\ \frac{{\partial {\mathbf{g}}_{j} }}{{\partial t_{f} }} = \frac{{\partial {\mathbf{g}}_{j} }}{{\partial {\mathbf{x}}_{j} }}\frac{{\partial {\mathbf{x}}_{j} }}{{\partial t_{f} }} + \frac{{\partial {\mathbf{g}}_{j} }}{{\partial t_{j} }}\frac{{\partial t_{j} }}{{\partial t_{f} }}. \hfill \\ \end{gathered}$$
(13)

The right-hand-side gradients of each term in Eq. (13) can be easily obtained from the established Jacobian using a recursive formula. As a result, it is possible that the straightforward composition of the KKT system matrix for robust SQP using a recursive formula. Also, it can reduce the burden of computation.

3.4 Time Integrator for Simulation

The accuracy and efficiency of time integrators have a great effect on DDSA. It is possible to adopt an efficient and accurate time integrator for simulation in this method. The pseudo-spectral time integrator which was developed in [17] is used in DDSA. The motion equation can be expressed as follows:

$${\dot{\mathbf{x}}}(t) = {\mathbf{f}}({\mathbf{x}}(t),{\mathbf{u}}(t),t),\quad t \in [t_{0} ,t_{f} ],\quad {\mathbf{x}} \in R^{n} ,\quad {\mathbf{u}} \in R^{m} .$$
(14)

Using a local affine transformation, the Eq. (14) can be transformed into Eq. (15):

$$\begin{gathered} \tau = \frac{{2t - (t_{f} + t_{0} )}}{{t_{f} - t_{0} }}, \hfill \\ \frac{{d{\mathbf{x}}}}{d\tau }\frac{d\tau }{{dt}} = {\mathbf{f}}({\mathbf{x}}(t),{\mathbf{u}}(t),t) ,\hfill \\ \frac{{d{\mathbf{x}}}}{d\tau } = \frac{dt}{{d\tau }}{\mathbf{f}}({\mathbf{x}}(t),{\mathbf{u}}(t),t) = \frac{{t_{f} - t_{0} }}{2}{\mathbf{f}}({\mathbf{x}}(t),{\mathbf{u}}(t),t). \hfill \\ \end{gathered}$$
(15)

Ref. 17 used the integration method after representing Eq. (15) by Eq. (16) when the initial state is specified with \({\mathbf{x}}_{0} = {\mathbf{x}}(t_{0} )\):

$${\mathbf{x}}_{j} = {\mathbf{x}}_{0} + \int_{{t_{0} }}^{{t_{j} }} {{\mathbf{f}}({\mathbf{x}}(t),{\mathbf{u}}(t),t)dt} .$$
(16)

Using the Legendre–Gauss–Lobatto (LGL) quadrature points \(\{ \tau_{j} \}_{j = 0}^{j = N}\) and the corresponding integration matrix \(\{ I_{jk} \}_{j = 0,k = 0}^{j = N,k = N}\), Eq. (16) can be transformed into Eq. (17):

$${\mathbf{x}}_{j} = {\mathbf{x}}_{0} + \frac{{t_{f} - t_{0} }}{2}\sum\limits_{k = 1}^{N} {I_{jk} {\mathbf{f}}({\mathbf{x}}_{k} )} .$$
(17)

This paper also adopts the Piccard iterative method to solve the Nonlinear algebraic equations (NAEs) shown in Eq. (17) and the state can be updated using the following formula:

$$\begin{aligned} ({\mathbf{x}}_{j} )_{iter + 1} = & {\mathbf{x}}_{0} + \frac{{t_{f} - t_{0} }}{2}\sum\limits_{k = 1}^{N} {I_{jk} {\mathbf{f}}\{ ({\mathbf{x}}_{k} )_{iter} \} } \\ j = & 1, \cdots ,N. \\ \end{aligned}$$
(18)

When \(iter\) represented the iteration sequence. Therefore, the iterative update of the state solution needs no time-consuming evaluation of the Jacobian matrix. This paper solves Eq. (18) with the prescribed tolerance defined by:

$$\varepsilon = \sqrt {\frac{1}{N \times n}\sum\limits_{k = 1}^{N} {\{ ({\mathbf{x}}_{j} )_{iter + 1} - ({\mathbf{x}}_{j} )_{iter} \}^{2} } } .$$
(19)

And an extremely few number of iterations are required even with condition of \(\varepsilon \le 10^{ - 8}\) for most of the present application. Therefore, it can be claimed that the present pseudo-spectral integrator can show the outperformance in computational efficiency and prediction accuracy over the explicit or other implicit methods. This point has already been demonstrated in Ref. [17].

3.5 Validation of Numerical Technique

For validation of the efficient approach, over ten NOCP examples have been practiced and were compared with the exact solution. This paper introduces the minimum terminal problem [19]. To observe the advantages of DDSA, this problem has been modified to increase the number of state variables:

$$\begin{gathered} \min J = - x_{1} (t_{f} ) ,\hfill \\ subject\,to \hfill \\ \dot{x}_{1} = x_{1} u - x_{1} u^{2} ,\hfill \\ \dot{x}_{j} = x_{j - 1} ,\,\,(j = 2,3,...M) ,\hfill \\ with\,\,\,x_{1} (0) = 1,x_{j} (0) = 0,\,t_{f} = 5. \hfill \\ \end{gathered}$$
(20)

The problem consists of 7 computational nodes, 100,000 maximum number of iterations, and \(10^{ - 5}\) tolerance of the KKT condition. Figure 3 shows that the numerical result with 30 collocation nodes and one state variable. The results of DDSA completely matched with the analytical optimal solution compared with the collocation method.

Fig. 3
figure 3

Comparison of numerical results of NOCP example: solution

Full size image

Figure 4 shows that the difference between the collocation method and DDSA. To compare the differences, the problems with various numbers of state variables and collections are solved. As the system becomes large, the computation time of both methods increases. However, more time was spent when using collocation method. Because the size of the KKT system matrix of DDSA is smaller than that of collocation, DDSA is more accurate and is computed faster than collocation. Moreover, it is more accurate and faster when collocation node increases, as shown in Fig. 4. Therefore, it has the advantage when a problem needs lots of collocation nodes. As a result, when using trajectory optimization problems of large systems like high-fidelity rotorcraft dynamic models, DDSA is an appropriate method to use (Fig. 5).

Fig. 4
figure 4

Comparison of numerical results of NOCP example: computation time and accuracy

Full size image
Fig. 5
figure 5

Illustration of point mass model

Full size image

4 Trajectory Optimization Problem of Rotorcraft Emergency Procedures

4.1 Rotorcraft Emergency Procedures and Model

In this paper, the application of the point-mass model is used for its simplicity and accuracy. This model is a smaller system than a high-fidelity rotorcraft model, which consists of longitudinal, rotor RPM dynamics (21)–(23), and power supplied (26) when the engine is shut down. Also, kinematics for height and horizontal distance (24), (25) are included.

The governing equations of this model are summarized below:

$$m_{h} \dot{u} = C_{T} \rho \left( {\pi R^{2} } \right)\left( {\Omega R} \right)^{2} \sin \alpha - \frac{1}{2}\rho f_{e} u\sqrt {u^{2} + w^{2} },$$
(21)
$$m_{h} \dot{w} = m_{h} g - C_{T} \rho \left( {\pi R^{2} } \right)\left( {\Omega R} \right)^{2} \cos \alpha - \frac{1}{2}\rho f_{e} w\sqrt {u^{2} + w^{2} },$$
(22)
$$I_{R} \Omega \dot{\Omega } = P_{S} - \frac{1}{\eta }\rho \left( {\pi R^{2} } \right)\left( {\Omega R} \right)^{3} C_{P},$$
(23)
$$\dot{x} = u,$$
(24)
$$\dot{h} = - w,$$
(25)
$$\tau_{P} \dot{P}_{S} = (P_{res} - P_{S} ).$$
(26)

The inflow model that consists of general momentum, the empirical vortex ring state, and ground effect are applied in this model. To consider control rates, control variables are changed those derivatives as \(\dot{C}_{T} ,\,\,\,\dot{\alpha }\). Therefore, the state variables \({\mathbf{x}} = (u{,}\,\,w{,}\,\,x{,}\,h,\,P,\,\,\Omega ,C_{T} ,\,\,\alpha )^{T}\) and control variables \({\mathbf{u}} = (\dot{C}_{T} ,\,\,\dot{\alpha })^{T}\) are used. Values of parameters used in the point-mass models of OH-58A and UH-60 are given in Table 1. Those data have been obtained from [1] and [21].

Table 1 Rotorcraft specification
Full size table

This model has been used in many studies for rotorcraft trajectory optimization problems. More details about this model are represented in [1], [2, 3] and Ref. [20, 21]. This model is applied for the application and validation of DDSA.

4.2 Rotorcraft Emergency Procedures

In the engine-failure condition, the rotorcraft must perform the appropriate emergency procedure for the situation. Single-engine rotorcraft performs emergency landing by autorotation when the engine fails during flight. Furthermore, twin-engine rotorcraft performs autorotation when all engine fails and performs appropriate emergency procedures when one engine fails. There is the Cat-A certification for multi-engine rotorcraft with the independent engine system. It requires that a helicopter can either continue flight or land safely at OEI situation. These procedures are well illustrated in Fig. 6. The minimum requirements of certification are four types of maneuvering performance in two types of helipad [4]. Two types of helipads are given as ground level and elevated helipad. When takeoff and landing, the four different maneuvers of continued takeoff (CTO), rejected takeoff (RTO), continued landing (CL), and balked landing (BL) [or rejected landing (RL)] are given. The RTO and CL are performed when OEI occurred before takeoff-decision-point (TDP) and landing-decision-point (LDP). The CTO and BL performed when OEI occurred after TDP and LDP. These emergency procedures are described in Fig. 6. The flight performance satisfying the flight speed and altitude requirements must be demonstrated. Also, it needs to consider the 1-s pilot delay which is the time for the pilot to recognize engine failure. In this paper, single-engine rotorcraft OH-58A is applied for autorotation problems, and twin-engine rotorcraft UH-60 is applied for Cat-A problems.

Fig. 6
figure 6

Trajectory of autorotation (a) and Cat-A operation at elevated helipad (b), (c) [1]

Full size image

4.3 NOCP Formulation of Emergency Procedures and Numerical Result

The different objective functions can be defined depending on the maneuver for appropriate situations. Typically, the autorotation problem is defined as minimize touchdown speed [22]. And, the Cat-A landing problems is defined as minimize the dispersion of touchdown points [1, 20]. Also, the minimum RPM drop problems are defined for CTO and BL problems. All problems of emergency procedures must be defined as minimum time problems. Path constraints for those defined appropriate values should satisfy the certification criteria and rotorcraft operation limits. The summary of problems is given in Table 2. Autorotation problems assume that the engine fails at low and high-altitude hover. Also, the Cat-A operation problems assume that OEI occurred at several points on the normal trajectory of backup takeoff and landing. More details of initial condition for Cat-A operation are represented in [4]. All optimizations were performed using the initial points which are a result of a 1-s simulation with no pilot response after the engine failure.

Table 2 NOCP definition of emergency procedures
Full size table

Problems of rotorcraft emergency procedure were solved using three horizon, 20 collocation nodes, and 1.0e-05 KKT condition tolerance. In a numerical technique, the computational stability of the robust SQP method depends on the appropriate scaling of design variables. Using appropriate scaling factors, the design variables and gradient for the robust SQP method are scaled to the order of 1. Some relationships have been used to determine the scaling factor. For example, the design variables of velocity are scaled using the main rotor nominal angular speed and rotor radius:

$$\tilde{u} = \frac{u}{{R\Omega_{0} }}.$$
(27)

Results of low- and high-altitude hovering autorotation maneuver are shown in Fig. 7. The results show that the rotorcraft increases the translation of kinetic energy as much as possible to decrease the rate of descent and make a soft landing. In the high-altitude hover, the rotorcraft has a steady-descent phase between 5 and 10 s. In this phase, the main-rotor RPM has been maintained or was increased. Also, high altitude can give pilot enough height for steady-state autorotation. However, in low-altitude hover maneuver, steady-descent phase is not possible. Finally, vertical decent movement and flare maneuver can be seen in both low- and high-altitude cases before touchdown.

Fig. 7
figure 7

Numerical results of autorotation problems: low-hover (left) and high-hover (Right)

Full size image

Figures 8 and 9 show the results of Cat-A operation. In the backup technique and landing procedure, the rotorcraft can safely land back to the target point when the OEI occurred before TDP and after LDP. However, it may require lots of control efforts. To safely land to the target point, the rotorcraft must perform the appropriate maneuver. If OEI occurs near the helipad during landing procedures, the RPM drop is occurred because of low airspeed to land. If OEI occurs in flight point after TDP and before LDP, the rotorcraft can safely operate without violating the performance limitation. Moreover, the result shows that CTO operation needs more time to reach the continued flight than BL operation and the rotor RPM drops because of low airspeed. However, the rotorcraft can recover the RPM by increasing airspeed up to safe takeoff speed \(V_{TOSS}\).

Fig. 8
figure 8

Numerical results of Cat-A takeoff: RTO (left) and CTO (right)

Full size image
Fig. 9
figure 9

Numerical results of Cat-A landing: CL (left) and BL (right)

Full size image

The available power of the engine may decrease due to the deterioration of the engine and the effect of the outer environment, etc. When OEI occurs, the rotorcraft with a less-capable engine must need to operate Cat-A procedure with another flight trajectory to satisfy its certificate requirement comparing with the original trajectory of Cat-A. The problems of Cat-A operation with a less-capable engine are solved in this paper. And the results are compared with the operations done with an original engine.

Figures 10 and 11 show the numerical result of Cat-A operation with a less-capable engine compared with an original engine. Figure 10 shows the optimal trajectory of RTO operation at 70ft height and CTO operation at 140ft height. The RTO operation with a less-capable engine is similar to the original procedure. However, the RPM of the less-capable engine drops under 85% of the reference RPM. Because it leads to loss of control, RTO operation with an 80% available power is dangerous. The result of the CTO operation shows that the rotorcraft with a less-capable engine can satisfy the requirement of certification, but it must maintain the RPM lower than the reference RPM. The maintained RPM of the rotorcraft with a 90% available power is about 98% of reference RPM, and those of the rotorcraft with an 80% available power is 92% of reference RPM. Also, it is dangerous, because some part of the optimal trajectory is below the takeoff surface when OEI occurs with an 80% available power. As a result, the TDP height for rotorcraft with a less-capable engine must raise to ensure sufficient altitude to safe perform CTO procedure, and the takeoff weight for those must lower than the original weight.

Fig. 10
figure 10

Comparison of the optimal takeoff trajectory between the original engine and a less-capable engine: RTO (left) and CTO (right)

Full size image
Fig. 11
figure 11

Comparison of the optimal landing trajectory between the original engine and a less-capable engine: CL (left) and BL (right)

Full size image

Figure 11 shows the optimal trajectory of CL operation at 35ft height and BL operation at 100ft height. The results of CL operation show that a rotorcraft with a less-capable engine can safely land, while the RPM decreases. Moreover, the result of BL operation shows that over 80% of reference power is sufficient to operate BL procedure. However, it needs more time and longer horizontal distance to achieve the requirement of certification. This numerical result needs to be validated by comparing flight test data. And, the objective function and constraints can be modified using test data for accurate predict.

5 Conclusion

This paper focused on the methodology of solving the trajectory optimization problem for rotorcraft emergency procedures. There are many numerical methods to solve the trajectory optimization problems. Among them, the collocation method is widely used, because it has high-convergence and can handle unstable systems. However, this method is not appropriate for solving problems with large systems. To solve the trajectory optimization problems with a high-fidelity rotorcraft model, the DDSA is appropriate because of the size and the instability of the system. Using the numerical result of NOCP examples, it is confirmed that the DDSA has more advantages for a large system than the collocation method. Also, this paper has proposed DDSA using Hermit spline interpolation, the recursive formula, and pseudo-spectral time integrator. This approach reduced the size of the KKT system matrix using a small number of design variables and by excepting for dynamic constraints. This approach seems like DMS. However, it is a very different methodology in point of control parameterized method, Jacobian evaluation, and integration method. Also, it is more effective and widely adoptable than DMS. This proposed numerical technique has been validated by solving NOCP examples and the trajectory optimization problems of rotorcraft emergency procedures using the point mass model. This study has solved the five emergency procedures which are autorotation, RTO, CTO, CL, and BL. Also, the problems of the Cat-A operation with a less-capable engine are solved using DDSA. The problem definition for predicting flight performance of emergency procedures can be defined as various problems containing minimize finial time. The numerical results can be demonstrated by comparing with flight test data. And it can be improved by modifying some problem definitions, constraints, and models. In present, this methodology can only solve the problems with the ordinary differential equation (ODE) system. However, the high-fidelity rotorcraft models can be defined in the differential–algebraic equation (DAE) systems. The consideration of the DAE system in this methodology is necessary to solve the problem with high-fidelity models. Because the numerical stability of the robust SQP method also affects this methodology, to further improve the methodology, the study of appropriate normalization of design variables also is necessary.