A user guide of CART and random forests with applications in FinTech and InsurTech

Abstract

In the realm of financial data analytics, machine learning techniques, particularly classification and regression trees (CARTs) and random forests, have shown remarkable efficiency. This article serves as a user guide for these methods, with an emphasis on their applicability and effectiveness in analyzing datasets in FinTech and InsurTech. In particular, we present several numerical examples and empirical studies, and demonstrate their superiority in handling data with a variety of input features, offering insights into their potential applications in the industries.

1 Introduction

Classification of data has long been one of the prime topics in industrial practice, and various methods have been proposed and commonly used for this purpose, such as the binary logistic regression and multinomial logit model that perform the task through linear feature combinations. However, the lack of interpretability for these methods, which is crucial from the regulatory perspective, makes it necessary for simpler and more explainable classification methods to be proposed. To this end, the Classification Tree or Decision Tree, a greedy algorithmic approach, offers a remarkable solution. It creates easy-to-follow rules for categorizing data, making it highly valuable in data mining and applicable in financial sectors for various tasks related to credit approval and relief of financial stress. Initially developed by Breiman, Friedman, Olshen, and Stone in Breiman et al. (1984), this method has gained widespread recognition in supervised learning, with continual research and development since then; also see (Gordon, 1999) for more recent developments.

For decades, the finance and insurance industries have been at the forefront of embracing new and innovative technologies. Their long-lasting relationship with AI can date back to the 1980 s. With the boom of data mining in the 1990s and the rise of decision trees, we have witnessed the long-term prosperity of machine learning in the fields of FinTech and InsurTech till today. As powerful and well-developed representatives of machine learning, CART models and their ensemble version of random forests have played an important role in many different practical scenarios, such as fraud detection, risk assessment and prediction, marketing analytics, as well as pricing and reserving in insurance. Indeed, in the era of big data, companies have to revolutionize how to manage the vast amount of data they collect. With rapid advancements in technology, the volume and types (namely structured, semi-structured, and unstructured) of data processed have significantly increased (Chakraborty and Kar 2017). Thanks to the development of high-performance computers and new effective algorithms, industries can have more choices beyond the traditional algorithms with low efficiency, and hence achieve a more efficient daily operation via the use of CARTs and random forests.

The flourishing of CART and random forests in the fields of finance and insurance is also reflected in the various works since the turn of the century. In the realm of finance, Smith et al. (2000) explored the use of various data mining techniques, including CART, in the insurance industry for the analysis of customer retention and claim patterns, and discussed how they could help to formulate strategic decisions for policy renewals and premium pricing. Viaene et al. (2002) evaluated the power of various commonly used methods for detecting frauds in automobile insurance; while Decision Tree performed slightly worse than other candidates, the authors did point out that an ensemble version of Decision Tree would yield better performance than almost all competitors. This claim was later realized by a novel fraud detection method proposed by Phua et al. (2004) combining back-propagation, naïve Bayesian, and CART with a stacking-bagging approach; more recent developments on the application of CART and random forests in fraud detection can be referred to Gepp et al. (2012); Phua et al. (2010); Varmedja et al. (2019). Moreover, Gepp et al. (2010) introduced decision trees as a method for predicting business failure, suggesting they may be more effective than traditional discriminant analysis, in response to the costly impact of major company failures. As for the field of insurance, Quan and Valdez (2018) demonstrated the use of multivariate decision tree models for insurance claim data, emphasizing their advantages over univariate models in accuracy and the ability to capture relationships among variables. Wüthrich (2018) explored the application of regression trees in individual claims reserving, and assessed its impact on accurately predicting claim costs and improving reserving processes in insurance. All these works serve as concrete evidence of the power and usefulness of CART and random forest, as well as their versatility on various objectives. It is therefore no wonder that they have been widely utilized in finance and insurance industries.

In particular, with the rise of the trendy topics of FinTech and Insurtech, the need for data-driven decision-making is greater than ever in history, and CART and random forests are certainly among the most popular choices for this purpose. To this end, we aim to provide a user guide of these tools, including both their theoretical principles and, more importantly, practical illustrations on real-life datasets with program codes in both Python and R, so as to provide some insights into these tools to the readers, as well as facilitate the plug-and-play need of them.

The rest of this article is arranged as follows. We begin with a concise introduction of the concept of entropy in information theory in Sect. 2, which is the fundamental building block of CART and random forests. We then discuss how the two pillars of CART, namely classification tree (a.k.a. decision tree) and regression tree, are constructed in Sects. 3 and 4, respectively; some practical considerations at this stage will also be mentioned. Section 5 introduces the random forest, the ensemble version of CART. We then move on to the programming perspective in Sect. 6 and investigate how these tools are trained and validated in Python and R using several illustrative examples. Finally, we conduct a comparative experiential study using two representative real-life datasets in finance and insurance to testify to the power of CART and random forest in Sect. 7.

2 Concepts of entropies

Typically, the construction of CARTs is based on the notion of entropy in information theory. Indeed, it is important to establish a comprehensive understanding of the concept of entropy in information theory, as it provides the foundational basis for making informed and accurate data splits. We first introduce several key information-theoretic quantities to be used later in this article.

2.1 Shannon and differential entropies

In 1948, Claude Shannon introduced the concept of entropy, derived from thermodynamics, into information theory; see (Shannon, 1948, 1949) for details. This entropy, often termed Shannon entropy in his honor, measures the deviation of a distribution from a uniform distribution. It plays a crucial role in information theory, especially in defining the capacity of a communication channel and gauging its efficiency in transmitting information.

Let $\textrm{x}$ be a discrete random variable whose support is denoted by ${\mathcal {X}}$, and p be its probability mass function. The Shannon entropy $H(\textrm{x})$ of $\textrm{x}$ is defined as:

$$\begin{aligned} H(\textrm{x}):= -{{\,\mathrm{\mathbb {E}}\,}}(\log _2 p(x)) = -\sum _{x \in {\mathcal {X}}} p(x) \log _2 p(x), \end{aligned}$$

(1)

adhering to the convention $0 \log _2 0 = 0$. For example, the Shannon entropy of a Bernoulli random variable $\textrm{x}$ with a success probability of $p$ is:

$$\begin{aligned} H(\textrm{x}) = -p \log _2 p - (1-p) \log _2(1-p). \end{aligned}$$

(2)

Note that although entropy is defined for random variables, it is fundamentally reliant on their distributions. In a dataset ${\mathcal {S}}$, the empirical estimation of entropy involves calculating the frequency of occurrence for each value in ${\mathcal {X}}$. The empirical probability in a dataset ${\mathcal {S}}$, denoted as $p_{{\mathcal {S}}}(x)$, is calculated as:

$$\begin{aligned} p_{{\mathcal {S}}}(x) = \frac{\text {number of occurrences of } x \text { in } {\mathcal {S}}}{\text {total data points in } {\mathcal {S}}}, \end{aligned}$$

helping to empirically estimate the entropy by $-\sum _{x \in {\mathcal {X}}} p_{{\mathcal {S}}}(x) \log _2 p_{{\mathcal {S}}}(x)$.

In the context of information theory, entropy is measured in binary bits, namely 0 or 1. As the entropy increases, the amount of distinct, useful information decreases,¹ and hence the randomness and chaotic information both increase. Moreover, the concept of Shannon entropy is closely linked with Fisherian statistical inference. For a random sample $x_1,\dots ,x_n$ from a discrete random variable $\textrm{x}$, the likelihood is $\prod _{i=1}^n p(x_i)$, and the average negative log-likelihood of $-\frac{1}{n}\sum _{i=1}^n \ln p(x_i)$ converges to $-{{\,\mathrm{\mathbb {E}}\,}}(\ln p(\textrm{x})) = -\sum _{x \in {\mathcal {X}}} p(x) \ln p(x)$ by the weak law of large numbers. This limit is exactly $H(\textrm{x})\cdot \ln 2$, equating the likelihood to $\left( \frac{1}{2^{H(\textrm{x})(1+o_p(1))}}\right) ^n$. Additionally, in information theory, the application of entropy is highly motivated for its role in data compression; for a sample $(x_1,\dots ,x_n)\in {\mathcal {X}}^n$, approximately $nH(\textrm{x})$ bits are needed for binary code compression with a large enough n; more details are discussed in Appendix A.1.

By the definition of Shannon entropy, it is clear that $H(\textrm{x}) \ge 0$. For a degenerate variable $\textrm{x}$, $H(\textrm{x})$ equals 0, indicating no uncertainty in $\textrm{x}$. In the case of a Bernoulli variable taking values 0 or 1, by Eq. (2), $H(\textrm{x})$ falls within the range [0, 1], reaching 1 when both outcomes are equally probable. For a discrete variable $\textrm{x}$ with $n$ values and probabilities $p_i$, $i=1,\dots ,n$, the entropy peaks when $p_i \equiv \frac{1}{n}$ for each $i$, yielding $H(\textrm{x}) = \log _2 n$ by using Jensen’s inequality.

For a continuous random variable $\textrm{x}$ with support ${\mathcal {X}}$ and a continuous density function $f(x)$, the concept of Shannon entropy evolves into what is known as differential entropy² (see (Shannon, 1948)). Unlike its discrete counterpart, differential entropy is defined as:

$$\begin{aligned} h(\textrm{x}):= {{\,\mathrm{\mathbb {E}}\,}}(\ln f(x)) = -\int _{{\mathcal {X}}} f(x) \ln f(x) \, dx. \end{aligned}$$

(3)

This form of entropy, however, does not share all properties of Shannon entropy, such as non-negativity and scaling invariance, and hence not a simple generalization of the latter. For example, take a normally distributed variable $\textrm{x} \sim {\mathcal {N}}(\mu ,\sigma ^2)$. The differential entropy $h(\textrm{x})$ is given by $h(\textrm{x})= \frac{1}{2}\left( 1 + \ln (2\pi \sigma ^2)\right)$, which is evidently negative if $\sigma ^2 < \frac{1}{2\pi e}$. Furthermore, as $\sigma ^2 \rightarrow 0$, $\textrm{x}$ becomes a degenerate distribution at $\mu$, and $h(\textrm{x})$ approaches $-\infty$, unlike Shannon entropy which approaches 0. Furthermore, differential entropy may not exist for certain distributions; for instance, consider the distribution with a density function $f(x) = \frac{\ln k}{x (\ln x)^2}$ for $x > k$, and 0 otherwise, where $k>1$, then it can be shown by routine calculations that its differential entropy is infinite.

2.2 Conditional entropy

The Shannon entropy and differential entropy mentioned above are unconditional, and hence useful in scenarios where there is no prior knowledge about the variable x. Meanwhile, it is more typical in real-world applications to have some pre-existing information from other source variables. Intuitively, this additional knowledge should decrease the level of uncertainty and, consequently, the entropy. For example, in a linguistic model designed to forecast upcoming texts, the range of potential subsequent words is significantly narrowed down once the current words are identified. Let us formalize this concept in the following manner. Consider a pair of discrete random variables $(\textrm{x}, \textrm{y})$ with the joint probability mass function $\mathbb {P}(\textrm{x}=x, \textrm{y}=y) =: p(x, y)$ for $x \in {\mathcal {X}}$ and $y \in {\mathcal {Y}}$. Our objective is to investigate how the knowledge of $\textrm{x}$ influences the uncertainty of $\textrm{y}$, thereby affecting its entropy. Utilizing the concept of conditional probability $p(y|x) = \mathbb {P}(\textrm{y}=y|\textrm{x}=x)$, we define the conditional entropy of $\textrm{y}$ given $\textrm{x}$ as:

$$\begin{aligned} H(\textrm{y}|\textrm{x}) {:}{=}-\sum _{x \in {\mathcal {X}}}\sum _{y \in {\mathcal {Y}}} p(x, y) \log _2 p(y|x). \end{aligned}$$

For the special case where $\textrm{y}$ is entirely determined by $\textrm{x}$, i.e., $\textrm{y} = f(\textrm{x})$ for a given function $f$, the conditional probability $p(y|x)$ is 1 when $y = f(x)$ and 0 otherwise, for all $x\in {\mathcal {X}}$, hence $H(\textrm{y}|\textrm{x}) = -\sum _{x \in {\mathcal {X}}} p(x, f(x)) \log _2 p(f(x)|x) = 0$.

We next investigate the relationship between conditional entropy and unconditional entropy. From the definition of $H(\textrm{y}|\textrm{x})$, we can express $p(x, y)$ in terms of the conditional probability $p(y|x)$ and rearrange the summation order to get:

$$\begin{aligned} H(\textrm{y}|\textrm{x})&= - \sum _{y \in {\mathcal {Y}}} \left( \sum _{x \in {\mathcal {X}}} p(x) p(y|x) \log _2 p(y|x) \right) . \end{aligned}$$

Let $\phi (x) {:}{=}x \log _2 x$ for $x > 0$. The inner summation can be represented as $\mathbb {E}(\phi (p(y|\textrm{x})))$ for each $y$. Given that $\phi '(x) = \frac{\ln x + 1}{\ln 2}$ and $\phi ''(x) = \frac{1}{x \ln 2} > 0$ for all $x > 0$, $\phi (x)$ is convex. This permits the application of Jensen’s inequality, leading to:

$$\begin{aligned} H(\textrm{y}|\textrm{x}) = - \sum _{y \in {\mathcal {Y}}} \mathbb {E}(\phi (p(y|\textrm{x})))\le - \sum _{y \in {\mathcal {Y}}} \phi (\mathbb {E}(p(y|\textrm{x}))) = \sum _{y \in {\mathcal {Y}}} p(y) \log _2 p(y) = H(\textrm{y}), \end{aligned}$$

(4)

which aligns with the intuition that additional information decreases the randomness or entropy of the original random variable. Similarly, for the case where $\textrm{y}$ is a continuous variable and $\textrm{x}$ is any type of variable with distribution function $F_{\textrm{x}}(x)$, the conditional differential entropy of $\textrm{y}$ given $\textrm{x}$ is defined using the conditional density $f(y|x)$³:

Consider, for instance, the bivariate normal variables $\textrm{x}$ and $\textrm{y}$, where both share the common marginal distribution ${\mathcal {N}}(\mu , \sigma ^2)$ and possess a correlation coefficient $\rho \in (-1, 1)$. It is evident that $\textrm{y}|\textrm{x}=x \sim {\mathcal {N}}(\mu (1 - \rho ) + \rho x, \sigma ^2(1 - \rho ^2))$. Consequently, the conditional differential entropy $h(\textrm{y}|\textrm{x})$ is equal to $h(\textrm{y}|\textrm{x}) = \frac{1}{2}\left( 1+\textrm{ln}\left( 2\pi \sigma ^2(1 - \rho ^2)\right) \right)$, which is less than $h(\textrm{y}) = \frac{1}{2}\left( 1+ \textrm{ln} \left( 2\pi \sigma ^2\right) \right)$, thereby illustrating a decrease in entropy.

As a remark, the conditional entropy $H(\textrm{y}|\textrm{x})$ can be reformulated as $H((\textrm{y}, \textrm{x})) - H(\textrm{x})$, where $H((\textrm{y}, \textrm{x}))$ is the joint entropy of $(\textrm{y},\textrm{x})$. The proof for the discrete case is straightforward as follows, while the proof in the continuous case is analogous:

$$\begin{aligned} H(\textrm{y}|\textrm{x})&= -\sum _{x \in {\mathcal {X}}} \sum _{y \in {\mathcal {Y}}} p(x, y) \log _2 p(y|x) = H((\textrm{y}, \textrm{x})) - H(\textrm{x}). \end{aligned}$$

(5)

2.3 Mutual information, relative entropy, and cross entropy

In the realm of information theory, mutual information uniquely quantifies the interdependence of two variables, symbolized as $\textrm{x}$ and $\textrm{y}$. This measure is given by $I(\textrm{x},\textrm{y}):=H(\textrm{y})-H(\textrm{y}|\textrm{x})$. Notably, it exhibits symmetry, expressed as $I(\textrm{x},\textrm{y})=H(\textrm{x})-H(\textrm{x}|\textrm{y})=I(\textrm{y},\textrm{x})$, which is straightforward from (5). Delving into entropy and its conditional counterpart, mutual information is bounded, namely $0\le I(\textrm{x},\textrm{y}) \le H(\textrm{y})$, underpinned by the inequalities $H(\textrm{y}) \ge H(\textrm{y}|\textrm{x})\ge 0$, as delineated in (4). Specifically, it reaches the maximum of $H(\textrm{y})$ when $\textrm{y}$ is completely determined by $\textrm{x}$, leading to $H(\textrm{y}|\textrm{x})=0$, while it reaches the minimum of 0 when $\textrm{x}$ and $\textrm{y}$ are independent, resulting in $H(\textrm{y}|\textrm{x})=H(\textrm{y})$.

Relative entropy and cross entropy serve as key indices for gauging disparities between two probability distributions. While these measures do not conform to the requirement of a metric, they retain certain metric-like qualities, such as nonnegativity.

Consider two discrete distributions P and Q, which also act as their respective probability mass functions, defined over a shared discrete domain ${\mathcal {X}}$,⁴ then the concept of relative entropy (also known as Kullback–Leibler divergence, refer to Kullback (1997)) from Q to P is defined as:

$$\begin{aligned} \mathbb {D}(P\Vert Q):= -{{\,\mathrm{\mathbb {E}}\,}}^P\left( \ln \left( \frac{Q(\textrm{x})}{P(\textrm{x})} \right) \right) = -\sum _{x\in {\mathcal {X}}} P(x) \ln \left( \frac{Q(x)}{P(x)}\right) , \end{aligned}$$

where ${{\,\mathrm{\mathbb {E}}\,}}^P$ signifies the expected value according to distribution P. For illustration, assume P and Q are Poisson distributions with parameters $\lambda$ and $\theta$ respectively. The relative entropy from Q to P is computed as

$$\begin{aligned} \mathbb {D}(P\Vert Q)&= \theta - \lambda - \lambda \ln (\theta /\lambda ) . \end{aligned}$$

Similarly, for binomial distributions $P = \textrm{Bin}(n, \alpha )$ and $Q = \textrm{Bin}(n, \beta )$, the relative entropy from Q to P is

$$\begin{aligned} \mathbb {D}(P\Vert Q)&= n\alpha \ln \left( \frac{\alpha }{\beta }\right) + n(\alpha - 1) \ln \left( \frac{1 - \beta }{1 - \alpha }\right) . \end{aligned}$$

These examples indicate that relative entropy inherently lacks symmetry, contravening the commutative nature typical of a metric, though this property may still hold in some special cases, e.g., when $n=1$ and $\alpha =1-\beta$ in the latter example above. Nevertheless, relative entropy does possess nonnegativity in general; to validate this, we apply Jensen’s inequality on the convex function $-\ln x$, then we have:

$$\begin{aligned} \mathbb {D}(P\Vert Q) = {{\,\mathrm{\mathbb {E}}\,}}^P\left( -\ln \left( \frac{Q(\textrm{x})}{P(\textrm{x})} \right) \right) \ge -\ln \left( {{\,\mathrm{\mathbb {E}}\,}}^P\left( \frac{Q(\textrm{x})}{P(\textrm{x})}\right) \right) = -\ln \left( \sum _{x\in {\mathcal {X}}} Q(x) \right) = 0. \end{aligned}$$

Similarly, if P and Q are now continuous over a common support ${\mathcal {X}}$, we define the relative entropy from Q to P analogously by replacing summation with integration:

$$\begin{aligned} \mathbb {D}(P\Vert Q): = -\int _{{\mathcal {X}}} P(x) \ln \left( \frac{Q(x)}{P(x)}\right) dx. \end{aligned}$$

For instance, if P adheres to a d-variate normal distribution with mean vector $\varvec{\mu }_P$ and covariance matrix $\varvec{\Sigma }_P$, and Q follows another d-variate normal distribution with mean vector $\varvec{\mu }_Q$ and covariance matrix $\varvec{\Sigma }_Q$, then the relative entropy from Q to P is:

$$\begin{aligned} \mathbb {D}(P\Vert Q)&= \frac{1}{2} \left( \ln \frac{|\varvec{\Sigma }_Q|}{|\varvec{\Sigma }_P|} - d + \textrm{tr} (\varvec{\Sigma }_Q^{-1} \varvec{\Sigma }_P) + (\varvec{\mu }_P - \varvec{\mu }_Q)^\top \varvec{\Sigma }_Q^{-1} (\varvec{\mu }_P - \varvec{\mu }_Q)\right) . \end{aligned}$$

When $\varvec{\Sigma }_P = \varvec{\Sigma }_Q$, the relative entropy from Q to P increases as the distance between $\varvec{\mu }_P$ and $\varvec{\mu }_Q$ grows. Conversely, if $\varvec{\mu }_P=\varvec{\mu }_Q$, discerning the change direction when $\varvec{\Sigma }_P \ne \varvec{\Sigma }_Q$ can be complex; while in the simplest one-dimensional scenario, with variances $\sigma _P^2$ and $\sigma _Q^2$, then regardless of the value of the correlation coefficient $\rho$, the relative entropy from Q to P simplifies to:

$$\begin{aligned} \mathbb {D}(P\Vert Q) = \frac{1}{2} \left( \frac{\sigma _P^2}{\sigma _Q^2} - \ln \frac{\sigma _P^2}{\sigma _Q^2} - 1 \right) , \end{aligned}$$

which intensifies as the ratio $\sigma _P^2/\sigma _Q^2$ deviates more significantly from 1.

Based on the relative entropy, the cross entropy for two discrete distributions P and Q is defined as follows:

$$\begin{aligned} H(P,Q):= {\tilde{H}}(P) + \mathbb {D}(P\Vert Q)=-\sum _{x\in {\mathcal {X}}} P(x) \ln Q(x), \end{aligned}$$

(6)

with ${\tilde{H}}(P):= -\sum _{x\in {\mathcal {X}}} P(x) \ln P(x)$ representing the scaled entropy of P. Note that it is different from the joint entropy $H((\textrm{x},\textrm{y}))$ in (5).

Given a fixed P, H(P) remains constant regardless of Q, establishing a correspondence between relative entropy and cross-entropy. This entropy framework extends to continuous distributions by substituting summation with integration. Cross entropy often plays the role of a loss function in deep learning, assessing the degree of similarity between the actual label distribution and the predicted distribution in a dataset.

3 Construction of classification trees

In this section, we shall introduce the infrastructure of a classification tree, and discuss how it is constructed and calibrated with the aid of entropy and information gain.

3.1 Classification tree

Consider a dataset ${\mathcal {S}} = { ({\varvec{x}}_i,y_i)}_{i=1}^n$ of size n where ${\varvec{x}}_i=(x_i^{(1)},x_i^{(2)},\dots ,x_i^{(p)})$ comprises p input variables, and $y_i$ is the associated label within ${\mathcal {Y}}=\{c_1,\dots ,c_M\}$. It is implicitly assumed that identical feature vectors (${\varvec{x}}_i \equiv {\varvec{x}}_{i'}$) imply identical labels ($y_i \equiv y_{i'}$). The feature vector space is denoted by ${\mathcal {D}}:=\prod _{j=1}^p {\mathcal {R}}(x^{(j)})$, with ${\mathcal {R}}(x^{(j)})$ representing the range of $x^{(j)}$. A classification tree (a.k.a. decision tree) segments ${\mathcal {D}}$ into M distinct subsets ${\mathcal {D}}_1,\dots ,{\mathcal {D}}_M$, creating a corresponding partition of ${\mathcal {S}}$ into ${\mathcal {S}}_1,\dots ,{\mathcal {S}}_M$, where

$$\begin{aligned} {\mathcal {S}}_k:=\{({\varvec{x}},y)\in {\mathcal {S}}:{\varvec{x}}\in {\mathcal {D}}_k\}. \end{aligned}$$

(7)

A classification tree is defined as an acyclic graph, where each internal node denotes an attribute. This attribute is described by specific quantitative relationships, derived from certain components of a feature vector ${\varvec{x}}$. Branches emerging from a node indicate the outcomes of decision rules. To illustrate, consider a binary classification tree, where each node evaluates a distinct component of ${\varvec{x}}$, denoted as $x^{(j)}$. If $x^{(j)}$ is less than a threshold $t^{(j)}$, the process follows the left branch; otherwise, it proceeds along the right branch. Descending through the tree involves continuously dividing the dataset into increasingly smaller subsets. Branch construction ceases at a particular leaf node when all the labels $y_i$ within that leaf belong predominantly to the same category. This terminal node, or leaf, is then classified as representing a “pure” class label $c_k$ in the set ${\mathcal {Y}}$. The path from the root to a leaf node represents a classification rule. The depth of the tree is the longest path length, or the maximum number of branches, from the root to any leaf node. This framework naturally raises the following questions:

• (1) At each node, which feature should be examined, and what criteria should guide the choice of this feature?

• (2) Specifically, in the context of a binary classification tree, how do we determine the appropriate threshold value, and in cases where an attribute offers a range of values, how should the number of branches be decided?

We shall discuss them in detail in the rest of this section.

3.2 Information gain

Information gain is pivotal in determining the optimal attributes for branching in a classification tree. At each decision node, the entropy of the empirical data distribution is computed, guiding the decision to further split the node based on the adequacy of the information gain. This essentially evaluates whether the split notably reduces uncertainty, as quantified by entropy. For each node, out of the p potential features, a specific feature $\textrm{x}^{(j)}$ is chosen for the split if it yields the maximum information gain. This gain is essentially the mutual information between the label y and the chosen feature $\textrm{x}^{(j)}$ for the subsample at the node. Specifically, consider $\textrm{x}^{(j_i)}$ as the selected attribute at node i with its associated subsample ${\mathcal {S}}^{(i)}$. The information gain IG$({\mathcal {S}}^{(i)},\textrm{x}^{(j_i)})$, which is a specific form of a goodness measure to be discussed further in (12), is conceived as the entropy difference on average before and after dividing ${\mathcal {S}}^{(i)}$ using $\textrm{x}^{(j_i)}$. It is defined as:

$$\begin{aligned} \textrm{IG}({\mathcal {S}}{(i)},\textrm{x}^{(j_i)})&:=I(\textrm{y}^{(i)},\textrm{x}^{(j_i)})=H(\textrm{y}^{(i)})-H(\textrm{y}^{(i)}|\textrm{x}^{(j_i)})\nonumber \\&= H(\textrm{y}^{(i)}) - \sum _{v \in {\mathcal {V}}(\textrm{x}^{(j_i)})} p_{\textrm{x}^{(j_i)}}(v) H(\textrm{y}^{(i,v)})\nonumber \\&=H(\textrm{y}^{(i)})) - \sum _{v\in {\mathcal {V}}(\textrm{x}^{(j_i)})} \frac{|{\mathcal {S}}^{(i,v)}|}{|{\mathcal {S}}^{(i)}|} H(\textrm{y}^{(i,v)}), \end{aligned}$$

(8)

where ${\mathcal {V}}(\textrm{x}^{(j_i)})$ represents all possible values of the attribute $\textrm{x}^{(j_i)}$ after the split, and ${\mathcal {S}}^{(i,v)}$ is the subset of samples from ${\mathcal {S}}^{(i)}$ where $\textrm{x}^{(j_i)}$ takes the value $v\in {\mathcal {V}}(\textrm{x}^{(j_i)})$, and $\textrm{y}^{(i)}$ and $\textrm{y}^{(i,v)}$ are labels of the subsamples ${\mathcal {S}}^{(i)}$ and ${\mathcal {S}}^{(i,v)}$, respectively. The unconditional entropy $H(\textrm{y}^{(i,v)})$ in (8) is derived from the conditional probabilities:

$$\begin{aligned}&\ {\hat{{{\,\mathrm{\mathbb {P}}\,}}}}\left( \textrm{y}^{(i)}=u\left| \textrm{x}^{(j'_n)}=v,\textrm{x}^{(j'_{n-1})}=v_{j'_{n-1}},\dots ,\textrm{x}^{(j'_1)}=v_{j'_1}\right. \right) \nonumber \\ =&\ \frac{\left| \left\{ ({\varvec{x}},y^{(i)})\in {\mathcal {S}}:y^{(i)}=u,x^{(j'_n)}=v,x^{(j'_{n-1})}=v_{j'_{n-1}},\dots ,x^{(j'_1)}=v_{j'_1}\right\} \right| }{\left| \left\{ ({\varvec{x}},y)\in {\mathcal {S}}:x^{(j'_n)}=v,x^{(j'_{n-1})}=v_{j'_{n-1}},\dots ,x^{(j'_1)}=v_{j'_1}\right\} \right| }, \end{aligned}$$

(9)

for all $u\in {\mathcal {Y}}$ and every $v\in {\mathcal {V}}(\textrm{x}^{(j'_n)})$. Here, $j'_n=j_i$ is the current node, with $j'_1,j'_2,\dots ,j'_{n-1}$ being the previously traversed nodes, starting from the root at $j'_1$ and proceeding along the corresponding branches to the current node $j'_n$. The value $v_{j'_j}$ is the corresponding value of the attribute $x^{(j'_j)}$ at the j-th node. For a visual representation, refer to Fig. 1. To simplify notations, we replace $H(\textrm{y}^{(i,v)})$ by an abused symbol $H({\mathcal {S}}^{(i,v)})$, which implies that we make reference to the subsample directly, rather than its associated labels, thereby avoiding any confusion. This approach aids the straightforward comparison of entropy across various subsamples.

Fig. 1

An illustration for splitting tree with a sample ${\mathcal {S}}^{(i)}$ at node i by using an attribute of $\textrm{x}^{(j_i)}$

To exemplify the concept of information gain, we consider a node with a sample size of 20 from a credit default dataset, ${\mathcal {S}}^{(1)} = \{(x_i^{(1)}={ \mathrm I},x_i^{(2)}=\textrm{S}), y_i\in \{\textrm{N},\textrm{Y}\}\}_{i=1}^{20}$. In this sample, 13 individuals did not default (N) on their loans, while 7 defaulted (Y). The first attribute, $x^{(1)}$, denotes “Income level” (I) and can be either “High income” (H) or “Low income” (L). The second attribute, $x^{(2)}$, represents “Sex” (S) and can be either “Female” (F) or “Male” (M). Within these 20 samples, 6 from the non-defaulting class (N) and 5 from the defaulting class (Y) are categorized as low income with $x^{(1)}=\textrm{L}$. The rest fall in the high-income category with $x^{(1)}= \textrm{H}$. On the other hand, 7 samples from class N and 3 from class Y are females with the attribute $x^{(2)}=\textrm{F}$, while the others are males with $x^{(2)}= \textrm{M}$; refer to Table 1 for details.

Table 1 20 credit default samples with Class N or Y as their label y; attributes are “Income level” $x^{(1)}=\textrm{I}$ and “Sex” $x^{(2)}=\textrm{S}$

Fig. 2

Selection of attribute $\textrm{x}^{(1)}$ or $\textrm{x}^{(2)}$ based on information gain

The information gain of two attributes is then given by:

$$\begin{aligned} \textrm{IG}({\mathcal {S}}^{(1)}, { \mathrm I})&= H({\mathcal {S}}^{(1)}) - \frac{11}{20} H({\mathcal {S}}_{\textrm{L}}) - \frac{9}{20} H({\mathcal {S}}_{\textrm{H}}) = 0.0435 ;\\ \textrm{IG}({\mathcal {S}}^{(1)}, \textrm{S})&= H({\mathcal {S}}^{(1)}) - \frac{10}{20} H({\mathcal {S}}_{\textrm{F}}) - \frac{10}{20} H({\mathcal {S}}_{\textrm{M}}) = 0.0080. \end{aligned}$$

Clearly, $\textrm{IG}({\mathcal {S}}^{(1)}, { \mathrm I}) > \textrm{IG}({\mathcal {S}}^{(1)}, \textrm{S})$, which indicates that “ Income level” is more effective than “Sex” for partitioning the data at this node. It is worth noting that there are some circumstances where $H({\mathcal {S}}_{\textrm{H}}) > H({\mathcal {S}}_{\textrm{F}})$ and $H({\mathcal {S}}_{\textrm{L}}) = H({\mathcal {S}}_{\textrm{M}})$, yet $\textrm{IG}({\mathcal {S}}^{(1)}, { \mathrm I}) > \textrm{IG}({\mathcal {S}}^{(1)}, \textrm{S})$; in such scenario, the individual entropies of child nodes derived from “ Income level” are higher than those from “Sex”, while their combined effect (average entropy) is lower once the proportional contributions of each child node are factored in. This phenomenon, more commonly known as the Simpson’s Paradox, highlights a situation where a clear-cut trend in separate groups vanishes or reverses when these groups are aggregated; also see (Wagner, 1982) for detailed discussions.

3.3 Other impurity measures for information

In addition to the entropies and mutual information previously discussed, we now introduce two additional prevalent impurity measures:

• 1. Gini-index For a discrete random variable $\textrm{x}$ with its probability mass function denoted as p(x) for each $x\in {\mathcal {X}}$, the Gini-index, denoted by G, is defined by:

  $$\begin{aligned} G(\textrm{x}):= 1 - \sum _{x\in {\mathcal {X}}}p^2(x). \end{aligned}$$

  (10)

• 2. Misclassification Error The misclassification error for a discrete random variable $\textrm{x}$ is given by:

  $$\begin{aligned} \text {Misclassification Error}(\textrm{x}):= 1 - \max _{x\in {\mathcal {X}}}p(x). \end{aligned}$$

  (11)

Refer to Fig. 3 for an illustration of the characteristic trends of entropy, Gini-index, and misclassification error when $\textrm{x}$ is modeled as a Bernoulli random variable with the success probability p. Apparently, for all these measures of impurity, their peak values are attained when $p=1-p=\frac{1}{2}$, indicating the equal likelihood of all outcomes. At this juncture, the respective node in a binary tree is in its “most impure” state.

Fig. 3

Graphical illustration of entropy, Gini-index, and misclassification error for a Ber(p) distribution as p varies

Similar to entropy, for a discrete random variable $\textrm{x}$ with n distinct outcomes, all impurity measures reach their respective maxima when the probabilities are uniformly distributed, i.e., $p(x)\equiv \frac{1}{n}$, indicating that each outcome is equally probable. The maximum values for these impurity measures under uniform distribution are as follows: (1) for entropy, it reaches $H(\textrm{x})=\log _2 n$ as discussed before; (2) for the Gini-index, the maximum is $G(\textrm{x})=1-\frac{1}{n}$, which can be shown using the Lagrange multiplier method; and (3) for misclassification error, it achieves $1-\frac{1}{n}$, derived from the condition $(\max _ip_i)\cdot n\ge \sum \limits _{i=1}^np_i=1$. In line with the principle of maximizing information gain for optimal attribute selection in node splitting, we typically evaluate the impurity of the parent node prior to splitting and compare it with the weighted average impurity of the resulting child nodes. Following the notations defined in Subsection 3.2, we define the goodness⁵ of an attribute $\textrm{x}^{(j_i)}$ at the node i in a similar manner as entropy:

$$\begin{aligned} \Delta \text {Im} (\textrm{x}^{(j_i)}):=\text {Im}({\mathcal {S}}^{(i)})-\sum _{v\in {\mathcal {V}}(\textrm{x}^{(j_i)})} \frac{|{\mathcal {S}}^{(i,v)}|}{|{\mathcal {S}}^{(i)}|}\text {Im}({\mathcal {S}}^{(i,v)}), \end{aligned}$$

(12)

where $\text {Im}(\cdot )$ represents a predetermined impurity measure, akin to one of those as previously discussed. The impurity measure applies to the probability distributions of labels, specifically to the conditional distribution in (9). To simplify our notation without causing significant confusion, we use $\text {Im}({\mathcal {S}}^{(i,v)})$ to denote the impurity measure associated with the conditional probability distribution of labels derived from the subsample ${\mathcal {S}}^{(i,v)}$. Additionally, for ease of reference, we equate the name of a node with that of its corresponding subsample. The chosen impurity measure is consistently applied across the development of the entire classification tree, and potentially even across an entire random forest (refer to Sect. 5 for more details). Our goal is to select an attribute $\textrm{x}^{(j_i)}$ that lowers the impurity measure the most, indicated by the largest value of $\Delta \text {Im}(\textrm{x}^{(j_i)})$.

Let us explore a straightforward example to demonstrate the computations using the various impurity measures mentioned before. Consider a dataset comprising 13 elements, roughly evenly split between two groups: 6 in group 1 and 7 in group 2. To decide how to split the root node into two child nodes, we evaluate two binary attributes, namely A and B, using the data presented in Table 2. For the sake of illustration, we employ the Gini index as the impurity measure.

Table 2 Number of elements in Groups 1 and 2 after splitting by either attribute A or B

The Gini-index at the parent node is:

$$\begin{aligned} G(\text {parent}) = 1 - \left( \frac{6}{13}\right) ^2 - \left( \frac{7}{13}\right) ^2 = 0.4970; \end{aligned}$$

similarly, we can calculate the Gini-index at each child node using A as the splitting attribute as $G_{\textrm{A}}(N_1)=0.4688$, $G_\textrm{A}(N_2)=0.32$; and using B as the splitting attribute, the corresponding Gini-index at each child node becomes $G_\textrm{B}(N_1)=0.4688$, $G_{\textrm{B}}(N_2)=0.48$. Therefore, the respective goodness measures for A and B are:

$$\begin{aligned} \Delta G(\textrm{A})&= G(\text {parent}) - \left( \frac{5+3}{13} \right) G_{\textrm{A}}(N_1) - \left( \frac{1+4}{13} \right) G_\textrm{A}(N_2) = 0.0854,\\ \Delta G(\textrm{B})&= G(\text {parent}) - \left( \frac{3+5}{13} \right) G_{\textrm{B}}(N_1) - \left( \frac{3+2}{13} \right) G_\textrm{B}(N_2) = 0.0239. \end{aligned}$$

Therefore, we conclude that attribute A is favored over B, as $\Delta G(\textrm{A}) = 0.0854 > 0.0239 = \Delta G(\textrm{B})$.

3.4 Splitting against continuous attributes

The methods studied before can be extended to identify the optimal split for a continuous attribute $\textrm{x}^{(j)}$. This involves segmenting the value range of $\textrm{x}^{(j)}$ into several non-overlapping, consecutive intervals, and calculating the impurity measure for each child node based on the probability mass distribution over these intervals. The crucial part is how to choose the potential splits, and a common way is as follows: we first sort the data with respect to the attribute, then compute the possible splitting points, typically the midpoints between each pair of adjacent values. We illustrate the idea with an example using a continuous attribute of Age to predict a binary outcome, “Buys Premium Subscription” (taking values of Yes or No) on a service, see the illustration in Fig. 4.

Fig. 4

Choosing the threshold value for the attribute Age with the smallest weighted Gini-index

As shown in Fig. 4, the black crosses represent individual data points, with the x-coordinate indicating the age and the vertical position indicating whether the person makes the subscription, and the red line shows the trend of weighted Gini-index after partitioning at each potential splitting point (the midpoints between consecutive ages, indicated by the solid dots), and the blue dashed line indicates the best split using this attribute, which in this case occurs at the age of 25, where the Gini-index is at its lowest of 0.3. To verify the result for this particular splitting, by noting that one child contains 2 data points both being “No”, and that the other contains 8 data points with 6 being “Yes” and 2 being “No”, the Gini-indices of the two child nodes are 0 and 0.375, respectively, and the weighted Gini-index for the split at this threshold can be calculated as:

$$\begin{aligned} \text {Weighted Gini} = \frac{2}{10} \times 0 + \frac{8}{10} \times 0.375 = 0.3. \end{aligned}$$

We can also compute the Gini-index for other candidate splitting points analogously, and then verify that the age of 25 is an optimal splitting point.

3.5 Overfitting in classification tree

Overfitting is a common issue where the model becomes too complex and starts to capture not only the underlying patterns in the training data but also the noise. In classification trees, this happens when the tree is too detailed and has too many branches. Ideally, there is an optimal time to stop the growth of the decision tree, ensuring that it maintains a sufficiently high accuracy while also possessing good generalization capabilities. This can be achieved via pre-pruning or post-pruning; we shall introduce the philosophy behind, it and also discuss some examples of commonly used pruning algorithms.

Pre-pruning is quite intuitive; it involves setting thresholds or criteria that determine when the growth of the tree should stop, such as fixing the maximum depth of the tree or the minimum number of samples required at a leaf node. However, pre-pruning methods share a common problem known as the “horizon effect”, namely they may cause the classification to stop too early before valuable partitions appear in subsequent steps.

On the other hand, post-pruning, also known as backward pruning, allows the tree to grow to a certain size first and remove branches that do not contribute significantly to the accuracy or other measures of the tree on validation data. There are two primary methods depending on where the pruning process begins:

• 1. Bottom-up pruning starts at the leaves of the tree and moves upward towards the root. A node (and its subtree) is pruned if removing it improves or maintains the performance of the tree according to a certain metric, like error rate or cost complexity.

• 2. Top-down pruning starts at the root of the tree and removes the subtree beneath a node if its “contributed reduction” in terms of entropy or other impurity measures is below a specified threshold.

Furthermore, deciding which branches to prune in a classification tree involves a careful evaluation of its structure and the impact of each split on the performance of the model. We here introduce three representative pruning techniques that are arguably more popular than the others:

(a) Reduced Error Pruning In this technique, we start at the leaves and evaluate the impact of removing each split (or subtree) on the validation set. A split is deleted if its removal does not decrease the accuracy of the tree. This approach is straightforward and effective in reducing the complexity of the tree without sacrificing accuracy.

(b) Cost complexity pruning The aim of this approach is to prevent overfitting by considering not only the original classification error $R({\mathcal {T}})$ but also the complexity of the tree. This is achieved by introducing a “penalty” term to the original misclassification rate $R({\mathcal {T}}):= \frac{1}{n}\sum _{\ell =1}^{T} \sum _{({\varvec{x}}_i,y_i) \in {\mathcal {T}}_\ell } \mathbbm {1}_{\{y_i \ne {\bar{y}}_{{\mathcal {T}}_\ell }\}}$, where T is the number of terminal leaf nodes in the tree, leading to the objective of constructing a tree that minimizes the following criterion:

$$\begin{aligned} R_\alpha ({\mathcal {T}}):= R({\mathcal {T}}) + \alpha T = \frac{1}{n}\sum _{\ell =1}^{T} \sum _{({\varvec{x}}_i,y_i) \in {\mathcal {T}}_\ell } \mathbbm {1}_{\{y_i \ne {\bar{y}}_{{\mathcal {T}}_\ell }\}} + \alpha T. \end{aligned}$$

(13)

Here, $\alpha$ represents a hyperparameter that controls the influence of model complexity. Given $\alpha \ge 0$, the objective is to find a subtree ${\mathcal {T}}(\alpha )$ within ${\mathcal {T}}$, denoted as ${\mathcal {T}}(\alpha ) \subseteq {\mathcal {T}}$, that minimizes $R_\alpha ({\mathcal {T}})$, defined as:

$$\begin{aligned} {\mathcal {T}}(\alpha ):= \mathop {\mathrm {arg\,min}}\limits _{\tilde{{\mathcal {T}}} \subseteq {\mathcal {T}}} R_\alpha (\tilde{{\mathcal {T}}}) = \mathop {\mathrm {arg\,min}}\limits _{\tilde{{\mathcal {T}}} \subseteq {\mathcal {T}}} \bigg ( R(\tilde{{\mathcal {T}}}) + \alpha {\tilde{T}} \bigg ). \end{aligned}$$

(14)

(c) Chi-squared pruning In the construction of a classification tree, we usually carry out a splitting whenever there is an Information Gain, without investigating whether the change in entropy holds statistical significance. This issue can be addressed by hypothesis testing, where the null hypothesis is that the feature used to split the data at a node is conditionally independent of the target variable, given all the classification rules leading to this node. Mathematically, let ${\mathcal {C}}^{(i)}$ be the collection of classification rules leading to the current node $j'_n=j_i$ in a built tree, in terms of the splitting attributes at the traversed nodes, $\textrm{x}^{(j_1')},\dots , \textrm{x}^{(j_{n-1}')}$, and a further splitting into q child nodes by $\textrm{x}^{(j_i)}$ is carried out, where the k-th child node ${\mathcal {S}}^{(i+1,k)}$ contains those data points with $\textrm{x}^{(j_i)}\in {\mathcal {X}}^{(j_i,k)}\subset {\mathcal {X}}^{(j_i)}$, for $k=1,\dots ,q$, such that $\bigsqcup _{k=1}^q{\mathcal {X}}^{(j_i,k)}={\mathcal {X}}^{(j_i)}$. The null hypothesis can now be written as $\textrm{x}^{(j_i)}\mid {\mathcal {C}}^{(i)}\perp \!\!\! \perp \textrm{y}\mid {\mathcal {C}}^{(i)}$, under which we have, for any $u\in {\mathcal {Y}}$ and $k=1,\dots ,q$,

$$\begin{aligned} \mathbb {P}(\textrm{y}=u\mid {\mathcal {C}}^{(i)},\textrm{x}^{(j_i)}\in {\mathcal {X}}^{(j_i,k)})&=\frac{\mathbb {P}(\textrm{y}=u,\textrm{x}^{(j_i)}\in {\mathcal {X}}^{(j_i,k)}\mid {\mathcal {C}}^{(i)})}{\mathbb {P}(\textrm{x}^{(j_i)}\in {\mathcal {X}}^{(j_i,k)}\mid {\mathcal {C}}^{(i)})}\\&=\frac{\mathbb {P}(\textrm{y}=u\mid {\mathcal {C}}^{(i)})\mathbb {P}(\textrm{x}^{(j_i)}\in {\mathcal {X}}^{(j_i,k)}\mid {\mathcal {C}}^{(i)})}{\mathbb {P}(\textrm{x}^{(j_i)}\in {\mathcal {X}}^{(j_i,k)}\mid {\mathcal {C}}^{(i)})}\\&=\mathbb {P}(\textrm{y}=u\mid {\mathcal {C}}^{(i)}). \end{aligned}$$

In particular, under this hypothesis, we expect that the child nodes will share the exact class distribution as that in the parent node, hence the splitting of the node using this feature will not essentially improve the prediction of the target variable in nature due to the independence; mathematically, this means $\frac{|({\varvec{x}},y)\in {\mathcal {S}}^{(i+1,1)}:y=u|}{|{\mathcal {S}}^{(i+1,1)}|}\approx \cdots \approx \frac{|({\varvec{x}},y)\in {\mathcal {S}}^{(i+1,q)}:y=u|}{|{\mathcal {S}}^{(i+1,q)}|}\approx \frac{|({\varvec{x}},y)\in {\mathcal {S}}^{(i)}:y=u|}{|{\mathcal {S}}^{(i)}|}$ for all $u\in {\mathcal {Y}}$. If we do not reject the null hypothesis, then for the sake of this independence test, the most commonly used tool is the celebrated Pearson’s chi-squared test statistic, which is also why the resulting pruning method is called chi-squared pruning.

Fig. 5

Example of chi-square pruning

Let us illustrate the idea of this approach using a simple example as shown in Fig. 5, where at a particular node of the tree as the parent node, the observations in classes A and B are displayed in red solid dots and black crosses, respectively. In particular, $N_{\textrm{L}}$ and $N_{\textrm{R}}$ are the numbers of nodes in left and right child nodes; the proportions of data points in classes A and B in the parent node are denoted by $P_{\textrm{A}}$ and $P_{\textrm{B}}$; $N_{AL}$ and $N_{BL}$ (resp. $N_{AR}$ and $N_{BR}$) are the actual numbers of class-A and class-B data points in the left (resp. right) child node, respectively, and their corresponding expected numbers are denoted similarly with E replacing N.

Recall that Pearson’s chi-squared test statistic is calculated as the sum of squared standardized differences between observed and expected frequencies of certain variables at each node; the general form of the test statistic, for M number of possible class labels and q number of child nodes in the splitting of concern, is:

$$\begin{aligned} K:=\sum _{\begin{array}{c} i=1,\dots ,M \\ j=1,\dots ,q \end{array}}\frac{(N_{ij} - E_{ij})^2}{E_{ij}}, \end{aligned}$$

(15)

where $N_{ij}$ (resp. $E_{ij}$) is the actual (resp. expected) number of class-i data points in the j-th child node, and it follows a $\chi ^2$ distribution with $(M-1)(q-1)$ degrees of freedom under the null hypothesis above. A lower value of the chi-squared test statistic, corresponding to a larger p-value, means that it is advisable to remove the split. To this end, we conduct the Pearson’s chi-squared test as follows:

• (1) We first calculate the test statistic as follows; note that $M=q=2$ in this particular example:

  $$\begin{aligned} K&= \frac{(N_{\textrm{AL}}-E_{\textrm{AL}})^2}{E_{\textrm{AL}}}+\frac{(N_\textrm{AR}-E_{\textrm{AR}})^2}{E_{\textrm{AR}}}+\frac{(N_{\textrm{BL}}-E_\textrm{BL})^2}{E_{\textrm{BL}}}+\frac{(N_{\textrm{BR}}-E_{\textrm{BR}})^2}{E_{\textrm{BR}}}\\&=\frac{(2-\frac{25}{9})^2}{\frac{25}{9}}+\frac{(3-\frac{20}{9})^2}{\frac{20}{9}}+\frac{(3-\frac{20}{9})^2}{\frac{20}{9}}+\frac{(1-\frac{16}{9})^2}{\frac{16}{9}}=1.1025. \end{aligned}$$

• (2) Under the null hypothesis, the degree of freedom of the $\chi ^2$ distribution is $(M-1)(q-1)=1$, then the p-value of the test can be computed as $\mathbb {P}(\chi ^2_1>1.1025)=0.2937>0.05$. Therefore, we do not reject the null hypothesis at a 5% significance level, suggesting that the split should be pruned as the amount of reduced entropy is of little statistical significance.

In summary, this statistical approach ensures that the complexity of the decision tree is balanced with its predictive power, leading to more robust and versatile models.

4 Regression tree

A regression tree is similar to a classification tree, with the key distinction that in regression trees, the target variable y spans a continuous range of values, as opposed to the categorical nature required for classification trees. Recall that the foundational inspiration of a classification tree involves dividing the space of feature vectors ${\mathcal {D}}$ into M more manageable regions, specifically ${\mathcal {D}}_1,\dots ,{\mathcal {D}}_M$. In this context, the predictor function ${\hat{f}}$, utilized for label prediction, is expressed as follows:

$$\begin{aligned} {\hat{f}}({\varvec{x}}) = \sum _{k=1}^M c_k \mathbbm {1}_{\{{\varvec{x}}\in {\mathcal {D}}_k\}}. \end{aligned}$$

(16)

Recall that constructing a classification tree ${\mathcal {T}}$ involves identifying a series of terminal leaf nodes, represented as $\{{\mathcal {T}}_1, \ldots , {\mathcal {T}}_T \}$, to minimize the possible misclassification rate $R({\mathcal {T}})$. In contrast, when creating a regression tree, the binary loss indicated by $\mathbbm {1}_{\{y_i\ne {\hat{y}}_{{\mathcal {T}}_\ell }\}}$ in the expression of $R({\mathcal {T}})$ is substituted by a squared loss function:

$$\begin{aligned} R({\mathcal {T}}):= \frac{1}{n}\sum _{\ell =1}^{T}\sum _{({\varvec{x}}_i,y_i)\in {\mathcal {T}}_\ell } (y_i-{\hat{y}}_{{\mathcal {T}}_\ell })^2, \end{aligned}$$

(17)

and the tree derived from minimizing (17) is typically referred to as a regression tree; $M = T$ represents the total number of divisions within the tree. In a standard approach, each terminal node ${\mathcal {T}}_\ell$ is assigned a unique continuous value, such as the average of the subsample at that node. This can be mathematically expressed as:

$$\begin{aligned} {\hat{y}}_{{\mathcal {T}}_\ell } = \frac{1}{|{\mathcal {T}}_\ell |} \sum _{({\varvec{x}}_i,y_i) \in {\mathcal {T}}_\ell } y_i, \quad \text {for } \ell =1,\dots ,T. \end{aligned}$$

(18)

Furthermore, the regression loss in (17) can be reformulated as:

$$\begin{aligned} R({\mathcal {T}}):= \frac{1}{n}\sum _{i=1}^n(y_i - {\hat{f}}({\varvec{x}}_i))^2, \end{aligned}$$

where the function ${\hat{f}}({\varvec{x}})$ is defined similarly to (16), except that the values $c_k$’s may assume any value within a continuous range. Considering this framework, a regression tree can be viewed as a variant of a threshold regression model, whose predictor function is given by:

$$\begin{aligned} {\hat{f}}({\varvec{x}})=\sum _{\ell =1}^T {\hat{f}}_\ell ({\varvec{x}}) \mathbbm {1}_{\{{\varvec{x}} \in {\mathcal {D}}_\ell \}}, \end{aligned}$$

where ${\hat{f}}_\ell$ is a specific regression function applicable within the domain ${\mathcal {D}}_\ell$, for $\ell =1,\dots ,T$.

Like classification trees, a regression tree is constructed using a top-down, greedy search method. Beginning at the root node, we identify the optimal splitting attribute that reduces the squared loss function to its minimum. This process is then repeated, moving to a subsequent child node. In our discussion, we concentrate primarily on the prevalent practice of binary splitting. However, it is important to note that binary splitting is not a requirement for regression trees. The approach we describe here can be readily generalized to accommodate scenarios where a parent node is divided into three or more child nodes.

Fig. 6

An illustration of splitting at a parent node with a dataset ${\mathcal {S}}$

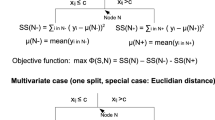
Consider ${\mathcal {S}} = \{(\varvec{x}_i, y_i)\}_{i=1}^n$ as the dataset at a given parent node. For a selected feature variable $\textrm{x}^{(j)}$ and a yet-to-be-determined attribute value $t^{(j)}$, our goal is to partition the dataset into two segments:

$$\begin{aligned} {\mathcal {S}}_-^{(j)} = \{({\varvec{x}}_i,y_i)\in {\mathcal {S}}:x_i^{(j)} < t^{(j)} \} \quad \text {and} \quad {\mathcal {S}}_+^{(j)} = \{({\varvec{x}}_i,y_i)\in {\mathcal {S}}: x_i^{(j)} \ge t^{(j)} \}, \end{aligned}$$

as visually represented in Fig. 6.

We define the mean label values for the subsamples at the two resulting child nodes as:

$$\begin{aligned} {\bar{y}}_{{\mathcal {S}}_-^{(j)}} = \frac{\sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}_-^{(j)}} y_i}{|{\mathcal {S}}_-^{(j)}|} \qquad \text {and} \qquad {\bar{y}}_{{\mathcal {S}}_+^{(j)}} = \frac{\sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}_+^{(j)}} y_i}{|{\mathcal {S}}_+^{(j)}|}. \end{aligned}$$

The efficacy of this split is quantified by the following mean squared error:

$$\begin{aligned} \frac{1}{|{\mathcal {S}}|}\left( \sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}_-^{(j)}} (y_i - {\bar{y}}_{{\mathcal {S}}_-^{(j)}})^2 +\sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}_+^{(j)}} (y_i - {\bar{y}}_{{\mathcal {S}}_+^{(j)}})^2\right) . \end{aligned}$$

(19)

Our objective is to identify the most effective combination of $\textrm{x}^{(j)}$ and $t^{(j)}$ that minimizes (19). For each feature $\textrm{x}^{(j)}$, we initially pinpoint the ideal $t^{(j)}$ that reduces (19) to its minimum, utilizing potential thresholds from a specific discretization approach (also see Subsection 3.4). Subsequently, we compare these minimum mean squared errors across all attributes and select the attribute yielding the lowest error. This process repeats until a stopping criterion is met at a terminal node ${\mathcal {T}}_\ell$, halting further splits. Common stopping criteria include:

• (i) the sample count of the node falls below a preset threshold $n_0$:

  $$\begin{aligned}|{\mathcal {T}}_\ell |<n_0; \quad \text {or}\end{aligned}$$

• (ii) the sum of squared errors at the node falls beneath a predetermined limit $\epsilon$:

  $$\begin{aligned} \sum _{({\varvec{x}}_i,y_i)\in {\mathcal {T}}_\ell }(y_i-{\hat{y}}_{{\mathcal {T}}_\ell })^2<\epsilon ;\text { or} \end{aligned}$$

• (iii) the reduction in mean squared error (19) from an additional split of the current node ${\mathcal {S}}$ into ${\mathcal {S}}_-^{(j)}$ and ${\mathcal {S}}_+^{(j)}$, using any feature variable $x^{(j)}$, is less than some threshold $\epsilon$:

  $$\begin{aligned} \max _j\left( \frac{1}{|{\mathcal {S}}|}\left( \sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}} (y_i - {\hat{y}}_{\mathcal {S}})^2 - \left( \sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}_-^{(j)}} (y_i - {\bar{y}}_{{\mathcal {S}}_-^{(j)}} )^2 +\sum _{({\varvec{x}}_i,y_i)\in {\mathcal {S}}_+^{(j)}} (y_i - {\bar{y}}_{{\mathcal {S}}_+^{(j)}})^2\right) \right) \right) <\epsilon . \end{aligned}$$

Once a regression tree is constructed, the predicted value of a test observation is the mean of the training observations in the region ${\mathcal {D}}_\ell$ where the test observation falls.

Fig. 7

Regression tree splitting algorithm for one attribute

Consider an illustrative example as shown in Fig. 7, which depicts a dataset with four distinct categories, encompassing a single feature variable $\textrm{x}$ and a label variable $\textrm{y}$, both of which are real-valued. The root node of the tree initiates the division of the dataset into two segments based on the condition $x<t_1$ or $x\ge t_1$. Subsequently, the mean values ${\hat{c}}_1$ and ${\hat{c}}_2$ for these segments are computed. Each of these segments is further subdivided into two smaller groups, using the thresholds $t_2$ and $t_3$. This results in distinct clusters, each aligned with a specific label.

Fig. 8

Illustrations of a feasible partition of a space of feature vectors caused by a regression tree, and an impossible one

While the regression tree model is frequently utilized, it is also important to note its limitations. The tree construction is inherently a greedy, top-down binary search, in the sense that each split decision is optimal given the results of previous splits at preceding nodes, making it locally optimal but not necessarily globally. Besides, some spatial partitions of ${\mathcal {D}}$ cannot be achieved by a regression tree. Take the case of two feature variables for instance, a regression tree may be able to partition ${\mathcal {D}}$ as shown in Fig. 8(a), yet it is never possible for any regression tree to achieve a partitioning such as the one in Fig. 8(b). Indeed, even the initial split in scenario (b) cannot be located, whereas in (a), the vertical line $x^{(1)} = s''_1$ can serve as the initial split, and the subsequent splitting steps are also viable. Last but not least, just like classification trees, the construction of regression trees is sometimes also subject to the overfitting issue, adversely affecting its performance on test data. This issue can likewise be mitigated by various pruning methods leading to a simpler tree with fewer splits, which might increase the variance of the tree but also improve its interpretability.

5 Random forest

The concept of a random forest stems from the principle of bagging. Starting with a training set ${\mathcal {S}}$, the approach involves generating B random subsets ${\mathcal {S}}_1, \ldots , {\mathcal {S}}_B$ from ${\mathcal {S}}$, where B is a pre-defined hyperparameter. Corresponding to each subset, B distinct tree models, with respective predictive functions ${\hat{f}}_1, \ldots , {\hat{f}}_B$, are constructed for classification and regression purposes. For each $b=1,\dots ,B$, we obtain ${\mathcal {S}}_b$ by sampling from ${\mathcal {S}}$ with replacement until $|{\mathcal {S}}_b|=n=|{\mathcal {S}}|$. Additionally, when dealing with a large number of features, say p of them, the construction of each tree for a subset ${\mathcal {S}}_b$ may be limited to a smaller number of features, let’s say $m \ll p$, so as to streamline the computational complexity. After training, the ensemble comprises B distinct tree models. For a new input vector ${\varvec{x}}$, the predictive outcome from the random forest is the mean of the predicted values from the B models in the case of regression:

$$\begin{aligned} {\hat{f}}_{\textrm{rf}} ({\varvec{x}}) = \frac{1}{B} \sum _{b=1}^B {\hat{f}}_b({\varvec{x}}); \end{aligned}$$

while it becomes the majority vote in the classification context. Also see Fig. 9 for a graphical illustration.

Fig. 9

A graphical illustration of random forest

The rationale for choosing random subsets of features in constructing different trees is to minimize correlation among these trees, thereby lowering the overall variance of the model beyond what is achieved through bagging alone. When certain features are exceptionally strong indicators for the target label, they tend to be repeatedly selected for splitting in multiple trees, leading to a collection of highly similar, or correlated, trees in the ensemble. This correlation among predictors does not contribute to enhancing prediction accuracy by variance reduction. The key to the effectiveness of model ensembling lies in the fact that good models usually concur on predictions, whereas less effective models tend to diverge. By amalgamating these models, the ensemble can spread out the errors, thereby diminishing variance. However, when bad models exhibit correlation, they are more inclined to produce concordant predictions, which can undermine the effectiveness of methods like majority voting or averaging.

6 Application in Python and R

6.1 Classification tree

In the context of both Python and R, the process of creating a classification tree involves iterative binary segmentation of predictor variables $\textrm{x}^{(j)}$, where $j=1,\ldots ,p$. This approach, which examines every possible division resulting from each predictor variable, renders the tree construction both computationally demanding and time-intensive. Commonly, subsequent to the tree’s assembly, an optimally chosen hyperparameter, denoted as $\alpha$, is employed for the tree pruning procedure. The optimal subtree, which minimizes the criterion outlined in (13), is selected as the definitive tree. From this tree, a series of clear and concise classification rules are then extracted.

In Python, the implementation of a classification tree is facilitated through the use of DecisionTreeClassifier, a component of the widely-utilized sklearn package within the tree class. The necessary libraries for constructing a classification tree in Python can be imported as demonstrated in Program 1.

The function plot_tree() is utilized in plotting the classification tree derived from DecisionTreeClassifier, while export_text() generates a textual description of the classification rules. The DecisionTreeClassifier in Python, noted for its user-friendliness, contains a variety of hidden options. Specifically, ccp_alpha represents the hyperparameter $\alpha$ for cost complexity pruning, with a default setting of 0. The parameter criterion determines the method for measuring impurity, set by default to gini for the Gini-index, as indicated in (10). Other alternatives for this parameter include entropy, corresponding to Shannon entropy as outlined in 1, and log_loss, related to differential entropy as mentioned in 3. Within the R environment, the construction of a classification tree is facilitated through the rpart() function, which is a part of the built-in rpart library.⁶, where the acronym rpart represents Recursive Partitioning and Regression Trees; also see Programme 2.

The function rpart() in R provides a variety of options. For example, to employ differential entropy, one can set parms=list(split="information"), while the Gini-index, denoted by gini, is the default option. Regarding cost complexity pruning, the default parameter of the function is $\alpha =0.01$, while users have the flexibility to define any non-negative value for $\alpha$, such as $\alpha =0.05$, which is achievable through control=rpart.control(cp=0.05). It is important to highlight the method parameter in rpart, with the possible values of class, anova, poisson, and exp; among them, class is ideal for classification tasks with a categorical target variable, anova is adopted for regression trees designed to minimize the total mean squared errors across all end nodes, poisson fits Poisson regression scenarios, and exp is applicable for constructing regression trees in survival analysis with exponential scaling. These trees, often labeled as survival trees, provide a nonparametric substitute for the renowned semiparametric Cox proportional hazards model.

HSI dataset: We next demonstrate the construction of a classification tree using the stock data from the Hong Kong market in 2018, stored in the file fin-ratio.csv, for the task of classifying whether a stock is a constituent of the Hang Seng Index (HSI); note that the data have not undergone outlier detection. See the programmes in Python and R in Programmes 3 and 4, respectively.

Fig. 10

Classification tree for the stock data in 2018 without removing outliers

The classification trees of Python and R in Fig. 10 look different but still agree with each other to a certain degree. What caused the difference will be discussed later. Here, we may focus on a tree generated by Python for simplicity. Below are the detailed classification rules along with the associated quality metrics:

• R1: If $\texttt {ln\_MV} \le 24.928$, then return as class = 0 (not HSI) (430/1).

• R2: If $\texttt {ln\_MV} > 24.9288$ and $\texttt {DY} \le 4.683$, then return as class = 0 (not HSI), (67/24).

• R3: If $\texttt {ln\_MV} \ge 24.9288$ and $\texttt {DY} > 4.683$, then return as class = 1 (HSI) (16/25).

The figures at the terminal nodes indicate the number of cases. For instance, in the subset where $\texttt {ln\_MV} \le 9.478$, the count is 430 for the “zero” group and 1 for the “one” group. With this in mind, given the only simple condition that $\texttt {ln\_MV} \le 9.478$, we can predict the stock is a Blue Chip with confidence.

A cross-tabulation table detailing this classification tree is available: refer to Programme 5 for the Python version and Programme 6 for the R version. According to the output, Python and R exhibit different performances and tree structures on the same dataset. If we take a closer look at Fig. 10, the first two layers of trees share the same threshold (cut-point) and structure, but the tree created by R is significantly larger, which means that the growth of the tree in Python is stopped earlier. This difference can be attributed to various other hyperparameters involved in tree construction. For instance, minsplit determines the minimum number of observations required in a node for a split to occur, and maxdepth defines the maximum depth of the tree, considering the root node as depth 0.

6.2 Regression tree

A medical insurance example In another scenario, we turn our attention to a case study aimed at forecasting the Premium Price set by a health insurance provider. This prediction is based on two key customer attributes: Age and Weight.⁷

Fig. 11

Regression tree for the medical premium data

Fig. 12

Premium price is color-coded from low (red, green) to high (blue, purple)

From Fig. 11, we observe that the regression tree utilizes four boundary points: 30 years and 47 years for the Age feature, and 70 kg and 95 kg for the Weight feature. These points partition the dataset ${\mathcal {R}}$ into five groups: ${\mathcal {R}}_1$, ${\mathcal {R}}_2$, ${\mathcal {R}}_3$, ${\mathcal {R}}_4$, and ${\mathcal {R}}_5$. The regression tree model yields the following insights:

• 1. Age is a primary determinant of the Premium Price for a customer. Customers younger than 30 years are assigned a lower premium, those between 30 and 47 years a medium premium, and customers older than 47 years a higher premium.

• 2. For customers younger than 47 years, Weight does not affect their premium.

• 3. For customers older than 47 years, Weight affects the Premium Price. In this age group, customers weighing less than 70 kg are charged a lower premium, those between 70 and 95 kg a medium premium, and customers over 95 kg a higher premium.

6.3 Random forest

Let us implement the random forest algorithm on the 2018 financial dataset using both Python and R. We then compare these outcomes with those derived from a solitary classification tree.

The observed misclassification rate is $0\%$, significantly surpassing the rate achieved with the classification tree in Programme 5.

The misclassification rate is calculated as $=\frac{28+17}{491+22}=7.51\%$, which is unexpectedly higher compared to the classification tree in Programme 6. It’s noteworthy that the total count of samples, $471+28+17+22 = 558$, does not equal 563 due to some predictions being NA.

This example illustrates that in each split of the tree-building process for a random forest, only a randomly chosen subset of $m=2$ features (specified as max_features=2 in Python and mtry=2 in R) from the original $p=6$ features is examined. This is the key distinction between random forest and standard bagging, where $m=p$. Here, since $2 = m < p = 6$, there’s a possibility for the random forest to underperform compared to a conventional classification tree. The chosen value of m here aligns with the rule of thumb that $m= \lfloor \sqrt{p}\rfloor$.

Credit Card Default Prediction In a rating system for credit card reliability, we collect information from potential clients to forecast their likelihood of future default. Let us consider a dataset that contains details on default payments, demographic attributes, credit information, payment histories, and billing records of credit card users in Taiwan between April and September 2005 (Lichman, 2013). This dataset is characterized by 26 distinct features including credit amount, gender, education level, marital status, and age. The assigned label is 1 if the client defaults in the subsequent month, and 0 otherwise. In the context of predictive analytics, we utilize both classification trees and random forests within Python (refer to Program 9) and R (refer to Program 10) environments for forecasting.

Fig. 13

Classification tree for the credit default dataset

From the results shown in Program 9, the calculated precision, recall, $F_1$-score, and accuracy values for the classification tree in Python are as follows:

$$\begin{aligned} \text {Precision}&= \frac{421}{421 + 198} = 0.680, \quad&\text {Recall}&= \frac{421}{421 + 870} = 0.326, \\ F_1\text {-score}&= \frac{2}{1/0.680 + 1/0.326} = 0.441, \quad&\text {Accuracy}&= \frac{421 + 4511}{6000} = 0.822. \end{aligned}$$

In a similar fashion, the precision, recall, $F_1$-score, and accuracy for the random forest model implemented in Python are:

$$\begin{aligned} \text {Precision}&= \frac{491}{491 + 275} = 0.641, \quad&\text {Recall}&= \frac{491}{491 + 800} = 0.380, \\ F_1\text {-score}&= \frac{2}{1/0.641 + 1/0.380} = 0.477, \quad&\text {Accuracy}&= \frac{491 + 4434}{6000} = 0.821. \end{aligned}$$

Moreover, as shown in Fig. 13a, Python’s decision-making process in the dataset focuses primarily on two out of the 26 feature variables, specifically PAY_0 and PAY_2, which correspond to the repayment status in September and August of 2005, respectively. These variables track the number of months a client’s payment is delayed, where-1 stands for no delay, and the maximum recorded delay is capped at 9 months. A notable insight is that a client is more likely to default if there’s a payment delay of several months, with the critical threshold identified as 2 months by Python. Correspondingly, from Fig. 13b, the R also partition PAY_0 with the same threshold of 2 months. The confusionMatrix() function from the caret package in R is used to calculate various performance metrics.

Clearly, both results from Python and R suggest that PAY_0 is the most crucial feature variable in training the classification tree, and we would like to determine if the same conclusion also holds in the random forest model. To this end, we can adopt the tools readily available in Python and R to measure the importance of feature variables; the following two metrics are the most commonly adopted criteria for this purpose, also see (Breiman, 2001):

• Mean Decrease in Impurity (MDI): The importance of a feature variable is computed by averaging the decrease in the impurity measure, which is specified during the training stage.⁸, over all trees in the forest where the feature variable in question is used; the larger the mean decrease, the higher the importance of the feature variable.

• Permutation Feature Importance (a.k.a. Mean Decrease in Accuracy (MDA)): This method involves shuffling the data of only the feature variable in question of the testing dataset, and calculate the decrease in accuracy of the permuted testing set against the original testing set; a larger decrease in model performance indicates a higher importance of the feature variable.

We here only illustrate the two approaches in Python, as shown in respective Programmes 11 and 12, and the corresponding visualizations are depicted in Figs. 14 and 15, respectively. It is clear that both metrics consistently suggest that PAY_0 is the most important feature variable in building the random forest model, which agrees with the result in CART. Readers can attempt in a similar manner to obtain the feature importance results in R.

Fig. 14

Feature importances of the random forest, using mean decrease in impurity, for the credit default dataset via Python in Programme 11

Fig. 15

Feature importances of the random forest, using permutation on full model, for the credit default dataset via Python in Programme 12

7 Experiential study

In this section, we shall look at two real-life experiential studies, and give a more general comparison with other common and competitive machine learning algorithms. To remove the randomness of the experiment result and emphasize the robustness of the model’s performance, the following procedure is adopted:

• 1. Training data are randomly selected without replacement from the original data, with the size $N_{train}$;

• 2. Randomly select $N_{test}$ number of data points without replacement from each label as the testing dataset;

• 3. Build and evaluate each of the candidate machine learning models, and repeat the process 100 times.

7.1 Bank churners

Banks provide consumer credit card services for annual fees and charges. Customer attrition is one of the major problems they feared, it is then crucial for banks to predict whether a given cardholder is likely to withdraw the credit card services. We aim to predict Attrition_Flag by 19 feature variables from both existing and attritted customers.⁹

Fig. 16

Accuracy comparison of various models for Bank Churners

The box plot in Fig. 16 displays a comparison of the accuracy of various machine learning models, including Random Forest and Decision Tree. The Random Forest model shows higher median accuracy and a smaller interquartile range (IQR) than the Decision Tree model. This suggests that the Random Forest model not only achieves higher accuracy on average, but also has a more consistent performance across different runs or datasets. In contrast, the Decision Tree model has a wider IQR, indicating more variability in its accuracy. The median accuracy of the Decision Tree is also lower than that of the Random Forest, suggesting its comparatively weaker performance than the latter, yet both of them can achieve significantly better performances in general than the other models. While we can tell that multilayered perceptron (MLP) seems to be less robust and has extreme outlier and K-nearest neighbors (KNN) shows the worst general performance.

Moreover, since it is more important for bankers to detect who has a higher chance to be attrited, $F_1$-score and Recall could be more effective measures in an unbalanced dataset, since models may increase their accuracy by simply predicting more majority labels. As displayed in Fig. 17, they show similar patterns, hence our conclusion above still remains valid.

Fig. 17

$F_1$ and Recall scores comparison of various models for Bank Churners

7.2 Default premium prediction

Insurance companies offer multiple services, such as life and health insurance, requiring policyholders to pay regular premiums for their policies. These premium payments become a significant part of the insurance companies’ cash flow once they are received. Nevertheless, policyholders sometimes delay or completely stop making these premium payments. Let us consider a dataset which records 10 feature variables on the personal profile details and premium payment history.¹⁰ The comparison of $F_1$ and Recall scores for different models are shown in Figs. 18 and 19, respectively.

Fig. 18

$F_1$-score comparison of various models for Default Premium Prediction

Fig. 19

Recall comparison of various models for Default Premium Prediction

It can be observed that both Decision Tree (DT) and Random Forest (RF) exhibit commendable performances, consistently ranking as the top two models. However, a notable divergence from the commonly expected trend is that the simpler Decision Tree model slightly outperforms its more complex ensemble counterpart of Random Forest. This counterintuitive result could be attributed to several factors that are specific to the nature and structure of the dataset in question. Given that the dataset is extremely imbalanced (95% majority), Decision Tree may benefit from its inherent simplicity and transparency, which allows it to overfit to the minority class, potentially capturing the nuances and patterns that a more generalized model like Random Forest might miss. This is because the latter typically averages the results of its numerous constituent trees, which can dilute the influence of the less represented class. Furthermore, the configuration and tuning of Random Forest, such as the number of trees and the depth of each tree, might not have been optimized for the particular characteristics of the imbalanced dataset. Under such scenarios, Decision Tree may outshine Random Forest by focusing more closely on the critical decision boundaries that define the minority class, resulting in a better performance as reflected by the evaluation metrics used in this study. It is a reminder that in the realm of machine learning, especially with imbalanced datasets, complexity is not always equal to superiority; rather, the tailored fit of a model to the specific data at hand is paramount.

Appendix

1.1 Entropy in information theory

In this section, we motivate the entropy concept introduced in Sect. 2 with its significance in information theory. For further details, readers may refer to Cover and Thomas (2006). Consider iid discrete random variables $\textrm{x}_1,\dots ,\textrm{x}_n \in {\mathcal {X}}$, all following a common probability mass function p(x). Applying the weak law of large numbers, we deduce the Asymptotic Equipartition Property (AEP), which is expressed as:

$$\begin{aligned} -\frac{1}{n}\log _2 p(\textrm{x}_1,\dots ,\textrm{x}_n) = -\frac{1}{n}\sum _{i=1}^n\log _2p(\textrm{x}_i) \overset{p}{\rightarrow } -{{\,\mathrm{\mathbb {E}}\,}}(\log _2p(\textrm{x})) = H(\textrm{x}), \end{aligned}$$

as n approaches infinity. For any chosen $\varepsilon > 0$ and $n \in \mathbb {N}$, we define a typical set $A^{(n)}_\varepsilon$, comprising sequences $(x_1,\dots ,x_n) \in {\mathcal {X}}^n$ that satisfy

$$\begin{aligned} 2^{-n(H(\textrm{x}) + \varepsilon )} \le p(x_1,\dots ,x_n) \le 2^{-n(H(\textrm{x}) - \varepsilon )}, \end{aligned}$$

(20)

or equivalently,

$$\begin{aligned} H(\textrm{x}) - \varepsilon \le -\frac{1}{n}\log _2 p(x_1,\dots ,x_n) \le H(\textrm{x}) + \varepsilon . \end{aligned}$$

Given that

$$\begin{aligned} 1 \ge {{\,\mathrm{\mathbb {P}}\,}}\left( (\textrm{x}_1,\dots ,\textrm{x}_n) \in A^{(n)}_\varepsilon \right)&= \sum \limits _{(x_1,\dots ,x_n) \in A^{(n)}_\varepsilon } p(x_1,\dots ,x_n) \\&\ge \left| A^{(n)}_\varepsilon \right| \cdot 2^{-n(H(\textrm{x}) + \epsilon )}, \end{aligned}$$

we conclude that the cardinality $\left| A^{(n)}_\varepsilon \right|$ is bounded by $2^{n(H(\textrm{x}) + \varepsilon )}$, and according to AEP’s properties, it holds that $\underset{n\rightarrow \infty }{\lim }\ {{\,\mathrm{\mathbb {P}}\,}}\left( (\textrm{x}_1,\dots ,\textrm{x}_n) \in A^{(n)}_\varepsilon \right) = 1$. Altogether, for sufficiently large n, the typical set $A^{(n)}_\varepsilon$ contains most of the sequences in ${\mathcal {X}}^n$. Owing to (20), sequences within $A^{(n)}_\varepsilon$ are nearly equally probable, and this provides a foundational idea of data compression.

Consider compressing a message $x^{(n)}=(x_1,\dots ,x_n)$, composed of n alphabets from ${\mathcal {X}}$, into a binary code. Our focus is on the average number of bits, denoted as $l(x^{(n)})$, needed to encode a generic message $x^{(n)}\in {\mathcal {X}}^n$. Assuming that the alphabets $\textrm{x}_1,\dots ,\textrm{x}_n$ are independent and identically distributed, we reformulate this as calculating the expected length, ${{\,\mathrm{\mathbb {E}}\,}}(l(\textrm{x}^{(n)}))$, for a random message $\textrm{x}^{(n)} = (\textrm{x}_1,\dots ,\textrm{x}_n)$. Dividing ${\mathcal {X}}^n$ into the typical set $A^{(n)}_\varepsilon$ and its complement $\overline{{A}^{(n)}_\varepsilon }$, we note that a maximum of $n(H(\textrm{x})+\varepsilon ) + 1$ bits is sufficient to represent sequences $x^{(n)} \in A^{(n)}_\varepsilon$. In contrast, sequences in $\overline{{A}^{(n)}_\varepsilon }$ can be encoded using at most $n\log _2 |{\mathcal {X}}| + 1$ bits. Based on AEP that ${{\,\mathrm{\mathbb {P}}\,}}(\textrm{x}^{(n)} \in A^{(n)}_\varepsilon ) \ge 1-o_n(1)$ and $o_n(1)\rightarrow 0$ as $n\rightarrow \infty$, we derive:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[l(\textrm{x}^{(n)})]&= \sum _{x^{(n)}\in {\mathcal {X}}^n}p(x^{(n)}) l(x^{(n)}) \\&= \sum _{x^{(n)} \in A^{(n)}_\varepsilon } p(x^{(n)}) l(x^{(n)}) + \sum _{x^{(n)} \not \in A^{(n)}_\varepsilon }p(x^{(n)})l(x^{(n)})\\&\le {{\,\mathrm{\mathbb {P}}\,}}(\textrm{x}^{(n)} \in A^{(n)}_\varepsilon ) (n(H(\textrm{x})+\varepsilon ) +1) + {{\,\mathrm{\mathbb {P}}\,}}( \textrm{x}^{(n)} \not \in A^{(n)}_\varepsilon )(n\log _2|{\mathcal {X}}| + 1) \\&\le n(H(\textrm{x})+\epsilon )+1 + o_n(1)(n\log _2|{\mathcal {X}}|+1) \\&= n(H(\textrm{x}) + \varepsilon '), \end{aligned}$$

where $\varepsilon ' = \varepsilon +\frac{1+o_n(1)}{n}+o_n(1)\log _2|{\mathcal {X}}|$. Hence,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\left( \frac{1}{n}l(\textrm{x}^{(n)}) \right) \le H(\textrm{x}) + \varepsilon ; \end{aligned}$$

Employing a similar argument, one can get that $\liminf \limits _{n \rightarrow \infty } \mathbb {E} \left( \frac{1}{n} l (\textrm{x}^{(n)}) \right) \ge H(\textrm{x})$. This leads to the conclusion that $\underset{n\rightarrow \infty }{\lim }{{\,\mathrm{\mathbb {E}}\,}}\left( \frac{1}{n}l(\textrm{x}^{(n)})\right) =H(\textrm{x})$, indicating that, on average, only $nH(\textrm{x})$ bits are necessary to code sequences in ${\mathcal {X}}^n$ for large n.