1 Introduction

The complementary risk problems suggested by Basu and Klein (1982) are arise in several areas, such as industrial reliability, public health, biomedical studies, demography, and actuarial science. In complementary risk analysis, the lifetime associated with a specific risk may not be observable; rather, we observe only the maximum lifetime value among all risks. In reliability studies, we observe only the maximum component lifetime of a parallel system. That is, the observable quantities for each component are the maximum lifetime value to failure among all risks, and the cause of failure. Whereas in competing risk scenario, in which the lifetime associated with a particular risk is not observable; rather, we observe only the minimum lifetime value among all risks. One can refer Lawless (2003), Crowder et al. (1991), and Cox and Oakes (1984) for the statistical procedures and extensive literature deal with these problems.

A difficulty arises if the risks are latent in the sense that there is no information about which factor was responsible for the component failure (or individual failure), that is the latent complementary risks, which can often be observed in field data. On many occasions, this information is not available, or it is impossible that the true cause of failure can be specified by an expert. In reliability, the components can be totally destroyed in the experiment. Furthermore, the true cause of failure can be masked from our view.

In modular systems, the need to keep a system running means that a module that contains many components can be replaced without the identification of the exact failing component. Goetghebeur and Ryan (1995) addressed the problem of assessing covariate effects based on a semi-parametric proportional hazards structure for each failure type when the failure type is unknown for some individuals. Reiser et al. (1995) considered statistical procedures for analyzing masked data, but their procedure cannot be applied when all observations have an unknown cause of failure. A comparison of two partial likelihood approaches for risk modeling with missing cause of failure is presented in Lu and Tsiatis (2005).

Louzada et al. (2011) introduced the complementary exponential geometric distribution, which is complementary to the exponential geometric model proposed by Adamidis and Loukas (1998), based on a complementary risk problem in the presence of latent risks, in the sense that there is no information about which factor was responsible for the component failure, but only the maximum lifetime value among all risks is observed. Louzada et al. (2013) introduced the complementary exponentiated exponential geometric distribution which considered a generalization to the complementary exponential geometric distribution. Jose et al. (2013) introduced the complementary exponential power series distribution with an increasing failure rate. Tojeiro et al. (2014) introduced the complementary Weibull geometric (CWG) as a complementary distribution to the Weibull-geometric (WG) model proposed by Barreto-Souza et al. (2011).

In this context, in this paper, we propose a new generalized family of complementary distributions conceived inside a latent complementary risk scenario, in which there is no information about which factor was responsible for the component failure (or individual failure), and only the maximum lifetime value among all risks is observed. This paper is focused on the construction of discrete version of complementary distributions, which are not studied in the literature.

The rest of the paper is organized as follows: In Sect. 2, we develop a new generalization of complementary distributions with illustrations. In Sect. 3, we discuss the various methods of discretization of continuous distributions. In Sect. 4, we introduce the discrete complementary Weibull-geometric (DCWG) distribution and its properties are discussed in Sect. 5. The estimates of unknown parameters of the model using maximum-likelihood estimation method are derived and their existence and uniqueness are established. Also, a simulation study is carried out to check the performance of the MLEs of the model parameters. These results are presented in Sect. 6. In Sect. 7, the empirical study of the flexibility of DCWG distribution by means of a practical data set is carried out. Finally, conclusions are presented in Sect. 8.

2 A new generalization of complementary distributions

Let \(X_1,X_2,\ldots ,\) be independent and identically distributed (i.i.d) random variables having cumulative distribution function (cdf) F(x) and let N be an integer-valued random variable independent of \(X_i\)’s.

Define \(Z= max(X_1,X_2,\ldots ,X_N)\). Then, the cdf of Z is

$$\begin{aligned} G(z)= & {} P(max(X_1,X_2,\ldots ,X_N)\le z)\nonumber \\= & {} \sum _n P(max(X_1,X_2,\ldots ,X_N)\le z/N=n) P(N=n) \nonumber \\= & {} \sum _n[P(X_i\le z)]^n P(N=n)\nonumber \\= & {} \sum _n F^n(z)P(N=n) = H(F(z), \end{aligned}$$
(1)

where F(z) is the common cdf of \(X_i\)’s and H(s) is the probability generating function (pgf) of N. Thus, we have the random variable Z has complementary distribution. For example, if \(X_i\)’s are i.i.d Pareto random variables and N is negative binomial, then we say that Z has complementary Pareto negative binomial distribution.

Since N be any integer-valued random variable taking values on \(\{1,2,3,\ldots \},\) we may take N as power series family or power series distribution. We know that binomial, negative binomial or geometric, Poisson, etc. are members in power series family. Let N be an integer-valued random variable having power series distribution on \(\{1,2,3,\ldots \},\) and the probability mass function (pmf) of N is

$$\begin{aligned} P(N=n)=\frac{a_n \theta ^n}{f(\theta )-a_0},\quad n=1,2,\ldots , \end{aligned}$$
(2)

where \(a_n>0, \theta >0\) and \(f(\theta )=\sum _{n=0}^\infty a_n \theta ^n.\)

The pgf of N is

$$\begin{aligned} H(s)= & {} \sum _{n=1}^\infty s^n P(N=n)\nonumber \\= & {} \sum _{n=1}^\infty s^n \frac{a_n \theta ^n}{f(\theta )-a_0} = \frac{f(\theta s)-a_0}{f(\theta )-a_0}. \end{aligned}$$
(3)

Hence, from Eq. (1), distribution function of \(Z=max(X_1,X_2,\ldots ,X_N),\) where \(X_i\)’s are i.i.d with cdf F(x) and N has the power series distribution is

$$\begin{aligned} G(z)=H(F(z))=\frac{f(\theta F(z))-a_0}{f(\theta )-a_0}. \end{aligned}$$
(4)

Thus, we can develop a number of families of distributions using complementary random variables. Some examples are:

2.1 Examples

  1. 1.

    Complementary family of distributions generated through Binomial\((n,\theta )\) distribution. Based on Eq. (4), the family is defined through the cdf

    $$\begin{aligned} G(z)=\frac{(1+\theta F(z))^n-1}{(1+\theta )^n-1}. \end{aligned}$$
    (5)

    For example, complementary exponential binomial is defined by the cdf

    $$\begin{aligned} G(z)=\frac{(1+\theta (1-\mathrm{e}^{-\lambda z}))^n-1}{(1+\theta )^n-1},\, \lambda>0,\,\theta>0,\,z>0. \end{aligned}$$
    (6)
  2. 2.

    Complementary family of distributions generated through Poisson (\(\theta \)) distribution. The family, based on Eq. (4), is defined through the cdf

    $$\begin{aligned} G(z)=\frac{e^{\theta F(z)}-1}{e^\theta -1}, \theta>0, z>0. \end{aligned}$$
    (7)

    As an example, the complementary Pareto type III Poisson distribution is defined through the cdf

    $$\begin{aligned} G(z)=\frac{\mathrm{e}^{\theta \frac{z^\alpha }{1+z^\alpha }}-1}{\mathrm{e}^\theta -1},\,\theta>0,\, \alpha>0,\, z>0. \end{aligned}$$
    (8)
  3. 3.

    Complementary family of distributions generated through geometric (\(\theta \)) distribution. The family is defined through the cdf

    $$\begin{aligned} G(z)=\frac{(1-\theta F(z))^{-1}-1}{(1-\theta )^{-1}-1},\, \theta>0, \,z>0. \end{aligned}$$
    (9)

    In this cdf G(z), when F(z) is Weibull, we get the complementary Weibull-geometric (CWG) distribution (Tojeiro et al. , 2014).

From the illustrations, it can be seen that we may be able to develop a number of new families of distributions based on complementary random variables.

Now, we consider the situation where N be a discrete random variable denoting the number of complementary risks related to the occurrence of an event of interest following a geometric distribution with pmf

$$\begin{aligned} P(N=n)=p(1-p)^{n-1}, \end{aligned}$$
(10)

where \(0<p<1\) and \(n=1,2,\ldots \) . Also, let \(X_i, i=1,2,\ldots ,\) denotes the time-to-event due to the ith complementary risk, which are independent of N. Then, for given \(N=n\), the random variable \(X_i\) is assumed to be i.i.d and follows the Weibull distribution \(W(\beta ,\alpha )\) with scale parameter \(\beta >0\), shape parameter \(\alpha >0\), and probability density function (pdf):

$$\begin{aligned} f(x_i;\beta ,\alpha )=\alpha \beta ^\alpha x_i^{\alpha -1} \mathrm{e}^{-(\beta x_i)^\alpha },\, x_i>0. \end{aligned}$$
(11)

In the latent complementary risks scenario, the number of causes N and the lifetime \(X_i\) (associated with a particular cause) are not observable (latent variables), but only the maximum lifetime \(Z=max(X_1,X_2,\ldots ,X_N)\) among all the causes is usually observed. Then, using Eq. (9) with \(\theta =1-p\), we get the CWG distribution. The cdf and survival function of CWG distribution, respectively, are

$$\begin{aligned} F(z)=\frac{p(1-\mathrm{e}^{-(\beta z)^\alpha })}{p+(1-p)\mathrm{e}^{-(\beta z)^\alpha }}, \end{aligned}$$
(12)

and

$$\begin{aligned} S(z)=\frac{\mathrm{e}^{-(\beta z)^\alpha }}{p+(1-p)\mathrm{e}^{-(\beta z)^\alpha }}. \end{aligned}$$
(13)

This distribution is complementary to the Weibull-geometric (WG) distribution proposed in Barreto-Souza et al. (2011).

The aim of this paper is to introduce new discrete distributions arising from complementary type random variables. These types of discrete distributions are not studied in the literature.

3 Discretization of continuous distributions

Developing the discrete analogues of continuous distributions has drawn much attention among the researchers and a number of papers in this area are appeared in various journals. In reliability analysis and lifetime modeling, there are situations where the data show discrete behavior, such as, the number of rounds fired a weapon till the first failure; the number of cycles successfully completed prior to the first failure when a particular device works in cycles, etc.

It is well known that the geometric distribution and negative binomial distribution are the discrete analogue of the exponential distribution and gamma distribution, respectively. Discrete version of the normal distribution was introduced in Lisman and van Zuylen (1972) and studied in Kemp (1997). Another version of discrete normal distribution was studied in Roy (2003). Nakagawa and Osaki (1975), Stein and Dattero (1984), and Padgett and Spurrier (1985) have proposed three different analogues of the discrete Weibull distribution which are further studied in Khan et al. (1989) and Kulasekera (1994).

Recently, several forms of discrete lifetime distributions derived from continuous distributions are proposed by many authors. Some of them are: discrete half-normal distribution in Kemp (2008); discrete Burr and Pareto distributions in Krishna and Pundir (2009); discrete inverse Weibull distribution in Jazi et al. (2010); discrete generalized exponential distribution in Gomez-Deniz (2010) and Nekoukhou et al. (2012); discrete modified Weibull distribution in Nooghabi et al. (2011); discrete gamma distribution in Chakraborty and Chakravarty (2012); discrete additive Weibull distribution in Bebbington et al. (2012); discrete generalized exponential distribution of the second type in Nekoukhou et al. (2013); discrete reduced modified Weibull distribution in Almalki and Nadarajah (2014); discrete Lindley distribution in Bakouch et al. (2014); discrete generalized Rayleigh distribution in Alamatsaz et al. (2016); discrete Weibull-geometric distribution in Jayakumar and Babu (2018); and discrete additive Weibull-geometric distribution in Jayakumar and Babu (2019). For more details on discretization of continuous distributions, see Chakraborty (2015).

There are different methods available for obtaining the discrete analogue Y of a continuous random variable X, which can be classified as follows:

  1. (i)

    Difference equation analogues of Pearsonian differential equation.

  2. (ii)

    The pmf of Y retains the form of the pdf of X and support of Y is determined from full range of X.

  3. (iii)

    The pmf of Y retains the form of the pdf of X and support of Y is determined from a subset of the range of X.

  4. (iv)

    Survival function (sf) of Y retains the form of the survival function of X and support of Y is determined from full range of X.

In method (ii), the pmf of the discrete random variable Yis derived as an analogue of the continuous random variable X with pdf \(f(x), - \infty< x < \infty \) as

$$\begin{aligned} P(Y=y)=\frac{f(y)}{\sum _{i=-\infty }^{\infty }f(i)},\quad y=0, \pm 1, \pm 2, \ldots . \end{aligned}$$
(14)

Because of the normalizing constant, the distribution generated through this technique may not always have a compact form. The discrete version of the complementary family of distributions generated through the Poisson (\(\theta \)) distribution given in Eqn.(7) is obtained as

$$\begin{aligned} P(Y=y)=\frac{g(y)}{\sum _{i=0}^{\infty }g(i)} = \frac{\mathrm{e}^{\theta F(y)}}{\sum _{i=0}^{\infty }\mathrm{e}^{\theta F(i)}}, \quad y=0,1,2, \ldots . \end{aligned}$$
(15)

For different choices of the cdf F(y), we will get different discrete families of complementary distributions generated through Poisson distribution.

The method (iv) is an easiest way to get the discrete version using the survival function. Suppose Y is the discrete version of a continuous random variable X, then its pmf is given by

$$\begin{aligned} P(Y=y) = S_X(y)-S_X (y+1); \quad y=0,1,2,\ldots . \end{aligned}$$
(16)

Using this method, the discrete version of the complementary family of distributions generated through geometric (\(\theta \)) is given by

$$\begin{aligned} P(Y=y)= & {} \frac{1-F(y)}{1-\theta F(y)}-\frac{1-F(y+1)}{1-\theta F(y+1)} \nonumber \\= & {} \frac{(1-\theta )(F(y+1)-F(y))}{(1-\theta F(y))(1-\theta F(y+1))}. \end{aligned}$$
(17)

By selecting different distributions for F(y) in Eq. (17), we get various discrete versions of complementary distributions generated through geometric compounding. Now, in the next section, we study extensively one of the members of such distributions called the discrete complementary Weibull geometric.

4 Discrete complementary Weibull-geometric distribution

Using the method (iv) explained in Sect. 3 and after a reparametrization, \(\rho =e^{-\beta ^\alpha },\) the pmf of the discrete analogue, say Y, of the CWG distribution is obtained as

$$\begin{aligned} P_{Y}(y;p,\rho ,\alpha ) = \frac{p(\rho ^{y^\alpha }-\rho ^{(y+1)^\alpha })}{[p+(1-p)\rho ^{y^\alpha }][p+(1-p)\rho ^{(y+1)^\alpha }]}, \end{aligned}$$
(18)

where \(y=0,1,2,\ldots , p>0,\alpha >0\) and \(0<\rho <1.\) Here, the parameter p and \(\rho \) can be interpreted as the concentration parameters, while \(\alpha \) is a shape parameter. We call this distribution as the discrete complementary Weibull-geometric (DCWG) distribution and is denoted as \(DCWG(p,\rho ,\alpha ).\) Now, we present some submodels of the DCWG distributions.

In particular, when \(\alpha =1,\) the pmf becomes

$$\begin{aligned} P_{Y}(y;p,\rho ) = \frac{p(\rho ^{y}-\rho ^{(y+1)})}{[p+(1-p)\rho ^{y}][p+(1-p)\rho ^{(y+1)}]}, \end{aligned}$$
(19)

which is called the discrete complementary exponential geometric distribution.

When \(p=1\), \(P_{Y}(y;\rho ,\alpha )=\rho ^{y^\alpha }-\rho ^{(y+1)^\alpha }\) which is the discrete Weibull distribution of Nakagawa and Osaki (1975).

When \(p= 1\) and \(\alpha = 2\), then \(P_{Y}(y;\rho )=\rho ^{y^2}-\rho ^{(y+1)^2}\) which is the discrete Rayleigh distribution of Roy (2004).

When \(p= 1\) and \(\alpha = 1\), then \(P_{Y}(y;\rho )=\rho ^{y}-\rho ^{(y+1)}\) which is the geometric distribution with parameter \(\rho .\)

When \(p\rightarrow 0+\), the DCWG tends to a degenerate distribution at zero.

5 Structural properties of the \(DCWG(p,\rho ,\alpha )\) distribution

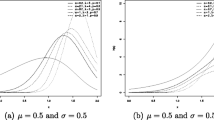
The shape of the pmf of \(DCWG(p,\rho ,\alpha )\) distribution for various choices of parameter values are shown in Fig. 1. It can be seen that the distribution is unimodal and highly positively skewed. For \(0<\alpha <1\), \(p>0\), and \(0<\rho <1\), we have \(p_Y(0)>p_Y(1)>p_Y(2)>\ldots .\), and hence, \(p_Y(y)\) is strictly decreasing function. Also note that when \(\alpha =1\), \(p_Y(y)\) is geometric, and when \(\alpha >1\), \(p_Y(y)\) is initially increasing to the maximum point and then decreasing.

Fig. 1
figure 1

Shape of pmf for various choices of parameter values

Full size image

5.1 Recurrence relation for probabilities

The recurrence relation for probabilities of \(DCWG(p,\rho ,\alpha )\) distribution is as follows:

$$\begin{aligned} P_{Y}(y+1)=\frac{(\rho ^{(y+1)^\alpha }-\rho ^{(y+2)^\alpha })(p+(1-p)\rho ^{y^\alpha })}{(\rho ^{y^\alpha }-\rho ^{(y+1)^\alpha })(p+(1-p)\rho ^{(y+2)^\alpha })}P_{Y}(y). \end{aligned}$$
(20)

From Gupta et al. (1997), the distribution is

  1. (a)

    log-concave if and only if \(\big \{ \frac{P_{Y}(y+1)}{P_{Y}(y)}\big \}_{y\ge 0}\) is decreasing,

  2. (b)

    log-convex if and only if \(\big \{ \frac{P_{Y}(y+1)}{P_{Y}(y)}\big \}_{y\ge 0}\) is increasing, and

  3. (c)

    geometric if \(\big \{ \frac{P_{Y}(y+1)}{P_{Y}(y)}\big \}_{y\ge 0}\) is constant.

All the above three cases are justified to the DCWG distribution based on the values of the parameters as shown by plots of pmf.

The cdf of \(DCWG(p,\rho ,\alpha )\) distribution is obtained as

$$\begin{aligned} F(y)=P(Y\le y)=1-S_{Z}(y+1)=\frac{p(1-\rho ^{(y+1)^\alpha })}{p+(1-p)\rho ^{(y+1)^\alpha }}, \end{aligned}$$
(21)

where \(y=0,1,2,\ldots ; p>0, 0<\rho <1\) and \(\alpha >0.\)

Remark 1

The cdf of \(DCWG(p,\rho ,\alpha )\) distribution can be expressed as

$$\begin{aligned} F(y)=\frac{1-\rho ^{(y+1)^\alpha }}{1-\left( \frac{p-1}{p}\right) \rho ^{(y+1)^\alpha }}. \end{aligned}$$
(22)

This becomes the discrete Weibull-geometric distribution of Jayakumar and Babu (2018), if \(0<\frac{p-1}{p}<1\) and is satisfied only if \(p\in (1,\infty ).\)

The survival function of \(DCWG(p,\rho ,\alpha )\) distribution is given by

$$\begin{aligned} S(y)=P(Y>y)=1-P(Y\le y)=\frac{\rho ^{(y+1)^\alpha }}{p+(1-p)\rho ^{(y+1)^\alpha }}. \end{aligned}$$
(23)

Hazard rate function (hrf) is given by

$$\begin{aligned} h(y)=\frac{P(Y=y)}{P(Y\ge y)}=\frac{1-\rho ^{(y+1)^\alpha -y^\alpha }}{1-\frac{p-1}{p}\rho ^{(y+1)^\alpha }}, \end{aligned}$$
(24)

provided that \(P(Y\ge y)>0.\)

Here note that as \(y\rightarrow 0,\) \(h(y)\rightarrow \frac{p(1-\rho )}{p+(1-p)\rho }.\) When \(p=1\), the distribution becomes the discrete Weibull distribution and has the following properties:

  • Decreasing failure rate for \(0<\alpha < 1\);

  • Increasing failure rate for \(\alpha >1\);

  • Constant failure rate for \(\alpha =1\).

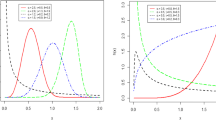
For \(\alpha =1\), we have \(\lim _{y\rightarrow \infty }h(y) \rightarrow 1-\rho \), and for \(0<\alpha <1\), \(\lim _{y\rightarrow \infty }h(y) \rightarrow 0\), and for \(\alpha >1\), \(\lim _{y\rightarrow \infty }h(y) \rightarrow 1.\) The shape of hazard rate function for various choices of parameter values are shown in Fig. 2. The hazard rate function is also showing the bathtub and unimodal (upside down bathtub) shapes.

Fig. 2
figure 2

Shape of hrf for various choices of parameter values

Full size image

5.2 Quantile function

The uth quantile \(\phi (u)\) of the \(DCWG(p,\rho ,\alpha )\) distribution is obtained as

$$\begin{aligned} \phi (u)=\lceil y_u \rceil = \bigg \lceil \bigg ( \frac{\ln (p(1-u))-\ln (p+(1-p)u)}{\ln (\rho )}\bigg )^{\frac{1}{\alpha }}-1\bigg \rceil , \end{aligned}$$
(25)

where \(\lceil y_u \rceil \) denotes the smallest integer greater than or equal to \(y_u\).

The median is

$$\begin{aligned} \phi (0.5)=\lceil y_{0.5} \rceil = \bigg \lceil \bigg ( \frac{\ln (p)-\ln (p+1)}{\ln (\rho )}\bigg )^{\frac{1}{\alpha }}-1\bigg \rceil . \end{aligned}$$
(26)

Let u follow U(0, 1) distribution, and then, using the expression given in Eq. (25), we can generate random samples from the \(DCWG(p,\rho ,\alpha )\) distribution.

5.3 Probability generating function

The pgf of \(DCWG(p,\rho ,\alpha )\) distribution is

$$\begin{aligned} P_{Y}(s)=1+(s-1)\sum _{y=1}^{\infty }\frac{s^{y-1}\rho ^{(y+1)^\alpha }}{p+(1-p)\rho ^{(y+1)^\alpha }}. \end{aligned}$$
(27)

The expressions for mean and variance are

$$\begin{aligned} E(Y)=\sum _{y=1}^{\infty }\frac{\rho ^{(y+1)^\alpha }}{p+(1-p)\rho ^{(y+1)^\alpha }}, \end{aligned}$$
(28)

and

$$\begin{aligned} V(Y)=\sum _{y=1}^{\infty }\frac{(2y-1)\rho ^{(y+1)^\alpha }}{p+(1-p)\rho ^{(y+1)^\alpha }}-\bigg [ \sum _{y=1}^{\infty }\frac{\rho ^{(y+1)^\alpha }}{p+(1-p)\rho ^{(y+1)^\alpha }}\bigg ]^2. \end{aligned}$$
(29)

The mean, variance, skewness, and kurtosis of \(DCWG(p,\rho ,\alpha )\) distribution for various choices of parameter values are numerically computed and presented in Table 1. The results show that this distribution is suitable for modeling both over- and under-dispersed data.

Table 1 Mean, variance, skewness, and kurtosis of the \(DCWG(p,\rho ,\alpha )\) distribution for various parameter values
Full size table

6 Inference on parameters of the \(DCWG(p,\rho ,\alpha )\) distribution

Consider a random sample \((y_1,y_2,\ldots ,y_n)\) of size n from \(DCWG(p,\rho ,\alpha ).\) Then, the likelihood function is given by

$$\begin{aligned} L=\prod _{i=1}^{n}\frac{p\left[ \rho ^{y_i^\alpha }-\rho ^{(y_i+1)^\alpha }\right] }{\left[ p+(1-p)\rho ^{y_i^\alpha }\right] \left[ p+(1-p)\rho ^{(y_i+1)^\alpha }\right] }. \end{aligned}$$
(30)

The log-likelihood function is

$$\begin{aligned} \ln L= & {} n \ln (p)+\sum _{i=1}^{n}\ln \left[ \rho ^{y_i^\alpha }-\rho ^{(y_i+1)^\alpha }\right] \nonumber \\&-\sum _{i=1}^{n}\ln \left[ p+(1-p)\rho ^{y_i^\alpha }\right] -\sum _{i=1}^{n}\ln \left[ p+(1-p)\rho ^{(y_i+1)^\alpha }\right] . \end{aligned}$$
(31)

The likelihood equations are respectively

$$\begin{aligned} \frac{\partial \ln L}{\partial p}= & {} \frac{n}{p}-\sum _{i=1}^{n}\frac{1-\rho ^{y_i^\alpha }}{p+(1-p)\rho ^{y_i^\alpha }}-\sum _{i=1}^{n}\frac{1-\rho ^{(y_i+1)^\alpha }}{p+(1-p)\rho ^{(y_i+1)^\alpha }}=0, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial \ln L}{\partial \rho }= & {} \sum _{i=1}^{n}\frac{y_i^\alpha \rho ^{y_i^\alpha -1}-(y_i+1)^\alpha \rho ^{(y_i+1)^\alpha -1}}{\rho ^{y_i^\alpha }-\rho ^{(y_i+1)^\alpha }} - (1-p)\sum _{i=1}^{n}\frac{y_i^\alpha \rho ^{y_i^\alpha -1}}{p+(1-p)\rho ^{y_i^\alpha }} \nonumber \\&- (1-p)\sum _{i=1}^{n}\frac{(y_i+1)^\alpha \rho ^{(y_i+1)^\alpha -1}}{p+(1-p)\rho ^{(y_i+1)^\alpha }} = 0, \end{aligned}$$
(33)

and

$$\begin{aligned} \frac{\partial \ln L}{\partial \alpha }= & {} \sum _{i=1}^{n}\frac{\ln (\rho )[y_i^\alpha \rho ^{y_i^\alpha }\ln (y_i)-(y_i+1)^\alpha \rho ^{(y_i+1)^\alpha }\ln (y_i+1)]}{\rho ^{y_i^\alpha }-\rho ^{(y_i+1)^\alpha }} \nonumber \\&- (1-p)\ln (\rho )\sum _{i=1}^{n}\frac{y_i^\alpha \rho ^{y_i^\alpha }\ln (y_i)}{p+(1-p)\rho ^{y_i^\alpha }} \nonumber \\&- (1-p)\ln (\rho )\sum _{i=1}^{n}\frac{(y_i+1)^\alpha \rho ^{(y_i+1)^\alpha }\ln (y_i+1)}{p+(1-p)\rho ^{(y_i+1)^\alpha }} = 0. \end{aligned}$$
(34)

The likelihood equations do not have explicit solutions and have to be obtained numerically using statistical softwares like nlm package in R programming. Let the estimators be \({\hat{\theta }}=({\hat{p}},{\hat{\rho }},{\hat{\alpha }})^T.\) Here, the DCWG family satisfies the regularity conditions which are fulfilled for the parameters in the interior of the parameter space, but not on the boundary. Hence, the vector \({\hat{\theta }}\) is consistent and asymptotically normal. That is, \(\sqrt{I_{Y}(\theta )}[{\hat{\theta }}-\theta ]\) converges in distribution to multivariate normal with zero mean vector and identity covariance matrix. The Fisher’s information matrix can be computed using the approximation

$$\begin{aligned} I_{Y}({\hat{\theta }}) \approx \left[ \begin{array}{ccccc} -\frac{\partial ^2 \ln L }{\partial p^2} \Big {|}_{{\hat{\theta }}} &{} -\frac{\partial ^2 \ln L }{\partial p \partial \rho }\Big {|}_{{\hat{\theta }}} &{} -\frac{\partial ^2 \ln L }{\partial p \partial \alpha }\Big {|}_{{\hat{\theta }}}\\ \\ -\frac{\partial ^2 \ln L }{\partial \rho \partial p}\Big {|}_{{\hat{\theta }}} &{} -\frac{\partial ^2 \ln L }{\partial \rho ^2}\Big {|}_{{\hat{\theta }}} &{} -\frac{\partial ^2 \ln L }{\partial \rho \partial \alpha } \Big {|}_{{\hat{\theta }}}\\ \\ -\frac{\partial ^2 \ln L }{\partial \alpha \partial p}\Big {|}_{{\hat{\theta }}} &{} -\frac{\partial ^2 \ln L }{\partial \alpha \partial \rho }\Big {|}_{{\hat{\theta }}} &{} -\frac{\partial ^2 \ln L }{\partial \alpha ^2}\Big {|}_{{\hat{\theta }}} \end{array} \right] , \end{aligned}$$
(35)

where \({{\hat{\theta }}}\) is the MLE of \({\theta }\). The existence and uniqueness of MLEs of the parameters of the \(DCWG(p,\rho ,\alpha )\) distribution are established when the other parameters are known as suggested in Popović et al. (2016) and are explained in the Theorems 1,2, and 3 (see Appendix).

6.1 Simulation study

This section explains the performance of the MLEs of the model parameters of the DCWG distribution using Monte Carlo simulation for various sample sizes and for selected parameter values. The algorithm for the simulation study is given below:

Step 1.:

Input the value of replication (N);

Step 2.:

Specify the sample size n and the values of the parameters \(p,\rho \) and \(\alpha \);

Step 3.:

Generate \(u_i\) from \(U(0,1), ~i=1,2,\ldots ,n\);

Step 4.:

Obtain the random observations from the DCWG distribution using Eq. (25);

Step 5.:

Compute the MLEs of the three parameters;

Step 6.:

Repeat steps 3–5, N times;

Step 7.:

Compute the parameter estimate, standard error of estimate, average bias, mean square error (MSE), and coverage probability (CP) for each parameter.

Here, the expected value of the estimator is

$$\begin{aligned} E({\hat{\theta }})=\frac{1}{N}\sum _{i=1}^{N}{\hat{\theta }}_i, E(SE({\hat{\theta }}))=\sqrt{\frac{1}{N}\sum _{i=1}^{N}\bigg (-\frac{\partial ^2 \log (L)}{\partial \theta _i^2}\bigg )}, \end{aligned}$$

Average Bias \(=\frac{1}{N}\sum _{i=1}^{N}({\hat{\theta }}_i-\theta )\), \(MSE({\hat{\theta }})=\frac{1}{N}\sum _{i=1}^{N}({\hat{\theta }}_i-\theta )^2\) and

CP = Probability of \(\theta _i \in \bigg ({\hat{\theta }}_i \pm 1.96\sqrt{-\frac{\partial ^2 \log (L)}{\partial \theta _i^2} }\bigg ).\)

We take random samples of size \(n=50\), 100, 200, and 500, respectively. The MLEs of the parameter vector \(\theta =(p,\rho ,\alpha )^T\) are determined by maximizing the log-likelihood function in Eq. (31) using the optim package in R programming based on each generated sample. This simulation is repeated 1000 times, and the average estimate and its standard error, average bias, MSE, and CP are computed and presented in Table 2. From Table 2, it can be seen that, as sample size increases, the estimates of bias and MSE decrease. Also note that the CP values are quite closer to the 95% nominal level.

Table 2 The parameter estimate, standard error, average bias, MSE, and CP for given parameters
Full size table

7 Data application

In this section, we analyze a real-life data set to prove empirically the flexibility of the DCWG distribution. We compare the fit of the DCWG distribution with the following discrete life time distributions:

  1. (a)

    Discrete Weibull-geometric (DWG) distribution (Jayakumar & Babu, 2018) having pmf

    $$\begin{aligned} P(X=x)=\frac{(1-p)(\rho ^{x^\alpha }-\rho ^{(x+1)^\alpha })}{(1-p\rho ^{x^\alpha })(1-p\rho ^{(x+1)^\alpha })};\\ \quad \alpha > 0,\, 0<p<1,\,0<\rho <1,\,x= 0,1,2,\ldots . \end{aligned}$$
  2. (b)

    Exponentiated discrete Weibull (EDW) distribution (Nekoukhou & Bidram, 2015) having pmf

    $$\begin{aligned} P(X=x)=(1-p^{(x+1)^\alpha })^\beta -(1-p^{x^\alpha })^\beta ; \\ \quad 0<p<1,\,\alpha>0,\,\beta >0,\,x=0,1,2,\ldots . \end{aligned}$$
  3. (c)

    Discrete modified Weibull (DMW) distribution (Nooghabi et al. , 2011) having pmf

    $$\begin{aligned} P(X=x)=\rho ^{x^\alpha c^x}-\rho ^{(x+1)^\alpha c^{(x+1)}};\\ \quad 0<\rho <1,\,\alpha >0,\,c \ge 1,\,x=0,1,2, \ldots . \end{aligned}$$
  4. (d)

    Discrete Weibull (DW) distribution (Nakagawa & Osaki, 1975) having pmf

    $$\begin{aligned} P(X=x)=\rho ^{x^\alpha }-\rho ^{(x+1)^\alpha };\\ \quad 0<\rho <1,\,\alpha >0,\,x=0,1,2, \ldots . \end{aligned}$$
  5. (e)

    Geometric (G) distribution having pmf

    $$\begin{aligned} P(X=x)=(1-\rho )\rho ^x; 0<\rho <1, x=0,1,2,\ldots . \end{aligned}$$

The values of the log-likelihood function (−log L), the K–S (Kolmogrov–Smirnov) statistic, AIC (Akaike Information Criterion), CAIC (Akaike Information Criterion with correction), BIC (Bayesian Information Criterion), and HQIC (Hannon–Quinn Information Criterion) are calculated for the six distributions to verify which distribution fits better to the data. The better distribution corresponds to smaller −log L, K \(-S\), AIC, CAIC, BIC, HQIC, and greater p value.

Here, \( AIC=-2 \log L+2k\), \(CAIC=-2\log L+\left( \frac{2kn}{n-k-1}\right) \), \(BIC=-2\log L+k \log n\), and \(HQIC=-2 \log L+2k \log (\log (n))\), where L is the likelihood function evaluated at the maximum-likelihood estimates, k is the number of parameters, and n is the sample size. We used the AdequacyModel package in R programming to obtain the MLE estimates and goodness-of-fit tests of the given data set.

The data set corresponds to daily ozone concentrations that were collected in New York during May–September, 1973 and were taken from Ferreira et al. (2012). This set of daily ozone-level measurements (in ppb = ppm \(\times \) 1000) are as follows:

7 115 79 31 9 8 45 61 23 28 19 23 35 59 21 23 32 48 22 44 28 4 7 65 24 13 18 11 27 44 21 73 12 1 10 110 23 28 36 30 85 89 20 80 41 6 97 122 32 135 34 21 82 73 16 14 23 52 168 24 18 39 20 45 13 14 71 108 9 18 11 29 16 21 46 16 37 63 44 13 12 59 84 7 20 64 118 36 37 50 76 23 13 39 85 14 49 9 96 30 32 16 78 14 64 78 91 18 40 35 47 20 77 66 97 11.

The descriptive statistics of the data set are presented in Table 3. To identify the shape of the hrf of the data set, we consider the Total Time on Test (TTT) plot and it is shown in Fig. 3. From the TTT plot, we can see that the hrf is an increasing function, and therefore, the DCWG distribution is appropriate for this data set.

Table 3 Descriptive statistics for the data set
Full size table
Fig. 3
figure 3

The TTT plots of the data set

Full size image

The parameter estimates and goodness-of-fit statistics for the data set are presented in Tables 4 and 5 .

Table 4 The parameter estimates of data set
Full size table
Table 5 The goodness-of-fit statistics for data set
Full size table

The −logL value shown in Table 4 is minimum for DCWG distribution. From Table 5, the values of AIC, CAIC, BIC, HQIC, and K–S are minimum, and p value is maximum for DCWG distribution. This shows that the DCWG distribution is a better model for this data set. Figure 4 shows the fitted pdf and cdf with the empirical distribution of the given data set.

Fig. 4
figure 4

Fitted pdf and cdf plots for the data set

Full size image

8 Conclusion

In this paper, we introduced a new generalized family of distributions generated from random maxima, which contains many distributions of which complementary Weibull-geometric distribution is a special case. Then, we proposed a new three-parameter discrete complementary Weibull-geometric (DCWG) distribution. This distribution is a generalization of discrete Weibull and geometric distributions. We studied the main mathematical and statistical properties including the quantile function and probability generating function of the DCWG distribution. The model parameters were estimated using maximum-likelihood estimation method and a simulation study is presented to illustrate the performance of the method. The existence and uniqueness of the MLE estimates were investigated. The DCWG distribution was applied to a practical data set to show its flexibility for data modeling.