Abstract
A new definition of connectedness of an object in a category with respect to a closure operator is given. It is shown that many of the classical results about connectedness of topological spaces, under mild conditions, hold in an arbitrary category. In particular it is shown that the image of a connected object is connected; that the union and the product of connected objects are connected. Several illustrative examples are provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Preliminaries
Closure operators and connectedness of objects in a category with respect to a closure operator have been investigated by several authors, [2,3,4,5,6,7,8, 12, 13], among others.
In the current paper, we give yet another definition of connectedness of an object in a category with respect to a closure operator.
In [13], the definition of connectedness is based on the idea that a topological space is connected if there is no nontrivial closed subset A of X, such that \(X{\setminus } A\) is closed too.
The definition given in this paper is based on the idea that a topological space is connected if there are no two non-empty closed subsets A and B of X, such that \(A\cap B=\emptyset \) and \(X=A\cup B\) (or equivalently \(X{\setminus } (A\cup B)=\emptyset \)).
It turns out that in a category, the connectedness (given in this paper) is generally stronger than that given in [13], and that under certain conditions the two coincide.
In [13], the category is assumed to be finitely complete and the class \({\mathcal {M}}\) of monomorphisms, on which the closure operator is defined, is assumed to be the right part of a proper and stable factorization structure; while in this paper, there is no assumption on the category and the class \({\mathcal {M}}\) is not as restricted.
We give several classical results about connectedness under mild hypotheses. In particular in Sect. 2, we give the definition of connectedness of an object in a category, providing several examples; in Sect. 3, we prove that the image of a connected object under a morphism is connected; in Sect. 4, we define two kind of unions (joins) and we prove that the union of mutually disjoint connected objects is connected; and in Sect. 5, we show that the product of two connected objects is connected.
Under conditions that the connectedness here and the one given in [13] coincide, the results not provided in [13], such as connectedness of union and connectedness of product of objects, can be deduced.
To this end, in the rest of this section, we establish some notation and give some preliminaries needed in the subsequent sections.
For a class \({\mathcal {M}}\) of morphisms, we denote by \({\mathcal {M}}/X\) the class of isomorphism classes of monomorphisms in \({\mathcal {M}}\) with codomain X.
Denoting by \(a\wedge b\) the diagonal of the pullback of a along b and calling it meet of a and b, we have:
Definition 1.1
A class \({\mathcal {M}}\) of monomorphisms in a category \({\mathcal {C}}\) is called a domain, if:
-
(1)
it contains all the identities;
-
(2)
it is stable under pullbacks, i.e., for all \(m\in {\mathcal {M}}/X\) and
 in \({\mathcal {C}}\), the pullback \(f^{-1}(m)\) of m along f exists and is in \({\mathcal {M}}/Y\);
in \({\mathcal {C}}\), the pullback \(f^{-1}(m)\) of m along f exists and is in \({\mathcal {M}}/Y\); -
(3)
for all \(X\in {\mathcal {C}}\), \({\mathcal {M}}/X\) is closed under binary meets;
-
(4)
for all \(X\in {\mathcal {C}}\), \({\mathcal {M}}/X\) has a minimum (also called zero).
A class \({\mathcal {M}}\) that satisfies only (1)–(3) is called a weak domain; and a domain that is closed under composition is called a strong domain.
We remark that conditions 1 and 2 yield that \({\mathcal {M}}\) contains all the isomorphisms and is closed under composition with isomorphisms, on both sides and that the meet induces a preorder, denoted by \(\le \), on \({\mathcal {M}}/X\) which is up to isomorphism a partial order.
Denoting the minimum of \({\mathcal {M}}/X\) by \(o_X:O_X\longrightarrow X\), we have:
Lemma 1.2
Let \({\mathcal {M}}\) be a strong domain.
-
(a)
Suppose that in the commutative triangle:
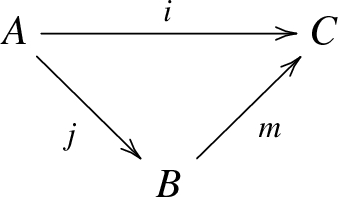
i, j, and m are in \({\mathcal {M}}\). Then, \(i=o_C\) if and only if \(j=o_B\). In this case, \(O_B=O_C\).
-
(b)
For all \(C\in {\mathcal {C}}\), \(o_{O_C}=1_{O_C}\).
Proof
(a) Suppose \(i=o_C\). Given \(k\in {\mathcal {M}}/B\), we have \(mk\in {\mathcal {M}}/C\). Therefore, \(i\le mk\), implying \(mj\le mk\). Therefore, \(j\le k\). Hence, \(j=o_B\).
Now, suppose that \(j=o_B\). Given \(k\in {\mathcal {M}}/C\), we have \(m^{-1}(k)\in {\mathcal {M}}/B\). Therefore, \(j\le m^{-1}(k)\), implying that \(mj\le mm^{-1}(k)\). Therefore, \(i=mj\le mm^{-1}(k)= kk^{-1}(m)\le k\).
(b) Given \(C\in {\mathcal {C}}\), let \(B=O_C\) and
 . By part (a), we have \(mo_B=o_C\). Therefore, \(mo_B=m\), implying that \(o_B=1_B\), as required. \(\square \)
. By part (a), we have \(mo_B=o_C\). Therefore, \(mo_B=m\), implying that \(o_B=1_B\), as required. \(\square \)
For \(a,b\in {\mathcal {M}}/X\), defining the joint negation \(\lnot \lbrace a,b\rbrace \) to be the largest element of \({\mathcal {M}}/X\) whose meet with both a and b is \(o_X\) and the negation \(\lnot a\) to be the largest element of \({\mathcal {M}}/X\) whose meet with a is \(o_X\), we have:
Lemma 1.3
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\) and \(a,b\in {\mathcal {M}}/X\). Then:
-
(a)
for all \(f\in {\mathcal {C}}\), \(f^{-1}(a\wedge b)=f^{-1}(a)\wedge f^{-1}(b)\).
-
(b)
for all \(m:M\longrightarrow X\) in \({\mathcal {M}}\), \(m^{-1}(o_X)=o_M\).
-
(c)
for all \(m\in {\mathcal {M}}\), \(m^{-1}(\lnot \{a,b\})=\lnot \{m^{-1}(a),m^{-1}(b)\}\).
Proof
All parts can be proved by straightforward computations. Parts (b) and (c) use Lemma 1.2. That \({\mathcal {M}}\) be a strong domain is needed only in (c). \(\square \)
2 Connectedness
Recall that, [8]:
Definition 2.1
Let \({\mathcal {M}}\) be a weak domain in \({\mathcal {C}}\). A closure operator \(\mathfrak {c}\), on \({\mathcal {C}}\), relative to \({\mathcal {M}}\) is a family \(\mathfrak {c}=(c_X)_{X\in {\mathcal {C}}}\) of maps \(c_X:{\mathcal {M}}/X\rightarrow {\mathcal {M}}/X\), such that for every \(X\in {\mathcal {C}}\):
-
(1)
(Extension) \(m\le c_X(m)\) for all \(m\in {\mathcal {M}}/X\);
-
(2)
(Monotonicity) if \(m\le m'\) in \({\mathcal {M}}/X\), then \(c_X(m)\le c_X(m')\);
-
(3)
(Continuity) \(c_X(f^{-1}(n))\le f^{-1}(c_Y(n))\) for all
 and \(n\in {\mathcal {M}}/Y\).
and \(n\in {\mathcal {M}}/Y\).
A morphism \(m\in {\mathcal {M}}/X\) is called \(\mathfrak {c}\)-closed if \(c_X(m)=m\) and \(\mathfrak {c}\)-dense if \(c_X(m)=1_X\).
Note that for any morphism  , if \(n\in {\mathcal {M}}/Y\) is \(\mathfrak {c}\)-closed, then so is \(f^{-1}(n)\in \mathcal M/X\); and that the conditions on \({\mathcal {M}}\) are weaker than those in [8], where \({\mathcal {M}}\) is assumed to be part of a factorization structure.
, if \(n\in {\mathcal {M}}/Y\) is \(\mathfrak {c}\)-closed, then so is \(f^{-1}(n)\in \mathcal M/X\); and that the conditions on \({\mathcal {M}}\) are weaker than those in [8], where \({\mathcal {M}}\) is assumed to be part of a factorization structure.
Definition 2.2
-
(a)
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\) and \(a,b\in {\mathcal {M}}/X\). b is said to be a quasi-complement of a if \(a\wedge b=o_X\) and \(\lnot \{a,b\}=o_X\). In this case, we also say that a and b are quasi-complements.
-
(b)
With a closure operator \(\mathfrak {c}\) on \({\mathcal {C}}\) relative to \({\mathcal {M}}\), we say that a and b are \(\mathfrak {c}\)-closed quasi-complements, if they are \(\mathfrak {c}\)-closed and quasi-complements.
Remark 2.3
The pseudo-complement \(\lnot a\) of a (if it exists), see [13], is a quasi-complement of a.
Definition 2.4
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). An object X of \({\mathcal {C}}\) is said to be \(\mathfrak {c}\)-connected if whenever a and b in \({\mathcal {M}}/X\) are \(\mathfrak {c}\)-closed quasi-complements, then \(a=o_X\) or \(b=o_X\).
Remark 2.5
If an object X is connected, then the only closed quasi-complement of a non-zero closed subobject of X must be \(o_X\). Therefore, by Remark 2.3, the closed pseudo-complement of a non-zero closed subobject of X (if it exists) is \(o_X\). Therefore, X is connected in the sense of [13]. The converse holds whenever for all non-zero closed subobjects a of X, if a non-zero closed quasi-complement of a exists, then the pseudo-complement of a exists and is closed.
Therefore, if the category \({\mathcal {C}}\) satisfies the conditions of [13], and the above condition holds, then the connectedness here and the one given in [13] coincide.
Example 2.6
Let \({\mathcal {C}}\) be the category Top of topological spaces.
-
(1)
Let \({\mathcal {M}}\) be the collection of initial monos and \(\mathfrak {c}\) be the Kuratowski closure operator. Then, a topological space is \(\mathfrak {c}\)-connected if and only if it is connected in the classical sense.
-
(2)
Let \({\mathcal {M}}\) be the collection of all monos. For each \(X\in {\mathcal {C}}\) and a in \({\mathcal {M}}/X\), define \(c_X(a)\) to be the inclusion
 with induced topology, where \(I_a\) is the image of A under a and \(\bar{I_a}\) is the Kuratowski closure of \(I_a\). One can verify that \(\mathfrak {c}=\{c_X(a):X\in {\mathcal {C}}, a\in {\mathcal {M}}/X\}\) is a closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Since \(a\in {\mathcal {M}}/X\) is \(\mathfrak {c}\)-closed if and only if it is initial and closed with respect to Kuratowsky closure operator, the \(\mathfrak {c}\)-connectedness coincides with the classical one.
with induced topology, where \(I_a\) is the image of A under a and \(\bar{I_a}\) is the Kuratowski closure of \(I_a\). One can verify that \(\mathfrak {c}=\{c_X(a):X\in {\mathcal {C}}, a\in {\mathcal {M}}/X\}\) is a closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Since \(a\in {\mathcal {M}}/X\) is \(\mathfrak {c}\)-closed if and only if it is initial and closed with respect to Kuratowsky closure operator, the \(\mathfrak {c}\)-connectedness coincides with the classical one.
Recalling that a preradical r in the category R-mod of R-modules is a subfunctor of the identity functor of R-mod, any preradical r gives a closure operator \(c^r\) of R-mod, such that for a mono
 , \(c^{r}_{A}(B)=\pi ^{-1}(r(A/I_m))\), where \(I_m\) is the image and \(\pi \) is the cokernel of m, [8].
, \(c^{r}_{A}(B)=\pi ^{-1}(r(A/I_m))\), where \(I_m\) is the image and \(\pi \) is the cokernel of m, [8].
Example 2.7
Let \({\mathcal {C}}\) be the category Ab of abelian groups and \({\mathcal {M}}\) be the collection of all monos.
-
(1)
For the preradical t defined by the torsion subgroup, \( t(A)=\lbrace a\in A: (\exists n\in Z) n>0\) and \(na=0\rbrace \) the corresponding closure operator \(c^t\), for \(m\in {\mathcal {M}}/A\) is given by: \(c^{t}_{A}(m)=\lbrace a\in A: (\exists n\in Z) n>0\) and \(na\in I_m\rbrace \).
-
(a)
Any abelian group A for which \(t(A)\ne 0\) is \(c^t\)-connected because for any \(c^t\)-closed m and n in \({\mathcal {M}}/A\), \(m\wedge n\ne 0\). Therefore, by Remark 2.5, it is connected in the sense of [13]. While for \(A={\mathbb {Z}}_2\oplus {\mathbb {Z}}\), for which \(t(A)\ne 0\), it is not connected in the sense of [7].
-
(b)
The free abelian group \({\mathbb {Z}}\) of integers is \(c^t\)-connected, because every non-zero \(m\in {\mathcal {M}}/{{\mathbb {Z}}}\) is \(c^t\)-dense. Therefore, it is connected in the sense of [13]. It can be verified that it is not in the sense of [7].
-
(c)
The group \(A={\mathbb {Z}}\oplus {\mathbb {Z}}\), where \(\oplus \) denotes the direct sum, is \(c^t\)-connected, because if b and c are any two non-zero \(c^t\)-closed members of \({\mathcal {M}}/A\), such that \(b\wedge c=0\), then for some integers \(m,n, r,s\in {\mathbb {Z}}\), \(I_b=\langle (m, n)\rangle \) and \(I_c=\langle (r, s)\rangle \), and so for
 , we have \(d\wedge b=d\wedge c=0\), implying that \((\{b,c\}\Rightarrow 0_A)\ne 0_A\) if it exists.
, we have \(d\wedge b=d\wedge c=0\), implying that \((\{b,c\}\Rightarrow 0_A)\ne 0_A\) if it exists.Connectedness in the sense of [13] follows. It can be shown that it is not connected in the sense of [7].
-
(a)
-
(2)
For the preradical f defined by the Frattini subgroup: \(f(A)=\cap \lbrace M: M\) is a maximal (proper) subgroup of \(A\rbrace \) the corresponding closure operator \(c^f\), for \(m\in {\mathcal {M}}/A\) is given by: \(c^{f}_{A}(m)=\cap \lbrace M:M\) is a maximal subgroup of A containing \(I_m\)\(\rbrace \).
-
(a)
\({\mathbb {Z}}_p\) is \(c^f\)-connected, because it does not have any nontrivial subgroup. Therefore, it is connectedness in the sense [13]. Simple verification shows that it is not in the sense of [7].
-
(b)
Consider the abelian group \(A={\mathbb {Z}}_p\oplus {\mathbb {Z}}_q\). Since \(({\mathbb {Z}}_p\oplus {\mathbb {Z}}_q)/({\mathbb {Z}}_p\oplus 0)\equiv {\mathbb {Z}}_q\), \(f(({\mathbb {Z}}_p\oplus {\mathbb {Z}}_q)/({\mathbb {Z}}_p\oplus 0))\equiv f({\mathbb {Z}}_q)=0\), implying that
 is \(c^f\)-closed. Similarly,
is \(c^f\)-closed. Similarly,  is \(c^f\)-closed. Since A is cyclic, the only nontrivial subgroups of A are \({\mathbb {Z}}_p\oplus 0\) and \(0\oplus {\mathbb {Z}}_q\). Therefore, if for \(m\in {\mathcal {M}}/A\), \(m\wedge a=0\) and \(m\wedge b=0\), then \(m=0\). This shows (a, b) is a \(c^f\)-closed partition of A. Therefore, A is not \(c^f\)-connected in the sense of [13], and therefore not \(c^f\)-connected. It can be shown that it is not connected in the sense of [7].
is \(c^f\)-closed. Since A is cyclic, the only nontrivial subgroups of A are \({\mathbb {Z}}_p\oplus 0\) and \(0\oplus {\mathbb {Z}}_q\). Therefore, if for \(m\in {\mathcal {M}}/A\), \(m\wedge a=0\) and \(m\wedge b=0\), then \(m=0\). This shows (a, b) is a \(c^f\)-closed partition of A. Therefore, A is not \(c^f\)-connected in the sense of [13], and therefore not \(c^f\)-connected. It can be shown that it is not connected in the sense of [7]. -
(c)
Let \(A={\mathbb {Z}}_{p^n}\) and \(n\ge 2\). The subgroups of \({{\mathbb {Z}}}_{p^n}\) are \(\langle p^i\rangle \) for \(i=0, ...,n \). Since \({\mathbb {Z}}_{p^n}/\langle p^i\rangle =Z_{p^{i}}\), we have \(f({\mathbb {Z}}_{p^n}/\langle p^i\rangle )=f({\mathbb {Z}}_{p^{i}})\). If \(i\ge 2\), then \(f({\mathbb {Z}}_{p^{i}})\ne 0\). Therefore, the only \(c^f\)-closed subgroup of \({\mathbb {Z}}_{p^n}\) is \(\langle p\rangle \). Thus, \({\mathbb {Z}}_{p^n}\) is \(c^f\)-connected. Therefore, it is \(c^f\)-connected in the sense of [13]. It is not connected in the sense of [7].
-
(a)
The following example shows connectedness and connectedness in the sense of [13] are not the same, due to non-existence of pseudo-complements.
Example 2.8
Let \({\mathcal {C}}\) be the category generated by the following preordered set:

\({\mathcal {M}}\) be the collection of all morphisms and consider the identity closure operator \(\mathfrak {c}\) on \({\mathcal {C}}\), relative to \({\mathcal {M}}\).
One can verify that \(a_n\wedge b_m=o_X\) and \(\lnot \lbrace a_n, b_m\rbrace =o_X\). Since \(a_n\) and \(b_m\) are \(\mathfrak {c}\)-closed and non-zero, X is not \(\mathfrak {c}\)-connected. However. for all n, \(A_n\) and \(B_n\) are \(\mathfrak {c}\)-connected.
Since neither \(a_n\) nor \(b_n\) has a pseudo-complement, there is no \(\mathfrak {c}\)-closed partition of X. Thus. X is \(\mathfrak {c}\)-connected in the sense of [13]. One can verify that it is \(\mathfrak {c}\)-connected in the sense of [7].
In the following example, connectedness and connectedness in the sense of [13] are not the same, this time due to non-closedness of pseudo-complement.
Example 2.9
Let \({\mathcal {C}}\) be the category generated by the following preordered set:

where the two triangles commute.
With \({\mathcal {M}}\) the collection of all morphisms, we define the closure operator \(\mathfrak {c}\) as follows:
In \({\mathcal {C}}/O, {\mathcal {C}}/A, {\mathcal {C}}/B, {\mathcal {C}}/C\), and \({\mathcal {C}}/D\), all morphisms are \(\mathfrak {c}\)-closed, while in \({\mathcal {C}}/X\), e and f are \(\mathfrak {c}\)-dense and the rest are \(\mathfrak {c}\)-closed.
The only \(\mathfrak {c}\)-closed subobjects of X are \(o_X, g, h\) and \(1_X\). One can easily verify that \(g\wedge h=o_X\) and \(\lnot \lbrace g,h\rbrace =o_X\), so that g and h are non-zero \(\mathfrak {c}\)-closed quasi-complements. Hence, X is not \(\mathfrak {c}\)-connected. However, \(\lnot g=f\) and \(\lnot h =e\). Therefore, in the sense of [13], X is \(\mathfrak {c}\)-connected.
3 Image of a Connected Object is Connected
In this section, we introduce the notion of fine epi and use it to show that the image of a connected object under a fine epi is connected.
Definition 3.1
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\). A morphism
 is said to be \({\mathcal {M}}\)-fine epi, if for any \(i:I\rightarrowtail Y\) in \({\mathcal {M}}\), \(f^{-1}(i)=o_X\) implies \(i=o_Y\).
is said to be \({\mathcal {M}}\)-fine epi, if for any \(i:I\rightarrowtail Y\) in \({\mathcal {M}}\), \(f^{-1}(i)=o_X\) implies \(i=o_Y\).
When the domain \({\mathcal {M}}\) is the collection of all the monos whose pullback along every morphism exist, then \({\mathcal {M}}\)-fine epi is also called fine epi.
Example 3.2
Let \({\mathcal {M}}\) be a domain and
 be a morphism in \({\mathcal {C}}\).
be a morphism in \({\mathcal {C}}\).
-
(1)
If \(f^{-1}(o_Y)\ne o_X\), then f is \({\mathcal {M}}\)-fine epi.
This follows from the fact that for \(i\in {\mathcal {M}}/Y\), \(f^{-1}(o_Y)\le f^{-1}(i)\).
-
(2)
If f is a retraction, then it is \({\mathcal {M}}\)-fine epi.
Let
 in \({\mathcal {M}}/Y\) be given, such that the following square is a pullback.
in \({\mathcal {M}}/Y\) be given, such that the following square is a pullback. 
Since \(i^{-1}(f)\) is a retraction, there is
 , such that \(i^{-1}(f)s=1_B\). To show \(i=o_Y\), let
, such that \(i^{-1}(f)s=1_B\). To show \(i=o_Y\), let
 be given in \({\mathcal {M}}/Y\). Since \(o_X\le f^{-1}(a)\), there is h, such that \(o_X=f^{-1}(a)h\). We have \(aa^{-1}(f)hs=ff^{-1}(a)hs=fo_Xs=ii^{-1}(f)s=i\), implying that \(i\le a\), as desired.
be given in \({\mathcal {M}}/Y\). Since \(o_X\le f^{-1}(a)\), there is h, such that \(o_X=f^{-1}(a)h\). We have \(aa^{-1}(f)hs=ff^{-1}(a)hs=fo_Xs=ii^{-1}(f)s=i\), implying that \(i\le a\), as desired. -
(3)
Suppose that all morphisms in \({\mathcal {C}}\) with domain \(O_X\) are mono. If f is stable regular epi, then f is \({\mathcal {M}}\)-fine epi.
With i as in part 2, \(i^{-1}(f)\) is regular epi. Since it is by hypothesis mono, it is an isomorphism. An argument similar to part 2 shows that \(i=o_Y\).
-
(4)
Suppose that \({\mathcal {C}}\) is balanced and all morphisms in \({\mathcal {C}}\) with domain \(O_X\) are mono. If f is stable epi, then f is \({\mathcal {M}}\)-fine epi.
-
(5)
With \({\mathcal {C}}\) the following poset, \(O\rightarrow A\) is epi but not \({\mathcal {M}}\)-fine epi, while \(A\rightarrow B\) is both epi and \({\mathcal {M}}\)-fine epi.
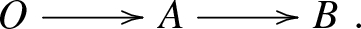
Extending the concept of essential module, [9], to essential homomorphism, by calling an R-module homomorphism
 essential if Y is an essential extension of f(X), which is equivalent to, for all \(y\in Y\), \(f(X)\cap Ry=0\) yields \(y=0\), we have:
essential if Y is an essential extension of f(X), which is equivalent to, for all \(y\in Y\), \(f(X)\cap Ry=0\) yields \(y=0\), we have:
Example 3.3
In the category Rmod of R-modules, with R a commutative ring with identity, a morphism
 is fine epi, if and only if it is not mono or it is essential mono. In particular, every essential, hence epi, is fine epi.
is fine epi, if and only if it is not mono or it is essential mono. In particular, every essential, hence epi, is fine epi.
Suppose that
 is fine epi and mono. Let \(y\in Y\), such that \(f(X)\cap Ry=0\). Since f is mono, we get \(f^{-1}(Ry)=0\). Since f is fine epi, \(Ry=0\) and so \(y=0\). Hence, f is essential mono.
is fine epi and mono. Let \(y\in Y\), such that \(f(X)\cap Ry=0\). Since f is mono, we get \(f^{-1}(Ry)=0\). Since f is fine epi, \(Ry=0\) and so \(y=0\). Hence, f is essential mono.
Conversely if f is not mono, then \(f^{-1}(0)\ne 0\). Therefore, by part (1) of Example 3.2, f is fine epi and if it is essential mono, then let
 be mono, such that \(f^{-1}(i)=0\). For \(b\in B\), set \(y=i(b)\). Since \(f^{-1}(Ry)=0\), we get \(f(X)\cap Ry=0\). Therefore, \(y=0\) and thus, \(b=0\). Hence, \(B=0\) as desired.
be mono, such that \(f^{-1}(i)=0\). For \(b\in B\), set \(y=i(b)\). Since \(f^{-1}(Ry)=0\), we get \(f(X)\cap Ry=0\). Therefore, \(y=0\) and thus, \(b=0\). Hence, \(B=0\) as desired.
Example 3.4
In the category Set of sets, a morphism is fine epi if and only if it is epi.
Suppose f is fine epi. Let
 be the inclusion. Then, \(f^{-1}(i)=\emptyset \). Thus, \(Y-f(X)=\emptyset \), and so, \(Y=f(X)\). Hence, f is epi. The converse is true by part 4 of Example 3.2.
be the inclusion. Then, \(f^{-1}(i)=\emptyset \). Thus, \(Y-f(X)=\emptyset \), and so, \(Y=f(X)\). Hence, f is epi. The converse is true by part 4 of Example 3.2.
Example 3.5
Let \(({\mathcal {C}},|\ |)\) be a concrete category over \({\mathcal {X}}\), [1], \({\mathcal {M}}_{{\mathcal {C}}}\) be a domain in \({\mathcal {C}}\) and \({\mathcal {M}}\) be a domain in \({\mathcal {X}}\). Suppose that \(|\ |\) takes \({\mathcal {M}}_{{\mathcal {C}}}\) elements to \({\mathcal {M}}\) elements, preserves pullbacks, and preserves and reflects zeros. If |f| is \({\mathcal {M}}\)-fine epi, then f is \({\mathcal {M}}_{{\mathcal {C}}}\)-fine epi. If in addition structured \({\mathcal {M}}\) elements lift to \({\mathcal {M}}_{{\mathcal {C}}}\) elements, then the converse is true.
In particular, in the construct Top of topological spaces, a morphism is fine epi if and only if it is surjective.
Let
 be in \({\mathcal {M}}_{{\mathcal {C}}}/Y\), such that \(f^{-1}(i)=o_X\). Since \(|\ |\) preserves pullbacks and zeros, \(|f|^{-1}(|i|))=o_{|X|}\). Now, |f| is \({\mathcal {M}}\)-fine epi, so \(|i|=o_{|Y|}\). Since \(|\ |\) reflects zeros, we get \(i=o_Y\).
be in \({\mathcal {M}}_{{\mathcal {C}}}/Y\), such that \(f^{-1}(i)=o_X\). Since \(|\ |\) preserves pullbacks and zeros, \(|f|^{-1}(|i|))=o_{|X|}\). Now, |f| is \({\mathcal {M}}\)-fine epi, so \(|i|=o_{|Y|}\). Since \(|\ |\) reflects zeros, we get \(i=o_Y\).
For the converse, let
 be in \({\mathcal {M}}/|Y|\), such that \(|f|^{-1}(i')=o_{|X|}\). Let
be in \({\mathcal {M}}/|Y|\), such that \(|f|^{-1}(i')=o_{|X|}\). Let
 be a lift in \({\mathcal {M}}_{{\mathcal {C}}}\), of \(i'\). By preservation of pullbacks, we have \(|f^{-1}(i)|=|f|^{-1}(i')=o_{|X|}\), and so, \(f^{-1}(i)=o_X\). Since f is \({\mathcal {M}}_{{\mathcal {C}}}\)-fine epi, \(i=o_Y\). Therefore, \(i'=|i|=o_{|Y|}\).
be a lift in \({\mathcal {M}}_{{\mathcal {C}}}\), of \(i'\). By preservation of pullbacks, we have \(|f^{-1}(i)|=|f|^{-1}(i')=o_{|X|}\), and so, \(f^{-1}(i)=o_X\). Since f is \({\mathcal {M}}_{{\mathcal {C}}}\)-fine epi, \(i=o_Y\). Therefore, \(i'=|i|=o_{|Y|}\).
Definition 3.6
A (weak, strong) domain \({\mathcal {M}}\) in \({\mathcal {C}}\) is said to have images, if for all
 , the map
, the map
 has a left adjoint f( ).
has a left adjoint f( ).
Example 3.7
Let \({\mathcal {M}}\) be a strong domain with images. If \(f:X\rightarrow Y\) is a morphism, such that for any \(i:B\rightarrow Y\) in \({\mathcal {M}}/Y\) for which \(f^{-1}(i)=o_X\), \((i^{-1}(f))(1_{O_X})=1_B\), then f is \({\mathcal {M}}\)-fine epi.
Let the morphism
 in \({\mathcal {M}}/Y\) be such that \(f^{-1}(i)=o_X\). The map
in \({\mathcal {M}}/Y\) be such that \(f^{-1}(i)=o_X\). The map
 being a left adjoint, preserves zeros and by part (2) of Lemma 1.2, \(o_{O_X}=1_{O_X}\). Therefore, \(o_B=i^{-1}(f)(o_{O_X})=i^{-1}(f)(1_{O_X})=1_B\). Thus, by part 1 of Lemma 1.2, \(o_Y=io_B=i1_B=i\).
being a left adjoint, preserves zeros and by part (2) of Lemma 1.2, \(o_{O_X}=1_{O_X}\). Therefore, \(o_B=i^{-1}(f)(o_{O_X})=i^{-1}(f)(1_{O_X})=1_B\). Thus, by part 1 of Lemma 1.2, \(o_Y=io_B=i1_B=i\).
Recalling that a collection \({\mathcal {M}}\) of morphisms is called a quasi-right factorization structure in \({\mathcal {C}}\), [11], if, for every \(f\in {\mathcal {C}}\), there is a smallest \(m\in {\mathcal {M}}\), called a quasi-right part of f, such that \(f\le m\); and that when \({\mathcal {M}}\) is a collection of monos whose pullbacks along every morphism exits, then a quasi-right factorization structure is a right factorization structure, we have:
Proposition 3.8
A weak domain \({\mathcal {M}}\) is a (quasi) right factorization structure in \({\mathcal {C}}\) if and only if it is a weak domain with images.
Proof
The proof for quasi-right factorization structure follows from the fact that for each \(f\in {\mathcal {C}}\) and \(i\in {\mathcal {M}}\), such that fi is defined, a quasi-right part of fi corresponds to f(i), [11]. Since, when \({\mathcal {M}}\) consists of monos, as is the case here, quasi-right factorization structures are right factorization structures, the result follows. \(\square \)
Example 3.9
Let the domain \({\mathcal {M}}\) be a quasi-right factorization structure in \({\mathcal {C}}\) that is closed under composition. If \(f:X\rightarrow Y\) is a morphism, such that for any \(i:B\rightarrow Y\) in \({\mathcal {M}}/Y\) for which \(f^{-1}(i)=o_X\), a quasi,right part of \(i^{-1}(f)\) is \(1_B\), then by Example 3.7, f is \({\mathcal {M}}\)-fine epi.
Also \({\mathcal {M}}\) is a right factorization structure, and since it is closed under composition, by [8], there is a collection \({\mathcal {E}}\), such that \(({\mathcal {E}}, {\mathcal {M}})\) is a factorization structure. Therefore, if \(f:X\rightarrow Y\) is a morphism, such that for any \(i:B\rightarrow Y\) in \({\mathcal {M}}/Y\) for which \(f^{-1}(i)=o_X\), the map \(i^{-1}(f)\) is in \({\mathcal {E}}\), then f is \({\mathcal {M}}\)-fine epi. In particular, if \({\mathcal {E}}\) is pullback stable, then every \({\mathcal {E}}\)-morphism is \({\mathcal {M}}\)-fine epi.
Saying a morphism f reflects (closed) quasi-complements, if whenever a and b are (closed) quasi-complements, then so are \(f^{-1}(a)\) and \(f^{-1}(b)\), we have:
Theorem 3.10
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose that
 is \({\mathcal {M}}\)-fine epi and f reflects closed quasi-complements. If X is \(\mathfrak {c}\)-connected, then so is Y.
is \({\mathcal {M}}\)-fine epi and f reflects closed quasi-complements. If X is \(\mathfrak {c}\)-connected, then so is Y.
Proof
Let a and b in \({\mathcal {M}}/Y\) be closed quasi-complements. Since X is \(\mathfrak {c}\)-connected and \(f^{-1}(a)\) and \(f^{-1}(b)\) are \(\mathfrak {c}\)-closed, \(f^{-1}(a)=o_X\) or \(f^{-1}(b)=o_X\). f being a fine epi, yields \(a=o_Y\) or \(b=o_Y\). Therefore, Y is \(\mathfrak {c}\)-connected. \(\square \)
Example 3.11
Since in the category Top and in every Topos, [10], implications and zeros are stable under pullbacks, every morphism reflects quasi-complements. Therefore, by Theorem 3.10, every fine epi preserves connectedness.
4 Union of Connected Objects is Connected
In this section, we first define two different joins (unions), and then, we show that the union of connected objects is connected in both cases, each under certain conditions.
Definition 4.1
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\). For i and j in \({\mathcal {M}}/X\), define \(i\preceq j\) if for any \(k\in {\mathcal {M}}/X\), \(k\wedge j=o_X\) implies \(k\wedge i=o_X\). We write \(i\sim j\), whenever \(i\preceq j\) and \(j\preceq i\).
Lemma 4.2
\(({\mathcal {M}}/X, \preceq )\) is a preordered class.
Proof
Obvious. \(\square \)
Definition 4.3
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\) and \(\lbrace a_{\alpha }:\alpha \in I\rbrace \subseteq {\mathcal {M}}/X\). \(a\in {\mathcal {M}}/X\) is called:
-
(a)
a join of \(\lbrace a_{\alpha }\rbrace \), denoted by \(\vee a_{\alpha }\), if it is a join relative to the preorder \(\le \).
-
(b)
a prime join of \(\lbrace a_{\alpha }\rbrace \), denoted by \(\curlyvee ^{^p} a_{\alpha }\), if for any \(b\in {\mathcal {M}}/X\), \(b\wedge a=o_X\) if and only if for all \(\alpha \in I\), \(b\wedge a_{\alpha }=o_X\).
Proposition 4.4
Let \({\mathcal {M}}\) be a domain in \({\mathcal {C}}\) and \(\lbrace a_{\alpha }:\alpha \in I\rbrace \subseteq {\mathcal {M}}/X\).
-
(a)
Both join and prime join, if they exist, are unique up to \(\sim \).
-
(b)
For any \(b\in {\mathcal {M}}/X\), \(b\wedge \curlyvee ^{^p} a_{\alpha }\sim \curlyvee ^{^p} (b\wedge a_{\alpha })\).
-
(c)
If \(\vee a_{\alpha }\) exists and commutes with meet, then \(\vee a_{\alpha }\) is a prime join.
Proof
Follows from straightforward computations. \(\square \)
Example 4.5
Let \({\mathcal {C}}\) be the category Top of topological spaces.
-
(1)
Let \({\mathcal {M}}\) be the collection of all monos. for
 in \({\mathcal {M}}/X\), let \(I_a=a(A)\) be the set image of A under a. One can easily verify that:
in \({\mathcal {M}}/X\), let \(I_a=a(A)\) be the set image of A under a. One can easily verify that:-
(a)
\(a\wedge b\) is the inclusion
 , where for \(i=a^{-1}(b)\) and \(j=b^{-1}(a)\), the topology of \(I_a\cap I_b\) is generated by the subbase \(\{i^{-1}(G),j^{-1}(H):G \hbox { open in A} \hbox { and } H \hbox { open in } B\}\).
, where for \(i=a^{-1}(b)\) and \(j=b^{-1}(a)\), the topology of \(I_a\cap I_b\) is generated by the subbase \(\{i^{-1}(G),j^{-1}(H):G \hbox { open in A} \hbox { and } H \hbox { open in } B\}\). -
(b)
\(a\le b\) if and only if \(I_a\subseteq I_b\) and that the inclusion
 is continuous, where \(I_a\) and \(I_b\) have topologies induced by the isomorphisms \(I_a\cong A\) and \(I_b\cong B\), respectively.
is continuous, where \(I_a\) and \(I_b\) have topologies induced by the isomorphisms \(I_a\cong A\) and \(I_b\cong B\), respectively. -
(c)
\(a\preceq b\) if and only if \(I_a\subseteq I_b\).
-
(d)
The negations of a and \(\{a,b\}\) in \({\mathcal {M}}/X\) are respectively the inclusions
 and
and  with induced topologies.
with induced topologies. -
(e)
\(\vee a_{\alpha }\) is the inclusion
 , with the coinduced topology from all \(I_{A_\alpha }\).
, with the coinduced topology from all \(I_{A_\alpha }\). -
(f)
\(\curlyvee ^{^p} a_{\alpha }\) is the inclusion
 , with any topology containing the induced topology.
, with any topology containing the induced topology.
-
(a)
-
(2)
Let \({\mathcal {M}}\) be the collection of all initial monos, i.e., monos with induced topology.
-
(a)
\(a\wedge b\) is the inclusion
 , with induced topology.
, with induced topology. -
(b)
\(a\le b\) if and only if \(I_a\subseteq I_b\). In this case, the inclusion
 is initial, where \(I_a\) and \(I_b\) have topologies induced by the isomorphisms \(I_a\cong A\) and \(I_b\cong B\), respectively.
is initial, where \(I_a\) and \(I_b\) have topologies induced by the isomorphisms \(I_a\cong A\) and \(I_b\cong B\), respectively. -
(c)
\(a\preceq b\) if and only if \(I_a\subseteq I_b\), i.e., \(a\preceq b\) if and only if \(a\le b\).
-
(d)
The negations of a and \(\{a,b\}\) in \({\mathcal {M}}/X\) are, respectively, the inclusions
 and
and  with induced topologies.
with induced topologies. -
(e)
\(\vee a_{\alpha }=\curlyvee ^{^p} a_{\alpha }\) is
 , with induced topology.
, with induced topology.
-
(a)
Example 4.6
Let \({\mathcal {C}}\) be the category Rmod of R-modules over a commutative ring R with identity and \({\mathcal {M}}\) be the collection of all monos. for  in \({\mathcal {M}}/X\), let \(I_a=a(A)\) be the set image of A under a. One can easily verify that:
in \({\mathcal {M}}/X\), let \(I_a=a(A)\) be the set image of A under a. One can easily verify that:
-
(1)
\(a\wedge b\) is
 , with submodule structure.
, with submodule structure. -
(2)
\(a\le b\) if and only if \(I_a\subseteq I_b\) and that the inclusion
 is a module homomorphism, where \(I_a\) and \(I_b\) have module structures induced by the isomorphisms \(I_a\cong A\) and \(I_b\cong B\), respectively.
is a module homomorphism, where \(I_a\) and \(I_b\) have module structures induced by the isomorphisms \(I_a\cong A\) and \(I_b\cong B\), respectively. -
(3)
\(a\preceq b\) if and only if
 is essential.
is essential. -
(4)
The negations, \(\lnot a\) and \(\lnot \{a,b\}\), do not exist in general.
-
(5)
\(\vee a_{\alpha }\) is the inclusion
 with submodule structure, where for each \(\alpha \), \(I_{a_\alpha }\) has the module structure induced by the isomorphism \(I_{a\alpha }\cong A_{\alpha }\).
with submodule structure, where for each \(\alpha \), \(I_{a_\alpha }\) has the module structure induced by the isomorphism \(I_{a\alpha }\cong A_{\alpha }\). -
(6)
The existence of \(\curlyvee ^{^p} a_{\alpha }\), in general, is not known.
Example 4.7
Let \({\mathcal {C}}\) be the category generated by the following preordered set:

which has pullbacks. Let \({\mathcal {M}}\) be the collection of all morphisms, \({\mathcal {A}}=\{a_i:i\in {\mathbb {N}}\}\subseteq {\mathcal {M}}/X\) and \(\emptyset \ne \mathcal {A'}\subseteq {\mathcal {A}}\).
Every \(a_i\) is a prime join of \({\mathcal {A}}'\). If \(\mathcal {A'}\) is finite, then the join of \(\mathcal {A'}\) is the \(a_i\in \mathcal {A'}\) with maximum index, which is a stable join as well; and if \(\mathcal {A'}\) is infinite, then the join of \(\mathcal {A'}\) is \(1_X\), which is not a stable join. Since for any \(b_{j}\), \(\bigvee _{a_i\in \mathcal {A'}}(a_i\wedge b_{j})=O\), but \((\bigvee _{a_i\in \mathcal {A'}}a_i)\wedge b_{j}=1_X\wedge b_{j}=b_j\), we conclude that \(1_X\) is not a prime join of \(\mathcal {A'}\).
For any \(a_i\) and \(b_j\), \(a_i\vee b_j=1_X\), which is not stable because \((a_i\vee b_j)\wedge a_{i+1}=1_X\wedge a_{i+1}=a_{i+1}\), but \((a_i\wedge a_{i+1})\vee (b_j\wedge a_{i+1})=a_i\vee 0=a_i\). One can verify that \(1_X\) is also a prime join of \(a_i\) and \(b_j\)
Example 4.8
Let \({\mathcal {C}}\) be the category generated by the preordered set:

which has pullbacks. Let \({\mathcal {M}}\) be the collection of all morphisms. One can easily verify that in \({\mathcal {M}}/X\), \(1_X\) is the join of b and c, and that \(ca'\), b and c are prime joins of b and c.
Example 4.9
Let \({\mathcal {C}}\) be the category generated by the preordered set:

which has pullbacks. Let \({\mathcal {M}}\) be the collection of all morphisms. Denoting the maps from A to \(D_i\) by \(a_i\), etc, and the maps from \(D_i\) to \(D_1\) by \(d_i\), consider \(a_1\) and \(b_1\) in \({\mathcal {M}}/{D_1}\). Neither a join nor a prime join of \(a_1\) and \(b_1\) exists.
Lemma 4.10
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\). Then, every \(m:M\longrightarrow X\) in \({\mathcal {M}}/X\) reflects quasi-complements.
Proof
Let \(a,b\in {\mathcal {M}}/X\) be quasi-complements. Using Lemma 1.3, we have \(m^{-1}(a)\wedge m^{-1}(b)=m^{-1}(a\wedge b)=m^{-1}(o_X)=o_M\), and \(\lnot \{m^{-1}(a),m^{-1}(b)\}=m^{-1}(\lnot \{a,b\})=m^{-1}(o_X)=o_M\). Hence, \(m^{-1}(a)\) and \(m^{-1}(b)\) are quasi-complements. \(\square \)
Theorem 4.11
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose that \(m:M\rightarrow X\) in \({\mathcal {M}}\) is \(\mathfrak {c}\)-dense and for any \(k\in {\mathcal {M}}/X\), \(m\preceq k\) implies \(c_X(m)\le c_X(k)\). If M is \(\mathfrak {c}\)-connected, then so is X.
Proof
Let i and j in \({\mathcal {M}}/X\) be closed quasi-complements. Using Lemma 4.10, \(m^{-1}(i)\) and \(m^{-1}(j)\) are closed quasi-complements. Since M is \(\mathfrak {c}\)-connected, \(m^{-1}(i)=o_M\) or \(m^{-1}(j)=o_M\). In case \(m^{-1}(i)=o_M\), by Lemma 1.2, we get \(m\wedge i=o_X\). Now, \(m\preceq j\), because if \(k\wedge j=o_X\), then \(k\wedge m \wedge i=o_X\) and \(k\wedge m\wedge j=o_X\) implies \(k\wedge m=o_X\). Now, by hypothesis, \(c_X(m)\le c_X(j)\). Since m is dense and j is closed, \(1_X\le j\), implying that \(j=1_X\). Since \(i\wedge j=o_X\), we get \(i=o_X\). Similarly, in case \(m^{-1}(j)=o_M\), we get \(j=o_X\). Hence, X is \(\mathfrak {c}\)-connected. \(\square \)
Calling a collection \(\{a_\alpha \}\subseteq {\mathcal {M}}/X\) mutually intersecting if for all \(\alpha \) and \(\beta \), \(a_\alpha \wedge a_{\beta }\ne o_X\), we have:
Theorem 4.12
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose that the mutually intersecting collection \(\lbrace a_{\alpha }:A_{\alpha }\rightarrow X\rbrace \subseteq {\mathcal {M}}/X\) has a join \(a:A\rightarrow X\) that commutes with meet. If for every \(\alpha \), \(A_{\alpha }\) is \(\mathfrak {c}\)-connected, then so is A.
Proof
Without loss of generality, we assume for all \(\alpha \), \(a_\alpha \not =o_X\). Let i and j in \({\mathcal {M}}/A\) be closed quasi-complements. Since a is a join of \(\lbrace a_{\alpha }\rbrace \), for each \(\alpha \), a morphism
 exists, such that \(a_{\alpha }=ab_{\alpha }\). By the fact that for every \(\alpha \), \(b_\alpha \) is in \({\mathcal {M}}\), Lemma 4.10 implies \(b_{\alpha }^{-1}(i)\) and \(b_{\alpha }^{-1}(j)\) are closed quasi-complements. Since \(A_\alpha \) is connected, for each \(\alpha \), \(b_{\alpha }^{-1}(i)=o_{A_{\alpha }}\) or \(b_{\alpha }^{-1}(j)=o_{A_{\alpha }}\).
exists, such that \(a_{\alpha }=ab_{\alpha }\). By the fact that for every \(\alpha \), \(b_\alpha \) is in \({\mathcal {M}}\), Lemma 4.10 implies \(b_{\alpha }^{-1}(i)\) and \(b_{\alpha }^{-1}(j)\) are closed quasi-complements. Since \(A_\alpha \) is connected, for each \(\alpha \), \(b_{\alpha }^{-1}(i)=o_{A_{\alpha }}\) or \(b_{\alpha }^{-1}(j)=o_{A_{\alpha }}\).
If there is \(\alpha _0\), such that \(b_{\alpha _0}^{-1}(i)\ne o_{A_{\alpha _0}}\), and there is \(\alpha _1\), such that \(b_{\alpha _1}^{-1}(j)\ne o_{A_{\alpha _1}}\), then by above \(b_{\alpha _0}^{-1}(j)=o_{A_{\alpha _0}}\) and \(b_{\alpha _1}^{-1}(i)=o_{A_{\alpha _1}}\). By Lemma 1.2, it follows that \((b_{\alpha _0}\wedge b_{\alpha _1})\wedge i=o_A\) and \((b_{\alpha _0}\wedge b_{\alpha _1})\wedge j=o_A\). Therefore, \(b_{\alpha _0}\wedge b_{\alpha _1}=o_A\). Thus, \(a_{\alpha _0}\wedge a_{\alpha _1}=a(b_{\alpha _0}\wedge b_{\alpha _1})=o_X\), which is a contradiction whether \(\alpha _0=\alpha _1\) or not. Therefore, either for every \(\alpha \), \(b_{\alpha }^{-1}(i)=o_{A_{\alpha }}\) or for every \(\alpha \), \(b_{\alpha }^{-1}(j)=o_{A_{\alpha }}\).
If for every \(\alpha \), \(b_{\alpha }^{-1}(i)=o_{A_{\alpha }}\), then \(a_{\alpha }\wedge (ai)=(ab_{\alpha })\wedge (ai)=a(b_\alpha \wedge i)=o_X\). Since a commutes with binary meet, \(a\wedge (ai)=o_X\). Therefore, \(ai=o_X\), implying that \(i=o_A\). Similarly if for every \(\alpha \), \(b_{\alpha }^{-1}(j)=o_{A_{\alpha }}\), then \(j=o_A\). Hence, either \(i=o_A\) or \(j=o_A\).\(\square \)
Example 4.13
Let Top be the category of topological spaces, \({\mathcal {M}}\) be the collection of initial monos, and \(\mathfrak {c}\) be the Kuratowski closure operator. By Example 2.6 and the fact that all the requirements of Theorem 4.12 are met, the theorem gives the known classic result about topological spaces.
Definition 4.14
Let \({\mathcal {M}}\) be a (weak) domain in \({\mathcal {C}}\). A closure operator \(\mathfrak {c}\) on \({\mathcal {C}}\) relative to \({\mathcal {M}}\) is said to be strongly continuous if for \(a:A\rightarrow X\) in \({\mathcal {M}}/X\) satisfying \(a\sim 1_X\), we have \(ac_A(i)=c_X(ai)\), for every \(i\in {\mathcal {M}}/A\).
Remark 4.15
If the preorders \(\preceq \) and \(\le \) on \({\mathcal {M}}/X\) coincide, then every closure operator relative to \({\mathcal {M}}\) is strongly continuous.
Example 4.16
Let \({\mathcal {C}}\) be the category Top of topological spaces.
-
(1)
Let \({\mathcal {M}}\) be the collection of all initial monos, [1]. Then, any closure operator relative to \({\mathcal {M}}\), in particular the Kuratowski closure operator, is strongly continuous, because for \(a\in {\mathcal {M}}/X\), \(a\sim 1_X\) if and only if \(a\cong 1_X\).
-
(2)
Let \({\mathcal {M}}\) be the collection of all monos and \(\mathfrak {c}\) be as in Example 2.6. \(\mathfrak {c}\) is not strongly continuous, because for
 , where \({\mathcal {T}}_1\supseteq {\mathcal {T}}_2\), \(a\sim 1_{(X,{\mathcal {T}}_1)}\), but it is not necessarily closed.
, where \({\mathcal {T}}_1\supseteq {\mathcal {T}}_2\), \(a\sim 1_{(X,{\mathcal {T}}_1)}\), but it is not necessarily closed.
Example 4.17
Let \({\mathcal {C}}\) be the category Ab of abelian groups.
-
(1)
The closure operator \(c^t\) introduced in Example 2.7 is not strongly continuous, because for \(a:\lbrace {\bar{0}}, {\bar{2}}\rbrace \hookrightarrow {\mathbb {Z}}_4\), \(a\sim 1_{{\mathbb {Z}}_4}\), but it is not \(c^t\)-closed.
-
(2)
Also the closure operator \(c^f\) introduced in Example 2.7 is not strongly continuous because for \(a:4{\mathbb {Z}}\hookrightarrow {\mathbb {Z}}\), \(a\sim 1_{{\mathbb {Z}}}\), but it is not \(c^f\)-closed.
Lemma 4.18
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\). Consider the following pullback square:

If \(a\preceq b\), then
-
(a)
\(a^{-1}(b)\sim 1_A\).
-
(b)
Let \(\mathfrak {c}\) be a strongly continuous closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). If \(j\in {\mathcal {M}}/B\) is \(\mathfrak {c}\)-closed, then so is \(a^{-1}(bj)\).
Proof
-
(a)
Let \(k\wedge a^{-1}(b)=o_A\). We have \((ak)\wedge b=a(k\wedge a^{-1}(b))=ao_A=o_X\). Since \(a\preceq b\), \((ak)\wedge a=o_X\). Therefore, \(ak=o_X\), and thus, by Lemma 1.2, \(k=o_A\).
-
(b)
Let \(d=b^{-1}(a)\). Since j is \(\mathfrak {c}\)-closed, \(d^{-1}(j)\) is \(\mathfrak {c}\)-closed. By part (a), we have \(a^{-1}(bj)=a^{-1}(b)d^{-1}(j)=a^{-1}(b)c_D(d^{-1}(j))=c_A(a^{-1}(b)d^{-1}(j))\)\(=c_A(a^{-1}(bj))\), as required.
\(\square \)
Lemma 4.19
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\), and let
 and
and
 be in \({\mathcal {M}}/X\), such that \(a\preceq b\). If \(i,j\in {\mathcal {M}}/B\) are quasi-complements, then so are \(a^{-1}(bi)\) and \(a^{-1}(bj)\).
be in \({\mathcal {M}}/X\), such that \(a\preceq b\). If \(i,j\in {\mathcal {M}}/B\) are quasi-complements, then so are \(a^{-1}(bi)\) and \(a^{-1}(bj)\).
Proof
Using Lemma 1.3, we have \(a^{-1}(bi)\wedge a^{-1}(bj)=a^{-1}(b(i\wedge j))=a^{-1}(o_X)=o_A\). To show \(\lnot \{a^{-1}(bi),a^{-1}(bj)\}=o_A\), let \(k\in {\mathcal {M}}/A\), such that \(k\wedge a^{-1}(bi)=o_A\) and \(k\wedge a^{-1}(bj)=o_A\). The former yields \(b(b^{-1}(ak)\wedge i)=ak\wedge bi=a(k\wedge a^{-1}(bi))=o_X\) and so by Lemma 1.2, \(b^{-1}(ak)\wedge i=o_B\); and the latter gives \(b^{-1}(ak)\wedge j=o_B\). We get \(b^{-1}(ak)=o_B\). Therefore, \(ak\wedge b=bb^{-1}(ak)=o_X\). Since \(a\preceq b\), \(ak\wedge a=o_X\), and since \(ak\le a\), \(ak=o_X\). Thus, \(k=o_A\). \(\square \)
Note that the above Lemma holds, when the inequality \(a\preceq b\) is replaced by the stronger inequality \(a\le b\).
Theorem 4.20
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a strongly continuous closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose that the mutually intersecting collection \(\lbrace a_{\alpha }:A_{\alpha }\rightarrow X\rbrace \subseteq {\mathcal {M}}/X\) has a prime join \(a:A\rightarrow X\). If for every \(\alpha \), \(A_{\alpha }\) is \(\mathfrak {c}\)-connected, then so is A.
Proof
Without loss of generality, we assume for all \(\alpha \), \(a_\alpha \not =o_X\). Let \(i,j\in {\mathcal {M}}/A\) be closed quasi-complements. Now suppose \(i\ne o_A\) and \(j\ne o_A\). By Lemma 1.2, we have \(ai\wedge a=ai\ne o_X\) and \(aj\wedge a=aj\ne o_X\). Since a is a prime join, there exist \(\alpha _0\) and \(\alpha _1\), such that \(ai\wedge a_{\alpha _0}\ne o_X\) and \(aj\wedge a_{\alpha _1}\ne o_X\). The former yields \(a_{\alpha _0}a_{\alpha _0}^{-1}(ai)\ne o_X\), implying that \(a_{\alpha _0}^{-1}(ai)\ne o_{A_{\alpha _0}}\) and the latter gives \(a_{\alpha _1}^{-1}(aj)\ne o_{A_{\alpha _1}}\). Since \(a_{\alpha _0}\preceq a\) and \(a_{\alpha _1}\preceq a\), by Lemma 4.19, \(a_{\alpha _0}^{-1}(ai)\) and \(a_{\alpha _0}^{-1}(aj)\) in \({\mathcal {M}}/{A_{\alpha _0}}\) and \(a_{\alpha _1}^{-1}(ai)\) and \(a_{\alpha _1}^{-1}(aj)\) in \({\mathcal {M}}/{A_{\alpha _1}}\), are closed quasi-complements.
Since \(A_{\alpha _0}\) and \(A_{\alpha _1}\) are \(\mathfrak {c}\)-connected, \(a_{\alpha _0}^{-1}(ai)\ne o_{A_{\alpha _0}}\) and \(a_{\alpha _1}^{-1}(aj)\ne o_{A_{\alpha _1}}\), we get \(a_{\alpha _0}^{-1}(aj)=o_{A_{\alpha _0}}\) and \(a_{\alpha _1}^{-1}(ai)=o_{A{\alpha _1}}\). We have \(a(a^{-1}(a_{\alpha _1})\wedge i)=a_{\alpha _1}\wedge ai=a_{\alpha _1}a_{\alpha _1}^{-1}(ai)=a_{\alpha _1}o_{A_{\alpha _1}}=o_X\), implying that \(a^{-1}(a_{\alpha _1})\wedge i=o_A\). Similarly, \(a^{-1}(a_{\alpha _0})\wedge j=o_A\). So \(a^{-1}(a_{\alpha _0}\wedge a_{\alpha _1})\wedge i=o_A\) and \(a^{-1}(a_{\alpha _0}\wedge a_{\alpha _1})\wedge j=o_A\), and thus, \(a^{-1}(a_{\alpha _0}\wedge a_{\alpha _1})=o_A\). Therefore, \(a\wedge (a_{\alpha _0}\wedge a_{\alpha _1})=o_X\), implying that \(a_{\alpha _0}\wedge a_{\alpha _1}=o_X\), which is a contradiction whether \(\alpha _0=\alpha _1\) or not. Therefore, either \(i=o_A\) or \(j=o_A\), as desired. \(\square \)
Remark 4.21
If the preorders \(\preceq \) and \(\le \) on \({\mathcal {M}}/X\) coincide, then Theorems 4.12 and 4.20 coincide.
The following proposition is needed in the next section.
Proposition 4.22
Let \({\mathcal {M}}\) be a strong domain in \({\mathcal {C}}\) and let \(\mathfrak {c}\) be a strongly continuous closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). For \(a:A\rightarrow X\) and \(b:B\rightarrow X\) in \({\mathcal {M}}/X\), such that \(a\sim b\), if A is \(\mathfrak {c}\)-connected, then so is B.
Proof
Let \(i,j\in {\mathcal {M}}/B\) be closed quasi-complements. Since \(a\preceq b\), by Lemma 4.18, \(a^{-1}(bi)\) and \(a^{-1}(bj)\) are \(\mathfrak {c}\)-closed and by Lemma 4.19, they are closed quasi-complements. Since A is \(\mathfrak {c}\)-connected, \(a^{-1}(bi)=o_A\) or \(a^{-1}(bj)=o_A\). If \(a^{-1}(bi)=o_A\), then by Lemma 1.2, \(a\wedge bi=o_X\). Since \(b\preceq a\), \(b\wedge bi=o_X\) and since \(bi\le b\), \(bi=o_X\). Thus, \(i=o_B\). Similarly, if \(a^{-1}(bj)=o_A\), then \(j=o_B\). \(\square \)
5 Product of Connected Objects is Connected
In this section, we prove that under certain conditions, the product of connected objects is connected.
Definition 5.1
Suppose \({\mathcal {C}}\) has a terminal object T and \({\mathcal {M}}\) is a weak domain in \({\mathcal {C}}\). For morphisms
 and
and
 in \({\mathcal {M}}\), an (s, t)-copy of X and Y is a prime join, in \({\mathcal {M}}/X\times Y\), of \(1_X\times s\) and \(t\times 1_Y\).
in \({\mathcal {M}}\), an (s, t)-copy of X and Y is a prime join, in \({\mathcal {M}}/X\times Y\), of \(1_X\times s\) and \(t\times 1_Y\).
Definition 5.2
Let \({\mathcal {C}}\) be a category with a strict initial object O. We say that a domain \({\mathcal {M}}\) in \({\mathcal {C}}\) has a common zero if for each object X, the unique map \(!_X:O\longrightarrow X\) belongs to \({\mathcal {M}}/X\).
Note that when \({\mathcal {M}}\) has a common zero, then for each object X, \(O_X=O\) and \(!_X=o_X:O\longrightarrow X\).
Proposition 5.3
Suppose \({\mathcal {C}}\) has a strict initial object O and a terminal object \(T\ne O\). Let \({\mathcal {M}}\) be a strong domain with a common zero in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a strongly continuous closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose also that there is a non-empty collection \(\{t_i:T\rightarrow X|i\in I\}\subseteq {\mathcal {M}}\), a morphism \(s:T\rightarrow Y\) in \({\mathcal {M}}\) and for each \(i\in I\), an \((s,t_i)\)-copy,
 , of X and Y. If
, of X and Y. If
 is a prime join of all the \(w_i\)’s and X and Y are \(\mathfrak {c}\)-connected, then so is W.
is a prime join of all the \(w_i\)’s and X and Y are \(\mathfrak {c}\)-connected, then so is W.
Proof
Since \(X\times T\cong X\), by Theorem 3.10, \(X\times T\) is \(\mathfrak {c}\)-connected. Similarly, \(T\times Y\) is \(\mathfrak {c}\)-connected. For each i, the pullback square:

shows that \((1_X\times s) \wedge (t_i\times 1_Y)\ne o_{X\times Y}\). Therefore, by Theorem 4.20, \(W_i\) is \(\mathfrak {c}\)-connected. Now, if \(w_i\wedge w_j=o_{X\times Y}\), then since \(w_j=(1_X\times s)\curlyvee ^{^p}(t_j\times 1_Y)\), we get \(w_i\wedge (1\times s)=o_{X\times Y}\). This in turn implies \((1\times s)\wedge (t_i\times 1)=o_{X\times Y}\), which is a contradiction. Hence, \(w_i\)s are mutually intersecting. By Theorem 4.20, W is \(\mathfrak {c}\)-connected. \(\square \)
Theorem 5.4
Suppose \({\mathcal {C}}\) has a strict initial object O, a terminal object \(T\ne O\), and for any object \(A\ne O\), there is a morphism  in \({\mathcal {C}}\). Let \({\mathcal {M}}\) be a strong domain with common zero in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a strongly continuous closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose also that the collection \({\mathcal {T}}=\{t_i:T\rightarrow X|i\in I\}\) of all morphisms from T to X is contained in \({\mathcal {M}}\), there exists a morphism \(s:T\rightarrow Y\) in \({\mathcal {M}}\), and that for each \(i\in I\), there exists an \((s,t_i)\)-copy of X and Y. If X and Y are \(\mathfrak {c}\)-connected, then so is \(X\times Y\).
in \({\mathcal {C}}\). Let \({\mathcal {M}}\) be a strong domain with common zero in \({\mathcal {C}}\) and \(\mathfrak {c}\) be a strongly continuous closure operator on \({\mathcal {C}}\) relative to \({\mathcal {M}}\). Suppose also that the collection \({\mathcal {T}}=\{t_i:T\rightarrow X|i\in I\}\) of all morphisms from T to X is contained in \({\mathcal {M}}\), there exists a morphism \(s:T\rightarrow Y\) in \({\mathcal {M}}\), and that for each \(i\in I\), there exists an \((s,t_i)\)-copy of X and Y. If X and Y are \(\mathfrak {c}\)-connected, then so is \(X\times Y\).
Proof
For each \(i\in I\), let
 be an \((s,t_i)\)-copy of X and Y. We show \(\curlyvee ^{^p}w_i=1_{X\times Y}\). Let
be an \((s,t_i)\)-copy of X and Y. We show \(\curlyvee ^{^p}w_i=1_{X\times Y}\). Let
 be in \({\mathcal {M}}/X\times Y\), such that for all \(i\in I\), \(a\wedge w_i=o_{X\times Y}\). So for all i, \(a\wedge (t_i\times 1_Y)=o_{X\times Y}\). If \(a\ne o_{X\times Y}\), then there is
be in \({\mathcal {M}}/X\times Y\), such that for all \(i\in I\), \(a\wedge w_i=o_{X\times Y}\). So for all i, \(a\wedge (t_i\times 1_Y)=o_{X\times Y}\). If \(a\ne o_{X\times Y}\), then there is
 in \({\mathcal {C}}\). Now, the composition
in \({\mathcal {C}}\). Now, the composition  is in \({\mathcal {T}}\) and so equals, say, \(t_j\). In the following diagram, all the squares are pullbacks:
is in \({\mathcal {T}}\) and so equals, say, \(t_j\). In the following diagram, all the squares are pullbacks:

This is a contradiction, because pullback of \(t_j\) along itself is \(1_T\). Therefore, \(a=o_{X\times Y}\). Thus, \(1_{X\times Y}\) is a prime join of \(w_i\)’s. By Proposition 5.3, \(X\times Y\) is \(\mathfrak {c}\)-connected. \(\square \)
Example 5.5
-
(1)
For \({\mathcal {C}}\) the category Top of topological spaces, it can be easily verified that the collection \({\mathcal {M}}\) of all the monos whose pullbacks along every morphism exists is a strong domain with common zero. By Examples 4.5 and 4.16, Theorem 5.4 generalizes the classical result.
-
(2)
For \({\mathcal {C}}\) a topos, [10], in which for any object \(A\ne O\), there is a morphism
 , by Theorem 5.4, product of connected objects is connected.
, by Theorem 5.4, product of connected objects is connected.
References
Adamek, J., Herrlich, H., Strecker, G.E.: Abstract and Concrete Categories. Wiley, New York (1990)
Castellini, G.: Connectedness with respect to a closure operator. Appl. Categ. Struct. 9, 285–302 (2001)
Castellini, G.: Categorical Closure Operators. Birkhäuser, Boston (2003)
Castellini, G., HajekClosure, D.: Operators and connectedness. Topol. Appl. 55, 29–45 (1994)
Castellini, G., Holgate, D.: A link between two connectedness notions. Appl. Categ. Struct. 11, 473–486 (2003)
Clementino, M.M.: On connectedness via closure operator. Appl. Categ. Struct 9, 539–556 (2001)
Clementino, M.M., Tholen, W.: Separation versus connectedness. Topol. Appl. 75, 143–181 (1997)
Dikranjan, D., Tholen, W.: Categorical Structure of Closure Operators. Kluwer Academic Publishers, Amsterdam (1995)
Enochs, E.E., Jenda, O.M.G.: Relative Homological Algebra. Walter de Gruyter, Berlin (2000)
Maclane, S., Moerdijk, I.: Sheaves in Geometry and Logic, A First Introduction to Topos Theory. Springer, Berlin (1992)
Mousavi, S.Sh, Hosseini, S.N.: Quasi right factorization structures as presheaves. Appl. Categ. Struct. 19, 741–756 (2011). https://doi.org/10.1007/s10485-010-9242-z
Preuss, G.: Relative connectedness and disconnectedness in topological categories. Quaest. Math. 2, 297–306 (1977)
Slapal, J.: Another approach to connectedness with respect to a closure operator. Appl. Categ. Struct. 17, 603–612 (2009)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Rahim Zaare-Nahandi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Shir Ali Nasab, A.R., Hosseini, S.N. Connectedness in a Category. Bull. Iran. Math. Soc. 46, 1195–1210 (2020). https://doi.org/10.1007/s41980-019-00320-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41980-019-00320-5



 in
in 
 and
and  with induced topology, where
with induced topology, where  , we have
, we have  is
is  is
is  in
in 
 , such that
, such that  be given in
be given in 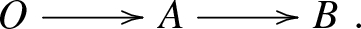
 in
in  , where for
, where for  is continuous, where
is continuous, where  and
and 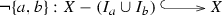 with induced topologies.
with induced topologies. , with the coinduced topology from all
, with the coinduced topology from all  , with any topology containing the induced topology.
, with any topology containing the induced topology. , with induced topology.
, with induced topology. is initial, where
is initial, where  and
and  with induced topologies.
with induced topologies. , with induced topology.
, with induced topology. , with submodule structure.
, with submodule structure. is a module homomorphism, where
is a module homomorphism, where  is essential.
is essential. with submodule structure, where for each
with submodule structure, where for each  , where
, where  , by Theorem
, by Theorem