1 Introduction

In the realm of engineering science, ensuring the reliability of devices is a pivotal concern. Device reliability denotes the probability that a system will function efficiently over a designated time frame and under specified operating conditions. Frequently lauded as a highly effective tool for analyzing lifetime data, reliability or survival functions play a crucial role in evaluating system performance. However, conventional data sources often fall short in providing accurate and precise information, leading to challenges in estimating probabilities with confidence. To surmount the obstacles posed by inaccurate and imprecise data, the innovative concept of fuzzy reliability has been introduced. The paradigm of fuzzy reliability stands out as a more robust and resilient concept compared to the classical reliability approach, dismantling the traditional reliance on precisely defined lifetime density parameters. In the real-world scenario, the lifetime of a system is inherently entwined with randomness and fuzziness, challenging the rigidity of conventional reliability paradigms. Zadeh (Zadeh 1968) introduced the fuzzy set theory. Since then, this theory has found applications across various mathematical and engineering disciplines, undergoing continuous refinement and adaptation by researchers and scientists. Lifetime random variables often come with precise parameters in their probability density distributions. However, the challenge arises when uncertainties and imprecisions in the data make it difficult to confidently determine these parameters. In such cases, a more practical approach involves treating the parameters as fuzzy quantities. A fuzzy set comprises elements or objects characterized by diverse levels of membership, each distinguished by a specific membership function. These degrees of membership typically fall within a range spanning from zero to one. Fuzzy sets play a pivotal role in addressing uncertainties and vagueness, proving to be indispensable mathematical tools in various domains beyond artificial intelligence, control theory, and decision analysis. They find extensive application in fields like pattern recognition, where ambiguity in data classification is prevalent. Additionally, fuzzy sets are instrumental in risk assessment and management, contributing significantly to the field of finance. In the realm of engineering, fuzzy logic controllers enhance system performance by accommodating imprecise inputs. Moreover, fuzzy sets have proven valuable in medical diagnosis, facilitating the interpretation of complex and ambiguous patient data. The adaptability of fuzzy sets makes them versatile tools in diverse disciplines, contributing to advancements in understanding and managing complex systems. Hashim (Hashim 2019) addressed the challenge of fuzzy reliability estimation within the context of the Lomax distribution. Neamah and Ali (Neamah and Ali 2020) delved into the intricacies of parameter estimation for fuzzy lifetime data, specifically focusing on the Frechet distribution. Pak et al. (Pak et al. 2014) explored the Bayesian approach to estimating the parameters of the Rayleigh distribution in the context of fuzzy lifetime data. Pak et al. (Pak et al. 2013a) drew inferences for the Weibull distribution based on fuzzy data. Further, Shafiq et al. (Shafiq et al. 2016) suggested the fuzzy estimators for the three-parameter lognormal distribution. The proposed estimators cover stochastic variation as well as fuzziness of the observations. Pak (Pak 2017) investigated the maximum likelihood estimation and Bayesian estimation for Lindley distribution when the available observations are reported in the form of fuzzy data. Huang and Zuo (Huang et al. 2006) proposed a new method to determine the membership function of the estimates of the parameters and the reliability function of multi-parameter lifetime distributions. Taha and Salman (Taha and Salman 2022) compared different estimation method for reliability function of Rayleigh distribution based on fuzzy lifetime data. Alharbi and Kamel (Alharbi and Kamel 2022) proposed the Fuzzy Bayesian estimation to get the best estimate of the unknown parameters of a two-parameter Kumaraswamy distribution from a frequentist point of view. Ali and Hasan (Ali and Hasan 2023) gave estimate of the parameters of the Topp leone-Kumaraswamy distribution using the informational standard Bayes estimation methods in light of different loss functions which are often random and fuzzy mixture in it and expressed in fuzzy numbers and leads to estimate the fuzzy reliability function within certain ranges of belonging to the fuzzy group. Sruthi and Kumar (Sruthi and Kumar 2021) considered the estimation of system reliability of a repairable system comprising of three identical and independent components with repair rate as well as failure rate of component, as fuzzy number. Shareef and Hussain (Shareef and Hussain 2023) used a beta membership function to study the classical method of obtaining estimation of the fuzzy reliability function of the new mixed distribution (Weibull-Raleigh-Exponential). Al-Noor and Al-Sultany (A-l Noor and A-l Sultany 2017) approximated non-Bayesian computational methods to estimate inverse Weibull parameters and reliability function with fuzzy data. The uncertainty is modeled using triangular fuzzy number. Sabry et al. (Sabry et al. 2021) derived inference of the reliability parameter of fuzzy stress strength \({R}_{F}=P(Y<X)\) is attached to the difference between stress and strength values when \(X\) and \(Y\) are independently distributed from inverse Rayleigh random variables. Nevertheless, fuzzy sets employ a sole attribute parameter, the membership degree, to signify both support and opposition, lacking the ability to depict a neutral state—neither supporting nor opposing. To overcome this limitation, Atanassov (Atanassov 1986) proposed the concept of intuitionistic fuzzy sets, serving as an extension to Zadeh's fuzzy set. In contrast to conventional fuzzy sets, intuitionistic fuzzy sets introduce an additional non-membership parameter, providing a more nuanced characterization of the inherent ambiguity within the objectively defined world. Zahra et al. (Roohanizadeh et al. 2022a) studied parameter and reliability estimation for the Pareto distribution, utilizing a generalized intuitionistic fuzzy number as the set parameter. Ebrahimnejad and Jamkhaneh (Ebrahimnejad and Jamkhaneh 2018) investigated the challenge of estimating reliability for the Rayleigh distribution, approaching the problem by treating the parameter as a generalized intuitionistic fuzzy number. Hu and Ren (Hu and Ren 2023) considered the reliability estimation of the Inverse Weibull distribution based on intuitionistic fuzzy lifetime data. Moreover, Roohanizadeh et al. (Roohanizadeh et al. 2022b) focused on different estimation approaches of two-parameter Weibull (TW) distribution based on the intuitionistic fuzzy lifetime data including, maximum likelihood and Bayesian estimation methodology. Kumar (Kumar 2021) determined the fuzzy reliability of different systems in which the lifetime of components is following fuzzy exponential distribution where fuzzy reliability function and its α-cut set are presented. In real-life situations, things can be uncertain due to randomness, fuzziness, or roughness. Sometimes, these uncertainties overlap, creating complex issues that can’t be solved with just one approach. Fuzzy stochastic theory is a solution, blending fuzzy set and probability theories to understand phenomena where randomness and fuzziness interact. Imagine it like a puzzle where pieces of randomness and fuzziness come together. Researchers use concepts like fuzzy random variables to make sense of it. For example, Huibert (Huibert 1978) suggested this idea.

This paper introduces a valuable Bayesian method for estimating parameters and reliability in the context of the one-parameter Weighted Exponential-Lindley distribution (WXLD) using intuitionistic fuzzy lifetime data. For this, Bayesian estimates of parameters and reliability are obtained under the SELF and LINEX loss functions utilizing the Lindley and T-K approximation. The rest of this paper is organized as follows: After this introduction, Sect. 1, provide an overview of the current state of reliability estimation for the WXLD lifetime model. Additionally, we explore the background and importance of fuzzy sets and intuitionistic fuzzy sets in this research. Moving on to the Sect. 2, we delve into the concepts of fuzzy sets and intuitionistic fuzzy sets, extending key ideas from probability theory to fuzzy set theory. In Sect. 3, we delve into the exploration of Bayes estimators under the framework of SELF, employing Lindley and T-K approximations, alongside the utilization of Monte Carlo simulation for estimation. Section 4 presents a numerical study elucidating the efficacy and performance of these methodologies. The practicality of the proposed method is validated with a real dataset in the Sect. 5. Lastly, the Sect. 6 draws conclusions, addresses limitations, and outlines potential directions for future research.

2 Preliminary knowledge and likelihood function

In this study, we proposed a distribution, called Weighted Exponential-Lindley distribution (WXLD) [Sharma and Kumar (Sharma and Kumar 2023)] which is a mixture of gamma (2, 1/θ) and one-parameter Exponential-Lindley distribution (XLD) [Chouia and Zeghdoudi (Chouia and Zeghdoudi 2021)] and it is described as follows:

Let a random variable \(X\sim \text{WXLD}(\theta )\) then the probability density function (pdf), Cumulative distribution function (cdf) and reliability functions are defined respectively as

$$f\left(x,\theta \right)=\frac{4{\theta }^{3}x(2+\theta +x){e}^{-2\theta x}}{(1+\theta {)}^{2}}, x\ge 0, \theta \ge 0$$
(1)
$$F(x,\theta )=1-{e}^{2\theta x}\left(\frac{2{\theta }^{2}{x}^{2}}{(1+\theta {)}^{2}}+2\theta x+1\right); x\ge 0, \theta \ge 0$$
(2)
$$and R\left(x\right)={e}^{-2\theta x}\left(\frac{2{\theta }^{2}{x}^{2}}{({1+\theta )}^{2}}+2\theta x+1\right)$$
(3)

The fuzzy set removes the uncertainty and vagueness which the classical set is failed to address. To do this, the fuzzy set added steady assessment in the grades of memberships of an element of a set through membership function. Mathematically it can be defined as:

Definition 1.

(Zadeh (Zadeh 1968)). Let X be a non-empty set. A fuzzy set A in X is characterized by its membership function \({\mu }_{A}:X\to \left[0, 1\right] and {\mu }_{A}\left(x\right) \text{degree of}\) membership of element x in fuzzy set A for each x \(\in X\) and A is completely determined by the set of tuples \(A=\left\{\left(x,{\mu }_{A}\left(x\right)\right)\right|x\in X\}\). Also, degree of non-membership of element \(x\in X\) in a fuzzy set \(A\) is denoted by \({v}_{A}(x)\) and is equal to \(1-{\mu }_{A}(x)\). From here it is clear that \(0<{\mu }_{A}\left(x\right)+{\nu }_{A}(x)\le 1\).

Atanassov (Atanassov 1986) introduced the concept of Intuitionistic Fuzzy Sets (IFS), which incorporates two essential parameters: membership degrees and non-membership degrees. This formulation enables a more comprehensive representation of the inherent characteristics of entities, providing a nuanced description of their attributes.

Definition 2.

Let X be a non-empty universal set. An IFS \(\widetilde{x}\) on universe of discourse X is given by \(\widetilde{x}\) = \(\left\{<x, {\mu }_{\widetilde{A}}\left(x\right), {\nu }_{\widetilde{A}}\left(x\right)>:x\in X\right\}\) with \({\mu }_{\widetilde{x}}\left(x\right):X\to \left[0, 1\right]\) and \({\nu }_{\widetilde{x}}\left(x\right):X\to \left[0, 1\right].\) \({\mu }_{\widetilde{x}}\left(x\right)\) and \({\nu }_{\widetilde{x}}\left(x\right)\) define the membership and degree of non-membership of the element \(x\in X\) to the set \(\widetilde{A}\), for every \(x\in X, 0\le {\mu }_{\widetilde{x}}\left(x\right)+{\nu }_{\widetilde{x}}\left(x\right)\le 1\) respectively and the degree of hesitation is \({\pi }_{\widetilde{x}}\left(x\right)=1-\left({\mu }_{\widetilde{x}}\left(x\right)+{\nu }_{\widetilde{x}}\left(x\right)\right).\)

Triangular Intuitionistic Fuzzy Numbers (TriIFNs) and Trapezoidal Intuitionistic Fuzzy Numbers (TraIFNs) stand out as unique categories within the realm of intuitionistic fuzzy numbers. These classes essentially broaden the scope of intuitionistic fuzzy numbers. The membership and non-membership functions for TriIFN having fuzzy number \(\widetilde{x}=(\alpha ,\beta ,\gamma )\) is

$${\mu }_{\widetilde{x}}\left(x\right)= \left\{\begin{array}{cc}\frac{x-\alpha }{\beta -\alpha }& \alpha \le x\le \beta \\ \frac{\gamma -x}{\gamma -\beta }& \beta \le x\le \gamma \\ 0& otherwise\end{array}\right.$$

and the Trapezoidal fuzzy number can be defined as \(\widetilde{x}=\left(\alpha ,\beta ,\gamma ,\eta \right)\) with the membership function

$${\mu }_{\widetilde{x}}\left(x\right)=\left\{\begin{array}{cc}\frac{x-\alpha }{\beta -\alpha }& \alpha \le x\le \beta \\ 1& \beta \le x\le \gamma \\ \frac{\eta -x}{\eta -\gamma }& \gamma \le x\le \eta \\ 0& otherwise\end{array}\right.$$

2.1 Intuitionistic fuzzy probability

In the subsequent section, we introduce novel conceptualizations of probability tailored to Intuitionistic Fuzzy Sets (IFSs). These innovative notions will serve as foundational elements in the discourse on estimation, specifically in the context of intuitionistic fuzzy observations.

Definition 3.

Given a probability space \(({\mathbb{R}}^{{\varvec{n}}},\boldsymbol{ }\boldsymbol{\wp }, \mathcal{P})\), the probability of an intuitionistic fuzzy observation \(\widetilde{x}\) within the realm of \({\mathbb{R}}^{{\varvec{n}}}\) is determined as follows:

$$\mathcal{P}\left(\widetilde{x}\right)={\int }_{{\mathbb{R}}^{{\varvec{n}}}}\frac{1-{\nu }_{\widetilde{x}}\left(x\right)+{\mu }_{\widetilde{x}}\left(x\right)}{2}d\mathcal{P}$$
(4)

Let X be a continuous random variable specified by \(\theta\) and having a pdf \(f(x,\theta )\). In the following, we define intuitionistic fuzzy conditional density, which is the conditional density of X given the intuitionistic fuzzy observation \(\tilde{x}\), as follows

$$f\left(x|\widetilde{x}\right)=\frac{u\left(x\right)f(x,\theta )}{{\int }_{\mathbb{R}}u\left(x\right)f\left(x,\theta \right)dx}, \forall x\in {\mathbb{R}}$$

Where,

$$u\left(x\right)=\frac{{1-\nu }_{\widetilde{x}}\left(x\right)+{\mu }_{\widetilde{x}}\left(x\right)}{2}$$

Subsequently, the likelihood function of \(\theta\) given IFS \(\widetilde{x}\) is defined as follows

$$L\left(\theta |\widetilde{x}\right)=\prod_{i=1}^{n}\mathcal{P}({\widetilde{x}}_{i}|\theta )=\prod_{i=1}^{n}{\int }_{\mathbb{R}}{u}_{i}\left(x\right)f\left(x|\theta \right)dx=\frac{{\left(4{\theta }^{3}\right)}^{n}}{{(1+\theta )}^{2n}}\prod_{i=1}^{n}\int x(2+\theta +x){e}^{-2\theta x}{u}_{i}\left(x\right)dx$$
(5)

Where, \(u_{i} \left( x \right) = \frac{{1 - \nu_{{\tilde{x}_{i} }} \left( x \right) + \mu_{{\tilde{x}_{i} }} \left( x \right)}}{2}\)

Corollary 1.

Introducing intuitionistic fuzzy conditional expectation involves utilizing intuitionistic fuzzy conditional density and an intuitionistic fuzzy observation \(\widetilde{x}=({\widetilde{x}}_{1}, {\widetilde{x}}_{2},\dots ,{\widetilde{x}}_{n})\). Given a random variable X, the intuitionistic fuzzy conditional expectation is expressed as follows:

$$E\left(X|\widetilde{x}\right)={\int }_{\mathbb{R}}xf\left(x|\theta \right)dx={\int }_{\mathbb{R}}x\frac{u\left(x\right)f(x,\theta )}{{\int }_{\mathbb{R}}u\left(x\right)f\left(x,\theta \right)dx}dx$$
(6)

Where, \(u\left( x \right) = \frac{{1 - \nu_{{\tilde{x}}} \left( x \right) + \mu_{{\tilde{x}}} \left( x \right)}}{2}\)

3 Bayesian estimation

In Bayesian statistical inference, the prior distribution is pivotal, embodying our existing knowledge or beliefs regarding the parameters. Its selection significantly influences the accuracy of estimating the posterior distribution. Opting for a suitable prior distribution is critical as it directly impacts the ultimate inference outcomes.

The gamma distribution stands out as a versatile continuous probability distribution, boasting numerous desirable attributes. This versatility renders it a frequent preference for parameter priors in Bayesian statistics. With the gamma distribution, we have the flexibility to adjust its parameters to align with various prior beliefs. Furthermore, its notable property of conjugacy streamlines posterior distribution computations. When employed as a prior distribution, the gamma distribution maintains its form when multiplied with the likelihood function, thus simplifying posterior distribution calculations. The pdf of the gamma distribution is:

$$\pi \left(\omega \right)=\frac{{\beta }^{\alpha }}{\Gamma (\alpha )}{\omega }^{\alpha -1}{e}^{-\beta \omega }, \omega >0, \alpha , \beta >0$$

In this section, we assume that the parameter \(\theta\) follows Gamma (a, b). i.e.,

$$\pi \left(\theta \right)=\frac{{b}^{a}}{\Gamma (a)}{\theta }^{a-1}{e}^{-b\theta }, \theta >0, a, b>0$$
(7)

In the Bayesian framework, the posterior distribution of \(\theta\) can be expressed as follows:

\({\pi }_{post}\left(\theta |\widetilde{x}\right)\propto L(\theta |\widetilde{x})\)×\(\pi (\theta )\)

$$\propto \frac{{b}^{a}}{\Gamma (a)}{\theta }^{a-1}{e}^{-b\theta }\times \prod_{i=1}^{n}{\int }_{0}^{\infty }{u}_{i}\left(x\right)f(x|\theta )dx$$
(8)

According to the Eq. (6), the Bayes estimator of the function \(g(\theta )\) of \(\theta\) under SELF is:

$${\theta }_{S}^{B}=E\left(g\left(\theta \right)|\widetilde{x}\right]=\frac{{\int }_{0}^{\infty }g(\theta ){\pi }_{post}\left(\theta |\widetilde{x}\right)d\theta }{{\int }_{0}^{\infty }{\pi }_{post}\left(\theta |\widetilde{x}\right)d\theta }$$
$$=\frac{{\int }_{0}^{\infty }g(\theta )L(\theta |\widetilde{x})\times \pi (\theta )d\theta }{{\int }_{0}^{\infty }L(\theta |\widetilde{x})\times \pi (\theta )d\theta }$$
$$=\frac{{\int }_{0}^{\infty }g(\theta ){e}^{W(\theta )}d\theta }{{\int }_{0}^{\infty }{e}^{W(\theta )}d\theta }$$
(9)

where, \(W\left(\theta \right)=\text{ln}\pi \left(\theta \right)+\text{ln}L\left(\theta |\widetilde{x}\right)\equiv \rho \left(\theta \right)+{L}^{*}(\theta )\) and \(E\left(g\left(\theta \right)|\widetilde{x}\right]\) indicates the posterior expectation. Equation (9) eludes analytical derivation, prompting us to employ two approximations: Lindley’s and T-K approximation, alongside a Markov Chain Monte Carlo (MCMC) method for its estimation.

3.1 Lindley approximation

Lindley's approach, initially introduced by Lindley (Lindley 1980), offers a method to approximate the ratio of two integrals, as presented in Eq. (9). In the context of a single-parameter scenario, Lindley's approximation for Eq. (9) takes the following form

$$g\left(\theta \right)+\frac{1}{2}{g}_{11}{\sigma }_{11}+{\rho }_{1}(\theta ){g}_{1}{\sigma }_{11}+\frac{1}{2}{L}_{3}^{*}{\sigma }_{11}^{2}{g}_{1}$$
(10)

where \(\rho (\theta )\) is the logarithm of prior distribution.

$$g_{1} = (dg(\theta ))/d\theta ,g_{1} 1 = (d^{2} g(\theta ))/(d\theta^{2} ),\rho_{1} = (d\rho (\theta ))/d\theta ,L_{3}^{*} = (\partial^{3} L^{*} (\theta ))/(\partial \theta^{3} ),\sigma_{1} 1 = [ - (?^{2} L^{*} (\theta ))/(\theta^{2} )]^{( - 1)}$$

We see that,\({\rho }_{1}=\frac{(a-1)}{\theta }-b\)

By evaluating all the expressions in Eq. (10) at the maximum likelihood estimate (MLE) of \(\theta\), we derive the approximation \({g}_{B}^{*}\) for Eq. (9). In our study, we have

$${L}^{*}\left(\theta \right)=3nlog\theta -2nlog\left(1+\theta \right)+\sum_{i=1}^{n}\text{log}\int 4x(2+\theta +x){e}^{-2\theta x}{u}_{i}\left(x\right)dx$$
(11)

Setting the partial derivative of the log-likelihood eq. (11) with respect to \(\theta\) equal to zero yields

$$\frac{\partial {L}^{*}\left(\theta \right)}{\partial \theta }=\frac{3n}{\theta }-\frac{2n}{\left(1+\theta \right)}-\sum_{i=1}^{n}\frac{\int \left\{2x\left(2+\theta +x\right){e}^{-2\theta x}+{e}^{-2\theta x}\right\}{xu}_{i}\left(x\right)dx}{\int x\left(2+\theta +x\right){e}^{-2\theta x}{u}_{i}\left(x\right)dx}=0$$
(12)

Due to the absence of a closed-form solution for likelihood Eq. (12), an iterative numerical approach becomes necessary to obtain the MLE. Specifically, the Newton–Raphson method is employed for determining the MLE of the parameter \(\theta\). The Newton–Raphson algorithm presents a direct method for estimating the parameters within a likelihood function, achieved through iterative procedures. If we denote the parameter value from the \({h}^{th}\) step as \({\widehat{\theta }}^{(h)}\), then at the \(\left(h+1\right)\) step of the iteration process, the updated parameter is obtained as follows:

$${\widehat{\theta }}^{(h+1)}={\widehat{\theta }}^{(h)}-\frac{\frac{\partial }{\partial \theta }{L}^{*}\left(\theta \right)|h}{\frac{{\partial }^{2}}{\partial {\theta }^{2}}{L}^{*}\left(\theta \right)|h}$$
(13)

where the notation \(A|h\), representing any partial derivative \(A\), signifies that the partial derivative is evaluated at \({\widehat{\theta }}^{(h)}\). To proceed with the Newton–Raphson method, we obtain the second-order derivative of the log-likelihood with respect to the parameter using the following procedure

$$\frac{{\partial }^{2}}{\partial {\theta }^{2}}{L}^{*}\left(\theta \right)=\frac{-3n}{{\theta }^{2}}+\frac{2n}{{(1+\theta )}^{2}}+\sum_{i=1}^{n}\left\{\frac{\int \left\{2x\left(2+\theta +x\right){e}^{-2\theta x}+{e}^{-2\theta x}\right\}{x}^{2}{u}_{i}\left(x\right)dx}{\int x\left(2+\theta +x\right){e}^{-2\theta x}{u}_{i}\left(x\right)dx}-{\left[\frac{\int 2{x}^{2}(2+\theta +x){e}^{-2\theta x}{u}_{i}\left(x\right)dx}{\int x\left(2+\theta +x\right){e}^{-2\theta x}{u}_{i}\left(x\right)dx}\right]}^{2}\right\}$$

The iteration process persists until convergence, defined as \(\left|{\widehat{\theta }}^{\left(h+1\right)}-{\widehat{\theta }}^{\left(h\right)}\right|<\epsilon\), where \(\epsilon\) is a predetermined threshold. The resulting estimate of \(\theta\) obtained via the Newton–Raphson algorithm is subsequently denoted as \(\widehat{\theta }\), representing the MLE.

Now, to apply Lindley’s form in Eq. (10), we obtain.

\({\sigma }_{11}=\frac{-3n}{{\widehat{\theta }}^{2}}+\frac{2n}{{(1+\widehat{\theta })}^{2}}+\sum_{i=1}^{n}\left\{\frac{\int \left\{2x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}+{e}^{-2\widehat{\theta }x}\right\}{x}^{2}{u}_{i}\left(x\right)dx}{\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}-{\left[\frac{\int 2{x}^{2}(2+\widehat{\theta }+x){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}{\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}\right]}^{2}\right\}\) and

$${L}_{3}^{*}\left(\theta \right)=\frac{6n}{{\widehat{\theta }}^{3}}-\frac{4n}{{\left(1+\widehat{\theta }\right)}^{3}}-\sum_{i=1}^{n}\left\{\frac{\int \left\{2x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}+{e}^{-2\widehat{\theta }x}\right\}{x}^{5}{u}_{i}\left(x\right)dx}{\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}+\frac{\left(\int {2x}^{2}{(2+\theta +x)e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx\right)\left(\int 2{x}^{3}{(2+\theta +x)e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx\right)}{{\left(\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx\right)}^{2}}\right\}+2\sum_{i=1}^{n}\left\{ \frac{\left(\int {x}^{2}{e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx\right)}{\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}\times \left(\frac{\int {x}^{3}{e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}{\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}-{\left[\frac{\int {x}^{2}{e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}{\int x\left(2+\widehat{\theta }+x\right){e}^{-2\widehat{\theta }x}{u}_{i}\left(x\right)dx}\right]}^{2}\right)\right\}$$

The approximate Bayes estimate of \(\theta\), denoted as \({\theta }_{BL}^{*}\), for the squared error loss function, is determined as the posterior mean of \(g\left(\theta \right)=\theta\), as specified by Eq. (10) in the following manner

$${\theta }_{BL}^{*}=\widehat{\theta }+{\rho }_{1}{\sigma }_{11}+\frac{1}{2}{L}_{3}^{*}{\sigma }_{11}^{2}$$
(14)

where, \({\rho }_{1}=\frac{a-1}{\widehat{\theta }}-b.\) Likewise, to compute the posterior mean of \(R(x)\), we define\(g\left(\theta \right)={e}^{-2\theta x}\left(\frac{2{\theta }^{2}{x}^{2}}{({1+\theta )}^{2}}+2\theta x+1\right)\) and

$${R}_{BL}^{*}\left(x\right)={e}^{-2\widehat{\theta }x}\left(\frac{2{\widehat{\theta }}^{2}{x}^{2}}{({1+\widehat{\theta })}^{2}}+2\widehat{\theta }x+1\right)\left\{1+\frac{1}{2}{x}^{4}{\sigma }_{11}-{x}^{2}\left[{\rho }_{1}{\sigma }_{11}+\frac{1}{2}{L}_{3}^{*}{\sigma }_{11}^{2}\right]\right\}$$
(15)

3.2 Tierney and Kadane’s approximation

Setting \(Q\left(\theta \right)=W(\theta )/n\) and \({Q}^{*}\left(\theta \right)=\left[\text{ln}g\left(\theta \right)+W(\theta )\right]/n\), the expression in Eq. (9) can be re-expressed as

$$E\left(g\left(\theta \right)|\widetilde{x}\right)=\frac{\underset{0}{\overset{\infty }{\int }}{e}^{n{Q}^{*}(\theta )}d\theta }{{\int }_{0}^{\infty }{e}^{nQ\left(\theta \right)}d\theta }$$
(16)

Following Tierney and Kadane (Tierney and Kadane 1986), we can approximate Eq. (16) as:

$${g}_{BT}^{*}(\theta )={\left(\frac{{\chi }^{*}}{\chi }\right)}^\frac{1}{2}\text{exp}\left\{n\left[{Q}^{*}\left({\overline{\theta }}^{*}\right)-Q(\overline{\theta }\right]\right\}$$
(17)

where \({\overline{\theta }}^{*}\) and \(\overline{\theta }\) maximize \({Q}^{*}(\theta )\) and \(Q(\theta )\), respectively and \({\chi }^{*}\) and \(\chi\) are the minus the inverse of the second derivatives of \({Q}^{*}(\theta )\) and \(Q(\theta )\) at \({\overline{\theta }}^{*}\) and \(\overline{\theta }\), respectively.

In this case, we have

$$W\left(\theta \right)=\frac{1}{n}\left\{m+\left(n+a-1\right)\text{log}\theta -\theta b+\sum_{i=1}^{n}log\frac{4{\theta }^{3}x(2+\theta +x){e}^{-2\theta x}}{(1+\theta {)}^{2}}{u}_{i}\left(x\right)dx\right\}$$

where \(m\) is a constant; therefore, \(\overline{\theta }\) can be obtained by solving the following equation:

$$\frac{\partial W(\theta )}{\partial \theta }=\frac{1}{n}\left\{\frac{n+a-1}{\theta }-b-\sum_{i=1}^{n}\frac{\int {x}^{2}{e}^{-2\theta x}{u}_{i}\left(x\right)dx}{\int x\left(2+\theta +x\right){e}^{-2\theta x}{u}_{i}\left(x\right)dx}\right\}=0$$

and from the second derivative of \(W(\theta )\), we have

$$\chi =-{\left[ \frac{{\partial }^{2}W(\theta )}{\partial {\theta }^{2}} |\theta =\overline{\theta }\right]}^{-1}$$

where

$$\frac{{\partial }^{2}W(\theta )}{\partial {\theta }^{2}}|\theta =\overline{\theta }=\frac{1}{n}\left\{-\frac{n+a-1}{{\overline{\theta }}^{2}}+\sum_{i=1}^{n}\left(\frac{\int {x}^{3}{e}^{-2\theta x}{u}_{i}\left(x\right)dx}{\int x\left(2+\theta +x\right){e}^{-2\theta x}{u}_{i}\left(x\right)dx}-{\left[\frac{\int {x}^{2}{e}^{-2\theta x}{u}_{i}\left(x\right)dx}{x\left(2+\theta +x\right){e}^{-2\theta x}{u}_{i}\left(x\right)dx}\right]}^{2}\right)\right\}$$

The expressions for \({W}^{*}\left(\theta \right), {\theta }_{BT}^{*}\) and \({R}_{BT}^{*}\) in Eq. (17) can be straightforwardly derived by applying the same rationale with \(g\left(\theta \right)=\theta\) and \(g\left(\theta \right)={e}^{-2\theta x}\) respectively.

3.3 MCMC method

In this section, we explore the utilization of MCMC methodologies, notably the Metropolis–Hastings (M-H) algorithm, to generate samples from the posterior density function. Subsequently, leveraging these samples, we compute the Bayes estimates. Based on the gamma prior \(\theta \sim Gamma \left(a, b\right)\) and the likelihood function, the posterior pdf of \(\theta\) can be written as

$${\pi }_{post}\left(\theta |\widetilde{x}\right)\propto \frac{{\theta }^{3n+a-1}}{{(1+2\theta )}^{2n}}{e}^{-b\theta }\prod_{i=1}^{n}x(2+\theta +x){e}^{-2\theta x}{u}_{i}\left(x\right)dx$$
(18)

Observing that the density function \({\pi }_{post}\left(\theta |\widetilde{x}\right)\) is unknown, our empirical findings suggest its resemblance to a normal distribution. Therefore, to produce random samples from \({\pi }_{post}\left(\theta |\widetilde{x}\right)\), we adopt the M-H algorithm, employing a normal proposal distribution as follows.

Step 1: Start with an initial guess value \({\theta }^{(0)}.\)

Step 2: Set \(l=1\).

Step 3: Generate \({\theta }^{(l)}\) from \({\pi }_{post}\left(\theta |\widetilde{x}\right)\) using M-H algorithm with the proposal distribution \(h(\theta )\equiv I\left(\theta >0\right)N(\widehat{\theta }, 1)\), where \(I(.)\) is the indicator function, as follows:

(a) Let \(u={\theta }^{(l-1)}\). Here we set \({\theta }^{(0)}\equiv \widehat{\theta }\).

(b) Generate \(v\) from the proposal distribution \(h\).

(c) Let \(s\left(u,v\right)=\text{min}\left\{1, \frac{{\pi }_{post}\left(v|\widetilde{x}\right)h(u)}{{\pi }_{post}\left(u|\widetilde{x}\right)h(v)}\right\}\).

(d) Accept \(v\) with probability \(p(u,v)\) or accept \(u\) with probability \(1-p(u,v)\).

Step 4: Compute \({R}^{\left(l\right)}\left(t\right)={e}^{-2{\theta }^{(l)}x}\left(\frac{2{{\theta }^{(l)}}^{2}{x}^{2}}{({1+{\theta }^{(l)})}^{2}}+2{\theta }^{(l)}x+1\right)\).

Step 5: Set \(l=l+1.\)

Step 6: Repeat steps 3–5, \(k\) times and obtain \({\theta }^{(l)}\) and \({R}^{\left(l\right)}\left(t\right)\) for \(l=1, 2,\dots .,k\).

Now, the Bayes estimates of the parameter \(\theta\) and reliability function \(R(t)\) with respect to SELF become

$${\theta }_{BM}^{*}={E}^{*}\left(\theta |\widetilde{x}\right)=\frac{1}{k}\sum_{l=1}^{k}{\theta }^{(l)}$$

and.

\({R}_{BM}^{*}\left(x\right)={E}^{*}\left(R(x)|\widetilde{x}\right)=\frac{1}{k}\sum_{l=1}^{k}{R}^{\left(l\right)}\left(x\right)\) respectively.

4 Numerical study

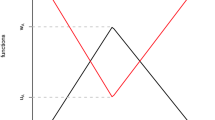
In this section, we showcase experimental findings aimed at examining the behaviors of various methods across different sample sizes. Initially, with a fixed \(\theta =1\) and varying values of \(n,\) we generated independent and identically distributed (i.i.d) random samples from WXLD. Subsequently, each instance of \(x\) underwent fuzzification using the fuzzy information system (f.i.s.) depicted in Fig. 1. Following that, we computed the Bayes estimates of the parameter \(\theta\) and the reliability function \(R\left(t\right)\) at \(t=1,\) for the fuzzy sample. We utilized Lindley’s approximation, T-K approximation and the MCMC technique for this computation. To ensure fair comparison, we adopted non-informative priors for \(\theta\), setting both shape and scale parameters to \(a=b=0\) in the Gamma distribution. Press (Press 2001) recommended employing very small non-negative values for the hyperparameters to maintain proper priors in such cases. We experimented with \(a=b=0.0002\) as suggested. The average values and mean squared errors (MSE) of the estimates over 10,000 replications are presented in Tables 1 and 2. The experimental findings indicated distinct outcomes when utilizing Lindley’s approximation versus the MCMC technique for computing Bayes estimates. Lindley’s approximation exhibited slower computational performance compared to the MCMC technique. Furthermore, irrespective of the method used, an increase in sample size corresponded to a reduction in the MSEs of the estimates. Regarding minimum MSEs, the T-K estimates typically outperformed both the Lindley and MCMC estimates for the parameter \(\theta\) and the reliability function \(R(t)\).

Fig. 1
figure 1

Fuzzy information system used to encode the simulated data

Full size image
Table 1 Average values (AV) and mean squared errors (MSE) of the Bayes estimates of \(\theta\) for various sample sizes \((n)\)
Full size table
Table 2 Average values (AV) and mean squared errors (MSE) of the Bayes estimates of reliability function \(R(t)\) for various sample sizes \((n)\)
Full size table

5 Real life application

To exemplify the practical application of the proposed methods, we will analyze real data obtained from an experiment conducted by Pak et al. (Pak et al. 2013b). In an experimental setup, a group of 25 ball bearings undergoes a life test. The performance of each ball bearing is tracked until it reaches a point of failure, with the failure times recorded as fuzzy numbers denoted by \({\widetilde{x}}_{i}=({\alpha }_{i}, {x}_{i}, {\beta }_{i})\). Here, \({\alpha }_{i}=0.05{x}_{i}, {\beta }_{i}=0.03{x}_{i}\) and the values of \({x}_{i}, i=1,\dots ,25\), are presented in Table 3. These fuzzy numbers represent the uncertainty surrounding each failure time, considering the potential variation in performance. The membership functions corresponding to these fuzzy numbers are defined as follows:

Table 3 Failures of 25 ball bearings data
Full size table
$${\mu }_{{\widetilde{x}}_{i}}\left(x\right)=\left\{\begin{array}{cc}\frac{x-({x}_{i}-{\alpha }_{i})}{{\alpha }_{i}}& {x}_{i}-{\alpha }_{i}\le x\le {x}_{i}\\ \frac{{x}_{i}+{\beta }_{i}-x}{{\beta }_{i}}& {x}_{i}\le x\le {x}_{i}+{\beta }_{i}\end{array}\right. i=1,...,25.$$

For these fuzzy data, the maximum likelihood estimate (MLE) of \(\theta\) is found to be approximately \(\widehat{\theta }=0.0912.\) Using the \(Gamma(2, 2)\) prior and employing Lindley’s approximation, the Bayes estimate of \(\theta\) \({\theta }_{B }^{*}\) is approximately 1.1237 with the reliability function \(R(t)\) evaluated at \(t=1\) yielding an estimate \({R}_{B}^{*}=0.9875.\) Also, Utilizing Tierney and Kadane’s approach, the Bayes estimates yield \({\theta }_{BT}^{*}=1.0256\) and \({R}_{BT}^{*}=0.9852\). We apply the M-H algorithm, using a proposal distribution of \(N(\widehat{\theta },1)\) to compute the Bayes estimates of \(\theta\) and the reliability function \(R(t)\). This yields \({\theta }_{BM}^{*}=1.1127\) and \({R}_{BM}^{*}=0.9824\), respectively.

6 Conclusions

In traditional reliability analysis using the Weighted Exponential-Lindley distribution, the assumption typically revolves around the availability of precise lifetime data, where observed lifetimes are considered exact real numbers. However, real-world scenarios often introduce complexities where experimental results may not be precisely recorded or measured. Instead, each observable event might only be associated with a fuzzy subset within the sample space. In our paper, we delve into the Bayesian estimation approach for both parameter estimation and reliability function determination of the WXLD, specifically tailored for cases where lifetime observations are represented by fuzzy numbers. This study introduced two approximation techniques: Lindley’s and Tierney and Kadane’s, in addition to employing a MCMC method.

for computing Bayes estimates. Following this, we conducted an extensive simulation study to assess the performance of these methodologies thoroughly. Our findings unequivocally indicate that the Tierney and Kadane procedure outperforms others, yielding the most precise parameter estimates, as evidenced by the Mean Squared Errors (MSEs) presented in Tables 1 and 2. Hence, it appears justifiable to advocate for the adoption of Tierney and Kadane's approximation method for estimating the unknown parameter \(\theta\) and reliability function \(R(t)\) derived from WXLD.

While this study offers valuable insights into Bayesian estimation approaches for the WXLD when dealing with fuzzy lifetime data, several limitations and avenues for future research exist. Firstly, the sensitivity of results to prior selection remains a concern, warranting further exploration into the impact of different prior specifications on estimation outcomes. Additionally, the assumption of consistency in the fuzziness of observed data across events may not always hold in practical scenarios, potentially introducing biases. Furthermore, while the proposed methodologies were validated using simulated datasets, validation with real-world data from diverse sources could enhance the robustness of the findings. Looking ahead, future research could focus on extending the Bayesian framework to accommodate multivariate settings and incorporate covariates to improve predictive accuracy. Robustness analyses, exploring the performance of estimation techniques under various model assumptions and the development of user-friendly software tools could further advance the applicability of these methods in reliability analysis across different industries.