1 Introduction

The basic reliability concept employing on a single-state or dual/binaries state methodology is now being generalized to permit parts and structures to possess a random limited variety of configurations. Binary modeling should be adequate for most reliable applications, however, for different types of utilization, especially gas/oil extraction and distribution frameworks, a multistate method is frequently necessary for the entire system. For instance, the velocity of supplied gases in the gasoline transit system serves as a measure of the network's well-being, and in the majority of cases, a binary model (100%, 0%) would be an inadequate description of the system (Aven 1988). The concept is similar for the simple series and simple parallel system, sometimes simple models are not necessary to derive the procedure that’s why, the complex and the k-out-of-n system are needed to demonstrate the 3-D model and to evaluate all the results. The forecasting of environmental changes is highly dependent on mathematical frameworks. The planners working with the environment, have an immediate requirement for a broad examination that can be easily utilized to determine the reliability of a system or to select among accessible frameworks. Leggett and Williams (1981) investigated the reliability index for these types of models. An illustrative example is also illustrated for the system which predicted the fluctuation in the atmosphere.

The significance of reliability has grown in the past decade, due to the complexity of bigger frameworks and the consequences of their breakdowns. In today's technological age, unreliability can risk human life in addition to generating ineffective operation and unsustainable servicing. Rushdi (1990) investigated the basic features of a threshold network and proposed an iterative method for calculating a precise model’s reliability. A real-life instance is offered, and the multi-threshold scenario is also examined throughout the work. Making the move from being concerned about reliability is undoubtedly tough because it necessitates a mental change; yet, difficult but not impossible (Aggarwal 1993). Wang et al. (2004) offered a methodology for bridging the separation between the old utilization of modeling outcomes, which gives no straightforward way for calculating reliability significance metrics, and the new use of simulation outcomes. The authors suggested several new reliability significance indices. These indices can be derived directly from simulation data, and their limiting values are standard reliability important indices. Ebneshahrashoob et al. (2005) analyzed the simple graph idea of availability concerning graph reliability to show how the recommended significance indices can be used and demonstrated. In addition, the authors obtained precise findings for particular subgroups of bipartite and tripartite graphs in terms of manageability. Benavides (2014) suggested a reliability framework that comprises numerous explication variables as needed but merely three unidentified factors allowing the engineer to obtain reliable data from multiple test operations and extend reliability results to various operating and construction aspects. In their work, Breneman et al. (2022) delved into the fundamentals of reliability engineering, quality, and safety engineering. They elaborated the concepts such as probability and discrete distributions also offering illustrative examples. Moreover, the paper explored the exponential distribution and covers essential aspects of reliability.

The consecutive 3-out-of-5:W system has been proposed in this manuscript. Some relevant concepts related to reliability have been discussed first. The schematic arrangement of the model of a consecutive 3-out-of-5:W system is constructed. After an illustration of the block diagram of the consecutive 3-out-of-5:W system, the methodology of the u-function and structure–function approach for the determination of the reliability function has been determined. The calculation has been evaluated by both methods. Once the reliability function is yielded, the tail-signature of the system has been calculated. Tail-signature is the key definition for the signature because by using tail-signature, the signature of the system has been deduced. After these outcomes, the minimal signature of the device would be evaluated. In the end, the estimated value of the consecutive 3-out-of-5 system and the estimated cost of the consecutive 3-out-of-5 system have been illustrated. All calculations have been done for both approaches.

The remainder portion of the work has been partitioned into the following sections and subsections, Sect. 2 provides a thorough explanation of the important concept in reliability or reliability-related notions i.e., universal generating function (u-function), structure–function approach, signature reliability, and consecutive k-out-of-n:W system. The system description for the consecutive 3-out-of-4:W system has been illustrated in Sect. 3. Sections 4 and 5 comprise the methodology for the u-function approach and structure–function approach respectively. The calculation for the reliability function, signature reliability, tail-signature, and all related metrics by using the u-function is presented in Sect. 6. The calculation for the reliability function, signature reliability, tail signature, and all related metrics by using the u-function is presented in Sect. 7. Section 8 comprises results and discussion. Section 9 presents the conclusion and related future work.

2 Relevant reliability concepts

Reliability concepts in systems engineering include various reliability indices such as the u-function approach, structure–function approach, and signature reliability. The u-function approach assesses system performance based on component states. The structure–function approach evaluates system reliability by analyzing the configuration of its components. Signature reliability focuses on the system’s performance signatures, providing insights into the overall reliability and robustness. A brief introduction to all these terms is as follows.

2.1 The u-function approach

To determine the reliability of diverse models, Ushakov (1986) presented the u-function approach. Using the conventional u-function method, Lisnianski et al. (1996) calculated the power system's reliability. The u-function method expands the well-known conventional moment-generating algorithm. In addition to evaluating the probability of the failure of the model, Levitin and Lisnianski (2001) used the u-function method to examine the reliability of the multi-state systems (MSS) and utilized it to investigate the proposed model, which was a complex arrangement of n linearly arranged components. The demonstrated method was a fusion of the u-function method with the aid of the genetic algorithm method. Levitin (2002) examined the reliability of the linear multi-state sliding window system (SWS) with different state elements. Levitin (2005) also examined the method and the algorithm of the u-function technique and how the reliability of various binary and sequential A-out-of-G systems can be calculated. The recursive techniques were used by Li and Zuo (2008) to evaluate the u-function of the multi-state weighted k-out-of-n systems. Kumar and Ram (2019) examined reliability by using the u-function and then computing the signature, tail signature, expected value, cost, Barlow-Proschan (B.P.) index, complex system, and bridge structure. With the aid of the u-function technique, Tyagi et al. (2021) proposed a real-life renewable system. The researchers also evaluated the reliability function along with a variety of parameters like, B.P. index, tail-signature, signature reliability, etc.

2.2 Structure–function approach

Marichal et al. (2011) demonstrated the non-independent and identically distributed (i.i.d.) conditions, the aforementioned notation remains valid for any consistent systems at any moment if and only if its individual states are negotiable. The criteria for deriving an alternate depiction of the system's reliability, in which the signature is swapped out for its non-i.i.d. extension, are also covered by the researchers. Finally, the authors addressed the requirements for the system's safety to have both models. Boland's formula, which necessitates knowing every value of the related structural function, can be utilized to deduce the signature of the device. But Marichal and Mathonet (2013) examined a novel methodology using derivatives and the diagonal component of the dependability function to effectively estimate the signature. An approach had been drawn up by Marichal et al. (2015) addressing the broad scenario of a structure divided into a finite number of disconnected modules arranged arbitrarily. Additionally, the researchers offered a usual equation for the device signature based on the signatures of the components. With the help of the appropriate vector of dominations, Marichal (2015) produced converting equations between the dependability function and the signature. For the calculation of any of these notions, the researchers also devised effective methods. Simple techniques like differentiation, coefficient extraction, and integration—are also discussed in this work to quickly calculate the signature from the dependability function. The reliability function is the key element in determining reliability as well as other factors. The proposed approach, like many other earlier ways, is a widely used technique for assessing the dependability function. The reliability function R can be constructed only from minor paths with ease and does not contain any additional paths. Before expanding each coproduct ∅ of the system, counting all the components that are present in it is used to simplify the corresponding geometric statement in terms of \({S}_{i}^{2}={S}_{i}.\)

2.3 Signature reliability

The possibility of an ith element's breakdown seems tragic to the entirety of the system, if it fails with an ith segment of an array that represents the signature of a system with i.i.d. member lifetime. Ghribi et al. (1997) devised a strategy to enhance software reliability, in this study the comparison of system signatures has been found and termed as an incredibly useful tools. In contrast to prior strategies the simply controlled data or technology modifies the program throughout the implementation. It is comprised of 2 stages: fault detection using a generation technique, and recovery from these flaws utilizing duplicated code functions. Triantafyllou and Koutras (2008) developed an algorithm for evaluating the signature of a reliability framework using a u-function technique. A simple adequate demand is also constructed for showing the non-preservation of the IFR attribute during the lifespan of the system by utilizing the system's signature. Marichal (2015) offered transformation formulations across the signature and the reliability function by using the associated span of dominance. The researcher also demonstrated how to simply estimate the signature from the dependability function using fundamental operations such as differentiation, coefficient extraction, and integration. Pandey et al. (2022) proposed a complex manufacturing system comprising parallel/series arrangements. The reliability function, signature reliability, lifespan, and cost rate using the u-function were also evaluated by the researchers. To assess the reliability of the model utilizing the u-function, Sadiya et al. (2022a, b) constructed a sophisticated solar water geyser device. The researchers also considered how reliable a system is after the evaluation of tail signature and signature reliability.

2.4 Consecutive k-out-of-n:W system

These systems serve as fundamental models for assessing the reliability of complex systems with redundant components, crucial in the aerospace, automotive, and telecommunications sectors. Understanding their behavior enables optimization of system design and maintenance strategies, enhancing overall reliability and safety. Insights gained inform decision-making processes, advancing engineering knowledge and improving real-world system performance. Thus, investigating consecutive k-out-of-n systems is imperative for ensuring the dependable operation of critical systems and advancing reliability engineering practices in various industries.

Chiang and Niu (1981) provided a recursion technique for calculating the reliability of the consecutive k-out-of-n:F systems. The researchers also provided precise higher and lower constraints for these systems. Chakravarthy and Gómez-Corral (2009) investigated the behavior of k-out-of-n dependability systems with spares and repairs for the use of matrix analytic formalism to numerically evaluate their performance. Eryılmaz (2009) investigated the reliability features of consecutive k-of-n networks with arbitrary dependent elements. The researchers also assess the most effective formulae for \({\varvec{n}}\le 2{\varvec{k}}\) for determining reliability metrics such as mean time to failure, failure rate, and mean residual lifetime. Wang (2016) investigated a k-out-of-n structure with a cold standby element assuming the common assumption that the element is operational at period t. The survival coefficient and average residual life function of such a system are calculated. Goliforushani et al. (2018) calculated the average cumulative life metric of a generalized k-out-of-n network under various situations, including whether the quantity of constituents in every module is equal or uneven, and whether the system's components are autonomous or interchangeable. Roy and Gupta (2021) investigated the reliability features of a k-of-n device featuring two cold standby elements. The authors also explained the structure's lifespan and constructed the reliability function, allowing us to determine the risk of device failure. Utilizing a structure–function method, Sadiya et al. (2022a, b) evaluated the reliability of a 2-out-of-4 system, three serially connected modules, and a bridge system. The researchers also looked at signature reliability and the tail-signature.

3 System description

The k-out-of-n system framework is an increasingly prevalent form of redundancy in complex and MSS systems with multiple applications. Both industrial and military systems utilized it for different purposes. The concept of the “k-out-of-n” arrangement implies a system layout in which only k out of n elements or modules must be functioning for the item to be functional. In these types of systems, it is necessary that k is either less than or equal to n. An additional spare tire is typically mounted on a car having four tires, for instance. Therefore, the car is safe to operate as long as at least four out of the five tires are in satisfactory condition. The k-out-of-n configuration is separated into two subcategories: k-out-of-n:W and k-out-of-n:F. A k-out-of-n:W structure necessitates at least k components to survive for the complete system of n components to succeed. A k-out-of-n:F system, on the other hand, signifies an arrangement that collapses if and only if at least k components collapse.

The series structure is capable of functioning if all of its parts and functions work effectively. This is an n-out-of-n system. The parallel system is a 1-out-of-n system since it can only function if at least single of its components is operating. The k-out-of-n systems are commonly used in a variety of technological applications. A reliability model with n components in a sequential manner is called a consecutive k-out-of-n:W system. The system will be working if k consecutive components are functioning.

The suggested study considers the consecutive k-out-of-n:W system, comprised of five components, three of which are in functioning order while the other two are collapsed/not operating. Finally, the system is operational, which is why it is referred to as a consecutive 3-out-of-5:W.

In this 3-out-of-5 structure shown in Fig. 1, the first and fourth units are linked together in a parallel pattern, and the second and fifth units are likewise connected. The third element is present and connected as a bridge in the middle. A minimum of three of the five components must have been in an operational position for this model to work properly.

Fig. 1
figure 1

The block-based representation of a consecutive 3-out-of-5:W system

Full size image

4 Methodology for u-function approach

4.1 Methodology for reliability function

The u-function is an effective tool to improve a wide range of complex and different types of systems for evaluating the device's reliability. In 1986, Ushakov introduced this technique to deduce the reliability measures of various devices. A polynomial function is applied to define a system’s probability in a given system. The u-function technique helps to define the effectiveness of the contributions of each unit that makes up a system as a whole, and then determines the system's effective distribution based on the effective distribution of its components. With the use of improved UGF, the study suggested a methodology that assessed the proposed device’s reliability utilizing algebraic calculations, the u-function makes it possible to estimate the overall effectiveness and dispersion of the entire system from the performance of its reliable elements (Ushakov 1986). The theoretical algorithm of the u-function for the reliability function determination is as follows:

  • Step 1: Calculate the effectiveness of each element by u-function.

  • Step 2: Allocate \({M}_{a}\left(z\right)={m}_{a}\left(z\right), \text{where} \,a=\text{1,2},\dots ,i.\)

  • Step 3: For \(a=2,\dots ,i, \text{obtain}\, {M}_{a}\left(z\right)={M}_{a-1}\left(z\right)\dots {m}_{a}(z)\).

  • Step 4: Obtain the function’s \(M\left(z\right)\) demonstrating the structure function as \(M\left(z\right)={M}_{i}\left(z\right) L,\) where \((F\left(\text{Z},\text{L}\right))=1(\text{Z}\ge \text{L})\).

  • Step 5: Evaluate the system reliability as \(P\left(F\left(\text{Z},\text{L}\right)\right)=\text{M}^{\prime}(1)\).

The proposed system is a consecutive 3-out-of-5 system computing value with reliabilities \({E}_{1},{E}_{2},\dots ,{E}_{5}.\)

Additionally, the UGF of the suggested model i.e., 3-out-of-5 system. The general u-function of a 3-out-of-5 system is as follows:

$${M}_{i}\left(z\right)={X}_{a}{z}^{a}+\left(1-{X}_{a}\right){z}^{0},$$
(1)

where \(a=\text{1,2},\text{3,4},5,{ and X}_{a}\) is the expression for the likelihood function, \({x}^{a}\) is the degree of the performance of the element, and \({x}^{0}\) is the degree of non-performance components.

An individual component’s u-function of the consecutive 3-out-of-5 system is as follows (Jafary and Fiondella 2016):

$$\begin{aligned}{M}_{1}\left(z\right)&={X}_{1}{z}^{1}+\left(1-{X}_{1}\right){z}^{0},\\ {M}_{2}\left(z\right)&={X}_{2}{z}^{1}+\left(1-{X}_{2}\right){z}^{0},\\ {M}_{3}\left(z\right)&={X}_{3}{z}^{1}+\left(1-{X}_{3}\right){z}^{0},\\ {M}_{4}\left(z\right)&={X}_{4}{z}^{1}+\left(1-{X}_{4}\right){z}^{0},\\ {M}_{5}\left(z\right)&={X}_{5}{z}^{1}+\left(1-{X}_{5}\right){z}^{0}.\end{aligned}$$

Following the steps of above-mentioned algorithm, the resulting function is as follows:

$$\begin{aligned}&M\left(z\right)={X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}+{X}_{1}\left(1-{X}_{2}\right){X}_{3}{X}_{4}{X}_{5}+{(1-X}_{1}){X}_{2}{X}_{3}{X}_{4}{X}_{5}+\left(1-{X}_{1}{)(1-X}_{2}\right){X}_{3}{X}_{4}{X}_{5}\\ &\quad +{X}_{1}{X}_{2}{(1-X}_{3}){X}_{4}{X}_{5}+{X}_{1}{(1-X}_{2})(1-{X}_{3}{)X}_{4}{X}_{5}+{(1-X}_{1}){X}_{2}{(1-X}_{3}){X}_{4}{X}_{5} +{X}_{1}{X}_{2}{X}_{3}(1-{X}_{4}){X}_{5} \\ &\quad +{X}_{1}{(1-X}_{2}){X}_{3}{(1-X}_{4}){X}_{5}+{(1-X}_{1}){X}_{2}{X}_{3}(1-{X}_{4}){X}_{5}{+X}_{1}{X}_{2}{(1-X}_{3}{(1-X}_{4}{)X}_{5}+{X}_{1}{X}_{2}{X}_{3}{X}_{4}{(1-X}_{5})+{X}_{1}{(1-X}_{2}{)X}_{3}{X}_{4}\left(1-{X}_{5}\right)\\&\quad +{(1-X}_{1}){X}_{2}{X}_{3}{X}_{4}{(1-X}_{5})+{X}_{1}{X}_{2}{(1-X}_{3}){X}_{4}{(1-X}_{5})+{X}_{1}{X}_{2}{X}_{3}{(1-X}_{4}{)(1-X}_{5}).\end{aligned}$$
(2)

By using the algorithm of the consecutive 3-out-of-5 system, the reliability of the system by using the u-function (Boland and Samaniego 2004). The following findings suggest that the system reliability estimates from the u-function of an individual component are nearly equivalent, and the resulting function is as follows:

$$\begin{aligned}&{=X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}+{X}_{1}{X}_{3}{X}_{4}{X}_{5}\\ \\ &\quad -{X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}+{X}_{2}{X}_{3}{X}_{4}{X}_{5}-{X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}\\ &\quad +{X}_{3}{X}_{4}{X}_{5}(1-{X}_{1}-{X}_{2}+{X}_{2}{X}_{2})+{X}_{1}{X}_{2}{X}_{4}{X}_{5}\\ &\quad -{X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}+{X}_{1}{X}_{4}{X}_{5}\left(1-{X}_{2}-{X}_{3}+{X}_{2}{X}_{3}\right)+{X}_{2}{X}_{4}{X}_{5}(1-{X}_{1}-{X}_{3}+{X}_{1}{X}_{3})+{X}_{1}{X}_{2}{X}_{3}{X}_{5}-{X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}\\ &\quad+{X}_{1}{X}_{3}{X}_{5}\left(1-{X}_{2}-{X}_{4}+{X}_{2}{X}_{4}\right)+{X}_{2}{X}_{3}\left(1-{X}_{1}-{X}_{4}-{X}_{1}{X}_{4}\right){X}_{1}{{X}_{2}X}_{5}\left(1-{X}_{3}-{X}_{4}+{X}_{3}{X}_{4}\right)\\ &\quad+{X}_{1}{X}_{2}{X}_{3}{X}_{4}+{X}_{1}{X}_{3}{X}_{4}-{X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}\left(1-{X}_{2}-{X}_{5}+{X}_{2}{X}_{5}\right)+{X}_{2}{X}_{3}{X}_{4}\left(1-{X}_{1}-{X}_{5}+{X}_{1}{X}_{5}\right)\\ &\quad +{X}_{1}{X}_{2}{X}_{4}\left(1-{X}_{3}-{X}_{5}+{X}_{3}{X}_{5}\right)+{X}_{1}{X}_{2}{X}_{3}\left(1-{X}_{4}-{X}_{5}+{X}_{4}{X}_{5}\right).\end{aligned}$$
(3)

4.2 Methodology for signature reliability and related metrics

The signature is defined for the system under consideration in the manner described below using the reliability measure. First, the system’s signature is assessed using the Boland formula (Boland and Samaniego 2004). The reliability function is considered during the calculation. The polynomial form acquired from the foregoing approach for calculating the reliability function to calculate the device’s reliability function using Taylor evaluation at ῳ = 1. The formula for the polynomial function is given as:

(4)

The following formula is used to estimate the values of the tail signature for the system with (q + 1)-tuple \({\mathbb{X}}=\left({\mathbb{X}}_{o} , \ldots , {\mathbb{X}}_{m}\right)\):

$${\mathbb{X}}_{b}=\sum_{a=b+1}^{z}{\mathbb{x}}_{a}= \frac{1}{\left(z-b\right)}\sum_{\left|N\right|=z-b}\emptyset \left({\mathbb{M}}\right).$$
(5)

As a result of using the aforementioned formulae to establish the system's tail signature, the following final formula is obtained (Marichal and Mathonet 2013):

$${\mathbb{T}}_{\mathbb{s}}=\frac{\left(m-s\right)!}{m!} {\mathcal{D}}^{s}R\left(1\right) , \quad s=\text{0,1},..,m.$$
(6)

The evaluation of the signature of the system with the help of the tail signature by using the formula below (Da et al. 2018):

$$\overline{\mathbb{S} }={\mathbb{T}}_{{\mathbb{s}}-1}- {\mathbb{T}}_{\mathbb{s}} ,\quad s=1, 2, \ldots , m .$$
(7)

The minimal signature \({M}_{s}\) is determined utilizing the coefficient of reliability function. With the help of a minimal signature, the expected lifetime of the system is calculated. Using the formula provided in evaluating Ě(ṫ) of the system as follows (Navarro et al. 2007):

(8)

where, is a vector coefficient that we can obtain by using minimal signature.

Next, the expected value \(E(X)\) of the elements of the proposed system will be evaluated which can be determined by using the formula as follows (Eryılmaz 2009):

(9)

Using Eq. (8) in the above formula, get the value of the predicted cost rate for the system (Kumar and Ram 2019):

(10)

The B.P. index of the proposed model can be computed by using the reliability function. As a result, the B.P. index is evaluated using the formula below:

$${BP}_{{I}^{(b)}} = {\int }_{0}^{1}({\delta }_{s}\text{l}) \left(\text{z}\right)\text{dz},\quad s = \text{1,2},\dots ,n.$$
(11)

At last, we will evaluate the cumulative signature of the system with the help of the formula as follows:

$${C}_{s}=D\left(a\right)* \frac{b!\left(m-a\right)!}{m!}\quad a=1, 2, \ldots,s.$$
(12)

5 Methodology for structure function approach

5.1 Reliability function estimation

Assume a product with m elements ([m], \(\emptyset\)), where [m] = {1,…, m} represents the set of its parts \(\emptyset\): \(\{ 0,1\}^m { } \to \{ 0,1\}\) and represents its organizing variable (which describes the application's structure as an average of the current state of its constituents). The framework is always semi-coherent, which denotes that none of the variables are decreasing and that it satisfies the conditions \(\emptyset \left( {0, \ldots ,0} \right) = 0\) for the breaking down stage and \(\emptyset \left( {1, \ldots 1} \right)\)\(=1\) for the operational stage. Considering the lifespans\({T}_{1}, {T}_{2},\dots ,{T}_{m-1},{T}_{m}\), as well as the unless and stated components are continuous and i.i.d. The following form should be used to express the reliability function:

$$\emptyset \left( {P_1 ,P_2 , \ldots ,P_{\text{n}} } \right) = { }P_4 P_5 \cup^* P_1 P_2 \cup^* P_4 P_3 P_2 \cup^* P_5 P_3 P_1 \cup^* \ldots \cup^* P_{{\text{n}} - 2} P_{{\text{n}} - 1} P_{\text{n}} .$$
(13)

Only the structure–function allows for the rapid extraction of the reliability parameter H(P), which can be used to improve the degree of alignment or decrease it from new perspectives. Bernoulli-type variables, often known as Bernoulli random variables, are the most fundamental type of random variable used here. According to their operating and contracting states, there are two alternative outcomes included: 1 and 0 (Marichal and Mathonet 2013).

5.2 Method for determining the signature and related metrics

The following steps are involved in figuring out a system's signature.

Step 1: Imagine that Boland's formula is used to find the signature \(\overline{\mathbb{S} }\) of any framework using the ith minimal lifespan m elements (Boland 2001),

$$\overline{\mathbb{S} }= \frac{1}{\left(\begin{array}{c}s\\ s-b+1\end{array}\right)} \sum_{\begin{array}{c}k\subseteq \left[\text{s}\right]\\ \left|\text{k}\right|=s-b+1\end{array}}\upvarphi (H)- \frac{1}{\left(\begin{array}{c}s\\ s-1\end{array}\right)} \sum_{\begin{array}{c}k\subseteq \left[\text{s}\right]\\ \left|\text{k}\right|=s-1 \end{array}}\upvarphi \left(H\right).$$
(14)

This study offers a method to do away with Boland's formula, which is needed to evaluate φ(K) for every \(k\subseteq \left[\text{s}\right],\) and instead identify the framework's signature simply from the configuration's dependability function (Marichal et al. 2011).

The dependability polynomial may be formed in a different approach to demonstrate the relationship between the dominance and signature vectors (Marichal 2015). The required polynomial terms are as follows:

$$H\left(R\right)= \sum_{j=1}^{m}{\alpha }_{j}\left(\begin{array}{c}m\\ j\end{array}\right){R}^{j}{Q}^{m-j},$$
(15)

where

$${\alpha }_{j}=\sum_{j=m-j+1}^{m}{S}^{0}\left(\begin{array}{c}m\\ j\end{array}\right)\text{for }j=1,\dots .m.$$
(16)

Step 2: The tail signature is evaluated for the entire model, which is the (m + 1)-tuple, \({S}^{*}= {(S}_{0}^{*}, \dots , {S}_{m}^{*}\)) (Navarro et al. 2007),

$${S}^{*}= \sum_{i=k+1}^{m}{S}^{0}= \frac{1}{\left(\begin{array}{c}m\\ m-i\end{array}\right)} \sum_{\left|H\right|=m-k}\upvarphi \left(\text{H}\right).$$
(17)

Step 3: Generate the polynomial reliability function using the Taylor expansion with R = 1 as the center, as follows (Marichal and Mathonet 2013):

$$P\left(R\right)={R}^{m}H\left(\frac{1}{R}\right).$$
(18)

Step 4: To evaluate the proposed system's tail signature (Navarro and Rychlik 2010).

$${S}^{*}= \frac{\left(m-k\right)!}{m!} {D}^{k} P\left(1\right), k=\text{0,1},\dots ,m.$$
(19)

The signature reliability can be conveniently assessed using “Bernstein polynomials”,

$$\left(\begin{array}{c}m\\ k\end{array}\right){S}_{k}^{*}=\text{coefficient of }\,{R}^{k}\,\text{of the Bernstein polynomial}.$$
(20)

Without using complex computations or additional broad equations, this simplified approach successfully identifies the device's tail signature.

Step 5: Determine the signature of a complex system using Eq. (6) (Navarro and Rubio 2009):

$${S}^{0}= {{S}^{*}}_{k-1}- {{S}^{*}}_{k},\quad k=\text{1,2},\dots ,m.$$
(21)

Determine a consecutive 3-out-of-5:W system's estimated lifetime \(E (T)\) for a system with independent components and a mean (μ = 1),

$$E\left(T\right)=\upmu \sum_{i=1}^{n}\frac{{e}_{i. }}{i}.$$
(22)

The system's capacity for prediction can be determined by employing the above equation for signature reliability,

$$E\left(X\right)=\sum_{i=1}^{n}i{S}^{0},\quad i=1,\dots ,n.$$
(23)

Furthermore, the cost rate of a complex system is as follows:

$$\text{Expected cost rate}= \frac{E\left(X\right) }{E(T)}.$$
(24)

The B.P. index of the i.i.d. is determined by the needs of the reliability function. The \(k\text{th}\) component of the shapely value, and thus the kth component of the B.P. index are the consequences for the degree of the reliability of the system (Shapley and Shubik 1954).

$$\text{B}.\text{P}= {\int }_{0}^{1}({\delta }_{b}P) \left(R\right)\text{d}R,\quad b=\text{1,2},\dots ,n.$$
(25)

where P denotes the dependability functions of the consecutive k-out-of-n: W system.

A simple method for determining the B.P. index utilizing the reliability metric P, ought to be more readily available than the notion described below (Blokus 2020):

$$I_{BP} = \sum \limits_{B \le [n]\{ m\} } \frac{1}{{a\left( {\begin{array}{*{20}c} {a - 1} \\ {\left| B \right|} \\ \end{array} } \right)}}\left( {\emptyset \left( {B \cup \left\{ a \right\}} \right) - \emptyset \left( B \right)} \right).$$
(26)

The procedure that follows can be used to calculate the system's cumulative signature. (Gertsbakh et al. 2011),

$${C}_{n}=B\left(n\right)*\frac{n!\left(x-n\right)!}{x!}, n=1,\dots ,z.$$
(27)

6 Reliability measures calculation for u-function approach

Considering a consecutive 3-out-of-5:W device consisting of three out of five working components. In which the components are connected in a complex manner not in series or not in parallel manner completely. Consequently, the proposed system is reliable (Levitin 2005). The structure–function of the system can be evaluated by formula (3):

$$\begin{aligned}&R={X}_{2}{X}_{3}+{X}_{3}{{X}_{4}X}_{5}+{X}_{1}{X}_{4}{X}_{5}+{X}_{2}{X}_{4}{X}_{5}+{X}_{1}{X}_{3}{X}_{5}\\ & \quad -{X}_{1}{X}_{2}{X}_{3}-{X}_{2}{X}_{3}{X}_{4}+{X}_{1}{X}_{2}{X}_{5}+{X}_{1}{X}_{3}{X}_{4}{+{X}_{2}X}_{3}{X}_{4}-2{X}_{1}{X}_{3}{X}_{4}{X}_{5}\\ &\quad -{X}_{1}{X}_{2}{X}_{4}{X}_{5}-{X}_{1}{X}_{2}{X}_{3}{X}_{5}-{X}_{1}{X}_{3}{X}_{4}{X}_{5}-2{X}_{2}{X}_{3}{X}_{4}{X}_{5}+3{X}_{1}{X}_{2}{X}_{3}{X}_{4}{X}_{5}.\end{aligned}$$
(28)

And now, if each component is uniformly dispersed and free of distribution for the proposed consecutive 3-out-of-5:W system, i.e.,

$${X}_{1}={X}_{2}={X}_{3}={X}_{4}={X}_{5}=X.$$

The reliability function of the proposed model is evaluated with the help of Owen's approach and yielded the form (Naaz et al. 2023):

$$R={X}^{2}+5{X}^{3}-8{X}^{4}+3{X}^{5}.$$

Now, the polynomial equation for the reliability function of the consecutive 3-out-of-5:W is as follows (Levitin 2002):

$$\begin{aligned}&R\left(X\right)={X}^{m}L\left(\frac{1}{{X}_{m}}\right),\\& R\left(X\right)=\left({X}^{2}+5{X}^{3}-8{X}^{4}+3{X}^{5}\right){x}^{-5},\\& R\left(X\right)={X}^{3}+5{X}^{2}-X+3,\\& R\left(S\right)=3-8X+5{X}^{2}+{X}^{3} ).\end{aligned}$$
(29)

To identify the consecutive 3-out-of-5:W system's tail signature \({\mathbb{T}}_{\mathbb{s}}\) by using Eq. (6) is as follows (Kumar and Singh 2019):

$$\begin{aligned}&{\mathbb{T}}_{\mathbb{s}}=\frac{\left(m-s\right)!}{m!} {\mathcal{D}}^{s}R\left(1\right) ,\quad s=0, 1, \ldots , m.\\ &{\mathbb{T}}_{1}=\frac{\left(5-0\right)!}{5!}{\mathcal{D}}{\prime}R\left(1\right)=1.\end{aligned}$$

Hence, all values of tail signature can be estimated similarly, the estimated values are as follows and tabulated in Table 1 (Naaz et al. 2022):

Table 1 The values of the tail signature of the consecutive 3-out-of-5:W system by using the binomial formula as follows:
Full size table

Tail signature \({\mathbb{T}}_{\mathbb{s}}=\left(1,\frac{3}{5},\frac{3}{10}\text{0,0},0\right)\).

To determine the signature reliability of the consecutive 3-out-of-5:W system by using Eq. (7) is as follows:

$$\begin{aligned}&\overline{\mathbb{S} }={\mathbb{T}}_{{\mathbb{s}}-1}- {\mathbb{T}}_{\mathbb{s}} , s=1, 2, \ldots , m. \\ &{\overline{\mathbb{S}} }_{1}={\mathbb{T}}_{1-1}- {\mathbb{T}}_{1}={s}_{0}-{s}_{1}=1-\frac{3}{5}=\frac{2}{5},\end{aligned}$$

so, the final values of the signature reliability are as follows:

$$\overline{s }=\left(\frac{2}{5},\frac{3}{10},\frac{3}{10},\text{0,0}\right).$$

Then, calculate the device's minimal signature of the consecutive 3-out-of-5:W system by using Eq. (8) as follows (Ram et al. 2023):

$${M}_{s}=\left(\text{0,1},5,-\text{8,3}\right).$$

Now to evaluate the expected lifespan the of the consecutive 3-out-of-5:W system by using Eq. (9) is as follows:

Now to determine the estimated cost rate by using Eq. (10) is as follows:

Utilizing the Eq. (28), consider the tentative values for the individual components as follows:

$${S}_{1}=0.4., {S}_{2}=0.5., {S}_{3}=0.6., {S}_{4}=0.7., {S}_{5}=0.8.$$

The overall reliability of the proposed system by using the above values is \(R=0.5144.\)

Utilizing Eq. (11), the B.P. index of the proposed consecutive 3-out-of-5:W system is as follows:

$${BP}_{I=}\left(\frac{1}{10},\frac{11}{60},\frac{4}{15},\frac{11}{60}, \frac{4}{15}\right).$$

Now to evaluate the cumulative signature of the proposed consecutive 3-out-of-5:W system by using Eq. (12) is as follows:

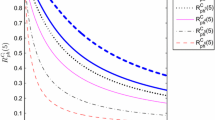
$$\begin{aligned}&{C}_{s}=D\left(a\right)* \frac{b!\left(m-a\right)!}{m!} \\ & a=1, 2, \ldots,s. \\& {C}_{s}=\left(\frac{1}{5},\frac{6}{5},\frac{45}{2},\text{272,0}\right).\end{aligned}$$

The cumulative signature of the consecutive 3-out-of-5:W system can be calculated with the help of Eq. (14) and tabulated as follows in Table 2.

Table 2 The cumulative signature of the consecutive 3-out-of-5:W system
Full size table

7 Reliability measures calculation for structure–function approach

Assuming a consecutive 3-out-of-5:W system as indicated in Fig. 1, which is in working condition and comprising five components from which at least three are functioning. The evaluation of several measures such as, reliability of the consecutive 3-out-of-5:W system, tail-signature, signature, cumulative signature, minimal signature, B.P. index, expected life-span, and estimated cost rate of the proposed consecutive 3-out-of-5:W system by using structure–function approach are evaluated as follows:

The related structural function of the consecutive 3-out-of-5:W system is:

$$\begin{aligned} &\emptyset (X_1 ,X_2 , \ldots ,X_5 ) = X_1 X_2 + X_4 X_5 + X_1 X_3 X_5 + X_2 X_3 X_4 \\& \quad - X_1 X_2 X_4 X_5 - X_1 X_2 X_3 X_5 - X_1 X_2 X_3 X_4 + X_1 X_3 X_4 X_5 - X_2 X_3 X_4 X_5 + 2X_1 X_2 X_3 X_4 X_5, \end{aligned}$$
(30)

The final reliability function of the consecutive 3-out-of-5:W system with the help of the structure–function approach is as follows:

$$H\left(X\right)={2X}^{2}+2{X}^{3}-5{X}^{4}+2{X}^{5}.$$
(31)

Utilizing Eq. (13), the expansion of the polynomial concerning R = 1 is as follows,

$$\begin{aligned}&H\left(X\right)={2-5X+2X}^{2}+2{X}^{3}. \\& H\left(X\right)=1\left(X-1\right)+5\left(X-1\right)+8{(X-1)}^{2}+2{(X-1)}^{3},\end{aligned}$$

or equivalently,

$$H\left(X+1\right)=1+5X+8{X}^{2}+2{X}^{3}.$$

The tail signature of the consecutive 3-out-of-5:W system can be estimated with the help of Eq. (20),

$${\mathbb{T}}_{\mathbb{s}}=\left(1, 1,\frac{4}{5} \frac{1}{5},\text{ 0,0}\right).$$

However, Table 3 shows the calculation for every component’s tail signatures and the new approach for determining the tail signature by employing (17).

Table 3 The values of the tail signature of the consecutive 3-out-of-5:W system by using the binomial formula
Full size table

As a result, using the tail signature's values and the previously described methods produce the findings shown below for the signature \(\overline{s }\) of the system is follows:

$$\overline{s }=\left(\frac{2}{5},\frac{3}{10},\frac{3}{10},\text{0,0}\right).$$

Utilizing the Eq. (30), consider the tentative values for the individual components as follows:

$${P}_{1}=0.4., {P}_{2}=0.5., {P}_{3}=0.6., {P}_{4}=0.7., {P}_{5}=0.8.$$

The overall reliability of the proposed system by using the above values is \(R=0.702.\)

To obtain the probable lifespan of a consecutive 3-out-of-5:W system now using a minimal signature is as follows,

$$E\left(T\right)=0.8167.$$

The minimal signature of the consecutive 3-out-of-5:W system is as follows,

$${M}_{s}=\left(0, 2, 2, -5, 2\right).$$

The value of the expected X of the consecutive 3-out-of-5:W system is,

$$E\left(X\right)=3.00.$$

Considering the value of the predicted X as a starting point, the cost price of the consecutive 3-out-of-5:W system is calculated as follows:

$$\text{cost price}=3.673.$$

By using Eq. (25), the B.P. index of the consecutive 3-out-of-5:W system can be obtained as,

$${I}_{BP}=\left(0.233, 0.233, 0.667, 0.233, 0.233\right).$$

The cumulative signature of the consecutive 3-out-of-5:W system can be calculated with the help of Eq. (27) and tabulated as follows in Table 4.

Table 4 The cumulative signature of the consecutive 3-out-of-5:W system
Full size table

8 Results and discussion

In this study, the reliability function and signature reliability of the consecutive k-out-of-n:W system are evaluated via two techniques (u-function technique and structure–function technique). The other metrics like tail signature, minimal signature, B-P index, system lifespan, and expected cost rate are also evaluated in the proposed work. This paper highlights the comparison between the results of both methods which are applied to the similar model. Based on reliability, if we provide the tentative values to an individual component, \(({S}_{1}, {P}_{1}=0.4., {S}_{2}, {P}_{2}=0.5., {S}_{3}, {P}_{3}=0.6., {S}_{4}, {P}_{4}=0.7., {S}_{5}, {P}_{5}=0.8.)\) the reliability of the system by using u-function is 0.5144 and by using structure function method is 0.702. Based on reliability, the structure–function method is appropriate for the proposed consecutive 3-out-of-5:W system. The cost price of the proposed 3-out-of-5:W system using the structure–function approach is \(3.673\) and by using the u-function approach, the value of the cost price is \(2.4782\). As well as the lifespan of the proposed system according to the u-function calculation is \(0.8167\) and \(0.7667\) is the result of the lifespan of the system by using the structure–function approach. Hence, based on lifespan and cost of the proposed consecutive 3-out-of-5:W system, the u-function method results better in comparison to structure–function approach. The values of the signature for an individual component of the consecutive 3-out-of-5:W system by using the structure–function approach is \({S}^{0}=(0, \frac{1}{5},\frac{3}{5},\frac{1}{5}0)\) and by using u-function methods the probability of the failure of the system is \(\overline{s }=\left(\frac{2}{5},\frac{3}{10},\frac{3}{10},0,0\right)\).

9 Conclusions and future work

In this paper, a consecutive 3-out-of-5:W system is examined using two approaches namely, the structure–function approach and u-function approach to evaluate the reliability function and signature reliability of the proposed 3-out-of-5:W system. This paper also determined the tail signature, system lifespan, B.P. index, and expected costs of the 3-out-of-5:W system. This study highlights the comparison between the outcomes yielded from both approaches. Based on simplicity, the structure–function approach is quite better than the u-function approach. The u-function method needs to evaluate the u-function for an individual component, which makes this method quite large and equations are more complicated. Instead, the system's signature can be calculated simply via structural function. It removes the big equations and collapses them into a streamlined formula that allows the tail signature to be easily analyzed. Signature reliability can also be simply assessed using the tail signature. Furthermore, both the approaches proposed in this work eliminate the requirement of Boland's formula, which is required to assess \(\mathbf{\upvarphi }(\mathbf{K})\) for every \({\varvec{k}}\subseteq \left[\mathbf{s}\right]\), and provides for the device's signature to be determined only based on the configuration reliability parameter. As a future work, the consecutive/weighted k-out-of-n system and bridge system can be considered with four and more than five working components by modeling the device. The tail signature and signature reliability can be calculated with the help of the reliability function using both approaches (u-function approach and structure–function approach).