Abstract
A milestone in the mathematical modeling of complex systems is the analysis of the significance of the system components. When examining the reliability, Birnbaum (1968) proposed measures of element significance. This direction of research into mathematical models of systems has led to many alternative analyzes. The aim of the article is to further expand the diagnostic capabilities of systems through a specialized analysis of their mathematical models. We propose, using the methods of game theory and stochastic processes, functionals that measure the structural reliability of the system and the operational performance related to maintenance. This allows for the construction of a new measure of significance, using knowledge of system design, reliability, and wear to optimize repair and maintenance. The considerations of this work are aimed at showing the ways of applying this approach to multi-state systems.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Birnbaum importance
- Barlow-Proschan importance
- Binary system
- Components importance
- Coherent system
- Cost-based importance
- Multistate system
- Natvig measure
- Risk-based importance
- Structural function
- Universal generating function
Subject Classifications: MSC 90B25 , 91B12 (62G10 62N05 90B25)
1 Introduction
1.1 Preliminaries
A systemFootnote 1, i.e. a complex structure with specific functionality is under investigation. The mathematical model of the system is based on the set theory as the family of subsets of a given set (set of elements) \(\boldsymbol{C}=\{c_1,\ldots ,c_n\}\) having some properties. An example is technical devices whose design is dictated by the need to perform specific functions. The constructed system should function in a planned and predictable manner. This property is a requirement that should also be considered in the design and construction (fabrication) process. The goal is therefore to reduce the risk (v. B.1) of a break in the planned operation of the system. So we have to model randomnessFootnote 2. For this purpose, we establish that all random phenomena are modeled using the probabilistic space \( (\Omega , {\mathcal F}, \mathbf{P} )\) (v. A).
Contemporary systems are characterized by their structural complexity. Its design is purposeful, which means that its purpose is to ensure the implementation of specific tasks. Due to the complexity of tasks and their multi-threading, the evaluation of functionality should be carried out on many levels. In short, the working complex system is able to be in many states. The first mathematical models of systems focused on component and structure reliability. This allowed a limitation to two-level assessments, the system (element) is operational or damaged (working or not working)Footnote 3. Already such an approach made it possible to methodologically support a designer with mathematical models, the analysis of which resulted in guidelines allowing for rational solutions in terms of the complexity of the structure and effective selection of elements so as to guarantee the reliability of the structure (system readiness) at the appropriate level for a sufficient time. Graph theory and the structures constructed in this theory are an excellent tool for modeling binary systems. The random graph is a good model of the binary systemFootnote 4. To put it simply, a coherent graph is a standby system model, and lack of consistency means no readiness. Turning off nodes and arcs in a connected graph leads to its decomposition, and thus destruction. Each operation of the system, the model of which is a random graph, leads to the moment in which the next disabled element of the structure leads to failure (lack of readiness). By analyzing the lifetime of the elements, it is possible to determine the order in which the elements are switched off and determine how often the failure of the tested element is the cause of the failure of the entire system. The more often an element is crucial, the greater its importance for the system. This line of reasoning led to the definition of Birnbaum’s [8] importance measure. There are known alternative results on the evaluation of the weight of components on the reliability of the system. The introduced measures of significance of elements on reliability will be the basis for the introduction of diagnostic algorithms about the possibility of which they wrote at the end of his seminal paper (cf. Birnbaum [8, 9] (v. Barlow et al. [7]). The indication of these algorithms is the subject of the authors’ study (v. Szajowski and Srednicka [37]).
The concept of significance measures (v. B.2) is essentially based on establishing a criterion against which we measure the significance of an element. [8] investigated the importance of the position of an element in a structure, valuing the elements whose failure less frequently decomposes the system. In order to determine the importance of the reliability (failure rate) of individual system components for the reliability of the entire system, measures sensitive to changes in the system and changes in component reliability are constructed. It also allows for the rationalization of the design and maintenance planning. The issues are complex due to the need to take into account both the effective reliability of the constructed system and the costs of maintaining it in readiness for a given period. Profitability analysis is of great importance. It is natural to formulate the problem by defining the overarching goal of minimizing costs while guaranteeing the expected level of reliability. In the whole process of analysis, the point of reference are two states (of the system and elements): functional or damaged. There are measures that are sensitive to a change of state, measure the importance of an element in relation to other elements, and the susceptibility of a system to a change of state from operation to failure. Thanks to this approach, it is possible to define weights for the cost of individual elements in a given time horizon, while ensuring a specific level of security or readiness. This approach can be found in the article by Wu and Coolen [39]. At the same time, other key goals and parameters of system analysis should not be forgotten. Their inclusion in the balanced model is possible with the use of natural methods of analysis when formulating many criteria based on elements of game theory.
We try to present the issue comprehensively, although there is currently no consistent approach to the method of determining the importance of elements in the system (v. B.3). This is one of the reasons why the loss of functionality of an element often does not significantly affect the system’s ability to perform most tasks. This aspect is emphasized by numerous examples presented in the literature, which show the significant impact of the state of the environment in which the systems are operated (time of day, weather conditions, environmental pollution). We write more about these issues in an earlier work (v. Szajowski and Średnicka [37]). From the analytical point of view, by introducing well-defined states of the system, referring, for example, to its function, one can investigate the meaning of structure elements in connection with the adopted description of its states.
As in binary systems, the rank of an element is determined by the availability of the system to scheduled tasks, so when evaluating elements of multi-state systems, the rank of an element in terms of state is determined by the availability of the system in this state.
The presented aspects relate to being in a fixed state, excluding the need for maintenance and repairs, including the costs of these activities (cost of parts, repair and maintenance time, penalties for unavailability). In system maintenance tasks, issues such as detecting failed components while the system is in that state are important in determining the importance of components to the steady state of the system. The element that should be checked first (because it is most suspected of a failure) can be treated as important for the efficient conduct of maintenance or repair (v. e.g. Ping [28]).
1.2 Investigation of Element Role in a Given State
If the system cannot be in the tested state, it is often important to determine the sequence of actions to restore the system to that state. To facilitate such analyzes, the weights (measures of significance regarding repair) of the elements should be determined. Otherwise, in these considerations, the measure of the importance of a component (group of components) in a given system is based on the quantification of the “role” of that component (group of components) and of the unavailability of the examined state of the system. Examples of such analyzes can be found in Fussell and Vesely [17], Barlow and Proschan [4], El-Neweihi et al. [13], El-Neweihi and Sethuraman [12] and Abouammoh et al. [1]. Defined measures (indicators) with significance allow to identify components (groups) that are probably responsible for “causing” the inability to use the analyzed state. In turn, the determination of these indicators leads to an effective control and maintenance principle, as well as to the optimization of spare parts storage and the optimal allocation of repairs to appropriate maintenance technicians of the relevant system components.
When examining the significance of the elements of binary systems, a few years after the publication of the results of Birnbaum and Proschan, it was noticed that similar solutions in the form of significance measures are used in parallel in the analysis of multi-person project management, voting analysis and other issues related to cooperative games (v. Ramamurthy [30]). As in the theory of cooperative games, the purpose of such research is to propose new importance measures for degrading components (v. Cao et al. [10]). The motivation is based on Shapley values, which can provide answers about how important players are to the whole cooperative game and what payoff each player can reasonably expect. The proposed importance measure characterizes how a specific degrading component contributes to the degradation of system reliability by using Shapley value. Degradation models are also introduced to assess the reliability of degrading components. The reliability of the system consisting independent degrading components is obtained by using structure functions, while the reliability of system comprising correlated degrading components is evaluated with a multivariate distribution. The ranking of degrading components according to this importance measure depends on the degradation parameters of components, system structure, and parameters characterizing the association of components. A reliability degradation of engineering systems and equipment are often attributed to the degradation of a particular component or set of components that are characterized by degrading features. This approach reflects the responsibility of each degrading component for the deterioration of system reliability. The results are also able to give timely feedback of the expected contribution of each degrading component to system reliability degradation.
1.3 Organization of the Paper
The rest of the paper is structured as follows. Section 2 provides the details of analysis of multistate systems. We start out, in Sect. 2.1, by showing how the coherency of multi-state systems is modeled. The remaining considerations are carried out on the assumption that the system is coherent. In the Sect. 2.3, we show what guidelines are to be provided by the constructed measures in the case of non-repairable systems (modules), and for whom these indicators are of interest. Other issues are interesting in the case of repairable systems and this is what the next Sect. 2.4 is about. The Sect. 3 describes the main problem of the paper, namely, the construction of a significance (importance) measure for an element or module of a system in the face of maintaining system consistency and activity. We recognize that the difficulty in maintaining the system is equal to the difficulty in maintaining its individual modules. These in turn are all the more important the more difficult it is to reconstruct them at the time of failure. The final Sect. 4 contains conclusions and suggestions for further research on diagnostics and maintenance of complex, multi-state systems. At the end of the work, and before the extensive bibliography, we have included a list of symbols, terms, and abbreviations. We chose them based on the belief that they may differ from those to which the reader is used to. In the next part, we have included end-notes to which we refer the reader when the main narrative requires them.
2 Multistate Systems
2.1 Coherent Multistate Systems
In the Sect. B.3 we mentioned coherent structures for binary system, while in this section we adapt the concept of coherence to the multistate systems. Many assumptions with given formulas regarding binary systems have natural continuation and analogous behavior in a multistate system, however are more complex Barlow and Wu [6].
Suppose we have specified the following objects (cf. [23, 26]):
-
a)
the set \(\boldsymbol{C}\) consisting of n ordered elements \(\boldsymbol{C}= \{1,2,...,n\}\) (elements collection, elements space )–it will be the space of elements;
-
b)
for every element \(i\in \boldsymbol{C}\) there is defined set of states \(\mathfrak C_i\) which is a completely ordered and finiteFootnote 5, i.e., \(\{(\mathfrak C_i, \prec _i)\}_{i \in \boldsymbol{C}}\) and \(|\mathfrak C_i|=w_i\in \mathbb {N}\);
-
c)
let \(\overrightarrow{x}^{\boldsymbol{A}}\) be an element of the set
 ;
; -
d)
if a subset \(\boldsymbol{A}\subset \boldsymbol{C}\), then \({\boldsymbol{C}} \backslash \boldsymbol{A}\equiv \boldsymbol{A}' \equiv \{ j \in {\boldsymbol{C}}| j\not \in \boldsymbol{A}\}\);
-
e)
if \({\boldsymbol{B}} \subset \boldsymbol{A}\subset {\boldsymbol{C}}\), then \(P_{\boldsymbol{B}}\) is a surjection \(P_{\boldsymbol{B}}: \mathfrak C_{\boldsymbol{A}} \rightarrow \mathfrak C_{\boldsymbol{B}} \)Footnote 6;
-
f)
if \(\Gamma \subset \mathfrak C_{\boldsymbol{A}} \) and \({\boldsymbol{B}} \subset {\boldsymbol{A}} \subset {\boldsymbol{C}}\), then \(P_{\mathfrak C_{\boldsymbol{B}}} \Gamma = \{ P_{\boldsymbol{B}} \overrightarrow{x}\in {\mathfrak C_{\boldsymbol{B}}} | \overrightarrow{x}\in \Gamma \}\), i.e., it is a subset of states indexed by \({\boldsymbol{B}}\)
-
g)
the partition of \({\boldsymbol{A}} \subset {\boldsymbol{C}}\) expressed as a family \({\mathcal B}=\{{\boldsymbol{B}}_j \}_{j=1}^m \), such that
-
1.
\({\boldsymbol{A}}=\displaystyle \bigcup _{j}^m {\boldsymbol{B}}_j \subset {\boldsymbol{C}}\), \( {\boldsymbol{B}}_i \cap {\boldsymbol{B}}_j = \emptyset \), for \(1\le i,j\le m\), \(i\ne j\);
-
2.
for every
 , \(1\le j\le m\), we have \(\overrightarrow{x}=(\overrightarrow{x}_1,\ldots ,\overrightarrow{x}_m)\in \mathfrak C_{\boldsymbol{A}}\) is such that \(P_{{\boldsymbol{B}}_j}\overrightarrow{x}=\overrightarrow{x}_j\);
, \(1\le j\le m\), we have \(\overrightarrow{x}=(\overrightarrow{x}_1,\ldots ,\overrightarrow{x}_m)\in \mathfrak C_{\boldsymbol{A}}\) is such that \(P_{{\boldsymbol{B}}_j}\overrightarrow{x}=\overrightarrow{x}_j\); -
3.
for every \(\overrightarrow{x}\in {\boldsymbol{A}}\subset {\boldsymbol{C}}\), \(\overrightarrow{x}=(\overrightarrow{x}^{{\boldsymbol{B}}_1},\ldots ,\overrightarrow{x}^{{\boldsymbol{B}}_m})\), where \(\overrightarrow{x}^{{\boldsymbol{B}}_j}= P_{{\boldsymbol{B}}_j}(\overrightarrow{x})=\overrightarrow{x}_j\), \(j=1,\ldots ,m\)
-
1.
-
h)
for \({\boldsymbol{A}}\subset {\boldsymbol{C}}\), \(i\in {\boldsymbol{A}}\), the state vector \((k_i,\overrightarrow{x}_{-i})\in \mathfrak C_{\boldsymbol{A}}\) is such that \(k_i\in \mathfrak C_i\) and
 .
.
Let there be a fixed space of elements \(\boldsymbol{C}= \{1,2,...,n\}\), the spaces of their states with an order established in them  , and the set of possible states of the system
, and the set of possible states of the system  .
.
Definition 1
The general system of n components is a triplet  where
where
-
1.
the mapping
 is surjection;
is surjection; -
2.
an inverse image of state set
 has following property. If
has following property. If 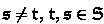 , then $$\begin{aligned} V_\mathfrak s(\phi ) \cap V_\mathfrak t(\phi ) = \emptyset , \end{aligned}$$
, then $$\begin{aligned} V_\mathfrak s(\phi ) \cap V_\mathfrak t(\phi ) = \emptyset , \end{aligned}$$where for any
 , \(V_\mathfrak L(\phi )\) is given by $$\begin{aligned} V_\mathfrak L(\phi ) = \{\overrightarrow{x}\in \mathfrak C_{\boldsymbol{C}}:\phi (\overrightarrow{x}) = \mathfrak l, \qquad \text {for }\mathfrak l\in \mathfrak L\}. \end{aligned}$$
, \(V_\mathfrak L(\phi )\) is given by $$\begin{aligned} V_\mathfrak L(\phi ) = \{\overrightarrow{x}\in \mathfrak C_{\boldsymbol{C}}:\phi (\overrightarrow{x}) = \mathfrak l, \qquad \text {for }\mathfrak l\in \mathfrak L\}. \end{aligned}$$For subset \(\mathfrak L=\{\mathfrak l\}\) we write \(V_\mathfrak l(\phi )\).
We define the natural classes of system by specifying the \(\phi \) mapping properties. We also specify the unique properties of the system.
- \(\alpha \):
-
A system
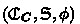 is increasing if and only if for every \(\overrightarrow{x},\vec {y} \in \mathfrak C_{\boldsymbol{C}}\), \( \overrightarrow{x}\preccurlyeq _{\mathfrak C_{\boldsymbol{C}}} \vec {y}\) we have
is increasing if and only if for every \(\overrightarrow{x},\vec {y} \in \mathfrak C_{\boldsymbol{C}}\), \( \overrightarrow{x}\preccurlyeq _{\mathfrak C_{\boldsymbol{C}}} \vec {y}\) we have  .
. - \(\beta \):
-
Component i is essential (relevant) for a system \(\phi \) if and only if

i.e., any changing the system state is possible by changing the state of the i-th element.
- \(\gamma \):
-
The system is called relevant if and only if every element is relevant to the system.
Definition 2
The system is called a coherent if and only if the mapping \(\phi \) is increasing and relevant.
Example 1
Various description of there same structure. Consider the layout of the elements connected according to the scheme in the Fig. 1. The set of all items is \( \boldsymbol{C}= \{c_1\ldots , c_5 \}\). The set of \( \boldsymbol{A}= \{c_1,c_2 \} \) elements is a series system with model \((\{0,1\}_{\boldsymbol{A}},\mathfrak A,\varphi _{\boldsymbol{A}})\), where \(\varphi _{\boldsymbol{A}}(x_1,x_2)=\prod _{j\in \boldsymbol{A}}x_j\in \mathfrak A=\{\mathfrak t_0,\mathfrak t_1\}\). The rest of the elements– \(\boldsymbol{B}=\{c_3,c_4,c_5\}\), forms another subsytem – which can take four states:  . For example, a combined car lamp with frosted glass gives different light intensity in different states. The user does not know which elements are functional and which are damaged – so the original model
. For example, a combined car lamp with frosted glass gives different light intensity in different states. The user does not know which elements are functional and which are damaged – so the original model

is useless in this case because the system has more than two states. We can propose for part B the model: \((\{0,1\}_{\boldsymbol{B}},\mathfrak B,\psi _{\boldsymbol{B}})\), where

and the model of hole system \((\{0,1\}_{\boldsymbol{C}},\mathfrak B,\phi )\) with the structure function

2.2 Introductory Characteristic for the Importance Measure
There are at least two major reasons why we should investigate a measure of importance of components in a system. First of them is a need to specify the elements of the system that contribute to its destruction to a greater extent and directly lower system reliability, which is why they should be subjected to more attentive observation, so one can focus on development while saving costs. The second reason is the ability to choose the most effective way to recognize system damage by creating a repair checklist helpful in further analysis. However, it must be emphasized that there is no universal measure that can be used anytime regardless of the circumstances. Such measures for the binary system based on the binary elements are presented in [37] (v. [30, Chap. 3]). In this chapter, following [24, Chap. 6] and paper cited therein, some extension of importance analysis of the elements based on the idea of multistate system is considered. The research aims attention on components’ importance measures that could be versatile, focusing on items that can be repaired at the specific period of time.
In practice, we can deal with systems in which the possible sets of the states of individual elements can be different and the states of the system are not of the same type as the states we assign to the elements of the system. However, in this analysis we can disregard the meaning of individual states. The important thing is that the number of states of individual elements is finite and there is an established order in the set of states. Where there may be ambiguities, we will label the states of the system with German Fracture letters with indexes and states of the elements by the Latin letters. To comply with the notations adopted in the former studies (v. [23]), the states are indexed from 0 to M, so if  ), then \(M=s\). We assume that low indices correspond to worse states, and higher ones to better ones. When switching from a multistate to a binary system, we can assume that the number of states has been reduced:
), then \(M=s\). We assume that low indices correspond to worse states, and higher ones to better ones. When switching from a multistate to a binary system, we can assume that the number of states has been reduced:  . For given states \(\overrightarrow{x}\in \mathfrak C_{\boldsymbol{C}}\) we have the state of the system
. For given states \(\overrightarrow{x}\in \mathfrak C_{\boldsymbol{C}}\) we have the state of the system  . A reduction to the binary system is determined by indication of the critical state
. A reduction to the binary system is determined by indication of the critical state  which by the order structure of
which by the order structure of  define maximal index of worse states \(j^\star \) is such that
define maximal index of worse states \(j^\star \) is such that  . Let
. Let  be such state. This choice of critical element reduce the state space as follows:
be such state. This choice of critical element reduce the state space as follows:  .
.
Following Natvig [23, p. 525], let us introduce notations:  ,
,  , where
, where  . Define
. Define  and
and  .
.
Definition 3
A multistate monotone system with the space of elements \(\boldsymbol{C}\) is called
-
a)
the multistate serial system if \( \phi _\mathbf{MSs }(\overrightarrow{x}) = \displaystyle \min _{1\le i \le n} x_i \);
-
b)
the multistate parallel system \( \phi _\mathbf{MPs }(\overrightarrow{x}) = \displaystyle \max _{1\le i \le n} x_i \).
Definition 4
A multistate monotone system with the space of elements \(\boldsymbol{C}\) and the structure function \(\phi \) is called strongly coherent if
and for every \(j \in \mathfrak M\setminus \{0\}\), \(i \in \boldsymbol{N}\) we have
where  and \(\mathfrak S_{i,j}^1=\mathfrak S_{i\boldsymbol{A}_{\mathfrak F}\prime }\).
and \(\mathfrak S_{i,j}^1=\mathfrak S_{i\boldsymbol{A}_{\mathfrak F}\prime }\).
Remark 1
Furthermore, let us assume that for \(i\in \boldsymbol{C}\), \(|\boldsymbol{C}|=n\) the i-th component has the random state \(X_i(t)\in \mathfrak C_i\) at time t. With the corresponding vector of independent random processes  we have description of the states of all elements of the system, and the corresponding state of the system is given by
we have description of the states of all elements of the system, and the corresponding state of the system is given by  . Without losing generality, we can use indexes of system components and state indexes, both for elements and for the entire system, instead of state names. In the following part we will denote the set of elements as \(\boldsymbol{N}\) (instead of \(\boldsymbol{C}\), \(|\boldsymbol{N}|=n\), and the sets of states \(\mathfrak C_{\cdot }\) and \(\mathfrak M\). If this does not lead to an ambiguity, it will be \(\mathfrak C_i = \mathfrak M=\{0, \ldots , M\}\). To emphasize the different sizes of state sets, where it is important, we will mark it by indexing state sets (e.g. \(\mathfrak M_r\)).
. Without losing generality, we can use indexes of system components and state indexes, both for elements and for the entire system, instead of state names. In the following part we will denote the set of elements as \(\boldsymbol{N}\) (instead of \(\boldsymbol{C}\), \(|\boldsymbol{N}|=n\), and the sets of states \(\mathfrak C_{\cdot }\) and \(\mathfrak M\). If this does not lead to an ambiguity, it will be \(\mathfrak C_i = \mathfrak M=\{0, \ldots , M\}\). To emphasize the different sizes of state sets, where it is important, we will mark it by indexing state sets (e.g. \(\mathfrak M_r\)).
2.3 Nonrepairable Coherent Multistate Systems
First, we will focus on multistate systems, where repair of the components is not permitted. Let assume that
-
a)
\(\mathfrak C_i=\mathfrak C\), where \(i\in \boldsymbol{N}\)
-
b)
\(X_i(t)\), for \(t \ge 0 \) and \(i\in \boldsymbol{N}\), is a Markov process on the probability space \((\Omega ,{\mathcal F},\mathbf{P} )\) with continuous time and the state space \(\mathfrak M_i\).
-
c)
\(X_i(0)=M_i\), which means that all components are in the properly functioning state \(M_i\), \(i\in \boldsymbol{N}\), at time \(t=0\).
Furthermore, let present some notation
where at time t: reliability of the i-th component to the level j is given by \(p_i^j(t)\) while \(p_{\phi }^j (r(t))\) is the reliability of the i-th component to the system [23]. To simplify, let us accept that for \(0\le l < k \le M\) we have \(\lambda _i^{(k,l)}(t)=0\). Moreover, let us assume that for each component i, time spent in state k before change to state \(k-1\), has a continuous distribution \(F_i^k(t)\) with density \(f_i^k(t)\). It is assumed that the times spent in particular states are independent random variables. Besides that, let us introduce row vector with dimension \(M+1\), such as
2.3.1 The Birnbaum’s Importance Measure
In [37] we discussed Birnbaum’s importance measure for the binary system, while in this Sect. 2.3.1 we propose a measure for a non-repairable and multi-state system - generalized weighted and not weighted Birnbaum’s measure. These measures help in judgment which components of the system are the most valuable and important for the faultless functioning and higher reliability of the system. Nevertheless, they measure importance only at fixed points of the time. Furthermore, they are not dependent on the i-th component, what means that the importance of the system is dependent on the operation of all components. Generalized Birnabaum’s measure \(I_B^{(i,k,j)}(t)\) is the probability at time t that the system is in such state, in which its functioning of i-th component in state k is decisive for the system to be in \(\{j,...,M\}\) states [23]. It is formulated as
where \(i\in \boldsymbol{N}\), and \(j,k\in \mathfrak M{\setminus }\{0\}\). Since \( \sum _{k=0}^M r_i^k(t)=1\) for \(i=1,...,n\), \(p_i^k(t)=1\), for \(k<1\), and \(p_i^k(t)=0\), for \(k>M\), then
When \(i\in \boldsymbol{N}\) and \( j,k\in \mathfrak M{\setminus }\{0\}\), we obtain
For case of \(M=1\) we have a corresponding Birnbaum’s importance measure (v. [37]).
In some cases, it is better to use the weighted Birnbaum’s measure for the multistate system. Hence, for critical state \(j\in \mathfrak M{\setminus }\{0\}\) an utility \(w'\) of being in particular states is assigned in such a way that \(w'(\mathfrak s)=w_j\mathbb {I}_{\{\mathfrak s\succeq \mathfrak s_j\}}(\mathfrak s)+w_j^c\mathbb {I}_{\mathfrak s\prec \mathfrak s_j}(\mathfrak s)\) where \(w_j \ge w_j^c\), \(\{w_j\}_{j=1}^M\) and \(\{w_j^c\}_{j=1}^M\) are nonincreasing. We have for the system leaving the set of states \(\{j,...,M\}\) a utility loss \(c_j=w_j - w_j^c\ge 0\). Without losing generality, we can additionally impose a condition \(\sum _{j=1}^M c_j =1\) on these losses.
The generalized weighted Birnbaum’s measure takes the form
while generalized Birnbaum measure is expressed by
We have \(\sum _{i=1}^n \hat{I}_B^{(i)}(t) = \sum _{i=1}^n I_B^{(i,j)}(t) = 1\).
2.3.2 The Barlow-Proschan Importance Measure
The Barlow-Proschan measure also helps in deciding, which components of the system are the most valuable for the proper functioning of the system and achieving its greater reliability. Moreover, the system failure reason can be identified via repair checklist generation. The Barlow and Proschan importance measure \(I_{B-P}^{(i)}\) of the i-th component is the probability that leaving the states \(\{1,...,M\}\) by the system converges in time with the jump down of the i-th component and is denoted as
where \(j\in \{0,...,M\}\), \(i=1,...,n\) and \(\sum _{i=1}^n I_{B-P}^{(i,j)} = 1\). For a binary case when \(M=1\), there is a following relationship
The Barlow-Proschan measure also occurs in generalized weighted form \(\hat{I}_{B-P}^i\) and the importance of the i-th component is denoted as
Weighted and nonweighted generalized Barlow-Proschan measure are in fact generalized Birnbaum measure’s weighted averages. These measures indicates that when component’s importance increases, the chance of this component to be the direct reason of the system worsening also increases.
2.3.3 The Natvig Importance Measure
The Natvig measure concentrates on how component’s transition between states influence performance of the system regarding the given system state.
For \(k\in \{0,...,M-1\}\) and \(i=1,...,n\) let introduce \(T_{i,k}\) which stands for the i-th component’s time of the jump into state k and \(T_{i,k}'\) is an assumed time of the i-th component’s jump into state k after it was believed to undergo a minimal repair at \(T_{i,k}\). Next, for \(j\in \{1,...,m\}\), \(k\in \{1,...,M\}\), \(i=1,...,n\) and interval \([T_{i,k-1},T_{i,k-1}']\) we have \(Y_{i,k,j}^1\) which is the system time in \(\{j,...,M\}\) states right away the i-th component changed it state from k to \(k-1\) and then instantly is a subject of the fictive minimal repair. Furthermore, \(Y_{i,k,j}^0\) has the same definition as \(Y_{i,k,j}^1\), however, at the end the i-th component does not undergo repair immediately, it stays in the state \(k-1\) for the whole interval \([T_{i,k-1},T_{i,k-1}']\), such that
Hence, for \(j\in \{1,...,M\}\), \(k\in \{1,...,M\}\), \(i=1,...,n\) and applying the expectation with assumption \(\mathbf {E}Z_{i,k,j} < \infty \) , we obtain from (3), the generalized Natvig importance measure of the i-th component \(I_N^{(i,j)}\) and its weighted version \(\hat{I}_N^{(i,j)}\), given by
Thus, the weighted Natvig measure may be interpreted as the extended, more sophisticated Barlow-Proschan’s weighted measure.
2.4 Repairable Coherent Multistate Systems
In this section we analyze importance measures of multistate systems, where components can be repaired after their failure. We assume that components are in state M at time \(t=0\), that is all of them are functioning properly. To simplify, we set the assumption of complete degradation from fully functioning state to the absolute failure state. Furthermore, in the repairable system for each component i, time spent in the state k before its transition to the state \(k-1\), has a fully continuous distribution \(F_i^k(t)\) with density \(f_i^k(t)\) and mean \(\mu _i^k\). Moreover, we accept that repair time of the i-th element has a density \(g_i(t)\), fully continuous distribution \(G_i(t)\) and mean \(\mu _i^0\) with independent times spent in particular states.
Let present the notation for such system
where \(a_i^j(t)\) at time t is the i-th component availability at level j and \(p_{\phi }^j(a(t))\) at time t is the system availability to level j. For \(j\in \mathfrak M\) and \(i\in \boldsymbol{N}\) there are corresponding availabilities
To simplify, let denote \(a(t) \equiv a\).
2.4.1 The Birnbaum Importance Measure
The generalized Birnbaum importance measure in the multistate repairable system is given by
where \(i=1,...,n\), \(j,k\in \{1,...,M\}\). From (1), (2) and (4) we may propose stationary measures for the same \(i,\ j,\ k\), expressed as
2.4.2 Universal Generating Function
Let us consider a multistate system in steady state with a constant demand w, (v. [20]), then we are able to extend the Birnbaum measure of the component importance
where \(p_{ij}\) stands for the probability of i-th component being in the specific state j with a rate of performance \(g_{ij}\) and A(w) is a multistate system’s steady-state availability with a constant demand w, given by
where \(j\in \mathfrak M{\setminus }\{0\}\), \(p_i\) is a steady-state probability that the system’s performance is equal \(g_i\) and \(F(g_i,w)\) is a function of acceptability.
Let introduce a universal generating function (UGF) u(z), for the i-th component with \(m_i\) number of states \(g_{ij}\) and corresponding probabilities \(p_{ij}\), Lisnianski [20], Qin et al. [29], we have
Therefrom, we have a u-function U(z), expressed by
Demand can be a variable and then it may be described with two vectors: \(w=\{w_1,...,w_M\}\), where \(w_i\) is a possible level of demand, and \(q =\{q_1,...,q_M\}\), where \(q_i\) is a matching steady-state probability. Then, the extended Birnbaum’s importance for any j-th component is given by
These importance measures depend on the i-th component’s system position, its performance level and system demand. The UGF method, due to the simpler calculations and not necesarlly using Markov approach, is an excellent choice of computing importance.
2.4.3 The Barlow-Proschan Importance Measure
For \(j,k \in \{1,...,M\}\) and \(i=1,...,n\) let introduce the number of jumps \(N_i^{(k)}(t)\) from state k to \(k-1\) of the i-th component in the time interval [0, t], \(\tilde{N}_i^{(k,j)}(t)\) which is the number of times in [0, t], when system leaves states \(\{j,...,M\}\) as a result of the i-th component jump from state k to \(k-1\) and \(\mathbf {E}N_i^{(k)}(t) \equiv M_i^{(k)}(t)\). From [4] for \(j,k \in \{1,...,M\}\) and \(i=1,...,n\), we have
with \(I_B^{(i,k,j)}(t)\) defined as (4). Thus, time dependent generalized Barlow and Proschan importance measure \(I_{B-P}^{(i,j)}(t)\) of the i-th component in the interval [0, t] in the multistate repairable system and the corresponding weighted importance measure \(\hat{I}_{B-P}^{(i)}(t)\) is given by
where \(0\le I_{B-P}^{(i,j)}(t) \le 1\) and \(\sum _{i=1}^n I_{B-P}^{(i,j)}(t)=1\),
where \(0\le \hat{I}_{B-P}^{(i)}(t) \le 1\) and \(\sum _{i=1}^n \hat{I}_{B-P}^{(i)}(t)=1\).
Denote \(\mu _i=\sum _{l=0}^M \mu _i^l\) and \(\bar{I}_{B}^{(i,j)}=\sum _{k=1}^MI_{B}^{(i,k,j)}\cdot \mu _i^{-1}\). From Barlow and Proschan [4] we introduce analogous stationary measures
where \(\hat{I}_{B-P}^{(i,j)}\) is the weighted average of \(I_{B-P}^{(i,j)}\), which is exactly the probability of component i downward jump being the reason that the system leaves \(\{j,...,M\}\) states.
Theorem 1
For the multistate repairable system in series, where \(\phi (x) = \min \limits _{1\le i\le n}x_i\), \(i=1,...,n\) and \(j \in \{1,...,M\} \), we have
Proof
Theorem 2
For the multistate repairable parallel system, where \(\phi (x) = \max \limits _{1\le i\le n}x_i\), \(i=1,...,n\) and \(j \in \{1,...,M\} \), we obtain
For the multistate system in series the stationary Barlow and Proschan importance measure of the component i decreases in \(\mu _i^k\) for \(k=j,...,M\), the weaker the more important, and unsatisfactory is not dependent on component’s mean time to repair.
Proof
The proof for the parallel system is analogous to the proof of the theorem 1
For the multistate system in parallel the stationary Barlow and Proschan importance measure of the component i also decreases in \(\mu _i^k\) for \(k=1,...,j-1\) and in the \(\mu _i^0\), hence the better the more significant. Nonetheless, in this case the measure depends on mean times to repair of the component and also on mean times to jumps downward.
Theorem 3
Let the component i be serial (\(\phi (x)=min(x_i,\phi (M_i,x))\)) or parallel (\(\phi (x)=max(x_i,\phi (0_i,x))\)) to the system. For \(j\in \{1,...,M\}\) and \(k\ne i\) let \(\sum _{l=j}^M \mu _i^l \le \mu _k^M\) in series case and \(\sum _{l=0}^{j-1} \mu _i^l \le \mu _k^0\) in the parallel case, then \(I_{B-P}^{(i,j)} \ge I_{B-P}^{(k,j)}\). In addition, the numerator has corresponding properties. Hence,
2.4.4 The Natvig Importance Measure
The Natvig measure for the multistate repairable systems is a natural extension of the one for nonrepairable system 2.3.3. For \(m=1,2,...\), \(k\in \{0,...,M\}\) and \(i=1,...,n\) we introduce the i-th component’s time of the m-th jump into state k given by \(T_{i,k,m}\) and the i-th component’s length of the m-th time of repair \(D_{i,m}\), such that
For the same i and m and \(k\in \{0,...,M-1\}\) we introduce a \(T_{i,k,m}'\), which is a fictive time of the i-th component’s m-th jump into state k after it was believed to undergo a fictive minimal repair at \(T_{i,k,m}\). Now, for the same i, m and \(j, k \in \{1,...,M\}\) we define \(Y_{i,k,j,m}^1\) as the time of the system in \(\{j,...,M\}\) states in the period \([min(T_{i,k-1,m,t},t), min(T_{i,k-1,m,t}',t)]\) immediately after the i-th component changes the state from k to \(k-1\) and then its prompt fictive minimal repair. \(Y_{i,k,j,m}^0\) is defined the same as \(Y_{i,k,j,m}^1\), however it is assumed that the i-th component stays in its state and does not undergo any repair. Hence, we have
To examine the effect of the fictitious minimal repairs, we need to sum up their contribution. Thus, for \(j\in \{1,...,M\}\), \(k\in \{1,...,M-1\}\), \(i=1,...,n\), and applying the expectation we obtain
Hence, for \(j,k\in \mathfrak M\setminus \{0\}\), \(i\in \boldsymbol{N}\) and assumption \(\mathbf {E}Y_{i,k,j}(t) < \infty \) , we obtain the generalized Natvig importance measure of the i-th component in the period of time [0, t] expressed by \(I_N^{(i,j)}(t)\) and its weighted version \(\hat{I}_N^{(i,j)}(t)\), given by
where \(0 \le I_N^{(i,j)}(t) \le 1\) and \(\sum _{i=1}^n I_N^{(i,j)}(t)= 1\),
where \(0 \le \hat{I}_N^{(i)}(t) \le 1\) and \(\sum _{i=1}^n \hat{I}_N^{(i)}(t) = 1\).
Theorem 4
For \(k \in \{1,...,M-1\}\)
The proof of the theorem can be found in Natvig [23]. Expressions in theorem 4 can be transformed into corresponding stationary importance measures by dividing by t and applying limit with respect to \(t\rightarrow \infty \) and renewal theory argument presented by Barlow and Proschan [4]:
where
Theorem 5
For the multistate repairable series system, where \(j \in \{1,...,M\} \) and \(i=1,...,n\), we have
and for parallel case we obtain
Thus, the stationary measures (8) for the multistate system in series give unsatisfactory results due to not being dependent on components’ mean time to repair. Unlike the series case, the stationary measure for the parallel system depend on mean time to repair as well as on the distribution of the downward transitions of components’ states.
2.4.5 The Natvig Measure - Dual Extension
Since the Natvig measure does not give satisfactory results for all multistate systems, we introduce its dual extension. Now, for \(m=1,2,...\) and \(i=1,...,n\), \(T_{i,M,m}'\) is a fictive time of the i-th component’s m-th jump into state M following a fictive minimal total failure at \(T_{i,M,m}\). For the same i, m and \(j \in \{1,...,M\}\) we define \(Y_{i,0,j,m}^1\) as the time of the system in \(\{0,...,j-1\}\) states in the period \([min(T_{i,M,m,t},t), min(T_{i,M,m,t}',t)]\) immediately after the i-th component state transition from 0 to M and its prompt fictive minimal total failure. \(Y_{i,0,j,m}^0\) is defined the same as \(Y_{i,k,j,m}^1\), however it is assumed that the i-th component stays in its state for the whole period. Hence, we have
To examine the effect, we need to sum up repair contributions at \(T_{i,M,m}\). Thus, for \(i=1,...,n\), \(j\in \{1,...,M\}\), \(m=1,2,...\), and applying the expectation, we obtain
Theorem 6
For \(j\in \{1,...,M\}\) and \(i=1,...,n\)
Hence, from (9) and Theorem 6, for \(j\in \{1,...,M\}\), \(i=1,...,n\), \(k\in \{0,...,M\}\), and assumption of \(\mathbf {E}Y_{i,k,j}(t) < \infty \), we obtain the dual generalized non-weighted and weighted Natvig measure, \(I_{D,N}^{(i,j)}(t)\) and \(\hat{I}_{D,N}^{(i)}(t)\) respectively, given by
where \(0 \le I_{D,N}^{(i,j)}(t) \le 1\) and \(\sum _{i=1}^n I_{D,N}^{(i,j)}(t) = 1\)
where \(0 \le \hat{I}_{D,N}^{(i)}(t) \le 1\) and \(\sum _{i=1}^n \hat{I}_{D,N}^{(i)}(t) = 1\). Moreover, for the same \(i,\ k,\ j\), and assumption of \(\mathbf {E}Y_{i,k,j}(t) < \infty \), we may introduce extended versions of (10a) - \(I_N^{*(i,j)}(t)\) and (10b) - \(\hat{I}_N^{*(i)}(t)\), denoted as
where \(0 \le I_N^{*(i,j)}(t) \le 1\), \(\sum _{i=1}^n I_N^{*(i,j)}(t) = 1\). We have \(\hat{I}_N^{*(i)}(t) = \sum _{j=1}^M c_j \cdot I_N^{*(i,j)}(t)\), where \(0 \le \hat{I}_N^{*(i)}(t) \le 1\) and \(\sum _{i=1}^n \hat{I}_N^{*(i)}(t) = 1\). Furthermore, corresponding stationary measures for (10) are
where
Theorem 7
For the multistate repairable series system, where \(j \in \{1,...,M\} \) and \(i=1,...,n\), we have
and for parallel case we obtain
Thus, for both parallel and series repairable multistate system, the extended generalized Natvig measures depend on the repair times distribution and on the component’s distribution of time to downward jumps, what gives a desirable results.
3 State Dependent Importance Measure
As in the case of binary systems and semi-coherent structures (v. [37]), also in multistate systems, we ask about the role (importance) of the structure element in maintaining it in the analyzed state. We focus on the element and its state \(c_{ij}\). The responsibility for that is the place of the element in the structure and an inner properties of it emanated by its state. These are the basis for assessing its meaning. The set of elements of the system should be described their states: \({\mathcal C}={\mathcal E}\times {\mathcal S}=\{(\overrightarrow{\mathbf{C }}_1,\overrightarrow{\mathbf{C }}_2,\ldots ,\overrightarrow{\mathbf{C }}_s): c_{ij}\in E\times S\}\), where vector components are the elements state. Let us imagine that each element has its administrator. If we treat the administrator of element in the system a player in a cooperative game, then in multi-state systems the tendency to remain in the examined state requires identifying the sets of elements (coalitions) responsible for that: the element and its state. The system may be in one of the numbered states \( j\in S =\{ 1,2,\ldots , K\} \). Let \(\mathfrak {P}_{ij}\) be a family of sets of states such that if \({\mathcal A}\in \mathfrak {P}_i\), \( c_{ij} \in {\mathcal A}\), then \({\mathcal A}{\setminus } \{c_{ij}\} \notin \mathfrak {P}_{ij}\). Let \(\bar{\mathfrak {P}}_{ij}\) be a family of sets created from sets of the \(\mathfrak {P}_{ij}\) family by removing critical elements. We will take such a family as the basis for the aggregation of structure elements and, similarly to the multiplayer model with stopping moments as strategies (v. Szajowski and Yasuda [35]), the signal to stop will be the agreement of the elements from the set belonging to this family \(\bar{\mathfrak {P}}_{ij}\) (the coalitions between elements are formed taking into account thier states).
Multi-player decision problems assume that each game participant has a preference function based on a scalar function defined on the states of a certain process. If the elements of the structure are assigned to conservators (hypothetical players) who take care of the condition of these elements so that they fulfill their functions properly, the mentioned function can estimate profits and losses resulting from the state of the element. In principle, this condition should be form the set S. However, in reality, it is the diagnostician who decides when to perform maintenance or replacement (and bear the cost of it). An element in a system usually lowers its efficiency (e.g., mating components in a driveline may need lubrication to reduce friction, which results in increased energy expenditure and lower system efficiency), but the maintenance downtime is wasted and cannot always be managed. The operating conditions of the system make it possible to determine the correct payment function (cost) for each maintenance technician. Each of the n (which are less or equal the number of the elements in the structure) conservators, observing the states on which its payment depends, decides whether to order a maintenance break or to carry out uninterrupted operation. For safety reasons and the structure of the system, it is clear whether such a decision of a single observer is effective - it can start work when the system is stopped, and the stoppage requires the consensus of conservators from some critical path.
To analyze the effects of action, we will use the model of the following antagonistic game with elements of cooperation defined by the \(\mathfrak {P}_{ij}\), which are defined by the functionality of the structure and the state of the element i. Further consideration in this section assume that the conditionality structure is determined by \(\mathfrak {P}_{ij}\).
Following the results of the author and Yasuda [35] the multilateral stopping of a Markov chain problem can be described in the terms of the notation used in the non-cooperative game theory (see [21, 22, 27]). To this end the process and utilities of its states should be specified.
Definition 5
(ISS-Individual Stopping Strategies). Let \((\overrightarrow{X}_n,{\mathcal F}_n,\mathbf{P }_x)\), \(n=0,1,2,\ldots ,N\), be a homogeneous Markov chain with the state space \((\mathbb {E},{\mathcal B})\).
-
The players are able to observe the Markov chain sequentially. The horizon can be finite or infinite: \(N\in \mathbb {N}\cup \{\infty \}\).
-
Each player has their utility function \(f_i: \mathbb {E}\rightarrow {\mathfrak {Re}} \), \(i=1,2,\ldots ,p\), such that \({\mathbf {E}}_x|f_i(\overrightarrow{X}_1)|<\infty \) and the cost function \(c_i: \mathbb {E}\rightarrow \mathfrak {Re} \), \(i=1,2,\ldots ,p\).
-
If the process is not stopped at moment n, then each player, based on \({\mathcal F}_n,\) can declare independently their willingness to stop the observation of the process.
Definition 6
(see [40]). An individual stopping strategy of the player i (ISS) is the sequence of random variables \(\{\sigma _n^i\}_{n=1}^N\), where \(\sigma _n^i:\Omega \rightarrow \{0,1\}\), such that \(\sigma _n^i\) is \({\mathcal F}_n\)-measurable.
The interpretation of the strategy is following. If \(\sigma _n^i=1\), then player i declares that they would like to stop the process and accept the realization of \(X_n\).
Definition 7
(SS–Stopping Strategy (the aggregate function).). Denote
and let \({\mathscr {S}}^i\) be the set of ISSs of player i, \(i=1,2,\ldots ,p\). Define \({\mathscr {S}}={\mathscr {S}}^1\times {\mathscr {S}}^2\times \ldots \times {\mathscr {S}}^p\). The element \(\sigma =(\sigma ^1,\sigma ^2,\ldots ,\sigma ^p)^T\in {\mathscr {S}}\) will be called the stopping strategy (SS).
The stopping strategy \(\sigma \in {\mathscr {S}}\) is a random matrix. The rows of the matrix are the ISSs. The columns are the decisions of the players at successive moments. The factual stopping of the observation process, and the players realization of the payoffs is defined by the stopping strategy exploiting p-variate logical function.
Let \(\delta :\{0,1\}^p\rightarrow \{0,1\}\) be the aggregation function. In this stopping game model the stopping strategy is the list of declarations of the individual players. The aggregate function \(\delta \) converts the declarations to an effective stopping time.
Definition 8
(An aggregated SS). A stopping time \(\tau _\delta (\sigma )\) generated by the SS \(\sigma \in {\mathscr {S}}\) and the aggregate function \(\delta \) is defined by
\((\inf (\emptyset )=\infty )\). Since \(\delta \) is fixed during the analysis we skip index \(\delta \) and write \(\tau (\sigma )=\tau _\delta (\sigma )\).
Definition 9
(Process and utilities of its states).
-
\(\{\omega \in \Omega : \tau _\delta (\sigma )=n\} =\bigcap \nolimits _{k=1}^{n-1}\{\omega \in \Omega : \delta (\sigma _k^1,\sigma _k^2,\ldots ,\sigma _k^p)=0\} \cap \{\omega \in \Omega :\delta (\sigma _n^1,\sigma _n^2,\ldots ,\sigma _n^p)=1\}\in {\mathcal F}_n\);
-
\(\tau _\delta (\sigma )\) is a stopping time with respect to \(\{{\mathcal F}_n\}_{n=1}^N\).
-
For any stopping time \(\tau _\delta (\sigma )\) and \(\mathfrak i\in \{1,2,\ldots ,p\}\) the payoff of player \(\mathfrak i\) is defined as follows (cf. [33]):
$$ f_i(X_{\tau _\delta (\sigma )})=f_i(X_n)\mathbb {I}_{\{\tau _\delta (\sigma )=n\}}+\limsup _{n\rightarrow \infty }f_i(X_n)\mathbb {I}_{\{\tau _\delta (\sigma )=\infty \}}. $$
Definition 10
(An equilibrium strategy (cf. [35])). Let the aggregate rule \(\delta \) be fixed. The strategy \({}^{*}\!\sigma =({}^{*}\!\sigma ^1,{}^{*}\!\sigma ^2,\ldots ,{}^{*}\!\sigma ^p)^T\in {\mathscr {S}}\) is an equilibrium strategy with respect to \(\delta \) if for each \(\mathfrak i\in \{1,2,\ldots ,p\}\) and any \(\sigma ^i\in {\mathscr {S}}^i\) we have
Definition 11
(Voting Game Importance). Let the aggregate rule \(\delta =h \) be fixed and the strategy \({}^{*}\!\sigma =({}^{*}\!\sigma ^1,{}^{*}\!\sigma ^2,\ldots ,{}^{*}\!\sigma ^p)^T\in {\mathscr {S}}\) be an equilibrium strategy with respect to \(\delta \). The voting game importance of the elements is the component of
The measure of significance of a structure element introduced in this way takes into account its role in the structure by the aggregation function h, it is normalized in the sense that the measures of all elements sum up to 1. It takes into account the external loads of elements, the cost of maintenance and repairs. Its use requires in-depth knowledge of the system and its components, which is a significant obstacle in its introduction into diagnostic practice. The hardest part is figuring out the payout functions (cost, risk, profit). The simplified version of the method may include in the payout functions only the operating risk with components in a condition requiring maintenance or repair, which is usually associated with less safety.
4 Concluding Remarks
4.1 Summary
Ensuring the reliability and secure performance of the simple as well as complex systems has an indisputable significance in system analysis. Therefore, the aim of the research was to answer the question how to recognize the most influential elements of the system to improve its reliability. This paper has demonstrated several approaches to the concept of importance measure depending on the parameters and assumptions characterizing the system.
This analysis showed that the importance measures first introduced by Birnbaum in 1968 became the foundation for further search of more convenient and versatile definitions of the importance of components in system reliability and the stable exploration of the multistate systems. Since then, the research has expanded in different directions but until nowadays the importance evaluation of highly complex structures such as networks may cause many computational problems. Besides, restrictions regarding coherence may exclude examination of certain systems. Therefore, this subject is under constant exploration.
4.2 Important Direction of Further Investigations
Wu and Coolen [39], when interpreting component importance, concluded that the importance of a component should depend on the following factors:
-
1.
The location of the component in the system.
-
2.
The reliability of the component.
-
3.
The uncertainty in the estimate of the component reliability and related cost.
-
4.
The costs of maintaining this component in a given time interval (0, t) and the state.
(v. also Rausand et al. [31]). The factor (3) highly depends on the statistical method implemented in the analyzes of exploratory data analyzes. Due to source of the data, the role of structure of the system to the reliability of it, the importance measure should take these elements into accounts. We are not observing the hidden state of the system directly and the information taken from the sensors should by interpreted and evaluated to infer on the hidden state of the elements and the system. The details of the construction needed, based on the results by Szajowski [36], are subject of a paper under editorial process. The works known to us show that betweenness centrality measure (v. Freeman [16]) is closely related to the Shapley value and Banzhaf value (v. Grofman and Owen [19]), and thus to importance measure in the reliability theory. While authors find it more convenient to use the terminology of reliability theory, the reader may as well transition to the terminology introduced by Freedman in community science. It would be at least potentially usable to discuss the various discoveries in general classification of the network elements by the game theory methods (v. e.g. Skibski et al. [34]).
Notes
- 1.
System (in Ancient Greek:
 – romanized: systema – a complex thing) – a set of interrelated elements realizing the assumed goals as a whole.
– romanized: systema – a complex thing) – a set of interrelated elements realizing the assumed goals as a whole. - 2.
The foundation of stochastic methods in the reliability theory can be found in the monograph by Barlow and Proschan [5].
- 3.
The definition of state “working” is defined as ready to perform some list of tasks.
- 4.
- 5.
An ordered set for which any two elements(i.e. states) can be compared–in this context every two states should be compared.
- 6.
The operator \(P_{\boldsymbol{B}}\) is sometimes denoted \(P_{\mathfrak C_{\boldsymbol{B}}}\).
- 7.
The list of symbols and abbreviations used in the work has been collected in the section abbreviation on page 25.
- 8.
With the same symbol, we denote the system and the analytical description of the system using the structure function wherever it does not lead to misunderstandings.
References
Abouammoh, A.M., El-Neweihi, E., Sethuraman, J.: The role of a group of modules in the failure of systems. Prob. Eng. Inf. Sci. 8(1), 89–101 (1994). https://doi.org/10.1017/S0269964800003223
Amrutkar, K.P., Kamalja, K.K.: An overview of various importance measures of reliability system. Int. J. Math. Eng. Manag. Sci. 2(3), 150–171 (2017)
Artzner, P., Delbaen, F., Eber, J.-M., Heath, D.: Coherent measures of risk. Math. Financ. 9(3), 203–228 (1999). https://doi.org/10.1111/1467-9965.00068. ISSN 0960-1627; 1467–9965/e
Barlow, R.E., Proschan, F.: Importance of system components and fault tree events. Stoch. Proc. Their Appl. 3(2), 153–173 (1975). https://doi.org/10.1016/0304-4149(75)90013-7. ISSN 0304-4149
Barlow, R.E., Proschan, F.: Mathematical Theory of Reliability. Classics in Applied Mathematics, vol. 17. SIAM, Philadelphia (1996). ISBN 0-89871-369-2. With contributions by Larry C. Hunter, Reprint of the 1965 original. https://doi.org/10.1137/1.9781611971194. MR 1392947
Barlow, R.E., Wu, A.S.: Coherent systems with multi-state components. Math. Oper. Res. 3(4), 275–281 (1978). https://doi.org/10.1287/moor.3.4.275. ISSN 0364-765X
Barlow, R.E., Fussell, J.B., Singpurwalla, N.D. (eds.) Reliability and Fault Tree Analysis. SIAM, Philadelphia (1975). Theoretical and applied aspects of system reliability and safety assessment, Conference held at the University of California, Berkeley, California, 3–7 September 1974, Dedicated to Professor Z. W. Birnbaum
Birnbaum, Z.W.: On the importance of components in a system. In: European Meeting 1968, Selected Statistical Paper, vol. 2, pp. 83–95 (1968)
Birnbaum, Z.W.: On the importance of different components in a multicomponent system. In: Krishnaiah, P. (ed.) Multivariate Analysis, II (Proceedings of Second International Symposium, Dayton, Ohio, 1968), pp. 581–592. Academic Press, New York (1969)
Cao, Y., Liu, S., Fang, Z.: Importance measures for degrading components based on cooperative game theory. Int. J. Qual. Reliabil. Manag. 37(2), 189–206 (2019). https://doi.org/10.1108/IJQRM-10-2018-0278
Do, P., Bérenguer, C.: Conditional reliability-based importance measures. Reliabil. Eng. Syst. Saf. 193, 106633 (2020). https://doi.org/10.1016/j.ress.2019.106633. ISSN 0951-8320
El-Neweihi, E., Sethuraman, J.: A study of the role of modules in the failure of systems. Probab. Eng. Inf. Sci. 5(2), 215–227 (1991). ISSN 0269-9648; 1469–8951/e
El-Neweihi, E., Proschan, F., Sethuraman, J.: A simple model with applications in structural reliability, extinction of species, inventory depletion and urn sampling. Adv. Appl. Probab. 10, 232–254 (1978). ISSN 0001-8678
Erdős, P., Rényi, A.: On random graphs. I. Publ. Math. Debrecen 6, 290–297 (1959). ISSN 0033-3883. MR 120167
Esary, J.D., Proschan, F.: Coherent structures of non-identical components. Technometrics 5, 191–209 (1963). ISSN 0040-1706; 1537–2723/e
Freeman, L.C.: A set of measures of centrality based on betweenness. Sociometry 40(1), 35–41 (1977). https://doi.org/10.2307/3033543. ISSN 00380431
Fussell, J., Vesely, W.: New methodology for obtaining cut sets for fault trees. Trans. Am. Nucl. Soc. 15(1), 262–263 (1972). 18. Annual American Nuclear Society Conference, Las Vegas, Nevada, 18 June 1972
Gilbert, E.N.: Random graphs. Ann. Math. Statist. 30, 1141–1144 (1959). https://doi.org/10.1214/aoms/1177706098. ISSN 0003-4851
Grofman, B., Owen, G.: A game theoretic approach to measuring degree of centrality in social networks. Soc. Netw. 4(3), 213–224 (1982/83). ISSN 0378-8733. https://doi.org/10.1016/0378-8733(82)90022-3
Lisnianski, A.: Multi-state System Reliability Analysis and Optimization for Engineers and Industrial Managers. Springer, London (2010). https://doi.org/10.1007/978-1-84996-320-6
Moulin, H.: Game theory for the Social Sciences. Studies in Game Theory and Mathematical Economic, New York University Press, New York (1982). ISBN 0- 8147-5386-8/hbk; 0-8147-5387-6/pbk. Transl. from the French by the author. Zbl 0626.90095
Nash, J.: Non-cooperative games. Ann. Math. 2(54), 286–295 (1951). https://doi.org/10.2307/1969529. ISSN 0003-486X. MR 43432
Natvig, B.: Measures of component importance in nonrepairable and repairable multistate strongly coherent systems. Methodol. Comput. Appl. Probab. 13(3), 523–547 (2011). https://doi.org/10.1007/s11009-010-9170-2. ISSN 1387-5841
Natvig, B.: Multistate systems reliability theory with applications. Wiley Series in Probability and Statistics, Wiley, Chichester (2011). https://doi.org/10.1002/9780470977088. ISBN 978-0-470-69750-4
Navarro, J., Arriaza, A., Suárez-Llorens, A.: Minimal repair of failed components in coherent systems. Eur. J. Oper. Res. 279(3), 951–964 (2019). ISSN 0377-2217. Zbl 1430.90217
Ohi, F.: Multistate coherent systems. In: Stochastic Reliability Modeling, Optimization And Applications, pp. 3–34. World Scientific Publishing, Co., Pte. Ltd. (2010). ISBN 9789814277440
Owen, G.: Game Theory, 4th edn. Emerald Group Publication, Limited, Bingley (2013). ISBN 987-1-7819-0507-4. MR 3443071
Ping, Z.: Measures of importance with applications to inspection policies. ProQuest LLC, Ann Arbor, MI (2004). ISBN 978-0496-73752-9. https://www.proquest.com/docview/305074799. Thesis (Ph.D.)–Univ. of Illinois at Chicago. MR 2705807
J. Qin, Y. Niu, and Z. Li. A combined method for reliability analysis of multi-state system of minor-repairable components. Eksploatacja niezawodnoŚć - Maint. Reliabil. 20(1) (2016). https://doi.org/10.17531/ein.2016.1.11
Ramamurthy, K.G.: Coherent Structures and Simple Games. Theory and Decision Library. Series C: Game Theory, Mathematical Programming and Operations Research, vol. 6. Kluwer Acadamic Publication Group, Dordrecht (1990). ISBN 0-7923-0869-7. https://doi.org/10.1007/978-94-009-2099-6
Rausand, M., Barros, A., Høyland, A.: System Reliability Theory. Models, Statistical Methods, and Applications. Wiley, Hoboken (2021). ISBN 978-1-119-37352-0. 2nd ed.: ISBN 0-471-47133-X. xix, 636 p. (2004)
Średnicka, M.: Importance measure in multi-state systems reliability. Master’s thesis, Wrocław Univ. of Sci. & Tech., Poland (2019). 40 p
Shiryayev, A.N.: Optimal Stopping Rules. Springer, New York (1978). English translation of
 by A. B. Aries
by A. B. AriesSkibski, O., Rahwan, T., Michalak, T. P., Wooldridge, M.: Enumerating connected subgraphs and computing the Myerson and Shapley values in graph-restricted games. ACM Trans. Intell. Syst. Technol. 10(2) (2019). https://doi.org/10.1145/3235026. ISSN 2157-6904
Szajowski, K., Yasuda, M.: Voting procedure on stopping games of Markov chain. In: Christer, A.H., Osaki, S., Thomas, L.C. (eds.) Stochastic Modelling in Innovative Manufacturing. Lecture Notes in Economics and Mathematical Systems, vol. 445, pp. 68–80. Springer, Heidelberg (1997). https://doi.org/10.1007/978-3-642-59105-1_6
Szajowski, K.J.: Rationalization of detection of the multiple disorders. Stat. Pap. 61(4), 1545-1563 (2020). ISSN 0932-5026; 1613-9798/e. https://doi.org/10.1007/s00362-020-01168-2. Zbl 1448.91017
Szajowski, K.J., Średnicka, M.: Operation comfort vs. the importance measure of system components. Math. Appl. 48(2), 191–226 (2020). ISSN 1730-2668. https://doi.org/10.14708/ma.v48i2.7058. MR 4243105
Tijs, S.: Introduction to Game Theory. Texts and Readings in Mathematics, vol. 23. Hindustan Book Agency, New Delhi (2003). ISBN 81-85931-37-2
Wu, S., Coolen, F.P.: A cost-based importance measure for system components: An extension of the Birnbaum importance. European J. Oper. Res. 225(1), 189–195 (2013). https://doi.org/10.1016/j.ejor.2012.09.034. ISSN 0377-2217
Yasuda, M., Nakagami, J., Kurano, M.: Multivariate stopping problems with a monotone rule. J. Oper. Res. Soc. Jpn. 25(4), 334–350 (1982). ISSN 0453-4514. https://doi.org/10.15807/jorsj.25.334. MR 692543
Funding
This research received no external funding. Springer remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Contributions
Both authors equally contributed to the conceptualization, methodology, formal analysis, investigation and writing–original draft preparation. Małgorzata Średnicka is responsible for the description of the importance measure concepts, examples, visualisation (v. [32]) and Krzysztof J. Szajowski is responsible for the project conceptualization and its administration.
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
Conflicts of Interest
The authors declare no conflict of interest.
Appendices
A List of Symbols
Abbreviations
The following abbreviations are used in this manuscript:
\(\emptyset \)-An empty set(p. 68) | \(\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}\)– The sets of elements |
and its subsets (p. 48) | |
\(\Omega _i,\mathfrak S\)– the sets of states (p. 48) | \(|\boldsymbol{A}|\)– the number of elements in \(\boldsymbol{A}\) (p. 48) |
| \(\boldsymbol{A}'={\boldsymbol{C}}\setminus \boldsymbol{A}\)–\(\boldsymbol{A}'\) is the complement |
product of sets (p. 48) | of \(\boldsymbol{A}\) to the space of elements \(\boldsymbol{C}\) (p. 48) |
\(\overrightarrow{x}=(x_1,x_2,\ldots ,x_n)\) | |
\(\overrightarrow{x}_{-j}=(x_1,\ldots ,x_{j-1},x_{j+1},\ldots ,x_n)\) | \((a,\overrightarrow{x}_{-j})=(x_1,\ldots ,x_{j-1},a,x_{j+1},\ldots ,x_n)\) |
\(\vec 1=(1,1,\ldots ,1)\) | \(\vec 0=(0,0,\ldots ,0)\) |
| \(\overrightarrow{x}^{J}=(x_{i_1},x_{i_2},\ldots ,x_{i_{|J|}})\in B^{|J|},\! J\subset \mathbf{N} \) |
\(\overrightarrow{x}^J=\overrightarrow{x}_{-(\mathbf{N} \setminus J)}\in B^{|J|},\) where \(J\subset \mathbf{N} \) | \(\left\langle \overrightarrow{x},\overrightarrow{y}\right\rangle \)– the inner product in \(\mathfrak {Re}^n\) |
\((a,\overrightarrow{x}_{-j})=(\overrightarrow{x}_{-j},a)=(x_1,\ldots ,x_{j-1},a,x_{j+1},\ldots ,x_n)\) | |
\(\overrightarrow{F}(t)=(F_1(t),F_2(t),\ldots ,F_n(t))\) | \(\prod ^{n}_{i=1}p_i=p_1\cdot p_2\cdot \ldots \cdot p_n\) (p. 58) |
\(\preceq \) | The partial ordering (p. 69) | ||
BS | Binary system (p. 67) | MSS | Multi-state system (p. 67) |
PRAs | Probabilistic Risk Assessments |
B Endnotes
1.1 B.1 Risk
It is difficult to define risk in general. In short, when we think about risk, we mean the possibility of an unexpected loss caused by an unpredictable event or harmful behavior (human, machine, animal, nature). One can think about the possibility of loss or injury. From the other side, the risk is the chance or probability that a person (a system) will be harmed or experience an adverse health (functioning) effect if exposed to a hazard. It may also apply to situations with property or equipment loss, or harmful effects on the environment. Therefore, we are talking about reducing ownership and loss as a result of a random event. Risk reduction means minimizing the chance of a loss occurring or limiting its size. To better understand the risk and the possibilities of risk management, the task of measuring risk has been set. The task is not formulated so that its solution is universal. This allowed to determine the desired properties of such measures [3].
1.2 B.2 General Idea of Importance Measure
The systems can be split into two categories: (i) binary systems (BS) and (ii) multistate systems (MSS).
There are four main classes of importance measures (v. Birnbaum [9], Amrutkar and Kamalja [2])
-
(I)
Reliability importance measure
-
(II)
Structural importance measure
-
(III)
Lifetime importance measure
-
(IV)
Failure and its recovery costs importance measure
The cost of failure (leaving the given state) and its recovery importance measure (IV) depends on the lifetime distribution of the component, its position in the system, and the loss related to the nonavailability of the system in the given state, diagnosis and repair. It is a new look at the importance of the components of a complex system. The analysis and significance measure proposed in this paper is based on the possibility of observing the components and a rational system maintenance policy, which consists in stopping the system for maintenance and repair at a time when it pays off to a sufficient number of components. The details are based on a cooperative analysis of costs and losses in the operation of such a system (v. Sect. 3, Szajowski and Yasuda [35]).
1.3 B.3 Review of Importance Measure Concepts
Since Birnbaum [8, 9] the importance measures were investigated and extended in various directions (v. Amrutkar and Kamalja [2]). The basis for the construction of significance measures is the observation that the binary system is well modeled by random graphs. The basis is the concept of structure.
Definition 12
(The structure). For a non-empty and finite set \(\boldsymbol{N}\)Footnote 7, we denote by \(\mathcal P\) the family of subsets \(\boldsymbol{N}\) having the following properties
-
(1)
\(\emptyset \in {\mathcal P}\)
-
(2)
\({\boldsymbol{N}}\in {\mathcal P}\);
-
(3)
\(\boldsymbol{S}\subseteq \boldsymbol{T}\subseteq {\boldsymbol{N}}\) and \(\boldsymbol{S}\in {\mathcal P}\) imply \(\boldsymbol{T}\in {\mathcal P}\).
The family \(\mathcal P\) is called structure.
This basic structure has been studied in many areas under a variety of names. Monograph by Ramamurthy [30] unified the definitions and concepts in two main fields of application, that is cooperative game theory (simple games) (v. Tijs [38, Chapt. 10]) and reliability theory (semi-coherent and coherent structures, v. Esary and Proschan [15], Barlow and Wu [6], Ohi [26]).
The relationships with cooperative games can be helpful in determining the importance of elements for the reliability of the system and at the same time a role in the possibility of efficient diagnosis in the event of a failure, as well as in determining the rules of the procedure for removing a failure. Removing the failure causes that the features of the element and the repaired module are restored. However, it should be remembered that the method of repair and the quality of the elements used reproduce the original features to varying degrees (v. e.g. Navarro et al. [25]). This has an impact on further operation, diagnosis and maintenance (uplift). Rules are easier to set when they are associated with objective measures of the features of components, modules, and the system. Analysis of significance measures in the context of repair helps to understand such relationships. Let us therefore establish these relationships (v. Do and Bérenguer [11]).
In game theory, consider the set \(\boldsymbol{C}=\{1,2,\ldots ,n\}\) of players and the power set \(2^{\boldsymbol{C}}\) of coalitions. A function \(\lambda :2^{\boldsymbol{C}}\rightarrow \{0,1\}\) is called a simple game on \(\boldsymbol{C}\) in characteristic function form if
-
(1)
\(\lambda (\emptyset )=0\);
-
(2)
\(\lambda (\boldsymbol{C})=1\);
-
(3)
\(\boldsymbol{S}\subseteq \boldsymbol{T}\subseteq \boldsymbol{C}\) implies \(\lambda (\boldsymbol{S})\le \lambda (\boldsymbol{T})\).
A coalition \(\boldsymbol{S}\subset \boldsymbol{C}\) is called winning if \(\lambda (\boldsymbol{S})=1\) and it is called blocking if \(\lambda (\boldsymbol{C}{\setminus } \boldsymbol{S})=0\). Indeed, the collection of winning (or blocking) coalitions in a simple game satisfies the three properties of the basic structure mentioned at the beginning.
In reliability theory, consider the set \(\boldsymbol{C}=\{1,2,\ldots ,n\}\) of components with which a system g has been built. The state of the system as well as any component can either be 0 (a failed state) or 1 (a functioning state). The knowledge of the system is represented by the knowledge of the structure function of the system, which is defined as a switching function (Boolean) \(g:\{0,1\}^n\rightarrow \{0,1\}\) of n variables (or n dimensional vector \(\vec {x}\))Footnote 8. The structure function g (simply the structure g) is called semicoherent if (1) g is monotone, i.e. \(\overrightarrow{x}\preceq \overrightarrow{y}\) implies \(g(\overrightarrow{x})\le g(\overrightarrow{y})\), and (2) \(g(\vec 0)=0\) and \(g(\vec 1)=1\).
The semicoherent structure can be called coherent when all its elements are significant. A subset \(\boldsymbol{A}\subset \boldsymbol{C}\) is called a path set of g, if \(g(\vec {1}^{\boldsymbol{A}},\vec {0}^{\boldsymbol{C}\setminus \boldsymbol{A}})=1\), i.e. the system is working if the items forming the set \(\boldsymbol{A}\) [resp. \(\boldsymbol{C}\setminus \boldsymbol{A}\)] are working [resp. failed]. Similarly, \(\boldsymbol{A}\subset {\boldsymbol{C}}\) is called a cut set of g, if \(g(\vec {0}^{\boldsymbol{A}},\vec {1}^{\boldsymbol{C}\setminus \boldsymbol{A}})=0\). Clearly, the assemblage of path [cut] sets of a semicoherent structure g satisfies the three properties of the basic structure mentioned at the beginning.
1.4 B.4 Cooperative Games vs. Semicoherent Systems
[30, Sect. 2] indicates the correspondence between the terminology of cooperative game theory and reliability by means of a list of equivalent notions: players or components; simple game or semicoherent structure; characteristic function or structure function; winning [blocking] coalition or path [cut] set; minimal winning [blocking] coalition or minimal path [cut] set. The review of the various types of simple games and semicoherent structures encountered in the literature are mentioned there. The most interesting is [30, Chap. 3], where a detailed study of the problem of assessing the importance [power] of components [players] comprising the system [game] is described. The emphasis is on the probabilistic approach to the quantification of relative importance.
Rights and permissions
Copyright information
© 2021 Springer-Verlag GmbH Germany, part of Springer Nature
About this chapter
Cite this chapter
Szajowski, K.J., Średnicka, M. (2021). Operation Comfort of Multistate System vs. The Importance of Its Components. In: Nguyen, N.T., Kowalczyk, R., Motylska-Kuźma, A., Mercik, J. (eds) Transactions on Computational Collective Intelligence XXXVI. Lecture Notes in Computer Science(), vol 13010. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-64563-5_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-64563-5_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-64562-8
Online ISBN: 978-3-662-64563-5
eBook Packages: Computer ScienceComputer Science (R0)





 ;
; ,
,  .
. is surjection;
is surjection; has following property. If
has following property. If 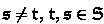 , then
, then  ,
, 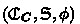 is increasing if and only if for every
is increasing if and only if for every  .
.

 – romanized: systema – a complex thing) – a set of interrelated elements realizing the assumed goals as a whole.
– romanized: systema – a complex thing) – a set of interrelated elements realizing the assumed goals as a whole. by A. B. Aries
by A. B. Aries –the Cartesian
–the Cartesian where
where