Wave-number space networks in plasma turbulence

Abstract

Turbulence commonly described in Fourier space due to its multi-scale nature can be formulated using wave-number space networks where each node represents a wave-vector on a discretized wave-number space grid that are connected to one another through triadic interactions denoted as three-body connections. This description that we call wave-number space network formulation, while being very inefficient for numerical implementation as compared for example to a pseudo-spectral formulation of the same equations on a regular grid, provides an alternative perspective and has conceptual advantages, such as the separation of the equations and the nonlinear interactions. The network represents, through its connections, the nonlinear interactions, and can be truncated by dropping nodes, or connections corresponding to considering only certain kinds of wave-numbers or certain kinds of interactions, without modifying the equations themselves. This guarantees that the underlying Hamiltonian structure of the equations remains unchanged, and therefore, one has the same conservation laws as the original system. Wave-number space networks can also be reduced by lumping nodes that have some similar characteristics together, in which case a reduction of the equations through some sort of closure becomes necessary, for which some possibilities are discussed. The network formulation can also be used for analyzing direct numerical simulations, and may be used for discovering key nodes as well as training models for constructing reduced systems. The goal of this review is to stimulate interest in thinking in terms of networks, while dealing with problems in plasma turbulence through a survey of what has been done in this subfield and what is possible for future studies, especially in the context of plasma turbulence.

1 Introduction

Transport of heat, particles, and momentum in tokamak plasmas can be caused by micro-turbulence, and regulated by meso-scale coherent structures, such as zonal flows (Diamond et al. 2005; Gürcan and Diamond 2015), geodesic acoustic modes (GAMs) (Winsor et al. 1968; Conway et al. 2021), or Alfvén eigenmodes (Mett and Mahajan 1992; Chen and Zonca 2016) that the turbulence in these devices naturally generates (or regulates), and their interactions. This makes the detailed understanding of plasma turbulence and its self-regulation through these flow patterns one of the key academic challenges that face the fusion community. Since the goal of the magnetized fusion program is to heat hydrogen ions to high enough temperatures to overcome the Coulomb barrier and instigate fusion reactions, the core of a magnetized fusion device is to be extremely hot. On the other hand, the region where the plasma touches the wall of the device, or the edge, should be kept at lower temperatures to avoid melting the wall or other plasma facing components. Details of this engineering problem, confounded by the complexities of heating, operation, and large scale magnetohydrodynamic (MHD) stability, result in a narrow range of available temperature gradients between the edge and the core regions, driving a multitude of small-scale instabilities, such as the ion and electron temperature gradient-driven modes [ITG (Coppi et al. 1967; Romanelli 1989) and ETG (Horton et al. 1988; Jenko et al. 2000)], where the source of the free energy is this background temperature gradient, trapped electron modes, or dissipative drift waves (Hasegawa and Wakatani 1983; Koniges et al. 1992) where the instability is a result of the nonadiabatic electron response or interchange (Sarazin and Ghendrih 1998; Scott 2005) or resistive ballooning modes (Zeiler et al. 1996; Beyer et al. 1999), where the instability source is the combination of magnetic curvature and pressure gradient forces.

There is actually a whole zoology of similar modes where the free energy sources may be the gradients of more exotic quantities (such as parallel velocity (D’Angelo 1965), current or resistivity (Garcia et al. 1985)), or any number of combinations of those. Given their potential importance, both linear and nonlinear physics of these different instability mechanisms and the resulting “micro-turbulence” have been studied thoroughly in the past (Kadomtsev 1965; Horton 1999), using various approaches, from linear to quasi-linear theory (Vedenov 1963; Bourdelle et al. 2007), using analytical methods as well as direct numerical simulations from simpler fluid systems (Beer and Hammett 1996), to gyrokinetics (Lee 1983; Brizard and Hahm 2007).

Albeit this multiplicity of physical mechanisms for small-scale instabilities in tokamaks, the variety of parameters that control their behavior, and the number of fluctuating fields that are involved in each instability, the generally agreed upon view seems to be that the “plasma turbulence” is nevertheless a generic notion that is somehow common in all these particular examples (Yoshizawa et al. 2001). That is, while the instability mechanism that drives the system unstable, and the waves that it generates are very different, the nonlinear “mode coupling” mechanism that is triggered as a result of the interactions of these unstable waves has a universal aspect (Sagdeev and Galeev 1969). However, it is also clear that plasma turbulence, especially the kind we find in tokamaks, is not exactly the “universal” in the same sense as the neutral fluid turbulence, which is usually described using the Kraichnan–Kolmogorov phenomenology of the turbulent cascade (Frisch 1995). Plasma turbulence is both similar to and different from neutral fluid turbulence and is peculiar in various respects such as the importance of waves and instabilities and therefore various resonant mechanisms (Dupree 1967; Krommes 2002) or the fact that the kinetic system provides a multitude of damping mechanisms (Kadomtsev 1968; Ter Haar 1965) and hence the coexistence of unstable and damped modes (Terry et al. 2006), which results in a turbulent “cascade”, without the presence of a clear inertial range.

In its most general formulation, the turbulent “cascade” in a bounded system can be thought of as percolation of a triad interaction network with a conserved quantity, like energy, where the network consists of discretized wave-numbers (Gürcan et al. 2020). In such a network, where each wave-number is a distinct node, each node interacts with a set of pairs, with which it satisfies the triadic interaction condition (i.e., ${\textbf{k}}+{\textbf{p}}+{\textbf{q}}=0$ where ${\textbf{k}},$ ${\textbf{p}}$ and ${\textbf{q}}$ are the interacting wave-numbers). For wave turbulence (Newell and Rumpf 2011), additional constraints such as resonance (or near resonance) among the frequencies of these wave-number nodes [e.g., $\omega \left( {\textbf{k}}\right) +\omega \left( {\textbf{p}}\right) -\omega \left( {\textbf{q}}\right) \approx 0$] can be invoked (Harper et al. 2013). Due to their triadic nature, the interactions in such a network are three-body interactions, and the resulting network is a three-body interaction network. We call such networks, wave-number space networks.

Consider a standard spectral formulation in a bounded system where the nonlinear term is computed through convolution sums. One can view the convolution, as a sum over the underlying three-body network consisting of all possible combinations of triadic interactions. The introduction of the concept of the “network” in this case is an equivalent but trivial reformulation of the convolution sum. The network in such an example can be a regular grid that does not change and is made up of a huge number of elements. Treating a convolution sum on a regular k-space grid as over an extended (but still somewhat regular) three-body network where each triadic interaction is handled as a separate connection increases the computational complexity of the problem considerably while introducing no apparent advantage. However, when we want to reduce the system, either dropping inactive nodes, or by lumping together nodes that play similar roles, the network approach, provides some advantages as well as an interesting perspective.

Networks appear in many problems in nature, and the discipline that is devoted to their study is called the network science (Barabási and Pósfai 2016). As neural networks have become extremely popular tools (LeCun et al. 2015) for multivariate multiple regression in science, policy, and technology in recent years, and the study of topology, structure and dynamics (Newman and Watts 1999; Watts and Strogatz 1998) of biological (Junker 2008), ecological (Landi et al. 2018), social (Wasserman and Faust 1994), and computer networks (Broder et al. 2000) has shown regular features in their complex self-adaptation (Barabási et al. 2000; Boccaletti et al. 2006), network science has become a central player in our quest to understanding complex aspects of natural systems (Barabasi 2011). Network science gives us tools that may provide insight into self organizing principles of these systems, such as the remarkable self-similarity that turbulent systems commonly demonstrate. It has been argued recently that turbulence can be formulated as a percolation on an evolving complex network, and some aspects of its behavior including intermittency can be related to generalities shared by other complex networks, such as food webs, or the Internet.

Use of the network abstraction to study nonlinear dynamics of turbulence also provides interesting prospects (Taira et al. 2016; Taira and Nair 2022), especially in the context of plasma turbulence. It may sometimes be possible to reduce complex networks by lumping together certain similar elements. It is common, for example, to describe food webs with species that play similar roles lumped together instead of labeling each distinct species separately (e.g., “whales” as a single node instead of every single species of whale as separate nodes). In the context of networks of wave-numbers, some regions in the wave-number domain may play similar roles and can be lumped together. For example, a description in terms of scales is a conceptual example of lumping together the wave-numbers that play similar roles in the turbulent cascade, relevant to homogeneous, isotropic turbulence. In the case of strong anisotropy, modes with wave-numbers, which has a vanishing component (e.g., zonal flows as $k_{x}=0$ modes in geophysical fluid dynamics or $k_{y}=0$ modes in fusion plasmas) can be considered as an important conceptual element of the anisotropic energy transfer in k-space (Smolyakov and Diamond 1999; Gürcan et al. 2009).

We know that, in the study of plasma turbulence, particular meso-scale structures play special roles in the turbulent self-organization. For example, the interactions between zonal flows and drift-wave turbulence are commonly referred to in the fusion community as predator–prey interactions (Malkov et al. 2001), where the zonal flows play the role of the predator and the underlying drift-wave turbulence that drives them, play the role of the prey. One can even use the Lotka–Volterra equation to model this state, and it is actually not unique to fusion plasmas, or zonal flows, but it is a feature of turbulent systems that are not very far from marginal stability conditions, such as the conditions one finds in transition to turbulence where only a finite number of modes would be initially excited (Goldenfeld and Shih 2017). In fact, also in fusion plasmas, one observes these predator–prey oscillations most clearly in near marginal stability conditions (Kobayashi et al. 2015), or in transitions, such as the Low-to-High confinement transition (Kim and Diamond 2003; Miki et al. 2013). The existence of this well-established analogy between a particular state of plasma turbulence—dominated by zonal flows—and an ecological system, nicely paves the way toward the extended analogy of plasma turbulence as a network of predator–prey relations, or a food web as it is called in ecology, and the consecutive natural step of abstraction of plasma turbulence in terms of “complex dynamical networks” of which food web is just an example.

The remainder of the paper is organized as follows. The introduction continues with a simple, concrete example commonly used in plasma physics to provide the context for the discussion on more abstract concepts into network formulation. Section 2 is devoted to primitive wave-number space networks (i.e., on regular rectangular grids), where the basic formulation is given in Sect. 2.1, and the network concepts of energy transfer among nodes are discussed through conservation laws in Sect. 2.2. Section 2.3 discusses the triadic instability assumption and phase dynamics, and Sect. 2.4 considers wave turbulence, and Sect. 2.5 examines how this basic formulation can be extended to multiple fields or kinetic systems, with Sect. 2.6 focusing on the effects of magnetic geometry, and localization of modes around rational surfaces. Section 3 gives some examples of truncated network models, with nested polyhedra models for fluids and MHD discussed in Sect. 3.1 and spiral chain models for two-dimensional turbulence discussed in Sect. 3.2. In Sect. 3.3, self-consistent quasi-linear models are discussed from the point of view of truncated network models. In Sect. 4, reductions of triadic networks are considered, with Sect. 4.1 describing how to deal with energy transfer in reduced networks and Sect. 4.2 illustrating closure on reduced networks through an eddy-damped quasi-normal Markovian approximation. Section 5 provides some examples of ad-hoc models, which starts by reinterpreting shell models as network models in Sect. 5.1 and then discussing small-world network versions of those and their dynamics in Sect. 5.2. Section 6 is dedicated to the use of wave-number space networks in analysis, with a short discussion of model extraction in Sect. 6.1. Section 7 is summary and discussions.

1.1 Elementary example: modulational instability

One of the earlier examples of reduced network models in fusion plasmas was based on what is sometimes called the i-delta equations, as the weakly nonadiabatic version of the Charney–Hasegawa–Mima system, using “a low order k-space”, consisting of a basic wave-number space network of 10 or so modes (Terry and Horton 1983). An even simpler example is the so-called modulational instability calculation, which requires at the minimum the most unstable mode, a zonal mode, and two sidebands, which means a minimum of 4 modes. The usual example of a modulational instability calculation involves considering the most unstable mode as the pump, and looking at the coupled evolution of the zonal flow and sidebands assuming the energy in these are initially much smaller compared to the pump mode, so that a linear stability analysis can be performed. Such a linear stability analysis of the coupled zonal-flow/sidebands system in the presence of the pump can be used to obtain the growth rate of the modulational instability as well as the most unstable $k_{x}.$ Of course, one can instead solve this low-order system numerically; however, in this case, if want the system to saturate, we need to add a second $k_{x}$ mode together with its sidebands (so a minimum of 7 modes), which will act as the sink. A similar system of interactions between zonal flows and drift waves were also considered in the past, using ballooning formalism and the gyrokinetic equation (Chen et al. 2000). More recently, a general network version similar to these systems was studied in detail for the Hasegawa–Wakatani model (Gürcan et al. 2022). Here, we use the Hasegawa–Wakatani case in the adiabatic (e.g., in the i-delta limit) as a simple elementary example to provide a “plasma physics” introduction to the topic. Consider the following:

Fig. 1

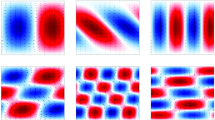
The dynamics and the network structure for the modulational instability example. The most unstable mode (i.e., $\Phi _{k0}$) acts as a pump, exciting the zonal mode (i.e., ${\overline{\Phi }}_{1}$) and the sidebands (i.e., $\Phi _{k1\pm }$). The nodes are shown in a reduced $k_{x}$–$k_{y}$ grid on the top right plot, which also acts as a legend for the main plot. The outer modes that are shown in gray circles are artificially damped, hence play the role of sink. In the final steady state, without any large scale friction, the energy in ${\overline{\Phi }}_{1}$ causes the interaction to effectively turn off. Introduction of large-scale friction would result in predator–prey-like oscillations

$$\begin{aligned} \frac{\partial }{\partial t}\left( 1+\chi _{k}\right) \Phi _{k}=-i\kappa k_{y}\Phi _{k}+\frac{1}{2}\sum _{\triangle }M_{kpq}\Phi _{p}^{*}\Phi _{q}^{*}, \end{aligned}$$

(1)

where $\Phi _{k}$ is the normalized electrostatic potential, $\chi _{k}\equiv k^{2}-i\delta _{k},$ where $\delta _{k}$ is defined through the relationship between the electron density and the electrostatic potential $n_{k}=\left( 1-i\delta _{k}\right) \Phi _{k},$ $\kappa$ is the normalized diamagnetic velocity, and $M_{kpq}$ is the nonlinear interaction coefficient whose form is not important for this example (see Sect. 6 for more details on definitions and normalizations). To study modulational instability, it is common to consider a subset of modes, such as

$$\begin{aligned} \Phi _{k}=\Phi _{k0}+\sum _{\ell }\left( {\overline{\Phi }}_{\ell }+\Phi _{k\ell +}+\Phi _{k\ell -}\right) , \end{aligned}$$

(2)

where $\Phi _{k0}$ is the most unstable mode (with $k_{y}=k_{y0}$ and $k_{x}=0$), ${\overline{\Phi }}_{\ell }$ are the zonal modes (with $k_{x}=k_{x\ell }$ and $k_{y}=0$), and $\Phi _{k\ell \pm }$ are the sidebands (with $k_{y}=k_{y0}$ and $k_{x}=\pm k_{x\ell }$) labeled by $\ell$ considering multiple radial wave-numbers. In general, we have $3n+1$ modes where n is the number of $k_{x}$ modes considered. We can, of course, also add other $k_{y}$ modes, but having only a single $k_{y}$ mode is sufficient for studying modulational instability. Note that for each mode ${\textbf{k}}={\textbf{k}}_{\ell },$ its Hermitian conjugate ${\textbf{k}}=-{\textbf{k}}_{\ell }$ should also be considered.

To have a stationary solution, we at least need to go to $n=2,$ and choose the $k_{x0}$ and $k_{y0}$ to correspond to the most unstable modes of the modulational instability and the linear instability, respectively, and introduce artificial damping on the equations for $\Phi _{k\pm 2}$ and ${\overline{\Phi }}_{2}.$ Such a system in the absence of zonal-flow damping (that is damping of the ${\overline{\Phi }}_{1},$ which is the primary modulationally unstable zonal component), evolves to a state of finite zonal flows and stays at that final state with stationary zonal flows. Figure 1 shows the results of the numerical integration of the low-order dynamical system that one gets from such a system (actually, we have used the full Hasegawa–Wakatani system with $C=10,$ $\kappa =1;$ see Sect. 6 for details).

2 Primitive wave-number space networks

2.1 Basic formulation

Consider a complex field $\psi _{{\textbf{k}}},$ which represents the Fourier transform of a real one through $\psi _{{\textbf{k}}}\equiv \frac{1}{L}\int _{L}\psi \left( {\textbf{x}}\right) {\textrm{e}}^{i{\textbf{k}}\cdot {\textbf{x}}}{\textrm{d}}^{n}{\textbf{x}}$ in a bounded domain L,  for which we can write

$$\begin{aligned} \partial _{t}\psi _{{\textbf{k}}}+i\omega _{{\textbf{k}}}\psi _{{\textbf{k}}}= \frac{1}{2}\sum _{\triangle }M_{{\textbf{k}}{\textbf{p}}{\textbf{q}}} \psi _{{\textbf{p}}}^{*}\psi _{{\textbf{q}}}^{*}, \end{aligned}$$

(3)

where $\omega _{{\textbf{k}}}$ is the complex frequency, whose imaginary part may represent the instability—or dissipation in small scales—and $M_{{\textbf{k}}{\textbf{p}}{\textbf{q}}}$ is the symmetrized nonlinear interaction coefficient. This template form may represent a number of different single field systems, such as for instance the Charney–Hasegawa–Mima system with $\omega _{{\textbf{k}}}=\frac{v_{*}k_{y}}{1+k^{2}}$ and $M_{\textbf{kpq}}\equiv \frac{\hat{{\textbf{z}}}\times {\textbf{p}} \cdot {\textbf{q}}\left( q^{2}-p^{2}\right) }{\left( 1+k^{2}\right) }$ where $v_{*}$ is the normalized background density gradient, and $L_{x}$ and $L_{y}$ are the box dimensions.

The wave-number on a two-dimensional regular square grid can be defined using two integer indices $\ell _{x}$ and $\ell _{y}$ as $k_{x}=2\pi \left( \ell _{x}-N_{x}/2\right) /L_{x}$ and $k_{y}=2\pi \left( \ell _{y}-N_{y}/2\right) /L_{y},$ where $L_{x,y}$ is the size of the domain and $N_{x,y}$ are the number of grid elements in each direction. We can flatten the two index variables into a single integer using for example the column major order linear storage formula $\ell =\ell _{x}+\ell _{y}N_{x}$ and use this as the node index. Note that in the general case of n dimensions, we can define the flattened node index via the usual $\ell =\ell _{1}+\sum _{i=2}^{n}\ell _{i}\prod _{j=1}^{i-1}N_{j}.$ This allows us to define the node wave-number ${\textbf{k}}_{\ell }\equiv \hat{\mathbf {{\textbf{x}}}}k_{x}\left( \ell _{x}\right) +\hat{{\textbf{y}}}k_{y}\left( \ell _{y}\right)$ as a vector and node variable $\psi _{\ell }\equiv \psi _{{\textbf{k}}_{\ell }}$ as a complex number denoted by the node label $\ell .$ This way, the whole regular grid of the n-dimensional wave-number domain can be thought of as a collection of $N=\prod _{j=1}^{n}N_{j}$ wave-number nodes.

We can thus write (3) as a dynamical equation for $\psi _{\ell }$ on a three-body network

$$\begin{aligned} \left( \frac{\partial }{\partial t}+i\omega _{\ell }\right) \psi _{\ell }=\frac{1}{2}\sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }}M_{{\ell \ell '\ell ''}}\psi _{\ell '}^{*}\psi _{\ell ''}^{*}, \end{aligned}$$

(4)

where ${\textbf{i}}_{\ell }$ denote the list of pairs that interact with the node $\ell .$ The list of pairs ${\textbf{i}}_{\ell }$ needs to be computed by going over all the nodes that satisfy the triad interaction condition ${\textbf{k}}_{\ell }+{\textbf{k}}_{\ell '}+{\textbf{k}}_{\ell ''}=0.$ Written in this way, Eq. (4) is exactly the same as Eq. (3) on a regular k-space grid. However, the former can be extended to irregular grids, or to a decimated Fourier space and can be more easily modified to incorporate the dynamics of an equivalent variable on a reduced network. Note also that the formulation of Eq. (4) can also be extended to windowed Fourier transforms, or wavelet coefficients, or any other similar decomposition such as the Galerkin decomposition, except that in that case, $\omega _{\ell }$ would be replaced by a nondiagonal matrix, representing an operator and constructing the interaction network (that is ${\textbf{i}}_{\ell }$ as connections and $M_{\ell \ell '\ell ''}$ as weights) may be nontrivial.

In practice, the formulation in (4) using a regular grid can be implemented in two steps. First, for each $\ell$, we find all possible $\ell ',\ell ''$ pairs that satisfy the triad interaction condition ${\textbf{k}}_{\ell }+{\textbf{k}}_{\ell '}+{\textbf{k}}_{\ell ''}=0$ and compute and record the interaction coefficients $M_{{\ell \ell '\ell ''}}.$ This constitutes our “network”, in that it is a list of all three-body connections between all the nodes of the network with particular weights for each connection in the form of interaction coefficients. Once the network is constructed, it can be stored and the complex dynamical variables $\psi _{\ell }$ corresponding to Fourier coefficients can be advanced on this network using (4).

Searching for all possible pairs that satisfy the triadic interaction condition is time-consuming, but it can be ameliorated by scanning $\ell$ and $\ell '$ while using ${\textbf{k}}_{\ell }\pm {\textbf{k}}_{\ell '}\pm {\textbf{k}}_{\ell ''}=0$ to solve for $\ell '',$ keeping only $k_{\ell '}<k_{\ell ''}$ part of the k-space consisting of only $k_{y}\ge 0$ modes (since the initial data are real). Notice that one can also impose additional resonance conditions in this step to implement weak wave-turbulence as a sparse network on a discrete regular grid (Kartashova 2009, 2010).

On a properly constructed regular grid, (4) and (3) are mathematically equivalent. This means that a numerical implementation of (4) as described above, and say a pseudo-spectral implementation of (3) with the same forcing, dissipation, and initial and boundary conditions, should give exactly the same evolution up to numerical precision. This can be verified, for example on a regular grid of resolution $N_{x}\times N_{y}=256\times 256,$ beyond which the network method starts to be impractical. This implies that $N_{\ell }=\left( N_{x}/2\right) \times \left( N_{y}/2\right) +\left( N_{x}/2-1\right) \times \left( N_{y}/2-1\right)$ independent nodes, since in a real-to-complex transform, we have $N_{y}/2+1$ independent wave-numbers in the y direction, with the last one being the Nyquist wave-number and $\Phi _{k_{x},0}=\Phi {}_{-k_{x},0}^{*}$ on the $k_{y}=0$ axis due to Hermitian symmetry. In such a network, the node that has the most connections is the smallest wave-number node that has $N_{t}=(N_{x}-2)\times (N_{y}-2)/2$ connections (i.e., triads that are connected to that node). Note also that for standard 2D turbulence, $\ell =0$ is unconnected, since $|k_{\ell '} |=|k_{\ell ''} |$ makes the interaction coefficient vanish. Since $M_{{\ell \ell '\ell ''}}=M_{{\ell \ell ''\ell '}},$ by choosing $\ell '>\ell '',$ and dropping the 1/2 in (4), we can reduce the maximum number of triads to $N_{t}=\left( N_{x}-2\right) \times \left( N_{y}-2\right) /4.$

Network formulation on a regular rectangular grid is extremely impractical for any kind of meaningful resolution, since its computational cost for a causal formulation scales with $N_{\ell }^{3},$ which would scale with $N^{9}$ (i.e., $N_{x}=N_{y}=N_{z}=N$) for three dimensions, and there exists many efficient techniques for dealing with turbulence on a regular grid. However, since the same approach can be used on a sparse network obtained from reduction such as the nested polyhedra models that we will see in Sect. 3.1, which can describe a very large range of scales using a relatively small number of nodes even in three dimensions, they can be extremely powerful for computations, as well. We argue that the effort of writing down the network formulation on a regular rectangular grid is nonetheless useful for establishing the connection to standard techniques, and to provide a basis on which we can apply network reduction. For example, if we know how to go from a regular rectangular grid to a particular reduced network form, we can apply the same reduction to the data from direct numerical simulations (DNS) that are usually on a rectangular grid (see Sect. 6 for some examples).

2.2 Conservation laws

If the nonlinear interaction coefficients in Eq. (4) have the symmetry

$$\begin{aligned} \sigma _{\ell }M_{{\ell \ell '\ell ''}}+ \sigma _{\ell '}M_{{\ell '\ell ''\ell }}+\sigma _{\ell ''}M_{{\ell ''\ell \ell '}}=0, \end{aligned}$$

(5)

where $\sigma _{\ell }$ is a coefficient that is a function of the node label $\ell$ (i.e., a function of the wave-number), and the quadratic quantity defined as

$$\begin{aligned} E_{\text {total}}^{\sigma }\equiv \sum _{\ell }\sigma _{\ell }|\psi _{\ell } |^{2} \end{aligned}$$

can be shown to be conserved by the nonlinear dynamics, since

$$\begin{aligned} \partial _{t}E_{\ell }^{\sigma }=\sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }}T_{\ell \ell '\ell ''}^{\sigma }+{\mathcal {P}}_{\ell }^{\sigma }-{\mathcal {D}}_{\ell }^{\sigma }, \end{aligned}$$

(6)

where ${\mathcal {P}}_{\ell }^{\sigma }$ is the production and ${\mathcal {D}}_{\ell }^{\sigma }$ is the dissipation of the conserved quantity labeled by $\sigma$ at the site of node $\ell .$ If we use Eq. (4), we get

$$\begin{aligned} {\mathcal {P}}_{\ell }^{\sigma }-{\mathcal {D}}_{\ell }^{\sigma }=2\gamma _{\ell }E_{\ell }^{\sigma }, \end{aligned}$$

since both energy injection at instability scales and the dissipation at small scales come from the form of the “linear growth rate” [i.e., $\gamma _{\ell }=\text {Im}\left( \omega _{\ell }\right)$] as a function of $k_{\ell }$ which actually becomes negative as we go to small scales due to dissipation. The transfer rate $T_{\ell \ell '\ell ''}$ in Eq. (6) represents the energy transfer from the nodes $\ell '$ and $\ell ''$ to the node $\ell ,$ which can be defined explicitly as

$$\begin{aligned} T_{\ell \ell '\ell ''}^{\sigma }\equiv \text {Re}\left[ \sigma _{\ell }M_{{\ell \ell '\ell ''}} \Phi _{\ell }\Phi _{\ell '}\Phi _{\ell ''}\right] . \end{aligned}$$

Since the interactions always appear as three-body interactions, we have $T_{\ell \ell '\ell ''}^{\sigma }+T_{\ell '\ell ''\ell }^{\sigma }+T_{\ell ''\ell \ell '}^{\sigma }=0$ as implied by Eq. (5). When we sum the Eq. (6) over all nodes, we find that the total amount of conserved quantity (e.g., energy) increases or decreases only as a result of the difference between its total injection and its total dissipation.

Fig. 2

The energy transfers in a network of triadic interactions between nodes 1–4, connected by two triads 123 and 134. The triad interactions are show in the form of little triangles, the transfer terms such as $t_{12}^{123}$ denote the energy transfer from node 1 to node 2 through the triad 123, which can also be denoted by $t_{12}^{3}.$ The total energy transfer between two nodes is the sum of the transfers through each triad, as shown for the case of two triads here with $t_{13}\equiv t_{13}^{134}-t_{31}^{123}$

Dropping the label $\sigma$ for convenience (e.g., considering energy), we can also write

$$\begin{aligned} \partial _{t}E_{\ell }=\sum _{\ell ',\ell ''}t_{\ell \ell '}^{\ell ''}+ {\mathcal {P}}_{\ell }-{\mathcal {D}}_{\ell }, \end{aligned}$$

(7)

where $t_{\ell \ell '}^{\ell ''}=\frac{1}{3}\left( T_{\ell \ell '\ell ''}-T_{\ell '\ell ''\ell }\right)$ represents the energy transfer from $\ell '$ to $\ell$ mediated by $\ell ''.$ Note that for a given triad, with the node labels 1, 2, and 3, we have $T_{123}=t_{12}^{3}+t_{13}^{2}=t_{12}^{3}-t_{31}^{2},$ meaning that the energy transferred from the nodes 3 and 2 to node 1 is the difference of the energy transferred from 2 to 1 mediated by 3 and the energy transferred from 1 to 3 mediated by 2 (see Fig. 2). This allows us to transform the three-body interaction network to a simple network with edges that are weighted by the other components of the triad, with multiple channels between the nodes.

We may further reduce the many connections between two nodes mediated by different third nodes, by summing over the third node as

$$\begin{aligned} \partial _{t}E_{\ell }=\sum _{\ell '}t_{\ell \ell '}+{\mathcal {P}}_{\ell }- {\mathcal {D}}_{\ell }, \end{aligned}$$

(8)

where $t_{\ell \ell '}\equiv \sum _{\ell ''}t_{\ell \ell '}^{\ell ''}.$ In Fig. 2, this corresponds to writing $t_{13}=t_{13}^{4}+t_{13}^{2}=t_{13}^{4}-t_{31}^{2}=t_{13}^{134}-t_{31}^{123}.$ The two connections in this example, $t_{13}^{134}$ and $t_{31}^{123},$ are part of two separate triad interactions, and therefore have two different phases (see below). Summing over all these different connections belonging to different triad interactions, having different phases, allows us to transform the system from a multigraph (a graph which has multiple edges between two nodes) to a simple graph (a graph with only one edge between two nodes) is an important reduction of the network topology. However, it results in loss of information, since once we sum multiple edges between two nodes into a single edge, there is no way to get back the different edges that make up that single combined edge. We also loose detailed information about the three-way relative phases that determine the direction of the flux through a given triad, since we sum over many triads to obtain the transfer between two nodes mediated by all possible third nodes.

2.3 Triadic instability assumption and phase dynamics

While the necessary condition for the existence of a link between the nodes in a three-body spectral network, representing turbulent mode coupling, is the triad interaction condition between the wave vectors, this link accommodating an actual transfer of energy between the nodes requires additional circumstances. Given three nodes and a triad, one may usually estimate the direction of energy transfer, through an analysis called the “instability assumption” (Waleffe 1993; Alexakis and Biferale 2018). In the fusion context, it would probably make more sense to call this “triadic instability assumption”, since instability in that context rather refers to the linear instability of the underlying system. In any case, the triadic instability condition suggests that, if we start with an initial state, such that $\psi _{\ell }\sim O\left( 1\right)$ but $\psi _{\ell '}\sim \psi _{\ell ''}\sim O\left( \epsilon \right) ,$ a linear stability analysis for the perturbations $\psi _{\ell '}$ and $\psi _{\ell ''}$ gives an instability condition

$$\begin{aligned} M_{{\ell '\ell ''\ell }}M_{{\ell ''\ell \ell '}}>0, \end{aligned}$$

(9)

which results in the growth of $\psi _{\ell '}$ and $\psi _{\ell ''}$ resulting in a transfer of energy. The growth can then be argued to continue until some kind of equipartition between the three nodes $\ell ,$ $\ell '$ and $\ell ''.$ For example for incompressible two dimensional turbulence, the interactions coefficients are $M_{kpq}=\frac{\hat{{\textbf{z}}}\times {\textbf{p}}\cdot {\textbf{q}} \left( q^{2}-p^{2}\right) }{k^{2}}$ [i.e., with $\ell ,\ell ',\ell ''\rightarrow k,p,q$], so that the instability condition $M_{pqk}M_{qkp}>0$ implies $\left( k^{2}-q^{2}\right) \left( p^{2}-k^{2}\right) >0,$ which is satisfied only if k is the middle wave-number. This is a consequence of the intermediate axis theorem for rigid body rotation and the equivalence of these two systems. More generally, the triadic instability assumption means that the transfer is from the node $\ell$ which has the interaction coefficient $M_{\ell \ell '\ell ''}$ that has the opposite sign to the other two $M_{{\ell '\ell ''\ell }}$ and $M_{{\ell ''\ell \ell '}},$ which has the same sign because of Eq. (9) resulting in $T_{\ell \ell '\ell ''}<0$ while $T_{\ell '\ell ''\ell }>0$ and $T_{\ell ''\ell \ell '}>0.$ This works even in the presence of linear growth and damping as long as the pump mode keeps increasing in amplitude, at some point, the nonlinear transfer mechanism will kick in. Note that while the actual three-wave system without any linear instability can be solved exactly using Jacobi elliptic functions (Abramowitz and Stegun 1964), the implications of these solutions to the triadic instability assumption, where we only consider the initial trends, which gives us an idea about the direction of the transfers, until we reach a stationary state either through statistical equipartition, or through the nonequilibrium steady state between production and dissipation through the nonlinear cascade processes.

However, as it invokes statistical steady states such as the equipartition, the analysis is usually based on the assumption that the phases are random in a turbulent field. This is reasonable as long as the phases of the legs of the triad that we are considering are not involved in some complicated conspiracy, like, for example, all three nodes of the triad staying in a phase-locked state for an extended period of time. For a system with internal free energy sources as it is usually the case for plasma turbulence, linear frequencies can provide the dominant term in the phase evolution of a given wave-number node. It may be that these frequencies, possibly modified by nonlinear effects such as the Doppler shift from large scale flows, etc., reorganize themselves locally to induce these phase-coherent states, which is in stark contrast to the case of random phase.

Substituting $\psi _{\ell }=A_{\ell }{\textrm{e}}^{i\phi _{\ell }}$ in (4) and assuming $M_{\ell \ell '\ell ''}\in {\mathbb {R}}$ for simplicity, we get

$$\begin{aligned} \partial _{t}A_{\ell }= & {} \gamma _{\ell }A_{\ell }+\frac{1}{2} \sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }} M_{{\ell \ell '\ell ''}}A_{\ell '}A_{\ell ''}\cos \left( \phi _{\ell }+\phi _{\ell '}+\phi _{\ell ''}\right) \end{aligned}$$

(10)

$$\begin{aligned} \partial _{t}\phi _{\ell }= & {} -\omega _{r\ell }-\frac{1}{2} \sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }} M_{{\ell \ell '\ell ''}}\frac{A_{\ell '}A_{\ell ''}}{A_{\ell }} \sin \left( \phi _{\ell }+\phi _{\ell '}+\phi _{\ell ''}\right) . \end{aligned}$$

(11)

Note that for the more general case of complex $M_{\ell \ell '\ell ''}$ the argument of the sine and cosine in Eqs. (10)–(11) would be replaced by $\left( \phi _{M_{\ell \ell '\ell ''}}+\phi _{\ell }+\phi _{\ell '}+\phi _{\ell ''}\right)$, where $\phi _{M_{\ell \ell '\ell ''}}=\arg \left( M_{\ell \ell '\ell ''}\right) .$ The complete problem of plasma turbulence, that we call the “primitive network”, that we usually solve in direct numerical simulations involves Eq. (4) or equivalently the Eqs. (11) and (10) or (6) on a network constructed from a regular rectangular grid of wave-number nodes in Fourier space.

However, the point of the network formulation is reduction, and there are many different ways one can reduce such a system depending on what the dominant processes are and what one wants to describe. For example, a blunt way to do reduction is to directly truncate the Fourier space, so that we have a reduced system, that is somehow supposed to represent the full system. If such a reduction is done using the original equations [i.e., Eq. (4)], it can typically give us a sense of what the coupled system does qualitatively, but unless the truncation is done respecting the statistical characteristics of the initial network, it would modify things like energy equipartition solutions, etc. In the same vein, we can keep the nodes but reduce the links, which corresponds to keeping the full regular rectangular grid in Fourier space, but only considering a certain class of interactions (e.g., certain kinds of triads). Self-consistent quasi-linear theory, commonly used in fusion and geophysical fluid dynamics applications where one keeps interactions with large scales (zonal flows and profiles) but drops the interactions among small-scale fluctuations can be considered as an example of this.

A different way to reduce the initial primitive network may be to use a closure scheme, which would allow us to lump different nodes and links together in groups instead of using truncation or dropping links. Such a lumping together of the nodes requires a closure that can represent multiple triadic interactions as a single triadic (or two-body) interaction, which in turn requires handling the statistics of phase relations. We can do this, for example, by invoking the random phase approximation, which would allow us to use direct interaction approximation (DIA) (Kraichnan 1959; Lesieur 1997) or the eddy-damped quasi-normal Markovian approximation (EDQNM) (Kraichnan 1976; Krommes 2002), thus resulting in a reduced system (say EDQNM equations) on a reduced network when we sum over groups of nodes.

Another interesting case arises, when the dynamics is dominated by interacting linear waves. In this limit, the resonant interactions between the linear frequencies $\omega _{\ell }$ result in a phase-locked state, which provides a natural closure for the system of equations. It would also provide a natural reduction of the network, since only those modes that also satisfy the resonant interaction condition, i.e., $\omega _{\ell }\pm \omega _{\ell '}\pm \omega _{\ell ''}=0$ are necessary and we can drop the others. It can also be argued, without actually invoking wave-turbulence closure, that the justification for using quasi-linear models in fusion plasmas is in fact the idea that the system lacks obvious three-wave-resonances without large-scale flows, which can be zonal flows, Geodesic acoustic modes (GAMs), or other large-scale structures, so that the resonant interactions always have to involve one of these flow structures (Holland et al. 2003).

2.4 Wave turbulence

Practicality of the network formulation relies on a suitable reduction of either the nodes or the interactions of its underlying wave-number space network. In this sense, wave-turbulence provides a compelling scenario, since it allows one to consider only a very small subset of all possible interactions due to the resonance condition. While, wave turbulence, which describes the evolution of an ensemble of weakly interacting waves (Newell and Rumpf 2011; Nazarenko 2011), obeying a linear dispersion relation, is strictly applicable only in the asymptotic limit with linearly stable waves, at the limit of infinite box size, it still presents a very powerful tool for understanding the role the resonant or quasi-resonant interactions play in the turbulent cascade. It can describe multiple statistical quantities using only a conserved quantity called the wave-quanta, commonly denoted by $N_{k}\equiv E_{k}/\omega _{k}$ where $E_{k}$ is the energy, which is equivalent to potential enstrophy in the Charney–Hasegawa–Mima case with proper zonal-flow response [apart from a factor of $1/|k_{y} |,$ which depends on the zonal-flow response]. Network formulation in the case of wave-turbulence is of great interest, and has been studied in some detail in the past, as one can obviously decouple the geometric study of the resonant manifold and the evolution of the wave-quanta on the said manifold resulting in a major conceptual simplification.

Being an asymptotic theory, it is common to make the assumption of infinite size in the study of wave-turbulence, which also sidesteps the issue of whether or not the discrete modes that are available in a finite system actually satisfy the resonance condition, since in that limit, one has a continuous k-space, hence an infinite number of nearly resonant modes (Nazarenko 2011). The usual wave-kinetic equation for the Charney–Hasegawa–Mima system can be written as follows Connaughton et al. (2015):

$$\begin{aligned} \frac{\partial n_{k}}{\partial t}=S\left[ n_{k}\right] +f_{k}-\gamma _{k}n_{k}, \end{aligned}$$

(12)

where the collision integral has the form

$$\begin{aligned} S\left[ n_{k}\right]&=4\pi \int W_{kpq}^{2}\bigg (n_{p}n_{q}-\sigma _{\omega _{k}\omega _{q}}n_{p}n_{k}- \sigma _{\omega _{k}\omega _{p}}n_{q}n_{k}\bigg )\nonumber \\&\quad \times \delta ^{2}\left( {\textbf{k}}-{\textbf{p}}- {\textbf{q}}\right) \delta \left( \omega _{k}-\omega _{p}- \omega _{q}\right) {\textrm{d}}^{2}p{\textrm{d}}^{2}q, \end{aligned}$$

(13)

and $\sigma$ denote the sign of its subscript, and the $W_{kpq}$ denote the nonlinear interaction coefficient in the wave interaction representation

$$\begin{aligned} W_{kpq}=-\frac{\hat{{\textbf{z}}}\times {\textbf{p}}\cdot {\textbf{q}}}{2} \sqrt{|\frac{p_{y}q_{y}}{k_{y}} |}\frac{\left( p^{2}-q^{2}\right) }{\left( 1+p^{2}\right) \left( 1+q^{2}\right) }. \end{aligned}$$

Some interesting observations for the Charney–Hasegawa–Mima system came out of the study of the wave-kinetic equation, such as the identification of an additional conservation law dubbed zonostrophy (Balk et al. 1991; Connaughton et al. 2015)

$$\begin{aligned} Z_{k}\equiv \arctan \left( \frac{\left( k_{x}+\sqrt{3}k_{y}\right) }{k^{2}}\right) - \arctan \left( \frac{\left( k_{x}-\sqrt{3}k_{y}\right) }{k^{2}}\right) - \frac{2\sqrt{3}}{\left( 1+k^{2}\right) }k_{y}. \end{aligned}$$

In the study of fusion plasmas, on the other hand, it is more common to use what is sometimes called weak turbulence theory (WTT), which is essentially the same thing as it involves the same underlying assumptions, except that one keeps the linear instability term, and the resulting kinetic equation is seen as a Markovian statistical closure in the same vein as the EDQNM. We can write the general form of the WTT equations somewhat symbolically as (Krommes 2002)

$$\begin{aligned} \partial _{t}C_{k}-2\gamma _{k}^{\text {lin}}C_{k}+2\text {Re} \eta _{k}^{\text {nl}}C_{k}=2F_{k}^{\text {nl}}, \end{aligned}$$

(14)

where $C_{k}\equiv \left\langle |\Phi _{k} |^{2}\right\rangle$

$$\begin{aligned} \eta _{k}^{\text {nl}}\approx -\sum _{\triangle }M_{kpq}M_{pkq}^{*} \theta _{kpq}^{*}\left( t\right) C_{q}, \end{aligned}$$

(15)

and

$$\begin{aligned} F_{k}^{\text {nl}}\approx \frac{1}{2}\sum _{\triangle }|M_{kpq} |^{2}\text {Re} \left[ \theta _{kpq}\left( t\right) \right] C_{p}C_{q} \end{aligned}$$

(16)

with

$$\begin{aligned} \theta _{kpq}\left( t\right) \equiv \pi \delta \left( \omega _{k}-\omega _{p}- \omega _{q}\right) . \end{aligned}$$

Note that the first term in (13) corresponds to the incoherent term, given in WTT by (16), and the last two terms in (13) can be combined, by exchanging p and q in one of the terms into the coherent term given in (15) [i.e., when multiplied by $n_{k}$ as it appears in (14)]. Multiplying $C_{k}$ by $\sigma _{k}$, we can write the equation for a conserved quantity $E_{k}^{\sigma }\equiv C_{k}\sigma _{k}.$ The advantage of this formulation is that we can use it on a reduced network, exactly the same way as we would use any other closure. An example for the EDQNM closure on a reduced network can be found in Sect. 4.2.

Wave turbulence on a discrete wave-number space network is also sometimes studied using the original equations (for example, the Charney–Hasegawa–Mima system) directly on a wave-number space network consisting of clusters of triads (Harper et al. 2013; Connaughton et al. 2015). In this case, using the wave interaction representation appears to be a mere convenience, since the equations are the same. However, since the resonance conditions, even including resonance broadening (Dupree 1966), make the topology of the k-space network, very sparse, since the large majority of interactions are effaced as a result of the resonance condition. This leads to the creation of clusters of connected triads, that may be isolated or weakly connected to one another, resulting in the blocking of the k-space cascade. Unlike strong turbulence case, each wave-number node in a wave-number space network of wave-turbulence is involved in only a few (if any) triads. This is a manifestation of the fact that the resonance condition, for example written for the Charney–Hasegawa–Mima case as

$$\begin{aligned} \frac{p_{y}+q_{y}}{1+p^{2}+q^{2}+2{\textbf{p}}\cdot {\textbf{q}}}- \frac{p_{y}}{\left( 1+p^{2}\right) }-\frac{q_{y}}{\left( 1+q^{2}\right) }=0, \end{aligned}$$

defines a curve for a given ${\textbf{q}}=k_{\ell },$ and only the points ${\textbf{p}}=k_{\ell '}$ that lie both on the discrete ${\textbf{k}}$-space grid and on the resonance manifold gets connected to this node. This makes it possible and somewhat practical to consider the wave-turbulence as a network of “triads” that are connected by nodes, in an inverted perspective to the point of view generally advocated in this review. A key observation in this case is that since unconnected clusters will independently conserve the quadratically conserved quantities, one has as many conserved quantities as the number of clusters $\times$ the number of nonlinearly conserved quantities if the system was fully connected (Harper et al. 2013). This makes the wave-turbulence cascade dependent on the topology of the network, getting blocked if the clusters remain unconnected, and with an explicit percolation phenomenon as the number of triads is increased (Bustamante and Hayat 2013).

The case of inhomogeneous wave-kinetics (Dubrulle and Nazarenko 1997; Smolyakov and Diamond 1999) is also of particular interest, especially in the context of self-consistent drift-wave/zonal flow evolution, with radial propagation as well as scattering in wave-number due to the effects of zonal flows. The wave-kinetic system that results is isomorphic to the Vlasov Equation, with wave quanta playing the role of the distribution function

$$\begin{aligned} \frac{\partial }{\partial t}N_{k}+\frac{\partial \omega }{\partial k}\frac{\partial N_{k}}{\partial x}-\frac{\partial \omega }{\partial x}\frac{\partial N_{k}}{\partial k_{x}}=C\left( N,N\right) +F_{k}, \end{aligned}$$

where $\omega =\omega _{k}-{\overline{u}}_{y}\left( x\right) k_{y}$ is the basic drift-wave-frequency Doppler shifted by the zonal flow ${\overline{u}}_{y}\left( x\right) ,$ $C\left( N,N\right)$ represents a collision integral describing mode coupling similar to (13) and $F_{k}$ is the forcing and dissipation which can be provided by a linear instability as well as external forcing and small-scale dissipation. The inhomogeneous wave-kinetic equation has proved extremely useful in the study of transport and turbulence in fusion plasmas, being applied in various problems ranging from momentum transport (Diamond et al. 2008) to turbulence spreading (Gürcan et al. 2005). Network formulation of the general class of kinetic systems of which the wave-kinetics is a member is discussed in the next section.

2.5 Formulation of kinetic theory

Going back to regular plasma or fluid turbulence, the form of Eq. (4) given in Sect. 2.1 is really strictly valid only for a single field system. Many plasma problems even when reduced fluid equations are used involve multiple fields. In this more general case, the different fields at a given node are likely to be coupled linearly, allowing also for the possibility of linear interactions between nodes (e.g., toroidal mode coupling in tokamak plasmas), we can write the more general network equation as

$$\begin{aligned} \partial _{t}\xi _{\ell }^{\alpha }+\sum _{\ell '}{\mathcal {L}}_{\ell \ell '}^{\alpha \beta } \xi _{\ell '}^{\beta }+\sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }} M_{\ell \ell '\ell ''}^{\alpha \beta \gamma }\xi _{\ell '}^{\beta *}\xi _{\ell ''}^{\gamma *}=0, \end{aligned}$$

(17)

where ${\mathcal {L}}_{\ell \ell '}^{\alpha \beta }$ is an arbitrary linear matrix, ${\textbf{i}}_{\ell }$ is the interaction network, and $M_{\ell \ell '\ell ''}^{\alpha \beta \gamma }$ are the nonlinear interaction coefficients. In the usual spectral formulation ${\mathcal {L}}_{\ell \ell '}^{\alpha \beta }={\mathcal {L}}_{\ell }^{\alpha \beta } \delta _{\ell \ell '},$ and one can in general define a set of alternative variables say $\chi _{\ell }^{\alpha }$ that diagonalizes the Greek indices to write the problem in terms its eigenmodes, in that particular case, we can write

$$\begin{aligned} \left( \partial _{t}+i\omega _{\ell }^{\alpha }\right) \chi _{\ell }^{\alpha }+ \sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }}M_{\ell \ell '\ell ''}^{\alpha \beta \gamma } \chi _{\ell '}^{\beta *}\chi _{\ell ''}^{\gamma *}=0 \end{aligned}$$

of course with a different M that describes the interactions between the eigenmodes, which can be computed using standard rules of linear algebra.

A fluid system with a finite number of moments is in fact a closure of the full kinetic system, so, in general, a distribution function can be written as a combination of a number of suitable functional forms. For instance, it is common to describe the distribution function of the Vlasov equation using Hermite polynomials (Grad 1949; Holloway 1996) as in

$$\begin{aligned} f\left( {\textbf{x}},v,t\right) =\frac{1}{N_{v}}\sum _{\ell ,\alpha } \xi _{\ell }^{\alpha }\left( t\right) H_{\alpha }\left( v\right) {\textrm{e}}^{i{\textbf{k}}_{\ell }x-v^{2}}, \end{aligned}$$

(18)

where $N_{v}$ is a normalization factor, and $H_{\alpha }$ is the Hermite polynomial of (integer) order $\alpha ,$ with hopefully only a finite number of Hermite polynomials being sufficient to describe its evolution. When used in conjunction with Eq. (18), the network equation of (17) describes the interactions between wave-number nodes that satisfy the triadic interaction conditions, where each node has a number of complex variables (indicated by the Greek indices) representing the coefficients of Hermite polynomials, which correspond to consecutive derivatives of Maxwellians.

In the same spirit, one can use a combination of Fourier–Bessel–Hermite (Plunk et al. 2010; Parker 2016) (or Fourier–Laguerre–Hermite (Mandell et al. 2018) ) expansion which handles, spatial, perpendicular and parallel velocity directions, respectively

$$\begin{aligned} f\left( {\textbf{x}},v_{\parallel },v_{\perp },t\right) =\sum _{\ell ,m,\alpha }F_{\ell m}^{\alpha }\left( t\right) J_{0}\left( \kappa _{m}v_{\perp }\right) H_{\alpha } \left( v_{\parallel }\right) {\textrm{e}}^{i{\textbf{k}}_{\ell }\cdot {\textbf{x}} -v_{\parallel }^{2}}. \end{aligned}$$

(19)

At this point, we can either flatten the indices $\alpha$ and m as before, so that we are left with a single index $\ell$ which represents the generalized wave-number in ${\textbf{x}},{\textbf{v}}$ space, so that some version of Eq. (4) can be used, or keep the form of Eq. (19) to write the wave-number space network equation in its general form as

$$\begin{aligned}&\partial _{t}f_{\ell m}^{\alpha } +\sum _{\ell '}{\mathcal {L}}_{\ell \ell '}^{\alpha \beta } f_{\ell 'm}^{\beta }\\&\quad +\sum _{\ell 'm';\ell ''m''\in {\textbf{i}}_{\ell }}M_{\ell \ell '\ell '';mm'm''}^{\alpha \beta \gamma }f_{\ell 'm'}^{\beta *}f_{\ell ''m''}^{\gamma *}=0; \end{aligned}$$

note that in gyrokinetics, $v_{\perp }$ appears as a label in the linear term (so no coupling between m’s), and the coupling condition for the triadic interactions can be written as ${\textbf{k}}_{m}+{\textbf{k}}_{m'}+{\textbf{k}}_{m''}=0$ where $\kappa _{m}\equiv |{\textbf{k}}_{m} |$ for $v_{\perp }$ space as well. Even though the condition for interaction in m is actually the same for that in $\ell ,$ because of the details of the way the system may be discretized in these different variables makes the actual computation of the interaction network topology rather complicated. There are actually many different alternatives to the above approach and the usual velocity space formulation with finite difference discretization can also be formulated as a complicated interaction matrix; however, since our focus is wave-number space networks, we pick a spectral formulation also in the velocity space variable as the natural choice.

Note, finally, that energy conservation for Eq. (17) can still be written using Eq. (6), with

$$\begin{aligned}{} & {} E_{\ell }^{\sigma }\equiv \xi _{\ell }^{\alpha }\sigma _{\ell }^{\alpha \beta }\xi _{\ell }^{*\beta }\\{} & {} T_{\ell \ell '\ell ''}^{\sigma }\equiv 2\text {Re}\left[ M_{\ell \ell '\ell ''}^{\beta \lambda \mu } \sigma _{\ell }^{\alpha \beta }\left( \xi _{\ell }^{*\alpha }\xi _{\ell '}^{*\lambda } \xi _{\ell ''}^{*\mu }\right) \right] \\{} & {} F_{\ell }^{\sigma }\equiv -\sum _{\ell '}2\text {Re}\left( {\mathcal {L}}_{\ell \ell '}^{\alpha \lambda }\sigma _{\ell }^{\alpha \beta }\xi _{\ell '}^{\lambda }\xi _{\ell }^{*\beta }\right) , \end{aligned}$$

so that we can write

$$\begin{aligned} P_{\ell }^{\sigma }=\left\{ \begin{array}{ll} F_{\ell }^{\sigma } &{} \quad \text {if}\ F_{\ell }^{\sigma }>0\\ 0 &{} \quad \text {if}\ F_{\ell }^{\sigma }>0 \end{array}\right. \quad \text {and}\quad D_{\ell }^{\sigma }=\left\{ \begin{array}{ll} 0 &{} \quad \text {if}\ F_{\ell }^{\sigma }>0\\ -F_{\ell }^{\sigma } &{} \quad \text {if}\ F_{\ell }^{\sigma }>0, \end{array}\right. \end{aligned}$$

where $\sigma _{\ell }^{\alpha \beta }=\sigma _{\ell }^{\beta \alpha }$ defines the conserved quantity.

2.6 Magnetic shear and rational surfaces

Strictly speaking, the examples that are given up to this point were written in Cartesian coordinates, and are therefore valid only in slab geometry. While one can easily transform everything to arbitrary curvilinear geometry, for example where one of the directions is aligned with the magnetic field as the natural geometry in magnetic fusion devices (D’haeseleer 1991), the actual details of using such coordinates are in fact nontrivial. This is partly due to the way some linear effects work in fusion plasmas, naturally allows an important reduction of the number of degrees of freedom. Among these effects, that of the magnetic shear stands out.

To understand the effect of magnetic shear, first consider the case of a sheared magnetic field in slab geometry with ${\textbf{B}}=B_{0}\left[ \hat{{\textbf{z}}}+\frac{x}{L_{s}}\hat{{\textbf{y}}}\right] .$ The parallel wave-number is then defined as $k_{\parallel }=k_{y}x/L_{s},$ and is therefore a function of the spatial variable x. We know that the Landau damping kills off any fluctuation with $k_{\parallel }v_{\text {th}}>\omega ,$ resulting in a reduction of the amplitude for any Fourier mode with $k_{\parallel }>\omega /v_{\text {th}}.$ This results in the amplitude of the fluctuations being localized to the region between the two Landau turning points $x_{\pm }=\pm |\frac{\omega L_{s}}{k_{y}v_{\text {th}}} |.$ Of course, a proper eigenmode analysis may incorporate various other effects, including the effect of an external, or self-generated flow shear, and thus give a more complete picture, but the basic concept of the localization of the drift-wave eigenmode due to Landau damping of higher k’s is rather generic.

A sheared slab can model the geometry of the magnetic field as a local approximation. For example, choosing the poloidal flux $\psi$ as a radial variable, $\theta$ as a poloidal variable with a period $2\pi ,$ and $\zeta$ as the toroidal variable, we can construct a generic toroidal coordinate system. Perturbations in such a system can be written in the general form as

$$\begin{aligned} \Phi \left( \psi ,\theta ,\zeta \right) =\sum _{n,m}\Phi _{nm} \left( \psi \right) {\textrm{e}}^{i\left( n\zeta -m\theta \right) }. \end{aligned}$$

(20)

Since the magnetic field is a function of $\psi$ and has the form of a helix wrapped around a torus, it is customary to define the toroidal winding number $q\left( \psi \right) \equiv \frac{{\textrm{d}}\zeta }{{\textrm{d}}\theta },$ which is the ratio of the number of times the magnetic field turns around the toroidal direction to the number of turns it makes in the poloidal direction, as “the safety factor” because of its importance in magnetic stability. For an axisymmetric tokamak with circular flux surfaces, this takes the familiar form $q=\frac{rB_{\phi }}{RB_{\theta }},$ where r and R are the minor and major radius variables. One can also define the effect of magnetic shear using the dimensionless parameter ${\hat{s}}\equiv rq'/q.$ More generally, the rate of change of the safety factor as a function of the poloidal flux $\psi$ determines the strength of the shear in the magnetic field in the $\psi$ direction. If we use a coordinates system that aligns itself to the magnetic field locally (like the so-called Clebsch coordinates described in some detail in D’haeseleer 1991), the effect enters through the nondiagonal terms in the metric tensor. However, at least in tokamaks, it is more customary to use toroidal coordinate $\phi$ as the direction of axisymmetry.

Since the magnetic field is sheared, each flux surface $\psi$ has a different pitch angle. The perturbations tend to be aligned to the field line (i.e., have $k_{\parallel }\approx 0$) as we discussed above. However, since they are also periodic in $\theta$ and $\zeta ,$ this can happen exactly, only when the perturbation is centered at what is called a “rational surface”, where $q\left( \psi \right) =m/n.$ This allows a perturbation of the form (20) to align itself to the magnetic field

$$\begin{aligned} \Phi \left( \psi ,\theta ,\zeta \right) =\sum _{n}\Phi _{n}\left( \psi \right) {\textrm{e}}^{in\left( \zeta -q\theta \right) }, \end{aligned}$$

(21)

and because of Landau damping, the perturbation with n and m such that $q\left( \psi \right) =m/n$ will be localized to its rational surface $\psi =\psi _{nm}$ defined by this relation.

The fact that plasma “turbulence” in tokamaks consists of modes localized to their rational surfaces has important implications for their network formulation. In this picture, the usual mode coupling through triads is largely restricted by the additional constraint that the interacting modes must have spatial overlap. Therefore, while the standard two-dimensional turbulence presents a very densely coupled network of interactions, the quasi-two-dimensional turbulence (since $k_{\parallel }\approx 0$) of tokamaks has a sparser interaction topology. This is true even when one includes a large number of toroidal and poloidal modes, so that rational surfaces are densely packed (i.e., each rational surface has many nearby neighbors).

Note that the nonlinear term of the underlying fluid equations due to advection by the ${\textbf{E}}\times {\textbf{B}}$ velocity, represented by the Poisson bracket, can be written in the coordinate system consisting of $\psi$ and $\alpha$ [so that ${\textbf{B}}=\nabla \psi \times \nabla \alpha$ say with $\alpha =\zeta -q\left( \psi \right) \theta$] as

$$\begin{aligned} \left[ \Phi ,\Omega \right] =\hat{{\textbf{b}}}\times \nabla \Phi \cdot \nabla \Omega = B\left( \frac{\partial \Phi }{\partial \psi }\frac{\partial \Omega }{\partial \alpha } -\frac{\partial \Phi }{\partial \alpha }\frac{\partial \Omega }{\partial \psi }\right) . \end{aligned}$$

2.6.1 Ballooning representation

When a perturbation of the form (20) is considered for a given n but for different values of m in toroidal geometry with a standard (e.g., increasing) profile of q,  the ${\textrm{e}}^{im\theta }$ factors from consecutive rational surfaces superpose in such a way that while at $\theta =0$, they add up, at $\theta =\pi$ they cancel. This causes an envelope-like dependence in $\theta$ direction with a maximum at $\theta =0$ direction, or the low field side of the tokamak (also called the bad curvature side). This envelope structure, which makes the modes expanded toward the low field side is called the “ballooning” structure. Details of the functional form of ballooning depend on the functional form of the localization of the Fourier modes around their rational surfaces. Since this ballooning structure suggests a slow variation of the envelope of the amplitude in $\theta$ variable [i.e., $f\left( \theta \right) {\textrm{e}}^{inq\theta }$ where the dependence of $f\left( \theta \right)$ on $\theta$ is “slow”], we are tempted to use an eikonal approximation. However, the fact that the $\theta$ variable is periodic complicates the issue.

To see this, consider a Gaussian centered at $\theta =0$ as the ballooning function $f\left( \theta \right) .$ For a periodic $\theta ,$ we can not write this simply as $f\left( \theta \right) ={\textrm{e}}^{-\theta ^{2}/2\sigma ^{2}}$ as it would have a discontinuity at $\theta =0.$ Instead, a basic first-order form

$$\begin{aligned} f\left( \theta \right) ={\textrm{e}}^{-\frac{\theta ^{2}}{2\sigma ^{2}}}+ {\textrm{e}}^{-\frac{\left( \theta -2\pi \right) ^{2}}{2\sigma ^{2}}} \end{aligned}$$

could be used (makes sense especially for $\sigma \ll 2\pi$), to remove the jump at $\theta =0.$ However, going back to (21), to avoid a jump in $\Phi ,$ the phase should also be continuous across the cut at $\theta =0$ (or $\theta =2\pi$), and thus, the actual form can be obtained by replacing $\theta \rightarrow \theta -2\pi$ in $f\left( \theta \right) {\textrm{e}}^{inq\theta }$ and adding this to itself. In other words, the ballooning function that removes the discontinuity at $\theta =0$ can be written as

$$\begin{aligned} f\left( \theta \right) ={\textrm{e}}^{-\frac{\theta ^{2}}{2\sigma ^{2}}}+ {\textrm{e}}^{-\frac{\left( \theta -2\pi \right) ^{2}}{2\sigma ^{2}}}{\textrm{e}}^{-i2\pi nq\left( r\right) }. \end{aligned}$$

Note that this particular example extends the range of $\theta$ from $[0,2\pi )$ to $[0,4\pi )$ or equivalently $(-2\pi ,2\pi ].$ If the ballooning function has a larger support, we need to extend the range of $\theta$ until the support is fully contained in the extended range. This leads us to introduce, what is called the ballooning representation, or the ballooning transform (Connor and Taylor 1987; Connor et al. 2004) as

$$\begin{aligned} \Phi ={\textrm{e}}^{-in\left( \phi -q\theta \right) }\sum _{p=-N}^{N}{\hat{\Phi }}\left( \theta -2\pi p\right) {\textrm{e}}^{-i2\pi nq\left( r\right) p}, \end{aligned}$$

where the function ${\hat{\Phi }}\left( \theta -2\pi j\right) \rightarrow {\hat{\Phi }}\left( \eta \right)$ is defined as a function of the extended ballooning angle $\eta ,$ such that the functional dependence on $\eta$ is simpler (e.g., the basic Gaussian form of $f\left( \eta \right) ={\textrm{e}}^{-\eta ^{2}/2\sigma ^{2}}$ in the example above). Note that here we have used a discrete version of the more common, continuum version of the ballooning transform for consistency with the network picture, as well as the conventions used in the rest of the paper.

The use of ballooning representation, as well as localization of the drift instabilities to rational surfaces, seems better adapted to the global physics of low n modes as opposed to high n micro-turbulence. However, the basic mechanism is independent of scale, and the approach is in fact used for gyrokinetic simulations of small-scale instabilities such as the ion temperature gradient driven (ITG) turbulence, or even those at electron gyroradius scales, such as the electron temperature gradient-driven (ETG) turbulence through the use of flux tube geometry (Beer et al. 1995).

The introduction of the concept of the flux tube, indeed, allows the reformulation of the problem of plasma turbulence using only a small portion of the whole toroidal volume. First, using magnetic flux coordinates, one switches to a coordinate system in which the magnetic field is a straight line (at each flux surface $\psi$), and then, the dependence of the magnetic field pitch angle to $\psi$ through $q\left( \psi \right)$ generates a “sheared slab” like coordinate system in these variables. This means that following Beer et al. (1995), we can define:

$$\begin{aligned} x=\frac{q_{0}}{B_{0}r_{0}}\left( \psi -\psi _{0}\right) ,\quad y=-\frac{r_{0}}{q_{0}}\left( \alpha -\alpha _{0}\right) ,\quad \text {z}=\theta , \end{aligned}$$

where $q_{0}=q\left( \psi _{0}\right) ,$ $B_{0}$ is the field at the magnetic axis and $r_{0}$ is the distance from the magnetic axis to the center of the box, to map the flux tube coordinates x,  y and z,  to the magnetic geometry of the tokamak. In this system, the equations go back to being quasi-two dimensional, with the possibility of a network formulation using $k_{x},$ $k_{y}$, etc., as discussed in earlier sections.

3 Truncation

The wave-number space network formulation is particularly useful for coming up with a reduction of the full system, when only a small number of wave-number nodes and/or triads are involved in the interaction. While in the general case, a proper reduction requires some kind of closure for the effects of the modes that are dropped in the reduced system, be it in the form of wave-number space nodes that do not contain much energy, higher moments of a kinetic distribution function or damped eigenmodes of a fluid system, a direct truncation of the system without any closure (or some kind of ad-hoc closure) is sometimes the simplest solution. Truncation may focus on dropping (i) wave-number space nodes (i.e., Fourier space truncation), (ii) triads (i.e., considering only a subset of interactions), or (iii) field variables (i.e., dropping higher order moments, or damped eigenmodes), or a combination of those. For example, quasi-linear theory is an example of dropping triadic interactions while keeping only those interactions with the large scales (profiles or zonal flows), without any attempt of closure for the effects of the rest of the modes. In contrast, if one uses eddy damping in such a system, this choice may represent an ad-hoc closure for the truncated modes. A straightforward truncation of the Fourier space using a geometrically scaled subset of wave-vectors is called the reduced wave-vector approximation (sometimes abbreviated as REWA) (Eggers and Grossmann 1991; Grossmann et al. 1996) and is the archetypical example of the truncated models that we discuss in this section. Such models tend to give very small intermittency corrections, as they have built-in self-similarity, but they can be very powerful for studying turbulence across a large range of scales.

3.1 Nested polyhedra models in 3D

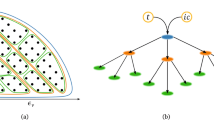
Nested polyhedra models (NPMs) are self-similar truncations of Fourier space based on nested polyhedra (Gürcan 2017a, 2018), resulting naturally in a finite set of complete triadic interactions at each scale. In these models, the wave-number space is discretized using nested, alternating icosahedron–dodecahedron pairs that are organized in such a way that the nodes of the resulting network form complete triads with nodes of the polyhedra from neighboring scales (see Fig. 3). Since the truncation is done at the level of the network, the underlying system of equations remains unchanged, and as there are only a finite number of nodes and links (i.e., three-body interactions), the resulting truncated system naturally respects the conservation properties of the original system. It is a nice example of the use of a truncated network to describe certain aspects (e.g., scale-by-scale energy transfer) of the complete system. It also illustrates neatly the separation of the issues of network topology (i.e., the regular grid is replaced by a Fourier space made up of vertices of the nested polyhedra) from those of model reduction (i.e., here, the equations are kept exactly the same, so there is no attempt at introducing even an ad-hoc closure). Nested polyhedra models can also be considered as an anisotropic generalization of shell models, used in studies of turbulence (Biferale 2003). Below, we discuss the NPM for both the Navier–Stokes and the MHD cases. The latter being more relevant for plasmas and providing a somewhat more general example than the Navier–Stokes case. While, in both cases, the model has the ability to represent anisotropy, since there is no source of anisotropy, the resulting turbulence remains isotropic.

Fig. 3

The numbering $n_{m}$ of the vertices of the a icosahedron (for an even m) as in Table 1 on the left and b dodecahedron (for an odd m) as in Table 2 on the right

The Navier–Stokes equation in Fourier space

$$\begin{aligned} \partial _{t}u_{{\textbf{k}}}^{i}+ik_{\kappa }\left[ \delta _{ij}- \frac{k_{i}k_{j}}{k^{2}}\right] \sum _{{\textbf{p}}+{\textbf{q}} =-{\textbf{k}}}u_{{\textbf{p}}}^{\kappa *}u_{{\textbf{q}}}^{j*}=0 \end{aligned}$$

(22)

can be discretized using a logarithmic alternating icosahedral/dodecahedral basis where ${\textbf{k}}=k_{n}\hat{{\textbf{k}}}_{m}$ with $k_{n}=g^{n}\lambda k_{0}$ is the logarithmically spaced wave-number magnitude with $g=\sqrt{\varphi }=\sqrt{\left( 1+\sqrt{5}\right) /2}$ and $\lambda =\sqrt{\sqrt{5}/3}$ for an icosahedron and $\lambda =1$ for a dodecahedron. The unit vector can be written as $\hat{{\textbf{k}}}_{m}=e_{m}^{j}=\left[ \sin \theta _{m}\cos \phi _{m}, \sin \theta _{m}\sin \phi _{m},\cos \theta _{m}\right]$ where $\theta _{m}$ and $\phi _{m}$ are to be picked from the angles corresponding to the icosahedral and the dodecahedral vertices. This choice comes from imposing the condition of forming triads with the vertices of three consecutive polyhedra. Defining

$$\begin{aligned} M_{nm}^{i\kappa j}=k_{nm}^{\kappa }\left[ \delta _{ij}-\frac{k_{nm}^{i}k_{nm}^{j}}{k_{n}^{2}}\right] . \end{aligned}$$

The nested polyhedra model can be written as

$$\begin{aligned}&\partial _{t}u_{n,m}^{i}+i{\overline{M}}_{nm}^{\kappa ij}\sum _{\left\{ m',m''\right\} } \bigg [ u_{n-2,m'}^{\kappa *}u_{n-1,m''}^{j*}+u_{n-1,m'}^{\kappa *}u_{n+1,m''}^{j*}\nonumber \\&\quad +u_{n+1,m'}^{\kappa *}u_{n+2,m''}^{j*}\bigg ], \end{aligned}$$

(23)

where the nth polyhedron is either an icosahedron or a dodecahedron, with ${\overline{M}}_{nm}^{i\kappa j}=M_{nm}^{i\kappa j}+M_{nm}^{ij\kappa }$ and the sum is computed over pairs of interacting nodes $m',m''$ of the consecutive shells as given in the interaction tables (Tables 1 and 2). When written in this form, the model has a clear resemblance to shell models and can actually be transformed into one by choosing the phases in a particular way. It can also be written using flattened indices and keeping only half of the nodes in each scale due to Hermitian symmetry

$$\begin{aligned} \left( \partial _{t}+\nu k_{\ell }^{2}\right) u_{\ell }^{\alpha }&=\sum _{\ell ',\ell ''={\textbf{i}}_{j}^{\ell }}M_{\ell }^{\alpha \beta \lambda }u_{\ell '}^{\beta c_{\ell '}}u_{\ell ''}^{\lambda c_{\ell ''}}\\&=\sum _{j=0}^{N_{\ell }}M_{\ell }^{\alpha \beta \lambda }u_{i_{j0}}^{\beta c_{j0}}u_{i_{j1}}^{\lambda c_{j1}}, \end{aligned}$$

where the Greek indices denote vector components, $i_{j0}$ and $i_{j1}$ are the two nodes $\ell '$ and $\ell ''$ that interact with the node $\ell$ in the interaction triad $t_{j}$ (i.e., $t_{j}\equiv \left[ \ell ,i_{j0}^{\ell },i_{j1}^{\ell }\right]$) that are to be taken from Tables 1 and 2 that gives ${\textbf{i}}_{j}^{\ell }=\left\{ i_{j0}^{\ell },i_{j1}^{\ell }\right\} .$ Here, we also define

$$\begin{aligned} u_{\ell }^{\alpha c_{\ell }}\equiv \left\{ \begin{array}{ll} u_{\ell }^{\alpha *} &{}\quad \text {if}\ c_{\ell }=1\\ u_{\ell }^{\alpha } &{} \quad \text {if}\ c_{\ell }=0 \end{array}\right. \end{aligned}$$

on the right-hand side. This is needed, because we one only keep half of the nodes of each polyhedra as in Fig. 3, which consist of 6 nodes for the icosahedron and 10 nodes for the dodecahedron, and the rest of the nodes can be obtained by reflection with respect to the origin [since ${\textbf{u}}\left( -{\textbf{k}}\right) ={\textbf{u}}^{*}\left( {\textbf{k}}\right)$]. The interaction tables are given in Tables 1 and 2, which replaces the adjacency matrix for this kind of network, and the flattened node index can be written as

$$\begin{aligned} \ell =\left\{ \begin{array}{ll} 8n+m_{n} &{}\quad n:\ \text {even}\\ \ell =8n+m_{n}+2 &{}\quad n:\ \text {odd} \end{array}\right. \end{aligned}$$

with $m_{n}$ being the node number within the polyhedron (basically the label of the discretized angle denoted by $\hat{{\textbf{k}}}_{m}$). Here, each node $\ell$ is connected to $N_{\ell }=9$ triads if it is an icosahedron node (i.e., n is even) or $N_{\ell }=15$ triads if it is a dodecahedron node (i.e., n is odd). A python implementation of the nested polyhedra model can be found at (Gürcan 2017b).

Table 1 $\ell =8n+m_{n},$ where $m_{n},$ which denotes the mth vertex of the nth polyhedron, is shown on the leftmost column, interacts with ${\textbf{i}}_{j}^{\left( \ell \right) }=\left\{ i_{0},i_{1}\right\} =\left\{ 8n-16+m_{n-2},8n-10+m_{n-1}\right\} ,$ $\left\{ 8n-10+m_{n-1},8n+6+m_{n+1}\right\}$ and $\left\{ 8n+6+m_{n+1},8n+16+m_{n+2}\right\}$ for an even n (i.e., an icosahedron node) where $m_{n},$ $m_{n\pm 1}$ and $m_{n\pm 2}$ are to be taken from their corresponding columns. Note that a bar over the integer value $m_{n}$ indicates $c_{j}=0$ (i.e., not conjugated), whereas no bar means $c_{j}=1$ (i.e., conjugated)

Table 2 $\ell =8n+m_{n}+2$ where $m_{n}$ is shown on the leftmost column, interacts with ${\textbf{i}}_{\ell }=\left\{ i_{0},i_{1}\right\} =\left\{ 8n-14+m_{n-2},8n-4+m_{n-1}\right\} ,$ $\left\{ 8n-4+m_{n-1},8n+12+m_{n+1}\right\}$ and $\left\{ 8n+12+m_{n+1},8n+18+m_{n+1}\right\}$ for an odd n (i.e., a dodecahedron node) where $m_{n},$ $m_{n\pm 1}$ and $m_{n\pm 2}$ are to be taken from their corresponding columns

3.1.1 MHD

The three-dimensional MHD equations can be written in the same wave-number space network as

$$\begin{aligned} \left( \partial _{t}+\nu k_{\ell }^{2}\right) u_{\ell }^{\alpha }&=\sum _{j=0}^{N_{\ell }}{\overline{M}}_{\ell }^{\alpha \beta \lambda }\left( u_{\ell _{j0}}^{\beta c_{j0}}u_{\ell _{j1}}^{\lambda c_{j1}}-b_{\ell _{j0}}^{\beta c_{j0}}b_{\ell _{j1}}^{\lambda c_{j1}}\right) \nonumber \\ \left( \partial _{t}+\eta k_{\ell }^{2}\right) b_{\ell }^{\alpha }&=\sum _{j=0}^{N_{\ell }}\delta M_{\ell }^{\alpha \beta \lambda }\left( u_{\ell _{j0}}^{\beta c_{j0}}b_{\ell _{j1}}^{\lambda c_{j1}}-b_{\ell _{j0}}^{\beta c_{j0}}u_{\ell _{j1}}^{\lambda c_{j1}}\right) , \end{aligned}$$

(24)

where ${\overline{M}}_{\ell }^{\alpha \beta \lambda }=M_{\ell }^{\alpha \beta \lambda } +M_{\ell }^{\alpha \lambda \beta },$ $\delta M_{\ell }^{\alpha \beta \lambda }=M_{\ell }^{\alpha \beta \lambda }-M_{\ell }^{\alpha \lambda \beta }$ and

$$\begin{aligned} M_{\ell }^{\alpha \beta \lambda }\left( k\right) =-ik_{\ell }^{\beta } \left[ \delta _{\alpha \lambda }-\frac{k_{\ell }^{\alpha }k_{\ell }^{\lambda }}{k_{\ell }^{2}}\right] . \end{aligned}$$

Note that the ratio of the largest wave-number to the smallest in an interacting triad in a nested polyhedra model is a constant around 62% (i.e., $1/\varphi$ where $\varphi =\left( 1+\sqrt{5}\right) /2$ is the golden ratio). Applying random forcing only on the velocity field at all the nodes of the shells $n=4$ and $n=5$ using a fixed time step $h_{f}\sim 10^{-3},$ larger than the maximum step size for the adaptive time stepping normally used, gives a steady-state wave-number spectrum that is consistent with Kolmogorov’s $k^{-5/3}$ spectrum as can be seen in Fig. 4. It is probably worth noting that the model is self-similar by construction (i.e., mono-fractal), shows no sign of intermittency in the sense that it follows the $S_{p}\left( k_{n}\right) \sim k_{n}^{-p/3}$ scaling in the inertial range, where $S_{p}\left( k_{n}\right) =\left\langle \frac{1}{N_{\ell }}\sum _{\ell }\left( \sum _{i}|u_{n\ell }^{i} |^{2}\right) ^{p/2}\right\rangle$ with $\left\langle \cdot \right\rangle$ denoting time average. The nested polyhedra approach for the MHD shows that such a model can easily handle the spectral evolution over 6 decades with a large possible variation of magnetic Prandtl number and describe one of the mechanisms by which the system can reach equipartition between kinetic and magnetic energies, when only the velocity field is stirred (i.e., dynamo action) (Gürcan 2018). Interestingly the system reaches steady state only when the velocity field is stirred through random forcing, whereas if the forcing is coherent, the large-scale magnetic field keeps accumulating.

Fig. 4

The wave-number spectrum with $Pr_{m}=1,$ $\nu =10^{-9},$ $N=60$, and $h_{f}=10^{-3}$ where $Pr_{m}\equiv \nu /\eta$ is the magnetic Prandtl number, N is the number of polyhedra, and $h_{f}$ is the random forcing time step. Kinetic (solid line) and magnetic (dotted line) energy spectra both follow the Kolmogorov’s $k^{-5/3}$ spectrum. The result is averaged over the polyhedra nodes and also from $t=460$ to $t=500$

3.2 Spiral chain models for 2D

In two dimensions, the basic equation of turbulence is that of Navier–Stokes, which can be written in wave-number space as a scalar equation for the Fourier transform of the stream function

$$\begin{aligned} \partial _{t}\Phi _{k}=\sum _{\triangle }\frac{\hat{{\textbf{z}}} \times {\textbf{p}}\cdot {\textbf{q}}\left( q^{2}-p^{2}\right) }{k^{2}} \Phi _{p}^{*}\Phi _{q}^{*}-D_{k}\Phi _{k}, \end{aligned}$$

where the sum over $\triangle$ represents a sum over ${\textbf{p}}$ and ${\textbf{q}}$, such that ${\textbf{k}}+{\textbf{p}}+{\textbf{q}}=0$ (with $p<q,$ since the interaction coefficient is symmetrized).

If it happens that a particular triad with $k<p<q$ satisfies the condition that $\eta \equiv \frac{\ln \left( q/k\right) }{\ln \left( p/k\right) }\in {\mathbb {Q}}$ (i.e., is rational), we can write $p=kg^{\ell }$ and $q=kg^{m}$ (i.e., $\eta =m/\ell$ and $g>1$ with $g\in {\mathbb {R}}$). Since not all triangles satisfy the condition $\eta \in {\mathbb {Q}},$ especially if we consider low-order rationals, only a select class of triangles can be represented by $p=kg^{\ell }$ and $q=kg^{m}$ with $\ell$ and m integers.

If we consider a “triad triplet”, that is a set of three triads that are obtained by scaling and rotating a given triad, such that the wave-vector ${\textbf{k}}$ appears first as the smaller, then as the middle and finally as the larger leg of the resulting triad and the contributions of each of those three triads to the equation for the wave-vector ${\textbf{k}},$ we can write

Fig. 5

The spiral chain $\ell =2,$ $m=3$ with $g=\sqrt{\rho }.$ The counter clock-wise primary spiral chain is shown in black dashed lines, while the clock-wise secondary spirals are shown in gray dashed lines. Note that as the energy travels along the primary chain, it gets exchanged between the 5 secondary chains. Finally, an interacting triad with ${\textbf{k}}={\textbf{k}}_{n}$ (black arrow, pointing right), ${\textbf{p}}={\textbf{k}}_{n-2}$ (red arrow, pointing up), and ${\textbf{q}}={\textbf{k}}_{n+1}$ (blue arrow, pointing left) is shown (i.e., ${\textbf{k}}+{\textbf{q}}-{\textbf{p}}=0$)

$$\begin{aligned} \partial _{t}\Phi _{n}&=k_{n}^{2}\sin \alpha _{qp}\bigg [g^{m+\ell } \left( g^{2m}-g^{2\ell }\right) \Phi _{n+\ell }^{*}\Phi _{n+m}^{*}\nonumber \\&\quad +g^{m-3\ell }\left( 1-g^{2m}\right) \Phi _{n-\ell +m}^{*}\Phi _{n-\ell }^{*}\nonumber \\&\quad +g^{\ell -3m}\left( g^{2\ell }-1\right) \Phi _{n-m}^{*}\Phi _{n-m+\ell }^{*}\bigg ], \end{aligned}$$

(25)

writing ${\textbf{k}}=k_{0}g^{n}\hat{{\textbf{k}}}_{n}$, so that $\Phi _{k}\rightarrow \Phi _{n}.$ Equation (25) is what we call the spiral chain model (Gürcan et al. 2019) of two-dimensional turbulence and it appears as a direct generalization of the two-dimensional shell models, since $m=2,$ $\ell =1$ gives the usual Gledzer–Ohkitani–Yamada (Ohkitani and Yamada 1989) model. Strictly speaking, the spiral chain models must have rotation by the same angle between its elements, which is true only for certain very particular values of g,  $\ell$, and m, even though the general form is also interesting but does not have a regular spiral structure in the wave-number space.

Considering, for example, $\ell =2,$ $m=3$ in (25), with $\theta _{n}=n\alpha ,$ so that $\alpha _{pk}=2\alpha ,$ $\alpha _{qp}=\alpha$ and $\alpha _{qk}=3\alpha .$ We can write the equations using the law of cosines for each angle, which gives two polynomial relations for g,  which can be solved for example for the case ${\textbf{k}}+{\textbf{p}}-{\textbf{q}}=0$ with $g=\sqrt{\rho }$ where $\rho$ is the plastic number defined as

$$\begin{aligned} \rho =\left( \frac{1}{2}\right) ^{1/3}\left[ \left( 1-\sqrt{\frac{23}{27}} \right) ^{1/3}+\left( 1+\sqrt{\frac{23}{27}}\right) ^{1/3}\right] \end{aligned}$$

and an angle $\alpha =\pi -\arccos \left( -g^{3}/2\right) .$ This particular spiral chain is shown in Fig. 5.

Generally speaking, spiral chain models are wave-number space networks where the nodes are organized in the form of spirals, and interact through exact triadic interactions. Since the structure is self-similar, if we take three nodes that interact, when we scale and rotate the system, the scaled versions of those three nodes also interact. If the spiral chain consists of a single set of $\ell ,$ m, and g values, it means that the whole spiral is constructed from a single triad that is rotated and scaled accordingly. However there are cases where multiple values of m and $\ell$ can be possible for a given value of g. Note that spiral chains can also be used to construct domain partitions instead of truncation.

Unfortunately, as numerical models, the spiral chain models suffer the same shortcomings as the shell models for describing 2D or quasi-2D systems. Phase evolution tending toward random makes these systems unable to reproduce a proper equipartition, since they lack the dependence of the number of degrees of freedom to scale that the linear grid has, and therefore, they fail, in particular, in reproducing the inverse cascade (Aurell et al. 1994). Note that this is a general problem related to the use of logarithmic spacing without paying attention to the statistical weight of each element, and not a problem related to the network formulation. However, this can be remedied using a closure that somehow gets rid of the phase dynamics, in which case the models become similar to differential approximation models (Lilly 1989; L’vov and Nazarenko 2006), but local over a fractal structure in wave-number space instead of the usual 1D k-space grid.

3.3 Self-consistent quasi-linear models

The usual formulation of quasi-linear theory deals with the computation of fluxes of transported quantities like particle density, temperature, or angular momentum using linear evolution equations for the fluctuations. When the profiles of these transported quantities also evolve in time, and the linear relations are computed at each time step given the local gradients of these evolving profiles (which may also include zonal flows and or other meso-scale flow structures), the resulting system is what we call self-consistent quasi-linear theory. One can also improve such a formulation by introducing renormalization (Dupree 1967; Gültekin and Gürcan 2019) to allow for nonlinear saturation through mode coupling. Otherwise, the saturation mechanisms of the regular quasi-linear models are based on profile flattening and/or corrugation coupled with turbulent generation and dissipation in different regions. In any case, self-consistent quasi-linear models without renormalization are also examples of truncation of the Fourier space, and one can also formulate them using a single poloidal mode, where only a single (usually most unstable) mode is considered (Bian et al. 2003; Sarazin et al. 2021) whose evolution is then coupled to the $k_{y}=0$ modes that represent the profiles and meso-scales.

To study general features of such a system, consider the generic system of equations

$$\begin{aligned} \partial _{t}\xi _{k}^{\alpha }+L_{k}^{\alpha \beta }\xi _{k}^{\beta }= \text {NL}_{k}^{\alpha }, \end{aligned}$$

(26)

where $\xi _{k}^{\alpha }$ are different fields which could be $\Phi _{k}$ and $n_{k}$, etc. for example in the Hasegawa–Wakatani model, or may represent various moments of a kinetic system and $L_{k}^{\alpha \beta }$ is a linear matrix operator. In general, the wave-number space network formulation focuses on computing, approximating, or modeling the nonlinear term $\text {NL}_{k}^{\alpha },$ which usually comes from an advection term in real space.

A single-mode self-consistent quasi-linear model consists of a formulation where the wave-number space grid consists of a single $k_{y}$ (e.g., the most unstable) mode in addition to the $k_{y}=0$ (e.g., zonal) mode. The equations remain the same, even though depending on the formulation, one may have different equations for zonal and nonzonal modes to begin with. One interesting aspect of such a system is that one can take a 2D pseudo-spectral solver and reduce the resolution $N_{x}\times N_{y}\rightarrow N_{x}\times 1.$ Note that in practice, a padded resolution of $N_{py}=6$ is needed to have a single nonzonal mode that is resolved (i.e., excluding the Nyquist frequency and the modes that are zeroed out as part of the 2/3 padding rule). This is a major truncation of the initial system, and the equations are not usually renormalized to take this truncation into account. The resulting self-consistent quasi-linear system describes the evolution of zonal modes, or “profiles” in the presence of a single most unstable mode that represents the fluctuations. The most unstable mode cannot couple to itself, because it is impossible to satisfy triadic interactions with three modes all having the same $k_{y}$, but it can couple to the zonal modes, which in this context are indistinguishable from profiles, even though the radial spatial resolution can be very high and, therefore, their spatiotemporal evolution very detailed.

Note that the matrix $L_{k}^{\alpha \beta }$ contains the linear physics, and computing its eigenvalues and eigenvectors, we can perform a simple local linear stability analysis. Once its $N_{f}$ eigenvalues ($N_{f}$ is the number of independent fields), are computed, and sorted with respect to their growth rates at each wave-number, we can pick the most unstable mode $k_{y0}.$ We would then setup the system, so that it would have a single $k\equiv k_{y0}$ (by choosing the box size $L_{y}=2\pi /k_{y0}$) and run it as a nonlinear system given by (26). Assuming the nonlinear term comes from $E\times B$ advection (or advection by a velocity field obtainable from a stream-function $\Phi$), we can write the equations by computing the inverse Fourier transforms in x as

$$\begin{aligned}{} & {} \partial _{t}{\overline{\xi }}^{\alpha }+\overline{{\mathcal {L}}}^{\alpha \beta } \left( \partial _{x}\right) {\overline{\xi }}^{\beta }=-\partial _{x}\left\langle {\widetilde{\xi }}_{k}^{\alpha }\partial _{y}{\widetilde{\Phi }}_{k}\right\rangle \end{aligned}$$

(27)

$$\begin{aligned}{} & {} \partial _{t}{\widetilde{\xi }}_{k}^{\alpha }+\widetilde{{\mathcal {L}}}_{k}^{\alpha \beta } \left( \partial _{x},ik\right) {\widetilde{\xi }}_{k}^{\beta }=-\partial _{x}{\overline{\Phi }} \cdot \partial _{y}\xi _{k}^{\alpha }+\partial _{y}{\widetilde{\Phi }}_{k}\partial _{x} {\overline{\xi }}^{\alpha }, \end{aligned}$$

(28)

where $k\equiv k_{y0}$ is used for simplicity. We can usually obtain $\Phi$ from $\xi _{k}^{\alpha }$ using something like $F\left( \xi _{k}^{\alpha },\Phi \right) =0,$ maybe through the relation between vorticity and potential if one of $\xi _{k}^{\alpha }$ represent the plasma vorticity as in Hasegawa–Wakatani system, or through the Poisson’s equation when $\xi _{k}^{\alpha }$ represent parts of the distribution function. Here, the linear operators for the “profiles” $\overline{{\mathcal {L}}}^{\alpha \beta }\left( \partial _{x}\right)$ are usually simple diagonal operators (unless we consider off diagonal transport terms due to geometry) representing diffusion or friction terms. In contrast, the linear operators $\widetilde{{\mathcal {L}}}_{k}^{\alpha \beta }\left( \partial _{x},ik\right)$ are usually not diagonal and contain the full linear physics for the mode most unstable mode k. Nonlinearly, the quasi-linear system contains (i) the local advection (hence including the effects of shear suppression) of the fluctuations by a background zonal flow profile, which is represented by the first term on the RHS of Eq. (28), (ii) drive due to gradients $\nabla {\overline{\xi }}^{\alpha }$ as well as the corrections by the corrugations in $\nabla {\overline{\xi }}^{\alpha }$ represented by the second term on the RHS of Eq. (28), and (iii) the radial self-consistent quasi-linear fluxes of the ${\overline{\xi }}^{\alpha }$’s represented by the RHS of Eq. (27). The roles of these different terms can be made clear by considering $\xi ^{\alpha }$ to be the ion temperature for example: (i) advection and shear suppression of fluctuations, (ii) corrections due to $\nabla {\overline{T}}$ to the linear dynamics normally imposed by the background temperature gradient, and (iii) the self-consistent quasi-linear fluxes $Q=-\left\langle {\widetilde{\xi }}_{k}^{\alpha }\partial _{y}{\widetilde{\Phi }}_{k}\right\rangle$ that can be computed using these fluctuations.

Considering multiple modes (already considering only two modes $k_{y0}$ and $k_{y1}$), the system starts to include mode coupling, even though it remains to be severely truncated. As a wave-number space model (i.e., going back to $k_{x}$ space), the truncation with respect to a full 2D system is rather clear. The same also applies to going from 3D to 2D by truncation, which works exactly the same way, or keeping only a few modes in the $k_{z}$ direction. All these examples can be seen as truncations of the wave-number space.

Another interesting example of the wave-number space truncation is the multi-mode self-consistent quasi-linear model, which results when we keep the full k-space resolution (i.e., $N_{x}\times N_{y}$ modes) but consider only interactions between zonal flows and fluctuations dropping interactions among fluctuations themselves. This can be done by re-writing Eqs. (27) and (28) by putting a sum over k in front of the RHS term of Eq. (27) and interpreting Eq. (28) as an equation valid for all $k\rightarrow k_{y}$ instead of a single $k_{y0}.$ The linear operator becomes a function of k and the physical meanings of the RHS terms remain the same. The only difference is that the self-consistent quasi-linear fluxes now include contributions from all the different k’s. The resulting multi-mode self-consistent quasi-linear model is equivalent to what is called the generalized quasi-linear theory in geophysical fluid dynamics. These models are truncations of the primitive wave-number space networks not the in the sense that we drop nodes from the network as in all the previous examples of this section including the single-mode self-consistent quasi-linear models, but in the sense that we drop links (i.e., triad interactions). In fact, we drop the overwhelming majority of the interactions, and keep only one kind of interaction, that is the interaction with the zonal modes hoping that this is the dominant kind of interaction in the full network.

4 Reduction

Since the turbulent cascade involves the nonlinear transfer of a conserved quantity (Energy, Enstrophy, etc.) from one scale to another, a reduced description of it can be based on the evolution of the relevant conserved quantity. The budget for the conserved quantity in a primitive network is given in Eq. (6). We will use energy in Navier–Stokes turbulence as an example, but the reduction procedure, which applies to the nonlinear term, can be invoked for any conserved quantity.

4.1 Energy transfer

Recalling Eq. (6) explicitly for energy $E_{\ell }$ of node $\ell$

$$\begin{aligned} \partial _{t}E_{\ell }=\sum _{\ell ',\ell ''\in {\textbf{i}}_{\ell }} T_{\ell \ell '\ell ''}+{\mathcal {P}}_{\ell }-{\mathcal {D}}_{\ell }, \end{aligned}$$

(29)

where ${\mathcal {P}}_{\ell }$ is the production and ${\mathcal {D}}_{\ell }$ is the dissipation at node $\ell$ and $T_{\ell \ell '\ell ''}$ is the energy transfer from the nodes $\ell ',\ell ''$ to the node $\ell .$ As the energy is conserved nonlinearly, we have $T_{\ell \ell '\ell ''}+T_{\ell '\ell ''\ell }+T_{\ell ''\ell \ell '}=0.$ Since Eq. (29) is written on a primitive network, each node $\ell$ represents a distinct discretized wave-number and we only have three-body interactions. To reduce it to a manageable size, one can consider a collection of subsets denoted by L that forms, what is called an exact cover of the set of nodes of the initial primitive network. This collection of subsets provides a partition of the wave-number space and the energy in each subset L can be computed simply as the sum of the energies of its constituents

Fig. 6

Example of a network reduction. Here, a shows the complete primitive network with only triadic interactions, b shows the collection of subsets, or lumps that are used to construct the reduced network, and c shows the resulting reduced network with both triadic and direct connections. Notice how the highlighted triad (blue if in color) gives rise to a direct interaction between the lumps L and $L'$, since both of its legs denoted by $\ell$ and $\ell '$ are in L,  while only one of its legs denoted by $\ell ''$ is in $L''$

$$\begin{aligned} E_{L}\equiv \sum _{\ell \in L}E_{\ell }. \end{aligned}$$

Similarly, the total production ${\mathcal {P}}_{L}=\sum _{\ell \in L}{\mathcal {P}}_{\ell }$ and dissipation ${\mathcal {D}}_{L}=\sum _{\ell \in L}{\mathcal {D}}_{\ell }$ in the partition can be defined as the sum of production and dissipation terms from each element contained within the partition. Note that for some systems with internal free energy source, it may be difficult to disentangle the two, and one may instead have to write the net production as ${\mathcal {P}}_{L}-{\mathcal {D}}_{L}=\sum _{\ell \in L}\left( {\mathcal {P}}_{\ell }-{\mathcal {D}}_{\ell }\right) .$ To write a budget equation for $E_{L}$ similar to Eq. (29), we also need to consider all possible channels of energy transfer to and from the partition L. Considering $\ell ,$ $\ell '$, and $\ell '',$ and noting that, by definition, we have $\ell \in L,$ we have four distinct possibilities, (i) all the nodes are in different partitions, i.e., $\ell '\in L'$ and $\ell ''\in L'',$ (ii) one of the interacting nodes is in L [e.g., $\ell '\in L'$ while $\ell ''\in L$] (iii) both $\ell '$ and $\ell ''$ are in the same partition that is different from L [e.g., $\ell '\in L'$ and $\ell ''\in L'$] (iv) both $\ell '$ and $\ell ''$ is also in L. In the first case, if $T_{\ell \ell '\ell ''}$ is positive, the energy is transferred from $L'$ and $L''$ to the partition L as a three-body interaction. The net contributions of all such nodes give us the net energy transfer between these three partitions, which we can write as $T_{LL'L''}.$ The second and third cases give the transfer between two partitions L and $L',$ and a sum over the transfers due to all such nodes gives us the net energy transfer from $L'$ to L,  which can be denoted by $T_{LL'}.$ Note that unlike $T_{LL'L''},$ this is a two-body interaction term, and it appears only in reduced networks. In the last case where all the nodes are in the same subset, since the energy is transferred from one internal node to another, there is no transfer in or out of L (see Fig. 6 as an example).

The resulting equation for reduced energy $E_{L}$ can be written as

$$\begin{aligned} \partial _{t}E_{L}-{\mathcal {P}}_{L}+{\mathcal {D}}_{L}= \sum _{L,L''}T_{LL'L''}+\sum _{L'}T_{LL'}, \end{aligned}$$

(30)

where

$$\begin{aligned} T_{LL'L''}=\sum _{\ell \in L,\ell '\in L',\ell ''\in L''}T_{\ell \ell '\ell ''} \end{aligned}$$

is the three-body energy transfer from $L'$ and $L''$ to L,  while

$$\begin{aligned} T_{LL'}=\sum _{\ell \in L}\sum _{\ell '\in L'}\sum _{\ell ''\in L'}T_{\ell \ell '\ell ''}-\sum _{\ell \in L'}\sum _{\ell '\in L}\sum _{\ell ''\in L}T_{\ell \ell '\ell ''} \end{aligned}$$

is the “direct” energy transfer from $L'$ to L,  which we can also write as

$$\begin{aligned} T_{LL'}=T_{LL'L'}-T_{L'LL}, \end{aligned}$$

so that it is obvious that $T_{L'L}=-T_{LL'}.$

Note that as the network is reduced, two-body interaction terms become more and more prevalent, and in the limit of only 2 partitions, we end up with a single direct energy transfer term between those two regions, which may represent a generalized predator–prey model as the ultimate reduced network dynamics. One interesting topological metric, which reveals the degree of reduction of a given k-space partition network is thus the ratio of the number of two- to three-body interactions, which would range from 0,  no reduction to 1,  complete reduction.

4.2 EDQNM closure on reduced networks

While reduction through lumping the nodes together, or partitioning allows us to lower the number of nodes and links in our wave-number space network, in general, it is not possible to write the transfer terms $T_{LL'L''}$ using the reduced variables $E_{L}.$ This means that Eq. (30) as written is not closed, and one has to make an assumption to close it. Actually, this is also true for (29), since we cannot write $T_{\ell \ell '\ell ''}$ in terms of $E_{\ell };$ however, one can always write an equation for the phase, $\phi _{\ell }$ similar to Eq. (11) and couple it to the Energy equation completely describe the system. In contrast, since the reduced transfer terms $T_{LL'L''}$ involve many different nodes, each of which having a different phase, and while it is possible to add energies, it is not meaningful to add phases to write single net phase for the whole partition, the closure in the reduced network becomes a necessity as opposed to a convenience that it was in the primitive network.

One of the simplest closures that is commonly used in the study of turbulence is the so-called eddy-damped quasi-normal Markovian (EDQNM) closure. In the context of the wave-number space network formulation, the EDQNM allows us to write

$$\begin{aligned} T_{\ell \ell '\ell ''}&=-\bigg [\Theta _{\ell \ell '\ell ''} |M_{{\ell \ell '\ell ''}} |^{2}\frac{k_{\ell }^{2}}{k_{\ell '}^{2} k_{\ell ''}^{2}}E_{\ell '}E_{\ell ''}\\&\quad +2\Theta _{\ell \ell '\ell ''}\frac{M_{{\ell \ell '\ell ''}} M_{\ell '\ell ''\ell }}{k_{\ell ''}^{2}}E_{\ell }E_{\ell ''}\bigg ] \end{aligned}$$

through a set of assumptions equivalent to random phases and Markovian statistics. This form allows us to write the transfer terms for the reduced network as

$$\begin{aligned} T_{LL'L''}&=\Theta _{LL'L''}\bigg [a_{LL'L''}E_{L'}E_{L''}\nonumber \\&\quad +b_{LL'L''}E_{L}E_{L''}+b_{LL''L'}E_{L}E_{L'}\bigg ], \end{aligned}$$

(31)

where

$$\begin{aligned}{} & {} a_{LL'L''}\equiv \frac{\sum _{\ell \in L,\ell '\in L',\ell ''\in L''}\Theta _{\ell \ell '\ell ''} |M_{{\ell \ell '\ell ''}} |^{2}\frac{k_{\ell }^{2}}{k_{\ell '}^{2} k_{\ell ''}^{2}}E_{\ell '}E_{\ell ''}}{\Theta _{LL'L''}E_{L'}E_{L''}}\\{} & {} b_{LL'L''}\equiv \frac{\sum _{\ell \in L,\ell '\in L',\ell ''\in L''}\Theta _{\ell \ell '\ell ''}\frac{M_{{\ell \ell '\ell ''}}M_{\ell '\ell ''\ell }}{k_{\ell ''}^{2}}E_{\ell }E_{\ell ''}}{\Theta _{LL'L''}E_{L}E_{L''}} \end{aligned}$$

and

$$\begin{aligned} \Theta _{LL'L''}\equiv \sum _{\ell \in L,\ell '\in L',\ell ''\in L''}\Theta _{\ell \ell '\ell ''}, \end{aligned}$$

and using $T_{LL'}=T_{LL'L'}-T_{L'LL}$ we can write:

$$\begin{aligned} T_{LL'}&=\bigg [\Theta _{LL'L'}a_{LL'L'}E_{L'}^{2}+2\Theta _{LL'L'} b_{LL'L'}E_{L}E_{L'}\nonumber \\&\quad -2\Theta _{L'LL}b_{L'LL}E_{L}E_{L'}-\Theta _{L'LL}a_{L'LL}E_{L}^{2} \bigg ]. \end{aligned}$$

(32)

Here, the network version of the triad interaction time can be written using its evolution equation

$$\begin{aligned} \partial _{t}\Theta _{LL'L''}+\left[ \eta _{L}+\eta _{L'}+\eta _{L''}\right] \Theta _{LL'L''}=1 \end{aligned}$$

(33)

with $\Theta _{LL'L''}\left( 0\right) =0$ and with

$$\begin{aligned} \eta _{L}&=\nu _{L}+\frac{1}{2}\sum _{L'L''}\Theta _{LL'L''} \left( b_{LL'L''}E_{L''}+b_{LL''L'}E_{L'}\right) \nonumber \\&\quad +\sum _{L'}\left( \Theta _{LL'L'}b_{LL'L'}-\Theta _{L'LL}b_{L'LL}\right) E_{L'}\nonumber \\&\quad -\frac{1}{2}\sum _{L'}\Theta _{L'LL}a_{L'LL}E_{L}. \end{aligned}$$

(34)

Note that on an arbitrary network partitioning, we cannot use the heuristic estimate [i.e., $\theta _{kpq}=\frac{1-{\textrm{e}}^{\left( \eta _{k}+\eta _{p}+ \eta _{q}\right) t}}{\eta _{k}+\eta _{p}+\eta _{q}}$ with $\eta _{k}\approx \nu k^{2}+c\sqrt{\int _{0}^{k}E\left( k'\right) k'^{2}{\textrm{d}}k'}$] for the eddy damping commonly used in this kind of closure, since the integral from 0 to k is meaningless on an arbitrary network. Instead, if we really must, we can use the even simpler one based on dimensional analysis

$$\begin{aligned} \eta _{L}\approx \nu _{L}+\lambda E_{L}^{1/2}k_{L}^{3/2} \end{aligned}$$

(35)

together with the “solution” of (33) written as

$$\begin{aligned} \Theta _{LL'L''}=\frac{1-{\textrm{e}}^{\left( \eta _{L}+ \eta _{L'}+\eta _{L''}\right) t}}{\eta _{L}+\eta _{L'}+\eta _{L''}}. \end{aligned}$$

(36)

The practical usefulness of the closure depend in practice on our ability to write its coefficients $a_{LL'L''},$ $b_{LL'L''}$, and $\Theta _{LL'L''}$ in terms of some average variables that we can associate with each subset L,  such as the average wave-number $k_{L}$ for example.

5 Ad-hoc models

Turbulent cascade can also be modeled through simpler models that do not necessarily come from a systematic reduction or truncation but are proposed based on a general idea of the cascade process and some aspects of conservation properties of the considered system. Dimensional analysis may be the simplest such example, but applying it directly to networks is not likely to provide us with any new insight. Shell models are another example, and they can actually be reformulated from a network perspective and allow us to talk about network topology vs. cascade in a simple framework (Gürcan 2021). We have also shown some examples of models that were obtained through truncation, such as the nested polyhedra models or the spiral chain models that basically had the same structure as the shell models, so the shell models can also be seen as generic versions of these models. It is also possible to use a formulation in terms of shells to describe the cascade processes of the full system as characterized by the data from direct numerical simulations. In this sense, the generic dynamical complex network model that uses shells as its nodes can be seen as a prototype of the cascade processes of the full system.

5.1 Shell models as networks

A straightforward generalization of the shell model concept to arbitrary range (i.e., m) interactions can be achieved using a set of wave-numbers $k_{n}=k_{0}g^{n},$ where g is a logarithmic scaling factor (e.g., $g=2$) and writing

$$\begin{aligned} \partial _{t}u_{n}&=i\alpha _{m}\bigg [ a_{n}^{m}u_{n+m}^{*} u_{n+m+1}^{*}+b_{n}^{m}u_{n+1}^{*}u_{n-m}^{*}\nonumber \\&\quad +c_{n}^{m}u_{n-1}^{*}u_{n-1-m}^{*}\bigg ]+f_{n}-\nu _{n}u_{n}, \end{aligned}$$

(37)

with

$$\begin{aligned} a_{n}^{m}&\equiv M_{n,n+m,n+m+1}\\ b_{n}^{m}&\equiv M_{n,n-m,n+1}\\ c_{n}^{m}&\equiv M_{n,n-1-m,n-1}, \end{aligned}$$

so that we have

$$\begin{aligned} \sigma _{n}a_{n}^{m}+\sigma _{n+m}b_{n+m}^{m}+\sigma _{n+m+1}c_{n+m+1}^{m}=0 \end{aligned}$$

as a consequence of the conservation law

$$\begin{aligned}&\sigma _{n}M_{n,n+m,n+m+1}+\sigma _{n+m}M_{n+m,n,n+m+1}\nonumber \\&\quad +\sigma _{n+m+1}M_{n+m+1,n,n+m}=0. \end{aligned}$$

(38)

Since the interaction coefficients are symmetrized, so that $M_{\ell nm}=M_{\ell mn}$ by construction, it is obvious that Eq. (38) is directly equivalent to Eq. (5). The choice of $M_{\ell nm}$ (and therefore the $\sigma _{n}$) define the kind of turbulence that can be described by Eq. (37). For example, the choice

$$\begin{aligned} M_{n,\ell ,\ell '}=\left\{ \begin{array}{ll} k_{\ell }+k_{\ell '} &{}\quad \text {if }n<\ell \\ -\left( \left( -1\right) ^{n-\ell }k_{\ell }+k_{\ell '}\right) &{}\quad \text {if } \ell <n \end{array}\right. \end{aligned}$$

corresponds to the usual three-dimensional Navier–Stokes turbulence which conserves energy

$$\begin{aligned} E=\sum _{n}|u_{n}|^{2} \end{aligned}$$

and what can be called helicity in the context of a shell model

$$\begin{aligned} H=\sum _{n}\left( -1\right) ^{n}k_{n}^{-1}|u_{n}|^{2}. \end{aligned}$$

The overall factor $\alpha _{m}$ in front of the nonlinearity in Eq. (37) denotes the average contribution from the geometric factor, and can be taken to have the form $\alpha _{m}=g^{-m}$ (e.g., Plunian and Stepanov 2007), $f_{n}$ is the forcing usually localized to a few shells and $-\nu _{n}$ is the viscosity, which may have the form of hyper- or hypo-viscosity depending on the details of the problem.

Note that the three terms in Eq. (37) come from a single triad form $t_{n}=\left( n,n+m,n+m+1\right)$ similarity transformed to $t_{n-m}=\left( n-m,n,n+1\right)$ and $t_{n-m-1}=\left( n-m-1,n-1,n\right) .$ Each of these triads introduce corresponding terms in the equations for each of its nodes. In other words, the triad $t_{n}=\left( n,n+m,n+m+1\right)$ contributes a term (i.e., $a_{n}^{m}u_{n+m}^{*}u_{n+m+1}^{*}$) to the equation for $u_{n},$ a second term (i.e., $b_{n+m}^{m}u_{n}^{*}u_{n+m+1}^{*}$) in the equation for $u_{n+m}$ and a third term (i.e., $c_{n+m+1}^{m}u_{n}^{*}u_{n+m}^{*}$) in the equation for $u_{n+m+1}.$ By keeping all the legs of all the triads, we can guarantee that we respect the conservation properties of the system with no additional effort.

Equation (37) is actually a network model with the simple interaction table ${\textbf{i}}_{n}=\left\{ \left( n+m,n+m+1\right) ,\left( n-m,n+1\right) ,\left( n-m-1,n-1\right) \right\} ,$ that is to be obtained from the triad list ${\textbf{t}}_{n}^{m}=\left\{ \left( n,n+m,n+m+1\right) ,\left( n-m,n,n+1\right) ,\left( n-m-1,n-1,n\right) \right\}$ for each n. The way it is written Eq. (37) has a single, fixed value of m,  which defines the elongation of the triangles involved in the reduction. Note that as we commonly take $g=2,$ Eq. (37) cannot be a truncation (since it would be impossible to satisfy ${\textbf{k}}_{n}+{\textbf{k}}_{n+m}+{\textbf{k}}_{n+m+1}=0$ with ${\textbf{k}}_{n}=k_{0}g^{n}\hat{{\textbf{k}}}_{n}$). It can be reduction however, since the wave-numbers are consistent with ${\textbf{k}}+{\textbf{p}}+{\textbf{q}}=0$ where $k_{n}<k<k_{n+1},$ $k_{n+m}<p<k_{n+m+1}$ and $k_{n+m+1}<q<k_{n+m+2}.$

5.2 Small-world network shell models

Picking $m=1$ in Eq. (37) gives us only local interactions, and the resulting model is exactly equivalent to the usual GOY model. The resulting regular lattice of the GOY model can be represented as a list of $N-2$ local triads $\left[ t_{012},t_{123},t_{234},\ldots ,t_{N-2,N-2,N}\right] .$ Going over this list and either replacing some of the local interactions with nonlocal ones [Watts–Strogatz strategy (Watts and Strogatz 1998)], or simply adding nonlocal interactions on top of existing local ones [Newman–Watts strategy (Newman and Watts 1999)], we get a small world network from a regular lattice (see Fig. 7). In practice, this is done by going over each of the elements of the list of triads and replacing or adding a nonlocal interaction with a probability p. Since the links are three-body interactions (and not two body as in simpler networks), we also need to choose in which sense the triad is elongated. A triad that is elongated “forward”, has the form $t_{n}^{m}=\left( n,n+m,n+m+1\right)$ and describes interactions with small scales where the scale n plays the role of large scale. On the other hand, a triad that is elongated backward has the form $t_{n}^{m}=\left( n,n-m,n-1\right)$ where the node n plays the role of one of the small-scale legs in an interaction involving a large-scale mode at $n-m.$ In practice, each time, we are adding a nonlocal interaction or replacing a local interaction with a nonlocal one, and we pick its direction to be forward with a probability $p_{f}$ or backward with a probability $1-p_{f}.$ In the end, we can choose $p_{f}=0,0.5$ or 1 and it does not seem to matter, since n itself is just a random node among all the possible nodes, so apart from the slight difference it makes for the edge nodes, we can choose all the nonlocal nodes to be forward without loss of generality. Note that the range of interaction m is also chosen to be a random number between 2 and $N-n-2$ for the forward interaction (or between 3 and $n-2$ for backward).

Fig. 7

The topology of a small-world network generated using the Newman–Watts strategy. The local triads are shown with shaded lines, whereas the nonlocal triads are shown in solid black. While the network is shown in a circular form, familiar in small world network studies, here, the nodes represents wave-number space shells with $k_{n}=k_{0}g^{n}$ and, as a result, $n=0$ is not connected back to $n=23$ by a local interaction

The act of reorganizing the nodes either by supplementing or replacing the local interactions with nonlocal ones is called rewiring. Note that in the process of rewiring, one goes back to the initial regular lattice of local interactions, and then applies the small-world construction algorithm (either Watts–Strogatz or Newman–Watts as described above), so that interactions do not accumulate or turn all the interactions into nonlocal ones. Rewiring acts on the list of triads. Once it is finished, we can compute the list of interactions ${\textbf{i}}_{\ell }=\left\{ \ell ',\ell ''\right\}$ and the nonlinear interaction coefficients $M_{\ell \ell '\ell ''}$ for each node using the triads that contain that node. This can be done in practice by going over the list of triads and when considering the triad $t_{n}^{m}=\left( n,n+m,n+m+1\right)$ adding $\left\{ n+m,n+m+1\right\}$ to ${\textbf{i}}_{n},$ $\left\{ n,n+m+1\right\}$ to ${\textbf{i}}_{n+m}$ and $\left\{ n,n+m\right\}$ to ${\textbf{i}}_{n+m+1}$ with the interaction coefficients (i.e., weights) $M_{n,n+m,n+m+1},$ $M_{n+m,n+m+1,n}$, and $M_{n+m+1,n,n+m}.$ As a result, one would have a different number of interactions for each node, and some of those interactions would be nonlocal, yet the energy would be conserved trivially, since we always consider all the contributions from each triad. For the Watts–Strogatz case, the model can be said to go from a regular shell model for $p=0$ to a shell model with random scale interactions for $p=1.$

Fig. 8

The steady-state spectra from the dynamical complex network models based on WS and NW rewiring strategies, compared with the GOY model, showing that all three models capture the $k^{-5/3}$ spectrum, while NW is slightly lower in amplitude as opposed to the other two, probably as a result of its extra connections, and therefore higher transfer efficiency

As the network is being manipulated by wiring and rewiring, the variables $u_{n}$ evolve according to the usual form of the equations, that we can write for instance as

$$\begin{aligned} \left( \partial _{t}+\nu k_{n}^{2}\right) u_{n}=\sum _{\ell ',\ell ''= {\textbf{i}}_{n}}M_{n,\ell ',\ell ''}u_{\ell '}^{*}u_{\ell ''}^{*}\;+f_{n}. \end{aligned}$$

(39)

It may be argued that while Eq. (39) represents the cascade of energy (or some other conserved quantity) in a given network topology, the randomized evolution of the network topology itself can be a proxy for further phase evolution that would enhance or impede energy transfer depending on the momentary alignment and synchronization of the phases of the (primitive) triads involved in the interaction. Notice that the variables $u_{n}$ already has some complex phases and their alignment already has consequences for the cascade, which already randomizes the evolution of shell models. However, since each shell model node does not represent a single wave-number node, those phases are ad-hoc replacements for some kind of average phase for a whole region. Energy transfer is actually enhanced or not, depending on the phase relations among many primitive triads that are involved in the interactions between three regions that are represented as a single three-body interaction among three shells. The turning on and off of nonlocal interactions may thus model a momentary phase synchronization in a nonlocal triad resulting in a burst of nonlocal transfer.

Further studies are needed to clarify both the meaning and the details of the evolution of wave-number space network topology in turbulent systems. Even if it is true that network topology can be used to represent phase synchronization, it is not clear how to describe the phase evolution of a turbulent system using rewiring rules. The question is similar to percolation, but is more complex as it involves three-body interactions. Here, we use random rewiring using one of the strategies described above to generate regularly rewired small-world network topologies, and solve Eq. (39) in such an evolving network, choosing the network rewiring time step to be larger than the time step for the evolution of the field variables. The results can be seen in Fig. 8.

Another interesting option would be to use quadratic conserved quantities, $E_{n}$ instead of the shell variables $u_{n}.$ This requires the use of a closure—for example, the EDQNM closure is discussed in Sect. 4.2—which gets rid of the complex phases completely. In such a formulation, the argument that the network evolution describes the phase dynamics becomes more transparent. For example, for a two-body interaction, if the phases of dominant triads involving nodes from the two regions L and $L'$ are aligned, the edge between L and $L'$ would be activated. An activate two-body interaction would add $T_{LL'}$ as defined in Eq. (32) and the corresponding term (e.g., $T_{L'L}$) in the equation for $E_{L'}.$ It can be seen that in the limit that most active interactions are two-body interactions, the problem of the turbulent cascade becomes that of percolation through a dynamical network, as the conserved quantity tries to go from the scale of injection to that of dissipation through a system represented by mostly neighboring interactions that can be turned on and off. The caveat is that the real system has an increasingly large number of triads as we go to smaller scales, allowing many possible paths for the cascade, and this is a key aspect of the statistical nature of the unreduced system.

6 Wave-number space networks for analysis

We can also use wave-number space networks for analysis of the data from numerical simulations (and possibly experiment as long as enough high-quality data is available). This usually involves projecting the full DNS data onto some reduced wave-number space consisting of a partition denoted by L,  to study the injection, transfer, and dissipation of some conserved quantity within that partition. For example, we can take Eq. (30) and compute each of its terms from their definitions using the data that we obtain from direct numerical simulations. Depending on the partitions, this may give us concrete information about the energy transfer between different parts of the k-space. For a given problem, say the dissipative drift waves described by the Hasegawa–Wakatani equations, different transfer terms may indicate energy transfer from energy containing scales, corresponding to most unstable modes to zonal flows and small-scale isotropic perturbations. In a wave-number space network formulation with three variables representing injection scales, zonal flows, and isotropic small scales, we can answer questions such as how much energy is transferred among different modes, or if the tertiary instability is actually important in zonal-flow saturation.

We can also do a primitive wave-number space network analysis, in which case we would compute each component of $T_{\ell \ell '\ell ''}$ in Eq. (29) for a reasonably low resolution numerical simulation. However, this is hard to represent graphically, and therefore can only be used to extract other useful information later on. For example, we can compute $t_{\ell \ell '},$ the net energy transfer between two nodes from all possible triadic interactions, as defined in Sect. 2.2, which can actually be represented graphically, or used in further reductions. An example of the network representation of the transfer tensor $t_{\ell \ell '},$ for a Hasegawa–Wakatani simulation with the minimum resolution of $16\times 16,$ is shown in Fig. 9. We can see that this is a zonal flow dominated case, where the energy is either transferred to zonal flows or is refracted to higher $k_{x}$, suggesting that a generalized quasi-linear description where only the interactions with the zonal flows are considered can be sufficient for describing this system in this limit. However, note that the implication that $k_{x}$ scattering comes mainly from zonal flows need to be shown by looking explicitly at the $t_{\ell \ell '}^{\ell ''}$ where $\ell ''$ (i.e., the mediator) is zonal vs. nonzonal for each pair. $\ell ,\ell '$ that is significant in the transfer network.

Fig. 9

The primitive wave-number space network of a $16\times 16$ k-space grid, where each node represents a separate k vector. The colored boxes in the background show the linear growth rate. The node size indicates the magnitude of kinetic energy and the node color indicates kinetic energy injection at that node. The arrows indicate the direction, with their width and color indicating the strength of energy transfer between the nodes. Energy transfer is shown as an arrow only if it is above a certain threshold, and zonal nodes with $k_{x}<0$ are removed because of Hermitian symmetry. We can see that most of the energy is localized at the zonal mode around $k_{x}\approx 1,$ even though this mode is removing energy from the system. We also see that the linearly most unstable mode is not the node that has the highest energy injection nonlinearly, and the injected energy either couples directly to the zonal flows or is refracted toward higher k probably by the action of the sheared flow

Recall that the two-dimensional Hasegawa–Wakatani system (Hasegawa and Wakatani 1983) consists of an equation of plasma vorticity

$$\begin{aligned} \frac{\partial }{\partial t}\nabla ^{2}\Phi +\hat{{\textbf{z}}}\times \nabla \Phi \cdot \nabla \nabla ^{2}\Phi =C\left( {\widetilde{\Phi }} -{\widetilde{n}}\right) +D_{\Phi }\left( \nabla ^{2}\Phi \right) \end{aligned}$$

(40)

coupled to an equation of continuity

$$\begin{aligned} \frac{\partial }{\partial t}n+\hat{{\textbf{z}}}\times \nabla \Phi \cdot \nabla n+\kappa \partial _{y}\Phi =C\left( {\widetilde{\Phi }} -{\widetilde{n}}\right) +D_{n}\left( n\right) , \end{aligned}$$

(41)

where $\Phi$ is the electrostatic potential normalized to T/e,  and n is the fluctuating part of the plasma density normalized to a background density $n_{0},$ x and y are the radial and the (locally) poloidal directions normalized to the sound Larmor radius $\rho _{s},$ $\kappa$ is the background density gradient that is assumed to be constant, normalized to the speed of sound, and C is the so-called adiabaticity parameter, which is a measure of the electron mobility in the parallel direction. With these, the $E\times B$ velocity is defined as ${\varvec{v}}_{E}=\hat{{\textbf{z}}}\times \nabla \Phi$ and the plasma vorticity becomes $\nabla ^{2}\Phi .$ Here, $\left\langle \Phi \right\rangle ={\overline{\Phi }}$ denotes averaging in y (i.e., poloidal) direction, so that ${\widetilde{\Phi }}\equiv \Phi -\left\langle \Phi \right\rangle .$ Finally, $D_{\Phi }$ and $D_{n}$ are functions representing viscosity and particle diffusion, respectively. For the standard form of kinematic viscosity, we can take $D_{\Phi }\left( \nabla ^{2}{\widetilde{\Phi }}\right) =\nu \nabla ^{4}{\widetilde{\Phi }}$ for fluctuations. In contrast, it makes sense to argue that for zonal flows, the dominant mechanism is large-scale friction, so that we can write $D_{\Phi }\left( \nabla ^{2}{\overline{\Phi }}\right) =-\nu _{ZF}\nabla ^{2}{\overline{\Phi }}.$ Normally, $D_{n}$ should be zero, but it is usually taken to have the same form with diffusion $D_{n}\left( {\widetilde{n}}\right) =D\nabla ^{2}{\widetilde{n}}$ for numerical stability.

The Hasegawa–Wakani model can be considered as a minimum nontrivial model of plasma turbulence, as it has all the key ingredients such as the linear instability and the ability to generate waves and zonal flows, but is otherwise one of the simplest possible models in plasma physics that describes the evolution of dissipative drift instabilities in the tokamak edge (Scott 1988; Koniges et al. 1992). It has the same nonlinear structure as that of the two-dimensional Navier–Stokes equations coupled with a passive scalar, or that of thermal convection in two dimensions. Therefore, the study of the Hasegawa–Wakatani system from a wave-number space network perspective is useful as a characteristic example for the kind of turbulence that one finds in fusion plasmas, as well as in other fields where similar equations are commonly used, such as solar or geophysical fluid dynamics. A simple pseudo-spectral implementation of this model provides us with a primitive network in the wave-number space.

Increasing the wave-number space resolution without increasing the wave-number space domain corresponds to increasing the box size and the number of grid elements by the same factor, resulting in a larger box with an unchanged real space grid element size, as shown in top plot of Fig. 10. This allows us to increase the resolution in wave-number space, which can then be reduced as in the bottom plot of Fig. 10 to “go back” to the low resolution case shown in Fig. 9. Of course, the details of the partitioning matters, and the choice shown in Fig. 10 imply a reduction where each reduced node represents a grid of $4\times 4$ primitive nodes apart from the $k_{x}=0$ or $k_{y}=0$ nodes, which represent $1\times 4$ and $4\times 1$ primitive nodes, respectively. The results from this reduced network are shown in Fig. 11 and are qualitatively consistent with the primitive network, with maybe more statistics and larger total energy because of the larger spatial extent.

Fig. 10

The box size and the resulting wave-number space resolution. The top plot shows the final snapshots, at $t=200,$ of the vorticity on the left and the density on the right of the two runs with the $64\times 64$ grid as the full box and the $16\times 16$ grid as the smaller box at the lower left corner. To construct the same network as in Fig. 9 through reduction, we partition the wave-number space grid as shown in the bottom plot (note that only a part of the k-space is shown for clarity). Both the $k_{y}=0$ and the $k_{x}=0$ modes have $1\times 4$ wave-number elements, whereas the rest of the nodes have $4\times 4$ elements each. The resulting network is shown in Fig. 11

To compute the transfer term from DNS, consider a simulation algorithm that advances the fields $\xi _{k}^{\alpha }$ according to Eq. (26), with the nonlinear term written explicitly as

$$\begin{aligned} \partial _{t}\xi _{k}^{\alpha }+L_{k}^{\alpha \beta }\xi _{k}^{\beta }= \text {NL}\left( \xi ^{\alpha },\Phi \right) _{k}, \end{aligned}$$

where ${\mathcal {L}}$ is the linear part of the problem and $\text {NL}\left( \xi ^{\alpha },\Phi \right) _{k}$ is the nonlinear part, which may, for example, represent the Poisson bracket as

$$\begin{aligned} \text {NL}\left( \xi ^{\alpha },\Phi \right) _{k}\equiv \left( \hat{{\textbf{z}}} \times \nabla \xi ^{\alpha }\cdot \nabla \Phi \right) _{k}. \end{aligned}$$

We would also usually have a relation between $\Phi _{k}$ and $\xi _{k}^{\alpha }$ for example as in the case where one of the fields, say $\xi _{k}^{1}$ represents vorticity, so that $\xi _{k}^{1}=-k^{2}\Phi _{k}.$

In this formulation, we can write

$$\begin{aligned} \left[ \partial _{t}\xi _{k}^{\alpha }\right] _{\text {lin}}=-L_{k}^{\alpha \beta }\xi _{k}^{\beta } \end{aligned}$$

and

$$\begin{aligned} \left[ \partial _{t}\xi _{k}^{\alpha }\right] _{\text {nl}}= \text {NL}\left( \xi ^{\alpha },\Phi \right) _{k}. \end{aligned}$$

Net injection of $E_{k}^{\sigma }\equiv \text {Re}\left[ \xi _{k}^{\alpha *} \sigma _{k}^{\alpha \alpha '}\xi _{k}^{\alpha '}\right]$ can then be written as

$$\begin{aligned} P_{k}^{\sigma }-D_{k}^{\sigma }\equiv \text {Re}\left( \xi _{k}^{*\alpha }\sigma _{k}^{ \alpha \alpha '}\left[ \partial _{t}\xi _{k}^{\alpha '}\right] _{\text {lin}}\right) , \end{aligned}$$

whereas the total transfer of $E_{k}^{\sigma }$ from all the other wave-numbers to the wave-number k takes the form

$$\begin{aligned} t_{k}=\sum _{k'}t_{k'k}\equiv \text {Re}\left( \xi _{k}^{\alpha *} \sigma _{k}^{\alpha \alpha '}\left[ \partial _{t}\xi _{k}^{\alpha '}\right] _{\text {nl}}\right) \end{aligned}$$

consistent with Eq. (8). Most of the numerical algorithms that deal with the Poisson bracket nonlinearity does so in real space because of the efficiency of doing so, either using finite differences directly using real space fields, or through the pseudo-spectral formulation based on back-and-forth fast Fourier transforms. This means that we have a quantity that is already summed over p and q as a result of the computation of $\left[ \partial _{t}\xi _{k}^{\alpha '}\right] _{\text {nl}}.$ To separate this, we can define a “band pass” filter that contains a single Fourier mode as $\varphi _{\ell '}\left( \xi ^{\alpha }\right) =\xi _{\ell '}^{\alpha } {\textrm{e}}^{i{\textbf{k}}_{\ell '}\cdot {\textbf{x}}},$ which sets all the other Fourier coefficients to zero. We can then compute

Fig. 11

The reduced wave-number space network of a $64\times 64$ wave-number space grid. Here, each node represents a partition containing $4\times 4$ wave-numbers (with the $k_{x}=0$ and $k_{y}=0$ nodes containing $1\times 4$ and $4\times 1$ elements as shown in the bottom plot of Fig. 10. As in Fig. 9, the background color shows the linear growth rate, and the node size and color indicate the magnitude and production rate of kinetic energy at that node. Again as in Fig. 9, the arrows indicate the direction, and the width and color of the lines indicate the strength of energy transfer between the nodes. Note also that the arrow lines are always curved in the counter clock-wise direction, so that we can infer their direction even when the arrow tip is not visible because of crowding. We used suitable thresholds and normalizations for both the nodes and the edges. Again, most of the energy is localized at the zonal mode around $k_{x}\approx 1.$ The relative differences between the zonal modes (an the transfer to them) and the others between Fig. 9 and the current figure suggest that when the resolution is increased by increasing the system size, so that the wave-number space resolution increases without changing the wave-number domain, the zonal-flow generation increases

$$\begin{aligned} t_{\ell \ell '}\equiv \text {Re}\left[ \xi _{\ell }^{\alpha *}\sigma _{\ell }^{\alpha \alpha '} \text {NL}\left( \xi _{\ell '}^{\alpha '}{\textrm{e}}^{i{\textbf{k}}_{\ell } \cdot {\textbf{x}}},\Phi \right) _{\ell }\right] \end{aligned}$$

(42)

switching to the node notation $\Phi _{\ell }\equiv \Phi _{k_{\ell }}\equiv {\hat{\Phi }}\left( k_{x\ell },k_{y\ell }\right) ,$ as the net transfer of $E^{\sigma }$ from $\ell '$ to $\ell$ (summed over all possible $\ell ''$). To do the same for a reduced network, we can either sum over $t_{\ell \ell '}$ by writing $t_{LL'}=\sum _{\ell \in L,\ell '\in L'}t_{\ell \ell '},$ or use the “band pass” filter for the region L,  defined as

$$\begin{aligned} \varphi _{L}\left( \xi ^{\alpha }\right) =\sum _{\ell \in L}\xi _{\ell }{\textrm{e}}^{i{\textbf{k}}_{\ell }\cdot {\textbf{x}}}, \end{aligned}$$

so that we can write using the larger filter

$$\begin{aligned} t_{LL'}=\sum _{\ell \in L}\text {Re}\left[ \xi _{\ell }^{\alpha *} \sigma _{\ell }^{\alpha \alpha '}\text {NL}\left( \varphi _{L'} \left( \xi ^{\alpha '}\right) ,\Phi \right) _{\ell }\right] . \end{aligned}$$

(43)

In other words, if we have a nonlinear function $\text {NL}\left( \xi ,\Phi \right)$ that computes the nonlinear terms of our system, we basically send it the band-pass-filtered ${\overline{\xi }}_{L'}=\varphi _{L'}\left( \xi \right)$ as the input variable $\text {NL}\left( {\overline{\xi }}_{L'},\Phi \right)$ to compute the effective nonlinear term involving the modes in that region $L'.$ Then, we multiply by $\sigma$ and $\xi _{\ell }^{*\alpha }$ and sum over $\ell \in L$ as in Eq. (43) to obtain the net transfer of the conserved quantity from the region $L'$ to region L. Repeating this for all possible $L'$ and L, we get the full network, as shown in Fig. 11.

6.1 Model extraction

In some cases where a reduced wave-number space network can actually be described by a closed system of equations of its reduced variables, say $E_{L},$ the numerical analysis can be used to “extract” that model directly from the data. Extraction of reduced models from data, especially “identification” when the data actually come from a nonlinear dynamical system with a reasonable number of degrees of freedom, has been a subject of great interest recently and is one of the more interesting methods of the booming field of data science, especially from the perspective of the study of complex dynamical systems. In this sense, the idea of using the data to extract a reduced model is simply an application of one of these methods to the problem in question somehow formulated in terms of networks.

However, methods, such as SINDy (Brunton et al. 2016; Kaptanoglu et al. 2021), apply directly to the data, and not exploit the advantage of having a model that we can query in different ways. The data that come out of a numerical simulation as discussed in the previous section would be a combination of many terms, linear and nonlinear terms, interactions with different fields, interactions with different wave-number space nodes, etc. All these are combined to form a single output data, or a list of outputs equal to the number of evolving field variables at each grid elements. For example, we may have a model for the linear physics, so that we can subtract that and concentrate on the nonlinear part, and try to decipher it using different nonlinear forms such as polynomials or a library of other nonlinear functions. The goal would be to minimize the difference between the $\left[ \partial _{t}\xi \right] _{\text {data}}$ and the $\left[ \partial _{t}\xi \right] _{\text {model}}={\mathcal {F}}_{\text {model}} \left( \xi _{\text {data}}\right) ,$ where ${\mathcal {F}}$ is a functional, while keeping the system as sparse as possible.

From a network perspective, where the primary objective may be to reduce a full system (i.e., the DNS) that we master completely, and can query as we want, by sending it filtered input to compute data that are separated into parts, the constraints on what can be done is quite different. We can, for instance, separate the linear and the nonlinear parts of $\left[ \partial _{t}\xi \right] =\left[ \partial _{t}\xi \right] _{\text {lin}}+ \left[ \partial _{t}\xi \right] _{\text {nl}}$ explicitly. We can also write $\left[ \partial _{t}\xi \right] _{\text {nl}}=\sum _{L'}t_{LL'}$ and compute each of $t_{LL'}$ using filtered inputs as discussed earlier in this section as a function of time. We can then do a linear regression, or nonlinear optimization to minimize the difference between the data $\left[ t_{LL'}\right] _{\text {data}}$ and the model for $\left[ t_{LL'}\right] _{\text {model}}={\mathcal {F}}_{\text {model}} \left( \xi _{L},\xi _{L'}\right) .$ Following SINDy, we can pose the optimization problem in such a way as to favor a sparse model. The advantage of being able to separate the data into its constituents that describe distinct interaction terms among its elements is weighed against the usual complexity of the underlying system and the fact that the reduction is almost never exact. Obviously, a complex nonlinear system, displaying multi-scale chaotic behavior, is unlikely to be fitted nicely with a close-enough reduced model. The slight error between the reduced model and the full system would probably result in a large difference in terms of the actual time traces. Note that the optimization can be done either by computing the differences in $\left[ {\textrm{d}}_{t}\xi \right] _{\text {model}}-\left[ {\textrm{d}}_{t}\xi \right] _{\text {data}},$ or the differences between $\xi _{\text {model}}-\xi _{\text {data}}$ by integrating the model in time with the given initial conditions from the data using $\xi _{\text {model}}=\xi _{\text {data}}\left( t=0\right) +\int _{0}^{t} \left[ \partial _{t}\xi \right] _{\text {model}}{\textrm{d}}t.$

Of course in cases where the system reduces itself to a nonlinear dynamical system of a very small degrees of freedom, the difference between the above methods where each interaction pair (or triple) is computed explicitly and compared to a model of that interaction explicitly vs. the sum of all the terms that contribute to a field variable is compared to a model of all the terms on the right-hand side for that variable is academic and both methods work equally well. The simplest such example is probably the case of the reduction of the data form four-dimensional gyrokinetic simulations near the instability threshold to a Lotka–Volterra predator–prey model (Kobayashi et al. 2015). In this case, because the system excites only a finite number of modes, which then interact with the zonal flows and saturate rapidly, the many degrees of freedom involved in these high-resolution simulations of the gyrokinetic equation reduces itself to an effective system of only two degrees of freedom corresponding roughly to the most unstable mode, and the zonal flow. The reduction to a predator–prey-like system works also in the case of interchange, and can be performed within the SINDy framework (Dam et al. 2017).

A similar case can be made for the use of machine learning for the development of reduced network models. Consider, for example, the case of a pseudo-spectral formulation with only two nonzonal modes in $k_{y}$ space (say k and $k'=2k$), whose evolution can be written in real space as

$$\begin{aligned} \partial _{t}\xi _{0}\left( x\right)&=N_{0k}\left( x\right) +N_{0k'}\left( x\right) \\ \partial _{t}\xi _{k}\left( x\right)&=N_{k0}\left( x\right) +N_{kk'}\left( x\right) \\ \partial _{t}\xi _{k'}\left( x\right)&=N_{k'0}\left( x\right) +N_{k'k}\left( x\right) , \end{aligned}$$

where

$$\begin{aligned} N_{0k}&=\left\langle \left[ \Phi _{k},\xi _{k}\right] \right\rangle ,\quad N_{k0}=\left[ {\overline{\Phi }},\xi _{k}\right] +\left[ \Phi _{k},{\overline{\xi }}\right] \\ N_{kk'}&=\left[ \Phi _{k'},\xi _{k}^{*}\right] +\left[ \Phi _{k}^{*},\xi _{k'}\right] ,\quad N_{k'k}=\left[ \Phi _{k},\xi _{k}\right] +\left[ \Phi _{k},\xi _{k}\right] . \end{aligned}$$

If we are to reduce this to a single-mode system

$$\begin{aligned} \partial _{t}\xi _{0}\left( x\right)&=N_{0k}\left( x\right) +F_{0}\left( x,k,\xi _{0},\xi _{k},\ldots \right) \\ \partial _{t}\xi _{k}\left( x\right)&=N_{k0}\left( x\right) +F_{k}\left( x,k,\xi _{0},\xi _{k},\ldots \right) , \end{aligned}$$

where $F_{0}$ and $F_{k}$ represent the effect of the effaced mode $k'$ on the two remaining modes; the zonal mode and the mode with the poloidal wave-number k. The argument for machine learning would be that we can train two “models” $F_{0}$ and $F_{k},$ which would allow for a closure of the system, using the data for $N_{0k'}\left( x\right)$ and $N_{kk'}\left( x\right)$, respectively. Furthermore, since such a simulation is reasonably cheap, the training data can be generated on demand in chunks.

7 Summary and conclusion

The goal of this review was to provide a different perspective into a well-known problem in nonlinear dynamics of fluids and plasmas. To achieve that, the basic formulation of the plasma turbulence in the context of fusion plasmas is revisited using wave-number space networks without going into particulars of the models or the physical systems in question. In their primitive form, these networks consist of nodes that represent elements in a discretized wave-number space grid and three-body interactions connecting those nodes. The fields generally representing the Fourier coefficients of various moments of the distribution function are evolved on this three-body interaction network where each node interacts with all the pairs with whom it satisfies the triadic interaction condition of ${\textbf{k}}+{\textbf{p}}+{\textbf{q}}=0$ imposed by the convolutions in Fourier space. Each link in such a three-body network is represented as a triangular node that is linked to three nodes that it links together, and each of its legs has an associated weight which is the nonlinear interaction coefficient. It is argued that the network formulation where we consider a list of nodes, and list of triads, provides a solid framework for model reduction. It is shown, for instance, that using a truncated wave-number space network that is obtained by dropping nodes, or triads from the original primitive network, one still respects all the same conservation laws as the original system without any effort.

Even though this review focuses on simple nonlinear models, such as two-dimensional Navier–Stokes equations or the Hasegawa–Wakatani system for plasma turbulence, some issues about the application of the network formalism to fusion plasmas, such as the effect of magnetic shear on mode localization around rational surfaces, or the link between the wave-number space and the flux tube formulation are briefly mentioned. Studies about the details of particular systems in realistic tokamak geometry are probably essential for future studies, if the wave-number space network formulation is to be useful for fusion applications.

Considering truncated networks, various examples from rather exotic, nested polyhedra models, to the well-known example of quasi-linear theory are evoked. It is clear that such models can reach incredible resolutions in comparison to direct numerical simulations on a regular rectangular grid. However, due to the fact that the number of triads increase as a function of scale on a regular grid, whereas it remains constant on a logarithmically scaled truncated network, they tend to underestimate intermittency and tend toward an incorrect statistical equipartition solution, which can be remedied by invoking simple closures. A detailed discussion of network reduction clarifies various mechanisms for the transfer of the quadratic conserved quantities (energy, enstrophy, etc.) of the original system. It is shown in particular that while a primitive network only has three-body interactions, a reduced network which groups together primitive nodes may also have two-body interactions as a result of two of the nodes of an interacting triad ending up in the same partition. Ad-hoc models that separate the evolution of the network topology and the evolution of the field variable on that network are discussed, in particular in the form of small-world network shell models, where the small-world aspect is achieved by randomly introducing some nonlocal interactions to the usual shell models of turbulence. It was argued that the evolution of the network topology could be used to model phase coherences that appear randomly in the evolution of a turbulent system. The (rather trivial) example of the EDQNM closure on a reduced network is also discussed, and it was shown that a simple reduced model based on random phase approximation that assumes Markovian statistics can be derived on a network. Finally, a discussion of how the transfer terms either in terms of transfer between three nodes $\ell ,$ $\ell '$ and $\ell ''$ in a primitive network or L and $L'$ and $L''$ in a reduced network can be computed from a direct numerical simulation by properly filtering the input fields in the nonlinear term. An example of this is given for the Hasegawa–Wakatani system. Possible application of the network formulation to model extraction or model training using machine learning algorithms is briefly discussed at the end, leaving the perspective open for future studies.