Introduction

The study of immersed bodies surrounded by external flows is crucial for the fluid mechanics. One of the associated concepts for studying the external flows is to utilize the boundary layer theory (BLT). In general, the coupling of BLT with the external flows characterizes the fluid behavior in an adverse pressure gradient (White 2011). It has found many practical applications in engineering industries, for example, to aerodynamics, hydrodynamics, turbulence, transportation, etc. (Sobey 2001). However, there may be one drawback to the BLT which is its failure in the separated flows (Sychev et al. 1998). To remove this limitation, an efficient computational fluid dynamics (CFD) simulation (Versteeg and Malalasekra 2007; Tu et al. 2012; Tannehill et al. 1997; Cebeci 2005; Sengupta 2004; Anderson 1995) was developed. It is worth noting that the CFD simulation is intended not only for the fluid behavior (Besthapu et al. 2017; Deng et al. 2012; Thepsonthi and Özel 2015; Hsiao 2016; Bezi et al. 2018; Mousazadeh et al. 2018; Shit et al. 2017), but also for chemical reactions (Ganapathirao et al. 2015; Ojjela and Kumar 2016; Hussain 2017; Shateyi and Marewo 2018), phase changes (Onyiriuka et al. 2018; Attia et al. 2015; Sheikholeslami and Rokni 2017), multiple flows (Raees et al. 2018; Gorla and Gireesha 2016; Jahan et al. 2018), etc.

Unlike the numerical CFD solutions, some analytic methods do not suffer from long runtime. Furthermore, due to the simplified boundary conditions involved in the CFD simulation (Houghton et al. 2013), an error usually occurs which cannot be neglected. It is noteworthy that although a large variety of analytical methods have been employed to investigate the NBVPs to date (Adesanya et al. 2018; Dehghan et al. 2015; Shahmohamadi and Rashidi 2016; Sayyed et al. 2018; Dib et al. 2015; Mohseni and Rashidi 2017; Khader and Megahed 2014; Lu et al. 2018; Nadeem et al. 2018, 2019), the RHA (Liao 1992, 2003), due to its convergence and effectiveness, can be considered as a powerful tool for discretizing the governing PDEs to an infinite series. In this way, Khoshrouye Ghiasi and Saleh (2018, 2019a, b, c, d) presented homotopic solutions to some problems arising in the BLT with the mixed boundary conditions. They compared and verified their findings with those obtained by the multi-step techniques such as Runge–Kutta and finite difference methods as well. In addition, they indicated that the RHA would be desirable if the NNFs are employed.

Due to the complexity of NNFs through porous media as well as the interaction between the particles (Goldsmith 1999), the RHA has been the centre of attention to date (Hashmi et al. 2017; Mustafa 2017; Abbas et al. 2010; Hayat et al. 2012a, b, 2016, 2017; Shehzad et al. 2018; Imtiaz et al. 2016). Moreover, the yield stress plays a crucial role in characterizing interaction threshold between the particles (Goldsmith 1999). According to rheology’s principle (Tanner 2000), accounting for the influence of constitutive law to describe the whole state of NNFs is essential, because the strain generated by the external forces is very large. It is to be noted that regardless of the flow history, the NNFs can be desirable in some processing technologies such as mixing, shear thinning/thickening, surface coating, etc.

As discussed above, although many efforts have been dedicated to investigate the BLT and NNFs simultaneously, there exist a few works concerning the NNF combined with NNF. Here, a brief summary of the most important works undertaken on the thermophysical analysis of NNF–NNF are reviewed. Raju et al. (2017) characterized numerically the magnetohydrodynamic (MHD) response of NNF–NNF over a variable thickness wall. They developed those reported by Khader and Megahed (2013) and showed that the effect of multiple slip can be ignored only in flow regions away from the stretching wall. Gireesha et al. (2017) accounted for the chemical reaction between the three dimensional (3-D) NNF–NNF. They also investigated the volumetric heat release with the magnetic field and nonlinear thermal radiation. They found that the buoyancy-induced flow over a deformable sheet is significantly affected by the mixed convection of NNFs. Kumaran et al. (2018) simulated thermodynamically NNF–NNF along the upwardly concave paraboloid of revolution. They showed that increasing the uniform Lorentz force, which is known as a resistance towards the velocity distribution, causes suppression of the thermal convection. They also found a remarkable agreement with the numerical solutions of heat transfer analysis in alumina–water fluid considering variable thermal conductivity which is reported by Animasaun and Sandeep (2016). Reddy et al. (2017) analyzed peristaltic transport of electrically conducting NNF–NNF through the NDSolve simulation carried out in Mathematica commercial software. They showed that the natural convection buoyancy-induced flow inside in an irregular channel varies with the uneven heating. However, one would expect the pressure loss not to be accelerated if the forced convection is regarded.

In this study, the unsteady Navier–Stokes, energy, and nanoparticle concentration equations are derived to investigate thermophysical characteristics of NNF–NNF over a permeable shrinking wall considering viscous dissipation and inclined magnetic field based on the Buongiorno mathematical model. For this purpose, the governing PDEs are undergone a similarity transformation and then converted to the ODEs. Furthermore, the RHA and its optimization have been employed to obtain the convergent series expressions. The results are compared and validated by those available numerical and analytical findings in the literature. To the best of author’s knowledge, no similar work exists to date.

Problem Formulation

Rheological Model

One of the most common NNFs is the Casson type which represents the Cauchy stress via the following constitutive equation (Casson 1959):

$$\tau = \left[ {\tau_{0}^{1/n} + \left( {\mu \dot{\gamma }} \right)^{1/n} } \right]^{n} ,$$
(1)

where \(\tau_{0}\) is the yield stress, \(\mu\) is the dynamic viscosity, \(\dot{\gamma }\) is the shear rate, and \(n \in {\mathbb{Z}}\) is the power-law index. It is to be noted that in the case when \(n = 1\), the Casson type reduces to an ideal Bingham plastic (Bingham 1922) (see “Appendix 1”).

An alternative NNF for describing the less resistance at higher shear rates is the Carreau–Yasuda type which is governed by Tropea et al. (2007):

$$\tau = \mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\left[ {1 + \left( {\varGamma \dot{\gamma }} \right)^{2\beta } } \right]^{{\left( {n - 1} \right)/2\beta }} ,$$
(2)

where \(\mu_{\infty }\) is an infinite shear rate viscosity, \(\mu_{0}\) is the zero shear rate viscosity, \(\varGamma\) is the relaxation time, and \(\beta > 0\) is a dimensionless parameter which accounts for the transition point between the zero shear rate and power-law regions. It should be mentioned here that for monomolecular polymers (i.e., \(\beta = 1\)), Eq. (2) reduces to the generalized Carreau type (Carreau 1972). Furthermore, since \(\dot{\gamma } = \sqrt {\frac{1}{2}\left( {\mathop {\mathbf{\gamma }}\limits^{.} :\mathop {\mathbf{\gamma }}\limits^{.} } \right)}\), and because \(\mu_{\infty }\) is assumed to be zero, we have

$$\mu = \mu_{0} \left[ {1 + \left( {\varGamma \dot{\gamma }} \right)^{2} } \right]^{{\left( {n - 1} \right)/2}} .$$
(3)

Governing Equations

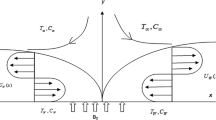
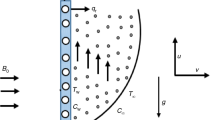
Utilizing the Buongiorno mathematical model in which the slip mechanisms between the nanoparticles can be modeled by means of the thermophoresis and Brownian diffusion (Buongiorno 2006), the governing PDEs take the following form:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(4)
$$\begin{aligned} \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} & = \upsilon \left[ {1 + \frac{1}{\lambda } + \frac{{3\left( {n - 1} \right)\varGamma^{2} }}{2}\left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]\frac{{\partial^{2} u}}{{\partial y^{2} }} \\&\quad+ g\left[ {\beta_{\text{T}} \left( {T - T_{\infty } } \right) + \beta_{\text{C}} \left( {C - C_{\infty } } \right)} \right] \\ & \quad - \,\frac{{\sigma B_{0}^{2} }}{\rho }u\sin^{2} \alpha , \\ \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} &= \frac{1}{{\rho c_{\text{p}} }}\left( {k\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{{\partial q_{\text{r}} }}{\partial y}} \right) \\&\quad+ \varepsilon \left[ {D_{\text{B}} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right], \end{aligned}$$
(6)
$$\frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }},$$
(7)

where \(\upsilon\) is the kinematic viscosity, \(\lambda\) is the Casson fluid parameter, \(g\) is the gravitational acceleration, \(\beta_{\text{T}}\) is the thermal expansion coefficient, \(T_{\infty }\) is the ambient temperature, \(\beta_{\text{C}}\) is the nanoparticle concentration expansion coefficient, \(C_{\infty }\) is the ambient nanoparticle concentration, \(\sigma\) is the electrical conductivity, \(B_{0}\) is the magnetic field strength, \(\rho\) is the density, \(\alpha\) is the inclination angle of magnetic field, \(c_{\text{p}}\) is the specific heat at constant pressure, \(k\) is the thermal conductivity, \(q_{\text{r}}\) is the radiation heat flux, \(\varepsilon = \left( {\rho c} \right)_{\text{p}} /\left( {\rho c} \right)_{\text{f}}\) is the ratio of effective heat capacity of the nanoparticle to the effective heat capacity of base fluid, \(D_{\text{B}}\) is the Brownian diffusion coefficient, and \(D_{\text{T}}\) is the thermophoresis diffusion coefficient.

The associated initial and boundary conditions are given below:

$$\begin{aligned} u & = 0, v = 0, T = T_{\infty } , C = C_{\infty } ,\quad {\text{at}}\;\;t = 0, \\ u & = U_{\text{w}} \left( {x,t} \right) = - \frac{bx}{1 - at}, v = V_{\text{w}} \left( {x,t} \right) = \frac{{v_{0} }}{{\left( {1 - at} \right)^{1/2} }}, \\T &= T_{\text{w}} = T_{\infty } + \frac{{bx^{2} T_{0} \left( {1 - at} \right)^{ - 3/2} }}{2\upsilon }, \\ C & = C_{\text{w}} = C_{\infty } + \frac{{bx^{2} C_{0} \left( {1 - at} \right)^{ - 3/2} }}{2\upsilon },\quad {\text{at}}\;\;y = 0, \\ u & \to 0, T \to T_{\infty } , C \to C_{\infty } ,\quad {\text{as}} \;\;y \to \infty , \\ \end{aligned}$$
(8)

where \(U_{\text{w}}\) is the velocity at the wall, \(b > 0\) is a constant with dimension (time)−1, \(a\) is a parameter corresponds to unsteadiness, \(V_{\text{w}}\) is the mass transfer rate, \(v_{0}\) is the suction/blowing parameter, \(T_{\text{w}}\) is the wall temperature, \(T_{0}\) is the reference temperature, \(C_{\text{w}}\) is the wall nanoparticle concentration, and \(C_{0}\) is the reference nanoparticle concentration.

The Rosseland approximation formula for the radiation heat flux presented in Eq. (6) takes the form (Rosseland 1931):

$$q_{\text{r}} = - \frac{{4\sigma_{\text{SB}} }}{{3a_{\text{R}} }}\frac{{\partial T^{4} }}{\partial y},$$
(9)

where \(\sigma_{\text{SB}} = 5. 6 6 9 7\times 1 0^{ - 8} \left[ {{\text{W}} {\text{m}}^{ - 2}\,{\text{K}}^{ - 4} } \right]\) and \(a_{\text{R}}\) are the Stefan–Boltzmann constant and mean spectral absorption coefficient, respectively. Assuming that the temperature discrepancy within the flow is very small (Khoshrouye Ghiasi and Saleh 2019c), \(T^{4}\) can be expanded in Taylor series as

$$T^{4} = T_{\infty }^{4} + 4T_{\infty }^{3} \left( {T - T_{\infty } } \right) + 6T_{\infty }^{2} \left( {T - T_{\infty } } \right)^{2} + \cdots \approx 4T_{\infty }^{3} T - 3T_{\infty }^{4} .$$
(10)

Upon substitution of Eq. (10) into Eq. (9) and differentiating this with respect to \(y\), Eq. (6) can be rewritten as follows:

$$\begin{aligned} \frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} &= \frac{1}{{\rho c_{\text{p}} }}\left( {k + \frac{{16\sigma_{\text{SB}} T_{\infty }^{3} }}{{3a_{\text{R}} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }} \\&\quad+ \varepsilon \left[ {D_{\text{B}} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right]. \end{aligned}$$
(11)

Introducing \(\eta = y\left( {\frac{b}{{\upsilon \left( {1 - at} \right)}}} \right)^{1/2}\), \(\varphi = x\left( {\frac{b\upsilon }{1 - at}} \right)^{1/2} f\left( \eta \right)\), \(\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}\), and \(\phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }}\), the non-dimensional form of governing ODEs is given by

$$\begin{aligned} & \left( {1 + \frac{1}{\lambda }} \right)\frac{{\partial^{3} f}}{{\partial \eta^{3} }} + \left( {f - \frac{{\bar{a}\eta }}{2}} \right)\frac{{\partial^{2} f}}{{\partial \eta^{2} }} \\&\quad- \left( {\frac{\partial f}{\partial \eta } + {\text{Ha}}^{2} \sin^{2} \alpha + \bar{a}} \right)\frac{\partial f}{\partial \eta } + \beta_{1} \theta + \beta_{2} \phi \quad \\&\quad+ \,\frac{{3\left( {n - 1} \right)}}{2}{\text{We}}\left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)^{2} \frac{{\partial^{3} f}}{{\partial \eta^{3} }} = 0, \\ & \frac{1}{ \Pr }\left( {1 + \frac{{4N_{\text{R}} }}{3}} \right)\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + \left( {f - \frac{{\bar{a}\eta }}{2} + {\text{Nb}}\frac{\partial \phi }{\partial \eta }} \right)\frac{\partial \theta }{\partial \eta }\\&\quad + {\text{Nt}}\left( {\frac{\partial \theta }{\partial \eta }} \right)^{2} = 0, \\ & \frac{{\partial^{2} \phi }}{{\partial \eta^{2} }} + {\text{Le}}\left( {f - \frac{{\bar{a}\eta }}{2}} \right)\frac{\partial \phi }{\partial \eta } + \frac{\hbox{Nt}}{\text{Nb}}\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} = 0, \\ \end{aligned}$$
(12)

where \(\eta\) is the similarity parameter, \(\varphi\) is the stream function, \(f\) is the similarity function, \(\theta\) is the non-dimensional temperature, \(\phi\) is the non-dimensional nanoparticle concentration, \(\bar{a} = a/b\) is the unsteadiness parameter, \({\text{Ha}}^{2} = \frac{{\sigma B_{0}^{2} }}{\rho b}\) is the Hartmann number, \(\beta_{1}\) is the thermal buoyancy (or mixed convection) parameter, \(\beta_{2}\) is the solute buoyancy parameter, \({\text{We}}^{2} = \frac{{\Gamma ^{2} b^{3} x^{2} }}{{\upsilon \left( {1 - at} \right)^{3} }}\) is the Weissenberg number, \({ \Pr } = \frac{{\mu c_{\text{p}} }}{k}\) is the Prandtl number, \(N_{\text{R}} = \frac{{4\sigma_{\text{SB}} T_{\infty }^{3} }}{{3a_{\text{R}} k}}\) is the radiation parameter, \({\text{Nb}} = \frac{{\varepsilon D_{\text{B}} }}{\upsilon }\left( {C_{\text{w}} - C_{\infty } } \right)\) is the Brownian motion parameter, \({\text{Nt}} = \frac{{\varepsilon D_{\text{T}} }}{{\upsilon T_{\infty } }}\left( {T_{\text{w}} - T_{\infty } } \right)\) is the thermophoresis parameter, and \({\text{Le}} = \upsilon /D_{\text{B}}\) is the Lewis number.

The associated boundary conditions are written as

$$\begin{aligned} & f = S, \frac{\partial f}{\partial \eta } = - 1, \theta = 1, \phi = 1, \quad {\text{at}}\;\;\eta = 0, \\& \frac{\partial f}{\partial \eta } \to 0, \theta \to 0, \phi \to 0,\quad {\text{as}}\;\;\eta \to \infty , \\ \end{aligned}$$
(13)

where \(S\) is the mass suction parameter.

Here, the non-dimensional skin friction coefficient, local Nusselt number, and local Sherwood number are given by

$$C_{\text{f}} = \frac{{2\tau_{\text{w}} }}{{\rho U_{\text{w}}^{2} }}, {\text{Nu}}_{x} = \frac{{xq_{\text{w}} }}{{k\left( {T_{\text{w}} - T_{\infty } } \right)}}, {\text{Sh}}_{x} = \frac{{xq_{\text{m}} }}{{D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}},$$
(14)

where

$$\tau_{\text{w}} = \mu \left( {1 + \frac{1}{\lambda }} \right)\left( {\frac{\partial u}{\partial y}} \right)_{y = 0} , q_{\text{w}} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} , q_{\text{m}} = - D_{\text{B}} \left( {\frac{\partial C}{\partial y}} \right)_{y = 0} .$$
(15)

It is to be noted that substitution of similarity transformations into Eqs. (14) and (15) gives the results:

$$\begin{aligned}& C_{\hbox{f}} {\text{Re}}_{x}^{1/2} = \left( {1 + \frac{1}{\lambda }} \right)\left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)_{\eta = 0} , {\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2} = - \left( {\frac{\partial \theta }{\partial \eta }} \right)_{\eta = 0} , \\&{\text{Sh}}_{x} {\text{Re}}_{x}^{ - 1/2} = - \left( {\frac{\partial \phi }{\partial \eta }} \right)_{\eta = 0} , \end{aligned}$$
(16)

where \({\text{Re}}_{x} = \frac{{\rho U_{\text{w}} x}}{\mu }\) is the local Reynolds number.

Solution Methodology

Let us consider the initial approximation of \(f\), \(\theta\) and \(\phi\) as follows:

$$f_{0} = S - 1 + e^{ - \eta } , \theta_{0} = \phi_{0} = e^{ - \eta } ,$$
(17)

which must satisfy the boundary conditions given in Eq. (13). According to the definition of homotopy, the auxiliary linear operators can be represented in the form:

$$L_{f} = \frac{{\partial^{3} f}}{{\partial \eta^{3} }} - \frac{\partial f}{\partial \eta }, L_{\theta } = \frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} - \theta , L_{\phi } = \frac{{\partial^{2} \phi }}{{\partial \eta^{2} }} - \phi ,$$
(18)

with the properties:

$$\begin{aligned}& L_{f} \left[ {C_{1} + C_{2} e^{\eta } + C_{3} e^{ - \eta } } \right] = 0, L_{\theta } = \left[ {C_{4} e^{\eta } + C_{5} e^{ - \eta } } \right] = 0,\\& L_{\phi } \left[ {C_{6} e^{\eta } + C_{7} e^{ - \eta } } \right] = 0, \end{aligned}$$
(19)

where \(C_{1}\) – \(C_{7}\) are the arbitrary constants. Using \(q \in \left[ { 0, 1} \right]\) as an embedding parameter, the zeroth-order deformation equations are given by

$$\begin{array}{*{20}l} {\left( {1 - q} \right){\text{L}}_{f} \left[ {f\left( {\eta ;q} \right) - f_{0} \left( \eta \right)} \right] = qh_{f} {\text{N}}_{f} \left[ {f\left( {\eta ;q} \right)} \right],} \hfill \\ {\left( {1 - q} \right){\text{L}}_{\theta } \left[ {\theta \left( {\eta ;q} \right) - \theta_{0} \left( \eta \right)} \right] = qh_{\theta } {\text{N}}_{\theta } \left[ {f\left( {\eta ;q} \right),\theta \left( {\eta ;q} \right),\phi \left( {\eta ;q} \right)} \right],} \hfill \\ {\left( {1 - q} \right){\text{L}}_{\phi } \left[ {\phi \left( {\eta ;q} \right) - \phi_{0} \left( \eta \right)} \right] = qh_{\phi } {\text{N}}_{\phi } \left[ {f\left( {\eta ;q} \right),\theta \left( {\eta ;q} \right),\phi \left( {\eta ;q} \right)} \right],} \hfill \\ \end{array}$$
(20)

where \(h_{f}\), \(h_{\theta }\), and \(h_{\phi }\) are the nonzero auxiliary parameters, and \(N_{f}\), \(N_{\theta }\), and \(N_{\phi }\) are the nonlinear operators which can be expressed as

$$\begin{aligned} &{\begin{aligned} N_{f} \left[ {f\left( {\eta ;q} \right)} \right] & = \left( {1 + \frac{1}{\lambda }} \right)\frac{{\partial^{3} f\left( {\eta ;q} \right)}}{{\partial \eta^{3} }} + \left( {f\left( {\eta ;q} \right) - \frac{{\bar{a}\eta }}{2}} \right)\frac{{\partial^{2} f\left( {\eta ;q} \right)}}{{\partial \eta^{2} }} - \left( {\frac{{\partial f\left( {\eta ;q} \right)}}{\partial \eta } + {\text{Ha}}^{2} \sin^{2} \alpha + \bar{a}} \right) \\ & \quad \times \,\frac{{\partial f\left( {\eta ;q} \right)}}{\partial \eta } + \beta_{1} \theta \left( {\eta ;q} \right) + \beta_{2} \phi \left( {\eta ;q} \right) + \frac{{3\left( {n - 1} \right)}}{2}{\text{We}}\left( {\frac{{\partial^{2} f\left( {\eta ;q} \right)}}{{\partial \eta^{2} }}} \right)^{2} \frac{{\partial^{3} f\left( {\eta ;q} \right)}}{{\partial \eta^{3} }}, \end{aligned}}\\ &{\begin{aligned} N_{\theta } \left[ {f\left( {\eta ;q} \right),\theta \left( {\eta ;q} \right),\phi \left( {\eta ;q} \right)} \right] & = \frac{1}{ \Pr }\left( {1 + \frac{{4N_{\text{R}} }}{3}} \right)\frac{{\partial^{2} \theta \left( {\eta ;q} \right)}}{{\partial \eta^{2} }} + \left( {f\left( {\eta ;q} \right) - \frac{{\bar{a}\eta }}{2} + {\text{Nb}}\frac{{\partial \phi \left( {\eta ;q} \right)}}{\partial \eta }} \right) \\ & \quad \times \,\frac{{\partial \theta \left( {\eta ;q} \right)}}{\partial \eta } + {\text{Nt}}\left( {\frac{{\partial \theta \left( {\eta ;q} \right)}}{\partial \eta }} \right)^{2} ,\end{aligned}} \\ &{\begin{aligned} N_{\phi } \left[ {f\left( {\eta ;q} \right),\theta \left( {\eta ;q} \right),\phi \left( {\eta ;q} \right)} \right] & = \frac{{\partial^{2} \phi \left( {\eta ;q} \right)}}{{\partial \eta^{2} }} + {\text{Le}}\left( {f\left( {\eta ;q} \right) - \frac{{\bar{a}\eta }}{2}} \right)\frac{{\partial \phi \left( {\eta ;q} \right)}}{\partial \eta } + \frac{\hbox{Nt}}{\text{Nb}}\frac{{\partial^{2} \theta \left( {\eta ;q} \right)}}{{\partial \eta^{2} }},\end{aligned}} \\ \end{aligned}$$
(21)

with the boundary conditions

$$\begin{aligned} f\left( {\eta ;q} \right) & = S, \frac{{\partial f\left( {\eta ;q} \right)}}{\partial \eta } = - 1, \theta \left( {\eta ;q} \right) = 1, \phi \left( {\eta ;q} \right) = 1, \quad {\text{at}}\;\;\eta = 0, \\ \frac{{\partial f\left( {\eta ;q} \right)}}{\partial \eta } & \to 0, \theta \left( {\eta ;q} \right) \to 0, \phi \left( {\eta ;q} \right) \to 0,\quad {\text{as}}\;\;\eta \to \infty . \\ \end{aligned}$$
(22)

It is to be noted that as \(q\) increases from 0 to 1, \(f\left( {\eta ;q} \right)\), \(\theta \left( {\eta ;q} \right)\), and \(\phi \left( {\eta ;q} \right)\) deform from the initial approximations to the exact solutions. Expanding \(f\left( {\eta ;q} \right)\), \(\theta \left( {\eta ;q} \right)\) and \(\phi \left( {\eta ;q} \right)\) in the Taylor series with respect to \(q\) gives

$$\begin{array}{*{20}l} {f\left( {\eta ;q} \right) = f_{0} \left( \eta \right) + \mathop \sum \limits_{m = 1}^{\infty } f_{m} \left( \eta \right)q^{m} ,} \hfill \\ {\theta \left( {\eta ;q} \right) = \theta_{0} \left( \eta \right) + \mathop \sum \limits_{m = 1}^{\infty } \theta_{m} \left( \eta \right)q^{m} ,} \hfill \\ {\phi \left( {\eta ;q} \right) = \phi_{0} \left( \eta \right) + \mathop \sum \limits_{m = 1}^{\infty } \phi_{m} \left( \eta \right)q^{m} ,} \hfill \\ \end{array}$$
(23)

where

$$\begin{aligned}& f_{m} \left( \eta \right) = \left( {\frac{1}{m!}\frac{{\partial^{m} f\left( {\eta ;q} \right)}}{{\partial q^{m} }}} \right)_{q = 0} , \theta_{m} \left( \eta \right) = \left( {\frac{1}{m!}\frac{{\partial^{m} \theta \left( {\eta ;q} \right)}}{{\partial q^{m} }}} \right)_{q = 0} , \\&\phi_{m} \left( \eta \right) = \left( {\frac{1}{m!}\frac{{\partial^{m} \phi \left( {\eta ;q} \right)}}{{\partial q^{m} }}} \right)_{q = 0} . \end{aligned}$$
(24)

With the proper choice of initial approximations, auxiliary linear operators, and auxiliary parameters, Eq. (23) converges at \(q = 1\) as

$$f\left( \eta \right) = \mathop \sum \limits_{m = 0}^{\infty } f_{m} \left( \eta \right), \theta \left( \eta \right) = \mathop \sum \limits_{m = 0}^{\infty } \theta_{m} \left( \eta \right), \phi \left( \eta \right) = \mathop \sum \limits_{m = 0}^{\infty } \phi_{m} \left( \eta \right).$$
(25)

Differentiating Eq. (20) \(m\) times with respect to \(q\), dividing them by \(m!\) and then setting \(q = 0\), the \(m\) th-order deformation equations are constructed as

$$\begin{array}{*{20}l} {L_{f} \left[ {f_{m} \left( \eta \right) - \chi_{m} f_{m - 1} \left( \eta \right)} \right] = h_{f} R_{f,m} \left( \eta \right),} \hfill \\ {L_{\theta } \left[ {\theta_{m} \left( \eta \right) - \chi_{m} \theta_{m - 1} \left( \eta \right)} \right] = h_{\theta } R_{\theta ,m} \left( \eta \right),} \hfill \\ {L_{\phi } \left[ {\phi_{m} \left( \eta \right) - \chi_{m} \phi_{m - 1} \left( \eta \right)} \right] = h_{\phi } R_{\phi ,m} \left( \eta \right),} \hfill \\ \end{array}$$
(26)

where

$$\chi_{m} = \left\{ {\begin{array}{*{20}l} {0, \quad n \le 1,} \hfill \\ {1, \quad n > 1,} \hfill \\ \end{array} } \right.$$
(27)
$$\begin{aligned} R_{f,m} \left( \eta \right) & = \left( {1 + \frac{1}{\lambda }} \right)\frac{{\partial^{3} f_{m - 1} }}{{\partial \eta^{3} }} + \mathop \sum \limits_{l = 0}^{m - 1} f_{l} \frac{{\partial^{2} f_{m - l - 1} }}{{\partial \eta^{2} }} - \frac{{\bar{a}\eta }}{2}\frac{{\partial^{2} f_{m - 1} }}{{\partial \eta^{2} }} - \mathop \sum \limits_{l = 0}^{m - 1} \frac{{\partial f_{l} }}{\partial \eta }\frac{{\partial f_{m - l - 1} }}{\partial \eta } \\ & \quad + \,\left( {{\text{Ha}}^{2} \sin^{2} \alpha + \bar{a}} \right)\frac{{\partial f_{m - 1} }}{\partial \eta } + \beta_{1} \theta_{m - 1} + \beta_{2} \phi_{m - 1} + \,\frac{{3\left( {n - 1} \right)}}{2}{\text{We}}\mathop \sum \limits_{l = 0}^{m - 1} \left( {\mathop \sum \limits_{i = 0}^{l} \frac{{\partial^{2} f_{l - i} }}{{\partial \eta^{2} }}\mathop \sum \limits_{j = 0}^{i} \frac{{\partial^{2} f_{j} }}{{\partial \eta^{2} }}\frac{{\partial^{3} f_{i - j} }}{{\partial \eta^{3} }}} \right), \\ R_{\theta ,m} \left( \eta \right) & = \frac{1}{ \Pr }\left( {1 + \frac{{4N_{\text{R}} }}{3}} \right)\frac{{\partial^{2} \theta_{m - 1} }}{{\partial \eta^{2} }} + \mathop \sum \limits_{l = 0}^{m - 1} f_{l} \frac{{\partial \theta_{m - l - 1} }}{\partial \eta } - \frac{{\bar{a}\eta }}{2}\frac{{\partial \theta_{m - 1} }}{\partial \eta } + {\text{Nb}}\mathop \sum \limits_{l = 0}^{m - 1} \frac{{\partial \phi_{l} }}{\partial \eta }\frac{{\partial \theta_{m - l - 1} }}{\partial \eta } + \,{\text{Nt}}\mathop \sum \limits_{l = 0}^{m - 1} \frac{{\partial \theta_{l} }}{\partial \eta }\frac{{\partial \theta_{m - l - 1} }}{\partial \eta }, \\ R_{\phi ,m} \left( \eta \right) & = \frac{{\partial^{2} \phi_{m - 1} }}{{\partial \eta^{2} }} + {\text{Le}}\mathop \sum \limits_{l = 0}^{m - 1} f_{l} \frac{{\partial \phi_{m - l - 1} }}{\partial \eta } - {\text{Le}}\frac{{\bar{a}\eta }}{2}\frac{{\partial \phi_{m - 1} }}{\partial \eta } + \frac{\hbox{Nt}}{\text{Nb}}\frac{{\partial^{2} \theta_{m - 1} }}{{\partial \eta^{2} }}, \\ \end{aligned}$$
(28)

with the boundary conditions

$$\begin{array}{*{20}l} {f\left( \eta \right) = 0, \frac{\partial f\left( \eta \right)}{\partial \eta } = 0, \theta \left( \eta \right) = 0, \phi \left( \eta \right) = 0, {\text{at}}\,\, \eta = 0,} \hfill \\ {\frac{\partial f\left( \eta \right)}{\partial \eta } \to 0, \theta \left( \eta \right) \to 0, \phi \left( \eta \right) \to 0, {\text{as}} \,\, \eta \to \infty .} \hfill \\ \end{array}$$
(29)

The general solutions of Eq. (26) in terms of particular solutions (i.e., \(f_{m}^{{ \star }} \left( \eta \right)\), \(\theta_{m}^{{ \star }} \left( \eta \right)\), and \(\phi_{m}^{{ \star }} \left( \eta \right)\)) can be written as

$$\begin{array}{*{20}l} {f_{m} \left( \eta \right) = f_{m}^{{ \star }} \left( \eta \right) + C_{1} + C_{2} e^{\eta } + C_{3} e^{ - \eta } ,} \hfill \\ {\theta_{m} \left( \eta \right) = \theta_{m}^{{ \star }} \left( \eta \right) + C_{4} e^{\eta } + C_{5} e^{ - \eta } ,} \hfill \\ {\phi_{m} \left( \eta \right) = \phi_{m}^{{ \star }} \left( \eta \right) + C_{6} e^{\eta } + C_{7} e^{ - \eta } ,} \hfill \\ \end{array}$$
(30)

where

$$\begin{aligned} &C_{1} = - \left( {f_{m}^{{ \star }} \left( 0 \right) + \frac{{\partial f_{m}^{{ \star }} \left( 0 \right)}}{\partial \eta }} \right), C_{2} = C_{4} = C_{6} = 0,\\& C_{3} = \frac{{\partial f_{m}^{{ \star }} \left( 0 \right)}}{\partial \eta }, C_{5} = - \theta_{m}^{{ \star }} \left( 0 \right), C_{7} = - \phi_{m}^{{ \star }} \left( 0 \right). \end{aligned}$$
(31)

To summarize the above-mentioned RHA, one can serve the following algorithm:

  1. 1.

    Set \(m = 1\).

  2. 2.

    Substitute Eq. (17) into Eq. (28) and find \(R_{f,1}\), \(R_{\theta ,1}\) and \(R_{\phi ,1}\).

  3. 3.

    Substitute \(R_{f,1}\), \(R_{\theta ,1}\), and \(R_{\phi ,1}\) into Eq. (26).

  4. 4.

    Determine \(C_{1}\) – \(C_{7}\) and find \(f_{1}\), \(\theta_{1}\), and \(\phi_{1}\).

  5. 5.

    Substitute \(f_{1}\), \(\theta_{1}\), and \(\phi_{1}\) into Eq. (26) and find \(R_{f,2}\), \(R_{\theta ,2}\) and \(R_{\phi ,2}\).

  6. 6.

    Repeat steps 2–4 \(m\) times.

  7. 7.

    Find \(f_{M}\), \(\theta_{M}\) and \(\phi_{M}\), where \(M\) is the number of iterations.

  8. 8.

    Check for convergence of the series expressions.

One way to accelerate the convergence of RHA is to find the optimal values of auxiliary parameters by minimizing the squared residual errors as follows (Liao 2010):

$$\begin{aligned} \Delta_{f,m} & = \frac{1}{r + 1}\mathop \sum \limits_{p = 0}^{r} \left\{ {N_{f} \left[ {\mathop \sum \limits_{d = 0}^{m} f\left( \eta \right)} \right]_{\eta = p\delta \eta } } \right\}^{2} {\text{d}}\eta , \\ \Delta_{\theta ,m} & = \frac{1}{r + 1}\mathop \sum \limits_{p = 0}^{r} \left\{ {N_{\theta } \left[ {\mathop \sum \limits_{d = 0}^{m} f\left( \eta \right),\mathop \sum \limits_{d = 0}^{m} \theta \left( \eta \right),\mathop \sum \limits_{d = 0}^{m} \phi \left( \eta \right)} \right]_{\eta = p\delta \eta } } \right\}^{2} {\text{d}}\eta , \\ \Delta_{\phi ,m} & = \frac{1}{r + 1}\mathop \sum \limits_{p = 0}^{r} \left\{ {N_{\phi } \left[ {\mathop \sum \limits_{d = 0}^{m} f\left( \eta \right),\mathop \sum \limits_{d = 0}^{m} \theta \left( \eta \right),\mathop \sum \limits_{d = 0}^{m} \phi \left( \eta \right)} \right]_{\eta = p\delta \eta } } \right\}^{2} {\text{d}}\eta , \\ \end{aligned}$$
(32)

where \(r = 2 0\) and \(\delta \eta = 0. 5\). It is worth noting that the total squared residual error (i.e., \(\Delta_{t,m} = \Delta_{f,m} + \Delta_{\theta ,m} + \Delta_{\phi ,m}\)) can be determined by Mathematica package BVPh2.0 (see “Appendix 2”).

Results and Discussion

This section is devoted entirely to finding the thermophysical characteristics of unsteady Casson–Carreau fluid over a permeable shrinking wall based on the Buongiorno mathematical model. To this end, the governing physical parameters, unless stated otherwise, are given in Table 1. It is to be noted that after estimating convergence region of the series expressions and comparing the RHA findings with those available in the open literature, an outline of how the governing physical parameters influence the results is also provided.

Table 1 Governing physical parameters
Full size table

Convergence Study

Table 2 tabulates the values of auxiliary parameters as well as its associated total squared residual errors at different orders of approximations (i.e., \(m\)) with the parameters, as given in Table 1. According to this table, the auxiliary parameters minimize when \(m\) is increased for all cases. Furthermore, it follows that the squared residual error achieves the minimum possible value when \(h_{f} = -\, 0. 7 2 3 5\), \(h_{\theta } = -\, 0. 9 9 1 1\), and \(h_{\phi } = -\, 1. 0 7 5 9\) are chosen. Therefore, it can be concluded that the above-mentioned auxiliary parameters are hereafter utilized in this study.

Table 2 Selection of \(h_{f}\), \(h_{\theta }\) and \(h_{\phi }\)
Full size table

Table 3 investigates the convergence of above-mentioned series expressions through the use of squared residual errors with the parameters, as presented in Table 1. It is seen from this table that the minimum values of squared residual errors can be found at \(m = 2 0\). Under these circumstances, one can expect the convergence of RHA to accelerate as fast as possible.

Table 3 Values of \(\Delta_{f,m}\), \(\Delta_{\theta ,m}\) and \(\Delta_{\phi ,m}\)
Full size table

Comparison and Validation

To verify the effectiveness of the present RHA, Fig. 1 illustrates the variation of skin friction coefficient versus different values of Hartmann number in both \(\alpha\) = 45° and \(9 0\)° with \(n = 1\), \({ \Pr } = 0. 7 1\), \(N_{\text{R}} = 1\), and \(\bar{a} = \beta_{1} = \beta_{2} = {\text{We}} = {\text{Nb}} = {\text{Nt}} = {\text{Le}} = S = 0\). This figure also represents a comparison between the RHA findings and those reported by Hakeem et al. (2016) obtained through the Runge–Kutta method. It is to be noted here that velocity slip at the boundary reported by Hakeem et al. (2016) is negligibly small.

Fig. 1
figure 1

Verification of the skin friction coefficient for a Casson type; a\(\alpha = 45{^\circ }\) and b\(\alpha = 90^\circ\)

Full size image

As it can be observed from Fig. 1, increasing the values of Hartmann number significantly decreases the skin friction coefficient in both cases. Furthermore, the present RHA agrees very well with those numerical findings reported by Hakeem et al. (2016).

Table 4 provides a comparison between the present RHA and those prepared by Bhattacharyya (2011) to show the effect of mass suction parameter in the calculation of skin friction coefficient. The inserted results in this table are given by \(\lambda \to \infty\), \(n = 1\) and \(\bar{a} = \beta_{1} = \beta_{1} = {\text{We}} = N_{\text{R}} = {\text{Nb}} = {\text{Nt}} = {\text{Le}} = 0\). Based on the results of Table 4, it is seen that increasing the suction parameter without considering its NNF terms increases the skin friction coefficient. Furthermore, the RHA findings are consistent with those prepared by Bhattacharyya (2011), because the insignificant relative error between them does not exceed 0.0008%.

Table 4 Values of the skin friction coefficient compared with those of Bhattacharyya (2011)
Full size table

According to the results depicted in Table 5, the present RHA is in an excellent agreement with the numerical findings provided by Pal et al. (2014) as well as those of Khan and Pop (2010). It is due to the fact that the present RHA and those reported by Pal et al. (2014) and Khan and Pop (2010) only suffer from a maximum relative error of at most 0.0058% and 0.0141%, respectively. Furthermore, Table 5 shows the variation of heat transfer rate versus different values of Prandtl number with \(\lambda \to \infty\), \(n = 1\), and \(\bar{a} = {\text{Ha}} = \alpha = \beta_{1} = \beta_{2} = {\text{We}} = N_{\text{R}} = {\text{Nb}} = {\text{Nt}} = {\text{Le}} = S = 0\).

Table 5 Values of the heat transfer rate compared with those of Pal et al. (2014) and Khan and Pop (2010)
Full size table

It is to be noted here that increasing the values of Prandtl number in Table 2 clearly increases the heat transfer rate. Therefore, in view of Fig. 1 and Tables 4 and 5, one can say that the present RHA, due to its accuracy and short run time, is desirable to have convergent and reliable series expressions.

Parametric Study

Based on the earlier studies (Khoshrouye Ghiasi and Saleh 2018; Zhang et al. 2016; El-Aziz and Afify 2016), the minimum boundary layer thickness would occur for large values of the unsteadiness parameter. It was shown that this parameter can also be regarded as the induced flow stabilizer. This issue is clearly seen in Fig. 2.

Fig. 2
figure 2

Variation of \(C_{\hbox{f}} {\text{Re}}_{x}^{1/2}\) versus \(\bar{a}\)

Full size image

Figure 2 represents the variation of skin friction coefficient versus different values of unsteadiness parameter for \(0. 1\le \lambda \le 0. 4\). According to this figure, by increasing the Casson fluid parameter, the skin friction coefficient is increased which is only due to a reduction in the diffusion-induced plasticity. However, Mabood et al. (2016) showed that this coefficient becomes relatively insensitive to \(\lambda\) in the case of temperature-dependent dynamic viscosity. It is worth noting that using this observation and the Vogel–Fulcher–Tamman (VFT) law (Vogel 1921), one can modify the temperature dependence of zero shear rate viscosity/relaxation time effectively.

In view of the results given in Table 6, it is seen that the thermal buoyancy parameter plays a more significant role in reducing the skin friction coefficient than that of the solute buoyancy one. This is because of the buoyancy force dominated by the viscous force. Furthermore, the buoyancy effects become more pronounced as the particle and fluid densities are quite different. It is to be mentioned here that a similar conclusion for entropy generation in a heterogeneous porous cavity has also been questioned by Zhuang and Zhu (2018).

Table 6 Combined effect of thermal and solute buoyancy parameters on the skin friction coefficient
Full size table

Figure 3 depicts the effect of viscoelasticity on the skin friction coefficient for both shear thinning (\(n < 1\)) and shear thickening (\(n > 1\)) fluids. Based on the results shown in this figure, increasing the values of Weissenberg parameter decreases the skin friction coefficient which is relevant to the enhancement of the drag force. In addition, since the viscoelasticity depends on the relaxation time, large values of \(\varGamma\) thicken the momentum boundary layer (Khan et al. 2018), and thereby decrease the velocity distribution. Hence, it can be inferred from Fig. 3 that the shear thinning/thickening effect causes little change to the momentum boundary layer thickness.

Fig. 3
figure 3

Variation of \(C_{\hbox{f}} {\text{Re}}_{x}^{1/2}\) versus \({\text{Ha}}\) for \(n = 0. 5\) and 1

Full size image

As shown in Fig. 4, it is obvious that the local Nusselt number is greatly affected by the Brownian motion and thermophoresis parameters simultaneously. Therefore, it is essential to account for the influence of mass diffusivity and temperature gradient with regard to the Brownian motion and thermophoresis parameters, respectively. However, it is to be noted that for large values of Brownian motion parameter, the temperature boundary layer thickness does not significantly vary.

Fig. 4
figure 4

Variation of \({\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2}\) versus \({\text{Nt}}\)

Full size image

Based on the results presented in Fig. 4, increasing the Browning motion/thermophoresis parameter clearly decreases the local Nusselt number particularly when it is subjected to the shear thickening effect. This is due to the fact that the thermophoresis can be introduced as a time-averaged motion influenced by the Brownian diffusion.

To investigate the effect of thermal radiation on the temperature distribution, the variation of local Nusselt number versus unsteadiness parameter is depicted in Fig. 5. It is seen from this figure that the heat energy which is generated by the radiation process can affect the temperature boundary layer thickness. Furthermore, Fig. 5 emphasizes on the fact that there exists a relationship between the thermal radiation and diffusion in describing the surface heat flux (Khader and Megahed 2014; Nadeem et al. 2019; Farooq et al. 2016). Using these important observations, one can conclude that in such systems the thermal radiation cannot be ignored.

Fig. 5
figure 5

Variation of \({\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2}\) versus \(\bar{a}\)

Full size image

Table 7 provides the variation of local Sherwood number versus \(\bar{a}\), \(\beta_{2}\), \({\text{Nb}}\), \({\text{Nt}}\), and \({\text{Le}}\) with both shear thinning and shear thickening fluids. According to this table, by increasing \({\text{Le}}\), the local Sherwood number is increased which is largely due to a reduction in the Brownian diffusion coefficient. Furthermore, Table 7 represents that the local Sherwood number is an enhancing function of \(\bar{a}\), \(\beta_{2}\) and \({\text{Nb}}\), while it is a diminishing function of \({\text{Nt}}\). At the end of this section, only the velocity, temperature and nanoparticle concentration distributions are listed in Table 8.

Table 7 Values of the local Sherwood number
Full size table
Table 8 Velocity, temperature, and nanoparticle concentration distributions
Full size table

Conclusions

The RHA was introduced in this work to investigate thermophysical characteristics of NNF–NNF over a permeable shrinking wall based on the Buongiorno mathematical model. The PDEs that govern the conservation of mass, momentum, energy, and nanoparticle concentration were converted to the ODEs in time via similarity transformation. The present RHA was also optimized by minimizing the squared residual errors at different orders of approximations. Here, the main results of the work can be summarized as follows:

  • Accounting for the effect of shear thinning/thickening fluid has little change to its momentum boundary layer thickness.

  • In case of \(\alpha = 4 5^\circ\) and \(90^\circ\), the RHA findings agree excellently with those reported by Hakeem et al. (2016).

  • The heat transfer rate is not affected by large values of the Brownian motion parameter. Moreover, the thermophoresis effect cannot be increased without considering the Brownian diffusion.

  • The nanoparticle concentration distribution becomes increasingly dependent on the Lewis number.