1 Introduction

For more than half a century, with the rapid development of nuclear technology, neutron detection technology has been required in several fields, including nuclear power plant control [1] and safety [2], nuclear decommissioning, irradiation facilities [3], medical applications such as boron neutron capture therapy, neutron logging, and nuclear security against illicit transportation of nuclear materials [4]. However, when it comes to the applications of neutron measurement, as a result of the fission process as well as the interaction between neutrons and the surrounding environment (e.g., inelastic scattering and slow neutron capture), gamma rays always accompany neutrons. Generally, both neutrons and gamma rays are easily detected but difficult to discriminate; therefore, discrimination of neutrons from gamma signals is necessary [5, 6]. With regard to this problem, the pulse shape discrimination (PSD) method has been widely used in many fields such as neutron flux monitoring, neutron diagnosis, nuclear medicine, nuclear safety, and nondestructive testing. For example, PSD is used in tokamak fusion devices [7] to monitor the neutron flux and diagnose the energy spectrum. This is an important and significant method. Specifically, according to the different attenuation rates of n–\(\upgamma\) signals in a scintillator [8], fractal spectrum [9], charge comparison [10, 11], rise time, pulse gradient [12], and intelligent screening methods [13, 14] are used for n–\(\upgamma\) discrimination. In addition, the pulse signals detected by the detector generally contain noise, and the difference between the neutron and gamma signals is insignificant. Moreover, the useless noise affects the performance and accuracy of discrimination; consequently, the pulse signal should be filtered and pre-processed beforehand, which can improve the performance of discrimination. Recently, many filtering methods have been developed; these include the Fourier transform [15, 16], wavelet transform [17, 18], moving-average filter [19], and Kalman filter [20]. The antinoise performance of the classification spectrum method and charge comparison method is discussed in Liu’s data [9]. Chen studied the time-domain discrimination method, which is more suitable for a seven-point-average running filter [11]. Based on the abovementioned previous studies, in this work, we compare the influence of different filtering methods on the performance of discrimination methods and determine an optimized filtering method for different discrimination methods.

The rest of our paper is organized as follows: The fundamental principles of the three discrimination methods and four filtering methods are introduced in Sect. 2. The valuation criteria and comparison of filtering effects are given in Sect. 3. The influence of the discrimination methods by using different filtering methods is discussed in Sect. 4. The conclusion of the work is presented in Sect. 5.

2 Principles of discrimination and filtering methods

2.1 Discrimination methods

2.1.1 Charge comparison

As a result of the inherent nature of n–\(\upgamma\) radiation, the ratio of charge of the slow component to the total charge in different pulse signals will be different for different decay speeds and afterglow effects. The total charge of the pulse signal and the charge of the slow component can be obtained by processing the pulse signals using a computer [21]. Then, the neutron and the \(\upgamma\) ray are discriminated by comparing the difference of (charge of the slow component)/(total charge) of different signals. The following is the formula for calculating the charge ratio R:

$$\begin{aligned} R = \frac{Q_{N}}{Q_{M}}, \end{aligned}$$
(1)

where \(Q_{N}\) and \({Q_{M}}\) are the charge of the slow component and the total charge of the pulse signal, respectively. Because of the slower attenuation speed of neutrons, the R value is larger than that of gamma rays.

2.1.2 Fractal spectrum

Fractal theory is based on the internal similarity between the same things, which means that, by selecting the appropriate dimension, their internal law can be clearly shown [22, 23]. The fractal spectrum method takes the spectrum as the fractal dimension and then discriminates the n–\(\upgamma\) pulse signal. After taking the logarithm of the power spectrum and frequency of n–\(\upgamma\) signals, an approximately linear relationship can be obtained. Through linear regression analysis, different regression coefficients can be obtained, by which n–\(\upgamma\) signals can be discriminated against. The pulse signal is converted into a frequency-domain signal by fast Fourier transform [24], whose formula is as follows:

$$\begin{aligned} F(k)=\sum \limits _{j=1}^N{f(j)w_N^{(j-1)(k-1)}}, \end{aligned}$$
(2)

where F is the data after the discrete Fourier transform, f is the original data, N is the calculation time of the Fourier transform, and

$$\begin{aligned} {w_N}=e^{(-2\pi i)/N}. \end{aligned}$$
(3)

The power spectrum is the mean square of the amplitude of the signal after the Fourier transform, which is defined as:

$$\begin{aligned} Pss={|F(k)|^2}/N. \end{aligned}$$
(4)

The power spectral density function can be obtained from formulas (2), (3), and (4), by which the logarithmic graph of spatial frequency power and spectral density (\(\log {Pss}\)–\(\log {w}\)) is drawn. It exhibits an approximately linear relationship. Subsequently, it was fitted by the following formula:

$$\begin{aligned} G(w)=G(w_0)\left( \frac{w}{w_0}\right) ^{-\alpha }, \end{aligned}$$
(5)

where G(w) is the power spectral density of the signal, w is the spatial frequency, \(w_0\) is the reference space frequency, and \(G(w_0)\) is the signal conversion coefficient (which is the signal power spectral density at \(w_0\)), and \(\alpha\) is the fitting coefficient. The fractal dimension is defined as follows:

$$\begin{aligned} D=2.5-\alpha . \end{aligned}$$
(6)

The n–\(\upgamma\) signals can then be discriminated according to the different fitting coefficients of neutrons and gamma rays.

2.1.3 Back-propagation neural network

A back-propagation neural network (BPNN) is a specific type of multilayer feed-forward network trained by an error back-propagation algorithm. It can learn and store a large number of input–output mapping relations and modify the weights of the network by back-propagation [25]. The model includes an input, a hidden layer, and an output layer. The learning process consists of two processes: forward propagation of the signal and backward propagation of the error. If the actual output of the output layer does not match the expected output (training signal), it enters an error back-propagation stage. The process of weight adjustment is the process of network learning and training, in which the hidden node output model is

$$\begin{aligned} {O_j}=f\left(\sum \limits {W_{ij}}\times {X_i}-{q_j}\right), \end{aligned}$$
(7)

and the output node output model is

$$\begin{aligned} {Y_k}=f\left(\sum \limits {T_{jk}}\times {O_j}-{q_k}\right), \end{aligned}$$
(8)

where \(X_i\) is the input, \(Y_k\) is the output, f is a nonlinear function, q is the threshold of the neural unit, and \(W_{ij}\) and \(T_{jk}\) are the weight matrices connecting \(X_i\) and \(O_j\) as well as \(O_j\) and \(Y_k\), respectively.

2.2 Filtering methods

2.2.1 Fourier transform

The Fourier transform transforms the time-domain signal into a frequency-domain signal. The low-amplitude frequency-domain information corresponding to the noise signal is removed, and then the frequency-domain signal is converted into the time-domain signal through the inverse Fourier transform to realize filtering. Because the pulse signal is discrete, a discrete Fourier transform (DFT) is used [26]. The positive transform formula for the DFT is as follows:

$$\begin{aligned} \begin{aligned} {F(u)}&=\sum \limits _{x=1}^N f(x) e^{-i \frac{2\pi }{N} xu} \\&=\sum \limits _{x=1}^N f(x) w_{N}^{xu} \quad (x=1,2,\dots ,N), \end{aligned} \end{aligned}$$
(9)

and the inverse transform formula for the DFT is as follows:

$$\begin{aligned} \begin{aligned} {f(x)}&={\frac{1}{N}}\sum \limits _{x=1}^N F(u) e^{i \frac{2\pi }{N} xu} \\&={\frac{1}{N}}\sum \limits _{x=1}^N F(u) w_{N}^{-xu} \quad (x=1,2,\dots ,N), \end{aligned} \end{aligned}$$
(10)

where \({w_N}=e^{{(-2\pi i)}/{N}}\) is the frequency, f(x) is the time-domain signal, F(u) is the frequency domain signal, and N is the length of the signal.

2.2.2 Wavelet transform

Wavelet analysis is the development and extension of Fourier analysis. The Fourier transform is the superposition of sine waves with different frequencies in the entire time domain, whereas the wavelet transform decomposes the signal into a series of attenuated wavelets [27], which can be used for scale transformation [28]. The Fourier transform of \(\psi (t) \in L^2 (R)\), defined as \(\psi (w)\). \(\psi (t)\) is called a basic wavelet when \(\psi (w)\) satisfies the admissible condition

$$\begin{aligned} {C_{\psi }}=\int _ R \mathrm {\frac{{|\psi (w)|^2}}{|w|} } \, \mathrm { d } w <\infty . \end{aligned}$$
(11)

After stretching and shifting, the following wavelet sequence is obtained:

$$\begin{aligned} {\psi _{a,b}(t)}=\frac{1}{\sqrt{|a|}}\psi \left( \frac{t-b}{a}\right) \quad a,b \in R,\;a\ne 0, \end{aligned}$$
(12)

where a is the stretching factor and b is the translation factor. The formulas for the wavelet transform and inverse wavelet transform are, respectively, as follows:

$$\begin{aligned} {W_{f}(a,b)}= & {} \langle f,\psi _{a,b}\rangle ={\sqrt{|a|}}\int _{-\infty }^{\infty }f(t)\psi \left( \frac{t-b}{a}\right) \mathrm {d}t, \end{aligned}$$
(13)
$$\begin{aligned} {f(t)}= & {} \frac{1}{C_{\psi }}\int _{R}\int _{R}\frac{1}{a^2}W_{f}(a,b)\psi \left( \frac{t-b}{a}\right) \mathrm {d}a\mathrm {d}b. \end{aligned}$$
(14)

2.2.3 Moving average

The moving-average smoothing filter is based on linear smoothing, which regards continuous sampling data as a queue with a fixed length of N. After a new measurement, the first datum of the queue is removed, the remaining \(N-1\) data are moved forward, and the new sampling data are inserted as the tail of the new queue. Finally, an arithmetic operation is performed on the queue to realize filtering [29, 30]. If the input signal is x and the data after the arithmetic operation are y, the calculation formula for the moving smoothing filter is as follows:

$$\begin{aligned} {Y(n)}=\frac{X(n)+X(n-1)+\cdots +X(n-N+1)}{N}. \end{aligned}$$
(15)

Taking \(N=5\) as an example gives

$$\begin{aligned} {Y(n)}=\frac{X(n)+X(n-1)+\cdots +X(n-4)}{5}. \end{aligned}$$
(16)

Equation (15) is the calculation formula for the moving-average smoothing filter. In this study, \(n = 5\) was selected to filter the pulse. This method is described as a moving-average filter.

2.2.4 Kalman filter

The Kalman filter uses the state-space model of signal and noise, updates the estimated value of the state variable by using the estimation value of the previous time and the observation value of the current time, and then it calculates the estimated value of the current time [31, 32]. Through the iterative operation, the filtering is completed. In principle, the operation of the Kalman filter includes two stages: prediction and update [33]. With regard to the mathematical expression of the Kalman filter [34], the evolution of the state sequence \(\{x_{k},k\in N\}\) of a target is denoted by

$$\begin{aligned} x_{k}=F_{k}{x_{k-1}}+v_{k-1}, \end{aligned}$$
(17)

where \(F_{k}\) is a known matrix, \(\{v_{k},k\in N\}\) is an independent and identically distributed (i.i.d.) process noise sequence, and N is the set of natural numbers. The objective of tracking is to recursively estimate \(x_{k}\) from the measurements

$$\begin{aligned} z_{k}=H_{k}x_{k}+n_{k}, \end{aligned}$$
(18)

where \(H_{k}\) is also a known matrix that defines the linear functions similar to \(F_{k}\) and \(\{n_{k},k\in N\}\) is an i.i.d. measurement noise sequence. Based on the aforementioned definitions, the recursive relationships of the Kalman filter algorithm are given as

$$\begin{aligned} {p(x_{k-1}|z_{1;k-1})}= & {} N(x_{k-1};{m_{k-1|k-1}},{P_{k-1|k-1}}), \end{aligned}$$
(19)
$$\begin{aligned} {p(x_{k}|z_{1;k-1})}= & {} N(x_{k};{m_{k|k-1}},{P_{k|k-1}}), \end{aligned}$$
(20)
$$\begin{aligned} {p(x_{k}|z_{1;k})}= & {} N(x_{k};{m_{k|k}},{P_{k|k}}), \end{aligned}$$
(21)

where

$$\begin{aligned} m_{k|k-1}= & {} F_{k}{m_{k-1|k-1}}, \end{aligned}$$
(22)
$$\begin{aligned} {P_{k|k-1}}= & {} Q_{k-1}+F_{k}{P_{k-1|k-1}}{F_{k}^{T}}, \end{aligned}$$
(23)
$$\begin{aligned} {m_{k|k}}= & {} m_{k|k-1}+K_{k}({z_{k}}-{H_{k}m_{k|k-1}}), \end{aligned}$$
(24)
$$\begin{aligned} {P_{k|k}}= & {} P_{k|k-1}-K_{k}{H_{k}P_{k|k-1}}, \end{aligned}$$
(25)

In these equations, N(x; m, p) is a Gaussian density with arguments x, mean m, and covariance P; p denotes the posterior probability density function; and \(Q_{k-1}\) and \(R_{k}\) represent the covariances of \(v_{k-1}\) and \(n_{k}\), respectively. The covariances of the innovation term \({z_{k}-{H_{k}}{m_{k|k-1}}}\) and the Kalman gain are, respectively, denoted as:

$$\begin{aligned} {S_{k}}= & {} H_{k}{P_{k|k-1}}{H_{k}^{T}}+R_{k}, \end{aligned}$$
(26)
$$\begin{aligned} {K_{k}}= & {} {P_{k|k-1}}{H_{k}^{T}}{S_{k}^{-1}}, \end{aligned}$$
(27)

where the transpose of a matrix M is defined by \(M^{T}\).

3 Valuation criteria and filtering effect

3.1 n–\(\upgamma\) pulse signals

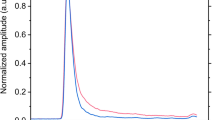
In our study, an \(^{241}\)Am–Be isotope neutron source, with an average energy of 4.5 MeV, was used as the radioactive source. A plastic scintillator (EJ299-33) and a digital oscilloscope with a 1 GS/s sampling rate and 200 MHz bandwidth were used to measure the n–\(\upgamma\) superposed field (with a trigger threshold set at 500 mV), in which 9414 pulse signals were obtained. The neutron pulse signals are compared with the gamma-ray pulse signals in Fig. 1. When the signals are normalized by their maximum amplitudes, it was observed that the luminous attenuation rate of the neutron pulse signals [35, 36] was significantly lower than that of the gamma pulse signals, where the two signals were normalized to their peak value.

Fig. 1
figure 1

Comparison of normalized n–\(\upgamma\) pulses

Full size image

3.2 Evaluation criteria for n–\(\upgamma\) discrimination effect

After discriminating the n–\(\upgamma\) pulse signals, two peaks were obtained. These could be fitted by a Gaussian function, as shown in Fig. 2. To evaluate the screening performance, the figure of merit (FOM) was introduced as the criterion [36]:

$$\begin{aligned} {FOM} = \frac{S}{\hbox {FWHM}_{n}+\hbox {FWHM}_{\gamma }}, \end{aligned}$$
(28)

where S is the distance between the two peaks and \(\hbox {FWHM}_{n}\) and \(\hbox {FWHM}_{\gamma }\) are the half-height widths of the neutron and gamma-ray peaks, respectively. For this evaluation criterion, the greater the FOM value, the better is the screening effect.

Fig. 2
figure 2

n–\(\upgamma\) screening effect evaluation criteria

Full size image

3.3 Filtering effect of the filtering methods

In this work, 9414 pulse data were measured in the experiment, and the subsequent algorithm analysis of the experimental data was performed using MATLAB software. Subsequently, the measured nuclear pulse signals were filtered using the four methods mentioned above. A comparison of the filtering results is presented in Fig. 3. Figure 3a–c show the performances of the Fourier transform filter (FTF), wavelet transform filter (WTF), moving-average filter (MAF), and Kalman filter (KF) compared to unfiltered original data (ORI). Figure 3a indicates that none of the four filtering methods caused pulse signal distortion on the whole. Figure 3c shows enlarged images of the pulse noise area, revealing that these four filtering methods reduced the noise in the pulse signals. The influence of the four filtering methods on the peak value is given in Table 1. From Table 1, it can be seen that the FTF based on the spectrum, WTF, and the MAF based on a linear, simple smoothing process will not cause peak distortion to pulse signal filtering, whereas the Kalman algorithm based on estimation causes a small amount of pulse peak distortion.

Fig. 3
figure 3

a Overall comparison of filtering effect. b Comparison of the influences to the peak changes by different filtering methods. c Comparison of the filtering effect of the falling edge by different filtering methods

Full size image
Table 1 Influence of the four filtering methods
Full size table

4 Influence of different filtering methods on the n–\(\upgamma\) discrimination algorithm

4.1 Charge comparison method

The rise time of the n–\(\upgamma\) pulse signals is \(\sim\)13 ns, and the attenuation time of the gamma pulse signals is \(140 \pm 10\) ns. The decay time of neutron pulse signals is \(170 \pm 15\) ns. The pulse signals between \(\sim\)15 ns before the peak and \(\sim\)200 ns after the peak were selected as the total component, and the pulse signals between T and 200 ns after the peak were selected as the slow component, where T, as mentioned previously, is the delay time. By changing the value of T, the optimal FOM values of the various charge comparison methods were obtained. MATLAB software was used to process the data offline. First, the original data were substituted into the charge comparison method for n–\(\upgamma\) discrimination. Then, the original data were filtered using the four filtering methods mentioned above, and the filtered data were replaced by the charge comparison method for n–\(\upgamma\) discrimination.

The discrimination of replacing a with b is shown in Fig. 4a, which show the results of the charge comparison method for the original data (ORI), FTF, WTF, MAF, and KF. Figure 4b shows the Gaussian fitting curves of the FOM distributions of neutrons and gamma rays, which are discriminated by using the four methods. The peaks on the left are gamma signals,and the peaks on the right are neutron signals. The FOM values of the n–\(\upgamma\) discrimination effect of the charge comparison method after filtering by using different filtering methods were fitted and calculated, and the screening times are given in Table 2.

Fig. 4
figure 4

a Comparison of the four screening methods with original data. b Gauss fitting FOM curves for the four screening methods

Full size image
Table 2 Discrimination time and FOM value of charge comparison method with different filtering methods
Full size table

Table 2 demonstrates that all four filtering methods have improved the discrimination process compared with the direct charge comparison method for the original data. Among them, the FTF and WTF exhibited greater improvement than did the other methods others, increasing discrimination by 6.79% and 5.49%, respectively. It took about \(\sim\)20 s for the unfiltered charge comparison method to distinguish 9414 pulse signals, and the time required for filtering by different filtering methods was slightly increased.

4.2 Fractal spectrum method

The results of many pulse signal discrimination intervals revealed that the FOM value of discrimination performance was better than the others when pulse signals between 38 ns after the peak and 130 ns after the peak were selected as the discrimination interval. Therefore, in this work, the pulse signals in this region were selected for n–\(\upgamma\) discrimination using different fractal spectrum methods. The filtered data were substituted into the fractal spectrum method for n–\(\upgamma\) discrimination. The results of the discrimination process are presented in Fig. 5a. Figure 5b shows the Gaussian fitting curves of the FOM distributions of neutrons and gamma rays screened by the corresponding methods. The FOM values of the fractal spectrum method for n–\(\upgamma\) screening after using different filtering methods were calculated and are given with the screening times in Table 3. Table 3 indicates that the MAF was only based on the simple, linear smoothing processing and that the discrimination between signals and noise was not significant; therefore, the fractal screening effect of the MAF is only 0.086% higher than that of the original pulse directly. The fractal discrimination effect after Kalman filtering increased by 3.04%, which means that the KF can effectively improve the effect of gamma-ray screening in the fractal spectrum method. After wavelet transform filtering, the effect of the fractal spectrum method was reduced, and after Fourier transform filtering, the filtering effect of the fractal spectrum method was improved by only 0.39%. This minor improvement was possibly because the wavelet transform and Fourier transform removed the useful frequency-domain information of the pulse signal noise, and the analysis dimension selected by the fractal spectrum method is the frequency domain. Consequently, it has little influence on the improvement of the discrimination effect. Moreover, this discrimination method is not suitable for real-time n–\(\upgamma\) discrimination because it takes \(\sim\)7 min.

Fig. 5
figure 5

a Comparison of the four screening methods with original data. b Gauss fitting FOM curves for the four screening methods

Full size image
Table 3 Discrimination time and FOM value for the fractal method with different filtering methods
Full size table

4.3 BPNN method

Before discriminating 9414 noisy pulse signals by using the BPNN, 7216 pulse signals with neutron and gamma characteristics were selected from 11,454 very-low-noise pulse signals. The falling edge of the signals was removed, which is attributed to the small difference between the neutron’s and gamma’s rising edges and the pulse signals to be discriminated containing more noise, which lowers the discrimination of the rising edge. Therefore, the falling edge and the corresponding charge ratio R were selected as the training set.

The FOM value of the n–\(\upgamma\) screening effect of the BPNN after using different filtering methods was calculated, and these, along with the screening times, are listed in Table 4 and shown in Fig. 6a, b. The filtering effect of the BPNN degrades after Kalman filtering. This is because signals with low noise that were smoothed by the Fourier transform were used as the training set, and the Kalman algorithm based on estimation has a poor smoothing effect on the signals, whereas the BPNN requires that the training set be highly similar to the prediction set. Consequently, it is not suitable for n–\(\upgamma\) screening in BPNNs. The other three filtering methods can improve the effect of n–\(\upgamma\) screening in the BPNN. The moving-average smoothing filter exhibited the most significant improvement on the n–\(\upgamma\) screening effect of the BPNN, and its FOM value reaches 1.5116, which is 8.48% higher than that of the original data.

Fig. 6
figure 6

a Comparison of the four screening methods with original data. b Gauss fitting FOM curves for the four screening methods

Full size image
Table 4 Discrimination time and FOM value of the BPNN with different filtering methods
Full size table

5 Conclusion

In this work, based on EJ299-33 plastic scintillation data, four filtering algorithms were used to filter the detected neutron and gamma signals. Three n–\(\upgamma\) screening methods were then applied to complete the filtering operation for the filtered pulse signals. By comparing the filtering performance with the final filtering effect, a better filtering method was found with each n–\(\upgamma\) screening algorithm. According to the calculation, in the charge comparison method, the Fourier transform filtering algorithm had the best adaptability, with an increase in 6.87%, the KF had the best adaptability effect of 3.04% in the fractal spectrum method, and the adaptability of the moving-average smoothing filter in BPNN screening exhibited an increase in 8.48%. Furthermore, the Kalman filtering algorithm has a significant influence on the peak value of the pulse, reaching 4.49%, and it has a certain impact on the energy resolution of the spectrum measurement after screening. In addition, the calculation time of the fractal spectrum method is the longest; this is not conducive to rapid realization of n–\(\upgamma\) discrimination, as it requires high performance of instrument calculations and is thus not suitable for real-time applications.