1 Introduction

Strange quark matter (SQM) is a new form of matter that contains deconfined up (u), down (d), and strange (s) quarks in \(\beta \)-equilibrium, with electric and color charge neutrality [1]. Since the early works of many authors [2–4], especially Witten’s conjecture that SQM might be absolutely stable [5], SQM has been an important topic in nuclear, astrophysics, and cosmology due to its far-reaching theoretical significance.

SQM may be produced in energetic heavy-ion collisions, or exist in cosmic rays and/or in the inner part of neutron stars. A neutron star could be converted to a quark star or hybrid star due to leptonic weak interactions, or seeded with slets by the self-annihilating weakly interacting massive particles [6]. Although many meaningful works have been done in the past decades, there are still many aspects left open [7]. For example, the stability and equation of state has not yet been definitively fixed and are still under active investigation [8].

A magnetic field has strong effects on the stability and properties of SQM [9, 10]. It is generally known that there exists a strong magnetic field in many compact objects. For example, the typical strength on the surface of a pulsar could be in the order of \({\sim }10^{12}\)  G [11]. The magnetic field in a magnetar could be as high as \(10^{13}\)–\(10^{15}\)  G or even higher [12, 13]. The origin of such strong magnetic fields is presently not well understood. A widely accepted theory is the magneto hydrodynamic dynamo mechanism, where a large magnetic field is generated by the rotating plasma of a protoneutron star [13]. Another model demonstrates magnetic flux conservation: the relatively small magnetic fields were amplified during the star collapse [14, 15].

In principle, the fundamental theory of strong interaction, i.e. quantum chromodynamics (QCD), can solve all problems in investigating SQM. Due to the non-perturbative difficulty at relatively lower densities, however, the motion equations are unable to be solved exactly from the first principle theory. Therefore, people usually resort to various models, e.g., the thermodynamically enhanced pQCD model [1, 16], conventional perturbation models [17–19], the Richard potential model [20, 21], the Nambu and Jona-Lasinio model [22], the field correlator method [23], the quark-cluster model [24, 25], the model with magnetic-field dependent coupling [26], the unification way to describe both slets and strange stars [27, 28], and many other models [29–41].

In order to include interactions between quarks, it is useful to adopt medium-dependent quark masses. There are two kinds of such masses. One is the chemical-potential and/or temperature dependent, which is normally called the quasiparticle model [42–53], the other is the density and/or temperature dependent [54–58]. In both cases, there are a lot of discussions on consistent thermodynamic treatments. It can be generally shown that the pressure at the minimum energy per baryon should be exactly zero [8, 59]. With this standard, many phenomenological models have to be ruled out.

In the case of chemical-potential dependent masses, one can have thermodynamic consistency by adding an additional term to the thermodynamic density [43]. In the density-dependent case, it is now clear that the original chemical potentials should be replaced with effective ones when the quark masses become density dependent [59]. These kind of models were previously called the density-dependent quark mass models. But its thermodynamic treatment is inconsistent. The most recent version is called the equivparticle model [8]. It is fully thermodynamically self-consistent due to the introduction of effective chemical potentials. The concept of an effective chemical potential is also shown to be useful in the extended bag model with a density-dependent bag constant [41].

Another important issue in the equivparticle model is the quark mass scaling, i.e. how to parameterize the density dependence of the quark masses. In the early stage, people mainly emphasize quark confinement, and the interaction part in the quark mass is parameterized to be inversely proportional to the baryon number density [54] for light quarks, and later extended to strange quarks [55]. According to the in-medium chiral condensate, it was shown that the interaction quark mass should be inversely proportional to the cubic root of the density [37]. This cubic root scaling was extended to a finite temperature [38]. It has also been extensively applied to the investigations of SQM-related physics, e.g. the QCD phase diagram [59], properties of SQM and slets [60] at zero and finite temperatures [38, 61], the damping time scale due to the coupling of the viscosity and r mode [62], and the quark–diquark equation of state and compact star structure [63] etc.

It is true that confinement interactions dominate at lower densities. With increasing densities, however, the perturbative interaction sets in, and becomes more and more important, and thus should be included. Recently, a new quark-mass scaling considering both the confinement and perturbative interactions was derived, and applied to the investigation of SQM and strange stars [8]. But the effect of a strong magnetic field was not considered there.

The purpose of the present paper is to study the properties of SQM in a strong magnetic field with the newly developed equivparticle model, which considers both the confinement and perturbative interactions. In the Sect. 2, we describe the thermodynamic formulas with emphasis on the thermodynamic consistency, while in Sect. 3, we study properties of magnetized SQM and present the results and discussions. Then, in Sect. 4, we study the mass–radius relation of magnetized strange stars. Section 5 is a short summary.

2 Themodynamic formulae

Let’s start with the energy of a relativistically moving free particle, i, with mass, \(m_i\), i.e.

$$\begin{aligned} \varepsilon _i=\sqrt{p_z^2+p_{\bot }^2+m_i^2}, \end{aligned}$$
(1)

where \(m_i\) is the particle mass, and \(p_z\) is the momentum along the z direction while \(p_{\bot }\) is the momentum component in the x–y plane or perpendicular to the z axis: \(p_{\bot }^2=p_x^2+p_y^2\). The corresponding thermodynamic potential density is

$$\begin{aligned} \Omega _{\mathrm {f}} = -\sum _i\frac{2g_i}{(2\pi )^3} \int \!\!\!\int \!\!\!\int \left( \mu _i-\varepsilon _i \right) \text{d}p_x\text{d}p_y\text{d}p_z, \end{aligned}$$
(2)

where \(g_i\) is the degeneracy factor with \(g_{\text {u}}=g_{\text {d}}=g_{\text {s}}=3\) and \(g_{\text {e}}=1\), while the extra factor 2 takes care of the spin degeneracy.

If a constant magnetic field with strength \(B_{\mathrm {m}}\) is present along the z direction, classically the movement of a fermion with a charge \(q_i\) (\(q_{\text {u}}=2/3, q_{\text {d}}=q_{\text {s}}=-1/3\), and \({q_{\text {e}}}=-1\)) is a regular helix whose axis is along the z axis and the projection on the x–y plane is a circle. Although the \(p_z\) can be still taken as a continuous variable, the component \(p_{\bot }\) perpendicular to the z direction should be quantized according to the Sommerfield’s rule:

$$\begin{aligned} p_{\bot }^2=2\nu |q_i|B_{\mathrm {m}}, \end{aligned}$$
(3)

where the integer quantum number, \(\nu \), is

$$\begin{aligned} \nu \equiv l+1/2-\text{sgn}(q_i)S, \end{aligned}$$
(4)

with l being the principle quantum number, \(S=1/2\) for spin-up particles, and \(S=-1/2\) for spin-down particles. The sign function sgn equals to 1 with a positive argument and to \(-1\) with a negative argument. So the energy level of the particle becomes

$$\begin{aligned} \varepsilon _{i,\nu }(p_z) =\sqrt{p_z^2+m_i^2+2\nu |q_i|B_{\mathrm {m}}} \equiv \sqrt{p_z^2+M_{i,\nu }^2}, \end{aligned}$$
(5)

where

$$\begin{aligned} M_{i,\nu }\equiv \sqrt{m_i^2+2\nu |q_i|B_{\mathrm {m}}}. \end{aligned}$$
(6)

For a given \(\nu \), one has two sets of (l, S) pair satisfying Eq. (4):

$$\begin{aligned} l= & {} \nu , S=\text{sign}(q_i)/2 \end{aligned}$$
(7)
$$\begin{aligned} l= & {} \nu -1, S=-\text{sign}(q_i)/2. \end{aligned}$$
(8)

But for \(\nu =0\), one has only the first pair. Therefore, the lowest energy level is singly degenerate, while others are all doubly degenerate.

Equation (3) means \(p_{\bot }\text{d}p_{\bot }=|q_i|B_{\mathrm {m}}\text{d}\nu \). Accordingly, we have \( \int \!\!\!\int \text{d}p_x\text{d}p_y =\int \!\!\!\int p_\bot \text{d}p_{\bot }\text{d}\theta =2\pi |q_i|B_{\mathrm {m}} \int \text{d}\nu , \) where \(\theta \) is the direction angle of \(\vec{p}_\bot \). For the quantized case, the following substitution rule is thus obvious:

$$\begin{aligned} \int \!\!\!\int \text{d}p_x\text{d}p_y =2\pi |q_i|B_{\mathrm {m}} \sum _\nu . \end{aligned}$$
(9)

Now applying this substitution to Eq. (2), and simultaneously replacing the degeneracy fact 2 for a spin with \(2-\delta _{\nu ,0}\), we immediately get the thermodynamic potential density for a system of free Fermions in a strong magnetic field:

$$\begin{aligned} \Omega _{\mathrm {M}}= & {} -\sum _i\frac{g_i|q_i|B_{\mathrm {m}}}{4\pi ^2} \sum _{\nu } (2-\delta _{\nu ,0}) \int ( \mu _i-\varepsilon _{i,\nu }) \text{d}p_z \nonumber \\\equiv & {} -\sum _i\sum _{\nu } \frac{f_{i,\nu }}{2} \int \left( \mu _i-\sqrt{p_z^2+M_{i,\nu }^2}\right) \text{d}p_z, \end{aligned}$$
(10)

where we have used \(f_{i,\nu }\equiv g_i|q_i|B_{\mathrm {m}}(2-\delta _{\nu ,0})/(2\pi ^2)\) to simplify notations.

For the system to be determined with a given set of chemical potentials, we need to determine the limits of the integration on \(p_z\) at a given \(\nu \). The normal way is to give the up limit of the respective single particle energy, i.e. the Fermi energy \(\epsilon _i\),

$$\begin{aligned} \sqrt{p_z^2+M_{i,\nu }^2}\le \epsilon _i. \end{aligned}$$
(11)

In this case, \(p_z\) is in the range \(|p_z|\le \sqrt{\epsilon _i^2-M_{i,\nu }^2}\). Therefore \(\Omega _{\mathrm {M}}\) becomes

$$\begin{aligned} \Omega _{\mathrm {M}} =-\sum _i \sum _{\nu =0}^{\nu _\mathrm {max}} f_{i,\nu } \int _{0}^{\sqrt{\epsilon _i^2-M_{i,\nu }^2}} \Big [\mu _i- \varepsilon _{i,\nu }(p_z)\Big ] \text{d}p_z. \end{aligned}$$
(12)

The Fermi energy should be linked to the chemical potential by minimizing the thermodynamic potential density with \({\partial \Omega _\mathrm {f}}/{\partial \epsilon _i}=0\) which requires

$$\begin{aligned} \sum _{\nu =0}^{\nu _\mathrm {max}} f_{i,\nu } \ (\mu _i-\epsilon _i) \ \frac{\epsilon _i}{\sqrt{\epsilon _i^2-M_{i,\nu }^2}} =0. \end{aligned}$$
(13)

This equation immediately gives \(\epsilon _i=\mu _i\), or the Fermi momentum is \(p_i=\sqrt{\mu _i^2-m_i^2}\). Then the \(\epsilon _i\) in Eq. (12) should be replaced by \(\mu _i\).

In the above derivation, we have, in fact, implicitly assumed that the quark mass, \(m_i\), is a constant. Now to consider medium effects, we let the quark masses be density dependent, i.e.

$$\begin{aligned} m_i=m_i(n_{\mathrm {b}}). \end{aligned}$$
(14)

We know from a recent study [8] that the original chemical potentials in this case should be replaced by the corresponding effective ones, i.e. \(\mu _i\rightarrow \mu _i^*\). By this substitution process, we immediately have

$$\begin{aligned} \Omega _0 =-\sum _i \sum _{\nu =0}^{\nu _\mathrm {max}} f_{i,\nu } \int _0^{\sqrt{{\mu _i^*}^2-M_{i,\nu }^2}} \Big [\mu _i^*- \varepsilon _{i,\nu }(p_z)\Big ] \text{d}p_z. \end{aligned}$$
(15)

The maximum \(\nu \) value is limited to make all \(\sqrt{{{\mu _i^*}^2}-M_{i,\nu }^2}\) meaningful. For this we should take

$$\begin{aligned} \nu _\mathrm {max} =\text{ int }\left( \frac{{\mu _i^*}^2-m_i^2}{2|q_i|B_{\mathrm {m}}} \right) , \end{aligned}$$
(16)

where the ‘int’ means taking the integer part.

Explicitly carrying out the integration gives

$$\begin{aligned} \Omega _0= & {} -\sum _i \sum _{\nu =0}^{\nu _\mathrm {max}} \frac{f_{i,\nu }}{2} \Bigg [ \left| \mu _i^*\right| \sqrt{{\mu _i^*}^2-M_{i,\nu }^2} \nonumber \\&\left. -M_{i,\nu }^2 \ln \frac{\left| \mu _i^*\right| +\sqrt{{\mu _i^*}^2-M_{i,\nu }^2}}{M_{i,\nu }} \right] . \end{aligned}$$
(17)

Then the particle number densities are obtained from \(n_i=-\partial \Omega _0/\partial \mu _i^*\), giving

$$\begin{aligned} n_i =\frac{g_i|q_i|B_{\mathrm {m}}}{2\pi ^2} \sum _\nu ^{\nu _\mathrm {max}} (2-\delta _{i,0})\sqrt{{\mu _i^*}^2-M_{i,\nu }^2}. \end{aligned}$$
(18)

The real chemical potential, \(\mu _i\), is connected to the effective one, \(\mu _i^*\), by

$$\begin{aligned} \mu _i =\mu _i^* + \sum _j \frac{\partial \Omega _0}{\partial m_j} \frac{\partial m_j}{\partial n_i} \equiv \mu _i^*-\mu _{\mathrm {I}}, \end{aligned}$$
(19)

where the second term is due to the density dependence of quark masses. Because \(n_{\mathrm {b}}=(n_{\text {u}}+n_{\text {d}}+n_{\text {s}})/3\), it is easy to get

$$\begin{aligned} \mu _{\mathrm {I}} =\mu _i^*-\mu _i =-\frac{1}{3} \frac{\mathrm {d}m_{\mathrm {I}}}{\mathrm {d}n_{\mathrm {b}}} \sum _j\frac{\partial \Omega _0}{\partial m_j}, \end{aligned}$$
(20)

where the summed derivative with respect to the quark masses is

$$\begin{aligned} \sum _j\frac{\partial \Omega _0}{\partial m_j} =\sum _i\sum _{\nu =0}^{\nu _\mathrm {max}} m_i\, f_{i,\nu }\, \text{ arccosh }\left( \frac{\mu _i^*}{M_{i,\nu }}\right) . \end{aligned}$$
(21)

Therefore, the interaction chemical potential is the same for all three flavor quarks. This is understandable due to the fact that the strong interaction is a color interaction.

The energy density is obtained by \(E=\Omega _0+\sum _i\mu _i^*n_i\):

$$\begin{aligned} E= & {} \sum _i \sum _{\nu =0} \frac{f_{i,\nu }}{2} \int _0^{\sqrt{{\mu _i^*}^2-M_{i,\nu }^2}}\sqrt{p_z^2+M_{i,\nu }^2}\, \text{d}p_z. \end{aligned}$$
(22)

After completing the integration, we can get

$$\begin{aligned} E= & {} \sum _i\frac{g_ie_iB_{\mathrm {m}}}{4\pi ^2} \sum _{\nu =0}^{\nu _\mathrm {max}}(2-\delta _{\nu ,0}) \Bigg [\mu _i^*\sqrt{{\mu _i^*}^2-M_{i,\nu }^2} \nonumber \\&\phantom { \sum _i } +M_{i,\nu }^2 \ln \frac{\mu _i^*+\sqrt{{\mu _i^*}^2-M_{i,\nu }^2}}{M_{i,\nu }} \Bigg ]. \end{aligned}$$
(23)

In principle, the longitudinal pressure and transverse pressure become different due to the magnetic field. But this difference only becomes obvious at an extremely high value of the magnetic field strength. Here we give the thermodynamically self-consistent pressure in the framework of the equivparticle model

$$\begin{aligned} P= & {} -\Omega _0 +\sum _{i,j} n_i \frac{\partial \Omega _0}{\partial m_j} \frac{\partial m_j}{\partial n_i} \nonumber \\= & {} -\Omega _0 +n_{\mathrm {b}}\frac{\mathrm {d}m_{\mathrm {I}}}{\mathrm {d}n_{\mathrm {b}}} \sum _j\frac{\partial \Omega _0}{\partial m_j}. \end{aligned}$$
(24)

Comparing Eq. (24) with the constant-mass case where \(P=-\Omega _0\), we find an additional term with the density derivative. It is because of this term that we can guarantee thermodynamic consistency.

3 The properties of MSQM

In the equivparticle model or the previous quark-mass–density-dependent model, the quark mass can be divided into two parts, i.e.

$$\begin{aligned} m_i=m_{0,i}+m_{\mathrm {I}}, \end{aligned}$$
(25)

where \(m_{0,i}\) is the current mass, and the interacting part, \(m_{\mathrm {I}}\), reflects the medium effects. The quark mass plays a key role in describing quark confinement. Originally, \(m_{\mathrm {I}}\) was parameterized as inversely proportional to the density [54]. Later, it was suggested to be inversely proportional to the cubic root of the density based on in-medium chiral condensates [37]. There are two forms of parameterizations related to the confinement interaction that dominates at lower densities. As is well known, perturbative interactions become more and more important with increasing density. To consider the perturbative effect, a new parametrization was recently formulated in Ref. [8] as

$$\begin{aligned} m_{\mathrm {I}}=\frac{D}{n_{\mathrm {b}}^{1/3}} +Cn_{\mathrm {b}}^{1/3}. \end{aligned}$$
(26)

The new parametrization considers both confinement and perturbative interactions. But it does not show explicit asymptotic freedom. One can easily find that, with increasing density, there exist a special density value \((D/C)^{3/2}\): when the density, \(n_{\mathrm {b}}\), is lower than this value, the interaction mass, \(m_{\mathrm {I}}\), as a whole decreases while it begins to increase unlimitedly when the density exceeds this special value. Therefore, the constant, C, in the second term of Eq. (26) should be a decaying function of the density. In fact, as has already been shown in Ref. [8], the quantity C is proportional to the square root of the QCD running coupling at the first-order level in perturbative QCD. However, the higher-order effects on the C variation is presently not available.

To eliminate the catastrophic increase at an extremely high density, we phenomenologically replace the constant, C, in Eq. (26) with a decaying function of the Woods–Saxon type [64]. This way, the quark mass formula becomes

$$\begin{aligned} m_{\mathrm {I}} = \frac{D}{n_{\mathrm {b}}^{1/3}} +C\left[ 1+\exp \left( \frac{n_{\mathrm {b}}-w}{n_\mathrm {a}}\right) \right] ^{-1}n_{\mathrm {b}}^{1/3}, \end{aligned}$$
(27)

where we have two new parameters: the asymptotic size, w, and diffuseness parameter, \(n_\mathrm {a}\). They are obviously not available from QCD presently, and have to be determined phenomenologically. In the present calculations, we take \(w=4\) fm\(^{-3}\) and \(n_\mathrm {a}=0.6\) fm\(^{-3}\).

Fig. 1
figure 1

Particle distributions in magnetized SQM. The quark fractions are plotted on the left axis. The electron number to the total quark number is very small, and is thus given on the right axis

Full size image
Fig. 2
figure 2

The chemical potentials of u and d quarks and the corresponding effective ones as functions of the density. The chemical potential for s quarks equal to that of d quarks, while the chemical potential of electron is the difference between u and u quarks

Full size image

Because of the weak interactions, the chemical potentials, \(\mu _i\) (\(i=\) u, d, s, e), satisfy the weak equilibrium conditions (neutrinos can hardly interplay with other particles, so they can enter and leave the system freely)

$$\begin{aligned} \mu _{\text {u}}+\mu _{\text {e}} =\mu _{\text {d}} = \mu _{\text {s}}. \end{aligned}$$
(28)

Because the difference between the real and effective chemical potentials is the same for all quark favors, the effective chemical potentials \(\mu _i^*\) (\(i=\) u, d, s) satisfy similar equalities as in Eq. (28):

$$\begin{aligned} \mu _{\text {u}}^*+\mu _{\text {e}}=\mu _{\text {d}}^*=\mu _{\text {s}}^*. \end{aligned}$$
(29)

Because electrons do not participate in weak interactions, the corresponding real chemical potential is equal to the effective one. It is, therefore, not necessary to distinguish them for electrons.

To be in accordance with conventional nuclear physics, the baryon number density of a SQM system is defined to be

$$\begin{aligned} n_{\mathrm {b}}=\frac{1}{3}\left( n_{\text {u}}+n_{\text {d}}+n_{\text {s}}\right) . \end{aligned}$$
(30)

At the same time, according to the charge of each flavor of quarks, the total electric charge density is

$$\begin{aligned} Q=\frac{2}{3}n_{\text {u}}-\frac{1}{3}n_{\text {d}}-\frac{1}{3}n_{\text {s}}-n_\text {e}. \end{aligned}$$
(31)

The charge neutrality condition requires \(Q=0\).

At a given density, \(n_{\mathrm {b}}\), we can numerically solve the equations in Eqs. (29)–(31) with the help of Eq. (18) for the four effective chemical potentials, \(\mu _i^*\) (\(i=\) u, d, s, e). Then, all other thermodynamic quantities can be calculated according to the formulas presented in the preceding section.

In Fig. 1, we show the particle distribution, \(n_i/(3n_{\mathrm {b}})\), the respective particle number density in unit of the total particle number density, as a function of the baryon number density for the parameters \(C=0.6\) and \(D^{1/2}={133}\,\mathrm{MeV}\). Because the electron content is much smaller than the quark’s, it is therefore separately plotted on the right axis. At extremely high density, the electron density tends to zero. Accordingly, all three quark fractions, \(n_i\), (\(i=\) u, d, s), approach to one third of the total baryon number density. With decreasing density, however, the difference between the quark fractions becomes gradually obvious: the d quark fraction increases, the s quark fraction decreases, while the u quark fraction is nearly constant.

The corresponding quark chemical potentials and their effective ones, \(\mu _i\) and \(\mu _i^*\) (\(i =\) u, d, s), are given in Fig. 2.

Fig. 3
figure 3

The energy per baryon as functions of the density for different parameters. The perturbative strength, parameter C and confinement parameter D 1/2 are indicated in the legend, while other parameters are fixed to be \(m_{0,u}=5\) MeV, \(m_{0,d}=10\) MeV, \(m_{0,s}=80\) MeV, \(w=4\) fm\(^{-3}\), \(n_\mathrm {a}=0.6\) fm\(^{-3}\), B m = 2 × 1018 G

Full size image

In Fig. 3, the energy per baryon of the MSQM system is plotted with different values of the parameters C and D, as indicated in the legend, for the fixed magnetic field strength \(B_{\mathrm {m}}=2\times 10^{18}\) G. On each curve, there is a minimum where the pressure calculated by Eq. (24) is exactly zero, showing the requirement of thermodynamic consistency. The position of the minimum is influenced by the parameters chosen. Generally speaking, the minimum energy per baryon will decease with increasing values of C because, in the stable regime, when there is a larger value for C, the corresponding D value can be smaller.

Fig. 4
figure 4

The minimum energy per baryon varies with the magnetic field strength

Full size image
Fig. 5
figure 5

The energy density of the magnetic field to that of the magnetized SQM at the minimum energy per baryon. The ratio \(B_{\mathrm {m}}^2/(2E_\mathrm {min})\) is obviously smaller than 0.1 if the field strength is less than \(2\times 10^{18}\) Gauss

Full size image

The minimum energy per baryon is strongly influenced by the external strong magnetic field strength. If there is no magnetic field, i.e. \(B_{\mathrm {m}}\) = 0, one will find that the lowest energy becomes higher. With increasing magnetic field strength, the minimum energy per baryon decreases. For the parameters where SQM is stable, the MSQM becomes more stable. To explicitly show the effects of the external magnetic field to the minimum energy, we give, in Fig. 4, the variation of the minimum energy per baryon with the external magnetic field strength for the three sets of parameters in Fig. 3 with \(D^{1/2}\) to be, respectively, 140, 133 and 129 MeV.

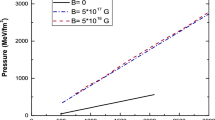
It should be pointed out that the pure magnetic field contribution is not included in the present calculations. This contribution should, in principle, be accounted for in a consistent study. In fact, many interesting investigations have considered both the matter and field contributions [32, 41, 65]. Because the origin of the strong magnetic fields in compact stars is still under discussion, the present paper is mainly interested in the effects on the mass–radius relation of MSQM stars when the asymptotic freedom is respected in the new quark mass scaling with perturbative interactions. To have an impression on the validity range of the present calculation, we use the relative importance ratio of the energy contribution from the pure magnetic field to that of the magnetized SQM, i.e., \(B_{\mathrm {m}}^2/(2E)\). In Fig. 5, we give the maximum value of this ratio, i.e., \(B_{\mathrm {m}}^2/(2E_\mathrm {min})\), where \(E_\mathrm {min}\) is the energy density corresponding to the minimum-energy state (the solids dots in Fig. 3) for each set of parameters. It is obvious that the ratio increases by increasing the magnetic field strength. At the present range of interest for \(B_{\mathrm {m}} < 2\times 10^{18}\) Gauss, however, the importance ratio is smaller than the ten percent at the minimum energy per baryon where the relative importance of the magnetic field contribution reaches its maximum. With increasing density, such as in a compact star, this ratio becomes much smaller. Therefore, the present calculations should be valid when the magnetic field strength does not obviously exceed the order of \(10^{18}\) Gauss.

4 Mass–radius relation of magnetized strange quark star

Neutron stars are interesting astronomical compact objects consisting of neutrons. Because the inner density is high, while SQM is possible if absolutely stable, it has long been speculated that there exist objects consisting completely of quarks, the so-called strange stars. In fact, many pulsars might be candidates for strange stars [27]. The structure of strange stars plays an important role in astrophysics, cosmology, and relevant nuclear physics.

Fig. 6
figure 6

The mass–radius relation of magnetized strange stars for the equations of state obtained in the last section (Fig. 3). The full dot on each cures is the maximum mass for that set of parameters

Full size image

As has been done in many investigations, we need to solve the Tolman–Oppenheimer–Volkov equation

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}r}=-\frac{GmE}{r^2}\frac{(1+P/E)\left( 1+4\pi ^2r^3P/m\right) }{1-2Gm/r}, \end{aligned}$$
(32)

with the subsidiary condition

$$\begin{aligned} m=\int ^r_0 4\pi E(r) r^2 \text{d}r. \end{aligned}$$
(33)

We now apply the equations of state obtained in this paper to solve for the mass–radius relation of magnetized strange stars. For a concrete description of the solving process, one may refer to Ref. [66].

In Fig. 6, we plot the mass–radius relation of magnetized strange stars for different sets of parameters. On each curve, there is a maximum mass indicated by a full dot. This dot separates the full cure into two parts. The quark stars on the right are mechanically stable, while those on the left are not mechanically stable, and thus surely do not exist.

The maximum star mass depends on the model parameters. For the parameter set with \(C=0.6\) and \(D^{1/2}=133\) MeV, the maximum star mass is close to 2 times the solar mass, while for the parameters with \(C=0.7\) and \(D^{1/2}=129\) MeV, the maximum mass can be even bigger [67, 68]. Only for the parameters \(C=0.4\) and \(D^{1/2}=156\) MeV, when MSQM is not absolutely stable, does the maximum mass become smaller.

5 Summary

We have investigated the properties of SQM in an external strong magnetic field with a new mass scaling. The new mass scaling not only considers both confinement and perturbative interactions, but also shows explicit asymptotic freedom.

The thermodynamic treatment follows the general formulas of the equivparticle model by the inclusion of effective chemical potentials. In this treatment, all the fundamental thermodynamic relations are still valid and is, thus, fully self-consistent.

With these new mass formulas and thermodynamic treatments, we studied the equation of state of magnetized quark matter and the structure of magnetized quark stars. It is found that a strong magnetic field can lower the minimum energy per baryon of MSQM. For parameters where SQM is not stable, MSQM can become absolutely stable. Because of perturbative interactions, the equations of state of MSQM becomes harder, which make the maximum star mass as large as more than two times the solar mass.