1 Introduction

Generalized structured component analysis (GSCA) and partial least squares path modeling (PLSPM) are two full-fledged approaches to component-based structural equation modeling (SEM) (Hwang and Takane 2014; Tenenhaus 2008). In component-based SEM, latent variables are conceptualized as components or weighted composites of indicators. These components are constructed to maximize the explained variances of either their indicators or endogenous components, as in principal component or canonical correlation analysis, or both. This is a key difference from factor-based SEM (i.e. covariance structural analysis (CSA) proposed by Jöreskog 1970, 1978), where latent variables are defined as factors to best explain the covariances of their indicators. Accordingly, component-based SEM are also called variance-based SEM, whereas factor-based SEM are called covariance-based SEM at times (Reinartz et al. 2009; Roldán and Sánchez-Franco 2012).

Although both GSCA and PLSPM fall within variance-based SEM, they involve different model specifications and estimation procedures. GSCA specifies three sub-models—weighted relation, structural, and measurement models—and derives a single optimization function unifying the sub-models. It allows for constructing two different modeling approaches, (i.e., GSCA with reflective indicators and GSCA with formative indicators) within one general modeling framework. On the other hand, PLSPM does not utilize a single objective function: each of the possible two modeling approaches (i.e., PLSPM with mode A and mode B) just modifies the specification of measurement model at a time.Footnote 1 Accordingly, unlike GSCA that uses a full information method with a global optimization function, PLSPM employs a limited information estimation method (Tenenhaus 2008). Despite such differences in model specification and estimation procedure, conceptually, PLSPM with mode A is compatible with GSCA with reflective indicators, in which the weight parameters are estimated to maximize the explained variances of indicators, as in principal component analysis (Hwang et al. 2015; Reinartz et al. 2009), as well as those of endogenous components. PLSPM with mode B is regarded as a counterpart of GSCA with formative indicators, explaining the variances of endogenous components only as much as possible, like canonical correlation analysis (Dijkstra 2017; Hwang et al. 2015).

In the literature, several simulation studies have assessed relative performances of GSCA and PLSPM under various simulation conditions. In Hwang et al. (2010), a simulation study was conducted to investigate the performance of GSCA with reflective indicators and PLSPM with mode A, varying sample sizes, data distributions, and model specifications. They found that the performance between the two approaches was similar when a model was specified without any cross-loadings. In other conditions where cross-loadings were specified, on average, GSCA with reflective indicators outperformed PLSPM with mode A (also see Hwang and Takane 2014, Chapter 2). However, the data used for this simulation study were generated under the assumption of covariance-based structural equation models, rendering it difficult to evaluate the comparative performance of variance-based SEM approaches (Hwang et al. 2010; Reinartz et al. 2009). Hence, it becomes necessary to develop a new data generating process (DGP) appropriate for variance-based SEM approaches.

Recently, a team of PLSPM researchers suggested a DGP for variance-based SEM (Becker et al. 2013; Dijkstra 2017) and evaluated the relative performance of GSCA with formative indicators, PLSPM with mode B, and sum-scores regression (i.e. a component’s scores are calculated by simply summing scores of its indicators) in terms of parameter recovery and statistical power (Hair et al. 2017). In Hair et al. (2017)’s study, GSCA with formative indicators and PLSPM with mode B turned out to produce consistent estimators under their DGP and performed better than the sum-scores regression. Between the two variance-based SEM approaches, GSCA with formative indicators provided more accurate estimates for the weight parameters than PLSPM with mode B, whereas they performed similarly in estimating path coefficients except for small sample sizes (N = 100). For small sample sizes, PLSPM with mode B was slightly better than GSCA with formative indicators, and the power of PLSPM with mode B was larger than that of GSCA with formative indicators.

Hair et al. (2017) made a meaningful contribution to variance-based SEM in that they initially evaluated the comparative performance of GSCA and PLSPM under structural equation models with components. Nevertheless, their study had limitations in (1) the range of the modeling approaches of GSCA and PLSPM considered and (2) the DGP they used for their simulation. First, Hair et al. (2017), compared GSCA with formative indicators and PLSPM with mode B only, although both GSCA and PLSPM could take other modeling approaches, as discussed earlier. Second, as will be explicated in Sect. 3, the components under their DGP were constructed with a set of arbitrarily chosen values for the weight parameters, rather than deriving the weight parameter values while considering the covariances of their indicators. Accordingly, these components may not capture the variances of both indicators and endogenous components well, and thus their DGP is hard to serve as a standard for evaluating all the variance-based SEM approaches. It is, therefore, required to develop a new DGP suited for variance-based SEM and to further assess the relative performance of all possible modeling approaches for both GSCA and PLSPM.

In this paper, we propose a new DGP for variance-based structural equation models with components that maximize the explained variances of their indicators and endogenous components. Under these structural equation models, all of the representatives for variance-based SEM—GSCA with reflective indicators, GSCA with formative indicators, PLSPM with mode A, and PLSPM with mode B—are evaluated using a Monte Carlo simulation.

The remainder of this article is organized as follows: In Sect. 2, we briefly review GSCA and PLSPM with respect to model specification and estimation process. In Sect. 3, a new data generating process for variance-based structural equation models is proposed. Its characteristics relative to that of the previous DGP are also discussed in detail. In Sect. 4, we report the design and results of our simulation. In the final section, the simulation results are summarized and their implications are discussed.

2 Overview of GSCA and PLSPM

GSCA and PLSPM have distinct model specifications. GSCA specifies three sub-models—weighted relation, structural, and measurement models. Let \({\mathbf{z}} = \left[ {\text{z}_{j} } \right] \in {\mathbf{\mathbb{R}}}^{J \times 1}\) denote the vector of observed variables or indicators where zj is the jth indicator and J is the number of indicators. Let \({\varvec{\upgamma}} = \left[ {\upgamma_{p} } \right] \in {\mathbf{\mathbb{R}}}^{P \times 1}\) denote the vector of latent variable or component, where γp is the pth component and P is the number of components. Both indicators and components are assumed to be standardized (i.e. Var(zj) = Var(γp) = 1). Let \({\mathbf{W}} = \left[ {\text{w}_{j,p} } \right] \in {\mathbf{\mathbb{R}}}^{J \times P}\) denote the component weight matrix, where wj,p is the weight assigned to the jth indicator to construct the pth component. Let \({\mathbf{C}} = \left[ {\text{c}_{p,j} } \right] \in {\mathbf{\mathbb{R}}}^{P \times J}\) denote the loading matrix where cp,j relates the pth component to the jth indicator. Let \({\mathbf{B}} = \left[ {\text{b}_{p*,p} } \right] \in {\mathbf{\mathbb{R}}}^{P \times P}\) denote the path coefficient matrix where bp*,p denotes the effect of the p*th component on the pth component. Let \({\boldsymbol{\upvarepsilon}} = [ {\upvarepsilon_{p} } ] \in {\mathbf{\mathbb{R}}}^{P \times 1}\) denote a residual vector where \(\upvarepsilon_{p}\) is the residual for the pth component. Let \({\mathbf{e}} = \left[ {\text{e}_{j} } \right] \in {\mathbf{\mathbb{R}}}^{J \times 1}\) denote a residual vector where ej is the residual for the jth indicator. The weighted relation, measurement, and structural models can be generally expressed as

$${\varvec{\upgamma}} = {\mathbf{W}}'{\mathbf{z}}$$
(1)
$${\varvec{\upgamma}} = {\bf B}'{\varvec{\upgamma}} + {\boldsymbol{\upvarepsilon}}$$
(2)
$${\mathbf{z}} = {\mathbf{C}} '{\varvec{\upgamma}} + {\mathbf{e}}.$$
(3)

In the weighted relation model (1), each latent variable or component is defined as a weighted composite of some observed variables, and the observed variables are considered indicators of the component. This sub-model identifies GSCA as a component-based SEM. The weight assigned to each indicator is determined for its component(s) to well explain the relations among the variables specified in the other two sub-models, (2) and (3). The structural model (2) specifies a series of directional relations among the components, whereas the relations between the components and their indicators are specified in the measurement model (3). Specifically, the measurement model (3) sets some indicators to be explained by their components, which, in effect, may allow the components to capture variances of the indicators better in estimation process of weight parameter. This type of indicator is called ‘reflective indicator’, whereas the indicator whose relation with its component is specified in the weighted relation model (1) only is called ‘formative indicator’. We named the GSCA modeling approach with reflective indicators only GSCA with reflective indicators and the one with formative indicators only GSCA with formative indicators for the sake of comparison between PLSPM with mode A and PLSPM with mode B. Note that GSCA with formative indicators virtually specifies two sub-models—(1) the weighted relation model and (2) the structural model.

Unlike GSCA, PLSPM specifies two sub-models only—structural (or inner) and measurement (or outer) model, the latter of which are differently specified in PLSPM with mode A and PLSPM with mode B (Tenenhaus et al. 2005). In the PLSPM with mode A, two sub-models can be written as follows:

$$\upgamma_{p} = \sum\limits_{p^* = 1,p^* \ne p}^{{P_{p} }} {\text{b}_{p^*,p} \upgamma_{p^*,p} } + \upvarepsilon_{p} \quad \forall p \in \{ 1,2, \ldots ,P\}$$
(4)
$$\text{z}_{j} = \text{c}_{p,j} \upgamma_{p} + \text{e}_{j} \quad \forall j \in \{ 1,2, \, \ldots ,J\} ,$$
(5)

where Pp is the number of the independent components for the pth component, \(\upgamma_{p}\) is the pth component, and \(\upgamma_{p^*,p}\) is the p*th independent component for the pth components. The measurement model used in PLSPM with mode A is called ‘reflective measurement model’ or ‘outwards directed model’. As in the GSCA sub-models, the structural and reflective measurement models of PLSPM with mode A specify the relations among components and between components and their indicators, respectively. They can also be re-expressed with the matrix notations for GSCA structural and measurement models in the same way. In this case, however, the path coefficient matrix, B, is a triangular matrix, implying that PLSPM does not allow reciprocal relations among components unless an additional statistical technique such as instrumental variables are utilized. For the loading matrix, C, zero constraints are imposed on all the off-diagonal blocks of its entries, which means that indicators can be explained by one component only in PLSPM with mode A. When cross-loadings and reciprocal relations are not specified, the structural and measurement models of PLSPM with mode A are equivalent to those of GSCA with reflective indicators.

On the other hand, while specifying the same structural model, PLSPM with mode B specifies different measurement model, called ‘formative measurement model’ or ‘inwards directed model.’ The formative measurement model can be expressed as

$$\upgamma_{p} = \sum\limits_{j = 1}^{{J_{p} }} {\text{w}_{j,p^*}\text{z}_{j} } + \upzeta_{p} \quad \forall p \in \{ 1,2, \, \ldots ,P\} ,$$
(6)

where Jp is the number of indicators for the pth component, \(\text{w}_{j,p^{*}}\) is the formative weight assigned to the jth indicator for the pth component, and ζp denote a residual for the pth component in formative measurement model. It implies that each component is defined by the weighted sum of its indicators as in (1) but with additional formative measurement errors: \(\upzeta_{p}\).

PLSPM is distinct from GSCA in that, regardless of its mode, PLSPM does not define latent variables as weighted composites of their indicators in model specification (Hwang et al. 2019; Lohmöller 1989). In the estimation process, however, PLSPM always computes component scores as if they specified the weight relation model (3) of GSCA. More specifically, in PLSPM with mode A, a score for a component is computed as a weighted sum of scores for the indicators which are specified to be affected by the component in the reflective measurement model (5). PLSPM with mode B computes component scores based on the specified formative measurement model (6) but with the values of formative measurement errors excluded. Consequently, it is reasonable to think that both PLSPM with mode A and PLSPM with mode B implicitly assume the same type of sub-model as the weight relation model (3) of GSCA, as follows:

$$\upgamma_{p} = \sum\limits_{j = 1}^{{J_{p} }} {\text{w}_{j,p} \text{z}_{j} } \quad \forall p \in \{ 1,2, \, \ldots ,P\} ,$$
(7)

where \(\text{w}_{j,p}\) corresponds to \(\text{c}_{p,j}\) for PLSPM with mode A and to \(\text{w}_{j,p^*}\) for PLSPM with mode B. In this respect, PLSPM has been classified as a component-based SEM with GSCA, and the models of PLSPM with mode A corresponds to those of GSCA with reflective indicators, while those of PLSPM with mode B does to those of GSCA with formative indicators.

Another distinction lies in the unification of model equations. Combining models from (1) to (3), GSCA builds a unified model as follows:

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {\mathbf{z}} \\\varvec{\upgamma}\\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}'} \\ {{\mathbf{B}}'} \\ \end{array} } \right]\varvec{\upgamma}+ \left[ {\begin{array}{*{20}c} {\mathbf{e}} \\ {\varvec{\upvarepsilon}} \\ \end{array} } \right] \\ & \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ {{\mathbf{W}}'} \\ \end{array} } \right]{\mathbf{z}} = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}'} \\ {{\mathbf{B}}'} \\ \end{array} } \right]{\mathbf{W}}'{\mathbf{z}} + \left[ {\begin{array}{*{20}c} {\mathbf{e}} \\ {\varvec{\upvarepsilon}} \\ \end{array} } \right] \\ & {\mathbf{V}}'{\mathbf{z}} = {\mathbf{A}}'{\mathbf{W}}'{\mathbf{z}} + {\mathbf{r}} \\ \end{aligned}$$
(8)

where \({\mathbf{V}}' = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ {{\mathbf{W}}'} \\ \end{array} } \right], \, {\mathbf{A}}' = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}'} \\ {{\mathbf{B}}'} \\ \end{array} } \right], \,\) and \({\mathbf{r}} = \left[ {\begin{array}{*{20}c} {\mathbf{e}} \\ {\varvec{\upvarepsilon}} \\ \end{array} } \right]\). In contrast, PLSPM does not integrate its sub-model equations (i.e. (4), (5) for PLSPM with mode A and (4), (6) for PLSPM with mode B) into one single equation and just leaves them as they are specified for each dependent variable. As will be explained below, this difference leads to the selection of different estimation process for each approach.

For parameter estimation, GSCA employs the full information estimation method owing to its global optimization function. The unification of sub-model Eqs. (8) allows GSCA to use the following global optimization function:

$$\varphi \, = \, \sum\limits_{i = 1}^{N} {{{\mathbf{r}}}_{i} '{\mathbf{r}}_{i} } = \sum\limits_{i = 1}^{N} {({\mathbf{V}}'{\mathbf{z}}_{i} - {\mathbf{A}}'{\mathbf{W}}'{\mathbf{z}}_{i} )'({\mathbf{V}}'{\mathbf{z}}_{i} - {\mathbf{A}}'{\mathbf{W}}'{\mathbf{z}}_{i} )} ,$$
(9)

where \({\mathbf{z}}_{i}\) denote a J by 1 vector of indicators for the ith observations (i = 1, 2, …, N), and ri denote the residuals for the ith observations. This function is equivalent to the sum of squared residuals for all the equations in GSCA model. Finding the values that minimize this function amounts to estimating parameters that maximize the explained variances of indicators and endogenous components. GSCA estimates the entire entries of A (i.e. loadings and path coefficients for GSCA with reflective indicators and path coefficients only for GSCA with formative indicators) and W (i.e. weights) alternatively and concurrently to minimize the optimization function using alternative least squares (ALS) algorithm. The alternating procedure continues until the value of the optimization function does not decrease more than the pre-determined convergence criterion. A detailed description of this algorithm can be found in Hwang and Takane (2014). In the full information method, estimation proceeds for the entire system of equations, thereby utilizing all the information from every equation. Accordingly, estimators of full information methods can be more efficient under correct model specification with sufficient sample (Bollen 1996; Fomby et al. 2011; Gerbing and Hamilton 1994).

Conversely, PLSPM does not have a single optimization criterion to be minimized and consequently relies on the limited information estimation method whereby parameters for each equation are estimated separately based solely on the information specific to the equation (Fomby et al. 2011, Chapter 22). In addition, the estimation process of PLSPM is utterly segregated and sequential. At the first stage, weights are estimated by the iterative process of two steps. Given the random initial values of component scores, component scores are updated at the first step as the weighted sum of the other components specified in (4), which is called inner estimates for components. With these inner estimates for components, weights are estimated at the second step in two different manners—mode A and mode B (Lohmöller 1989). Under mode A, weights are estimated to regress indicators on a component with the specified relations in (5), while the loading relating the pth component to the jth indicator, \(\text{c}_{p,j} ,\) is considered equivalent to the weight of the jth indicator to construct the pth component, \(\text{w}_{j,p}\). Because of the basic design setting that each indictor is explained by one component only, weights become the correlation between a component and its indicators. On the other hand, Mode B estimates weights by regressing a component on its indicators using the formative relations specified in (6). Then, using the weight estimates obtained from either mode A or mode B, component scores are computed as weighted sums of each set of indicators and standardized so that the variance of each component is equivalent to 1. These component score estimates are called outer estimates. Given the outer estimates for components, the 1st step proceeds again. These two steps iterate and stop when the estimates do not alter more than the convergence criterion. With the final component score estimates and specified relations in (4) and (5), path coefficients and loadings are estimated by ordinary least squares at the second stage. Note that, even in PLSPM with mode B, loadings are estimated at this stage by regressing indicators on their components as if they assumed the reflective measurement model (5). You may see more detailed explanation on this algorithm in Tenenhaus et al. (2005). It is known that limited information methods may render estimators more robust to model misspecification in general (Bollen 1996; Fomby et al. 2011; Gerbing and Hamilton 1994).

There is no distributional assumption on the data for both GSCA and PLSPM, so they estimate standard error or confidence interval of the estimates via the bootstrap method (Efron 1979).

3 Data generating process for variance-based structural equation models

We first explain how data have been generated from a structural equation model with several layers of endogenous components in a recursive structural model but without cross-loadings and cross-weights in the measurement and weight relation models. This extant DGP is an expansion of the ones proposed by Becker et al. (2013) and Cho et al. (2019) and corresponds to the one specified in Dijkstra (2017), which has been used in Sarstedt et al. (2016)’s and Hair et al. (2017)’s simulation study. In the DGP, weight parameter values are arbitrarily manipulated by an experimenter, thereby not reflecting information on covariances of indicators. We discuss the intrinsic limitations of this DGP as a standard for evaluating all the variance-based SEM techniques and propose a new DGP tailored to variance-based SEM.

The general variance-based structural equation model can be defined as a class of (1) the weighted relation model, (2) the structural model and (3) the measurement model. Without cross-loadings and cross-weights specified, the variance-based structural equation model can be seen as a set of (7) the weight relation model, (4) the structural model and (5) the reflective measurement models as well, from which we generated data for our simulation study. To facilitate the explanations on the DGP for this model, we initially re-express the general variance-based structural equation model while splitting components into the exogenous and endogenous components, and specify additional restrictions imposed on the model where cross-loadings and cross-weights are not specified. The notations used in Sect. 2 still retain. In addition, let \({\mathbf{z}} = \left[ {\begin{array}{*{20}c} {{\mathbf{z}}_{\text{X}} } \\ {{\mathbf{z}}_{\text{Y}} } \\ \end{array} } \right]\), where \({\mathbf{z}}_{\text{X}}\) is a JX by 1 vector of indicators for exogenous components, JX is the number of the indicators for exogenous components, \({\mathbf{z}}_{\text{Y}}\) is a JY by 1 vector of indicators for endogenous components, and JY is the number of the indicators for endogenous components. Let \({\varvec{\Sigma}}\text{z} = \left[ {\begin{array}{*{20}c} {{\varvec{\Sigma}}\text{z}_{\text{X}} } & {{\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}} } \\ {{\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}} '} & {{\varvec{\Sigma}}\text{z}_{\text{Y}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{\Sigma}}\text{z}_{1} } & \cdots & {{\varvec{\Sigma}}\text{z}_{1} \text{z}_{p} } & \cdots & {{\varvec{\Sigma}}\text{z}_{1} \text{z}_{P} } \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ {{\varvec{\Sigma}}\text{z}_{1} \text{z}_{p} '} & \ddots & {{\varvec{\Sigma}}\text{z}_{p} } & \ddots & {{\varvec{\Sigma}}\text{z}_{p} \text{z}_{P} } \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ {{\varvec{\Sigma}}\text{z}_{1} \text{z}_{P} '} & \cdots & {{\varvec{\Sigma}}\text{z}_{p} \text{z}_{P} '} & \cdots & {{\varvec{\Sigma}}\text{z}_{P} } \\ \end{array} } \right] \in {\mathbb{R}}^{J \times J}\) denote a J by J covariance matrix of indicators, where \({\varvec{\Sigma}}\text{z}_{\text{X}}\) is a JX by JX covariance matrix of indicators for exogenous components, \({\varvec{\Sigma}}\text{z}_{\text{Y}}\) is a JY by JY covariance matrix of indicators for endogenous components, \({\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}}\) is a JX by JY cross-covariance matrix of indicators for exogenous and endogenous components, \({\varvec{\Sigma}}\text{z}_{p}\) is a Jp by Jp covariance matrix of indicators for the pth component, Jp is the number of the indicators for the pth component and \({\varvec{\Sigma}}\text{z}_{p} \text{z}_{p*}\) is a cross-covariance matrix of indicators for the pth and p*th components. \({\boldsymbol{\Sigma}}\text{z}\) is assumed to be positive definite, implying that all the indicators are linearly independent. Let \({\varvec{\upgamma}} = \left[ {\begin{array}{*{20}c} {{\varvec{\upgamma}}_{\text{X}} } \\ {{\varvec{\upgamma}}_{\text{Y}} } \\ \end{array} } \right]\), where \({\varvec{\upgamma}}_{\text{X}}\) is a PX by 1 vector of exogenous components and \({\varvec{\upgamma}}_{\text{Y}}\) is a PY by 1 vector of endogenous components. Let \({\varvec{\Sigma}}{{\upgamma}}_{\text{X}}\) denote a PX by PX covariance matrix of exogenous components and \({\varvec{\Sigma}}\upgamma_{\text{Y}}\) denote a PY by PY covariance matrix of endogenous components. Let \({\mathbf{e}} = \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{\text{X}} } \\ {{\mathbf{e}}_{\text{Y}} } \\ \end{array} } \right] = [{\mathbf{e}}_{1} ', \ldots ,{\mathbf{e}}_{p} ', \ldots {\mathbf{e}}_{P} ']'\), where \({\mathbf{e}}_{\text{X}}\) is a JX by 1 vector of residuals for the indicators forming exogenous components, \({\mathbf{e}}_{\text{Y}}\) is a JY by 1 vector of residuals for the indicators forming endogenous components, and \({\mathbf{e}}_{p}\) denote a Jp by 1 vector of residuals for the indicators forming the pth components. Let \({\varvec{\Sigma}}\text{e} = \left[ {\begin{array}{*{20}c} {{\varvec{\Sigma}}\text{e}_{\text{X}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{\Sigma}}\text{e}_{\text{Y}} } \\ \end{array} } \right] \in {\mathbb{R}}^{{J \times J}}\) denote a J by J covariance matrix of residuals, where \({\varvec{\Sigma}}\text{e}_{\text{X}}\) is a JX by JX covariance matrix of residuals for the indicators related to exogenous components and \({\varvec{\Sigma}}\text{e}_{\text{Y}}\) is a JY by JY covariance matrix of residuals for the indicators related to exogenous components. Let \({\varvec{\upvarepsilon}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{\upvarepsilon}}^{*} } \\ \end{array} } \right]\), where \({\varvec{\upvarepsilon}}^{*}\) is a PY by 1 vector of errors for the endogenous components. Let \({\varvec{\Sigma}}\upvarepsilon^{*} = {\text{diag}}\left( {[\delta_{1} , \ldots ,\delta_{k} \ldots ,\delta_{{P_{Y} }} ]} \right)\) denote the PY by PY covariance matrix of errors for the endogenous components, where δk is the variance of the error for the kth endogenous component and diag() is an operator to convert a vector or matrix argument into a block-diagonal matrix. Let \({\mathbf{W}} = \left[ {\begin{array}{*{20}c} {{\mathbf{W}}_{\text{X}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{W}}_{\text{Y}} } \\ \end{array} } \right]\), where \({\mathbf{W}}_{\text{X}}\) is a JX by PX matrix of weights of the indicators for exogenous components, and \({\mathbf{W}}_{\text{Y}}\) is a JY by PY matrix of weights of the indicators for endogenous components. Let \({\mathbf{B}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {{\mathbf{B}}_{\text{X}} } \\ {\mathbf{0}} & {{\mathbf{B}}_{\text{Y}} } \\ \end{array} } \right]\), where \({\mathbf{B}}_{\text{X}}\) is a PX by PX matrix of path coefficients relating exogenous components to endogenous components and \({\mathbf{B}}_{\text{Y}}\) is a PY by PY upper triangular matrix of path coefficients relating endogenous components among themselves. Let \({\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{\text{X}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{C}}_{\text{Y}} } \\ \end{array} } \right]\), where \({\mathbf{C}}_{\text{X}}\) is a PX by JX matrix of loading relating exogenous components to their indicators, and \({\mathbf{C}}_{\text{Y}}\) is a PY by JY matrix of loadings relating endogenous components to their indicators. Then, the general variance-based structural equation model is re-written as

$${\varvec{\upgamma}}_{\text{X}} = {\mathbf{W}}_{\text{X}} '{\mathbf{z}}_{\text{X}}$$
(10)
$${\varvec{\upgamma}}_{\text{Y}} = {\mathbf{W}}_{\text{Y}} '{\mathbf{z}}_{\text{Y}} ,$$
(11)
$${\varvec{\upgamma}}_{\text{Y}} = {\bf B}_{\text{X}} '{\varvec{\upgamma}}_{\text{X}} + {\bf B}_{\text{Y}} '{\varvec{\upgamma}}_{\text{Y}} + {\varvec{\upvarepsilon}}^{*} .$$
(12)
$${\mathbf{z}}_{\text{X}} = {\mathbf{C}}_{\text{X}} '{\varvec{\upgamma}}_{\text{X}} + {\mathbf{e}}_{\text{X}}$$
(13)
$${\mathbf{z}}_{\text{Y}} = {\mathbf{C}}_{\text{Y}} '{\varvec{\upgamma}}_{\text{Y}} + {\mathbf{e}}_{\text{Y}}$$
(14)

where \({\text{Cov}}({\varvec{\upgamma}}_{p} ,{\mathbf{e}}_{p} ) = 0\), and \({\text{Cov}}({\varvec{\upgamma}}_{\text{X}} ,{\varvec{\upvarepsilon}}^{*} ) = 0\). When the model does not include cross-loadings and cross-weights, we can impose additional zero constraints on the off-diagonal submatrix of W, C and \({\varvec{\Sigma}\text{e}}\), so that \({\mathbf{C}} = {\text{diag}}\left( {[{\mathbf{c}}_{1} , \ldots ,{\mathbf{c}}_{p} \ldots ,{\mathbf{c}}_{P} ]} \right)\), \({\mathbf{W}} = {\text{diag([}}{\mathbf{w}}_{1} , \ldots ,{\mathbf{w}}_{p} , \ldots ,{\mathbf{w}}_{P} ] )\), and \({\varvec{\Sigma}}\text{e} = {\text{diag}}\left( {[{\varvec{\Sigma}}\text{e}_{1} , \ldots ,{\varvec{\Sigma}}\text{e}_{p} , \ldots ,{\varvec{\Sigma}}\text{e}_{P} ]} \right)\), where cp is a vector of loadings relating the pth component to its indicators, wp is a vector of weights of the indicators for the pth component, and \({\varvec{\Sigma}}\text{e}_{p}\) is a Jp by Jp covariance matrix of residuals for the indicators forming the pth component. Also, it can be additionally postulated that \({\text{Cov}}({\varvec{\upgamma}}_{p} ,{\mathbf{e}}_{p^*} ) = 0 \, \forall p,p^* \in \{ 1,2, \ldots ,P\} \, , \, p \ne p^*\), followed by \({\text{Cov(}}{\varvec{\upgamma}},{\mathbf{e}}) = {\mathbf{0}}\).

A covariance matrix of \({\varvec{\Sigma}}\text{z}\), a matrix needed for data generation, would be obtained by the following steps:

Step 1: For each p, prescribe the values of \({\varvec{\Sigma}}\text{z}_{p}\), BX, BY, \({\varvec{\Sigma} \upgamma }_{\text{X}}\), and unstandardized weight vectors for the pth components, denoted as \({\tilde{\mathbf{w}}}_{p}\). With the pre-determined values of \({\tilde{\mathbf{w}}}_{p}\), wp would be re-calculated as \(\frac{{{\tilde{\mathbf{w}}}_{p} }}{{\sqrt {{\tilde{\mathbf{w}}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} {\tilde{\mathbf{w}}}_{p} } }}\), because the variance of γp is expressed as

$${\text{Var}}(\upgamma_{p} ) = \frac{1}{N}{\text{E}}({\mathbf{w}}_{p} '{\mathbf{z}}_{p} '{\mathbf{z}}_{p} {\mathbf{w}}_{p} ) = {\mathbf{w}}_{p} '\frac{1}{N}{\text{E}}({\mathbf{z}}_{p} '{\mathbf{z}}_{p} ){\mathbf{w}}_{p} = {\mathbf{w}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} {\mathbf{w}}_{p} ,$$
(15)

where E(X) is the expectation of a random variable, X. As an alternative to prescribing \({\tilde{\mathbf{w}}}_{p}\), wp satisfying \({\mathbf{w}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} {\mathbf{w}}_{p} = 1\) can be directly chosen as well.

Step 2: Given the values of either \({\tilde{\mathbf{w}}}_{p}\) and wp, calculate cp as follows:

$${\mathbf{c}}_{p} = {\mathbf{w}}_{p}^{{\prime }} \mathbf{\Sigma} \text{z}_{p}$$
(16)

This Eq. (16) is derived from \({\text{Cov}}(\upgamma_{p} ,{\mathbf{e}}_{p} ) = {\mathbf{0}}\), because

$$\begin{aligned} & {\text{Cov}}({{\upgamma }}_{p} ,{\mathbf{e}}_{p} ) \\ & \quad = {\text{C}}ov({{\upgamma }}_{p} ,{\mathbf{z}}_{p} - {\mathbf{c}}_{p} '{\mathbf{w}}_{p} '{\mathbf{z}}_{p} ) = {\text{C}}ov({\mathbf{w}}_{p} '{\mathbf{z}}_{p} ,({\mathbf{I}} - {\mathbf{c}}_{p} '{\mathbf{w}}_{p} '){\mathbf{z}}_{p} ) \\ & \quad = {\mathbf{w}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} ({\mathbf{I}} - {\mathbf{c}}_{p} '{\mathbf{w}}_{p} ')' = {\mathbf{w}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} - {\mathbf{w}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} {\mathbf{w}}_{p} {\mathbf{c}}_{p} \\ & \quad = {\mathbf{w}}_{p} '{\varvec{\Sigma}}{\text{z}}_{p} - {\mathbf{c}}_{p} . \\ \end{aligned}$$

Step 3: Calculate \({\varvec{\Sigma}}\text{e}_{p}\). As \({\text{Var}}({\mathbf{e}}_{p} )\)\(= {\text{Var}}({\mathbf{z}}_{p} - {\mathbf{c}}_{p} '{\mathbf{w}}_{p} '{\mathbf{z}}_{p} )\), this becomes equivalent to \({\varvec{\Sigma}}\text{e}_{p} = ({\mathbf{I}} - {\mathbf{c}}_{p} '{\mathbf{w}}_{p} '){\varvec{\Sigma}}\text{z}_{p} ({\mathbf{I}} - {\mathbf{w}}_{p} {\mathbf{c}}_{p} )\),

Step 4: Construct matrices of CX, CY, WX, WY, ΣeX and ΣeY from the determined values of cp, wp and \({\varvec{\Sigma}}\text{e}_{p}\) in earlier steps.

Step 5: Determine \(\varvec{\Sigma} \upgamma_{\text{Y}}\). From (12), \(\upgamma_{\text{Y}}\) becomes \(\mathbf{\gamma}_{\text{Y}} = ({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} ')^{ - 1} {\mathbf{B}}_{\text{X}} '{\varvec{\upgamma}}_{\text{X}} + ({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} ')^{ - 1} \text{e}^{*}\). Thus, the covariance matrix of \(\upgamma_{\text{Y}}\) can be expressed as

$${\varvec{\Sigma}}{{\upgamma }}_{\text{Y}} = ({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} ')^{ - 1} ({\mathbf{B}}_{\text{X}} '\mathbf{\Sigma} {{\upgamma }}_{\text{X}} {\mathbf{B}}_{\text{X}} + \varvec{\Sigma} {{\upvarepsilon^*}})({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} )^{ - 1} .$$
(17)

From (17), the diagonal entries of \({\varvec{\Sigma}\upvarepsilon^*}\) are numerically determined such that the diagonal entries of \({\varvec{\Sigma}}{{\upgamma }}_{\text{Y}}\) are equal to one, since \({\varvec{\Sigma}}\upvarepsilon^*\) cannot be expressed as a function of other matrices like (17) for \({\varvec{\Sigma}}{{\upgamma }}_{\text{Y}}\). A nonlinear optimization function or package developed for various programming software can be utilized to find a numerical solution for \({\varvec{\Sigma}}\upvarepsilon^*\), for instance, fminsearch function in MATLAB or optimr package in R.

Step 6: Determine \({\varvec{\Sigma}}\text{z}_{\text{X}}\), \({\varvec{\Sigma}}\text{z}_{\text{Y}}\) and \({\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}}\). Inserting the prescribed or determined values in earlier steps, \({\varvec{\Sigma}}\text{z}_{\text{X}} = {\mathbf{C}}_{\text{X}} '\varvec{\Sigma} {{\upgamma }}_{\text{X}} {\mathbf{C}}_{\text{X}} + {\varvec{\Sigma}}\text{e}_{\text{X}}\) and \({\varvec{\Sigma}}\text{z}_{\text{Y}} = {\mathbf{C}}_{\text{Y}} '{\varvec{\Sigma}}{{\upgamma }}_{\text{Y}} {\mathbf{C}}_{\text{Y}} + {\varvec{\Sigma}}{\text{e}}_{\text{Y}}\). Afterwards, \({\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}}\) is obtained by \({\varvec{\Sigma}}\text{z}_{\text{X}}\text{z}_{\text{Y}} = {\mathbf{C}}_{\text{X}} '{\varvec{\Sigma}}{{\upgamma }}_{\text{X}} {\mathbf{B}}_{\text{X}} ({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} )^{ - 1} {\mathbf{C}}_{\text{Y}}\). It follows from

$$\begin{aligned} & {\text{Cov}}({\mathbf{Z}}_{\text{X}} ,{\mathbf{Z}}_{\text{Y}} ) \\ & \quad = {\text{Cov}}({\mathbf{C}}_{\text{X}} '{\varvec{\upgamma}}_{\text{X}} + {\mathbf{e}}_{\text{X}} ,{\mathbf{C}}_{\text{Y}} '{\varvec{\upgamma}}_{\text{Y}} + {\mathbf{e}}_{\text{Y}} ) \\ & \quad = {\mathbf{C}}_{\text{X}} '{\text{Cov}}({\varvec{\upgamma}}_{\text{X}} ,{\varvec{\upgamma}}_{\text{Y}} ){\mathbf{C}}_{\text{Y}} \\ & \quad = {\mathbf{C}}_{\text{X}} '{\text{Cov}}({\varvec{\upgamma}}_{\text{X}} ,({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} ')^{ - 1} {\mathbf{B}}_{\text{X}} '{\varvec{\upgamma}}_{\text{X}} + ({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} ')^{ - 1} {\varvec{\upvarepsilon}}^{*} ){\mathbf{C}}_{\text{Y}} \\ & \quad = {\mathbf{C}}_{\text{X}} '{\varvec{\Sigma}}\upgamma_{\text{X}} {\mathbf{B}}_{\text{X}} ({\mathbf{I}} - {\mathbf{B}}_{\text{Y}} )^{ - 1} {\mathbf{C}}_{\text{Y}} . \\ \end{aligned}$$

Now, we have \({\varvec{\Sigma}}\text{z} = \left[ {\begin{array}{*{20}c} {{\varvec{\Sigma}}\text{z}_{\text{X}} } & {{\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}} } \\ {{\varvec{\Sigma}}\text{z}_{\text{X}} \text{z}_{\text{Y}} '} & {{\varvec{\Sigma}}\text{z}_{\text{Y}} } \\ \end{array} } \right]\) and can generate data from a multivariate distribution with the zero mean vector and the \({\varvec{\Sigma}}\text{z}\). By generating data based on the above steps of DGP with the structural equation model specified in Hair et al. (2017), the equivalent results on the relative performance of GSCA with formative indicators and PLSPM with mode B were obtained (see the Table 1 in the Supplementary material).

This extant DGP is of significance as an initial proposal for variance-based structural equation models. Dijkstra (2017) analytically showed that the components in this DGP are canonical variables, implying that the components are constructed to maximize the explained variances of the endogenous components, and it was empirically verified in Hair et al. (2017)’s simulation study: the estimators of GSCA with formative indictors and PLS with mode B were consistent. In the abovementioned DGP, however, values of the weight parameters were arbitrarily chosen regardless of covariances of indicators in Step 1. Except for scaling constraint of weights, no functional relations between weights and covariances of indicators are considered in the DGP. Simply put, the extant DGP has no mechanism of accounting for the variances of indicators when forming the components. This result may be against many researchers’ expectation that the components would also reflect the information about indicators and adequately explain their variances. Consequently, the extant DGP is not concordant with GSCA with reflective indicators and PLSPM with mode A, which aim to form components that explain the variances of indicators as well as those of endogenous components. When applied to the data generated from the extant DGP, GSCA with reflective indicators and PLSPM with mode A are expected to produce biased estimates (see the Table 2 in Supplementary material).

Addressing this concern, we propose a new DGP specifying the functional relation between weights of indicators for components and their covariance matrix. In this DGP, weights of indicators for a component are initially determined to well explain the variances of the indicators given the covariances of the indicators. Set the values of \({\varvec{\Sigma}}{\text{z}}_{p}\) for p = 1, 2, …, P. Then, wp is obtained by,

$${\mathbf{w}}_{p} = ({\varvec{\Sigma}}{\text{z}}_{p} )^{{ - \frac{1}{2}}} {\mathbf{u}}_{1,p}$$
(18)

where \(({\varvec{\Sigma}}{\text{z}}_{p} )^{{ - \frac{1}{2}}} = {\mathbf{U}}_{p} ({\mathbf{D}}_{p} )^{{ - \frac{1}{2}}} {\mathbf{U}}_{p} '\), \({\mathbf{D}}_{p} = {\text{diag}}\left( {[\text{d}_{1} ,\text{d}_{2} , \ldots ,\text{d}_{Jp} ]} \right)\) is a Jp by Jp diagonal matrix of eigenvalues of \({\varvec{\Sigma}}{\text{z}}_{p}\) arranged in a descending order, \({\mathbf{U}}_{p} = [{\mathbf{u}}_{1,p} ,{\mathbf{u}}_{2,p} , \ldots ,{\mathbf{u}}_{Jp,p} ]\) is a Jp by Jp matrix of eigenvectors corresponding to the eigenvalues, and \({\mathbf{u}}_{1,p}\) is the eigenvector corresponding to the largest eigenvalue, \(\text{d}_{1}\). The rest of the procedures are the same as in the previous DGP.

We delineate the procedure to derive (18). The first step is to find the deterministic relation between the weights of indicators and the amount of explained variances of the indicators by their weighted composites. Let R 2p denote a Jp by 1 vector of the explained variances of indicators forming the pth components relative to the entire variances of indicators. The average R 2p is the mean of the elements of R 2p . Since the model does not involve cross-loadings and cross-weights and every indicator and component is standardized, those relations can be expressed as follows:

$$\begin{aligned} & {\text{average}}\,{\mathbf{R}}_{p}^{2} \\ & \quad = J_{p}^{ - 1} {\text{trace}}({\text{Cov}}({\mathbf{c}}_{p} '\upgamma_{p} )) \\ & \quad = J_{p}^{ - 1} {\text{trace}}({\mathbf{c}}_{p} '{\varvec{\Sigma}}\upgamma_{p} {\mathbf{c}}_{p} ) \\ & \quad = J_{p}^{ - 1} {\text{trace}}(({\mathbf{w}}_{p} '{\varvec{\Sigma}}\text{z}_{p} )'{\mathbf{w}}_{p} '{\varvec{\Sigma}}\text{z}_{p} ) \\ & \quad = J_{p}^{ - 1} {\text{trace}}({\mathbf{w}}_{p} '({\varvec{\Sigma}}\text{z}_{p} )^{2} {\mathbf{w}}_{p} ) \\ & \quad = J_{p}^{ - 1} {\mathbf{w}}_{p} '({\varvec{\Sigma}}\text{z}_{p} )^{2} {\mathbf{w}}_{p} \\ \end{aligned}$$
(19)

Then, finding the weights with which the composite of indicators maximizes its capability to explain the variances of the indicators amounts to solving the following optimization problem,

$$\mathop {\text{Max}}\limits_{{{\mathbf{w}}_{p} }} \, {\mathbf{w}}_{p} '({\varvec{\Sigma}}\text{z}_{p} )^{2} {\mathbf{w}}_{p} \;{\text{subject}}\;{\text{to}}\;{\mathbf{w}}_{p} '{\varvec{\Sigma}}\text{z}_{p} {\mathbf{w}}_{p} = 1.$$
(20)

This is the constrained quadratic optimization problem on the ellipsoid (Gallier and Quaintance 2019, Chapter 37.3). Since \({\varvec{\Sigma}}\text{z}_{p}\) is positive definite, it can be orthogonally diagonalized as

$${\varvec{\Sigma}}\text{z}_{p} = {\mathbf{U}}_{p} {\mathbf{D}}_{p} {\mathbf{U}}'_{p} .$$
(21)

Let \(({\varvec{\Sigma}}\text{z}_{p} )^{{\frac{1}{2}}}\) and \(({\varvec{\Sigma}}\text{z}_{p} )^{{ - \frac{1}{2}}}\) be defined by

$$\begin{aligned} ({\varvec{\Sigma}}\text{z}_{p} )^{{\frac{1}{2}}} & = {\mathbf{U}}_{p} ({\mathbf{D}}_{p} )^{{\frac{1}{2}}} {\mathbf{U}}_{p} ' \\ ({\varvec{\Sigma}}\text{z}_{p} )^{{ - \frac{1}{2}}} & = {\mathbf{U}}_{p} ({\mathbf{D}}_{p} )^{{ - \frac{1}{2}}} {\mathbf{U}}_{p} '. \\ \end{aligned}$$
(22)

They are the inverse matrix of each other so that

$$({\varvec{\Sigma}}\text{z}_{p} )^{{\frac{1}{2}}} ({\varvec{\Sigma}}\text{z}_{p} )^{{ - \frac{1}{2}}} = {\mathbf{U}}_{p} ({\mathbf{D}}_{p} )^{{\frac{1}{2}}} {\mathbf{U}}_{p} '{\mathbf{U}}_{p} ({\mathbf{D}}_{p} )^{{ - \frac{1}{2}}} {\mathbf{U}}_{p} ' = {\mathbf{I}}$$
(23)

By (21) and (22), the reparameterization of \({\mathbf{w}}_{p}\) as \({\mathbf{w}}_{p} = ({\varvec{\Sigma}}\text{z}_{p} )^{{ - \frac{1}{2}}} {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p}\) transforms (20) into well-known constrained quadratic optimization problem on the unit sphere,

$$\mathop {\text{Max}}\limits_{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p} }} \, {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p} '{\varvec{\Sigma}}\text{z}_{p} {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p} \;{\text{subject}}\;{\text{to}}\;{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p} '{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p} = 1.$$
(24)

The solution for (24) is \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} }}_{p} = {\mathbf{u}}_{1,p}\), that is, \({\mathbf{w}}_{p} = ({\varvec{\Sigma}}\text{z}_{p} )^{{ - \frac{1}{2}}} {\mathbf{u}}_{1,p}\), at which the largest value of the objective function, \({\mathbf{w}}_{p} '({\varvec{\Sigma}}\text{z}_{p} )^{2} {\mathbf{w}}_{p} \,\), is attained as d1. You may see the detailed explanation for (24) from Chapter 7 in Lay et al. (2015) or Chapter 18.4 in Gallier and Quaintance (2019).

The components constructed from this new DGP can be interpreted in three different ways. Firstly, they can be seen as principal components because the vector of weights for each component is determined in the same manner as for the first principal component in the principal component analysis. Secondly, those components can be also classified as canonical components, as they still satisfy all the relations among the parameters specified in the previous DGP. The new DGP just additionally specifies the relations between the weights of indicators and their covariances. Lastly, the components in the new DGP can be regarded as the one constructed to explain the variances of all the dependent variables specified in both measurement and structural models concurrently as much as possible. We name this type of components nomological components in that they can correspond to the concepts defined by the entire nomological network including both observed and latent variables (Cronbach and Meehl 1955). Accordingly, all the variance-based SEM techniques, whether to consider maximizing explained variances of either indicators or endogenous components only or both in constructing components (i.e. whether to construct principal, canonical or nomological components), can be adopted to analyze data from this new DGP, and thus, we can call this DGP a DGP for variance-based structural equation models. This is the condition where PLSPM with mode A and PLSPM with mode B are perfectly matched with each other and may work well asymptotically according to Dijkstra (2017). We employed this DGP for empirically evaluating the relative performance of both PLSPM with mode A and PLSPM with mode B and their counterparts, GSCA with reflective indicators and GSCA with formative indicators in our simulation study.

4 Simulation

We undertook a comprehensive examination of four SEM approaches—GSCA with reflective, GSCA with formative indicators, PLSPM with mode A, and PLSPM with mode B in parameter recovery and hypothesis testing under variance-based structural equation models. For simplicity, GSCA with reflective indicators and GSCA with formative indicators are abbreviated to GSCAR and GSCAF, while PLSPM with mode A and PLSPM with mode B to PLSA and PLSB, respectively. We considered three simulation design factors: sample size (N = 100, 250, 500, 1000), the number of indicators per component (Nind = 2, 4, 6, 8), and the average correlation within the indicators for a component (r = 0.2, 0.4, 0.6). In total, our experiment was comprised of 48 simulation conditions (4 sample sizes × 4 indicator numbers × 3 average correlations).

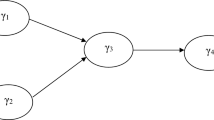
We specified a variance-based structural equation model with two exogenous and five endogenous components, as in Hair et al. (2017) (Fig. 1). This model reflects the American Customer Satisfaction Index model (ACSI; Fornell et al. 1996) which is one of the most influential variance-based structural equation models in studying the behavior of consumer satisfaction (e.g. Anderson and Fornell 2002; Eklöf and Westlund 2002; Rego et al. 2013). To mirror the reality, we assigned various values of different signs to path coefficients: two null values (i.e. b2 = b6 = 0), two small values (i.e. b3 = b12 = 0.15), two medium values (i.e. b5 = 0.3, b8 = −0.3), and six large values (i.e. b1 = b9 = b11 = 0.5, b4 = b7 = b10 = −0.5). Two exogenous components were correlated to each other by 0.3 (i.e. \({\varvec{\Sigma}}\upgamma_{\text{X}}\) = \(\left[ {\begin{array}{*{20}c} 1 & {.3} \\ {.3} & 1 \\ \end{array} } \right]\)).

Fig. 1
figure 1

A variance-based structural equation model with two exogenous components and five endogenous components specified for the simulation study. Note that measurement models are omitted for a simpler depiction

Full size image

Given the number of indicators per component and the value of the average correlation among the indicators for a component, individual correlations among the indicators for a component are randomly chosen to construct their covariance matrix, \({\varvec{\Sigma}}\text{z}_{p}\). Once \({\varvec{\Sigma}}\text{z}_{p}\) is determined, we applied this matrix to every block of indicators. The range of individual correlations for each condition was [0.1, 0.3] for r = 0.2, [0.2, 0.6] for r = 0.4, [0.4 0.8] for r = 0.6. For each experimental condition, we have \({\varvec{\Sigma}}\text{z}_{p}\), BX, BY, and \({\varvec{\Sigma}}\upgamma_{\text{X}}\), from which we derived the covariance matrix of entire indicators with all the true parameter values via the DGP for variance-based structural equation models (see Tables 4–7 in Supplementary materials). We generated 500 random samples from the multivariate normal distribution with a zero vector of mean and Σz obtained under each condition, to which, in turn, the four variance-based SEM approaches were applied. Based on their estimates, we evaluated three properties of estimators of each approach—bias, consistency, and relative efficiency—, and their performance in hypothesis testing—type I error and statistical power. Note that, in GSCAF, loadings were additionally estimated as in PLSB, though GSCAF does not estimate loading parameters in general. As explained in Sect. 2, the post examination on directional relations between components and their indicators are always conducted in PLSB. With the component scores computed on the final weight estimates, indicators are regressed on their components by OLS to obtain loading estimates. We applied the same procedure to GSCAF and computed loading estimates. These loading estimates have the same meaning as those in GSCAR and PLSF—how strongly correlated the components are with its indicators, but their absolute values may be smaller on average since variances of indicators are not considered in the estimation of weight parameters.

For bias and consistency, we calculated the relative bias (RB) of an estimator (\(\hat{\uptheta }\)):

$${\text{RB}}(\hat{\uptheta }) = \frac{\text{E}{(\hat{{\uptheta} }) - \uptheta }}{\uptheta } \approx \frac{{\frac{1}{Nrep}\sum\limits_{i = 1}^{Nrep} {(\hat{\uptheta }_{i} )} - \uptheta }}{\uptheta },$$
(25)

where θ is the parameter to be estimated by \(\hat{\uptheta }\), Nrep is the number of replications in an experiment, and \(\hat{\uptheta }_{i}\) is an estimate for θ given the ith sample. Estimators whose absolute value of the relative bias was larger than 10% were treated as unacceptably biased ones (e.g. Bollen et al. 2007; Hwang et al. 2010). If the relative bias of an estimator becomes close to zero with larger sample size and the value is below 10% with the largest sample size, the estimator was regarded as being empirically consistent. On the other hand, to assess the relative efficiency of the estimators, we computed root mean squared error (RMSE). Root mean squared error (RMSE),

$${\text{RMSE(}}\hat{\uptheta }) = \sqrt {\text{E}((\hat{\uptheta } - \uptheta )^{2} )} \approx \sqrt {\frac{1}{Nrep}\sum\limits_{i = 1}^{Nrep} {(\hat{\uptheta }_{i} - } \uptheta )^{2} }$$
(26)

is a metric to quantify errors of an estimator. An estimator with lower RMSE can be said to be more efficient than the others with higher RMSE. RMSE may serve as a better criterion in estimating expected errors of an estimator than mean absolute error (MAE) when errors are expected to follow normal distribution rather than uniform distribution (Chai and Draxler 2014).

Table 1 depicts the average RB values of the estimators for each sub-model (i.e. averaged over the entire weights in the weighted relation model), for each approach, given the simulation condition. The average RBs were calculated with the absolute RB values of estimators and did not consider the estimators for the parameter of zero value. As shown in Table 1, GSCAR and PLSA provided unbiased and consistent estimators across all the simulation conditions. Their average RBs were less than 10% across the sample sizes, irrespective of the level of r and Nind, and became close to zero as N increased. GSCAF and PLSB also produced unbiased and consistent estimators in general. Their average RBs were less than 10% except for that N was small (i.e. 100) and Nind was large (i.e. 8), and tended to zero value as N increased. In those exceptional cases, average RBs of GSCAF and PLSB estimators for weights and loadings were more than 10% (e.g. 12.39 and 10.18 for weights and loadings of GSCAF, and 15.60 and 13.42 for weights and loadings of PLSB when N = 100, Nind = 8, and r = 0.6), whereas only GSCAF estimators had the average RBs greater than 10% for path coefficients (e.g. 28.46 for path coefficients of GSCAF, and 8.99 for path coefficients of PLSB when N = 100, Nind = 8, and r = 0.6). Overall, GSCAR and PLSA estimators yielded smaller RBs than GSCAF and PLSB, and the difference was enlarged as r and Nind got larger and N got smaller.

Table 1 Relative bias expressed as a percentage (RB) of the estimators of each approach per experimental condition in the simulation study
Full size table

Table 2 presents the average RMSE values of the estimators for each sub-model, for each approach, given the simulation condition. The average RMSE was computed as the mean of the absolute values of estimators in the same sub-models. As Table 2 exhibits, estimators of GSCAR and PLSA were more efficient than those of GSCAF and PLSB in general. Specifically, GSCAF and PLSB estimators yielded larger RMSE values than GSCAR and PLSA estimators for weights and loadings, and this gap did not disappear even with the large size of sample (i.e. N = 1000), across every condition. With respect to path coefficients, the RMSEs of GSCAF and PLSB estimators were still larger than those of GSCAR and PLSA estimators when N = 100 or 250, but the difference in RMSEs became smaller as N increased. Between the GSCAR and PLSA, the estimators of GSCAR were at least equivalent to or more efficient than those of PLSA in general. Aside from the four conditions (i.e. r = 0.6, Nind = 6 or 8, and N = 100 or 250) of the 48 conditions, the RMSEs of GSCAR estimators for weights were less than or equal to those of PLSA estimators. For loading parameters, GSCAR estimators led to equivalent or smaller RMSEs on average than PLSA estimators across all the conditions. On the other hand, GSCAR and PLSA showed no substantial difference in the RMSEs of the estimators for path coefficients.

Table 2 Root mean square error (RMSE) of the estimators of each approach per experimental condition in the simulation study
Full size table

For the purpose of testing the utility of each approach as a tool for hypothesis testing, we calculated their type I error and statistical power. We constructed a 95% confidence interval for each estimate via 100 bootstrap sampling and calculated the relative frequency of the cases where the confidence interval failed to contain a zero value. That frequency can be interpreted as empirical type I error for the parameter of zero value and as statistical power for the parameter of nonzero value. Table 3 shows the average type I errors over the two null path coefficients for each approach in all the experimental conditions. Overall, every approach succeeded in controlling type I error around at 0.05 level (i.e. deviated from 0.05 by 0.02 or less), except GSCAF. GSCAF controlled type I error too strictly when N = 100 and Nind = 6 or 8 so that its value was 0.01 or even 0.00. Table 4 depicts the average statistical power for the parameters in each sub-model, varying N, Nind, and r. GSCAR and PLSA tended to have power equal to or higher than GSCAF and PLSB across all the simulation conditions. In particular, inequality between the two groups (i.e. GSCAR and PLSA versus GSCAF and PLSB) was observed to a greater degree when weight and path coefficients were estimated with a small size of sample relative to the large number of indicators (e.g. N = 100 and Nind  ≥  6). In comparison of GSCAR with PLSA, GSCAR showed better performance in power than PLSA given a small or medium size of sample (i.e. N  ≤  250) in general, but the difference was negligible.

Table 3 Type I error obtained from variance-based SEM approaches across different experimental conditions in the simulation study
Full size table
Table 4 Statistical power of variance-based SEM approaches across different experimental conditions in the simulation study
Full size table

5 Summary and discussions

In this paper, we uncovered the limitation of previous DGPs for variance-based SEM and proposed a new DGP where components are constructed to well explain the variances of their indicators as well as those of endogenous components. Along with the development of the DGP for variance-based structural equation models, GSCA with reflective indicators and PLSPM with mode A were properly evaluated. Our simulation study showed that all modeling approaches of variance-based SEM were able to provide consistent and acceptably unbiased estimators for the parameters of variance-based structural equation models. This result not only serves as empirical evidence to substantiate the appropriateness of the DGP proposed in this paper, but also cements GSCA’s and PLSPM’s positions as variance-based SEM approaches.

GSCA with reflective indicators and PLSPM with mode A turned out to recover parameters in a more efficient manner than GSCA with formative indicators and PLSPM with mode B under variance-based structural equation models. It would be attributed from the fact that the former approaches estimate weights while considering the variances of indicators as well as those of endogenous components. In addition, we found that compared to PLSPM with mode A, GSCA with reflective indicators provided more efficient estimators for weights and loadings. For the path coefficients, though, there were no substantial differences between PLSPM with mode A and GSCA with reflective indicators. These patterns were the same for GSCA with formative indicators and PLSPM with mode B, which is in accord with the simulation result of Hair et al. (2017).

In terms of hypothesis testing, GSCA with reflective indicators and PLSPM with mode A outperformed GSCA with formative indicators and PLSPM with mode B as well. While GSCA with reflective indicators and PLSPM with mode A controlled type I error at the pre-specified significance level (i.e. 0.05) equally well, GSCA with reflective indicators showed slightly higher power than PLSPM with mode A. Notably, GSCA with formative indicators outperformed PLSPM with mode B in statistical power. This tendency became more salient when the true path coefficient was prescribed to be low (i.e., b = 0.15; see Table 3 in Supplementary materials). This result is in contrast to the one reported by Hair et al. (2017) that PLSPM with mode B was better than GSCA with formative indicators in statistical power. The different results between the two studies may be due to the differences in prescribed signs of the path coefficients in a given structural model: given that standard errors are fixed, a statistical power is likely to be affected by the magnitude of biases, which are further dependent upon the signs of path coefficients in the structural model. We observed that a change in the sign of a path coefficient in DGP also influenced patterns of biases for all the other path coefficients in both GSCA and PLSPM. The effect was rather arbitrary so that some changes were advantageous to GSCA and the other to PLSPM. In this sense, higher power of PLSPM with mode B or GSCA with formative indicators in each study could stem from the prescribed values of path coefficients being advantageous to either of them.

Lastly, our simulation showed that the effects of the number of indicators per component and correlation between indicators for each component were different across modeling approaches of variance-based SEM. GSCA with reflective indicators and PLSPM with mode A benefited from the large number of indicators per component and the high level of average correlation between indicators for a component, as in factor analysis (Marsh et al. 1998), whereas those conditions rather had negative impacts on GSCA with formative indicators and PLSPM with mode B. This finding is consistent with Becker et al. (2013), in which an increase in correlation between indicators was found to be associated with lower RMSE for PLSPM with mode A but higher RMSE for PLSPM with mode B. According to their explication, high correlations between indicators can lead to multicollinearity, subsequently aggravating stability of weight estimation, especially for PLSPM with mode B. With indicators for a component being more correlated to each other, the multicollinearity problem is expected to be worse. Conversely, PLSPM with mode A is relatively free from this issue as it estimates weights by correlation (Becker et al. 2013; Rigdon 2012). However, it cannot be a sufficient reason why PLSPM with mode A or GSCA with reflective indicators performs better, despite of the risk of multicollinearity. It may be reasonable to conjecture that including additional indicators leads to an increase in the number of equations to be considered in estimating weight parameters for GSCA with reflective indicators and PLSPM with mode A, which in turn, would make their estimation process more stable.

Based on our findings, we provide a couple of recommendations for practitioners to utilize variance-based SEM approaches. First, if you want to construct nomological components in SEM framework or run SEM using the measures based on principal component analysis, you should select GSCA with reflective indicators or PLSPM with mode A. Without the prior preference on the two approaches, we suggest using GSCA with reflective indicators since it can help construct components more precisely. Using GSCA with formative indicators or PLSPM with mode B is recommended in particular case when the construction of components is specifically aimed at explaining the variances of endogenous components only.

Second, if you use GSCA with reflective indicators or PLSPM with mode A, it would be acceptable to increase the number of indicators with high correlation if possible. On the other hand, when drawing on GSCA with formative indicators or PLSPM with mode B, you should sift a few indicators with low correlation through a set of candidate indicators. However, you need to be cautious to add or remove indicators because such change may alter the conceptual meaning of components (Bollen 2017; Jarvis et al. 2003).

In spite of our comprehensive investigation on relative performances of the four SEM approaches, we overlooked two important criteria to evaluate their performance. The first one is another important property of an estimator—robustness to model-misspecification. As mentioned in Sect. 2, the limited estimation method adopted in PLSPM might allow PLSPM to be robust to model-misspecification, even though, in Hwang et al. (2010) and Hwang and Takane (2014)’s simulation study, the evidence to support this hypothesis was not found under factor-based structural equation models. On the other hand, GSCA with reflective indicators and PLSPM with mode A could be practically more robust to model-misspecification. SEM techniques are typically applied after all measurements are sufficiently validated (Bollen 1989; Chin 1998). In other words, SEM techniques are generally utilized in the situation where researchers are unsure of the true structural model but with validated measurement tools. In this case, GSCA with formative indicators and PLSPM with mode B would be subject to biased estimates for path coefficients, because their estimation of weights is contingent solely on allegedly specified paths among components. In contrast, GSCA with reflective indicators and PLSPM with mode A consider the variances of indicators as well in weights estimation, which may allow their estimators to be more robust against model-misspecification. Further research is required to test these hypotheses on the relative robustness under the various model constellations with components.

The second missing criteria is the one in the utterly different framework from parameter recovery—predictability. GSCA and PLSPM are essentially “prediction-oriented” approaches to SEM in that they can predict individual scores of every endogenous variable specified in the model, beyond simply estimating parameters (Cho et al. 2019; Sharma et al. 2018; Wold 1982). However, their relative predictive performance has never been properly evaluated even though its importance was acknowledged in the variance-based SEM scholarly community (Shmueli et al. 2016). Thus, the future research to compare the two variance-based SEM approaches needs to consider their performance on predictability. The DGP proposed in this paper may facilitate this future research.