Bearing fault diagnosis algorithm based on granular computing

Abstract

Granular computing, as an emerging soft computing classification method, provides a theoretical framework for solving complex classification problems based on information granulation and is one of the core technologies for simulating human thinking and solving complex classification problems in the current computational intelligence field. In this paper, we propose a design method of bearing fault diagnosis model based on granular computing: Convolutional Neural Networks-Granular Computing (CNN-GC). The method consists of two main components: fault features extraction and fault types determination. In this case, the bearing fault features are extracted using a convolutional neural network (CNN) with hyperparameter optimization to obtain bearing fault features with different output dimensions; fault types determination is obtained by using the extracted fault features as the input of hypersphere information granule based on granular computing. Compared with existing bearing fault diagnosis models, the CNN-GC model proposed in this paper, which accomplishes the conversion from numerical space to grain space, can obtain more accurate values and better grain size results. The superiority of the CNN-GC model in terms of accuracy and interpretability was demonstrated by the Case Western Reserve University(CWRU) bearing dataset.The experimental results show an accuracy rate of 99.8$\%$.

1 Introduction

With the continuous development of industrial automation, fault diagnosis plays an increasingly important role in protecting industrial production equipment. In recent years, with the continuous development of deep learning (Bas et al. 2021), intelligent diagnostic algorithms represented by CNN and deep neural networks (DNN) (Moosavi-Dezfooli 2016) are beginning to be used in fault diagnosis. CNN was first proposed by Lecun et al. (1998), which is used to process data with an obvious grid shape. Zhang et al. (2018) synthesized the implementation of fault diagnosis algorithms at home and abroad, the core part of which can be reduced to two parts: extraction of fault features and classification of fault determination results, and searched for an optimal combination to detect and separate and identify faults occurring in the system to improve the accuracy of fault diagnosis. Common types of bearing failures are shown in Fig. 1, which include stripping, burning, cracking defects, cage breakage, scuffing and seizing, and rusting and corrosion. As the core component of mechanical structure, rolling bearing occupies an absolute position in mechanical technology, representing the national level of scientific and technological manufacturing. Whether the healthy operation of rolling bearing plays a decisive role in industrial production. Therefore, this paper will be devoted to the diagnostic study of bearing faults to achieve health monitoring of bearings (Li et al. 2019; Wang et al. 2018).

Fig. 1

Common types of faulty bearings

In terms of fault features extraction, Lu et al. (2017) proposed an auto-coding algorithm for fault diagnosis, through which the frequency domain features of the input are extracted and input into its AE model. Ejegwa (2019) proposes the application of improved Pythagorean fuzzy sets to fault features extraction and their application to medical diagnosis. Zhu et al. proposed an SAE-based DN for hydraulic pump fault diagnosis, with feature extraction by DNN and Fourier transform of the extracted features as input to the model. Harmouche et al. (2014) proposed Global Spectrum Analysis for feature extraction of input signals. Janssens et al. (2016) first performed a discrete Fourier transform on the signal of the bearing of the gearbox through the CNN, converting the vibration signal from the time domain to the frequency domain, and finally input it to the CNN for features extraction.

In terms of the classification algorithm based on granular computing, Amezcua and Melin (2019) proposed a new Fuzzy Learning Vector Quantization (FuzzLVQ) method, implemented using a modular architecture based on the granular method, to further improve its performance in complex classification problems. Yao and Yao (2002) proposed to combine the concept of granular computing with decision tree, and form a granular classification induction algorithm by using granular computing model to learn the classification rules of progressive training data. Kaburlasos et al. (2014) proposed a Granular K Nearest Neighbors(GKNN) classifier, which can process numerical data and calibration data. Singh and Huang (2020) propose a quadruple decision method using interval-valued fuzzy sets, rough sets, and granular calculations to improve the accuracy of classification results. Kim et al. (2006) proposed a genetic algorithm-based construction method of information particle fuzzy classifier. In this method, sufficient information granules are generated by genetic algorithm first, and then fuzzy sets are constructed by further analysis of the content of information granules to form an interpretable fuzzy classifier. The validity of the classifier is verified by iris data. Hu et al. (2018) constructed a fuzzy classifier by using a particle swarm optimization algorithm to form an interaction matrix for the connection strength of input spatial information particles and input samples. Kumar et al. (2019) combined fuzzy information granulation and neural networks (NNs) to construct a granular neural networks (GNNs). In the GNNs, all operations are changed to be performed based on the information granules rather than on the values of the data itself.

Starting from the core part of fault diagnosis, the fault features extraction and fault classification results are studied respectively. Finally, a combined CNN-GC fault diagnosis model is proposed. The current fault diagnosis algorithm of rolling bearings mainly has the following problems:

• 1. When extracting fault features, it relies heavily on manual experience and an expert database, and different features need to be extracted for different industrial equipment or fault attributes, which lacks flexibility and generalization, thus causing the fault diagnosis algorithms to be different in different articles; at the same time, the experimental data used for fault diagnosis are mostly time-dependent, and retaining as many features in the time domain as possible is the key to diagnostic accuracy.

• 2. To maximize the model performance at the granularity level, the traditional information granulation method ignores its numerical performance, resulting in the final granularity model cannot meet the requirements of accurate prediction at the numerical and granularity level in practical applications (Lu et al. 2021).

• 3. The depth of the neural network, through training the model that contains a large number of parameters, and these parameters are just some fixed values, each network consists of network and network between the hidden layer of specific meaning not clear know, unable to a better understanding of the relationship between the input and output model, can be interpreted.

To solve the above problems, this paper proposes a new CNN-GC approach for supervised fault diagnosis. The conventional CNN is used for features extraction of faults, and the faults are classified based on the extracted features through hyperspherical information granules based on granular computing (Fu et al. 2020). Compared with existing fault diagnosis model design methods, CNN-GC has the following innovations:

• 1. In terms of structure, through the multilayer iteration of convolutional and pooling layers of CNN, the extracted features are dimensionalized, and then the dimensionalized results are input into the hypersphere information granules to diagnose and classify the fault types, which enhances the interpretability while retaining the “end-to-end” characteristics of traditional CNN. The information granules can be expressed linguistically to increase the readability of the network and reduce the black-box characteristics caused by too many parameters of the neural network (Guidotti et al. 2018).

• 2. The information granulation model of CNN-GC under multiple granularities (Lu et al. 2015) proposed in this paper acts directly on the original time-domain signal to maximize the preservation of features on the original time-domain data and can produce both more accurate values and better granularity outputs, suggesting a model that can be used for complex classification problems.

• 3. Hyperspherical information granules have previously been used only on some synthetic datasets and traditional public datasets. In this paper, by combining them with CNN, they are applied to practical industrial scenarios, and their application scenarios can continue to be extended subsequently.

This paper is structured as follows. Section 2 focuses on the fundamentals involved in this paper. Section 3 describes in detail the bearing fault diagnosis model proposed in this paper: CNN-GC. Section 4 conducts experimental validation and carries out some comparative tests. Section 5 provides a series of conclusions and identifies further research.

2 Basic knowledge

In this section, we introduce some of the fundamentals involved in the CNN-GC algorithm, mainly including CNN and hypersphere information granules.

2.1 CNN

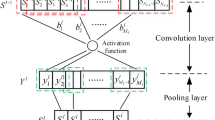
CNN is a kind of feedforward neural network with deep structure and volume computation and is one of the representative algorithms of deep learning. Typical neural networks include filtering level, which is mainly used for feature extraction, and classification level, which is based on the former. The filtering level contains convolutional, activation, and pooling layers and the classification level contains fully connected and softmax layers (Zhao and Liu 2019). In this paper, CNN is designed to process one-dimensional signals, and its basic principle is shown in Fig. 2.

Fig. 2

Basic principles of one-dimensional CNN

Figure 2 contains an input layer, two convolutional layers, two pooling layers, a flatten layer, a fully connected layer, and a softmax layer. After the input signal passes through this neural network, the final output is obtained from the softmax layer.

In this paper, Max Pooling is used to implement downsampling, which has the advantage of obtaining position-independent features for periodic time-domain signals (Zhang et al. 2018). The one-dimensional pooling operation is shown in Fig. 3, where the input layer has a feature width of 8 and a depth of 4. The original features are reduced to output features with a width of 4 and a depth of 4 by a pooling operation with both step sizes of 2.

Fig. 3

One-dimensional pooling operation diagram

2.2 Hypersphere information granules

Granular computing is a world view and methodology to look at the objective world. It is a new method to simulate human thinking and solve complex problems in the field of artificial intelligence. It emphasizes the multi-level and multi-perspective understanding and description of the real world, to obtain a granular structure representation of problems. In the face of complex data information, granular computing can divide it into several simple entities according to their attributes and characteristics, that is, a series of data sets that are indistinguishable, similar, or similar in function or close in physical distance, that is, a series of information particles (Fu et al. 2020). People extract the similarity of features from the data samples and divide and abstract the data into several specific categories of data blocks. Each data block is an “information particle”. By combining and summarizing the information particles, a “particle description” of each category of data (Gacek and Pedrycz 2006; Ouyang et al. 2021) can be formed, which is information granulation. For example, when we distinguish different leaves, we can distinguish them according to their shape, color, edge lines, and so on, which is a process of information granulation.

Hypersphere information granules definition (Fu et al. 2020): Consider a normalized n-dimensional data set $X=\left\{ x_{t} \mid x_{t} \in [0,1]^{n}, t=1,2, \ldots , N\right\}$, based on n dimensional data set X construct an expression form of information granule as follows:

$$\begin{aligned} \Omega =\left\{ x_{k} \mid \left\| x_{k}-v\right\| \le \rho , x_{k} \in X\right\} \end{aligned}$$

(1)

where, v and $\rho$ represent the center and radius of the constructed information particle respectively the symbol representing the constructed information center and radius of grain, $\Vert \cdot \Vert$ represents the Euclidean distance. The information grain represented by the formula can simultaneously summarize the features of all n dimensions of the data set X. When the data dimension n = 2, the geometric form of information grain $\Omega$ is a circle with v as the center and $\rho$ as the radius, which includes all the samples in the data set X falling inside the circle. When the data dimension n = 1, the geometric form of information particle $\Omega$ is a line segment. When the data dimension n = 3, the geometry of the information particle $\Omega$ is a ball, which is uniformly called supersphere information particle for convenience. Figure 4 illustrates the hypersphere information grain constructed by information granulation in a two-dimensional space.

Fig. 4

Hypersphere information granule $\Omega$ expressed in form of a circle with center ${\varvec{v}}$ and radius $\rho$ for the two-dimensional dataset X

Considering the construction of a reasonable and unique semantic hypersphere information granules based on numerical data, the information granules need to satisfy the following two requirements:

• 1. Coverage (information grain is reasonable): The information grain constructed based on the original numerical data should cover as many valuable samples from the original data set as possible. The more valuable samples are covered, the more features of the original data can be included in the information grain, and the information grain is considered reasonable. Specifically, the coverage of the hyperspherical information granule $\Omega$ defined on the dataset X can be defined by the following equation:

  $$\begin{aligned} {\text {Cov}}(\Omega )={\text {card}}\left\{ {\varvec{x}}_{k} \mid \left\| {\varvec{x}}_{k}-{\varvec{v}}\right\| \le \rho , {\varvec{x}}_{k} \in {\varvec{X}}\right\} \end{aligned}$$

  (2)

  where, ${\text {card}}\{\cdot \}$ represents the number of samples of the dataset X that are included in the hypersphere information granule $\Omega$.

• 2. Specificity (information grains are special): Information grains constructed based on raw numerical data should have a more explicit location and semantics. This means that the size of the constructed information granules should be as small as possible because the smaller the information granules contain fewer data samples, the more unique semantics they have, and the higher the specificity. Typically, the specificity of hypersphere information granules can be quantified using a monotonic non-increasing function on the size of the hypersphere information granules. Specifically, the specificity of a hyperspherical information granule $\Omega$ defined on a data set X can be defined by the following equation:

  $$\begin{aligned} {\text {Spec}}(\Omega )=1-\frac{\rho }{\rho _{\max }} \end{aligned}$$

  (3)

  Here $\rho _{\max }$ is a constant representing the farthest value in the distance from the center ${\varvec{v}}$ of all samples in the data set X. Therefore, the specificity of the hypersphere information granules depends only on the radius $\rho$ of the hypersphere information granules.

An increase in coverage leads to a decrease in specificity and vice versa, as shown in Fig. 5. When constructing hypersphere information granules around multidimensional numerical data, it is also necessary to balance and compromise the two properties.

Fig. 5

The relationship between coverage and specificity of hypersphere information granule in the two-dimensional case

Specifically, the values of the center ${\varvec{v}}$ and the radius $\rho$ are determined to make the product of the coverage and specificity obtain the maximum value, i.e.

$$\begin{aligned} \underset{{\varvec{v}}, \rho }{\arg \max }\{{\text {Cov}}(\Omega ) \times {\text {Spec}}(\Omega )\}. \end{aligned}$$

(4)

The $\arg \max$ here represents the value of the center ${\varvec{v}}$ and radius $\rho$ when finding the maximum value of let ${\text {Cov}}(\Omega ) \times {\text {Spec}}(\Omega )$.

3 Bearing fault diagnosis algorithm: CNN-GC

CNN-GC is an algorithm that combines CNN and granular computing. Specifically, CNN is used to first extract features from the existing data, and then the multiple data attributes extracted are used as input to hypersphere information granule to perform classification prediction, which in turn leads to a bearing fault diagnosis analysis model by which classification can be executed on whether the bearing is faulty and the fault category.

3.1 Features extraction

The input data is expanded into a 1-dimensional feature vector after being processed by multiple convolutional and pooling layers, and the expansion is shown in Fig. 6, which shows the output of a 4 $\times$ 2-dimensional pooling layer expanded into an 8 $\times$ 1 one-dimensional vector.

Fig. 6

Expansion diagram of pooling layer

In CNN-GC, the output of the last pooling layer is tiled into an n-dimensional features vector through a fully connected layer as the input to the hypersphere information granules. When the obtained n-dimensional feature vectors cannot meet the requirements of classification accuracy and precision in the next step, the relevant parameters involved in the convolution and pooling layers, etc., can be considered to adjust the output results to be maximized.

3.2 Hypersphere information granule formation

The formation of hypersphere information granules contains two parts: the merging mechanism and the elimination mechanism (Fu et al. 2020).

3.2.1 Merging mechanism

The c data subsets ${\varvec{D}}_{1}, {\varvec{D}}_{2}, \ldots , {\varvec{D}}_{c}$ are divided. Each data subset ${\varvec{D}}_{1}, {\varvec{D}}_{2}, \ldots , {\varvec{D}}_{c}$ is first clustered separately with the help of a fuzzy C-mean clustering algorithm to obtain the respective clustering prototypes for each subset; a prototype merging mechanism is proposed to control the coarseness of the division to obtain a series of smaller-sized data blocks on no data subset, and the class parameters of the clusters on each data subset are set to R.

Consider the ith subset

$${\varvec{D}}_{i}=\left\{ {\varvec{x}}_{i k}=\left[ x_{i k 1}, x_{i k 2}, \ldots , x_{i k n}\right] \mid {\varvec{x}}_{i k} \in [0,1]^{n}\right\}$$

where, $k=1,2, \ldots , N_{i}$ of the dataset ${\varvec{D}}$. After performing fuzzy C-mean clustering on this subset, a matrix containing R clustering prototypes of size $R \times n$ can be generated, i.e., ${\varvec{V}}_{i}=\left[ {\varvec{v}}_{i 1}, {\varvec{v}}_{i 2}, \ldots , {\varvec{v}}_{i p}, {\varvec{v}}_{i q}, \ldots , {\varvec{v}}_{i R}\right] ^{T}=\left[ v_{i s h}\right] _{\begin{array}{c} s=1,2, \ldots , R \\ h=1,2, \ldots , n. \end{array}}$ These initial clustering prototypes in matrix ${\varvec{V}}_{i}$ can then be merged according to the distance between them, with the following merging mechanism.

First calculate the distance between two pairs of prototypes in matrix ${\varvec{V}}_{i}$ to construct an $R \times R$ upper triangular distance matrix $M=\left[ d_{r w}\right] _{\begin{array}{c} r=1,2, \ldots , R \\ w=1,2, \ldots , R \end{array}}$, where $d_{r w}=\left\| {\varvec{v}}_{i r}-{\varvec{v}}_{i w}\right\|$. Obviously, all entries in this upper triangular distance matrix that are not zero represent the distance between two pairs of clustered prototypes. Subsequently, the two closest cluster prototypes can be found by selecting the element with the smallest value in M. Assuming that the element with the smallest value is located in row p and column q of the matrix M $(p \ne q, p, q \in \{1,2, \ldots , R\})$, i.e., the smallest value of $d_{p q}$, it can be determined that ${\varvec{v}}_{i p}$ and ${\varvec{v}}_{i q}$ are the two closest initial cluster prototypes. If the minimum distance $d_{p q}$ is greater than a predefined threshold $d_{t h}$, then the two prototypes ${\varvec{v}}_{i p}$ and ${\varvec{v}}_{i q}$ will remain in the prototype matrix ${\varvec{V}}_{i}$. If $d_{p q}$ is less than $d_{t h}$, it means that the two prototypes are too close and need to be merged into a new prototype using the following equation:

$$\begin{aligned} {\varvec{v}}_{i j}^{\text {new }}=\frac{\sum _{k=1}^{N_{i}}\left( u_{p k}+u_{q k}\right) ^{m} {\varvec{x}}_{i k}}{\sum _{k=1}^{N_{i}}\left( u_{p k}+u_{q k}\right) ^{m}}, \end{aligned}$$

(5)

where, m is the fuzzification factor in fuzzy C-mean clustering, and $u_{p k}$ and $u_{q k}$ represent the affiliation of the kth sample ${\varvec{x}}_{i k}$ in the data subset ${\varvec{D}}_{i}$ to ${\varvec{v}}_{i p}$ and ${\varvec{v}}_{i q}$, respectively, which can be calculated using the following equation:

$$\begin{aligned} u_{s k}=\left[ \sum _{e=1}^{c}\left( \frac{\left\| x_{i k}-v_{i s}\right\| ^{2}}{\left\| x_{i k}-v_{i e}\right\| ^{2}}\right) ^{\frac{2}{m-1}}\right] ^{-1}, s=p, q. \end{aligned}$$

(6)

Once the new prototype is obtained by merging, the pth and qth rows of the prototype matrix ${\varvec{V}}_{i}$ are removed and the new prototype ${\varvec{v}}_{i j}^{\text {new }}$ is added to its last row. At this point, the prototype matrix ${\varvec{V}}_{i}$ is updated to ${\varvec{V}}_{i}=\left[ {\varvec{v}}_{i 1}, {\varvec{v}}_{i 2}, \ldots , {\varvec{v}}_{i R}, {\varvec{v}}_{i j}^{\text {new }}\right] ^{T}$, and the number of rows is changed from R to $R-$ 1. At the same time, the upper triangular distance matrix M, which records the distance between two prototypes, is updated by recalculating the distance between two prototypes to the size of $(R-1) \times (R-1)$. The above prototype merging mechanism is repeated until the minimum value in the matrix M is greater than the predefined threshold $d_{\text {t h}}$, which means that the prototype merging is completed and there are no two prototypes closer to $d_{\text {t h}}$.

Take the ith data subset ${\varvec{D}}_{i}$ of the data set ${\varvec{D}}$ as an example, and construct hypersphere information grains, namely $\Omega _{i 1}, \Omega _{i 2}, \ldots , \Omega _{i R_{i}}$, on each of the Ri data chunks $\left( {\varvec{D}}_{i 1}, {\varvec{D}}_{i 2}, \ldots , {\varvec{D}}_{i R_{i}}\right)$ divided by it. The lth data chunk of the known data subset ${\varvec{D}}_{i}$ is denoted as $D_{i l}$, and its center is the prototype of the data chunk ${\varvec{v}}_{i l}^{\text {new }}$, $l=1,2, \ldots , R_{i}$. Here it can be determined that the lth merged prototype ${\varvec{v}}_{i l}^{\text {n e w}}$ is the center of the hypersphere information grain $\Omega _{i l}$ to be constructed on the data nugget, so the whole hypersphere information grain can be determined by determining the radius $\rho _{i l}$.

Regarding the coverage and specificity of the hypersphere pheromone, to determine the radius $\rho _{i l}$, perhaps two requirements are satisfied: (1) the hypersphere pheromone $\Omega _{i l}$ can encompass as many samples as possible in ${\varvec{D}}_{i l}$; (2) the hypersphere pheromone $\Omega _{i l}$ should be as small in volume as possible. These two properties of the hypersphere information grain can be quantified by the following two equations:

$$\begin{aligned} \text { global } {\text {Cov}}_{\mathrm {i}}=\sum _{l=1}^{R_{i}} {\text {local}} {\text {Cov}}\left( \Omega _{\mathrm {il}}\right) , \end{aligned}$$

(7)

$$\begin{aligned} \text { global Spec }_{\mathrm {i}}=\sum _{l=1}^{R_{i}} {\text {local}} {\text {Spec}}\left( \Omega _{\mathrm {il}}\right) . \end{aligned}$$

(8)

It can be seen that the two are still in conflict and can be balanced by adjusting the values of center and radius. Since the centers of the hyperspheres $\Omega _{i 1}, \Omega _{i 2}, \ldots , \Omega _{i R_{i}}$ to be constructed have been determined to be the prototypes ${\varvec{v}}_{i 1}^{\text {new }}, {\varvec{v}}_{i 2}^{\text {new }}, \ldots , {\varvec{v}}_{i R_{i}}^{\text {new }}$ obtained by merging the data subsets ${\varvec{D}}_{i}$, it is only necessary to determine the radii of each hypersphere $\rho _{i 1}, \rho _{i 2}, \ldots , \rho _{i R_{i}}$ to complete the reconciliation of the two, as in the following equation:

$$\begin{aligned} \underset{\rho _{i 1}, \rho _{i 2}, \ldots , \rho _{i R_{i}}}{\arg \max }\left\{ \text { global } {\text {Cov}}_{\mathrm {i}} \times \text { global Spec }_{\mathrm {i}}\right\} . \end{aligned}$$

(9)

To solve this problem, the differential evolutionary optimization algorithm is still used. The specific process means first constructing a population containing a set of candidate solutions, each of which is a randomly generated set of vectors, i.e., $\left[ \rho _{i 1}, \rho _{i 2}, \ldots , \rho _{i R_{i}}\right]$. Then this population starts to evolve iteratively towards maximizing the $\text { global } {\text {Cov}}_{i} \times \text { global } {\text {Spec}}_{i}$ value. Each of these evolutionary steps generates some new individuals of the population by change and crossover operations. When the number of evolved generations reaches the maximum, the best candidate solutions $\rho _{i 1}^{\text {opt}}, \rho _{i 2}^{\text {opt}}, \ldots , \rho _{i R_{i}}^{\text {opt}}$ of Eq. C are obtained, and thus the hypersphere infograins $\Omega _{i 1}, \Omega _{i 2}, \cdots , \Omega _{i R_{i}}$ on the data subset of ${\varvec{D}}_{i}$. where the lth hypersphere infograins are denoted as $\Omega _{i l}=\left\{ {\varvec{x}}_{i k} \mid \left\| {\varvec{x}}_{i k}-{\varvec{v}}_{i l}^{\text {new }}\right\| \le \rho _{i l}^{o p t}, {\varvec{x}}_{i k} \in {\varvec{D}}_{i l}\right\}$, Next, these This joint hypersphere information grain can characterize the structure of the data subset Di whose class label is $L_{i}$ more accurately than a single hypersphere information granule. For other data subsets of the data set ${\varvec{D}}$, the same method as above is used to construct the corresponding joint hypersphere information grain. Through the above steps, the corresponding joint hypersphere information granules ${\varvec{\Omega }}_{1}, {\varvec{\Omega }}_{2}, \ldots , {\varvec{\Omega }}_{c}$, where, ${\varvec{\Omega }}_{i}=\Omega _{i 1} \cup \Omega _{i 2} \cup \ldots \cup \Omega _{i R_{i}}, \quad i=1,2, \ldots , c$ are obtained for each data subset on the whole data set ${\varvec{D}}$.

3.2.2 Elimination mechanism

Each joint hypersphere information granule carries a semantic-implying which class the data it covers belongs to, which requires that these joint hypersphere information granules do not overlap two by two to form the final granule classification model.

For any two joint hypersphere information granules ${\varvec{\Omega }}_{a}=\Omega _{a 1} \cup \Omega _{a 2} \cup \cdots \cup \Omega _{a R_{a}}$ and ${\varvec{\Omega }}_{b}=\Omega _{b 1} \cup \Omega _{b 2} \cup \cdots \cup \Omega _{b R_{b}}$, they contain $R_{a}$ and $R_{b}$ hypersphere information granules, where, $a \ne b, a, b=1,2, \cdots , c$. The pth hypersphere information granule in ${\varvec{\Omega }}_{a}$. The pth hypersphere information granule $\Omega _{a p}=\left\{ {\varvec{x}}_{a k} \mid \left\| {\varvec{x}}_{a k}-{\varvec{v}}_{a p}^{\text {new}}\right\| \le \rho _{a p}^{\text {opt}}, {\varvec{x}}_{a k} \in {\varvec{D}}_{a p}\right\}$ in ${\varvec{\Omega }}_{a}$ and the qth hypersphere information granule $\Omega _{b q}=\left\{ {\varvec{x}}_{b k} \mid \left\| {\varvec{x}}_{b k}-{\varvec{v}}_{b q}^{\text {new }}\right\| \le \rho _{b q}^{\text {opt}}, {\varvec{x}}_{b k} \in {\varvec{D}}_{b q}\right\}$ in $\mathbf {\Omega }_{b}$, if the distance between the centers of $\Omega _{a p}$ and $\Omega _{b q}$, i.e.,$d_{a b}=\left\| v_{a p}^{\text {new}}-v_{b q}^{\text {new}}\right\|$, is less than the sum of their two radii, i.e., $\rho _{a p}^{o p t}+\rho _{b q}^{\text {opt}}$, it means that $\Omega _{a p}$ and $\Omega _{b q}$ are overlapping.

To eliminate the overlap between two of the c joint hypersphere information granules ${\varvec{\Omega }}_{1}, {\varvec{\Omega }}_{2}, \ldots , {\varvec{\Omega }}_{c}$, the position relationship between the two joint hypersphere information granules are considered, and while keeping the center unchanged, the first step is to change the radius so that the two are in a tangent state. Subsequently, the tangency point is moved along the line between the centers of the two hypersphere information granules ${\varvec{v}}_{a p}^{\text {new}}$ and ${\varvec{v}}_{b q}^{\text {new}}$, and the optimal radii $\rho _{a p}^{\text {adj}}$ and $\rho _{b q}^{\text {adj}}$ are calculated by the following equation:

$$\begin{aligned} \underset{\rho _{a p}^{\text {adj}}, \rho _{b q}^{\text {adj}}}{\arg \max }\left\{ A\times B\right\} \end{aligned}$$

(10)

where, $A = ({\text {Cov}}\left( \Omega _{a p}\right) +{\text {Cov}}\left( \Omega _{b q} \right) )$ $B = ({\text {Spec}}\left( \Omega _{a p}\right) +{\text {Spec}}\left( \Omega _{b q}\right) )$.

As a result, two new hypersphere information granules are formed without overlapping each other, and then the position relationship between the hypersphere information granules contained in ${\varvec{\Omega }}_{a}$ and ${\varvec{\Omega }}_{b}$ is repeatedly calculated and the overlap is eliminated in the above way by an iterative mechanism. At this point, the overlap between the joint hypersphere information granules is eliminated, and the final hypersphere information granules are formed.

3.3 Bearing fault analysis model

In summary, the bearing fault diagnosis model contains two components: feature extraction and hypersphere information granule execution classification. The specific execution process of the model is shown in Algorithm 1.

In this paper, the entire bearing fault diagnosis model is split into two sets of inputs and outputs. Firstly, suitable x,y,z parameters are selected in the CNN algorithm, then the CNN is used to extract features from the raw data according to the different classes of faults, the extracted n-dimensional features are normalized, while the class labels are assigned according to the different types of faults as secondary inputs, and finally the faults are classified through a merging mechanism (Sect. 3.2.1) and an elimination mechanism (Sect. 3.2.2) formed by hypersphere information granules (Joshi 2021).

4 Experimental verification

All data need to be normalized pre-processed before the experiment, as shown in the Eq. (11).

$$\begin{aligned} X_{\text {norm}}=\frac{X-X_{\min }}{X_{\max }-X_{\min }}, \end{aligned}$$

(11)

where, $X_{\text {norm}}$ is the normalized data, X is the original data, $X_{\max }$ and $X_{\min }$ are the maximum and minimum values of the original data set respectively. Subsequently, a data classification algorithm based on joint hypersphere information grains was invoked on each dataset to build the corresponding grain classification model based on the basic framework of two-stage grain description (Pedrycz et al. 2015). The fuzzification factor m in the Fuzzy c-means clustering (FCM) (Bezdek 2013) used to divide each data subset is set to 2. The number of prototypes generated by clustering R = 10, and then the number of prototypes ultimately used to divide data subsets is controlled by adjusting the value of distance threshold $d_{\text {th}}$ during prototype combination, so the threshold $d_{\text {th}}$ is constantly iterated from 0 to 1 with a step size of 0.05.

In CNN-GC, ten-fold cross-validation is used for hypersphere information granule classification experiments. The input dataset is divided into 10 parts, of which 9 parts are used as training data and 1 part is used as test data, and the average value is obtained in 10 experiments. The results of the cross-validation of the classification model on each dataset are constructed, and the classification results are expressed in the form of “Mean”, named $Q_{\text {Acc}}$.

4.1 The experimental data

4.1.1 The data source

Experimental data for this paper were obtained from the Rolling Bearing Data Center at CWRU (https://engineering.case.edu/bearingdatacenter). The CWRU bearing center data acquisition system is shown in Fig. 7. The experimental platform consists of a 2hp motor (left side of the figure) (1 hp = 746 W), a torque sensor (middle), a power meter (right) and electronic control equipment (not shown). A single point of failure was laid out on the bearing using EDM technology with a failure diameter of 0.007 inch, 0.014 inch, and 0.021 inch (1 inch = 2.54 cm). The diagnosed bearing had a total of 3 defect locations, Inner Race, Ball, and Outer Race, for a total of 9 damage states, with each damage Each damage state includes 4 types of load: 0 hp (corresponding to motor speed 1797 rpm), 1 hp (corresponding to motor speed 1772 rpm), 2 hp (corresponding to motor speed 1750 rpm) and 3 hp (corresponding to motor speed 1730 rpm) as shown in Table 1. The faulty bearing used is an SKF bearing. The acceleration sensor was used to collect the vibration signal in the experiment, and the sensor was placed on the motor housing by using a magnetic base. The sampling frequency of the system was divided into 12 kHz and 48 kHz (12,000 and 48,000 data points per second, respectively).

Fig. 7

Schematic diagram of bearing acquisition system

Table 1 Fault types

4.1.2 Data pre-processing

To facilitate the training of the CNN, the signal x is normalized for each segment, see Eq. (11). A total of 2 data sets were prepared in the experiment, as shown in Table 2. Each data set contains 9 damage states and 1 normal state, 10 states, in total. Data sets 1 and 2 correspond to the DE side at 12 kHz and the DE side at 48 kHz, respectively. 1000 samples were taken for each state (250 samples for each load case) to form a complete data set with a total of 10,000 samples. The experiments were performed with 2048 data points for each diagnosis. The samples were enhanced using a data set enhancement technique, by which is meant that there is an overlap between the signal of each segment and its subsequent segment.

Table 2 Datasets

4.2 Proposed method demonstration

4.2.1 Features extraction

In this paper, features extraction of the input data is performed by convolutional and pooling layers in CNN, and the ReLU activation function is added after the convolutional layer to map the originally linearly indistinguishable multidimensional features to another space. A Batch Normalization (BN) layer is added between the convolutional layer and the activation layer to reduce internal covariate transfer (Szegedy et al. 2017), improve the training efficiency of the network, and enhance the generalization ability of the network. One-hot coding is used for the input sample data (Sun et al. 2016).

In the experiments, the number of network layers of the CNN was specified as 3, 4, 5, 6 by hyperparameter tuning, the dimension of the extracted features was specified as $2^{n}$, and the output results were obtained as shown in Table 3. The highest accuracy of the fault diagnosis type was obtained when the convolutional and pooling layers were both 3 and the feature dimension was 128 (i.e. n = 7), and this was named 3-128 for the convenience of writing below, and so on, yielding “4-512”, “5-128 ”, “6-128”.

Table 3 Features extraction

4.2.2 Classification of hypersphere information granules

The extracted features are put into the hypersphere information granule classification algorithm for classification in turn, and the classification results are shown in Table 4, and the classification results are determined based on the classification accuracy, which is expressed in the form of “Mean”, named $Q_{\text {Acc}}$.

Table 4 Experimental results with different feature dimensions

As can be seen from Table 4, the number of features extracted to different dimensions by hyperparameter tuning into the hypersphere information grain can be obtained with different classification accuracies, and the highest accuracy for each dataset is marked in bold. In general, as the number of network layers increases, the higher the accuracy of hypersphere classification. The experimental results show that the reasonable information granulation method for numerical data proposed for this paper is feasible in the classification problem, and the application of this method can construct granular classification models with simple rules and reliable classification accuracy.

4.3 Comparative tests

As can be seen from Table 4, by adjusting the parameters such as the size, step size, and several convolutional kernels in CNN-GC as well as the number of layers of convolutional and pooling layers, the feature results in various dimensions are obtained, and when the number of convolutional and pooling layers is fixed, the higher the dimensionality of the extracted features is, the higher the accuracy of classification is.

In this paper, the final classification results are visualized by using the t-SNE algorithm, which reduces the feature expressions to 2 dimensions. The visualization results of Dataset1 are shown in Fig. 8. (1)–(4) correspond to the visualization results of Dataset1 in different dimensions in Table 3 in order, where the black triangles represent the clustering centers of hypersphere information grains.

Fig. 8

Visualization of the results of Dataset1

The CNN-GC algorithm proposed in this paper is compared with other fault diagnosis algorithms, as shown in Table 4. Other fault diagnosis algorithms mainly include Sparse self-coding (Tan et al. 2015), HDN (Gan and Wang 2016), SPNN (Sun et al. 2016b), SVM, DNN (Jia et al. 2016), and WDCNN (Zhang et al. 2018). All these fault diagnosis algorithms were also acted on the CWRU bearing dataset and different accuracy rates were obtained.

It can be seen from Table 4 that the CNN-GC algorithm in this paper significantly outperforms other algorithms in bearing fault diagnosis by 0.1% on Dataset1 and 0.2% on Dataset2 compared to existing algorithms.

In addition to this, it can be seen that, within a certain range, as the number of network layers increases, the recognition rate of fault diagnosis continues to improve. Too high or too low a dimensionality of the extracted features will affect the accuracy of the final recognition, this is because too low a dimensionality will make the extracted features incomplete and too high a dimensionality will interfere with the granulation model of the second input and prevent correct recognition.

5 Conclusion

In this paper, we focus on the model design of bearing fault diagnosis based on hypersphere iterative granularity. Firstly, through the convolutional layer of CNN, the pooling layer performs features extraction on the input data, and then the extracted features are put into the hypersphere information grain, and finally, the bearing fault type is judged according to the classification results. In the feature extraction of the input data using CNN, this paper obtained the feature extraction results for network layers 3–6 by hyperparameter optimization, which in turn the corresponding classification results were obtained at the hypersphere information granule. When validated on the CWRU dataset of faulty bearings, the accuracy was up to 99.8$\%$, i.e. the type of failure of the bearing could be accurately predicted.

The classification model constructed by the proposed classification algorithm based on joint hypersphere information grains can capture the various data structure features of the dataset from an intuitive perspective, and the resulting joint information grains can fit the geometric distribution shape of each class of samples in the original dataset under fixed parameters, thus realizing feature extraction to construct classification rules and achieving positive prediction for fault diagnosis.

The CNN-GC proposed in this paper improves the interpretability of the classification model without reducing the accuracy rate compared with other bearing fault diagnosis methods. CNN-GC can be applied to other industrial parts in the future, and CNN can also be combined with hyperboxes (Lu et al. 2018), hypercubes, constructing other forms of information granules to achieve granular descriptions (Lu et al. 2020), reducing the bias caused in classification problems through ensemble learning (Liu and Cocea 2017), and solving classification modeling problems in more complex scenarios.