A Theoretical Framework for Risk–Cost-Optimized Maintenance Strategy for Structures

Abstract

This paper presents a theoretical framework for developing a risk–cost optimised maintenance strategy for structures during their whole service life. A time-dependent reliability method is employed to determine the probability of structural failure and a generic form of stochastic model is developed for structural responses. To facilitate practical application of the proposed framework, a general algorithm is developed and programmed in a user-friendly manner. The merit of the proposed framework is that, in predicting when, where and what maintenance is required for the structure, all structural components and multi-failure modes are considered. It is found in the paper that, to ensure the safe and serviceable operation of the structure as a whole, some components need maintenance multiple times for different failure modes, whilst other components need “do nothing”. It is also found that ignorance of correlation amongst structural components and failure modes would underestimate the risk of structural failures in longer term and that the components with higher cost of structural failures require more maintenance actions. The paper concludes that the proposed framework can equip structural engineers, operators and asset managers with a tool for developing a risk–cost optimal maintenance strategy for structures under their management.

1 Introduction

Civil infrastructure plays a pivotal role in a nation’s economy, prosperity, social wellbeing, quality of life and the health of its population. This has been well recognized by industry, business, community and political leaders all over the world. However, due to its long-term service, coupled with exposure to aggressive environment and increased demands, deterioration of infrastructure has led to unserviceable or unsafe operation, and in some cases, catastrophic collapses of both underground and aboveground infrastructure. Various cases of catastrophic failures of infrastructure, such as I-35W Mississippi River bridge [1], Sasago tunnel in Tokyo [2] and underground water mains [3], are well documented.

The deterioration of infrastructure is clearly the main cause of structural damage and collapse. This is a severe global problem with consequences becoming more and more catastrophic. One apparent solution is to replace the deteriorated infrastructure; however, this is very costly. For example, the replacement cost for a tunnel structure is estimated at $250 million/km [4] and the estimated replacement cost for national and non-national highway system bridges in the US alone is about $52 billion [5]. More importantly, due to the ever-increasing scarcity of resources, this solution is not sustainable and impractical for some types of infrastructure, such as the underground structures.

To ensure the safe and serviceable operation of infrastructure, maintenance or intervention, including repairs, strengthening, instalment, etc., for infrastructure as a structural system is essential. The problem is how to determine when, where and what to maintain for a structure at a minimal risk and with effective cost. Lack of effective maintenance strategy has resulted in a situation where safe structures or components have been routinely maintained unnecessarily, whilst unserviceable or near-failure structures or components have not been maintained timely, leading to avoidable failures. It is well known that the maintenance cost is very high for certain types of structures and problems. For example, in the US, the annual cost for the problem of reinforcement corrosion is about $100 billion [6]. The annual cost of maintenance for tunnels could be as high as $150 K/km [7]. Furthermore, the cost of structural failures is beyond estimate when it involves casualties. Evidently, a change of such situation demands a risk–cost-optimized maintenance strategy as proposed here.

Various frameworks have been proposed to formulate strategies for inspection, maintenance and decision-making for deteriorated structures using reliability-based methods. These maintenance strategies are based on optimisation of inspection/repair times through minimisation of the total costs of inspection, repair and failure [8,9,10]. In addition to cost, risk, defined as the product of probability of failure and cost, is also used in optimisation of maintenance strategies [11,12,13]. Multi-objective optimisations considering reliability, risk and cost have also been investigated [14, 15]. A review of the key aspects involved in the maintenance and operation of structures under uncertainty can be found in [16]. These strategies have been applied to a variety of structural problems, e.g., reinforced concrete (RC) bridges subjected to de-icing salts [17], steel bridges subjected to corrosion [18] and offshore steel structures subjected to fatigue [19].

A thorough review of the available frameworks for maintenance strategy shows that a comprehensive maintenance strategy, capable of considering multiple structural components with different failure modes and using advanced time-dependent reliability methods, has not been fully developed. Although there have been some studies that consider different failure modes, categorized as ultimate and serviceability limit states [20], most of these studies consider only a single failure mode, either ultimate [18] or serviceability [21, 22]. Whilst maintenance strategies based on the probability of structure as a system failure rather than its component failure can be found in the literature [23,24,25], these studies only consider one failure mode for each structural component. Integration of structural components and failure modes into a single system has not been investigated previously. More importantly, in these studies, the probability of system failure has not been used as a basis for calculating the structural risk but only used as an indicator to determine the time for maintenance. Finally, only a few maintenance strategies based on advanced time-dependent reliability methods, e.g., the first passage probability method, can be found [26]. Most of the current maintenance strategies employ the Monte Carlo simulation technique without considering the correlation in the deterioration process over time for calculating the probability of failure.

The intention of this paper is to propose a framework for developing a risk–cost-optimized maintenance strategy for structural systems. The first-passage probability method is employed to determine the probability of structural failure. A generic form of stochastic model is proposed for structural response with various failure modes. To facilitate the practical application of the proposed framework, an algorithm is developed and programmed in a user-friendly manner. Two examples are provided to illustrate the application of the developed algorithm to corrosion-affected reinforced concrete structures. The significance of the proposed framework is that it can predict when, where and what to maintain for a structure to ensure its safe and serviceable operation during its whole lifespan. Timely maintenance has the potential to extend the service life of a structure and in some cases save lives.

2 Formulation of Maintenance Strategy

The conceptual design of the proposed maintenance strategy is based on the following idea. A structure or its component is to be maintained only when it fails (defined as undesirable behaviour). The failure should be predicted with sufficient confidence before it is too late to fix. A structure consists of many components, some of which are redundant. Thus, a structural system should be modelled as a series system for non-redundant components and as a parallel system for redundant components. Similarly, a component can fail in many modes, that can be categorised as ultimate and serviceability limit states. Serviceability limit states represent the state of operation of the system, while ultimate limit states represent the state of safety or collapse. Violation of any ultimate limit state constitutes the structural failure. Therefore, a series system is appropriate for ultimate failure modes. On the other hand, the violation of one serviceability limit state does not necessarily lead to safety concern or collapse. A realistic model for combining serviceability and ultimate limit states would be complex. To avoid this complexity, it is assumed that failure of all serviceability limit states constitutes the system failure. Thus, the parallel system is appropriate for assessment of serviceability failures [27, 28]. With this assumption, the ultimate and serviceability limit states can be related. Failure of components can be modelled as a system, which is a combination of series system for ultimate failures and parallel system for serviceability failures (referred to as component subsystem). This concept can be logically illustrated in Fig. 1.

Fig. 1

Concept of structural system failure

Since failure is not only random but also time variant, a time-dependent (i.e., when) reliability method should be used to determine the probability of the basic failure, i.e., a component (i.e., where) failure by a certain mode (i.e., what). This results in when, where and what maintenance actions are required for the structural system. The rationale for a risk–cost optimization is that, whilst keeping the probability of ultimate failure under control (to ensure safety), only when the probability of serviceability failure reaches an acceptable limit, the maintenance would be warranted. This means that if the probability of failure for serviceability limit states is less than a certain level, no maintenance action is required. However, if this level is reached, maintenance action is warranted. The merit of this rationale is to minimize the regular inspections for condition assessment without compromising the safety of the structure. The decision on when, where and what maintenance actions are required is based on the probability of system failure as schematically illustrated in Fig. 2. The maintenance actions, e.g., repair, strengthening, etc. take place on components for a given mode as shown in Fig. 2, where the first maintenance action at time t₁ (when) is determined by system failure and this action is on component 3 (where; the highest probability of three) for the given failure mode (what).

Fig. 2

Rationale for maintenance strategy

The above idea for risk–cost optimization can be mathematically formulated as follows:

$$\begin{aligned} & {\text{Minimize}}:\;\sum\limits_{i = 1}^{\text{Nr}} {\sum\limits_{j = 1}^{\text{Nc}} {\sum\limits_{k = 1}^{\text{Nm}} {\left( {[p_{\text{sys}} (t_{i} ) - p_{\text{sys}} (t_{i - 1} )] \times \frac{{{\text{CF}}_{jk} (t_{i} )}}{{(1 + i_{r} )^{{t_{i} }} }} + \frac{{{\text{CP}}_{jk} (t_{i} )}}{{(1 + i_{r} )^{{t_{i} }} }}} \right)} } } \\ & {\text{Subject}}\;{\text{to}}:\;p_{\text{u}} (t_{i} ) \le p_{\text{u,a}} ;p_{\text{s}} (t_{i} ) \ge p_{\text{s,a}} ;p_{\text{sys}} (t_{i} ) \le p_{\text{sys,a}} ;t_{i} - t_{i - 1} \ge \Delta t_{\hbox{min} } ;0 < t_{i} < t_{L} , \\ \end{aligned}$$

(1)

where t_i is the maintenance time with i refereeing to time sequence, N_r is the number of maintenance actions, N_c is the number of components in the system and N_m is the number of failure modes. In Eq. (1), CP_jk is the cost (including the annual discount rate) of maintenance action for jth component due to kth failure mode and CF_jk is the corresponding cost of failure (including the consequences). p_s and p_s,a are the probability and acceptable probability of serviceability failure, p_u and p_u,a are the probability and the acceptable probability of ultimate failure and p_sys and p_sys,a are the probability and the acceptable probability of system failure, respectively. Finally, Δt_min is the minimum time interval between two consecutive maintenance actions and t_L is the designed or expected lifetime of the structure. As it can be seen in Eq. (1), all the cost terms are converted to the present value (PV) by [29]:

$${\text{PV}} = \frac{{C_{jk} }}{{(1 + i_{r} )^{t} }},$$

(2)

where i_r represents the annual discount rate.

In Eq. (1), the optimization variables are a sequence of times for maintenance actions, i.e., t_i (i = 1, 2, …, N_r). At each optimized maintenance time, the critical structural component and failure mode are identified as outputs. These outputs will form the maintenance strategy for the structure; that is, when (t_i), where (component j) and what type of maintenance (failure mode k) is required for the structure during its service life (t_L) at an acceptable (minimum) risk (p_sys,a) and with effective cost. To ensure the safe and serviceable operation of the structure p_u,a and p_s,a probability limits are imposed. Types of maintenance are related to types of structural failure represented by a limit state, the attainment of which is quantified by a probability p_s or p_u, respectively. For example, for concrete structures, these maintenance actions may include (1) superficial patching for concrete cracking, (2) major repair for concrete delamination and (3) overall structural strengthening for rupture (or end of service life). It needs to be noted that how to maintain is beyond the scope of the paper assuming that after maintenance actions the structure is reinstated to a proportion of its original state with a maximum proportion of 100%.

As acknowledged in Sect. 1, various frameworks for maintenance strategy have been proposed (see above references). The essential difference between the maintenance strategy proposed herein and others is that the optimization variables of the former are related to components and failure modes. More importantly, the methods of time-dependent reliability as well as system reliability are employed in developing the strategy. This provides direct guidance on the types and times of maintenance to be carried out. It also facilitates practical applications of the proposed strategy since the design and assessment criteria are serviceability and ultimate limit states, as used by practitioners. A technical difference is that the estimation of p_sys is based on the first-passage probability method in conjunction with the system reliability as will be described below. Moreover, the maintenance strategy proposed herein has considered multiple failure modes for both components and structural system in the risk–cost optimization. Correlation amongst failure modes is also considered in the evaluation of probability of structural system failure. It needs to be noted that the proposed maintenance strategy also covers the “do-nothing” option of the conventional maintenance strategies since to determine when to do it implies “do nothing” at other times.

3 Probability of Structural Failure

A key contribution of the proposed maintenance strategy is the employment of upcrossing method in determining the probability of structural failure and in the risk–cost objective function. Although time-dependent reliability theory has been well established, it is briefly introduced in the paper for completeness of the developed maintenance strategy.

In assessing the risk of failures for a structure, a performance criterion should be established for the structure. In the theory of structural reliability, this criterion is expressed in the form of a limit state function as follows:

$$G(L,S,t) = L(t) - S(t),$$

(3)

where S(t) is the structural response (or load effect), L(t) is an acceptable limit for structural response (or structural resistance) and t is the time. With the limit state function of Eq. (3), the probability of structural failure, p_f, can be determined by

$$p_{t} (t) = P\left[ {G(L,S,t) \le 0} \right] = P\left[ {S(t) \ge L(t)} \right],$$

(4)

where P denotes the probability of an event. Equation (4) represents a typical upcrossing problem, which can be dealt with using time-dependent reliability methods [27]. Time-dependent reliability problems are those in which either all or some of the basic random variables are modelled as stochastic processes. To calculate the probability of failure for deteriorating structural systems, as is formulated in Eq. (4), different analytical and numerical methods can be used [30]. In this paper, the first passage probability method, which is an analytical method, is used for calculating the time-dependent probability of failure. The method allows for the correlation in the deterioration process over time. Other analytical methods based on the Gamma process, which is a form of Markov processes, can also be employed but these processes are memoryless and not able to account for the correlation in time. One of the limitations in first-passage probability method is that analytical solutions are only available for cases in which either the load effect or the resistance are modelled as stochastic process. Furthermore, few solutions for non-Gaussian stochastic processes have been developed [31, 32]. Although the formulated maintenance strategy, i.e., Eq. (1), is general, any time-dependent reliability methods can be used in determining the probability of failure over time.

For the problems involving stochastic process of structural response, S(t), the structural reliability depends on the time that is expected to elapse before the first occurrence of S(t) upcrossing a critical limit (the threshold) L(t) sometime during a given time interval [0, t_L]. Equivalently, the probability of the first occurrence of such an excursion is the probability of structural failure p_f(t) during that time interval. This is known as “first-passage probability” and under the assumption of Poisson processes, it can be expressed as follows (Melchers 1999):

$$p_{t} (t) = 1 - \left[ {1 - p_{\text{f}} (0)} \right]{\text{e}}^{{ - \int\limits_{0}^{t} {v{\text{d}}\tau } }} ,$$

(5)

where p_f(0) is the probability of structural failure at time t = 0 and υ is the mean rate for the response process S(t) to upcross the threshold L(t). In many practical problems, the mean upcrossing rate υ is small so that Eq. (5) can be approximated as follows:

$$p_{t} (t) = p_{\text{f}} (0) + \int\limits_{0}^{t} {v{\text{d}}\tau } .$$

(6)

The upcrossing rate in Eq. (6) can be determined by Rice formula (e.g., [27]) as follows:

$$v = v_{L}^{ + } = \int\limits_{L}^{\infty } {(\dot{S} - \dot{L}} )f_{{S\dot{S}}} (L,\dot{S}){\text{d}}\dot{S},$$

(7)

where $\nu_{L}^{ + }$ is the upcrossing rate of the response process S(t) relative to the threshold L, $\dot{L}$ is the slope of L with respect to time, $\mathop {\dot{S}\left( t \right)}$ is the time derivative process of S(t) and $f_{{S\dot{S}}} \left( \right)$ is the joint probability density function for S and $\dot{S}$. An analytical solution to Eq. (7) has been derived in [33] when S(t) is a Gaussian process and the threshold L is deterministic. This is expressed as follows:

$$v = v_{L = \det }^{ + } = \frac{{\sigma_{{\dot{S}|S}} }}{{\sigma_{S} }}\phi \left( {\frac{{L - \mu_{S} }}{{\sigma_{S} }}} \right)\left\{ {\phi \left( {\frac{{\dot{L} - \mu_{{\dot{S}|S}} }}{{\sigma_{{\dot{S}|S}} }}} \right) - \frac{{\dot{L} - \mu_{{\dot{S}|S}} }}{{\sigma_{{\dot{S}|S}} }}\varPhi \left( {\frac{{\dot{L} - \mu_{{\dot{S}|S}} }}{{\sigma_{{\dot{S}|S}} }}} \right)} \right\},$$

(8)

where $\nu_{L = \det }^{ + }$ denotes the upcrossing rate when the threshold L is deterministic, $\phi$() and $\varPhi$() are standard normal density and distribution functions, respectively, μ and σ denote the mean and standard deviation of S and $\mathop S\limits^{ \cdot }$, represented by subscripts, and “|” denotes the condition.

Since it is unlikely that the structural response exceeds a critical limit at the beginning of structural service, the probability of structural failure at t = 0 is zero, i.e., p_f(0)=0. Furthermore, since in most practical applications, the critical limit L(t) is a constant, such as prescribed in design codes and standards, the solution to Eq. (8) can be further simplified as follows:

$$\upsilon = \upsilon_{L = \det }^{ + } = \frac{{\sigma_{{\dot{S}|S}} }}{{\sigma_{S} }}\phi \left( {\frac{{L - \mu_{S} }}{{\sigma_{S} }}} \right)\left[ {\phi \left( {\frac{{ - \mu_{{\dot{S}|S}} }}{{\sigma_{{\dot{S}|S}} }}} \right) + \frac{{\mu_{{\dot{S}|S}} }}{{\sigma_{{\dot{S}|S}} }}\varPhi \left( {\frac{{\mu_{{\dot{S}|S}} }}{{\sigma_{{\dot{S}|S}} }}} \right)} \right].$$

(9)

For a given Gaussian stochastic process with mean function μ_S(t) and auto-covariance function C_SS(t_i,t_j), all variables in Eq. (9) can be determined, according to the theory of stochastic processes [see, e.g., 27, 34] as outlined in “Appendix”. To apply Eq. (9) in the risk–cost optimization of Eq. (1), the main effort lies in developing stochastic models of structural response S(t). This will be dealt with in the next section.

The probability of system failure depends on the configuration of the structural components and identified failure modes. It needs to be noted that a component failure is treated as system failure because there are many failure modes, i.e., limit state functions, by which the component can fail. In this study, a method proposed by [9] for finding the probability of system failure for series systems is used. Using some basic set theory transformation, intersection of events is transformed into a union of events so that the method proposed by [9] can be used. Other methods such as the Monte Carlo simulation can also be employed for calculating the probability of system failure.

4 Modelling of Structural Response

As may be appreciated, the structural response, S(t), is not only random but also time variant, depending on many factors, such as material properties, geometry, stress conditions, defects and so on. It is, therefore, well justified to model the structural response as a stochastic process, expressed in terms of primary contributing factors, which are treated as basic random variables. It follows that the structural response is a function of basic random variables as well as time and can be expressed as follows:

$$S(t) = f(a,b,c, \ldots ,t),$$

(10)

where a, b, c,… are the basic random variables, the probabilistic information of which is (presumed) available and t is the time. With this treatment, the statistics of S(t) can be obtained using the technique of Monte Carlo simulation. The basic procedure of Monte Carlo simulation is to take samples from the known probability distribution functions of basic random variables, i.e., a, b, c,… These samples are then substituted into Eq. (10) to obtain a realization of structural response S(t). This procedure is repeated several times (known as the sample size) so that the statistics of S(t), e.g., mean and standard deviation, and the probability density function of S(t), if needed, can be obtained.

To develop a generic model for structural response, a random variable, ξ_S, is introduced. ξ_S is defined in such a way that its mean is unity, i.e., E(ξ_S) = 1.0 and its coefficient of variation, λ_S, is a constant and can be estimated from simulation results as described above. Thus, Eq. (10) can be expressed as a stochastic process:

$$S(t) = S_{S} (t)\xi_{S} ,$$

(11)

where S_S(t) is treated as a deterministic function to be obtained from research and/or design codes. The mean and auto-covariance functions of S(t) are (see, e.g., [35])

$$\mu_{S} (t) = E[S(t)] = S_{S} (t)E[\xi_{S} ] = S_{S} (t),$$

(12)

$$C_{SS} (t_{i} ,t_{j} ) = \lambda_{S}^{2} \rho_{S} S_{S} (t_{i} )S_{S} (t_{j} ),$$

(13)

where ρ_S is (auto-)correlation coefficient for S(t) between two points in times t_i and t_j. With μ_S and $C_{SS} (t_{i} ,t_{j} )$, Equations (30) to (35) can be used to determine all terms of S(t) used in Eq. (9).

Evidently, the stochastic model of structural response, i.e., S(t), is case specific. For the example of corrosion-induced concrete cracking as measured by crack width, w(t), Eq. (12) can be embodied as follows (for details refer to [36]):

$$w(t) = w_{c} (t) \cdot \xi_{w} ,$$

(14)

where w_c(t) is treated as a deterministic time function and ξ_w is a random variable to account for all randomness of the basic random variables contributing to crack width. In Eq. (14), a model for w_c has been developed in [37] which can be expressed in terms of basic random variables as follows:

$$w_{\text{c}} = \frac{{4\pi d_{\text{s}} }}{{(1 - v_{\text{c}} )(a/b)^{\sqrt \alpha } + (1 + v_{\text{c}} )(b/a)^{\sqrt \alpha } }} - \frac{{2\pi bf_{\text{t}} }}{{E_{\text{ef}} }},$$

(15)

where d_s is the thickness of corrosion products, a and b are the inner and outer radii of the thick-wall cylinder for concrete cracking model (see Fig. 3), α is the stiffness reduction factor, υ_c is Poisson’s ratio of concrete, f_t is the tensile strength of concrete and E_ef is the effective elastic modulus of concrete.

Fig. 3

Schematic representation of corrosion-induced concrete cracking

With the model of Eq. (14), the mean and auto-covariance functions of w(t) can be determined accordingly as demonstrated in the example. Other examples on the formulation of deterioration process for different deterioration processes can be found in the current literature [26, 36].

5 Algorithm for Risk–Cost Optimization

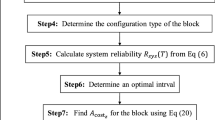
Although each term in Eq. (1) has been determined individually, the optimization itself is computationally involved and complex. In this paper, a numerical algorithm is proposed for the optimization. The flowchart of the proposed algorithm is presented in Fig. 4 and the optimization steps are described as follows.

Fig. 4

Flowchart for risk–cost optimization

• 1. For a given lifetime, t_L, identify all the failure modes (N_m is the total number of failure modes) for each component (N_c is the total number of structural components). Then categorize the identified failure modes into serviceability and ultimate limit states.

• 2. Establish limit state function for each failure mode as per Eq. (3) and formulate stochastic models of S(t) as per Eq. (11).

• 3. Set a number for the required maintenance actions, N_r.

• 4. For a given initial time t₀ (usually zero), calculate the probability of failure for all failure modes of each component by Eq. (9) and the probability of failure for component subsystem (consisting of all the failure modes; see Fig. 1b) and for structural system (consisting of all the structural components; see Fig. 1a). The probability of structural system failure is based on the configuration and correlation of components and failure modes. Check if all the constraints in Eq. (1) are satisfied.

• 5. Set the maintenance time for all failure modes of all components as t_r = t₀.

• 6. At a given time t₁ = t₀ + Δt₁, in which Δt₁ > Δt_min, repeat Step 4 for the probability of failure for all failure modes, components and the structure (p_s, p_u, p_sys) at time t₁ − t_r.

• 7. Check all the constraints shown in Eq. (1). If the constraints are not satisfied, repeat Steps 6–7 until all the constraints are satisfied; otherwise, go to Step 8.

• 8. Rank all components of the structure (system) based on risk. Component with the highest contribution to risk is the critical component and needs to be fixed. This gives where to maintain.

• 9. For the critical component identified in Step 8, rank failure modes based on risk calculated using the normalized probability of failure, i.e., $\frac{p}{{p_{\text{a}} }} \times {\text{Cost}}$. The failure mode with the highest risk is the critical failure mode that needs to be fixed. This gives what to fix.

• 10. For the critical component and failure mode identified in Steps 8 and 9, calculate the corresponding cost formulated in Eq. (1) at time t_r = t₁.

• 11. Set t₂ = t₁ + Δt₂ (Δt₂ > Δt_min) and repeat Steps 6–10, until all the required number of maintenance actions are completed, i.e., i = N_r.

• 12. Calculate the total cost for all the maintenance times t_i (i = 1, 2, …, N_r) using Eq. (1).

• 13. Iterate Steps 5–12 to minimize the total cost for different sequences of time t_i (i = 1, 2, …, N_r), satisfying all the constraints of Eq. (1).

• 14. For different N_r, repeat Steps 3–13 to minimize the objective function, until an optimum number of maintenance actions, N^Opt_r, which has the minimum cost for all N_r, is reached.

The outputs of the risk–cost optimization are the maintenance action times (t_i values). At each maintenance time, the algorithm determines the critical component and failure mode as output. In each optimization procedure, the number of maintenance actions is given. The optimum number of N_r, i.e., N^Opt_r, returns the minimum maintenance cost. The influence of the number of maintenance actions for each failure mode has been considered by solving the optimization problem for several different values for the number of maintenance actions and comparing the resulted optimal costs. This method of dealing with the number of maintenance actions is also used in other researchers, e.g., [8] and [9].

The search for optimum times t_i with given constraints is an iterative procedure. Different optimization algorithms such as sequential quadratic programming (SQP) can be employed for solving this nonlinear constraint optimization problem. One of the issues in the gradient-based optimization algorithms is that they rely on an initial point input for finding the local minimum. Mori and Ellingwood [8] have suggested that for testing the validity of a solution, several different starting points be tried. On the other hand, smart algorithms, e.g., the evolutionary algorithms [38] are more robust and versatile in finding the optimum of complex problems with nonlinear constrains. In this study, the above flowchart was coded using the Genetic Algorithm.

6 Worked Examples

6.1 Example I

To illustrate the application of the developed algorithm for the proposed maintenance strategy, a reinforced concrete (RC) bridge girder with three spans is used as a worked example. These spans, shown in Fig. 5, are the components of the bridge girder which is considered as structural system connected in series. For each component, four structural responses represented by four failure modes or limit states are considered (as component subsystem). Two of these are shear and flexural failures which are ultimate limit states, while the other two are excessive corrosion-induced crack width and deflection, which are serviceability limit states. For failure analysis, the ultimate limit states are considered as series system and the serviceability limit states as parallel system.

Fig. 5

System representation of the example structure

Decisions on maintenance actions for flexural and shear strength limit states are based on the residual strength. If the residual flexural or shear strength decreases below an acceptable level, i.e., L in Eq. (3), a maintenance action is required. Deflection is governed by the stiffness of each span. Therefore, controlling the residual stiffness is an appropriate means for limiting the deflection. Similar to residual strength models, if the residual stiffness decreases to an unacceptable level, the maintenance action is required. Treatment of crack-induced crack width is slightly different. An analytical time-dependent model is utilized for predicting the crack width, in which excessive crack width warrants a maintenance action. Due to deterioration, residual flexural and shear strengths and stiffness are decreasing gradually, while the crack width is increasing. The deterioration models for the considered failure modes, i.e., S_s(t) function in Eq. (12), are taken from studies of Li and Melchers [35] and Li et al. [36] as an example for illustration of the application of the proposed framework. These are summarized in Table 1 for all components and failure modes. Due to different environmental and loading conditions, the deterioration processes for different components and failure modes are generally not the same. Therefore, in this example, to differentiate the deterioration processes in each component and failure mode, different rates of deterioration are assumed to each component. In the application of the proposed framework to real-world structures, the information of deterioration rate can be collected from site condition assessment. In this example, it is assumed that after each maintenance action, the repaired component is reinstated to its original condition.

Table 1 Stochastic models for different components and failure modes

It should be noted that the deterioration models for flexural and shear strengths and the stiffness represents the normalized (with respect to the initial value) residual values. It is assumed that if the residual strength or stiffness is less than 70% of the initial value, ultimate failure would occur. For the crack limit state, the deterioration function represents growth of corrosion-induced crack over time. If the crack width exceeds 0.30 mm, this serviceability limit state is violated. In Fig. 11, the probability of failure for each of the considered failure modes over the lifetime of the bridge structure is shown. The bridge is designed for a 100-year service life, i.e., t_L = 100.

These models are just used for illustration purpose to demonstrate the application of the proposed framework. For ultimate limit states, maintenance actions are performed before the probability of failure exceeds an acceptable level, i.e., p_u,a, as is formulated in Eq. (1). For serviceability limit states, if the probability of failure exceeds an acceptable level, p_s,a, maintenance action is warranted. In this example, formulation of the limit states is in a way that for failure modes 1–3, due to deterioration, residual capacity is gradually decreasing, while for failure mode 4, damage due to deterioration is increasing with time. Therefore, decisions for maintenance action of each failure mode can be formulated as follows:

$${\text{Failure}}\,{\text{Mode}}\, 1 :\;\,p_{\text{f1}} = P\left[ {S_{1} (t) - L_{1} \le 0} \right] \le p_{\text{u,a}} ,$$

(16a)

$${\text{Failure}}\,{\text{Mode}}\, 2 :\;\,p_{\text{f2}} = P\left[ {S_{2} (t) - L_{2} \le 0} \right] \le p_{\text{u,a}} ,$$

(16b)

$${\text{Failure}}\,{\text{Mode}}\, 3 :\;\,p_{\text{f3}} = P\left[ {S_{3} (t) - L_{3} \le 0} \right] \ge p_{\text{s,a}} ,$$

(16c)

$${\text{Failure}}\,{\text{Mode}}\, 4 :\;\,p_{\text{f4}} = P\left[ {S_{4} (t) - L_{4} \ge 0} \right] \ge p_{\text{s,a}} .$$

(16d)

In the application of the proposed framework to real-world structures, the information of deterioration rate can be collected from site condition assessment. In this example, loading is assumed as lifetime maximum so that failure is determined by resistance deterioration. In Fig. 6, the probability of failure for each of the considered failure modes over 100 years of lifetime is shown.

Fig. 6

Probability of failure for different components and failure modes

In the evaluation of the probability of system failure, correlation among failure modes can be determined using some analytical methods or the Monte Carlo simulation. In the absence of real statistical data, engineering judgement can be used to set the correlation amongst failure mode. For instance, if some of the failure modes are due to corrosion, they will be correlated. In this study, correlation among failure modes is assumed. The following equation shows the assumed correlation matrix for limit sates representing different failure modes, i.e., G_m1–G_m4.

$$\begin{aligned} \;\;\;\;\;\;\begin{array}{*{20}c} {G_{m1} } & {\;G_{m2} } & {G_{m3} } & {G_{m4} } \\ \end{array} , \hfill \\ \begin{array}{*{20}c} {G_{m1} } \\ {G_{m2} } \\ {G_{m3} } \\ {G_{m4} } \\ \end{array} \left[ {\begin{array}{*{20}c} {1.0} & {0.2} & {0.5} & {0.5} \\ {} & {1.0} & {0.2} & {0.2} \\ {} & {{\text{Sym}} .} & {1.0} & {0.5} \\ {} & {} & {} & {1.0} \\ \end{array} } \right], \hfill \\ \end{aligned}$$

(17)

where G_m1, G_m2, G_m3 and G_m4 are the limit states for failure modes 1–4 (see Fig. 5a). It is also assumed that the correlation between components of the system is 0.50. According to the method proposed by [9], the probability of system failure for a series system with correlated components can be calculated as follows:

$$p_{\text{f}} \simeq 1 - \varPhi_{n} \left( {\bar{\beta };\bar{\rho }} \right),$$

(18)

where $\bar{\beta } = (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} )$ is the vector of reliability indices for all components of the series system and $\bar{\rho }$ is the correlation matrix for the components. Φ_n is the n-dimensional standardized normal distribution function. To determine the probability of failure for the subsystem of failure modes (refer to Fig. 5a), using some basic set theory expressions, the probability of system failure is transferred to the probability of failure for a set of series systems as follows:

$$p_{\text{f,mode}} = \text{P} \left[ {G_{m1} < 0 \cup G_{m2} < 0 \cup \left( {G_{m3} < 0 \cap G_{m4} } \right)} \right],$$

(19a)

$$\therefore\, p_{\text{f,mode}} = \text{P} \left[ {\left( {G_{m1} < 0 \cup G_{m2} < 0 \cup G_{m3} < 0} \right) \cap \left( {G_{m1} < 0 \cup G_{m2} < 0 \cup G_{m4} < 0} \right)} \right],$$

(19b)

$$\begin{aligned} \therefore\, p_{\text{f,mode}} = & \text{P} \left( {G_{m1} < 0 \cup G_{m2} < 0 \cup G_{m3} < 0} \right) + \text{P} \left( {G_{m1} < 0 \cup G_{m2} < 0 \cup G_{m4} < 0} \right), \\ \,\,\,\,\,\,\,\,\,\,\,\;\;\;\;\,\,\, & - \text{P} \left( {G_{m1} < 0 \cup G_{m2} < 0 \cup G_{m3} < 0 \cup G_{m4} < 0} \right), \\ \end{aligned}$$

(19c)

$$\begin{aligned} \therefore\, p_{\text{f,mode}} \simeq & \left[ {1 - \varPhi_{3} \left( {\beta_{m1} ,\beta_{m2} ,\beta_{m3} ),\bar{\rho }_{123} } \right)} \right] + \left[ {1 - \varPhi_{3} \left( {\beta_{m1} ,\beta_{m2} ,\beta_{m4} ),\bar{\rho }_{124} } \right)} \right] \\ \;\;\;\;\;\;\;\;\,\,\,\,\,\,\,\,\, & - \left[ {1 - \varPhi_{4} \left( {\beta_{1} ,\beta_{2} ,\beta_{3} ,\beta_{4} ),\bar{\rho }_{1234} } \right)} \right], \\ \end{aligned}$$

(19d)

where p_f,mode denotes the probability of system failure for subsystem of failure modes. β_m1, β_m2, β_m3 and β_m4 are the reliability indices for modes 1–4. $\bar{\rho }_{123}$, $\bar{\rho }_{124}$ and $\bar{\rho }_{1234}$ are the correlation matrices containing the correlation coefficients among the indexed failure modes. Φ₃ and Φ₄ are the three and four-dimensional standardized normal distribution functions. The probability of system failure for the whole bridge girder in this worked example is based on a system of three components connected in series as is shown in Fig. 5b). Considering the system shown in Fig. 5 and the result of time-dependent reliability shown in Fig. 6a–d, the probability of system failure can be calculated. In Fig. 7, results of probability of system failure with and without considering correlation over 100 years of structural lifetime are shown. For the case study considered in this worked example, the effect of correlation amongst failure modes and components on probability of system failure is not considerable in the short term but becomes significant in the longer term. The ignorance of correlation would underestimate the risk of structural failures in longer term. This vindicates the employment of the first passage probability method which allows for the correlation in the system.

Fig. 7

Probability of system failure

In the proposed framework, the maintenance actions including repair, strengthening and instalment depend on the failure mode. It is assumed that the cost of maintenance for all components of the system is equal, with relative cost of maintenance for ultimate failures being five times that of serviceability failures. The acceptable upper limit probability of failure for ultimate limit states is taken as 0.015. For serviceability limit states, an acceptable lower limit of 0.10 is used. Furthermore, the failure probability of structural system is limited to 0.10. The annual discount rate is assumed to be 3%. It is also assumed that the minimum number of years between successive maintenance actions is 3. To investigate the sensitivity of optimized maintenance strategy to different costs of failure, three costs of failure to cost of maintenance ratios, CF/CP, of 10, 100 and 200 are considered (refer to Eq. 1).

By substituting the stochastic models of S(t) and solution to the probability of failure in Eq. (1), the optimized maintenance strategy can now be derived. To find the optimized maintenance times, a generic computer code was programmed in MATLAB [39]. The genetic algorithm method is used to minimize the risk function defined in Eq. (1). For a given number of maintenance actions, the program can provide the maintenance times that minimize the risk. Furthermore, the program also identifies the component and failure mode that need maintenance at each maintenance time. After conducting a sensitivity analysis, it was considered appropriate to set the population size, crossover probability and mutation probability as 500, 0.80 and 0.05, respectively, for the genetic algorithm solution.

The outputs of the optimization form the maintenance strategy, that is, when, where and what to maintain for the infrastructure at a minimum system risk and effective cost. For the case of six maintenance actions and the cost of failure to cost of maintenance ratio, CF/CP, of 100, the optimized maintenance times for all components are shown in Fig. 8. As it can be seen, all the system constraints (upper limit of 0.10) are satisfied, and in each maintenance action, the most critical component is fixed. It is worth noting that all the failure modes satisfy the requirement of serviceability and ultimate limit states as the constraints of the optimization procedure (see Eq. 1).

Fig. 8

Optimized maintenance strategy for six maintenance actions, CF/CP = 100

As previously mentioned, the influence of the number of maintenance actions can be considered by solving the optimization problem for several different values of N_r. The N_r value with the minimum cost is the optimal value. In Fig. 9, the process of optimizing N_r for different cost of failure to cost of maintenance ratios is shown. As it can be seen, by increasing the cost of failure to achieve the minimum cost, more maintenance actions are required. It should be noted that the optimization procedure shows that to satisfy the constraints in Eq. (1), at least six maintenance actions are required. Figure 9 effectively corroborates the validity of the formulation of risk–cost optimization, i.e., Eq. (1) in which an optimal solution exists.

Fig. 9

Optimum number of maintenance actions for different cost of failure to cost of repair ratios (C0 is a reference cost)

For instance, for the highest cost of failure to cost of maintenance action, performing 13 maintenance actions is the optimum number of maintenance actions. Results of the optimum maintenance strategy for N_r = 13 are presented in Table 2. As it can be seen, in some cases, a component is fixed two times for a specific failure mode. For instance, for failure mode 2, component number 2 is twice fixed at 11 and 63 years, respectively. On the other hand, for some components, no maintenance action is required for some of the failure modes. For example, component number 2 requires no maintenance action for failure mode 4 during its whole lifetime. Clearly knowing when, where and what to maintain for the structure will also provide economic benefits in addition to the safety and serviceability of the structure. This is the significance of the present paper.

Table 2 The optimized maintenance strategy with CF/CP = 200 and optimum N^Opt_r = 13

6.2 Example II

In the second example, a deck from a bridge located in a coastal area in Melbourne is considered. Geometry and material properties of the cross section of the simply supported deck girders and the reinforcement are shown in Fig. 10. Due to corrosion, three of the girders in one span of the bridge are degrading.

Fig. 10

Geometry and material properties of concrete girders

Analysis of the inspection data shows that these girders degrade with different rates. The estimated corrosion current densities in girders 1–3 are 0.25, 0.50 and 0.75 μA/cm², respectively. It should be noted that according to Faraday’s law, a corrosion current density of 0.50 μA/cm² corresponds to an expected steel loss of 11.6 μm/year. As failure of one of these girders impairs function of the bridge deck, for the reliability analysis, the girders in the span can be connected in series. Each girder is subjected to two ultimate failure modes that are flexural and shear. For serviceability, two failure modes are excessive deflection and corrosion-induced crack. According to the proposed model in this study, the serviceability failure modes are connected in parallel, and the resulted subsystem is connected to the ultimate failure modes in series. This constitutes the failure mode system (see Fig. 1).

To derive statistics of the resistance related to each of the failure modes, some statistical models for geometry and material properties are needed. In Table 3, all the required statistics for the basic random variables are shown.

Table 3 Statistics of the basic random variables

In what follows, formulation of the limit states required for the considered failure modes is shown. Using the basic statistics, shown in Table 3, and by employing the Monte Carlo technique, time-dependent functions for the degradation processes are obtained. These processes will then be used to find the probability of failure within the proposed maintenance strategy. The probabilistic procedure to derive statistics of each stochatic process follows the models presented in Eq. (11).

6.2.1 Flexural Strength Model

Due to the corrosion process, the rebar area is decreasing over time. For the case of general corrosion, the reduced area can be calculated as follows:

$$A_{\text{s}} (t) = A_{\text{s0}} \left[ {1 - 0.0232i_{\text{corr}} t} \right]^{2} ,$$

(20)

where A_s0 is the area of an uncorroded rebar, i_corr is the corrosion rate measured as a current density expressed in µA/cm² and t is time since corrosion initiation in years. Following reduction of rebar area, the overall flexural strength of the bridge girder is degrading with time. In this study, the limit state function is based on the deterioration of flexural strength of girder cross section and expressed as follows:

$$g_{\text{M}} = M_{\text{m}} (b,h,c,f_{\text{c}}^{'} ,f_{\text{y}} ,i_{\text{corr}} ,t)\xi_{\text{M}} - M_{\text{a}} ,$$

(21)

where M_m() is the expected flexural strength as a function of basic random variables and time. ξ_M is a random variable, which accounts for variability in the degradation process of flexural strength [35]. The standard procedure described in the ACI 318 [44] can be used to calculate this strength. The variables b, h, c, f′_c, f_y, i_corr are the basic random variables (see Table 3). With this treatment, statistics of the flexural strength can be obtained using the technique of Monte Carlo technique.

M_a in Eq. (21) is the minimum acceptable strength. It has been shown [26, 35] that it may be appropriate to take the acceptable limit for strength deterioration as 70% of the original strength, i.e., M_a/M₀ = 0.70.

6.2.2 Shear Strength Model

The limit state for shear strength, which is an ultimate limit state, is similar to that of the flexural strength. Due to the reduction of shear reinforcement and other factors such as damage on concrete area due to corrosion-induced cracks, the shear strength of reinforced concrete (RC) girder cross section deteriorates over time. The limit state function for the shear failure can be formulated as follows:

$$g_{\text{V}} = V(t) - V_{\text{a}} ,$$

(22)

where V(t) is the shear strength expressed as a function of time and V_a is the acceptable residual shear strength. It is assumed that reduction of shear strength to more than 50% of the original shear strength is not acceptable, i.e., V_a/V₀ = 0.50. This is due to the fact that flexural strength generally governs the design of RC beams, leading to beams with higher reserve capacity in shear.

Higgins et al. [45] compared different models for predicting residual shear capacity of corrosion-damaged RC cross sections due to rebar corrosion and deterioration of concrete cross section. They showed that an analytical model based on the ACI 318 code for shear strength was able to conservatively predict the residual shear capacity of the RC cross sections. They also found that average stirrup area provided the best prediction of the shear strength. The analytical model proposed by Higgins et al.is adopted in this research. Damage to the RC cross section due to corrosion-induced cracks, which leads to spalling of side concrete, was considered through reduction of the cross-section width. Based on empirical evidence and theoretical computation from observed cover damage due to corrosion Higgins et al. proposed the following expression for the reduced cross section width:

$$b_{\text{eff}} = b - \left[ {2(d_{\text{s}} + c) - \frac{s}{5.5}} \right]\;\;{\text{for}}\;\;s < 5.5(d_{\text{s}} + c),$$

(23)

where d_s (12 mm in this study) is the diameter of stirrups, c (100 mm in this study) is the concrete cover to stirrups and s (200 mm in this study) is stirrups spacing. The above expression represents the final reduced width. To have a time-dependent cross section width and by assuming uniformly distributed, the following model for cross section width of damaged RC sections results:

$$b_{\text{eff}} (t) = b - \left[ {2(d_{\text{s}} + c) - \frac{s}{5.5}} \right]\frac{t}{{t_{\text{L}} }},$$

(24)

where t_L is the lifetime of the structure. Combining the traditional method of calculating the shear capacity based on the ACI 318 code, the general corrosion models and concrete cross-sectional damage, the residual shear capacity of a RC cross section can be calculated as follows:

$$V(t) = V_{\text{m}} (t)\xi_{\text{V}} ,$$

(25a)

$$V_{\text{m}} (t) = 0.33\sqrt {f_{\text{c}}^{'} } b_{\text{eff}} (t)d + \frac{{A_{\text{v}} (t)}}{s}f_{\text{y}} d,$$

(25b)

where V_m(t) is the mean shear strength function and ξ_V accounts for variability in the shear strength. Using the Monte Carlo technique, statistics of the residual shear strength over the lifetime of the structures can be calculated.

6.2.3 Deflection Model

Controlling the maximum structural deflection is one of the serviceability limit states. In general, the deflection of a structural member can be expressed as follows:

$$\Delta = \kappa \cdot q,$$

(26)

where q is the distributed load applied on the structure and c is a coefficient to convert load to deflection, i.e., load effect, to be determined from structural analysis. For example, for a simply supported reinforced concrete girder, $\kappa = \frac{{5l^{4} }}{{384E_{\text{eff}} I_{\text{e}} }}$, where l is the span length and K = E_effI_e is the effective flexural stiffness of the RC girder. For corrosion-affected RC structures, the deflection increases even under the constant load (q) due to corrosion-induced concrete cracking, spalling and de-bonding between the reinforcement and concrete (this is in addition to creep and shrinkage). In this paper, reduction of effective structural stiffness, which is directly related to increase of deflection, is used for defining the deflection serviceability limit state. In line with deterioration process models developed for the residual flexural and shear strengths, a similar deterioration model is developed for the residual stiffness. The limit state function for deflection be expressed as follows:

$$g_{\text{D}} = K_{\text{m}} (t)\xi_{\text{K}} - K_{\text{a}} ,$$

(27)

where K_a is the acceptable residual stiffness. It is assumed that reduction of flexural stiffness to 0.25 of the initial stiffness is a violation to the deflection limit state, i.e., K_a/K₀ = 0.25. ξ_K is a variable introduced to account for variability in the stiffness and K_m(t) is the mean of deterioration function for deflection which is increasing with time. Reduction of flexural rigidity over time would lead to increase of deflection. In this study, a theoretical model, in which the reduction in the rebar area contributes to the reduction of cracked moment of inertia, is developed. Considering a fully cracked section, the flexural stiffness can be expressed as a function of time as follows:

$$K_{\text{m}} (t) = E_{\text{c}} \left[ {\frac{{bd_{\text{n}} (t)^{3} }}{3} + \frac{{E_{\text{s}} }}{{E_{\text{c}} }}A_{\text{s}} (t)\left( {d - d_{\text{n}} (t)} \right)^{2} } \right],$$

(28)

where d_n(t) is the depth of the neutral axis, which is calculated by balancing the second moment of area for top and bottom sides of the neutral axis. Monte Carlo technique was used to evaluate the mean and coefficient of variation of the deterioration process for stiffness over time.

6.2.4 Crack Model

As may be appreciated, the cracking process of concrete is a very random phenomenon, depending on many factors, such as concrete properties, geometry, stress conditions, defects in the concrete and so on. The problem becomes worse when the crack is induced by the expansion of corrosion products which itself is also very uncertain. To define the related serviceability limit state, corrosion-induced crack width, which is expressed as a function of time, is compared with the acceptable crack width which is taken from guidelines in design codes and standards:

$$g_{\text{C}} = w_{\text{a}} - w(t).$$

(29)

It is assumed that the acceptable crack width, w_a, is 0.3 mm. Similar to other random processes, the corrosion-induced crack width can be expressed as a product of a mean crack function over time and a random variable accounting for uncertainty (see Eq. 14). In Eq. (14), ξ_w is a random variable with a mean of 1.0 and a coefficient of variation which is obtained using the Monte Carlo technique. In this study, an analytical model developed by Li et al. [37], shown in Eq. (15), is used for estimating the crack width as a function of time. It follows that the crack width is a function of basic random variables as well as time. With values of basic variables in Table 3, a realization of the crack width can be generated.

6.2.5 Results

For service life prediction and derivation of optimal maintenance strategy, 100-year time is considered. By employing stochastic degradation models described in the previous sections, the probability of failure for all the structural components (concrete girders) and all the considered failure modes can be calculated as shown in Fig. 11.

Fig. 11

Probability of failure for different girders and failure modes

In the development of the optimal maintenance strategy, it is assumed that the acceptable probability of failure for the ultimate limit states is 0.05. Considering this limit, for shear failure mode, all components need repair within the 100-year period. For the serviceability limit states, repair action is warranted once the probability of failure exceeds 0.25. Furthermore, the acceptable probability of system failure is taken as 0.15. The expected cost of failure to that of repair is 1000, while it is assumed that the maintenance and repair actions for ultimate limit states are 5 times those for the serviceability limit states. As a constraint, repair actions are set to be at least three years apart. The results of the probability of system failure based on 7 repair actions during the 100-year period are shown in Fig. 12.

Fig. 12

Typical optimized maintenance strategy for six maintenance actions, N_r = 7

From the results in Fig. 12, it can be clearly seen that some structural components need multiple repairs, while others need only one repair action. By changing the number of repair actions, N_r, the optimum number of repair actions that results in the minimum total cost can be determined. In Fig. 13, results of the optimization for number of repair actions are shown. As it can be seen, performing 14 repair/maintenance actions results in the minimum expected cost.

Fig. 13

Optimum number of maintenance actions (C_F/C_R = 1000)

The components and the failure models requiring repairs are shown in Table 4.

Table 4 The optimized maintenance strategy for the bridge deck (N^Opt_r = 14)

Results of the optimum maintenance strategy shown in Table 4 show that the girder with higher degradation rate requires more maintenance attention. Also, the shear failure mode is more critical than the flexural failure mode; therefore, more repair is needed for shear.

7 Conclusion

A theoretical framework for developing a risk–cost-optimized maintenance strategy for a structural system during its whole service life has been formulated in this paper. In this framework, the first-passage probability method has been employed and a generic form of stochastic model for structural responses has been developed to determine the probability of structural failure. To facilitate the practical application of the proposed framework, an algorithm has been developed and programmed in a user-friendly manner with two worked examples. The merit of the proposed framework is that in predicting when, where and what maintenance is required for the structure, all structural components and multi-failure modes have been considered. It has been found in the paper that, to ensure the safe and serviceable operation of the structure as a whole, some components need maintenance multiple times for different failure modes, whilst other components need “do nothing”. The significance of this finding is that timely maintenance on needed components for identified failure modes can help prevent avoidable collapses and prolong the service life of the structure, yielding economic benefits. It has also been found that ignorance of correlation amongst components and failure modes would underestimate the risk of structural failures in longer term, and that the components with higher cost of structural failures require more maintenance actions. It can be concluded that the proposed framework provides a tool for structural engineers, operators and asset managers to develop a risk–cost-optimized maintenance strategy for structures under their management.

Appendix

According to the theory of stochastic processes (Papoulis and Pillai 2002), all variables in Eq. (9) can be determined, for a given Gaussian stochastic process with mean function μ_S(t), and auto-covariance function $C_{SS} (t_{i} ,t_{j} )$, as follows:

$$\mu_{{\dot{S}|S}} = E[\dot{S}|S = L] = \mu_{{\dot{S}}} + \rho \frac{{\sigma_{{\dot{S}}} }}{{\sigma_{S} }}(L - \mu_{S} ),$$

(30)

$$\sigma_{{\dot{S}|S}} = \left[ {\sigma_{{\dot{S}}}^{2} (1 - \rho^{2} )} \right]^{1/2} ,$$

(31)

where

$$\mu_{{\dot{S}}} = \frac{{{\text{d}}\mu_{S} (t)}}{{{\text{d}}t}},$$

(32)

$$\sigma_{{\dot{S}}} = \left[ {\frac{{\partial^{2} C_{\text{SS}} (t_{i} ,t_{j} )}}{{\partial t_{i} \partial t_{j} }}|_{i = j} } \right]^{1/2} ,$$

(33)

$$\rho = \frac{{C_{{S\dot{S}}} (t_{i} ,t_{j} )}}{{\left[ {C_{SS} (t_{i} ,t_{j} ) \cdot C_{{\dot{S}\dot{S}}} (t_{i} ,t_{j} )} \right]^{1/2} }},$$

(34)

and the cross-covariance function is

$$C_{{S\dot{S}}} (t_{i} ,t_{j} ) = \frac{{\partial C_{\text{SS}} (t_{i} ,t_{j} )}}{{\partial t_{j} }}.$$

(35)

Based on the above relationships, all the variables in Eq. (9) can be determined.