1 Introduction

Nonlinear second-order systems include a widely used mechanical and electromechanical systems such as robot manipulator, spacecraft, underwater vehicle, wind turbine and vibrating systems (Colombo et al. 2020; Jiang et al. 2022; He et al. 2022; Nguyen et al. 2020). The variety of applications has motivated many researchers in the last decades to control the second order systems by different strategies (Li et al. 2021; Jimenez-Rodriguez et al. 2019; Bartolini et al. 1997; Li et al. 2022). Bartolini et al. (1997) solved the tracking problem of nonlinear second-order systems by classical minimum-time optimal control method. A tracking control scheme using reinforcement learning is proposed to steer both position and velocity of a class of second-order systems (Li et al. 2022). A multi-agent second-order system is controlled by a neural network-based controller which can ensure that the tracking errors between the following agent and leader will converge to a narrow neighborhood of zero (Wen et al. 2015). A velocity observer-based feedback controller is developed for second-order systems with the application to a robot (Homayounzade and Keshmiri 2011). A finite-time sliding mode control that employs a disturbance observer is presented for second-order systems (Miranda-Colorado 2019).

Most research conducted on the control of second-order systems tried to solve the tracking problem without attention to the practical limitations (Ghiasi et al. 2010). In this respect, the limitation on the control input plays a significant role in finding the feasible control signal. This restriction results from the limited capacity of actuators like DC motors, which can just generate a finite amount of torque. Neglecting the input constraint in designing the controllers has a negative effect on the closed-loop system performance. To address this problem, various methods have been employed for input-constrained control by taking into consideration one or multiple requirements like stability, practical implementations, simplicity in computations, robustness, optimality and generality. One solution incorporates static or dynamic nonlinear models to represent the saturation within the system model (Gui et al. 2015). Another solution is to use anti-windup schemes jointed to the main controllers to counteract the impact of input saturation within the control systems (Tsai et al. 2011). Proportional derivative controller integrated with a dynamic compensation (Su and Swevers 2014) and intelligent methods plus Barrier Lyapunov functions (Ma and Huang 2020) are also proposed as alternative solutions for the saturated control problems. Ding and Zheng (2016) designed terminal sliding mode control for nonlinear second-order systems with input saturation. In all of the reviewed methods, optimization is not the primary procedure to solve the constraint issue for finding the control laws. Meanwhile, the stability and universality of the previously mentioned approaches might still lack clarity.

The optimality of solutions for constrained nonlinear systems can be achieved through dynamic programming or calculus of variation as the classical optimal control methods (Kirk 2004). Because of high computations of these methods, some approximation methods based on piecewise functions (Loxton et al. 2009) Haar functions (Marzban and Razzaghi 2010), adaptive dynamic programming (ADP) (Liu et al. 2013), hybrid functions (Mashayekhi et al. 2012) and adaptive neural network approaches (Li et al. 2017) are applied to approximate the control input. Alternatively, modern optimal methods such as model predictive control (MPC) have been introduced to find the constrained control inputs at each sampling time by solving an optimization problem online (Silva et al. 2019). Although MPC strategies are suitable for linear systems, extending them to nonlinear systems introduces new challenges. It is difficult or impossible to find analytical solution for the optimization problem in the nonlinear problems. The numerical solutions also involve high computations, making them unsuitable for online implementations. Importantly, the stability analysis of NMPC methods in the presence of constraints requires further research.

In the current paper, in order to overcome the time-consuming problem in the optimization-based nonlinear methods reviewed above, a control strategy is proposed for the second-order systems based on a continuous predictive approach. This approach, unlike the conventional discrete predictive control, leads to the closed form control laws with no need to the optimization process at each sampling time. The proposed approach leads to feedback linearization-like method when the constraints are dropped and the uncertainties of the system are ignored (Moradi Nerbin et al. 2017; Lu 1995; Abdi et al. 2018; Rafatnia and Mirzaei 2022). For the uncertain systems, the tracking error is decreased by selecting small values for the prediction time as a free parameter of the controller (Mirzaeinejad et al. 2016; Rafatnia and Mirzaei 2022). In the present study, the constrained version of the continuous predictive approach is developed by minimizing the expanded performance index in the presence of input constraints. The Karush–Kuhn–Tucker (KKT) theorem is used to analytically solve the resultant constrained optimization problem. How to solve the KKT conditions in a straight-forward manner for the second-order system is demonstrated in this paper. Importantly, the boundedness of the tracking error and its derivative for the second order system is provided by equating the constrained solution with the solution obtained from an optimal controller with a time-varying weight on the control input.

It is important to note that the constrained controller, developed for the second order system, requires a precise mathematical model to reach the desired performance. However, there are various sources of perturbations, including un-modelled dynamics, uncertain parameters and external disturbances, deteriorating the performance of model-based control system (Razmjooei et al. 2022). Different control methods have been suggested by the researchers to deal with uncertainties and disturbances. Among these studies, two commonly used techniques can be distinguished as robust and adaptive control methods (Yi and Zhai 2019; Hu et al. 2022; Cruz-Ortiz et al. 2022). In the paper, an extended state observer (ESO) is utilized to enhance the nominal model considered for the second-order systems (Xiong et al. 2015). The ESO has been applied in various applications like robot control (Yue et al. 2014) and flight control (Li et al. 2014). The paper integrates the constrained controller with the ESO to develop an adaptive constrained controller. The resultant control system can continuously adapt itself by using the observer information about the perturbations without increasing the order of main system.

For a case study, the position control problem of a lever arm as a second-order system is selected to examine the proposed controller. In the simulation study, the NMPC has been used as a comparative method to show the performance and applicability of the proposed constrained controller. For experimental implementation, a platform for lever arm control is fabricated to verify the proposed controller under various maneuvers of trajectory tracking. An experimental assessment is conducted to compare the efficiency of a constrained controller with and without an observer, considering different trajectories. Also, an adaptive backstepping controller is implemented to be compared with the ESO-based constrained controller in the presence of perturbations.

The paper is organized as follows: In Sect. 2, the problem formulation in a general form is presented and the design and analysis of the control system are proposed. In this section, the constrained controller is firstly design, supposing that the perturbation term in the model of the second order system is known. Then, the ESO algorithm is presented to estimate the perturbation term. In Sect. 3, the results of the proposed control method are presented for a lever arm under computer simulations and experimental implementations. Finally, Sect. 4 gives the conclusion.

2 Control Problem Definition

The aim of this study is controlling a widely used class of second-order systems in the presence of input constraint caused by limited capacity of actuators, and perturbations caused by model uncertainties and external disturbances. The dynamic of the many practical systems like Euler–Lagrange systems is derived as Jiang et al. (2022); Li et al. (2022); Miranda-Colorado (2019)

$$\begin{aligned} \ddot{x}=f(x,\dot{x})+bu+d. \end{aligned}$$
(1)

where \(x\in R\) is the generalized position and \(\dot{x} \in R\) is the generalized velocity. \(u \in R\) is the control input that is manipulated to control the generalized position with the bounded generalized velocity. In addition, d is the unexpected external disturbance, respectively. Considering \(\eta (x,\dot{x},d)=f(x,\dot{x})+d\) as the perturbation term, and \(x_1=x\) and \(x_2=\dot{x}\) as the states of the system, the state-space form of (1) is represented as follows:

$$\begin{aligned} \left\{ \begin{array}{lc} \dot{x}_{1}=x_{2}, \\ \dot{x}_{2}=\eta (x,\dot{x},d)+b u, \\ y = x_1. \end{array}\right. \end{aligned}$$
(2)

Assumption: It is supposed that \(\eta (x,\dot{x},d)\) is a bounded function, and also \(b\ne 0\) is a constant (Li et al. 2021, 2022; Miranda-Colorado 2019).

There is often a constraint on the control input of the system due to the limited capacity of the onboard actuators. In this study, the admissible range for the control input is considered as follows

$$\begin{aligned} u=\big \{u \in R \ \ |\ \ U_{\text {min}}\le u \le U_{\text {min}}\big \}. \end{aligned}$$
(3)

The other challenge with the state space Eq. (2) is the perturbations existing in \(\eta (x,\dot{x},d)\), making the system model improper for the constrained controller design. One strategy to deal with this challenge is using the estimation methods. In this paper, the ESO is used to upgrade the nominal model toward the actual system. In this high-gain observer, \(y = x_1\) is considered as the system output.

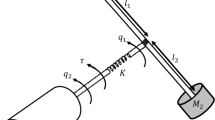
The structure of the ESO-based constrained control system is shown in Fig. 1. By using the information of measurable output, the ESO aims to estimate the uncertainty term \(\eta (x,\dot{x},d)\) to minimize the difference between the nominal model and the actual model. Consequently, assuming an reliable dynamic model for the system, the constrained controller is initially designed based on the model outlined in (2). Subsequently, the supervisor updates the control law by utilizing information received from the observer. Therefore, the ESO-based constrained controller adapts itself with reality to track the desired trajectories.

Fig. 1
figure 1

Block diagram of the ESO-based controller

Full size image

2.1 Constrained Controller Design

In this section, the control law is developed using an optimization approach by assuming that the perturbation term \(\eta (x,\dot{x},d)\) is known. In this approach, the quadratic point-wise performance index defined as a weighted combination of the current control signal and the next tracking error is considered to be minimized as Mirzaeinejad and Mirzaei (2011); Jafari et al. (2015)

$$\begin{aligned} J=\frac{1}{2}{[x_{1}(t+h)-x_{1d}(t+h)]^2}+\frac{1}{2}wu^2, \end{aligned}$$
(4)

in which h is the prediction time, and \(x_{1d}\) is the desired output. The weighting factor w shows the relative importance of control energy and tracking accuracy. By increasing w, the control input is reduced at the cost of decreasing the tracking accuracy. The term \({{x}}_1\left( t+h\right)\) is approximated by the qth-order Taylor series expansion at the present time t

$$\begin{aligned} x_1(t+h)={x_1}(t)+h\dot{x}_1(t)+\frac{h^{2}}{2!}{\ddot{x}}_1(t)+...+\frac{h^{q}}{q!}{x}_1^{(q)}(t). \end{aligned}$$
(5)

For the control algorithm, the order of Taylor series expansion in (5) is limited to the relative degree of the expanded control variable (Moradi Nerbin et al. 2017; Lu 1995). The second-order system has the relative degree, \(\rho =2\), for \({{x}}_1\) because the control input u appears explicitly in the second derivative of \({{x}}_1\) for the first time according to the system model defined by (1) and (2).

Remark 1

By limiting the expansion order equal to the relative degree of the control variable, the control input is supposed to be constant in the predictive interval between t and \(t+h\). This means zero control order and is sufficient for control variables with low relative degrees. Increasing the control order causes complexity in the calculation of the control input (Mirzaeinejad et al. 2016; Malekshahi and Mirzaei 2012).

By considering the perturbation term \(\eta\) as a known factor, in the following, the output and its desired value is expanded by the second-order Taylor series:

$$\begin{aligned} x_{1}(t+h)&=x_{1}(t)+hx_{2}(t)+\frac{h^2}{2}(\eta +bu). \end{aligned}$$
(6)
$$\begin{aligned} x_{1d}(t+h)&=x_{1d}(t)+h\dot{x}_{1d}(t)+\frac{h^2}{2}\ddot{x}_{1d}(t). \end{aligned}$$
(7)

By substituting Eqs. (6) and (7) into (4), the performance index is rewritten in terms of current states and variables as

$$\begin{aligned} \begin{aligned} J&=\frac{1}{2}{\left[ (x_{1}-x_{1d})+h(x_{2}-\dot{x}_{1d}) +\frac{h^2}{2}(\eta +bu-\ddot{x}_{1d})\right] ^2}\\&\quad +\frac{1}{2}wu^2. \end{aligned} \end{aligned}$$
(8)

By using the system dynamics described by Eq. (1), the performance index (8) is written in terms of the system states and input in the present time. Accordingly, the optimal control law for a second-order system is obtained by applying the subsequent necessary condition for optimality, which relates to the quadratic performance index (8):

$$\begin{aligned} \frac{\partial {J}}{\partial {u}}=0, \end{aligned}$$
(9)

which leads to

$$\begin{aligned} u=-\frac{2\kappa }{bh^2}\left[ e_{1}+h(x_{2}-\dot{x}_{1d})+\frac{h^2}{2}(\eta -\ddot{x}_{1d})\right] , \end{aligned}$$
(10)

where \(e(t) = x_1-x_{1d}\), and the reduction factor, which incorporates the control weighting factor, is defined as follows:

$$\begin{aligned} \kappa =\frac{1}{1+4h^{-4}b^{-2}w}, \end{aligned}$$
(11)

where \(0\le \kappa \le 1\) for \(w\ge 0\). By increasing the weighting factor w, the reduction factor \(\kappa\) is reduced to limit the control input. When \(w=0\), then \(\kappa =1\). In this case, the control input with no intentional reduction is given as

$$\begin{aligned} u=-\frac{2}{bh^2}\left[ e_{1}+h(x_{2}-\dot{x}_{1d})+\frac{h^2}{2}(\eta -\ddot{x}_{1d})\right] . \end{aligned}$$
(12)

Using the control law (12) in the model (2), the closed loop dynamics is achieved as

$$\begin{aligned} \dot{x}_2=f-\frac{2}{h^2}\left[ e_{1}+h(x_{2}-\dot{x}_{1d})+\frac{h^2}{2}(\eta -\ddot{x}_{1d})\right] , \end{aligned}$$
(13)

that leads to the following error dynamics:

$$\begin{aligned} \ddot{e}_1+\frac{2}{h}\dot{e}_1+\frac{2}{h^2}e_1=0. \end{aligned}$$
(14)

Remark 2

By deriving the control laws (10) and (12) in the closed forms, the prediction time h is considered as a free parameter of the control law, not a step size of integration. This free parameter should be adjusted to achieve a desired behaviour for the closed loop system. Since the parameter h is selected positive, the linear error dynamics (14) is exponentially stable. This result indicates that the truncation error in Taylor series expansion with the order limited to the relative degree does not influence the control performance as mentioned in Remark 1. The parameter h also influences the time constant of the closed-loop system (14). The poles of the closed loop system (14) are determined as \(\frac{-1}{h}(1+j)\). It is seen that, h affects the place of poles and consequently the system response. Faster responses are achieved with smaller values of h.

For the constrained control problem, the performance index (8) is minimized subject to the satisfaction of constraints (3). One strategy for restricting the control input within a specified range is the increasing of the weighting factor w in the control law (10). For a constant value of w, the control input is decreased during the process at the cost of increased tracking errors at all times even when the control input is within the range.

As an alternative optimal approach, the constrained controller is developed in which the input constraint is considered in finding the control law. To achieve this aim, the expanded performance index (8) with \(w=0\) has to be minimized in the presence of the input constraints (3). As a result, the following constrained optimization problem needs to be solved to determine the optimal control law:

$$\begin{aligned} \begin{aligned}&\text {minimize} \ \ \ J(u(t),\ x(t), h, w=0) \ \ \ \\&\text {subject to} \ \ \ U_{\text {min}}\le u \le U_{\text {max}}. \end{aligned} \end{aligned}$$
(15)

The analytical solution to the constrained optimization problem (15) is achieved by applying the KKT theorem. Accordingly, the input constraint with upper and lower bounds is written as two constraints in the following standard form:

$$\begin{aligned} \begin{aligned} p_1(u)&=u-U_{\text {max}}, \\ p_2(u)&=-u+U_{\text {min}}. \end{aligned} \end{aligned}$$
(16)

Then, the KKT conditions for optimality can be expressed as Rao (2019):

$$\begin{aligned}&\frac{\partial J}{\partial u}+\sum _{i=0}^{2}{{\lambda }_{i}}\frac{\partial p_{i}}{\partial u}=0,\ i=1, 2 \end{aligned}$$
(17)
$$\begin{aligned}&\lambda _{i}p_{i}=0\ \ \ i=1, 2 \end{aligned}$$
(18)
$$\begin{aligned}&p_{i}\le 0\ \ \ \ \ \ i=1, 2 \end{aligned}$$
(19)
$$\begin{aligned}&{\lambda }_{i}\ge 0\ \ \ \ \ \ i=1, 2 \end{aligned}$$
(20)

where \(\lambda _1\) and \(\lambda _2\) denote Lagrange multipliers.

Theorem 1

For the affine system (1)–(2) having single input, \(u\in R\), with upper and lower constraints, the constrained solution leads to the simple saturation of the unconstrained control.

Proof

The KKT conditions (17) to (20) include some equalities and inequalities that are solved simultaneously by considering activity or inactivity of constraints. According to (18), the inactive constraints imply \(p_i\le 0\) and \(\lambda _i=0\), while for active constraints \(\lambda _i\ne 0\) and \(p_i=0\). In the mentioned problem, both constraints cannot be active simultaneously. Therefore, when one of the constraints becomes active, its Lagrange multiplier takes a non-zero value, and the control input is readily determined using the constraint equation with equality sign \((p_i=0)\), as specified in (18). Accordingly, the non-zero Lagrange multiplier corresponding to inactive constraint can be calculated by solving Eq. (17). During instances when none of the constraints are active, all Lagrange multipliers are zero, resulting in an optimal solution without constraints. Consequently, the constrained control law for the second-order system is derived as follows:

$$\begin{aligned} u_{\text {cons}}=\left\{ \begin{array}{lc} U_{\text {max}} &{} \text {if} \ \ \ \ \ p_1\ge 0, \ p_2< 0 \\ u_{\text {unc}} &{} \text {if} \ \ \ \ \ p_1\le 0, \ p_2\le 0\\ U_{\text {min}} &{} \text {if} \ \ \ \ \ p_1 < 0, \ p_2\ge 0 \end{array}\right. \end{aligned}$$
(21)

where \(u_{\text {unc}}\) is the unconstrained control law presented in (12). Note that for the second-order system (1)–(2), the form of performance index (4) or (8) is parabolic having a single minimum. Therefore, a feasible solution with bounded Lagrange multipliers exist for KKT conditions.

According to the error dynamics (14), the unconstrained control system with \(w=0\) is exponentially stable. On the other hand, from Theorem 1, the optimal constrained solution given in (21) is a simple saturation of the unconstrained optimal control law with \(w=0\). This solution can be achieved, equivalently, by online regulating of the weighting factor w in the control law (10). In other words, the saturated control input (21) can be achieved by tuning the reduction factor in the unconstrained control law (10). Consequently, the coefficient \(\kappa\) is occasionally reduced from 1 to avoid surpassing the allowable input value. The coefficient \(\kappa\) corresponding to the maximum input is derived from (10) as follows:

$$\begin{aligned} \kappa ={-u_{\text {cons}}\frac{bh^2}{2}}{\left[ e_{1}+h(x_{2}-\dot{x}_{1d})+\frac{h^2}{2}(\eta -\ddot{x}_{1d})\right] }^{-1}. \end{aligned}$$
(22)

For other times when the control input is within the admissible range, the coefficient \(\kappa\) will be equal to 1, that means no reduction on the control input.

In the following, two different approaches are conducted to show the boundedness of tracking error under the control input (21) when the control input is weighted with a time-varying variable to decrease \(\kappa\). Equivalently, the boundedness of saturation solution is provided.

Theorem 2

The tracking error of generalized position and its derivative in the closed-loop system under the control law (10) are uniformly bounded for any \(0\le \kappa \le 1\).

Proof

The closed loop dynamics in terms of \(\kappa\) is derived by applying Eq. (10) into Eq. (1) as follows:

$$\begin{aligned} \ddot{e}_1+\frac{2\kappa }{h}\dot{e}_1+\frac{2\kappa }{h^2}e_1=(1-\kappa )({\eta }-\ddot{x}_{1d}). \end{aligned}$$
(23)

The right hand-side of Eq. (23) is created due to the limiting of the control input that causes some tracking errors. For \(\kappa = 1\), the closed loop dynamics (23) is changed to Eq. (14) indicating no constraint case. Assuming that the function \(\eta\) in (2) is bounded and considering \(|\eta -\ddot{x}_{1d}|<\Gamma\), Eq. (23) can be written as

$$\begin{aligned} {\ddot{e}}_1(t)+\frac{2\kappa }{h}{\dot{e}}_1+\frac{2\kappa }{h^{2}}{e}_1<(1-\kappa )\Gamma . \end{aligned}$$
(24)

By using the solution of the second-order differential equation, followed by the application of the comparison lemma (Khalil 2001), it is established that

$$\begin{aligned} e_1 \le Ae^{\frac{-\kappa }{h}t}\left( \text {sin}{\frac{\sqrt{\kappa (2-\kappa )}}{h}t}+\phi \right) +\frac{(1-\kappa )\Gamma h^2}{2\kappa }. \end{aligned}$$
(25)

The positive value of h indicates that

$$\begin{aligned} \lim _{t\rightarrow \infty } e_1(t)=\frac{(1-\kappa )\Gamma h^2}{2\kappa }. \end{aligned}$$
(26)

Substituting Eq. (11) in (26) leads to

$$\begin{aligned} \lim _{t\rightarrow \infty } e_1(t)=\frac{2\Gamma w}{h^2b^2}. \end{aligned}$$
(27)

From equation (27), it can be deduced that, for any specified \(\epsilon > 0\), selecting the prediction time h as \(h^2 > \frac{2w\Gamma }{b^2\epsilon }\) guarantees the convergence of \(e_1\) towards the following compact set:

$$\begin{aligned} |{e_1}|<\epsilon . \end{aligned}$$
(28)

To assess the boundedness of \(\dot{e}_1(t)\) for the second-order system, one can examine a potential candidate for the Lyapunov function in the form of

$$\begin{aligned} V=\frac{\kappa }{h^2}e^2_1+\frac{1}{2}\dot{e}^2_1>0. \end{aligned}$$
(29)

The first time derivative of V gives

$$\begin{aligned} \dot{V}=\frac{{\dot{\kappa }}}{h^2}e_1^2+\frac{2\kappa }{h^2}e_1\dot{e}_1+\dot{e}_1\ddot{e}_1. \end{aligned}$$
(30)

When the control input reaches the constraint, \(\kappa\) is equivalently reduced from 1 to decrease the control input, so \({\dot{\kappa }}\) in Eq. (30) becomes negative until the saturation is removed and the system returns to the unconstrained solution. For the un-constrained solution, \(\kappa =1\) and \({\dot{\kappa }}=0\). Therefore, Eq. (30) is simplified to

$$\begin{aligned} \dot{V}=-\frac{2}{h}\dot{e}^2_1<0, \end{aligned}$$
(31)

that indicates the asymptotic stability of closed loop system. For the saturated times, considering a negative value for \({\dot{\kappa }}\) and replacing Eq. (23) into (30) gives

$$\begin{aligned} \dot{V}=\dot{e}_1(\left( 1-\kappa \right) \left( {\eta }-\ddot{x}_{1d}\right) ) -\left[ \frac{\left| {\dot{\kappa }}\right| }{h^2}e_1^2+\frac{2\kappa }{h}\dot{e}_1^2\right] . \end{aligned}$$
(32)

Considering the upper bound for \(\left| ({\eta }-\ddot{x}_{1d})\right| <\Gamma\), gives

$$\begin{aligned} \dot{V}\le |\dot{e}_1|(1-\kappa )\Gamma -\left[ \frac{\left| {\dot{\kappa }}\right| }{h^2}e_1^2+\frac{2\kappa }{h}\dot{e}_1^2\right] \le |\dot{e}_1|(1-\kappa )\Gamma -\frac{2\kappa }{h}\dot{e}_1^2. \end{aligned}$$
(33)

Further investigation on the inequality (33) is done by applying the inequality \(\alpha \beta \le n\alpha ^{2}+\frac{\beta ^{2}}{4n}\) for any real \(\alpha\), \(\beta\) and \(n>0\). By considering \(n=\frac{\kappa }{h}>0\)

$$\begin{aligned} \dot{V}&\le \frac{\kappa }{h}\dot{e}_1^2+\dfrac{h\Gamma ^2 \left( 1-\kappa ^2\right) }{4\kappa }-\frac{2\kappa }{h}\dot{e}_1^2, \end{aligned}$$
(34)
$$\begin{aligned} \dot{V}&\le \frac{h\Gamma ^2(1-\kappa )^2}{4\kappa }-\frac{\kappa }{h}\dot{e}_1^2. \end{aligned}$$
(35)

Using (28) and (29), the inequality (35) is rewritten as

$$\begin{aligned} \dot{V}\le -\frac{2\kappa }{h}V+\frac{2\kappa ^2}{h^3}\epsilon ^2+\frac{h\Gamma ^{2}(1-\kappa )^2}{4\kappa }. \end{aligned}$$
(36)

By taking \(\frac{2\kappa ^2}{h^3}{|\epsilon |}^2+\frac{h\Gamma ^2(1-\kappa )^2}{4\kappa }=N\), the inequality (36) is written as

$$\begin{aligned} \dot{V}\le -\frac{2\kappa }{h}V+N. \end{aligned}$$
(37)

Applying the comparison lemma, the solution of the first-order differential equation results in:

$$\begin{aligned} V(t)\le \left( V(0)-\frac{hN}{2\kappa }\right) e^{\frac{-2\kappa }{h}t}+\frac{hN}{2\kappa }. \end{aligned}$$
(38)

Due to the positive values of \(\kappa\) and h, the Lyapunov function remains bounded as can be observed

$$\begin{aligned} \lim _{t\rightarrow \infty }V(t)=\frac{hN}{2\kappa }. \end{aligned}$$
(39)

The boundedness of the Lyapunov function (29), coupled with the convergence of the error \(e_1\) within a compact set as indicated by (28) result the boundedness of \(\dot{e}_1\).

Remark 3

As deduced from Theorem 2, it is imperative to avoid selecting an overly small prediction time h to ensure the system’s tracking error remains within acceptable bounds under input constraints. On the other hand, the smaller value for h leads to the faster response of the systems as indicated in Remark 2. Therefore, a reasonable value for the prediction time should be selected. This issue will be investigated in the results section.

2.2 Design of ESO

In this section, the ESO algorithm is utilized to estimate the perturbation term \(\eta (x,\dot{x},d)\) for using in the constrained control law developed in the previous section. By defining the perturbation term as an extera state \(x_3=\eta (x,\dot{x},d)\), the augmented state-space model of the system can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{lc} \dot{x}_1=x_2,\\ \dot{x}_2 =x_3+bu,\\ \dot{x}_3=\Upsilon (t),\\ y=x_1 \end{array}\right. \end{aligned}$$
(40)

The equations of ESO are presented as

$$\begin{aligned} \left\{ \begin{array}{lc} \dot{{\hat{x}}}_1={\hat{x}}_2-\Omega _1({\hat{x}}_1-y)\\ \dot{{\hat{x}}}_2={\hat{x}}_3-\Omega _2({\hat{x}}_1-y),\\ \dot{{\hat{x}}}_3=-\Omega _3({\hat{x}}_1-y), \end{array}\right. \end{aligned}$$
(41)

in which \(\Omega _{i \ (i = 1, 2,3)}\) represent the observer gains. With the appropriate selection of gains, the observer provides a good estimate for the system states, encompassing the additional state \(x_3\). The error dynamics is derived by subtracting (41) from (40) as

$$\begin{aligned} \left\{ \begin{array}{lc} \dot{{\tilde{e}}}_1={\tilde{e}}_2-\Omega _1{\tilde{e}}_1,\\ \dot{{\tilde{e}}}_2={\tilde{e}}_3-\Omega _2{\tilde{e}}_1,\\ \dot{{\tilde{e}}}_3=-\Omega _3{\tilde{e}}_1+\Upsilon (t), \end{array}\right. \end{aligned}$$
(42)

in which \({\tilde{e}}_i={\hat{x}}_i-x_i\ (i =1,2,3)\) represents the error of estimation. According to Eq. (42), the error dynamics is linear. Therefore, by selecting appropriate gains, the observer stability is assured, assuming that \(\Upsilon (t) = {\dot{\eta }}\) remains bounded. The following theorem gives a scheme for selecting the gains \(\Omega _{i \ (i=1,2,3)}\) to produce the desired response.

Theorem 3

By selecting \(\Omega _1=3/\epsilon\), \(\Omega _2=3/\epsilon ^2\) and \(\Omega _3=1/\epsilon ^3\), in which \(\epsilon >0\) is an adjustable parameter, the estimation error dynamics described by (42) remains bounded under the condition of bounded \(\Upsilon (t)\).

Proof

By selecting \(\Omega _1=3/\epsilon\), \(\Omega _2=3/\epsilon ^2\) and \(\Omega _3=1/\epsilon ^3\) in (42), the resulting dynamics can be expressed as

$$\begin{aligned} \begin{bmatrix} \dot{{\tilde{e}}}_1\\ \dot{{\tilde{e}}}_2 \\ \dot{{\tilde{e}}}_3 \end{bmatrix}= \Psi \begin{bmatrix} {\tilde{e}}_1\\ {\tilde{e}}_2\\ {\tilde{e}}_3 \end{bmatrix} - G\Upsilon (t), \end{aligned}$$
(43)

where \(\Psi = \begin{bmatrix} -3/\epsilon &{} 1 &{} 0 \\ -3/\epsilon ^2 &{} 0 &{} 1 \\ -1/\epsilon ^3 &{} 0 &{} 0 \end{bmatrix}\) and \(G = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\). The eigenvalues of \(\Psi\) are found as \(\lambda _i = -1/\epsilon\) \((i=1,2,3)\). Consequently, the matrix \(\Psi\) will be Hurwitz for a given positive \(\epsilon\), ensuring the bounded-input bounded output (BIBO) stability for the error dynamics. Solving (43) yields

$$\begin{aligned} {\tilde{e}}(t) = e^{Et}{\tilde{e}}(0)+\int _{0}^{t}e^{E(t-\tau )}G\Upsilon (\tau )d\tau , \end{aligned}$$
(44)

where \({\tilde{e}}=[{\tilde{e}}_1 \ {\tilde{e}}_2 \ {\tilde{e}}_3]^T\). Since \(\epsilon\) is a positive value

$$\begin{aligned} \lim _{t\rightarrow \infty }{\tilde{e}}(t)= \int _{0}^{t}e^{E(t-\tau )}G\Upsilon (\tau )d\tau . \end{aligned}$$
(45)

Based on Eq. (45), for any given \(\epsilon >0\) and under the assumption of bounded \(\Upsilon (u)\), the estimation error converges to a compact set Chen (1984).

Remark 4

The positioning of eigenvalues and the convergence speed of the ESO as a high-gain observer, are impacted by the adjustable parameter \(\epsilon\). Any decrease in the value of \(\epsilon\) leads to a fast response for the observer. However, decreasing the adjustable parameter \(\epsilon\) increases the sensitivity to modeling errors and measurement noise, potentially resulting in increased estimation errors. Moreover, there is a risk of numerical errors during the solution of the set of differential equations at each sampling time for smaller values of \(\epsilon\).

3 Case Study (A Lever Arm)

According to Fig. 2, a lever arm consisting of a massless arm with two lumped masses at the end-points is examined as a case study for the second-order system.

Fig. 2
figure 2

The schematic of the lever arm

Full size image

In this structure, the kinematic and potential energies are obtained as follows:

$$\begin{aligned} T&=\frac{1}{2}I_o{\dot{\theta }}^{2}, \end{aligned}$$
(46)
$$\begin{aligned} V_{g}&=(m_{1}r_{1}-m_{2}r_{2})g\sin {\theta }. \end{aligned}$$
(47)

Here, \(I_o\) represents the moment of inertia, \(m_1\) and \(m_2\) are the lumped masses located at the end points of the arm, and \(\theta\) represents the angular displacement of the arm. The governing equation for the lever arm using the Lagrange method is given as

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial {T}}{\partial {{\dot{\theta }}}}\right) -\frac{\partial {T}}{\partial {\theta }}+\frac{\partial {V_{g}}}{\partial {\theta }}=\tau , \end{aligned}$$
(48)

which leads to

$$\begin{aligned} I_{o}\ddot{\theta }+G(\theta )=\tau , \end{aligned}$$
(49)

where \(I_{o}=m_1r_1^2+m_2r_2^2\) is the lever arm inertia and \(G=(m_1gr_1-m_2gr_2)\text {cos}\theta\) denotes the gravity term. \(\tau\) represents the torque of motor. By defining \(\theta =x_{1}\), \({\dot{\theta }}=x_{2}\), the state-space model of the lever arm is formulated as

$$\begin{aligned} \left\{ \begin{array}{lc} \dot{x}_{1}=x_{2}, \\ \dot{x}_{2}=f(x)+a\tau , \end{array}\right. \end{aligned}$$
(50)

where

$$\begin{aligned} f(x)=-I_o^{-1}G,\ a=I_o^{-1}. \end{aligned}$$
(51)

3.1 Simulation Results

In the simulation study, the dynamic model of the lever arm system is assumed to be accurate. Therefore, the constrained controller is examined without the ESO observer. The parameters of the lever arm are taken as \(m_{1}=0.5 \) (kg), \(m_{2}=0.6\) (kg), \(r_{1}=0.14 \) (m), \(r_{2}=0.15 \) (m). Also, the admissible range for the control input is considered as \(-0.98 \le \tau \le 0.98 \) (N m). Three distinct prediction times, including \(h=0.05\), \(h=0.2\), and \(h=0.4\), are examined for the proposed control system.

At first, the outcomes of the unconstrained control strategy for three distinct prediction times are illustrated in Fig. 3. Note that, the input constraint is dropped in these results. As mentioned before, the unconstrained version of the control strategy performs as a feedback linearization control. The results confirm that a reduction in the prediction time h leads to a decrease in both settling time and the speed of responses. However, this reduction is accompanied by an increase in torque magnitudes. The settling time for \(h=0.05\) is considerably smaller compared to the other cases at the cost of higher control inputs. The obtained results are in full alignment with the outcomes of Remark 2 in Sect. 2 for the unconstrained control. However, the computed torques for the unconstrained controller exceed admissible ranges and are unfeasible for practical realization. To decrease the applied torques, the prediction time h seems to be increased. However, it negatively affect the speed of the response. According to the results of Fig. 3, the settling time for \(h=0.4\) is high while the control input is still out of the specified range. Consequently, the unconstrained controller with high values of h is found to be inefficient for limiting the control input and the application of the constrained controller is required. Note that, \(h=0.4\) is removed at the rest of the results because of its high settling time.

Fig. 3
figure 3

The simulation results of the unconstrained control for step trajectory, a Angular displacement, b Tracking error, c Control input

Full size image

The constrained controller is evaluated in the simulation results, considering the maximum allowable torques that the actuator can apply. The results for \(h=0.05\) and 0.2 are shown in Fig. 4. Since the unconstrained controller demands larger control input for lower prediction time value \((h=0.05)\), the constrained controller often encounters more saturations. This result is in complete agrement with the result of Theorem 2. Consequently, it is crucial to choose a suitable prediction time that is neither too large nor too small. The suitable value for the simulated system can be found \(h = 0.2\). The system slows down for higher values like \(h = 0.4\), and the control input becomes more saturated for smaller values like \(h = 0.05\). Equivalently, it is obvious that the reduction factor is changed between 0 and 1 according to Fig. 4d. When \(\kappa =1\), there is no limitation on the control signal. However, during saturation, the factor \(\kappa\) is decreased to reduce the control input \(\tau\).

Fig. 4
figure 4

The simulation results of the constrained control for step trajectory, a Angular displacement, b Tracking error, c Control input, d Reduction factor

Full size image

To assess the effectiveness of the suggested constrained control approach in comparison to alternative constrained strategies, the achieved outcomes are contrasted with those of the conventional NMPC outlined in Appendix 1, considering time-varying trajectories. Both control methods utilize identical non-linear lever arm models and constraints. According to Fig. 5, the performance of two methods in satisfying the constraints are similar. However, the simulation times for the proposed controller and NMPC running on the same PC are 1.75 (sec) and 72.8 (sec), respectively. This result indicates that the proposed constrained controller is much faster than the NMPC. This is for the reason that the NMPC, unlike the proposed method, uses the online optimization for calculation of the control inputs at each sampling time. These comparative results indicate the capability of the proposed method for online implementation.

Fig. 5
figure 5

The simulation results of the constrained control for time-varying trajectory in comparing with NMPC, a Angular displacement, b Tracking error, c Control input

Full size image

In order to show the independency of the proposed constrained controller on the selected value for the prediction time (\(h=0.2\)), the controller is tested under the harmonic trajectories according to Fig. 6. The results indicate the superior performance of the proposed method in tracking the mentioned trajectory with admissible control inputs. Also, the simulation times are 1.73 (s) and 85.05 (s) for the proposed method and NMPC, respectively. Therefore, the proposed method is fast and easy to implement compared to the common NMPC method.

Fig. 6
figure 6

The simulation results of the constrained control for harmonic trajectory in comparing with NMPC, a Angular displacement, b Tracking error, c Control input

Full size image

3.2 Experimental Evaluation of the Proposed Control System

To implement the proposed control system in the real environment, a platform for a lever arm is designed and fabricated. The fabricated platform containing a lever-arm with two end-point masses is shown in Fig. 7. The derive pulleys and conveyor tail connect the DC motor to the arm. The MEMS-grade MPU6050 inertial measurement unit (IMU) is employed to measure the angular velocity of the arm at a frequency of 50 Hz, as depicted in Fig. 7. Additionally, the HN3806 two-phase encoder provides the angular displacement of the arm with an accuracy of 0.3 degrees. The measured data sent to the Simulink software through the serial connection, is used to calculate the control signal. Finally, the pulse-width modulation (PWM) input is sent to a 12-volt DC motor to complete the hardware in the loop structure. In this setup, two Arduino UNO boards serve as input–output (IO) hardware, while the analysis and calculation of the control input are executed on a laptop computer equipped with an Intel(R) Core(TM) i7 CPU 6500U running at 2.50 GHz and 4 MB cache. Note that, the admissible range of the control input due to the limited capacity of actuator is considered as \(-0.98 \le \tau \le 0.98 \) (N m). On the another hand, in simulation studies, the impact of the time-delay is dropped. However in the real system, time delay from the sensor signal and control input can be clearly seen.

3.2.1 Results Without Perturbations

In this section, the results of the proposed controller are presented by assuming no external disturbances and parametric uncertainties. Additionally, the gyroscope data is incorporated in these results to provide the angular velocity of the lever-arm. Figures 8 and 9 show the obtained results of the proposed control method during two desired trajectories. The results clearly show a good performance in tracking the desired trajectories by the proposed control method. It is necessary to say that when the reduction factor is equal to one, the control input is in the admissible range, and there is no reduction in the control input. However, the reduction factor is reduced during saturation to limit the control input \(\tau\). The NMPC algorithm used as a comparative method in the simulation studies is not applicable for the online implementation in the experimental setup because of its too high running time.

Fig. 7
figure 7

Experimental setup

Full size image
Fig. 8
figure 8

The experimental results of the constrained control for the periodic path, a Angular displacement, b Tracking error, c Control input, d Reduction factor

Full size image
Fig. 9
figure 9

The experimental results of the constrained control for time-varying path, a Angular displacement, b Tracking error, c Control input, d Reduction factor

Full size image

3.2.2 Results with Perturbations

In the following, the effectiveness of the proposed ESO-based constrained controller is assessed by incorporating \(20\%\) parametric uncertainty in the lever arm lengths and an external disturbance \(d=0.3\sin (0.5t)\). The pseudo-code of the proposed hardware in the loop mechanization is outlined in Algorithm 1. The results of the ESO-based constrained controller for three values of the free parameter \(\epsilon\) in the observer are compared in Fig. 10. As illustrated in Fig. 10, for a higher value for \(\epsilon =0.1\), the controller couldn’t properly follow the desired path. This shows that larger values of \(\epsilon\) may not effectively provides the dynamics of lever-arm behavior. Based on Remark 4, a decrease in the free parameter \(\epsilon\) leads to a substantial reduction in the estimation error; nevertheless, there is some flexibility in reducing the value of \(\epsilon\). When the value of \(\epsilon\) is much smaller, as in the case of \(\epsilon =0.01\), the system becomes sensitive to modeling and measurement errors, resulting in fluctuations as illustrated in Fig. 10b. Numerical errors may also arise when employing much smaller values for the observer gain. The control inputs associated with three different values of \(\epsilon\) are depicted in Fig. 10c. The outcomes shows that the fluctuations observed for \(\epsilon =0.01\) result in a more saturated control input. Therefore, \(\epsilon\) should be chosen appropriately, avoiding both excessively large and excessively small to mitigate substantial errors and fluctuations in the system responses and control input. Based on the results, the choice of \(\epsilon =0.02\) is considered reasonable for the present application.

Algorithm 1
figure a

The proposed control method pseudo-code

Full size image
Fig. 10
figure 10

The experimental results of the ESO-based controller for different \(\epsilon\), a Angular displacement, b Tracking error, c Control input, d Reduction factor

Full size image

Figure 11 illustrates a comparison among the estimated states and the unknown term (\({\hat{x}}_3\)) for three different free parameters of \(\epsilon\). It is clearly seen that, reducing the parameter \(\epsilon\) until an acceptable range can reduce the estimation errors. Note that, the gyroscope data is used to calculate the estimation error of the second state \({\tilde{e}}_2\).

Fig. 11
figure 11

The estimation results for different \(\epsilon\), a Angular displacement error, b Angular velocity error, c Unknown term

Full size image

To evaluate the proposed method under various conditions, a time-varying reference trajectory is used. The outcomes are then compared with those obtained from the controller without utilizing the estimated unknown term. Figure 12 illustrates that the ESO-based controller outperforms the controller without ESO, demonstrating significantly enhanced performance. This is attributed to the fact that the estimator tries to improve the precision of the controller by incorporating the perturbation term. Therefore, the ESO-based controller, employing the ESO, demonstrates superior performance in reducing the tracking error. In addition, the controller without ESO brings high control input to compensate for the perturbations. Therefore, the difference between the ESO-based controller and the controller without ESO is emphasized in the tracking accuracy of the reference path with lower control efforts. This is because the ESO-based method, as an adaptive control approach, utilizes perturbation information to calculate the control input at each sampling time. In contrast, the controller without ESO attempts to reduce the tracking error by increasing the control effort.

Fig. 12
figure 12

The comparative experimental results of the controller with and without ESO for time-varying path, a Angular displacement, b Tracking error, c Control input, d Reduction factor

Full size image

To assess the efficiency of the proposed observer-based controller in compensating for the perturbations, the obtained results are compared with those extracted by an adaptive back-stepping controller (ABSC), addressed in the Appendix. In this case, the periodic path is determined. Note that, the amplitude and frequency of the external disturbance are unknown for both controller. According to Fig. 13, the tracking error of the proposed ESO-based controller is lower than that of the ABSC. The ABSC controller couldn’t estimate the perturbation term accurately, unlike the ESO. Note that the adaptive control laws like ABSC often require primary information of the unknown terms.

Fig. 13
figure 13

The comparative experimental results between the proposed method and ABSC for the time-varying path, a Angular displacement, b Tracking error, c Control input

Full size image

4 Conclusion

In this study, a nonlinear optimal controller with input constraints is analytically designed for a class of second-order systems. The optimality of the constrained solution is provided by solving an optimization problem based on the response prediction of nonlinear systems. The stability of the constrained controller is analyzed to show the convergence of the tracking errors towards the compact sets in terms of the prediction time. Consequently, it is essential to strike a balance when selecting the prediction time, avoiding both excessively large and excessively small values. Opting for a prediction time that is too large leads to slow responses, while choosing a prediction time that is too small results in more saturated control input, deteriorating the responses of the system. The ESO is employed to compensate for uncertainties and external disturbances, updating the proposed constrained controller to match real conditions. Simulation studies are carried out for a lever arm, and the proposed control schemes have been compared with NMPC. The results show that the proposed controller is much faster than NMPC. Therefore, it is able to be online implemented on a fabricated platform containing a lever arm. The proposed control method is verified with different tests. The results demonstrate the efficacy of the proposed control method in minimizing tracking errors in the presence of input limitations. The comparative results with the ABSC indicate superior performance for the proposed method in compensating for uncertainties and external disturbances. The extension of the proposed methodology to address more complex second-order systems with multi inputs opens avenues for future research and improvements.