1 Introduction

Nowadays robotic arms are widely applicable in many industries such as automotive engineering, aerospace engineering, and ocean engineering (Dwivedy and Eberhard 2006). Many robotic arms cannot be considered as rigid bodies since their geometrical properties and manufactured materials result in a flexible structure for these arms. One of the most familiar examples of such systems is the robotic manipulators mounted on exploring aerospace vehicles. These arms are significantly flexible because of their long length. Considering the fact that in robotic performances, accuracy is one of the most critical parameters, this flexibility may increase the end-effector error. Thus, in order to compensate for the aforementioned errors and increase the accuracy of the system, the flexibility of the arm requires to be considered. Considering the flexibility of the arm increases the engaged degrees of freedom and states of the system. When the flexibility of a robotic system is considered in modeling, not only the slow dynamic movement of the arm as a rigid body should be studied, but also the fast dynamic related to the vibrational response of the arm beam needs to be modeled and its related PDE equations should be coupled with the ODE equations of the main system.

Some modeling methods for the planner flexible manipulators have been proposed so far. A partial differential equation model of a planner single-link flexible manipulator is derived in Jiang et al. (2018). However, the partial differential equation model is not suitable for both dynamic analysis and controller design of the system. There are three popular approaches through which the model can be reduced to ODE. Assumed mode method (Gao et al. 2019), finite element method (Mohamed and Tokhi 2004), and the lumped parameter model (Sun et al. 2017). Amongst these studies, the assumed mode method is more applicable in researches, since the dynamic behavior of a flexible manipulator can be presented more accurately using the model with lower dimensions (El-Badawy et al. 2010).

As can be seen, in the mentioned studies, the flexibility of the robotic arm is modeled in two dimensions by the use of two generalized coordinates. This simplifying assumption is in contrast to the real behavior of a robotic arm which actually has deformation in three dimensions (3D).

There are a few studies in which the manipulators would be modeled spatially in 3D space based on their original PDE formulations. The orientation and the vibrations of the manipulator should be considered simultaneously when a flexible manipulator moves within 3D space. Liu et al. (2018), the model of a coupled 3D flexible manipulator is derived using Hamilton principle and unit quaternion, and the resultant model is described with the aid of a set of PDEs and ODEs.

On the other hand, all of these researches have another significant simplification named linear modeling. This assumption again decreases the accuracy of modeling of the robotic arm and its related vibrating response since the geometrical properties and material structure of these beams form a nonlinear dynamic system with nonlinear PDE equations.

Sharf (1995) considered the spin-up of a flexible beam and compared the different approaches for modeling the axial shortening on the basis of nonlinear strain–displacement relations. Damaren and Shart ( 1995), Du et al. (1996), Al-Bedoor and Hamdan (2001), Martins et al. (2002), Abe (2009) and Fazel et al. (2013) investigated the dynamics of flexible manipulators with geometric nonlinearity using the finite deformation theory and showed that the effect of the nonlinearity on the dynamic responses of a manipulator is not negligible when large bending deformations occur. Therefore, it can be concluded that it is necessary to consider the effects of geometric nonlinearity to design controllers for this kind of manipulators undergoing large flexural deformations.

3D and nonlinear modeling of flexible robotic arms increase the accuracy of simulation of this system, but the actual vibration of the system and its related deviation from set-point needs to be compensated by the aid of some improvement algorithms. Thus, a proper nonlinear controller is proposed in this paper to reduce the unwanted vibration of these arms and increase their accuracy.

The vibration control of flexible link manipulators has also received significant interest in the literature. The control schemes developed can be classified into two categories: feedback control and open-loop control. The main feedback control strategies, which use the measurements of system states to control the vibrations in a closed-loop way, include the proportional-integral-derivative control (Tokhi and Azad 1996), delayed feedback control (Qiu and Wu 2015), positive position feedback control (Shan et al. 2005), linear quadratic regulator (Chan and Modi 1990), adaptive control (Liu et al. 2016), sliding-mode control (Chang and Chen 1998), fuzzy control (Subudhi and Morris 2003), and artificial neural networks-based control (Talebi et al. 2000). The last two items are numerical methods which are not preferable for robotic applications since their efficiency for online and real-time processes is not good. These closed-loop controllers have a good compensating effect on the main dynamic of the system while the oscillatory response of the flexible arm cannot be properly controlled. The open-loop control strategies, which filter the inputs to produce a desirable motion with minimal vibrations, include the optimal trajectory planning (Heidari et al. 2013), and the input shaping method (Mohamed and Tokhi 2004; Díaz et al. 2010). Again, using these open-loop approaches alone do not result in a robust response in the whole dynamics of the flexible system. Ren et al. (2020) and Zhao et al. (2019, 2021) used the boundary control method to control the flexible manipulator. Here, the linear dynamic system is modeled in two-dimensional space. The advantage of this control method is for trajectory tracking. On the other hand, for the systems with parametric uncertainties, such as non-linear dynamics and unknown payload, the design of this type of controller is challenging.

The aforementioned controlling strategies are either open-loop which cannot compensate for the uncertainties and disturbances or closed-loop with a delay which is not suitable for controlling the fast dynamic response of the arm vibrating response. In this paper, a combination of an open-loop vibrational controller, i.e., input shaping (IS) with a closed-loop controller of feedback linearization is proposed to compensate the vibrational response of the system and dynamic error of the system simultaneously.

Input shaping is one of the algorithms in which the feedforward term is used for controlling the system. Input shaping suppresses the tip vibration by reshaping the desired trajectory in order to produce a new commanded trajectory that does not excite the resonance frequency of the flexible manipulator. The first advantage of this control method is its efficiency toward damping the vibrations instantly, resulting in zero residual vibration. Another benefit of the mentioned method is its good robustness and fast convergence rate. This method was first introduced in Singer and Seering (1990). The IS method is one of the subdivisions of the finite impulse response filters. In (Mohamed and Tokhi 2004) using the IS method, a smooth path is designed to transfer the flexible robot with small deflections, in a rest-to-rest motion. Additionally, the IS method is compared with the other finite impulse response filters. Ghorbani et al. (2019) have studied several shaping methods including ZV, ZVD and EI, with negative and positive amplitudes for the systems which include both rigid and flexible motions. Experimental investigations corresponding to the development of feed-forward and feedback controls are presented in Mohamed et al. (2005). A collocated PD controller has initially been developed in this paper for controlling rigid body motion. Afterward, feed-forward control based on input shaping and low-pass filtering technique has been developed which is equipped with strain feedback and PD control for increasing the efficiency of the designed vibration control of the manipulator. Singer and Seering (1990), an efficient dynamic modeling and tracking/vibration integrated control for a parallel manipulator was done. In addition, in formulation, the servo motor dynamics were considered.

In most of the researches, the system dynamic modeling has been simplified. These simplifications have been applied for ease of analysis, increasing the stabilization, and increasing the efficiency of the designed controller. It should be noted that some of these assumptions and simplifications have a significant impact on the system response. One of the most important assumptions that should be considered in the modeling is the number of engaged mode shapes required to discretize the equations. Here the required number of engaged mode shapes is extracted by analyzing the convergence of the response. The second important item which should be taken into account is the number of the engaged generalized coordinates for the system which works in three-dimensional space. The vibrational response of this system is performed so far in 2-dimensional space. Here it is shown that modeling the system in three dimensions will increase the accuracy of the system response since the model states are more compatible with the real system. However, this improvement also increases the number of equations.

There are also simplifications in the field of controlling the flexible arm. For example, most of the traditional studies have linearized the system around their related equilibrium points and have employed linear controllers such as proportional-derivative or optimal linear control methods. On the other hand, in most similar researches the main purpose of the controller is to control the slow dynamics of the main system states while the solution is proposed to control or reduce the fact dynamics of the system vibrations. Dynamic linearization of the system around a point can only control the system locally and decreases the active workspace of the arm. Therefore, in this paper, global linearization is employed and the controller design is based on nonlinear system dynamics.

The aforementioned controllers are employed so far have been implemented on 2D models or linear systems for which both of them do not deliver a real perspective of the efficiency of the proposed controllers. In this paper, closed-loop input shaping is designed and implemented for 3D nonlinear model of which is the most accurate model of these systems.

As a result, to provide a real model of a flexible robotic arm and reduce its related vibrations at the same time with compensating its dynamic errors, a nonlinear 3D robotic arm is modeled in this paper and a closed-loop input shaping controller is designed and implemented for it to control the fast and slow dynamics of the system simultaneously. To cover the mentioned target, a 3D flexible model of a robotic arm is extracted considering geometric nonlinear effects and its related kinematics and kinetics are derived. The kinematic of the system is extracted using the Jacobian matrix and the dynamic formulation of the system is provided employing Lagrange equation. Euler–Bernoulli model is employed to model the beam of the robotic arm and assumed mode is used to discretize the system. Then a closed-loop input shaping controller is designed and implemented on the system. The open-loop input shaping improves the input of the system in a way to reduce the vibrating response of the beam while feedback linearization compensates for its dynamic error related to uncertainties or disturbances. In order to show the superiority of the proposed 3D nonlinear model of the system, the arm is modeled in MATLAB and its related results are compared with previous models. In addition, to verify the efficiency of the proposed controlling strategy, some analytic and comparative simulation scenarios are conducted in MATLAB. It will be shown that the improved model provides a more realistic scheme of the dynamic system, and the proposed controller has a significant effect on compensating the vibration and error of the system through which the accuracy of the flexible robotic arm can be improved.

2 Kinematics

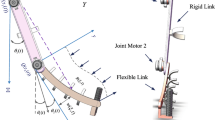
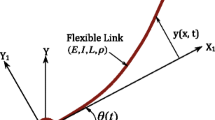
In order to check the necessity of 3D and nonlinear modeling of a robotic arm, a new model needs to be developed here in order to compare its related response with previous simplified models. In addition, the coupled model of the robotic arm and beam vibration is required to control the arm movement and its related vibrations. Thus, the dynamic equation of a nonlinear 3D flexible arm is derived here. The arm is considered here as an Euler–Bernoulli beam in two-plane bending. Axial deformation of the beam is also considered in this model which has nonlinear effects on the beam vibration in the flexible arm system. The general scheme of the considered system is shown in Fig. 1. Axes \({X}_{i}{Y}_{i}{Z}_{i}\) constitutes an inertia frame while \({X}_{b}{Y}_{b}{Z}_{b}\) is the body-fixed frame whose origin is on the arm’s joint. The workspace rigid position of the arm is described by the aid of two joint space angles \({\theta }_{1}\) and \({\theta }_{2}\) which are controlled by torques \({\tau }_{1}\) and \({\tau }_{2}\). The corresponding deflections with respect to the body-fixed frame are denoted by \(y(x,t)\) and \(z(x,t)\). Here \(x\) and \(t\) are the independent spatial and time variable, respectively. Also, \(u(x,t)\) is the axial deformation of the beam. Thus, the position vector of the point \(p\) in the body-fixed frame is:

$${r}_{b}={\left[x+u(x,t) \; y\left(x,t\right)\; z (x,t)\right]}^{T}$$
(1)

The relationship of each coordinate system can be represented by two rotation transformation matrices. Let \({R}_{r}({\theta }_{1})\) and \({R}_{r}({\theta }_{2})\) to be the rigid joint rotation matrices for rotating degrees of \({\theta }_{1}\) and \({\theta }_{2}\) as:

$$\begin{aligned} R_{r} \left( {\theta_{1} } \right) &= \left[ {\cos\cos \theta_{1}\; 0\;\sin\sin \theta_{1}\; 0\; \;1\;0 - \sin\sin \theta_{1}\;0\;\cos\cos \theta_{1} } \right] \hfill \\ R_{r} \left( {\theta_{2} } \right) &= \left[ {\cos\cos \theta_{2} - \sin\sin \theta_{2}\;0\;\sin\sin \theta_{2} \cos\cos \theta_{2}\;0\;0\;0\;1} \right] \hfill \\ \end{aligned}$$
(2)

The position vector of the system in the inertial coordinate frame can be computed as:

$${r}_{i}={R}_{r}\left({\theta }_{1}\right)\cdot {R}_{r}\left({\theta }_{2}\right)\cdot {r}_{b}$$
(3)

The orientation of the body fixed frame \({X}_{b}{Y}_{b}{Z}_{b}\) with respect to inertia frame \({X}_{i}{Y}_{i}{Z}_{i}\) is denoted by \(\theta ={\left[0\;{\theta }_{1}\;{\theta }_{2} \right]}^{T}\) where \({\theta }_{1}\) and \({\theta }_{2}\) are the rotation angles about \({Y}_{i}\) and \({Z}_{i}\) axis, respectively. In addition, the corresponding angular velocity of the body-fixed frame \({X}_{b}{Y}_{b}{Z}_{b}\) with respect to the inertia frame is presented by vector \(\omega ={\left[0\; {\omega }_{1}\;{\omega }_{2} \right]}^{T}\). The vector \(r\) can be defined as:

$${r}_{b}=D+d$$
(4)

where \(D={\left[x\;0\;0\right]}^{T}\) and \(d={\left[u(x,t) y\left(x,t\right) z (x,t)\right]}^{T}\). Here the vector \(d\) represents the beam deformation at point \(p\) relative to the body-fixed frame.

Fig. 1
figure 1

Schematic of 3D flexible robotic manipulator

Full size image

3 Dynamic Modeling

The time derivative of the position vector in the inertia frame and body-fixed frame is expressed by \({\dot{r}}_{i}\) and \({\dot{r}}_{b}\), respectively; considering the relative velocity relation we have:

$${\dot{r}}_{i}={\dot{r}}_{b}+\omega \times {r}_{b}=\dot{d}+\omega \times {r}_{b}$$
(5)

Therefore, the kinetic energy of the system including the hub, beam and tip mass will be as follows:

$$K=\frac{1}{2}\left({\omega }^{T}{I}_{h}\omega +\rho {\int }_{0}^{l}{\left[{\dot{r}}_{i}\right]}^{T}\left[{\dot{r}}_{i}\right]{\rm d}x+{m}_{p}{\left[{\dot{r}}_{i,}\right]}_{x=l}^{T}{\left[{\dot{r}}_{i}\right]}_{x=l}\right)$$
(6)

where \({m}_{p}\) and \({I}_{h}\) are the tip mass and the inertia of the joints, respectively. The inertia of the joints, assuming the symmetry of the beam, can be stated as follow:

$${I}_{h}=\left[{I}_{1}\;0\;0\;0\;{I}_{2}\;0\;0\;0 \;{I}_{3}\right]$$
(7)

The potential energy of the system with neglecting of gravity can be expressed as:

$$U=\frac{EI}{2}{\int }_{0}^{l}\left({\kappa }_{y}^{2}+{\kappa }_{z}^{2}\right)\mathrm{d}x$$
(8)

where \({\kappa }_{y}^{2}\) and \({\kappa }_{z}^{2}\) are the nonlinear curvatures of the beam about \({Z}_{b}\) and \({Y}_{b}\) axis, respectively, that can be computed as follows:

$$\begin{aligned} \kappa_{1}^{2} &= \left( {\frac{{\partial^{2} y}}{{\partial x^{2} }}} \right)^{2} \left\{ {1 + \left( {\frac{\partial y}{{\partial x}}} \right)^{2} + \cdots } \right\} \hfill \\ \kappa_{2}^{2} &= \left( {\frac{{\partial^{2} z}}{{\partial x^{2} }}} \right)^{2} \left\{ {1 + \left( {\frac{\partial z}{{\partial x}}} \right)^{2} + \cdots } \right\} \hfill \\ \end{aligned}$$
(9)

Assume mode method is used to discretize the continuous system. To meet this goal, the transversal deformations of the beam are assumed to be a multiplication of mode shape function by a time function as follows:

$$\begin{aligned} y\left( {x,t} \right) & = \mathop \sum \limits_{i = 1}^{n} \phi_{i} \left( x \right)\eta_{i} \left( t \right) \\ z\left( {x,t} \right) & = \mathop \sum \limits_{i = 1}^{n} \psi_{i} \left( x \right)\xi_{i} \left( t \right) \\ \end{aligned}$$
(10)

where \({\phi }_{i}\left(x\right)\) and \({\psi }_{i}(x)\) are the vibrating modes for a non-rotating cantilever beam. In addition, \({\eta }_{i}\left(t\right)\) and \({\xi }_{i}(t)\) are general coordinates. It is also assumed that the neutral axis of the flexible manipulator is in-extensional; hence the inextensibility condition can be expressed as:

$$\sqrt{{\left(1+{u}^{{\prime}}\right)}^{2}+{{y}^{^{\prime}}}^{2}+{{z}^{{\prime}}}^{2}}-1=0$$
(11)

The above equation can be expanded up to the second-order for \(y\) and \(z\). Solving for \({u}^{{\prime}}\) and neglecting the terms of order higher than three we obtain:

$${u}^{{\prime}}=\sqrt{1-{{y}^{{\prime}}}^{2}-{{z}^{^{\prime}}}^{2}}-1\approx -\frac{1}{2}\left({{y}^{{\prime}}}^{2}+{{z}^{{\prime}}}^{2}\right)$$
(12)

Finally, \(u\) can be expressed as:

$$u\left(x,t\right)=-\frac{1}{2}{\int }_{0}^{x}\left({{y}^{{\prime}}}^{2}+{{z}^{{\prime}}}^{2}\right)\,{\rm d}x$$
(13)

The equation of motion for the flexible manipulator, considering one mode for each deformation, can be then obtained using the following Lagrange approach:

$$\frac{\partial }{\partial t}\left(\frac{\partial L}{\partial \dot{q}}\right)-\frac{\partial L}{\partial q}=Q$$
(14)

where \(L=K-U\) and \(q\), \(Q\) are as follows:

$$\begin{aligned} q &= \left[ {\theta_{1}\;\theta_{2}\;\eta_{1}\;\zeta_{1} } \right] \hfill \\ Q &= \left[ {\tau_{1}\;\tau_{2}\;0\;0} \right] \hfill \\ \end{aligned}$$
(15)

By substituting Eqs. (10) and (13) into Eqs. (6) and (8) and applying the Lagrange formulation, the equations of motion of the system are obtained as follows:

$$M\ddot{q}+C\dot{q}+K=Q$$
(16)

where M is inertia, C is centripetal and K is elastic matrices as follows:

$$\begin{aligned} M & = \left[ {M_{rr}\;M_{rf}\;M_{fr}\;M_{ff} } \right]\quad C = \left[ {C_{rr}\;C_{rf}\;C_{fr}\;C_{ff} } \right] \\ K & = \left[ {0\;0\;K_{1}\;\xi^{3}+ K_{2} \xi } \right]^{T} \\ \end{aligned}$$
(17)

There are four coupled dynamic states here including the first rotation angle of the arm, the second rotation angle of the arm, the first mode shape of the arm, and the second mode shape of the arm [Eq. (15)]. Considering the fact that these four generalized coordinates are coupled, in order to explain the system in state space and extract the related controlling input, it is required to state the dynamic formulations in a matrix form of size 4.

4 Control Schemes

In this section, the proposed control schemes for controlling the position of the arm and simultaneously reducing its vibration are introduced. To cover this goal, a combination of a feed-forward control based on input shaping and a feedback control based on feedback linearization is proposed here. Initially, a collocated feedback linearization control is developed in order to control the rigid body motion of the flexible manipulator. Afterward, the calculated controlling signal is modified according to the input shaping method to reduce the vibrational response of the arm.

4.1 Feedback Linearization Control

In this section, using the feedback linearization technique, the rigid motion of the flexible manipulator is controlled. For this purpose, the equations of motion of the system described in the previous section are rewritten in the following form:

$${M}_{rr}{\ddot{q}}_{r}+{M}_{rf}\ddot{\xi }+{C}_{rr}{\dot{q}}_{r}+{C}_{rf}\dot{\xi }=\tau$$
(18)
$${M}_{fr}{\ddot{q}}_{r}+{M}_{ff}\ddot{\xi }+{C}_{fr}{\dot{q}}_{r}+{C}_{ff}\dot{\xi }+{K}_{1}{\xi }^{3}+{K}_{2}\xi =0$$
(19)

where \({q}_{r}={\left[{\theta }_{1}\;{\theta }_{2} \right]}^{T}\) are the main dynamic generalized coordinate of the system, \(\xi ={\left[\eta\;\zeta \right]}^{T}\) is the vibrating generalized coordinate and \(\tau ={\left[{\tau }_{1}\;{\tau }_{2} \right]}^{T}\) is the controlling torques of the motors. Index r refers to the main dynamic parameters of the system while index f shows the vibrating parameters. \({M}_{rr}\) and \({M}_{ff}\) are positive definite inertia matrices and hence invertible. \(\ddot{\xi }\) can be found from Eq. (19) as:

$$\ddot{\xi }=-{M}_{ff}^{-1}\left({M}_{fr}{\ddot{q}}_{r}+{C}_{fr}{\dot{q}}_{r}+{C}_{ff}\dot{\xi }+{K}_{1}{\xi }^{3}+{K}_{2}\xi \right)$$
(20)

where the mentioned matrices for our case study are:

$$\begin{array}{ll} {M_{rf} = \left[ {M_{13}\;M_{14}\;M_{23}\;M_{24} } \right]} \hfill & {M_{rr} = \left[ {M_{11}\;M_{12}\;M_{21}\;M_{22} } \right]} \hfill \\ {M_{ff} = \left[ {M_{33}\;M_{34}\;M_{43}\;M_{44} } \right]} \hfill & {M_{fr} = \left[ {M_{31}\;M_{32}\;M_{41}\;M_{42} } \right]} \hfill \\ {C_{rf} = \left[ {C_{13}\;C_{14}\;C_{23}\;C_{24} } \right]} \hfill & {C_{rr} = \left[ {C_{11}\;C_{12}\;C_{21}\;C_{22} } \right]} \hfill \\ {C_{ff} = \left[ {C_{33}\;C_{34}\; C_{43}\; C_{44} } \right]} \hfill & {C_{fr} = \left[ {C_{31}\;C_{32}\;C_{41}\;C_{42} } \right]} \hfill \\ {K_{2} = \left[ {K_{21}\;0\;0\;K_{22} } \right]} \hfill & {K_{1} = \left[ {K_{11}\;0\;0\;K_{12} } \right]} \hfill \\ \end{array}$$
(21)

Substituting (20) into (18), the dynamic equation of the system can be expressed as:

$$N{\ddot{q}}_{r}=\tau -D$$
(22)

where

$$\begin{aligned} N & = M_{rr} - M_{rf} M_{ff}^{ - 1} M_{fr} \\ D & = C_{rr} \dot{q}_{r} + C_{rf} \dot{\xi } - M_{rf} M_{ff}^{ - 1} \left( {C_{fr} \dot{q}_{r} + C_{ff} \dot{\xi } + K_{1} \xi^{3} + K_{2} \xi } \right) \\ \end{aligned}$$
(23)

The required torque of the motors according to feedback linearization control can therefore be defined for the system as:

$$\tau =N\nu +D$$
(24)

where \(\nu\) the outer loop input of feedback linearization and must be determined according to pole placement approach. By applying Eq. (24) to Eq. (22), nonlinear terms disappear and the linear system of Eq. (22) will be achieved:

$${\ddot{q}}_{r}=\nu$$
(25)

Considering \(e={q}_{r}-{q}_{d}\) as the error of the states, the input \(\nu\) can be supposed as follows:

$$\nu ={\ddot{q}}_{d}-{k}_{1}\dot{e}-{k}_{2}e$$
(26)

where \({k}_{1}\) and \({k}_{2}\) are positive parameters and \({q}_{d}\) is the desired state. Substituting (26) into (25), the error dynamic of the system is:

$$\ddot{e}+{k}_{1}\dot{e}+{k}_{2}e=0$$
(27)

The controlling gains should be tuned according to pole placement technique.

4.2 Input Shaping

One of the most useful shaping methods is input shaping. This method is real-time and robust. Input shaping is designed to reduce, or eliminate command-induced system vibrations. The formulation that shows the impulse times and impulse amplitudes is written in a matrix form. The first row indicates the time by which each impulse is delayed while the second row indicates the amplitude of the related impulses. Each impulse can be completely defined by one column: a time delay and amplitude value. A generic input shaper depicted in matrix form is shown in the following equation. Note that the first impulse (\({A}_{1}\)) occurs at time \({t}_{1}=0\) for all input shapers described in this section.

$$\left[ {0\;t_{2}\;t_{3}\;\ldots\;A_{1}\;A_{2}\;A_{3}\;\ldots } \right]$$
(28)

The oldest and simplest input shaper is the Zero Vibration (ZV) shaper. This input shaper is designed to filter the signals which excite the natural frequency of the system. A ZV shaper has two impulses. The related formulation describing the ZV shaper is:

$$\left[{t}_{1} \;{t}_{2} \;{A}_{1}\; {A}_{2} \right]=\left[0\; \frac{\pi }{{\omega }_{d}}\; \frac{1}{1+\gamma } \;\frac{\gamma }{1+\gamma }\right]$$
(29)

where \(\gamma =\exp\exp \left(\frac{\xi \pi }{\sqrt{1-{\xi }^{2}}}\right) .\)

Also, \(\xi\) and \({\omega }_{d}\) are the damping ratio and damped natural frequency of the oscillatory mode addressed by the ZV shaper. However, the ZVD shaper is more preferable since it has an additional constraint and thus increases the robustness of the controller. In this method, not only the vibration is forced to be decreased to zero at the modeled frequency, but also the related derivatives of the vibration amplitudes with respect to frequency are forced to be reduced to zero. The corresponding formulation of the ZVD shaper can be written as:

$$\left[{t}_{1}\;{t}_{2}\;{t}_{3}\;{A}_{1}\;{A}_{2}\;{A}_{3} \right]=\left[0\;\frac{\pi }{{\omega }_{d}}\;\frac{2\pi }{{\omega }_{d}}\;\frac{1}{{\gamma }^{2}+2\gamma +1}\;\frac{2\gamma }{{\gamma }^{2}+2\gamma +1}\;\frac{{\gamma }^{2}}{{\gamma }^{2}+2\gamma +1}\right]$$
(30)

where \(\gamma\) was introduced in Eq. (29). If the robustness corresponding to the damping ratio variation wants to be also included, the shaper will consist of four impulses as follow:

$$IS=\left[0\;{t}_{2}\;{t}_{3}\;{t}_{4}\;{A}_{1}\;{A}_{2}\;{A}_{3}\;{A}_{4} \right]=\left[0\;\frac{\pi }{{\omega }_{d}}\;\frac{1}{{{\gamma }^{3}+3\gamma }^{2}+3\gamma +1}\;\frac{3\gamma }{{{\gamma }^{3}+3\gamma }^{2}+3\gamma +1}\;\frac{2\pi }{{\omega }_{d}}\;\frac{3\pi }{{\omega }_{d}}\;\frac{3{\gamma }^{2}}{{{\gamma }^{3}+3\gamma }^{2}+3\gamma +1}\;\frac{{\gamma }^{3}}{{{\gamma }^{3}+3\gamma }^{2}+3\gamma +1}\right]$$
(31)

The vibration reduction can be accomplished by the aforementioned open-loop strategy while the same motion can be covered simultaneously by filtering the input according to the above-mentioned method. Therefore, the shaped inputs are as follows:

$$\begin{aligned} \tau_{s1} &= \tau_{1} *IS \hfill \\ \tau_{s2} &= \tau_{2} *IS \hfill \\ \end{aligned}$$
(32)

4.3 Feedback Linearization Control Employed by Input Shaper

The input shaping method is an excellent means to form rest-to-rest commands which do not excite oscillatory motions. However, its open-loop nature limits its usage for the cases in which the system is subject to external disturbances or parameter uncertainties. However, this method cannot be used to control the rigid motion of a flexible system. On the other hand, the feedback linearization method is not designed to reduce the vibrations of a flexible manipulator. Therefore, it is proposed in this paper to combine these two methods to guide the flexible arm within a desired motion at the same time by reducing its related vibrations.

There are two methods by which the input shaper can be implemented on a closed-loop controller. In the first method, the shaper is located within the feedback loop. This method is called closed-loop input shaping and permits the shaper to act directly on the plant. This implementation ensures that the control signal is always fully shaped. However, the controlling gains of closed-loop input shaping should be tuned so that the stability of the system could be assured subject to the time delay caused by the input shaper. This kind of combination is suitable for a system that is under unwanted disturbances. The second approach is to place the input shaper outside the loop. In this case, the inputs of the shaper are the desired states of the system and the outputs of the shaper are the shaped desired states as follows:

$${q}_{s}={q}_{d}*IS$$
(33)

where \({q}_{s}\) is the shaped desired states. Therefore, the input \(\nu\) for this case is found as follows:

$$\nu ={\ddot{q}}_{s}-{k}_{1}{\dot{e}}_{s}-{k}_{2}{e}_{s}$$
(34)

where \({e}_{s}={q}_{r}-{q}_{s}\). Since the external disturbances are ignored here, this method of outside-the-loop input shaping is used in this paper (Fig. 2).

Fig. 2
figure 2

Controlling flowchart of input shaping method

Full size image

The overall scheme of the proposed controller flowchart is depicted in Fig. 3. As can be seen, the error signals which are supposed to be employed for calculation the outer loop signal of feedback linearization are filtered firstly by the aid of the aforementioned shaper.

Fig. 3
figure 3

Controlling flowchart of shaped feedback linearization method

Full size image

5 Simulation Verification of Modeling

The cycle time is set on 0.001 S The reason is contributed to the fact that in order to observe the complete performance of a vibrating system, the cycle time should be less than the period related to the vibrating states of the system. Considering the fact that the range of frequency of the system considering its mass and elasticity mode is about 3.42395 HZ thus the selected cycle time of 0.001 S can show all of the vibrating performance of the system properly. In order to verify the accuracy of the modeling, the effect of considered modes and the necessity of nonlinear modeling, some simulation scenarios are studied in this section.

5.1 Verification of the Developed Model

Ren et al. (2020), a planar nonlinear vibration of a single link robot is studied using FEM. To investigate the accuracy of the developed model, vibration along one lateral direction is analytically extracted in this paper and its response is compared with the results of the mentioned paper. Consider the input moment of Fig. 4a as the input of the system. A comparison of the system response between the mentioned reference and the presented model of this paper is depicted in Fig. 4b.

Fig. 4
figure 4

Simulation verification: a input moment of paper (Ren et al. 2020), b comparison of the system response between paper (Ren et al. 2020) and this study

Full size image

A good agreement can be observed which shows the correctness of the nonlinear vibration model of the robotic beam.

5.2 Effect of the Number of Modes

In order to verify the proposed controlling method, it is necessary to examine it on a real plant. Here instead of the real robotic arm, the direct dynamics of the mentioned robotic arm is employed as the plant which is subject to control. However, since this arm is flexible, modeling the direct dynamics of the arm is extremely dependent on the number of engaged vibrating modes. This is contributed to the fact that each mode has a dependent differential equation that needs to be coupled to the main dynamics of the arm. As a result, the proper number of the engaged vibrating mode needs to be extracted first, so that the number of the coupled equations for the simulation plant can be identified. The modes which could be excited during this simulation should be considered as the required engaged mode which is defined in this section.

Here, the effect of included modes in discretization of the system is investigated for the two first modes. Since the mechanical and geometrical specifications of the studied arm are similar along with two lateral directions, the effect of the number of modes is investigated for a two-dimensional arm.

The simulation is performed for a robotic arm with the parameters presented in Table 1:

Table 1 Specification of the system
Full size table

To check the arm response, the first torque input is considered zero while the second torque is implemented according to Fig. 5.

Fig. 5
figure 5

The bang-bang input applied to the system

Full size image

The system response including \({\theta }_{2}\) and beam deflection along \({Y}_{b}\) are compared for one and two included modes.

It can be seen that the effect of considering the second mode is negligible for the present arm and thus the second mode is neglected in the analysis (Figs. 6, 7 and 8).

Fig. 6
figure 6

Effect of the different number of assume modes: a vibration responses of the flexible arm, b rigid motion responses of the flexible arm

Full size image
Fig. 7
figure 7

Effect of the different nonlinear terms on the vibration response

Full size image
Fig. 8
figure 8

Rigid states of the arm using FL controller: a angular positions of the arm, b angular velocities of the arm

Full size image

5.3 Investigation of the Effect of Nonlinear Terms

The nonlinear terms which can be observed in the modeling of the system are related to two sources: geometrical and inertia. The geometrical nonlinearity has hardening effect while the inertia one has softening effect in the first mode. Here, the geometric nonlinearity is dominant; so, the effective nonlinearity is of hardening type. This behavior is reflected in response amplitude. In order to investigate this effect, a comparison study is performed between the response of a linear arm and a nonlinear one. Figure 9 shows the effect of different sources of nonlinearities on the deflection of arm tip. This figure proves that the nonlinear modeling of the system is inevitable to obtain accurate results.

Fig. 9
figure 9

Tip deflections of the arm using FL controller

Full size image

It can be seen that the response amplitude of the system in which its related nonlinearities are considered is sensibly different compared to the simplified linear system and this difference is considerable. This study shows that the simplification related to linearizing the vibrating model of the system is not an acceptable approximation and thus considering the nonlinear effects on modeling and simulation of the flexible robotic arm is necessary.

6 Simulation Verification of the Proposed Controller

In this section, the efficiency of the proposed compound controller is investigated in vibration reduction of the modeled flexible robotic arm. In order to show the superiority of the proposed compound controller over traditional ordinary controllers, the system is firstly controlled using an ordinary feedback linearization method and its results are compared with the proposed controller in which the controlling input is modified using the input shaping method.

6.1 Controlling the System Using Feedback Linearization Method

Here, a nonlinear feedback-based controller is employed to manage and improve the dynamic response and vibrating behavior of the flexible robotic arm simultaneously. Note that the flexibility of the system increases the number of engaged states of the system while the feedback of the rigid states of the beam \({\theta }_{1}\), \({\theta }_{2}\) is just sensed and fed to the controller to be employed for constructing the controlling input of this controlling method.

Here, a regulation process is supposed to be performed with zero initial conditions for the angular position and deflection of the beam. The setpoint of the rigid motion of the system is supposed as follows:

$$\theta_{1} = 0.2\quad {\text{and}}\quad \theta_{2} = 0.5\,{\text{rad}}$$

Also, the final velocity and acceleration of the arm are set to be zero, and of course, the desired set point of vibrational deflections of the beam along all of its directions is supposed to be zero. According to the mentioned formulation of Sect. 4, the internal controlling input is:

$$\nu =-{k}_{1}\dot{q}-{k}_{2}(q-{q}_{d})$$
(35)

For this regulation process, the following controlling inputs are tuned so that the Eigen-values related to the main rigid states would be −2:

$$k_{1} = \left[ { - 4\;0\;0 \;- 4 } \right]\quad k_{2} = \left[ { - 4\; 0\; 0\; - 4 } \right]$$
(36)

The extracted elements related to the matrices and vectors of \(N=N({\theta }_{1},{\theta }_{2},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\zeta }_{1},{\eta }_{1},{\dot{\zeta }}_{1},{\dot{\eta }}_{1})\) and \(D=D({\theta }_{1},{\theta }_{2},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\zeta }_{1},{\eta }_{1},{\dot{\zeta }}_{1},{\dot{\eta }}_{1})\) are calculated and can be observed in the Appendix. In Fig. 8 the actual response of the beam angle which is controlled using the FL method can be seen.

It can be observed that the desired angular position and velocity of the beam are obtained using this controller within 4 s. The overshoot of the second angle is larger since the initial error of this state is larger. The corresponding response of the robot deflection can also be observed in Fig. 9.

It can be seen that the amplitude of the workspace vibration along Y is more than X, and this is contributed to the fact that the required torque of the second motor is more than the first one to compensate for more initial error of the second angle. The related controlling input of the motors using the FL method is extracted as Fig. 10.

Fig. 10
figure 10

The required controlling inputs based on the FL method

Full size image

As was expected, the controlling input is oscillatory to compensate for the flexible nature of the beam. Also, as mentioned before, the required torque amplitude of the second motor is more than the first one to realize the desired set point of both angles during a unique time period.

6.2 Investigating the Effect of Nonlinearity Terms in Designing the Controller

Note that, the mentioned nonlinear terms which exist in the nature of the studied system, not only significantly affect the modeling of the robot plant, and deliver a more realistic model of the system with less parameter uncertainties, but also help us to design a more efficient controller for the system since the controller is nonlinear and extremely dependent on considering the real nonlinear terms which should be taken into account in its feed-forward portion of controlling signal. Here, this necessity is shown by comparing the response of the real nonlinear plant of the flexible arm between two controllers in which the nonlinear terms are considered in one and are ignored in the other. In Fig. 11a, b this comparison can be observed.

Fig. 11
figure 11

Comparison of the angular position of the arm using FL method between linear and non-linear models: a first angular position, b second angular position

Full size image

It can be seen that the system in which the nonlinearities are considered in the designed controller can be controlled properly while the system which is controlled using the controller with the linearized formulation of the model is unstable and its response has diverged. This shows that for controlling the real nonlinear vibrating system of the flexible robotic arm, the nonlinear modeling and its usage in the controller is inevitable (Fig. 12).

Fig. 12
figure 12

Comparison of the tip deflection using FL method between linear and non-linear models: a tip deflection in the y-direction, b tip deflection in the z-direction

Full size image

6.3 Controlling the System Using the Proposed Shaped Feedback Linearization Method

In the previous section, the flexible robotic arm was controlled using an ordinary FL method. It was seen that the required motors’ torque and workspace movement of the arm using this method are oscillatory since the feedback of vibrating states is not included in designing the controlling input. Besides the destructive effect of this vibrating response on the accuracy of the system, producing this oscillatory torque using the ordinary motors is either impossible or extremely harmful for the system since a considerable shock will be implemented on the devices. That’s why a new controller compound of FL and input shaping method is proposed here to control the arm and reduce its related vibrations simultaneously. The parameters of the input shaper can be evaluated by the aid of the natural frequency of the system while the gains of FL are again selected using pole placement. For previous regulation movement, a comparison between the response of the system controlled by simple FL and the proposed compound controller is shown in Fig. 13.

Fig. 13
figure 13

Comparison of the rigid states of the arm between FL and shaped FL methods: a angular positions of the arm, b angular velocities of the arm

Full size image

As expected, a delay can be observed for the system in which the input is shaped by the designed input shaper and this is contributed to the fact that the dynamic of the input shaping section of the controller increases the final time constant of the system. The related comparison for the deflection of arm tip can be seen in Fig. 14.

Fig. 14
figure 14

Comparison of the tip deflection between FL and shaped FL methods: a tip deflection in the y direction, b tip deflection in the z-direction

Full size image

It can be seen that the vibrating response of the arm workspace is significantly decreased using the proposed input shaping in the employed FL controller. The amplitude of the vibrations is decreased by about 0.13 m along Y and about 0.05 m along Z-direction. This unwanted vibration reduction increases the accuracy of the system and makes it possible to use them for more accurate applications. Also, as stated before, the proposed controller can decrease the required oscillatory torque of the motors as follow (Fig. 15) which increases the effective lifetime of the devices.

Fig. 15
figure 15

Comparison of controlling inputs between FL and shaped FL methods

Full size image

Finally, the comparison of the workspace response of the robot, considering the kinematics of the system can be extracted as Fig. 16a–c show.

Fig. 16
figure 16

Comparison of workspace response between FL and shaped FL methods: a workspace response X, b workspace response Y, c workspace response Z

Full size image

It can be seen that not only the vibrating deflections of the system is reduced, but also the rigid motion of the arm is controlled appropriately without any vibrating response. Again, here, a short delay needs for the proposed controller to shape the input and reduce the unwanted vibrations of all of the rigid and vibrating states and also their related torque profiles.

Finally, in order to investigate the robustness of the proposed controlling method against the parametric uncertainties, a 30% parametric uncertainty related to the arm module of elasticity has been engaged in the simulation (The actual value of the module of elasticity is 8 \(N {m}^{2}\) and the value included in the controller design is 11 \(N {m}^{2}\)). The results of the closed-loop system are compared to the performance of the system equipped with inverse dynamics. According to the following profiles, which show the X, Y and Z coordinates of the end-effector movement, it can be concluded that the proposed controller is robust enough against the parametric uncertainties (Fig. 17).

Fig. 17
figure 17

Comparison of the proposed controller robustness with inverse dynamics against the parametric uncertainties

Full size image

7 Conclusion

In this paper, a 3D flexible robotic arm with nonlinear vibration was modeled and a new nonlinear feedback controller was designed and implemented based on the shaped feedback linearization method in order to reduce the vibration of the flexible arm and increase its accuracy. The robotic formulation of the link was derived considering its rigid and vibrational motions along longitudinal and lateral directions simultaneously. Kinematic of the flexible robot was first calculated in order to make a relation between its joint space and workspace. Then, considering both of geometrical and inertia nonlinearities of the beam, the kinetic and dynamic model of the considered flexible arm was derived using Lagrange method, and the model response was analyzed. In order to increase the accuracy and guarantee the stability of the robotic arm in the presence of flexibility, a new compound nonlinear feedback controller was developed employing the shaped feedback linearization method and its efficiency was compared with the ordinary FL method. The accuracy of the modeled system was proved by simulating the system in MATLAB and comparing the response of the system with the results of previous references using the FEM method. A good agreement of the response showed the correctness of the 3D modeling. Then, the effect of the number of included modes was investigated and it was observed that considering the second mode does not have a significant effect on the accuracy of the system and can be ignored to increase the speed of the system process and its real-time and online applicability. On the other hand, investigating the response of the system in which the nonlinearities are considered and its comparison with the system in which these items are ignored showed that the vibrating amplitude of the nonlinear model which is more close to a real system is significantly less than the approximated linearized one and this observation shows the necessity of considering the nonlinearities of the system. It was also seen that another reason to consider the nonlinear terms is in designing a controller for the system. It was shown that the approximated linearized inverse dynamic of the system, which should be used as the feed-forward controlling term of the designed controller, causes instability of the real nonlinear system while considering the nonlinearities in feed-forward not only provides the stability of the system but also results in a good accuracy for the regulation process of the system. Moreover, comparing the results of the closed-loop system using the ordinary FL method and the proposed shaped FL method showed that the former one cannot control the vibrating deflections of the system since their related feedback is not used in the corresponding controlling input, and this phenomenon results in oscillatory torque of the motors, which is not desired. However, the proposed shaped FL method can control all of the rigid and vibrational states of the system simultaneously with good accuracy and no fluctuation in the system. Finally, with the aid of a simulation study, it was proved that the proposed controller is also robust against the parametric uncertainties, especially the parameter related to the elasticity module of the arm. Thus, it can be concluded that nonlinear modeling of the system together with the proposed shaped FL method can successfully control the robot motions with good accuracy and robustness while its related deflections can also be reduced significantly at the same time that guarantees the robot stability.