Transient Thermal and Mechanical Stress Analysis of 2D-Functionally Graded Finite Cylinder: A Truly Meshless Formulation

Abstract

The applications of thick cylinders are increasing in many industries such as aero-space, marine, automotive and oil industry. The working conditions in some cases need design and manufacturing of cylinders with functionally graded properties. In this study, the transient axi-symmetric response of two-dimensional functionally graded (2D-FG) thick hollow cylinders in which material properties are graded in radial and axial directions is studied. The cylinder is subjected to axi-symmetric transient thermal and mechanical loading conditions. The governing equations of the cylinder are obtained from the equilibrium equations of elasticity in the weak form. The meshless local Petrov–Galerkin formulation is presented to discretize the governing equations of 2D-FG cylinder to a system of linear differential equations. The Crank–Nicolson and the Newmark method are employed for time integration of the equations. The accuracy of the results is examined by comparison of the predictions with analytical methods and available results in the open literature. In the numerical results, steady state and transient response of 2D-FG cylinder which is subjected to time-dependent mechanical load and transient thermal load are investigated and the propagation of displacement and stress waves in the FG cylinder are studied. It is seen that the presented formulation is accurate and efficient for steady state and transient response analysis of FG cylinders in thermo-mechanical loading conditions. The effect of FG parameters and loading parameter on the response of the cylinder is studied.

1 Introduction

The composition of several different materials as functionally graded material can be used in order to optimize the responses of structures subjected to thermal and mechanical loads. Functionally graded materials are non-homogeneous materials made from two or more constituent in which the volume fraction of constituents varies gradually with predefined pattern to give a non-uniform microstructure with continuously graded macro properties. The FG materials are designed to possess desirable properties for specific applications in thermo-mechanical loading conditions, especially for high rate thermal loadings. The homogeneous and FG hollow cylinders have many industrial applications such as in aerospace and automobile industries. The analysis of transient thermal and mechanical stresses in FG cylinders which are subjected to thermo-mechanical loading is of great importance. Analytical and computational studies have been carried out for investigation of the behavior of FG cylinders. A brief review of analytical and numerical methods for analysis of thermo-mechanical loading of FG cylinders is presented here. Reddy and Chin (1998) studied the dynamic thermo-elastic response of functionally graded cylinders and plates by finite element method. Horgan and Chan (1999) investigated the effects of material inhomogeneity on the response of linearly elastic isotropic radially graded hollow circular cylinders or disks under uniform internal or external pressure. Zimmerman and Lutz (1999) derive an exact solution for the problem of uniformly heating of a functionally graded cylinder whose elastic moduli and thermal expansion coefficient vary linearly with radius. El-Abbasi and Meguid (2000) developed finite element formulation to study the thermo-elastic behavior of FG plate and shells. Awaji and Sivakumar (2001) used the finite difference method to analyze one-dimensional transient temperature distributions in a circular hollow cylinder that was composed of functionally graded ceramic–metal-based materials.

Kim and Noda (2002) have adopted a Green's function approach based on the laminate theory for solving the two-dimensional unsteady temperature field and the associated thermal stresses in an infinite hollow circular cylinder made of FG material with radially graded properties. The general theoretical analysis of steady-state thermal stresses for a long hollow thick cylinder made of functionally graded material is developed by Jabbari et al. (2002). Nemat-Alla (2003) introduced a two-dimensional functionally graded materials (2D-FGM) to withstand super high temperatures and to give more reduction in thermal stresses. Liew et al. (2003) presented a solution for analysis of thermal stress behavior of hollow circular cylinders of functionally graded material. Sladek et al. (2005) analyzed the static stress distribution in anisotropic FG cylinder by the MLPG method. Kordkheili and Naghdabadi (2007) presented an analytical thermo-elasticity solution for hollow finite-length cylinders made of functionally graded materials exposed to thermal loads, internal pressure and axial loadings. Thermo-mechanical analysis of functionally graded hollow circular cylinders subjected to mechanical loads and linearly increasing boundary temperature was carried out by Shao and Ma (2008). Asgari and Akhlaghi (2011) studied the steady state thermal stress of thick hollow circular cylinder with finite length made of two-dimensional functionally graded material using the graded finite element method. Hosseini et al. (2011) studied the thermo-elasticity and thermal shock in radially FG long cylinder using coupled thermo-elasticity theory and meshless method.

Ponnusamy and Rajagopal (2011) studied the wave propagation in transversely isotropic thermoelastic solid cylinder with arbitrary cross-section. Arshad et al. (2011) presented vibration frequency of a bi-layered cylindrical shell composed of two independent FG layers which are functionally graded through the thickness of the layers. Foroutan et al. (2011) studied the static response of radially FG cylinders with finite length subjected to mechanical loading by mesh-free method. Lee et al. (2012) studied an inverse algorithm and applied the discrepancy principle to simultaneously estimate the unknown time-dependent inner and outer boundary heat fluxes in a functionally graded hollow circular cylinder. Darabseh et al. (2012) studied the transient thermo-elastic response of a thick hollow radially FG cylinder under thermal loading and Green–Lindsay generalized theory of thermo-elasticity.

Mollarazi et al. (2012) studied the free vibration analysis of radially functionally graded axi-symmetric cylinder by meshless method. Dai et al. (2013) utilized finite difference method to analyze the response of a long hollow cylinder made of functionally graded materials under dynamic symmetric radially mechanical and thermal loadings. Xie et al. (2013) studied two-dimensional thermo-elastic dynamic responses of a long radially functionally graded hollow cylinder subjected to non-axi-symmetrical thermal and mechanical loads by the finite difference method. Wu and Kuo (2013) developed a unified formulation based on the principle of virtual displacements (PVDs) for simply supported functionally graded sandwich hollow cylinders for the quasi-three-dimensional bending and free vibration analyses. Ebrahimi and Najafizadeh (2014) studied the free vibration of two-dimensional functionally graded cylindrical shell by Love's first approximation classical shell theory and generalized differential quadrature (GDQ) and generalized integral quadrature (GIQ) methods. Shojaeefard and Najibi (2014) studied transient heat conduction in hollow thick temperature-dependent 2D-FGM cylinders subjected to transient axisymmetric thermal loads using the graded finite element method. Karakas and Daloglu (2015) developed graded harmonic finite element method based on three-dimensional elasticity theory to study the mechanical stress and natural frequency of 2D-axi-symmetric structures. Foroutan and Shirzadi (2016) developed an axi-symmetric Hermition collocation method based on the strong form of governing equation to study the free vibration of radially functionally graded cylinder. Dai and Dai (2016) presented a semi-analytical approach to study the displacement and stress fields in a functionally graded (FG) hollow circular disk, rotating with an angular acceleration under a changing temperature field.

Najibi and Shojaeefard (2016) utilized finite element method to investigate mechanical behavior of thick hollow finite length cylinder made of two dimensional functionally graded materials. Xu and Yu (2017) studied elastic wave propagation in functionally graded cylinder using time domain spectral finite element method. Niu et al. (2019) investigated the free vibrations of the rotating pretwisted functionally graded composite cylindrical panels reinforced with the graphene platelets by first-order shear deformation theory and Chebyshev-Ritz method. Talebitooti (2019) studied the free vibration and critical speed of pressurized rotating FG cylindrical shell based on the three-dimensional theory and layerwise theory.

As seen, the semi-analytical methods and numerical approaches are employed for analysis of functionally graded cylinders. The numerical approaches for analysis of FG cylinders mostly include the finite element method and finite difference method. The meshless methods are used for static stress analysis and free vibration analysis of FG cylinders. To the best knowledge of authors, the transient thermal stress in the 2D-functionally graded cylinders by the meshless method is not studied in the open literature. Although the finite element method is used for transient stress analysis in 1D-FG cylinders, the finite element method has some difficulties and disadvantages, such as its needs to mesh of elements, discontinuities of derivations of shape functions in boundary of elements, and difficulties in construction of higher-order shape functions. In order to overcome the difficulties, the meshless methods are developed in recent two decades, which does not need element mesh, either for purposes of interpolation of the solution variables, or for the integration of the equations. Different meshless methods, such as Discrete Elements method (DEM) Nayroles et al. (1992), Element Free Galerkin (EFG) method (Belytschko et al. 1994), H-p Clouds method (Duarte and Oden 1996), Reproducing Kernel Particle method (RKPM) (Liu et al. 1995) and meshless local Petrov–Galerkin method (MLPG) (Atluri and Zhu 2000), have been presented in the past years. For more information, the differences and similarities of these methods are referred to researches of Atluri et al. (1999) and Belytschko (2002). Due to advantages of meshless methods, the meshless methods, especially the MLPG method, are used for analysis of various problems in engineering and science. For example, Lin and Atluri (2000) proposed MLPG to solve steady convection diffusion problems, in one and two dimensions. Liu and Gu (2000) proposed coupled MLPG/finite element method and a coupled MLPG/boundary element method to improve the solution efficiency for continuum mechanics problems. This paper focuses on the coupling of MLPG method with FEM and BEM. Ching and Batra (2001) augmented the MLPG method with the enriched basis functions and successfully predicted the singular stress fields near a crack tip. Gu and Liu (2001) developed MLPG formulation for free and forced vibration analyses of solid structures. Qian et al. (2003) used two meshless local Petrov–Galerkin formulations, namely MLPG1 and MLPG5, to analyze infinitesimal deformations of a homogeneous and isotropic thick elastic plate with a higher-order shear and normal deformable plate theory. Wang et al. (2005) presented a new meshless method for steady state heat conduction problem in anisotropic and inhomogeneous materials. Haitao and Yuanhan (2007) presented a meshless virtual boundary method and employed it for 2D elasticity problems. Mahmoodabadi et al. (2011) employed meshless local Petrov–Galerkin method for 3D steady-state heat conduction problems. Ahmadi and Aghdam (2010a, b) developed generalized plane-strain meshless method for micromechanical modeling of unidirectional composite to study micro-stresses in composite materials. Ahmadi et al. (2011) developed a meshless formulation to study the heat transfer in heterogeneous materials and studied the heat transfer and thermal conductivity of composite materials. Hematiyan et al. (2014) presented an efficient technique for evaluation of a domain integral in which the integrand is defined by its values at a discrete set of nodes with highly varying density. Ahmadi and Aghdam (2015) and Ahmadi (2017) presented a suitable meshless formulation for modeling the elastic–plastic and failure behavior of heterogeneous materials in micromechanics. Zheng et al. (2015) and Mavric and Sarler (2017) developed meshless formulation for analysis of transient coupled thermoelasticity problems under thermal and mechanical shock loading.

Khosravifard et al. (2017) developed a new numerical strategies based on meshless methods for the analysis of linear fracture mechanics problems of stationary as well as propagating cracks with minimum computational labor Abdollahifar et al. (2019) developed meshless local. Petrov–Galerkin (MLPG) method to study transient dynamic stress intensity factor in FGM plates. Memari and Azar (2020) described a combined way based on FE and MLPG1 methods to take the advantages of two numerical techniques in fracture mechanics to numerically solve stationary dynamic fracture and quasi-static linear elastic crack propagation problems. Jenabidehkordi et al. (2020) presented a novel approach for investigating the fracture and mechanical behavior of polymer-matrix composites at the mesoscale and takes advantage of the peridynamics equation of motion and its nonlocality. Liaghat et al. (2021) proposed an efficient iterative inverse procedure for identification of distribution of loads that had led to a specific crack propagation path in a fractured component. Recently, Ahmadi (2021) studied dynamic behavior of 2D-functionally graded nonlocal nanobeams using meshless method and the first-order shear deformation (FSDT) beam theory.

In this study, a truly meshless formulation is developed to study the transient response of 2D-FG axi-symmetric cylinders and the transient response of 2D-functionally graded cylinder with finite length which is subjected to axi-symmetric time-dependent mechanical and thermal load is studied. The presented method is a truly meshless method and the thermo-mechanical properties of the cylinder are considered to be graded in both radial and axial directions of the cylinder. The governing equations of the cylinder are obtained using the thermo-elasticity theory. A formulation based on meshless local Petrov–Galerkin (MLPG) method is developed to obtain the governing equations of the cylinder as a system of linear differential equations. The governing equations are integrated numerically in the time domain with Crank–Nikolson and Newmark time integration techniques and transient response of the cylinder subjected to thermo-mechanical loading is obtained. The transient and steady state displacement and radial, axial and hoop stresses in 2D-FG cylinder are studied, and the effect of parameters on the response of the cylinder is investigated.

2 Formulation

A thick hollow cylinder made of 2D-FG material with the cylindrical coordinate system rθz is considered in which r indicates radial coordinate, z indicates the axial coordinate, and θ is the circumferential coordinate of the cylinder. The cylinder length is L, the inner radius is R_i, and the outer radius is R_o. The cylinder is subjected to axi-symmetric internal and (or) external pressure P_i(z, t) and P_o(z, t), and the axi-symmetric thermal loading conditions in inner and (or) outer surface. The edge conditions of the cylinder at z = 0 and z = L, and the volume fraction of the FG basic constituents of the cylinder are supposed to be axi-symmetric. Due to the axi-symmetric nature of the problem, the cross-section of the cylinder in r-z plane is shown in Fig. 1. The displacement field of the cylinder is considered as u_r = u_r(r,z,t), u_z = u_z(r,z,t), and u_θ = 0, where u_r and u_z and u_θ are displacements in the r and z and θ directions. Regarding to axi-symmetric conditions, the equilibrium equations in the radial and axial directions can be written as Sadd (2009)

$$ \frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\partial \sigma_{rz} }}{\partial z} + \frac{1}{r}(\sigma_{r} - \sigma_{\theta } ) + b_{r} = \rho (r,z)\ddot{u}_{r} $$

(1)

$$ \frac{{\partial \sigma_{rz} }}{\partial r} + \frac{{\partial \sigma_{z} }}{\partial z} + \frac{1}{r}(\sigma_{rz} ) + b_{z} = \rho (r,z)\ddot{u}_{z} $$

(2)

where b_r and b_z are body force. The equation of heat transfer for the cylinder can be considered as

$$ - \frac{1}{r}\frac{\partial }{\partial r}(rq_{r} ) - \frac{\partial }{\partial z}(q_{z} ) + g = \rho (r,z)c_{p} (r,z)\frac{\partial T}{{\partial t}} $$

(3)

Fig. 1

An axisymmetric finite cylinder, the coordinate system, and the 2D subdomains Ω_s^I

where g is the heat source, ρ(r,z) is mass density, and c_p(r,z) is specific heat capacity and are functions of r and z coordinates.

2.1 Local Weak Formulation

An axi-symmetric formulation based on meshless local Petrov Galerkin (MLPG) method is derived for solution of the problem. The MLPG method is based on the local weak form of the governing equations over the local subdomains. The cross section of the cylinder with rz plane is shown in Fig. 1, and called Ω. The cylinder volume can be obtained by rotation of Ω about the z-axis. The number of N nodes and N local area Ω_s^I (I = 1, 2, …, 3) with arbitrary shape are considered in the domain Ω. Revolution of the local area Ω_s^I about z-axis makes a volume (ring) which is called local volume V_s^I. In this study, Ω_s^I are called 2D subdomain and V_s^I are so-called 3D subdomain. Due to the axi-symmetric nature of the problem, the local weak form is written over the three-dimensional subdomains V_s^I. For achieving the weak formulation, Eq. (1) and Eq. (2) are multiplied in weight function w(r,z) and integrated over the subdomain volume V_s^I as Atluri and Zhu (2000)

$$ \int\limits_{{V_{s}^{I} }} {w(\frac{1}{r}\frac{\partial }{\partial r}(r\sigma_{r} ) + \frac{{\partial \sigma_{rz} }}{\partial z} - \frac{1}{r}\sigma_{\theta } + b_{r} - \rho \ddot{u}_{r} ){\text{d}}V} = \int\limits_{0}^{2\pi } {\int\limits_{{\Omega_{s}^{I} }} w (\frac{1}{r}\frac{\partial }{\partial r}(r\sigma_{r} ) + \frac{{\partial \sigma_{rz} }}{\partial z} - \frac{1}{r}\sigma_{\theta } + b_{r} - \rho \ddot{u}_{r} ){\text{d}}Ar{\text{d}}\theta } $$

(4)

$$ \int\limits_{{V_{s}^{I} }} {w(\frac{1}{r}\frac{\partial }{\partial r}(r\sigma_{rz} ) + \frac{{\partial \sigma_{z} }}{\partial z} + b_{z} - \rho \ddot{u}_{z} ){\text{d}}V = } \int\limits_{0}^{2\pi } {\int\limits_{{\Omega_{s}^{I} }} w (\frac{1}{r}\frac{\partial }{\partial r}(r\sigma_{rz} ) + \frac{{\partial \sigma_{z} }}{\partial z} + b_{z} - \rho \ddot{u}_{z} ){\text{d}}Ar{\text{d}}\theta } = 0 $$

(5)

Generally Ω^I_s may have arbitrary shape in the r-z section of the cylinder and called local subdomain, V_s^I is the volume of rotation of Ω_s^I around z-axis as 2π radian and dA = drdz. Also, the weak form of (3) can be obtained in the same procedure as

$$ \int\limits_{{V_{s}^{I} }} {w(( - \frac{1}{r}\frac{\partial }{\partial r}(rq_{r} ) - \frac{{\partial q_{z} }}{\partial z} + g - \rho c_{p} \dot{T}){\text{d}}Ar{\text{d}}\theta = } \int\limits_{0}^{2\pi } {\int\limits_{{\Omega_{s}^{I} }} {w( - \frac{1}{r}\frac{\partial }{\partial r}(rq_{r} ) - \frac{{\partial q_{z} }}{\partial z} + g} } - \rho c_{p} \dot{T}){\text{d}}Ar{\text{d}}\theta = 0 $$

(6)

It must be considered that due to axi-symmetric conditions, the integrand in (4), (5) and (6) is not as a function of circumferential coordinate θ. Therefore, integration over θ can be done easily and Eqs. (4), (5) and (6) are simplified and rewritten as

$$ \int\limits_{{\Omega_{s}^{I} }} ( w\frac{{\partial (r\sigma_{r} )}}{\partial r} + wr\frac{{\partial \sigma_{rz} }}{\partial z} - w\sigma_{\theta } + wrb_{r} ){\text{d}}r{\text{d}}z - \alpha \int\limits_{{\Gamma_{{su_{r} }}^{I} }} {w(u_{r} - \overline{u}_{r} } ){\text{d}}\Gamma = \int\limits_{{\Omega_{s}^{I} }} {w\rho \ddot{u}_{r} } r{\text{d}}r{\text{d}}z $$

(7)

$$ \int\limits_{{\Omega_{s}^{I} }} {(w} \frac{{\partial (r\sigma_{rz} )}}{\partial r} + wr\frac{{\partial \sigma_{z} }}{\partial z} + wrb_{z} ){\text{d}}r{\text{d}}z - \alpha \int\limits_{{\Gamma_{{su_{z} }}^{I} }} {w(u_{z} - \overline{u}_{z} } ){\text{d}}\Gamma = \int\limits_{{\Omega_{s}^{I} }} w \rho \ddot{u}_{z} r{\text{d}}r{\text{d}}z $$

(8)

$$ \int\limits_{{\Omega_{s}^{I} }} {( - w\frac{{\partial (rq_{r} )}}{\partial r} - } wr\frac{{\partial q_{z} }}{\partial z} + wrg){\text{d}}r{\text{d}}z + \alpha \int\limits_{{\Gamma_{sT}^{I} }} {w(T - \overline{T}} ){\text{d}}\Gamma = \int\limits_{{\Omega_{s}^{I} }} {w\rho c_{p} \dot{T}\,r{\text{d}}r{\text{d}}z} \, $$

(9)

In equations (7) to (9), the terms which include α is the penalty terms and added to the weak form in order to impose the essential boundary conditions to the equations, and α is a large number which is known as penalty parameter. $\Gamma_{{su_{r} }}^{I}$, $\Gamma_{{su_{z} }}^{I}$ and $\Gamma_{sT}^{I}$ are the parts of the subdomain in which u_r, u_z and temperature T are prescribed, respectively. In general $\Omega_{s}^{I}$ could have arbitrary shape and its boundary i.e. $\partial \Omega_{s}^{I}$ consists of three parts $\partial \Omega_{s}^{I} = L_{s}^{I} \cup \Gamma_{st}^{I} \cup \Gamma_{su}^{I}$, in which $L_{s}^{I}$ is part of the local boundary that is located totally inside the global domain, and $\Gamma_{st}^{I}$ and $\Gamma_{su}^{I}$ are parts of $\partial \Omega_{s}^{I}$ coincides with the global traction boundary and the global essential boundary, respectively. Also the part of $\partial \Omega_{s}^{I}$ that coincides with the Dirichlet boundary is shown by $\Gamma_{sT}^{I}$, and the part that coincides with Neumann boundary is shown by $\Gamma_{sq}^{I}$ and the part that coincides with convection boundary is shown by $\Gamma_{sh}^{I}$. By employing the divergence theorem, (7), (8) and (9) can be written as

$$ \begin{gathered} - \int\limits_{{\Omega_{s}^{I} }} {(rw_{,r} \sigma_{r} + rw_{,z} \sigma_{rz} + w\sigma_{\theta } ){\text{d}}r{\text{d}}z + } \int\limits_{{L_{s}^{I} }} {rw(\sigma_{r} n_{r} + \sigma_{rz} n_{z} ){\text{d}}\Gamma + } \hfill \\ \int\limits_{{\Gamma_{st}^{I} }} {rw\overline{t}_{r} {\text{d}}\Gamma - \alpha \int\limits_{{\Gamma_{sur}^{I} }} {w(u_{r} - \overline{u}_{r} )} } {\text{d}}\Gamma + \int\limits_{{\Omega_{s}^{I} }} {wb_{r} r{\text{d}}r{\text{d}}z = } \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z)\ddot{u}_{r} wr{\text{d}}r{\text{d}}z} \hfill \\ \end{gathered} $$

(10)

$$ \begin{gathered} - \int\limits_{{\Omega_{s}^{I} }} {(rw_{,r} \sigma_{rz} + rw_{,z} \sigma_{z} ){\text{d}}r{\text{d}}z + } \int\limits_{{\Gamma_{s}^{I} }} {rw(\sigma_{rz} n_{r} + \sigma_{z} n_{z} ){\text{d}}\Gamma + } \hfill \\ \int\limits_{{\Gamma_{st}^{I} }} {rw\overline{t}_{z} {\text{d}}\Gamma - \alpha \int\limits_{{\Gamma_{suz}^{I} }} {w(u_{z} - \overline{u}_{z} )} } {\text{d}}\Gamma - \int\limits_{{\Omega_{s}^{I} }} {wb_{z} r{\text{d}}r{\text{d}}z = } \int\limits_{{\Omega_{s}^{I} }} {\rho w\ddot{u}_{z} r{\text{d}}r{\text{d}}z} \hfill \\ \end{gathered} $$

(11)

$$ \begin{gathered} \int\limits_{{\Omega_{s}^{I} }} {(rw_{,r} q_{r} + r} w_{,z} q_{z} ){\text{d}}r{\text{d}}z - \int\limits_{{L_{s}^{I} }} {wr(q_{r} n_{r} + q_{z} n_{z} ){\text{d}}\Gamma } - \int\limits_{{\Gamma_{sq}^{I} }} {wr\overline{q}_{n} {\text{d}}\Gamma } - \int\limits_{{\Gamma_{sh}^{I} }} {wrh(T - T_{\hbar } ){\text{d}}\Gamma } \hfill \\ + \int\limits_{{\Omega_{s}^{I} }} {wg\,r{\text{d}}r{\text{d}}z} + \alpha \int\limits_{{\Gamma_{sT}^{I} }} {w(T - \overline{T}} ){\text{d}}\Gamma = \int\limits_{{\Omega_{s}^{I} }} {w\rho c_{p} \dot{T}\,r{\text{d}}r{\text{d}}z} \hfill \\ \end{gathered} $$

(12)

Notice that the weight function w(r,z) of the local subdomain Ω_s^I is chosen as a bell-type function whose maximum value is on the Ith node, and w(r,z) vanishes on the boundary of Ω_s^I that is located totally inside the global domain i.e. L^I_s. Therefore, the integrations over L^I_s are eliminated from (10), (11) and (12). The weight function of the Ith subdomain Ω_s^I is shown by w^I(r,z). In this study, for the circular subdomains the quadratic weight function is used as Ahmadi (2017); Memari et al. (2020)

$$ w^{I} ({\mathbf{x}}) = \left\{ {\begin{array}{*{20}c} {1 - 6(\frac{{d_{I} }}{{R_{s}^{I} }})^{2} + 8(\frac{{d_{I} }}{{R_{s}^{I} }})^{3} - 3(\frac{{d_{I} }}{{R_{s}^{I} }})^{4} } & {0 \le d_{I} \le R_{s}^{I} } \\ 0 & {d_{I} \ge ~R_{s}^{I} } \\ \end{array} } \right. $$

(13)

where R_s^I is the radius of the support domain of Ω_s^I and d_I is the distance of X to the center of Ω_s^I. Other types of weight function can be used. More details can be found in Liu (2009).

In order to obtain the governing equations in the matrix form, the matrices σ, W^I and ε_v are defined as

$$ \begin{gathered} {{\varvec{\upsigma}}} = \{ \begin{array}{*{20}c} {\sigma_{r} } & {\sigma_{z} } & {\sigma_{rz} } & {\sigma_{\theta } } \\ \end{array} \}^{T} \hfill \\ {\mathbf{W}}^{I} = \left[ {\begin{array}{*{20}c} {w^{I} } & {0} \\ {0} & {w^{I} } \\ \end{array} } \right]_{2x2} ,\,\,{{\varvec{\upvarepsilon}}}_{{\mathbf{v}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {w_{,r}^{I} } & {0} & {w_{,z}^{I} } & {\frac{{w^{I} }}{r}} \\ \end{array} } \\ {\begin{array}{*{20}c} {0} & {w_{,z}^{I} } & {w_{,r}^{I} } & {0} \\ \end{array} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(14)

and the matrix of displacement u, traction t, body force b and N is defined as

$$ {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} {u_{r} } \\ {u_{z} } \\ \end{array} } \right\},\,\,{\mathbf{b}} = \left\{ {\begin{array}{*{20}c} {b_{r} } \\ {b_{z} } \\ \end{array} } \right\},\,\,{\overline{\mathbf{t}}} = \left\{ {\begin{array}{*{20}c} {\overline{{t_{r} }} } \\ {\overline{{t_{z} }} } \\ \end{array} } \right\},\,\,{\mathbf{N}} = \left[ {\begin{array}{*{20}c} {n_{r} } & {0} & {n_{z} } & {0} \\ {0} & {n_{r} } & {n_{z} } & {0} \\ \end{array} } \right] $$

(15)

By employing (14) and (15), the equilibrium equation of elasticity in (10) and (11) is written in the matrix form as

$$ \begin{gathered} - \int\limits_{{\Omega_{s}^{I} }} {{{\varvec{\upvarepsilon}}}_{{\mathbf{v}}} {{\varvec{\upsigma}}}\,rdrdz + } \int\limits_{{\Gamma_{s}^{I} }} {{\mathbf{W}}^{I} {\mathbf{N\sigma }}\,rd\Gamma + } \int\limits_{{\Gamma_{st}^{I} }} {{\mathbf{W}}^{I} {\overline{\mathbf{t}}}\,rd\Gamma } \hfill \\ - \alpha \int\limits_{{\Gamma_{su}^{I} }} {{\mathbf{W}}^{I} {\mathbf{u}}\,d\Gamma } + \alpha \int\limits_{{\Gamma_{su}^{I} }} {{\mathbf{W}}^{I} {\overline{\mathbf{u}}}\,d\Gamma } + \int\limits_{{\Omega_{s}^{I} }} {{\mathbf{W}}^{I} {\mathbf{b}}\,rdrdz} \, = \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z){\mathbf{W}}^{I} {\mathbf{\ddot{u}}}\,rdrdz} \hfill \\ \end{gathered} $$

(16)

and the energy equation in (12) is written as

$$ \begin{gathered} \int\limits_{{\Omega_{s}^{I} }} {{\overline{\mathbf{B}}}_{v}^{I} {\mathbf{q}}rdrdz} + \int\limits_{{\Gamma_{sq}^{I} }} {rw^{I} {\overline{\mathbf{N}}\mathbf{q}}d\Gamma } - \int\limits_{{\Gamma_{sh}^{I} }} {hw^{I} (T - T_{\infty } )d\Gamma } - \alpha \int\limits_{{\Gamma_{sT}^{I} }} {w^{I} (T - \overline{T})} d\Gamma \hfill \\ + \int\limits_{{\Omega_{s}^{I} }} {w^{I} g\,rdrdz} = \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z)c_{p} (r,z)w^{I} \dot{T}rdrdz} \hfill \\ \end{gathered} $$

(17)

where in (17), h is thermal convection coefficient on Γ_sh, T_∞ is the ambient temperature, and

$$ {\overline{\mathbf{B}}}_{v}^{I} = [w_{,r}^{I} ,\,\,\,w_{,z}^{I} ],\,\,\,{\overline{\mathbf{N}}} = [n_{r} ,\,\,\,n_{z} ],\,\,\,{\mathbf{q}} = \{ \begin{array}{*{20}c} {q_{r} ,} & {q_{z} } \\ \end{array} \}^{T} $$

(18)

The stress matrix σ and matrix of heat flux q can be obtained as

$$ \begin{gathered} {{\varvec{\upsigma}}} = {\mathbf{D\varepsilon }} - {\hat{\mathbf{D}}}(T - T_{0} ),\,\,\, \hfill \\ {\mathbf{q}} = - {\hat{\mathbf{K}}}\{ T_{,r} ,\,\,\,T_{,z} \}^{T} \hfill \\ \end{gathered} $$

(19)

and the strain matrix ε is defined as

$$ {{\varvec{\upvarepsilon}}} = \{ \begin{array}{*{20}c} {\varepsilon_{r} ,} & {\varepsilon_{z} ,} & {\varepsilon_{rz} ,} & {\varepsilon_{\theta } } \\ \end{array} \}^{T} = \{ \begin{array}{*{20}c} {\frac{{\partial u_{r} }}{\partial r},} & {\frac{{\partial u_{z} }}{\partial z},} & {\frac{1}{2}(\frac{{\partial u_{r} }}{\partial z} + \frac{{\partial u_{z} }}{\partial r}),} & {\frac{{u_{r} }}{r}} \\ \end{array} \}^{T} $$

(20)

and ${\mathbf{D}}$, ${\hat{\mathbf{D}}}$ and ${\hat{\mathbf{K}}}$ for the FG material are given as

$$ \begin{gathered} {\mathbf{D}} = \frac{E(r,z)}{{({1} + \nu )({1} - {2}\nu )}}\left[ {\begin{array}{*{20}c} {{1} - \nu } & \nu & {0} & \nu \\ \nu & {{1} - \nu } & {0} & \nu \\ {0} & {0} & {{0}{\text{.5}}({1} - {2}\nu )} & {0} \\ \nu & \nu & {0} & {{1} - \nu } \\ \end{array} } \right]\, \hfill \\ \hfill \\ \,{\hat{\mathbf{D}}} = \frac{E(r,z)\alpha (r,z)}{{({1 - 2}\nu )}}[\begin{array}{*{20}c} 1 & 1 & 0 & 1 \\ \end{array} ]^{T} ,\,\,\,\,{\hat{\mathbf{K}}} = \left[ {\begin{array}{*{20}c} {k_{r} (r,z)} & {0} \\ {0} & {k_{z} (r,z)} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(21)

where in the above equations E(r,z) is the module of elasticity, ν is the Poisson ratio, α (r,z) is the coefficient of thermal expansion, and k_r(r,z) and k_z(r,z) are the thermal conductivities in the r and z directions.

2.2 Discretization Approach

The displacement and temperature field are written in the discrete form. In this study, the moving least square (MLS) approximation method is employed to discretize the governing equations according to the discrete nodal values. By employing the MLS approximation method, the displacement field and the temperature field are broken down based on the virtual nodal values of displacement and temperature as Atluri and Zhu (2000)

$$ \begin{gathered} u_{r} = \phi^{J} \hat{u}_{r\,J} \hfill \\ u_{z} = \phi^{J} \hat{u}_{z\,J} \hfill \\ T = \phi^{J} \hat{T}_{J} \hfill \\ \end{gathered} $$

(22)

where ϕ^J is the interpolation (shape) function and $\hat{u}_{r\,J}$, $\hat{u}_{z\,J}$ and $\hat{T}_{J}$ are fictitious nodal values. The displacement matrix u which is defined in (15) can be written as Atluri and Zhu (2000); Ahmadi (2017) 

$$ {\mathbf{u}} = {{\varvec{\Phi}}}_{J} {\hat{\mathbf{U}}}_{J} $$

(23)

where

$$ {{\varvec{\Phi}}}_{J} = \left[ {\begin{array}{*{20}c} {\phi^{J} } & 0 \\ 0 & {\phi^{J} } \\ \end{array} } \right],\,\,\,\,{\hat{\mathbf{U}}}_{J} = \left\{ {\begin{array}{*{20}c} {\hat{u}_{r} } \\ {\hat{u}_{z} } \\ \end{array} } \right\}_{J} $$

(24)

and the strain matrix and temperature gradient matrix are obtained as follows:

$$ \begin{gathered} {{\varvec{\upvarepsilon}}} = {\mathbf{B}}_{J} {\hat{\mathbf{U}}}_{J} , \hfill \\ \{ \begin{array}{*{20}c} {T_{,r} ,} & {T_{,z} } \\ \end{array} \}^{T} = {\overline{\mathbf{B}}}_{J} \hat{T}_{J} \hfill \\ \end{gathered} $$

(25)

where B_J and ${\overline{\mathbf{B}}}_{J}$ are defined as

$$ {\mathbf{B}}_{J} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \phi^{J} }}{\partial r}} & 0 & {\frac{{\partial \phi^{J} }}{\partial z}} & {\frac{{\phi^{J} }}{r}} \\ 0 & {\frac{{\partial \phi^{J} }}{\partial z}} & {\frac{{\partial \phi^{J} }}{\partial r}} & 0 \\ \end{array} } \right]^{T} ,\,\,{\overline{\mathbf{B}}}_{J} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \phi^{J} }}{\partial r}} \\ {\frac{{\partial \phi^{J} }}{\partial z}} \\ \end{array} } \right] $$

(26)

The discrete form of Eq. (16) and (17) can be obtained by substituting from Eqs. (19), (23) and (25), into (16) and (17) as

$$ \begin{gathered} - \int\limits_{{\Omega_{s}^{I} { }}} {{{\varvec{\upvarepsilon}}}_{{\mathbf{v}}} {\mathbf{DB}}_{J} {\hat{\mathbf{U}}}_{J} r{\text{d}}r{\text{d}}z + \int\limits_{{\Omega_{s}^{I} { }}} {} {{\varvec{\upvarepsilon}}}_{{\mathbf{v}}} {\hat{\mathbf{D}}}(\phi^{J} \hat{T}_{J} - T_{0} )r{\text{d}}r{\text{d}}z{ + }\int\limits_{{_{s}^{J} { } }} {{\mathbf{W}}^{I} {\mathbf{NDB}}_{J} {\hat{\mathbf{U}}}_{J} r{\text{d}}} } \hfill \\ + \int\limits_{{_{st}^{I} }} {{\mathbf{W}}^{I} {\overline{\mathbf{t}}}r{\text{d}}} - \alpha \int\limits_{{_{su}^{I} }} {{\mathbf{W}}^{I} {{\varvec{\Phi}}}_{J} {\hat{\mathbf{U}}}_{J} } {\text{d + }}\alpha \int\limits_{{_{su}^{I} }} {{\mathbf{W}}^{I} } {\overline{\mathbf{U}}}{\text{d + }}\int\limits_{{\Omega_{s}^{I} }} {{\mathbf{W}}^{I} {\mathbf{b}}r{\text{d}}r{\text{d}}z} = \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z)\,{\mathbf{W}}^{I} {{\varvec{\Phi}}}_{J} \,{\mathbf{\ddot{\hat{U}}}}_{J} \,r{\text{d}}r{\text{d}}z} \hfill \\ \end{gathered} $$

(27)

and

$$ \begin{gathered} - \int\limits_{{\Omega_{s}^{I} }} {{\mathbf{B}}_{v}^{I} } {\mathbf{\hat{K}\overline{B}}}\hat{T}_{J} r{\text{d}}r{\text{d}}z + \int\limits_{{\Gamma_{sq}^{I} }} {rw^{I} {\mathbf{\overline{N}\overline{q}}}{\text{d}}\Gamma } - \int\limits_{{\Gamma_{sh}^{I} }} {w^{I} h(\phi^{J} \hat{T}_{J} - T_{\infty } ){\text{d}}\Gamma } \hfill \\ - \alpha \int\limits_{{\Gamma_{sT}^{I} }} {w^{I} (\phi^{J} \hat{T}_{J} - \overline{T})} {\text{d}}\Gamma + \int\limits_{{\Omega_{s}^{I} }} {w^{I} g\,r{\text{d}}r{\text{d}}z} = \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z)c_{p} (r,z)w^{I} \phi^{J} \dot{\hat{T}}_{J} r{\text{d}}r{\text{d}}z} \hfill \\ \end{gathered} $$

(28)

Equations (27) and (28) can be written in the standard form as

$$ {\mathbf{M}}_{IJ} {\mathbf{\ddot{\hat{U}}}}_{J} + {\mathbf{K}}_{IJ} \,{\hat{\mathbf{U}}}_{J} = {\mathbf{F}}_{I} \, $$

(29)

$$ {\mathbf{C}}_{{{\mathbf{IJ}}}} \dot{\hat{T}}_{{\mathbf{J}}} {\mathbf{ + \overline{K}}}_{{{\mathbf{IJ}}}} \,\hat{T}_{{\mathbf{J}}} {\mathbf{ = \overline{F}}}_{{\mathbf{I}}} $$

(30)

where M_IJ, K_IJ and F_I are defined as follows:

$$ {\mathbf{M}}_{IJ} = \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z)\,{\mathbf{W}}_{I} {{\varvec{\Phi}}}_{J} \,r{\text{d}}r{\text{d}}z} $$

(31)

$$ {\mathbf{K}}_{IJ} = \int\limits_{{\Omega_{s}^{I} }} {\varepsilon_{v} {\mathbf{DB}}_{J} r{\text{d}}r{\text{d}}z} - \int\limits_{{ _{s}^{I} }} {\,{\mathbf{W}}^{I} {\mathbf{NDB}}_{J} r{\text{d}}} + \alpha \int\limits_{{ _{s}^{I} }} {{\mathbf{W}}^{I} {{\varvec{\Phi}}}_{J} } {\text{d}} $$

(32)

$$ {\mathbf{F}}_{I} = \int\limits_{{\Omega { }_{s}^{I} }} {{{\varvec{\upvarepsilon}}}_{{\mathbf{v}}} {\hat{\mathbf{D}}}(\phi^{J} \hat{T}_{J} - T_{0} )r{\text{d}}r{\text{d}}z} + \int\limits_{{{ }_{st} }} {{\mathbf{W}}^{I} {\overline{\mathbf{t}}}r{\text{d}}} + \alpha \int\limits_{{{ }_{su} }} {\mathbf{W}}^{I} {\overline{\mathbf{U}}}{\text{d + }}\int\limits_{{\Omega { }_{s} }} {{\mathbf{b}}r{\text{d}}r{\text{d}}z} $$

(33)

and C_IJ, ${\overline{\text{K}}}_{IJ}$ and ${\overline{\text{F}}}_{I}$ are defined as follows:

$$ C_{IJ} = \int\limits_{{\Omega_{s}^{I} }} {\rho (r,z)c_{p} (r,z)w^{I} \phi^{J} r{\text{d}}r{\text{d}}z} $$

(34)

$$ \overline{K}_{IJ} = \int\limits_{{\Omega_{s}^{I} }} {{\mathbf{B}}_{v}^{I} } {\mathbf{\hat{K}\overline{B}}}r{\text{d}}r{\text{d}}z + \int\limits_{{\Gamma_{sh}^{I} }} {wh\phi^{J} {\text{d}}\Gamma } + \alpha \int\limits_{{\Gamma_{sT}^{I} }} {w^{I} \phi^{J} } {\text{d}}\Gamma $$

(35)

$$ \overline{F}_{I} = \int\limits_{{\Omega_{s}^{I} }} {w^{I} g\,r{\text{d}}r{\text{d}}z} + \int\limits_{{\Gamma_{sq}^{I} }} {rw^{I} {\mathbf{\overline{N}\overline{q}}}{\text{d}}\Gamma } + \int\limits_{{\Gamma_{sh}^{I} }} {w^{I} hT_{\infty } {\text{d}}\Gamma } + \alpha \int\limits_{{\Gamma_{sT}^{I} }} {w^{I} \overline{T}} {\text{d}}\Gamma $$

(36)

Numerical integration with Gauss–Legendre quadrature rule is used to calculate the integrations over Ω_s^I. As seen in Fig. 1, depending on the position of the subdomain, the subdomains are chosen as circle, half of circle or quarter of circle. The subdomains of the nodes that are located on the edges are chosen as half circles, the subdomains of the nodes that are located on the corners are quarter of circles, and the other subdomains are circles. The radius of the subdomains is chosen so that the subdomains of nodes that are close to boundaries do not exceed the boundaries of global domain.

The two-dimensional integration over the circular subdomains with radius R_s^I can be written as

$$ \int\limits_{{\Omega_{s}^{I} }} {f(r,z){\text{d}}r{\text{d}}z = } \int\limits_{0}^{2\pi } {\int\limits_{0}^{{R_{s}^{I} }} {f(\rho ,\varphi )\rho {\text{d}}\rho {\text{d}}\varphi } = } \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {f(\xi ,\eta )\rho } } \det {\mathbf{J}}_{e} {\text{d}}\xi {\text{d}}\eta $$

(37)

where ρ and ϕ show the polar coordinates that are assigned to the center of circular subdomains Ω_s^I, ξ = 2ρ/R_s^I-1 and η = ϕ/π−1 and det J_e = (π) × (R_s^I/2) =    πR_s^I/2. Now, according to Gauss–Legendre quadrature rule, the integral can be obtained as Atkinson (1988)

$$ \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {g(\xi ,\eta )} } \det {\mathbf{J}}_{e} {\text{d}}\xi {\text{d}}\eta \approx \sum\limits_{i = 1}^{{n_{\rho } }} {\sum\limits_{j = 1}^{{n_{\varphi } }} {W_{i} W_{j} g(\xi_{i} ,\eta_{j} )} } \det {\mathbf{J}}_{e} $$

(38)

The Gauss–Legendre sample points for numerical integration over one of the circular subdomains with n_ρ = n_ϕ = 10 are presented in Fig. 2. As said before, the subdomains Ω_s^I may have overlaps and the method doesn't need background mesh to calculate the integrals. The integration on half circles and quarter of circles can be obtained with the same procedure, but in (37), integration for half circles and quarter of circles must be done on [0, π] and [0, π/2], respectively.

Fig. 2

Gauss–Legendre sample points for numerical integration over circular subdomain

3 MLS Procedure

A concise summary of moving least square (MLS) approximation is given here. Let u(x) be a function of a field variable defined in the domain Ω. The approximation of u(x) at point x is denoted by u^h(x). According to moving least square (MLS) approximation, the field function can be approximated as Atluri and Zhu (2000); Liu (2009):

$$ u({\mathbf{x}}) = {\mathbf{p}}^{T} ({\mathbf{x}}){\mathbf{a}}({\mathbf{x}}) \forall {\mathbf{x}} \in \Omega_{x} $$

(39)

where p^T(x) is a complete monomial basis of order m and a(x) is a vector of coefficients that is function of space coordinate. p^T(x) can be expressed as

$$ {\mathbf{p}}^{T} ({\mathbf{x}}) = [p_{1} ({\mathbf{x}}),p_{2} ({\mathbf{x}}),...,p_{m} ({\mathbf{x}})] $$

(40)

m is the number of terms of monomials (polynomial basis). In 2-D problems p^T(x) express for m = 3 and m = 6 as Liu (2009) 

$$ {\mathbf{p}}^{T} ({\mathbf{x}}) = [1,x^{1} ,x^{2} ]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m = 3 $$

(41)

$$ {\mathbf{p}}^{T} ({\mathbf{x}}) = [1,x^{1} ,x^{2} ,(x^{1} )^{2} ,x^{1} x^{2} ,(x^{2} )^{2} ]\,\,\,\,\,\,\,\,\,\,m = 6 $$

(42)

in which x¹ and x² are the special coordinates. The coefficient vector a(x) is determined by minimizing J(x), which is defined as Liu (2009) 

$$ J({\mathbf{x}}) = \mathop \sum \limits_{i}^{n} w_{i} ({\mathbf{x}})[{\mathbf{p}}^{T} ({\mathbf{x}}_{i} )a({\mathbf{x}}) - \hat{u}_{i} ]^{2} $$

(43)

where w_i(x) is the weight function of MLS approximation. a(x) is achieved by minimizing J(x), and a(x) is substituted to (39), and interpolation function is obtained as

$$ u^{h} ({\mathbf{x}}) = \mathop \sum \limits_{i = 1}^{n} \phi_{i} ({\mathbf{x}}) \hat{u}_{i} $$

(44)

The MLS shape function ϕ_i(x) is obtained as

$$ \phi_{i} ({\mathbf{x}}) = \mathop \sum \limits_{j = 1}^{m} p_{j} ({\mathbf{x}})[{\mathbf{A}}^{ - 1} ({\mathbf{x}}){\mathbf{B}}({\mathbf{x}})]_{ji} $$

(45)

where A is called the MLS moment matrix given by

$$ {\mathbf{A}} = \mathop \sum \limits_{i}^{n} w_{i} ({\mathbf{x}}){\mathbf{p}}({\mathbf{x}}_{{\mathbf{i}}} ){\mathbf{p}}^{T} ({\mathbf{x}}_{{\mathbf{i}}} ) $$

(46)

and B is given by

$$ {\mathbf{B}} = [w_{1} ({\mathbf{x}}){\mathbf{p}}({\mathbf{x}}_{{\mathbf{1}}} ), w_{2} ({\mathbf{x}}){\mathbf{p}}({\mathbf{x}}_{{\mathbf{2}}} ), \ldots , w_{n} ({\mathbf{x}}){\mathbf{p}}({\mathbf{x}}_{{\mathbf{n}}} )] $$

(47)

Here it should be noted that $\hat{u}_{i}$ is the fictitious nodal values and ϕ_i(x) is usually called the shape function of the MLS approximation. The partial derivatives of ϕ_i(x) are obtained as

$$ \phi_{i,k} = \mathop \sum \limits_{j = 1}^{m} [p_{j,k} ({\mathbf{A}}^{ - 1} {\mathbf{B}})_{ij} + p_{j} ({\mathbf{A}}^{ - 1} {\mathbf{B}}_{,k} + {\mathbf{A}}^{ - 1}_{k} {\mathbf{B}})_{ji} ] $$

(48)

The spline weight function as defined in (49) is used in this study.

$$w_{i} ({\mathbf{x}}) = \left\{ {\begin{array}{*{20}c} { - 6(\frac{{d_{i} }}{{r_{i} }})^{2} + 8(\frac{{d_{i} }}{{r_{i} }})^{3} - 3(\frac{{d_{i} }}{{r_{i} }})^{4} } & {0 \le d_{i} \le r_{i} } \\ 0 & {d_{i} \ge ~r_{i} } \\ \end{array} } \right. $$

(49)

where d_i=$\left|{\varvec{x}}-{{\varvec{x}}}_{i}\right|$ is the distance from node I which is located at point x_i to point x, and r_i is the size of the support for the weight function w_i(x). More details can be found in Atluri and Zhu (2000); Liu (2009).

4 Solution of Transient Problems

Two numerical integration methods are employed for transient solution of the governing equations of problem in (29) and (30). The Crank–Nicolson method and the Newmark method are used for time integration.

4.1 The Crank–Nicolson Method

In this method, the second-order finite element equations in (29) must be written as the first-order equations in time as Eslami (2014)

$$ {\mathbf{A\dot{x}}} + {\mathbf{Bx}} = {\mathbf{F}} $$

(50)

To integrate Eq. (50) in the time domain, two states of ${\mathbf{x}}$, separated by time increment Δt and denoted by ${\mathbf{x}}_{t}$ and ${\mathbf{x}}_{t + \Delta t}$, are considered. According to the trapezoidal rule, ${\mathbf{x}}_{t}$ and ${\mathbf{x}}_{t + \Delta t}$ are related as

$$ {\mathbf{x}}_{t + \Delta t} = {\mathbf{x}}_{t} + ((1 - \beta ){\dot{\mathbf{x}}}_{t} + \beta {\dot{\mathbf{x}}}_{t + \Delta t} )\Delta t $$

(51)

where 0 ≤ β ≤ 1 is a constant which may be selected by the analyst. Equation (50) is written at times t and t + Δt, and the first equation is multiplied by (1-β), and the second equation is multiplied by β to obtain the following equations

$$ (1 - \beta )({\mathbf{A\dot{x}}}_{{\mathbf{t}}} + {\mathbf{Bx}}_{{\mathbf{t}}} ) = (1 - \beta ){\mathbf{F}}_{{\mathbf{t}}} $$

(52)

$$ \beta ({\mathbf{A}}\,{\dot{\mathbf{x}}}_{t + \Delta t} + {\mathbf{Bx}}_{t + \Delta t} ) = \beta {\mathbf{F}}_{t + \Delta t} $$

(53)

It is assumed that the matrices A and B are constant by time. These two equations are added, and Eq. (51) is used to eliminate the time derivatives of ${\mathbf{x}}$. The resulting equation is solved for ${\mathbf{x}}_{{{\mathbf{t + \Delta t}}}}$, which yields Eslami (2014)

$$ (\frac{1}{\Delta t}{\mathbf{A}} + \beta {\mathbf{B}}){\mathbf{x}}_{{{\mathbf{t + \Delta t}}}} = (\frac{1}{\Delta t}{\mathbf{A}} - (1 - \beta ){\mathbf{B}}){\mathbf{x}}_{{\mathbf{t}}} + (1 - \beta ){\mathbf{F}}_{{\mathbf{t}}} + \beta {\mathbf{F}}_{{{\mathbf{t + \Delta t}}}} $$

(54)

This equation is used to calculate the matrix X at the time t + Δt in terms of its value at time t. The stability of the solution algorithm depends on the numerical value of $\Delta$t, which is inversely proportional to the stability parameter β. Different values of β are associated with various numerical schemes. The value β = 0 provides the forward finite difference method, β=1 provides backward finite difference method, and the Crank–Nicolson, or trapezoidal rule, is associated with β = 1/2. More details about stability and accuracy of this method can be found in Eslami (2014).

4.2 The Newmark Method

In the Newmark method, the matrix of velocity ${\dot{\mathbf{x}}}$ and displacement ${\mathbf{x}}$ at time t +$\Delta$t are approximated as Eslami (2014)

$$ {\dot{\mathbf{x}}}_{{{\mathbf{t}} + \Delta t}} = {\dot{\mathbf{x}}}_{{\mathbf{t}}} + [(1 + \alpha ){\mathbf{\ddot{x}}}_{t} + \alpha {\mathbf{\ddot{x}}}_{{{\mathbf{t}} + \Delta t}} ]\Delta t $$

(55)

$$ {\mathbf{x}}_{{{\mathbf{t}} + \Delta t}} = {\mathbf{x}}_{{\mathbf{t}}} + {\dot{\mathbf{x}}}_{{\mathbf{t}}} \Delta t + [(\frac{1}{2} - \beta ){\mathbf{\ddot{x}}}_{{\mathbf{t}}} + \beta {\mathbf{\ddot{x}}}_{{{\mathbf{t}} + \Delta t}} ](\Delta t)^{2} $$

(56)

where the coefficients α and β are parameters which determine the accuracy and stability of the technique. The finite element equations for dynamic problems is written for time t + Δt as

$$ {\mathbf{M}}\,{\mathbf{\ddot{x}}}_{t + \Delta t} + {\mathbf{C}}\,{\dot{\mathbf{x}}}_{t + \Delta t} + {\mathbf{K}}\,{\mathbf{x}}_{t + \Delta t} = {\mathbf{F}}_{t + \Delta t} $$

(57)

Equation (56) is solved for ${\mathbf{\ddot{x}}}_{{{\mathbf{t}} + \Delta t}}$ and the result are then substituted in Eq. (55) and an expression is obtained for ${\dot{\mathbf{x}}}_{{{\mathbf{t}} + \Delta t}}$. The two expressions which are obtained for ${\dot{\mathbf{x}}}_{{{\mathbf{t}} + \Delta t}}$ and ${\mathbf{\ddot{x}}}_{{{\mathbf{t}} + \Delta t}}$ are substituted in Eq. (57) and the resulting expression is solved for ${\mathbf{x}}_{{{\mathbf{t}} + \Delta t}}$ and the following relation is obtained as Eslami (2014)

$$ {\hat{\mathbf{K}}\mathbf{x}}_{{{\mathbf{t}} + \Delta t}} = {\hat{\mathbf{F}}} $$

(58)

where

$$ {\hat{\mathbf{K}}} = {\mathbf{K}} + \frac{\alpha }{\beta (\Delta t)}{\mathbf{C}} + (\frac{{1}}{{\beta (\Delta t)^{{2}} }}){\mathbf{M}} $$

(59)

$$ {\hat{\mathbf{F}}} = {\mathbf{F}}_{t + \Delta t} + {\mathbf{M}}(\frac{{1}}{{\beta \Delta t^{2} }}{\mathbf{x}}_{t} + \frac{{1}}{\beta \Delta t}{\dot{\mathbf{x}}}_{t} + (\frac{{1}}{{{2}\beta }} - {1}){\mathbf{\ddot{x}}}_{t} ) + {\mathbf{C}}(\frac{\alpha }{\beta \Delta t}{\mathbf{x}}_{t} + (\frac{\alpha }{\beta } - 1){\dot{\mathbf{x}}}_{t} + \Delta t(\frac{\alpha }{2\beta } - 1){\mathbf{\ddot{x}}}_{t} ) $$

(60)

With the given initial values of ${\mathbf{x}}_{0}$, ${\dot{\mathbf{x}}}_{0}$ and ${\mathbf{\ddot{x}}}_{0}$, the method can be used to march through the time. The method for α = 1/2 and β = 1/4 is called the average acceleration method.

5 Functionally Graded Material

In the functionally graded materials (FGMs), the material properties change continuously between two or more material properties. The 2D-FGMs are usually made by continuous gradation of three or four distinct material phases such as ceramics or metals. The volume fractions of the constituents vary in a predetermined composition profile.

In this study, it is supposed that the material properties of the cylinder are axi-symmetric, and are 2D FG in radial and axial directions. The inner surface of the cylinder is made of two ceramic which is denoted by c₁ and c₂, and the outer surface is made of two metals denoted by m₁ and m₂. The bottom of inner surface of cylinder is pure c₁, and the top of the inner surface is pure c₂. Also the bottom of outer surface is pure m₁, and the top of outer surface is pure m₂. Now consider the volume fractions of axi-symmetric 2D-FGM cylinder of internal radius R_i, external radius R_o, and finite length L as shown in Fig. 3 changes continuously in two direction as.

$$ V_{c1} (r,z) = (1 - (\frac{{r - R_{i} }}{{R_{o} - R_{i} }})^{{n_{r} }} )(1 - (\frac{z}{L})^{{n_{z} }} ) $$

(61)

$$ V_{c2} (r,z) = (1 - (\frac{{r - R_{i} }}{{R_{o} - R_{i} }})^{{n_{r} }} )(\frac{z}{L})^{{n_{z} }} $$

(62)

$$ V_{m1} (r,z) = (\frac{{r - R_{i} }}{{R_{o} - R_{i} }})^{{n_{r} }} (1 - (\frac{z}{L})^{{n_{z} }} ) $$

(63)

$$ V_{m2} (r,z) = (\frac{{r - R_{i} }}{{R_{o} - R_{i} }})^{{n_{r} }} (\frac{z}{L})^{{n_{z} }} $$

(64)

where n_r and n_z are parameters that represent the power exponent of volume fraction distributions in r and z directions. For example, the volume fraction of the first ceramic material is V_c1(r = R_i, z = 0) = 1 and the volume fraction changes continuously to V_c1(r = R_o, z = 0) = V_c1(r = R_i, z = L) = V_c1(r = R_o, z = L) = 0. The volume fractions of the other materials change in two direction. In the special cases, n_z = 0 and n_r ≠ 0 represent 1D FG cylinder where inner surface is c₂ and outer surface is m₂, n_z ≠ 0 and n_r = 0 represents 1D axial FG cylinder where bottom surface is m₁ and top surface is m₂, and n_r = n_z = 0 represents homogeneous m₂ cylinder. According to the rule of mixture, a material property, P, at any arbitrary point (r, z) in the 2D-FGM cylinder is determined linear combination of volume fractions and material properties of the basic materials as.

$$ P = P_{c1} V_{c1} + P_{c2} V_{c2} + P_{m1} V_{m1} + P_{m2} V_{m2} $$

(65)

Fig. 3

Two-dimensional distribution of material properties in the 2D-FG cylinder—module of elasticity

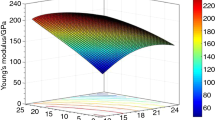
The distribution of a material parameter (module of elasticity) in the r-z section of 2D-FG cylinder is shown in Fig. 3.

6 Numerical Results and Discussion

The numerical results are presented for response of FG cylinder subjected to mechanical and thermal loading. The thermo-mechanical properties of basic constituents of the 2D-FGM cylinder are presented in Table 1.

Table 1 Mechanical properties of basic constituents of the 2D-FGM cylinder

It should be noted that Poisson’s ratio is assumed to be constant through the body. This assumption is reasonable because of the small differences between the Poisson’s ratios of basic materials. The variation of a material property such as heat conduction coefficient is considered as Eq. (65). In this study, the penalty parameter is chosen as E_m1 × 10⁸. At first, the convergence and accuracy of the numerical results are investigated.

6.1 Convergence Study

The convergence of numerical results of present meshless method by increasing the number of nodes is studied in this section. To this aim, a homogeneous cylinder with R_i = 0.5, R_o = 1.5 and L = 1 is considered. The inner surface of the cylinder is subjected to constant pressure P_i and the outer surface is stress-free. Analytical solution is available for long and homogeneous cylinder subjected to uniform internal pressure in the plane strain condition Sadd (2009). In the meshless solution, the boundary conditions on the top and bottom edges of the cylinder are considered in such a way that its behavior is similar to a long cylinder i.e. u_z(r, z = 0) = u_z(r, z = L) = 0. The inner surface of the cylinder is subjected to pressure P_i = 1 MPa. The nodes are distributed uniformly in the solution domain in square array. The convergence of the radial stress σ_r at the mid-point of the cylinder wall i.e. (r = (R_i + R_o)/2, z = L/2) by increasing the number of nodes is shown in Fig. 4. The analytical value of the stress at this point is shown in this figure. As seen in Fig. 4, the predicted values of σ_r converge to the analytical value of stress by increasing the number of nodes. For the number of nodes greater than 13 × 13 = 169 nodes, the stress converged to the analytical value.

Fig.4

Convergence of radial stress at point r = (R_i + R_o)/2, z = L/2 by increasing the number of nodes

The number of nodes, the size of subdomains Ω_s^I and the size of support domain in the MLS approximation (r_i in Eq. (49)) influence the numerical results of the meshless formulation.

In the construction of shape function with MLS approximation, r_i (see Eq. (49)) is a parameter that must be chosen in the solution procedure. In this study, r_i is chosen as r_i = α_s × d_i, where d_i is the distance of node I to the nearest neighborhood node. Also, the subdomains Ω_s^I are chosen as circles around node I with radius R_s^I = β_s × d_i, where α_s and β_s are parameters that control the size of supports domain and subdomains. The effect of α_s and β_s on the predictions of the present method is studied in Table 2. The radial stress σ_r and SR=σ_{r Meshless}/σ_{r Analytic} at point (r = (R_i + R_o)/2, z = L/2) are presented in Table 2, and the effect of α_s and β_s on the predictions of the meshless method is investigated. The results are presented for grid of 13 × 13 nodes. The prediction of analytical method at this point is σ_r = -0.2593P_i. It is seen in Table 2 that for 4.5 ≤ α_s ≤ 5.5 and 1 ≤ β_s ≤ 2 the agreement between predictions of present method and analytical method increases.

Table 2 Effect of α_s and β_s on the prediction of the meshless formulation

6.2 Comparison of Results

At first, the predictions of present study are compared with the predictions of analytical solution for homogeneous cylinder. Analytical solution is available for stress distribution in long cylinder in the plane strain conditions which is subjected to uniform internal and external pressure and steady state radial temperature distribution (Sadd 2009). In the meshless solution, the boundary conditions of the cylinder are considered in such a way that it is similar to a long cylinder i.e. u_z(r, z = 0) = u_z(r, z = L) = 0, and uniform internal pressure P_i is applied to inner side of the cylinder. The dimensions of the cylinder are considered as R_i = 1 m, R_o = 1.5 m and L = 0.5 m.

The distribution of radial stress σ_r and hoop stress σ_θ through the thickness of the homogeneous aluminum cylinder at z = 0.5L which is subjected to internal pressure are presented in Fig. 5, and compared with the results of analytical solution. Also the distribution of thermal stress σ_θ and σ_r in the cylinder which is subjected to thermal loading is presented in Fig. 6. The inner surface of the cylinder is kept at T_i = 100 °C, and the outer surface is kept at T_o = 25 °C, and the stress-free initial temperature of the cylinder is considered as T₀ = 25 °C. As seen, there are good agreements between the predictions of present meshless solution and the predictions of analytical solution for mechanical and thermal loading.

Fig. 5

Distribution of σ_θ and σ_r in the cylinder subjected to internal pressure—comparison of results

Fig. 6

Distribution of σ_θ and σ_r in aluminum cylinder subjected to thermal loading—comparison of results

Also, the predictions of present method are compared with the predictions of analytical solution for long and radially FG cylinder reported by Jabbari et al. (2002). They presented an analytical solution for long radially FG cylinder which is subjected to internal pressure, and 1D steady state temperature distribution in radial direction. The geometrical and mechanical properties of the inner surface of cylinder are chosen the same as Jabbari et al. (2002), R_i = 1 m, R_o = 1.2 m, E_i = 200GPa, α_i = 1.2 × 10^–6/^°C, and ν = 0.3. The distribution of radial stress σ_r and hoop stress σ_θ through the cylinder thickness is shown in Figs. 7,  8, and compared with the prediction of analytical solution (Jabbari et al. 2002). In these figures, m is the power law index of FG material. The cylinder is subjected to the loading conditions as T(R_i) = T_i = 10 °C and T(R_o) = 0 °C and P(R_i) = P_i = 50 MPa, P(R_o) = 0.

Fig. 7

Comparison of predictions of present method and analytical method for distribution of σ_r at z = L/2

Fig. 8

Comparison of predictions of present method and analytical method for distribution of σ_θ at z = L/2

The steady state temperature distribution in the cylinder thickness, whose inner surface is kept at T_i = 10˚C and outer surface is kept at T_o = 0 °C, is provided in Fig. 9 for m = 2 and m = −2. As it is observed, there is very good agreement between the predictions of MLPG method and analytical solution (Jabbari et al. 2002). Figures 5, 6, 7, 8, 9 show there are good agreements between the predictions of present method and predictions of analytical solutions. It is concluded that the present method is accurate for prediction of the thermo-mechanical response of FG cylinders.

Fig. 9

Comparison of predictions of present method and analytical method for distribution of temperature at z = L/2

6.3 Transient Mechanical Loading of FGM Cylinder

In the transient loading, the cylinder is subjected to time-dependent internal pressure as (66). The internal pressure is assumed to be zero at t = 0, and increases exponentially as a function of time to its final value P_i as

$$ P(t) = P_{i} (1 - \exp ( - \frac{t}{{t_{f} }})) $$

(66)

where t_f is a time parameter which controls the rate of increasing the pressure. The increasing rate of the applied pressure decreases by increasing t_f. At t = 4t_f, the applied pressure is 98.17% of the final value, i.e., P(t = 4t_f) = 0.9817P_i. The pressure–time diagram for t_f = 20T₁ and t_f = 40T₁ is given in Fig. 10, where T₁ = 2π/ω₁ is the time period of first nonzero natural frequency of the cylinder.

Fig. 10

Time history of applied internal pressure of cylinder for two different values of t_f

The mechanical properties of basic constituents of the 2D-FGM cylinder are considered according to Table 1, and the Poisson’s ratio is taken to be 0.3. The dimensions of the cylinder are considered as; R_i = 1 m, R_o = 1.5 m and L = 1 m, and the edge of the cylinder at z = 0 and z = L are free. The first four axi-symmetric natural frequency of the cylinder for n_r = 1 and n_z = 0 are ω₁ = 746.1 Hz, ω₂ = 832.5 Hz, ω₃ = 2185.5 Hz, and ω₄ = 3260.1 Hz. The corresponding mode shapes are presented in Fig. 11.

Fig. 11

Mode shapes of the FG cylinder for n_r = 1, n_z = 0 and n_r = n_z = 1

The response of the cylinder due to the applied transient pressure is studied in this section. In order to verify the accuracy of time integration, the time integration of equations is done by the Crank–Nicolson and Newmark method, and the results are compared. The cylinder is subjected to internal pressure with t_f = 0.5T₁ and t_f = 5T₁ (T₁ = 2π/ω₁ = 1/746.1 = 1.3403 ms is the time period of first natural frequency), and the transient response of the cylinder which is obtained by Newmark and Crank–Nicholson method is compared. In the Nicolson method, β is taken as β = 0.50005 and in the Newmark method α and β are chosen as α = 0.5 and β = 0.25, and the time step is chosen Δt = T₁/14.

The time history of the radial displacement at the inner surface of the cylinder at z = 0.5L is presented in Fig. 12 for t_f = 0.5T₁ and t_f = 5T₁. It is observed that the predictions of Crank–Nicolson method and Newmark method are in very close agreement. The accuracy of time integration is verified by comparison of results of two methods in Fig. 12. The dimensionless displacement is defined as u^* = uE_m2/R_iP_i.

Fig. 12

Comparison of the results of Crank–Nicolson and Newmark method at (r = R_i, z = 0.5L) of FG cylinder, n_r = 1, n_z = 0, Δt = T₁/14

To study the effect of loading rate on the response of the cylinder, the cylinder is subjected to internal pressure with t_f = T₁, t_f = 2T₁, t_f = 10T₁ and t_f = 50T₁ and the effect of loading rate on the response of the cylinder is studied. The radial displacement at (r = R_i, z = L/2) for (n_r = 1, n_z = 0) and (n_r = 1, n_z = 1) is presented in Fig. 13. It is seen in Fig. 12 and Fig. 13 that for very rapid loading rate in which t_f is comparable with T₁, i.e. t_f = 0.5T₁, t_f = T₁ and t_f = 2T₁, t_f = 5T₁, the response of the cylinder is oscillatory, and the amplitude of oscillation is considerable. As seen in Fig. 13, the amplitude of oscillation for t_f = 10T₁ is small, and the amplitude of oscillation for t_f = 50T₁ is very small and can be ignored. It is seen that the load increasing rate significantly affects the transient response of the cylinder. When the loading rate of the cylinder is very fast, so that t_f is comparable with T₁, it makes the natural frequencies of the cylinder to be excited and oscillatory response is observed. For t_f >  > T₁, such as t_f = 50T₁, the loading can be considered as quasi static and the natural frequencies of the cylinder are not exited. As seen in Fig. 12 and Fig. 13a, the oscillation frequency of displacements is constant in these figures, but in Fig. 13b, at least two frequencies are seen in the time response of the cylinder. In the 2D-FG cylinder with n_r = n_z = 1, due to non-symmetric material properties, more than one frequency is seen in the time response of the cylinder.

Fig. 13

Effect of loading rate on the response of 1D- and 2D-FG cylinder at (r = R_i, z = 0.5L) (a) (n_r = 1, n_z = 0) (b) (n_r = 1, n_z = 1)

The time response of 2D-FG cylinder for various values of n_r and n_z is presented in Fig. 14. For all values of n_r and n_z which are presented in Fig. 14, the distribution of mechanical properties is 2D in the rz plane, and at least two frequencies are seen in the time response of the cylinder.

Fig. 14

Effect of power law index n_r and n_z on the response of 2D-FG cylinder, t_f = T₁

The hoop stress and radial stress at various thickness of the FG cylinder (n_r = 1, n_z = 0) for t_f = 2T₁ are shown in Fig. 15 and Fig. 16. R_m = (R_i + R_o)/2 is the mean radius of the cylinder, and R₁ = (R_i + R_m)/2 and R₂ = (R_m + R_o)/2. As seen the mean value of hoop stress increases monotonically, but σ_θ have an oscillatory part with frequency ω₁. Although the time history of displacement at the inner surface of the cylinder in Fig. 13 is oscillatory, it is seen in Fig. 16 that as expected, the predicted radial stress at the inner surface is not oscillatory and is equal to the applied internal pressure, and the radial stress at the traction free outer surface of the cylinder at r = R_o vanishes. The radial stress in the cylinder wall has an oscillatory part. The bullet circles in the next figures show the steady state values of stress which are obtained by static solution of the problem at the final pressure P(t) = P_i. As seen at t >  > t_f, the mean value of hoop stress and radial stress is equal to the value of static solution which is shown by bullet circles in the figures.

Fig. 15

Transient radial stress in the thickness of cylinder at z = L/2, (n_r = 1, n_z = 0, t_f = 2T₁)

Fig. 16

Transient radial stress in the thickness of FG cylinder at z = L/2, (n_r = 1, n_z = 0, t_f = 2T₁)

The radial stress σ_r, hoop stress σ_θ and axial stress σ_z in the FG cylinder (n_r = 1, n_z = 0) for t_f = 50T₁ are shown in Figs. 17, 18 and  19. As seen for t_f >  > T₁, i.e. t_f = 50T₁, there is no oscillation in the transient response of the cylinder. As seen, the stresses start from zero and increase monotonically. The final value of transient solution is equal to the value of static steady state solution at final pressure P = P_i.

Fig. 17

Transient radial stress σ_r(t) in the thickness of the FG cylinder (n_r = 1, n_z = 0, t_f = 50T₁)

Fig. 18

Transient hoop stress σ_θ (t) in the thickness of the FG cylinder (n_r = 1, n_z = 0, t_f = 50T₁)

Fig. 19

Transient axial stress σ_z(t) in the thickness of the FG cylinder (n_r = 1, n_z = 0, t_f = 50T₁)

The response of 2D-FG cylinder with n_r = n_z = 1 is studied in the next figures. The mode shapes and natural frequency of the cylinder are shown in Fig. 11. In this cylinder, the material properties are not uniform through the length of the cylinder. The radial stress and hoop stress in the cylinder which is subjected to internal pressure with t_f = 2T₁ are presented in Figs. 20 and 21. As seen in Fig. 20, due to non-uniform material properties in the axial direction, more than one oscillation frequency is seen in the response of the cylinder. The time history of radial stress at the bottom, center and top of the cylinder at r = R_m are shown in Fig. 22.

Fig. 20

Transient hoop stress σ_θ (t) in the 2D-FG cylinder (n_z = n_r = 1, t_f = 2T₁)

Fig. 21

Transient radial stress σ_r(t) in the 2D-FG cylinder (n_z = n_r = 1, t_f = 2T₁)

Fig. 22

Transient radial stress σ_r(t) in the 2D-FG cylinder at z = L/4, z = L/2 and z = 3L/4, (n_z = n_r = 1, t_f = 2T₁)

6.3.1 Thermal Loading of FGM Cylinder

Transient temperature and thermal stress in the FG cylinder are studied in this section. A thick hollow cylinder of inner radius R_i = 0.1 m, outer radius R_o = 0.15 m, and length L = 0.1 m, which is subjected to thermal loading is considered.

At first, the accuracy of present method for prediction of temperature distribution in the cylinder is studied. For this aim, the inner surface of the cylinder is subjected to T_i = 100 °C, the outer surface is subjected to T_o = 25 °C, and the top and bottom surface of the cylinder are isolated. The steady state temperature distribution through the thickness of the cylinder at z = L/2 is shown in Fig. 23 for (n_r = 0, n_z = 0) and (n_r = 1 n_z = 0). As seen, there is good agreement between the predictions of present method and analytical steady state solution for temperature distribution.

Fig. 23

Distribution of temperature through the thickness of cylinder at z = L/2-comparison of results

The contour plots for distribution of temperature in the thickness of FG cylinder for various values of n_r and n_z are presented in Fig. 24. As seen in Fig. 24, for n_z = 0 the temperature is uniform in the length of the cylinder, and for n_z ≠ 0, the temperature gradient is seen through the length of the cylinder.

Fig. 24

Contour plots of steady-state temperature distribution for various n_r and n_z

6.3.2 Transient Temperature

To study the transient temperature, 2D-FG cylinder with n_r = n_z = 1 with initial steady state and stress-free temperature T₀ = 25 °C is considered. The temperature in the inside of the cylinder suddenly increases to T_I∞ = 100 °C, and the following convection conditions are considered. The ambient temperature is T_B∞ = T_T∞ = T_o∞ = 25 °C, and the convection coefficients are considered as h_B = h_T = h_O = 10 W/m²K and h_I = 100 W/m²K, where subscripts B, T, I and O represent the bottom, top, inner and outer sides of the cylinder. The transient temperature and transient thermal stress in the cylinder are studied. The transient temperature in some points of the cylinder at inner surface R_i, outer surface R_o and mid-radius R_m of the cylinder at z = L/2 and z = 0 are shown in Fig. 25. The time step of numerical integration is chosen as Δt = 5 s. The circle bullets show the steady state temperature which is obtained from the steady state solution of the problem. As seen, the temperature of the cylinder increases and gets the final steady state value after about 1016 s. In order to show the temperature distribution pattern, the contours of temperature distribution at t = 100 s and t = 1016 s are shown in Fig. 26.

Fig. 25

Transient temperature at some points of the 2D-FG cylinder n_r = n_z = 1

Fig. 26

Contour plots of transient temperature distribution in the 2D-FG cylinder at t = 100 s and t = 1016 s, n_r = n_z = 1

7 Transient Thermal Stress

The transient thermal stress in the cylinder due to the transient temperature distribution is studied in the following. The axial displacement on the top and bottom surface of the cylinder is restricted as u_z(r,0) = u_z(r, L) = 0. The radial displacement of inner surface of the cylinder at different times is shown in Fig. 27. Although the boundary conditions of cylinder and the loading are symmetric with respect to z = L/2, the displacement is not symmetric. As seen in Fig. 27, the transient displacement of inside surface of 2D-FG cylinder gets its final value equal to the steady state solution.

Fig. 27

Distribution of radial displacement of inner surface of the cylinder at various times, n_r = n_z = 1

The transient thermal stresses at some nodes of the cylinder are shown in Figs. 28, 29 and 30. The time history of radial thermal stress σ_r at z = L/4 and z = L/2 is presented in Fig. 28. As seen, the radial thermal stress at traction free outer surface of the cylinder vanishes at all times. The hoop thermal stress σ_θ and axial thermal stress σ_z are presented in Fig. 29 and Fig. 30. The hoop stress is tensile at R_i and is compressive at R_m and R_o, and σ_z is compressive in the mentioned points. The thermal stresses increase to the final steady state values. It should be noticed that the results of the steady state solution are shown by circle in these figures.

Fig. 28

Transient radial thermal stress σr in the 2D-FG cylinder, n_r = n_z = 1

Fig. 29

Transient hoop thermal stress σ_θ in the 2D-FG cylinder, n_r = n_z = 1

Fig. 30

Transient axial thermal stress σz in the 2D-FG cylinder, n_r = n_z = 1

The contour plots of radial and hoop thermal stress distribution at t = 100 s and t = 1016 s are shown in Fig. 31. The stress distribution in the cylinder with n_r = 1, n_z = 0 in which the bottom surface is restricted in the axial direction, i.e. u_z(r, z = 0) = 0, and the top surface is free is studied in Figs. 32, 33 and 34. The contours of thermal stresses in the steady state conditions are presented in Fig. 35.

Fig. 31

Contour plots of stress distribution in 2D-FG cylinder (n_r = n_z = 1) at t = 100 s and t = 1016 s

Fig. 32

Transient radial thermal stress σr in the FG cylinder, n_r = 1, n_z = 0

Fig. 33

Transient hoop thermal stress σ_θ in the FG cylinder, n_r = 1, n_z = 0

Fig. 34

Transient axial thermal stress σz in the FG cylinder, n_r = 1, n_z = 0

Fig. 35

Contour plots of steady state stress distribution in FG cylinder, n_r = 1, n_z = 0

8 Conclusion

The commercial finite element software cannot systematically model the functional graded material, especially the 2D-FGMs. For this purpose, a meshless formulation is presented for 2D-functionally graded cylinders which are subjected to time-dependent mechanical and thermal loading conditions. The equilibrium equation of elasticity and equation of heat conduction are written in the weak form, and a meshless formulation is developed to discretize the transient governing equations to a system of linear differential equations in time domain. The Crank–Nikolson and Newmark time integration methods are employed for time integration of the equations. The transient response of the cylinder subjected to mechanical and thermal loading is studied, and the effects of parameters on the response of cylinder are investigated. The disadvantages of finite element method in solution of the same problems, including the discontinuity of derivatives of shape function at the boundary of elements, its need to mesh of elements and the difficulties to create shape functions with high degree of continuity in finite element method are eliminated in this formulation. It is observed that the proposed formulation is an effective and efficient method for analyzing thick cylinders with desired functionally graded material properties. In the numerical results, the effect of mechanical parameters such as loading rate, boundary conditions and FG power index on the transient stress and displacement is investigated. It is seen that transient loading with high rate excited the natural frequencies of the cylinder.