Assessment of Vibrational Frequencies and Static Characteristics of Multilayered Skew Magneto-Electro-Elastic Plates: A Finite Element Study

Abstract

This article presents a finite element (FE) model for free vibration and static analysis of layered skew magneto-electro-elastic (SMEE) plates by incorporating the shear deformation theory. The coupled constitutive equations of the MEE materials are used to derive the FE model accounting the effect of electro-elastic and magneto-elastic couplings. The displacement, electric potential and magnetic potential are considered as primary variables, while the stresses, electric displacement and magnetic induction are derived from the primary variables using constitutive equations. Influence of boundary conditions and material stacking sequences on the natural frequency, displacement and stresses of the SMEE plates has been investigated. Particular emphasis has been put on studying the effect of skew angles and aspect ratios on the natural frequencies, stresses, electric displacement and magnetic induction. The present study reveals that skew angle and aspect ratio significantly influence the structural behavior of SMEE plates.

1 Introduction

Recently, the study of smart structures has gained traction with its ability to design and establish multifunctional components. As the interest of smart structures is vested in next-generation smart transportation systems, sensors and actuators, aerospace applications, marine applications, medical instruments and energy harvesting, just to name a few, a new era of smart structures composed of smart composites has emerged (Ray et al. 1994; Zhang et al. 2015; Datta and Ray 2016). In particular, magneto-electro-elastic (MEE) composites composed of piezoelectric (BaTiO₃) and magnetostrictive (CoFe₂O₄) materials have attracted the attention of researchers. The MEE composites exhibit a unique ability to convert one form of the energy into other (among mechanical, electric and magnetic). This new class of composites exhibits a coupled property called the magneto-electric effect along with the electro-elastic and the magneto-elastic effects, which is absent in individual constituents of the MEE composites. For an applied load on a traditional structure, reaction is a function of geometry and material property. However, in the case of smart structures with MEE composites, electric and magnetic fields have their influence along with material property and geometry. The increasing demand for structures that are more adaptable to the applied load might have motivated the recent developments in MEE composites. Extensive research has been carried out to assess the structural behavior of magneto-electro-elastic plates (Pan 2001; Pan and Heyliger 2002, 2003; Pan and Han 2005; Liu 2011). The magneto-electric effect in composites of piezoelectric and piezomagnetic phase was theoretically investigated by Nan (1994). Free vibration characteristics of the MEE structures have been extensively studied by many researchers through various methodologies (Buchanan 2004; Li et al. 2014; Anandkumar et al. 2007; Liu and Chang 2010; Bhangale and Ganesan 2005; Ramirez et al. 2006; Razavi and Shooshtari 2015; Shooshtari and Razavi 2016). Subsequently, the behavior of MEE plates under static loads is extensively investigated and well established through many methods (Lage et al. 2004; Moita et al. 2009; Liu et al. 2016; Bhangale and Ganesan 2006). Kattimani and Ray (2014a, b, 2015) investigated on the control of geometrically nonlinear vibrations of MEE plates and shells using 1–3 piezoelectric composite. Kondaiah et al. (2015, 2017) evaluated the MEE sensor patch for pyroeffects. Ebrahimi and Barati (2016, 2017a, b) extensively investigated the FG nano-MEE structures. The behavioral study of MEE plate for free vibration and large deflection was established by Milazzo (2014a, b, 2016; Chen et al. 2015) via various methodologies. The static behavior of anisotropic multilayered MEE hollow sphere was studied by Vinyas and Kattimani (2017a). Vinyas and Kattimani (2017b, c) and Ebrahimi et al. (2017a) investigated the static behavior of stepped functionally graded and multiphase MEE plates subjected to different thermal loads. Ebrahimi et al. (2017b) and Kattimani (2017) investigated the vibration characteristics of porous smart structures. Recently, Carrera et al. (2017) obtained the nonlinear vibration characteristics of multiferroic plates and shells. Recently, Carrera unified formulation is used by many researchers to assess the structural characteristics of the MEE plates (Carrera and Valvano 2017; Cinefra et al. 2017; Zappino et al. 2017; Kumar et al. 2017; Nair and Durvasula 1973).

Skew plates and laminates are of importance in many engineering applications as geometric changes implemented to the rectangular plate influence various response characteristics. In addition, such plates specifically exhibit high strength to weight ratio and excellent fatigue resistance capturing the attention of many researchers. Extensive research has been carried out to study the effect of skew angle on free vibration and static analysis of skew composite plates (Naghsh and Azhari 2015; Upadhyay and Shukla 2012; Liew and Wang 1993; Kanasogi and Ray 2013). Active vibration control of skew composite plates was studied by Garg et al. (2006)). McGee et al. (1994) developed a higher-order shear deformation theory to analyze the vibration behavior of different skew laminates. Higher-order shear deformation theory has been incorporated to analyze the natural vibrations of rhombic plates by Butalia et al. (1990). Chen et al. (2014) critically analyzed the response of skew plates under bending using a Heterosis element. Recently, Kiran and Kattimani (2017, 2018a, b, c) and Kiran et al. (2018) have investigated the structural behavior of various rectangular and skew MEE structures. The comprehensive literature review reveals that extensive research has been published on free vibration and static analysis of the multilayered MEE plates and fiber-reinforced skew composite plates. However, to the best of the author’s knowledge, no research has been reported on the free vibration and static analysis of layered skew magneto-electro-elastic plates. Consequently, this paper presents the development of FE model for the free vibration and the static analysis of layered SMEE plates using 1–2 shear deformation theory. Special attention has been paid to study the effect of skew angle on the natural frequencies, displacements, potentials, induced stresses, electric displacement and magnetic induction of the SMEE plates. Effect of aspect ratios, layer stacking sequence and boundary conditions on the behavior of SMEE plates has been thoroughly investigated.

2 Problem Description and Governing Equation

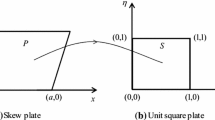
A schematic diagram of a skew magneto-electro-elastic plate with coordinate system is illustrated in Fig. 1a, while Fig. 1b illustrates the two-dimensional x–y plane of the skew MEE plate. The length, the width and the total thickness of the plate are a, b and H, respectively. The skew angle of the SMEE plate is α. The SMEE plate consists of three layers of equal thickness h_i (i = 1, 2, 3). The top and the bottom layers are made of identical material either piezoelectric (BaTiO₃) commonly represented by B or magnetostrictive (CoFe₂O₄) commonly represented by F, while the middle layer is of the other material, i.e., magnetostrictive or piezoelectric. Based on the stacking sequence of the material, the MEE composite is called B/F/B or F/B/F indicating the top/middle/bottom layer, respectively, in which, B stands for BaTiO₃ and F stands for CoFe₂O₄. Since the structure is composed of layers of dissimilar materials, the kinematics of deformation of the SMEE plate may be difficult to define by using an equivalent single layer displacement theory because of the fact that the material properties of the adjacent continua of the overall plate differ in order. Hence, the 1–2 shear deformation theory (Hildebrand et al. 1949; Tessler 1993) has been incorporated to derive the deformations of the SMEE plate.

Fig. 1

a SMEE plate with B/F/B stacking sequence, b the two-dimensional x–y plane of the skew SMEE plate

Consequently, the axial displacements u and v at any point in the SMEE plate along the x- and y-direction, and the transverse displacement w at any point in the SMEE plate can be expressed as (Hildebrand et al. 1949; Tessler 1993)

$$\begin{aligned} & u(x,y,z,t) = u_{0} (x,y,t) + z\theta_{x} (x,y,t) \\ & v(x,y,z,t) = v_{0} (x,y,t) + z\theta_{y} (x,y,t) \\ & w(x,y,z,t) = w_{0} (x,y,t) + z\theta_{z} (x,y,t) + z^{2} \kappa_{z} (x,y,t) \\ \end{aligned}$$

(1)

where $u_{0}$ and $v_{0}$ are the translational displacements at any point on the midplane of the plate along x- and y-direction, while $w_{0}$ is the transverse displacement along z-direction at any point in the SMEE plate. θ_x and θ_y denote the generalized rotation of the normal to the middle plane of the SMEE plate about the y- and x-axis, respectively. θ_z and $\kappa_{z}$ are the generalized rotational displacements for the SMEE plate with respect to the thickness coordinate. For the ease of computation, rotational and translational displacements are considered separately as follows:

$$\left\{ {d_{t} } \right\} = \left[ {u_{0} \,\,v_{0} \,\,w_{0} } \right]^{\text{T}} ,\quad \{ d_{r} \} = [\theta_{x} \,\,\theta_{y} \,\,\theta_{z} \,\,\kappa_{z} ]^{\text{T}}$$

(2)

To overcome the shear locking in thin structures and to emphasize the computation of elemental stiffness matrices linked with the transverse shear deformation, the selective integration rule has been employed. To address such specific need, the state of strain at any point in the plate is separated by in-plane and transverse normal strain vector $\varepsilon_{b}$ and the transverse shear strain vector $\varepsilon_{s}$ expressed as follows:

$$\{ \varepsilon_{b} \} = [\varepsilon_{x} \,\,\varepsilon_{y} \,\,\varepsilon_{z} \,\,\gamma_{xy} ]^{\text{T}} ,\quad \{ \varepsilon_{s} \} = [\gamma_{xz} \,\,\gamma_{yz} ]^{\text{T}}$$

(3)

where $\varepsilon_{x}$, $\varepsilon_{y}$ and $\varepsilon_{z}$ represent the normal strains along x-, y- and z-direction, respectively; $\gamma_{xy}$ represents the in-plane shear strain, $\gamma_{xz}$ and $\gamma_{yz}$ are the transverse or out-of-plane shear strains. Making use of the displacement field given in Eq. (1) and from the linear strain–displacement relations, the strain vectors $\varepsilon_{b}$ and $\varepsilon_{s}$ defining the state of in-plane, transverse normal and transverse shear strain at any point in the SMEE plate can be expressed as

$$\{ \varepsilon_{b}^{k} \} = \{ \varepsilon_{bt} \} + [Z_{1} ]\{ \varepsilon_{rb} \} ,\quad \{ \varepsilon_{s}^{k} \} = \{ \varepsilon_{ts} \} + [Z_{2} ]\{ \varepsilon_{rs} \}$$

(4)

wherein k designates the layer number for the overall plate, the transformation matrices [Z₁] and [Z₂] are expressed as

$$\begin{aligned} \left[ {Z_{1} } \right] &= \left[ {\begin{array}{*{20}c} z & 0 & 0 & 0 & 0 \\ 0 & z & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & {2z} \\ 0 & 0 & z & 0 & 0 \\ \end{array} } \right],\quad \left[ {Z_{2} } \right] &= \left[ {\begin{array}{*{20}c} 1 & 0 & z & 0 & {z^{2} } & 0 \\ 0 & 1 & 0 & z & 0 & {z^{2} } \\ \end{array} } \right] \end{aligned}$$

(5)

while the generalized strain vectors appearing in Eq. (4) are given by

$$\{ \varepsilon_{bt} \} = \left[ {\frac{{\partial u_{0} }}{\partial x}\quad \frac{{\partial v_{0} }}{\partial y}\quad 0\quad \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right],\{ \varepsilon_{ts} \} = \left[ {\frac{{\partial w_{0} }}{\partial x}\quad \frac{{\partial w_{0} }}{\partial y}} \right]\quad {\text{and}}\quad \{ \varepsilon_{rb} \} = \left[ {\frac{{\partial \theta_{x} }}{\partial x}\quad \frac{{\partial \theta_{y} }}{\partial y}\quad \frac{{\partial \theta_{x} }}{\partial x} + \frac{{\partial v_{0} }}{\partial x}\quad \theta_{z} \quad \kappa_{z} } \right]$$

(6)

Analogous to the strain vectors given in Eq. (3), the state of stress at any point in the SMEE plate can be written as follows:

$$\{ \sigma_{b} \} \, = [\sigma_{x} \,\,\sigma_{y} \,\,\sigma_{z} \,\,\tau_{xy} ]^{\text{T}} ,\quad \{ \sigma_{s} \} \, = [\tau_{xz} \,\,\tau_{yz} ]^{\text{T}}$$

(7)

in which $\sigma_{x}$, $\sigma_{y}$ and $\sigma_{z}$ are the normal stresses along x-, y- and z-directions, respectively; $\tau_{xy}$ is the in-plane shear stress; $\tau_{{\varvec{xz}}}$ and $\tau_{yz}$ are the transverse shear stresses along xz- and yz- direction, respectively. Considering the effect of coupled fields, the constitutive equations for the SMEE plate can be expressed as follows:

$$\left\{ {\sigma_{b}^{k} } \right\} = \left[ {\bar{C}_{b}^{k} } \right]\left\{ {\varepsilon_{b}^{k} } \right\} - \left\{ {e_{b}^{k} } \right\}E_{z} - \left\{ {q_{b}^{k} } \right\}H_{z} ,\quad \left\{ {\sigma_{s}^{k} } \right\} = \left[ {\bar{C}_{s}^{k} } \right]\left\{ {\varepsilon_{s}^{k} } \right\}$$

(8a)

$$D_{z} = \left\{ {e_{b}^{k} } \right\}^{T} \left\{ {\varepsilon_{b}^{k} } \right\} + \xi_{33}^{k} E_{z} + d_{33} H_{z}$$

(8b)

$$B_{z} = \left\{ {q_{b}^{k} } \right\}^{T} \left\{ {\varepsilon_{b}^{k} } \right\} + d_{33}^{k} E_{z} + \mu_{33} H_{z}$$

(8c)

where k = 1, 2, 3 designates the layer number starting from the bottom layer of the overall SMEE plate and

$$\left[ {\bar{C}_{b}^{k} } \right] = \left[ {\begin{array}{*{20}c} {\bar{C}_{11}^{k} } & {\bar{C}_{12}^{k} } & {\bar{C}_{13}^{k} } & {\bar{C}_{16}^{k} } \\ {\bar{C}_{12}^{k} } & {\bar{C}_{22}^{k} } & {\bar{C}_{23}^{k} } & {\bar{C}_{26}^{k} } \\ {\bar{C}_{13}^{k} } & {\bar{C}_{23}^{k} } & {\bar{C}_{33}^{k} } & {\bar{C}_{36}^{k} } \\ {\bar{C}_{16}^{k} } & {\bar{C}_{26}^{k} } & {\bar{C}_{36}^{k} } & {\bar{C}_{66}^{k} } \\ \end{array} } \right],\quad \left[ {\bar{C}_{s}^{k} } \right] = \left[ {\begin{array}{*{20}c} {\bar{C}_{55}^{k} } & {\bar{C}_{45}^{k} } \\ {\bar{C}_{45}^{k} } & {\bar{C}_{44}^{k} } \\ \end{array} } \right]$$

(9)

where $\left[ {\bar{C}_{b}^{k} } \right]$ and $\left[ {\bar{C}_{s}^{k} } \right]$ are the transformed coefficient matrices, $\xi_{33}^{k}$ and $\mu_{{{33}}}$ are the dielectric constant and the magnetic permeability constant, respectively; $d_{33}$ is the electromagnetic coefficient. Since the plate is considered to be thin, the electric displacement, the electric field, the magnetic induction and the magnetic field along the z-direction are only considered and represented by D_z, E_z, B_z and H_z, respectively. The electric coefficient matrix $\left\{ {e_{b}^{k} } \right\}$ and the magnetic coefficient matrix $\left\{ {q_{b}^{k} } \right\}$ are given by

$$\left\{ {e_{b}^{k} } \right\} = \left\{ {e_{31} \,\,e_{32} \,\,e_{33} \,\,e_{36} } \right\}^{\text{T}} ,\quad \left\{ {q_{b}^{k} } \right\} = \left\{ {q_{31} \,\,q_{32} \,\,q_{33} \,\,q_{36} } \right\}^{\text{T}}$$

(10)

Employing the principle of virtual work the governing equations for the SMEE plate is established as

$$\begin{aligned} & \sum\limits_{k = 1}^{3} {\left( {\int\limits_{{\varLambda^{k} }} {\delta \left\{ {\varepsilon_{b}^{k} } \right\}\left\{ {\sigma_{b}^{k} } \right\}{\text{d}}\varLambda^{k} + } } \right.} \left. {\int\limits_{{\varLambda^{k} }} {\delta \left\{ {\varepsilon_{s}^{k} } \right\}\left\{ {\sigma_{s}^{k} } \right\}{\text{d}}\varLambda^{k} + \int\limits_{{\varLambda^{k} }} {\delta \left\{ {d_{t} } \right\}^{T} \rho^{k} \left\{ {\ddot{d}_{t} } \right\}{\text{d}}\varLambda^{k} } } } \right) - \int\limits_{{\varLambda^{t} }} {\delta E_{z}^{t} D_{z}^{t} {\text{d}}\varLambda^{t} } \\ & \quad \quad - \int\limits_{{\varLambda^{b} }} {\delta E_{z}^{b} D_{z}^{b} {\text{d}}\varLambda^{b} } - \int\limits_{{\varLambda^{m} }} {\delta H_{z}^{m} B_{z}^{m} d\varLambda^{m} } - \int\limits_{{A^{el} }} {\delta \left\{ {d_{t} } \right\}^{T} F_{t} {\text{d}}A^{el} } = 0 \\ \end{aligned}$$

(11)

where $\varLambda^{k}$ (k = 1, 2, 3) indicates the volume of the respective layer, $F_{t}$ is the applied surface traction force on the top surface area A^el, ρ^k denotes the mass density of the kth layer and $\delta$ is the symbol representing the first variation. $\varLambda^{t}$, $\varLambda^{b}$ and $\varLambda^{m}$ represent the volume of the top piezoelectric, the bottom piezoelectric and the middle magnetostrictive layer, respectively. $E_{z}^{t}$, $E_{z}^{b}$ and $D_{z}^{t}$, $D_{z}^{b}$ are the electric fields and the electric displacements of the top and bottom layers of the SMEE plate, whereas $H_{z}^{m}$ and $B_{z}^{m}$ are the magnetic field and magnetic induction in the middle layer, respectively. The transverse electric field (E_z) is related to the electric potential and the transverse magnetic field (H_z) is related to the magnetic potential in accordance with the Maxwell’s equation as follows:

$$E_{z}^{t} = - \frac{{\partial \phi^{t} }}{\partial z},\quad E_{z}^{b} = - \frac{{\partial \phi^{b} }}{\partial z}\,\,{\text{and}}\,\,H_{z}^{m} = - \frac{{\partial \psi^{m} }}{\partial z}$$

(12)

where t/b/m represents the top/bottom/middle layer of the SMEE plate, respectively, depending on the stacking sequence of the layers. It is assumed that the interfaces between the piezoelectric and magnetostrictive layers are suitably grounded. In addition, the thickness of the layers of the SMEE plate is very small. Hence, the variation of the electric potential and the magnetic potential functions can be assumed linear across the thickness of the layers. Thus, the electric potential functions $\phi^{t}$ and $\phi^{b}$, respectively, for the top and bottom piezoelectric layers while the magnetic potential distribution field $\psi^{m}$ in the magnetostrictive layer of the SMEE plate can be expressed as

$$\phi^{t} = \frac{{z - z_{b} }}{h}\phi_{1} ,\quad \phi^{b} = - \frac{{z - h_{2} }}{h}\phi_{2} \quad {\text{and}}\quad \psi^{m} = \frac{{z - h_{2} }}{h}\bar{\psi }$$

(13)

where $z_{b}$ is the z-coordinate of the bottom surface of the top piezoelectric layer, h₂ is the z-coordinate of the top surface of the bottom piezoelectric layer, $\phi_{1}$ and $\phi_{2}$ are the electric potentials on the top and the bottom surfaces of the top and the bottom layers, and $\bar{\psi }$ is the magnetic potential on the bottom surface of the middle magnetostrictive layer.

3 Finite Element Formulation for Skew Magneto-Electro-Elastic Plate

The SMEE plate is discretized by using eight nodded iso-parametric elements. Defining the coordinate of the SMEE plate as illustrated in Fig. 1b, the two opposite boundaries are lined y = 0 and y = b cos α and the two opposite skewed edges are defined by the lines x = y tan α and x = a + y tan α. In accordance with Eq. (2), the generalized displacement vectors $\left\{ {d_{ti} } \right\}$ and $\left\{ {d_{ri} } \right\}$ associated with the ith node (where, i = 1, 2, 3, …, 8) of an element can be expressed as

$$\left\{ {d_{ti} } \right\} = [u_{0i} \,\,v_{0i} \,\,w_{0i} ]^{\text{T}} \,\,{\text{and}}\,\,\left\{ {d_{ri} } \right\} = [\theta_{xi} \,\,\theta_{yi} \,\,\theta_{zi} \,\,\phi_{zi} ]^{\text{T}}$$

(14)

At any point within the element, the generalized displacement vectors $\left\{ {d_{t} } \right\}$ and $\left\{ {d_{r} } \right\}$, the magnetic potential vector $\left\{ \psi \right\}$ and the electric potential vector $\left\{ \phi \right\}$ can be expressed in terms of nodal generalized displacement vectors $\left\{ {d_{t}^{el} } \right\}$ and $\left\{ {d_{r}^{el} } \right\}$, the nodal magnetic potential vector $\left\{ {\psi^{el} } \right\}$ and the nodal electric potential vector $\left\{ {\phi^{el} } \right\}$, respectively, as follows:

$$\begin{aligned} & \left\{ {d_{t} } \right\} = [n_{t} ]\left\{ {d_{t}^{el} } \right\},\quad \left\{ {d_{r} } \right\} = [n_{r} ]\left\{ {d_{r}^{el} } \right\}, \\ & \quad \left\{ \phi \right\} = \left[ {\phi_{1} \,\,\phi_{2} } \right]^{\text{T}} = \, \left[ {n_{\phi } } \right]\left\{ {\phi^{el} } \right\}\quad {\text{and}}\quad \left\{ {\psi^{m} } \right\} = \left[ {n_{\psi }^{m} } \right]\left\{ {\psi_{m}^{el} } \right\} \\ \end{aligned}$$

(15)

where $\left[ {n_{t} } \right]$, $\left[ {n_{r} } \right]$, $\left[ {n_{\phi } } \right]$ and $\left[ {n_{\psi } } \right]$ are the (3 × 24), (4 × 32), (2 × 16) and (1 × 8) shape function matrices, respectively. The detailed matrices corresponding to shape functions are provided in Eq. (39) of “Appendix”. I_t and I_r are the (3 × 3) and (5 × 5) identity matrices, respectively. $N_{i}$ is the shape function of natural coordinate associated with the ith node. $\phi_{1i}$, $\phi_{2i}$ (where i = 1, 2, 3, …, 8) are the electric potential degrees of freedom, and $\bar{\psi }_{i}$ are the magnetic potential degrees of freedom. Using Eqs. (12)–(15), the transverse electric field for the top and the bottom layer ($E_{z}^{\text{t}}$, $E_{z}^{\text{b}}$) and the transverse magnetic field for the middle layer ($H_{z}^{\text{m}}$) are given by

$$E_{z}^{\text{t}} = - \frac{1}{h}\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\left[ {n_{\phi } } \right]\left\{ {\phi^{el} } \right\},\quad E_{z}^{\text{b}} = - \frac{1}{h}\left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]\left[ {n_{\phi } } \right]\left\{ {\phi^{el} } \right\}\,\,{\text{and}}\,\,H_{z}^{\text{m}} = - \frac{1}{h}\left[ {n_{\psi } } \right]\left\{ {\psi^{el} } \right\}$$

(16)

Now, using Eq. (4) and shape function vectors, the generalized strain vectors at any point within the element can be expressed in terms of the nodal generalized strain vectors as follows:

$$\begin{aligned} & \left\{ {\varepsilon_{bt} } \right\} = \left[ {b_{tb} } \right]\left\{ {d_{t}^{el} } \right\},\quad \left\{ {\varepsilon_{br} } \right\} = \left[ {b_{rb} } \right]\left\{ {d_{r}^{el} } \right\} \\ & \left\{ {\varepsilon_{ts} } \right\} = \left[ {b_{ts} } \right]\left\{ {d_{t}^{el} } \right\},\quad \left\{ {\varepsilon_{rs} } \right\} = \left[ {b_{rs} } \right]\left\{ {d_{r}^{el} } \right\} \\ \end{aligned}$$

(17)

in which $\left[ {b_{tb} } \right]$, $\left[ {b_{rb} } \right]$, $\left[ {b_{ts} } \right]$ and $\left[ {b_{rs} } \right]$ are the nodal strain–displacement matrices. The explicit form of the matrices is given in “Appendix”. Substituting Eqs. (4), (8), (16) and (17) into (11) and simplifying, we obtain the elemental equations of motion for the SMEE plate as follows:

$$\left[ {M^{el} } \right]\left\{ {\ddot{d}_{t}^{el} } \right\} + \left[ {k_{tt}^{el} } \right]\left\{ {d_{t}^{el} } \right\} + \left[ {k_{tr}^{el} } \right]\left\{ {d_{r}^{el} } \right\} + \left[ {k_{t\phi }^{el} } \right]\left\{ {\phi^{el} } \right\} + \left[ {k_{t\psi }^{el} } \right]\left\{ {\psi^{el} } \right\} = \left\{ {F_{t}^{el} } \right\}$$

(18)

$$\left[ {k_{tr}^{el} } \right]^{\text{T}} \left\{ {d_{t}^{el} } \right\} + \left[ {k_{rr}^{el} } \right]\left\{ {d_{r}^{el} } \right\} + \left[ {k_{r\phi }^{el} } \right]\left\{ {\phi^{el} } \right\} + \left[ {k_{r\psi }^{el} } \right]\left\{ {\psi^{el} } \right\} = 0$$

(19)

$$\left[ {k_{t\phi }^{el} } \right]^{\text{T}} \left\{ {d_{t}^{el} } \right\} + \left[ {k_{r\phi }^{el} } \right]^{\text{T}} \left\{ {d_{r}^{el} } \right\} - \left[ {k_{\phi \phi }^{el} } \right]\left\{ {\phi^{el} } \right\} = 0$$

(20)

$$\left[ {k_{t\psi }^{el} } \right]^{\text{T}} \left\{ {d_{t}^{el} } \right\} + \left[ {k_{r\psi }^{el} } \right]^{\text{T}} \left\{ {d_{r}^{el} } \right\} - \left[ {k_{\psi \psi }^{el} } \right]\left\{ {\psi^{el} } \right\} = 0$$

(21)

The matrices and the vectors appearing in Eqs. (18)–(21) are the elemental mass matrix $\left[ {M^{el} } \right]$, the elemental elastic stiffness matrices $\left[ {k_{tt}^{el} } \right]$, $\left[ {k_{tr}^{el} } \right]$ and $\left[ {k_{rr}^{el} } \right]$, the elemental electro-elastic coupling stiffness matrices and the elemental magneto-elastic coupling stiffness matrices are $\left[ {k_{t\phi }^{el} } \right]$, $\left[ {k_{r\phi }^{el} } \right]$ and $\left[ {k_{t\psi }^{el} } \right]$, $\left[ {k_{r\psi }^{el} } \right]$, respectively; $\left\{ {F_{t}^{el} } \right\}$ is the elemental mechanical load vector; $\left[ {k_{\phi \phi }^{el} } \right]$ and $\left[ {k_{\psi \psi }^{el} } \right]$ are the elemental electric and elemental magnetic stiffness matrices, respectively. The elemental matrices and vectors are detailed in Eq. (40) of “Appendix.”

3.1 Skew Boundary Transformation

In case of skew MEE plates, the supported adjacent edges of the boundary element are not parallel to the global axes (x, y, z). Hence, in order to specify the boundary conditions at the skew edges of the plate, the displacements u¹, v¹ and w¹ at any point on the skew edges of the local coordinates must be restrained along the x¹-, y¹- and z¹-direction. The boundary conditions can be specified conveniently by transforming the element matrices corresponding to the global axis to the local axis along the edges. A simple transformation relation can be expressed between the local degrees of freedom and the global degrees of freedom for the generalized displacement vectors of a point lying on the skew edges of the plate as follows:

$$\left\{ {d_{t} } \right\} = \left[ {L_{t} } \right]\left\{ {d_{t}^{1} } \right\},\quad \left\{ {d_{r} } \right\} = \left[ {L_{r} } \right]\left\{ {d_{r}^{1} } \right\}$$

(22)

$$\left\{ {d_{t}^{1} } \right\} \, = \, \left[ {u_{0}^{1} \,\,\,v_{0}^{1} \,\,\,w_{0}^{1} } \right]^{\text{T}} ,\quad \left\{ {d_{r}^{1} } \right\} = \left[ {\theta_{x}^{1} \,\,\,\theta_{y}^{1} \,\,\,\theta_{z}^{1} \,\,\,\kappa_{z}^{1} } \right]^{\text{T}} ,$$

(23)

where $\left\{ {d_{t} } \right\}$, $\left\{ {d_{r} } \right\}$ and $\left\{ {d_{t}^{l} } \right\}$, $\left\{ {d_{r}^{1} } \right\}$ are the displacements on the global and the local edge coordinate system, respectively. $\left[ {L_{t} } \right]$ and $\left[ {L_{r} } \right]$ are the transformation matrices for a node on the skew boundary and are given by

$$\left[ {L_{t} } \right] = \left[ {\begin{array}{*{20}c} c & s & 0 \\ { - s} & c & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],\quad \left[ {L_{r} } \right] = \left[ {\begin{array}{*{20}c} c & s & 0 & 0 \\ { - s} & c & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

(24)

in which $c = \cos \alpha$ and $s = \sin \alpha$, the skew angle of the plate is α. It may be noted that for the nodes which do not lie on the skew edges, the transformation from global coordinates to the local coordinates is not required. The transformation matrices in such cases are the diagonal matrices in which the values of the principal diagonal elements are unity. The elemental stiffness matrices of the element containing the nodes laying on the skew edges are given as follows:

$$\begin{aligned} & \left[ {\overline{k}_{tt}^{el} } \right] = \left[ {T_{1} } \right]^{\text{T}} \left[ {k_{tt}^{el} } \right]\left[ {T_{1} } \right],\quad \left[ {\overline{k}_{tr}^{el} } \right] = \left[ {T_{1} } \right]^{\text{T}} \left[ {k_{tr}^{el} } \right]\left[ {T_{2} } \right], \\ & \left[ {\overline{k}_{rr}^{el} } \right] = \left[ {T_{2} } \right]^{\text{T}} \left[ {k_{rr}^{el} } \right]\left[ {T_{2} } \right],\quad \left[ {M^{el} } \right] = \left[ {T_{1} } \right]^{\text{T}} \left[ {M^{el} } \right]\left[ {T_{1} } \right] \\ \end{aligned}$$

(25)

where the transformation matrices [T₁] and [T₂] are given by

$$\begin{aligned} \left[ {T_{1} } \right] & = \left[ {\begin{array}{*{20}c} {\left[ {L_{t} } \right]} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} \\ {\tilde{o}} & {\left[ {L_{t} } \right]} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} \\ {\tilde{o}} & {\tilde{o}} & {\left[ {L_{t} } \right]} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} \\ {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\left[ {L_{t} } \right]} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} \\ {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\left[ {L_{t} } \right]} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} \\ {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\left[ {L_{t} } \right]} & {\tilde{o}} & {\tilde{o}} \\ {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\left[ {L_{t} } \right]} & {\tilde{o}} \\ {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\tilde{o}} & {\left[ {L_{t} } \right]} \\ \end{array} } \right]; \\ \left[ {T_{2} } \right] & = \left[ {\begin{array}{*{20}c} {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o} } & {\left[ {L_{r} } \right]} \\ \end{array} } \right] \\ \end{aligned}$$

(26)

in which $\tilde{o}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{o}$ are the (3 × 3) and (4 × 4) null matrices, respectively, and the number of $\left[ {L_{t} } \right]$ and $\left[ {L_{r} } \right]$ matrices is equal to the number of nodes in the element. The elemental equations of motion are assembled to obtain the global equations of motion of the SMEE plate as follows:

$$\left[ M \right]\left\{ {\ddot{d}_{t} } \right\} + \left[ {k_{tt}^{g} } \right]\left\{ {d_{t} } \right\} + \left[ {k_{tr}^{g} } \right]\left\{ {d_{r} } \right\} + \left[ {k_{t\phi }^{g} } \right]\left\{ \phi \right\} + \left[ {k_{t\psi }^{g} } \right]\left\{ \psi \right\} = \left\{ {F_{t} } \right\}$$

(27)

$$\left[ {k_{tr}^{g} } \right]^{\text{T}} \left\{ {d_{t} } \right\} + \left[ {k_{rr}^{g} } \right]\left\{ {d_{r} } \right\} + \left[ {k_{r\phi }^{g} } \right]\left\{ \phi \right\} + \left[ {k_{r\psi }^{g} } \right]\left\{ \psi \right\} = 0$$

(28)

$$\left[ {{k}_{{{t}\phi }}^{{g}} } \right]^{\text{T}} \left\{ {{d}_{{t}} } \right\} + \left[ {{k}_{{{r}\phi }}^{{g}} } \right]^{\text{T}} \left\{ {{d}_{{r}} } \right\} - \left[ {{k}_{\phi \phi }^{{g}} } \right]\left\{ \phi \right\} = 0$$

(29)

$$\left[ {k_{t\psi }^{g} } \right]^{\text{T}} \left\{ {d_{t} } \right\} + \left[ {k_{r\psi }^{g} } \right]^{\text{T}} \left\{ {d_{r} } \right\} - \left[ {k_{\psi \psi }^{g} } \right]\left\{ \psi \right\} = 0$$

(30)

where $\left[ M \right]$ is the global mass matrix; $\left[ {k_{tt}^{g} } \right]$, $\left[ {k_{tr}^{g} } \right]$ and $\left[ {k_{rr}^{g} } \right]$ are the global elastic stiffness matrices; $\left[ {k_{t\phi }^{g} } \right]$ and $\left[ {k_{r\phi }^{g} } \right]$ are the global electro-elastic coupling stiffness matrices; $\left[ {k_{t\psi }^{g} } \right]$ and $\left[ {k_{r\psi }^{g} } \right]$ are the global magneto-elastic coupling stiffness matrices; $\left\{ {F_{t} } \right\}$ is the global mechanical load vector; $\left[ {\varvec{k}_{\phi \phi }^{\varvec{g}} } \right]$ and $\left[ {k_{\psi \psi }^{g} } \right]$ are the global electric and the global magnetic stiffness matrices, respectively. Solving the global equations of motion (Eqs. (28)–(30)) to obtain global generalized displacement vector $\left\{ {d_{t} } \right\}$ and $\left\{ {d_{r} } \right\}$ by condensing the global degrees of freedom for $\left\{ \phi \right\}$ and $\left\{ \psi \right\}$ in terms of $\left\{ {d_{r} } \right\}$ is as follows:

$$\begin{aligned} \left\{ \psi \right\} & = \left[ {k_{\psi \psi }^{g} } \right]^{ - 1} \left[ {k_{t\psi }^{g} } \right]^{T} \left\{ {d_{t} } \right\} + \left[ {k_{\psi \psi }^{g} } \right]^{ - 1} \left[ {k_{r\psi }^{g} } \right]^{T} \left\{ {d_{r} } \right\}, \\ \left\{ \phi \right\} & = \left[ {k_{\phi \phi }^{g} } \right]^{ - 1} \left[ {k_{t\phi }^{g} } \right]^{T} \left\{ {d_{t} } \right\} + \left[ {k_{\phi \phi }^{g} } \right]^{ - 1} \left[ {k_{r\phi }^{g} } \right]^{T} \left\{ {d_{r} } \right\}, \\ \left\{ {d_{r} } \right\} & = - \left[ {K_{3} } \right]^{ - 1} \left[ {K_{2} } \right]^{T} \left\{ {d_{t} } \right\} \\ \end{aligned}$$

(31)

Now, substituting Eq. (31) in Eq. (27) and upon simplification, we obtain the global equations of motion in terms of the global translational degrees of freedom as follows:

$$\begin{aligned} & \left[ M \right]\left\{ {\ddot{d}_{t} } \right\} + \left( {\left[ {K_{1} } \right] - \left[ {K_{2} } \right]\left[ {K_{3} } \right]^{ - 1} \left[ {K_{2} } \right]^{\text{T}} } \right)\left\{ {d_{t} } \right\} = \left\{ {F_{t} } \right\}, \\ & \left[ M \right]\left\{ {\ddot{d}_{t} } \right\} + \left[ K \right]\left\{ {d_{t} } \right\} = \left\{ {F_{t} } \right\} \\ & \quad {\text{and}}\quad \left[ K \right] = \left( {\left[ {K_{1} } \right] - \left[ {K_{2} } \right]\left[ {K_{3} } \right]^{ - 1} \left[ {K_{2} } \right]^{\text{T}} } \right) \\ \end{aligned}$$

(32)

The global matrices in Eq. (32) are provided in Eq. (41) of “Appendix.”

4 Results and Discussion

This section comprises the investigation of SMEE plate to assess its free vibration and static response characteristics. The influence of skew angle and stacking sequence on the structural behavior of the SMEE plate is explicitly studied. In addition, the influence of geometric parameters such as boundary condition and aspect ratio on the SMEE plate is thoroughly investigated. The validity of the proposed FE formulation is established considering different benchmark solutions available in the literature. The SMEE plate considered for the numerical studies consists of three layers with a magnetostrictive layer sandwiched between two piezoelectric layers forming the stacking sequence B/F/B. In the case of the F/B/F stacking sequence, the piezoelectric layer is sandwiched between the two magnetostrictive layers. The SMEE plate with three layers of equal thickness has the following geometry: a = b = 1 m and the total thickness H = 0.3 m. The material properties for the BaTiO₃ and the CoFe₂O₄ are tabulated in Table 1. The skew boundary conditions considered for the analysis of the SMEE plate are given as follows:

• (a) Simply supported boundary condition

  at x = y tanα, x = a + y tanα

  $$v_{0}^{1} = \,w_{0}^{1} = \theta_{y}^{1} = \theta_{z}^{1} = \phi^{1} = \psi^{1} = 0$$

  (33)

  at y = 0, y = b cosα

  $$u_{0} = w_{0} = \theta_{z} = \phi = \psi = 0$$

• (b) Clamped–clamped boundary condition

  at x = y tanα, x = a + y tanα

  $$u_{0}^{1} = v_{0}^{1} = w_{0}^{1} = \theta_{x}^{1} = \theta_{y}^{1} = \theta_{z}^{1} = \phi^{1} = \psi^{1} = 0$$

  (34)

  at y = 0, y = b cosα

  $$u_{0} = v_{0} = w_{0} = \theta_{x} = \theta_{y} = \theta_{z} = \phi = \psi = 0$$

• (c) Free edge boundary condition

  at x = y tanα, x = a + y tanα:

  $$u_{0}^{1} = v_{0}^{1} = w_{0}^{1} = \theta_{x}^{1} = \theta_{y}^{1} = \theta_{z}^{1} = \phi^{1} = \psi^{1} \ne 0$$

  (35)

  at y = 0, y = b cosα:

  $$u_{0} = v_{0} = w_{0} = \theta_{x} = \theta_{y} = \theta_{z} = \phi = \psi \ne 0$$

Table 1 Material properties of BaTiO₃ and CoFe₂O₄.

4.1 Validation of Present FE Model

The validity of the proposed FE formulation and the code generated are verified with the various benchmark solutions available in the literature. To the best of the authors’ knowledge, the studies pertaining to structural behavior of SMEE plate are unavailable in the open literature. Hence, the results are verified for the rectangular MEE plate reported by Naghsh and Azhari (2015). For the identical geometric parameters and material properties of Naghsh and Azhari (2015), the natural frequencies of the skew MEE plate with the skew angle α = 0 are computed for different mesh size to understand the convergence behavior in Table 2. The element employed displayed a good convergence property, and hence a 20 × 20 mesh is found to be sufficient to model the whole plate. Further, the same mesh size is employed for all subsequent analysis. In addition, the transverse shear stresses across the thickness of the SMEE plate for the B/F/B and the F/B/F stacking sequence with α = 0 are presented in Figs. 2 and 3. It may be seen from these figures that the results are in excellent agreement with those of Lage et al. (2004) and Moita et al. (2009). In addition, the FE formulation for the MEE plate can be degenerated to study the purely elastic laminated composite plates. Hence to verify the correctness of the transformation matrix generated, the free vibration behavior of skew laminated composite plate is studied. It is notable from Tables 3 and 4 that the results reported from the present FE model display a good agreement with the results available in the literature facilitating the further investigation on SMEE plates.

Table 2 Non-dimensional natural frequency modes for clamped B/F/B plate

Fig. 2

Transverse shear stress (τ_xz) across the thickness for a B/F/B, b F/B/F MEE plate (α = 0)

Fig. 3

Influence of α on au, bv, cϕ, dψ, eσ_xx, fσ_yy, gτ_xy, hτ_xz, iD_z, jB_z of the simply supported B/F/B SMEE plate (a/b = 1, H = 0.3 m)

Table 3 Normalized frequency parameter $\lambda = \omega b^{2} /\pi^{2} h(\rho /E_{2} )^{1/2}$ for the clamped laminated composite plate (a/H = 10)

Table 4 Non-dimensional frequency parameter $\lambda = \omega b^{2} /\pi^{2} h(\rho /E_{2} )^{1/2}$ for the simply supported laminated composite plate (a/H = 10)

4.2 Free Vibration Analysis of Skew Magneto-Electro-Elastic Plates

In this section, the free vibration behavior of skew magneto-electro-elastic plate is investigated. The influence of the introduced skew angle on the natural frequency of the SMEE plate is finely presented. In addition, the influence of stacking sequence and geometric parameters is extensively studied. Table 5 presents the natural frequencies for different skew angle. In addition, Table 5 also presents the influence of stacking sequence and the boundary condition on the natural frequency of the plate. The increase in skew angle increases the natural frequency of the SMEE plate. It is interesting to note that the natural frequency increases rapidly for α = 45°. This increase in natural frequency can be attributed to the reduction in the area of the SMEE plate. Also, the plate stiffness considerably increases with the increase in skew angle contributing to higher natural frequency. Further, the F/B/F-stacked SMEE plate attains a higher natural frequency than B/F/B plate. It is due to the fact that the F/B/F plate possesses larger stiffness and elastic property with two magnetostrictive layers. Furthermore, it can be noticed from Table 5 that the fully clamped plate attains the higher natural frequency over simply supported and FCFC SMEE plate. It can be attributed to the increase in flexural rigidity at the plate edges with higher constraints and hence the higher natural frequency. Consequently, Table 6 presents the corresponding mode shapes/contours for the clamped B/F/B SMEE plate at various skew angles. It can be observed that the increase in skew angle causes the modes to shift toward the corners of the plate.

Table 5 Normalized natural frequencies for SMEE plate (a = 1 m, a = b, H = 0.3 m)

Table 6 Contour plots for B/F/B clamped SMEE plate (a = 1 m, a = b, H = 0.3 m)

Influence of different aspect ratio (a/H) for various skew angles on the natural frequencies of the simply supported and fully clamped B/F/B SMEE plate is tabulated in Tables 7 and 8, respectively. Similarly, Tables 9 and 10 present the same for F/B/F SMEE plate. It may be observed from these tables (Tables 7, 8, 9, 10) that the increase in aspect ratio decreases the natural frequencies for different skew angles. It can be attributed to the thin plate which possesses lower stiffness over thick plate and hence lower natural frequency. Further, it is interesting to note that the effect of aspect ratio on the natural frequencies is significant as compared to the effects of skew angle, boundary conditions and the stacking sequences.

Table 7 Normalized natural frequencies for different aspect ratios (a = 1 m, a = b, B/F/B, SSSS)

Table 8 Normalized natural frequencies for different aspect ratios (a = 1 m, a = b, B/F/B, CCCC)

Table 9 Normalized natural frequencies for different aspect ratios (a = 1 m, a = b, F/B/F, SSSS)

Table 10 Normalized natural frequencies for different aspect ratios (a = 1 m, a = b, F/B/F, CCCC)

4.3 Static Analysis of SMEE Plates

In this section, the static analysis of the plate subjected to a sinusoidal load is presented. Equation (36) represents the sinusoidal distributed load with an applied force F₀ on the top surface of the SMEE plate (Lage et al. 2004). The geometrical parameters of the SMEE plate are similar to that of dimensions of the free vibration analysis. The results are obtained at a point x = 0.75 m, y = 0.25 m and for the nearest Gauss points to these nodes.

$$F_{t} = F_{0} \sin \left( {\frac{\pi x}{a}} \right)\sin \left( {\frac{\pi y}{b}} \right)$$

(36)

The effect of skew angle on the primary and secondary parameters is presented in Fig. 3a–j. The displacements (u and v) decrease with the increase in skew angle as depicted in Fig. 3a, b. This can be attributed to the increase in stiffness of the plate with the increase in skew angle and thereby results in lower displacements. The electric potential shown in Fig. 3c decreases with the increase in skew angle, while the magnetic potential in Fig. 3d is higher for α = 45°. The effect of skew angle on the stresses of the simply supported B/F/B SMEE plate is presented in Fig. 3e–h. It may be observed from these figures that the normal stresses (σ_xx and σ_yy) are compressive on the top layer and tensile in the bottom layer with zero stress in the midplane of the SMEE plate. The normal stress components are discontinuous at the interface of the layers of dissimilar materials. It can be attributed to the difference in material properties and displacement gradient across the thickness. It may also be noticed from these figures that the effect of skew angle on the stress components is minimum for α = 45°. A similar trend has been observed for the in-plane shear stress (τ_xy). The magnitude of transverse shear stress (τ_xz) also decreases with the increase in the skew angle. Further, it has been observed from the results that the stiffness of the SMEE plate changes with the change in skew angle, thereby directly affecting various plotted parameters. It may also be observed that the transverse shear stress (τ_xz) is zero at the top and the bottom layers of the plate while satisfying the continuity at the interface of the layers exhibiting the maximum at the midplane. It is interesting to note that the transverse shear stress (τ_xz) is significantly reduced with the increase in plate skew angle by α = 0° to α = 45°. This reduction in interlayer stresses signifies the lower the occurrence of delamination at higher skew angle. Figure 3i, j illustrate the effect of the skew angle on the electric displacement (D_z) and magnetic induction (B_z), respectively. From these figures, it may be observed that the electric displacement (D_z) varies linearly in the top and the bottom layers, while the effect of skew angle appears to be negligible in the middle layer. Electric displacement (D_z) decreases with the increase in the skew angle as the electric potential decreases for higher skew angles. A similar trend has been noticed in the behavior of the magnetic induction (B_z) also. The minimum electric displacement and magnetic induction are observed for α = 45°.

4.3.1 Effect of Geometrical Parameters and Stacking Sequence

This section includes the assessment of influence of geometric parameters such as the boundary condition and the aspect ratio on the static behavior of the SMEE plate. In addition, the effect of material stacking sequence on the static response characteristics of SMEE plate is also presented. The influence of different boundary restraints applied to the SMEE plate is presented in Fig. 4a–j. The displacements (u and v) shown in Fig. 4a, b are lower for the simply supported (SSSS) plate in comparison with the fully clamped (CCCC) plate. The increase in flexural rigidity in the plate edges contributes to the lower displacements for CCCC plate. The electric and the magnetic potential are higher for fully clamed plate as depicted in Fig. 4c, d. The stresses σ_xx and τ_xy are higher for fully clamped plate, while the stress σ_yy in the y-direction is higher for SSSS plate. The transverse shear stress is higher for fully clamped plate in comparison with SSSS plate as shown in Fig. 4h. The electric displacement is higher for CCCC plate, while the magnetic induction is seen to be higher for SSSS plate as shown in Fig. 4i, j. In addition, the effect of aspect ratio on the stresses, electric displacement and magnetic induction is investigated. Figures 5 and 6 illustrate the variation of normal stresses (σ_xx and σ_yy) for different aspect ratios for the skew angles α = 15° and 45°, respectively. From these figures, it can be observed that the normal stresses decrease with the increase in aspect ratios for the skew angles α = 15° and 45°, respectively. The in-plane shear stress (τ_xy) presented in the Fig. 7a, b shows minimal variation for all the aspect ratios and skew angles considered. The transverse shear stress (τ_xz), the electric displacement (D_z) and the magnetic induction (B_z) are presented in Figs. 8, 9 and 10, respectively. It may be noticed from these figures that the transverse shear stress (τ_xz), the electric displacement (D_z) and the magnetic induction (B_z) follow a similar trend of the normal stresses. Further, the effect of material stacking sequence on the static response characteristics of the SMEE plate is presented in Fig. 11a–j. The displacements (u and v) are higher for B/F/B plate over F/B/F plate. This can be attributed to the lower stiffness associated with B/F/B plate in comparison with F/B/F plate. The electric potential in the B/F/B SMEE plate and the magnetic potential in the F/B/F SMEE plate are observed to be constant in the middle layer, while it varies linearly in the top and the bottom. However, the electric potential in F/B/F plate and the magnetic potential in B/F/B plate are found to be zero at the top and the bottom layer. The stresses are found to be higher for B/F/B stacking sequence over F/B/F stacking. The electric displacement in the B/F/B SMEE plate and the magnetic induction in the F/B/F SMEE plate are observed to be zero in the middle layer, while it varies linearly in the top and bottom layers. However, the electric displacement in F/B/F plate and the magnetic induction in the B/F/B plate are found to be zero at the top and the bottom layers, while they varied linearly in the middle layer.

Fig. 4

Influence of boundary condition on au, bv, cϕ, dψ, eσ_xx, fσ_yy, gτ_xy, hτ_xz, iD_z, jB_z of the B/F/B SMEE plate (a/b = 1, H = 0.3 m)

Fig. 5

Normal stress (σ_xx) for different aspect ratios aα = 15°, bα = 45° (a/b = 1)

Fig. 6

Normal stress (σ_yy) for different aspect ratios aα = 15°, bα = 45° (a/b = 1)

Fig. 7

In-plane shear stress (τ_xy) for different aspect ratios aα = 15°, bα = 45° (a/b = 1)

Fig. 8

Transverse shear stress (τ_xz) for different aspect ratios aα = 15°, bα = 45° (a/b = 1)

Fig. 9

Electric displacement (D_z) for different aspect ratios aα = 15°, bα = 45° (a/b = 1)

Fig. 10

Magnetic induction (B_z) for different aspect ratios aα = 15°, bα = 45° (a/b = 1)

Fig. 11

Influence of stacking sequence on au, bv, cϕ, dψ, eσ_xx, fσ_yy, gτ_xy, hτ_xz, iD_z, jB_z of the B/F/B SMEE plate (a/b = 1, H = 0.3 m)

5 Conclusion

In this paper, a finite element analysis has been carried out to investigate the free vibration and static behavior of the layered skew magneto-electro-elastic plates. The kinematics of the SMEE plate is described by layerwise shear deformation theory. The transformation matrix between the global and local degrees of freedom for the nodes lying on the skew edges has been successfully incorporated to investigate the behavior of the SMEE plate. The natural frequencies of the SMEE plate increase with an increase in the skew angle for both the plates of B/F/B and F/B/F stacking sequence. However, for α = 45° the increase in natural frequency is rapid. In addition, F/B/F SMEE plate produces higher natural frequency over B/F/B plate. The displacements and the electric potential decreases with the increase in skew angle, while the magnetic potential is higher for α = 45°. The magnitude of the normal stresses decreases with the increase in a skew angle which may be attributed to the increase in SMEE plate stiffness with the increase in the skew angle. Further, it is observed that the transverse shear stresses in the thickness direction decrease with the increase in the skew angle, while the influence on the in-plane shear stresses is marginal. The boundary condition, the aspect ratio and the stacking sequence exhibit noticeable influence on the induced magnetic, electric and the elastic fields. The results presented here may serve as a benchmark for further analysis of the SMEE structures.

Appendix

The nodal strain–displacement matrices [b_tb], [b_rb], [b_ts] and [b_rs] appearing in the Eq. (16) are given by

$$\begin{aligned} & \left[ {b_{tb} } \right] = \left[ {b_{tb1} \,\,b_{tb2} \,\,.\,\,.\,\,.\,\,b_{tb8} } \right],\quad \left[ {b_{rb} } \right] = \left[ {b_{rb1} \,\,b_{rb2} \,\,.\,\,.\,\,.\,\,b_{rb8} } \right], \\ & \left[ {b_{ts} } \right] = \left[ {b_{ts1} \,\,b_{ts2} \,\,.\,\,.\,\,.\,\,b_{ts8} } \right]\,\,{\text{and}}\,\,\left[ {b_{rs} } \right] = \left[ {b_{rs1} \,\,b_{rs2} \,\,.\,\,.\,\,.\,\,b_{rs8} } \right] \\ \end{aligned}$$

(37)

The various sub-matrices [b_tbi], [b_rbi], [b_tsi] and [b_rsi] (i = 1, 2, 3, …, 8) are as follows

$$\left[ {b_{tbi} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial n_{i} }}{\partial x}} & 0 & 0 \\ 0 & {\frac{{\partial n_{i} }}{\partial y}} & 0 \\ {\frac{{\partial n_{i} }}{\partial y}} & {\frac{{\partial n_{i} }}{\partial x}} & 0 \\ \end{array} } \right];\left[ {b_{tsi} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial n_{i} }}{\partial x}} \\ 0 & 0 & {\frac{{\partial n_{i} }}{\partial y}} \\ \end{array} } \right];\left[ {b_{rbi} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial n_{i} }}{\partial x}} & 0 & 0 & 0 \\ 0 & {\frac{{\partial n_{i} }}{\partial y}} & 0 & 0 \\ {\frac{{\partial n_{i} }}{\partial y}} & {\frac{{\partial n_{i} }}{\partial x}} & 0 & 0 \\ 0 & 0 & {n_{i} } & 0 \\ 0 & 0 & 0 & {n_{i} } \\ \end{array} } \right];\left[ {b_{rsi} } \right] = \left[ {\begin{array}{*{20}c} {n_{i} } & 0 & 0 & 0 \\ 0 & {n_{i} } & 0 & 0 \\ 0 & 0 & {\frac{{\partial n_{i} }}{\partial x}} & 0 \\ 0 & 0 & {\frac{{\partial n_{i} }}{\partial y}} & 0 \\ 0 & 0 & 0 & {\frac{{\partial n_{i} }}{\partial x}} \\ 0 & 0 & 0 & {\frac{{\partial n_{i} }}{\partial y}} \\ \end{array} } \right]$$

(38)

The shape function matrices and vectors in Eq. (15) are given as follows:

$$\begin{aligned} \left\{ {d_{t}^{el} } \right\} &= \left[ {\left\{ {d_{t1}^{el} } \right\}^{\text{T}} \,\,\left\{ {d_{t2}^{el} } \right\}^{\text{T}} \,.\,\,.\,\,.\,\,\left\{ {d_{t8}^{el} } \right\}^{\text{T}} } \right]^{\text{T}} ,\quad \left\{ {d_{r}^{el} } \right\} = \left[ {\left\{ {d_{r1}^{el} } \right\}^{\text{T}} \,\,\left\{ {d_{r2}^{el} } \right\}^{\text{T}} \,\,.\,\,.\,\,.\,\,\left\{ {d_{r8}^{el} } \right\}^{\text{T}} } \right]^{\text{T}} , \\ \left\{ {\phi^{el} } \right\} &= \, \left\{ {\phi_{11} \,\,\phi_{21} \,\,\phi_{12} \,\,\phi_{22} \,\,.\,\,.\,\,.\,\,\,\phi_{18} \,\,\phi_{28} } \right\}^{\text{T}} \, ,\quad \left\{ {\psi^{el} } \right\} \, = \, \left\{ {\psi_{1} \,\,\psi_{2} \,\,.\,\,.\,\,.\,\,\psi_{8} } \right\}^{\text{T}} , \\ \left[ {n_{t} } \right] &= \left[ {n_{t1} \,\,n_{t2} \,\,.\,\,.\,\,.\,\,\,n_{t8} } \right]^{\text{T}} ,\quad \left[ {n_{r} } \right] = \left[ {n_{r1} \,\,n_{r2} \,\,.\,\,.\,\,.\,\,\,n_{r8} } \right]^{\text{T}} \, \\ \end{aligned}$$

$$\left[ {n_{\phi } } \right] = \left[ {\begin{array}{*{20}c} {n_{{\phi_{11} }} } & 0 & {n_{{\phi_{12} }} } & 0 & {\,\,.\,\,.\,\,.\,\,} & {n_{{\phi_{18} }} } & 0 \\ 0 & {n_{{\phi_{21} }} } & 0 & {n_{{\phi_{22} }} } & {\,\,.\,\,.\,\,.\,\,} & 0 & {n_{{\phi_{28} }} } \\ \end{array} } \right]^{\text{T}} ,\quad \left[ {n_{\psi } } \right] = \left[ {n_{\psi 1} \, n_{\psi 2} \,\,.\,\,.\,\,.\,\,\,n_{\psi 8} } \right]^{\text{T}} ,$$

$$n_{ti} = N_{i} I_{t} ,\,\,n_{ri} = N_{i} I_{r}$$

(39)

The elemental matrices and vectors appearing in Eqs. (18)–(21) are given by

$$\begin{aligned} & \left[ {k_{tt}^{el} } \right] = \left[ {k_{tb}^{el} } \right] + \left[ {k_{ts}^{el} } \right],\quad \left[ {k_{tr}^{el} } \right] = \left[ {k_{trb}^{el} } \right] + \left[ {k_{trs}^{el} } \right],\quad \left[ {k_{rr}^{el} } \right] = \left[ {k_{rrb}^{el} } \right] + \left[ {k_{rrs}^{el} } \right], \\ & \left[ {k_{t\phi }^{el} } \right] = \left[ {k_{\phi t}^{el} } \right]^{\text{T}} ,\quad \left[ {k_{t\psi }^{el} } \right]\,\, = \left[ {k_{\psi t}^{el} } \right]\,^{\text{T}} , \\ & \left[ {k_{t\phi }^{el} } \right] = \int\limits_{0}^{{a_{el} }} {\int\limits_{0}^{{b_{el} }} {\left[ {b_{tb} } \right]^{\text{T}} \left[ {D_{t\phi } } \right]} } \,\left[ {n_{\phi } } \right]{\text{d}}x\,{\text{d}}y,\quad \left[ {k_{r\phi }^{el} } \right] = \,\int\limits_{0}^{{a_{el} }} {\int\limits_{0}^{{b_{el} }} {\left[ {b_{rb} } \right]^{\text{T}} \left[ {D_{r\phi } } \right]} } \,\left[ {n_{\phi } } \right]{\text{d}}x\,{\text{d}}y, \\ & \left[ {k_{t\psi }^{el} } \right] = \int\limits_{0}^{{a_{el} }} {\int\limits_{0}^{{b_{el} }} {\left[ {b_{tb} } \right]^{\text{T}} \left[ {D_{t\psi } } \right]} } \,\left[ {n_{\psi } } \right]{\text{d}}x\,{\text{d}}y,\quad \left[ {k_{r\psi }^{el} } \right] = \,\int\limits_{0}^{{a_{el} }} {\int\limits_{0}^{{b_{el} }} {\left[ {b_{rb} } \right]^{\text{T}} \left[ {D_{r\psi } } \right]} } \,\left[ {n_{\psi } } \right]{\text{d}}x\,{\text{d}}y, \\ \end{aligned}$$

(40)

where $\left[ {D_{t\phi } } \right]$, $\left[ {D_{r\phi } } \right]$, $\left[ {D_{t\psi } } \right]$, $\left[ {D_{r\psi } } \right]$, $\left[ {D_{\phi \phi } } \right]$ and $\left[ {D_{\psi \psi } } \right]$ are the rigidity matrices appearing in Eq. (40) are given as follows:

$$\begin{aligned} & \left[ {D_{t\phi } } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left\{ {e_{b} } \right\}\frac{1}{h}\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]{\text{d}}z }+ \int\limits_{{h_{1} }}^{{h_{2} }} {\left\{ {e_{b} } \right\}\frac{1}{h}\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]{\text{d}}z} ,\quad \left[ {D_{t\psi } } \right] = \int\limits_{{h_{2} }}^{{h_{3} }} {\left\{ {q_{b} } \right\}\frac{1}{h}} {\text{d}}z, \\ & \left[ {D_{r\phi } } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {z_{1} } \right]^{T} \left\{ {e_{b} } \right\}\frac{1}{h}\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]{\text{d}}z }+ \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {z_{1} } \right]^{T} \left\{ {e_{b} } \right\}\frac{1}{h}\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]{\text{d}}z} ,\quad \left[ {D_{r\psi } } \right] = \int\limits_{{h_{2} }}^{{h_{3} }} {\left[ {z_{1} } \right]^{T} \left\{ {q_{b} } \right\}\frac{1}{h}} {\text{d}}z \\ & \left[ {D_{\phi \phi } } \right] = \frac{{\xi_{33} }}{h}\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],\quad D_{\psi \psi } = \frac{1}{h}\mu_{33} \\ \end{aligned}$$

The global matrices in Eq. (32) are given as follows:

$$\begin{aligned} & \left[ {K_{1} } \right] = \left[ {k_{tt}^{g} } \right] + \left[ {k_{t\phi }^{g} } \right]\left[ {k_{\phi \phi }^{g} } \right]^{ - 1} \left[ {k_{t\phi }^{g} } \right]^{\text{T}} + \left[ {k_{t\psi }^{g} } \right]\left[ {k_{\psi \psi }^{g} } \right]^{ - 1} \left[ {k_{t\psi }^{g} } \right]^{\text{T}} , \\ & \left[ {K_{2} } \right] = \left[ {k_{tr}^{g} } \right] + \left[ {k_{t\phi }^{g} } \right]\left[ {k_{\phi \phi }^{g} } \right]^{ - 1} \left[ {k_{r\phi }^{g} } \right]^{\text{T}} + \left[ {k_{t\psi }^{g} } \right]\left[ {k_{\psi \psi }^{g} } \right]^{ - 1} \left[ {k_{r\psi }^{g} } \right]^{\text{T}} , \\ & \left[ {K_{3} } \right] = \left[ {k_{rr}^{g} } \right] + \left[ {k_{r\phi }^{g} } \right]\left[ {k_{\phi \phi }^{g} } \right]^{ - 1} \left[ {k_{r\phi }^{g} } \right]^{\text{T}} + \left[ {k_{r\psi }^{g} } \right]\left[ {k_{\psi \psi }^{g} } \right]^{ - 1} \left[ {k_{r\psi }^{g} } \right]^{\text{T}} . \\ \end{aligned}$$

(41)