Vibration Analysis of Thick Functionally Graded Micro-plates Using HOSNDPT and Modified Couple Stress Theory

Abstract

This paper develops a micro-scale vibration analysis of micro-plates using higher-order shear and normal deformable plate theory in conjunction with modified couple stress theory. The present model includes one material length scale parameter which takes into account the size effects. The equations of motions and boundary conditions are derived using Hamilton’s principle. Analytical solutions for the free vibration problem of simply supported rectangular micro-plates are obtained. Numerical results are presented to illustrate the effect of small scale on the dynamic response of functionally graded micro-plates. The results show that the size-dependent effect increases the stiffness of the micro-plate and consequently increases the natural frequencies.

1 Introduction

Functionally graded materials (FGMs) are non-homogeneous composites that identify with their smooth and continuous variations in one or more directions. They are usually a combination of two different materials. Most popular FGMs are made of two components: one is metal and the other is ceramic. This combination is in order to achieve a composition with specific characteristics. FGMs have many advantages such as improved stress distribution, high thermal resistance, high toughness and reduced stress intensity factor. Recently, FGMs have found many applications in micro- and nano-scale devices and systems. Some of these applications are thin films (Fu et al. 2003; Lu et al. 2011), atomic force microscopes (AFMs) (Rahaeifard et al. 2009), micro- and nano-electromechanical systems (MEMS and NEMS) (Witvrouw and Mehta 2005; Lee et al. 2006) and so on. As the material size scales reduce to the micron scales, the stiffness and strength of materials increase because of material size effect. It is well known that classical continuum theories do not include the size effect in micro-scale structures. In order to overcome this deficiency, many higher-order theories such as classical couple stress theory with two material length scale parameters (Mindlin and Tiersten 1962; Toupin 1962; Koiter 1964), strain gradient theory with three material length scale parameters (Lam et al. 2003), micro-polar theory (Eringen 1967), non-local elasticity theory (Eringen 1972), surface elasticity (Gurtin et al. 1998) and modified couple stress theory with one material length scale parameter (Yang et al. 2002) have been developed to characterize the size effect in micro-scale structures. Based on the modified couple stress theory, many size-dependent beam and plate models have been developed to consider the size effects in small-scale structures. Park and Gao (2006) developed Euler–Bernoulli beam model for bending analysis of micro-beams. Ma et al. (2008) used Timoshenko beam model for micro-beams. Asghari et al. (2010) considered the Von-Karman nonlinear strains in the Timoshenko beam model. Euler–Bernoulli beam model for buckling analysis of axially loaded micro-beams was utilized by Akgöz and Civalek (2011). Their model was employed by Kong et al. (2008) and Kahrobaiyan et al. (2010) to study the vibration of micro-beams. Ke and Wang (2011) developed a Timoshenko beam model to study the size effect on dynamic stability of functionally graded (FG) micro-beams. Tsiatas (2009) first developed a Kirchhoff plate model (CPT) for static analysis of micro-plates. Yin et al. (2010) and Jomehzadeh et al. (2011) used the model presented by Tsiatas (2009) to study the vibration of micro-plates. This model was used by Akgöz and Civalek (2012) to study the vibration of nano-plates. Asghari and Taati (2013) dealt with classical (Kirchhoff) plate theory (CPT) of FG micro-plates. On the other hand, CPT does not consider shear deformation effect, so it provides accurate results for thin homogeneous plates only and is not suitable for thick plates. Using CPT for moderately thick plates leads to overestimation of results. Ma et al. (2011) and Ke et al. (2012) used the first-order shear deformation theory (FSDT) to develop a size-dependent model for accounting the shear deformation effects. In view of difficulties in determining shear correction factor, FSDT is not a convenient model, whereas it predicts sufficiently accurate results for moderately thick plates. Roque et al. (2013) used modified couple stress theory with meshless method to study the bending of simply supported isotropic micro-plates. Eshraghi et al. (2016) introduced solution methods capable of treating static bending and free vibration problems involving thermally loaded functionally graded annular and circular micro-plates using modified couple stress theory. Thai and Vo (2013) studied the static and dynamic behavior of functionally graded micro-plates. They used modified couple stress theory and sinusoidal shear deformation theory.

Behavior of thick structures in macro- and micro-scales was studied by some researchers (Arbind et al. 2014; Akgöz and Civalek 2015, 2017). Batra and Vidoli (2002) used virtual work principle to determine higher-order shear and normal deformable plate theory for thick plates with linear elastic incompressible anisotropic material. No shear correction factor was used, and vibration analysis of simply supported rectangular plates was investigated. The proposed higher-order shear and normal deformable plate theory is the closest theory to the three-dimensional elasticity solution. According to this theory, Legendre polynomials in thickness direction are used to approximate the displacement field components. Ghayesh et al. (2017) investigated the vibration analysis of geometrically imperfect three-layered shear deformable micro-beams. They considered both hardening and softening nonlinear behavior. Xiao et al. (2008) used meshless local Petrov–Galerkin method with radial basis function to study the static behavior of thick laminated composite elastic plates. They applied higher-order shear and normal deformable plate theory and considered different boundary conditions. Mohseni et al. (2017) studied the bending analysis of micro-plates based on the higher-order shear and normal deformable plate theory. They considered functionally graded distribution of material properties through the thickness.

In this paper, thick plates’ model is developed for free vibration analysis of rectangular FG micro-plates using modified couple stress theory. Variational formulation based on Hamilton’s principle is used in order to obtain the equations of motions and boundary conditions. A solution is determined for FG micro-plates with all edges simply supported (Navier solution). The natural frequencies are obtained for rectangular micro-plates with different material length scale parameters, various thickness ratios, various aspect ratios and some power law indices. The results indicate that the size length scale parameter has a significant effect when the thickness of the micro-plate becomes small.

2 Theoretical Formulation

2.1 Modified Couple Stress Theory

The modified couple stress theory which was proposed by Yang et al. (2002) is a modification of the classical couple stress theory. According to this theory, the virtual strain energy of a linear elastic micro-plate can be expressed as

$$\delta U = \int_{V} {\left( {\sigma_{ij} \delta \varepsilon_{ij} + m_{ij} \delta \chi_{ij} } \right){\text{d}}V}$$

(1)

where σ_ij are the Cartesian components of the stress tensor, ɛ_ij are the components of the strain tensor, m_ij are the components of deviatoric part of the symmetric couple stress tensor and χ_ij are the components of symmetric curvature tensor, so that

$$\chi_{ij} = \frac{1}{2}\left( {\frac{{\partial \theta_{i} }}{{\partial x_{j} }} + \frac{{\partial \theta_{j} }}{{\partial x_{i} }}} \right)\quad i,j = 1,2,3$$

(2)

where θ_i are the components of rotation vector that in terms of displacement components are

$$\theta_{1} = \frac{1}{2}\left( {\frac{{\partial u_{3} }}{{\partial x_{2} }} - \frac{{\partial u_{2} }}{{\partial x_{3} }}} \right)$$

(3a)

$$\theta_{2} = \frac{1}{2}\left( {\frac{{\partial u_{1} }}{{\partial x_{3} }} - \frac{{\partial u_{3} }}{{\partial x_{1} }}} \right)$$

(3b)

$$\theta_{3} = \frac{1}{2}\left( {\frac{{\partial u_{2} }}{{\partial x_{1} }} - \frac{{\partial u_{1} }}{{\partial x_{2} }}} \right)$$

(3c)

Also u₁, u₂ and u₃ are the Cartesian components of displacement field in x₁, x₂ and x₃ direction, respectively.

2.2 Kinematics

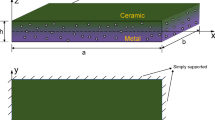
Consider a functionally graded (FG) micro-plate as shown in Fig. 1, where x₁x₂-plane coincides with the middle surface of the plate and the x₃-axis is perpendicular to this plane. As shown in Fig. 1, l₁ is the length of the plate along x₁ direction, l₂ is the width of the plate along x₂ direction and h is the thickness of the plate along x₃ direction. Using prescribed Cartesian coordinate, the infinitesimal deformations and displacement field of FG micro-plate based on the higher-order shear and normal deformable plate theory (HOSNDPT) are described as (Batra and Vidoli 2002)

$$u_{i} (x_{1} ,x_{2} ,x_{3} ,t) = v_{\alpha } (x_{1} ,x_{2} ,x_{3} ,t)\delta_{i\alpha } + w(x_{1} ,x_{2} ,x_{3} ,t)\delta_{i3} \quad \alpha = 1,2$$

(4)

where

$$v_{\alpha } (x_{1} ,x_{2} ,x_{3} ,t) = L_{a} (x_{3} )v_{\alpha }^{a} (x_{1} ,x_{2} ,t)$$

(5a)

$$w(x_{1} ,x_{2} ,x_{3} ,t) = L_{a} (x_{3} )w^{a} (x_{1} ,x_{2} ,t)$$

(5b)

and a = 0, 1, 2, …, k. Also, L_a(x₃) are the orthonormal Legendre polynomials with the following properties as

$$L^{\prime}_{a} (x_{3} ) = D_{ab} L_{b} (x_{3} )$$

(6)

where L ^′ _a (x₃) is the first derivative of the orthonormal Legendre polynomial with respect to x₃.

Fig. 1

Geometry of FG micro-plate

Matrix D shows the matrix of differentiation coefficients. Hence, for k = 7, the general matrix D is defined as follows:

$$\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {\sqrt 3 } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\sqrt {15} } & 0 & 0 & 0 & 0 & 0 & 0 \\ {\sqrt 7 } & 0 & {\sqrt {35} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {3\sqrt 3 } & 0 & {3\sqrt 7 } & 0 & 0 & 0 & 0 \\ {\sqrt {11} } & 0 & {\sqrt {35} } & 0 & {3\sqrt {11} } & 0 & 0 & 0 \\ 0 & {\sqrt {39} } & 0 & {\sqrt {91} } & 0 & {\sqrt {143} } & 0 & 0 \\ {\sqrt {15} } & 0 & {5\sqrt 3 } & 0 & {3\sqrt {15} } & 0 & {\sqrt {195} } & 0 \\ \end{array} } \right]$$

(7)

According to Einstein’s notation, repeated indices are summed even if they appear as a subscript and a superscript.

Hence, by considering the linear form of Von-Karman relations for strain–displacement equations, they are simplified as

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right) \quad \ i,j=1,2,3$$

(8)

and also,

$$v_{1} = L_{a} (x_{3} )v_{1}^{a}$$

(9a)

$$v_{2} = L_{a} (x_{3} )v_{2}^{a}$$

(9b)

$$w = L_{a} (x_{3} )w^{a}$$

(9c)

2.3 Constitutive Relations

As explained earlier, it is assumed that the micro-plate is made of functionally graded materials where material properties are expressed by the power law function in the thickness direction as

$$\varGamma (x_{3} ) = (\varGamma_{c} - \varGamma_{m} )\left( {\frac{1}{2} + \frac{{x_{3} }}{h}} \right)^{N} + \varGamma_{m}$$

(10)

In the above equation, $\varGamma_{c}$ and $\varGamma_{m}$ are the values of a typical material property, such as Young’s modulus (E), density (ρ) or Lamè constants (λ, μ) of the ceramic and metal parts, respectively. In addition, N is the power law index denoting the volume fraction of the exponent. Constitutive relations for a linear elastic micro-plate in modified couple stress theory are

$$\sigma_{ij} = 2\mu \varepsilon_{ij} + \lambda \varepsilon_{kk} \delta_{ij}$$

(11)

$$\varepsilon_{kk} = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}$$

(12)

$$m_{ij} = 2\mu l^{2} \chi_{ij}$$

(13)

where ɛ_kk is the dilatation strain tensor and δ_ij is Kronecker delta. Also, Lamè constants, μ and λ in terms of engineering constants, are $\mu = \frac{{E(x_{3} )}}{2(1 + \nu )}$ and $\lambda = \frac{{E(x_{3} )\nu }}{(1 + \nu )(1 - 2\nu )}$. It must be noted that the Poisson’s ratio (ν) of FG micro-plate is considered to be constant due to its small variation through the thickness of the micro-plate. In Eq. (13), l is called the material length scale parameter which is regarded as a material property measuring the effect of couple stress. This parameter can be determined from torsion test of slim cylinder (Chong et al. 2001) or bending test of thin beams (Lam et al. 2003).

2.4 Equations of Motion

Hamilton’s principle is used herein to derive the equations of motion and boundary conditions (Reddy 2002). Hence,

$$\int_{0}^{T} {\left( {\delta U + \delta W - \delta K} \right){\text{d}}T} = 0$$

(14)

where U is the strain energy, W is the work done by external forces, K is the kinetic energy and T denotes time.

Using the variational approach, variation of strain energy δU is given by

$$\begin{aligned} \delta U = & \int_{\varOmega } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left[ {\left( {\sigma_{11} \delta \varepsilon_{11} + \sigma_{22} \delta \varepsilon_{22} + \sigma_{33} \delta \varepsilon_{33} + \sigma_{12} \delta \gamma_{12} + \sigma_{13} \delta \gamma_{13} + \sigma_{23} \delta \gamma_{23} } \right) + \left( {m_{11} \delta \chi_{11} + m_{22} \delta \chi_{22} } \right.} \right.} } \\ & \left. {\left. { + \,m_{33} \delta \chi_{33} + \,2m_{12} \delta \chi_{12} + 2m_{13} \delta \chi_{13} + 2m_{23} \delta \chi_{23} } \right)} \right]{\text{d}}x_{1} {\text{d}}x_{2} {\text{d}}x_{3} \\ \end{aligned}$$

(15)

so that

$$\begin{aligned} \delta U = & \int_{\varOmega } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\left[ {\sigma_{11} L_{a} (x_{3} )\delta v_{1,1}^{a} + \sigma_{22} L_{a} (x_{3} )\delta v_{2,2}^{a} + \sigma_{33} D_{ab} L_{b} (x_{3} )\delta w^{a} + \sigma_{12} \left( {L_{a} (x_{3} )\delta v_{1,2}^{a} + L_{a} (x_{3} )\delta v_{2,1}^{a} } \right)} \right.} \right.} } \\ & \left. { + \,\sigma_{13} \left( {D_{ab} L_{b} (x_{3} )\delta v_{1}^{a} + L_{a} (x_{3} )\delta w_{,1}^{a} } \right) + \sigma_{23} \left( {D_{ab} L_{b} (x_{3} )\delta v_{2}^{a} + L_{a} (x_{3} )\delta w_{,2}^{a} } \right)} \right] + \left[ {\frac{1}{2}m_{11} \left( {L_{a} (x_{3} )\delta w_{,12}^{a} } \right.} \right. \\ & \left. { - \,D_{ab} L_{b} (x_{3} )\delta v_{2,1}^{a} } \right) + \frac{1}{2}m_{22} \left( {D_{ab} L_{b} (x_{3} )\delta v_{1,2}^{a} - L_{a} (x_{3} )\delta w_{,12}^{a} } \right) + \frac{1}{2}m_{33} \left( {D_{ab} L_{b} (x_{3} )\delta v_{2,12}^{a} } \right. \\ & \left. { - \,D_{ab} L_{b} (x_{3} )\delta v_{1,2}^{a} } \right) + \frac{1}{2}m_{12} \left( {L_{a} (x_{3} )\delta w_{,22}^{a} - D_{ab} L_{b} (x_{3} )\delta v_{2,2}^{a} + D_{ab} L_{b} (x_{3} )\delta v_{1,1}^{a} - L_{a} (x_{3} )\delta w_{,11}^{a} } \right) \\ & + \,\frac{1}{2}m_{13} \left( {D_{ab} L_{b} (x_{3} )\delta w_{,2}^{a} - D_{ab} D_{bc} L_{c} (x_{3} )\delta v_{2}^{a} + L_{a} (x_{3} )\delta v_{2,11}^{a} - L_{a} (x_{3} )\delta v_{1,12}^{a} } \right) \\ & \left. {\left. { + \,\frac{1}{2}m_{23} \left( {D_{ab} D_{bc} L_{c} (x_{3} )\delta v_{1}^{a} - D_{ab} L_{b} (x_{3} )\delta w_{,1}^{a} - L_{a} (x_{3} )\delta v_{2,12}^{a} - L_{a} (x_{3} )\delta v_{1,22}^{a} } \right)} \right]} \right\}{\text{d}}x_{1} {\text{d}}x_{2} {\text{d}}x_{3} \\ \end{aligned}$$

(16)

Consider the following force and moment resultants:

$$M_{\alpha \beta }^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma_{\alpha \beta } L_{a} (x_{3} ){\text{d}}x_{3} }$$

(17a)

$$T_{i}^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma_{i3} L_{a} (x_{3} ){\text{d}}x_{3} }$$

(17b)

$${\mathcal{M}}_{\alpha \beta }^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {m_{\alpha \beta } L_{a} (x_{3} ){\text{d}}x_{3} }$$

(17c)

$$\tau_{i}^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {m_{i3} L_{a} (x_{3} ){\text{d}}x_{3} }$$

(17d)

Substituting relations (17) in Eq. (16) and simplifying the results leads to

$$\begin{aligned} \delta U = & \int_{\varOmega } {\left[ {\left( {M_{11}^{a} \delta v_{1,1}^{a} + M_{22}^{a} \delta v_{2,2}^{a} + T_{33}^{b} D_{ab} \delta w^{a} + M_{12}^{a} \delta v_{1,2}^{a} + M_{12}^{a} \delta v_{2,1}^{a} + T_{1}^{b} D_{ab} \delta v_{1}^{a} + T_{1}^{a} \delta w_{,1}^{a} + T_{2}^{b} D_{ab} \delta v_{2}^{a} } \right.} \right.} \\ & \left. { + \,T_{2}^{b} \delta w_{,2}^{a} } \right) + \frac{1}{2}\left( {{\mathcal{M}}_{11}^{a} \delta w_{,12}^{a} - {\mathcal{M}}_{11}^{b} D_{ab} \delta v_{2,1}^{a} + {\mathcal{M}}_{22}^{b} D_{ab} \delta v_{1,2}^{a} - {\mathcal{M}}_{22}^{a} \delta w_{,12}^{a} + \tau_{3}^{b} D_{ab} \delta v_{2,1}^{a} - \tau_{3}^{b} D_{ab} \delta v_{1,2}^{a} } \right. \\ & + \,{\mathcal{M}}_{12}^{a} \delta w_{,22}^{a} - {\mathcal{M}}_{12}^{b} D_{ab} \delta v_{2,2}^{a} + {\mathcal{M}}_{12}^{b} D_{ab} \delta v_{1,1}^{a} - {\mathcal{M}}_{12}^{a} \delta w_{,11}^{a} + \tau_{1}^{b} D_{ab} \delta w_{,2}^{a} - \tau_{1}^{c} D_{ab} D_{bc} \delta v_{2}^{a} + \tau_{1}^{a} \delta v_{2,11}^{a} \\ & \left. {\left. { - \,\tau_{1}^{a} \delta v_{1,12}^{a} + \tau_{2}^{c} D_{ab} D_{bc} \delta v_{1}^{a} - \tau_{2}^{b} D_{ab} \delta w_{,1}^{a} - \tau_{2}^{a} \delta v_{2,12}^{a} - \tau_{2}^{a} \delta v_{1,22}^{a} } \right)} \right]{\text{d}}x_{1} {\text{d}}x_{2} {\text{d}}x_{3} \\ \end{aligned}$$

(18)

Also, variation of the work done by external forces can be obtained as (Reddy and Kim 2012)

$$\begin{aligned} \delta W = & \int_{V} {\left( {\bar{f}_{1} \delta v_{1} + \bar{f}_{2} \delta v_{2} + \bar{f}_{3} \delta w + \bar{c}_{1} \delta \theta_{1} + \bar{c}_{2} \delta \theta_{2} + \bar{c}_{3} \delta \theta_{3} } \right){\text{d}}x_{1} {\text{d}}x_{2} {\text{d}}x_{3} } + \int_{{\varOmega^{ + } }} {\left( {q_{1}^{t} \delta v_{1} + q_{2}^{t} \delta v_{2} + q_{3}^{t} \delta w} \right){\text{d}}x_{1} {\text{d}}x_{2} } \\ & + \,\int_{{\varOmega^{ - } }} {\left( {q_{1}^{b} \delta v_{1} + q_{2}^{b} \delta v_{2} + q_{3}^{b} \delta w} \right){\text{d}}x_{1} {\text{d}}x_{2} } + \int_{s} {\left( {\bar{t}_{1} \delta v_{1} + \bar{t}_{2} \delta v_{2} + \bar{t}_{3} \delta w} \right){\text{d}}s} \\ \end{aligned}$$

(19)

In Eq. (19), $\bar{f}_{i} ,\,\,\bar{c}_{i} ,\,\,q_{i}^{{}}$ and $\bar{t}_{i} \,(i = 1,2,3)$ are body forces (per unit volume), body couples (per unit volume), distributed transverse loads on the plate surfaces (superscripts t and b indicate top and bottom) and surface forces, respectively. Also V, Ω and S denote the volume, surface and lateral surface of the micro-plate, respectively. Replacing Eqs. (9) in Eq. (19) leads to the following relation:

$$\begin{aligned} \delta W = & \int\limits_{\varOmega } {\int\limits_{ - h/2}^{h/2} {\left( {\left( {\bar{f}_{1} L_{a} (x_{3} )\delta v_{1}^{a} + \bar{f}_{2} L_{a} (x_{3} )\delta v_{2}^{a} + \bar{f}_{3} L_{a} (x_{3} )\delta w^{a} } \right) + \frac{1}{2}\bar{c}_{1} \left( {L_{a} (x_{3} )\delta w_{,2}^{a} - D_{ab} L_{b} (x_{3} )\delta v_{2}^{a} } \right)} \right.} } \\ & \left. { + \,\frac{1}{2}\bar{c}_{2} \left( {D_{ab} L_{b} (x_{3} )\delta v_{1}^{a} - L_{a} (x_{3} )\delta w_{,1}^{a} } \right) + \frac{1}{2}\bar{c}_{3} \left( {L_{a} (x_{3} )\delta v_{2,1}^{a} - L_{a} (x_{3} )\delta v_{1,2}^{a} } \right)} \right){\text{d}}x_{1} {\text{d}}x_{2} {\text{d}}x_{3} \\ & + \,\int_{\varOmega } {\left( {q_{1}^{t} L_{a} \left( {\frac{h}{2}} \right)\delta v_{1}^{a} + q_{2}^{t} L_{a} \left( {\frac{h}{2}} \right)\delta v_{2}^{a} + q_{3}^{t} L_{a} \left( {\frac{h}{2}} \right)\delta w^{a} + q_{1}^{b} L_{a} \left( { - \frac{h}{2}} \right)\delta v_{1}^{a} + q_{2}^{b} L_{a} \left( { - \frac{h}{2}} \right)\delta v_{2}^{a} } \right.} \\ & \left. { + \,q_{3}^{b} L_{a} \left( { - \frac{h}{2}} \right)\delta w^{a} } \right){\text{d}}x_{1} {\text{d}}x_{2} + \int_{s} {\left( {\bar{t}_{1} L_{a} (x_{3} )\delta v_{1}^{a} + \bar{t}_{2} L_{a} (x_{3} )\delta v_{2}^{a} + \bar{t}_{3} L_{a} (x_{3} )\delta w^{a} } \right){\text{d}}s} \\ \end{aligned}$$

(20)

so that

$$\begin{aligned} \delta W = & \int_{\varOmega } {\left( {F_{1}^{a} \delta v_{1}^{a} + F_{2}^{a} \delta v_{2}^{a} + F_{3}^{a} \delta w^{a} + \frac{1}{2}c_{1}^{a} \delta w_{,2}^{a} - \frac{1}{2}c_{1}^{b} D_{ab} \delta v_{2}^{a} + \frac{1}{2}c_{2}^{b} D_{ab} \delta v_{1}^{a} - \frac{1}{2}c_{2}^{a} \delta w_{,1}^{a} + \frac{1}{2}c_{3}^{a} \delta v_{2,1}^{a} } \right.} \\ & \left. { - \,\frac{1}{2}c_{3}^{a} \delta v_{1,2}^{a} } \right){\text{d}}x_{1} {\text{d}}x_{2} + \int_{s} {\left( {t_{1}^{a} \delta v_{1}^{a} + t_{2}^{a} \delta v_{2}^{a} + t_{3}^{a} \delta w^{a} } \right){\text{d}}s} \\ \end{aligned}$$

(21)

It should be noted that variation of work done by the external forces is simplified using Reddy’s definitions (Reddy and Kim 2012) as

$$f_{i}^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {L_{a} (x_{3} )\bar{f}_{i} {\text{d}}x_{3} }$$

(22a)

$$t_{i}^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {L_{a} (x_{3} )\bar{t}_{i} {\text{d}}x_{3} }$$

(22b)

$$c_{i}^{a} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {L_{a} (x_{3} )\bar{c}_{i} {\text{d}}x_{3} }$$

(22c)

$$F_{i}^{a} = q_{i}^{t} L_{a} \left( {\frac{h}{2}} \right) + q_{i}^{b} L_{a} \left( { - \frac{h}{2}} \right) + f_{i}^{a}$$

(22d)

Also, variation of kinetic energy is expressed as

$$\delta K = \int_{\varOmega } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left( {\frac{{\partial v_{1} }}{\partial t}\frac{{\partial \delta v_{1} }}{\partial t} + \frac{{\partial v_{2} }}{\partial t}\frac{{\partial \delta v_{2} }}{\partial t} + \frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}} \right){\text{d}}x_{1} {\text{d}}x_{2} {\text{d}}x_{3} } }$$

(23)

Replacing Eqs. (9) in Eq. (23) and simplifying the relations results in

$$\delta K = \int_{\varOmega } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left( {L_{a} (x_{3} )\dot{v}_{1}^{a} L_{b} (x_{3} )\delta \dot{v}_{1}^{b} + L_{a} (x_{3} )\dot{v}_{2}^{a} L_{b} (x_{3} )\delta \dot{v}_{2}^{b} + L_{a} (x_{3} )w_{1}^{a} L_{b} (x_{3} )\delta w_{1}^{b} } \right){\text{d}}x_{`} {\text{d}}x_{2} {\text{d}}x_{3} } }$$

(24)

Let

$$R_{ab} = R_{ba} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho L_{a} (x_{3} )L_{b} (x_{3} ){\text{d}}x_{3} }$$

(25)

Therefore, Eq. (24) is simplified as

$$\delta K = \int_{\varOmega } {R_{ab} \left( {\dot{v}_{1}^{a} \delta \dot{v}_{1}^{b} + \dot{v}_{2}^{a} \delta \dot{v}_{2}^{b} + \dot{w}^{a} \delta \dot{w}^{b} } \right){\text{d}}x_{1} {\text{d}}x_{2} }$$

(26)

By substituting Eqs. (18), (21) and (26) into Eq. (14) and integrating by parts, the following equations of motion for FG micro-plates based on the HOSNDPT and modified couple stress theory are determined:

$$\begin{aligned} & \delta v_{1}^{a} :\left( {R_{ba} \ddot{v}_{1}^{b} + T_{1}^{b} D_{ab} + \frac{1}{2}\tau_{2}^{c} D_{ab} D_{bc} + F_{1}^{a} + \frac{1}{2}c_{2}^{b} D_{ab} - \frac{{\partial M_{11}^{a} }}{{\partial x_{1} }} - \frac{1}{2}\frac{{\partial {\mathcal{M}}_{12}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{{\partial M_{12}^{a} }}{{\partial x_{2} }} - \frac{1}{2}\frac{{\partial {\mathcal{M}}_{22}^{b} }}{{\partial x_{2} }}D_{ab} } \right. \\ & \quad \left. { + \,\frac{1}{2}\frac{{\partial \tau_{3}^{b} }}{{\partial x_{2} }}D_{ab} + \frac{1}{2}\frac{{\partial c_{3}^{a} }}{{\partial x_{2} }} - \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial \tau_{1}^{a} }}{{\partial x_{1} }}} \right) - \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial \tau_{2}^{a} }}{{\partial x_{2} }}} \right)} \right) = 0 \\ \end{aligned}$$

(27a)

$$\begin{aligned} & \delta v_{2}^{a} :\left( {R_{ba} \ddot{v}_{2}^{b} + T_{2}^{b} D_{ab} - \frac{1}{2}\tau_{1}^{c} D_{ab} D_{bc} + F_{2}^{a} - \frac{1}{2}c_{1}^{b} D_{ab} - \frac{{\partial M_{12}^{a} }}{{\partial x_{1} }} + \frac{1}{2}\frac{{\partial {\mathcal{M}}_{11}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{{\partial M_{22}^{a} }}{{\partial x_{2} }} + \frac{1}{2}\frac{{\partial {\mathcal{M}}_{12}^{b} }}{{\partial x_{2} }}D_{ab} } \right. \\ & \quad \left. { - \,\frac{1}{2}\frac{{\partial \tau_{3}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{1}{2}\frac{{\partial c_{3}^{a} }}{{\partial x_{1} }} + \frac{1}{2}\frac{\partial }{{\partial x_{1} }}\left( {\frac{{\partial \tau_{1}^{a} }}{{\partial x_{1} }}} \right) + \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial \tau_{2}^{a} }}{{\partial x_{1} }}} \right)} \right) = 0 \\ \end{aligned}$$

(27b)

$$\begin{aligned} & \delta w^{a} :\left( {R_{ba} \ddot{w}^{b} + T_{3}^{b} D_{ab} + F_{3}^{a} + \frac{1}{2}\frac{{\partial \tau_{2}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{1}{2}\frac{{\partial \tau_{1}^{b} }}{{\partial x_{2} }}D_{ab} + \frac{1}{2}\frac{{\partial c_{2}^{a} }}{{\partial x_{1} }} - \frac{1}{2}\frac{{\partial c_{1}^{a} }}{{\partial x_{2} }} - \frac{{\partial T_{1}^{a} }}{{\partial x_{1} }} - \frac{{\partial T_{2}^{a} }}{{\partial x_{2} }} - \frac{1}{2}\frac{\partial }{{\partial x_{1} }}\left( {\frac{{\partial {\mathcal{M}}_{12}^{a} }}{{\partial x_{1} }}} \right)} \right. \\ & \quad \left. { + \,\frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial {\mathcal{M}}_{11}^{a} }}{{\partial x_{1} }}} \right) - \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial {\mathcal{M}}_{22}^{a} }}{{\partial x_{1} }}} \right) + \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial {\mathcal{M}}_{12}^{a} }}{{\partial x_{2} }}} \right)} \right) = 0 \\ \end{aligned}$$

(27c)

For an FG micro-plate without body forces, body couples and surface tractions, equations of motion are reduced to

$$\begin{aligned} & \delta v_{1}^{a} :\left( {R_{ba} \ddot{v}_{1}^{b} + T_{1}^{b} D_{ab} + \frac{1}{2}\tau_{2}^{c} D_{ab} D_{bc} - \frac{{\partial M_{11}^{a} }}{{\partial x_{1} }} - \frac{1}{2}\frac{{\partial {\mathcal{M}}_{12}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{{\partial M_{12}^{a} }}{{\partial x_{2} }} - \frac{1}{2}\frac{{\partial {\mathcal{M}}_{22}^{b} }}{{\partial x_{2} }}D_{ab} + \frac{1}{2}\frac{{\partial \tau_{3}^{b} }}{{\partial x_{2} }}D_{ab} } \right. \\ & \quad \left. { - \,\frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial \tau_{1}^{a} }}{{\partial x_{1} }}} \right) - \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial \tau_{2}^{a} }}{{\partial x_{2} }}} \right)} \right) = 0 \\ \end{aligned}$$

(28a)

$$\begin{aligned} & \delta v_{2}^{a} :\left( {R_{ba} \ddot{v}_{2}^{b} + T_{2}^{b} D_{ab} - \frac{1}{2}\tau_{1}^{c} D_{ab} D_{bc} - \frac{{\partial M_{12}^{a} }}{{\partial x_{1} }} + \frac{1}{2}\frac{{\partial {\mathcal{M}}_{11}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{{\partial M_{22}^{a} }}{{\partial x_{2} }} + \frac{1}{2}\frac{{\partial {\mathcal{M}}_{12}^{b} }}{{\partial x_{2} }}D_{ab} - \frac{1}{2}\frac{{\partial \tau_{3}^{b} }}{{\partial x_{1} }}D_{ab} } \right. \\ & \left. {\quad + \,\frac{1}{2}\frac{\partial }{{\partial x_{1} }}\left( {\frac{{\partial \tau_{1}^{a} }}{{\partial x_{1} }}} \right) + \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial \tau_{2}^{a} }}{{\partial x_{1} }}} \right)} \right) = 0 \\ \end{aligned}$$

(28b)

$$\begin{aligned} & \delta w^{a} :\left( {R_{ba} \ddot{w}^{b} + T_{3}^{b} D_{ab} + \frac{1}{2}\frac{{\partial \tau_{2}^{b} }}{{\partial x_{1} }}D_{ab} - \frac{1}{2}\frac{{\partial \tau_{1}^{b} }}{{\partial x_{2} }}D_{ab} - \frac{{\partial T_{1}^{a} }}{{\partial x_{1} }} - \frac{{\partial T_{2}^{a} }}{{\partial x_{2} }} - \frac{1}{2}\frac{\partial }{{\partial x_{1} }}\left( {\frac{{\partial {\mathcal{M}}_{12}^{a} }}{{\partial x_{1} }}} \right) + \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial {\mathcal{M}}_{11}^{a} }}{{\partial x_{1} }}} \right)} \right. \\ & \quad \left. { - \,\frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial {\mathcal{M}}_{22}^{a} }}{{\partial x_{1} }}} \right) + \frac{1}{2}\frac{\partial }{{\partial x_{2} }}\left( {\frac{{\partial {\mathcal{M}}_{12}^{a} }}{{\partial x_{2} }}} \right)} \right) = 0 \\ \end{aligned}$$

(28c)

Using the variational approach and Hamilton’s principle, boundary conditions are derived besides the equations of motion. Hence, they are

$$\left( {t_{1}^{a} + \left( {M_{11}^{a} + \frac{1}{2}{\mathcal{M}}_{12}^{b} D_{ab} + \frac{1}{2}\frac{{\partial \tau_{1}^{a} }}{{\partial x_{1} }}} \right)n_{1} } \right) + \left( {M_{12}^{a} + \frac{1}{2}{\mathcal{M}}_{22}^{b} D_{ab} - \frac{1}{2}\tau_{3}^{b} D_{ab} - \frac{1}{2}c_{3}^{a} + \frac{1}{2}\frac{{\partial \tau_{2}^{a} }}{{\partial x_{2} }}} \right)n_{2} = 0$$

(29a)

$$\left( {t_{2}^{a} + \left( {M_{12}^{a} - \frac{1}{2}{\mathcal{M}}_{11}^{b} D_{ab} + \frac{1}{2}\tau_{3}^{b} D_{ab} + \frac{1}{2}c_{3}^{a} - \frac{1}{2}\frac{{\partial \tau_{1}^{a} }}{{\partial x_{1} }}} \right){\mathbf{n}}_{1} + \left( {M_{22}^{a} - \frac{1}{2}{\mathcal{M}}_{12}^{b} D_{ab} - \frac{1}{2}\frac{{\partial \tau_{2}^{a} }}{{\partial x_{2} }}} \right){\mathbf{n}}_{2} } \right) = 0$$

(29b)

$$\left( {t_{3}^{a} + \left( {T_{1}^{a} - \frac{1}{2}\tau_{2}^{b} D_{ab} - \frac{1}{2}c_{2}^{a} + \frac{1}{2}\frac{{\partial {\mathcal{M}}_{12}^{a} }}{{\partial x_{1} }}} \right){\mathbf{n}}_{1} } \right) + \left( {T_{2}^{a} + \frac{1}{2}\tau_{1}^{b} D_{ab} + \frac{1}{2}c_{1}^{a} - \frac{1}{2}\frac{{\partial {\mathcal{M}}_{11}^{a} }}{{\partial x_{1} }} + \frac{1}{2}\frac{{\partial {\mathcal{M}}_{22}^{a} }}{{\partial x_{1} }} - \frac{1}{2}\frac{{\partial {\mathcal{M}}_{12}^{a} }}{{\partial x_{2} }}} \right){\mathbf{n}}_{2} = 0$$

(29c)

where $({\mathbf{n}}_{1} ,{\mathbf{n}}_{2} ,{\mathbf{n}}_{3} )$ are unit outward normal vectors in (x₁, x₂, x₃) directions, respectively.

Clearly, when the size effects are neglected, i.e., l = 0, the present model is reduced to the relations for FG plate shown by Sheikholeslami and Saidi (2013).

Further, considering harmonic motion, the solutions of Eqs. (28) are assumed as

$$v_{\alpha }^{a} (x_{1} ,x_{2} ,t) = e^{i\omega t} V_{\alpha }^{a} (x_{1} ,x_{2} )$$

(30a)

$$w^{a} (x_{1} ,x_{2} ,t) = e^{i\omega t} W^{a} (x_{1} ,x_{2} )$$

(30b)

where $i = \sqrt { - 1}$ and ω is the frequency of motion.

Replacing Eqs. (30) in Eqs. (28), system homogenous equations are determined where the Eigen values are the natural frequency.

2.5 Analytical Solutions

In this section, an analytical solution for free vibration of simply supported rectangular micro-plates is presented. Based on the Navier approach, the displacement components are approximated using double series solution as

$$V_{1}^{a} (x_{1} ,x_{2} ) = \sum\limits_{m,n = 0}^{\infty } {\tilde{V}_{1}^{amn} \cos \left( {\frac{{m\pi x_{1} }}{{l_{1} }}} \right)\sin \left( {\frac{{n\pi x_{2} }}{{l_{2} }}} \right)}$$

(31a)

$$V_{2}^{a} (x_{1} ,x_{2} ) = \sum\limits_{m,n = 0}^{\infty } {\tilde{V}_{2}^{amn} \sin \left( {\frac{{m\pi x_{1} }}{{l_{1} }}} \right)\cos \left( {\frac{{n\pi x_{2} }}{{l_{2} }}} \right)}$$

(31b)

$$W^{a} (x_{1} ,x_{2} ) = \sum\limits_{m,n = 0}^{\infty } {\tilde{W}^{amn} sin\left( {\frac{{m\pi x_{1} }}{{l_{1} }}} \right)sin\left( {\frac{{n\pi x_{2} }}{{l_{2} }}} \right)}$$

(31c)

where m and n are integers that show the mode numbers and $(\tilde{V}_{1}^{amn} ,\tilde{V}_{2}^{amn} ,\tilde{W}^{amn} )$ are coefficients of the components of the displacement field.

According to the Navier solution, the components of the displacement field are extended using double trigonometric series so that the boundary conditions of the plate (Eqs. 29) are satisfied.

Using Eqs. (31), a homogenous system of equations is obtained. Solving the resulted characteristic equation leads to determining the natural frequencies.

3 Numerical Results and Discussions

In order to validate the results, a comparison is made with the available results in the literature. Hence, consider a simply supported micro-plate made of epoxy with the following properties (Reddy 2011):

$$E = 14.4\;{\text{GPa}},\rho = 1220\;{\text{kg/m}}^{3} ,\nu = 0.3,l = 17.6 \times 10^{ - 6} \;{\text{m}}$$

(32)

In Tables 1 and 2, dimensionless natural frequency $\bar{\omega } = \omega \frac{{l_{1}^{2} }}{h}\sqrt {\frac{\rho }{E}}$ of simply supported homogeneous square micro-plate is compared with the shown natural frequencies by Yin et al. (2010) (based on classical plate theory (CPT)) and by Thai and Kim (2013) (based on third-order shear deformable plate theory (TSDT)), respectively. Also, in Table 3 the non-dimensional natural frequencies $\tilde{\omega } = \omega h\sqrt {\frac{{\rho_{c} }}{{E_{c} }}}$ obtained from HOSNDPT and the results based on the TSDT (Thai and Kim 2013) are compared, while the order of Legendre polynomial is 5. According to these tables, it is clear that there is a good agreement between the presented results and those shown in the literature.

Table 1 Comparison of dimensionless natural frequency $\bar{\omega }$ for square homogeneous micro-plate

Table 2 Comparison of dimensionless natural frequency $\bar{\omega }$ for square homogeneous micro-plate

Table 3 Comparison of dimensionless natural frequency $\bar{\omega }$ for square FG micro-plate

In order to have a numerical study, it is assumed that FG micro-plate is made of alumina and aluminum with the following material properties (Salamat-Talab et al. 2012):

$$E_{m} = 70\;{\text{GPa}},\rho_{m} = 2702\;{\text{kg/m}}^{3} ,E_{c} = 380\;{\text{GPa}},\rho_{c} = 3800\;{\text{kg/m}}^{3} ,\nu = 0.3$$

(33)

Also, the material length scale parameter is 17.6 × 10⁻⁶ m (Lam et al. 2003). In Table 4, the convergence of results versus different orders of Legendre polynomial is tabulated. Based on the table, it is clear that for thin micro-plates results converge for small values of k, but for thick micro-plates, they converge for bigger values of k; thus, in the following, fifth-order theory of HOSNDPT is used.

Table 4 Convergence of natural frequency $\bar{\omega }$ versus variation of Legendre polynomial order

In Tables 5, 6 and 7, non-dimensional natural frequencies are presented where variations of different parameters are considered. Based on the tables, it is clear that considering material length scale parameter leads to increasing the stiffness of micro-plate; therefore, dimensionless natural frequencies increase as the material length scale parameter increases. Also, it is inferred that increasing the power law index, N, leads to decreasing the dimensionless natural frequencies. According to the tables, aspect ratio of the micro-plate, l₁/l₂,  affects the responses. As shown in Table 7, the natural frequency is influenced by the side-to-thickness ratio (l₁/h).

Table 5 Dimensionless natural frequency $\bar{\omega }$ of square FG micro-plate

Table 6 Dimensionless natural frequency $\bar{\omega }$ for rectangular homogeneous (N = 0) micro-plate

Table 7 Dimensionless natural frequency $\bar{\omega }$ for rectangular FG micro-plate

Figure 2 shows the effect of the material length scale parameter l on dimensionless natural frequency $\bar{\omega }$ of a square micro-plate. According to this figure, increasing the material length scale parameter increases the dimensionless natural frequency. Also, as the length of micro-plate increases, the dimensionless natural frequency increases. According to this figure, variation of results is more apparent for plates with thickness near to the material length scale parameter.

Fig. 2

Effect of the material length scale parameter l on dimensionless natural frequency $\bar{\omega }$ for a square micro-plate

The effect of material properties on dimensionless natural frequency $\bar{\omega }$ of a square FG micro-plate is depicted in Fig. 3. Based on the figure, increasing the power law index reduces the dimensionless natural frequency of FG micro-plate. Also, changes in dimensionless natural frequencies are more considerable for micro-plates with thickness/material length scale ratio less than 3.

Fig. 3

Effect of the material properties on the dimensionless natural frequency $\bar{\omega }$ of a square FG micro-plate

Figure 4 shows the effect of the length-to-thickness ratio on dimensionless natural frequency $\bar{\omega }$ of a square micro-plate. According to this figure, variation of natural frequencies is more apparent for smaller values of length-to-thickness ratio.

Fig. 4

Effect of the thickness ratio l₁/h on the dimensionless natural frequency $\bar{\omega }$ of a square micro-plate

4 Conclusions

In the present paper, free vibration analysis of thick functionally graded micro-plates was investigated. Higher-order shear and normal deformable plate theory in conjunction with modified couple stress theory with one length scale parameter was used. Comparing the results with the available results in the literature shows that the presented model and solution have good agreement with the other results. An analytical solution for free vibration of simply supported FG micro-plate was presented. According to the numerical results, it is inferred that the inclusion of micro-structures affects the micro-plate behavior so that the equivalent flexural rigidity increases. Thus, modeling micro-plates with classical plate theories leads to inaccurate results. Also, it is seen that increasing the material length scale parameter increases the non-dimensional natural frequencies. In addition, increasing the power law index reduces the dimensionless natural frequencies. Numerical study indicates that while the thickness of micro-plate is the same as the material length scale parameter, variation of result is more apparent. This change in results vanishes as the ratio of thickness to material length scale parameter increases. As depicted in figures, increasing the aspect ratio increases the dimensionless natural frequencies.