On the Nonlinear Vibrations of Polymer Nanocomposite Rectangular Plates Reinforced by Graphene Nanoplatelets: A Unified Higher-Order Shear Deformable Model

Abstract

This paper presents a unified higher-order shear deformable plate model to numerically examine the nonlinear vibration behavior of thick and moderately thick polymer nanocomposite rectangular plates reinforced by graphene platelets (GPLs). Four distribution patterns of graphene nanoplatelet nanofillers across the plate thickness are considered. The effective material properties of graphene platelet-reinforced polymer (GPL-RP) nanocomposite plate are approximately calculated by employing the modified Halpin–Tsai model and rule of mixture. Using a generalized displacement field, a unified mathematical formulation is derived based on Hamilton’s principle in conjunction with von Kármán geometrical nonlinearity. By selecting appropriate shape functions, the proposed unified nonlinear plate model can be reduced to that on the basis of Mindlin, Reddy, parabolic, trigonometric and exponential shear deformation plate theories. The investigation of nonlinear vibration behavior is performed by employing a multistep numerical solution approach. In this regard, the discretization process is done through the generalized differential quadrature method. Then, the discretized governing equations are solved by employing the numerical-based Galerkin technique, periodic time differential operators and pseudo-arc length continuation algorithm. A detailed parametric study is carried out to examine the effect of GPL distribution pattern, weight fraction, geometry of GPL nanofillers and boundary constraints on the nonlinear vibration characteristics of the GPL-RP nanocomposite rectangular plates.

1 Introduction

New advanced materials with improved properties play a key role in developing various fields of technology. Polymer nanocomposites have been recognized as excellent materials that can be used in novel devices and systems for applications in industrial and engineering fields (Hule and Pochan 2007; Zhang et al. 2012; Lee et al. 2013; Kurahatti et al. 2010). The discovery of fullerene in 1985 by Kroto et al. (1985) and then carbon nanotubes (CNTs) in 1991 by Iijima (1991), graphene by Novoselov et al. (2004) and its associated allotropes (Fennimore et al. 2003) resulted in the revolutionary changes in the area of polymer nanocomposites. Because of the outstanding mechanical, electrical, chemical and physical properties of graphene and CNTs (Allen et al. 2007; Bianco et al. 2005; Ji et al. 2010; Stankovich et al. 2006; Qiu et al. 2015), these discoveries led to focusing both the scientific and industrial communities on the CNTs and graphenes (Kiani 2014, 2015a, b; Ansari et al. 2018) as well as the carbon nanotubes- and graphenes-reinforced polymer nanocomposites. For instance, these advanced materials are among the best candidates to employ in manufacturing the wind turbines, medical implants and light gasoline tanks (Du and Cheng 2012; Das and Prusty 2013) and temperature sensors (Das and Prusty 2013; Potts et al. 2011). However, some problems such as bundling of CNTs caused by the van der Waals interaction between the nanotubes and walls, and difficulty in uniformly dispersing the CNTs in polymer matrices resulted in increasing use of the two-dimensional allotropes of carbon such as graphenes as reinforcements within the polymers. This considerable attention is due to their relatively low fabrication cost, excellent dispersion, superior mechanical properties and large surface area as well as the stronger bonding between the polymers and graphene nanofillers (Fu et al. 2008; Terrones and Terrones 2003).

The investigations on the polymer nanocomposite structures can be categorized mainly into two classes of analyses. In the first group, many studies have been carried out on both static and dynamic behaviors of various structures such as beams, plates and shells reinforced by CNTs on the basis of the linear and nonlinear models (Tornabene et al. 2016; Zhu et al. 2012; Rafiee et al. 2013; Alibeigloo 2013; Ke et al. 2013; Ansari et al. 2014a; Jam and Kiani 2015; Wattanasakulpong and Ungbhakorn 2013; Moradi-Dastjerdi et al. 2013; Ansari et al. 2016a, b). The number of investigations fitting to the first class is quite large. The second group is concerned with the analysis of the linear and nonlinear mechanical behaviors of polymer nanocomposite structures reinforced by graphene nanoplatelets. Compared to the first class, the second class of analysis, associated with the analysis of graphene nanoplatelet-reinforced structures, is not large. Herein, the paper reviews a few studies belonging to the aforementioned two classes of analysis.

Starting with the first class of analyses, by employing the Timoshenko beam model, Ritz method and a direct iterative approach, the nonlinear free vibration of FG-CNTRC beams was examined by Ke et al. (Ke et al. 2010). On the basis of the first-order shear deformation theory and element-free IMLS-Ritz method, the postbuckling of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) rectangular plates with edges elastically restrained against translation and rotation was examined by Zhang et al. (2016). Gholami et al. (2017) employed the higher-order shear deformation beam theory and an efficient multistep numerical solution approach in order to examine the imperfection sensitivity on the nonlinear resonant dynamics of imperfect FG-CNTRC beams with different edge supports. Zhang et al. (2014) contributed to the field by examining the nonlinear bending of FG-CNTRC cylindrical panels, employing the kp-Ritz method with kernel particle function. Ansari et al. (2015) utilized a numerical solution strategy to analyze the forced vibration of FG-CNTRC plates under the harmonic transverse loading. Fan and Wang (2016) employed the higher-order shear deformation theory and two-step perturbation technique so as to investigate the nonlinear bending and postbuckling of matrix cracked hybrid-laminated FG-CNTRC rectangular plates. Based on the third-order shear deformation plate theory and von Kármán hypothesis, Ansari and Gholami (2016) numerically investigated various parameters such as volume fraction of CNTs, distribution pattern of CNTs and boundary conditions on the frequency- and force-response curve of thick and moderately thick FG-CNTRC rectangular plates. Wu et al. (2017) contributed to the field by analyzing the effect of geometric imperfection on the postbuckling equilibrium path of FG-CNTRC beams.

A limited research work has been dedicated to the second class of analysis, conserved with the mechanical behaviors of polymer nanocomposite structures reinforced by graphene platelets (Shen et al. 2017a, b; c; d). In this regard, the buckling and postbuckling of graphene platelet-reinforced polymer (GPL-RP) nanocomposite Timoshenko beams was analyzed by Yang et al. (2017). Kitipornchai et al. (2017) contributed to the field by examining the influences of porosity distributions on the free vibration and elastic buckling of GPL-RP nanocomposite porous beams. The dynamic stability of GPL-RP Timoshenko beams in thermal environments was investigated by Wu et al. (2017). Furthermore, Chen et al. (2017) investigated the geometrically nonlinear free vibration and postbuckling of GPL-RP nanocomposite porous beams. By proposing a linear first-order shear deformable plate model, Song et al. (2017) analyzed the free and forced vibration of GPL-RP nanocomposite rectangular plates using Navier solution technique. Feng et al. (2017) used the Timoshenko beam theory and Ritz method to investigate the nonlinear bending of GPL-RP nanocomposite beams. Within the framework of the first-order shear deformation theory, Wu et al. (2017) used a differential quadrature-based iteration technique to study the thermal buckling and postbuckling of GPL-RP nanocomposite rectangular plates. On the basis of the three-dimensional elasticity theory, an analytical solution approach was provided by Yang et al. (2017a; b) in order to examine the thermoelastic bending of GPL-RP nanocomposite rectangular, circular annular plates under the uniform transverse load in the thermal environment. Gholami and Ansari (2017) developed a sinusoidal shear deformable plate model to numerically investigate the nonlinear bending of GPL-RP nanocomposite rectangular plates with various boundary conditions. Moreover, Feng et al. (2017) utilized the Ritz method in conjunction with a direct iterative scheme to study the nonlinear free vibration of GPL-RP nanocomposite Timoshenko beams.

There are various plate theories which can be employed to provide the equations of motion of nanocomposite plates. In this regard, one can mention the Kirchhoff or classical plate theory, Mindlin or first-order shear deformation plate theory and higher-order shear deformation plate theories. Each of these theories includes some advantages and disadvantages. For instance, the Kirchhoff plate theory, as the simplest plate theory, is established on the basis of the Kirchhoff–Love’s assumptions. Applying these assumptions results in neglecting the impacts of transverse shear deformation and rotary inertia and makes this theory suitable only for thin plates. Therefore, the shear deformation plate theories are usually used in order to describe the mechanical characteristics of the thick and moderately thick plates. One can categorize the shear deformation theories into the first- and higher-order theories. To accurately use the first-order shear deformation plate theory, a shear correction factor which depends on different quantities such as boundary, loading and geometries should be used. Although the use of higher-order shear deformation plate theories results in more complicated equation, the need for any shear correction factor is eliminated. Furthermore, unlike the first-order shear deformation theory, these theories satisfy the zero transverse shear stress conditions on the upper and lower plate surfaces. Hence, the higher-order shear deformation theories are quite interesting in analyzing the thick and moderately thick plates. Some of the proposed higher-order shear deformation theories existing in the literature include the Reddy plate theory (Reddy 1984), parabolic shear deformation plate theory, trigonometric shear deformation plate theory (Touratier 1991) and exponential shear deformation plate theory (Karama et al. 2003).

To the best of the authors’ knowledge, to date, no work can be found in the open literature about the nonlinear free vibration analysis of GPL-RP nanocomposite rectangular plates with various edge conditions on the basis of the higher-order shear deformation plate theory. Hence, in this study, the nonlinear vibration of thick and moderately thick GPL-RP nanocomposite rectangular plates with various edge supports is numerically examined by proposing a unified higher-order shear deformable plate model and constructing the backbone curve as the nonlinear frequency ratio versus the maximum vibration amplitude. Four distribution patterns of GPL nanofillers across the plate thickness are considered. The effective material properties of GPL-RP nanocomposite plate are computed using the modified Halpin–Tsai model and rule of mixture. Afterward, the GPL-RP nanocomposite rectangular plate is modeled on the basis of a unified higher-order shear deformation theory through use of the von Kármán geometric nonlinearity taking into account the effects of rotary inertia and transverse shear deformation. The nonlinear governing equations and associated boundary conditions are developed via the Hamilton’s principle. The proposed plate model can be degenerated to that on the basis of Mindlin, Reddy, parabolic, trigonometric and exponential shear deformation plate theories. In the following, to solve the nonlinear vibration problem, the achieved nonlinear partial differential equations are transformed into a system of nonlinear algebraic equations by employing a multistep numerical solution approach including the generalized differential quadrature (GDQ) method, Galerkin technique and time periodic discretization and then solved via the pseudo-arc length continuation algorithm to obtain the backbone curve of GPL-RP nanocomposite. The influences of GPL distribution pattern, weight fraction, geometry of GPL nanofillers and boundary conditions on the natural frequency and backbone curve of the GPL-RP nanocomposite rectangular plates are studied in detail.

This paper is organized as follows: in Sect. 2, first, the effective material properties of GPL-RP nanocomposites are calculated. Then, a unified nonlinear mathematical formulation of FG GPL-RP nanocomposite rectangular plates on the basis of a generalized higher-order shear deformation plate theory is presented in Sect. 2. A numerical multistep solution approach for geometrically nonlinear vibration analysis of FG GPL-RP nanocomposite plates is developed in Sect. 3. Numerical results and discussion are given in Sect. 4, and the final section discusses the concluding remarks.

2 Unified Nonlinear Higher-Order Shear Deformable Plate Model

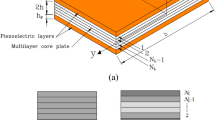
Consider a FG GPL-RP nanocomposite plate with length a, width b and thickness h made of the polymer matrix and GPLs nanofillers as illustrated in Fig. 1. It is assumed that the FG GPL-RP nanocomposite plate is made of even N_L layers with same thickness h_L= h/N_L. In each individual layer, the uniform or random dispersion can be considered for the GPLs. Furthermore, in order to have a FG distribution, it is assumed that the GPL weight fraction changes layer-wisely through the thickness of the GPL-RP nanocomposite plate. Moreover, it should be remarked that in general, no chemical bonding exists between a graphene nanoplatelet and the surrounding polymer matrix. In this case, only non-bonded electrostatic and van der Waals (vdW) interactions are considered between a graphene nanoplatelet and the surrounding polymer matrix. Electrostatic interactions can be neglected in comparison with vdW interactions, due to the fact that vdW interactions contribute more significantly in three higher orders of magnitude than electrostatic energy. Furthermore, the nanofiller used in this study consists of graphene nanoplatelet and surrounding interphase generated due to non-bonded van der Waals interaction between graphene and polymer matrix (For more details, refer to Mahmoodi and Vakilifard 2017; Shokrieh et al. 2017; Shokrieh and Rafiee 2010; Mortazavi et al. 2013).

Fig. 1

Schematic view of a GPL-RP nanocomposite plate

In this section, first, the effective material properties of GPL-RP nanocomposites are discussed and then the process of development of a unified nonlinear higher-order shear deformable plate model for FG GPL-RP nanocomposite rectangular plates is explained.

2.1 Effective Material Properties of the GPL-RP Nanocomposites

In this subsection, the effective material properties of GPL-RP nanocomposites are achieved. In this regard, it is assumed that the GPL nanofillers can be distributed through the thickness of plates as four distribution patterns, namely U-GPLRC, X-GPLRC, O-GPLRC and A-GPLRC. The schematic view of these four distribution patterns is illustrated in Fig. 2. For the U-GPLRC pattern, the GPL content in all layers is the same, while in the case of X-GPLRC pattern, the highest GPL nanofillers located on both top and bottom surfaces of the GPL-RP nanocomposite plate and the middle-plane includes the lowest GPL contents. Furthermore, in the case of the A-GPLRC distribution pattern, the GPL weight fraction gradually increases from the top surface so that the bottom surface includes the highest GPL nanofillers. Also, for the O-GPLRC distribution pattern, the middle-plane includes the highest GPL weight fraction and both top and bottom planes contain the minimum GPL contents.

Fig. 2

Schematic view of various GPL distribution patterns

For various GPL distribution patterns, the volume fractions of GPLs of the kth layer can be considered as follows Yang et al. (2017), Song et al. (2017):

$${\text{U}} - {\text{GPLRC}}:\quad\quad V_{GPL}^{\left(k \right)}= V_{\text{GPL}}^{*},$$

(1a)

$${\text{X}} - {\text{GPLRC}}:\quad\quad V_{GPL}^{\left(k \right)}=2V_{\text{GPL}}^{*} \left| {2k - N_{\text{L}} - 1} \right|/N_{\text{L}},$$

(1b)

$${\text{O}} - {\text{GPLRC}}:\quad\quad V_{GPL}^{\left(k \right)}=2V_{\text{GPL}}^{*} \left({1 - \left| {2k - N_{\text{L}} - 1} \right|/N_{\text{L}}} \right),$$

(1c)

$${\text{A}} - {\text{GPLRC}}:\quad\quad V_{GPL}^{\left(k \right)}=V_{\text{GPL}}^{*} \left({2k - 1} \right)/N_{\text{L}},$$

(1d)

where $k=1,2, \ldots,N_{\text{L}}$. Also, $V_{\text{GPL}}^{*}$ signifies the total volume fraction of GPLs which can be calculated as

$$V_{\text{GPL}}^{*}=\frac{{w_{\text{GPL}}}}{{w_{\text{GPL}} + \left({1 - w_{\text{GPL}}} \right)\left({\rho_{\text{GPL}}/\rho_{\text{m}}} \right)}},$$

(2)

in which ρ_m and ρ_GPL stand for the mass densities of matrix and GPLs, respectively. Also, w_GPL is the GPL weight fraction.

The material properties of nanocomposites reinforced with a low content of GPLs can be achieved by the modified Halpin–Tsai model (Affdl and Kardos 1976; Hull and Clyne 1996; Harris 1986). For nanocomposites reinforced with a low content of GPLs, the accuracy of this modified micromechanics model for estimating the material properties of PLRCs is validated by the experimental results provided by Rafiee et al. (2009). By utilizing the Halpin–Tsai micromechanics technique, the effective Young’s modulus of GPL-RP nanocomposites can be approximately computed as follows Affdl and Kardos (1976), Hull and Clyne (1996), Harris (1986):

$$E_{\text{eff}}=\frac{3}{8}E_{\text{L}} + \frac{5}{8}E_{\text{T}},$$

(3)

in which E_L and E_T stand for the longitudinal and transverse moduli for a unidirectional lamina. The Halpin–Tsai model can be utilized to approximately calculate these moduli as follows Affdl and Kardos (1976):

$$E_{\text{L}}=\frac{{1 + \xi_{\text{L}} \eta_{\text{L}} V_{\text{GPL}}}}{{1 - \eta_{\text{L}} V_{\text{GPL}}}}E_{\text{m}},E_{\text{T}}=\frac{{1 + \xi_{T} \eta_{\text{T}} V_{\text{GPL}}}}{{1 - \eta_{T} V_{\text{GPL}}}}E_{\text{m}},$$

(4)

where the parameters η_L and η_T are computed as

$$\eta_{\text{L}}=\frac{{E_{\text{GPL}}/E_{\text{m}} - 1}}{{E_{\text{GPL}}/E_{\text{m}} + \xi_{\text{L}}}},\eta_{\text{T}}=\frac{{E_{\text{GPL}}/E_{\text{m}} - 1}}{{E_{\text{GPL}}/E_{\text{m}} + \xi_{\text{T}}}},$$

(5)

In Eq. (5), the Young’s modulus of the polymer matrix and GPLs are denoted by E_m and E_GPL, respectively. Moreover, the parameters ξ_L and ξ_T are obtained as

$$\xi_{\text{L}}=2\left({\frac{{a_{\text{GPL}}}}{{h_{\text{GPL}}}}} \right),\xi_{\text{T}}=2\left({\frac{{b_{\text{GPL}}}}{{h_{\text{GPL}}}}} \right),$$

(6)

where a_GPL, b_GPL and h_GPL are, respectively, the average length, width and thickness of GPLs.

Furthermore, by implementing the rule of mixture, the effective mass density ρ_ef and effective Poisson’s ratio ν_eff are achieved as follows:

$$\rho_{\text{eff}}=\rho_{\text{m}} V_{\text{m}} + \rho_{\text{GPL}} V_{\text{GPL}},$$

(7a)

$$\nu_{\text{eff}}=\nu_{\text{m}} V_{\text{m}} + \nu_{\text{GPL}} V_{\text{GPL}},$$

(7b)

in which ρ_m, ν_m, ρ_GPL and ν_GPL are, respectively, the mass density and Poisson’s ratio corresponding to the polymer matrix and GPLs. It is remarked that in present investigation, the subscripts “m” and “GPL” refer to the matrix and GPLs, respectively.

2.2 Geometrically Nonlinear Governing Equations

In this subsection, a unified geometrically nonlinear higher-order shear deformable plate model for the GPL-RP nanocomposite rectangular plates is developed. The GPL-RP nanocomposite rectangular plate is defined in a Cartesian coordinate system $\left({0 \le x_{1} \le a,0 \le x_{2} \le b, - h/2 \le x_{3} \le h/2} \right)$ where x₁ and x₂ are the direction along with the length and width of plate, respectively, and x₃ is perpendicular to the in-plane surface and points outwards. The displacement vector of a given point located on the GPL-RP nanocomposite rectangular plate is considered as the following unified form:

$${\mathbf{u}}\left({t,x_{1},x_{2},x_{3}} \right)=\tilde{u}_{i} {\mathbf{e}}_{i}=\left({u_{\alpha} - x_{3} w_{,\alpha} + \chi \left({x_{3}} \right)\left({\psi_{\alpha} + w_{,\alpha}} \right)} \right){\mathbf{e}}_{\alpha} + w{\mathbf{e}}_{3}.$$

(8)

in which $\tilde{u}_{i};\left({i=1,2,3} \right)$ indicate the elements of an arbitrary point through the axes $x_{i};\left({i=1,2,3} \right)$, respectively, and t is the time. It is remarked that in present analysis, $i,j=1,2,3$ and $\alpha,\beta=1,2$. Furthermore, u₁, u₂ and w are the displacements along x₁, x₂ and x₃ axes, respectively. Moreover, ψ₁ and ψ₂ are, respectively, the rotations about x₂ and x₁ axes. Furthermore, χ(x₃) indicates the generalized shape function illustrating the stress distribution and transverse shear deformation across the thickness of the GPL-RP nanocomposite plate. In order to achieve the displacement filed of different shear deformation plate theory, one can consider the shape function as the following form:

$$\begin{aligned} & {\text{Mindlin\,plate\,theory}}\left({\text{MPT}} \right):\chi \left({x_{3}} \right)=x_{3}, \\ & {\text{Reddy\,plate\,theory}}\left({\text{RPT}} \right):\chi \left({x_{3}} \right)=x_{3} \left({1 - \frac{{4x_{3}^{2}}}{{3h^{2}}}} \right), \\ & {\text{Parabolic\,shear\,deformable\,plate\,theory\,}}\left({\text{PSDPT}} \right):\chi \left({x_{3}} \right)=x_{3} \left({\frac{5}{4} - \frac{{5x_{3}^{2}}}{{3h^{2}}}} \right), \\ & {\text{Trigonometric\,shear\,deformable\,plate\,theory\,}}\left({\text{TSDPT}} \right):\chi \left({x_{3}} \right)=\frac{h}{\pi}\sin \left({\frac{{\pi x_{3}}}{h}} \right), \\ & {\text{Exponential\,shear\,deformable\,plate\,theory}}\left({\text{ESDPT}} \right):\chi \left({x_{3}} \right)=x_{3} e^{{- 2\left({x_{3}/h} \right)^{2}}} \\ \end{aligned}$$

(9)

By assuming the von Kármán nonlinear strain–displacements relation for the unified displacement field defined in Eq. (8), one can express the nonzero components of strain tensor in terms of displacement gradients as follows:

$$\varepsilon_{\alpha \beta}=\varepsilon_{\alpha \beta}^{0} + \chi_{1} \varepsilon_{\alpha \beta}^{1} + \chi_{2} \varepsilon_{\alpha \beta}^{2},\gamma_{\alpha 3}=2\varepsilon_{\alpha 3}=\chi_{3} \gamma_{\alpha 3}^{0},$$

(10)

where

$$\begin{aligned} \varepsilon_{\alpha \beta}^{0} &=\frac{1}{2}\left({u_{\alpha,\beta} + u_{\beta,\alpha} + w_{,\alpha} w_{,\beta}} \right),\varepsilon_{\alpha \beta}^{1}=w_{,\alpha \beta},\varepsilon_{\alpha \beta}^{2}=\frac{1}{2}\left({\psi_{\alpha,\beta} + \psi_{\beta,\alpha}} \right), \\ \gamma_{\alpha 3}^{0} &=\psi_{\alpha} + w_{,\alpha},\chi_{1}=\chi \left({x_{3}} \right) - x_{3},\chi_{2}=\chi \left({x_{3}} \right),\chi_{3}=\frac{{{\text{d}}\chi \left({x_{3}} \right)}}{{{\text{d}}x_{3}}}. \\ \end{aligned}$$

(11)

where in mathematical formulation, the symbol comma indicates the partial differentiation with respect to the geometric coordinates.

Furthermore, the stress–strain relations corresponding to the kth layer of GPL-RP nanocomposite plate can be expressed as

$$\left\{{\begin{array}{*{20}c} {\sigma_{11}} \\ {\sigma_{22}} \\ {\sigma_{12}} \\ {\sigma_{13}} \\ {\sigma_{23}} \\ \end{array}} \right\}^{\left(k \right)}=\left[{\begin{array}{*{20}c} {Q_{11}} & {Q_{12}} & 0 & 0 & 0 \\ {Q_{12}} & {Q_{22}} & 0 & 0 & 0 \\ 0 & 0 & {Q_{66}} & 0 & 0 \\ 0 & 0 & 0 & {Q_{55}} & 0 \\ 0 & 0 & 0 & 0 & {Q_{44}} \\ \end{array}} \right]^{\left(k \right)} \left\{{\begin{array}{*{20}c} {\varepsilon_{11}} \\ {\varepsilon_{22}} \\ {\gamma_{12}} \\ {\gamma_{13}} \\ {\gamma_{23}} \\ \end{array}} \right\}^{\left(k \right)}$$

(12)

in which σ₁₁ and σ₂₂ are the normal stress components; σ₁₂, σ₁₃ and σ₂₃ represent the shear stresses and $\gamma_{12}=2\varepsilon_{12}$. Furthermore, $Q_{ij}^{\left(k \right)}$. indicates the reduced material stiffness coefficients compatible with the plane-stress conditions for the kth layer, which are computed as follows:

$$Q_{11}^{\left(k \right)}=Q_{22}^{\left(k \right)}=\frac{{E_{\text{eff}}}}{{1 - \nu_{\text{eff}}^{2}}},Q_{12}=\frac{{\nu_{\text{eff}} E_{\text{eff}}}}{{1 - \nu_{\text{eff}}^{2}}},Q_{44}^{\left(k \right)}=Q_{55}^{\left(k \right)}=Q_{66}^{\left(k \right)}=\frac{{E_{\text{eff}}}}{{2\left({1 + \nu_{\text{eff}}} \right)}}.$$

(13)

Then, the in-plane force resultants (N_αβ) and bending moment resultants (M_αβ) as well as the higher-order bending moments (P_αβ) and transverse forces (Q_α) caused by the stress components σ_αβ and σ_α3 can be defined as

$$\left\{{N_{\alpha \beta},M_{\alpha \beta},P_{\alpha \beta},Q_{\alpha}} \right\}=\mathop \sum \limits_{l=1}^{{N_{\text{L}}}} \mathop \int \limits_{{x_{3l}}}^{{x_{3l + 1}}} \left\{{\sigma_{\alpha \beta}^{\left(l \right)},\gamma_{1} \sigma_{\alpha \beta}^{\left(l \right)},\gamma_{2} \sigma_{\alpha \beta}^{\left(l \right)},\kappa_{\text{s}} \gamma_{3} \sigma_{\alpha 3}^{\left(l \right)}} \right\}dx_{3}$$

(14)

where κ_s represents the shear correction factor and equals 5/6 for MPT and 1 for higher-order shear deformation plate theories.

These quantities defined in Eq. (14) can be expressed in the following matrix form

$$\left\{ {\begin{array}{*{20}c} {N_{{11}} } \\ {N_{{22}} } \\ {N_{{12}} } \\ {M_{{11}} } \\ {M_{{22}} } \\ {M_{{12}} } \\ {P_{{11}} } \\ {P_{{22}} } \\ {P_{{12}}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c}{A_{{11}} } & {A_{{12}} } & 0 & {B_{{11}} } & {B_{{12}} } & 0 & {C_{{11}} } & {C_{{12}} } & 0 \\ {A_{{12}} } & {A_{{22}} } & 0 & {B_{{12}} } & {B_{{22}} } & 0 & {C_{{12}} } & {C_{{22}} } & 0 \\ 0 & 0 & {A_{{66}} } & 0 & 0 & {B_{{66}} } & 0 & 0 & {C_{{66}} } \\ {B_{{11}} } & {B_{{12}} } & 0 & {D_{{11}} } & {D_{{12}} } & 0 & {F_{{11}} } & {F_{{12}} } & 0 \\ {B_{{12}} } & {B_{{22}} } & 0 & {D_{{12}} } & {D_{{22}} } & 0 & {F_{{12}} } & {F_{{22}} } & 0 \\ 0 & 0 & {B_{{66}} } & 0 & 0 & {D_{{66}} } & 0 & 0 & {F_{{66}} } \\ {C_{{11}} } & {C_{{12}} } & 0 & {F_{{11}} } & {F_{{12}} } & 0 & {H_{{11}} } & {H_{{12}} } & 0 \\ {C_{{12}} } & {C_{{22}} } & 0 & {F_{{12}} } & {F_{{22}} } & 0 & {H_{{12}} } & {H_{{22}} } & 0 \\ 0 & 0 & {C_{{66}} } & 0 & 0 & {F_{{66}} } & 0 & 0 & {H_{{66}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{{11}}^{0} } \\ {\varepsilon _{{22}}^{0} } \\ {\gamma_{{12}}^{0} } \\ {\varepsilon _{{11}}^{1} } \\ {\varepsilon_{{22}}^{1} } \\ {\gamma _{{12}}^{1} } \\ {\varepsilon_{{11}}^{3} } \\ {\varepsilon _{{22}}^{3} } \\ {\gamma_{{12}}^{3} } \\ \end{array} } \right\},$$

(15a)

$$\left\{{\begin{array}{*{20}c} {Q_{1}} \\ {Q_{2}} \\ \end{array}} \right\}=\left[{\begin{array}{*{20}c} {A_{55}} & 0 \\ 0 & {A_{44}} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} {\gamma_{13}^{0}} \\ {\gamma_{23}^{0}} \\ \end{array}} \right\}$$

(15b)

in which the parameters A_ij, B_ij, C_ij, D_ij, F_ij and H_ij are defined as

$$\begin{aligned} \left\{{A_{IJ},B_{IJ},C_{IJ},D_{IJ},F_{IJ},H_{IJ}} \right\} &=\mathop \sum \limits_{l=1}^{{N_{\text{L}}}} \mathop \int \limits_{{x_{3l}}}^{{x_{3l + 1}}} Q_{IJ}^{\left(l \right)} \left\{{1,\Upsilon_{1},\Upsilon_{2},\Upsilon_{1}^{2},\Upsilon_{1} \Upsilon_{2},\Upsilon_{2}^{2}} \right\}dx_{3};\left({I,J=1,2,6} \right), \\ A_{ij} &=\kappa_{\text{s}} \mathop \sum \limits_{l=1}^{{N_{\text{L}}}} \mathop \int \limits_{{x_{3l}}}^{{x_{3l + 1}}} Q_{IJ}^{\left(l \right)} \Upsilon_{3}^{2} dx_{3};\left({I,J=4,5} \right). \\ \end{aligned}$$

(16)

Now, the variation of the potential strain energy expression of the thick and moderately thick GPL-RP nanocomposite rectangular plates is given below:

$$\begin{aligned} \delta\Pi_{s} &=\mathop \int \limits_{A} \mathop \int \limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{ij} \delta\varepsilon_{ij} dx_{3} dA=\mathop \sum \limits_{l=1}^{{N_{\text{L}}}} \mathop \int \limits_{A} \mathop \int \limits_{{x_{3l}}}^{{x_{3l + 1}}} \sigma_{ij}^{\left(l \right)} \delta\varepsilon_{ij} dx_{3} \\ &=\mathop \int \limits_{A} \left\{{N_{\alpha \beta} \delta\varepsilon_{\alpha \beta}^{0} + M_{\alpha \beta} \delta\varepsilon_{\alpha \beta}^{1} + P_{\alpha \beta} \delta\varepsilon_{\alpha \beta}^{2} + Q_{\alpha} \delta\gamma_{\alpha 3}^{0}} \right\}dA, \\ \end{aligned}$$

(17)

where A signifies the surface area of the GPL-RP nanocomposite plate.

Also, the variation of kinetic energy of shear deformable GPL-RP nanocomposite plates can be given as

$$\begin{aligned} \delta \Pi_{T} &=\mathop \int \limits_{A} \mathop \int \limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} \rho \dot{\tilde{u}}_{i} \delta \dot{\tilde{u}}_{i} {\text{d}}z{\text{d}}A=\mathop \sum \limits_{l=1}^{{N_{\text{L}}}} \mathop \int \limits_{A} \mathop \int \limits_{{x_{3l}}}^{{x_{3l + 1}}} \rho^{\left(l \right)} \dot{\tilde{u}}_{i} \delta \dot{\tilde{u}}_{i} dx_{3} \\ &=\mathop \int \limits_{A} \left\{{I_{0} \left({\dot{u}_{\alpha} \delta \dot{u}_{alpha} + \dot{w}\delta \dot{w}} \right) + I_{1} \dot{u}_{\alpha} \delta \dot{w}_{,\alpha} + I_{1} \dot{w}_{,\alpha} \delta\dot{u}_{\alpha} + I_{2} \dot{\psi}_{\alpha} \delta\dot{u}_{\alpha}} \right. \\ & \quad \left. {+\,I_{2} \dot{u}_{\alpha} \delta \dot{\psi}_{\alpha} + I_{3} \dot{w}_{,\alpha} \delta \dot{\psi}_{\alpha} + I_{3} \dot{\psi}_{\alpha} \delta\dot{w}_{,\alpha} + I_{4} \dot{w}_{,\alpha} \delta\dot{w}_{,\alpha} + I_{5} \dot{\psi}_{\alpha} \delta \dot{\psi}_{\alpha}} \right\}dA, \\ \end{aligned}$$

(18)

where the differentiation with respect to the time is denoted by symbol dot. Also, $I_{J};\left({J=0, \ldots,5} \right)$ can be calculated as

$$\left\{{I_{0},I_{1},I_{2},I_{3},I_{4},I_{5}} \right\}=\mathop \sum \limits_{l=1}^{{N_{\text{L}}}} \mathop \int \limits_{{x_{3l}}}^{{x_{3l + 1} }} \rho^{\left(l \right)} \left\{{1,\gamma_{1},\gamma_{2},\gamma_{1} \gamma_{2},\gamma_{1}^{2},\gamma_{2}^{2}} \right\}dx_{3},$$

(19)

Now, substituting Eqs. (11) into (17) and employing the chain rule and divergence theorem results in the following expression for the variation of strain potential energy of GPL-RP nanocomposite rectangular plates

$$\begin{aligned} \delta \Pi_{\text{s}} &=\mathop \int \limits_{\text{A}} \left\{{- N_{\alpha \beta,\alpha} \delta u_{\beta} + \left[{- Q_{\alpha,\alpha} + M_{\alpha \beta,\alpha \beta} - \left({N_{\alpha \beta} w_{,\beta}} \right)_{,\alpha}} \right]\delta w + \left({- P_{\alpha \beta,\alpha} + Q_{\beta}} \right)\delta \psi_{\beta}} \right\}{\text{d}}A \\ & \quad + \mathop {\oint}\limits_{\text{S}} \left({N_{nn} \delta g_{n} + N_{ns} \delta g_{s} + \left({Q_{n} - V_{n}} \right)\delta w + P_{nn} \delta \theta_{n} + P_{ns} \delta \theta_{s} + M_{nn} \delta \frac{\partial w}{\partial n}} \right){\text{d}}S \\ \end{aligned}$$

(20)

where

$$\begin{aligned} g_{n} &=n_{\alpha} u_{\alpha},g_{s}=- n_{2} u_{1} + n_{1} u_{2}, \\ N_{nn} &=N_{\alpha \beta} n_{\alpha} n_{\beta},N_{ns}=\left({N_{22}-N_{11}} \right)n_{1} n_{2} + N_{12} \left({n_{1}^{2}-n_{2}^{2}} \right), \\ M_{nn} &=M_{\alpha \beta} n_{\alpha} n_{\beta},M_{ns}=\left({M_{22}-M_{11}} \right)n_{1} n_{2} + M_{12} \left({n_{1}^{2}-n_{2}^{2}} \right), \\ P_{nn} &=P_{\alpha \beta} n_{\alpha} n_{\beta},P_{ns}=\left({P_{22}-P_{11}} \right)n_{1} n_{2} + P_{12} \left({n_{1}^{2}-n_{2}^{2}} \right), \\ Q_{n} &=n_{\alpha} \left({N_{\alpha \beta} w_{\beta} + Q_{\alpha}} \right),V_{n}=n_{\alpha} \left({M_{\alpha \beta,\beta}} \right) + M_{ns,s}, \\ \end{aligned}$$

(21)

Also, n_α is the direction cosines of the outward unit normal to the boundary of the middle-plane.

Now, using the Hamilton’s principle and implementation of the fundamental lemma of the calculus of variations results in the following geometrically nonlinear mathematical formulation of governing equations of motion for the GPL-RP nanocomposite rectangular plates

$$N_{\alpha \beta,\alpha}=I_{0} \ddot{u}_{\beta} + I_{1} \ddot{w}_{,\beta} + I_{2} \ddot{\psi}_{\beta},$$

(22a)

$$Q_{\alpha,\alpha}-M_{\alpha \beta,\alpha \beta} + \left({N_{\alpha \beta} w_{,\beta}} \right)_{,\alpha}=I_{0} \ddot{w}-I_{1} \ddot{u}_{\alpha,\alpha}-I_{3} \ddot{\psi}_{\alpha,\alpha}-I_{4} \ddot{w}_{,\alpha \alpha},$$

(22b)

$$P_{\alpha \beta,\alpha}-Q_{\beta}=I_{2} \ddot{u}_{\beta} + I_{3} \ddot{w}_{,\beta} + I_{5} \ddot{\psi}_{\beta},$$

(22c)

Furthermore, the essential and natural boundary conditions associated with the governing Eq. (22) are achieved as

$$\delta g_{n}=0\qquad or\,N_{nn}=0$$

(23a)

$$g_{s}=0\qquad or\,N_{ns}=0$$

(23b)

$$\delta w=0\qquad or\,\left({Q_{n}-V_{n}} \right)=0$$

(23c)

$$\delta \theta_{n}=0\qquad or\, P_{nn}=0$$

(23d)

$$\delta \theta_{s}=0\qquad or\, P_{ns}=0$$

(23e)

$$\delta \frac{\partial w}{\partial n}=0\qquad or\, M_{nn}=0$$

(23f)

One can express the geometrically nonlinear governing Eq. (22) in terms of components of displacement field by substituting the relations defined in (11) and (15) into (22) as the following form:

$$\begin{aligned} & A_{11} u_{1,11} + \left({A_{12} + A_{66}} \right)u_{2,12} + A_{66} u_{1,22} + B_{11} w_{,111} + \left({B_{12} + 2B_{66}} \right)w_{,122} \\ & \quad \, + C_{11} \psi_{1,11} + \left({C_{12} + C_{66}} \right)\psi_{2,12} + C_{66} \psi_{1,22} + Z_{1}=I_{0} \ddot{u}_{1} + I_{1} \ddot{w}_{,1} + I_{2} \ddot{\psi}_{1}, \\ \end{aligned}$$

(24a)

$$\begin{aligned} & A_{66} u_{2,11} + \left({A_{12} + A_{66}} \right)u_{1,12} + A_{22} u_{2,22} + \left({B_{12} + 2B_{66}} \right)w_{,112} + B_{22} w_{,222} \\ & \quad \, + C_{12} \psi_{1,12} + C_{22} \psi_{2,22} + C_{66} \left({\psi_{1,12} + \psi_{2,11}} \right) + Z_{2}=I_{0} \ddot{u}_{2} + I_{1} \ddot{w}_{,2} + I_{2} \ddot{\psi}_{2}, \\ \end{aligned}$$

(24b)

$$\begin{aligned} & A_{55} \left({\psi_{1,1} + w_{,11}} \right) + A_{44} \left({\psi_{2,2} + w_{,22}} \right)-B_{11} u_{1,111}-\left({B_{12} + 2B_{66}} \right)u_{2,112} \\ & \quad - \left({B_{12} + 2B_{66}} \right)u_{1,122} - B_{22} u_{2,222} - D_{11} w_{,1111} - 2\left({D_{12} + 2D_{66}} \right)w_{,1122} \\ & \quad - D_{22} w_{,2222} - F_{11} \psi_{1,111} - \left({F_{12} + 2F_{66}} \right)\left({\psi_{2,112} + \psi_{1,122}} \right) - F_{22} \psi_{2,222} + Z_{3} \\ & \quad=I_{0} \ddot{w} - I_{1} \left({\ddot{u}_{1,1} + \ddot{u}_{2,2}} \right) - I_{3} \left({\ddot{\psi}_{1,1} + \ddot{\psi}_{2,2}} \right) - I_{4} \left({\ddot{w}_{,11} + \ddot{w}_{,22}} \right), \\ \end{aligned}$$

(24c)

$$\begin{aligned} & C_{11} u_{1,11} + \left({C_{12} + C_{66}} \right)u_{2,12} + C_{66} u_{1,22} + F_{11} w_{,111} + \left({F_{12} + 2F_{66}} \right)w_{,122} + H_{11} \psi_{1,11} \\ & \quad + \left({H_{12} + H_{66}} \right)\psi_{2,12} + H_{66} \psi_{1,22} - A_{55} \left({\psi_{1} + w_{,1}} \right) + Z_{4}=I_{2} \ddot{u}_{1} + I_{3} \ddot{w}_{,1} + I_{5} \ddot{\psi}_{1}, \\ \end{aligned}$$

(24d)

$$\begin{aligned} & C_{66} u_{2,11} + \left({C_{12} + C_{66}} \right)u_{1,12} + C_{22} u_{1,22} + \left({F_{12} + 2F_{66}} \right)w_{,112} + F_{22} w_{,222} + H_{12} \psi_{1,12} \\ & \quad + H_{22} \psi_{2,22} + H_{66} \left({\psi_{1,12} + \psi_{2,11}} \right) - A_{44} \left({\psi_{2} + w_{,2}} \right) + Z_{2}=I_{2} \ddot{u}_{2} + I_{3} \ddot{w}_{,2} + I_{5} \ddot{\psi}_{2}, \\ \end{aligned}$$

(24e)

where

$$Z_{1}=A_{11} w_{,1} w_{,11} + A_{12} w_{,12} w_{,2} + A_{66} \left({w_{,12} w_{,2} + w_{,1} w_{,22}} \right),$$

(25a)

$$Z_{2}=A_{12} w_{,1} w_{,12} + A_{22} w_{,2} w_{,22} + A_{66} \left({w_{,2} w_{,11} + w_{,1} w_{,12}} \right),$$

(25b)

$$\begin{aligned} Z_{3} &=- B_{11} \left({w_{,11}^{2} + w_{,1} w_{,111}} \right) - B_{12} \left({w_{,112} w_{,2} + w_{,12}^{2}} \right) \\ & \quad - 2B_{66} \left({w_{,112} w_{,2} + w_{,11} w_{,22} + w_{,12}^{2} + w_{,1} w_{,122}} \right) - B_{12} \left({w_{,11} w_{,12} + w_{,1} w_{,122}} \right) \\ & \quad - B_{22} \left({w_{,222} w_{,2} + w_{,22}^{2}} \right) + \left({N_{11} w_{,1}} \right)_{,1} + \left({N_{22} w_{,2}} \right)_{,2} + \left({N_{12} w_{,2}} \right)_{,1} + \left({N_{12} w_{,1}} \right)_{,2}, \\ \end{aligned}$$

(25c)

$$Z_{4}=C_{11} w_{,1} w_{,11} + C_{12} w_{,12} w_{,2} + C_{66} \left({w_{,12} w_{,2} + w_{,1} w_{,22}} \right),$$

(25d)

$$Z_{5}=C_{12} w_{,1} w_{,12} + C_{22} w_{,22} w_{,2} + C_{66} \left({w_{,11} w_{,2} + w_{,1} w_{,12}} \right).$$

(25e)

In a similar way, one can express the natural boundary conditions in terms of the components of displacement field.

In the current investigation, the nonlinear free vibration of GPL-RP nanocomposite plates with three types of edge supports, namely all edges simply supported (SSSS), all edges clamped (CCCC) and two opposite edges clamped—the remaining edges simply supported (CSCS), will be studied. In the case of MPT (i.e., first-order shear deformation plate theory), the associated boundary conditions can be mathematically written as follows:

• a. SSSS edge supports

  $$\begin{aligned} u_{1} &=u_{2}=w=\psi_{2}=P_{11}=0\qquad at\,edges\,x_{1}=0,a \\ u_{1} &=u_{2}=w=\psi_{1}=P_{22}=0\qquad at\,edges\,x_{2}=0,\,b \\ \end{aligned}$$

  (26a)

• b. CCCC edge supports

  $$\begin{aligned} u_{1} &=u_{2}=w=\psi_{1}=\psi_{2}=0\qquad at\,edges\,x_{1}=0,\,a\\ u_{1} &=u_{2}=w=\psi_{1}=\psi_{2}=0\qquad at\,edges\,x_{2}=0,b \\ \end{aligned}$$

  (26b)

• c. CSCS edge supports

  $$\begin{aligned} u_{1} &=u_{2}=w=\psi_{1}=\psi_{2}=0\qquad at\,edges\,x_{1}=0,a \\ u_{1} &=u_{2}=w=\psi_{1}=P_{22}=0\qquad at\,edges\,x_{2}=0,b \\ \end{aligned}.$$

  (26c)

Moreover, for the higher-order shear deformation plate theories, one can mathematically express the edge conditions as the following form:

• a. SSSS edge supports

  $$\begin{aligned} u_{1} &=u_{2}=w=\psi_{2}=P_{11}=M_{11}=0\qquad at\,edges\,x_{1}=0,a \\ u_{1} &=u_{2}=w=\psi_{1}=P_{22}=M_{22}=0\qquad at\,edges\,x_{2}=0,b \\ \end{aligned}$$

  (27a)

• b. CCCC edge supports

  $$\begin{aligned} u_{1} &=u_{2}=w=\psi_{1}=\psi_{2}=w_{,1}=0\qquad at\,edges\,x_{1}=0,a\\ u_{1} &=u_{2}=w=\psi_{1}=\psi_{2}=w_{,2}=0\qquad at\,edges\,x_{2}=0,b \\ \end{aligned}$$

  (27b)

• c. CSCS edge supports

  $$\begin{aligned} u_{1} &=u_{2}=w=\psi_{1}=\psi_{2}=w_{,1}=0\qquad at\,edges\,x_{1}=0,\,a \\ u_{1} &=u_{2}=w=\psi_{1}=P_{22}=M_{22}=0\qquad at\,edges\,x_{2}=0,b \\ \end{aligned}$$

  (27c)

3 Solution Approach

An efficient multistep numerical solution methodology including the GDQ method (Shu 2000), numerical-based Galerkin approach, time periodic differential scheme, pseudo-arc length continuation algorithm (Keller 1977; De Borst et al. 2012) and modified Newton–Raphson method is utilized for the geometrically nonlinear free vibration analysis of GPL-RP nanocomposite plates with different edge conditions. The basic idea is that applying the GDQ method results in converting the nonlinear partial differential governing equations of motion and edge conditions into a set of nonlinear algebraic equations. Then, the discretized governing equations are transformed into a reduced form of time-dependent Duffing-type equations by applying the numerical-based Galerkin approach. Applying the time periodic differential scheme results in discretizing the set of Duffing-type equations in the time domain, from which the backbone curve of GPL-RP nanocomposite plate as the nonlinear frequency ratio versus the maximum vibration amplitude is then obtained by the simultaneous use of the pseudo-arc length continuation technique in conjugation with the modified Newton–Raphson method.

On the basis of the GDQ method, the discretized form of a two-variable function f(x₁, x₂) with its pth- and qth-order derivatives with respect to the x₁ and x₂ can be written as

$$\frac{{\partial^{p + q} f\left({x_{1},x_{2}} \right)}}{{\partial x_{1}^{p} \partial x_{2}^{q}}}=\left({{\mathbf{D}}_{{x_{2}}}^{\left(q \right)} \otimes {\mathbf{D}}_{{x_{1}}}^{\left(p \right)}} \right){\mathbf{f}}.$$

(28)

in which the weighting coefficients matrices of the pth- and qth-order derivatives in the x₁ and x₂ directions are denoted by ${\mathbf{D}}_{{x_{1}}}^{\left(p \right)}$ and ${\mathbf{D}}_{{x_{2}}}^{\left(q \right)}$, respectively. Furthermore, the symbol $\otimes$ signifies the Kronecker product (see “Appendix 1”). Also, f is the discretized form of two-variable function which is expressed in the form of the column vector as follows:

$${\mathbf{f}}=\left[{f\left({x_{1}}_1,{x_{2}}_1 \right), \ldots,\,f\left({x_{1}}_N,{x_{2}}_1 \right),f\left({x_{1}}_1,{x_{2}}_2 \right), \ldots,f\left({x_{1}}_N,{x_{2}}_2 \right), \ldots,f\left({x_{1}}_1,{x_{2}}_M \right), \ldots,f\left({x_{1}}_N,{x_{2}}_M \right)} \right]^{\text{T}},$$

(29)

where $x_{{1_{i}}}$ and $x_{{2_{i}}}$ are the grid point through the x₁- and x₂-axes, respectively. Due to the most convergence and stability (Tornabene 2009), the shifted Chebyshev–Gauss–Lobatto distribution is used to generate these grid points as follows:

$$\begin{aligned} x_{{1_{i}}}=\frac{a}{2}\left({1 - \cos \frac{i - 1}{N - 1}\pi} \right),\quad i=1,2,3, \ldots,N \hfill \\ x_{{2_{i}}}=\frac{b}{2}\left({1 - \cos \frac{j - 1}{M - 1}\pi} \right),\quad i=1,2,3, \ldots,M \hfill \\ \end{aligned}$$

(30)

Moreover, N and M are the number of gird points through the x₁- and x₂-directions, respectively.

Also, the weighting coefficients matrix ${\mathbf{D}}^{\left(r \right)}=D_{ij}^{\left(r \right)}=W_{ij}^{\left(r \right)}$ is obtained via a recursive method as follows:

$$D_{ij}^{\left(r \right)}=\left\{\begin{aligned} I_{ij} ,{\text{where}}\,I_{ij} {\text{is\,a\,}}N \times N\,{\text{identity\,matrix}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,r=0 \hfill \\ \frac{{P\left({x_{i}} \right)}}{{\left({x_{i} - x_{j}} \right)P\left({x_{j}} \right)}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i,j=1, \ldots,N{\text{\,and}}\,i \ne j{\text{\,and}}\,r=1 \hfill \\ r\left[{W_{ij}^{\left(1 \right)} W_{ii}^{{\left({r - 1} \right)}} - \frac{{W_{ij}^{{\left({r - 1} \right)}}}}{{x_{i} - x_{j}}}} \right],i \ne j\,{\text{and}}\, - \mathop \sum \limits_{{\begin{array}{*{20}c} {k=1} \\ {k \ne i} \\ \end{array}}}^{N} W_{ik}^{\left(r \right)},i=j\,\,\,\,i,j=1, \ldots,N\,{\text{and}}\,r\ge 2 \hfill \\ \end{aligned} \right.$$

(31)

where $P\left({x_{i}} \right)=\mathop \prod \nolimits_{k=1;i \ne k}^{N} \left({x_{i} - x_{k}} \right)$. Applying the GDQ method on the governing equations, (24) gives a set of time-dependent ordinary differential equations which can be expressed in a matrix form as follows:

$${\mathbf{M}}{\ddot{\mathbf{X}}} + {\mathbf{KX}} + {\mathbf{K}}_{nl} \left({\mathbf{X}} \right)={\mathbf{0}}$$

(32)

where ${\mathbf{X}}=\left\{{{\mathbf{u}}_{1}^{\text{T}},{\mathbf{u}}_{2}^{\text{T}},{\mathbf{w}}^{\text{T}},{\varvec{\uppsi}}_{1}^{\text{T}},{\varvec{\uppsi}}_{2}^{\text{T}}} \right\}^{\text{T}}$ signifies the vector associated with the 5 NM unknown generalized coordinates; K and M are, respectively, the stiffness and mass matrices. Moreover, ${\mathbf{K}}_{{{\mathbf{nl}}}} \left({\mathbf{X}} \right)$ is the nonlinear stiffness vector. K, M and ${\mathbf{K}}_{{{\mathbf{nl}}}} \left({\mathbf{X}} \right)$ can be expressed as

$${\mathbf{K}}=\left[{\begin{array}{*{20}c} {{\mathbf{K}}_{11}} & {{\mathbf{K}}_{12}} & {{\mathbf{K}}_{13}} & {{\mathbf{K}}_{14}} & {{\mathbf{K}}_{15}} \\ {{\mathbf{K}}_{21}} & {{\mathbf{K}}_{22}} & {{\mathbf{K}}_{23}} & {{\mathbf{K}}_{24}} & {{\mathbf{K}}_{25}} \\ {{\mathbf{K}}_{31}} & {{\mathbf{K}}_{32}} & {{\mathbf{K}}_{33}} & {{\mathbf{K}}_{34}} & {{\mathbf{K}}_{35}} \\ {{\mathbf{K}}_{41}} & {{\mathbf{K}}_{42}} & {{\mathbf{K}}_{43}} & {{\mathbf{K}}_{44}} & {{\mathbf{K}}_{45}} \\ {{\mathbf{K}}_{51}} & {{\mathbf{K}}_{52}} & {{\mathbf{K}}_{53}} & {{\mathbf{K}}_{54}} & {{\mathbf{K}}_{55}} \\ \end{array}} \right],\,\,{\mathbf{M}}=\left[{\begin{array}{*{20}c} {{\mathbf{M}}_{11}} & {\mathbf{0}} & {{\mathbf{M}}_{13}} & {{\mathbf{M}}_{14}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{22}} & {{\mathbf{M}}_{23}} & {\mathbf{0}} & {{\mathbf{M}}_{25}} \\ {{\mathbf{M}}_{31}} & {{\mathbf{M}}_{32}} & {{\mathbf{M}}_{33}} & {{\mathbf{M}}_{34}} & {{\mathbf{M}}_{35}} \\ {{\mathbf{M}}_{41}} & {\mathbf{0}} & {{\mathbf{M}}_{43}} & {{\mathbf{M}}_{44}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{52}} & {{\mathbf{M}}_{53}} & {\mathbf{0}} & {{\mathbf{M}}_{55}} \\ \end{array}} \right],$$

(33a)

$${\mathbf{K}}_{nl} \left({\mathbf{X}} \right)=\left[{{\mathbf{K}}_{{u_{1}}} \left({\mathbf{X}} \right)^{\text{T}},{\mathbf{K}}_{{u_{2}}} \left({\mathbf{X}} \right)^{\text{T}},{\mathbf{K}}_{w} \left({\mathbf{X}} \right)^{\text{T}},{\mathbf{K}}_{{\psi_{1}}} \left({\mathbf{X}} \right)^{\text{T}},{\mathbf{K}}_{{\psi_{2}}} \left({\mathbf{X}} \right)^{\text{T}}} \right]^{\text{T}},$$

(33b)

The discretized components of K_ij, M_ij and ${\mathbf{K}}_{nl} \left({\mathbf{X}} \right)$ are provided in “Appendix 2”.

Now, to reduce the dimensions of discretized Eq. (32) and consequently decrease the computational cost, the numerical-based Galerkin approach (Gholami and Ansari 2016) is employed. In this regard, first, the nonlinear terms of Eq. (32) are neglected and the solution of linear free vibration problem is assumed as ${\mathbf{X}}={\tilde{\mathbf{X}}}e^{{j\tilde{\omega}_{\text{L}} t}}$. After imposing the discretized form of boundary conditions into the stiffness matrix and inserting the assumed solution into the linearized equation, a generalized eigenvalue problem is achieved as the following form:

$${\mathbf{K}}{\tilde{\mathbf{X}}}=\tilde{\omega}_{\text{L}}^{2} {\mathbf{M}}{\tilde{\mathbf{X}}},{\tilde{\mathbf{X}}}=\left[{{\tilde{\mathbf{u}}}_{1}^{\text{T}},{\tilde{\mathbf{u}}}_{2}^{\text{T}},{\tilde{\mathbf{w}}}^{\text{T}},{\tilde{\varvec{\uppsi}}}_{1}^{\text{T}},{\tilde{\varvec{\uppsi}}}_{2}^{\text{T}}} \right]^{\text{T}}$$

(34)

where $\tilde{\omega}_{\text{L}}$ is the linear frequency. By solving Eq. (34), one can achieve the linear frequencies of the GPL-RP nanocomposite plate and related mode shapes. By choosing the first m mode shapes, the solution of Eq. (34) can be expressed as follows:

$${\mathbf{X}}={\varvec{\Phi}} {\mathbf{q}}$$

(35)

where the reduced unknown generalized displacement vector and a sparse matrix are specified by q and Φ, respectively, and can be written as

$$\begin{aligned} {\mathbf{q}}^{\text{T}}_{{\left({5m} \right) \times 1}}=\left[{q_{{u_{1}}}^{\left(1 \right)},q_{{u_{1}}}^{\left(2 \right)}, \ldots,q_{{u_{1}}}^{\left(m \right)},q_{{u_{2}}}^{\left(1 \right)},q_{{u_{2}}}^{\left(2 \right)}, \ldots,q_{{u_{2}}}^{\left(m \right)},} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {q_{w}^{\left(1 \right)},q_{w}^{\left(2 \right)}, \ldots,q_{w}^{\left(m \right)},q_{{\psi_{1}}}^{\left(1 \right)},q_{{\psi_{1}}}^{\left(2 \right)}, \ldots,q_{{\psi_{1}}}^{\left(m \right)},q_{{\psi_{2}}}^{\left(1 \right)},q_{{\psi_{2}}}^{\left(2 \right)}, \ldots,q_{{\psi_{2}}}^{\left(m \right)}} \right]^{\text{T}}, \hfill \\ \end{aligned}$$

(36a)

$${\varvec{\Phi}}=\left[{\begin{array}{*{20}c} {{\varvec{\Phi}}_{{u_{1}}}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{\Phi}}_{{u_{2}}}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\varvec{\Phi}}_{w}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{\Phi}}_{{\psi_{1}}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{\Phi}}_{{\psi_{2}}}} \\ \end{array}} \right],$$

(36b)

in which

$$\begin{aligned} {\varvec{\Phi}}_{{u_{1}}} &=\left[{{\tilde{\mathbf{u}}}_{{1_{NM \times 1}}}^{(1)}, \ldots,{\tilde{\mathbf{u}}}_{{1_{NM \times 1}}}^{(m)}} \right],{\varvec{\Phi}}_{{u_{2}}}=\left[{{\tilde{\mathbf{u}}}_{{2_{NM \times 1}}}^{(1)}, \ldots,{\tilde{\mathbf{u}}}_{{2_{NM \times 1}}}^{(m)}} \right],{\varvec{\Phi}}_{w}=\left[{{\tilde{\mathbf{w}}}_{NM \times 1}^{\left(1 \right)}, \ldots,{\tilde{\mathbf{w}}}_{NM \times 1}^{\left(m \right)}} \right], \\ {\varvec{\Phi}}_{{\psi_{1}}} &=\left[{{\tilde{\varvec{\uppsi}}}_{{1_{NM \times 1}}}^{(1)}, \ldots,{\tilde{\varvec{\uppsi}}}_{{1_{NM \times 1}}}^{(m)}} \right],{\varvec{\Phi}}_{{\psi_{2}}}=\left[{{\tilde{\varvec{\uppsi}}}_{{2_{NM \times 1}}}^{(1)}, \ldots,{\tilde{\varvec{\uppsi}}}_{{2_{NM \times 1}}}^{(m)}} \right]. \\ \end{aligned}$$

(37)

The matrix Φ including the first m mode shapes can be regarded as the Galerkin basis functions. By substituting relation (35) into (32), one can obtain the residual vector as follows:

$${\mathbf{R}}={\mathbf{M}}{\varvec{\Phi}} {\ddot{\mathbf{q}}} + {\mathbf{K}}{\varvec{\Phi}} {\mathbf{q}} + {\mathbf{K}}_{nl} \left({\varvec{\Phi }}{{\mathbf{q}}} \right)$$

(38)

According to the numerical-based Galerkin technique, one can define a matrix operator as the following form to multiply each equation by the associated mode shape and then integrate over the space domain

$${\mathbf{G}}_{m \times 5NM}={\varvec{\Phi}}^{\text{T}} \left[{\begin{array}{*{20}c} {{\mathbf{S}}_{1} \otimes {\mathbf{S}}_{2}} & 0 & 0 & 0 & 0 \\ 0 & {{\mathbf{S}}_{1} \otimes {\mathbf{S}}_{2}} & 0 & 0 & 0 \\ 0 & 0 & {{\mathbf{S}}_{1} \otimes {\mathbf{S}}_{2}} & 0 & 0 \\ 0 & 0 & 0 & {{\mathbf{S}}_{1} \otimes {\mathbf{S}}_{2}} & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{S}}_{1} \otimes {\mathbf{S}}_{2}} \\ \end{array}} \right],$$

(39)

where S₁ and S₂ represent the integral matrix operators defined in “Appendix 1”. Equation (39) is multiplied by (38), which gives the following relation:

$${\tilde{\mathbf{M}}}{\ddot{\mathbf{q}}} + {\tilde{\mathbf{K}}\mathbf{q}} + {\tilde{\mathbf{K}}}_{{{\mathbf{nl}}}} \left({\mathbf{q}} \right)={\mathbf{0}}$$

(40)

in which ${\tilde{\mathbf{M}}}$ and ${\tilde{\mathbf{K}}}$ signify the reduced mass and stiffness matrices, respectively, and

$${\tilde{\mathbf{M}}}={\mathbf{GM}}{\varvec{\Phi}},{\tilde{\mathbf{K}}}={\mathbf{GK}}{\varvec{\Phi}},{\tilde{\mathbf{K}}}_{nl} \left({\mathbf{q}} \right)={\mathbf{GK}}_{nl} \left({\varvec{\Phi}}{{\mathbf{q}}} \right),$$

(41)

Equation (41) represents the Duffing-type equation.

Now, after applying $\tau=t/T$ and ${\tilde{\omega}}_{\text{NL}}=2\pi/T$ ($\tilde{\omega}_{\text{NL}}$ denotes the nonlinear frequency) and selecting the discrete points in the time domain

$$\tau_{i}=\frac{i}{{N_{t}}},\quad 0 < \tau_{i} \le 1,i=1,2, \ldots,N_{t}=2k$$

(42)

in which N_t represents the number of discrete points, the time periodic discretization approach (Shojaei et al. 2014; Ansari et al. 2014b) can be employed to achieve the discretized form of Eq. (40), which can be expressed as follows:

$$\left({\frac{{\omega_{\text{NL}}}}{2\pi}} \right)^{2} {\tilde{\mathbf{M}QD}}_{\tau}^{{\left(2 \right)}T}+ {\tilde{\mathbf{K}Q}} + {\tilde{\mathbf{K}}}_{nl} \left({\mathbf{Q}} \right)={\mathbf{0}}$$

(43)

where ${\mathbf{D}}_{\tau}^{\left(2 \right)}$ signifies the time differentiation matrix operator defined as follows:

$$\left\{\begin{array}{ll}\begin{array}{l}b_{11}=- \frac{{N_{t}^{2}}}{12} - \frac{1}{6}\\ {b_{i,1}= \frac{{\left({- 1} \right)^{i - 2}}}{{2\sin^{2} \frac{{\pi \left({i - 1} \right)}}{{N_{t}}}}}}\\ b_{1,j}= \frac{{\left({- 1} \right)^{{N_{t}- j}}}}{{2\sin^{2} \frac{{\pi \left({N_{t}- j + 1} \right)}}{{N_{t}}}}}\\{b_{i + 1,j + 1}= b_{i,j}}\end{array},& i,j=2,3,4, \ldots,N_{t},\,{\mathbf{D}}_{\tau}^{\left(2 \right)}= \left({2\pi} \right)^{2} \left[{b_{i,j}} \right]\end{array}\right.$$

(44)

in which ${\mathbf{D}}_{\tau}^{\left(2 \right)}$ is Teoplitz matrix.Equation (43) can be written as

$$\left({\left({\frac{{\tilde{\omega}_{\text{NL}}}}{2\pi}} \right)^{2} \left({{\mathbf{D}}_{\tau}^{\left(2 \right)}\otimes {\tilde{\mathbf{M}}}} \right) + \left({{\mathbf{I}}_{\tau}\otimes {\tilde{\mathbf{K}}}} \right)} \right)vec\left({\mathbf{Q}} \right) + vec\left({{\tilde{\mathbf{K}}}_{nl} \left({\mathbf{Q}} \right)} \right)={\mathbf{0}}$$

(45)

where I_τ is an N_t× N_t identity tensor and vec(Q) indicates the vectorization of the matrix Q.

Now, using the pseudo-arc length continuation algorithm (Keller 1977) as an efficient approach for approximating the solution set of a system of nonlinear algebraic equations, in conjugation with the modified Newton–Raphson method enables us to solve the set of nonlinear algebraic Eq. (45) and accordingly achieve the nonlinear free vibration characteristics of the GPL-RP nanocomposite rectangular plates with various edge conditions via plotting frequency–response curves.

4 Numerical Results and Discussion

The developed unified nonlinear higher-order plate model in conjunction with the multistep numerical solution approach outlined in the previous sections is employed to study the effect of distribution patterns of weight fraction, geometries of GPL nanofillers and edge supports on the nonlinear free vibration characteristics of the GPL-RP nanocomposite rectangular plates through numerical examples. To this end, epoxy with Young’s modulus of E_M= 3.0GPa and Poisson’s ratio of V_M= 0.34 is considered as the polymer matrix (Yasmin and Daniel 2004). Unless otherwise specified, the material properties and geometries of GPLs are considered as: Young’s modulus of E_GPL = 1.01TPa, Poisson’s ratio of v_GPL = 0.186, length of a_GPL = 2.5 μm, width of b_GPL = 1.5 μm and thickness of h_GPL = 1.5 nm, as given in Rafiee et al. (2009), Liu et al. (2007). Also, unless otherwise indicated, it is assumed that the total thickness of the GPL-RP nanocomposite rectangular plate is h = 0.045 m and the subsequent numerical results are computed on the basis of PSDPT. Furthermore, the total number of layers is considered N_L= 10 (Song et al. 2017).

Defining the following nondimensional maximum amplitude (Non. Dim. Max. Amplitude), i.e., w_max = W_max/h and nondimensional linear and nonlinear frequencies $\left\{{\omega_{\text{L}},\omega_{\text{NL}}} \right\}=\left\{{\tilde{\omega}_{\text{L}},\tilde{\omega}_{\text{NL}}} \right\}a\sqrt {\rho_{\text{m}} \left({1 - \nu_{\text{m}}^{2}} \right)/E_{\text{m}}}$ ($\tilde{\omega}_{\text{L}}$ and $\tilde{\omega}_{\text{NL}}$ are the dimensional linear and nonlinear frequencies, respectively), the backbone curve indicating the nonlinear-to-linear frequency ratio versus the maximum nondimensional transverse vibration amplitude is provided.

In order to verify the correctness and accuracy of presented results predicted by the developed higher-order shear deformable plate model, the first four fundamental frequency parameters $\tilde{\omega}_{\text{L}} h\sqrt {\rho_{\text{m}}/E_{\text{m}}}$ of GPL-RP nanocomposite rectangular plate with simply supported edge conditions achieved by the present model and numerical solution approach are compared with those given by Song et al. (2017), as provided in Table 1. Good agreement can be seen between the present results and those given by Song et al. (2017) which clearly demonstrates the reliability of the proposed model and numerical calculations for the analysis of GPL-RP nanocomposite rectangular plates.

Table 1 Comparison study of frequency parameters of GPL-RP nanocomposite plates with various GPL distribution patterns $\left({a/h=b/h=10,w_{\text{GPL}}= 0.1\%} \right)$

Figure 3 provides a comparison between the nonlinear free vibration response of GPL-RP nanocomposite plates associated with different plate theories. The nonlinear frequency response of the GPL-RP nanocomposite rectangular plate is illustrated as the nonlinear frequency ratio $\omega_{\text{NL}}/\omega_{\text{L}}$ versus nondimensional maximum (i.e., Non. Dim. Max.) amplitude curves for various boundary conditions. It can be seen that the nonlinear-to-linear frequency ratios predicted by the higher-order shear deformation plate theories are greater than those predicted by Mindlin plate theory. It should be remarked that unlike the MPT, in higher-order shear deformable plate models, the transverse shear deformation and rotary inertia effects are taken into formulation without needing the shear correction factor. It is remarked that in following, the numerical results are obtained on the basis of PSDPT.

Fig. 3

Nonlinear free vibration response curve of GPL-RP nanocomposite plates with X-GPLRC distribution pattern corresponding to various plate theories $\left({a/h=b/h=10,w_{\text{GPL}}= 0.3\%} \right)$

Figure 4 illustrates the influence of GPL weight fraction on the nonlinear frequency ratio $\omega_{\text{NL}}/\omega_{\text{L}}$ versus nondimensional maximum (i.e., Non. Dim. Max.) amplitude curves for GPL-RP nanocomposite rectangular plate with various boundary conditions. Note that the numerical results in this example are provided for the X-GPLRC distribution pattern. As displayed, for all considered boundary conditions, a typical spring hardening behavior (i.e., increasing the nonlinear frequency ratio with increasing the maximum vibration amplitude) is exhibited. An increase in the GPL weight fraction results in higher linear and nonlinear frequencies but a smaller nonlinear frequency ratio. Moreover, the increase in GPL weight fraction leads to weaker hardening behavior. These are due to the fact that adding more GPLs results in increasing the stiffness of the GPL-RP nanocomposite rectangular plates and hence an increase in the values of linear and nonlinear frequencies and a reduction in the nonlinear frequency ratio of system happen. Furthermore, it can be seen that the effect of adding GPLs on the nonlinear frequency ratio is more pronounced for small GPL weight fractions and it is negligible for higher values of GPL weight fractions. Also, the stronger end conditions such as fully clamped boundary conditions show the lowest typical spring hardening behavior.

Fig. 4

Nonlinear free vibration response curve of GPL-RP nanocomposite plates with various GPL weight fractions and boundary conditions $\left({a/h=b/h=10} \right)$

In addition to the GPL weight fraction, the nonlinear frequency response of GPL-RP nanocomposite plates is strongly dependent on the GPL distribution pattern. Graphically illustrated in Fig. 5 is the influence of GPL distribution pattern on the nonlinear frequency response curve and natural frequency of GPL-RP nanocomposite rectangular plates. The results show that the plate with X-GPLRC distribution pattern has the highest natural frequency, but the lowest nonlinear frequency ratio among various GPL distribution patterns. In contrast, the plates made of pure epoxy and O-GPLRC distribution pattern have the lowest linear natural frequency and the highest nonlinear frequency ratios, respectively. Moreover, the results confirm that the nonlinear frequency ratios of plates made of pure epoxy and U-GPLRC and A-GPLRC distribution patterns are the same. According to the provided results, it can be concluded that more distribution of GPL nanofillers near the upper and bottom surfaces of GPL-RC nanocomposite plate results in the bending resistance of system being more intense and consequently increasing the total bending stiffness and natural frequencies and decreasing the typical spring hardening behavior.

Fig. 5

Nonlinear free vibration response curve of GPL-RP nanocomposite plates with various GPL distribution patterns $\left({a/h=b/h=10,w_{\text{GPL}}= 0.2\%} \right)$

The effect of length-to-thickness ratio of GPLs nanofillers on the nonlinear free vibration response curve and natural frequency of GPL-RP nanocomposite rectangular plates with different boundary conditions is studied in Fig. 6. The X-GPLRC distribution pattern is considered in the numerical computations. Moreover, the thickness of GPLs is assumed to be constant. It can be seen that a rise in the length-to-thickness ratio of GPLs leads to the considerable increase in natural frequency and decreasing the nonlinear frequency ratio of system. In fact, because of intensifying the bending rigidity and strength of GPL-RP nanocomposite rectangular plates, the hardening spring behavior of system decreases when the length-to-thickness ratio of GPLs nanofillers increases. It is to be noted that this behavior may be due to the better load transforming from the matrix to the GPLs with the reinforcement of polymer matrix by the GPLs with larger length-to-thickness ratios. Also, it can be found that this reduction in the typical spring hardening behavior is more considerable for the smaller length-to-thickness ratios of GPLs.

Fig. 6

Nonlinear free vibration response curve of GPL-RP nanocomposite plates with various length-to-thickness ratio of GPL nanofillers $\left({a_{\text{GPL}}/h_{\text{GPL}}} \right)\,\left({a/h=b/h=10,w_{\text{GPL}}= 0.3\%} \right)$

Figure 7 presents the effect of length-to-width ratio of GPL nanofillers on the nonlinear free vibration curve and natural frequency of GPL-RP nanocomposite rectangular plates with X-GPLRC distribution pattern. The width of GPLs is assumed to be constant. Although the increase in length-to-width ratio of GPLs has a negligible effect on the nonlinear frequency ratio and typical spring hardening behavior of GPL-RP nanocomposite plates, for a given amount of GPLs, due to increasing the surface contact area between the polymer matrix and GPLs nanofillers and consequently supplying better load transfer, it results in increasing the structural stiffness. Therefore, the linear and nonlinear frequencies of GPL-RP nanocomposite plates increase with increasing the length-to-width ratio of GPL nanofillers. It can be seen that increasing the length-to-width ratio of GPLs results in decreasing the maximum deflection and subsequently increasing the hardening-type behavior. It indicates that the total stiffness of GPL-RP nanocomposite plates increases when the length-to-thickness ratio of GPLs increases.

Fig. 7

Nonlinear free vibration response curve of GPL-RP nanocomposite plates with various length-to-width ratio of GPL nanofillers $\left({a_{\text{GPL}}/w_{\text{GPL}}} \right)\,\left({a/h=b/h=10,w_{\text{GPL}}/h_{\text{GPL}}= 50,w_{\text{GPL}}= 0.3\%} \right)$

5 Concluding Remarks

Nonlinear free vibration of thick and moderately thick GPL-RP nanocomposite rectangular plates with various edge supports was investigated by a multistep numerical solution approach. The modified Halpin–Tsai model and rule of mixture were used to estimate the effective material properties of GPL-RP nanocomposites with four distribution patterns of graphene nanoplatelet nanofillers across the plate thickness. Furthermore, by selecting a generalized displacement field, a unified nonlinear mathematical formulation was derived using Hamilton’s principle in conjunction with von Kármán geometric nonlinearity. The proposed unified nonlinear plate model has the capability of being reduced to that on the basis of Mindlin, Reddy, parabolic, trigonometric and exponential shear deformation plate theories. Solving the nonlinear vibration problem was performed using a multistep numerical solution method. In this regard, after discretization process using the GDQ method, a reduced form of Duffing-type equation was achieved by applying the numerical-based Galerkin method. Then, TPD scheme and pseudo-arc length continuation algorithm were utilized to obtain the backbone curve of GPL-RP nanocomposite plates as the nonlinear frequency ratio versus the maximum vibration amplitude. A detailed parametric study was carried out to examine the effects of GPL distribution pattern, weight fraction, geometry of GPL nanofillers, length-to-thickness and boundary constraints on nonlinear vibration of the GPL-RP nanocomposite rectangular plates.

The nonlinear vibration analysis of higher-order shear deformable GPL-RP nanocomposite rectangular plates revealed:

• (a) Due to increasing the stiffness of GPL-RP nanocomposite plates, adding further GPLs into polymer results in increasing linear and nonlinear frequencies and decreasing the typical spring hardening behavior of system. However, the effect of adding GPLs on the nonlinear frequency ratio is more pronounced for small GPL weight fractions.

• (b) Distribution of GPL nanofillers near the upper and bottom surfaces of GPL-RC nanocomposite plate leads to further intensifying the bending resistance of plate and consequently increasing the total bending stiffness and natural frequencies and decreasing the typical spring hardening behavior.

• (c) Due to better load transformation capability to form the matrix to GPLs, the hardening spring behavior of nanocomposite plate decreases with increasing the length-to-thickness ratio of GPLs nanofillers. However, this reduction in the typical spring hardening behavior is more pronounced for the smaller length-to-thickness ratios of GPLs.

• (d) The effect of length-to-width ratio of GPL nanofillers on the nonlinear frequency ratio of nanocomposite plate is negligible. However, increasing the length-to-width ratio of GPL nanofillers increases the linear and nonlinear frequencies.

Appendices

Appendix 1

Definition

If A is an m-by-n matrix and B is a p-by-q matrix, the Kronecker product ${\mathbf{A}} \otimes {\mathbf{B}}$ is an mp-by-nq block matrix and defined as

$${\mathbf{A}} \otimes {\mathbf{B}}=\left[{\begin{array}{*{20}c}{a_{11} {\mathbf{B}}} &\cdots& {a_{1n} {\mathbf{B}}}\\ \vdots&\ddots&\vdots \\{a_{m1} {\mathbf{B}}} &\cdots& {a_{mn} {\mathbf{B}}}\\ \end{array}} \right]_{mp \times nq}$$

(b) Integral Matrix Operators

$$\mathop \int \limits_{{x_{1}}}^{{x_{N}}} f\left(x \right)dx=\left({\mathop \sum \limits_{r=0}^{N - 1} {\tilde{\mathbf{X}}}^{\left(r \right)} {\mathbf{D}}_{x}^{\left(r \right)}} \right){\mathbf{F}}={\mathbf{S}}_{x} {\mathbf{F}},\,{\mathbf{S}}_{x}= \left[{S_{x}} \right]_{1 \times N}$$

where ${\mathbf{D}}_{x}^{\left(r \right)}$ denotes the GDQ differential operator, and

$$\begin{aligned} {\tilde{\mathbf{X}}}^{\left(r \right)}&= \left[{\frac{{\left({x_{2}- x_{1}} \right)^{r + 1}}}{{2^{r + 1} \left({r + 1} \right)!}}, \ldots,\frac{{\left({x_{i + 1}- x_{i}} \right)^{r + 1}- \left({x_{i - 1}- x_{i}} \right)^{r + 1}}}{{2^{r + 1} \left({r + 1} \right)!}}, \ldots, - \frac{{\left({x_{N - 1}- x_{N}} \right)^{r + 1}}}{{2^{r + 1} \left({r + 1} \right)!}}} \right], \\ & \quad \quad \quad& \quad \quad \quad& \quad \quad \quad& \quad \quad \quad i=2,3, \ldots,N - 1 \\\end{aligned}$$

Appendix 2

The discretized components of K_ij, M_ij and ${\mathbf{K}}_{nl} \left({\mathbf{X}} \right)$ are as

$$\begin{aligned} {\mathbf{K}}_{11}&= A_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ A_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{12}= \left({A_{12}+ A_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{13}&= B_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}+ \left({B_{12}+ 2B_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{14}&= C_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ C_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{15}= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{21}&= \left({A_{12}+ A_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},\quad{\mathbf{K}}_{22}= A_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ A_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}, \\{\mathbf{K}}_{23}&= \left({B_{12}+ 2B_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ B_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{24}= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},\\{\mathbf{K}}_{25}&= C_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ C_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)},{\mathbf{K}}_{31}=- B_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}- \left({2B_{66}+ B_{12}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{32}&=- B_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}- \left({B_{12}+ 2B_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}, \\{\mathbf{K}}_{33}&= A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ A_{44} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}- D_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(4 \right)}- 2\left({D_{12}+ 2D_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}- D_{22} {\mathbf{D}}_{{x_{2}}}^{\left(4 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\{\mathbf{K}}_{34}&= A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}+ F_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},\\{\mathbf{K}}_{35}&= A_{44} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ F_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\{\mathbf{K}}_{41}&= C_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ C_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}} {\mathbf{K}}_{42}= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{43}&=- A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}+ F_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{44}&= H_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}- A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}+ H_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{45}= \left({H_{12}+ H_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{51}&= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},{\mathbf{K}}_{52}= C_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ C_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}, \\{\mathbf{K}}_{53}&=- A_{44} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ F_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\{\mathbf{K}}_{54}&= \left({H_{12}+ H_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},{\mathbf{K}}_{55}= H_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ H_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}- A_{44} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}. \\\end{aligned}$$

(46)

$$\begin{aligned} {\mathbf{M}}_{11}&= {\mathbf{M}}_{22}= I_{0} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{M}}_{33}= I_{0} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}- I_{4} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right), \\{\mathbf{M}}_{44}&= {\mathbf{M}}_{55}= I_{5} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}.{\mathbf{M}}_{14}= {\mathbf{M}}_{41}= {\mathbf{M}}_{25}= {\mathbf{M}}_{52}= \varvec{I}_{2} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{M}}_{13}=- {\mathbf{M}}_{31}= I_{1} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{M}}_{23}&=- {\mathbf{M}}_{32}= I_{1} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{M}}_{34}=- {\mathbf{M}}_{43}=- I_{3} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},{\mathbf{M}}_{35}=- {\mathbf{M}}_{53}=- I_{3} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\\end{aligned}$$

(47)

Also, one can be written the components of the nonlinear stiffness vector as follows

$$\begin{aligned} {\mathbf{K}}_{{u_{1}}} \left({\mathbf{X}} \right) &= A_{11} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) + \left({A_{12}+ A_{66}} \right)\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \\ & \quad+ A_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right), \\{\mathbf{K}}_{{u_{2}}} \left({\mathbf{X}} \right) &= A_{22} \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({A_{12}+ A_{66}} \right)\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \\ & \quad+ A_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right), \\{\mathbf{K}}_{w} \left({\mathbf{X}} \right) &= \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right)\left({{\mathbf{N}}_{11}\circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) + \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right)\left({{\mathbf{N}}_{22}\circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right) \\ & \quad+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right)\left({{\mathbf{N}}_{12}\circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right) + \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right)\left({{\mathbf{N}}_{12}\circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{11} \left({\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- \left({B_{12}+ 2B_{66}} \right)\left({\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{66} \left({\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{12} \left({\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{22} \left({\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right), \\{\mathbf{K}}_{{\psi_{1}}} \left({\mathbf{X}} \right) &= C_{11} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{\varvec{x}_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) + \left({C_{12}+ C_{66}} \right)\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \\ & \quad+ C_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right), \\\end{aligned}$$

$$\begin{aligned} {\mathbf{K}}_{{\psi_{2}}} \left({\mathbf{X}} \right)=C_{22} \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({C_{12}+ C_{66}} \right)\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + C_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right). \hfill \\\end{aligned}$$

(48)

where

$$\begin{aligned} {\mathbf{N}}_{11}&= A_{11} \left[{\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{u}}_{1}+ \frac{1}{2}\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right] \\ & \quad+ A_{12} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{u}}_{2}+ \frac{1}{2}\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right] + C_{11} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{1}\\ & \quad+ C_{12} \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{2}+ B_{11} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}} + B_{22} \left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}, \\{\mathbf{N}}_{22}&= A_{22} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{u}}_{2}+ \frac{1}{2}\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right] \\ & \quad+ A_{12} \left[{\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{u}}_{1}+ \frac{1}{2}\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right] + C_{22} \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{2}\\ & \quad+ C_{12} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{1}+ B_{22} \left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}} + {\text{B}}_{12} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}, \\{\mathbf{N}}_{12}&= A_{66} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{u}}_{1}+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{u}}_{2}+ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right] \\ & \quad+ C_{66} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{1}+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{2}} \right] \\ & \quad+ B_{66} \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{1}+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{2}+ 2\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right). \\\end{aligned}$$

(49)

where ${\mathbf{I}}_{{x_{1}}}$ and ${\mathbf{I}}_{{x_{2}}}$ are, respectively, N × N and M × M identity tensors and ° indicates the Hadamard product.